Adult-capture assays as a tool to measure insecticide resistance in Anopheles malaria vectors: a modeling comparison with larval-capture assays

Systematic, long-term, and spatially representative monitoring of insecticide resistance in mosquito populations is urgently needed to quantify its impact on malaria transmission, and to combat failing interventions when resistance emerges. Resistance assays on wild-caught adult mosquitoes (known as adult-capture) offer an alternative to the current protocols, which recommend larval capture. Adult-capture assays can be done in a shorter time frame, in more locations, and in the absence of an insectary. However, unlike insectary-raised mosquitoes, a group of adults captured in the wild represents different ages and may have previous exposure to insecticides. Since age and prior exposure are critically important in determining the likelihood of death during the assay, taking these factors into account is important for assessing the relative utility of the assay. Currently such quantitative assessments are lacking. We developed a discrete-time deterministic model to simulate the mosquito life cycle, including insecticide exposure due to insecticide-treated bed nets. We incorporated non-lethal effects of insecticide exposure demonstrated in laboratory experiments and the impact of multiple exposure to insecticides on mosquito death rates during the assay. We then sampled from this population using both larval-captured and adult-captured mosquito collection and simulated insecticide resistance assays. To quantify possible biases in adult-capture assays, we compared the results of these assays to the true resistance allele frequency in the population. In simulated samples of 100 test mosquitoes, reflecting WHO-recommended sample sizes, we found that adult-capture samples had a 94% positive predictive value (PPV) for resistance at the WHO’s 10% resistance cutoff, and a 97% negative predictive value (NPV), compared to 98% PPV and 19% NPV for larval-captured samples. Bias in the adult-capture assays was primarily dependent on the level of insecticide resistance rather than coverage of bed nets or exposure heterogeneity. Using adult-captured mosquitoes for resistance assays may have advantages over larval-capture collection in many settings, and in our model does not appear to be significantly less accurate than larval-capture, especially when used to categorize resistance under the binary WHO criteria. These results suggest that adult-captured assays could be deployed for resistance monitoring programs at a more widespread scale.

Introduction

Insecticides used to target the Anopheles mosquito vectors of the Plasmodium parasite have long been a cornerstone of global malaria control. The vast reduction of malaria transmission observed over the past decades is largely attributed to insecticide-based interventions (Bhatt et al., 2015; World Malaria Report 2023, 2023), but following increased use over the past two decades—most intensely in sub-Saharan Africa—resistance to these insecticides is now widespread (Ranson and Lissenden, 2016). There is recent evidence that increasing resistance may be impacting the efficacy of vector control tools, consistent with stalled progress in malaria control since 2019 (Alonso and Noor, 2017; World Malaria Report 2023, 2023). However, this has been difficult to quantify as insecticide resistance assays are not easily employable in all settings (Toé et al., 2014; Hemingway et al., 2016). In addition, there remain important gaps in the data on the intensity and spread of resistance in wild populations (Mnzava et al., 2015; Moyes et al., 2019, 2020). Practical, cost-effective techniques for routine resistance monitoring are urgently needed, both to understand the impact of insecticide resistance on malaria transmission and to signal the need for alternative interventions when resistance emerges (Kont et al., 2023).

Resistance to at least one class of insecticides is reported in the majority of malaria-endemic countries (World Malaria Report 2023, 2023). Insecticide resistance, broadly, is caused by four different mechanisms: target site resistance, metabolic resistance, cuticular resistance, and behavioral resistance (Suh et al., 2023). While there are individual molecular markers for some of these mechanisms, resistance from target site resistance, metabolic resistance, and cuticular resistance can all be measured using a bioassay, or simply assay, in which mosquitoes are exposed to insecticide and then assessed for survival.

In spite of this complexity, insecticide resistance is typically categorized as a binary measure (confirmed resistant or not) in WHO susceptibility tests, based on a threshold of 10% of mosquitoes surviving exposure to insecticide after 24 hours (World Health Organization, 2022). A secondary cutoff of 2% survival is used as a measure of “suspected resistance.” Monitoring insecticide resistance is one of the main pillars of the Global Plan for Insecticide Resistance Management in malaria vectors (GPIRM), and sentinel sites are directed to monitor populations at least annually (World Health Organization, 2012). Their recommendations for prolonging the efficacy of insecticide interventions are dependent on local insecticide resistance levels, although the evidence base for these recommendations is poor (Madgwick and Kanitz, 2022; Hobbs et al., 2023).

Systematic, long-term, and spatially representative monitoring, however, requires increased sampling of mosquito populations beyond the current system. The WHO’s ‘Test procedures for insecticide resistance monitoring in malaria vector mosquitoes’ advises that control programs select sentinel sites that will be representative of both the eco-epidemiological zones and malaria intensities in their region (World Health Organization, 2016). However, neither of these variables are static over time—malaria prevalence changes in response to malaria interventions, and eco-epidemiological zones change in response to interventions as well as climate and land use change (Ryan et al., 2015, 2020; Rodó et al., 2021). Thus, sentinel sites are likely to become less representative of the insecticide resistance landscape over time. In addition, the GPIRM emphasizes the importance of monitoring and responding to insecticide resistance at the local level (World Health Organization, 2012) because Anopheles populations cluster at a relatively small geographic scale (Carter et al., 2000; World Health Organization, 2012). High resolution monitoring of insecticide resistance is important in order to allow for local-level decision making, as well as to understand the changing distribution of insecticide resistance. Although the importance of insecticide resistance monitoring is well outlined, there remain large gaps in data in many malaria-endemic regions, both geographically and temporally (Mnzava et al., 2015; Moyes et al., 2019, 2020). Recent work used spatial modeling methods to try and fill in the gaps in resistance data across sub-Saharan Africa, constructing annual maps of predicted resistance level by district (Moyes et al., 2020). However, many locations still have insufficient data, leaving inferred results unable to capture geographic heterogeneity in resistance levels.

The WHO’s current field protocol for testing resistance recommends using mosquitoes raised from collected larvae or the first generation (F1) progeny of collected adults, both of which require access to mosquito rearing facilities and take a week or longer to rear to the correct age for testing (World Health Organization, 2012, 2022). Larval collection is generally easier than adult collection to obtain a large number of individuals. However, resistance assays conducted on wild-caught adult mosquitoes–which we will refer to here as adult-capture assays–offer an alternative with some benefits, and are already in use for capturing mosquitoes that are difficult to find at the larval stage (Hargreaves et al., 2003; Rakotoson et al., 2017; Matowo et al., 2021).

First, insecticide bioassays are not necessarily a good predictor of the failure of vector control tools or of malaria infection risk (Thomas and Read, 2016; Kleinschmidt et al., 2018). While larval testing under standardized conditions is a good indicator of technical resistance—to borrow language from Namias et al.—that is the genetic change that leads to reduced susceptibility in lab-controlled bioassays—testing on wild adults may actually be a better indicator of practical resistance—the change in the mosquito that leads to mosquito control failure in field settings (Namias et al., 2021). In addition to allowing for collection of vector species that are not easily found at the larval stage, sampling adults may better represent the mosquitoes of interest: as they are the vectors that directly contribute to transmission, resistance in adult mosquitoes may be a better representation of “real world” resistance. Samples collected as adults may also have a lower likelihood of pseudo-replication due to relatedness within larval samples collected from the same breeding site. It is therefore possible that testing for insecticide susceptibility on mosquitoes in less standardized conditions could help shed light on the connection between measured resistance and vector control efficacy (Namias et al., 2021). A second advantage of adult-capture assays, though they are more labor intensive with respect to sampling, is that they may be conducted in the absence of rearing facilities and in a shorter time frame, as there is no need to wait for eggs or larvae to grow to adulthood, lending this method more flexibility. Adult-capture assays therefore have potential as a tool for increasing the spatial coverage of insecticide resistance monitoring, and developing more systematic monitoring programs.

Despite these potential advantages, assays on wild-caught adult mosquitoes are not currently recommended by the WHO. This is in part due to age and exposure heterogeneity in adult sampled mosquitoes, and in part due to the difficulty of collecting a large number of adult mosquitoes. Unlike mosquitoes raised from larvae, which are tested at a standardized age (usually 3-5 days), mosquitoes captured as adults have unknown age at the time of testing and are likely to have a variety of insecticide exposure histories, including the number of past exposures, the timing of exposures, and their duration. Laboratory experiments have shown that insecticide resistance declines with mosquito age (Rajatileka et al., 2011). Resistance also appears to decrease when mosquitoes were previously exposed to insecticides, weakening even resistant mosquitoes (Viana et al., 2016). These heterogeneities and dynamic aspects of resistance measured in adult mosquitoes must be considered to compare adult capture assay results with standard methods, and to adjust for real-world settings.

In the absence of studies directly comparing insecticide resistance from adult mosquito samples to that of larval samples, mathematical models offer transparent frameworks to account for the likely impact of aging and exposure heterogeneities among adult mosquitoes. Dynamical models have a long history in the context of malaria interventions, because they capture the nonlinearities inherent in biological populations that may not be intuitive, and they distill the most important dynamic factors likely to affect complex phenomena like patterns of resistance. Here, we developed a mathematical model of the mosquito life cycle to examine the impacts of heterogeneity in age and exposure history of wild adult mosquitoes on measured assay survival in simulated adult-capture samples. We modeled a mosquito population with inherited insecticide resistance, incorporating variations in insecticide susceptibility due to age and insecticide exposure history. Using this model, we have quantified how sampling from heterogeneous adult mosquito populations could impact the categorical results of insecticide resistance assays, including the positive and negative predictive values. We also compared adult- and larval-capture assays as measures of the true resistance frequency in the modeled population. We find that adult mosquito sampling offers a practical complementary approach for monitoring insecticide resistance in malaria-endemic regions.

Materials and methods

Mosquito life cycle model

We developed a discrete-time deterministic model of the mosquito life cycle (Figure 1) that includes a single allele to determine resistance. We assumed that insecticide exposure occurs only through exposure to vector control—in this case, pyrethroid-treated long lasting insecticide treated nets (LLINs), and therefore only when mosquitoes are blood feeding. As female mosquitoes take blood meals throughout their life cycles, the model allows for multiple exposures to insecticide. Blood feeding occurs every fourth day (labeled “feed” in Figure 1 and Supplementary Figure S1). Resistance is conferred by a single gene locus, with either susceptible (S) or resistant (R) alleles. There are three possible genotypes: homozygous susceptible (SS), heterozygous resistant (SR), and homozygous resistant (RR). In this population, the phenotypic characteristics of the heterozygous resistant mosquitoes are halfway between those of the homozygous susceptible and homozygous resistant phenotypes. Offspring genetics follows Mendelian inheritance patterns, and mating is random and not preferential based on genetics. We assumed that males do not undergo selection from insecticide resistance.

Figure 1

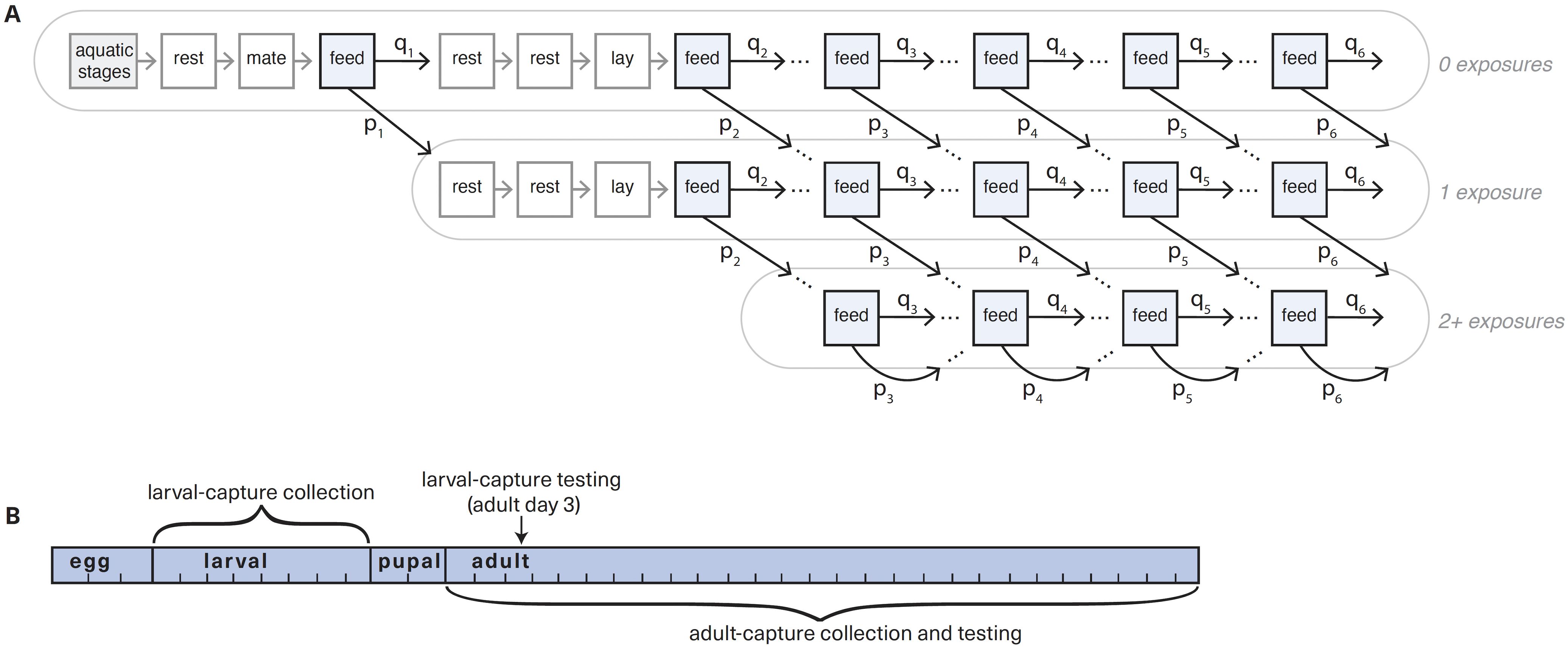
Figure 1. Mosquito life cycle model and sampling schematics. (A) Simplified schematic of mosquito population model for a single genotype, with exposure days highlighted blue. The aquatic stage (in grey) is split into three components: the egg stage is 3 days, larval stage is 5, and pupal stage is 2 days. In adult (non-aquatic) stages, each compartment represents a single day. Mosquitoes have the opportunity for exposure on each feeding (highlighted), which varies by heterogeneity parameter s and is determined by past exposure history. The number of past exposures is not tracked beyond 2 exposures. The first full gonotrophic cycle is shown, while later cycles are abbreviated to show only feeding days (i.e. 2 rest and 1 laying days hidden). The fully elaborated diagram is shown in Supplementary Figure S1. Daily mortality and egg laying also not shown for ease of visualization. (B) Timeline for larval-capture (upper) and adult-capture (lower) collection and testing.

The mosquito life cycle was modeled in single day timesteps: mosquitoes lay eggs every fourth day, three days after blood feeding (Figure 1; Supplementary Figure S1). Mosquito longevity in the model was capped at 26 days (Childs et al., 2016). The model has daily mortality, meaning that a proportion of mosquitoes die each day. In egg and pupal stages, mortality is a fixed constant (Supplementary Table S1). In the larval stage, mortality follows a Ricker-type nonlinear survival function, which is a density-dependent function that limits the population size, leading to higher mortality when the population is larger and lower mortality when the population is smaller (Li, 2004). In adult mosquitoes, the daily mortality rate is based on age, genotype, and exposure history (Supplementary Figure S2). In addition, adult mosquitoes can experience immediate mortality due to encounters with LLINs on feeding days.

In mosquitoes with any resistance (heterozygous and homozygous resistant genotypes), we modeled the mortality effects caused by insecticide exposure as observed in experimental lab conditions in (Viana et al., 2016). These effects occur via two mechanisms: an increased risk of immediate mortality upon subsequent exposures to insecticide, and an increase in the rate of daily mortality for the rest of the mosquito’s life regardless of further exposure (Supplementary Figure S2B). Parameters for the mortality effects in homozygous resistant mosquitoes were based on data from the resistant Tiassele strain in (Viana et al., 2016), which were exposed to Permanet 2.0 LLINs every four days to mimic natural exposure from blood feeding using the WHO cone bioassay. Daily mortality in homozygous susceptible mosquitoes was based on an entirely susceptible lab strain from (Childs et al., 2016; Viana et al., 2016). Gompertz-Makeham survival curves were fitted to the daily mortality data from both of these references (see Supplementary Material) to obtain both immediate and daily mortality parameters for mosquitoes with and without a history of insecticide exposure (Supplementary Tables S2, S3). In the absence of insecticide exposure, homozygous resistant mosquitoes have higher daily mortality than homozygous susceptible mosquitoes, leading to a fitness cost of insecticide resistance. While there may be other fitness costs linked to resistance, such as reduced egg production or decreased sexual competitiveness, we did not include these in the model.

Insecticide exposure

Insecticide coverage is a parameter input for each simulation of the model, and determines the probability p of insecticide exposure at each blood feed. Coverage is often taken to mean what fraction of households receive LLINs. However, to account for outdoor biting and net failure, we multiplied the input coverage by a parameter for “LLIN effectiveness” (assumed to be 80%) to reduce the probability of exposure on each feed. Mosquitoes in this model blood feed up to six times, leading to a maximum of six potential insecticide exposures. To simplify the model, we only explicitly tracked up to two past exposures (Figure 1).

We expect some level of heterogeneity in the number of times any given mosquito will encounter insecticides. For example, due to the spatial distribution of bed nets, some mosquitoes may be feeding in proximity to households that are entirely protected by LLINs, encountering them each time they feed, and others may be feeding in proximity to households that are never protected by LLINs (Carter et al., 2000). However, this quantity is difficult to measure for wild mosquitoes, and we do not explicitly include space in the model. In order to account for this, we use a proxy parameter, which we call the exposure heterogeneity parameter, or simply heterogeneity parameter. This allows for the probability of future insecticide exposures to depend on a mosquito’s past exposures (see Supplementary Material).

The heterogeneity parameter s modifies the probability of exposure on all blood feeds f after the first feed (Supplementary Figure S3). We varied s between 0 and 1 in increments of 0.1: when s = 0, there is completely random mixing, and the probability of exposure on each feed is probabilistically determined based on the insecticide coverage parameter, regardless of the mosquito’s exposure history. When s = 1, the mosquito’s exposure on future feeds is completely determined by whether or not it was exposed on its first feed. The probabilities of exposure, p, and of non-exposure, q, were calculated as follows, depending on exposure on past feeds f:

Exposed on previous feed: E₊(f-1)

$$\mathrm{p}(\mathrm{f})|{\mathrm{E}}_{+}(\mathrm{f}-1)=\mathrm{p}(\mathrm{f}-1)+\mathrm{s}*\mathrm{q}(\mathrm{f}-1)$$

$$\mathrm{q}(\mathrm{f})|{\mathrm{E}}_{+}(\mathrm{f}-1)=\mathrm{q}(\mathrm{f}-1)-\mathrm{s}*\mathrm{q}(\mathrm{f}-1)$$

Unexposed on previous feed: E_-(f-1)

$$\mathrm{p}(\mathrm{f})|{\mathrm{E}}_{‐}(\mathrm{f}-1)=\mathrm{p}(\mathrm{f}-1)-\mathrm{s}*\mathrm{p}(\mathrm{f}-1)$$

$$\mathrm{q}(\mathrm{f})|{\mathrm{E}}_{‐}(\mathrm{f}-1)=\mathrm{q}(\mathrm{f}-1)+\mathrm{s}*\mathrm{p}(\mathrm{f}-1)$$

Both the level of exposure heterogeneity, s, and the resistance allele frequency in the population impact the proportion of mosquitoes exposed to insecticides on a given day for a given insecticide coverage (Supplementary Figure S3).

Constructing the sampling population dataset

For each combination of insecticide coverage and heterogeneity parameter values, we generated a mosquito population from which we simulated sampling adult or larval mosquitoes. To do so, we ran the model starting with 1% resistance allele frequency in the population until it reached an equilibrium resistance allele frequency, or for 25 years. “True resistance” in the modeled population was calculated as the resistance allele frequency in the whole population:

$$\begin{array}{c}True resistance (Resistance allele frequency)\hfill \\ =(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.*SR+RR)/(SS+SR+RR)\hfill \end{array}$$

For all combinations of these parameters, the final equilibrium resistance was either 0% or 100%.

Insecticide resistance assay simulations

To compare the results of insecticide resistance assays using each collection strategy, we simulated assays by drawing individual mosquitoes from the simulated population. In order to capture variation in the insecticide resistance frequency, we took samples of mosquitoes on 100 days drawn randomly with replacement across the time series. To avoid sampling from unstable population dynamics that occur at earlier time points in the simulations with very high insecticide coverage, we excluded the first year of each simulation. For each assay type, larval or adult, 200 mosquitoes were sampled randomly from a single day (and associated resistance frequency) such that 100 of these mosquitoes were “exposed” to insecticide and 100 were used as controls. Due to the increased difficulty of capturing adult mosquitoes compared to larvae, we also simulated assays on the same days with only 100 mosquitoes in each assay (50 exposed and 50 unexposed). On each day, each of these assays were conducted with a random sample of mosquitoes 100 times in order to capture sampling variability.

For adult-capture assays, we drew mosquitoes randomly from the adult population on the day of collection to determine their genotype, age, and exposure history. The probability of mortality for each adult mosquito in the assay is a function of age, exposure history, genotype, and whether they are in the exposure or control sample (Table 1). To determine whether an individual mosquito dies in the assay, we drew from a binomial distribution using that probability. For the larval-capture assays, we drew mosquitoes randomly from the larval population on the day of collection to determine their genotype. In the assay, each larvally-captured mosquito has the mortality probability of a three day old adult with no exposure history. This would be equivalent to collecting as larvae and raising them in an insectary, and performing the assay three days after emergence. Because the test is conducted on mosquitoes captured as larvae, we assumed no exposure history.

Table 1

Table 1. Mortality parameters used for each simulated assay test group.

To adjust for mortality observed in the control, we corrected the results of each assay using Abbott’s formula (Abbott, 1987):

$$Corrected mortality=100*\frac{(\%mortality in exposed-\% morality in controls)}{(100-\%mortality in controls)}$$

The WHO recommends using Abbott’s formula when mortality in controls is > 5%. However, we used the adjustment regardless of control mortality in order to directly compare adult to larval sampling. Our outcome of interest was corrected survival, which is 1 – corrected mortality.

Comparison of sampling methods

To measure the difference between the results from the adult-capture and larval-capture assays, we calculated a “survival difference” by subtracting the mean of adult-capture survival from the mean of larval-capture survival. By this measure, a positive survival difference value means that the observed mean survival is higher in adult-capture assays, and a negative survival difference means that survival is higher in larval-capture assays.

Measures of test performance

Because the WHO uses a survival of 10% or higher as a measure of “confirmed resistance,” and of 2% or higher as a measure of “suspected resistance,” we evaluated the sensitivity, specificity, positive predictive value (PPV), and negative predictive value NPV) for each of these assays in our simulated mosquito populations (Supplementary Figure S4). A test’s sensitivity is the probability that a test will return a positive result given that the true state is positive, whereas specificity is the probability that a test will return a negative result given that the true state is negative. The test’s PPV is the probability that the true state is positive given that a test is positive, and NPV is the probability that the true state is negative given that the result of a test is negative. We calculated and reported each of these probabilities for both the adult- and larval-capture assays to compare the performance of these assays as predictive tests at both the 2% and 10% cutoffs.

Assumptions

We made several important simplifying assumptions in order to make a parsimonious model of this complex biological system. For simplicity in the model, we assumed that resistance is determined at a single, two-allele locus. In reality insecticide resistance has multiple causes of varying genetic complexity (Martinez-Torres et al., 1998; Mulamba et al., 2014; Balabanidou et al., 2016; Ingham et al., 2020). Although this modeling assumption is a simplification of the true mechanisms determining resistance, other modeling research has suggested that monogenic and polygenic models have consistency in qualitative results (Hobbs and Hastings, 2024). In addition, we assumed that insecticide exposure only occurs via LLINs (as opposed to other routes such as indoor residual spraying, larvicide, or agricultural exposure). We examine the impact of this assumption in our sensitivity analyses. We incorporated a fitness cost of resistance through daily mortality only, by using a higher daily mortality in insecticide resistant mosquitoes compared to susceptible mosquitoes. In addition, we assumed a decreased lifespan among resistant mosquitoes that survive after exposure, based on the data in Viana et al. (2016), which found that exposure to insecticides has a detrimental effect on mosquitoes’ health even if they do not die immediately. Finally, we simplified the structure of the mosquito life cycle, assuming a strict 4-day gonotrophic cycle. In the field, the duration of this cycle likely varies between mosquitoes and from one cycle to the next.

Sensitivity analyses

We conducted several sensitivity analyses to examine the impacts of these modeling assumptions. We examined our fitness cost assumption by repeating our simulations using the homozygous resistant mortality curves for all genotypes in the model, and again using an intermediate mortality curve for the heterozygous resistant mosquitoes—the mean of the homozygous resistant mortality and homozygous susceptible mortality for each day. We checked the sensitivity of our results to the assumption of 50% dominance of resistance, varying to 25% (heterozygous resistant mosquitoes are more similar to homozygous susceptible mosquitoes) and 75% (heterozygous resistant mosquitoes are more similar to homozygous resistant mosquitoes). We also looked at the sensitivity of our results to the assumption we derive from survival data in Viana et al. (2016) that there is a longevity effect (increasing daily mortality) in resistant mosquitoes that survive exposure. In addition, we examined our assumption around the duration of the gonotrophic cycle, using a 3-day rather than 4-day cycle. While neither of these perfectly represent the blood-feed frequencies in the field, which vary, this allowed us to understand the impact of this assumption on our model results. In both scenarios, mosquitoes have a maximum of six gonotrophic cycles, and the maximum lifespan is 26 days. Finally, we ran a sensitivity analysis challenging our assumption that insecticide exposure only occurs through LLINs, incorporating insecticide selection during the larval stage to reflect the possibility of environmental larvicides. We imposed either a low or high additional mortality rate on each day of the larval stage.

All code was written in R and can be found on GitHub at github.com/iholmdahl/adult_capture_IR.

Results

We ran the population model for 10 years starting with 1% resistance allele frequency in 5% increments of insecticide coverage, from 0% to 95%, and in 10% increments of the heterogeneity parameter, from 0% to 100%. Despite always starting with an almost entirely susceptible population, the population always reached either a fully susceptible (0% resistant allele frequency) or fully resistant (100% resistant allele frequency) equilibrium during this time (Figure 2). The population became fully resistant when insecticide coverage was 70% or higher, and fully susceptible when insecticide coverage was 25% or lower. The precise coverage at which the population became fully resistant depends on parameter choices, and biological interpretation requires precise knowledge of a particular setting. The amount of time it took for the population to become fully resistant also depended on the coverage and degree of heterogeneity, with higher coverage and lower heterogeneity each leading to faster emergence of resistance (Supplementary Figure S5).

Figure 2

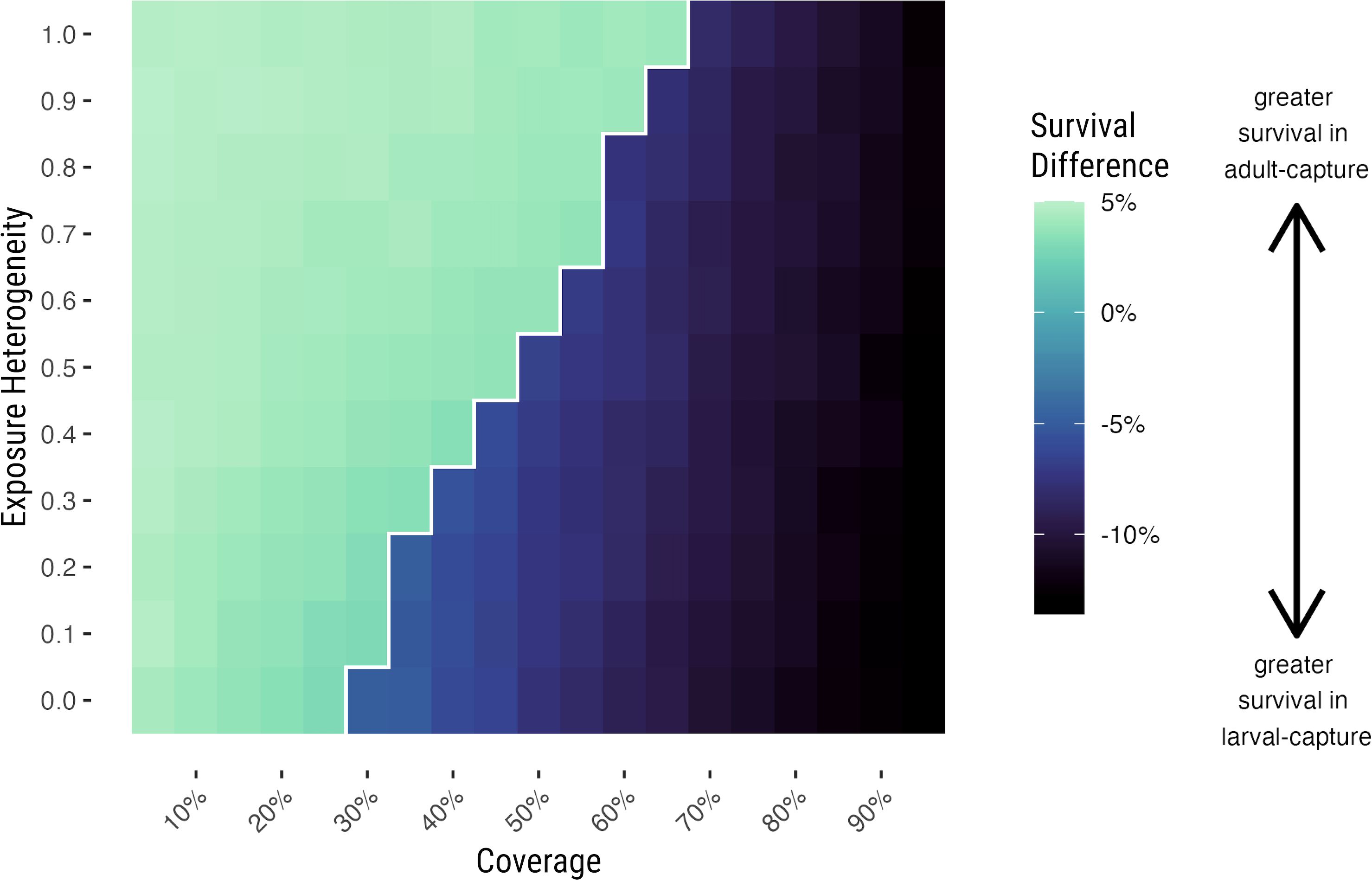
Figure 2. Difference between adult-capture and larval-capture assay results at equilibrium is determined by population resistance and insecticide coverage. Survival difference between mean results from adult-capture and larval-capture assays across a range of insecticide coverage (x-axis) and heterogeneity parameter (y-axis) values, conducted when the population resistance is at equilibrium. The color scale indicates the difference between mean survival from simulated assays using adult capture compared to larval capture, i.e. adult-capture survival – larval-capture survival. Negative values indicate that when the population is at equilibrium, observed survival is lower in adult capture than larval capture, on average; positive values indicate that observed survival is higher in adult capture than larval capture. The light area to the left of the white contour line has 0% resistance at equilibrium, while the darker area to the right has 100% resistance at equilibrium.

The assumption of greater heterogeneity in the population led to a higher coverage required to reach the fully resistant equilibrium. When the heterogeneity parameter was equal to one, meaning that whether or not a mosquito was exposed on its first blood feed determined exposure on all of its future blood feeds, the population became fully resistant when insecticide coverage was 70% or higher. When the heterogeneity parameter is equal to zero, the population became fully resistant when insecticide coverage was as low as 30% or greater (Figure 2).

To understand the implications of using adult-capture samples rather than larval-capture samples when the population is either fully resistant or fully susceptible, we simulated assays when the population was at equilibrium using each method and directly compared their results (Figure 2). The difference between modeled bioassay survival using adult-capture vs larval-capture depended on the level of resistance in the population. In a population that is completely susceptible, adult-capture simulations overestimated resistance by approximately 3-5%. In a population that is entirely resistant, adult-capture assays underestimated resistance by 5-15%.

This difference is driven by the relative exposure history of the population at different levels of population resistance. In a predominantly resistant population, many resistant mosquitoes have survived at least one insecticide exposure, and prior exposure makes resistant adults more susceptible to insecticide exposure (Viana et al., 2016). A sample of the adult population will include many mosquitoes that will die even though they are homozygous resistant because they already have been exposed previously, making the population appear less resistant than it truly is.

The magnitude of this difference in the resistant population depends on coverage (i.e. varies horizontally in Figure 2), with higher levels of coverage leading to a larger difference between adult and larval-capture assay results. It does not, however, appear to differ by the degree of exposure heterogeneity (i.e., vertically in Figure 2). We interpret this to mean that the bias in an adult-capture assay is driven primarily on the level of resistance in the population, with coverage as a secondary determining factor.

While some populations may be either fully susceptible or fully resistant, it is more likely that a population in the field will have an intermediate level of resistance. To investigate the difference between these two sampling methods in a non-equilibrium population, we sampled from the population at varying levels of resistance allele frequency. We also sampled at varying levels of the heterogeneity parameter and insecticide coverage. When we aggregated across exposure heterogeneity and coverage, assays based on larval- or adult-capture both measured true resistance relatively well, but with an observed bias in the adult-capture sample tests (Figure 3A). Assays conducted with 50 mosquitoes in each of the exposed and control groups, rather than 100, performed similarly, although individual test results had a wider variance (Supplementary Figure S6).

Figure 3

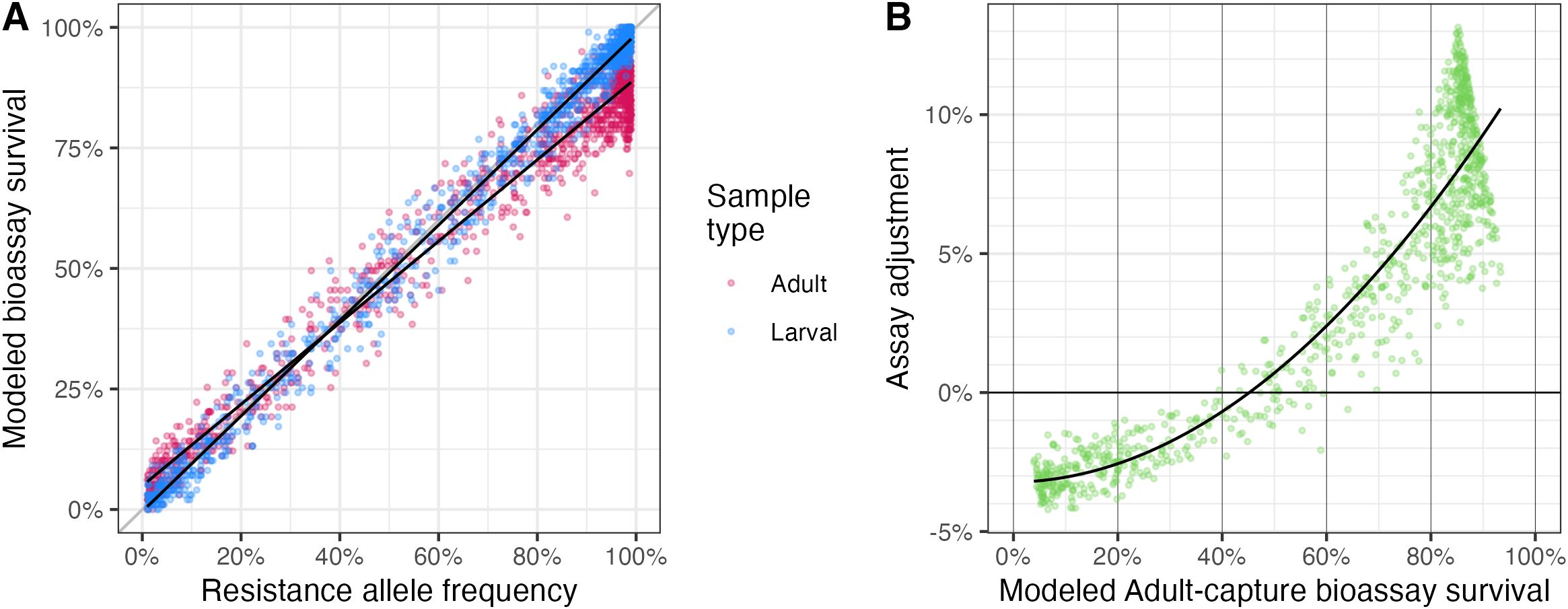
Figure 3. Resistance assay results in adult-capture vs larval-capture samples in a population with varied resistance allele frequency. (A) Measured survival by resistance allele frequency, from assays simulated with 100 mosquitoes in each of the exposed and control groups collected by either larval (blue) or adult (red) capture. (B) Adjustment proposed for adult-capture assays, to align with larval-capture results which more closely reflect true resistance allele frequency. Points show the mean difference between adult capture and true resistance for each combination of resistance level, insecticide coverage, and exposure heterogeneity.

As was observed in the equilibrium populations, there is a bias in adult capture tests, where resistance is overestimated at lower levels of resistance allele frequency and underestimated at higher levels of resistance allele frequency. This is also driven predominantly by the exposure history of the population: in a mostly resistant population, resistant mosquitoes are likely to have a history of exposure to insecticides, and will therefore be more likely to die in a resistance assay than an unexposed resistant mosquito in a larval assay. On the other hand, in a mostly (but not entirely) susceptible population, resistant mosquitoes are disproportionately overrepresented in a sample of wild adults because they are able to survive insecticide exposure (whereas susceptible mosquitoes of the same age will have died when exposed). At intermediate levels of resistance allele frequency (~50%), these two effects counter each other, and both bioassays will measure the same level of survival (Figure 3A).

To “correct” for this difference between these two sampling methods, we took the mean of 100 adult-capture samples and the mean of 100 larval-capture samples for a given day (associated with a resistance allele frequency). We then subtracted to find the difference in mean bioassay result at each value of resistance allele frequency (Figure 3B). Depending on the level of resistance, the bias in the adult-capture model ranged from a mean 3% overestimate of resistance at very low resistance allele frequencies to a mean 11% underestimate of resistance at very high resistance allele frequencies. These results are similar to when the population was at equilibrium (Figure 2). We then modeled this survival difference against adult assay survival using a quadratic function, generating a correction model function (black line in Figure 3B).

We tested this correction model by applying it to adult-capture assays and, alongside the results of unadjusted adult-capture and larval-capture assay results, compared the results of this correction to the true resistance allele frequency. Using this adjustment (Figure 3B), the bias in the adult-capture assays was reduced: the mean square error (MSE) of the adjusted adult-capture (0.0038) was lower than in the unadjusted adult-capture (0.0059), but was still greater than in the larval-capture (0.0018) (Table 2).

Table 2

Table 2. Model performance comparisons.

Finally, to evaluate the performance of adult-capture assays compared to larval-captured assays in a field context, we estimated the sensitivity, specificity, and negative and positive predictive values of adult-capture and larval-capture assays simulated in our model. We generated these for both the 10% “confirmed resistance” threshold and the 2% “suspected resistance” threshold used by the WHO. Although continuous measures of resistance are important for understanding the strength of resistance in a population, these categorical cutoffs remain a standard part of field malaria programs.

Assays done with adult-capture samples correctly identified “confirmed resistance” (10% or higher) 99.5% of the time with samples of 100 tested and 100 controls (Table 3), and 98.5% of the time with samples of 50 tested and 50 controls (Supplementary Table S4). This was higher than those done with larval samples, which had a sensitivity of 98.4% (n =100) and 97.3% (n = 50), respectively (Table 3; Supplementary Table S4). Larval-capture samples, however, correctly identified insecticide susceptibility (<10%) 91.1% (n=100) and 89.9% (n=50) of the time, which was higher than adult-capture samples (73.1% with samples of n = 100, and 72.7% with samples of n = 50).

Table 3

Table 3. Test performance comparisons for Confirmed Resistance (10%).

In field contexts, positive predictive values (PPV) and negative predictive values (NPV) are particularly relevant, as the true resistance allele frequency is unknown. We evaluated PPV and NPV across the entire dataset, which ranged from 0 to 100% resistance allele frequency. With adult-capture samples, results showing “confirmed resistance” (i.e. >10% resistance allele frequency) were truly >10% resistant 94% of the time when n=100 and 93.8% of the time when n=50. With larval-capture samples, the corresponding PPVs were slightly higher (97.9% and 97.6%, respectively). However, the NPV was much higher using adult-capture samples than larval-capture: with 100 samples each for test and control groups, NPV was 97% for adult-capture samples and 19.2% with larval-capture samples. The NPV was similar with n=50 (92.1% and 19.2%, respectively).

The results for suspected resistance (>2%) followed similar trends to those for confirmed resistance, although specificity and NPV were lower for both sampling methods and specificity in particular was much lower for adult-capture (Table 4). Sensitivity was 99.8% (n=100) and 98.9% (n=50) for adult-capture samples, compared to 98.3% (n=100) and 96.5% (n=50) using larval capture (Table 4; Supplementary Table S5. Specificity, however, was 19.4% (n=100) and 5.1% (n=100) using adult capture compared to 60.2% (n=100) and 48.7% (n=50) using larval capture. Using adult-capture samples, PPV was 96.0% (n = 100) and 96.5% (n=50) compared to 97.7% (n=100) and 98.2% (n=50) using larval-capture samples. NPV for this category of resistance was particularly low for larval-capture samples. Using larval-capture samples, NPV was 4.2% for both sample sizes compared to 54.6% (n=100) and 44.3% (n=50) for adult-capture.

Table 4

Table 4. Test performance comparisons for Suspected Resistance (2%).

Practical interpretation

At lower levels of resistance, the percent resistance measured by an assay will determine the categorical resistance classification, and small errors can lead to categorical misclassification. In Figure 3B, we propose a correcting adjustment to the adult capture assays so they can more accurately determine the true resistance in a population. Once such an adjustment is applied, it is possible, as shown in Figure 4, to see how results of the adult resistance assay indicate the actual resistance allele frequency at lower levels of resistance. This figure is intended as a guide to interpret the true resistance (i.e., the population resistance allele frequency) given the results of an adult-capture resistance assay. When resistance measures 5% or lower in an adjusted resistance assay, the mean resistance allele frequency in the population is actually <1%. When resistance from the adjusted resistance assay is larger, it tracks linearly with the true resistance, with a correction. Thus, it is possible to determine an estimate of the true resistance by using the adjusted adult resistance assay.

Figure 4

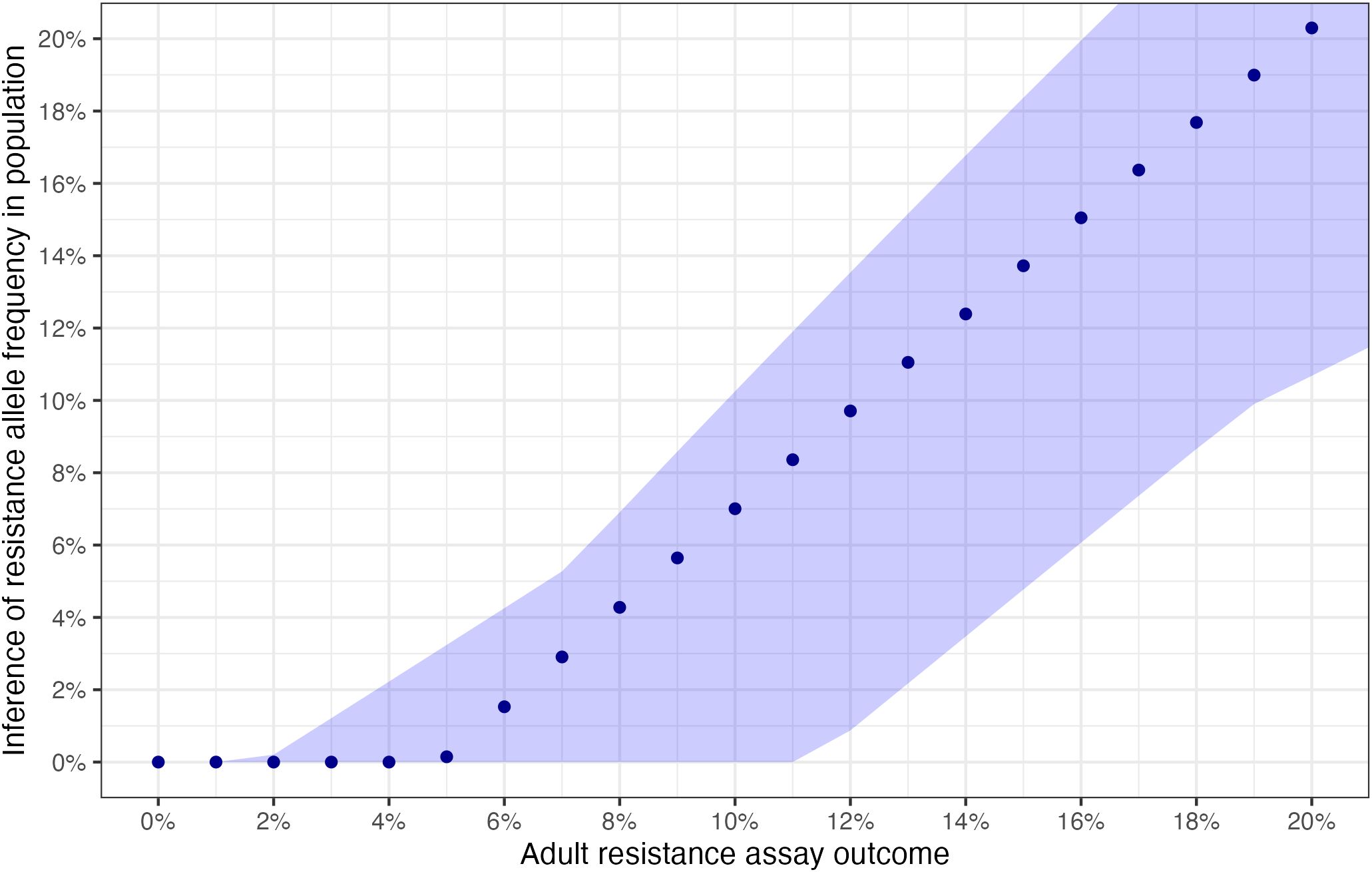
Figure 4. Interpretation of true resistance from adjusted assay survival. Points indicate the modeled mean resistance allele frequency for each assay survival % under the standard model parameterization. Assay survival shown here is already adjusted for mortality in the control group using Abbott’s correction formula. The range ribbon shows the variation in mean resistance allele frequency for each observed survival % across all sensitivity analyses.

Parameters used in the modeling may not precisely reflect the values in a particular field location. To assess the sensitivity of the assay outcomes to changes in the chosen parameters, we employ several sensitivity analyses, which test our assumptions of parameters governing both the mosquito life cycle and effects of insecticide exposure. Throughout, adult-capture remained a good predictor of true resistance. Under all sensitivity analyses, the relationship between adult-capture and larval-capture assays were qualitatively similar to that of the primary analysis (Supplementary Figure S7). The range of variation from the sensitivity analyses appears in Figure 4 as the shaded area around the points indicating the variation in mean assay results across all sensitivity analyses.

We also reconstructed the adjustment curve for each sensitivity analysis, which were qualitatively similar to the primary analysis (Supplementary Figure S7). In each, the mean resistance measurement using adult-captured assays was higher on average than that using larval-capture assays at low resistance, and lower than that using larval-capture assays at high resistance (Supplementary Figure S7). The resistance allele frequency at which mean adult-capture assays were equal to the mean of larval-capture assays ranged from 40%-52% resistance for all analyses apart from the analysis with a shortened gonotrophic cycle, which intersected at 56%. Adjustment curves generated in sensitivity analyses diverged from those in the original analysis the most at very high or very low resistance levels, in particular, for those with high larvicide exposure, 3-day gonotrophic cycle, and no mortality related fitness cost. At higher resistance levels, mean adult-capture survival was up to 11% lower than mean larval-capture survival, in the model 25% dominance of resistance (Supplementary Figure S7, purple line). At lower resistance levels, the mean adult survival was up to 11.5% higher than the mean larval survival in the model with a 3-day (rather than 4-day) gonotrophic cycle. The adjustment curve generated by the model with a 3-day gonotrophic cycle had the greatest divergence from the other model results, leading to a much larger overestimate of resistance in the adult-capture assays at low levels of resistance (Supplementary Figure S7, green line).

Discussion

Insecticide resistance represents a major threat to the gains in malaria control achieved over the past two decades. Monitoring the spread and strength of insecticide resistance is a key component of surveillance for malaria control programs, and current approaches are lacking particularly with respect to spatial representation. This is, in part, connected to the limitations of current resistance assay protocols. Given the importance of insecticide resistance in limiting disease control, it is important to fully consider how monitoring insecticide resistance can be improved. Here, we used a mathematical model of a mosquito population to compare the results of simulated adult- and larval-capture assays. We found that, despite bias in assays using adult-capture, they may still be a good measure of resistance, particularly around the WHO categorical resistance cutoffs.

Although capturing adult mosquitoes is a more labor-intensive process than capturing larvae, there are settings in which adult-capture may be a more practical strategy for insecticide resistance monitoring than larval-capture (Supplementary Table S6). Adult-capture can be done without the need for raising mosquitoes from larvae, and is therefore more portable, which may allow for testing in more remote and varied locations. In addition, they require much less time following collection—tests can be conducted immediately after collection, provided there are sufficient mosquitoes sampled, as opposed to the week or more required to raise larvae or F1 progeny to the correct age in the insectary. These advantages could allow for a shift beyond the current sentinel site model, towards more systematic monitoring over geographic regions. However, adult-capture does have its challenges. Collection must be done carefully, to avoid damaging the mosquitoes, and taxonomic identification without damaging specimens requires expertise. While adult-capture does not require the same insectary capacity as raising mosquitoes from larvae, it still requires some infrastructure so that mosquitoes can be kept alive for testing. These challenges must be considered locally before promoting the use of adult sampling over larval sampling.

Despite these challenges, adult-capture may in fact be a more representative way of monitoring the mosquitoes that are driving malaria transmission (World Health Organization, 2012). In theory, also supported by our model, larval-capture results are a very good measure of true resistance in the full mosquito population. However, this depends upon the assumption that the larvae are drawn from the same population that we are interested in measuring, i.e. the mosquitoes that are actively biting humans and, thus, likely contributing to malaria transmission. This may not be the case in the field: larval collections, in particular, may overrepresent a small portion of the mosquito population (due to egg laying behavior) and adult-capture can more easily target mosquitoes that are actively seeking out humans for blood feeding. The results of this modeling study show that even when there is bias in adult-capture assay results, it has a relatively comparable sensitivity and positive predictive value and therefore may be an improvement over larval-capture if the logistical challenges can be overcome.

One limitation of this model is that it relies on a single data set to parameterize the mortality of resistant mosquitoes following multiple exposures. For this reason, we are not able to model multiple Anopheles species, which often overlap in a single ecological setting. In addition, some field experiments have demonstrated greater survival in adult-captured mosquitoes than measured in the birth cohorts, which appears counter to the results of the lab work in Viana et al. (Hughes et al., 2020). However, from our simulated bioassays we show that adult-capture can yield either higher or lower mortality than larval-capture, depending on true population resistance.

Field experiments that directly compare larval- and adult-captured assays in regions with varying levels of resistance are necessary in order to understand whether adult-capture could be used to replace larval-capture assays. We hope that these modeling results, showing that the theoretical potential for using adult-capture samples for resistance assays, is a step towards motivating additional future investigation into this question.

The model framework is not intended to perfectly capture every detail of real-world contexts; rather, it examines the impact of assumptions about the most important drivers of heterogeneities in resistance patterns in the context of variable mosquito age and exposure. Our results demonstrate that adult-capture, in addition to the current standard larval-capture, could be a useful and consistent measure of resistance. Field experiments should be conducted to validate our results, which could allow adult-capture to be prioritized moving forward as an alternative strategy for wide scale testing to the methods currently recommended.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material. The modeling code can be found at github.com/iholmdahl/adult_capture_IR. Further inquiries can be directed to the corresponding author.

Author contributions

IH: Conceptualization, Formal analysis, Investigation, Methodology, Validation, Visualization, Writing – original draft, Writing – review & editing. CB: Conceptualization, Formal analysis, Methodology, Supervision, Visualization, Writing – original draft, Writing – review & editing, Validation. LC: Conceptualization, Formal analysis, Methodology, Supervision, Visualization, Writing – original draft, Writing – review & editing, Investigation, Validation.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors acknowledge helpful conversations and feedback from Hilary Ranson, Flaminia Catteruccia, and Neil Hobbs.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fmala.2025.1489687/full#supplementary-material

References

Abbott W. S. (1987). A method of computing the effectiveness of an insecticide. 1925. J. Am. Mosq. Control Assoc. 3, 302–303.

PubMed Abstract | Google Scholar

Alonso P., Noor A. M. (2017). The global fight against malaria is at crossroads. Lancet 390, 2532–2534. doi: 10.1016/S0140-6736(17)33080-5

PubMed Abstract | Crossref Full Text | Google Scholar

Balabanidou V., Kampouraki A., MacLean M., Blomquist G. J., Tittiger C., Juárez M. P., et al. (2016). Cytochrome P450 associated with insecticide resistance catalyzes cuticular hydrocarbon production in Anopheles Gambiae. Proc. Natl. Acad. Sci. U.S.A. 113, 9268–9273. doi: 10.1073/pnas.1608295113

PubMed Abstract | Crossref Full Text | Google Scholar

Bhatt S., Weiss D. J., Cameron E., Bisanzio D., Mappin B., Dalrymple U., et al. (2015). The effect of malaria control on Plasmodium falciparum in Africa between 2000 and 2015. Nature. 526, 207–211. doi: 10.1038/nature15535

PubMed Abstract | Crossref Full Text | Google Scholar

Carter R., Mendis K. N., Roberts D. (2000). Spatial targeting of interventions against malaria. Bull. World Health Organization. 78, 1401–1411.

Google Scholar

Childs L. M., Cai F. Y., Kakani E. G., Mitchell S. N., Paton D., Gabrieli P., et al. (2016). Disrupting mosquito reproduction and parasite development for malaria control. PloS pathogens. 12, e1006060. doi: 10.1371/journal.ppat.1006060

PubMed Abstract | Crossref Full Text | Google Scholar

Hargreaves K., Hunt R. H., Brooke B. D., Mthembu J., Weeto M. M., Awolola T. S., et al. (2003). Anopheles arabiensis and An. quadriannulatus resistance to DDT in South Africa. Med. veterinary entomology. 17, 417–422. doi: 10.1111/j.1365-2915.2003.00460.x

PubMed Abstract | Crossref Full Text | Google Scholar

Hemingway J., Ranson H., Magill A., Kolaczinski J., Fornadel C., Gimnig J., et al. (2016). Averting a malaria disaster: will insecticide resistance derail malaria control? Lancet 387, 1785–1788. doi: 10.1016/S0140-6736(15)00417-1

PubMed Abstract | Crossref Full Text | Google Scholar

Hobbs N. P., Hastings I. M. (2024). Mathematical methodology for dynamic models of insecticide selection assuming a polygenic basis of resistance. bioRxiv. doi: 10.1101/2024.04.30.591816

Crossref Full Text | Google Scholar

Hobbs N. P., Weetman D., Hastings I. M. (2023). Insecticide resistance management strategies for public health control of mosquitoes exhibiting polygenic resistance: A comparison of sequences, rotations, and mixtures. Evolutionary applications. 16, 936–959. doi: 10.1111/eva.13546

PubMed Abstract | Crossref Full Text | Google Scholar

Hughes A., Lissenden N., Viana M., Toé K. H., Ranson H. (2020). Anopheles Gambiae populations from Burkina Faso show minimal delayed mortality after exposure to insecticide-treated nets. Parasites Vectors 13, 17. doi: 10.1186/s13071-019-3872-2

PubMed Abstract | Crossref Full Text | Google Scholar

Ingham V. A., Anthousi A., Douris V., Harding N. J., Lycett G., Morris M., et al. (2020). A sensory appendage protein protects malaria vectors from pyrethroids. Nature. 577, 376–380. doi: 10.1038/s41586-019-1864-1

PubMed Abstract | Crossref Full Text | Google Scholar

Kleinschmidt I., Bradley J., Knox T. B., Mnzava A. P., Kafy H. T., Mbogo C., et al. (2018). Implications of insecticide resistance for malaria vector control with long-lasting insecticidal nets: a WHO-coordinated, prospective, international, observational cohort study. Lancet Infect. diseases. 18, 640–649. doi: 10.1016/S1473-3099(18)30172-5

PubMed Abstract | Crossref Full Text | Google Scholar

Kont M. D., Lambert B., Sanou A., Williams J., Ranson H., Foster G. M., et al. (2023). Characterising the intensity of insecticide resistance: A novel framework for analysis of intensity bioassay data. Curr. Res. Parasitol. vector-borne Dis. 4, 100125. doi: 10.1016/j.crpvbd.2023.100125

PubMed Abstract | Crossref Full Text | Google Scholar

Li J. (2004). Simple mathematical models for interacting wild and transgenic mosquito populations. Math. biosciences. 189, 39–59. doi: 10.1016/j.mbs.2004.01.001

PubMed Abstract | Crossref Full Text | Google Scholar

Madgwick P. G., Kanitz R. (2022). Modelling new insecticide-treated bed nets for malaria-vector control: how to strategically manage resistance? Malaria J. 21, 102. doi: 10.1186/s12936-022-04083-z

PubMed Abstract | Crossref Full Text | Google Scholar

Martinez-Torres D., Chandre F., Williamson M. S., Darriet F., Bergé J. B., Devonshire A. L., et al. (1998). Molecular characterization of pyrethroid knockdown resistance (kdr) in the major malaria vector Anopheles Gambiae s.s. Insect Mol. Biol. 7, 179–184. doi: 10.1046/j.1365-2583.1998.72062.x

PubMed Abstract | Crossref Full Text | Google Scholar

Matowo N. S., Martin J., Kulkarni M. A., Mosha J. F., Lukole E., Isaya G., et al. (2021). An increasing role of pyrethroid-resistant Anopheles funestus in malaria transmission in the Lake Zone, Tanzania. Sci. Rep. 11, 13457. doi: 10.1038/s41598-021-92741-8

PubMed Abstract | Crossref Full Text | Google Scholar

Mnzava A. P., Knox T. B., Temu E. A., Trett A., Fornadel C., Hemingway J., et al. (2015). Implementation of the global plan for insecticide resistance management in malaria vectors: progress, challenges and the way forward. Malaria J. 14, 173. doi: 10.1186/s12936-015-0693-4

PubMed Abstract | Crossref Full Text | Google Scholar

Moyes C. L., Athinya D. K., Seethaler T., Battle K. E., Sinka M., Hadi M. P., et al. (2020). Evaluating insecticide resistance across African districts to aid malaria control decisions. Proc. Natl. Acad. Sci. United States America. 117, 22042–22050. doi: 10.1073/pnas.2006781117

PubMed Abstract | Crossref Full Text | Google Scholar

Moyes C. L., Wiebe A., Gleave K., Trett A., Hancock P. A., Padonou G. G., et al. (2019). Analysis-ready datasets for insecticide resistance phenotype and genotype frequency in African malaria vectors. Sci. data. 6, 121. doi: 10.1038/s41597-019-0134-2

PubMed Abstract | Crossref Full Text | Google Scholar

Mulamba C., Riveron J. M., Ibrahim S. S., Irving H., Barnes K. G., Mukwaya L. G., et al. (2014). Widespread pyrethroid and DDT resistance in the major malaria vector Anopheles funestus in East Africa is driven by metabolic resistance mechanisms. PloS One 9, e110058. doi: 10.1371/journal.pone.0110058

PubMed Abstract | Crossref Full Text | Google Scholar

Namias A., Jobe N. B., Paaijmans K. P., Huijben S. (2021). The need for practical insecticide-resistance guidelines to effectively inform mosquito-borne disease control programs. eLife 10. doi: 10.7554/eLife.65655

PubMed Abstract | Crossref Full Text | Google Scholar

Rajatileka S., Burhani J., Ranson H. (2011). Mosquito age and susceptibility to insecticides. Trans. R. Soc. Trop. Med. Hygiene 105, 247–253. doi: 10.1016/j.trstmh.2011.01.009

PubMed Abstract | Crossref Full Text | Google Scholar

Rakotoson J.-D., Fornadel C. M., Belemvire A., Norris L. C., George K., Caranci A., et al. (2017). Insecticide resistance status of three malaria vectors, Anopheles Gambiae (s.l.), An. funestus and An. mascarensis, from the south, central and east coasts of Madagascar. Parasites Vectors 10, 396.

PubMed Abstract | Google Scholar

Ranson H., Lissenden N. (2016). Insecticide resistance in African anopheles mosquitoes: A worsening situation that needs urgent action to maintain malaria control. Trends Parasitol. 32, 187–196. doi: 10.1016/j.pt.2015.11.010

PubMed Abstract | Crossref Full Text | Google Scholar

Rodó X., Martinez P. P., Siraj A., Pascual M. (2021). Malaria trends in Ethiopian highlands track the 2000 “slowdown” in global warming. Nat. Commun. 12, 1555. doi: 10.1038/s41467-021-21815-y

PubMed Abstract | Crossref Full Text | Google Scholar

Ryan S. J., McNally A., Johnson L. R., Mordecai E. A., Ben-Horin T., Paaijmans K., et al. (2015). Mapping physiological suitability limits for malaria in Africa under climate change. Vector-Borne Zoonotic Dis. 15, 718–725. doi: 10.1089/vbz.2015.1822

PubMed Abstract | Crossref Full Text | Google Scholar

Ryan S. J., Lippi C. A., Zermoglio F. (2020). Shifting transmission risk for malaria in Africa with climate change: a framework for planning and intervention. Malaria J. 19, 170. doi: 10.1186/s12936-020-03224-6

PubMed Abstract | Crossref Full Text | Google Scholar

Suh P. F., Elanga-Ndille E., Tchouakui M., Sandeu M. M., Tagne D., Wondji C., et al. (2023). Impact of insecticide resistance on malaria vector competence: a literature review. Malaria J. 22, 19. doi: 10.1186/s12936-023-04444-2

PubMed Abstract | Crossref Full Text | Google Scholar

Thomas M. B., Read A. F. (2016). The threat (or not) of insecticide resistance for malaria control. Proc. Natl. Acad. Sci. United States America 113, 8900–8902. doi: 10.1073/pnas.1609889113

PubMed Abstract | Crossref Full Text | Google Scholar

Toé K. H., Jones C. M., N’Fale S., Ismail H. M., Dabiré R. K., Ranson H. (2014). Increased pyrethroid resistance in malaria vectors and decreased bed net effectiveness, Burkina Faso. Emerging Infect. Dis. 20, 1691–1696. doi: 10.3201/eid2010.140619

PubMed Abstract | Crossref Full Text | Google Scholar

Viana M., Hughes A., Matthiopoulos J., Ranson H., Ferguson H. M. (2016). Delayed mortality effects cut the malaria transmission potential of insecticide-resistant mosquitoes. Proc. Natl. Acad. Sci. United States America 113, 8975–8980. doi: 10.1073/pnas.1603431113

PubMed Abstract | Crossref Full Text | Google Scholar

World Health Organization (2012). Global plan for insecticide resistance management in malaria vectors (World Health Organization). Available at: https://apps.who.int/iris/handle/10665/44846.

Google Scholar

World Health Organization (2016). Test procedures for insecticide resistance monitoring in malaria vector mosquitoes (2d edition) (World Health Organization). Available at: https://www.who.int/publications/i/item/9789241511575.

Google Scholar

World Health Organization (2022). Manual for monitoring insecticide resistance in mosquito vectors and selecting appropriate interventions. (Genève, Switzerland: World Health Organization).

Google Scholar

World Malaria Report 2023 (2023). World Malaria Report 2023 (Genève, Switzerland: World Health Organization).

Google Scholar