
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Lab Chip Technol., 10 July 2024
Sec. Micro- and Nano-fluidics
Volume 3 - 2024 | https://doi.org/10.3389/frlct.2024.1438672
This article is part of the Research TopicInsights in Micro- and Nano-fluidicsView all 3 articles
A general theory is developed for the time dependent transient electrophoretic mobility of spherical colloidal particles in a salt-free liquid medium containing only counterions when a step external electric field is suddenly applied to the colloidal suspension. It is found that as in the case of the steady electrophoretic mobility in a salt-free medium, there is a certain critical value of the particle surface charge separating two cases, that is, the low-surface-charge case and the high-surface-charge case. In the latter case the counterion condensation takes place near the particle surface. For the low-surface charge case, the transient electrophoretic mobility agrees with that of a sphere in an electrolyte solution in the limit of very low electrolyte concentrations. For the high-surface-charge case, however, the transient mobility becomes independent of the particle surface charge because of the counterion condensation effects. A simple expression is derived for the ratio of the transient electrophoretic mobility to the steady electrophoretic mobility, which is found to take the same form irrespective of the magnitude of the particle surface charge. Using this equation, it is now possible to predict how the system will approach its final steady state.
The fundamental theories of electrophoresis developed in colloid and interface science have recently attracted significant attention in micro- and nano-fluidic lab-on-a-chip systems for the manipulation of liquids and colloidal particles. According to the standard theories of electrophoresis (von Smoluchowski, 1921; Hückel, 1924; Henry, 1931; Overbeek, 1943; Booth, 1950; Wiersema et al., 1966; O’Brien and White, 1978; Ohshima et al., 1983; Delgado, 2001; Dukhin and Goetz, 2001; Spasic and Hsu, 2005; Masliyah and Bhattacharjee, 2006; Ohshima, 2006; Lee, 2018), the zeta potential of colloidal particles is crucial in determining the stability of colloidal suspensions (Derjaguin and Landau, 1941; Verwey and Overbeek, 1948). Usually, the zeta potential is calculated from the electrophoretic mobility of the particles under a constant electric field, known as steady electrophoresis. In contrast, transient electrophoresis involves the non-steady motion of colloidal particles in a liquid medium when subjected to a sudden step electric field. Over time, the transient electrophoretic mobility tends to its static value. Understanding this relaxation time is vital for designing effective electrophoresis measurement systems. The theory of transient electrophoresis originated from Morison (Morrison, 1969; Morrison, 1971) and Ivory (Ivory, 1983; Ivory, 1984), was expanded by Keh and others (Keh and Tseng, 2001; Huang and Keh, 2005; Keh and Huang, 2005; Chiang and Keh, 2015a; Lai and Keh, 2020; Li and Keh, 2020; Lai and Keh, 2021), and has been further developed by various researchers (Khair, 2012; Ohshima, 2022a; Ohshima, 2022b; Ohshima, 2022c; Ohshima, 2023b). Many studies cover different particle types and extend to transient dynamic electrophoresis and transient gel electrophoresis. A lot of theoretical studies exist on transient electrophoresis, covering various particle types such as spherical rigid particles (Morrison, 1971; Ivory, 1984; Huang and Keh, 2005; Keh and Huang, 2005; Chiang and Keh, 2015a; Lai and Keh, 2021; Ohshima, 2022a), cylindrical rigid particles (Morrison, 1971; Li and Keh, 2020; Ohshima, 2022b), porous particle (Chiang and Keh, 2015b; Lai and Keh, 2020; Yu and Keh, 2024), soft particles (Ohshima, 2022c) and particles with a slip surface (Ohshima, 2023b). Beyond the aforementioned transient free-solution electrophoresis theories, there are also theories on transient gel electrophoresis, which deal with the transient electrophoretic behavior of colloidal particles (Ivory, 1984) in a polymer gel medium (Saad, 2018; Saad and Faltas, 2018; Saad, 2019; Sherief et al., 2021; Ohshima, 2023c; Ragab, 2023; Ayman et al., 2024). In addition, there are theories on the transient dynamic electrophoresis, which refers to the transient dynamic electrophoresis of colloidal particles when a dynamic electric field is suddenly applied (Ohshima, 2023a; Ohshima, 2024a). Further, there are theories on transient electrophoresis of colloidal particles in a multi-particle suspension (Chiang and Keh, 2015a; Ohshima, 2024b).
The above-mentioned theories of transient electrophoresis deal with colloidal particles in an electrolyte solution, or, in a salt-containing medium. When colloidal particles are suspending in a liquid medium containing only counterions, that is, in a salt-free liquid medium, a remarkable phenomenon called the counterion condensation effect occurs, especially in the case of highly charged colloidal particles (Ohshima, 2002a; Ohshima, 2002b; Ohshima, 2003a; Ohshima, 2003b; Carrique et al., 2010; Delgado et al., 2016; Luo and Keh, 2021). Chang (Chang, 2009; Chang, 2010; Chang, 2012) presented theoretical studies on the transient electroosmotic flow of a salt-free solution in a cylindrical microcapillary and found that the counterion condensation effect occurs when the microcapillary wall is highly charged.
In the present paper we focus on the transient electrophoresis in a salt-free medium. In micro- and nano-fluidic lab-on-a-chip systems, the importance of understanding the electrophoresis theory of charged colloidal particles in a salt-free medium, compared to salt-containing systems, lies in the precision and control it offers. Salt-free conditions eliminate interference from electrolyte ions, enabling more accurate manipulation of particle behavior within confined channels. This advanced control is crucial for applications such as separation, sorting, and sensing within lab-on-a-chip platforms, where even small variations in mobility of colloidal particles can have a significantly impact on their performance. Moreover, insights gained from studying salt-free electrophoresis contribute to the development of novel techniques for precise particle manipulation and analysis in micro- and nano-fluidic devices, advancing their capabilities in various fields such as biotechnology, medicine, and environmental monitoring. We derive here a simple closed form expression for the time dependent transient electrophoretic mobility of spherical colloidal particles suspended in a salt-free medium when a step external electric field is suddenly applied to the colloidal suspension.
Let us consider a suspension of spherical colloidal particles of radius a, mass density ρp, and surface charge density σ or total surface charge Q = 4πa2σ in a salt-free liquid medium of relative permittivity εr, mass density ρ0, and viscosity η containing only counterions. We employ Kuwabara’s cell model for a concentrated suspension of colloidal particles (Kuwabara, 1959). In addition to Kuwabara’s cell model, Happel’s cell model (Happel, 1958) is also known. The reason for adopting Kuwabara’s model is that in the steady electrophoresis problem, Kuwabara’s cell model correctly yields the Smoluchowski mobility equation in the limit of the dilute case. We thus assume that each spherical particle is surrounded by a spherical free volume of radius R, within which counterions are distributed so that electroneutrality is satisfied. The particle volume fraction ϕ is given by
We treat the dilute case, ϕ «1. Let the valence of the counterions and the average concentration (number density) in the absence of the applied electric field be −z and n0, respectively. Then we have
where e is the elementary electric charge. Eq. 2 is the electroneutrality condition. The right-hand side of Eq. 2 is the total amount of charge resulting from the counterions in the spherical free volume with a radius R.
We suppose that at time t = 0, a step electric field E(t) is suddenly applied to the particle suspension, viz.,
where E0 is constant. Then the particles start to move with a time-dependent transient electrophoretic velocity U(t) in the direction parallel to E0. We define the transient electrophoretic mobility μ(t) of the particle as U(t)= μ(t)E(t) =μ(t)E0. The origin of the spherical polar coordinate system (r, θ, ϕ) is held fixed at the center of the representative particle and the polar axis (θ = 0) is set parallel to E0. Let λc be the drag coefficient of the counterions. The main assumptions in our analysis are as follows. (i) The applied field E(t) is weak so that U(t) is proportional to E(t) and terms of higher order in E(t) may be neglected. (i) The applied electric field E(t) is weak so that U(t) is proportional to E(t) and terms of higher order in E(t) may be neglected so that the convection term ρ0 (u·∇)u involving the square of the liquid velocity u (r, t) in the Navier-Stokes equation can be neglected. (ii)The slipping plane (at which the liquid velocity relative to the particle becomes zero) is located on the particle surface (at r = a). (iii) Counterions cannot penetrate the particle surface. (iv) The fluid vorticity ω is zero at the outer surface of the free volume, following Kuwabara’s model (Kuwabara, 1959).
The fundamental electrokinetic equations for the flow velocity u (r, t) of the liquid at position r and time t and that of the counterions v(r, t) are similar to those for the dynamic electrophoresis of spherical colloidal particles in a salt free medium (Ohshima, 2003b), viz.,
where p (r, t) is the pressure, ρc (r, t) is the charge density resulting from the counterions of concentration (number density) n(r, t), ψ(r, t) is the electric potential outside the sphere, μc(r, t)is the electrochemical potential of the counterions, μc0 is a constant term in μc(r, t), which corresponds to the standard electrochemical potential of counterions, FH(t) and FE(t) are, respectively, the hydrodynamic and electric forces acting on the particle, ε0 is the permittivity of a vacuum, k is the Boltzmann constant, and T is the absolute temperature. Eq. 5 are the Navier-Stokes equation and the equations of continuity for an incompressible flow. Eq. 6 expresses that the flow v(r, t) of the counterions is caused by the liquid flow u(r, t) and the gradient of the electrochemical potential μc(r, t) given by Eq. 9 of the counterions. Eq. 7 is the continuity equation for the counterions. Eqs 10, 11 and are, respectively, the Poisson equation and the equation of motion of the particle.
The initial condition for u (r, t) is given by
The slipping plane (at which the liquid velocity u (r, t) relative to the particle is zero) is assumed to be located on the particle surface (at r = a), viz.,
According to Kuwabara’s cell model (Kuwabara, 1959), we assume that at the outer surface of the unit cell (r = R) the liquid velocity is parallel to the electrophoretic velocity U(t) of the particle, viz.,
where
Also, we assume that on the outer surface of the unit cell (r = R) the gradient of the electric potential is parallel to the applied field E(t), viz.,
where E(t) is the magnitude of E(t). Finally, we adopt the boundary condition that no electrolyte ions can penetrate the particle surface, viz,
For a weak field E(t) [assumption (i)], we may write
where the quantities with superscript (0) refer to those at equilibrium, δn (r, t), δψ(r, t), δμc (r, t), δρc (r, t) are small quantities, and
and
with
Here we have set the equilibrium electric potential ψ(0) (r) to be zero at points where the volume charge density ρc(r) resulting from counterions equals its average value (−zen0). We define the equilibrium surface potential as ψ(0) (a)−ψ(0) (R). The boundary conditions for ψ(0) (r) at the particle surface r = a and at the outer surface of the free volume r =R are
Further, symmetry considerations permit us to write
Here Φ(r, t), Y(r, t), and h(r, t) are functions of r and t.
By substituting Eq. 27–29 into Eqs 4–7, and neglecting the products of the small quantities, we obtain the following equation for h(r, t), ϕi(r, t), and Y(r, t):
with
where y(r) is the scaled equilibrium electric potential, ν is the kinematic viscosity of the liquid.
The initial and boundary conditions (Eqs 12–16) and the equation of the motion of the particle (Eq. 11) can be rewritten as those for h(r, t) and Y(r, t) as follows.
The transient electrophoretic mobility μ(t) can be obtained from Eq. 39, viz.,
Eq. 31 for h(r, t) is most easily solved by using the Laplace transformation with respect to time t. We introduce the Laplace transforms
and the Laplace transform of Eq. 42 is
The Laplace transform of Eq. 29 thus gives
By solving Eq. 50 subject to Eqs 37–41 and using Eq. 49, we obtain the following general expression for the Laplace transform
where
Eq. 51 is the general expression Laplace transform of the transient electrophoretic mobility μ(t) of a spherical colloidal particle in a salt-free liquid medium. The transient mobility μ(t) can be obtained from Eq. 51 by the numerical inverse Laplace transformation. It can be shown that as in the case of steady electrophoresis in salt-free media, the electrophoretic mobility is determined almost solely by the second term of the right-hand side of Eq. 51 (Ohshima, 2002a; Ohshima, 2003a; Ohshima, 2003b), viz.,
This term comes from the contribution of the pressure due to the counterions at the outer surface of the free volume (at r = R). Further, for the dilute case (ϕ ≪ 1) we may approximate
By substituting Eq. 25 into Eq. 43 and using Eq. 8, we have for the dilute case
An accurate analytic expression for the equilibrium potential distribution around a spherical particle in a salt-free medium for the dilute case (ϕ ≪ 1) has already been derived (Ohshima, 2002a). The expressions for ψ(0) (a) and ψ(0) (R) are given below.
Case 1. (low-surface-charge case)
is satisfied, then
If the zeta potential ζ is identified as the surface potential defined by ψ(0) (a)−ψ(0) (R), then we have
which is the Coulomb potential. That is, in the low-surface-charge case, the expression for the zeta potential ζ of a particle in a salt-free medium agrees with the limiting form of the zeta potential of a particle in an electrolyte solution with a very low electrolyte concentration.
Case 2. (high-surface-charge-case)
is satisfied, then
from which
Eq. 71 demonstrates that in the high-surface-charge case, unlike in the low-surface-charge case, the zeta potential ζ is no longer given by the Coulomb potential (Eq. 67) but by a more complicated equation (Eq. 71). Eq. 71 depends less on Q than Eq. 67 and becomes a function of the particle volume fraction ϕ, as the counter ion condensation occurs in the vicinity of the particle surface.
By substituting the above results into Eq. 63, we obtain the following results:
Case 1. (low-surface- charge case)
Case 2. (high-surface- charge case)
In the limit of s→0, Eqs 72, 73 become the steady electrophoretic mobility μs = μ(∞) at t = ∞ of spherical colloidal particles in a salt free medium (Ohshima, 2002a), that is,
Case 1. (low-surface- charge case)
Case 2. (high-surface- charge case)
The transient electrophoretic mobility μ(t) can be obtained analytically from Eqs 72, 73 by the inverse Laplace transformation. The result is
Case 1. (low-surface- charge case)
Case 2. (high-surface- charge case)
with
where erfc(z) is the complementary error function, defined by
We see that Eq. 76 for the low-surface-charge case agrees with the low κa limiting form of the transient electrophoretic mobility μ(t) of a spherical colloidal particle of radius a in an electrolyte solution of the Debye-Hückel parameter κ (Ohshima, 2022a). For the high-surface-charge case, the transient electrophoretic mobility μ(t) deviates from Eq. 76 and given by Eq. 77, which is independent of Q. In other words, in the high-surface-charge case, as Q increases, the zeta potential ζ does not increase linearly with Q (Eq. 71). This is because the number of counterions condensed near the particle surface increases, which tends to suppress the rise in the zeta potential. Consequently, the particle zeta potential depends less on Q.
It follows from Eqs 74–77 that the ratio of the transient electrophoretic mobility μ(t) to the steady mobility μs = μ(∞) in a salt-free medium is always simply given by
for both cases 1 (low-surface- charge case) and 2 (high-surface- charge case), irrespective of the magnitude of the particle surface charge Q.
Figure 1 illustrates the ratio μ(t)/μs calculated with Eq. 82 as a function of scaled time νt/a2 for four values of the mass density ratio ρp/ρ0, showing how μ(t) reaches the corresponding steady value μs. It is observed that the transient mobility μ(t) of heavier particles with larger mass density ρp requires a longer time to reach its steady value μs. Figure 2 gives a 3-D plot of the ratio μ(t)/μs calculated with Eq. 82 as a function of scaled time νt/a2 and the mass density ratio ρp/ρ0, which covers wider ranges of νt/a2 and the mass density ratio ρp/ρ0.
Figures 1, 2 show that the relaxation time required for μ(t) to reach its steady value μs becomes longer as the mass density ratio ρp/ρ0 increases. An approximate expression for the relaxation time T can be derived as follows. As a crude approximation, Eq. 82 reduces to
with
where T can be regarded as the relaxation time.
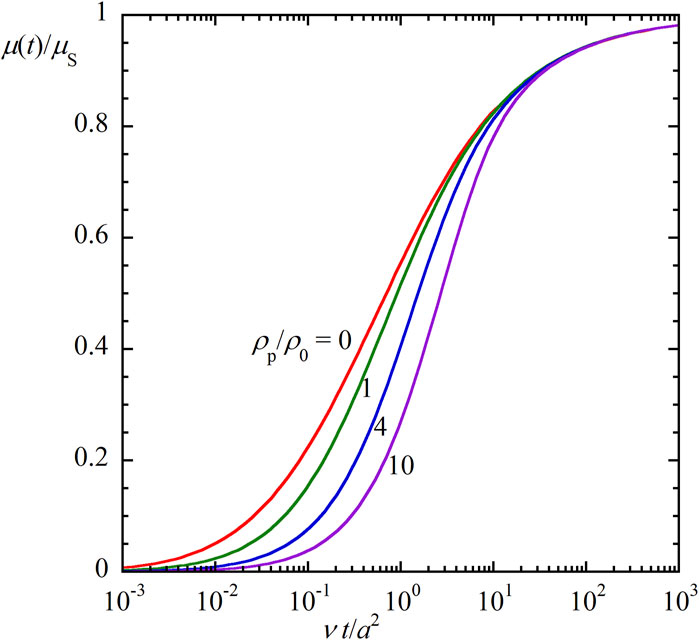
Figure 1. The ratio μ(t)/μs of the transient electrophoretic mobility μ(t) to the steady electrophoretic mobility μs for spherical colloidal particles of radius a and mass density ρp in a salt-free liquid medium of mass density ρ0 and kinematic viscosity ν as a function of the scaled time νt/a2 for four values of the mass density ratio ρp/ρ0 (ρp/ρ0 = 0, 1, 4, and 10).
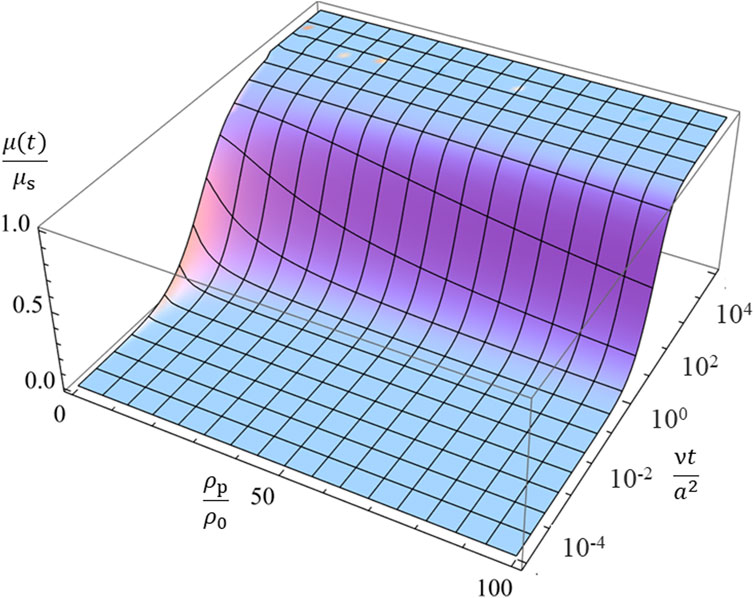
Figure 2. The 3-D plot of the ratio μ(t)/μs of the transient electrophoretic mobility μ(t) to the steady electrophoretic mobility μs for spherical colloidal particles of radius a and mass density ρp in a salt-free liquid medium of mass density ρ0 and kinematic viscosity ν as a function of the scaled time νt/a2 and the mass density ratio ρp/ρ0.
We have developed a theory of the transient electrophoresis of colloidal particles in a salt-free medium, which provides vital information for designing effective electrophoresis measurement systems related to micro- and nano-fluidic lab-on-a-chip technologies. We first derived a general expression (Eq. 51 for the Laplace transform
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
HO: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing.
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ayman, M., Saad, E. I., and Faltas, M. S. (2024). Transient electrophoresis of a conducting cylindrical colloidal particle suspended in a Brinkman medium. Z. fur Angew. Math. Phys. 75 (2), 53–23. doi:10.1007/s00033-023-02182-8
Booth, F. (1950). The cataphoresis of spherical, solid non-conducting particles in a symmetrical electrolyte. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 203 (1075), 514–533. doi:10.1098/rspa.1950.0154
Carrique, F., Ruiz-Reina, E., Arroyo, F. J., and Delgado, Á. V. (2010). Dynamic electrophoretic mobility of spherical colloidal particles in realistic aqueous salt-free concentrated suspensions. J. Phys. Chem. B 114 (18), 6134–6143. doi:10.1021/jp102350d
Chang, S. H. (2009). Transient electro-osmotic flow in cylindrical microcapillaries containing salt-free medium. Biomicrofluidics 3 (1), 12802. doi:10.1063/1.3064113
Chang, S. H. (2010). Electroosmotic flow in slit microchannel containing salt-free solution. Eur. J. Mech. B/Fluids 29 (5), 337–341. doi:10.1016/j.euromechflu.2010.04.003
Chang, S. H. (2012). Electroosmotic flow in a dissimilarly charged slit microchannel containing salt-free solution. Eur. J. Mech. B/Fluids 34, 85–90. doi:10.1016/j.euromechflu.2012.01.020
Chiang, C. C., and Keh, H. J. (2015a). Startup of electrophoresis in a suspension of colloidal spheres. Electrophoresis 36 (24), 3002–3008. doi:10.1002/elps.201500316
Chiang, C. C., and Keh, H. J. (2015b). Transient electroosmosis in the transverse direction of a fibrous porous medium. Colloids Surfaces A Physicochem. Eng. Aspects 481, 577–582. doi:10.1016/j.colsurfa.2015.06.021
Delgado, Á. V., Carrique, F., Roa, R., and Ruiz-Reina, E. (2016). Recent developments in electrokinetics of salt-free concentrated suspensions. Curr. Opin. Colloid and Interface Sci. 24, 32–43. doi:10.1016/j.cocis.2016.06.004
Derjaguin, B. V., and Landau, D. L. (1941). Theory of the stability of strongly charged lyophobic sols and of the adhesion of strongly charged particles in solutions of electrolytes. Acta Physicochim. USSR 14, 633–662.
Dukhin, A. S., and Goetz, J. P. (2001). Ultrasound for characterizing colloids. Particle sizing, zeta potential, rheology. Amsterdam: Elsevier.
Happel, J. (1958). Viscous flow in multiparticle systems: slow motion of fluids relative to beds of spherical particles. AIChE J. 4 (2), 197–201. doi:10.1002/aic.690040214
Henry, D. C. (1931) The cataphoresis of suspended particles. Part I.—the equation of cataphoresis, Proc. R. Soc. A Math. Phys. Eng. Sci., 133, 106–129. doi:10.1098/rspa.1931.0133
Huang, Y. C., and Keh, H. J. (2005). Transient electrophoresis of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 21 (25), 11659–11665. doi:10.1021/la051171q
Ivory, C. F. (1983). Transient electroosmosis: the momentum transfer coefficient. J. Colloid And Interface Sci. 96 (1), 296–298. doi:10.1016/0021-9797(83)90032-2
Ivory, C. F. (1984). Transient electrophoresis of a dielectric sphere. J. Colloid And Interface Sci. 100 (1), 239–249. doi:10.1016/0021-9797(84)90432-6
Keh, H. J., and Huang, Y. C. (2005). Transient electrophoresis of dielectric spheres. J. Colloid Interface Sci. 291 (1), 282–291. doi:10.1016/j.jcis.2005.04.108
Keh, H. J., and Tseng, H. C. (2001). Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 242 (2), 450–459. doi:10.1006/jcis.2001.7797
Khair, A. S. (2012). Transient phoretic migration of a permselective colloidal particle. J. Colloid Interface Sci. 381 (1), 183–188. doi:10.1016/j.jcis.2012.05.038
Kuwabara, S. (1959). The forces experienced by randomly distributed parallel circular cylinders or spheres in a viscous flow at small Reynolds numbers. J. Phys. Soc. Jpn. 14 (4), 527–532. doi:10.1143/JPSJ.14.527
Lai, Y. C., and Keh, H. J. (2020). Transient electrophoresis of a charged porous particle. Electrophoresis 41 (3–4), 259–265. doi:10.1002/elps.201900413
Lai, Y. C., and Keh, H. J. (2021). Transient electrophoresis in a suspension of charged particles with arbitrary electric double layers. Electrophoresis 42 (21–22), 2126–2133. doi:10.1002/elps.202000336
Lee, E. (2018). Theory of electrophoresis and diffusiophoresis of highly charged colloidal particles. Amsterdam: Elsevier B.V.
Li, M. X., and Keh, H. J. (2020). Start-Up electrophoresis of a cylindrical particle with arbitrary double layer thickness. J. Phys. Chem. B 124 (44), 9967–9973. doi:10.1021/acs.jpcb.0c07436
Luo, R. H., and Keh, H. J. (2021). Electrophoresis and electric conduction in a salt-free suspension of charged particles. Electrophoresis 42 (21–22), 2134–2142. doi:10.1002/elps.202100181
Masliyah, J. H., and Bhattacharjee, S. (2006). Electrokinetic and colloid transport phenomena. Hoboken: John Wiley and Sons.
Morrison, F. A. (1969). Transient electrophoresis of a dielectric sphere. J. Colloid And Interface Sci. 29 (4), 687–691. doi:10.1016/0021-9797(69)90221-5
Morrison, F. A. (1971). Transient electrophoresis of an arbitrarily oriented cylinder. J. Colloid And Interface Sci. 36 (1), 139–145. doi:10.1016/0021-9797(71)90250-5
O’Brien, R. W., and White, L. R. (1978). Electrophoretic mobility of a spherical colloidal particle. J. Chem. Soc. Faraday Trans. Chem. Soc. Faraday Trans. 22 Mol. Chem. Phys. 74, 1607–1626. doi:10.1039/F29787401607
Ohshima, H. (2002a). Electrophoretic mobility of a cylindrical colloidal particle in a salt-free medium. J. Colloid Interface Sci. 255 (1), 202–207. doi:10.1006/jcis.2002.8650
Ohshima, H. (2002b). Electrophoretic mobility of a spherical colloidal particle in a salt-free medium. J. Colloid Interface Sci. 248 (1), 499–503. doi:10.1006/jcis.2002.8232
Ohshima, H. (2003a). Dynamic electrophoretic mobility of spherical colloidal particles in a salt-free medium. J. Colloid Interface Sci. 265 (2), 422–427. doi:10.1016/S0021-9797(03)00470-3
Ohshima, H. (2003b). Numerical calculation of the electrophoretic mobility of a spherical particle in a salt-free medium. J. Colloid Interface Sci. 262 (1), 294–297. doi:10.1016/S0021-9797(03)00190-5
Ohshima, H. (2022a). Approximate analytic expression for the time-dependent transient electrophoretic mobility of a spherical colloidal particle. Molecules 27 (16), 5108. doi:10.3390/molecules27165108
Ohshima, H. (2022b). Transient electrophoresis of a cylindrical colloidal particle. Fluids 7 (11), 342. doi:10.3390/fluids7110342
Ohshima, H. (2022c). Transient electrophoresis of a spherical soft particle. Colloid Polym. Sci. 300 (12), 1369–1377. doi:10.1007/s00396-022-05029-2
Ohshima, H. (2023a). Transient dynamic electrophoresis of a spherical colloidal particle. Electrophoresis 45 (July), 706–711. doi:10.1002/elps.202300153
Ohshima, H. (2023b). Transient electrophoresis of a spherical colloidal particle with a slip surface. Electrophoresis 44 (23), 1795–1801. doi:10.1002/elps.202200242
Ohshima, H. (2023c). Transient gel electrophoresis of a spherical colloidal particle. Gels 9 (5), 356. doi:10.3390/gels9050356
Ohshima, H. (2024a). Transient dynamic electrophoresis of a soft particle. Electrophoresis. doi:10.1002/elps.202300247
Ohshima, H. (2024b). Transient electrophoresis of spherical colloidal particles in a multi-particle suspension. Colloid Polym. Sci. doi:10.1007/s00396-024-05269-4
Ohshima, H., Healy, T. W., and White, L. R. (1983). Approximate analytic expressions for the electrophoretic mobility of spherical colloidal particles and the conductivity of their dilute suspensions. J. Chem. Soc. Faraday Trans. 2 79 (11), 1613. doi:10.1039/F29837901613
Overbeek, J. T. G. (1943) Beih. Theor. Elektrophorese Relaxationseffekt, 54, 287–364. doi:10.1007/BF02556774
Ragab, K. E. (2023). An investigation of the transient electrophoresis of conducting colloidal particles in porous media using a cell model. Chin. J. Phys. 85 326–344. doi:10.1016/j.cjph.2023.07.024
Saad, E. I. (2018). Start-up Brinkman electrophoresis of a dielectric sphere for Happel and Kuwabara models. Math. Methods Appl. Sci. 41 (18), 9578–9591. doi:10.1002/mma.5314
Saad, E. I. (2019). Unsteady electrophoresis of a dielectric cylindrical particle suspended in porous medium. J. Mol. Liq. 289, 111050. doi:10.1016/j.molliq.2019.111050
Saad, E. I., and Faltas, M. S. (2018). Time-dependent electrophoresis of a dielectric spherical particle embedded in Brinkman medium. Z. fur Angew. Math. Phys. 69 (2), 43–18. doi:10.1007/s00033-018-0939-4
Sherief, H. H., Faltas, M. S., and Ragab, K. E. (2021). Transient electrophoresis of a conducting spherical particle embedded in an electrolyte-saturated Brinkman medium. Electrophoresis 42 (16), 1636–1647. doi:10.1002/elps.202100063
Spasic, A., and Hsu, J. P. (2005). Finely dispersed particles. Micro-. nano-, atto-engineering (Boca Raton: Taylor and Francis).
Verwey, E. J. W., and Overbeek, J. T. G. (1948). Theory of the stability of lyophobic colloids. Amsterdam: Elsevier B.V.
von Smoluchowski, M. (1921). “Elektrische endosmose und strömungsströme,” in Handbuch der Elektrizität und des Magnetismus, Band II Stationäre ströme. Editor E. Greatz (Leipzig: Barth).
Wiersema, P. H., Loeb, A. L., and Overbeek, J. T. G. (1966). Calculation of the electrophoretic mobility of a spherical colloid particle. J. Colloid And Interface Sci. 22 (1), 78–99. doi:10.1016/0021-9797(66)90069-5
Yu, C. W., and Keh, H. J. (2024). Transient slow motion of a porous sphere. Fluid Dyn. Res. 56 (1), 015503. doi:10.1088/1873-7005/ad220c
Keywords: transient electrophoresis, transient electrophoretic mobility, salt-free medium, laplace transform, step electric field
Citation: Ohshima H (2024) Transient electrophoresis of colloidal particles in a salt-free medium. Front. Lab. Chip. Technol. 3:1438672. doi: 10.3389/frlct.2024.1438672
Received: 26 May 2024; Accepted: 17 June 2024;
Published: 10 July 2024.
Edited by:
Xiangchun Xuan, Clemson University, United StatesReviewed by:
Gaojin Li, Shanghai Jiao Tong University, ChinaCopyright © 2024 Ohshima. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hiroyuki Ohshima, b2hzaGltYUBycy5ub2RhLnR1cy5hYy5qcA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.