Benjamin Owen- Institute for Multiscale Thermofluids, School of Engineering, University of Edinburgh, Edinburgh, United Kingdom
Inertial microfluidics allows for passive, label-free manipulation of particles suspended in a fluid. Physical experiments can understand the underlying mechanisms to an extent whereby inertial microfluidic devices are used in real-world applications such as disease diagnostics. However, design processes are often iterative and device optimisation can be improved. Numerical modelling has complementary capabilities to physical experiments, with access to full flow field data and control of design parameters. Numerical modelling is used to uncover the fundamental mechanisms in inertial microfluidics and provides evidence for physical experiments. In recent years, numerical modelling has been increasingly coupled to machine learning algorithms to uncover additional physics and provide fast solutions. In this perspective, I discuss the role numerical modelling will play in future inertial microfluidic device research and the opportunities to combine numerical modelling with machine learning algorithms. Two key areas for future research applying machine learning are highlighted; fast predictions of flow fields and the optimisation of design parameters. Developments in these areas would significantly reduce the resources required in device design and have the potential to uncover new applications.
1 Introduction to inertial microfluidics
Inertial microfluidic devices are able to manipulate particles based on their geometric and mechanical properties (Zhou and Papautsky, 2013). One key application is size- and softness-based separation of particles. Particles are suspended in a pressure-driven fluid through a channel with a Reynolds number, (a non-dimensional quantity indicating the ratio of inertial to viscous forces) that is larger than in traditional microfluidic devices. Increasing the Reynolds number is achieved through increasing the fluid flow rate through the device, allowing for a higher throughput of samples. The Reynolds number is also sufficiently high for inertial forces to be relevant to the overall flow physics as first observed by Segre and Silberberg (1961).
The main inertial forces acting on a single particle are the shear gradient lift force and the wall-induced force (Martel and Toner, 2014). The shear-gradient lift force is caused by the u-shaped nature of the fluid velocity profile across the channel cross-section due to the no-slip condition at the wall as shown in Figure 1A. Since the particle has a finite size, there is a velocity gradient across the particle in the lateral direction, resulting in the shear-gradient lift force which usually pushes the particle towards the channel wall as shown by the blue arrow in Figure 1A. The second force, the wall-induced force, is caused by the increase in fluid pressure between the wall as shown in Figure 1B. The wall-induced force pushes the particle away from the wall.
FIGURE 1. Depiction of the two main inertial forces acting on a particle in an inertial microfluidic device: (A) shear gradient lift force and (B) wall-induced force. The balance of the two forces dictates the location of the lateral equilibrium position of the particle.
At given lateral positions in the channel cross-section, the shear-gradient lift force and the wall-induced force will balance, resulting in lateral equilibrium positions of the particle, often referred to as the Segré-Silberberg effect. The location of the lateral equilibrium positions are dependent on the geometric and mechanical properties of the particle such as size, shape and softness (Kilimnik et al., 2011). As a result, particles with different properties can be separated. When the concentration of particles within the flow is large, a distinct lateral equilibrium position may not exist due to overpopulation (Krüger et al., 2014). However, focusing streams can still exist where particles migrate towards equilibrium positions without being able to reach equilibrium. These focusing stream are also dependent on the geometric and material particle properties and therefore particle type separation can still occur.
Another physical phenomena that exists in inertial microfluidic flows is the axial ordering of particles often called particle trains (Schaaf and Stark, 2020). Particles that migrate to their lateral equilibrium positions will also form trains with a consistent inter-particle spacing between them. If the concentration of the suspension is too high the trains can break down and transition into focusing streams.
The physical phenomena of lateral equilibrium positions and axial-ordering can be exploited for a number of applications. The property-dependent lateral equilibrium positions can be used for passive, label-free manipulation of biological cells. This manipulation can be as simple as creating cell-rich or cell-free volumes. Particles can be separated or focused based on their properties which in turn can be utilised for diagnostic purposes, e.g., the detection of circulating tumour cells (CTCs) in blood samples (Zhou et al., 2019). Crucially, cells remain viable after passing through an inertial microfluidic device. This retention of viability opens up opportunities to culture cells, e.g., CTC-based organoids used to test the effectiveness of drugs (De Angelis et al., 2022).
The axial ordering of particles can be exploited in applications such as flow cytometry and cell encapsulation. In flow cytometry, cells pass through fluorescence sensors to accurately measure physical and chemical properties. The axial ordering of particles in flow cytometry with a consistent inter-particle spacing ensures robust measurements are taken (Wu et al., 2023). In cell encapsulation, a single cell is placed within a droplet. Tuning of droplet generation is well understood (Lashkaripour et al., 2019). However, ensuring a single particle is placed within each droplet is non-trivial. Encapsulation devices can suffer from Poisson statistics leading to empty droplets or doublets, reducing efficiency of the device and requiring post-generation sifting to output the desired single cell droplets. Consistent axial ordering via inertial microfluidics has been shown to overcome Poisson statistics (Shahrivar and Del Giudice, 2022).
Experimental (Segre and Silberberg, 1961), numerical (Chun and Ladd, 2006), and analytical (Asmolov, 1999) studies of inertial flows set the foundations for the seminal study of the application of the phenomena to microfluidics by Di Carlo et al. (2007), coining the term “inertial microfluidics.” The authors demonstrated that inertial microfluidics has the ability to passively and continuously separate cells of different sizes at high throughput. Since then, many further investigations have been conducted with a near linear growth in published studies as shown in Figure 2. The majority of these studies use physical experiments. However, in recent times the use of numerical modelling has increased leading to a larger rate of increase of numerical to experimental studies.
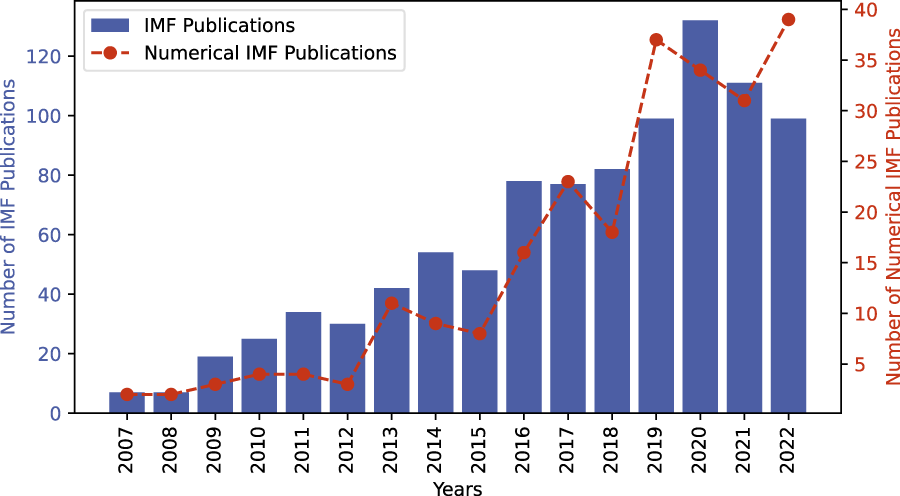
FIGURE 2. Comparison of the overall number of published studies in the field of inertial microfluidics: experimental and numerical (blue) and number of published numerical studies in inertial microfluidics (red)1.
2 Introduction to artificial intelligence and machine learning
Artificial intelligence (AI) and machine learning has experienced a boom in interest in recent years. Applications include language translation and image recognition, allowing users to classify large datasets quickly and accurately. Machine learning algorithms can identify underlying patterns within datasets and predict future behaviour. To be used for prediction, machine learning algorithms require existing datasets to train on. The level of user engagement with the training data classifies machine learning algorithms into supervised, unsupervised and reinforcement learning methods (Sarker, 2021).
In supervised learning, the algorithm is trained on labeled data, meaning the input data is paired with the correct output. The algorithm learns to map the input to the output, making predictions or decisions based on that mapping. Common algorithms used in supervised learning include linear or non-linear regression for regression tasks and classification algorithms such as decision trees, support vector machines, and neural networks for classification tasks. Generating and labeling the input data for supervised learning can be time consuming.
Unsupervised learning involves working with unlabeled data. The algorithm explores the data without any supervision or guidance, identifying patterns or structures within it. Unlike supervised learning, there are no explicit ground truths, and the algorithm is left to discover the inherent structure of the data on its own. Common techniques in unsupervised learning include clustering, where the algorithm groups similar data points together, and dimensionality reduction, where the algorithm simplifies the data while preserving its essential features.
Reinforcement learning is a type of machine learning where an agent learns how to behave in an environment by performing actions and receiving rewards. The agent explores the environment and learns to make a sequence of decisions that maximize a reward metric over time. The number of iterations required to optimise performance can often be large, meaning that the time taken for an iteration to occur should be minimised in order to find a solution within an acceptable time frame.
In recent years, machine learning has been successfully applied to a number of applications in the field of fluid mechanics, from turbulence modeling (Guastoni et al., 2021) to flow control (Rabault et al., 2019) and is rapidly becoming a core technology for computational fluid dynamics. While a limited number of recent studies have used machine learning for inertial microfluidic studies (Su et al. 2021), the recent advances in machine learning and numerical modelling coupling have yet to be fully exploited in inertial microfludics1.
The increase in interest in numerical modelling of inertial microfluidics and machine learning in the general fluid mechanics field leads to the focus of this perspective article. What are the future applications of numerical modelling in inertial microfluidics and how can it be used in conjunction with recent advances in machine learning? I discuss the advantages and disadvantages of both physical experiments and numerical modelling in Section 3.1 and highlight how they complement each other. I highlight numerical modelling studies to date which have mainly focused on investigating fundamental physical mechanisms (Section 3.2) and supplementing experimental studies through the control of design parameters (Section 3.3). In Section 4.1 I discuss the current state-of-the-art for inertial microfluidics and machine learning before providing an overview of how machine learning has been applied to the broader field of fluid mechanics, and the potential avenues for cross-exploitation in inertial microfluidics in Section 4.2. In Section 4.3 I discuss some of the challenges that must be overcome in order to more widely apply machine learning to inertial microfluidics.
3 Numerical modelling in inertial microfluidics
Numerical modelling in inertial microfluidics generally falls into the category of computational fluid dynamics (CFD). Originally developed for aerospace research, CFD has been applied to many applications including energy generation (Hewitt et al., 2017), automotive design (Ashton et al., 2016) and cardiovascular disease (Morris et al., 2016). A number of numerical methods exist including lattice Boltzmann, finite volume, finite element, finite difference, and smoothed particle hydrodynamics. Each method has advantages and disadvantages depending on a given application. The choice of the method often involves a judgement on which method is most suited to a given application as well as the user’s existing expertise. For more detailed technical discussion of numerical modelling in inertial microfluidics, the interested reader is directed to recent reviews on the subject (Razavi Bazaz et al., 2020; Owen et al., 2023). In this section I will discuss how numerical modelling and physical experiments compliment each other in Section 3.1. I will then provide a brief overview on how numerical modelling has mainly been utilised in inertial microfluidics: uncovering the fundamental physics in Section 3.2 and supplementing experimental studies through the control of design parameters in Section 3.3.
3.1 Synergy of numerical modeling and physical experiments
Numerical modelling complements physical experiments. Numerical modelling can give access to entire datasets, e.g., it is possible to view the full fluidic field at any time and at any location within the domain. In contrast, physical experiments can generally only view particle positions in one or two planes due to physical constraints placing high-speed cameras while images can only be taken for a fraction of a second. Furthermore, measurements taken by high-speed cameras generally focus only on the particle behaviour due to the difficulty of measuring fluid behaviour. An advantage of physical experiments is that they inherently represent real-world devices. In contrast, a real-world representation in a numerical model would either have a prohibitively high computational cost and complexity or the physical model may not yet exist, e.g., a real-world representation of a white blood cell. As such, a numerical modeller must use expertise and judgement to decide which physical mechanisms to include within the simulation and develop models if they do not yet exist. Figure 3 shows an example of how numerical modelling and physical experiments can be used together to further our understanding of inertial microfluidic devices.
FIGURE 3. Complementary physical experiments adapted from Zhou et al. (2019) and numerical simulations (unpublished). Physical experiments can provide real-world images of particle behaviour obtained through microscopes in a limited number of planes and positions. Samples collected at the outlets of physical experiments provide quantitative device performance data such a output purity and separation efficiency. Numerical simulations can provide comprehensive particle and fluid behaviour in the device using a model of the system. Note that experimental images at the inlet and outlet are stacked and represent a number of time instances, aggregated. Numerical images are of a single time instance.
3.2 Uncovering fundamental physics
Given the complementary advantages and disadvantages discussed in Section 3.1, numerical modelling is suited to investigating the fundamental physics of inertial microfluidics. The physics involved in inertial microfluidics is dependent on a large number of geometric properties of the channel, geometric and material properties of the particle, and properties of the suspending fluid. A selection of the major contributors to the overall physics are shown in Figure 4. Numerical modelling can take a simplified representation and investigate the effect of one or two key parameters at a time. For example, previous studies have used large parameter sweeps to investigate the effect of particle size and softness on the focusing behaviour of single particles (Kilimnik et al., 2011), and on pair and train formation (Schaaf et al., 2019; Owen and Krüger, 2022).
FIGURE 4. (A) Key parameters in inertial microfluidics: For a given application, parameters may be constrained. Some parameters are more likely to be constrained, e.g. the size and softness of a target particle, while others may be design parameters that should be optimised for the given constrained parameters. NB: Size in Geometric Properties refers to the scale factor of the device with same axial and cross-sectional shape, while Size in Particle Properties refers to a characteristic length, usually particle radius or diameter. The ratio of the two sizes provides the confinement of the system. (B–G) Example Geometric Properties. Axial shape: (B) straight, (C) curved. Cross-sectional shape: (D) square, (E) rectangular, (F) circular, (G) triangular. Dashed line in (B) and (C) is the channel centreline. Particles in (D–G) show each lateral equilibrium position associated with the cross-section type.
Numerical modelling can also analyse specific parts of a system in detail, and translate systems to alternative reference frames to ease analysis. Kahkeshani et al. (2016) used these capabilities to investigate the mechanism of the self-assembly of particles into pairs. Through the use of co-moving reference frames and parameter space sweeps of initial lateral positions, they demonstrated the existence of attractors (forces of attraction) between particles. These attractors can be used to predict the preferred spacing between particles for a given flow Reynolds number, identifying the transfer of preferred spacing as Reynolds number increases.
Numerical modelling can be used to create non-physical scenarios to disentangle competing effects. Prohm and Stark (2014) used this capability to neglect the lateral motion of a particle as it passed through a channel. By placing the particle at carefully selected locations within the cross-section, the authors were able to create inertial lift force maps for a given channel cross-section, particle size, and Reynolds number. These force maps were used to predict the lateral motion of a particle in the cross-section as well as identifying stable and unstable equilibrium positions.
3.3 Controlling design parameters
Numerical modelling can be used to efficiently optimise device design parameters, both in terms of time and cost. This is particularly true when investigating device geometric design parameters that would require the redesign and fabrication of multiple physical devices if conducted via physical experiments. One such example was published by Palumbo et al. (2020) who used numerical modelling to optimise a helical spiral channel for size-based particle sorting. They investigated the effect of various geometric parameters such as channel pitch, diameter, taper angle, depth, and width, within the same study (
A typical particle-resolved simulation may take approximately 24 h using 36 cores on a high performance computing cluster. Assuming 10 simulations can be run in parallel on the cluster, a numerical study of 200 simulations would take approximately 1 month to generate data. Furthermore, most of this time would require low human effort given that simulations are automated once they have been started and simulations are deterministic and therefore one simulation is sufficient per device design. In contrast, physical experiments require high human effort, including sample preparation and set-up of devices, calibration of equipment, and data collection once the experiment is running. A typical device may take 1 h to set-up and perform the experiment. Given, each device design should be tested at least three times to ensure repeatability of results, an experimental study would take approximately 3 months of high human effort time to complete.
While numerical modelling offers the opportunity to perform large parameter sweeps for a single parameter, it is still constrained when investigating the coupled behaviour of two or more parameters as the number of required simulations grows with xn where x is the number of points within the parameter sweep, and n is the number of parameters under investigation. As a result, parameter sweeps with multiple dependent parameters can quickly become prohibitively large, even with the enhanced performance with using numerical modelling. In Section 4 I discuss how machine learning may address this issue.
4 Integration of numerical modelling with machine learning
The use of artificial intelligence and machine learning has grown significantly in recent years. Well-known applications include language translation and image recognition. It has also been successfully applied to fluid mechanics, while a limited number of recent studies have used machine learning for inertial microfluidic studies. I will discuss the current state-of-the-art for inertial microfluidics and machine learning in Section 4.1. In Section 4.2 I will provide an overview of how machine learning has been applied to the broader field of fluid mechanics, and the potential avenues for cross-exploitation in inertial microfluidics before briefly discussing some of the challenges that must be overcome in order to apply machine learning to inertial microfluidics in Section 4.3.
4.1 State-of-the-art in machine learning applied to inertial microfluidics
Machine learning is a branch of artificial intelligence where algorithms are developed to solve problems that would be too costly to solve via human-developed algorithms. Artificial neural networks (ANNs) are an increasingly popular method for machine learning and have been shown to perform well. ANNs evaluate example data, referred to as “training data,” recognise patterns and learn to complete a task, often without the need for further instruction. The interested reader is directed to detailed review of ANN methodology and their applications (Abiodun et al., 2019).
While the use of machine learning has yet to be fully exploited in inertial microfluidics, some recent papers have successfully explored its potential applications in this field. Su et al. (2021) used an ANN to provide fast predictions of inertial lift forces on rigid, spherical particles through straight channels with rectangular, triangular or semi-circular cross-sections. These inertial lift force predictions were integrated into a reduced-order simulation to estimate the lateral equilibrium position of a given particle size, channel aspect ratio and flow Reynolds number without directly modelling the particle itself. As a result, computational time and cost is significantly reduced in comparison to a simulation where the particle is fully resolved. ANNs have also been used in the prediction of microcirculatory networks. Ebrahimi and Bagchi (2022) used particle resolved 3D simulations to train an ANN to provide time dependent flow behaviour and red blood cell distributions through capillary networks, accounting for the cell-cell interactions that are crucial to the network behaviour that traditional 1D network models omit.
Machine learning has also been used in the classification of measurements obtained through physical experiments of inertial microfluidics for disease diagnosis. Guillou et al. (2021) used a bespoke inertial device to identify different mechanical properties in white blood cells. Based on these properties, they used a logistic regression model to determine the likelihood of sepsis. This device has recently obtained FDA approval and is currently used in clinical practice (Sorrells et al., 2023).
4.2 The potential for cross-exploitation of machine learning in fluid mechanics and inertial microfluidics
The integration of machine learning with numerical modelling and CFD in particular, has surged in recent years. A number of different machine learning methods exist and have been successfully integrated into various fluid mechanics-based applications as shown in Figure 5. Here I focus on two promising areas where machine learning can be applied in inertial microfluidics: fast flow field prediction and design parameter optimisation. Readers who are interested in a broader discussion of machine learning application to fluid mechanics are directed to a recent review of the subject (Brunton et al., 2020). I first focus on fast flow-field predictions.
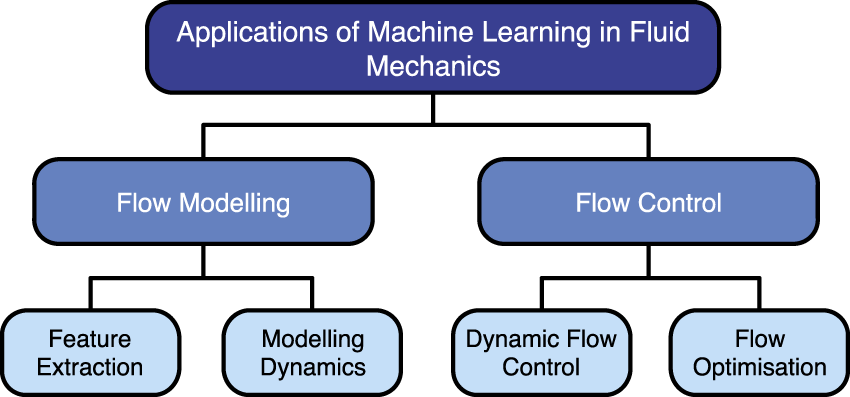
FIGURE 5. Areas where machine learning has been applied to fluid mechanics.
A popular method for fast flow field predictions is physics-informed neural networks (PINNs). PINNs allow for the governing physical equations to be integrated into neural network training so that they are trained to satisfy both the governing equations and training data, resulting in smaller training dataset size requirements. PINNs have successfully been applied to a range of applications within fluid mechanics such as supersonic flows and thrombus formation (Cai et al., 2021). Application of PINNs to inertial microfluidics could allow the simulation of scenarios that would be too computationally expensive to predict via numerical modelling alone. Examples include the particle-resolved dense suspension flows and complex geometries where periodic boundary conditions cannot be exploited.
The second promising area for the application of machine learning algorithms in inertial microfluidics is design parameter optimisation. By coupling fast flow-field predictions with reward-based learning algorithms, is it possible to explore parameter spaces significantly larger than is realistic via numerical modelling alone, allowing multiple coupled parameters to be explored simultaneously. Rabault et al. (2019) demonstrated this capability for flow control applications, using a deep-reinforcement and artificial neural network framework to optimise a time-dependent jet for drag reduction using a modest computation resources. Such a task would be prohibitively expensive via numerical modelling and parameter space exploration alone, even accounting for user expertise and prior knowledge in flow control.
4.3 Challenges when applying machine learning and numerical modelling to inertial microfluidics
While the advancement of the inertial microfluidic field with numerical modeling and machine learning algorithms is potentially transformative, developing such algorithms is non-trivial, with a number of challenges that must be overcome.
One significant challenge is the time and cost associated with generating datasets used to train the algorithms. In the case of unsupervised learning, where larger training datasets are often required, generating the dataset can often be prohibitive with access required to significant compute hardware for extended periods of time. For example, a typical particle-resolved simulation may take approximately 24 h using 36 cores on a high-performance computing cluster. For a training dataset of around 1,000 simulations, the datasets can easily exceed a year of total compute time with costs in excess of £15,000 (£0.02 per core hour). Given that the motivation for employing machine learning algorithms is often to reduce time and costs associated with individual simulations, it is important to identify applications where the training costs do not exceed the benefit of the machine learning algorithm output. While efforts have been made to reduce or transfer training data between models, for example Kim and Lee (2020) demonstrated that a neural network could accurately predict flow behavior in flow with Reynolds numbers three times larger than the datasets used to train the model, generating sufficient training data remains a significant barrier to overcome.
Key physical parameter identification is another challenge with the use of machine learning in inertial microfluidics. The underlying physical mechanisms in inertial microfluidics are not fully understood and are the subject of ongoing research. In particular, it may be the case that current numerical models are missing critical aspects of the physical model that are required to train machine learning algorithms. One such example is the representation of cells. Numerical models of red blood cells are relatively mature having been extensively investigated in other research fields (Owen et al., 2018). As a result, existing models that are representative of real-world behaviour can be exploited in inertial microfluidics. In comparison, white blood cells are more mechanically and geometrically complex than red blood cells to model with representative numerical models yet to be developed.
5 Conclusion
Inertial microfluidics is a method to manipulate particles based on their geometric and mechanical properties. Exploitation of the inertial forces allows for passive, label-free separation of particles based on their size, softness and shape, while maintaining cell viability for personalised therapeutics. The increased Reynolds number also brings the additional benefit enhancing throughput, making it possible to process larger samples efficiently.
Early efforts focused on physical experiments. However, in recent times interest in numerical modelling in inertial microfluidics has increased due to the complementary capabilities of physical experiments and numerical modelling. In particular, the ability of physical experiments to inherently represent the real-world is complemented by the ability of numerical models to access complete data sets for fluid and particle behaviour. Such behaviour is dependent on a large number key parameters such as geometric and mechanical fluid and particle properties. Numerical modelling has the ability to model non-physical scenarios in order to isolate the effects of individual parameters. It also has the ability to perform large parameter space studies to identify trends and underlying mechanisms. However, when the effects of multiple parameters are coupled, such parameter space studies can become prohibitively large.
Machine learning algorithms have been subject to significant interest in many applications including fluid mechanics. Recent studies have demonstrated that machine learning is able to provide fast flow field predictions and to optimise parameters for a given target performance within a system. These capabilities have yet to be fully exploited within inertial microfluidics. However, they have the potential to allow for multiple coupled parameters to be explored simultaneously, providing fast prediction of the flow field, reducing computational time, and allowing larger parameter spaces to be explored. Machine learning also has the capability to identify underlying complex patterns, opening up the opportunity to identify previously unknown, underlying physical mechanisms and provide efficient device design optimisation. However, in order to fully realise the potential of machine learning algorithms, numerical models must be further developed to incorporate the key physical parameters that govern inertial mechanisms and be able to provide sufficient training data within a suitable time frame and budget.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
BO: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Project administration, Visualization, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article. BO is funded through by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (803553) and by the US-UK Fulbright Commission, All-Disciplines Fulbright Award.
Acknowledgments
The author would like thank Prof. Timm Krüger for his invaluable guidance and feedback.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The reviewer SRB declared a past co-authorship with the author BO to the handling editor.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Footnotes
1Number of IMF studies Scopus query: TITLE-ABS-KEY (“inertial microfluidics”) OR TITLE-ABS-KEY (“inertial focusing”) OR TITLE-ABS-KEY (“inertial migration”) OR TITLE-ABS-KEY (“inertial separation”) AND PUBYEAR
References
Abiodun, O. I., Kiru, M. U., Jantan, A., Omolara, A. E., Dada, K. V., Umar, A. M., et al. (2019). Comprehensive review of artificial neural network applications to pattern recognition. IEEE Access 7, 158820–158846. doi:10.1109/ACCESS.2019.2945545
Ashton, N., West, A., Lardeau, S., and Revell, A. (2016). Assessment of RANS and DES methods for realistic automotive models. Comput. Fluids 128, 1–15. doi:10.1016/j.compfluid.2016.01.008
Asmolov, E. S. (1999). The inertial lift on a spherical particle in a plane Poiseuille flow at large channel Reynolds number. J. Fluid Mech. 381, 63–87. doi:10.1017/S0022112098003474
Brunton, S. L., Noack, B. R., and Koumoutsakos, P. (2020). Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 52, 477–508. doi:10.1146/annurev-fluid-010719-060214
Cai, S., Mao, Z., Wang, Z., Yin, M., and Karniadakis, G. E. (2021). Physics-informed neural networks (PINNs) for fluid mechanics: a review. Acta Mech. Sin. 37, 1727–1738. doi:10.1007/s10409-021-01148-1
Chun, B., and Ladd, A. J. (2006). Inertial migration of neutrally buoyant particles in a square duct: an investigation of multiple equilibrium positions. Phys. Fluids 18, 2176587. doi:10.1063/1.2176587
De Angelis, M. L., Francescangeli, F., Nicolazzo, C., Signore, M., Giuliani, A., Colace, L., et al. (2022). An organoid model of colorectal circulating tumor cells with stem cell features, hybrid EMT state and distinctive therapy response profile. J. Exp. Clin. Cancer Res. 41, 86–15. doi:10.1186/s13046-022-02263-y
Di Carlo, D., Irimia, D., Tompkins, R. G., and Toner, M. (2007). Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. 104, 18892–18897. doi:10.1073/pnas.0704958104
Ebrahimi, S., and Bagchi, P. (2022). Application of machine learning in predicting blood flow and red cell distribution in capillary vessel networks. J. R. Soc. Interface 19, 20220306. doi:10.1098/rsif.2022.0306
Guastoni, L., Güemes, A., Ianiro, A., Discetti, S., Schlatter, P., Azizpour, H., et al. (2021). Convolutional-network models to predict wall-bounded turbulence from wall quantities. J. Fluid Mech. 928, A27. doi:10.1017/jfm.2021.812
Guillou, L., Sheybani, R., Jensen, A. E., Di Carlo, D., Caffery, T. S., Thomas, C. B., et al. (2021). Development and validation of a cellular host response test as an early diagnostic for sepsis. PLoS ONE 16, e0246980. doi:10.1371/journal.pone.0246980
Hewitt, S., Margetts, L., and Revell, A. (2017). Building a digital wind farm. Archives Comput. Methods Eng. 25, 879–899. doi:10.1007/s11831-017-9222-7
Kahkeshani, S., Haddadi, H., and Di Carlo, D. (2016). Preferred interparticle spacings in trains of particles in inertial microchannel flows. J. Fluid Mech. 786, R3. doi:10.1017/jfm.2015.678
Kilimnik, A., Mao, W., and Alexeev, A. (2011). Inertial migration of deformable capsules in channel flow. Phys. Fluids 23, 3664402. doi:10.1063/1.3664402
Kim, J., and Lee, C. (2020). Prediction of turbulent heat transfer using convolutional neural networks. J. Fluid Mech. 882, A18. doi:10.1017/jfm.2019.814
Krüger, T., Kaoui, B., and Harting, J. (2014). Interplay of inertia and deformability on rheological properties of a suspension of capsules. J. Fluid Mech. 751, 725–745. doi:10.1017/jfm.2014.315
Lashkaripour, A., Rodriguez, C., Ortiz, L., and Densmore, D. (2019). Performance tuning of microfluidic flow-focusing droplet generators. Lab a Chip 19, 1041–1053. doi:10.1039/C8LC01253A
Martel, J. M., and Toner, M. (2014). Inertial focusing in microfluidics. Annu. Rev. Biomed. Eng. 16, 371–396. doi:10.1146/annurev-bioeng-121813-120704
Morris, P. D., Narracott, A., von Tengg-Kobligk, H., Silva Soto, D. A., Hsiao, S., Lungu, A., et al. (2016). Computational fluid dynamics modelling in cardiovascular medicine. Heart 102, 18–28. doi:10.1136/heartjnl-2015-308044
Owen, B., Bojdo, N., Jivkov, A., Keavney, B., and Revell, A. (2018). Structural modelling of the cardiovascular system. Biomechanics Model. Mechanobiol. 17, 1217–1242. doi:10.1007/s10237-018-1024-9
Owen, B., Kechagidis, K., Bazaz, S. R., Enjalbert, R., Essmann, E., Mallorie, C., et al. (2023). Lattice-Boltzmann modelling for inertial particle microfluidics applications -A tutorial review. Adv. Phys. X 8, 2246704. doi:10.1080/23746149.2023.2246704
Owen, B., and Krüger, T. (2022). Numerical investigation of the formation and stability of homogeneous pairs of soft particles in inertial microfluidics. J. Fluid Mech. 937, A4–A31. doi:10.1017/jfm.2022.85
Palumbo, J., Navi, M., Tsai, S. S., Spelt, J. K., and Papini, M. (2020). Inertial particle separation in helical channels: a calibrated numerical analysis. AIP Adv. 10, 0030930. doi:10.1063/5.0030930
Prohm, C., and Stark, H. (2014). Feedback control of inertial microfluidics using axial control forces. Lab a Chip 14, 2115–2123. doi:10.1039/c4lc00145a
Rabault, J., Kuchta, M., Jensen, A., Réglade, U., and Cerardi, N. (2019). Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 865, 281–302. doi:10.1017/jfm.2019.62
Razavi Bazaz, S., Mashhadian, A., Ehsani, A., Saha, S. C., Krüger, T., and Ebrahimi Warkiani, M. (2020). Computational inertial microfluidics: a review. Lab a Chip 20, 1023–1048. doi:10.1039/c9lc01022j
Sarker, I. H. (2021). Machine learning: algorithms, real-world applications and research directions. SN Comput. Sci. 2, 160–221. doi:10.1007/s42979-021-00592-x
Schaaf, C., Rühle, F., and Stark, H. (2019). A flowing pair of particles in inertial microfluidics. Soft Matter 15, 1988–1998. doi:10.1039/C8SM02476F
Schaaf, C., and Stark, H. (2020). Particle pairs and trains in inertial microfluidics. Eur. Phys. J. E 43, 50. doi:10.1140/epje/i2020-11975-6
Segre, G., and Silberberg, A. (1961). Radial particle displacements in Poiseuille flow of suspensions. Nature 189, 209–210. doi:10.1038/189209a0
Shahrivar, K., and Del Giudice, F. (2022). Beating Poisson stochastic particle encapsulation in flow-focusing microfluidic devices using viscoelastic liquids. Soft Matter 18, 5928–5933. doi:10.1039/d2sm00935h
Sorrells, M. G., Seo, Y., Magnen, M., Broussard, B., Sheybani, R., Shah, A. M., et al. (2023). Biophysical changes of leukocyte activation (and NETosis) in the cellular host response to sepsis. Diagnostics 13, 1435. doi:10.3390/diagnostics13081435
Su, J., Chen, X., Zhu, Y., and Hu, G. (2021). Machine learning assisted fast prediction of inertial lift in microchannels. Lab a Chip 21, 2544–2556. doi:10.1039/d1lc00225b
Wu, C., Wei, X., Men, X., Xu, Y., Bai, J., Wang, Y., et al. (2023). Open flow cytometer with the combination of 3D hydrodynamic single cell focusing and confocal laser-induced fluorescence detection. Talanta 258, 124424. doi:10.1016/j.talanta.2023.124424
Zhou, J., Kulasinghe, A., Bogseth, A., O’Byrne, K., Punyadeera, C., and Papautsky, I. (2019). Isolation of circulating tumor cells in non-small-cell-lung-cancer patients using a multi-flow microfluidic channel. Microsystems Nanoeng. 5, 8. doi:10.1038/s41378-019-0045-6
Keywords: particle separation, particle focusing, physics-informed neural networks, reinforcement learning, disease diagnostics
Citation: Owen B (2024) Accelerating the development of inertial microfluidic devices using numerical modelling and machine learning. Front. Lab. Chip. Technol. 3:1328004. doi: 10.3389/frlct.2024.1328004
Received: 25 October 2023; Accepted: 16 January 2024;
Published: 02 February 2024.
Edited by:
David Collins, The University of Melbourne, AustraliaReviewed by:
Sajad Razavi Bazaz, Children’s Cancer Institute, AustraliaCopyright © 2024 Owen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Benjamin Owen, benjamin.owen@ed.ac.uk