- 1Department of Psychology, Vanderbilt University, Nashville, TN, United States
- 2Department of Biological Sciences, Vanderbilt University, Nashville, TN, United States
- 3Vanderbilt Brain Institute, Vanderbilt University, Nashville, TN, United States
We report in a companion paper that in the mouse brain, in contrast to the 1,000-fold variation in local neuronal densities across sites, capillary density (measured both as capillary volume fraction and as density of endothelial cells) show very little variation, of the order of only fourfold. Here we confirm that finding in the rat brain and, using published rates of local blood flow and glucose use at rest, proceed to show that what small variation exists in capillary density across sites in the rat brain is strongly and linearly correlated to variations in local rates of brain metabolism at rest. Crucially, we show that such variations in local capillary density and brain metabolism are not correlated with local variations in neuronal density, which contradicts expectations that use-dependent self-organization would cause brain sites with more neurons to have higher capillary densities due to higher energetic demands. In fact, we show that the ratio of endothelial cells per neuron serves as a linear indicator of average blood flow and glucose use per neuron at rest, and both increase as neuronal density decreases across sites. In other words, because of the relatively tiny variation in capillary densities compared to the large variation in neuronal densities, the anatomical infrastructure of the brain is such that those sites with fewer neurons have more energy supplied per neuron, which matches a higher average rate of energy use per neuron, compared to sites with more neurons. Taken together, our data support the interpretation that resting brain metabolism is not demand-based, but rather limited by its capillary supply, and raise multiple implications for the differential vulnerability of diverse brain areas to disease and aging.
Introduction
The brain, which together with the liver is the most energy-consuming organ in the human body, maintains its functionality through a nearly constant supply of energy through its circulatory system (Aschoff et al., 1971; Mintun et al., 2002), even as variations in neuronal activity cause local changes in rate of blood flow and ensuing rates of energy use (Kety, 1956; Iadecola, 2017). While such local changes are consistent with the dominant demand-based view of brain metabolism, according to which the increasing requirements for energy posed by increasing levels of neuronal activity are met by increased energy supply (based on the seminal findings of Attwell and Laughlin (2001)), the demand-based framework fails to explain how come local increases in rates of energy supply and use do not translate into overall, brain-wide increases in energy supply and use. Instead, local increases in neuronal firing activity and ensuing rates of energy supply and use are always accompanied by decreases elsewhere in the brain, such that overall, the blood supply and energy economy of the brain as a whole remains stable over time (Mintun et al., 2002).
Such a trade-off in activity across brain sites would be possible if there were a third party governing energy demands and allocation at all times, one that decreases energy allocation to one site as it increases energy allocation to another. Such a scenario seems unlikely in the highly distributed system that is the mammalian brain.
A much simpler alternative is that blood circulation in the brain works as a closed system, as it does in the body as a whole, with no variation in circulating blood volume, such that increased circulation to one part happens at the expense of decreased circulation to another part. The simplest scenario in which the brain would operate as one such closed system, with limited blood resources in the form of a constant rate of blood flow, is one where the brain functions at near capacity already at “rest” (Herculano-Houzel and Rothman, 2022). The anatomical circumstances that would allow near-capacity function at rest would occur in any organ whose capillaries were always patent – unlike in skeletal muscle, the gastrointestinal tract, or the penis, for example, where massive capillary recruitment parallels variations in activity (Shepherd, 1982; Andersson, 2011; Skattebo et al., 2020). Indeed, the brain is one such organ with a constitutively patent capillary bed, where variations in sleep-waking states and in levels of waking activity occur with hardly any significant capillary recruitment (Kuschinsky and Paulson, 1992; Zoccoli et al., 1996; Jesperson and Ostergaard, 2012).
We propose in an accompanying manuscript a new framework of brain metabolism that views energy use in the brain as constitutively near maximum and constrained by blood supply to brain tissue, whose rate is ultimately limited by the density of capillaries in the brain (Krogh, 1919; Gjedde, 2005; Herculano-Houzel and Rothman, 2022). In a previous study, we found that capillary densities in the mouse brain are not variable in coordination with neuronal densities across sites, a finding that refutes a basic expectation of the demand-based view of brain metabolism1, but only supports a supply-limited framework if local capillary densities are found to correlate strongly, and linearly, with local rates of blood flow. Moreover, while the demand-based view of brain metabolism predicts local rates of blood flow and energy use to correlate with neuronal densities, our supply-limited view predicts independence between neuronal local densities and metabolic rates.
Previous studies showed that local capillary densities indeed correlate strongly, and linearly, with local rates of blood flow, with highest rates and densities in the inferior colliculus and lowest in the white matter (Klein et al., 1986; Borowsky and Collins, 1989). Here we determine capillary densities (measured both as capillary volume fraction and as endothelial cell densities) in different anatomically identified areas of the rat brain and compare those densities to reported measurements of local blood flow and rate of glucose use in matching areas. We find that local capillary densities, but not neuronal densities, are indeed a strong and linear predictor of local rates of blood flow and glucose use in the resting rat brain, meeting the necessary condition for a supply-limited framework of brain metabolism.
Materials and Methods
Experimental Design
Our goal with this study was simply to determine whether local variations in capillary density across sites in the rat brain correlate closely with local variations in rate of glucose use at rest reported in the literature. To this end, therefore, only cell densities and capillary density (measured as capillary volume fraction) are required, not absolute quantities. We used structured illumination confocal imaging under high magnification to allow quantification of cell and capillary densities in thin optical sections of multiple structures in the brain of three adult Sprague-Dawley rats. This approach is based on our finding in an accompanying paper that 2D and 3D quantifications of cellular density and capillary fraction give equivalent results, with similarly strong relationships between capillary density and capillary fraction, and across densities of the different cell types (Ventura-Antunes and Herculano-Houzel, in review), and leverages the efficiency of using 2D analysis with the high resolution and thin optical section provided by high magnification with a 63x objective in confocal imaging. Structures were chosen to match locations, listed in Table 1, with measured local rates of glucose use and/or blood flow at rest reported in the literature (Sokoloff et al., 1977; McCulloch et al., 1982; Nakai et al., 1983; Gjedde and Diemer, 1985; Levant and Pazdernik, 2004). These reports in the literature, in turn, were selected for their use of similar methods, and for their reasonably extensive analysis of multiple, and overlapping, brain sites, necessary for the present analysis. Brain capillaries were revealed by immunohistochemistry against collagen IV, which labels the basal lamina of blood vessels. Immunohistochemistry against the neuronal marker NeuN (Mullen et al., 1992) was used to reveal neurons; glial cells were identified by exclusion of neurons and capillary-associated cells from the total number of cell nuclei visualized with DAPI. In each location, we quantified capillary area fraction (which is identical to volume fraction), densities of neurons, glial, and capillary-associated (heretofore “endothelial”) cells. Analysis consisted of determining whether those variables were correlated with reported rates of glucose use at rest across locations and animals.
Experimental Animals
We obtained three brains of adult male Sprague-Dawley rats from BrainBits (Springfield, IL, United States). According to the supplier, animals were aged 2–2.5 months, weighed 300-400 g, and were housed in a thermally controlled environment at 27°C with ad libitum access to chow and water. We opted to only examine male animals for consistency given resource limitations that precluded inclusion of sufficient numbers of both males and females for relevant comparison in this study. The animals were perfused through the heart with 0.9% saline, followed by 4% paraformaldehyde in phosphate buffer, and shipped in 4% paraformaldehyde. Brains were washed in 0.1M phosphate buffer then immersed for 2 days in 30% sucrose in 0.1M phosphate buffer for cryoprotection. Using a sliding microtome (American Optical Corp., Southbridge, MA, United States, Model 860), the ensemble of cerebellum and brainstem were cut into a series of 50 μm thick sagittal sections, and the remaining cerebrum was cut into a series of 50 μm coronal sections. All sections were stored at –20°C in antifreeze solution (30% polyethylene glycol and 30% glycerol in 0.1 M phosphate buffer) until use.
Immunofluorescence
One in every eight sections of the cerebrum and one in four of the cerebellum and brainstem were subjected to immunohistochemistry with anti-NeuN antibody to reveal neurons, anti-collagen IV to reveal cells intimately associated with capillaries (vascular fraction), and counterstaining with DAPI (Figures 1A–C). Nuclei that overlapped with capillaries were considered “endothelial cells”; by elimination, cells without anti-NeuN and anti-Collagen IV labeling were counted as glial cells (Figure 1D).
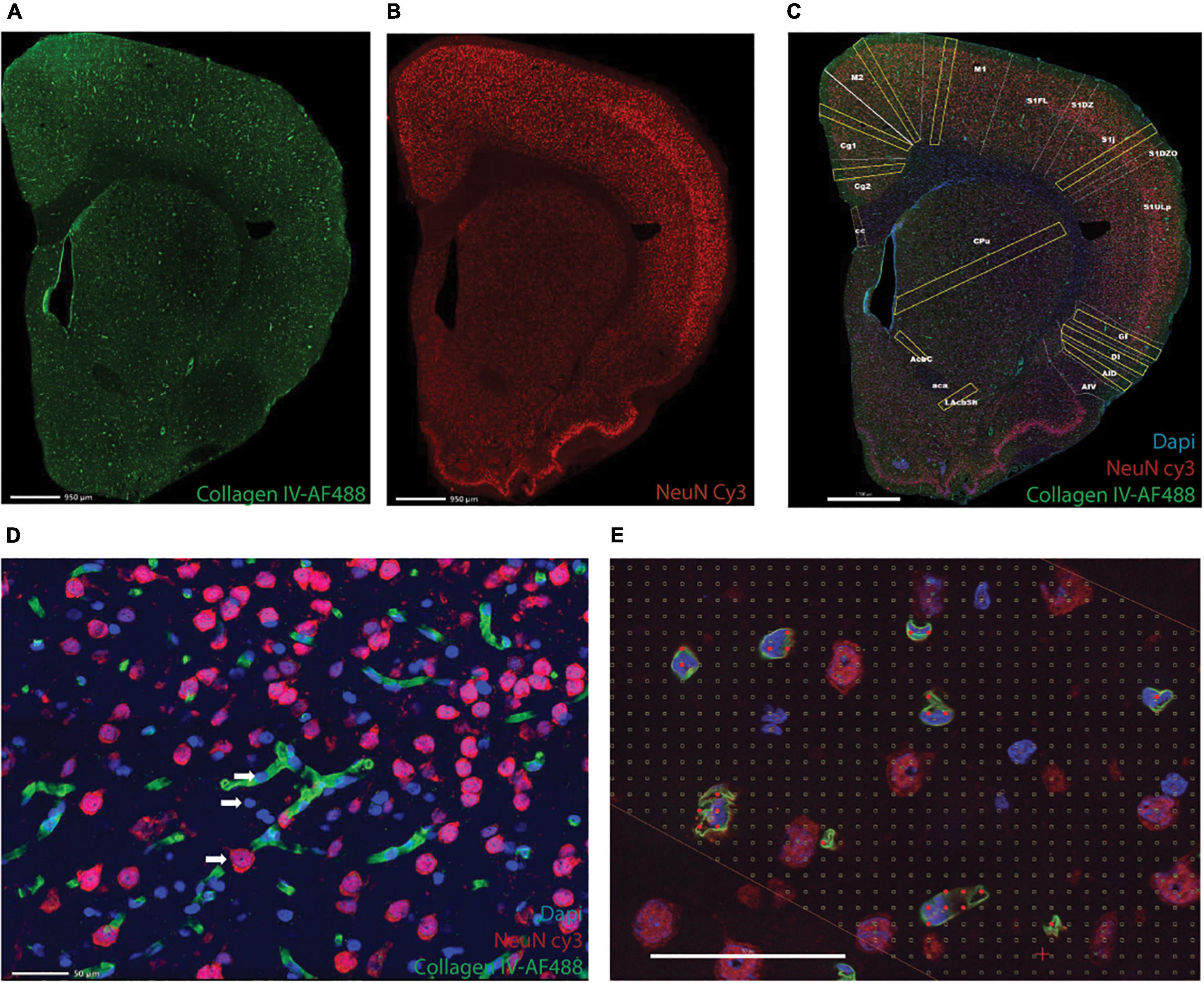
Figure 1. Triple labeling reveals microvasculature, neurons, and all cell nuclei. Shown is an example of a full image montage acquired at 5x magnification of a coronal section of the rat cerebrum labeled with AF 488-anti-collagen IV to reveal microvasculature (A), Cy3-anti-NeuN to reveal neuronal nuclei (B), and counterstained with DAPI to reveal all cell nuclei (C, merged images). Scale bars in (A–C), 950 μm. (D) Example of an area inside one of the ROIs in (C), imaged using a 63x objective to reveal neurons (red), microvasculature and associated cells (endothelial cell nuclei, in blue, juxtaposed to capillaries, in green), and glial cells (blue). (E) Example of a Cavalieri grid used to estimate the microvascular fraction in each ROI. Scale bars in (D,E) 50 μm.
Each section was washed in phosphate buffer (PB), heated for 1 h at 70°C in a 0.1 M solution of boric acid, pH 9.0, then incubated in blocking buffer [phosphate buffer containing 3% normal goat serum (Sigma-Aldrich, Saint Louis, MO, United States, LG9023) and 2% bovine serum albumin (Sigma-Aldrich- A2058)] for 1 h. Sections were then incubated during 48 h at 4°C in blocking buffer containing rabbit polyclonal anti-collagen IV antibody (Abcam, Boston, MA, United States, Ab6586) at a 1:500 dilution, followed by 2 h at 4°C in a 1:500 dilution of Alexa Fluor 488 goat anti-rabbit secondary antibody (Abcam, Ab150077). Sections were only then stained with Cy3-conjugated rabbit anti-NeuN primary polyclonal antibody (Millipore, Burlington, MA, United States, ABN78C3) diluted 1:500 in PB, during 72 h at 4°C under continuous stirring. All sections were labeled with DAPI (4’,6-Diamidino-2-Phenylindole Dilactate, from stock solution at 20 mg/l) to provide counterstaining for identification of brain structures and allow visualization of all cell nuclei in each section. The sections were then mounted on glass slides and coated with Vectashield (Vector Labs, Burlingame, CA, United States, Cat. number H-1400) for viewing under fluorescence microscopy.
Microscopy
Two-dimensional montages of the entirety of each processed brain section were acquired under magnification with a 5x objective for documentation and careful matching to an atlas (Paxinos and Watson, 2006) for the placement of regions of interest (ROIs). These ROIs, delineated as detailed below, were then imaged at 63x magnification (Plan-ApoChromat objective), which gives a depth of field of 0.5 μm with oil and an optical plane of 0.5 μm, using two Zeiss AxioImager M2 microscopes equipped with Apotome 2 structured illumination (Carl Zeiss, Jena, Germany) operated by StereoInvestigator software (Williston, VT, United States). A total of 135 sections were imaged for the cerebrum and cerebellum/brainstem of three rat brains, respectively: 31 and 23 sections in rat 01, 20 and 17 sections in rat 02, and 31 and 13 sections in rat 03.
Structures Analyzed
In each of the three rats, we analyzed a total of 53 brain structures in the cerebrum, midbrain, hindbrain and cerebellum (listed in Table 1). In the composite micrograph of each section, we drew a rectangle as long as necessary to span the entirety of each recognizable target structure, taking care to avoid any vessels obviously larger than capillaries. Rectangles placed in cortical structures were at least 0.5 mm wide at the pial surface. Each of these rectangles constituted one ROI. A total of 1734 ROIs were imaged initially across the three animals (respectively, 1,167, 236, and 330), then an additional 392 ROIs were placed in the three animals (respectively, 131, 131, and 130) in 22 structures matching those with reported rates of blood flow and glucose use at rest reported in the literature (Sokoloff et al., 1977; McCulloch et al., 1982; Nakai et al., 1983; Gjedde and Diemer, 1985; Levant and Pazdernik, 2004).
Estimates of local cell densities were obtained by classifying and counting every DAPI-labeled cell contained in each ROI exclusively as neuronal (if it expressed NeuN), “endothelial” (if it did not express NeuN and, was immediately associated with collagen IV-labeled capillaries), or glial (if it neither expressed NeuN nor was immediately associated with capillaries). Numbers of cells were then divided by the area sampled.
Estimates of capillary fraction in the tissue were performed using a Cavalieri probe (Gundersen and Jensen, 1987) using StereoInvestigator software (Microbrightfield, Williston, VT). As established previously (see text footnote 1), a Cavalieri estimator grid with 4 microns distance between points was placed in each ROI for estimating the fractional area occupied by capillaries. Capillary fractional area (which we transformed into percentages) was calculated as the ratio between grid points in the ROI that fell on capillaries identified by anti-collagen IV staining (Figure 1E) and all points in the ROI.
Statistical Analysis
All analyses were performed in JMP14 PRO, using non-parametric Spearman correlation coefficients to test the correlation between variables, and least-squares regression of raw or log-transformed values to linear functions to determine the slope of power function relationships across variables.
Results
We first analyzed a total of 387,809 cells in 2,301 ROIs located in 53 structures in the brain of three rats. We find that across all 1,734 ROIs, microvasculature amounts to 3.36 ± 1.78% (mean ± standard deviation) of the area of the parenchyma in brain sections, and therefore presumably a similar 3.36 ± 1.78% of the volume of the parenchyma as well (Figure 2A). The standard deviation indicates a coefficient of variation of 53.0% around the mean capillary fraction across all sites, with 50% of sites with fractional microvasculature values between 2.06 and 4.37%. As we found in the mouse brain (Ventura-Antunes and Herculano-Houzel, in review), there is only a ca. fourfold variation in average local capillary fraction measured across structures (Table 1), from the lowest values in the white matter of the corpus callosum (1.27 ± 0.71%) and internal capsule (1.76 ± 0.45%) to the highest values in the superior olive (6.26 ± 1.53%), dentate nucleus of the cerebellum (5.80 ± 1.33%) and superior colliculus (4.21 ± 1.47%).
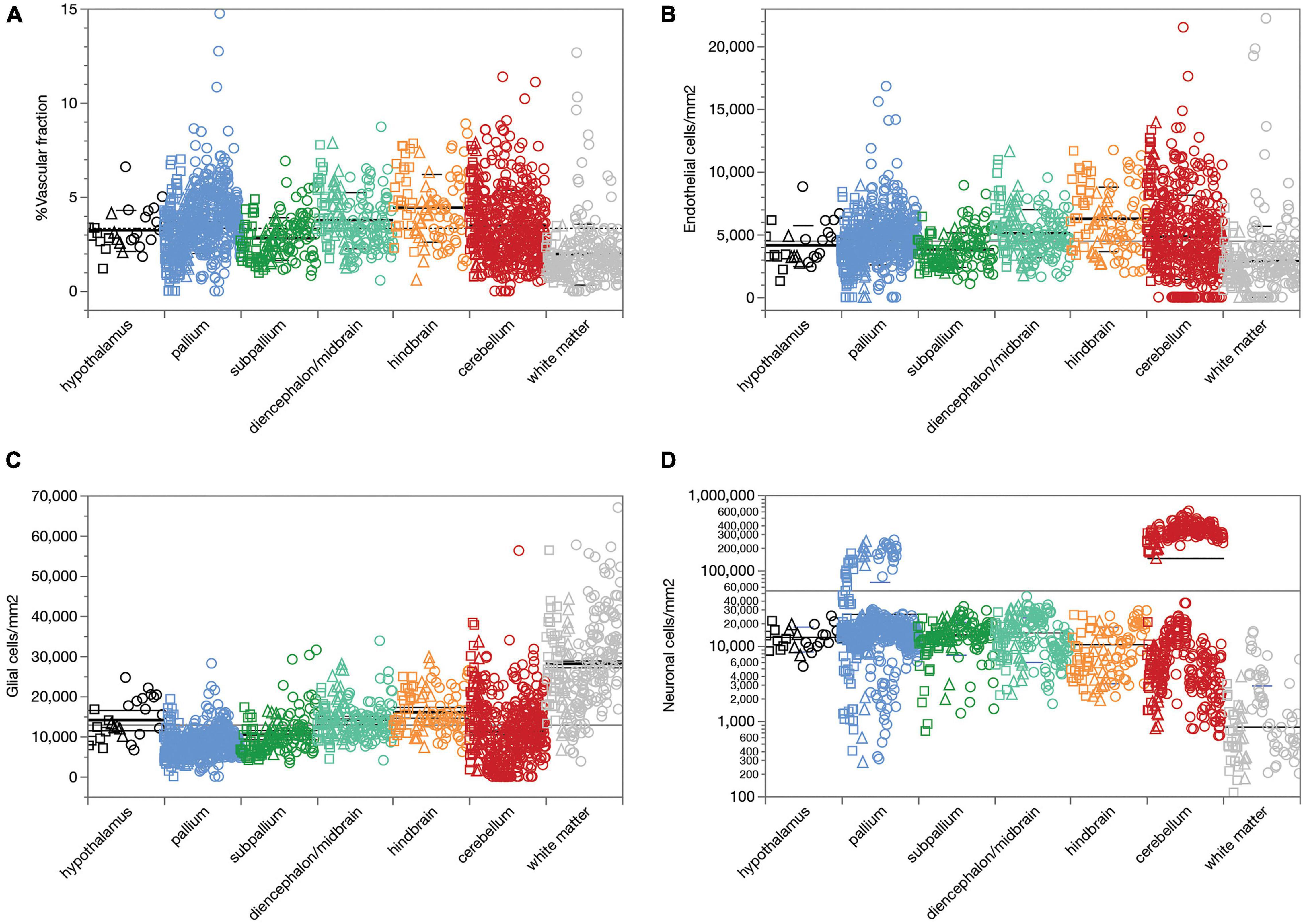
Figure 2. Average capillary fraction, in% of parenchyma surface or volume, and cellular densities across sites and structures in the different brain subdivisions of three rat brains. Different symbols indicate each of three animals (circles, squares, triangles). Bars indicate means and standard deviation for each brain subdivision; long line indicates grand mean across all sites. (A) Capillary fraction. Grand mean of 3.36 ± 1.78% (n = 1733 sites) indicated by dotted line. Means ± SD: hypothalamus, 3.22 ± 1.09% (n = 27 sites); pallium, 3.65 ± 1.63% (n = 587 sites); subpallium, 2.80 ± 1.13% (n = 133 sites); diencephalon/midbrain, 3.76 ± 1.49% (n = 165 sites); hindbrain, 4.42 ± 1.80% (n = 96 sites); cerebellum, 3.50 ± 1.89% (n = 494 sites); white matter, 1.96 ± 1.62% (n = 231 sites). (B) Endothelial cell densities. Means ± SD, cells/mm2: hypothalamus, 4,122 ± 1,633 (n = 27 sites); pallium, 4,609 ± 1,983 (n = 587 sites); subpallium, 3,797 ± 1,382 (n = 134 sites); diencephalon/midbrain, 5,100 ± 1,911 (n = 165 sites); hindbrain, 6,245 ± 2,572 (n = 96 sites); cerebellum, 4,817 ± 3,355 (n = 494 sites); white matter, 2,877 ± 2,820 (n = 231 sites). (C) Glial cell densities. Means ± SD, cells/mm2: hypothalamus, 14,602 ± 5,027 (n = 27 sites); pallium, 8,276 ± 3,171 (n = 587 sites); subpallium, 10,436 ± 4,961 (n = 134 sites); diencephalon/midbrain, 14,157 ± 4,649 (n = 165 sites); hindbrain, 16,024 ± 5,353 (n = 96 sites); cerebellum, 11,152 ± 8,010 (n = 494 sites); white matter, 28,047 ± 11,309 (n = 231 sites). (D) Neuronal cell densities. Means ± SD, cells/mm2: hypothalamus, 13,140 ± 4,753 (n = 27 sites); pallium, 26,463 ± 44,103 (n = 587 sites); subpallium, 14,135 ± 6,525 (n = 134 sites); diencephalon/midbrain, 14,950 ± 8,866 (n = 165 sites); hindbrain, 10,511 ± 7,343 (n = 96 sites); cerebellum, 146,162 ± 170,169 (n = 494 sites); white matter, 840 ± 2,130 (n = 231 sites).
We find that endothelial cells comprise 14.10 ± 9.11% of all cells and 30.36 ± 18.67% of the non-neuronal cells in the rat brain parenchyma, ranging between 10.88 ± 0.73% of all cells in the nucleus accumbens to 27.26 ± 1.85% in the molecular layer of the hippocampal dentate gyrus (Table 1). As in the mouse brain (Ventura-Antunes and Herculano-Houzel, in review), the percentage of cells in the rat parenchyma that compose the capillary bed is about threefold higher than the microvascular tissue fraction, which suggests that individual endothelial cells are on average smaller than neurons and non-neuronal cells in the tissue.
Similarly, we find that compared to neuronal densities, endothelial cell densities are very stable across structures in the rat brain, at an overall density of 4,504 ± 2,666 cells/mm2 across all 1,734 sites analyzed (Figure 2B). The standard deviation indicates a coefficient of variation (CV) of 59.0%, similar to the 53% found for mean capillary fraction, with 50% of the sites with endothelial cell densities between 2,834 and 5,737 cells/mm2. As found for capillary fraction, there is a relatively small, ca. 4.5-fold variation in local average endothelial cell densities measured across structures, from the lowest values in the corpus callosum (2,058 ± 1,311 cells/mm2) to the highest in the cerebellar dentate nucleus (9,620 ± 2,262 cells/mm2; Table 2). Glial cell densities are similarly consistent across structures, with an overall density of 12,975 ± 9,186 cells/mm2 across all 1,734 sites, 50% of sites with glial cell densities between 7,095 and 16,207, and a CV of 70.9%, with noticeably higher glial cell densities only in white matter structures (Figure 2C). In contrast, neuronal cell densities are enormously diverse, even when analysis is restricted to gray matter sites (although there are consistently detectable neurons in white matter structures). Overall, we find an average neuronal density of 54,012 ± 111,192 neurons/mm2, with a large CV of 205.9%, 50% of sites with neuronal densities between 3,780 and 20,246 neurons/mm2, and local averages ranging from as few as 794 ± 772 neurons/mm2 in the hippocampal CA1 to as many as 137,624 ± 65,597 and 337,953 ± 71,200 neurons/mm2 in the granular layers of the hippocampal dentate gyrus and cerebellar cortex (Table 2 and Figure 2D; notice the logarithmic scale, in comparison to the linear scale in Figures 2A–C).
Our estimates of the local capillary area fraction correlate strongly, and linearly, with endothelial cell density across all sites (Spearman correlation, ρ = 0.742, p < 0.0001; Figure 3A, linear fit, r2 = 0.457, p < 0.0001). Similarly strong correlations across all three animals examined are found for each brain subdivision (Figure 3A), which validates the use of endothelial cell density as a surrogate indicator of capillary density across all sites within the brain of a species.
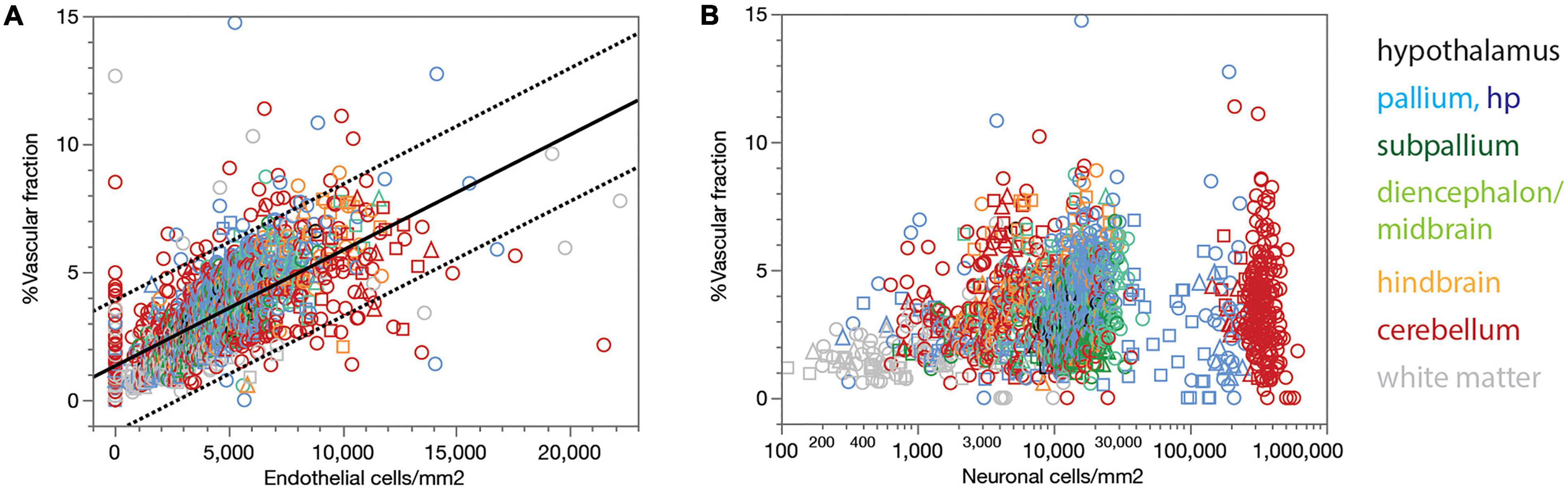
Figure 3. Local vascular fraction increases with endothelial cell density but does not accompany local neuronal density consistently across brain structures. (A) Local vascular fraction varies as a linear function of endothelial cell densities across all ROIs of all three animals, and also across sites within each brain subdivision. Spearman correlation across all sites: ρ = 0.742, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.790, p < 0.0001; pallium, ρ = 0.711, p < 0.0001; subpallium, ρ = 0.765, p < 0.0001; diencephalon/midbrain, ρ = 0.801, p < 0.0001; hindbrain, ρ = 0.806, p < 0.0001; cerebellum, ρ = 0.654, p < 0.0001; white matter, ρ = 0.670, p < 0.0001. (B) Local vascular fraction correlates significantly with local neuronal density across sites within several brain structures, but not consistently across structures, such that highly disparate neuronal densities occur with similar vascular fractions across structures. Spearman correlation across all sites: ρ = 0.286, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.437, p = 0.0226; non-hippocampal pallium, ρ = 0.419, p < 0.0001; whole pallium, ρ = 0.250, p < 0.0001; subpallium, ρ = 0.099, p = 0.2594; diencephalon/midbrain, ρ = 0.243, p = 0.0017; hindbrain, ρ = 0.248, p = 0.0005; cerebellum, ρ = 0.027, p = 0.5511; white matter, ρ = –0.002, p = 0.9766.
Although the microvasculature is the sole source of energy to neurons in the brain, we find that local capillary volume fraction is only poorly correlated with neuronal density across all brain sites (Spearman correlation, ρ = 0.286, p < 0.0001), and clearly not in a universal manner (Figure 3B). Besides the much larger variation in neuronal density than in capillary volume fraction, we find that neuronal densities spanning two orders of magnitude across structures occur with similar (and similarly small) capillary fractions (Figure 3B). Importantly, while significant positive correlations exist between local capillary fraction and neuronal density across sites within some structures, notably the hypothalamus and non-hippocampal pallium, they are not evident within all structures in the rat brain, and also not aligned across brain structures (Figure 3B).
Local endothelial cell densities, like local capillary volume fractions, are not consistently correlated with local neuronal densities across brain sites (Figure 4A). Although higher local neuronal densities are significantly positively correlated with higher local endothelial cell densities within several structures, notably the hypothalamus, non-hippocampal pallium and hindbrain (see figure legend), the correlation across all sites and structures is only poor. Indeed, the entire range of local neuronal densities occurs across structures in the rat brain that share similar endothelial cell densities (Figure 4A).
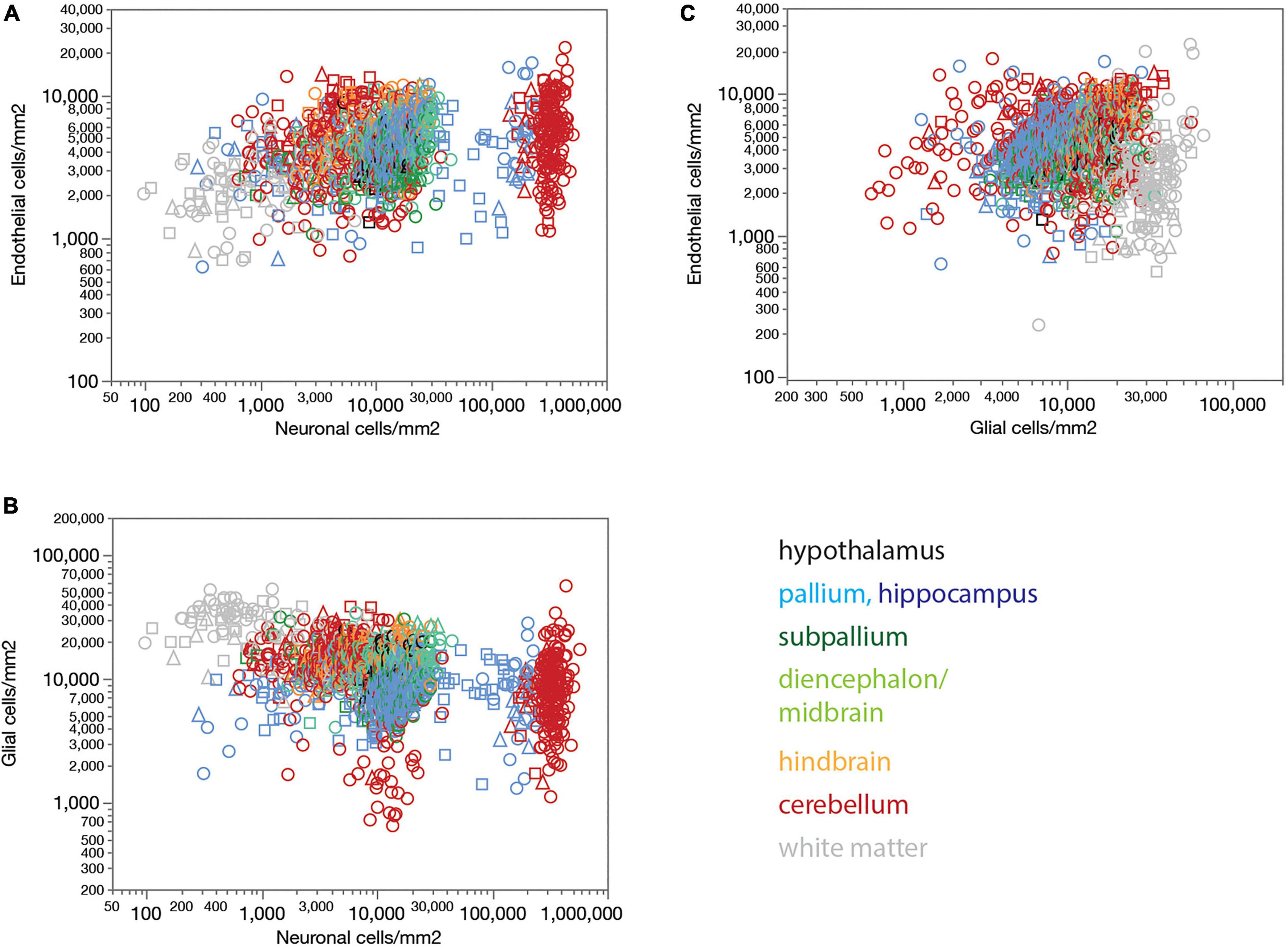
Figure 4. Endothelial, neuronal, and glial cell densities are not universally correlated across structures in the rat brain. (A) Local endothelial cell density correlates significantly with local neuronal density across sites within several brain structures, but not consistently across structures, such that highly disparate neuronal densities occur with similar endothelial cell densities across structures. Spearman correlation across all sites: ρ = 0.283, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.434, p = 0.0239; pallium, ρ = 0.332, p < 0.0001; non-hippocampal pallium, ρ = 0.484, p < 0.0001; subpallium, ρ = 0.195, p = 0.0242; diencephalon/midbrain, ρ = 0.369, p < 0.0001; hindbrain, ρ = 0.469, p < 0.0001; cerebellum, ρ = 0.053, p < 0.0001; white matter, ρ = –0.097, p = 0.1436. (B) Local glial cell density correlates significantly with local neuronal density across sites within several brain structures, but not consistently across structures, such that highly disparate neuronal densities occur with similar endothelial cell densities across structures. Spearman correlation across all sites: ρ = –0.420, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.392, p = 0.0432; pallium, ρ = 0.265, p < 0.0001; non-hippocampal pallium, ρ = 0.441, p < 0.0001; subpallium, ρ = –0.098, p = 0.2597; diencephalon/midbrain, ρ = 0.280, p = 0.0003; hindbrain, ρ = 0.322, p = 0.0014; cerebellum, ρ = –0.427, p < 0.0001; white matter, ρ = –0.128, p = 0.0529. (C) Local endothelial cell density correlates significantly with local glial density across sites within several brain structures, notably in the gray matter, but not consistently across structures. Spearman correlation across all sites: ρ = 0.057, p = 0.0182. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.748, p < 0.0001; pallium, ρ = 0.405, p < 0.0001; non-hippocampal pallium, ρ = 0.547, p < 0.0001; subpallium, ρ = 0.182, p = 0.0355; diencephalon/midbrain, ρ = 0.339, p < 0.0001; hindbrain, ρ = 0.554, p < 0.0001; cerebellum, ρ = 0.117, p < 0.0001; white matter, ρ = 0.113, p = 0.0854; non-cortical gray matter, ρ = 0.550, p < 0.0001.
Local glial cell densities are also much less variable than neuronal densities across brain structures and species. There is a detectable negative correlation between local glial and neuronal densities across all structures and animals in the whole dataset, but no consistent trend within each structure (Figure 4B). Moreover, correlations within brain structures have the opposite sign, with no shared, universal relationship between neuronal and glial cell densities. As found for local endothelial cell densities, the entire, wide range of local neuronal densities occurs across sites with similar local glial cell densities (Figure 4B).
Interestingly, while there is no detectable universal correlation between local glial and endothelial cell densities across all structures, densities of these two subtypes of non-neuronal cells are strongly correlated within and across gray matter structures, though not white matter structures (Figure 4C).
The lack of a universal correlation between local densities of endothelial cells (or vascular fraction) and neuronal densities across brain structures in the rat, combined with the relatively uniform densities of endothelial cells, results in a universal relationship between the ratio of endothelial cells per neuron (E/N) and local neuronal densities that span over three orders of magnitude across brain structures (Figure 5A). E/N values scale across structures, and even within each structure, accompanying local neuronal density, such that the lower the local density of neurons, the larger the E/N ratio (Figure 5A). Thus, in order of decreasing neuronal density, there are on average over 60 neurons per endothelial cell in the cerebellar granular layer (E/N 0.016 ± 0.012), 24 neurons per endothelial cell in the hippocampal granular layer of the dentate gyrus (E/N 0.042 ± 0.048), 3 neurons per endothelial cell in the hypothalamus and non-hippocampal pallium (E/N 0.355 ± 0.278, 0.339 ± 0.134, respectively), 2.5 neurons per endothelial cell in the subpallium (E/N 0.411 ± 0.511), 2 neurons per endothelial cell in the diencephalon/midbrain (E/N 0.483 ± 0.367), just over 1 neuron per endothelial cell in the hindbrain (E/N 0.875 ± 0.606), 1.218 ± 1.647 endothelial cells for every neuron in the cerebellar molecular layer, and 2.506 ± 2.897 endothelial cells for every neuron in hippocampal sites excluding the granular layer of the dentate gyrus.
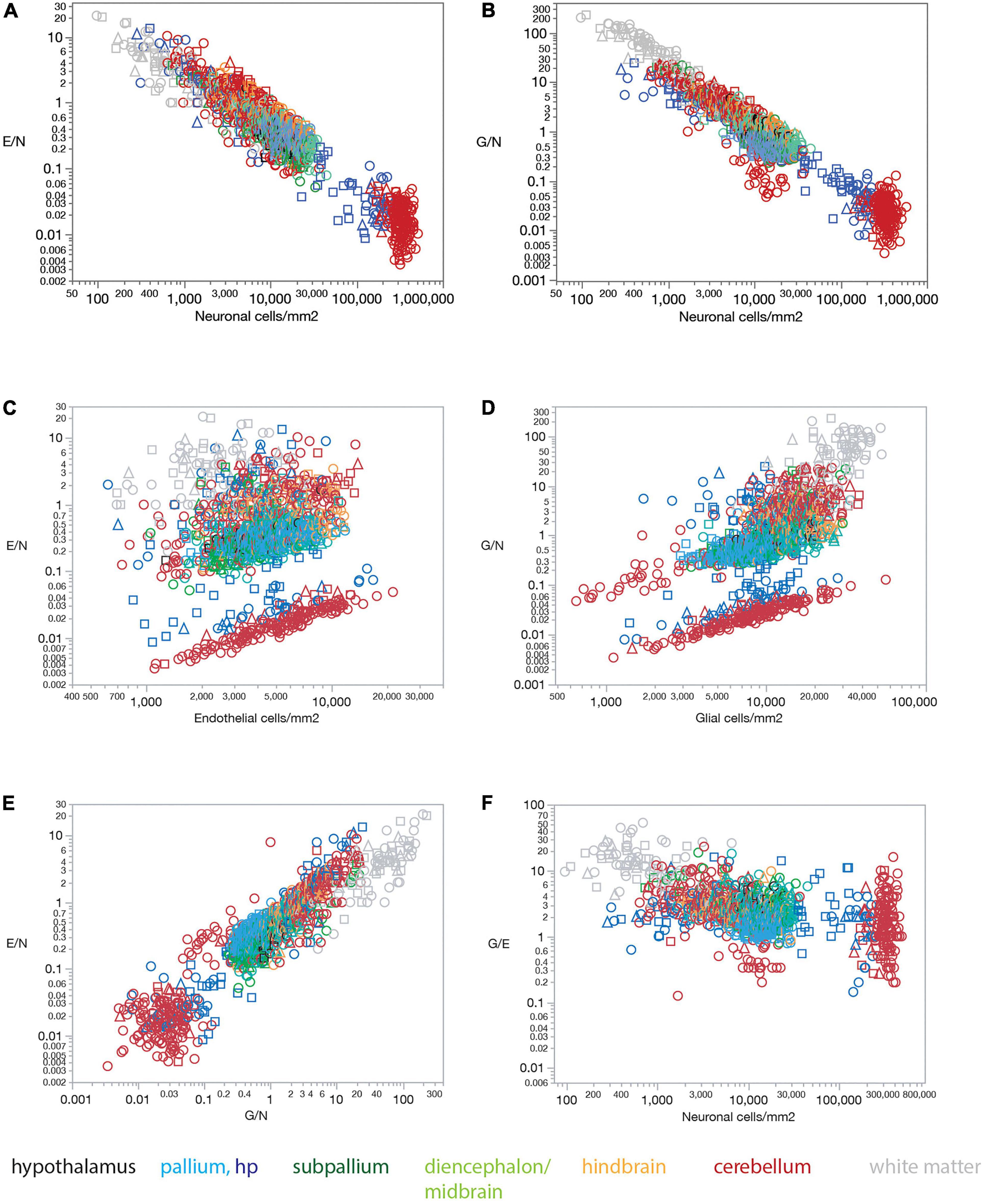
Figure 5. Ratios of endothelial and glial cells per neuron increase with decreasing local neuronal density across sites and structures in all three rat brains. (A) The ratio of endothelial cells per neuron E/N varies uniformly with neuronal density across brain sites and structures. Spearman correlation across all sites: ρ = –0.833, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = –0.451, p = 0.0182; pallium, ρ = –0.688, p < 0.0001; non-hippocampal pallium, ρ = –0.451, p < 0.0001; subpallium, ρ = –0.747, p < 0.0001; diencephalon/midbrain, ρ = –0.813, p < 0.0001; hindbrain, ρ = –0.847, p < 0.0001; cerebellum, ρ = –0.822, p < 0.0001; white matter, ρ = –0.867, p < 0.0001. (B) The ratio of glial cells per neuron G/N varies uniformly with neuronal density across brain sites and structures. Spearman correlation across all sites: ρ = –0.873, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = –0.496, p = 0.0085; pallium, ρ = –0.719, p < 0.0001; non-hippocampal pallium, ρ = –0.458, p < 0.0001; subpallium, ρ = –0.690, p < 0.0001; diencephalon/midbrain, ρ = –0.885, p < 0.0001; hindbrain, ρ = –0.907, p < 0.0001; cerebellum, ρ = –0.829, p < 0.0001; white matter, ρ = –0.953, p < 0.0001. (C) The ratio of endothelial cells per neuron E/N does not vary uniformly with endothelial cell density across brain sites and structures. Spearman correlation across all sites: ρ = 0.202, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.482, p = 0.0108; pallium, ρ = 0.310, p < 0.0001; non-hippocampal pallium, ρ = 0.507, p < 0.0001; subpallium, ρ = 0.419, p < 0.0001; diencephalon/midbrain, ρ = 0.192, p = 0.0133; hindbrain, ρ = 0.033, p = 0.7536; cerebellum, ρ = 0.411, p < 0.0001; white matter, ρ = 0.377, p = 0.0001. (D) The ratio of glial cells per neuron G/N does not vary uniformly with glial cell density across brain sites and structures. Spearman correlation across all sites: ρ = 0.664, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.507, p = 0.0069; pallium, ρ = 0.360, p < 0.0001; non-hippocampal pallium, ρ = 0.544, p < 0.0001; subpallium, ρ = 0.721, p < 0.0001; diencephalon/midbrain, ρ = 0.161, p = 0.0389; hindbrain, ρ = 0.063, p = 0.5401; cerebellum, ρ = 0.752, p < 0.0001; white matter, ρ = 0.586, p < 0.0001. (E) The ratio of endothelial cells per neuron E/N varies uniformly with the ratio of glial cells per neuron G/N across brain sites and structures. Spearman correlation across all sites: ρ = 0.834, p < 0.0001. Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.670, p < 0.0001; pallium, ρ = 0.747, p < 0.0001; non-hippocampal pallium, ρ = 0.574, p < 0.0001; subpallium, ρ = 0.705, p < 0.0001; diencephalon/midbrain, ρ = 0.803, p < 0.0001; hindbrain, ρ = 0.875, p < 0.0001; cerebellum, ρ = 0.736, p < 0.0001; white matter, ρ = 0.843, p < 0.0001. (F) The ratio of glial cells per endothelial cell G/E remains relatively constant across sites and brain subdivisions with different neuronal densities. Spearman correlation across all sites: ρ = –0.515, p < 0.0001 (average G/E, 3.854 ± 5.212). Spearman correlation within brain subdivisions: Hypothalamus, ρ = 0.012, p = 0.9542 (average G/E, 3.584 ± 1.011); pallium, ρ = –0.121, p = 0.0037 (average G/E, 1.994 ± 1.418); non-hippocampal pallium, ρ = –0.019, p = 0.6908 (average G/E, 1.780 ± 0.593); subpallium, ρ = –0.170, p = 0.0498 (average G/E, 3.139 ± 2.299); diencephalon/midbrain, ρ = –0.108, p = 0.1687 (average G/E, 3.122 ± 1.763); hindbrain, ρ = –0.263, p = 0.0095 (average G/E, 2.881 ± 1.332); cerebellum, ρ = –0.465, p < 0.0001 (average G/E, 2.769 ± 2.683); white matter, ρ = 0.008, p = 0.9032 (average G/E, 12.936 ± 9.692).
Similarly, and as reported previously (Herculano-Houzel, 2014), the lack of a universal correlation between local densities of glial and neuronal cell densities across brain structures in the rat, combined with the relatively uniform densities of glial cells, results in a universal relationship between the ratio of glial cells per neuron (G/N) and local neuronal densities across brain structures (Figure 5B).
In contrast, the ratio of endothelial cells per neuron (E/N) and the ratio of glial cells per neuron (G/N) fail to vary consistently with endothelial cell density (Figure 5C) or glial cell density (Figure 5D). Thus, we find that the lower the local density of neurons, the larger the E/N and G/N ratios (Figures 5A,B), in a manner that applies for grey matter structures, white matter structures, and both together. Such universality strongly supports and extends to the E/N ratio our previous model that proposes that with relatively constant densities of non-neuronal cells, the relevant variable for determining G/N is simply local neuronal density (Herculano-Houzel, 2014; Mota and Herculano-Houzel, 2014). Because local neuronal density correlates with the inverse of average local neuronal cell size (estimated for entire cells, including soma and all arbors; Mota and Herculano-Houzel, 2014), these findings imply that the fewer and larger neurons are at a brain site, the more endothelial and glial cells are available per neuron.
In further support of local neuronal densities as the sole, or main, variable of consequence to determining cell type ratios across brain sites, we find that local E/N and G/N ratios are strongly, directly, and universally correlated across brain sites, such that sites with lower neuronal densities (that is, larger neurons) have both more endothelial and glial cells for every neuron (Figure 5E). As expected from this finding that E/N and G/N increase together, the G/E ratio remains fairly constant across sites and structures as neuronal density varies, at an overall average of typically about 2–3 glial cells per endothelial cell in gray matter structures, except for a much larger ratio of 13 glial cells per endothelial cell in the white matter (Figure 5F).
Figure 6 shows that our findings also apply when data are averaged across all sites within each brain structure before analysis. Mean capillary fraction is strongly and linearly correlated with endothelial cell density across brain structures (Figure 6A), but there is only a weak correlation between either mean capillary fraction or mean endothelial cell density and mean neuronal density across structures (Figures 6B,C). This analysis also makes evident that while mean capillary fraction and endothelial cell densities are highest in hindbrain and cerebellar structures, and lowest in white matter structures (Figures 6A–C), there is at least a 30-fold variation in average neuronal density across structures whose mean average capillary fraction varies only twofold, between 2 and 4% of the tissue (Figure 6C). As a consequence of the much larger variation in neuronal density than in endothelial (or glial) cell density across brain structures, the E/N ratio decreases tightly together with increasing neuronal densities (Figure 6D), although with clearly larger E/N ratios in hindbrain and cerebellar structures (consistently with the larger vascular fraction of these structures), and E/N increases together with increasing G/N ratios across structures (Figure 6E), resulting in average G/E ratios of between 1.5 and 4 across structures (Figure 6F).
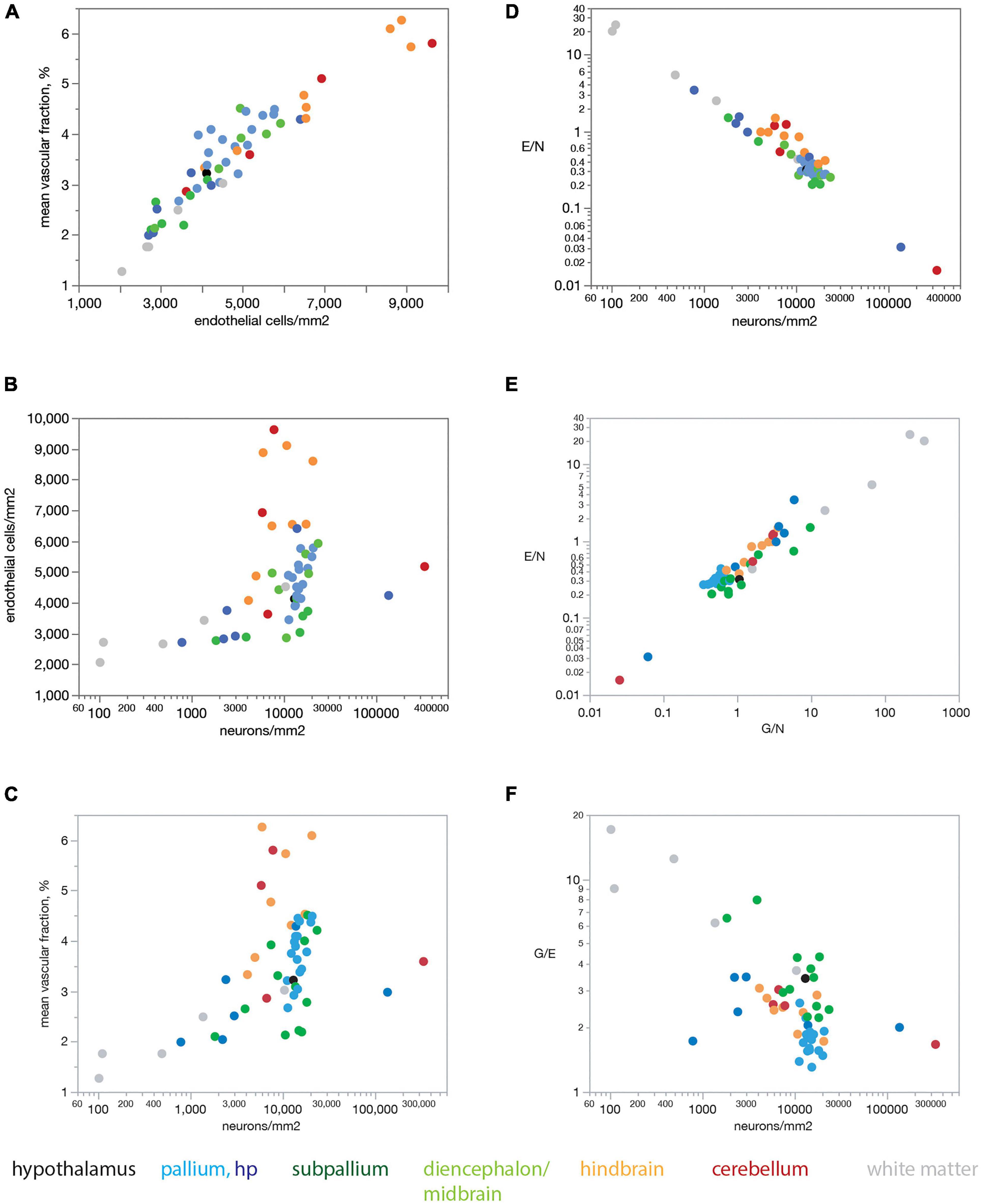
Figure 6. Mean endothelial cell densities correlate with mean capillary fraction but not neuronal density across structures in the rat brain, resulting in E/N ratios that correlate with neuronal density and G/N ratios across structures. Each point represents the average value for one of the brain structures as listed in Tables 1, 2. Data points are color-coded according to the key below the graphs. (A) Mean capillary fraction varies as a linear function of endothelial cell density across structures in the rat brain (Spearman correlation ρ = 0.936, p < 0.0001; linear fit, r2 = 0.888, p < 0.0001). (B) Weak correlation between mean endothelial cell density and mean neuronal density across structures in the rat brain (Spearman correlation ρ = 0.440, p = 0.0001). (C) Weak correlation between mean capillary fraction and mean neuronal density across structures in the rat brain (Spearman correlation ρ = 0.480, p = 0.0010). (D) Mean ratio of endothelial cells per neuron (E/N) decreases uniformly with increasing neuronal cell density across brain sites and structures (Spearman correlation ρ = –0.878, p < 0.0001; power fit, r2 = 0.943, p < 0.0001). (E) The ratio of endothelial cells per neuron E/N varies uniformly and linearly with the ratio of glial cells per neuron G/N across brain structures (Spearman correlation ρ = 0.860, p < 0.0001; power fit, r2 = 0.891, p < 0.0001). (F) The average ratio of glial cells per endothelial cell G/E is correlated with average neuronal densities across brain structures (Spearman correlation ρ = –0.550, p < 0.0001).
Endothelial cell densities and capillary volume fraction are easily quantified in fixed brains, and could constitute measurements of great scientific value for examining brain metabolism if they served as proxies of measurements of brain metabolism at rest that can only be obtained in living brains. To address this possibility, we compared data we acquired from 392 ROIs in 22 structures in the brains of three rats selected to match sites with published data of rates of blood flow and glucose use in the non-stimulated (“resting”) rat brain acquired in five independent studies (Sokoloff et al., 1977; McCulloch et al., 1982; Nakai et al., 1983; Gjedde and Diemer, 1985; Levant and Pazdernik, 2004). Figure 7 shows that local rates of resting glucose utilization measured with autoradiographic methods by other groups are strongly and consistently correlated with our measured local capillary fraction (Figure 7A) and endothelial cell densities (Figure 7B), even though the absolute values of local rates of glucose use disagree across studies (different colors in Figure 7). Importantly, we find that local rates of glucose use at rest are not significantly correlated with either neuronal (Figure 7C) or glial cell densities (Figure 7D) measured in the same locations in the rat brain. These data suggest that local endothelial cell densities and capillary fraction are valid proxies for local rates of glucose use in the rat brain at rest, and that these rates bear no relationship with the numbers of neurons or glial cells present in the volume measured.
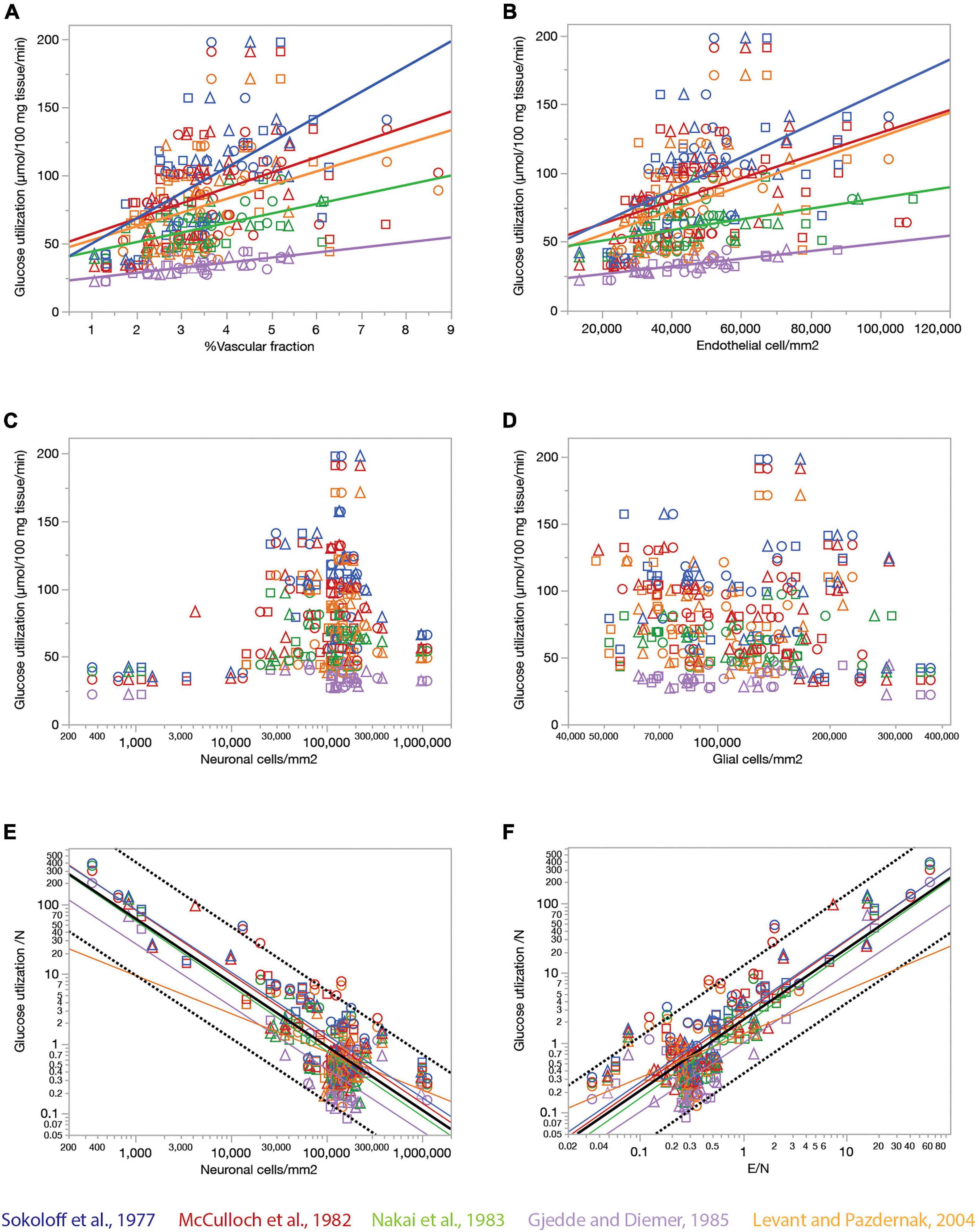
Figure 7. Relationship between local rates of glucose utilization at rest (data from the literature) and capillary fraction, cell densities, and E/N ratio (our data). Each data point refers to one brain structure in the list below. Each dataset is depicted in a different color according to the key. Data from each of three rats are shown separately as indicated by the symbols (circles, triangles, and squares). (A) Local rates of glucose utilization reported in the literature correlate with capillary fraction in the same structures in our data. Linear fits are plotted for each dataset. All linear correlations are significant (p < 0.0001 unless noted otherwise), with r2 = 0.450 (Gjedde and Diemer, 1985), 0.381 (Sokoloff et al., 1977), 0.289 (Nakai et al., 1983), 0.211 (McCulloch et al., 1982), and 0.157, p = 0.0006 (Levant and Pazdernik, 2004). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = 0.671 (Sokoloff et al., 1977), ρ = 0.610 (Gjedde and Diemer, 1985); ρ = 0.575 (McCulloch et al., 1982); ρ = 0.511 (Nakai et al., 1983); ρ = 0.439, p = 0.0001 (Levant and Pazdernik, 2004); ρ = 0.446 (all data). (B) Local rates of glucose utilization reported in the literature are linearly correlated with local density of endothelial cells in our data. All linear correlations are significant (p < 0.0001 unless noted otherwise), with r2 = 0.457 (Gjedde and Diemer, 1985), 0.299 (Sokoloff et al., 1977), 0.222 (Nakai et al., 1983), 0.205 (McCulloch et al., 1982) and 0.180, p = 0.0002 (Levant and Pazdernik, 2004). Spearman correlation coefficients (all values of p < 0.0001): ρ = 0.622 (Sokoloff et al., 1977), ρ = 0.609 (Gjedde and Diemer, 1985); ρ = 0.604 (McCulloch et al., 1982); ρ = 0.510 (Nakai et al., 1983); ρ = 0.480 (Levant and Pazdernik, 2004); ρ = 0.445 (all data). (C,D) Local rates of glucose utilization are not significantly correlated with neuronal density (C; all values of p > = 0.01) or with glial cell density (D; all values of p > = 0.01) across structures. (E) The estimated rate of glucose utilization per neuron decreases linearly with neuronal density. Power fit exponent, r2 (all p-values < 0.0001): –0.896 ± 0.089, r2 = 0.722 (Gjedde and Diemer, 1985); –0.898 ± 0.065, r2 = 0.771 (Sokoloff et al., 1977); –0.922 ± 0.066, r2 = 0.699 (McCulloch et al., 1982); –0.932 ± 0.076, r2 = 0.729 (Nakai et al., 1983); –0.546 ± 0.133, r2 = 0.197, p = 0.0001 (Levant and Pazdernik, 2004); –0.913 ± 0.037, r2 = 0.662 (all data). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = –0.651 (Sokoloff et al., 1977), ρ = –0.627, p = 0.0370 (Gjedde and Diemer, 1985); ρ = –0.641 (McCulloch et al., 1982); ρ = –0.664 (Nakai et al., 1983); ρ = –0.207, p = 0.0837 (Levant and Pazdernik, 2004); ρ = –0.524 (all data). (F) The estimated rate of glucose utilization per neuron increases linearly with the ratio of endothelial cells per neuron. Power fit exponent, r2 (all p-values < 0.0001): 0.986 ± 0.105, r2 = 0.694 (Gjedde and Diemer, 1985); 1.021 ± 0.070, r2 = 0.791 (Sokoloff et al., 1977); 1.040 ± 0.069, r2 = 0.730 (McCulloch et al., 1982); 1.041 ± 0.085, r2 = 0.727 (Nakai et al., 1983); 0.626 ± 0.120, r2 = 0.284 (Levant and Pazdernik, 2004); 1.016 ± 0.039, r2 = 0.683 (all data). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = 0.778 (Sokoloff et al., 1977), ρ = 0.446, p = 0.0035 (Gjedde and Diemer, 1985); ρ = 0.732 (McCulloch et al., 1982); ρ = 0.749 (Nakai et al., 1983); ρ = 0.345, p = 0.0032 (Levant and Pazdernik, 2004); ρ = 0.630 (all data). Structures analyzed: amygdala, auditory cortex, cerebellar cortex, cerebellar dentate nucleus, other cerebellar nuclei, cerebellar white matter, cochlear nucleus, corpus callosum, entorhinal cortex, globus pallidus, habenula (lateral), hippocampus, hypothalamus, inferior colliculus, inferior olive, insular cortex, nucleus accumbens, sensorimotor cortex, superior colliculus, superior olive, striatum, substantia nigra, thalamus, vestibular nucleus, visual cortex.
Our data also allow the estimation of an average rate of glucose utilization per neuronal unit (that is, one neuron and its associated glial cells) and how it varies across sites. Strikingly, we find that the average rate of glucose use per neuronal unit varies uniformly, and negatively, with local average neuronal density across the various sites in the rat brain, such that the smaller the local neuronal density, the higher the rate of glucose use per neuron (Figure 7E). At the same time, the rate of glucose use per neuronal unit increases together, and linearly, with the ratio of endothelial cells per neuron across brain sites (Figure 7F). Taken together, these results suggest that given the fairly even distribution of capillary densities across structures in the rat brain, the more the neurons found in a certain volume, sharing the blood supplied by the capillaries in that volume, the less glucose is used per neuronal unit per unit time in the resting brain.
The rate of glucose use by brain structures may or may not be limited by the rate of glucose supply by blood flow to the brain, for instance because of the possibility of variation in expression of glucose transporters (Choeiri et al., 2005), and also in the case that the anatomy of the blood supply system provides much more glucose than is actually used in physiological conditions. Although some of the studies whose datasets we used showed that resting rates of glucose use are linearly correlated to capillary density across sites in the rat brain (Klein et al., 1986; Borowsky and Collins, 1989), which is consistent with supply-limitation of rates of glucose use at rest, we did not wish to assume that rates of glucose use at rest are determined by rates of blood flow through the capillaries in the local volume. To determine whether local capillary density correlates with local rates of blood supply, and whether the ratio between numbers of endothelial cells and the neurons they serve might determine how much blood, and therefore energy, is supplied per individual neuronal unit, we crossed our data on local densities of capillaries (the vascular fraction), endothelial, glial and neuronal cells with three published datasets on rates of blood flow in the resting rat brain (McCulloch et al., 1982; Nakai et al., 1983; Gjedde and Diemer, 1985; Figure 8). In each of these three datasets, local rates of glucose use are tightly, and linearly, correlated with local rates of blood flow measured in different brain structures (r2 = 0.874, p < 0.0001, and r2 = 0.578, p < 0.0001, respectively).
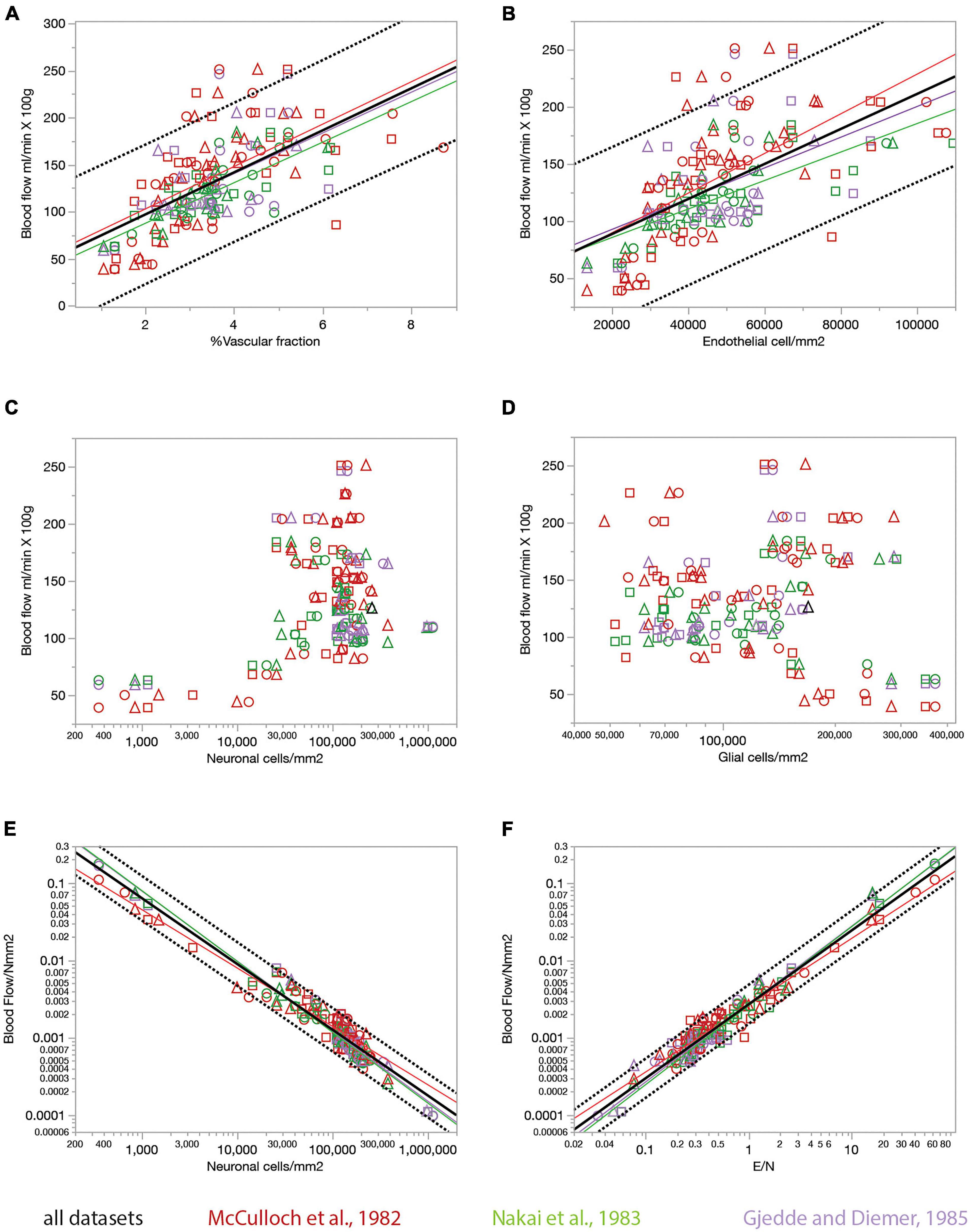
Figure 8. Relationship between local rates of blood flow at rest (data from the literature) and capillary fraction, cell densities, and E/N ratio (our data). Each data point refers to one brain structure in the list below. Each dataset is depicted in a different color according to the key. Data from each of three rats are shown separately as indicated by the symbols (circles, triangles, and squares). (A) Local rates of blood flow at rest reported in the literature correlate with capillary fraction in the same structures in our data. Linear fits are plotted for each dataset. All linear correlations are significant (p < 0.0001 unless noted otherwise), with r2 = 0.310, p = 0.0002 (Gjedde and Diemer, 1985), 0.620 (Nakai et al., 1983), 0.376 (McCulloch et al., 1982), and 0.392 (all data, plotted). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = 0.546, p = 0.0002 (Gjedde and Diemer, 1985); ρ = 0.740 (McCulloch et al., 1982); ρ = 0.774 (Nakai et al., 1983); ρ = 0.673 (all data). (B) Local rates of blood flow at rest reported in the literature are linearly correlated with local density of endothelial cells in our data. All linear correlations are significant (p < 0.0001 unless noted otherwise), with r2 = 0.223, p = 0.0018 (Gjedde and Diemer, 1985), 0.524 (Nakai et al., 1983), 0.397 (McCulloch et al., 1982), and 0.364 (all data). Spearman correlation coefficients (all values of p < 0.0001): ρ = 0.468, p = 0.0022 (Gjedde and Diemer, 1985); ρ = 0.764 (McCulloch et al., 1982); ρ = 0.761 (Nakai et al., 1983); ρ = 0.661 (all data). (C,D) Local rates of blood flow at rest are not significantly correlated with neuronal density (C, p = 0.8381 and 0.4166 for the Gjedde and Nakai datasets, respectively, though ρ = 0.375, p = 0.0010 for the McCulloch dataset) or with glial cell density (D; all values of p > = 0.08) across structures. (E) The estimated rate of blood flow at rest per neuron decreases linearly with neuronal density. Power fit exponent, r2 (all p-values < 0.0001): –0.907 ± 0.030, r2 = 0.960 (Gjedde and Diemer, 1985); –0.756 ± 0.028, r2 = 0.913 (McCulloch et al., 1982); –0.917 ± 0.023, r2 = 0.969 (Nakai et al., 1983); –0.546 ± 0.133, –0.852 ± 0.017, r2 = 0.939 (all data). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = –0.874 (Gjedde and Diemer, 1985); ρ = –0.890 (McCulloch et al., 1982); ρ = –0.964 (Nakai et al., 1983); ρ = –0.908 (all data). (F) The estimated rate of blood flow at rest per neuron increases linearly with the ratio of endothelial cells per neuron. Power fit exponent, r2 (all p-values < 0.0001): 1.009 ± 0.036, r2 = 0.954 (Gjedde and Diemer, 1985); 0.866 ± 0.026, r2 = 0.941 (McCulloch et al., 1982); 1.023 ± 0.024, r2 = 0.973 (Nakai et al., 1983); 0.957 ± 0.017, r2 = 0.951 (all data). Spearman correlation coefficients (all values of p < 0.0001 unless noted otherwise): ρ = 0.863 (Gjedde and Diemer, 1985); ρ = 0.913 (McCulloch et al., 1982); ρ = 0.960 (Nakai et al., 1983); ρ = 0.921 (all data). Structures analyzed: amygdala, auditory cortex, cerebellar cortex, cerebellar dentate nucleus, other cerebellar nuclei, cerebellar white matter, cochlear nucleus, corpus callosum, entorhinal cortex, globus pallidus, habenula (lateral), hippocampus, hypothalamus, inferior colliculus, inferior olive, insular cortex, nucleus accumbens, sensorimotor cortex, superior colliculus, superior olive, striatum, substantia nigra, thalamus, vestibular nucleus, visual cortex.
We find that rates of blood flow/min.100 g correlate positively and even more strongly than rates of glucose use with the capillary fractions and endothelial cell densities we measured in the same brain structures, such that structures with higher blood flow rates have proportionately higher capillary fraction (Figure 8A) and densities of endothelial cells (Figure 8B). Once more, we find that local rates of blood flow are not correlated with local densities of neurons or glial cells (Figures 8C,D).
The ratio between local rate of blood flow and local neuronal density indicates how much blood supply is available per neuronal unit per unit time. We find that this ratio is strongly linearly and inversely proportional to neuronal density (Figure 8E), like the rate of glucose use per neuronal unit (Figure 7E), with less blood supplied per neuronal unit in those locations where neuronal densities are higher. Consequently, as could be expected at this point, local variations in rate of blood flow per neuronal unit are strongly linearly correlated with the ratio of endothelial cells per neuron (Figure 8F), such that sites with more endothelial cells available per neuron also have higher rates of blood supplied per neuron.
Finally, to address the multiple correlations across the variables examined, we performed principal component analysis of the main variables available for each brain structure: local densities of endothelial cells, neurons, and glial cells; E/N and G/N ratios; rates of blood flow and glucose use; and rates of blood flow and glucose use per neuron. Strikingly, we find that rates of blood flow per neuron, glucose use per neuron, E/N and G/N ratios load very strongly in the first factor (factor loading, 0.943, 0.935, 0.952, and 0.965, respectively), together with glial cell density (factor loading, 0.599), accounting for 44.5% of the variance in the data. In the second factor, rates of blood flow and glucose use load together with endothelial cell density (factor loading, 0.993, 0.712, and 0.578, respectively), accounting cumulatively for 67.4% of variance in the data. Notably, local neuronal density does not load significantly in either factor, indicating that neuronal density is a truly independent variable in the dataset.
Discussion
Here we find that, as we reported in the mouse (Ventura-Antunes and Herculano-Houzel, in review), capillary fraction and endothelial cell densities vary little across sites in the rat brain, compared to the highly variable neuronal cell densities across sites, with no consistent or universal correlation between capillary fraction (or endothelial cell densities) and neuronal or glial cell densities across those sites. Crucially, at the same time, we find that the small variations that do occur in local capillary fraction and endothelial cell density correlate strongly with independent measurements of local blood flow rate and glucose use at rest, while these measurements of local metabolic rates in the resting brain again bear no systematic relationship to local densities of neurons or glial cells. Most importantly, crossing our data on cellular distribution in the rat brain to published data on metabolism in matching brain sites revealed that the average resting rates of blood supply and glucose use per neuronal unit are strongly and linearly predicted by the anatomical ratio of endothelial cells per neuron across brain sites. Given that there is no other source of oxygen and glucose to the brain other than the capillary bed, it follows that local capillary density, which we confirm to correlate strongly with local rates of blood flow at rest, must be limiting to the rate at which energy (in the form of both oxygen and glucose, no matter the stoichiometry of their use) is delivered to brain sites, regardless of how many neurons are found at each location. Local capillary density must remain limiting to rates of energy delivery even in the case of variations in expression of glucose transporters, which necessarily occurs on top of limitations imposed by capillary density, for it is not possible to transport to neurons glucose that never arrived at a brain site because of limited capillary delivery. Moreover, since oxygen transport from hemoglobin to brain tissue depends exclusively on diffusion, and not on carriers or transporters, its availability is ultimately limited by the anatomy of the supply network – that is, by the density of the capillary bed. Thus, we propose that while variations in local capillary density are relatively minimal across sites in the rat brain, they are highly consequential to brain metabolism by determining the rate of energy supply to diverse numbers of neurons across locations in the brain. This proposition is fully developed into a supply-limited framework of brain metabolism in a companion paper (Herculano-Houzel and Rothman, 2022).
It is undisputed that sensory stimulation and other forms of focused mental activity increase local neuronal activity and brain metabolism (reviewed in Leithner and Royl (2014)), which in principle might appear to make our present anatomical study of questionable relevance to advancing our understanding of brain metabolism. Additionally, it could be argued that the capillary bed is plastic and can respond with proliferation to changes in activity. For example, dark-rearing and visual deprivation causes the visual cortex to develop with decreased vascularization (Toga, 1987; Argandoña and Lafuente, 1996), whereas complex visual experience leads to increased capillary density in the visual cortex (Sirevaag et al., 1988). We refute such likely criticism in two main ways. First, exactly because it is self-organized, the anatomy of the brain microvasculature at rest is a reflection of the history of brain activity (Black et al., 1987; Isaacs et al., 1992). For that reason, the resting, steady-state energy availability of the adult brain at rest, as well as its steady-state rate of energy use, is a reflection of its past history of activity, and represents an adequate supply. That past history reflected in the current distribution of capillaries captured in the images that we quantify includes any use-dependent modifications in local capillary density. Thus, understanding the distribution of capillaries in the brain provides unique insight into the self-organizing principles that govern brain metabolism at steady-state.
While we acknowledge that direct implications of our quantitative findings on the capillary distribution of fixed rat brains are currently limited to the resting (undisturbed awake) rat brain, the second argument for the relevance of our steady-state findings to the dynamically changing awake brain is our recent demonstration that local capillary densities are indeed a fundamental determinant of rates of brain metabolism also during sensory stimulation, even in the so-called “state of neurovascular uncoupling,” during which rates of blood flow increase much more than rates of oxygen use by brain tissue (Herculano-Houzel and Rothman, 2022, see companion paper). Increases in local rates of blood flow in the stimulated brain, presumably driven by variations in neuronal activity, are due to local changes in arterial dilation and increases in blood pressure, without capillary recruitment (Kuschinsky and Paulson, 1992; Jesperson and Ostergaard, 2012; Leithner and Royl, 2014). The increased local rate of blood flow would lead to a proportionally increased rate of oxygen transfer from blood to brain tissue if that rate weren’t already near maximal, constrained by the combination of capillary surface area (and thus capillary density), hemoglobin oxygenation (which is typically already saturated at rest, at 100% of arterial values), and hematocrit (which, on this time scale, is unchanging). Because there is no effective capillary recruitment in the awake brain, the increase in rate of oxygen use in the stimulated brain is only modest, and no longer linearly coupled to the increase rate of blood flow – but, importantly, the increased rate of oxygen use remains fully predictable by local capillary density (Herculano-Houzel and Rothman, 2022).
One of the strengths of our approach is that it allows the establishment of parallels between local capillary density (and thus local rate of blood flow) and local numbers of neurons and glial cells. While we did not measure actual rates of blood delivery per neuron, our finding that the ratio of endothelial cells per neuron is a strong linear predictor of average rate of blood flow per neuronal unit allows us to predict the implications to brain physiology, just like the capillary-to-muscle fiber ratio of skeletal muscle is regarded as a critical determinant of muscle metabolic capacity (Hepple et al., 1985; Wagner, 2000). We find that the economy of the working brain balances sites where as many as 60 neurons share blood supplied by a single endothelial cell, such as the granular layer of the cerebellum; sites where only two neurons (as in the thalamus and midbrain) or three neurons (as in the non-hippocampal pallium) share a single endothelial cell’s worth of blood supply; sites where there is about one endothelial cell for every neuron (as in the hindbrain); and sites where endothelial cells exceed the number of neuronal cell bodies consuming the energy they supply (as in the molecular layers of the hippocampus and cerebellum). With the much smaller variation in endothelial cell density (and therefore capillary density) than in neuronal density, it appears that the particular density at which neurons occur at different brain sites determines the economy of energy distribution amongst neighboring neurons, with more competition for energy in those sites where more neurons share the limited resources transported in the blood.
It is possible that some of the variation we find in cell densities and capillary fraction are due to unequal shrinkage of different brain structures during fixation and immunohistochemical processing. However, in the event of enough differential shrinkage across sites to affect the correlations that we report, we would expect that densities of both neurons and endothelial cells would be affected similarly at each site, which would artificially increase the chances that we find strong positive correlations between these two variables across sites. Our main finding of no strong or consistent correlation between neuronal and endothelial cell densities is thus the opposite of what one would expect if variable tissue shrinkage were a significant issue in our dataset.
By showing that variations in local capillary densities are at the same time very limited but also directly and linearly correlated to local rates of blood flow and glucose use at rest, our study raises an important new issue of what determines local capillary densities in the developing and in the steady-state adult brain. Activity-dependent formation of new capillaries is a possibility (Toga, 1987; Sirevaag et al., 1988; Argandoña and Lafuente, 1996), presumably leading to higher capillary densities in sites of higher neuronal activity, especially during development. However, the lack of correlation between local neuronal density and capillary density in the rat (this study) and mouse brain (Ventura-Antunes and Herculano-Houzel, in review) as well as between local density of synapses and capillary density in the mouse (Ventura-Antunes and Herculano-Houzel, in review), when the rate of energy use by neurons is believed to be heavily dependent on synaptic activity (Attwell and Laughlin, 2001), puts into question the extent to which local differences in intrinsic or stimulus-driven neuronal activity might drive variations in local capillary density. Moreover, the recent observation that endothelial cells in the adult mouse brain are as old as the neurons that they feed (Arrojo e Drigo et al., 2019) raises doubts regarding the magnitude of the impact of activity-dependent changes in capillary density in adult animals. On the other hand, the physics of scaling of distribution networks predicts that capillary densities should be determined by the size of the system (Banavar et al., 2002), which is consistent with the small degree of variation that we report here. It will be interesting to pursue the question of what determines the small but consequential variations in local capillary densities in the brain that we report here.
An important incidental finding of the present study is that endothelial cells and glial cells appear to vary together in numbers and density across gray matter structures, with a somewhat constant ratio of about three glial cells to every endothelial cell in these structures. Astrocytic endfeet are closely associated with endothelial cells, and astrocytes play a key role in providing neurons with energy substrates either directly removed or transformed from substances transferred from the blood (Magistretti and Pellerin, 1996). Given that astrocytes are only about 5–10% of non-neuronal cells of the rodent brain (Herculano-Houzel et al., 2006; Sun et al., 2017), our finding of an average of ca. 3 glial cells per endothelial cell suggests that there is at most one astrocyte per endothelial cell in the different gray matter structures in the rat brain, even though non-quantitative microscopy indicates, from the early studies of Ramón y Cajal (1995), that individual capillaries are covered by multiple astrocytic endfeet. Combined with the realization that astrocytes are actually a minority of glial cells (Sun et al., 2017), our finding of ca. 3 glial cells per endothelial cell suggests that the various endfeet that cover each endothelial cells very likely originate from the same individual astrocyte, and at best the few neighboring astrocytes that tile that territory, such that, overall, each astrocyte contacts at most a couple of endothelial cells simultaneously. It will be interesting to investigate directly this quantitative relationship in the future. Until then, the small and at best 1:1 ratio of astrocytes to endothelial cells that we suggest points to yet another way in which brain metabolism is constrained by supply, given that glial cells, like endothelial cells, occur at a narrow range of densities, and therefore the number of neurons served by every astrocyte depends simply on how many neurons occur within the territory of an individual astrocyte (Herculano-Houzel, 2014). Thus, we propose that neuronal metabolism is limited not only in how much blood is supplied to their territory by capillaries, but also by how many other neurons share their astrocytic support.
It follows that those brain areas with higher neuronal densities (because these are not compensated by increased capillary density) should be particularly susceptible to alterations that disrupt blood supply and astrocyte-supported metabolism, such as ischemia, metabolic diseases, and aging. We thus predict that brain structures with lower E/N ratios, and not simply those brain areas with highest metabolic rates, should be the most vulnerable and the first parts of the brain to be afflicted once blood supply is compromised. For instance, the entorhinal cortex, one of the first cortical areas to be affected in Alzheimer’s disease, is one such area of fairly low metabolic rate, but with its high neuronal density, it actually has the lowest E/N ratio of the non-hippocampal pallium (0.024, or 42 neurons to each endothelial cell), followed by the hippocampal dentate gyrus (0.126, or 8 neurons to each endothelial cell; Table 3), another highly vulnerable structure. Consistently with our proposition that neuronal competition for a limited capillary supply is a determinant factor in brain health and disease, it is now increasingly recognized that cerebrovascular pathology contributes to dementia and clinically diagnosed Alzheimer’s disease (Arvanitakis et al., 2016), and blood flow reductions that impair the hemodynamic responses are increasingly recognized in normal aging (Brown and Thore, 2011) as well as in the early stages of Alzheimer’s disease (Sweeney et al., 2018).
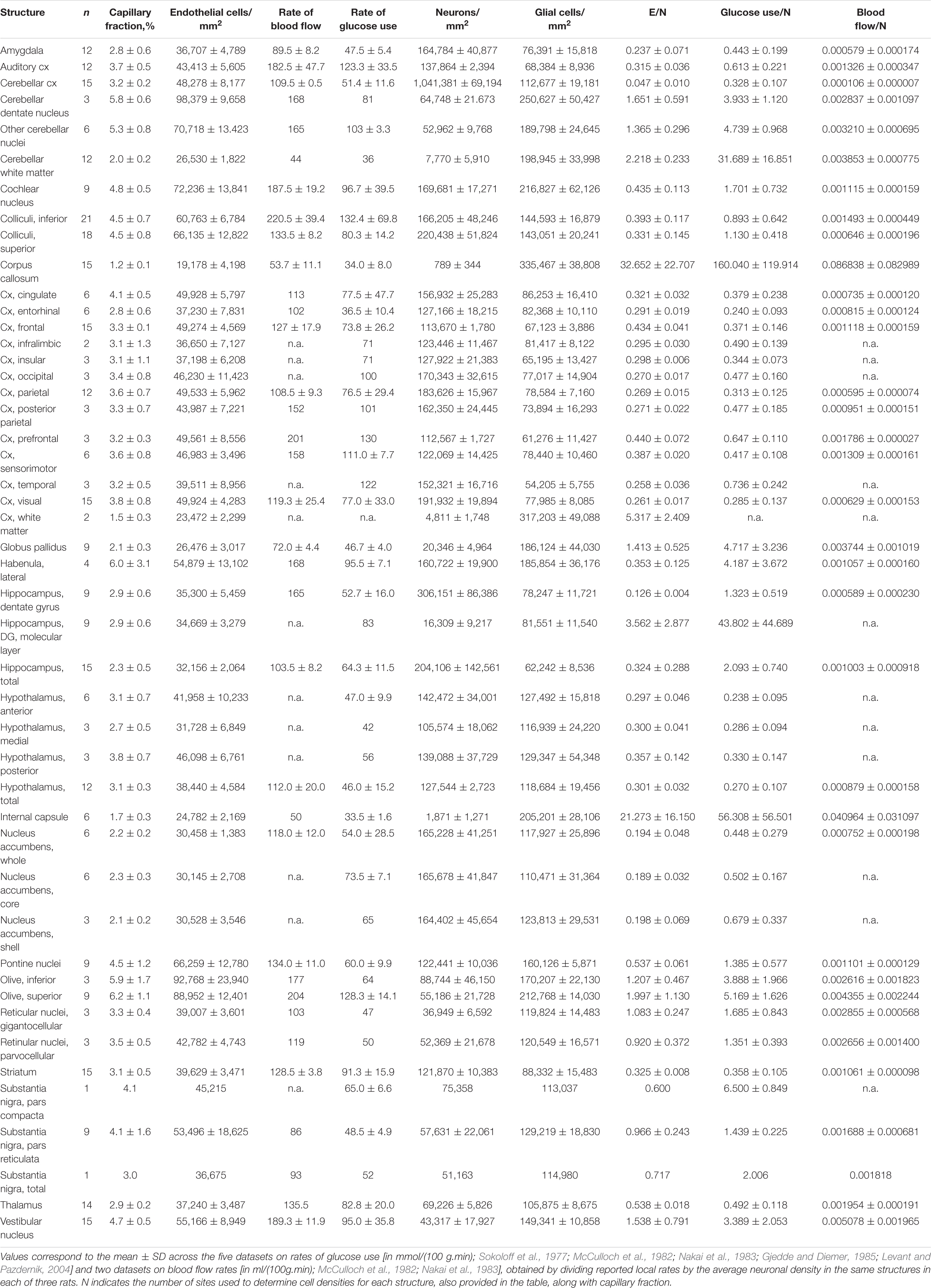
Table 3. Average rates of glucose use/neuron and blood flow/neuron in different structures of the rat brain.
Recognizing that the relative ratio of local neuronal densities to local capillary density is of such potentially fundamental relevance to brain health raises new questions about how local capillary density is determined, which is complicated by the fact that our understanding of the source of variations in local neuronal size that lead to variations in neuronal density across brain sites remains lacking. During the early stages of development, the radial glial cells that give rise to early neurons and form migrating routes for these newly generated cells (Rakic, 1972) also guide the formation and stabilization of a primitive vascular network (Ma et al., 2013). It is likely that multiple factors influence the formation of what will ultimately be the capillary bed of the brain, but our companion study in the mouse indicates that synaptic density is not one of them (see text footnote 1). We plan to study the parallel development of the distribution of capillaries and neurons in different mammalian species to shed light on the sources of variation in capillary density, and in particular on the origin of the higher capillary densities in hindbrain structures reported here. One testable hypothesis to be examined is that the accentuated growth of neuronal arbors that occurs in the cerebral cortex during neuronal differentiation pushes already formed capillaries away from one another, thus leading to lower capillary densities in the cerebral cortex than those observed in the hindbrain. Another possibility is that there are fundamental differences between the anatomy and physiology of the vascularization of the cerebrum and of the hindbrain, which indeed branch off from two different main arteries: the internal carotid and the basilar artery. It will be interesting to investigate how that difference could also account for the higher capillary densities that we report in territories vascularized by the basilar artery.
Finally, our observations strongly indicate that local capillary fraction and/or endothelial cell density in the rat brain serve as accurate proxies for local metabolic rate, especially blood flow rate, across brain structures. Because local capillary fraction and endothelial cell densities (which we find to be linearly correlated to each other) are readily quantifiable in thin 2D sections of fixed brains, they show great promise in serving as proxies for studies of how brain metabolism scales across species. To that end, it will be necessary to determine whether the same relationship between capillary density and rate of blood flow at rest is shared across mammalian species. However, together with the observation that the capillary bed is the most restrictive portion of the circulatory system to blood flow (Gould et al., 2017), the finding that resting brain metabolic rate scales consistently across mammalian species (Herculano-Houzel, 2011) strongly suggests that the relationship between capillary density and rate of blood flow is shared universally across mammalian species. In the case that such a universal relationship is confirmed, we will finally be able to extend studies of brain metabolism to a wide range of mammalian species that would be impossible to examine alive, but whose fixed brains are approachable.
Data Availability Statement
The original contributions presented in this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Ethics Statement
Ethical review and approval was not required for the animal study because brains were purchased from BrainBits already perfused.
Author Contributions
SH-H conceived the study. LV-A and OD executed all data acquisition. All authors analyzed the data. SH-H and LV-A wrote the manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Douglas Rothman for insightful discussions. Supported by the James S. McDonnell Foundation and Vanderbilt University.
Footnotes
- ^ Ventura-Antunes, L., and Herculano-Houzel, S. (2022). Energy supply per neuron is constrained by capillary density in the mouse brain. Front. Integr. Neurosci.
References
Andersson, K. E. (2011). Mechanisms of penile erection and basis for pharmacological treatment of erectile dysfunction. Pharmacol. Rev. 63, 811–859. doi: 10.1124/pr.111.004515
Argandoña, E. G., and Lafuente, J. V. (1996). Effects of dark-rearing on the vascularization of the developmental rat visual cortex. Brain Res. 732, 43–51. doi: 10.1016/0006-8993(96)00485-4
Arrojo e Drigo, R., Lev-Ram, V., Tyagi, S., Ramachandra, R., Deerinck, T., Bushong, E., et al. (2019). Age mosaicism across multiple scales in adult tissues. Cell Metab. 30, 343–351. doi: 10.1016/j.cmet.2019.05.010
Arvanitakis, Z., Capuano, A. W., Leurgans, S. E., Bennett, D. A., and Schneider, J. A. (2016). Relation of cerebral vessel disease to Alzheimer’s disease dementia and cognitive function in elderly people: a cross-sectional study. Lancet Neurol. 15, 934–943. doi: 10.1016/S1474-4422(16)30029-1
Aschoff, J., Günther, B., and Kramer, K. (1971). Energiehaushalt und Temperaturregulation. Munich: Urban and Schwarzenberg.
Attwell, D., and Laughlin, S. B. (2001). An energy budget for signaling in the grey matter of the brain. J. Cereb. Blood Flow Metab. 21, 1133–1145. doi: 10.1097/00004647-200110000-00001
Banavar, J. R., Damuth, J., Maritan, A., and Rinaldo, A. (2002). Supply-demand balance and metabolic scaling. Proc. Natl. Acad. Sci. U.S.A. 99, 10506–10509. doi: 10.1073/pnas.162216899
Black, J. E., Sirevaag, A. M., and Greenough, W. T. (1987). Complex experience promotes capillary formation in young rat visual cortex. Neurosci. Lett. 83, 351–355. doi: 10.1016/0304-3940(87)90113-3
Borowsky, I. W., and Collins, R. C. (1989). Metabolic anatomy of brain: a comparison of regional capillary density, glucose metabolism, and enzyme activities. J. Comp. Neurol. 288, 401–413. doi: 10.1002/cne.902880304
Brown, W. R., and Thore, C. R. (2011). Cerebral microvascular pathology in aging and neurodegeneration. Neuropathol. Appl. Neurobiol. 37, 56–74. doi: 10.1111/j.1365-2990.2010.01139.x
Choeiri, C., Staines, W., Miki, T., Seino, S., and Messier, C. (2005). Glucose transporter plasticity during memory processing. Neuroscience 130, 591–600. doi: 10.1016/j.neuroscience.2004.09.011
Gjedde, A. (2005). The pathways of oxygen in brain I. Delivery and metabolism of oxygen.. Adv. Exp. Med. Biol. 566, 269–275. doi: 10.1007/0-387-26206-7_36
Gjedde, A., and Diemer, N. H. (1985). Double-Tracer Study of the Fine Regional Blood—Brain Glucose Transfer in the Rat by Computer-Assisted Autoradiography. J. Cerebr. Blood Flow Metab. 5, 282–289. doi: 10.1038/jcbfm.1985.36
Gould, I. G., Tsai, P., Kleinfeld, D., and Linninger, A. (2017). The capillary bed offers the largest hemodynamic resistance to the cortical blood supply. J. Cereb. Blood F low Metab. 37, 52–68. doi: 10.1177/0271678x16671146
Gundersen, H. J. G., and Jensen, E. B. (1987). The efficiency of systematic sampling in stereology and its prediction. J. Microscopy. 147, 229–263. doi: 10.1111/j.1365-2818.1987.tb02837.x
Hepple, R. T., Hogan, M. C., Stary, C., Bebout, D. E., Mathieu-Costello, O., and Wagner, P. D. (1985). Structural basis of muscle O(2) diffusing capacity: evidence from muscle function in situ. J. Appl. Physiol. 88, 560–566. doi: 10.1152/jappl.2000.88.2.560
Herculano-Houzel, S. (2011). Scaling of brain metabolism with a fixed energy budget per neuron: implications for neuronal activity, plasticity and evolution. PLoS One 6:e17514. doi: 10.1371/journal.pone.0017514
Herculano-Houzel, S. (2014). The glia/neuron ratio: how it varies uniformly across brain structures and species and what that means for brain physiology and evolution. Glia 62, 1377–1391. doi: 10.1002/glia.22683
Herculano-Houzel, S., Mota, B., and Lent, R. (2006). Cellular scaling rules for rodent brains. Proc. Natl. Acad. Sci. USA 103, 12138–12143. doi: 10.1073/pnas.0604911103
Herculano-Houzel, S., and Rothman, D. L. (2022). From a demand-based to a supply-limited framework of brain metabolism. Front. Integr. Neurosci. 16:818685. doi: 10.3389/fnint.2022.818685
Iadecola, C. (2017). The neurovascular unit coming of age: a journey through neurovascular coupling in health and disease. Neuron 96, 17–42. doi: 10.1016/j.neuron.2017.07.030
Isaacs, K. R., Anderson, B. J., Alcantara, A. A., Black, J. E., and Greenough, W. T. (1992). Exercise and the brain: angiogenesis in the adult rat cerebellum after vigorous physical activity and motor skill learning. J. Cereb. Blood Flow Metab. 12, 110–119. doi: 10.1038/jcbfm.1992.14
Jesperson, S. N., and Ostergaard, L. (2012). The roles of cerebral blood flow, capillary transit time heterogeneity, and oxygen tension in brain oxygenation and metabolism. J. Cereb. Blood Flow Metab. 32, 264–277. doi: 10.1038/jcbfm.2011.153
Kety, S. (1956). Human cerebral blood flow and oxygen consumption as related to aging. J. Chron. Dis. 3, 478–486. doi: 10.1016/0021-9681(56)90146-1
Klein, B., Kuschinsky, W., Schrock, H., and Vetterlein, F. (1986). Interdependency of local capillary density, blood flow, and metabolism in rat brains. Am. J. Physiol. 251, H1333–H13340. doi: 10.1152/ajpheart.1986.251.6.H1333
Krogh, A. (1919). The number and distribution of capillaries in muscles with calculations of the oxygen pressure head necessary for supplying the tissue. J. Physiol. 52, 409–415. doi: 10.1113/jphysiol.1919.sp001839
Kuschinsky, W., and Paulson, O. B. (1992). Capillary circulation in the brain. Cerebrovasc. Brain Metab. Rev. 4, 261–286.
Leithner, C., and Royl, G. (2014). The oxygen paradox of neurovascular coupling. J. Cereb. Blood Flow Metab. 34, 19–29. doi: 10.1038/jcbfm.2013.181
Levant, B., and Pazdernik, T. L. (2004). Differential effects of ibogaine on local cerebral glucose utilization in drug-naïve and morphine-dependent rats. Brain Res. 1003, 159–167. doi: 10.1016/j.brainres.2003.12.032
Ma, S., Kwon, H. J., Johng, H., Zang, K., and Huang, Z. (2013). Radial glial neural progenitors regulate nascent brain vascular network stabilization via inhibition of Wnt signaling. PLoS Biol. 11:e1001469. doi: 10.1371/journal.pbio.1001469
Magistretti, P., and Pellerin, L. (1996). Cellular bases of brain energy metabolism and their relevance to functional brain imaging: evidence for a prominent role of astrocytes. Cereb. Cx 6, 50–61. doi: 10.1093/cercor/6.1.50
McCulloch, J., Kelly, P. A., Grome, J. J., and Pickard, J. D. (1982). Local cerebral circulatory and metabolic effects of indomethacin. Am. J. Physiol. -Heart Circulat. Physiol. 243, H416–H423. doi: 10.1152/ajpheart.1982.243.3.H416
Mintun, M. A., Vlassenko, A. G., Shulman, G. L., and Snyder, A. Z. (2002). Time-related increase of oxygen utilization in continuously activated human visual cortex. NeuroImage 16, 531–537. doi: 10.1006/nimg.2002.1114
Mota, B., and Herculano-Houzel, S. (2014). All brains are made of this: a fundamental building block of brain matter with matching neuronal and glial masses. Front. Neuroanat. 8:127. doi: 10.3389/fnana.2014.00127
Mullen, R. J., Buck, C. R., and Smith, A. M. (1992). NeuN, a neuronal specific nuclear protein in vertebrates. Develop 116, 201–211. doi: 10.1242/dev.116.1.201
Nakai, M., Iadecola, C., Ruggiero, D. A., Tucker, L. W., and Reis, D. J. (1983). Electrical stimulation of cerebellar fastigial nucleus increases cerebral cortical blood flow without change in local metabolism: Evidence for an intrinsic system in brain for primary vasodilation. Brain Res. 260, 5–49. doi: 10.1016/0006-8993(83)90762-x
Paxinos, G., and Watson, C. (2006). The rat brain in stereotaxic coordinates: hardcover edition. Amsterdam: Elsevier.
Rakic, P. (1972). Mode of cell migration to superficial layers of fetal monkey neocortex. J. Comp. Neurol. 145, 61–83. doi: 10.1002/cne.901450105
Ramón y Cajal, S. (1995). Histology of the nervous system of man and vertebrates (trans. Swanson N, Swanson LW). New York, NY: Oxford University Press.
Shepherd, A. P. (1982). Role of capillary recruitment in the regulation of intestinal oxygenation. Am. J. Physiol. 242, G435–G441. doi: 10.1152/ajpgi.1982.242.5.G435
Sirevaag, A. M., Black, J. E., Shafron, W. T., and Greenough, W. T. (1988). Direct evidence that complex experience increases capillary branching and surface area in visual cortex of young rats. Dev. Brain Res. 43, 299–304. doi: 10.1016/0165-3806(88)90107-1
Skattebo, O., Calbet, J. A. L., Rud, B., Capelli, C., and Hallén, J. (2020). Contribution of oxygen extraction fraction to maximal oxygen uptake in healthy young men. Acta Physiol. 230:e13486.
Sokoloff, L., Reivich, M., Kennedy, C., Des Rosiers, M. H., Patlak, C. S., Pettigrew, K. D., et al. (1977). The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat. J. Neurochem. 28, 897–916. doi: 10.1111/j.1471-4159.1977.tb10649.x
Sun, W., Cornwell, A., Li, J., Peng, S., Osorio, M. J., Aalling, N., et al. (2017). SOX9 is an astrocyte-specific marker in the adult brain outside the neurogenic regions. J. Neurosci. 37, 4493–4507. doi: 10.1523/jneurosci.3199-16.2017
Sweeney, M. D., Kisler, K., Montagne, A., Toga, A. W., and Zlokovic, B. V. (2018). The role of brain vasculature in neurodegenerative disorders. Nat. Neurosci. 21, 1318–1331. doi: 10.1038/s41593-018-0234-x
Toga, A. W. (1987). The metabolic consequence of visual deprivation in the rat. Dev. Brain Res. 37, 209–217. doi: 10.1016/0165-3806(87)90242-2
Wagner, P. D. (2000). Diffusive resistance to O2 transport in muscle. Acta Physiol. Scand. 168, 609–614. doi: 10.1046/j.1365-201x.2000.00712.x
Keywords: metabolism, capillary density, brain vasculature, brain energetics, neuronal density
Citation: Ventura-Antunes L, Dasgupta OM and Herculano-Houzel S (2022) Resting Rates of Blood Flow and Glucose Use per Neuron Are Proportional to Number of Endothelial Cells Available per Neuron Across Sites in the Rat Brain. Front. Integr. Neurosci. 16:821850. doi: 10.3389/fnint.2022.821850
Received: 24 November 2021; Accepted: 07 March 2022;
Published: 10 June 2022.
Edited by:
Rodrigo Clemente Vergara, Universidad Metropolitana de Ciencias de la Educación, ChileReviewed by:
Claude Messier, University of Ottawa, CanadaSergio Vicencio-Jimenez, Johns Hopkins Medicine, United States
Copyright © 2022 Ventura-Antunes, Dasgupta and Herculano-Houzel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Suzana Herculano-Houzel, c3V6YW5hLmhlcmN1bGFub0B2YW5kZXJiaWx0LmVkdQ==
†ORCID: Suzana Herculano-Houzel, orcid.org/0000-0002-1765-3599; Lissa Ventura-Antunes, orcid.org/0000-0001-5508-0990; Oisharya Moon Dasgupta, orcid.org/0000-0002-0329-4871
‡Present address: Lissa Ventura-Antunes, Vanderbilt University Medical Center, Nashville, TN, United States
 Lissa Ventura-Antunes
Lissa Ventura-Antunes Oisharya Moon Dasgupta
Oisharya Moon Dasgupta Suzana Herculano-Houzel
Suzana Herculano-Houzel