Shivendra G. Tewari
Manoj K. Gottipati
Vladimir Parpura- 1Molecular and Integrative Physiology, University of Michigan, Ann Arbor, MI, USA
- 2Department of Neurobiology, University of Alabama at Birmingham, Birmingham, AL, USA
Research in neuroscience has come a long way since it was first hypothesized, in the early twentieth century, that dynamic changes in ion permeability underlie an event termed as action potential (Bernstein, 1912). Research along the same lines in the 1950s by Hodgkin and Huxley (1952) elucidated the dependence of action potential on the permeability of potassium and sodium ions—a theory achieved using quantitative analysis of potassium, sodium, and leak currents. Using mathematical modeling, they suggested that potassium and sodium conduits exist in distinct states (open, closed, or inactive) during an action potential; this was at a time when the composition of excitable membrane was largely unknown. Their mathematical model revolutionized the field of neurobiology and still forms the basis for many of the current mathematical models. Over the past several years, as more information on different channel types became available, more complex neuronal action potential models accounting for several channel types have been built (Traub et al., 1994; Bower and Beeman, 1995); a comparison between the original Hodgkin-Huxley model and a more detailed contemporary model is shown in Figures 1A–C.
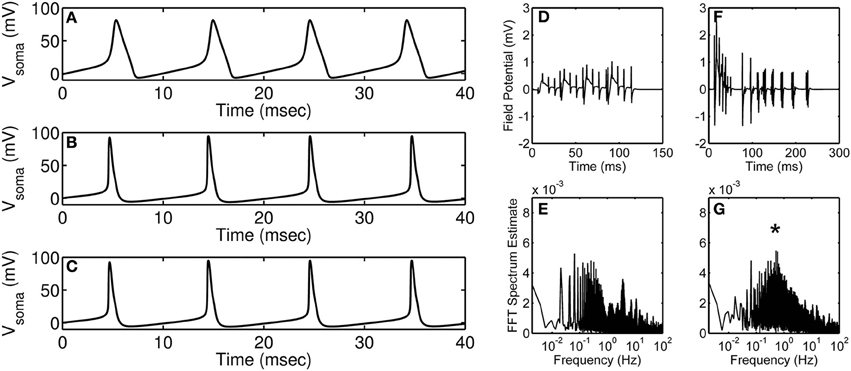
Figure 1. Modeling of action potential discharges and the effect of astrocyte on accumulated neural discharges. (A) Hodgkin-Huxley squid axon model (Hodgkin and Huxley, 1952) injected with 35 μA·cm−2 current. (B,C) Branching dendrite model of a rodent CA3 pyramidal neuron (Traub et al., 1994) injected with 15 nA current into the soma compartment; (B) Control (wild-type) neuron modeling, and (C) Modeling of action potential discharges of a neuron with calcium-activated potassium channel knocked out. Simulations were obtained using published models and parameters. Model simulated field potentials of CA1 pyramidal neurons in the absence (D) and the presence (F) of peri-synaptic astrocyte. FFT spectrum analysis of the model simulated field potentials in the absence (E) and the presence (G) of astrocyte. (D–G) are modified and reproduced from Tewari and Parpura (2013). Asterisk denotes the astrocyte induced peak in the FFT spectrum.
With the hindsight, detailed models have been successful in emulating neuronal firing patterns observed in vivo or in situ. Primarily, computation of such detailed models has been possible due to significant technological advances that help solve differential equations in multiple dimensions. On one hand, detailed mathematical models are necessary to account for all the known proteins but on the other hand these detailed models possess redundant parameters which will lead to an unnecessary increase in the cost of computation. For example, consider the situation in Figures 1B,C where a detailed hippocampal CA3 region pyramidal neuron model is simulated under control conditions (B) and by knocking out its calcium-activated potassium channel (C). It is apparent from the figure that under both the conditions the action potential generated is unchanged, which indicates that incorporating all of the “known” proteins need not necessarily lead to a significant change in the model output of interest (in this case, an action potential). It is worth mentioning that the model described above involves only 897 ordinary differential equations, which is far less than the number of equations in a model accommodating all the neurons in the CA3-CA1 region [estimated to be ~20 × 106 (West and Gundersen, 1990)]; the amount of redundancy in the latter model could be overwhelming and pruning the less significant proteins would aide in generating a region specific or whole-brain simulation. Of course, it is a “brigade” of interconnected neurons (identified experimentally by local field potential recordings), but not a single neuron per se, that plays a role in performing a task (Miller and Cohen, 2001; Buschman et al., 2012). This may contribute to an additional level of redundancy that needs to be assessed and optimized in order to successfully model the CA3-CA1 region.
An important player left out of the discussion above is the peri-synaptic astrocyte. In recent years, it has been demonstrated that the astrocytes can: (1) facilitate or depress synaptic plasticity (De Pittà et al., 2015), (2) synchronize CA1 neuronal firing (Fellin et al., 2004), (3) modulate extracellular field potentials (Lee et al., 2014), (4) repair damaged synapses (Wade et al., 2012), and/or (5) initiate epileptic discharges (Reato et al., 2012; Tewari and Parpura, 2013). It has also been hypothesized that astrocytes can (1) store memories (Caudle, 2006), (2) promote motor-skill learning (Padmashri et al., 2015), and (3) modulate sleep (Halassa et al., 2009). Considering this overwhelming evidence of the involvement of astrocytes in brain activity, it has become important to integrate the effect of astrocyte signaling while simulating region specific neural oscillations or whole-brain rhythms. In the past decade, efforts have been made to integrate detailed models of different neurons on a large scale to mimic brain region specific neural oscillation patterns (Traub et al., 2005; Reimann et al., 2013), however, astrocytes have been left out of their calculations.
Recently, there have been attempts to include astrocytes in modeling of synaptic transmission. For example, Figures 1D–G show simulations from Tewari and Parpura (2013) performed in the absence (Figures 1D,E) and the presence (Figures 1F,G) of astrocyte signaling. Briefly, these model simulations show an effect of extra-synaptic signaling on the amplitude and the frequency of neural oscillations. The amplitude of neural oscillations is represented by field potentials and the frequency of neural oscillations is estimated using fast Fourier transform (FFT). It is apparent from these simulations that the presence of astrocyte increases the amplitude of neural oscillations (compare Figure 1D and Figure 1F) and also orchestrates neural firing to occur at a certain frequency (note “asterisk” in Figure 1G). Note that these simulations were performed under minimal recurrent synapses within a neural population which suggests that both neural oscillation amplitude and frequency would change depending upon astrocyte input.
Two types of modeling issues have been introduced above, (1.) which arises due to redundant model parameters and (2.) which arises due to the structural limitations of the model (e.g., ignoring glio-transmission in a model of CA3-CA1 region). To avoid these issues, as mentioned earlier, two things need to be considered before even initiating mathematical analysis of an experimental dataset:
(a) The extent to which a given mathematical model can mimic a biological response.
(b) Level of details that can be ignored in an experimental data-set without significant loss in the biological question being addressed.
Action potentials generated using the famous Hodgkin-Huxley model (shown in Figure 1A) could be considered today as the case (2) as some of the details we know today are not included in the model. However, it is noteworthy that the time taken to simulate the Hodgkin-Huxley model is more than 500 times less as compared to the more elaborate Traub model (shown in Figure 1B), which can be considered as the case (1). Although the action potentials generated using these two models are noticeably different, there are methods available that can help build on (improve) the Hodgkin-Huxley model in a parsimonious way or reduce the Traub model to be computationally less expensive. The first step toward building a new model (or modifying an old model) should be to gather as much data as possible (from literature and/or experiments). The models developed should be checked for parsimony using Akaike information criterion (Bozdogan, 1987) or Bayesian information criterion (Neath and Cavanaugh, 2012). The best practice for estimating the parameters is to use a global optimization (Vinnakota and Bugenhagen, 2013) technique along with a local optimization technique (Byrd et al., 1999). Moreover, sensitivity analysis methods are very useful in identifying sensitive or insensitive parameters to facilitate model reduction (Saltelli et al., 2008), and should be applied before parameter estimation.
Future models of synaptic plasticity need to integrate the effect of astrocytes on the frequency of neural synchrony in different brain regions. It is understandable that prediction of region specific firing patterns would involve the integration of all possible neuron-astrocyte-neuron interactions in the region of interest which can be computationally challenging. For example, simulation of the network model presented in Figures 1D–G takes about 48 h on a laptop computer. Therefore, it is really important to employ modeling strategies which lead to simplified, computationally tractable and biologically relevant mathematical models.
Author Contributions
All authors listed, have made substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We acknowledge the support by the National Institutes of Health (The Eunice Kennedy Shriver National Institute of Child Health and Human Development award HD078678 for VP; and National Institute of General Medical Sciences award P50-GM094503 for ST).
References
Bernstein, J. (1912). Elektrobiologie: Die Lehre von den Elektrischen Vorgangen im Organismus auf Moderner Grundlage Dargestellt. Wiesbaden: Springer Fachmedien Wiesbaden.
Bower, J. M., and Beeman, D. (1995). The Book of GENESIS: Exploring Realistic Neural Models with the GEneral NEural SImulation System. Internet Edition.
Bozdogan, H. (1987). Model selection and Akaike's information criterion (AIC): The general theory and its analytical extensions. Psychometrika 52, 345–370. doi: 10.1007/BF02294361
Buschman, T. J., Denovellis, E. L., Diogo, C., Bullock, D., and Miller, E. K. (2012). Synchronous oscillatory neural ensembles for rules in the prefrontal cortex. Neuron 76, 838–846. doi: 10.1016/j.neuron.2012.09.029
Byrd, R. H., Hribar, M. E., and Nocedal, J. (1999). An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 9, 877–900. doi: 10.1137/S1052623497325107
Caudle, R. M. (2006). Memory in astrocytes: a hypothesis. Theor. Biol. Med. Model. 3:2. doi: 10.1186/1742-4682-3-2
De Pittà, M., Brunel, N., and Volterra, A. (2015). Astrocytes: orchestrating synaptic plasticity? Neuroscience doi: 10.1016/j.neuroscience.2015.04.001. [Epub ahead of print].
Fellin, T., Pascual, O., Gobbo, S., Pozzan, T., Haydon, P. G., and Carmignoto, G. (2004). Neuronal synchrony mediated by astrocytic glutamate through activation of extrasynaptic NMDA receptors. Neuron 43, 729–743. doi: 10.1016/j.neuron.2004.08.011
Halassa, M. M., Florian, C., Fellin, T., Munoz, J. R., Lee, S. Y., Abel, T., et al. (2009). Astrocytic modulation of sleep homeostasis and cognitive consequences of sleep loss. Neuron 61, 213–219. doi: 10.1016/j.neuron.2008.11.024
Hodgkin, A. L., and Huxley, A. F. (1952). A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544. doi: 10.1113/jphysiol.1952.sp004764
Lee, H. S., Ghetti, A., Pinto-Duarte, A., Wang, X., Dziewczapolski, G., Galimi, F., et al. (2014). Astrocytes contribute to gamma oscillations and recognition memory. Proc. Natl. Acad. Sci. U.S.A. 111, E3343–E3352. doi: 10.1073/pnas.1410893111
Miller, E. K., and Cohen, J. D. (2001). An integrative theory of prefrontal cortex function. Ann. Rev. Neurosci. 24, 167–202. doi: 10.1146/annurev.neuro.24.1.167
Neath, A. A., and Cavanaugh, J. E. (2012). The Bayesian information criterion: background, derivation, and applications. Wiley Interdiscip. Rev. 4, 199–203. doi: 10.1002/wics.199
Padmashri, R., Suresh, A., Boska, M. D., and Dunaevsky, A. (2015). Motor-skill learning is dependent on astrocytic activity. Neural Plast. 2015:938023. doi: 10.1155/2015/938023
Reato, D., Cammarota, M., Parra, L. C., and Carmignoto, G. (2012). Computational model of neuron-astrocyte interactions during focal seizure generation. Front. Comput. Neurosci. 6:81. doi: 10.3389/fncom.2012.00081
Reimann, M. W., Anastassiou, C. A., Perin, R., Hill, S. L., Markram, H., and Koch, C. (2013). A biophysically detailed model of neocortical local field potentials predicts the critical role of active membrane currents. Neuron 79, 375–390. doi: 10.1016/j.neuron.2013.05.023
Saltelli, A., Ratto, M., Andres, T., Campolongo, F., Cariboni, J., Gatelli, D., et al. (2008). Global Sensitivity Analysis: The Primer. Chichester: John Wiley & Sons.
Tewari, S., and Parpura, V. (2013). A possible role of astrocytes in contextual memory retrieval: An analysis obtained using a quantitative framework. Front. Comput. Neurosci. 7:145. doi: 10.3389/fncom.2013.00145
Traub, R. D., Contreras, D., Cunningham, M. O., Murray, H., LeBeau, F. E., Roopun, A., et al. (2005). Single-column thalamocortical network model exhibiting gamma oscillations, sleep spindles, and epileptogenic bursts. J. Neurophysiol. 93, 2194–2232. doi: 10.1152/jn.00983.2004
Traub, R. D., Jefferys, J. G., Miles, R., Whittington, M. A., and Tóth, K. (1994). A branching dendritic model of a rodent CA3 pyramidal neurone. J. Physiol. 481(Pt 1), 79–95. doi: 10.1113/jphysiol.1994.sp020420
Vinnakota, K. C. Bugenhagen, S. M. (2013). “Optimization and parameter estimation: genetic algorithms,” in Encyclopedia of Systems Biology, eds W. Dubitzky, O. Wolkenhauer, K.-H. Cho, and H. Yokota (New York, NY: Springer), 1600–1604. doi: 10.1007/978-1-4419-9863-7_291
Wade, J., McDaid, L., Harkin, J., Crunelli, V., and Kelso, S. (2012). Self-repair in a bidirectionally coupled astrocyte-neuron (AN) system based on retrograde signaling. Front. Comput. Neurosci. 6:76. doi: 10.3389/fncom.2012.00076
Keywords: neurons, astrocytes, mathematical model, parameter estimation
Citation: Tewari SG, Gottipati MK and Parpura V (2016) Mathematical Modeling in Neuroscience: Neuronal Activity and Its Modulation by Astrocytes. Front. Integr. Neurosci. 10:3. doi: 10.3389/fnint.2016.00003
Received: 01 December 2015; Accepted: 14 January 2016;
Published: 04 February 2016.
Edited by:
Ye Chen, Navy Medical Research Center, USAReviewed by:
Abdelmalik Moujahid, University of the Basque Country UPV/EHU, SpainCopyright © 2016 Tewari, Gottipati and Parpura. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shivendra Tewari, dGV3YXJpc2dAZ21haWwuY29t;
Vladimir Parpura, dmxhZEB1YWIuZWR1