
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Immunol., 12 March 2024
Sec. Cancer Immunity and Immunotherapy
Volume 15 - 2024 | https://doi.org/10.3389/fimmu.2024.1363144
This article is part of the Research TopicMathematical Modeling and Computational Predictions in OncoimmunologyView all 10 articles
Mechanistic learning refers to the synergistic combination of mechanistic mathematical modeling and data-driven machine or deep learning. This emerging field finds increasing applications in (mathematical) oncology. This review aims to capture the current state of the field and provides a perspective on how mechanistic learning may progress in the oncology domain. We highlight the synergistic potential of mechanistic learning and point out similarities and differences between purely data-driven and mechanistic approaches concerning model complexity, data requirements, outputs generated, and interpretability of the algorithms and their results. Four categories of mechanistic learning (sequential, parallel, extrinsic, intrinsic) of mechanistic learning are presented with specific examples. We discuss a range of techniques including physics-informed neural networks, surrogate model learning, and digital twins. Example applications address complex problems predominantly from the domain of oncology research such as longitudinal tumor response predictions or time-to-event modeling. As the field of mechanistic learning advances, we aim for this review and proposed categorization framework to foster additional collaboration between the data- and knowledge-driven modeling fields. Further collaboration will help address difficult issues in oncology such as limited data availability, requirements of model transparency, and complex input data which are embraced in a mechanistic learning framework
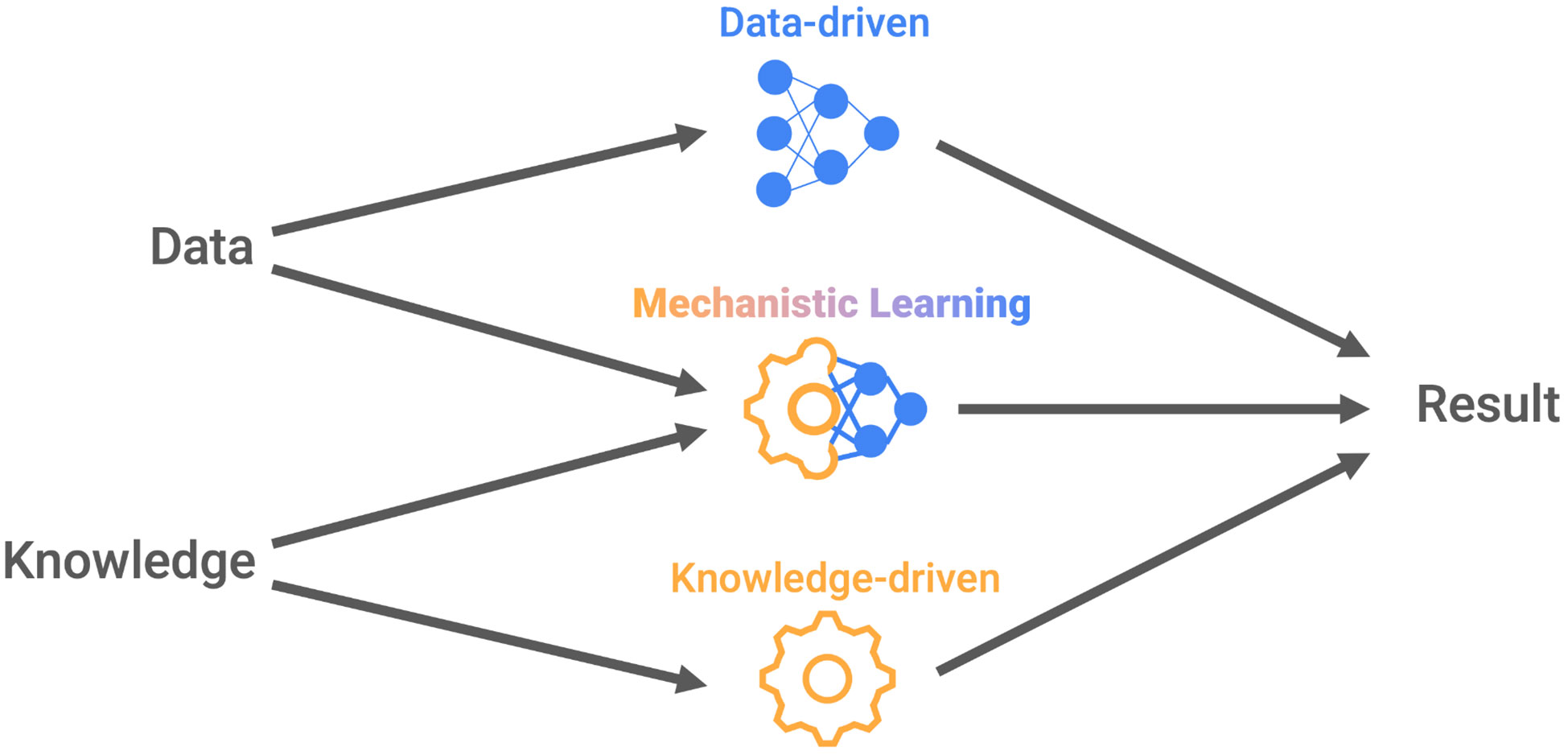
Graphical Abstract Data and knowledge both drive the progress of research and are the cornerstones of modeling. Depending on the emphasis, both data-driven (exemplified by machine and deep learning) and knowledge-driven (exemplified by mechanistic mathematical modeling) models generate novel results and insights. Mechanistic learning describes approaches that employ both data and knowledge in a complimentary and balanced way.
An increasing understanding of cancer evolution and progression along with growing multi-scale biomedical datasets, ranging from molecular to population level, is driving the research field of mathematical oncology (1). Mathematical oncology aims to bridge the gaps between medicine, biology, mathematics, and computer science to advance cancer research and clinical care. Both data and understanding of cancer biology contribute to this aim. Furthermore, modeling in the context of clinical application poses a range of challenges that need to be met in order to ensure practical translation: data sparsity, heterogeneity, and source bias need to be accounted for, while the complexity of the model has to remain balanced regarding flexibility, interpretability, and explainability. Finally, one must consider the risk of model overfitting, together with robustness and generalization strength.
Data science may be defined as “a set of fundamental principles that support and guide the principled extraction of information and knowledge from data” (2). Here, problem-solving is approached from the perspective of a learning process accomplished through observing diverse examples (3). Relationships between various types of input data (e.g., omics and imaging) and outcomes (e.g., overall survival) are abstracted where a mechanistic understanding of a relationship is missing or otherwise not accounted for. In this context, we refer to it as “data-driven” modeling. For oncology, data-driven approaches address a variety of applications to further scientific progress and task automation. Prime examples include predictions of drug response, tumor subtyping, and outcome as well as auto-segmentation of tumors on imaging.
An alternative is to formulate a specific guess on how relevant variables interact between input and output through the formulation of a mathematical model. Bender defines a mathematical model as an “abstract, simplified, mathematical construct related to part of reality and created for a particular purpose” (4). Here the formulation of deliberate approximations of reality through equations or rules is key (5). In turn, the quality and limits of this approximation, which we refer to as “knowledge-driven” modeling, are validated with data. Independent of the use of a data science or a mathematical modeling formulation, “data” and “knowledge” are indispensable. The emphasis on data and knowledge may vary leading to the terminology of “data-driven” and “knowledge-driven” modeling (6). The fluid boundaries between these concepts motivate their combination.
The evolving field of mechanistic learning (7, 8) aims to describe synergistic combinations of classical mathematical modeling and data science (9, 10). In this review, we provide an overview of the key aspects of these approaches, explain possible ways of combining them, present a selection of examples, and discuss how mechanistic learning can thrive in mathematical oncology. In doing so, we aim to draw awareness to similarities and synergies between knowledge- and data-driven modeling, noting that this combination could help push mathematical oncology into the clinic as reliable, data-supported, and explainable models in the context of oncology (11).
As per definition, data- and knowledge-driven modelling are complementary perspectives for approaching research questions. Here, we address similarities and differences to understand synergies at the interface of these fluid concepts.
According to Rockne et al. (1), the goal of knowledge-driven modeling is to describe the behavior of complex systems based on an understanding of the underlying mechanisms rooted in fundamental principles of biology, chemistry, and physics. While the formulation of the “model”, i.e. the approximation of reality, is flexible, the overarching aim is to gain a deeper understanding of processes driving the system’s behavior often through simulation and analysis of unobserved scenarios. Here, mathematical formulas or systematic processes are purposefully crafted to reflect key aspects of reality with inevitable simplifying assumptions. For example, dimensionality is reduced, dynamic processes are approximated as time-invariant, or biological pathways are reduced to key components (12). Conceptualizing these assumptions requires a deep understanding of the biomedical processes and modeling goals. These demands are met through interdisciplinary collaboration and validation. In the absence of experimental data, it is still possible to analyze and simulate to expose dynamics emerging from model building blocks (13–15). These extrapolations beyond the range of validation data are rooted in the confidence in the quality of the approximation of the biomedical reality, i.e. the quality of the knowledge and its implementation.
It is tempting to suggest that knowledge-driven models are inherently interpretable. Yet, the implementation of chains of relationships can formulate complex inverse problems. Subsequently, post hoc processing through parameter identifiability and sensitivity analyses is key (16, 17). This can identify previously unknown interactions between system components to generate hypotheses for experimental and clinical validation.
Knowledge-driven modeling has successfully been applied to investigate different aspects of cancer including somatic cancer evolution and treatment. We refer the interested reader to recent review articles (18, 19) covering for instance different fractionation schemes for radiotherapy (20, 21), the onset and influence of treatment-induced tumor resistance (22), or cancer evolution (23). A popular application of knowledge-driven models is the simulation of in silico trials for hypothesis generation in simulated cohorts (24–26).
A common understanding of data-driven modeling (e.g. - machine learning, deep learning and classical statistics) is the creation of insight from empirical examples (27). A performance metric (28, 29) is optimized to uncover patterns and relationships between input data and output task. The validity of data-driven models should be studied carefully, in particular the dependency of the results on the chosen performance metric (29). It is also key to consider the optimization convergence. If this process fails, the model will be uninformative.
Purely data-driven models do not readily leverage the community’s understanding of the system under study but instead often employ highly parameterized models. The many degrees of freedom allow flexibility to approximate complex and mechanistically unknown relationships, e.g. deep neural networks act as “universal function approximators’’ (30). New information can be extracted from the data through this structuring but the extensive parameterization may obscure how the decision process is formed. Post hoc processing is required to uncover the nature of the approximated relationship through interpretability and explainability analysis (31). The models’ flexibility also makes them vulnerable to overfitting. Appropriately large amounts of training data and stringent data splits for fitting (training) and validation (32) are necessary to mitigate this risk. Data quantity and quality, i.e. its task specificity and ability to cover a variety of relevant scenarios, are equally important.
Generally, the application focus differs from that of knowledge-driven models. Generalization beyond the observed data space is often challenging (33). It is essential to rely on robust training regimes (34) and consider model limitations as performance is compromised in scenarios not (sufficiently) covered by data (33).
In summary, data-driven approaches are powerful tools for knowledge generation. In oncology, data-driven approaches have previously contributed substantially to scientific progress and process automation (35). To name just a few examples, (un-)supervised machine learning has greatly supported areas of drug response prediction (36, 37) and molecular tumor subtype identification (38, 39), whereas generative models and deep learning have revolutionized computer vision tasks such as volumetric tumor segmentation (40, 41), image-based outcome predictions (42, 43) and automated intervention planning.
Table 1 summarizes and contrasts key characteristics of the extremes of purely data- and knowledge-driven modeling, yet boundaries between these models remain fluid for many applications. The fundamental steps of data- and knowledge-driven modeling have parallels despite varying terminology: a subset of data is used to construct and calibrate the model, then further data is necessary for validation and refinement. In data-driven modeling, we first formulate the learning task (i.e. identifying features, labels, and loss function), and architecture selection. In knowledge-driven modeling, we start by deriving equations/mathematical rules. Both algorithms are subsequently compared to real-world data to optimize hyperparameters (i.e., structural model implementations) and to learn model parameters for fitting. The same optimization principles apply but the extent to which mechanistic priors are accounted for in the design of the objective function varies. Finally, validation, ideally on independently sourced data, is performed to assess the model’s performance.
Given these similarities and differences, it is important to account for possible challenges upon combining approaches. Model bias or conflicting information generated by addressing the same task with differently motivated approaches needs to be carefully considered. At the same time, there exists ample room to harness synergies between knowledge and data-driven modeling under the umbrella of mechanistic learning. Specifically, differences regarding data requirements, model complexity, extrapolation, and application regimes imply that a combination of both approaches may mitigate individual limitations. For example, parameters of a mechanistic mathematical model can be estimated by a deep learning algorithm from complex multi-omics data or knowledge-driven descriptions can be used to constrain the large range of possible solutions of a complex data-driven approach to a meaningful subset. In the following sections, we provide a detailed overview of how these combinations can be achieved and provide real-world application examples to motivate these.
“Mechanistic learning” (7, 8) can take on many facets by shifting the emphasis of the “data” and “knowledge” paradigms upon model design and fitting. While a partition of mechanistic learning into simulation-assisted machine learning, machine-learning-assisted simulation, and a hybrid class for approaches falling between these definitions is intuitive at first (44), it fails to describe the variety of hybrid approaches. We suggest a more abstract classification (Figure 1):
● Sequential - Knowledge-based and data-driven modeling are applied sequentially building on the preceding results
● Parallel - Modeling and learning are considered parallel alternatives to complement each other for the same objective
● Extrinsic - High-level post hoc combinations
● Intrinsic - Biomedical knowledge is built into the learning approach, either in the architecture or the training phase
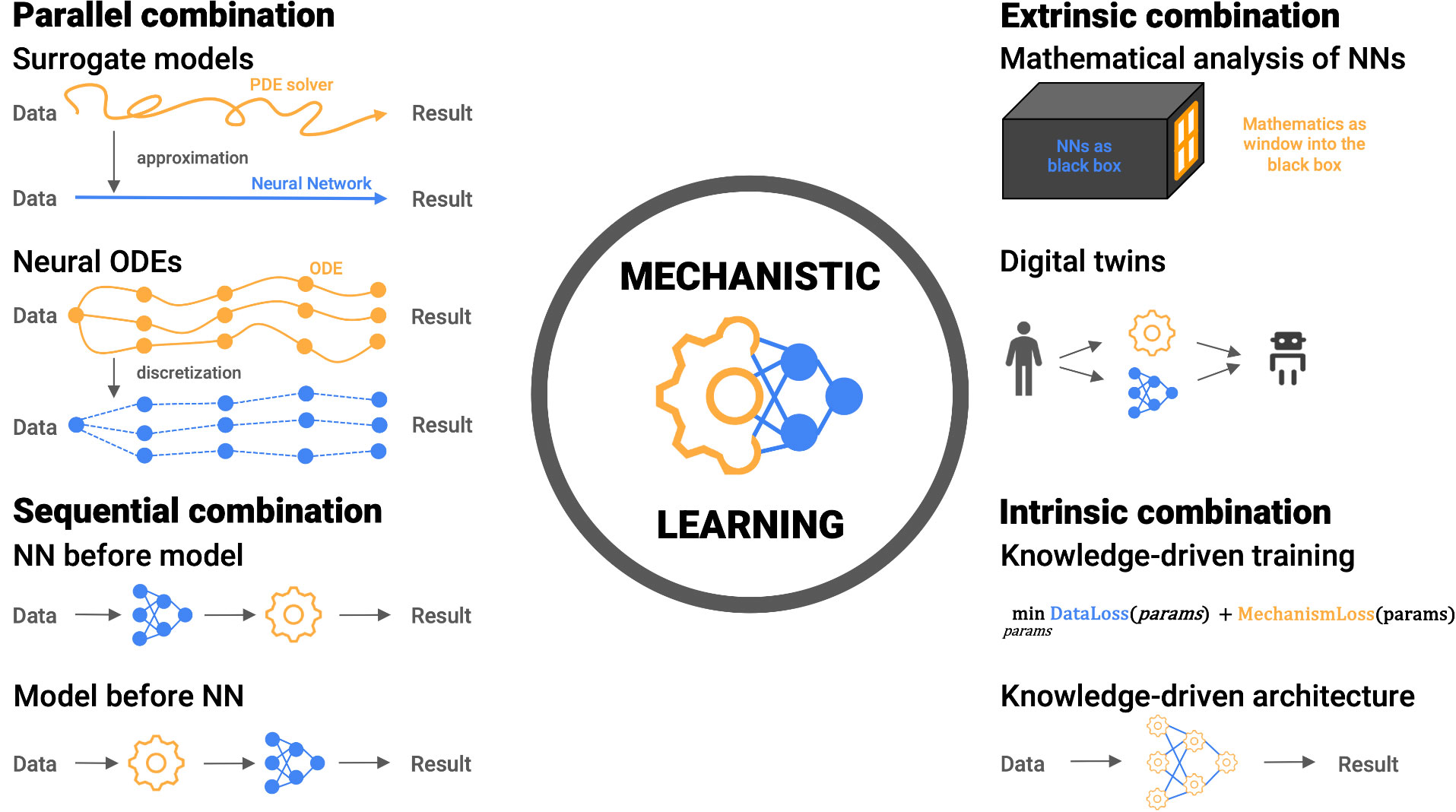
Figure 1 Examples of mechanistic learning structured in four combinations: Parallel combinations (top left) with examples of surrogate models and neural ordinary differential equations (ODEs). Data- and knowledge-driven models act as alternatives to complement each other for the same objective. Sequential combinations (bottom left) apply data- and knowledge-driven models in sequence to ease the calibration and validation steps. Extrinsic combinations (top right) combine knowledge-driven and data-driven modeling at a higher level. For example, mathematical analysis of data-driven models and their results or as complementary tasks for digital twins. Intrinsic combinations (bottom right), like physics- and biology-informed neural networks include the knowledge-driven models into the data-driven approaches. Knowledge is included in the architecture of a data-driven model or as a regularizer to influence the learned weights.
Whereas sequential and parallel combinations make a deliberate choice of aspects of data- and knowledge-driven models to coalesce, extrinsic and intrinsic combinations actively interlace these. Thus, the complexity with respect to implementation and interpretation grows from sequential to intrinsic combinations. While most implementations readily fit into one of these four classes, we emphasize that we do not consider the combinations as discrete encapsulated instances. Instead, we view all synergistic combinations on a continuous landscape between the two extremes of purely knowledge- and data-driven models (Figure 2).
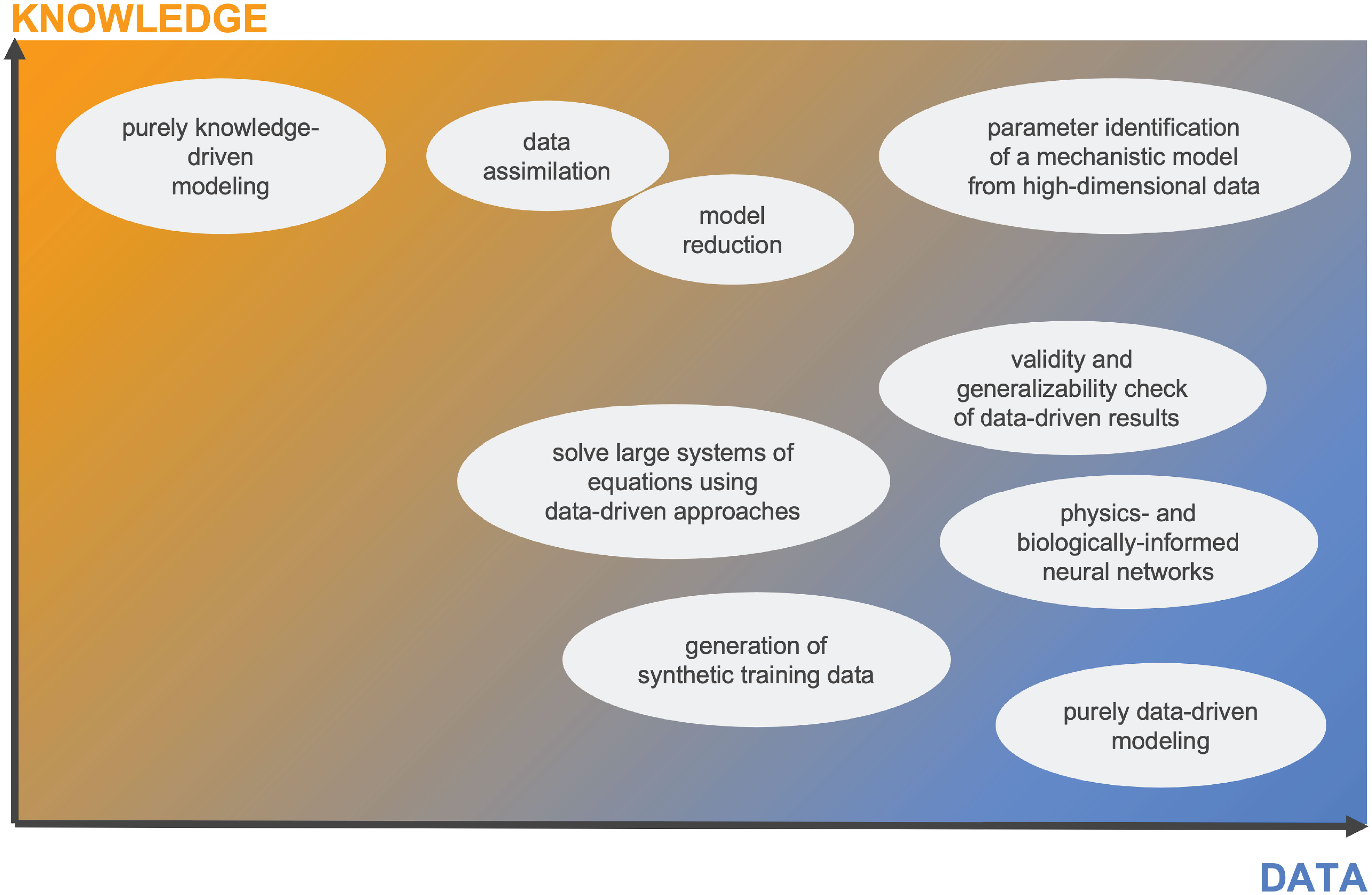
Figure 2 The mechanistic learning landscape shows room for the combination of data-driven and knowledge-driven modeling. We suggest that purely data-driven or purely knowledge-driven models represent the extremes of a data-knowledge surface with ample room for combinations in different degrees of synergism. Further, in the left-bottom corner with almost no data nor knowledge, any modeling or learning technique is limited.
Sequential approaches harness knowledge and data-driven aspects as sequential and computationally independent tasks by disentangling the parameter/feature estimation and forecasting steps. They strive to attain mechanistic learning objectives by interlinking inputs from one approach with another. This could involve utilizing data-driven methods for estimating mechanistic model parameters or implementing feature selection in a data-driven model guided by mechanistic priors. Although sequential frameworks are straightforward to implement and interpret, often their computational demands increase significantly, taking into account both computational requirements and the limitations inherent in the individual approaches (e.g., data requirements, accuracy of prior knowledge).
In medical science, data availability remains a key challenge (45). However, there often exists a strong hypothesis regarding the driving features of a specific prediction task. A simple but effective means of improving the performance of data-driven algorithms is a deliberate choice of model architecture, data preprocessing, and model inputs. For example, focusing the input of a deep neural network to disease-relevant subregions of an image boosted classification performance in a data-limited setting (46), and expert-selected features were used to reduce data requirements of image processing tasks dimensionality and data requirements of image processing tasks (47). Similarly important is a deliberate choice of model architecture (48–50). For instance, while convolutional blocks are the staple for computer vision tasks, similar approaches exist for sequential data (e.g. sequence-to-sequence transformers, recurrent neural networks, or graph-based models (51, 52)). While no mechanistic modeling is conducted per se deliberate feature and architecture selection includes additional information. Ultimately, features can also be identified by knowledge-driven modeling (53, 54).
Feature engineering is the process of designing input features from raw data (55). This process can be guided by a deeper understanding of the underlying mechanisms, including physical and biochemical laws or causal relationships.
Aspects of a mechanistic model can serve as input features to or outputs from machine learning models. This strategy of “mechanistic feature engineering”, was used by Benzekry et al. to predict overall survival in metastatic neuroblastoma patients (56). First, a mechanistic model of metastatic dissemination and growth was fitted to patient-specific data. Then, a multivariate Cox regression model predicted overall survival from available clinical data with or without patient-specific mechanistic model parameters. They found that including the fitted mechanistic model parameters greatly enhanced the predictive power of the regression. One problem in this truly sequential setting is that it is difficult to address uncertainty propagation. Therefore, a challenging limitation persists, as the propagation of uncertainties and prediction errors may amplify within the context of the complete framework.
A common problem in knowledge-driven modeling for longitudinal predictions is parameter identifiability and fitting given limited data and complex systems of equations. The bottleneck lies in the lack of a detailed understanding of the mechanistic relation between input data and desired output, rather than a purely computational limitation.
Similar to using mechanistic feature engineering for data-driven model inputs, data-driven approaches can also be employed to discover correlations within unstructured, high-dimensional data to provide inputs to knowledge-driven models. Depending on the specific application a range of methods are possible: imaging data are preprocessed by convolutional architectures, whereas omics data could be processed with network analysis, graph-based, or standard machine learning models. These correlations are then harnessed to predict the parameters of a mechanistic approach. Importantly, each model is implemented and trained/fitted independently, implying a high-level, yet easily interpretable combination. This sequential combination harnesses the ability of data-driven models to extract information in the form of summarizing parameters from high dimensional and heterogeneous data types. Importantly, the type of data required for such analysis needs to meet the criteria of knowledge-driven (e.g., longitudinal information) and data-driven (e.g., sufficient sample size) approaches alike - this may restrict applicability in light of limited data quality or excessive noise. Similarly, limitations such as robustness and prediction performance for the estimated parameters should be considered.
In practice, Perez-Aliacar et al. (57) predicted parameters of their mechanistic model of glioblastoma evolution from fluorescent microscopy images. This combination of models has also been suggested in the context of data-driven estimation of pharmacokinetic parameters for drugs (58). Moreover, data-driven models enable parameter inference by studying parameter dependencies of simulation results through approximate Bayesian computation (59, 60) or genetic algorithms (61).
Another sequential construct consists in using machine learning models to predict the residuals of a mechanistic model prediction. Kielland et al. utilized this technique to forecast breast cancer treatment outcomes under combination therapy from gene expression data (62). Initially, a mechanistic model of the molecular mechanisms was calibrated with cell line data to enable patient-specific predictions. Subsequently, various machine learning models were employed to predict the residuals of the mechanistic model from the available expression of more than 700 genes. While the performance of the combined strategy was comparable to using machine learning alone, it offered three advantages. First, the mechanistic model provided a molecular interpretation of treatment response. Additionally, this approach facilitated the discovery of important genes not included in the mechanistic model. Hence, this approach can potentially incorporate emerging biological knowledge and new therapeutics without additional data required for machine learning alone. Note that this sequential strategy facilitates the inclusion of both mechanistically understood features and others that may not be as clear, a common scenario in treatment forecasting.
In summary, sequential combinations are attractive due to their clear path toward implementation and interpretation with limitations due to prerequisites on data, mechanistic understanding or uncertainty propagation. While future directions may dive deeper into harnessing more complex input data (e.g. multi-omics, multimodal) for mechanistic model inputs, the technical advancement for sequential combinations remains dictated by the progress in the individual fields.
Parallel combinations blend advantages of purely data- or knowledge-driven models without changing the anticipated evaluation endpoint. These are alternatives for the same task as a purely data- or knowledge-driven approach and hence aspects concerning data requirements, implementation, model robustness, and performance can be compared. This makes them attractive for high-stakes decision scenarios, such as clinical application (e.g. tumor growth prediction).
Many phenomena in oncology can be readily formulated using large systems of equations. However, solving large models comes at a high computational cost. Utilizing methods such as model order reduction aids in optimizing the computational efficiency of the solving process. This approach typically demands substantial mathematical expertise and is not suitable for time- or resource-constrained scenarios such as real-world clinical deployment. Neural networks, as universal function approximators, offer an efficient alternative. In practice, data-driven models are trained on numerical simulation results and approximate a solution to the system of equations. The inference step of the successfully trained model takes a fraction of the computational resources compared to the full mechanistic model (63, 64).
A related concept is the generation of vast amounts of “synthetic” training data (65) based on a small set of “original” data points. While synthetic training data can improve the accuracy of many learning-based systems, care needs to be taken to prevent encoding faulty concepts or misleading biases into the training data that are not present in reality (66, 67). Any uncertainty or bias introduced during the training of the synthetic data generator is inherent in the resulting samples. This limitation could easily be overlooked within downstream tasks, underscoring the importance of meticulously designing a surrogate model.
For example, Ezhov et al. (68) introduced a deep learning model performing inverse model inference to obtain the patient-specific spatial distribution of brain tumors from magnetic resonance images, addressing the computational limitations of previous partial differential equation (PDE)-based spatial tumor growth and response models. A similar brain tumor growth model based on an encoder-decoder architecture trained on 6,000 synthetic tumors generated from a PDE model (69).
The term “neural ordinary differential equation”, or “neural ODE” originated from the notion of viewing neural networks as discretized ODEs or considering ODEs to be neural networks with an infinite amount of layers (70–72). In that sense, the knowledge-driven approaches using ODEs and the data-driven approach using neural networks are parallel perspectives of the same concept. While not every data-driven model can be interpreted as discretized ODEs and not every question for ODEs can be answered by a discretization to a neural network, neural ODEs can often be a helpful concept to translate between knowledge- and data-driven modeling. More generally, a neural ODE can also be seen as a differential equation that uses a neural network to parameterize the vector field. As such, this approach offers advantages over neural networks, including high-capacity function approximation and easy trainability, together with the extensive available theory and tools for the numerical treatment of differential equations. In addition, the continuous-time regime of differential equations allows treating irregular time series data in a natural way (73).
Neural ODEs have already been used for a variety of tasks in oncology ranging from genome-wide regulatory dynamics (74) and breast tumor segmentation in medical images (75) to time-to-event modeling (76). Importantly, neural ODEs can generate realistic synthetic data, such as longitudinal patient trajectories. As these synthetic patient data are anonymous, regularly sampled, and complete (i.e. no missing data) they address key challenges of medical data analytics: data privacy, limited data, missing data, variable data quality, and sampling time points. Synthetic patients can be shared across institutes as high-quality samples to train large-scale models, ensuring compliance with international data privacy regulations (77).
While oncology research generates vast amounts of data, extracting and consolidating mechanistic understanding from data is a laborious process reliant on human experts. Symbolic regression allows for automated and data-driven discovery of governing laws expressed as algebraic or differential equations. This method finds a symbolic mathematical expression that accurately matches a dataset of label-feature pairs. Two prominent symbolic regression techniques are genetic programming-based optimization (78) and sparse regression (79). In genetic programming, closed-form expressions are represented as trees and evolved such that trees with high goodness-of-fit are selected for further exploration. In sparse regression strategies, the target expression is assumed to be a linear combination of certain “basis functions”, and L1 regularization is used to select and weight a small combination of them.
Despite remarkable success in physics (78), symbolic regression applications in oncology are still scarce. In one example, by Brummer et al. (80), sparse regression was employed to estimate a system of ODEs from in vitro CAR T-cell glioma therapy data. Compared to knowledge-based models, this data-driven approach offers new insights into the biological dynamics as the model form is not constrained.
However, estimating derivatives from high noise and sparse longitudinal measurements, like many from clinical oncology, remains challenging. Several groups have used variational formulations of ODEs and PDEs in the optimization step without relying on estimating derivatives from noisy and sparse data (81–83). Bayesian approaches applied to genetic programming have also proven successful in situations where existing non-Bayesian approaches failed (84). Other promising directions in oncological research are Koopman theory (85) and the universal differential equation framework (86), where neural networks are used to model all or part of a differential equation, facilitating the discovery of governing equations, or parts of them, in cases where data are limited.
Extrinsic combinations make use of both mechanistic and data-driven approaches to address different aspects of the same problem or to post-process the output of a data-driven implementation.
Originating from analogies in manufacturing and engineering, the concept of digital twins (87–89) has recently gained interest in the oncology community. A digital twin is an in silico patient “twin” that recapitulates important patient characteristics and is used to simulate alternative treatment strategies and forecast disease progression (90). In the context of precision medicine, this implies that alternative treatment scenarios are simulated with the digital twin to select an optimal strategy. Hence, predictive modeling of longitudinal information regarding the expected patient trajectory is provided. The computational framework behind the digital twin can be based on mechanistic, data-driven, or a combined set of algorithms. We highlight the potential of combining mechanistic and data-driven modeling as side-by-side tasks, covering different aspects of one unifying digital twin.
Typically, for mechanistic digital twins, a mathematical framework describes the dynamics of tumor size, morphology, composition, and other biomarkers (91). The data-driven analogy is represented by machine learning algorithms, e.g., k-nearest neighbors but also more advanced architectures, to provide a prediction of the endpoint of interest based on established databases (92, 93). Both knowledge- and data-driven models enable the real-time adaptation of treatment protocols by simulating a range of scenarios. Importantly, harnessing the strengths of each method should be considered for optimal results. For instance, a data-driven prediction task could inform on patient subgrouping and identify likely outcomes, whereas mechanistic modeling would explore personalized treatment alternatives. Generally, digital twins can also serve as “virtual controls” to benchmark the efficacy of the patient’s current treatment regimen (94, 95). Wu et al. provide an in-depth review regarding the specific application example of digital twins for oncology applications including a mention of the roles of data-driven image analysis and knowledge-driven modeling. The trade-off between application focus and computational complexity of a digital twin has to be considered in light of the data available which may restrict the feasible complexity and performance. Limitations, such as the requirement for longitudinal data, the complexity of mid-treatment adjustment in clinical settings, and the overall complexity regarding a high-stakes decision process need to be accounted for (89).
Data-driven approaches are trained to optimize a performance metric, but performance alone is not driving a model’s application in (clinical) practice. Here, quantification of the uncertainty of model results, model robustness, as well as interpretability to explain why a model arrived at a certain conclusion are equally important (96). These questions are usually studied under the term explainable AI; for a survey we refer to Roscher et al. (97). Progress in advanced explainable AI dictates a mechanistic interpretation of a model’s decision-making process (98).
Addressing many of the questions related to deep learning is only possible using mathematical methods, i.e., challenges in the field of data-driven models are transformed to mathematical conjectures that are subsequently (dis)proven. This approach ensures that the results generated by models are mathematically reliable and transparent and thus better suited for clinical implementations.
Numerous examples underscore this point and provide motivation for employing intricate architecture designs based on mathematical formulations. A specific instance involves learning a specialized representation that elucidates cancer subtyping from multi-omics inputs, including transcriptomic, proteomic, or metabolomic data (77).
Data assimilation techniques bridge numerical models and observational data through optimization of starting conditions. Typical examples are Kalman or particle filter methods (99, 100), which can improve the accuracy of numerical predictions. For the interpretation and validation of simulation results, tools from data-driven modeling can be used to detect patterns in simulations (101). This approach is already performed in research fields outside the oncology domain (102). A prime example is the post-processing of complex numerical weather forecasting predictions using deep learning to boost overall performance (103, 104). Within oncology applications, machine learning and Bayesian statistics have also been used for uncertainty quantification which is important for clinical translation (105–107).
This combination incorporates a mechanistic formulation within a machine learning model either upon training as a contribution to the formulated objective function or a priori as a way of choosing the architecture of the data-driven model. As such, these are densely interconnected combinations.
Mechanism-informed neural networks such as physics-informed neural networks (PINNs) (108, 109) use mechanistic regularization upon training, i.e., equation-regularization, by guiding the possible solutions to physically relevant ones. The loss function combines performance loss with a regularization term assessing the deviation from a predefined set of equations. This approach reduces overfitting and ensures physically meaningful predictions. The final neural network will not satisfy the equations exactly but approximate them for the areas where training data is available. PINNs can be valuable for deciding whether an equation can be used to describe data by considering several related equations as regularizers.
Equation-regularization has previously been shown to enhance both the performance and interpretability of data-driven architectures. In the context of oncology, one example includes the modeling of tumor growth dynamics (110). Ayensa-Jiménez et al (111) used physically-guided NNs with internal variables to model the evolution of glioblastoma as a “go-or-grow” process given constrained resources such as metabolites and oxygen. The model-free nature of their approach allows for the incorporation of data from various boundary conditions and external stimuli, resulting in accurate tumor progression predictions even under different oxygenation conditions.
Rather than optimizing a network architecture through regularization, biology-informed neural networks constrain the model architecture to biological priors from the start. Typically in the context of network analysis, biological priors such as known interactions between genes and/or transcription factors are translated to nodes and edges in a graph (112, 113). The network is constrained to an established connectivity profile which greatly reduces the model complexity compared to a fully connected network. Similar to transfer learning where a different data-rich scenario is used to pretrain a model prior to refining specific weights on the limited target data, this approach uses expert insight to preset connections and weights. Lagergren et al. (114) proposed biology-informed neural networks that learn the nonlinear terms of a governing system, eliminating the need for explicitly specifying the mechanistic form of a PDE as is the case for PINNs. They tested their approach on real-world biological data to uncover previously overlooked mechanisms. Another example is given by Przedborski et al. (115) who used biology-informed neural networks to predict patient response to anti-PD-1 immunotherapy and present biomarkers and possible mechanisms of drug resistance. Their model offers insights for optimizing treatment protocols and discovering novel therapeutic targets. Indeed, this approach has found several applications, e.g., for the prediction of prostate cancer (112) and drug discovery (116). Despite similar naming conventions, biology- and physics-informed neural networks refer to distinct approaches. The latter distinguishes itself by integrating biological realism and enhancing interpretability for applications that predominately rely on multi-scale, multi-source data (such as omics). However, profound insight regarding the formulated biological process is indispensable. PINN applications regularize, i.e. do not strictly constrain implying more flexibility yet less interpretability.
Finally, in the context of generative approaches, differential equations have previously been incorporated into (deep) neural networks through variational autoencoders. While current examples were obtained from medical applications other than oncology (117, 118), they represent elegant solutions to allow for dynamic deep learning despite limited data, given careful hyperparameter tuning.
Hierarchical nonlinear models, also referred to as nonlinear mixed effects models, are a widely used framework to analyze longitudinal measurements on a number of individuals, when interest focuses on individual-specific characteristics (119). For instance, early in drug development, pharmacokinetics studies are carried out to gain insights into within-subject pharmacokinetics processes of absorption, distribution, and elimination (120). Typically, a parametric nonlinear model describing drug concentration change over time (individual-level model) is coupled with a linear model describing the relation between pharmacokinetic parameters and individual features (population-level model). One of the simplest population-level models is the random intercept model, which models individual parameter values as normally distributed around a typical value. This enables information sharing through each individual’s contribution to determine the typical value, while simultaneously allowing individual parameters that match the observed measurements. Moreover, in contrast to the sequential approach (section 3.1.3), hierarchical models allow for the propagation of uncertainty between the individual-level and population-level models. Applications in oncology range from tumor growth (121) to mutational dynamics in circulating tumor DNA (122) or metastatic dissemination (123).
Interestingly, hierarchical models have the potential to benefit from more sophisticated data-driven approaches to integrate high-throughput data, such as omics or imaging (8). This can be done by changing the linear covariate model with more complex machine learning algorithms able to capture complex relations between the parameters of the individual-level model and the high dimensional covariates (124, 125), and/or by using Bayesian inference (38).
Recently, machine and deep learning have become ubiquitous given their indisputable potential to learn from data (126). However, it is evident that medical applications, especially in oncology, are currently constrained by the extent and diversity of available data. Moreover, clinical translation involves high-stakes decisions that need to be backed up by evidence. The oncology field must address the critical challenges of limited data availability, model transparency, and complex input data. To overcome these bottlenecks, we need data-efficient, comprehensible, and robust solutions. Despite the growing interest in mechanistic mathematical modeling for medical applications, the success and opportunity of data-driven models must be taken into account. Strategically integrating knowledge- and data-driven modeling in mechanistic learning represents a logical progression to tackle the challenges in mathematical oncology. It aims to facilitate accurate, personalized predictions, leading to a more comprehensive understanding of cancer evolution, progression, and response.
Here, we identified opportunities for synergistic combinations and provided a snapshot of the current state-of-the-art for how such combinations are facilitated for oncology applications. We highlighted similarities in the mathematical foundation and implementation structure of optimization processes and pointed out differences with respect to data requirements and the role of knowledge and data in these approaches. It is important to structure the growing landscape of models at the interface of data- and knowledge-driven implementations. We hence propose systemizing combinations in four general categories: sequential, parallel, intrinsic, and extrinsic combinations. While sequential and parallel combinations are intuitive and easily implemented, intrinsic and extrinsic combinations incorporate a stronger degree of interlacing that requires a deeper understanding of both data science and mathematical theory. The choice of analysis tool should always keep in mind the quality, size, and type of data and knowledge in light of the underlying research question. An intentional combination of machine learning and mechanistic mathematical modeling can then leverage the strengths of both approaches to tackle complex problems, gain deeper insights, and develop more accurate and robust solutions. Mechanistic learning can take on many facets and is foreseen to grow in importance in the context of mathematical oncology with a particular focus on explainable AI, handling of limited data (e.g. efficient architecture design, data augmentation), and generation of precision oncology solutions. In this review, we discussed only the core concepts. Given the fluid boundaries between data- and knowledge-driven models and in light of the variety of approaches within each of these domains, an exhaustive listing of all combinations is infeasible. However, several future directions stand out. For instance, hybrid modeling with Bayesian statistics, deep generative approaches, or specific training regimes, including semi-supervised (contrastive) or reinforcement learning, are worth mentioning. Finally, despite the positive notion regarding mechanistic learning, certain limitations persist within both separate and combined approaches. Specifically ethical considerations should be addressed. These may arise from data privacy, algorithmic bias, or the clinical implementation of hybrid models.
Finally, with this work we strive to motivate a more active exchange between machine learning and mechanistic mathematical modeling researchers given the many parallels in terms of methodologies and evaluation endpoints, and the powerful results produced by mechanistic learning.
JM: Conceptualization, Formal analysis, Visualization, Writing – original draft, Writing – review & editing. CJ: Conceptualization, Supervision, Writing – review & editing. PM: Conceptualization, Supervision, Writing – review & editing. AK: Conceptualization, Writing – original draft, Writing – review & editing. SB: Conceptualization, Formal analysis, Project administration, Writing – original draft, Writing – review & editing.
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. JM was supported by NSF 1735095 - NRT: Interdisciplinary Training in Complex Networks and Systems. CJ was supported by the Swiss National Science Foundation (Ambizione Grant [PZ00P3_186101]). PM was supported in part by Cancer Moonshot funds from the National Cancer Institute, Leidos Biomedical Research Subcontract 21X126F, and by an Indiana University Luddy Faculty Fellowship. AK-L’s work was funded by the research centers BigInsight (Norges Forskningsråd project number 237718) and Integreat (Norges Forskningsråd project number 332645). SB was supported by the Botnar Research Center for Child Health Postdoctoral Excellence Programme (#PEP-2021-1008). Open access funding by ETH Zurich.
We thank Alexander Zeilmann and Saskia Haupt for many fruitful discussions and helpful contributions without which this manuscript would not have been possible. The collaboration that led to the design of this manuscript was fostered during the 2023 Banff International Research Station (BIRS) Workshop on Computational Modelling of Cancer Biology and Treatments (23w5007) initiated by Prof. M. Craig and Dr. A. Jenner.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1. Rockne RC, Scott JG. Introduction to mathematical oncology. JCO Clin Cancer Inform. (2019) 1–4. doi: 10.1200/CCI.19.00010
2. Provost F, Fawcett T. Data science and its relationship to big data and data-driven decision making. Big Data. (2013) 1:51–9. doi: 10.1089/big.2013.1508
3. Géron A. Hands-on Machine Learning with Scikit-Learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems. Sebastopol, California, USA:O’Reilly (2019).
5. Murray JD. Mathematical Biology: I. An Introduction Vol. 17. New York, NY: Springer New York (2002).
6. Obot OU, Attai KF, Onwodi GO. Integrating knowledge-driven and data-driven methodologies for an efficient clinical decision support system. In: Connolly TM, Papadopoulos P, Soflano M, editors. Advances in Medical Technologies and Clinical Practice. (Hershey, Pennsylvania, USA: IGI Global) (2022). p. 1–28.
7. Ciccolini J, Barbolosi D, André N, Barlesi F, Benzekry S. Mechanistic learning for combinatorial strategies with immuno-oncology drugs: can model-informed designs help investigators? JCO Precis Oncol. (2020) 4(4):486–91. doi: 10.1200/PO.19.00381
8. Benzekry S. Artificial intelligence and mechanistic modeling for clinical decision making in oncology. Clin Pharmacol Ther. (2020) 108:471–86. doi: 10.1002/cpt.1951
9. Baker RE, Peña J-M, Jayamohan J, Jérusalem A. Mechanistic models versus machine learning, a fight worth fighting for the biological community? Biol Lett. (2018) 14:20170660. doi: 10.1098/rsbl.2017.0660
10. Lorenzo G, Ahmed SR, Hormuth DA, Vaughn B, Kalpathy-Cramer J, Solorio L, et al. Patient-specific, mechanistic models of tumor growth incorporating artificial intelligence and big data. (2023). doi: 10.48550/ARXIV.2308.14925
11. Hatzikirou H. Combining dynamic modeling with machine learning can be the key for the integration of mathematical and clinical oncology: Comment on “Improving cancer treatments via dynamical biophysical models” by M. Kuznetsov, J. Clairambault, V. Volpert. Phys Life Rev. (2022) 40:1–2. doi: 10.1016/j.plrev.2022.01.002
12. Blair RH, Trichler DL, Gaille DP. Mathematical and statistical modeling in cancer systems biology. Front Physiol. (2012) 3. doi: 10.3389/fphys.2012.00227
13. Altrock PM, Liu LL, Michor F. The mathematics of cancer: integrating quantitative models. Nat Rev Cancer. (2015) 15:730–45. doi: 10.1038/nrc4029
14. Khajanchi S, Nieto JJ. Mathematical modeling of tumor-immune competitive system, considering the role of time delay. Appl Math Comput. (2019) 340:180–205. doi: 10.1016/j.amc.2018.08.018
15. Yasemi M, Jolicoeur M. Modelling cell metabolism: A review on constraint-based steady-state and kinetic approaches. Processes. (2021) 9:322. doi: 10.3390/pr9020322
16. Renardy M, Hult C, Evans S, Linderman JJ, Kirschner DE. Global sensitivity analysis of biological multiscale models. Curr Opin Biomed Eng. (2019) 11:109–16. doi: 10.1016/j.cobme.2019.09.012
17. Wieland F-G, Hauber AL, Rosenblatt M, Tönsing C, Timmer J. On structural and practical identifiability. Curr Opin Syst Biol. (2021) 25:60–9. doi: 10.1016/j.coisb.2021.03.005
18. Rockne RC, Scott JG. The 2019 mathematical oncology roadmap. Phys Biol. (2019) 16:041005. doi: 10.1088/1478-3975/ab1a09
19. McDonald TO, Cheng Y-C, Graser C, Nicol PB, Temko D, Michor F. Computational approaches to modelling and optimizing cancer treatment. Nat Rev Bioeng. (2023) 1:695–711. doi: 10.1038/s44222-023-00089-7
20. Ghaderi N, Jung J, Brüningk SC, Subramanian A, Nassour L, Peacock J. A century of fractionated radiotherapy: how mathematical oncology can break the rules. Int J Mol Sci. (2022) 23:1316. doi: 10.3390/ijms23031316
21. McMahon SJ, Prise KM. Mechanistic modelling of radiation responses. Cancers. (2019) 11:205. doi: 10.3390/cancers11020205
22. Yin A, Moes DJAR, Hasselt JGC, Swen JJ. & Guchelaar, H. A review of mathematical models for tumor dynamics and treatment resistance evolution of solid tumors. CPT Pharmacomet Syst Pharmacol. (2019) 8:720–37. doi: 10.1002/psp4.12450
23. Beerenwinkel N, Schwarz RF, Gerstung M, Markowetz F. Cancer evolution: mathematical models and computational inference. Syst Biol. (2015) 64:e1–e25. doi: 10.1093/sysbio/syu081
24. Brüningk SC, Peacock J, Whelan CJ, Brady-Nicholls R, Yu H-HM, Sahebjam S, et al. Intermittent radiotherapy as alternative treatment for recurrent high grade glioma: a modeling study based on longitudinal tumor measurements. Sci Rep. (2021) 11:20219. doi: 10.1038/s41598-021-99507-2
25. Sung W, Hong TS, Poznansky MC, Paganetti H, Grassberger C. Mathematical modeling to simulate the effect of adding radiation therapy to immunotherapy and application to hepatocellular carcinoma. Int J Radiat Oncol. (2022) 112:1055–62. doi: 10.1016/j.ijrobp.2021.11.008
26. Wang H, et al. In silico simulation of a clinical trial with anti-CTLA-4 and anti-PD-L1 immunotherapies in metastatic breast cancer using a systems pharmacology model. R Soc Open Sci. (2019) 6:190366. doi: 10.1098/rsos.190366
27. Igual L, Seguí S. Introduction to data science. In: Introduction to Data Science. Springer International Publishing, Cham (2017). p. 1–4.
28. Sharma M. State-of-the-art in performance metrics and future directions for data science algorithms. J Sci Res. (2020) 64:221–38. doi: 10.37398/JSR
29. Wang Q, Ma Y, Zhao K, Tian Y. A comprehensive survey of loss functions in machine learning. Ann Data Sci. (2022) 9:187–212. doi: 10.1007/s40745-020-00253-5
30. Lu Y, Lu J. A universal approximation theorem of deep neural networks for expressing probability distributions. In: Larochelle H, Ranzato M, Hadsell R, Balcan MF, Lin H, editors. Advances in Neural Information Processing Systems, vol. 33. Curran Associates, Inc., Cambridge, Massachusetts, USA (2020). p. 3094–105.
31. Linardatos P, Papastefanopoulos V, Kotsiantis S. Explainable AI: A review of machine learning interpretability methods. Entropy. (2020) 23:18. doi: 10.3390/e23010018
32. Yeom S, Giacomelli I, Fredrikson M, Jha S. (2018). Privacy risk in machine learning: analyzing the connection to overfitting, in: 2018 IEEE 31st Computer Security Foundations Symposium (CSF), IEEE, Oxford. (IEEE, New York, New York, USA), pp. 268–82. doi: 10.1109/CSF.2018.00027
33. Cao X, Yousefzadeh R. Extrapolation and AI transparency: Why machine learning models should reveal when they make decisions beyond their training. Big Data Soc. (2023) 10. doi: 10.1177/20539517231169731
34. Augustin M, Meinke A, Hein M. Adversarial robustness on in- and out-distribution improves explainability. In: Vedaldi A, Bischof H, Brox T, Frahm J-M, editors. Computer Vision – ECCV 2020, vol. 12371. Springer International Publishing, Cham (2020). p. 228–45.
35. Kann BH, Hosny A, Aerts HJWL. Artificial intelligence for clinical oncology. Cancer Cell. (2021) 39:916–27. doi: 10.1016/j.ccell.2021.04.002
36. Baptista D, Ferreira PG, Rocha M. A systematic evaluation of deep learning methods for the prediction of drug synergy in cancer. PloS Comput Biol. (2023) 19:e1010200. doi: 10.1371/journal.pcbi.1010200
37. Baptista D, Ferreira PG, Rocha M. Deep learning for drug response prediction in cancer. Brief Bioinform. (2021) 22:360–79. doi: 10.1093/bib/bbz171
38. Lee SY. Bayesian nonlinear models for repeated measurement data: an overview, implementation, and applications. Mathematics. (2022) 10:898. doi: 10.3390/math10060898
39. Liu X, Yoo C, Xing F, Oh H, Fakhri GE, Kang J-W, et al. Deep unsupervised domain adaptation: A review of recent advances and perspectives. (2022). doi: 10.48550/arXiv.2208.07422
40. Jiang H, Diao Z, Yao Y-D. Deep learning techniques for tumor segmentation: a review. J Supercomput. (2022) 78:1807–51. doi: 10.1007/s11227-021-03901-6
41. Jyothi P, Singh AR. Deep learning models and traditional automated techniques for brain tumor segmentation in MRI: a review. Artif Intell Rev. (2022) 56:2923–69. doi: 10.1007/s10462-022-10245-x
42. Kaur I, Doja MN, Ahmad T. Data mining and machine learning in cancer survival research: An overview and future recommendations. J Biomed Inform. (2022) 128:104026. doi: 10.1016/j.jbi.2022.104026
43. Lu S-C, Xu C, Nguyen CH, Geng Y, Pfob A, Sidey-Gibbons C. Machine learning–based short-term mortality prediction models for patients with cancer using electronic health record data: systematic review and critical appraisal. JMIR Med Inform. (2022) 10:e33182. doi: 10.2196/33182
44. von Rueden L, Mayer S, Sifa R, Bauckhage C, Garcke J. Combining machine learning and simulation to a hybrid modelling approach: current and future directions. In: Berthold MR, Feelders A, Krempl G, editors. Advances in Intelligent Data Analysis XVIII. Springer International Publishing, Cham (2020). p. 548–60.
45. Rajpurkar P, Chen E, Banerjee O, Topol EJ. AI in health and medicine. Nat Med. (2022) 28:31–8. doi: 10.1038/s41591-021-01614-0
46. Brüningk SC, Hensel F, Lukas LP, Kuijs M, Jutzeler CR, Rieck B. (2021). Back to the basics with inclusion of clinical domain knowledge - A simple, scalable and effective model of Alzheimer’s Disease classification, in: Proceedings of the 6th Machine Learning for Healthcare Conference, PMLR., pp. 730–54.
47. Rawat RR, Ruderman D, Macklin P, Rimm DL, Agus DB. Correlating nuclear morphometric patterns with estrogen receptor status in breast cancer pathologic specimens. NPJ Breast Cancer. (2018) 4:32. doi: 10.1038/s41523-018-0084-4
48. Culos A, Tsai AS, Stanley N, Becker M, Ghaemi MS, McIlwain DR, et al. Integration of mechanistic immunological knowledge into a machine learning pipeline improves predictions. Nat Mach Intell. (2020) 2:619–28. doi: 10.1038/s42256-020-00232-8
49. Fabris F, Freitas AA. New KEGG pathway-based interpretable features for classifying ageing-related mouse proteins. Bioinformatics. (2016) 32:2988–95. doi: 10.1093/bioinformatics/btw363
50. Zhang W, Chien J, Yong J, Kuang R. Network-based machine learning and graph theory algorithms for precision oncology. NPJ Precis Oncol. (2017) 1:1–15. doi: 10.1038/s41698-017-0029-7
51. Gaudelet T, Day B, Jamasb AR, Soman J, Regep C, Liu G, et al. Utilizing graph machine learning within drug discovery and development. Brief Bioinform. (2021) 22:bbab159. doi: 10.1093/bib/bbab159
52. Li MM, Huang K, Zitnik M. Graph representation learning in biomedicine and healthcare. Nat Biomed Eng. (2022) 6:1353–69. doi: 10.1038/s41551-022-00942-x
53. Kather JN, Charoentong P, Suarez-Carmona M, Herpel E, Klupp F, Ulrich A, et al. High-throughput screening of combinatorial immunotherapies with patient-specific in silico models of metastatic colorectal cancer. Cancer Res. (2018) 78:5155–63. doi: 10.1158/0008-5472.CAN-18-1126
54. Bull JA, Byrne HM. Quantification of spatial and phenotypic heterogeneity in an agent-based model of tumour-macrophage interactions. PloS Comput Biol. (2023) 19:e1010994. doi: 10.1371/journal.pcbi.1010994
55. Zheng A, Casari A. Feature engineering for machine learning: principles and techniques for data scientists. Beijing: Boston: O’Reilly (2018).
56. Benzekry S, Sentis C, Coze C, Tessonnier L, André N. Development and validation of a prediction model of overall survival in high-risk neuroblastoma using mechanistic modeling of metastasis. JCO Clin Cancer Inform. (2021) 5(5):81–90. doi: 10.1200/CCI.20.00092
57. Pérez-Aliacar M, Doweidar MH, Doblaré M, Ayensa-Jiménez J. Predicting cell behaviour parameters from glioblastoma on a chip images. A deep learning approach. Comput Biol Med. (2021) 135:104547. doi: 10.1016/j.compbiomed.2021.104547
58. Mavroudis PD, Teutonico D, Abos A, Pillai N. Application of machine learning in combination with mechanistic modeling to predict plasma exposure of small molecules. Front Syst Biol. (2023) 3:1180948. doi: 10.3389/fsysb.2023.1180948
59. Pesonen H, Simola U, Köhn‐Luque A, Vuollekoski H, Lai X, Frigessi A, et al. ABC of the future. Int Stat Rev. (2022) 91(2):243–68. doi: 10.1111/insr.12522
60. Rocha HL, Godet I, Kurtoglu F, Metzcar J, Konstantinopoulos K, Bhoyar S, et al. A persistent invasive phenotype in post-hypoxic tumor cells is revealed by fate mapping and computational modeling. iScience. (2021) 24. doi: 10.1101/2020.12.30.424757
61. Akasiadis C, Ponce-de-Leon M, Montagud A, Michelioudakis E, Atsidakou A, Alevizos E, et al. Parallel model exploration for tumor treatment simulations. Comput Intell. (2022) 38:1379–401. doi: 10.1111/coin.12515
62. Kielland A. Integrating Biological Domain Knowledge in Machine Learning Models for Cancer Precision Medicine. Oslo: University of Oslo (2023).
63. Gu Y, Ng MK. Deep neural networks for solving large linear systems arising from high-dimensional problems. (2022). doi: 10.48550/ARXIV.2204.00313
64. Jiang Z, Jiang J, Yao Q, Yang G. A neural network-based PDE solving algorithm with high precision. Sci Rep. (2023) 13:4479. doi: 10.1038/s41598-023-31236-0
65. Nikolenko SI. Synthetic Data for Deep Learning Vol. 174. . Cham: Springer International Publishing (2021). doi: 10.1007/978-3-030-75178-4
66. Gherman IM, Abdallah ZS, Pang W, Gorochowski TE, Grierson CS, Marucci L. Bridging the gap between mechanistic biological models and machine learning surrogates. PloS Comput Biol. (2023) 19:e1010988. doi: 10.1371/journal.pcbi.1010988
67. Rocha HL, de O. Silva JV, Silva RS, Lima EABF, Almeida RC. Bayesian inference using Gaussian process surrogates in cancer modeling. Comput Methods Appl Mech Eng. (2022) 399:115412. doi: 10.1016/j.cma.2022.115412
68. Ezhov I, Scibilia K, Franitza K, Steinbauer F, Shit S, Zimmer L, et al. Learn-Morph-Infer: A new way of solving the inverse problem for brain tumor modeling. Med Image Anal. (2023) 83:102672. doi: 10.1016/j.media.2022.102672
69. Jain RK, Gupta A, Ali WH, Lermusiaux PFJ. GlioMod: spatiotemporal-aware glioblastoma multiforme tumor growth modeling with deep encoder-decoder networks. (2022). doi: 10.1101/2022.11.06.22282010
70. Chen RTQ, Rubanova Y, Bettencourt J, Duvenaud D. Neural ordinary differential equations. (2019). doi: 10.48550/arXiv.1806.07366
71. Weinan E. A proposal on machine learning via dynamical systems. Commun Math Stat. (2017) 5:1–11. doi: 10.1007/s40304-017-0103-z
72. Haber E, Ruthotto L. Stable architectures for deep neural networks. Inverse Probl. (2018) 34:014004. doi: 10.1088/1361-6420/aa9a90
73. Kidger P. On neural differential equations. Doctoral thesis, Mathematical Institute, University of Oxford. (2022), 231 pp. doi: 10.48550/arXiv.2202.02435
74. Hossain I, Fanfani V, Quackenbush J, Burkholz R. Biologically informed NeuralODEs for genome-wide regulatory dynamics. (2023). doi: 10.21203/rs.3.rs-2675584/v1
75. Ru J, Lu B, Chen B, Shi J, Chen G, Wang, et al. Attention guided neural ODE network for breast tumor segmentation in medical images. Comput Biol Med. (2023) 159:106884. doi: 10.1016/j.compbiomed.2023.106884
76. Moon I, Groha S, Gusev A. SurvLatent ODE: A Neural ODE based time-to-event model with competing risks for longitudinal data improves cancer-associated Venous Thromboembolism (VTE) prediction. (2022). doi: 10.48550/arXiv.2204.09633
77. Wendland P, Birkenbihl C, Gomez-Freixa M, Sood M, Kschischo M, Fröhlich H. Generation of realistic synthetic data using Multimodal Neural Ordinary Differential Equations. NPJ Digit Med. (2022) 5:1–10. doi: 10.1038/s41746-022-00666-x
78. Schmidt M, Lipson H. Distilling free-form natural laws from experimental data. Science. (2009) 324:81–5. doi: 10.1126/science.1165893
79. Brunton SL, Proctor JL, Kutz JN. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc Natl Acad Sci. (2016) 113:3932–7. doi: 10.1073/pnas.1517384113
80. Brummer AB, Xella A, Woodall R, Adhikarla V, Cho H, Gutova M, et al. Data driven model discovery and interpretation for CAR T-cell killing using sparse identification and latent variables. Front Immunol. (2023) 14. doi: 10.3389/fimmu.2023.1115536
81. Kacprzyk K, Qian Z, van der Schaar M. D-CIPHER: discovery of closed-form partial differential equations. International Conference on Learning Representations. ICLR, Appleton WI (2022). doi: 10.48550/arXiv.2206.10586
82. Messenger DA, Bortz DM. Weak SINDy for partial differential equations. J Comput Phys. (2021) 443:110525. doi: 10.1016/j.jcp.2021.110525
83. Qian Z, Kacprzyk K, van der Schaar M. D-CODE: discovering closed-form ODEs from observed trajectories. International Conference on Learning Representations. ICLR, Appleton WI (2022). Available at: https://openreview.net/forum?id=wENMvIsxNN.
84. Guimerà R, Reichardt I, Aguilar-Mogas A, Massucci FA, Miranda M, Pallarès J, et al. A Bayesian machine scientist to aid in the solution of challenging scientific problems. Sci Adv. (2020) 6:eaav6971. doi: 10.1126/sciadv.aav6971
85. Brunton SL, Budišić M, Kaiser E, Kutz JN. Modern koopman theory for dynamical systems. SIAM Rev. (2022) 64:229–340. doi: 10.1137/21M1401243
86. Rackauckas C, Ma Y, Martensen J, Warner C, Zubov K, Supekar R, et al. Universal differential equations for scientific machine learning. (2021). doi: 10.48550/arXiv.2001.04385
87. Hernandez-Boussard T, Macklin P, Greenspan EJ, Gryshuk AL, Stahlberg E, Syeda-Mahmood T, et al. Digital twins for predictive oncology will be a paradigm shift for precision cancer care. Nat Med. (2021) 27:2065–6. doi: 10.1038/s41591-021-01558-5
88. Kaul R, Ossai C, Forkan ARM, Jayaraman PP, Zelcer J, Vaughan S, et al. The role of AI for developing digital twins in healthcare: The case of cancer care. WIREs Data Min Knowl Discovery. (2023) 13:e1480. doi: 10.1002/widm.1480
89. Wu C, Lorenzo G, Hormuth DA, Lima EABF, Slavkova KP, DiCarlo JC. Integrating mechanism-based modeling with biomedical imaging to build practical digital twins for clinical oncology. Biophys Rev. (2022) 3:021304. doi: 10.1063/5.0086789
90. Fertig EJ, Jaffee EM, Macklin P, Stearns V, Wang C. Forecasting cancer: from precision to predictive medicine. Med. (2021) 2:1004–10. doi: 10.1016/j.medj.2021.08.007
91. Sager S. Digital twins in oncology. J Cancer Res Clin Oncol. (2023) 149:5475–5477. doi: 10.1007/s00432-023-04633-1
92. Mourtzis D, Angelopoulos J, Panopoulos N, Kardamakis D. A smart ioT platform for oncology patient diagnosis based on AI: towards the human digital twin. Proc CIRP. (2021) 104:1686–91. doi: 10.1016/j.procir.2021.11.284
93. Wan Z, Dong Y, Yu Z, Lv H, Lv Z. Semi-supervised support vector machine for digital twins based brain image fusion. Front Neurosci. (2021) 15. doi: 10.3389/fnins.2021.705323
94. Swanson KR, Rostomily RC, Alvord EC. A mathematical modelling tool for predicting survival of individual patients following resection of glioblastoma: a proof of principle. Br J Cancer. (2008) 98:113–9. doi: 10.1038/sj.bjc.6604125
95. Jackson PR, Juliano J, Hawkins-Daarud A, Rockne RC, Swanson KR. Patient-specific mathematical neuro-oncology: using a simple proliferation and invasion tumor model to inform clinical practice. Bull Math Biol. (2015) 77:846–56. doi: 10.1007/s11538-015-0067-7
96. Molnar C. Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. Munich, Germany: Christoph Molnar (2022).
97. Roscher R, Bohn B, Duarte MF, Garcke J. Explainable machine learning for scientific insights and discoveries. IEEE Access. (2020) 8:42200–16. doi: 10.1109/Access.6287639
98. Ladbury C, Zarinshenas R, Semwal H, Tam A, Vaidehi N, Rodin AS, et al. Utilization of model-agnostic explainable artificial intelligence frameworks in oncology: a narrative review. Transl Cancer Res. (2022) 11(10):3853–3868. doi: 10.21037/tcr
99. Kim Y, Bang H, Kim Y, Bang H. Introduction to kalman filter and its applications. In: Introduction and Implementations of the Kalman Filter. IntechOpen, London, United Kingdom (2018).
100. Elfring J, Torta E, van de Molengraft R. Particle filters: A hands-on tutorial. Sensors. (2021) 21:438. doi: 10.3390/s21020438
101. Macklin P. When seeing isn’t believing: how math can guide our interpretation of measurements and experiments. Cell Syst. (2017) 5:92–4. doi: 10.1016/j.cels.2017.08.005
102. Ozik J, Collier N, Heiland R, An G, Macklin P. Learning-accelerated discovery of immune-tumour interactions. Mol Syst Des Eng. (2019) 4:747–60. doi: 10.1039/C9ME00036D
103. Grönquist P, Yao C, Ben-Nun T, Dryden N, Dueben P, Li S, et al. Deep learning for post-processing ensemble weather forecasts. Philos Trans R Soc Math Phys Eng Sci. (2021) 379:20200092. doi: 10.1098/rsta.2020.0092
104. Li W, Pan B, Xia J, Duan Q. Convolutional neural network-based statistical post-processing of ensemble precipitation forecasts. J Hydrol. (2022) 605:127301. doi: 10.1016/j.jhydrol.2021.127301
105. Liang B, Tan J, Lozenski L, Hormuth DA, Yankeelov TE, Villa U, et al. Bayesian inference of tissue heterogeneity for individualized prediction of glioma growth. IEEE Trans Med Imaging. (2023) 42(10). doi: 10.1109/TMI.2023.3267349
106. Lipkova J, Angelikopoulos P, Wu S, Alberts E, Wiestler B, Diehl C, et al. Personalized radiotherapy design for glioblastoma: integrating mathematical tumor models, multimodal scans, and bayesian inference. IEEE Trans Med Imaging. (2019) 38:1875–84. doi: 10.1109/TMI.42
107. Lima EABF, Faghihi D, Philley R, Yang J, Virostko J, Phillips CM, et al. Bayesian calibration of a stochastic, multiscale agent-based model for predicting in vitro tumor growth. PloS Comput Biol. (2021) 17:e1008845. doi: 10.1371/journal.pcbi.1008845
108. Cuomo S, Di Cola VS, Giampaolo F, Rozza G, Raissi M, Piccialli F. Scientific machine learning through physics–informed neural networks: where we are and what’s next. J Sci Comput. (2022) 92:88. doi: 10.1007/s10915-022-01939-z
109. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys. (2019) 378:686–707. doi: 10.1016/j.jcp.2018.10.045
110. Zhu A. Accelerating parameter inference in diffusion-reaction models of glioblastoma using physics-informed neural networks. SIAM Undergrad Res Online. (2022) 15. doi: 10.1137/22S1472814
111. Ayensa-Jiménez J, Doweidar MH, Sanz-Herrera JA, Doblare M. Understanding glioblastoma invasion using physically-guided neural networks with internal variables. PloS Comput Biol. (2022) 18:e1010019. doi: 10.1371/journal.pcbi.1010019
112. Elmarakeby HA, Hwang J, Arafeh R, Crowdis J, Gang S, Liu D, et al. Biologically informed deep neural network for prostate cancer discovery. Nature. (2021) 598:348–52. doi: 10.1038/s41586-021-03922-4
113. Yazdani A, Lu L, Raissi M, Karniadakis GE. Systems biology informed deep learning for inferring parameters and hidden dynamics. PloS Comput Biol. (2020) 16:e1007575. doi: 10.1371/journal.pcbi.1007575
114. Lagergren JH, Nardini JT, Baker RE, Simpson MJ, Flores KB. Biologically-informed neural networks guide mechanistic modeling from sparse experimental data. PloS Comput Biol. (2020) 16:e1008462. doi: 10.1371/journal.pcbi.1008462
115. Przedborski M, Smalley M, Thiyagarajan S, Goldman A, Kohandel M. Systems biology informed neural networks (SBINN) predict response and novel combinations for PD-1 checkpoint blockade. Commun Biol. (2021) 4:877. doi: 10.1038/s42003-021-02393-7
116. Greene CS, Costello JC. Biologically informed neural networks predict drug responses. Cancer Cell. (2020) 38:613–5. doi: 10.1016/j.ccell.2020.10.014
117. Hackenberg M, Harms P, Pfaffenlehner M, Pechmann A, Kirschner J, Schmidt T, et al. Deep dynamic modeling with just two time points: Can we still allow for individual trajectories? Biom J. (2022) 64:1426–45. doi: 10.1002/bimj.202000366
118. Qian Z, Zame W, Fleuren L, Elbers P, van der Schaar M. Integrating expert ODEs into neural ODEs: pharmacology and disease progression. In: Advances in Neural Information Processing Systems, vol. 34. Curran Associates, Inc., Red Hook, New York, USA (2021). p. 11364–83.
119. Davidian M, Giltinan DM. Nonlinear models for repeated measurement data: An overview and update. J Agric Biol Environ Stat. (2003) 8:387–419. doi: 10.1198/1085711032697
120. Bonate PL, Vicini P. Preclinical pharmacokinetic–pharmacodynamic modeling and simulation in drug. In: Preclinical Drug Development. CRC Press, Boca Raton, Florida, USA (2010).
121. Ribba B, Holford N, Magni P, Trocóniz I, Gueorguieva I, Girard P, et al. A review of mixed-effects models of tumor growth and effects of anticancer drug treatment used in population analysis. CPT Pharmacomet Syst Pharmacol. (2014) 3:113. doi: 10.1038/psp.2014.12
122. Janssen JM, Verheijen RB, Van Duijl TT, Lin L, Van Den Heuvel MM, Beijnen JH, et al. Longitudinal nonlinear mixed effects modeling of EGFR mutations in ctDNA as predictor of disease progression in treatment of EGFR -mutant non-small cell lung cancer. Clin Transl Sci. (2022) 15:1916–25. doi: 10.1111/cts.13300
123. Bigarré C, Bertucci F, Finetti P, Macgrogan G, Muracciole X, Benzekry S. Mechanistic modeling of metastatic relapse in early breast cancer to investigate the biological impact of prognostic biomarkers. Comput Methods Programs Biomed. (2023) 231:107401. doi: 10.1016/j.cmpb.2023.107401
124. Lai TL, Shih M-C, Wong SP. A new approach to modeling covariate effects and individualization in population pharmacokinetics-pharmacodynamics. J Pharmacokinet Pharmacodyn. (2006) 33:49–74. doi: 10.1007/s10928-005-9000-2
125. Knights J, Chanda P, Sato Y, Kaniwa N, Saito Y, Ueno H, et al. Vertical integration of pharmacogenetics in population PK/PD modeling: A novel information theoretic method. CPT Pharmacomet Syst Pharmacol. (2013) 2:25. doi: 10.1038/psp.2012.25
126. Fox G, Glazier JA, Kadupitiya JCS, Jadhao V, Kim M, Qui, et al. (2019). Learning everywhere: pervasive machine learning for effective high-performance computation, in: 2019 IEEE International Parallel and Distributed Processing Symposium Workshops (IPDPSW), IEEE, New York, New York, USA. pp. 422–9. doi: 10.1109/IPDPSW.2019.00081
Keywords: mathematical modeling, machine learning, deep learning, ODE (ordinary differential equation), mechanistic learning
Citation: Metzcar J, Jutzeler CR, Macklin P, Köhn-Luque A and Brüningk SC (2024) A review of mechanistic learning in mathematical oncology. Front. Immunol. 15:1363144. doi: 10.3389/fimmu.2024.1363144
Received: 29 December 2023; Accepted: 20 February 2024;
Published: 12 March 2024.
Edited by:
Heiko Enderling, University of Texas MD Anderson Cancer Center, United StatesReviewed by:
Jaya Lakshmi Thangaraj, University of California, San Diego, United StatesCopyright © 2024 Metzcar, Jutzeler, Macklin, Köhn-Luque and Brüningk. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Sarah C. Brüningk, c2FyYWguYnJ1ZW5pbmdrQGhlc3QuZXRoei5jaA==
†ORCID: John Metzcar, orcid.org/0000-0002-0142-0387
Catherine R. Jutzeler, orcid.org/0000-0001-7167-8271
Paul Macklin, orcid.org/0000-0002-9925-0151
Alvaro Köhn-Luque, orcid.org/0000-0002-5192-5199
Sarah C. Brüningk, orcid.org/0000-0003-3176-1032
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.