
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
MINI REVIEW article
Front. Immunol. , 28 August 2017
Sec. Microbial Immunology
Volume 8 - 2017 | https://doi.org/10.3389/fimmu.2017.00995
This article is part of the Research Topic Integrative Computational Systems Biology Approaches in Immunology and Medicine View all 24 articles
Although combinatorial antiretroviral therapy (cART) potently suppresses the virus, a sterile or functional cure still remains one of the greatest therapeutic challenges worldwide. Reservoirs are infected cells that can maintain HIV persistence for several years in patients with optimal cART, which is a leading obstacle to eradicate the virus. Despite the significant progress that has been made in our understanding of the diversity of cells that promote HIV persistence, many aspects that are critical to the development of effective therapeutic approaches able to purge the latent CD4+ T cell reservoir are poorly understood. Simultaneous purging strategies known as “kick-kill” have been pointed out as promising therapeutic approaches to eliminate the viral reservoir. However, long-term outcomes of purging strategies as well as the effect on the HIV reservoir are still largely fragmented. In this context, mathematical modeling can provide a rationale not only to evaluate the impact on the HIV reservoir but also to facilitate the formulation of hypotheses about potential therapeutic strategies. This review aims to discuss briefly the most recent mathematical modeling contributions, harnessing our knowledge toward the uncharted territory of HIV eradication. In addition, problems associated with current models are discussed, in particular, mathematical models consider only T cell responses but HIV control may also depend on other cell responses as well as chemokines and cytokines dynamics.
According to UNAIDS estimates for the year 2015, 36 million persons are infected with the HIV worldwide, and there are approximately 2.3 million new infections and 1.6 million AIDS-related deaths that occurred that year (1). Combined antiretroviral therapies (cART) are not able to eradicate the virus and HIV rebounds if therapy is discontinued. Upon HIV infection, a subset of latently infected cells carrying transcriptionally inactive integrated proviral DNA (the HIV reservoir) is rapidly established (2, 3). These cells are the main force behind HIV persistence under cART and, therefore, the main obstacle for an HIV cure (4–6). Thus far, there is only one reported case of a potential cure, known in the popular press as the Berlin patient (7). Unfortunately, the unique circumstances of the Berlin patient case would make it highly implausible to achieve a cure on large scales (8).
Two different approaches are envisaged for curing HIV infection: a sterilizing cure if there is a complete eradication of the virus and infected cells; and a functional cure if there is permanent control of viral replication without therapy (2). There was a growing recognition that a cure for HIV infection could be feasible (4, 8, 9). Recent clinical observations have hypothesized that an early initiation of cART is crucial to a progressive contraction of the latent HIV reservoir (“shrink”). This could possibly be accomplished with simultaneous strategies that activate (“kick” or “shock”) the latent reservoir and increase the clearance of virus-infected cells (“kill”), known as a “kick-kill” or “shock-kill” strategy (10, 11). The time window to intervene at an early stage of infection, while reservoirs are limited, is envisaged to be narrow but critical to the performance of an effective “shrink-kick-kill” strategy (Figure 1).
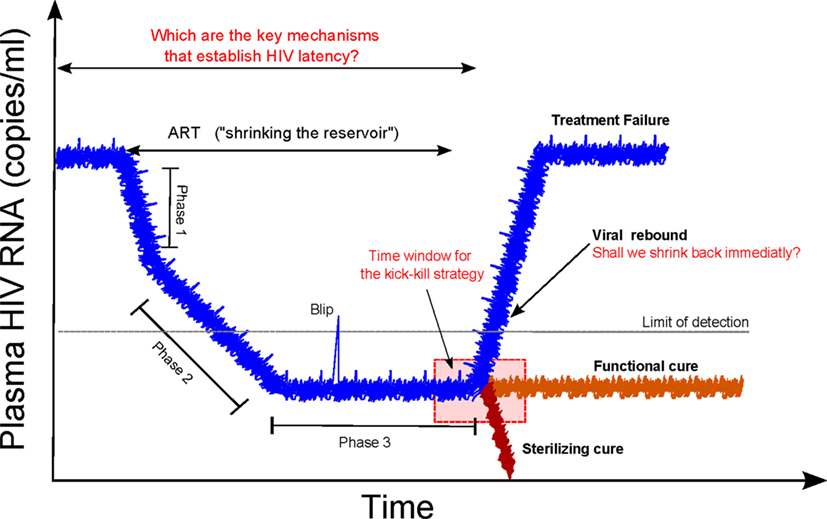
Figure 1. Shrink-kick-kill strategies toward an HIV cure. HIV undergoes three phases after cART initiation. The first phase describes the rapid decay of productively infected cells, e.g., activated CD4+ T cells. The second phase is led by cells that possess a half-life of about 14 days, which are not completely identified but are possibly macrophages and dendritic cells. The third phase is a low but stable level of residual viremia giving a plateau phase, which contains occasional viremic episodes (called blips). This third phase has been attributed to long-term reservoirs maintained by activation of latently infected memory CD4+ T cells. Recently, it has been hypothesized that tailoring a kick-kill strategy after cART cessation could lead to a sterilizing cure or a functional cure, i.e., achieving a controlled viremia below detection. This figure is a modification from Ref. (11).
Disentangling the leading mechanisms of HIV reservoirs is essential for the design of optimal therapeutic strategies. Although there are animal models such as the non-human primate and the BLT humanized mouse available to recapitulate HIV infection or even eradication, they are not perfect (12). Mathematical models can serve as a framework to interpret data of ongoing clinical trials, to evaluate the long-term of new therapeutic interventions, and to tailor future clinical trials. HIV modeling research twisted in a new dimension when the two works from Perelson et al. (13) and Nowak and Bangham (14) obtained a mathematical interpretation of viral decay data presented in HIV patients treated with anti-HIV drugs. Since then, modeling HIV infection has been a very active research topic over the past decades. Most of these modeling works initially aimed to represent the basic relation between the host cells and virus (15–21). In addition, significant efforts were invested to understand HIV disease progression (22–29), viral persistence (30–34), drug resistance (35–39), and optimal cART scheduling (40–46) among many others. Mathematical modeling was also pointed out as a tool to assess the potential of “kick-kill” strategies on long-term outcomes from short-term studies (47).
This short review focuses on discussing briefly the uncharted territory of HIV eradication as well as the most recent mathematical modeling contributions aiming to shed light on major clinical implications toward an HIV cure, see Table 1.
A very debatable question in HIV research has been if the existence of an HIV latent cellular reservoir is maintained by long-lived resting memory CD4+ T cells or through residual virus replication that replenishes the HIV reservoir (2, 56). Till now, latently infected resting memory CD4+ T cells are the only cell type in which it has been clearly demonstrated that replication-competent virus can persist for several years in patients (4, 57–59).
Memory CD4+ T cells represent the largest lymphocyte population in the adult human body and play critical roles in maintaining a life-long immune defense against specific pathogens (60). Reservoir maintenance is disputable, it has been mainly attributed to the replenishment of the pool, presumably by homeostatic or antigen-driven clonal proliferation and de novo infection of memory CD4+ T cells, ensuring the continuous replenishment of the HIV reservoir (57). Recent works from different labs (4, 57–59) revealed a progressive reduction of the size of the blood latent reservoir around a core of less-differentiated memory subsets (central memory and stem cell-like memory CD4+ T cells). These works indicated an extreme stability of different sub-reservoirs, the size of which is directly related to cumulative plasma virus exposure before the onset of cART (58, 59), stressing the importance of early initiation of effective cART. Nevertheless, very recent studies demonstrated that the viral reservoir is seeded rapidly after SIV infection of rhesus monkeys, even before detectable viremia (61). Therefore, the multifactorial mechanisms of HIV reservoirs and their establishment according to the time of optimal cART are still a matter of debate.
The VISCONTI study (9) dissected for the first time that the initiation of cART at very early stages of infection could decrease the size of the HIV reservoirs. In this study, cART was provided for 3 years after primary infection (PHI) to 14 patients and then interrupted. This study revealed that the 14 patients presented a sustained control for a median of 7 years named as posttreatment controllers (PTCs), implying that perhaps the nature of the viral reservoir (levels of TCM cells) could play an important role in controlling the infection in the absence of cART. Note that PTCs are not the only ones that can control HIV infection, a small group of individuals identified in 2005 showed the ability to control HIV infection in the absence of cART named as “Elite controllers (ECs)” (62). Although both ECs and PTCs can control the HIV infection, ECs can naturally maintain undetectable viral loads mainly attributed to a measurably stronger CTL response than non-controllers. Note that ECs undetectable viral loads are not only due to strong CTL but also other cell types, HLA type, and cytokines and chemokines (63).
Although the VISCONTI study revealed crucial information for a successful therapeutic strategy inducing viral remission, it left open several questions, in particular, how can we increase the probability of HIV-infected patients becoming PTC? The answer is not intuitive, in this direction, Hill et al. (48) proposed a mathematical model based on a two-type branching process assuming only four types of events: a latently infected cell can either activate or die, an actively infected cell can either die or produce a collection of virions that results in the infection of other cells. The model provided a relevant prediction that it might not be necessary to deplete completely the reservoir pool to prevent viral rebound, representing a PTC. The reasoning behind these predictions is that the high variability in viral progeny generated from actively infected cells increases the probability that the progeny of an activated provirus will go extinct because of stochastic diffusion. Hill et al. (48) results suggested that in order to achieve the goal of eradication for 95% of patients, a 5.8 logs reduction in the reservoir size may be necessary. Alternatively, to reach 1 year average without rebound, approximately 2,000-fold reduction would be required (48).
Controverting Hill et al. (48) predictions, Pinkevych et al. (49) combined data from four independent clinical cohorts of patients with cART interruption together using a simple model with exponential phase with a “shoulder” that represents the time for drug “washout” and viral growth. Pinkevych et al. (49) estimated that viral replication is initiated on average once every 6 days approximately, which is about 24 times lower than previous estimations. Furthermore, the model indicated that a modest 50–70-fold reduction of the reservoir would be required for 1 year without viral rebound after cART interruption. Six months later, Hill et al. (64) questioned the estimation approach by Pinkevych et al. (49). Mathematical models including modest interpersonal variations in Ref. (64) were also able to explain the observed variation in rebound times, rejecting the simplifying assumption of homogeneity in Ref. (49). In response to the critic of Hill et al. (64), Pinkevych et al. (65) derived an analytical approximation incorporating multiple reactivation events and consequently fitted to four datasets. Overall, fitting results in Ref. (65) indicated similar results to their original work (49). Furthermore, Pinkevych et al. (65) argued back to the work in Hill et al. (48) for using reactivation rates from previous publications that were not based on data on reactivation from latency after treatment interruption.
In a separate modeling lab, Conway et al. (50) tested the immune system response led by cytotoxic T cell (CTL) would be sufficient to control the infection due to the rate of new productively infected cells is small. To this end, using ordinary differential equations (ODEs), numerical simulations in Ref. (50) pointed out that for very strong CTL responses, HIV infection would be controlled in a similar fashion as with the ECs. Moreover, within the first 6 months of cART interruption, the model represented qualitatively similar the viral rebound to those reported in some individuals in the VISCONTI study. Interestingly, the model analysis reveals that not only a very low latent reservoir size is necessary to guarantee PTCs but also the CTL strength. A shortcoming of the Conway et al. model is the missing quantitative information to precise CD8+ T response leading to a subjective selection of the model and parameters.
The central dogma for an HIV cure is to reverse latency of resting CD4+ T cells that harbor replication competent proviruses (30), but at the same time, a major challenge in “purging” treatment strategies is the reduction of the virus without causing global T cell activation (66). The ability to induce HIV viremia or at least cell surface expression of viral proteins and presentation of viral antigens is a fundamental requirement for enabling the immune-mediated killing of latently infected cells and, thus, defines the key goal of latency-reversing agents (LRAs) in eradication strategies (11). These agents include histone methyltransferase inhibitors and histone deacetylases (HDAC) inhibitors (67). The potential to activate HIV production from latently infected cell lines and resting CD4+ T cells from HIV-infected patients on suppressive cART is under large debate last 5 years (11, 68). Thus far, multiple HDAC inhibitors can potently activate viral production in vitro, however, results of initial clinical trials in HIV-infected patients are just very recently published (10, 69, 70).
Essential steps in the life cycle of HIV within host cells, cell-associated HIV RNA markers, have been identified and currently used in several clinical trials as a surrogate to measure the degree of HIV persistence (71). Among HIV RNA markers, unspliced RNA (UsRNA) also referred as cell-associated unspliced (CA-US) is more easy to detect and thus several studies have linked to virus persistence (71).
For vorinostat, a promising LRA, 20 HIV-infected individuals on suppressive cART were treated with 400 mg of vorinostat for 14 days and then followed by 70 days (69). Although highly variable outcomes among the participants, vorinostat induced a significant and sustained increase UsRNA. Ke et al. (51) proposed three different models based on ODEs to further understand how latently infected cells respond dynamically to vorinostat: a direct activation model, a delay activation model, and a multistage delayed model. The model analysis in Ref. (51) revealed that a multistage delayed activation model could recapitulate the short-term and the long-term changes induced by vorinostat in UsRNA in most of the participants. This can be interpreted as latently infected cells may need to go through several stages before becoming sustainably activated. Clinically relevant for HIV persistence, parameter estimates by Ke et al. (51) evoked the idea that vorinostat treatment may not induce killing of transcriptionally activated cells leading to a minimal or absent reduction in reservoir size.
Another important LRA is romidepsin, Søgaard et al. (70) reported in a small clinical trial of six HIV-infected individuals who received romidepsin once weekly for 3 weeks while keeping cART. In contrast to vorinostat that did not induce plasma HIV RNA, romidepsin treatment promoted in five patients an increase of plasma HIV RNA to detectable levels ranging from 46 to 103 copies/ml. However, romidepsin and vorinostat did not alter the size of the HIV reservoir (72). To demonstrate that romidepsin may successfully activate the latent reservoir, Policicchio et al. (52) developed a non-human primate (NH) model to capture the characteristics of PTCs. Unexpectedly, stopping cART 7 days after romidepsin administration showed that viral rebound occurred as early as 3 days after cART interruption. Note that the average time of viral rebounds in humans is approximately 8 weeks (73). Employing a simple mathematical model of viral production, Policicchio et al. (52) indicated that the slopes of plasma viral load increase after romidepsin treatment are related to the intensification of viral replication attributed to romidepsin. Fitting results showed that the estimated slope was 0.418 log10/day.
Thus far, in clinical trials, HDACs have demonstrated an increase of UsRNA in total but a minimal reduction in reservoir size. Based on simple mathematical models assuming “direct activation,” Petravic et al. (53) suggested that several mechanisms such as maintenance and clearance of the reservoirs as well as other mechanisms may significantly impact the relationship between HIV reactivation and the reduction of latently infected cells. In particular, Petravic et al. (53) considered the impact of panobinostat and romidepsin, both drugs revealed 3–4 increased of CA-RNA in clinical trials. On one hand, cells reactivated with panobinostat have a long life span (half-life >1 month) suggesting a modest increase in reactivation rate (approximately 8%). On the other hand, cells activated with romidepsin have a short life span (2 days), implying that HIV reactivation rate may have doubled with romidepsin (53).
Overall, it is envisaged that additional interventions will be needed to eliminate efficiently latently infected cells (69). It is, therefore, very likely that HDACs will form part of a multipronged strategy (74). Consequently, mathematical models merging dynamics from different HDAC inhibitors may help to propose “kick” strategies to eliminate latently infected cells to achieve the ultimate goal of HIV eradication.
Purging strategies reached a new level of complexity due to recently published works addressing the frequency of CTL escape mutations in archived proviruses, indicating an unexpected and exceptionally dynamic nature of the latent reservoir (75). Although cART is started early, the vast majority of latent viruses carry CTL mutations that render infected cells unrecognizable by CTLs directed at common epitopes. While the non-protective responses may not be harmful per se, they may dominate and suppress the true protective ones. Thus, it is critical to (re)focus T-cell responses on the protective, biologically conserved epitopes of the HIV-1-proteome by effective vaccination (76). However, the biggest obstacle for vaccine development is the HIV-1 variability and escape from mounted responses. T-cell strategies focus on vaccine-elicited responses on the most conserved regions of the HIV-1 proteome are very promising, due to these are common to most variants and cause replicative fitness loss if mutated (76, 77). In this context, the best “kill” strategy could be based on innovative vaccines aiming to induce CD8+ T cell responses in conserved regions of the HIV-1 proteome.
To the best knowledge of the author, there is not any mathematical work to evaluate vaccines aiming to induce CD8+ T cell responses. Till now, mathematical models have focused on incorporating affinity antibody maturation (54, 55). Using agent-based simulations of the Germinal Center (GC) reaction, simulation results from Wang et al. (55) suggested that the induction of cross-reactive antibodies occurs with low probability because of conflicting forces by different antigens, ultimately frustrating affinity maturation. Wang et al. (55) provided a critical prediction that sequential immunization with different antigens would be preferred over a cocktail for induction of cross-reactive antibodies. In a similar vein, Luo et al. (54) proposed a Markov process model to simulate coevolving multi-type virus and antibodies populations. Simulations results provided also the hint that competitive exclusion by autologous antibodies could avoid the appearance of broadly neutralizing antibodies.
HIV modeling is on uncharted territory. Modeling “kill” strategies aiming to induce CD8+ T cell responses in cooperation with a combination of HDAC inhibitors has the potential to advance understanding toward HIV eradication. There are at the moment several clinical trials based on “kick-kill” therapies such as the RIVER study (78), for which a long-term follow-up out to 5 years is envisaged. Furthermore, several mechanisms may be underestimated in mathematical modeling research. Recent experimental evidence revealed that clonal proliferation of infected cell may play a central role maintaining the reservoirs (79). On the other hand, viral control may not be only associated with restoration of CD8+ T cells (80). Mathematical models presented till now assume only T cell responses as a main component. However, further modeling efforts including host factors and immune responses responsible for the HIV elite status may uncover clues for the design of therapeutic vaccines and functional cures (63). Ultimately, mathematical models of HIV compartments (e.g., different places where the virus is present) and sanctuaries (e.g., limited penetration of drugs that maintains persistent replication) are needed to weight HIV persistence.
Above all, the difference in opinion of modeling approaches between Pinkevych et al. and Hill et al. points out that there is a great need to unify the efforts in modeling practices such as develop good practice guidelines for reporting parameter fitting results. Although assuming there exists a model that represents properly the problem at hand, model fitting to experimental data is subject to a large number of factors that can distort parameter estimates (81). Efforts in dealing with errors in parameter estimation shall be well documented in next mathematical models to strengthen and support further development toward HIV eradication.
EAHV conceived and wrote the manuscript.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by the Alfons und Gertrud Kassel-Stiftung.
2. Eisele E, Siliciano RF. Redefining the viral reservoirs that prevent HIV-1 eradication. Immunity (2012) 37(3):377–88. doi:10.1016/j.immuni.2012.08.010
3. Barré-Sinoussi F, Ross AL, Delfraissy J-F. Past, present and future: 30 years of HIV research. Nat Rev Microbiol (2013) 11(12):877–83. doi:10.1038/nrmicro3132
4. Deeks SG, Autran B, Berkhout B, Benkirane M, Cairns S, Chomont N, et al. Towards an HIV cure: a global scientific strategy. Nat Rev Immunol (2012) 12(8):607–14. doi:10.1038/nri3262
5. Lewin SR, Deeks SG, Barré-Sinoussi F. Towards a cure for HIV-are we making progress? Lancet (2014) 384(9939):209–10. doi:10.1016/S0140-6736(14)61181-8
6. Murray AJ, Kwon KJ, Farber DL, Siliciano RF. The latent reservoir for HIV-1: how immunologic memory and clonal expansion contribute to HIV-1 persistence. J Immunol (2016) 197(2):407–17. doi:10.4049/jimmunol.1600343
7. Hütter G, Nowak D, Mossner M, Ganepola S, Müssig A, Allers K, et al. Long-term control of HIV by CCR5 Delta32/Delta32 stem-cell transplantation. N Engl J Med (2009) 360(7):692–8. doi:10.1056/NEJMoa0802905
8. Passaes CP, Sáez-Cirión A. HIV cure research: advances and prospects. Virology (2014) 45(4–455):340–52. doi:10.1016/j.virol.2014.02.021
9. Sáez-Cirión A, Bacchus C, Hocqueloux L, Avettand-Fenoel V, Girault I, Lecuroux C, et al. Post-treatment HIV-1 controllers with a long-term virological remission after the interruption of early initiated antiretroviral therapy ANRS VISCONTI study. PLoS Pathog (2013) 9(3):e1003211. doi:10.1371/journal.ppat.1003211
10. Archin NM, Liberty AL, Kashuba AD, Choudhary SK, Kuruc JD, Crooks AM, et al. Administration of vorinostat disrupts HIV-1 latency in patients on antiretroviral therapy. Nature (2012) 487(7408):482–5. doi:10.1038/nature11286
11. Van Lint C, Bouchat S, Marcello A. HIV-1 transcription and latency: an update. Retrovirology (2013) 10(1):67. doi:10.1186/1742-4690-10-67
12. Policicchio BB, Pandrea I, Apetrei C. Animal models for HIV cure research. Front Immunol (2016) 7:12. doi:10.3389/fimmu.2016.00012
13. Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science (1996) 271(5255):1582–6. doi:10.1126/science.271.5255.1582
14. Nowak MA, Bangham CR. Population dynamics of immune responses to persistent viruses. Science (1996) 272(5258):74–9. doi:10.1126/science.272.5258.74
15. Mohri H, Bonhoeffer S, Monard S, Perelson AS, Ho DD. Rapid turnover of T lymphocytes in SIV-infected rhesus macaques. Science (1998) 279:1223–7. doi:10.1126/science.279.5354.1223
16. Perelson AS, Nelson PW. Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev (1999) 41(1):3–44. doi:10.1137/S0036144598335107
17. Perelson AS. Modelling viral and immune system dynamics. Nat Rev Immunol (2002) 2(1):28–36. doi:10.1038/nri700
18. Markowitz M, Louie M, Hurley A, Sun E, Di Mascio M, Perelson AS, et al. A novel antiviral intervention results in more accurate assessment of human immunodeficiency virus type 1 replication dynamics and T-cell decay in vivo. J Virol (2003) 77(8):5037–8. doi:10.1128/JVI.77.8.5037-5038.2003
19. Xia X. Modelling of HIV infection: vaccine readiness, drug effectiveness and therapeutical failures. J Process Control (2007) 17(3):253–60. doi:10.1016/j.jprocont.2006.10.007
20. Dalal N, Greenhalgh D, Mao X. A stochastic model for internal HIV dynamics. J Math Anal Appl (2008) 341(2):1084–101. doi:10.1016/j.jmaa.2007.11.005
21. Noecker C, Schaefer K, Zaccheo K, Yang Y, Day J, Ganusov VV. Simple mathematical models do not accurately predict early SIV dynamics. Viruses (2015) 7(3):1189–217. doi:10.3390/v7031189
22. Kirschner E, Webb F. Immunotherapy of HIV-1 infection. J Biol Syst (1998) 6(1):71–83. doi:10.1142/S0218339098000091
23. Bajaria SH, Webb G, Cloyd M, Kirschner D. Dynamics of naive and memory CD4+ T lymphocytes in HIV-1 disease progression. J Acquir Immune Defic Syndr (2002) 30(1):41–58. doi:10.1097/00042560-200205010-00006
24. Yates A, Stark J, Klein N, Antia R, Callard R. Understanding the slow depletion of memory CD4+ T cells in HIV infection. PLoS Med (2007) 4(5):948–55. doi:10.1371/journal.pmed.0040177
25. Hogue IB, Bajaria SH, Fallert BA, Qin S, Reinhart TA, Kirschner DE. The dual role of dendritic cells in the immune response to human immunodeficiency virus type 1 infection. J Gen Virol (2008) 89(9):2228–39. doi:10.1099/vir.0.83600-0
26. Althaus CL, De Boer RJ. Dynamics of immune escape during HIV/SIV infection. PLoS Comput Biol (2008) 4(7):1–9. doi:10.1371/journal.pcbi.1000103
27. Hadjiandreou M, Conejeros R, Vassiliadis VS. Towards a long-term model construction for the dynamic simulation of HIV infection. Math Biosci Eng (2007) 4(3):489–504. doi:10.3934/mbe.2007.4.489
28. Chang H, Astolfi A. Enhancement of the immune system in HIV dynamics by output feedback. Automatica (2009) 45(7):1765–70. doi:10.1016/j.automatica.2009.03.016
29. Hernandez-Vargas EA, Middleton RH. Modeling the three stages in HIV infection. J Theor Biol (2013) 320:33–40. doi:10.1016/j.jtbi.2012.11.028
30. Finzi D, Hermankova M, Pierson T, Carruth LM, Buck C, Chaisson RE, et al. Identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy identification of a reservoir for HIV-1 in patients on highly active antiretroviral therapy. Science (1997) 278:1295–300. doi:10.1126/science.278.5341.1295
31. Rong L, Perelson AS. Asymmetric division of activated latently infected cells may explain the decay kinetics of the HIV-1 latent reservoir and intermittent viral blips. Math Biosci (2009) 217(1):77–87. doi:10.1016/j.mbs.2008.10.006
32. Conway JM, Coombs D. A stochastic model of latently infected cell reactivation and viral blip generation in treated HIV patients. PLoS Comput Biol (2011) 7(4):e1002033. doi:10.1371/journal.pcbi.1002033
33. Zhang J, Perelson AS. Contribution of follicular dendritic cells to persistent HIV viremia. J Virol (2013) 87(14):7893–901. doi:10.1128/JVI.00556-13
34. Conway JM, Perelson AS. Residual viremia in treated HIV+ individuals. PLoS Comput Biol (2016) 12(1):e1004677. doi:10.1371/journal.pcbi.1004677
35. Bonhoeffer S, Nowak MA. Pre-existence and emergence of drug resistance in HIV-1 infection. Proc Biol Sci (1997) 264(1382):631–7. doi:10.1098/rspb.1997.0089
36. Hernandez-Vargas EA, Colaneri P, Middleton RH, Blanchini F. Discrete-time control for switched positive systems with application to mitigating viral escape. Int J Robust Nonlin Control (2010) 21(10):1093–111. doi:10.1002/rnc.1628
37. Rosenbloom D, Hill A, Rabi S, Siliciano RF, Nowak MA. Antiretroviral dynamics determines HIV evolution and predicts therapy outcome. Nat Med (2012) 18(9):1378–85. doi:10.1038/nm.2892
38. Hernandez-Vargas EA, Colaneri P, Middleton RH. Switching strategies to mitigate HIV mutation. IEEE Trans Control Syst Technol (2014) 22(4):1623–8. doi:10.1109/TCST.2013.2280920
39. Moreno-Gamez S, Hill AL, Rosenbloom DIS, Petrov DA, Nowak MA, Pennings PS. Imperfect drug penetration leads to spatial monotherapy and rapid evolution of multidrug resistance. Proc Natl Acad Sci U S A (2015) 112(22):E2874–83. doi:10.1073/pnas.1424184112
40. Perelson AS, Essunger P, Cao Y, Vesanen M, Hurley A, Saksela K, et al. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature (1997) 387(6629):188–91. doi:10.1038/387188a0
41. D’Amato RM, D’Aquila RT, Wein LM. Management of antiretroviral therapy for HIV infection: analyzing when to change therapy. Manage Sci (2000) 46(9):1200–13. doi:10.1287/mnsc.46.9.1200.12235
42. Joshi HR. Optimal control of an HIV immunology model. Optimal Control Appl Method (2002) 23(4):199–213. doi:10.1002/oca.710
43. Zurakowski R. Nonlinear observer output-feedback MPC treatment scheduling for HIV. Biomed Eng (2011) 10(1):40. doi:10.1186/1475-925X-10-40
44. Hernandez-Vargas EA, Colaneri P, Middleton RH. Optimal therapy scheduling for a simplified HIV infection model. Automatica (2013) 49(9):2874–80. doi:10.1016/j.automatica.2013.06.001
45. Haering M, Hordt A, Meyer-Hermann M, Hernandez-Vargas EA. Computational study to determine when to initiate and alternate therapy in HIV infection. Biomed Res Int (2014) 2014:472869. doi:10.1155/2014/472869
46. Rivadeneira PS, Moog CH, Stan G-B, Brunet C, Raffi F, Ferré V, et al. Mathematical modeling of HIV dynamics after antiretroviral therapy initiation: a review. Biores Open Access (2014) 3(5):233–41. doi:10.1089/biores.2014.0024
47. Freedberg KA, Possas C, Deeks S, Ross AL, Rosettie KL, Di Mascio M, et al. The HIV cure research agenda: the role of mathematical modelling and cost-effectiveness analysis. J Virus Erad (2015) 1(4):245–9.
48. Hill AL, Rosenbloom DIS, Fu F, Nowak MA, Siliciano RF, Faria VG, et al. Predicting the outcomes of treatment to eradicate the latent reservoir for HIV. Proc Natl Acad Sci U S A (2014) 111(43):15597–15597. doi:10.1073/pnas.1406663111
49. Pinkevych M, Cromer D, Tolstrup M, Grimm AJ, Cooper DA, Lewin SR, et al. HIV reactivation from latency after treatment interruption occurs on average every 5-8 days-implications for HIV remission. PLoS Pathog (2015) 11(7):1–19. doi:10.1371/journal.ppat.1005000
50. Conway JM, Perelson AS. Post-treatment control of HIV infection. Proc Natl Acad Sci U S A (2015) 112(17):5467–72. doi:10.1073/pnas.1419162112
51. Ke R, Lewin SR, Elliott JH, Perelson AS. Modeling the effects of vorinostat in vivo reveals both transient and delayed HIV transcriptional activation and minimal killing of latently infected cells. PLoS Pathog (2015) 11(10):e1005237. doi:10.1371/journal.ppat.1005237
52. Policicchio BB, Xu C, Brocca-Cofano E, Raehtz KD, He T, Ma D, et al. Multi-dose romidepsin reactivates replication competent SIV in post-antiretroviral rhesus macaque controllers. PLoS Pathog (2016) 12(9):1–35. doi:10.1371/journal.ppat.1005879
53. Petravic J, Rasmussen TA, Lewin SR, Kent SJ, Davenport MP. Relationship between measures of HIV reactivation and the decline of latent reservoir under latency-reversing agents. J Virol (2017) 91(9):e2092–2016. doi:10.1128/JVI.02092-16
54. Luo S, Perelson AS. Competitive exclusion by autologous antibodies can prevent broad HIV-1 antibodies from arising. Proc Natl Acad Sci U S A (2015) 112(37):11654–9. doi:10.1073/pnas.1505207112
55. Wang S, Mata-Fink J, Kriegsman B, Hanson M, Irvine DJ, Eisen HN, et al. Manipulating the selection forces during affinity maturation to generate cross-reactive HIV antibodies. Cell (2015) 160(4):785–97. doi:10.1016/j.cell.2015.01.027
56. Lafeuillade A. Eliminating the HIV reservoir. Curr HIV/AIDS Rep (2012) 9(2):121–31. doi:10.1007/s11904-012-0115-y
57. Chomont N, El-Far M, Ancuta P, Trautmann L, Procopio FA, Yassine-Diab B, et al. HIV reservoir size and persistence are driven by T cell survival and homeostatic proliferation. Nat Med (2009) 15(8):893–900. doi:10.1038/nm.1972
58. Buzon MJ, Sun H, Li C, Shaw A, Seiss K, Ouyang Z, et al. HIV-1 persistence in CD4+ T cells with stem cell-like properties. Nat Med (2014) 20(2):139–42. doi:10.1038/nm.3445
59. Jaafoura S, de Goer de Herve MG, Hernandez-Vargas EA, Hendel-Chavez H, Abdoh M, Mateo MC, et al. Progressive contraction of the latent HIV reservoir around a core of less-differentiated CD4(+) memory T Cells. Nat Commun (2014) 5(5407):1–8. doi:10.1038/ncomms6407
60. Chahroudi A, Silvestri G, Lichterfeld M. T memory stem cells and HIV: a long-term relationship. Curr HIV/AIDS Rep (2015) 12(1):33–40. doi:10.1007/s11904-014-0246-4
61. Whitney JB, Hill AL, Sanisetty S, Penaloza-MacMaster P, Liu J, Shetty M, et al. Rapid seeding of the viral reservoir prior to SIV viraemia in rhesus monkeys. Nature (2014) 512(7512):74–7. doi:10.1038/nature13594
62. Lambotte O, Chaix M-L, Gasnault J, Goujard C, Lebras P, Delfraissy JF, et al. Persistence of replication-competent HIV in the central nervous system despite long-term effective highly active antiretroviral therapy. AIDS (2005) 19(2):217–8. doi:10.1097/00002030-200501280-00018
63. Genovese L, Nebuloni M, Alfano M. Cell-mediated immunity in elite controllers naturally controlling HIV viral load. Front Immunol (2013) 4:86. doi:10.3389/fimmu.2013.00086
64. Hill AL, Rosenbloom DIS, Siliciano JD, Siliciano RF. Insufficient evidence for rare activation of latent HIV in the absence of reservoir-reducing interventions. PLoS Pathog (2016) 12(8):4–9. doi:10.1371/journal.ppat.1005679
65. Pinkevych M, Kent SJ, Tolstrup M, Lewin SR, Cooper DA, Søgaard OS, et al. Modeling of experimental data supports HIV reactivation from latency after treatment interruption on average once every 5–8 days. PLoS Pathog (2016) 12(8):8–11. doi:10.1371/journal.ppat.1005740
66. Rasmussen TA, Schmeltz Søgaard O, Brinkmann C, Wightman F, Lewin SR, Melchjorsen J, et al. Comparison of HDAC inhibitors in clinical development: effect on HIV production in latently infected cells and T-cell activation. Hum Vaccin Immunother (2013) 9(5):993–1001. doi:10.4161/hv.23800
67. Xing S, Siliciano RF. Targeting HIV latency: pharmacologic strategies toward eradication. Drug Discov Today (2013) 18(11–12):541–51. doi:10.1016/j.drudis.2012.12.008
68. Cillo AR, Sobolewski MD, Bosch RJ, Fyne E, Piatak M, Coffin JM, et al. Quantification of HIV-1 latency reversal in resting CD4+ T cells from patients on suppressive antiretroviral therapy. Proc Natl Acad Sci U S A (2014) 111(19):7078–83. doi:10.1073/pnas.1402873111
69. Elliott JH, Wightman F, Solomon A, Ghneim K, Ahlers J, Cameron MJ, et al. Activation of HIV transcription with short-course vorinostat in HIV-infected patients on suppressive antiretroviral therapy. PLoS Pathog (2014) 10(10):e1004473. doi:10.1371/journal.ppat.1004473
70. Søgaard OS, Graversen ME, Leth S, Olesen R, Brinkmann CR, Nissen SK, et al. The depsipeptide romidepsin reverses HIV-1 latency in vivo. PLoS Pathog (2015) 11(9):e1005142. doi:10.1371/journal.ppat.1005142
71. Pasternak AO, Lukashov VV, Berkhout B. Cell-associated HIV RNA: a dynamic biomarker of viral persistence. Retrovirology (2013) 10(1):41. doi:10.1186/1742-4690-10-41
72. Gunst JD, Tolstrup M, Rasmussen TA, Søgaard OS. The potential role for romidepsin as a component in early HIV-1 curative efforts. Exp Rev Anti Infect Ther (2016) 14(5):447–50. doi:10.1586/14787210.2016.1164031
73. SPARTAC. Short-course antiretroviral therapy in primary HIV infection. N Engl J Med (2013) 368(3):207–17. doi:10.1056/NEJMoa1110039
74. Wightman F, Ellenberg P, Churchill M, Lewin SR. HDAC inhibitors in HIV. Immunol Cell Biol (2012) 90(1):47–54. doi:10.1038/icb.2011.95
75. Deng K, Pertea M, Rongvaux A, Wang L, Durand CM, Ghiaur G, et al. Broad CTL response is required to clear latent HIV-1 due to dominance of escape mutations. Nature (2015) 517(7534):381–5. doi:10.1038/nature14053
76. Hanke T. Conserved immunogens in prime-boost strategies for the next-generation HIV-1 vaccines. Expert Opin Biol Ther (2014) 14(5):601–16. doi:10.1517/14712598.2014.885946
77. Ferguson AL, Mann JK, Omarjee S, Ndung’u T, Walker BD, Chakraborty AK. Translating HIV sequences into quantitative fitness landscapes predicts viral vulnerabilities for rational immunogen design. Immunity (2013) 38(3):606–17. doi:10.1016/j.immuni.2012.11.022
78. Fidler S, Babiker A. River Study – Protocol Viral Eradication a Two-Arm (Proof of Concept) Randomised Phase II Trial Version (2016). Technical report. London.
79. Hosmane NN, Kwon KJ, Bruner KM, Capoferri AA, Beg S, Rosenbloom DIS, et al. Proliferation of latently infected CD4(+) T cells carrying replication-competent HIV-1: potential role in latent reservoir dynamics. J Exp Med (2017) 214(4):959–72. doi:10.1084/jem.20170193
80. Bruel T, Hamimi C, Dereuddre-Bosquet N, Cosma A, Shin SY, Corneau A, et al. Long-term control of Simian immunodeficiency virus (SIV) in cynomolgus macaques not associated with efficient SIV-specific CD8 + T-cell responses. J Virol (2015) 89(7):3542–56. doi:10.1128/JVI.03723-14
Keywords: HIV infection, HIV cure, reservoirs, mathematical modeling, LRA, ART, vaccination
Citation: Hernandez-Vargas EA (2017) Modeling Kick-Kill Strategies toward HIV Cure. Front. Immunol. 8:995. doi: 10.3389/fimmu.2017.00995
Received: 12 June 2017; Accepted: 04 August 2017;
Published: 28 August 2017
Edited by:
Juarez Antonio Simões Quaresma, Federal University of Pará, BrazilReviewed by:
David Andrew Moskowitz, Northwestern University, United StatesCopyright: © 2017 Hernandez-Vargas. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Esteban A. Hernandez-Vargas, dmFyZ2FzQGZpYXMudW5pLWZyYW5rZnVydC5kZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.