- 1Department of Primary Education, Research Center of Psychophysiology and Education, National and Kapodistrian University of Athens, Athens, Greece
- 2Department of Education and Human Sciences, University of Modena and Reggio Emilia, Reggio Emilia, Italy
Introduction
Mathematics is a complex subject including different domains such as arithmetic, arithmetic problem solving, geometry, algebra, probability, statistics, calculus, … that implies mobilizing a variety of basic abilities associated with the sense of quantity, symbols decoding, memory, visuospatial capacity, logics, to name a few. Students with difficulties in any of the these abilities or in their coordination, may experience mathematical learning difficulties. Understanding the cognitive nature of the various mathematical domains, as well as the mechanisms mediating cognitive development, has fascinated researchers from different fields: from mathematics education to developmental and cognitive psychology and neuroscience.
The field of cognitive psychology has a long history in the studies of cognitive difficulties involved in developing the representation and learning general use of numbers in mathematics (e.g., Campbell, 2005). However, as Fletcher et al. (2007) note, there are “no consistent standards by which to judge the presence or absence of LDs [learning difficulties] in math” (p. 207), and there is still disagreement concerning the question of a definition, operational criteria, and prevalence (Lanfranchi et al., 2008; Mazzocco, 2008). In general, the term Mathematical Learning Difficulty (MLD) is used broadly to describe a wide variety of deficits in math skills, typically pertaining the domains of arithmetic and arithmetic problem solving. We will use MLDs to refer to learning difficulties in these domains as well as other mathematical domains like the ones mentioned above.
Within the field of mathematics education, many frameworks and theories have been developed to analyze teaching and learning processes and difficulties involved with these and other mathematical tasks (e.g., Freudenthal, 1991; Schoenfeld, 1992, 2011; Bharath and English, 2010). Recently, the field has shown interest in perspectives from cognitive neuroscience (e.g., Grabner and Ansari, 2010).
Although developmental and classification models in these fields have been developed (for example, Geary and Hoard, 2005; Desoete, 2007; von Aster and Shalev, 2007), to our knowledge, no single framework or model can be used for a comprehensive and fine interpretation of students' mathematical difficulties, not only for scientific purposes, but also for informing mathematics educators. As mathematics educators1, we believe that reaching a model that combines existing hypotheses on MLD, based on known cognitive processes and mechanisms, could be used to provide a mathematical profile for every student.
Our aims with this contribution are to: (1) provide an overview of the most relevant hypotheses in the present day's literature regarding possible deficits that lead to MLD and of possible classifications of MLD subtypes; (2) and to build on such literature, using a multi-deficit neurocognitive approach, to propose a classification model for MLD describing four basic cognitive domains within which specific deficits may reside.
In order to reach our first objective we will describe the current hypotheses on neurocognitive deficits that may lead to MLD specifically related to numbers, and then we will provide examples of the most relevant classifications of MLD, based on a possible deficit in basic cognitive functions.
Hypotheses for Difficulties in the Learning of Numbers
Certainly deficits that lead to difficulties in processing numbers are of primary importance among the hypotheses for MLD. The literature refers to two preverbal or non-symbolic systems for processing quantities: (1) the object tracking system (OTS) that is precise, limited by its absolute set size, and that creates an object file with concrete information for each objects observed simultaneously (Brannon and Roitman, 2003; Xu, 2003; Fayol and Seron, 2005; van Herwegen et al., 2008; Cordes and Brannon, 2009; Cantlon et al., 2010; Piazza, 2010); (2) the approximate number system (ANS) that is extensible to very large quantities, operates on continuous dimensions, and yields and approximate evaluation in accordance with Weber's law (Xu and Spelke, 2000; Mix et al., 2002; Halberda and Feigenson, 2008; Piazza, 2010).
The main hypotheses based on deficits in these systems and other mechanisms specific to numerical processing have been reviewed by Andersson and Östergren (2012), and classified into the following categories:
- defective ANS;
- defective OTS;
- defective numerosity-coding;
- access deficit;
- multiple deficit.
Classifications of MLD and the Hypothesis of Domain General Cognitive Deficit
As noted in the introduction, acquiring basic mathematical skills requires possessing, building and promoting a range of abilities. The core systems of number, seem to be quite important in understanding the nature of the development of numerical cognition, but these are not the only systems upon which success in mathematics lies. Many researchers have attempted to describe subtypes in MLD (Geary, 1990; Rourke, 1993; Fuchs and Fuchs, 2002; Geary, 2004; Geary and Hoard, 2005). Geary was one of the first who tried to connect “Mathematics Disorder” with neuropsychological deficits (Geary, 1994). He posited three key subtypes of deficits (confirmed in Geary and Hoard, 2005):
- procedural (left hemisphere), in which children present a delay in acquiring simple arithmetic strategies, which may be a result of verbal working memory deficits, but also deficits in conceptual knowledge.
- semantic memory (left hemisphere), in which children show deficits in retrieval of facts because of a long term memory deficit.
- spatial (right hemisphere), in which children show deficits in the spatial representation of number.
In general, Geary's classification and the others proposed in the literature (for a review see: Desoete, 2004, 2007; Stock et al., 2006) lead to the identification of the 3 subtypes listed, as well as, one based on a number knowledge deficit. However such classifications are not completely satisfactory because in general the profiles of the children met in practice do not appear to belong to any subtype, but instead be constituted of several characteristics pertaining different subtypes (Desoete, 2007).
We believe this to be the case, because the subtypes are not characterized by basic cognitive processes, such as working memory (WM), long term memory (semantic memory), executive functions, fact retrieval and, by extension, calculation and fluency. Together with the existing hypotheses of domain specific deficits in number processing that we have presented in section Hypotheses for Difficulties in the Learning of Numbers, we support an additional hypothesis of a domain general cognitive deficit underlying MLD (Geary, 2004; Geary and Hoard, 2005), which emanates from converging evidence showing that such cognitive functions are involved in mathematical performance in both adults and children (Fuchs et al., 2005; Andersson, 2007, 2008; Swanson et al., 2008).
Classification Model of Mathematical Learning Difficulties
Taking into account the literature presented as well as unpublished clinical observations, we propose a classification model for MLD (Table 1) describing four basic cognitive domains within which specific deficits may reside. For each subtype we also list specific systems involved and typical mathematical difficulties.
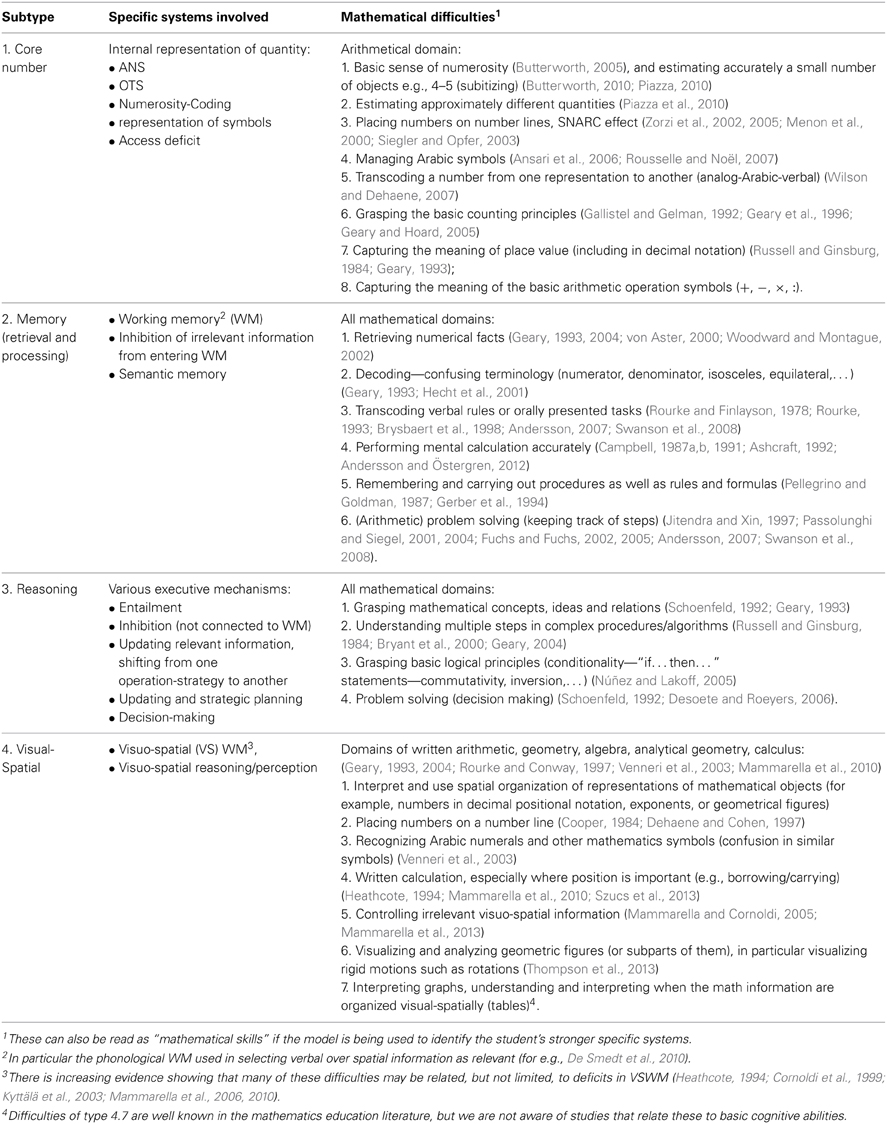
Table 1. Classification model for MLD, proposing 4 subtypes, possible specific systems involved, and typical mathematical difficulties encountered.
An analysis of a student's performance on a set of well-designed tasks can lead to the singling out of specific areas of difficulty (and strength), by comparing the specific systems and difficulties implied in each incorrect (or correct) answer to the tasks. The student's profile will be then described as a single subtype or as a combination of subtypes in which types of mathematical tasks and possible deficits to specific systems are highlighted.
Conclusions
We conclude highlighting the innovative value of the present etiological model. First, we may refer to it as being multidimensional in that it proposes a transition from the one-dimensional “Dyscalculia” to the multidimensional “Mathematical Learning Difficulties,” bringing into the picture mathematical domains other than the ones typically considered by the MLD literature until today. This leads to the second important feature: the model has direct implications for the field of mathematics education and may become an important tool for educators involved both in primary or secondary education. This is because the model allows to identify mathematical profiles of students early on, and these can be used to design more effective and comprehensive intervention programs, focusing on the students' strengths to compensate weaknesses and provide motivation. In fact, we believe, that in general intervention should focus mostly on the students' strengths, because this can have positive effects on motivation, while attempts to address students' weaknesses directly are likely to contribute to de-motivation and further failures. Moreover, educators, from researchers to teachers, can use the model to easily create tasks for working with their students.
Finally, the suggested classification model of MLD is expected to be clinically useful, as has been observed during a first study of its validity, the results of which will be soon submitted for publication. However we note that the model is at an early phase of development, and it can and will be improved through further research.
Footnotes
- ^The authors hold graduate and post graduate degrees in mathematics and mathematics education.
References
Andersson, U. (2007). The contribution of working memory to children's mathematical word problem solving. Appl. Cogn. Psychol. 21, 1201–1216. doi: 10.1002/acp.1317
Andersson, U. (2008). Working memory as a predictor of written arithmetical skills in children: the importance of central executive functions. Br. J. Educ. Psychol. 78, 181–203. doi: 10.1348/000709907X209854
Andersson, U., and Östergren, R. (2012). Number magnitude processing and basic cognitive functions in children with mathematical learning disabilities. Learn. Individ. Differ. 22, 701–714. doi: 10.1016/j.lindif.2012.05.004
Ansari, D., Dhital, B., and Siong, S. C. (2006). Parametric effects of numerical distance on the intraparietal sulcus during passive viewing of rapid numerosity changes. Brain Res. 1067, 181–188. doi: 10.1016/j.brainres.2005.10.083
Ashcraft, M. H. (1992). Cognitive arithmetic: a review of data and theory. Cognition 44, 75–106. doi: 10.1016/0010-0277(92)90051-I
Bharath, S., and English, L. D. (2010). Theories of Mathematics Education: Seeking New Frontiers. New York, NY: Springer.
Brannon, E., and Roitman, J. (2003). “Nonverbal representations of time and number in animals and human infants,” in Functional and Neural Mechanisms of Interval Timing, ed W. H. Meck (Boca Raton, FL: CRC Press), 143–182.
Bryant, D. P., Bryant, B. R., and Hammill, D. D. (2000). Characteristic behaviors of students with LD who have teacher-identified math weaknesses. J. Learn. Disabil. 33, 168–177. doi: 10.1177/002221940003300205
Brysbaert, M., Fias, W., and Noel, M. P. (1998). The Whorfian hypothesis and numerical cognition: is “twenty-four” processed the same way as “four and twenty”? Cognition 66, 51–77. doi: 10.1016/S0010-0277(98)00006-7
Butterworth, B. (2005). The development of arithmetical abilities. J. Child Psychol. Psychiatry 46, 3–18. doi: 10.1111/j.1469-7610.2004.00374.x
Butterworth, B. (2010). Foundational numerical capacities and the origins of dyscalculia. Trends Cogn. Sci. 14, 534–541. doi: 10.1016/j.tics.2010.09.007
Campbell, J. I. D. (1987a). Network interference and mental multiplication. J. Exp. Psychol. Learn. 13, 109–123. doi: 10.1037//0278-7393.13.1.109
Campbell, J. I. D. (1987b). Production, verification, and priming of multiplication facts. Mem. Cogn. 15, 349–364. doi: 10.3758/BF03197037
Campbell, J. I. D. (1991). Conditions of error priming in number-fact retrieval. Mem. Cogn. 19, 197–209. doi: 10.3758/BF03197119
Cantlon, J., Safford, K., and Brannon, E. (2010). Spontaneous analog number representations in 3-year-old children. Dev. Sci. 13, 289–297. doi: 10.1111/j.1467-7687.2009.00887.x
Cooper, R. G. (1984). “Early number development: discovering number space with addition and subtraction,” in Origins of Cognitive Skills, ed C. Sophian (New Jersey, NJ: Erlbaum), 157–192.
Cordes, S., and Brannon, E. (2009). Crossing the divide: infants discriminate small from large numerosities. Dev. Psychol. 45, 1583–1594. doi: 10.1037/a0015666
Cornoldi, C., Rigoni, F., Tressoldi, P. E., and Vio, C. (1999). Imagery deficits in nonverbal learning disabilities. J. Learn. Disabil. 32, 48–57. doi: 10.1177/002221949903200105
Dehaene, S., and Cohen, L. (1997). Cerebral pathways for calculation: double dissociation between rote verbal and quantities knowledge of arithmetic. Cortex 33, 219–250. doi: 10.1016/S0010-9452(08)70002-9
De Smedt, B., Taylor, J., Archibald, L., and Ansari, D. (2010). How is phonological processing related to individual differences in children's arithmetic skills? Dev. Sci. 13, 508–520. doi: 10.1111/j.1467-7687.2009.00897.x
Desoete, A. (2004). Children with Mathematics Learning Disabilities in Belgium. J. Learn. Disabil. 37, 50–61. doi: 10.1177/00222194040370010601
Desoete, A. (2007). Students with mathematical disabilities in Belgium: from definition, classification and assessment to STICORDI devices. Adv. Learn. Behav. Disabil. 20, 121-221. doi: 10.1016/S0735-004X(07)20008-4
Desoete, A., and Roeyers, H. (2006). Metacognitive macroevaluations in mathematical problem solving. Learn. Instr. 16, 12-25. doi: 10.1016/j.learninstruc.2005.12.003
Fayol, M., and Seron, X. (2005). “About numerical representations: insights from neuropsychological, experimental, and evolutionary studies,” in Handbook of Mathematical Cognition, ed J. J. Campbell (New York, NY: Psychology Press), 3–22.
Fletcher, J. M., Lyon, G. R., Fuchs, L. S., and Barnes, M. A. (2007). Learning Disabilities: From Identification to Intervention. New York, NY: Guilford Press.
Freudenthal, H. (1991). Revisiting Mathematics Education: China Lectures. Norwell, MA: Kluwer Academic Publishers.
Fuchs, L. S., Compton, D. L., Fuchs, D., Paulsen, K., Bryant, J. D., and Hamlett, C. L. (2005). The prevention, identification, and cognitive determinants of math difficulty. J. Educ. Psychol. 97, 493–513. doi: 10.1037/0022-0663.97.3.493
Fuchs, L. S., and Fuchs, D. (2002). Mathematical problem-solving profiles of students with mathematics disabilities with and without comorbid reading disabilities. J. Learn. Disabil. 35, 563-557. doi: 10.1177/00222194020350060701
Fuchs, L. S., and Fuchs, D. (2005). Enhancing mathematical problem solving for students with disabilities. J. Spec. Educ. 39, 45-57. doi: 10.1177/00224669050390010501
Gallistel, C., and Gelman, R. (1992). Preverbal and verbal counting and computation. Cognition 44, 43–74. doi: 10.1016/0010-0277(92)90050-R
Geary, D. C. (1990). A componential analysis of an early learning deficit in mathematics. J. Exp. Child Psychol. 49, 363–383. doi: 10.1016/0022-0965(90)90065-G
Geary, D. C. (1993). Mathematical disabilities: cognitive, neuropsychological, and genetic components. Psychol. Bull. 114, 345–362. doi: 10.1037/0033-2909.114.2.345
Geary, D. C. (1994). Children's Mathematical Development. Washington, DC: American Psychological Association.
Geary, D. C. (2004). Mathematics and learning disabilities. J. Learn. Disabil. 37, 4–15. doi: 10.1177/00222194040370010201
Geary, D. C., Bow-Thomas, C. C., Liu, F., and Siegler, R. S. (1996). Development of arithmetical competencies in Chinese and American children: influence of age, language, and schooling. Child Dev. 67, 2022–2044. doi: 10.2307/1131607
Geary, D. C., and Hoard, M. (2005). “Learning disabilities in arithmetic and mathematics: theoretical and empirical perspectives,” in Handbook of Mathematical Cognition, ed J. I. D. Campbell (New York, NY: Psychology Press), 253–267.
Gerber, M., Semmel, D., and Semmel, M. (1994). Computer-based dynamic assessment of multidigit multiplication. Except. Child. 61, 114–125.
Grabner, R. H., and Ansari, D. (2010). Promises and potential pitfalls of a ‘cognitive neuroscience of mathematics learning’. ZDM 42, 655–660. doi: 10.1007/s11858-010-0283-4
Halberda, J., and Feigenson, L. (2008). Developmental change in the acuity of the “Number Sense”: the Approximate Number System in 3-, 4-, 5-, and 6-year-olds and adults. Dev. Psychol. 44, 1457–1465. doi: 10.1037/a0012682
Heathcote, D. (1994). The role of visuospatial working memory in the mental addition of multi-digit addends. Curr. Psychol. Cogn. 13, 207–245.
Hecht, S. A., Torgesen, J. K., Wagner, R., and Rashotte, C. (2001). The relationship between phonological processing abilities and emerging individual differences in mathematical computation skills: a longitudinal study of second to fifth grades. J. Exp. Child Psychol. 79, 192–227. doi:10.1006/jecp.2000.2586
Jitendra, A., and Xin, Y. P. (1997). Mathematical word-problem-solving instruction for students with mild disabilities and students at risk for math failure: a research synthesis. J. Spec. Educ. 30, 412–438. doi: 10.1177/002246699703000404
Kyttälä, M., Aunio, P., Lehto, J., Van Luit, J., and Hautamäki, J. (2003). Visuospatial working memory and early numeracy. Educ. Child Psychol. 20, 65–76.
Lanfranchi, S., Lucangeli, D., Jerman, O., and Swanson, H. L. (2008). Math disabilities: Italian and US perspectives. Adv. Learn. Behav. Disabil. 21, 277–308. doi: 10.1016/S0735-004X(08)00011-6
Mammarella, I. C., and Cornoldi, C. (2005). Difficulties in the control of irrelevant visuospatial information in children with visuospatial learning disabilities. Acta Psychol. 118, 211–228. doi: 10.1016/j.actpsy.2004.08.004
Mammarella, I. C., Cornoldi, C., Pazzaglia, F., Toso, C., Grimoldi, M., and Vio, C. (2006). Evidence for a double dissociation between spatial-simultaneous and spatial-sequential working memory in visuospatial (nonverbal) learning disabled children. Brain Cogn. 62, 58–67. doi: 10.1016/j.bandc.2006.03.007
Mammarella, I. C., Giofrè, D., Ferrara, R., and Cornoldi, C. (2013). Intuitive geometry and visuospatial working memory in children showing symptoms of nonverbal learning disabilities. Child Neuropsychol. 19, 235–249. doi: 10.1080/09297049.2011.640931
Mammarella, I. C., Lucangeli, D., and Cornoldi, C. (2010). Spatial working memory and arithmetic deficits in children with nonverbal learning difficulties. J. Learn. Disabil. 43, 455–468. doi: 10.1177/0022219409355482
Mazzocco, M. M. (2008). “Defining and differentiating mathematical learning disabilities and difficulties,” in Why Is Math So Hard for Some Children? The Nature and Origins of Mathematical Learning Difficulties and Disabilities, eds D. B. Berch and M. M. Mazzocco (Baltimore, MD: Brookes Publishing Company), 29–47.
Menon, V., Rivera, S. M., White, C. D., Glover, G. H., and Reiss, A. L. (2000). Dissociating prefrontal and parietal cortex activation during arithmetic processing. Neuroimage 12, 357–365. doi: 10.1006/nimg.2000.0613
Mix, K. S., Huttenlocher, J., and Levine, S. C. (2002). Quantitative Development in Infancy and Early Childhood. New York, NY: Oxford University Press.
Núñez, R., and Lakoff, G. (2005). “The cognitive foundations of mathematics: the role of conceptual metaphor,” in Handbook of Mathematical Cognition, ed J. I. D. Campbell (New York, NY: Psychology Press), 109–125.
Passolunghi, M. C., and Siegel, L. S. (2001). Short-term memory, working memory, and inhibitory control in children with difficulties in arithmetic problem solving. J. Exp. Child Psychol. 80, 44-57. doi: 10.1006/jecp.2000.2626
Passolunghi, M. C., and Siegel, L. S. (2004). Working memory and access to numerical information in children with disability in mathematics. J. Exp. Child Psychol. 88, 348-367. doi: 10.1016/j.jecp.2004.04.002
Pellegrino, J. W., and Goldman, S. J. (1987). Information processing and elementary mathematics. J. Learn. Disabil. 20, 23–32. doi: 10.1177/002221948702000105
Piazza, M. (2010). Neurocognitive start-up tools for symbolic number representations. Trends Cogn. Sci. 14, 542–551. doi: 10.1016/j.tics.2010.09.008
Piazza, M., Facoetti, A., Trussardi, A. N., Berteletti, I., Conte, S., Lucangeli, D., et al. (2010). Developmental trajectory of number acuity reveals a severe impairment in developmental dyscalculia. Cognition 116, 33–41. doi: 10.1016/j.cognition.2010.03.012
Rourke, B. P. (1993). Arithmetic disabilities, specific and otherwise: a neuropsychological perspective. J. Learn. Disabil. 26, 214–226. doi: 10.1177/002221949302600402
Rourke, B. P., and Conway, J. A. (1997). Disabilities of arithmetic and mathematical reasoning: perspectives from neurology and neuropsychology. J. Learn. Disabil. 30, 34–46. doi: 10.1177/002221949703000103
Rourke, B. P., and Finlayson, M. A. I. (1978). Neuropsychological significance of variations in patterns of academic performance: verbal and visualspatial abilities. J. Abnorm. Child Psych. 6, 121–133. doi: 10.1007/BF00915788
Rousselle, L., and Noël, M. P. (2007). Basic numerical skills in children with mathematics learning disabilities: a comparison of symbolic vs. non-symbolic number magnitude processing. Cognition 102, 361–395. doi: 10.1016/j.cognition.2006.01.005
Russell, R. L., and Ginsburg, H. P. (1984). Cognitive analysis of children's mathematical difficulties. Cogn. Instr. 1, 217–244.
Schoenfeld, A. (1992). “Learning to think mathematically: problem solving, metacognition, and sense making in mathematics,” in Handbook of Research on Mathematics Teaching and Learning, eds D. A. Grouws and the NCTM (New York, NY: Maxwell Macmillan International), 334–370.
Schoenfeld, A. (2011). How We Think: A Theory of Goal-Oriented Decision Making and its Educational Applications. New York, NY: Routledge.
Siegler, R. S., and Opfer, J. E. (2003). The development of numerical estimation: evidence for multiple representations of numerical quantity. Psychol. Sci. 14, 237–243. doi: 10.1111/1467-9280.02438
Stock, P., Desoete, A., and Roeyers, H. (2006). “Focussing on mathematical disabilities: a search for definition, classification and assessment,” in Learning Disabilities New Research, ed S. V. Randall (Hauppauge, NY: Nova Science Publishers), 29–62.
Swanson, H. L., Jerman, O., and Zheng, X. (2008). Growth in working memory and mathematical problem solving in children at risk and not at risk for serious math difficulties. J. Educ. Psychol. 100, 343–379. doi: 10.1037/0022-0663.100.2.343
Szucs, D., Devine, A., Soltesz, F., Nobes, A., and Gabriel, F. (2013). Developmental dyscalculia is related to visuospatial memory and inhibition impairment. Cortex 49, 2674–2688. doi: 10.1016/j.cortex.2013.06.007
Thompson, J. M., Nuerk, H.-C., Moeller, K., and Kadosh, R. C. (2013). The link between mental rotation ability and basic numerical representations. Acta Psychol. 144, 324–331. doi: 10.1016/j.actpsy.2013.05.009
van Herwegen, J., Ansari, D., Xu, F., and Karmiloff-Smith, A. (2008). Small and large number processing in infants and toddlers with Williams syndrome. Dev. Sci. 11, 637–643. doi: 10.1111/j.1467-7687.2008.00711.x
Venneri, A., Cornoldi, C., and Garuti, M. (2003). Arithmetic difficulties in children with visuospatial learning disability (VLD). Child Neuropsychol. 9, 175–183. doi: 10.1076/chin.9.3.175.16454
von Aster, M. (2000). Developmental cognitive neuropsychology of number processing and calculation: varieties of developmental dyscalculia. Eur. Child Adolesc. Psychiatry 9, 41–58. doi: 10.1007/s007870070008
von Aster, M., and Shalev, R. S. (2007). Number development and developmental dyscalculia. Dev. Med. Child Neurol. 49, 868–873. doi: 10.1111/j.1469-8749.2007.00868.x
Wilson, A. J., and Dehaene, S. (2007). “Number sense and developmental dyscalculia,” in Human Behavior, Learning and the Developing Brain, 2nd Edn., eds D. Coch, K. W. Fischer, and G. Dawson (New York, NY: Guilford Press), 212–238.
Woodward, J., and Montague, M. (2002). Meeting the challenge of mathematics reform for students with LD. J. Spec. Educ. 36, 89–101. doi: 10.1177/00224669020360020401
Xu, F. (2003). Numerosity discrimination in infants: evidence for two systems of representations. Cognition 89, B15–B25. doi:10.1016/S0010-0277(03)00050-7
Xu, F., and Spelke, E. S. (2000). Large number discrimination in 6-month-old infants. Cognition 74, B1–B11. doi:10.1016/S0010-0277(99)00066-9
Keywords: core deficits, dyscalculia, internal representation of numbers, mathematical learning difficulties, multi-deficit model, number sense
Citation: Karagiannakis G, Baccaglini-Frank A and Papadatos Y (2014) Mathematical learning difficulties subtypes classification. Front. Hum. Neurosci. 8:57. doi: 10.3389/fnhum.2014.00057
Received: 29 July 2013; Accepted: 24 January 2014;
Published online: 10 February 2014.
Edited by:
Zoe Theodoridou, St. Luke's Hospital, GreeceReviewed by:
Roi Cohen Kadosh, Cohen Kadosh Laboratory, UKDaniela Lucangeli, University of Padova, Italy
Copyright © 2014 Karagiannakis, Baccaglini-Frank and Papadatos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:am9obmthcmFnaWFuQG1hdGgudW9hLmdy
 Giannis Karagiannakis
Giannis Karagiannakis Anna Baccaglini-Frank
Anna Baccaglini-Frank Yiannis Papadatos1
Yiannis Papadatos1