
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Hum. Neurosci. , 07 February 2011
Sec. Speech and Language
volume 5 - 2011 | https://doi.org/10.3389/fnhum.2011.00004
This article is part of the Research Topic Origins and consequences of rhythmic cortical activity View all 17 articles
Rhythmic neural synchronization is found throughout the brain during many different tasks and even at rest. Beyond their underlying mechanisms, the question of their role is still controversial. Modeling can bring insight on this difficult question. We review here our recent modeling results concerning this issue in different situations. During rest, we show how local rhythmic synchrony can induce a spatiotemporally organized spontaneous activity at the brain level. Then, we show how rhythmic synchrony decreases reaction time in attention and enhances the strength and speed of information transfer between different groups of neurons. Finally, we show that when rhythmic synchrony creates firing phases, the learning with spike timing-dependent plasticity of repeatedly presented input patterns is greatly enhanced.
Rhythmic neural synchronization is commonly found in the brain and involves a number of different frequency bands. Such activity is found during the execution of a number of tasks (Tallon-Baudry, 2009) and even when a subject is at rest (Nir et al., 2008). The origin of such rhythms has received quite a lot of attention either experimentally or in modeling studies and a number of mechanisms have been found. The issue of their role is far less clear, as a general consensus has not been attained. On one side, as rhythmic neural activity correlates with a number of cognitive processes and behavior, its role is believed to be important for information processing (Fries, 2009). On the other side, it is believed that this rhythmic synchrony is just concomitant to information processing but do not participate in it. Two facts make this question difficult to answer. Direct evidence of the role of rhythmic synchrony can be obtained by manipulating these rhythms but only few results have been obtained for the induced behavioral (Stopfer et al., 1997) and neural activity (Sohal et al., 2009) changes. Second, the way information is processed in the brain is not sufficiently characterized to attribute a well-defined role to rhythmic synchrony. As modeling allows a more complete and deeper investigation, this approach appears as a convenient tool to explore this question.
Based on our recent modeling work, we review here evidence for a constructive role of rhythmic neural activity in different situations. First, we show how local rhythmic synchrony can induce a spatiotemporally organized spontaneous activity at the brain level during rest (Deco et al., 2009). Then, we show how rhythmic synchrony contributes positively to attention (Buehlmann and Deco, 2008) and information transfer between different neural pools (Buehlmann and Deco, 2010). Finally, we show how the learning of repeatedly presented input patterns by spike timing-dependent plasticity (STDP) can be enhanced by rhythmic synchrony (Masquelier et al., 2009). As we just review here the main results of these studies, we redirect the interested reader to the original references for more details.
A growing body of neuroimaging research has documented that, in the absence of an explicit task – the so-called “resting state,” the brain exhibits structured spatiotemporal patterns of activity. In particular, analysis of the fMRI blood oxygen level-dependent (BOLD) fluctuations (<0.1 Hz) during such conditions has revealed the existence of consistent networks, called resting state networks (Biswal et al., 1995). Among them, the so-called default-mode network is believed to play an important role (Shulman et al., 1997; Gusnard and Raichle, 2001; Greicius et al., 2003; Fox et al., 2005; Raichle and Mintun, 2006). Although this network could be associated with daydreaming, free association, stream of consciousness, or inner rehearsal in humans, similar patterns have been found in anesthetized monkeys, demonstrating that this network reveals intrinsic properties of the brain (Vincent et al., 2007). Since, a series of other networks has been identified (Mantini et al., 2007). These findings using the hemodynamic BOLD signal are supported by direct measurements of the neural activity: namely, even for distant regions, the slow fluctuations (<0.1 Hz) of the neural firing rate and of the gamma band power of the local field potential (LFP) can be correlated (Nir et al., 2008).
To understand the origin of this type of activity, a large-scale model of the brain is necessary. This can be done by considering the network of anatomically connected brain regions, such as the one known for the macaque via the CoCoMac database (Kötter, 2004; Kötter and Wanke, 2005), as shown in Figure 1A. At this large-scale, propagation delays are taken into account, via the choice of an axonal conduction velocity and the use of inter-regional distances. At the local level, the underlying network of excitatory and inhibitory spiking neurons, considered homogeneous for simplicity, can be modeled using the classical reduced model of a Wilson–Cowan unit (Wilson and Cowan, 1972), where noise is added. When each unit is driven under its oscillatory threshold – above which a gamma oscillation develops, it is shown that for a sufficiently large coupling all units oscillate, the network activity exhibiting an irregular dynamics. We divide the network in two structural communities (see Figure 1B), calculate the level of synchrony of each community using an analog of the Kuramoto (1984) order parameter and also calculate the BOLD signal using a hemodynamic model (Friston et al., 2003). We observe slow fluctuations of the communities synchrony levels and of their calculated BOLD signal (Figure 2). These fluctuations get anticorrelated for an intermediate range of noise levels (Figure 2), in line with the experimental observations (Fox et al., 2005). Note the optimal noise level where the anticorrelation is maximal, indicating the presence of stochastic resonance.
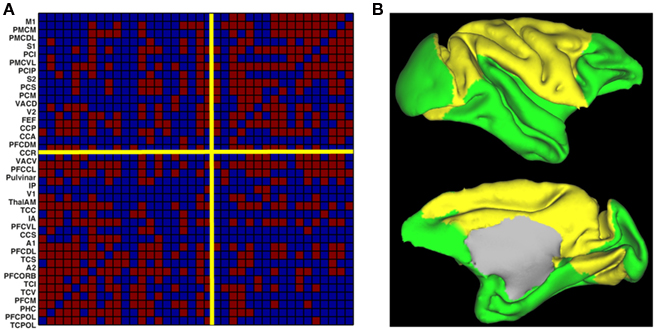
Figure 1. Structure of the large-scale model of the macaque brain. (A) Structural connectivity matrix (existing connections in red) between the 33 regions of the CoCoMac database. The network is separated in two communities (yellow separation lines). (B) Cortical surface representation of the two communities (yellow and green). Figure adapted from Deco et al. (2009).
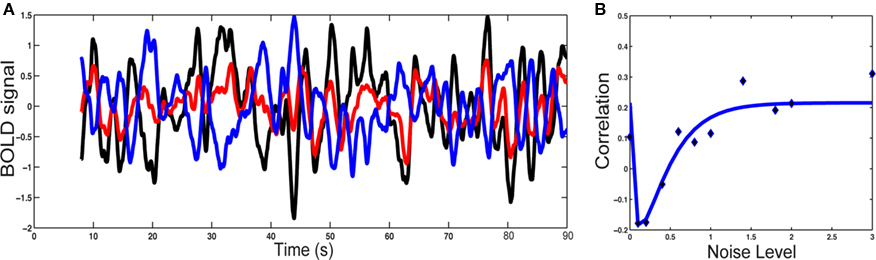
Figure 2. Blood oxygen level-dependent signal analysis. (A) BOLD fluctuations for each community (1: black; 2: red) and for the difference (blue). (B) Correlation between the synchronization level of the two communities versus the noise level: simulations (points) and non-linear least-squared fitting (curve). Note the stochastic resonance effect: there is an optimal noise level for which both communities are maximally anticorrelated. Figure adapted from Deco et al. (2009).
In area V4 of behaving monkeys, attention has been shown to modulate the firing rate of neurons whose receptive fields contain the attended stimulus. When the receptive field contains one stimulus, attention increases the firing rate. When two stimuli are presented, the firing rate increases if the stronger stimulus is attended but decreases when the weaker one is attended. This behavior is called biased competition (Moran and Desimone, 1985; Desimone and Duncan, 1995). Furthermore, associated with an increase of gamma frequency range power of the LFP with attention, neurons activated by an attended stimulus exhibit increased gamma frequency synchronization compared with neurons activated by a distractor stimulus1 (Fries et al., 2001). Although rate and gamma synchrony modulations occur simultaneously, it is not clear if and how they are mechanistically related.
A number of theoretical studies have investigated the neural mechanisms subserving attention. In the presence of a gamma oscillation, a number of these studies have found that attentional modulations could be reproduced (Niebur et al., 1993; Tiesinga et al., 2004; Borgers et al., 2005, 2008; Buia and Tiesinga, 2006, 2008; Borgers and Kopell, 2008; Buehlmann and Deco, 2008; Zeitler et al., 2008; Ardid et al., 2010). In other studies (Deco and Rolls, 2005; Hugues and Jose, 2010), it was found that attentional modulations could be induced by a top-down bias to a non-oscillating asynchronous network. In conclusion, while network gamma oscillations could help, these results demonstrate that they are not mandatory to induce attentional modulations. We review here a study investigating this question further.
Biased competition has been implemented in a network of excitatory and inhibitory spiking neurons (see Figure 3A), where attention is modeled as an additional input to the neurons encoding the attended stimulus (Deco and Rolls, 2005). When the attentional effects on gamma synchronization are included (Buehlmann and Deco, 2008), the model results are compatible with the experiments: when a stimulus is presented there is correlated neural activity in the gamma frequency band, and its power is stronger in the neurons encoding the attended stimulus than in the neurons encoding the unattended stimulus. By increasing the AMPA synaptic conductance and decreasing simultaneously the NMDA one to preserve charge entry, we can create a gamma oscillation in the network and increase its power. When the gamma power level is increased, the attentional rate modulation decreases monotonically but the gamma modulation first increases up to a maximum and then decreases (Figure 3B). These results suggest that rate and gamma modulations can occur independently of each other and are therefore not concomitant effects. However, if the rate modulation is accompanied by a gamma modulation, reaction times are found to be shorter, implying a behavioral relevance for gamma synchronization.
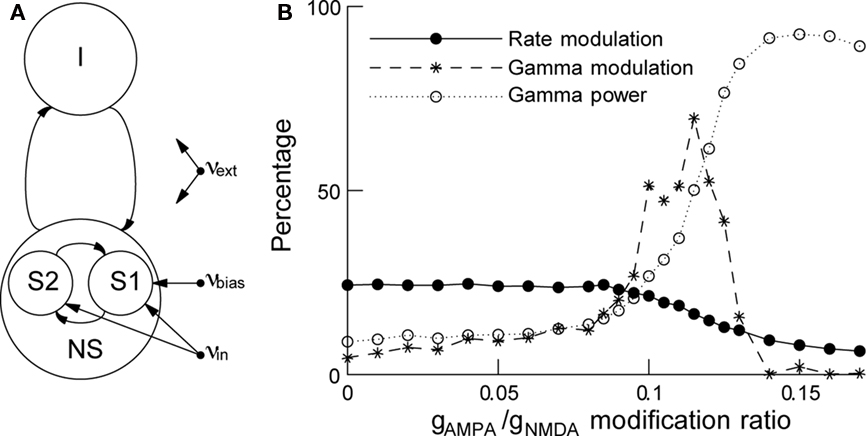
Figure 3. In attention, rate and gamma modulations are not concomitant effects. (A) Schematic representation of the network. The network consists of excitatory and inhibitory spiking neurons, with full synaptic connectivity. All neurons receive as external inputs (Poissonian) spike trains characterized by their rate. The excitatory neurons are organized in three pools: the non-specific neurons (NS) and the two selective pools (S1, S2) that receive the input encoding the stimulus (with rate νin). One of the two selective pools gets an additional bias (νbias). All neurons get also an input (νext) that simulates the spontaneous activity in the surrounding cerebral cortex. (B) Rate modulation (solid curve) and gamma modulation (dashed curve) as a function of the modification ratio gAMPA/gNMDA for excitatory synaptic conductances. Increasing this ratio increases rhythmic gamma band power (dotted curve), decreases the rate modulation monotonically while gamma modulation peaks around gAMPA/gNMDA ≈ 0.12. Either of the two modulations can be dominant, depending on the gamma power. Figure adapted from Buehlmann and Deco (2008).
One potential role of rhythmic neural activity may be to enhance communication between neural pools. In fact, an experimental study has shown that the correlation of neural activity in two neural clusters depends on the phase relation of the neural activity in the two clusters (Womelsdorf et al., 2007). This result suggests that effective connectivities in a network can be maximized or minimized by synchronization, a hypothesis also known as communication through coherence (CTC; Fries, 2005). In a similar modeling framework (see Figure 4A), general effects of gamma synchronization on information transfer between two neural pools were studied by measuring the transfer entropy (TE) between these two clusters (Buehlmann and Deco, 2010). TE is an information theoretical measure that quantifies the statistical coherence between systems and is able to distinguish between shared and transported information (Schreiber, 2000). In accordance with the experiments we found that (i) there is an optimal phase relation at which TE is highest between the two groups of neurons, (ii) TE increases as a function of the gamma power (Figure 4B), and (iii) the time required to reach 50% of the TE after stimulus onset decreases as a function of gamma power (Figure 4C). Taken together, these findings support the CTC hypothesis and, as rhythmic neural synchronization makes information transport more efficient, they suggest that it has a behavioral relevance.
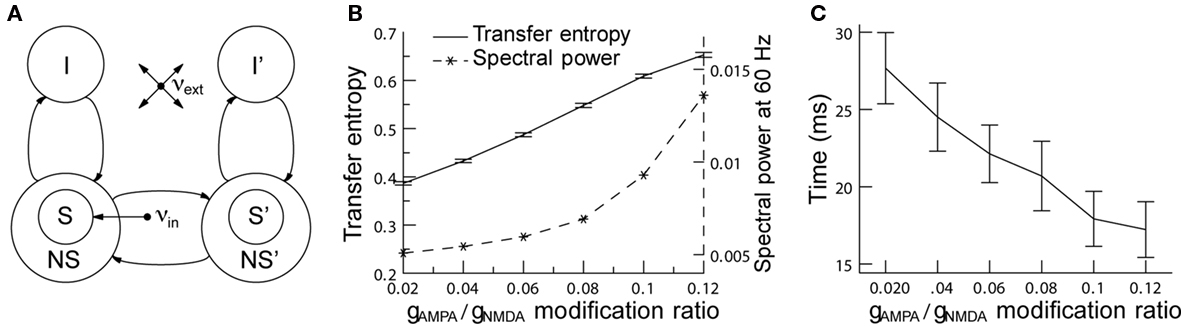
Figure 4. Increasing network gamma frequency band power leads to mean transfer entropy increase and time for information transfer decrease. (A) Schematic representation of the network. The network consists of two parts. In each part, there are excitatory (S, NS) and inhibitory (I) spiking neuron pools, which are interconnected. The connectivity is full. The selective pool (S) receives the external input (νin) and has strong recurrent connections. The two parts of the network are connected via the selective pools by both feedforward and feedback connections. All neurons get also an input (νext) that simulates the spontaneous activity in the surrounding cerebral cortex. (B) When the modification ratio gAMPA/gNMDA increases, both gamma power (dashed line) and TE (solid line) increase. (C) Rise times of TE as a function of the modification ratio. Information starts flowing after stimulus onset when, consequently, TE starts rising. The plot shows the time required to reach 50% of the average TE. TE clearly rises faster for higher gamma band power. In both graphics, error bars indicate 95% confidence intervals; averaged over 100 trials. Figure adapted from Buehlmann and Deco (2010).
Recent experiments have established that in cortex information can be encoded in the spike times of neurons relative to the phase of a background oscillation in the LFP – a phenomenon referred to as “phase-of-firing coding” (PoFC; Montemurro et al., 2008; Kayser et al., 2009; Vinck et al., 2010). These firing phase preferences could result from combining an oscillatory drive with a stimulus-dependent current that would produce the variations in preferred phases (Hopfield, 1995), a mechanism that has experimental support in vitro (Tiesinga et al., 2002; Schaefer et al., 2006; McLelland and Paulsen, 2009). However, it remains unknown if such a firing activity can be decoded, that is if downstream neurons can respond selectively to patterns of phases in their inputs and if this behavior can be learnt.
A recent modeling study has shown that PoFC has a major impact on downstream learning and decoding when associated with the now well-established STDP (Masquelier et al., 2009). STDP is a physiological mechanism of activity-driven synaptic regulation, where an excitatory synapse receiving a spike before a postsynaptic one is emitted is potentiated (Long-Term Potentiation) whereas its strength is weakened the other way around (Long-Term Depression). STDP has been observed both in vivo and in vitro, in many species (from insects to mammals) and in many brain areas (see Caporale and Dan, 2008 for a review).
Specifically, a single neuron equipped with STDP (Figure 5) can robustly detects a randomly repeating pattern of input currents hidden in a subset of its afferents when it is encoded in their firing phases (Figure 6). The oscillatory drive improves the spike times’ reliability, by decreasing their sensitivity to initial conditions and avoiding jitter accumulation, so that they depend mainly on the current input values. The ability of STDP to detect repeating spike patterns had been noted before in continuous activity (Masquelier et al., 2008), but it turns out that oscillations greatly facilitate learning, which is possible even when only a small fraction of the afferents (∼10%) exhibits PoFC. A benchmark with more conventional rate-based codes demonstrated the superiority of oscillations and PoFC for both STDP-based learning and speed of decoding, which only takes one oscillatory cycle.
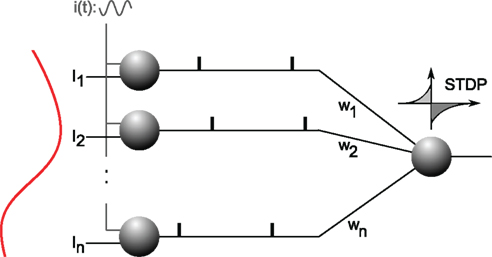
Figure 5. Neural architecture. Excitatory afferent neurons 1, …, n (on the left) receive individual input currents I1, …, In plus a common oscillatory drive i(t), which leads to a current-to-phase conversion: the stronger the current the earlier a neuron fires during an oscillation cycle. Afferents project with plastic weights w1, …, wn to one downstream neuron equipped with STDP. This neuron will gradually become selective to the spike wave corresponding to the repeating current pattern. Figure adapted from Masquelier et al. (2009).
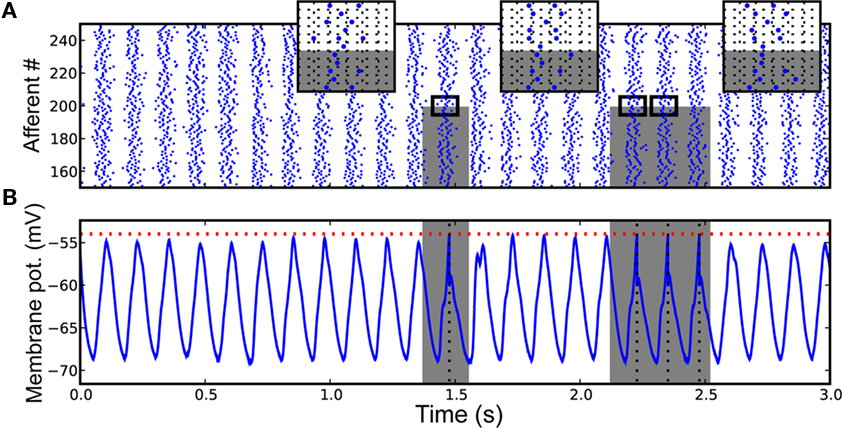
Figure 6. Downstream neuron input and response after learning (A) Input spike trains from afferents 150, …, 250, for the [0, 3]-s period. Spikes come in waves because of the oscillatory drive. Gray rectangles designate the periods where the pattern is presented, and the afferents that are involved in it (0, …, 199 here). Three inserts [horizontal grid size = 1 rad (in phase) = 20 ms] zoom on adequate periods to illustrate that the spike phases of the afferents involved in the pattern are the same (except for the noise) for different pattern presentations, which is not true for other afferents (200, …, 1999 here). The repetition of the pattern spike wave allows the pattern to be learned by STDP. (B) Postsynaptic membrane potential as a function of time: it oscillates at the same frequency as the afferents (and possibly with a phase lag due to conduction delays), but reaches the threshold if and only if the pattern is presented. See Masquelier et al. (2009) for details. Figure adapted from Masquelier et al. (2009).
Simultaneously resetting all the afferents’ potentials every now and then is a similar alternative to adding a common oscillatory drive, which also leads to reproducible spike times that STDP can pick. This may be a valid description of what happens during discrete sensory processing such as saccades or sniffs (Uchida et al., 2006), or with “stimulus onset paradigms,” in which a given sensory system is in a spontaneous state before being presented with a stimulus. But the fact that periods of oscillatory activity are found throughout the brain, and the suggestion that they could be particularly useful for the continuous cognitive processes, in which no reference time such as stimulus onsets is available, means that the oscillatory drive model may be of great practical importance.
Even if they are still speculative, these results suggest how two simple mechanisms present in the brain may combine constructively to induce a kind of temporal coding: oscillations allow information to be encoded in the spike phases, and STDP provides an appealing mechanism to learn how to decode them. Consistent with our scheme a growing body of experimental evidence in animals and humans demonstrates that successful Long-Term Memory encoding correlates with increased oscillatory activity across a broad range of frequencies (from the theta to the gamma frequency bands), in both sensory and associative areas (see Jensen et al., 2007; Klimesch et al., 2008; Tallon-Baudry, 2009 for recent reviews).
In this review, we have presented recent modeling results which suggest that rhythmic neural synchronization can have a variety of roles. During rest, when the brain is close to a spontaneous state, we have found that if local rhythms are sustained, they tend to form synchronized clusters of brain regions, creating in this way spatiotemporally organized activity at the brain scale level. Rhythmic synchrony was also found to decrease reaction time in attention and enhance information transfer between different groups of neurons, in line with the CTC hypothesis (Fries, 2005). Finally, when rhythmic synchrony creates firing phases (PoFC), the learning with STDP of repeatedly presented input patterns is greatly enhanced.
Among the mechanisms we have considered in this review on rhythmic neural synchronization, PoFC, CTC, and STDP involve spike timing and may be at work simultaneously. An interesting issue is to understand how they relate to each other in the brain, and if they facilitate each other or not. An oscillation in a network, either of intrinsic or extrinsic origin, can induce PoFC in the discharge of its neurons, the mean input to a neuron controlling generally its mean firing phase with respect to this oscillation. When a first neural network projects to a second one, and that both exhibit an oscillation in the same frequency band, the phase to which the incoming spikes arrive to the second network relative to its oscillation (taking into account an eventual conduction delay) is believed to play a role in the effective communication between the two networks (CTC; Fries, 2005; Womelsdorf et al., 2007). The information conveyed from the first network spikes will be “filtered” by the second, some neurons having a more important effect on the second network activity than others due to their firing phase. Note that beyond these phenomena at the individual neuron level, the phase between the oscillations in the two networks will also depend on the global behavior of the neural populations in these networks.
In the case where synapses between these two networks are equipped with STDP, learning will of course depend on the relative timing between the spikes in the first and in the second network, and therefore on the firing phases in the case of oscillatory networks. This learning will sculpt the connectivity between these networks, potentiating some synapses, and depressing others, which can change the interaction between the two networks and the relative phase of their oscillations and in turn how synapses evolve. What controls this complex dynamical process is a fundamental issue to understand how brain connectivity evolves with experience, but still very little is known. However, it is reasonable to think that selection of incoming information can be done in this way. Consider two neural groups A and B, projecting on a second network, all of them oscillating in the same frequency band. Depending on the mean phase of A and B spikes, the patterns of A spikes may be learned with STDP (following the results presented in section ‘Role of Rhythmic Neural Synchronization in Learning with Spike Timing-dependent Plasticity’), but synapses from B neurons may be systematically depressed. This selection mechanism may be flexible, the phase relationships changing for example with the context: in the previous example, the learning of the patterns of B spikes would then become possible, while the patterns of A spikes would be forgotten. Note that, as STDP is a slow process, this mechanism will occur on a much longer timescale than communication occurs.
At a broader level, these results show that rhythmic synchrony can have an important impact on the efficiency of neural communication at different scales, by providing a temporal organization of neural activity. However, these findings should also be investigated experimentally to check if the modeling hypotheses are appropriate and the rhythms sufficiently strong so that these effects are effectively present.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors were supported by the FP7 European Project Brainsync, the Fyssen Foundation, the Spanish Research Project BFU2007-61710, and CONSOLIDER INGENIO 2010 (Bilingualism and Cognitive Neuroscience).
Ardid, S., Wang, X. J., Gomez-Cabrero, D., and Compte, A. (2010). Reconciling coherent oscillation with modulation of irregular spiking activity in selective attention: gamma-range synchronization between sensory and executive cortical areas. J. Neurosci. 30, 2856–2870.
Biswal, B., Yetkin, F., Haughton, V., and Hyde, J. (1995). Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 34, 537–541.
Borgers, C., Epstein, S., and Kopell, N. J. (2005). Background gamma rhythmicity and attention in cortical local circuits: a computational study. Proc. Natl. Acad. Sci. U.S.A. 102, 7002–7007.
Borgers, C., Epstein, S., and Kopell, N. J. (2008). Gamma oscillations mediate stimulus competition and attentional selection in a cortical network model. Proc. Natl. Acad. Sci. U.S.A. 105, 18023–18028.
Borgers, C., and Kopell, N. J. (2008). Gamma oscillations and stimulus selection. Neural Comput. 20, 383–414.
Buehlmann, A., and Deco, G. (2008). The neuronal basis of attention: rate versus synchronization modulation. J. Neurosci. 28, 7679–7686.
Buehlmann, A., and Deco, G. (2010). Optimal information transfer in the cortex through synchronisation. PLoS Comput. Biol. 6, e1000934. doi: 10.1371/journal.pcbi.1000934
Buia, C. I., and Tiesinga, P. H. (2006). Attentional modulation of firing rate and synchrony in a model cortical network. J. Comput. Neurosci. 20, 247–264.
Buia, C. I., and Tiesinga, P. H. (2008). Role of interneuron diversity in the cortical microcircuit for attention. J. Neurophysiol. 99, 2158–2182.
Caporale, N., and Dan, Y. (2008). Spike timing-dependent plasticity: a Hebbian learning rule. Annu. Rev. Neurosci. 31, 25–46.
Chalk, M., Herrero, J. L., Gieselmann, M. A., Delicato, L. S., Gotthardt, S., and Thiele, A. (2010). Attention reduces stimulus-driven gamma frequency oscillations and spike field coherence in V1. Neuron 66, 114–125.
Deco, G., Jirsa, V., McIntosh, A. R., Sporns, O., and Kötter, R. (2009). Key role of coupling, delay, and noise in resting brain fluctuations. Proc. Natl. Acad. Sci. U.S.A. 106, 10302–10307.
Deco, G., and Rolls, E. T. (2005). Neurodynamics of biased competition and cooperation for attention: a model with spiking neurons. J. Neurophysiol. 94, 295–313.
Desimone, R., and Duncan, J. (1995). Neural mechanisms of selective visual-attention. Annu. Rev. Neurosci. 18, 193–222.
Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., and Raichle, M. E. (2005). The human brain is intrinsically organized into dynamics, anticorrelated functional networks. Proc. Natl. Acad. Sci. U.S.A. 102, 9673–9678.
Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends Cogn. Sci. 9, 474–480.
Fries, P. (2009). Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 32, 209–224.
Fries, P., Reynolds, J. H., Rorie, A. E., and Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. Science 291, 1560–1563.
Friston, K., Harrison, L., and Penny, W. (2003). Dynamic causal modelling. Neuroimage 19, 1273–1302.
Greicius, M. D., Krasnow, B., Reiss, A., and Menon, V. (2003). Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc. Natl. Acad. Sci. U.S.A. 100, 253–258.
Gusnard, D., and Raichle, M. (2001). Searching for a baseline: functional imaging and the resting human brain. Nat. Rev. Neurosci. 2, 685–694.
Hopfield, J. (1995). Pattern recognition computation using action potential timing for stimulus representation. Nature 376, 33–36.
Hugues, E., and Jose, J. V. (2010). A unified and quantitative network model to describe spatial attention in area V4. J. Physiol. (Paris) 104, 84–90.
Jensen, O., Kaiser, J., and Lachaux, J.-P. (2007). Human gamma-frequency oscillations associated with attention and memory. Trends Neurosci. 30, 317–324.
Kayser, C., Montemurro, M. A., Logothetis, N. K., and Panzeri, S. (2009). Spike-phase coding boosts and stabilizes information carried by spatial and temporal spike patterns. Neuron 61, 597–608.
Klimesch, W., Freunberger, R., Sauseng, P., and Gruber, W. (2008). A short review of slow phase synchronization and memory: evidence for control processes in different memory systems? Brain Res. 1235, 31–44.
Kötter, R. (2004). Online retrieval, processing, and visualization of primate connectivity data from the cocomac database. Neuroinformatics 2, 127–144.
Kötter, R., and Wanke, E. (2005). Mapping brains without coordinates. Philos. Trans. R. Soc. Lond. B Biol. Sci. 360, 751–766.
Mantini, D., Perrucci, M., Del Gratta, C., Romani, G., and Corbetta, M. (2007). Electrophysiological signatures of resting state networks in the human brain. Proc. Natl. Acad. Sci. U.S.A. 104, 13170–13175.
Masquelier, T., Guyonneau, R., and Thorpe, S. J. (2008). Spike timing dependent plasticity finds the start of repeating patterns in continuous spike trains. PLoS ONE 3, e1377. doi: 10.1371/journal.pone.0001377
Masquelier, T., Hugues, E., Deco, G., and Thorpe, S. J. (2009). Oscillations, phase-of-firing coding, and spike timing-dependent plasticity: an efficient learning scheme. J. Neurosci. 29, 13484–13493.
McLelland, D., and Paulsen, O. (2009). Neuronal oscillations and the rate-to-phase transform: mechanism, model and mutual information. J. Physiol. 587(Pt 4), 769–785.
Montemurro, M. A., Rasch, M. J., Murayama, Y., Logothetis, N. K., and Panzeri, S. (2008). Phase-of-firing coding of natural visual stimuli in primary visual cortex. Curr. Biol. 18, 375–380.
Moran, J., and Desimone, R. (1985). Selective attention gates visual processing in the extrastriate cortex. Science 229, 782–784.
Niebur, E., Koch, C., and Rosin, C. (1993). An oscillation-based model for the neuronal basis of attention. Vision Res. 33, 2789–2802.
Nir, Y., Mukamel, R., Dinstein, I., Privman, E., Harel, M., Fisch, L., Gelbard-Sagiv, H., Kipervasser, S., Andelman, F., Neufeld, M. Y., Kramer, U., Arieli, A., Fried, I., and Malach, R. (2008). Interhemispheric correlations of slow spontaneous neuronal fluctuations revealed in human sensory cortex. Nat. Neurosci. 11, 1100–1108.
Schaefer, A. T., Angelo, K., Spors, H., and Margrie, T. W. (2006). Neuronal oscillations enhance stimulus discrimination by ensuring action potential precision. PLoS Biol. 4, e163. doi: 10.1371/journal.pbio.0040163
Shulman, G., Fiez, J., Corbetta, M., Buckner, R., Miezin, F., Raichle, M., and Petersen, S. (1997). Common blood flow changes across visual tasks: II. Decreases in cerebral cortex. J. Cogn. Neurosci. 9, 648–663.
Sohal, V. S., Zhang, F., Yizhar, O., and Deisseroth, K. (2009). Parvalbumin neurons and gamma rhythms enhance cortical circuit performance. Nature 459, 698–702.
Stopfer, M., Bhagavan, S., Smith, B. H., and Laurent, G. (1997). Inpaired odour discrimination on desynchronization of odour-encoding neural assemblies. Nature 390, 70–74.
Tallon-Baudry, C. (2009). The roles of gamma-band oscillatory synchrony in human visual cognition. Front. Biosci. 14, 321–332.
Tiesinga, P. H., Fellous, J. M., Salinas, E., Jose, J. V., and Sejnowski, T. J. (2004). Inhibitory synchrony as a mechanism for attentional gain modulation. J. Physiol. Paris 98, 296–314.
Tiesinga, P. H. E., Fellous, J. M., Jose, J. V., and Sejnowski, T. J. (2002). Information transfer in entrained cortical neurons. Network 13, 41–66.
Uchida, N., Kepecs, A., and Mainen, Z. F. (2006). Seeing at a glance, smelling in a whiff: rapid forms of perceptual decision making. Nat. Rev. Neurosci. 7, 485–491.
Vincent, J., Patel, G. H., Fox, M. D., Snyder, A. Z., Baker, J. T., Van Essen, D. C., Zempel, J. M., Snyder, L. H., Corbetta, M., and Raichle, M. E. (2007). Intrinsic functional architecture in the anaesthetized monkey brain. Nature 447, 83–86.
Vinck, M., Lima, B., Womelsdorf, T., Oostenveld, R., Singer, W., Neuenschwander, S., and Fries, P. (2010). Gamma-phase shifting in awake monkey visual cortex. J. Neurosci. 30, 1250–1257.
Wilson, H., and Cowan, J. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24.
Womelsdorf, T., Schoffelen, J. M., Oostenveld, R., Singer, W., Desimone, R., Engel, A. K., and Fries, P. (2007). Modulation of neuronal interactions through neuronal synchronization. Science 316, 1609–1612.
Keywords: oscillations, resting state, attention, communication, learning
Citation: Deco G, Buehlmann A, Masquelier T and Hugues E (2011) The role of rhythmic neural synchronization in rest and task conditions. Front. Hum. Neurosci. 5:4. doi: 10.3389/fnhum.2011.00004
Received: 31 May 2010;
Accepted: 07 January 2011;
Published online: 07 February 2011.
Edited by:
Thilo Womelsdorf, Robarts Research Institute London, CanadaReviewed by:
Miles A. Whittington, Newcastle University, UKCopyright: © 2011 Deco, Buehlmann, Masquelier and Hugues. This is an open-access article subject to an exclusive license agreement between the authors and Frontiers Media SA, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Gustavo Deco, Unit for Brain and Cognition, Department of Information and Communication Technologies, Universitat Pompeu Fabra, Roc Boronat, 138, 08018 Barcelona, Spain. e-mail:Z3VzdGF2by5kZWNvQHVwZi5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.