- Department of Electrical and Computer Engineering, Northeastern University, Boston, MA, United States
The convincing performances of deep neural networks (DNNs) can be degraded tremendously under malicious samples, known as adversarial examples. Besides, with the widespread edge platforms, it is essential to reduce the DNN model size for efficient deployment on resource-limited edge devices. To achieve both adversarial robustness and model sparsity, we propose a robustness-aware search framework, an Adversarial Neural Architecture Search by the Pruning policy (ANAS-P). The layer-wise width is searched automatically via the binary convolutional mask, titled Depth-wise Differentiable Binary Convolutional indicator (D2BC). By conducting comprehensive experiments on three classification data sets (CIFAR-10, CIFAR-100, and Tiny-ImageNet) utilizing two adversarial losses TRADES (TRadeoff-inspired Adversarial DEfense via Surrogate-loss minimization) and MART (Misclassification Aware adveRsarial Training), we empirically demonstrate the effectiveness of ANAS in terms of clean accuracy and adversarial robust accuracy across various sparsity levels. Our proposed approach, ANAS-P, outperforms previous representative methods, especially in high-sparsity settings, with significant improvements.
1 Introduction
Deep neural networks (DNNs) have demonstrated remarkable progress in various tasks, including image classification (Yu et al., 2022; Xin et al., 2024), object detection (Li et al., 2022; Yang et al., 2022), and language modeling (Vaswani et al., 2017; Dao et al., 2023). However, despite their achievements, several challenges may limit their wide applications. On one hand, reliability and security concerns restrict the extensive real-world deployment of DNNs. For instance, adversaries can introduce imperceptible perturbations to benign inputs, named adversarial examples (Luo et al., 2018; Xiao et al., 2018; Bai et al., 2023), resulting in extremely bad inference performance. To enhance the dependability and safety of DNNs, research on trustworthy artificial intelligence has been actively investigated, where considerable efforts are devoted to robustifying DNNs (Apruzzese et al., 2019; Boopathy et al., 2020; Tramer et al., 2020) that can effectively defend against adversarial examples (Sun et al., 2022; Chen et al., 2023). On the other hand, DNNs may suffer from substantial over-parameterization with enormous computational overhead and massive memory requirements (Li et al., 2020; Yuan et al., 2021a).
To achieve high accuracy performance, the models typically cost a huge number of parameters, ranging from millions to billions (Mahajan et al., 2018; Yuan L. et al., 2021). Thus, they heavily rely on powerful Graphics Processing Units (GPUs) for training and can hardly deploy on resource-limited edge devices, such as mobile phones. To deal with this problem, many research efforts are devoted to exploring the potential of compact and sparse networks (Liu et al., 2021; Gong et al., 2022b; You et al., 2022), aiming for faster inference speed and smaller storage (Yuan et al., 2021b; Wu et al., 2022) compared to dense models without compromising the accuracy performance.
Several methods aim to obtain sparse and robust models from the pruning perspective, such as alternating direction method of multipliers (ADMM; Ye et al., 2019), Dynamic Network Rewiring (DNR; Kundu et al., 2021), HYDRA (Ye et al., 2019), and Masking Adversarial Damage (MAD; Lee et al., 2022). However, the previously mentioned methods either depend on carefully crafted scoring metrics or exhibit poor generalization at high sparsity. The most relevant work is ANP-VS (Madaan et al., 2020), which employs a regularized loss for pruning dense networks. Nevertheless, their pruning approach also performs poorly with high pruning ratios.
To simplify the training and pruning pipelines with enhanced robustness-sparsity trade-offs for DNNs, we propose a channel pruning and width search framework, Adversarial Neural Architecture Search by the Pruning policy (ANAS-P), for identifying the sparsity mask and improving the adversarial robustness. ANAS-P consists of three training stages. The first stage is to conduct common adversarial training to prepare a pretrained robust model. The, in the second step, the pruning policy is learned by minimizing the adversarial loss with the constraint for model computations measured by multiply-accumulate operations (MACs). Specifically, the binary convolutional (CONV) mask, titled Depth-wise Differentiable Binary Convolutional indicator (D2BC), is attached after each CONV layer to select the appropriate number of CONV channels in the DNN. Finally, the pruned (or searched) network is fine-tuned via the adversarial loss used in the first step.
Compared with traditional adversarial pruning methods with manually designed metrics to sort the significance of the weights and determine the corresponding pruning policy, our method can automatically learn the weight importance and the pruning policy based on the trainable masks to achieve better adversarial robustness by the adversarial model itself, which is more straightforward and efficient. Furthermore, in contrast to adversarial Neural Architecture Search (NAS) approaches (Guo et al., 2020; Devaguptapu et al., 2021; Cheng et al., 2023) with tremendous computing costs for large search space, our ANAS-P is instead dedicated to updating the model parameters and sparsity masks simultaneously without significant computation and memory costs.
We conduct numerous experiments to validate the effectiveness of ANAS-P on CIFAR-10, CIFAR-100 and Tiny-ImageNet data sets. The proposed ANAS-P outperforms previous adversarial model compression approaches, especially at high sparsity levels. For example, ANAS-P only has a minor decrease of 0.75% in clean accuracy and a reduction of 4.58% in robust accuracy for VGG-16 under AutoAttack at the sparsity of 99% on CIFAR-10, while the baselines suffer from more significant robust accuracy loss (larger than 18.4%).
To summarize, the contributions of our work are the following:
- We introduce an adversarial pruning framework to search for the appropriate per-layer width with the D2BC mask that is learnable with model weights directly.
- The proposed ANAS-P can train the model weights and the sparsity masks simultaneously, thus greatly saving on the computational costs for the search.
- Through extensive experiments, we empirically validate ANAS-P in terms of clean accuracy and robust accuracy against various adversarial attacks for different sparsity levels.
2 Related work
2.1 Adversarial attacks and adversarial training
In general, adversarial attacks (Goodfellow et al., 2015; Carlini and Wagner, 2017; Madry et al., 2018; Croce and Hein, 2020a; Sriramanan et al., 2020) introduce imperceptible perturbations into the clean inputs to generate adversarial examples, deceiving the DNN's decision-making. Specifically, Fast Gradient Sign Method (Goodfellow et al., 2015) attacks the model with one-step gradient descent, while Projected Gradient Descent (PGD; Madry et al., 2018), and Carlini and Wagner (2017) achieve stronger attack performance with iterative multistep gradient descent. Aside from their detrimental effects, adversarial examples are frequently utilized for model robustness evaluation, as seen in AutoAttack (AA; Croce and Hein, 2020b), which uses ensembles' multiple attack strategies to conduct a fair and dependable validation of model adversarial robustness.
Although many works (Xu et al., 2019; Chen et al., 2020; Freitas et al., 2020; Zhou et al., 2021; Gong et al., 2022a) are committed to investigating and addressing the fragility of DNNs, adversarial training is one of the most effective methods. It trains DNNs on adversarial examples by solving the min-max optimization. PGD-based adversarial training (Madry et al., 2018) yields strong defensive impact (Madry et al., 2018), but the clean accuracy drops (Su et al., 2018; Tsipras et al., 2018). In pursuit of enhancing the trade-off between clean accuracy and adversarial robustness, TRadeoff-inspired Adversarial DEfnese via Surrogate-loss minimization (TRADES; Zhang et al., 2019) and Misclassification Aware adveRsarial Training (MART; Wang et al., 2020) incorporate both the natural error term and the robustness regularization term in their training losses. Moreover, efficient adversarial training (Shafahi et al., 2019; Zhang et al., 2020, 2022; Chen et al., 2022; Li et al., 2023) accelerates the entire training significantly.
2.2 Adversarial model pruning
Adversarial robustness has been studied in the field of compressed DNNs recently. To cope with the issue that adversarial robustness is at odds with high model sparsity (Guo et al., 2018), several works have focused on both model sparsity and robustness. ADMM (Ye et al., 2019) conducts adversarial training and weight pruning jointly. From the adversarial latent feature level, vulnerability suppression (Madaan et al., 2020) is proposed to prune the model by a novel regularized training loss. Furthermore, the dynamic pruning approach is adopted during adversarial training via weight regrowth (Kundu et al., 2021). However, all these approaches either generalize poorly to ultra-sparse networks or are limited to one adversarial training objective. To achieve end-to-end robust learning, adversarial sparse training is proposed via Bayesian connectivity sampling (Özdenizci and Legenstein, 2021).
Another category considers pruning and retraining adversarially pretrained DNNs under the heuristic weight magnitude criterion. HYDRA (Sehwag et al., 2020) attains model compression from the robustness-aware importance score. MAD (Lee et al., 2022) determines the pruning score via the second-order information of adversarial loss. While their approaches are compatible with diverse adversarial losses, the pruning metric requires elaborate design. What is more, the assumption that weights with smaller magnitudes are less crucial for robustness may not always hold true. Following the assumption that pruning smaller weights may lead to inferior robustness performance. Besides, early pruning of small weights prevents them from contributing to robustness and accuracy later. Consequently, layers at the initial stage are continuously pruned and induce irreversible pruning and overexploitation. In contrast, our method with the D2BC mask layer is independent of the weight magnitudes and allows direct binary training.
3 Methodology
In this section, we present our proposed approach, ANAS-P, followed by detailed discussions on how to design the model pruning or channel search effectively.
3.1 Width search with D2BC layer
To achieve both sparsity and robustness, the width search is executed within each CONV layer to select the number of CONV channels autonomously. Precisely, we attach a D2BC indicator layer, which is a depth-wise 1 × 1 CONV layer, after each CONV layer to function as the per-layer trainable mask in the adversarial setting. The formulation is as follows:
where ⊙ stands for the convolution operation. represents the weight parameters with o output channels, i input channels, and kernel size k×k in the lth CONV layer. denotes the output features of lth layer (with the D2BC mask layer) with o channels, s×s′ feature size and bs batch sizes. is the weights of the trainable D2BC mask.
Each element of ml serves as the channel pruning indicator for the homologous output channel of wl⊙al−1. The pruning policy is determined by the magnitude of the elements ml. To be more specific, the elements of ml with smaller values signify the pruning of channels, whereas larger elements indicate the preservation of the corresponding channels. Subsequently, channel pruning is converted to a binarization problem via a threshold as shown:
where is the element-wise binarized ml, which is initialized randomly between 0 and 1. And the thres is manually set to 0.5 in our case.
However, during the training phase, the binary mask with the non-differentiable binarization operation for each CONV layer leads to challenges for back propagation. In quantization tasks, the straight-through estimator (STE) approach (Bengio et al., 2013) was initially proposed to circumvent non-differentiable problems (Yin et al., 2019; Spallanzani et al., 2022). Thus, to address the aforementioned issue, we incorporate the STE (Bengio et al., 2013) to directly pass the gradients through the binarization, as follows:
By leveraging binarization and the STE method, we can design a trainable mask that effectively indicates whether the corresponding channel should be pruned or preserved. We emphasize the following advantages by incorporating the STE with the D2BC layers in the pruning task:
• Our approach simplifies the mask generation and training process compared to other more complex techniques like Differentiable Markov Channel Pruning (DMCP) by a Markov process (Guo et al., 2020) or softmax function in Differentiable Network Channel Pruning (DNCP; Zheng et al., 2022). Instead, our binary masks are simply generated through a threshold and trained directly via the STE.
• It can facilitate the concurrent training of the sparsity mask and model parameters to enable the end-to-end channel pruning, thus saving search efforts compared with previous adversarial NAS methods (Guo et al., 2020; Mok et al., 2021; Cheng et al., 2023), which train multiple epochs for each architecture candidate.
• In contrast to magnitude-based adversarial pruning (Sehwag et al., 2020; Lee et al., 2022), our approach decouples the trainable masks from the original model weights, thereby overcoming the aforementioned shortcomings of magnitude-based pruning. Instead of obtaining the trade-off between the accuracy and sparsity with suboptimal solutions in previous magnitude-based pruning, the model weights in our method focus on improving the accuracy while the pruning function is handled by the sparsity mask.
• Pruned channels are allowed to recover freely and contribute to accuracy dynamically. During training, if the D2BC mask layer identifies a channel for pruning, the corresponding weights are not updated. Consequently, the information in pruned channels is retained, preventing the suboptimal gradient updating by zero elements in D2BC layers. In contrast, other pruning methods (Gui et al., 2019; Rakin et al., 2019; Ye et al., 2019; Kaur et al., 2022) corrupt weights in pruned layers by forcing them toward zero values. Later, if the mask is updated from 0 to 1, the corresponding pruned channel can be recovered to contribute to the accuracy again.
3.2 Adversarial training loss
Adversarial training (Madry et al., 2018) promotes model robustness against adversarial examples under perturbative inputs by solving the min–max optimization as follows:
where θ denotes the model parameter, x and y are the data point and label from the training data set ; δ means adversarial perturbations injected into x under the constraint with the constant strength ϵ, that is, △: = {||δ||∞ ≤ ϵ}; and is the training loss. During adversarial training, the optimization first achieves the inner maximization for adversarial attacks, followed by minimizing the outer training error with respect to the model parameters θ. The conventional procedure for generating adversarial examples involves multi-iteration to modify the more formidable adversary, for example:
where the projection utilizes the sign of gradients at step t with step size α.
In order to reach the trade-off between natural and robust errors, TRADES (Zhang et al., 2019) combines the natural loss with the regularization term for both natural examples and the corresponding adversarial ones by
where λ is a coefficient controlling the relative importance of two terms and B(x, ϵ) indicates a neighborhood of .
Furthermore, MART (Wang et al., 2020) highlights the influence of misclassified examples, as shown:
where fy(θ; x) depends on ground truth label y.
3.3 Adversarial pruning loss
Equipped with the D2BC layer, the network parameters and the pruning masks are trained via gradient descent optimizers simultaneously. The overall training objective is to achieve robustness and model sparsity as follows:
where ol/il indicates output/input channels with feature size and kernel size kl×kl in the lth CONV layer. is l2-norm between the current model's Multiply-Accumulate Operations (MACs) and target MACs that is constrained by global CONV sparsity (i.e., [50%, 90%, 99%]). derives from in Equations 1 or 2, and γ controls the relative strength of two losses.
3.4 Pruned Layer Compression
After the model pruning, for the deployment of the pruned model, the subsequent procedure involves converting the large sparse models into compact dense models by compressing the layers based on their sparsity masks, as formulated in the following:
where o0 and o1 refer to the number of 0 and 1 in the mask, respectively, (o0+o1 = o), and ⊕ implies the channel-wise concatenated operation. With this procedure, the pruned channels are effectively removed from the layers. Thus, the overhead is efficiently reduced by avoiding the computations of pruned channels.
3.5 Framework with D2BC mask layer
In the framework, we perform a per-layer width architecture search to achieve both model sparsity and robustness. The search space contains the width for each CONV layer in the network, which is too large to be explored with a heuristic method. Therefore, we propose the per-layer width search as shown in Figure 1, where the models (i.e., VGG-16 and ResNet18) are composed of D2BC mask layers, shown in Figure 2, and pruning is determined automatically by the D2BC parameters. The overall three-stage training is summarized in Figure 3, including adversarial pretraining, adversarial neural architecture search by pruning, and adversarial fine-tuning.
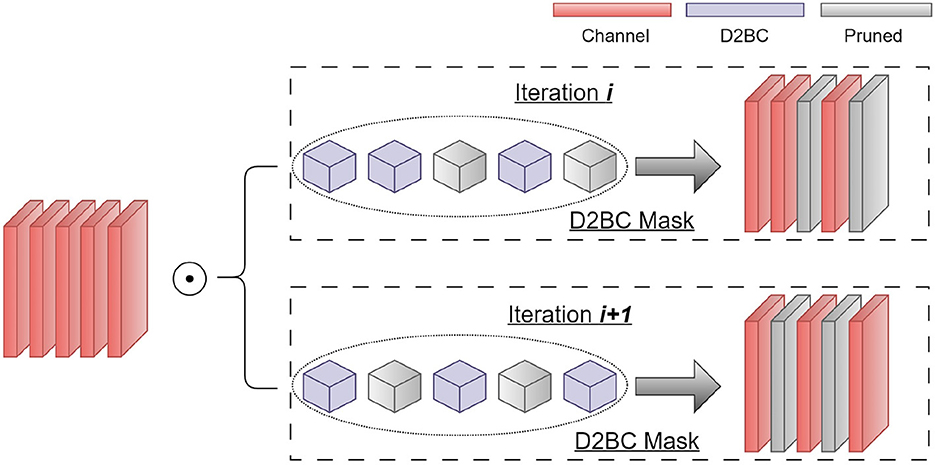
Figure 1. Architecture of Depth-wise Differentiable Binary Convolutional (D2BC) indicator in the per-layer width search.
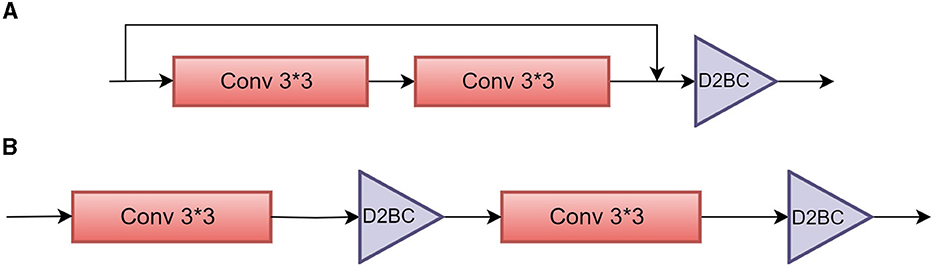
Figure 2. Schematic view of Depth-wise Differentiable Binary Convolutional (D2BC) mask in ResNet-18 and VGG-16. (A) The binary mask in ResNet-18 is applied after the residual block, enabling the simultaneous removal of both channels from the convolutional (CONV) output and channels from the identity path. (B) Instead, the binary layer in VGG-16 is immediately attached after each CONV layer in VGG-16.

Figure 3. The training pipeline overview, which includes three stages: (1) adversarial pretraining, (2) adversarial neural architecture search by the Depth-wise Differentiable Binary Convolutional pruning mask, and (3) adversarial fine-tuning.
4 Experiments
4.1 Experimental setup
4.1.1 Data sets and models
To demonstrate the effectiveness and generality of the proposed ANAS-P, we consider two networks: ResNet-18 (He et al., 2016) and VGG-16 (Simonyan and Zisserman, 2015) on three standard data sets in various scales, including CIFAR-10, CIFAR-100 (Krizhevsky and Hinton, 2009), and TinyImageNet-200 (Deng et al., 2009).
4.1.2 Adversarial loss and pruning
In our experiments, we utilize two representative adversarial training losses including TRADES (Zhang et al., 2019) and MART (Wang et al., 2020) in three training stages, consisting of adversarial pretraining, adversarial pruning, and fine-tuning. For the pretraining, pruning, and fine-tuning phases, either Equations 1 or 2 is leveraged as the adversarial loss function to learn robust representations, while Equation 3 is used as the pruning loss for the adversarial pruning stage. Our ANAS-P investigates different model sparsity ratios from small to large, including [50%, 90%, 99%] to optimize the D2BC masks. Note that all pruning approaches in this work only prune CONV layers.
4.1.3 Baselines
We compare ANAS-P with robust learning without sparsity, such as TRADES (Zhang et al., 2019) and MART (Wang et al., 2020; i.e., the dense adversarial training). Additionally, we take into account the adversarial pruning baselines, including ADMM (Ye et al., 2019) and HYDRA (Sehwag et al., 2020), which are consistent with our empirical settings.
4.1.4 Evaluation metrics
We evaluate the performance of models using the following metrics: clean accuracy, which represents the percentage of correctly classified benign examples, and adversarial robust accuracy, which denotes the percentage of correctly classified adversarial examples perturbed by the corresponding adversarial attacks. To assess the truly reliable adversarial robustness, we use a PGD attack (Madry et al., 2018; PGD-50-10) with the standard magnitude (ϵ = 8/255), 50 steps as well as 10 restarts at the step-size α = 2/255 under l∞-norm. Moreover, Auto-PGD (A-PGD; Croce and Hein, 2020b) with momentum parameter ρ = 0.75 and AA (Croce and Hein, 2020b) are introduced to evaluate diverse aspects of model robustness.
4.1.5 Training details
The entire training consists of three stages: adversarial pretraining with 100 epochs, adversarial pruning via the D2BC mask with 20 epochs, and adversarial fine-tuning with 40 epochs. For the adversarial pretraining phase, we follow the same setting as TRADES (Zhang et al., 2019) and MART (Wang et al., 2020). Afterward, the model is initialized with the parameters of the pretrained backbone obtained in the first phase, and the coefficient γ in the overall training loss in Equation 3 is set to 0.01. SGD optimizers are utilized for both ANAS-P and dense adversarial training, with momentum set to 0.9, and weight decay of 2 × 10−4 and 3.5 × 10−3 in TRADES (Zhang et al., 2019) and MART (Wang et al., 2020), respectively. The learning rate is initialized as 1 × 10−4 and reduced by half at the 10 and 15 epochs during the searching phase and at the 30 and 35 epochs during adversarial fine-tuning.
4.2 Experimental results
4.2.1 CIFAR-10/100
We consider both dense adversarial training (Zhang et al., 2019; Wang et al., 2020) and adversarial pruning baselines (Ye et al., 2019; Sehwag et al., 2020) to investigate how sparsity influences the model's clean accuracy and adversarial robust accuracy. For a fair comparison, all model configurations are identical and the compression is dedicated to CONV layers. As shown in Table 1, we report the performance of the VGG-16 or ResNet-18 model trained with TRADES (Zhang et al., 2019) or MART (Wang et al., 2020) on CIFAR-10 at three pruning ratios.
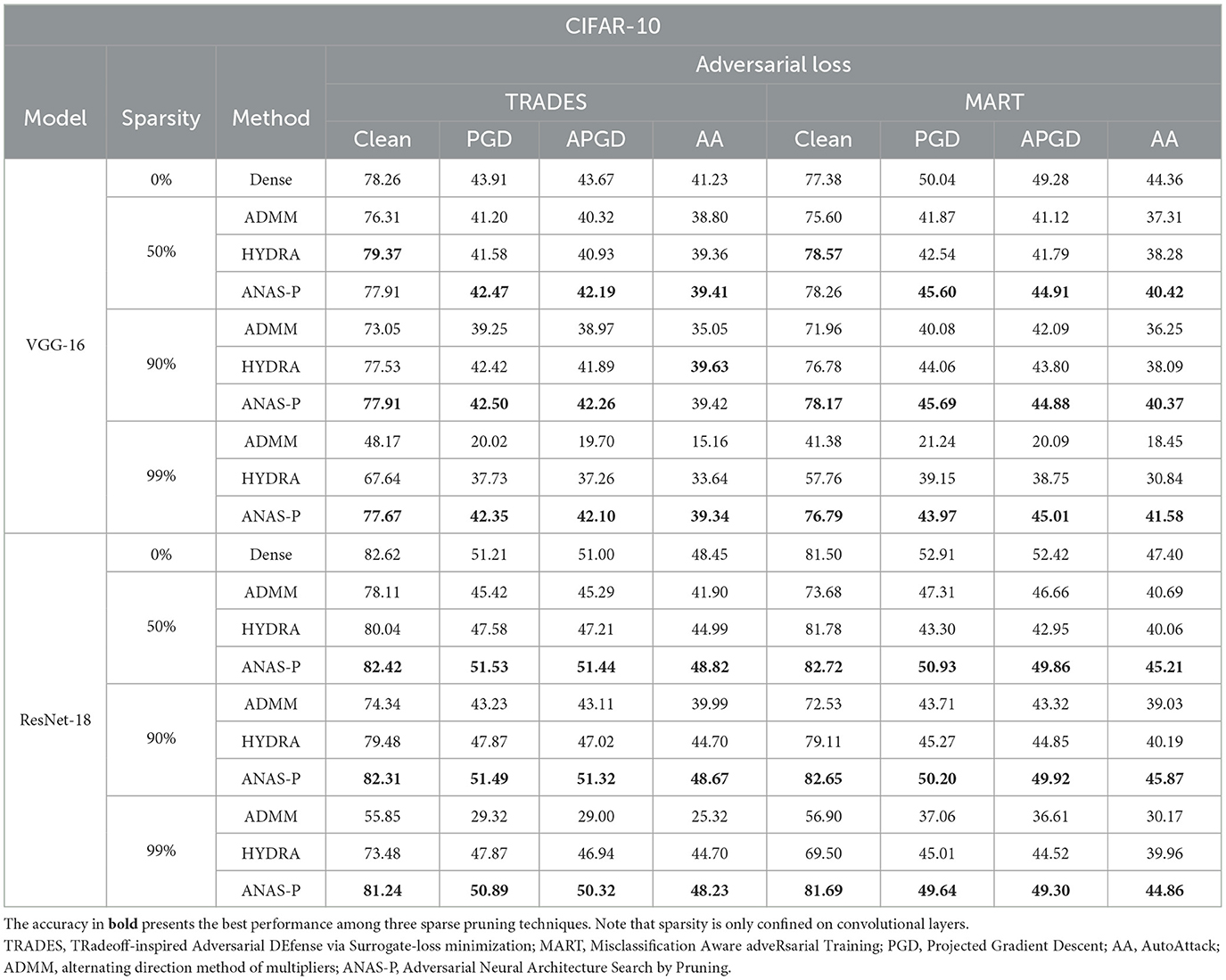
Table 1. Comparisons with dense adversarial training methods and robustness-ware pruning approaches with compression ratio [50%,90%,99%] on CIFAR-10 trained with VGG-16, ResNet-18.
As observed, from low to high sparsity levels, all three adversarial pruning methods witness the degradation in benign accuracy and adversarial robust accuracy compared with two dense robust learning strategies. With respect to the VGG-16 model, the proposed ANAS-P outperforms ADMM and HYDRA under two adversarial objectives (TRADES and MART) in terms of the adversarial robust accuracy under three different adversarial attacks (PGD, A-PGD, and AA). Specifically, we find that ADMM and HYDRA suffer from a significant clean and robust accuracy drop at 99% sparsity, for example, from 78.26% to 48.17% for ADMM and to 67.64% for HYDRA on clean accuracy or from 41.23 to 15.16% for ADMM and to 33.64% for HYDRA on AA, when adversarial loss is TRADES. In contrast, ANAS-P only decreases the clean accuracy by 0.75% and the robust accuracy under AA by 4.58%. A similar smaller performance loss is observed on MART as well. Nevertheless, the performance of the sparse ResNet-18 models is superior to compressed VGG-16 in benign and adversarial accuracy. What is more, the ResNet-18 model pruned with TRADES at 50 and 90% sparsity ratios achieves higher robust accuracy under attacks of PGD, APGD and AA than dense baselines, where the improvements are 0.86% at most. Our ANAS-P is the leading method (especially at high sparsity levels), with better robustness compared with adversarial pruning baselines.
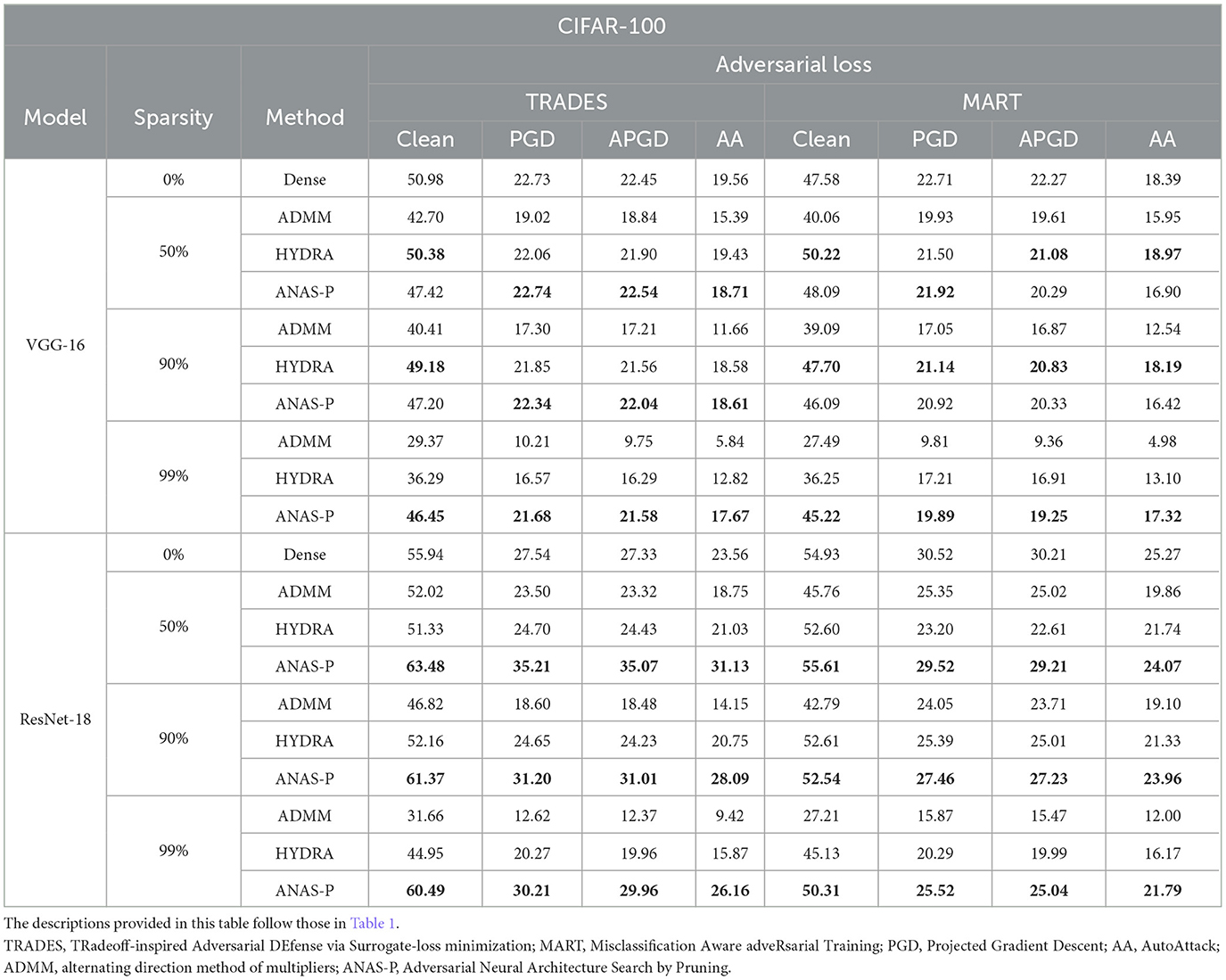
The evaluations are further extended to CIFAR-100 in Table 2. For the pruned VGG-16 model with high sparsity levels (such as 99% sparsity ratio), robustness evaluated under three adversarial attacks is superior to that achieved by ADMM and HYDRA. For example, VGG-16 pruned with MART at 99% sparsity decreases the PGD accuracy slightly by only 12.42% with the proposed ANAS-P, while ADMM and HYDRA result in a significant degradation of 56.80% (from 22.71 to 9.81%) and 24.22% (from 22.71 to 17.21%), respectively. Besides, for the ResNet-18 model, the experiments demonstrate our superior performance compared with two pruning baselines across all three sparsity levels in terms of both clean and robust accuracy for different adversarial training objectives (TRADES and MART). In particular, when the ResNet-18 model is pruned with TRADES, the clean and robust accuracy is even higher than those of the dense training, where the clean and PGD accuracy improvements are as high as 13.48% (from 55.94 to 63.48%) and 27.85% (from 27.54 to 35.21%) for 50% sparsity, respectively. Moreover, the ResNet-18 model trained with MART at 99% sparsity achieves a remarkable 17.54% (from 45.13 to 50.31%) increase in clean accuracy and a significant 34.66% (from 19.99 to 25.04%) improvement in APGD in comparison to HYDRA.
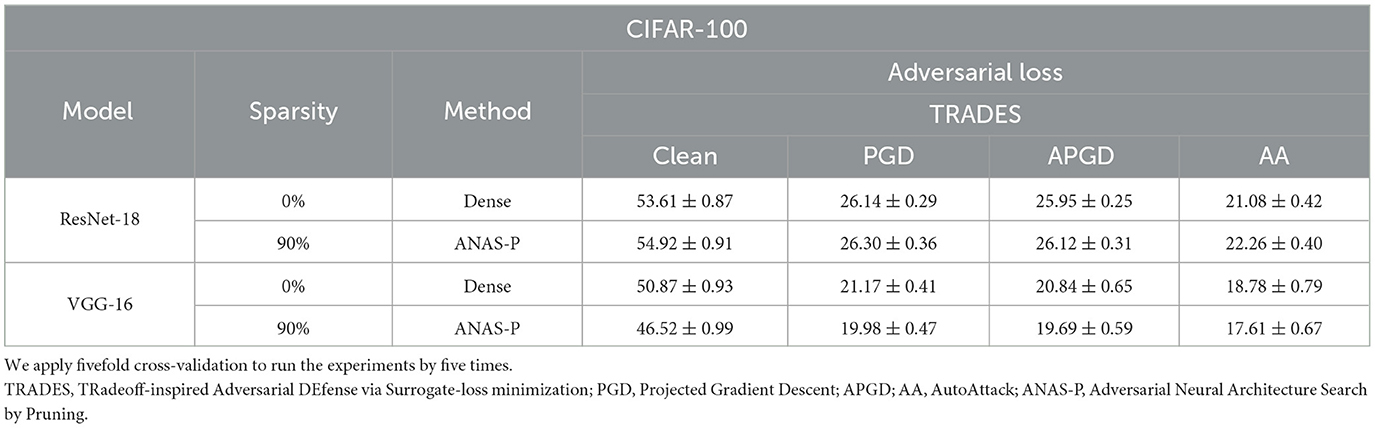
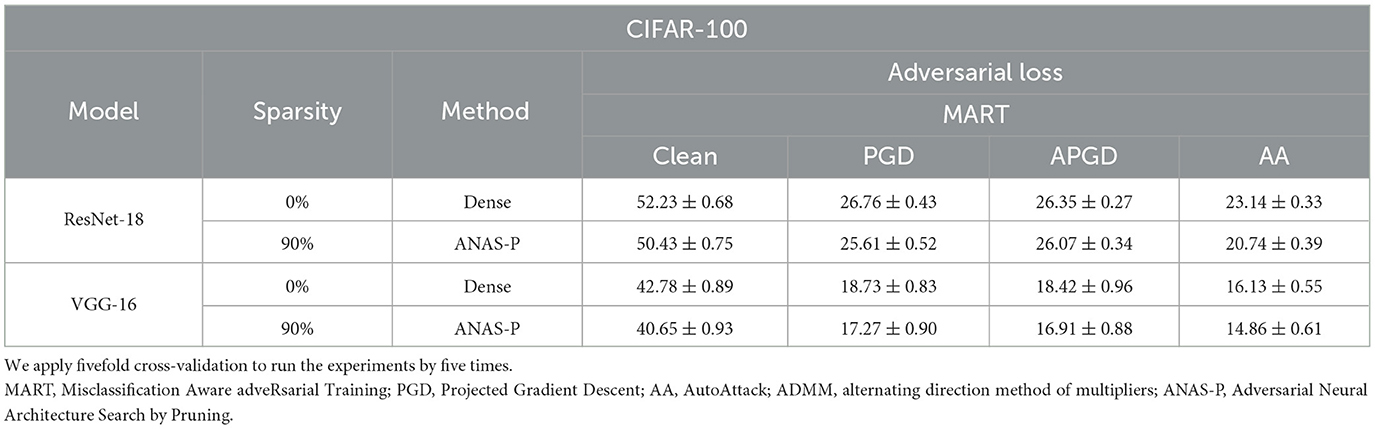
To avoid coincidence in a single division of the data and prove our method on different data, we further adopt K-fold cross-validation including the following steps: (a) Shuffle the original training data set randomly, (b) split the shuffled data set into K groups, and (c) for each group, we use this group as the test set and the rest K - 1 groups as the training set to train and test (learn and test) following our proposed method. Note that we repeat the learn-and-test K times as there are K groups in total. Here we set K equal to 5 and report the mean and the standard deviation of the results. We do not set K to a large value (such as 100) since adversarial training is computationally expensive in typical. As presented in Tables 3, 4, the standard deviation of our method is small, demonstrating our robustness for different data subsets.
4.2.2 Tiny-ImageNet
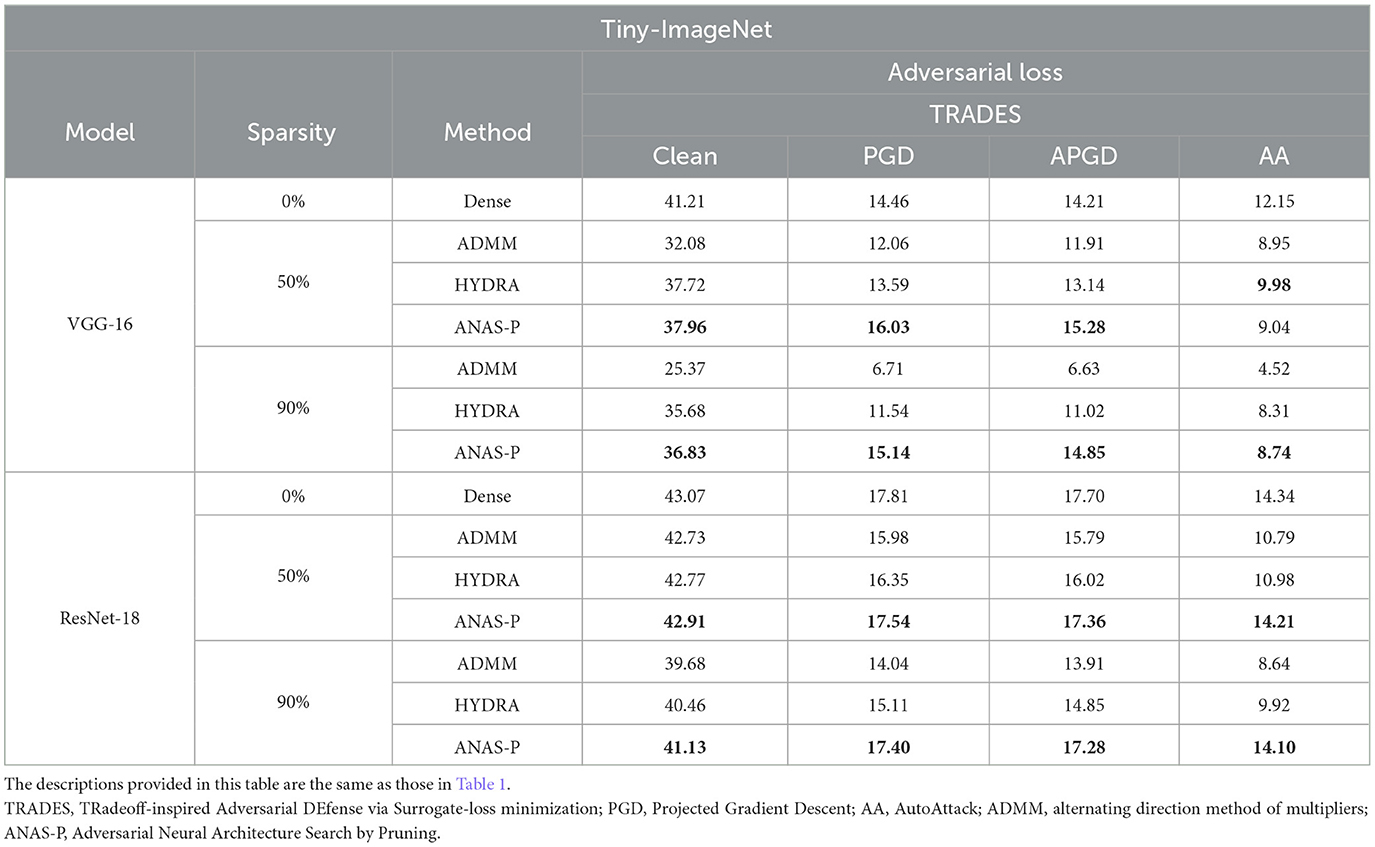
To strengthen our evaluation, we extend our experiments on Tiny-ImageNet with the larger image size in Table 5. The VGG-16 and ResNet-18 models are pruned under TRADES at the sparsity of 50 and 90%. ANAS-P, which yields the highest PGD-based robustness among the three pruning methods, advances the PGD and APGD robustness of VGG-16 by 10.86 and 7.53% for 50% sparsity, respectively, as well as 4.70 and 4.50% for 90% sparsity, respectively. Despite a slight impairment in benign and robust accuracy, the sparse ResNet-18 model pruned by ANAS-P remains superior to the network compressed via two other baselines, ADMM and HYDRA. At a CONV pruning ratio of 90%, ANAS-P merely encounters a 4.50% performance drop in clean accuracy and a 2.37% decrease in AA adversarial robust accuracy.
On all three data sets, ResNet-18 shows better clean and robust accuracy than VGG-16 regardless of the sparsity level. The potential impact factor is the architecture difference, with ResNet-18 consisting of residual blocks via the identity mapping, while VGG-16 is built on the stacked convolutional layers. When the dense network layers go deeper, the residual design helps solve the vanishing gradient problem and improves the representation ability of networks. The benefits of the residual layout generalize to the sparse and robust models.
4.3 Ablation study
4.3.1 Masking threshold
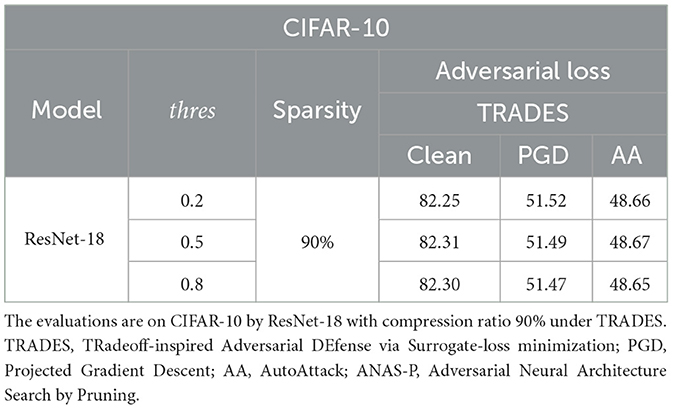
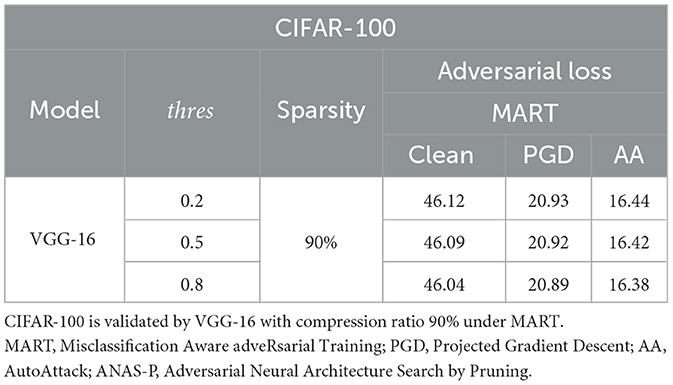
We conduct ablation studies on ANAS-P with three masking thresholds ([0.2, 0.5, 0.8]). The tests are on CIFAR-10 and CIFAR-100 by ResNet-18 and VGG-16 in Tables 6, 7. The differences between the three binarization thresholds in terms of both standard accuracy and robustness are marginal. We choose the medium value 0.5 as the final masking threshold.
4.3.2 Adversarial attack strength
Figure 4 illustrates our PGD evaluations with varying attack strengths for the trained sparse models at the sparsity of 99%, in comparison to HYDRA. The robustness is measured with three PGD attack intensities ([4/255, 8/255, 16/255]) for VGG-16 trained on CIFAR-10 with TRADES and for ResNet-18 trained on CIFAR-100 with MART. The results indicate that ANAS-P outperforms HYDRA across different PGD attack intensities.
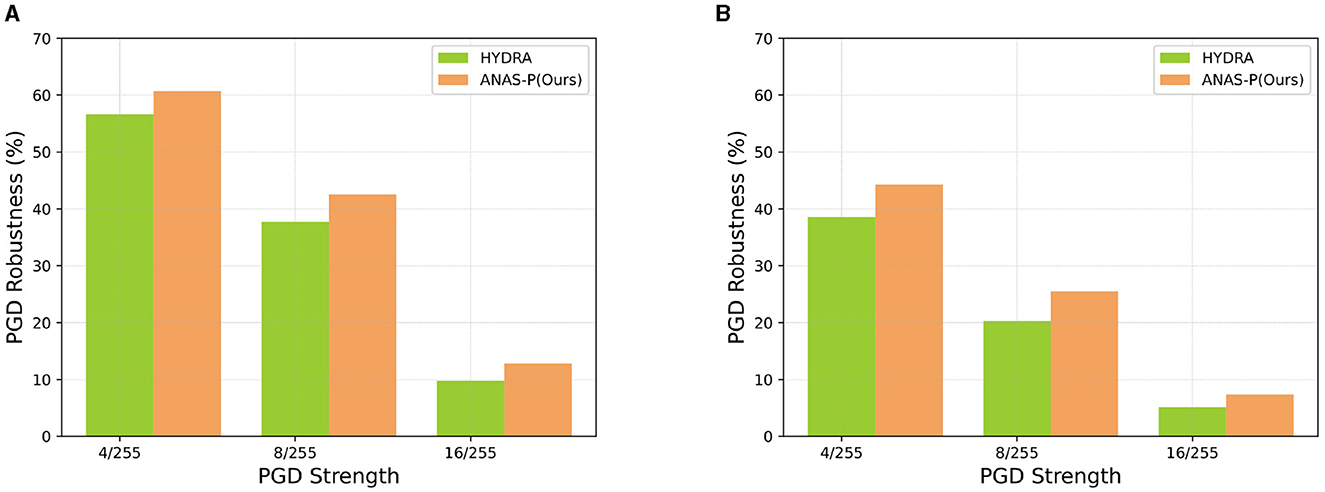
Figure 4. HYDRA and ANAS-P prune ResNet-18 and VGG-16 at the sparsity of 99%, which are evaluated by PGD with three attack strengths ([4/255, 8/255, 16/255]). (A) VGG-16 is trained on CIFAR-10 by TRADES. (B) ResNet-18 is on CIFAR-100 by MART. ANAS-P, Adversarial Neural Architecture Search by Pruning; PGD, Projected Gradient Descent.
4.3.3 Pruning loss penalty intensity
Figure 5 investigates how the parameter γ in Equation 3 impacts both standard and robust accuracy (AA evaluation). We consider VGG-16 trained on CIFAR-100, with the TRADES and MART loss under 90% sparsity. The observation is that with the increase of γ, the penalty imposed by is dominated over , leading to the deterioration of the model's clean accuracy and robustness. Therefore, we set the default value of γ to 0.01 in the experiments for optimal performance.
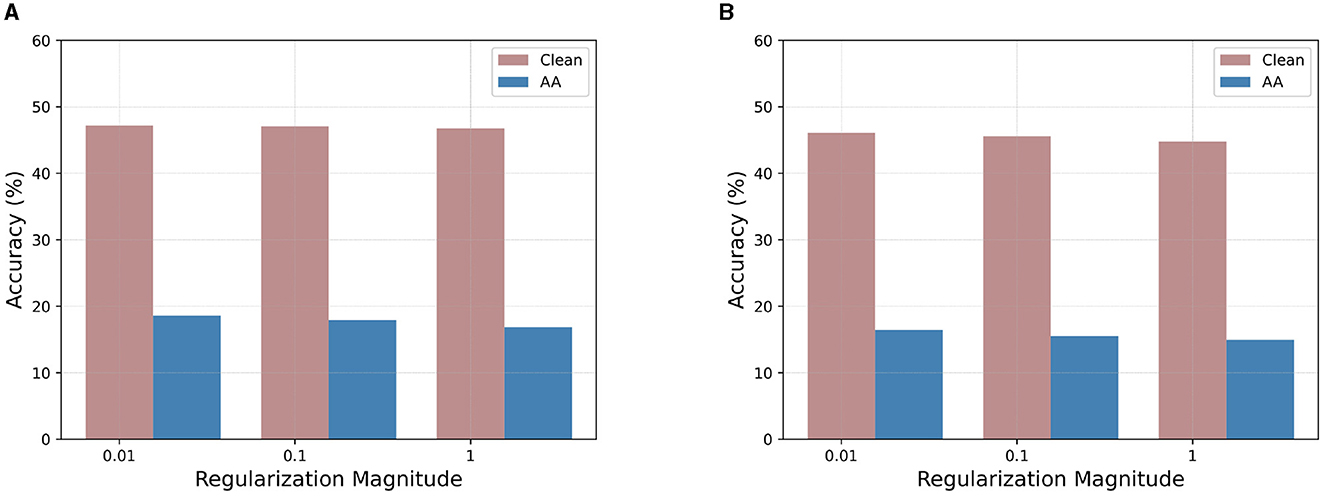
Figure 5. Effects of pruning loss coefficient magnitudes on 90% sparse VGG-16 evaluated under AA attack with different pruning regularization magnitudes on CIFAR-100. (A) VGG-16 by TRADES. (B) VGG-16 by MART. TRADES, TRadeoff-inspired Adversarial DEfense via Surrogate-loss minimization; MART, Misclassification Aware adveRsarial Training; AA, AutoAttack.
5 Discussion and conclusion
5.1 Discussion
Research on adversarial robustness in sparse models is crucial for the widespread real-world applications of DNNs. Our work makes a significant contribution to trustworthy and efficient artificial intelligence by pruning models while maintaining adversarial robustness. By advancing the understanding of adversarially robust sparse models, our proposed techniques can be applied to the deployment of sparse robust models in resource-constrained environments, such as mobile devices.
5.2 Conclusion
This article proposes ANAS-P, a robustness-aware neural architecture search framework by channel pruning to achieve sparsity and adversarial robustness. The D2BC mask is utilized for conducting a layer-width search per CONV layer. Extensive experiments conducted in two adversarial training settings demonstrate the effectiveness of our adversarial pruning approach in searching CONV-sparse and robust models.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
Author contributions
YL: Writing – original draft, Conceptualization, Investigation, Methodology, Software, Validation, Visualization, Writing – review & editing. PZ: Conceptualization, Methodology, Writing – review & editing, Writing – original draft. RD: Software, Validation, Visualization, Writing – review & editing. TZ: Software, Validation, Visualization, Writing – review & editing. YF: Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing. XX: Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing. XL: Funding acquisition, Project administration, Resources, Supervision, Writing – review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was supported by the Office of Naval Research Federal Award (Contract No. N00014-21-C-1111 with Subcontract No. 555072-78052) to Northeastern University.
Acknowledgments
We are grateful for the Office of Naval Research for sponsoring this study. We express our sincere gratitude to Yushu Wu and Yanyu Li for their valuable insights and constructive feedback on our methodology design and numerical experiments. Their contributions significantly enhance the quality of our work.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Apruzzese, G., Colajanni, M., Ferretti, L., and Marchetti, M. (2019). “Addressing adversarial attacks against security systems based on machine learning,” in 2019 11th international conference on cyber conflict (CyCon), volume 900 (Tallinn: IEEE), 1–18. doi: 10.23919/CYCON.2019.8756865
Bai, Y., Wang, Y., Zeng, Y., Jiang, Y., and Xia, S.-T. (2023). Query efficient black-box adversarial attack on deep neural networks. Pattern Recognit. 133:109037. doi: 10.1016/j.patcog.2022.109037
Bengio, Y., Léonard, N., and Courville, A. C. (2013). Estimating or propagating gradients through stochastic neurons for conditional computation. arXiv [Preprint]. arXiv:1305.2982. doi: 10.48550/arXiv.1305.2982
Boopathy, A., Liu, S., Zhang, G., Chen, P.-Y., Chang, S., Daniel, L., et al. (2020). “Visual interpretability alone helps adversarial robustness,” in International Conference on Machine Learning (ICML).
Carlini, N., and Wagner, D. (2017). “Towards evaluating the robustness of neural networks,” in IEEE Symposium on Security and Privacy (S&P) (San Jose, CA: IEEE). doi: 10.1109/SP.2017.49
Chen, A., Lorenz, P., Yao, Y., Chen, P.-Y., and Liu, S. (2023). “Visual prompting for adversarial robustness,” in ICASSP 2023-2023 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) (Rhodes Island: IEEE), 1–5. doi: 10.1109/ICASSP49357.2023.10097245
Chen, J., Cheng, Y., Gan, Z., Gu, Q., and Liu, J. (2022). Efficient robust training via backward smoothing. Proc. AAAI Conf. Artif. Intell. 36, 6222–6230. doi: 10.1609/aaai.v36i6.20571
Chen, T., Liu, S., Chang, S., Cheng, Y., Amini, L., Wang, Z., et al. (2020). “Adversarial robustness: from self-supervised pre-training to fine-tuning,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Seattle, WA: IEEE). doi: 10.1109/CVPR42600.2020.00078
Cheng, Z., Li, Y., Dong, M., Su, X., You, S., Xu, C., et al. (2023). “Neural architecture search for wide spectrum adversarial robustness,” in Proceedings of the AAAI Conference on Artificial Intelligence (Washington, DC: AAAI). doi: 10.1609/aaai.v37i1.25118
Croce, F., and Hein, M. (2020a). “Minimally distorted adversarial examples with a fast adaptive boundary attack,” in International Conference on Machine Learning (ICML) (PMLR), 2196–2205.
Croce, F., and Hein, M. (2020b). “Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks,” in International Conference on Machine Learning (ICML) (PMLR).
Dao, T., Fu, D. Y., Saab, K. K., Thomas, A. W., Rudra, A., and Ré, C. (2023). “Hungry Hungry Hippos: towards language modeling with state space models,” in International Conference on Learning Representations (ICLR).
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., Fei-Fei, L., et al. (2009). “Imagenet: a large-scale hierarchical image database,” in 2009 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Miami, FL: IEEE), 248–255. doi: 10.1109/CVPR.2009.5206848
Devaguptapu, C., Agarwal, D., Mittal, G., Gopalani, P., and Balasubramanian, V. N. (2021). “On adversarial robustness: a neural architecture search perspective,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops (Montreal, BC: IEEE). doi: 10.1109/ICCVW54120.2021.00022
Freitas, S., Chen, S.-T., Wang, Z. J., and Chau, D. H. (2020). “Unmask: adversarial detection and defense through robust feature alignment,” in 2020 IEEE International Conference on Big Data (Big Data) (Atlanta, GA: IEEE), 1081–1088. doi: 10.1109/BigData50022.2020.9378303
Gong, Y., Yao, Y., Li, Y., Zhang, Y., Liu, X., Lin, X., et al. (2022a). “Reverse engineering of imperceptible adversarial image perturbations,” in International Conference on Learning Representations (ICLR) (OpenReview.net).
Gong, Y., Zhan, Z., Zhao, P., Wu, Y., Wu, C., Ding, C., et al. (2022b). “All-in-one: a highly representative dnn pruning framework for edge devices with dynamic power management,” in Proceedings of the 41st IEEE/ACM International Conference on Computer-Aided Design (ICCAD) (New York, NY: ACM), 1–9. doi: 10.1145/3508352.3549379
Goodfellow, I. J., Shlens, J., and Szegedy, C. (2015). Explaining and harnessing adversarial examples. arXiv [Preprint]. doi: 10.48550/arXiv.1412.6572
Gui, S., Wang, H., Yang, H., Yu, C., Wang, Z., Liu, J., et al. (2019). “Model compression with adversarial robustness: a unified optimization framework,” in Advances in Neural Information Processing Systems (NIPS) (Vancouver, BC: MIT Press), 32.
Guo, S., Wang, Y., Li, Q., and Yan, J. (2020). “DMCP: differentiable Markov channel pruning for neural networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (Seattle, WA: IEEE). doi: 10.1109/CVPR42600.2020.00161
Guo, Y., Zhang, C., Zhang, C., and Chen, Y. (2018). “Sparse dnns with improved adversarial robustness,” in Advances in neural information processing systems (NIPS), 31.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Identity mappings in deep residual networks,” in European conference on computer vision (ECCV) (Cham: Springer), 630–645. doi: 10.1007/978-3-319-46493-0_38
Kaur, S., Fioretto, F., and Salekin, A. (2022). Deadwooding: robust global pruning for deep neural networks. arXiv [Preprint]. abs/2202.05226.
Krizhevsky, A., and Hinton, G. (2009). Learning multiple layers of features from tiny images. [Master's thesis]. Department of Computer Science, University of Toronto, Toronto, ON.
Kundu, S., Nazemi, M., Beerel, P. A., and Pedram, M. (2021). “DNR: a tunable robust pruning framework through dynamic network rewiring of DNNS,” in Proceedings of the 26th Asia and South Pacific Design Automation Conference, ASPDAC '21 (New York, NY: Association for Computing Machinery), 344–350. doi: 10.1145/3394885.3431542
Lee, B.-K., Kim, J., and Ro, Y. M. (2022). “Masking adversarial damage: finding adversarial saliency for robust and sparse network,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (New Orleans, LA: IEEE). doi: 10.1109/CVPR52688.2022.01470
Li, B., Pandey, S., Fang, H., Lyv, Y., Li, J., Chen, J., et al. (2020). “Ftrans: energy-efficient acceleration of transformers using fpga,” in Proceedings of the ACM/IEEE International Symposium on Low Power Electronics and Design (New York, NY: ACM), 175–180. doi: 10.1145/3370748.3406567
Li, F., Zhang, H., Liu, S., Guo, J., Ni, L. M., Zhang, L., et al. (2022). “DN-DETR: accelerate detr training by introducing query denoising,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (New Orleans, LA: IEEE), 13619–13627. doi: 10.1109/CVPR52688.2022.01325
Li, Y., Zhao, P., Lin, X., Kailkhura, B., and Goldhahn, R. (2023). “Less is more: data pruning for faster adversarial training,” in The Proceedings of the AAAI Conference on Artificial Intelligence Workshop on Artificial Intelligence Safety (SafeAI 2023) (Washington, DC: AAAI).
Liu, S., Chen, T., Chen, X., Atashgahi, Z., Yin, L., Kou, H., et al. (2021). Sparse training via boosting pruning plasticity with neuroregeneration. Adv. Neural Inform. Process. Syst. 34, 9908–9922. doi: 10.5555/3540261.3541019
Luo, B., Liu, Y., Wei, L., and Xu, Q. (2018). “Towards imperceptible and robust adversarial example attacks against neural networks,” in Proceedings of the AAAI Conference on Artificial Intelligence, Vol. 32 (New Orleans, LA: AAAI). doi: 10.1609/aaai.v32i1.11499
Madaan, D., Shin, J., and Hwang, S. J. (2020). “Adversarial neural pruning with latent vulnerability suppression,” in Proceedings of the 37th International Conference on Machine Learning (PMLR).
Madry, A., Makelov, A., Schmidt, L., Tsipras, D., and Vladu, A. (2018). “Towards deep learning models resistant to adversarial attacks,” in International Conference on Learning Representations (ICLR) (Vancouver, BC: OpenReview.net).
Mahajan, D., Girshick, R., Ramanathan, V., He, K., Paluri, M., Li, Y., et al. (2018). Exploring the limits of weakly supervised pretraining. Cham: Springer. doi: 10.1007/978-3-030-01216-8_12
Mok, J., Na, B., Choe, H., and Yoon, S. (2021). “Advrush: searching for adversarially robust neural architectures,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) (Montreal, QC: IEEE), 12322–12332. doi: 10.1109/ICCV48922.2021.01210
Özdenizci, O., and Legenstein, R. (2021). “Training adversarially robust sparse networks via bayesian connectivity sampling,” in International Conference on Machine Learning (ICML) (PMLR), 8314–8324.
Rakin, A. S., He, Z., Yang, L., Wang, Y., Wang, L., Fan, D., et al. (2019). Robust sparse regularization: simultaneously optimizing neural network robustness and compactness. arXiv [Preprint]. arXiv:1905.13074. doi: 10.48550/arXiv.1905.13074
Sehwag, V., Wang, S., Mittal, P., and Jana, S. (2020). Hydra: Pruning Adversarially Robust Neural Networks (Curran Associates, Inc.).
Shafahi, A., Najibi, M., Ghiasi, M. A., Xu, Z., Dickerson, J., Studer, C., et al. (2019). “Adversarial training for free!” in Advances in Neural Information Processing Systems (NeurIPS) (Vancouver, BC: Curran Associates, Inc.).
Simonyan, K., and Zisserman, A. (2015). “Very deep convolutional networks for large-scale image recognition,” in International Conference on Learning Representations (ICLR) (San Diego, CA: OpenReview.net).
Spallanzani, M., Leonardi, G. P., and Benini, L. (2022). “Training quantised neural networks with ste variants: the additive noise annealing algorithm,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) (New Orleans, LA: IEEE), 470–479. doi: 10.1109/CVPR52688.2022.00056
Sriramanan, G., Addepalli, S., Baburaj, A., and Venkatesh, B. R. (2020). Guided adversarial attack for evaluating and enhancing adversarial defenses. Adv. Neural Inform. Process. Syst. 33, 20297–20308. doi: 10.5555/3495724.3497428
Su, D., Zhang, H., Chen, H., Yi, J., Chen, P.-Y., Gao, Y., et al. (2018). “Is robustness the cost of accuracy?-a comprehensive study on the robustness of 18 deep image classification models,” in Proceedings of the European Conference on Computer Vision (ECCV) (Cham: Springer). doi: 10.1007/978-3-030-01258-8_39
Sun, L., Dou, Y., Yang, C., Zhang, K., Wang, J., Philip, S. Y., et al. (2022). Adversarial attack and defense on graph data: a survey. IEEE Trans. Knowl. Data Eng. 35, 7693–7711. doi: 10.1109/TKDE.2022.3201243
Tramer, F., Carlini, N., Brendel, W., and Madry, A. (2020). On adaptive attacks to adversarial example defenses. Adv. Neural Inform. Process. Syst. 33, 1633–1645. doi: 10.5555/3495724.3495862
Tsipras, D., Santurkar, S., Engstrom, L., Turner, A., and Madry, A. (2018). Robustness may be at odds with accuracy. arXiv [Preprint]. arXiv:1805.12152. doi: 10.48550/arXiv.1805.12152
Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). “Attention is all you need,” in Advances in Neural Information Processing Systems (NeurIPS).
Wang, Y., Zou, D., Yi, J., Bailey, J., Ma, X., Gu, Q., et al. (2020). “Improving adversarial robustness requires revisiting misclassified examples,” in International Conference on Learning Representations (ICLR) (OpenReview.net).
Wu, Y., Gong, Y., Zhao, P., Li, Y., Zhan, Z., Niu, W., et al. (2022). “Compiler-aware neural architecture search for on-mobile real-time super-resolution,” in European Conference on Computer Vision (ECCV) (Cham: Springer), 92–111. doi: 10.1007/978-3-031-19800-7_6
Xiao, C., Li, B., yan Zhu, J., He, W., Liu, M., and Song, D. (2018). “Generating adversarial examples with adversarial networks,” in Proceedings of the Twenty-Seventh International Joint Conference on Artificial Intelligence (IJCAI) (Stockholm: AAAI Press). doi: 10.24963/ijcai.2018/543
Xin, Y., Du, J., Wang, Q., Yan, K., and Ding, S. (2024). Mmap: multi-modal alignment prompt for cross-domain multi-task learning. Proc. AAAI Conf. Artif. Intell. 38, 16076–16084. doi: 10.1609/aaai.v38i14.29540
Xu, K., Liu, S., Zhang, G., Sun, M., Zhao, P., Fan, Q., et al. (2019). Interpreting adversarial examples by activation promotion and suppression. arXiv [Preprint]. arXiv:1904.02057. doi: 10.48550/arXiv.1904.02057
Yang, J., Li, C., Dai, X., and Gao, J. (2022). “Focal modulation networks,” in Advances in Neural Information Processing Systems (NIPS).
Ye, S., Xu, K., Liu, S., Lambrechts, J.-H., Zhang, H., Zhou, A., et al. (2019). “Adversarial robustness vs model compression, or both?” in International Conference on Computer Vision (ICCV) (Seoul: IEEE). doi: 10.1109/ICCV.2019.00020
Yin, P., Lyu, J., Zhang, S., Osher, S., Qi, Y., Xin, J., et al. (2019). “Understanding straight-through estimator in training activation quantized neural nets,” in International Conference on Learning Representations (ICLR) (New Orleans, LA: OpenReview.net).
You, H., Li, B., Sun, Z., Ouyang, X., and Lin, Y. (2022). Supertickets: drawing task-agnostic lottery tickets from supernets via jointly architecture searching and parameter pruning. Berlin: Springer. doi: 10.1007/978-3-031-20083-0_40
Yu, J., Wang, Z., Vasudevan, V., Yeung, L., Seyedhosseini, M., Wu, Y., et al. (2022). Coca: Contrastive captioners are image-text foundation models.
Yuan, G., Behnam, P., Li, Z., Shafiee, A., Lin, S., Ma, X., et al. (2021a). “Forms: fine-grained polarized reram-based in-situ computation for mixed-signal dnn accelerator,” in 2021 ACM/IEEE 48th Annual International Symposium on Computer Architecture (ISCA) (Valencia: IEEE), 265–278. doi: 10.1109/ISCA52012.2021.00029
Yuan, G., Ma, X., Niu, W., Li, Z., Kong, Z., Liu, N., et al. (2021b). “Mest: accurate and fast memory-economic sparse training framework on the edge,” in Advances in Neural Information Processing Systems (NIPS) (MIT Press), 34.
Yuan, L., Chen, D., Chen, Y.-L., Codella, N. C. F., Dai, X., Gao, J., et al. (2021). Florence: A new foundation model for computer vision. arXiv [Preprint]. abs/2111.11432.
Zhang, H., Yu, Y., Jiao, J., Xing, E. P., Ghaoui, L. E., Jordan, M. I., et al. (2019). “Theoretically principled trade-off between robustness and accuracy,” in International Conference on Machine Learning (ICML) (Long Beach, CA: PMLR).
Zhang, J., Xu, X., Han, B., Niu, G., Cui, L., Sugiyama, M., et al. (2020). ‘Attacks which do not kill training make adversarial learning stronger,” in Proceedings of the 37th International Conference on Machine Learning (ICML) (PMLR).
Zhang, Y., Zhang, G., Khanduri, P., Hong, M., Chang, S., Liu, S., et al. (2022). “Revisiting and advancing fast adversarial training through the lens of bi-level optimization,” in International Conference on Machine Learning (ICML) (Baltimore, MD: PMLR), 26693–26712.
Zheng, Y.-J., Chen, S.-B., Ding, C. H. Q., and Luo, B. (2022). Model compression based on differentiable network channel pruning. IEEE Trans. Neural Netw. Learn. Syst. 34, 10203–10212. doi: 10.1109/TNNLS.2022.3165123
Keywords: efficient AI, neural network sparsity, neural architecture search, adversarial robustness, adversarial pruning
Citation: Li Y, Zhao P, Ding R, Zhou T, Fei Y, Xu X and Lin X (2024) Neural architecture search for adversarial robustness via learnable pruning. Front. High Perform. Comput. 2:1301384. doi: 10.3389/fhpcp.2024.1301384
Received: 24 September 2023; Accepted: 18 June 2024;
Published: 16 September 2024.
Edited by:
Tongping Liu, University of Massachusetts Amherst, United StatesReviewed by:
Weiwen Jiang, George Mason University, United StatesHui Zhang, ByteDance Ltd., United States
Copyright © 2024 Li, Zhao, Ding, Zhou, Fei, Xu and Lin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yize Li, bGkueWl6ZUBub3J0aGVhc3Rlcm4uZWR1; Xue Lin, eHVlLmxpbkBub3J0aGVhc3Rlcm4uZWR1
 Yize Li
Yize Li Pu Zhao
Pu Zhao Ruyi Ding
Ruyi Ding Tong Zhou
Tong Zhou Yunsi Fei
Yunsi Fei Xiaolin Xu
Xiaolin Xu Xue Lin
Xue Lin