
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Genet. , 20 March 2023
Sec. Computational Genomics
Volume 14 - 2023 | https://doi.org/10.3389/fgene.2023.1158337
DNA is a practical storage medium with high density, durability, and capacity to accommodate exponentially growing data volumes. A DNA sequence structure is a biocomputing problem that requires satisfying bioconstraints to design robust sequences. Existing evolutionary approaches to DNA sequences result in errors during the encoding process that reduces the lower bounds of DNA coding sets used for molecular hybridization. Additionally, the disordered DNA strand forms a secondary structure, which is susceptible to errors during decoding. This paper proposes a computational evolutionary approach based on a synergistic moth-flame optimizer by Levy flight and opposition-based learning mutation strategies to optimize these problems by constructing reverse-complement constraints. The MFOS aims to attain optimal global solutions with robust convergence and balanced search capabilities to improve DNA code lower bounds and coding rates for DNA storage. The ability of the MFOS to construct DNA coding sets is demonstrated through various experiments that use 19 state-of-the-art functions. Compared with the existing studies, the proposed approach with three different bioconstraints substantially improves the lower bounds of the DNA codes by 12–28% and significantly reduces errors.
The natural objective of DNA-encoding methods is to provide high-density, error-free, and stable DNA codes by dynamic programming (Yim et al., 2014; Erlich and Zielinski, 2017; Organick et al., 2018; Lu et al., 2023). However, the computational capacity of dynamic programming remains infeasible with big digital data and biological sequences. Consequently, substantial efforts have been invested in finding efficient heuristic/optimization algorithms to tackle this feasibility (Cao et al., 2020a). These algorithms produce upper and lower bounds in DNA sequence data by dynamic programming. A sequence
Biotechnology and bioengineering recently played a vital role in DNA computation as nanobiotechnology synthesizes DNA. Research communities are still combating errors in DNA-coding sets with different computational methods (Grass et al., 2015; Yazdi et al., 2017; Deng et al., 2019). One of the computational methods is evolutionary computation, which comprises a set of biologically inspired algorithms. For example, the author showed the chaos whale optimization with sine and cosine functions to construct the DNA sequence set (Li et al., 2021b). Similarly, Xiaoru and Ling (2021) delivered an evolutionary-based equilibrium optimization with a random search model to overcome the error rate in DNA-coding sets. These studies contributed significantly to advancing evolutionary approaches in DNA storage. However, the results still lacked an improvement in the diversity of the sampled population.
For this purpose, the effectiveness of the optimization algorithm will have to increase by designing the mutation strategies. Wang et al. (2020) considered the differential evaluation algorithm with a two-level local search strategy to improve convergence. The general purpose of such strategies is to avoid the local minima and prevent the population from being similar. The improvement in evolutionary algorithms by mutation strategies also significantly impacts the improvement of the lower bounds of DNA-coding sets. A multi-verse optimizer (MVO) was made synergistic by damping the strategy to gain a stable state in global search, and it also reported 4–16% of improved DNA-coding sets (Cao et al., 2020b). Rasool et al. (2022a) used the opposition-based learning (OBL) mutation strategy (Dong et al., 2017) for three-dimensional search space with a meta-heuristic algorithm (Mirjalili, 2015) to generate the DNA-coding sets for data storage. The codes generated by the improved algorithm (MFOL) enhanced the DNA-coding sets over the altruistic algorithm (Limbachiya et al., 2018).
Nevertheless, these evolutionary studies have performed well by enhancing the efficiency of optimization algorithms by the mutation strategies, but they focus on particular biological coding constraints. The satisfaction of these constraints controls the oligonucleotide errors in the DNA sequences (Sager and Stefanovic, 2006; Song et al., 2018; Li et al., 2021b; Cao et al., 2022). For instance, the GC-content and Hamming distance constraints were considered for the oligonucleotide libraries construction by reducing the hybridization errors (Aboluion et al., 2012; Organick et al., 2018; Yang et al., 2020; Rasool et al., 2022b). However, the current approaches and algorithms of DNA code construction by the lower-bound computation do not satisfy the reverse-complement (RC) constraints. However, unsatisfactory reverse-complement constraints are relatively crucial in DNA codes with a high rate of errors, which cause the DNA stability for storage (Sager and Stefanovic, 2006; Yin et al., 2010).
In short, the conventional optimization algorithms have evolved for lower-bound improvements. Still, various functions’ convergence abilities have declined, which was improved by different mutation strategies with different purposes. However, the lower bounds of DNA-coding sets were insufficient for robust DNA storage due to non-specific hybridization errors (Cao et al., 2020b). Although these errors have been tackled by a few biological coding constraints, the extent of error avoidance was low because DNA sequences overlapped, creating non-specific hybridization that formed the secondary structure. DNA sequences with such a structure make the chemical reaction unstable and inactivate DNA synthesis and sequencing (Song et al., 2021). Thus, the coding sets of DNA storage are still facing the lowest global optimal performance with different evolutionary algorithms and mutation strategies to store more information in a shorter sequence with a minimum error.
Thus, in this paper, a bioengineering-based evolutionary approach has been proposed to solve the aforementioned problems. This approach integrates the MFO (Mirjalili, 2015) with two customized mutation strategies (MFOS) and practically applies it to construct DNA-coding sets. We customized the original mutation strategies for compatibility with the optimization algorithms to improve the lower bounds for the DNA code construction. Then, as the main objective of this study, MFOS is used with combinatorial constraints (GC-content, Hamming distance, no-runlength, and RC constraints) to construct DNA-coding sets. The computational RC constraint significantly increases the number of DNA strands (codes) and avoids further non-specific hybridization. The experiments are performed on 19 benchmark functions, and the Wilcoxon rank-sum test is used to evaluate the improved algorithm’s quality. The performance is compared with six existing evolutionary algorithms. The overall contribution of the proposed approach produced DNA-coding sets with improved lower bounds and coding rates compared to previous studies. It is a collaborative effort of information technology and biotechnology domains to solve a bioinformatics-based computational problem for DNA data storage. The following are the noteworthy contributions of this study:
• A novel evolutionary approach is proposed to construct DNA-coding sets by using the MFOS algorithm with two customized mutation strategies for speedy convergence and powerful exploration and exploitation capabilities.
• The novelty of this study is the practical implication of the MFOS algorithm with DNA coding constraints to improve the lower bounds and coding rates of the DNA codes by storing larger data files in the shorter sequence of DNA, and the results are compared with the existing literature.
• Computational RC constraints are satisfied to generate stable DNA codes with our two theorems by eliminating the undesired non-specific hybridization errors due to the secondary structure in DNA sequences. Additionally, an empirical thermodynamic analysis is performed on the RC constraints to validate the DNA coding sets and compare them with the prior constraints.
The rest of this paper is organized as follows. Section 2 briefs the existing DNA coding constraints. Section 3 introduces the evolutionary approach. Section 4 describes the experimental procedure, Section 5 provides result evaluation, and Section 6 reports the conclusion and future work.
The crucial part of DNA data storage is to construct DNA sequences with minimum errors during the synthesis and sequencing processes. These complicated processes are prone to insertion, substitution, and deletion errors (Yim et al., 2014; Wang et al., 2022). These errors with each nucleotide occur due to the consecutive repetitive subsequences, homopolymers, and GC-content with the minimum and maximum bases. The prior benchmark coding constraints (Cao et al., 2020b), including GC-content, no-runlength (NL), and Hamming distance, have also been used to construct DNA sequences by avoiding those errors. Additionally, this study introduces computation reverse-complement constraints to overcome further non-specific hybridization errors and the secondary structure during the DNA synthesis and sequences with the following mechanism.
A DNA code with length n will be a set of codes (
In retrospective studies (Cao et al., 2020b; Rasool et al., 2022a), some sequences were similar among the set of DNA sequences, including reverse or reverse-complement, and then non-specific hybridization occurred, which caused errors by forming the secondary structure (SS). A sequence structure in which a set of pairs of nucleotides support a secondary structure is known as the stem, while the number of repeated nucleotides is known as the stem length. The secondary structure is a result of similar sequences with base-pairing connections in which one sequence folds back to itself (Heckel et al., 2019). DNA sequence with a secondary structure makes chemical reaction less active, which causes the redundancy of that DNA sequence during the synthesis and sequencing process. Thus, the secondary structure must be unfolded before reading such sequences in the wet lab. Constructing robust DNA codes with fewer resources and errors will be helpful. This problem motivated us to put forward a novel solution that must deliver sufficiently different DNA sequences among a set of sequences by evading the secondary structure.
To avoid the SS before DNA reading, one can eliminate the base–pair connection by selecting a sequence with appropriate nucleotides that must have a sufficient code rate,
Theorem 1. A DNA sequence with length
The proposed evolutionary approach leverages the development of the MFO (Mirjalili, 2015) with DNA coding constraints. The MFO algorithm is selected because it can solve the challenging constraints and unknown search space problems for several applications, i.e., sequence compression problems, which motivated us to generalize this algorithm with DNA coding constraints. Moth belongs to the butterfly family with various similar characteristics. It has a particular navigation mechanism known as transverse orientation (TO) to fly by using the moonlight. The TO mechanism empowers the moth to fly by regulating a fixed angle by the Moon’s focal point, which allows it to fly long distances. Meanwhile, the moth often collides with human-made light due to being closer than moonlight, which distracts the moth from the destination. However, the moth endures in preserving the same angle, which causes its deadly spiral path. Eventually, this behavior supports the convergence of the moth toward the light. This concept provides a mathematical optimizer algorithm termed a moth-flame optimizer (MFO) for object convergence (Mirjalili, 2015).
This evolutionary algorithm has two candidate solutions, moth and flame, and one problem variable is the position of the moth during flight. Thus, a moth can fly by changing the position in 1/2/3 or hyper dimension of space. The moth candidate solution can be considered in the following matrix
where
An evolutionary population-based algorithm also considers an array of fitness values for all moths. The first row of
Meanwhile, the second candidate solution of MFO, the flame, also has a similar matrix
where
It should be noted that moth and flame are both solutions. However, the difference between these solutions is the mechanism we conducted with them to update them in all iterations of processes. The moth’s solution flies in a circular search space by acting as a search agent. In contrast, the flame is the destination solution for the moth in that search space. Hence, the moth struggles to reach the destination as an optimal solution by flying around the search space. Overall, this algorithm (Mirjalili, 2015) mechanism is based on the following three tuples to optimize the problem for an optimal solution.
where
The
where
The spiral function is a key component of the MFO, which decides the moth movement with respect to flames. A conceptual model is drawn in Figure 1 for the moth location updates according to the flame. The vertical axis indicates the position of a moth in one dimension, and the horizontal axis presents the possible position update for the next location. The dashed black lines display the locations that can be used for the next position of the moth in the green horizontal line concerning the orange horizontal line of a flame. The exploitation and exploration processes can be determined in the search space. Moth uses one dimension to explore and exploit the search space of flame. Exploitation emerges if the next position between the moth and flame is inside the search space, as directed by arrow 2. In contrast, exploration appears if the position updates between the moth and flame are outside the space, as indicated by arrow 1, 3–5 in Figure 1. Exploration and exploitation can be observed by following three rules.
1) A moth may converge by altering the random number
2) The lower random number is the closest distance to the flame.
3) The position frequency increases automatically as the moth comes closer to the flame.
For an effective possible solution, finding the best solution can be considered a flame candidate solution. The
where the variables
The evolutionary mechanism of this algorithm permits the moth to attain the best position in the local and global search space. However, a problem can occur that causes the MFO algorithm (Mirjalili, 2015) to fall into the local optima due to only updating the moth position corresponding to the flame and in one dimension. If all moths update the position with respect to only a single flame, all will be converged due to flying toward a flame in the search space that causes the exploration. In contrast, if all moths update the position with only
Meanwhile, the computation time complexity is a crucial metric for evaluating the algorithm run time. It is based on algorithm structure and parameter settings, i.e., number of candidates, location updates, maximum iterations, number of variables, and sorting mechanism. The Quicksort method has been adopted with a time complexity of
where
In summary, the MFO (Mirjalili, 2015) has the capability to explore and exploit the solution in the search space, while Levy flight enables MFO for the candidate solution to acquire tiny flight with profound exploration and exploitation ability, and the OBL mutation strategy is concerned with the opposite directions for the optimal solution. These strategies significantly improve the MFOS capabilities for jumping from the local area to the promising global areas. The nest subsection investigates the practical implication of constrained optimization with an improved evolutionary approach. The pseudocode of the improved evolutionary algorithm is presented in Algorithm 1. The information about mutation strategies mentioned in Algorithm 1 is provided in Note 02 in the Supplementary Materials.
Algorithm 1. Pseudocode of the improved MFOS algorithm.
Input: The population size N for 2 candidate solutions (Q, R), moth location (L), moth FitnessFunction (
Output: Optimal global solution Xm
1: Initialize random population Xi;
2: for (each moth Xi) do
3: Calculate Qf and Rf population using Eqs 1, 2;
4: if (population N converge), then
5: Update L for lb & ub using Eqs 5, 6;
6: else
7: Update Qf and Rf with Eqs 3, 4; end if end for
8: for synergy of mutation strategies with Eq. (9) and OBL; do
9: if (iteration reaches), then
10: Compute global solution;
11: else
12: Re-run mutation strategies;
13: else if
14: Calculate fitness of population; end else if
15: end if
16: end for
Return: Optimal global solution Xm.
In order to solve the multi-objective problem of the DNA data storage, the proposed meta-heuristic evolutionary algorithm is applied to the DNA coding constraints (Section 2) to find the lower bounds of DNA code words on coding sets,
Algorithm 2. Pseudocode of constraints satisfactory criteria with MFOS.
Input: Sequence length (
Output: DNA coding sets
1: Initialize individual constraint
2: for (constraints satisfaction) do
3: Update
4: if (error occurrence), then
5: remove SS using Theorem 1;
6: else if
7: maximum iteration using Theorem 2 for best
8: if (lower bounds improved), then
9: constraint satisfied;
10: else
11: update DNA coding constraint; end if
12: end else if
13:
14: end if
15: end for
Return: Improved DNA coding sets
The following are MFOS’s fundamental steps to construct DNA storage coding sets with constraints
• The Universe population N is initialized with the best candidate solution from moth and flame, and MFOS algorithm parameters are set with possible DNA coding that follows the particular constraints (GC, No-runlength, and Hamming distance).
• The DNA storage coding set is performed with the initial Universe population, and globally optimal solutions are secured with the current fitness of the candidate solution.
• The lower and upper bounds are computed with Eqs 5, 6 for the candidate solution, updating its exploration and exploitation position with Eq. 3.
• The updated position is executed with two mutation strategies (Levy flight and OBL) to assign the global search space to the candidate for the improved MFOS algorithm.
• The DNA-coding sets with
• If the results of combinatorial constraints satisfy the improved coding rate and find the lower bounds in a higher number of codes, then the new output will be the best DNA data storage coding sets C.
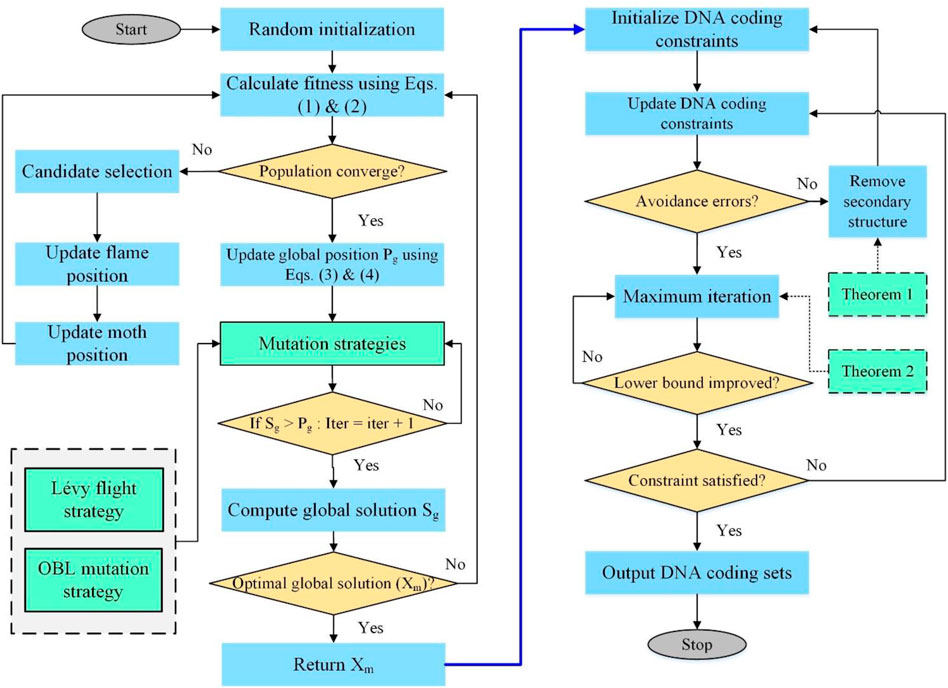
FIGURE 2. Schematic of the improved MFOS evolutionary approach with combinatorial DNA coding constraints.
These critical steps have been followed in constructing DNA codes for data storage.
The implementation was conducted in an integrated environment of different tools. All the evolutionary algorithms are executed on MacBook 2.4 GHz Intel Q-Core i5, 8 GB 2133 MHz DDR3, language Python with 3.8.11v, Google’s Collaboratory, and 3-dimensional convergence plots into MATLAB R2018b. In the proposed work, an image file (horse.png1) is converted into binary data by using the python package (TransBin). The binary data are mapped through the quarterly number (A-0, T-1, C-2, and G-3) of DNA bases (A, T, C, and G) for the construction of DNA code words. The proposed MFOS evolutionary algorithm is programmed in Magma software (Cannon et al., 2011) by varying the sequence lengths and Hamming distance. The DNA coding constraint-based theorems are used to generate the least-errors DNA codes with high density and coding ratio. As a result,
All mainstream functions have been implemented with identical conditions. The number of iterations for each function is set at 500, and the number of moths or population size is adjusted to 50. The MFOS convergence rate directly depends on the population size with crossover and mutation probabilities. The higher the crossover, the greater the exploration ability. Typically, the crossover probability is adjusted in the 0.6–1.0 range. In contrast, mutation probability is often considered lower as compared to crossover, i.e., 0.005 to 0.05 (Wang et al., 2020). It should be noted that the moth number of candidate solutions (i.e., flame) must be selected on an experimental basis. The larger the number of candidates’ solutions, the larger the chances of achieving the global optimum. In this study, the number of moths is reasonably estimated up to 30 times to eliminate the randomness of the optimizer results. However, this number can be 10 or 20 as well for different varieties of experiments. The summary of these operators and their parameter selections is presented in Table 1.
MFOS is a heuristic algorithm based on the MFO algorithm (Mirjalili, 2015), which must be executed almost 10 times to deliver significant results. It is a general standard that an evolutionary optimizer performing for
• The lowest average score is the highest algorithm performance.
• The minimum standard deviation score is the maximum stability of the algorithm.
In addition, the proposed algorithm MFOS is compared with the original MFO (Mirjalili, 2015) and various well-known and popular optimizer algorithms to validate the performance, for example, the Firefly Algorithm (FFA) (Emary et al., 2015), Grey Wolf Optimizer (GWO) (Mirjalili et al., 2014), Differential Evolution (DE) (Zhang et al., 2011), Multi-Verse Optimizer (MVO) (Mirjalili et al., 2016), and Harris Hawks Optimization (HHO) (Heidari et al., 2019). The FFA is a multi-objective optimizer for various domains and still has multiple variants. GWO achieved suitable compromises between exploration and exploitation. Recently, the MVO algorithm has been popular in DNA coding constraints in various DNA-based storage studies, i.e., DMVO (Cao et al., 2020b). HHO is a swarm-based algorithm that supports multiple iterations. A statistical test is computed from the benchmark functions to ensure the result’s originality. A non-parametric Wilcoxon rank-sum test (Kim and Kim, 1996) is adopted to evaluate and compare the results of MFO and MFOS algorithms.
Furthermore, the MFOS algorithm is applied in the Magma program with DNA coding constraints, i.e., GC-content and RC constraint, to assess the DNA storage effectiveness by the coding sets. The received lower-bound values are compared with a state-of-the-art Altruistic algorithm (Limbachiya et al., 2018) and two recent optimizer algorithms [KMVO (Cao et al., 2020a) and DMVO (Cao et al., 2020b)]. In addition, this study reported the lower bounds of DNA codes with RC constraint and compared the results with previous work, MFOL (Rasool et al., 2022a). A thermodynamic analysis is performed on coding constraints and compared with the newly introduced RC constraint to validate it by the computation of temperature variance.
A general trend exhibits the improved performance of our evolutionary algorithm in many functions. The improved AVG and SD values in the results prove that strategic combination is more effective in gaining convergence for the global optimum than MFO and the other five algorithms. Further evaluations are reported in Note 04 in the Supplementary Materials.
The convergence curve is a key criterion for evaluating the optimizer’s convergence speed and ability to jump out from the local optima. This study re-executed experiments on the specific mainstream functions by using five moths over 500 iterations. These functions are selected based on the best performance from Tables 1, Table 2, and 3 given in Note 03 in the Supplementary Materials. Two metrics, search history and convergence rate, are adopted to affirm the convergence of the improved MFOS algorithm. Search history is a qualitative metric that plots the 3D representation curves with the sequence of different iterations. It may also be seen from the 3D representation that fluctuation-flow are greatly dependent on the iteration sequence with different values. These observations guarantee the MFOS’s effectiveness for the optimized problem to attain the balanced transition between exploration and exploitation. In addition, the convergence rate is a quantitative metric that plots the best candidate’s fitness in each iteration. The fitness reduction with the passage of iterations empowers the MFOS convergence. To analyze the effectiveness of the Levy flight and OBL mutation strategies, Figure 3 illustrates the comparison of the original MFO, our MFOS, and the other five algorithms. In the unimodal F2 function, although the MFO secured the optimal global solution, it failed to jump out from the local optima in its early fitness. In contrast, the MFOS algorithm converges more speedily than the MFO and attains the optimal global solution after almost 100 iterations. Meanwhile, our optimizer attained optimal solution at 50 iterations in the F12 function. In contrast, the MFO fell into the local optima. Likewise, in the composite F18 function, the MFO curve tends to be horizontal with no more extended convergence, while the MFOS easily and rapidly converges and accesses the global optima due to its mutation strategies. In summary, the search-based meta-heuristic MFOS convergence curves are empirically insured by quantitative metrics. It is observed that the improved algorithm exhibits competitive results over the state-of-the-art optimizers by endowing a balanced nature between exploration and exploitation.
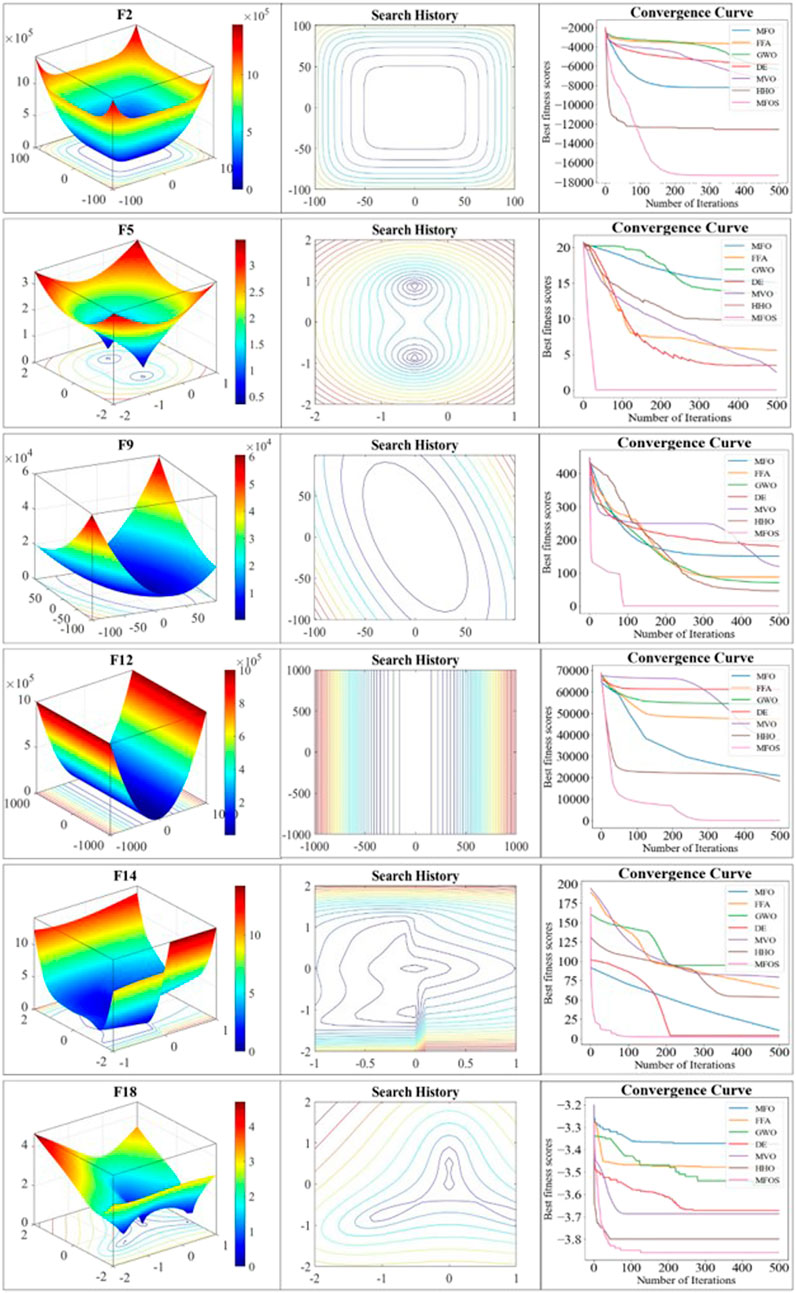
FIGURE 3. Convergence efficiency of unimodal (F2 and F5), multimodal (F9 and F12), and composite (F14 and F18) functions with 3D search space, search history, and curves.
Rank-sum statistical tests are used for doubtful distribution; without consideration, either the object is known or unknown. A popular rank-sum test proposed by Wilcoxon is an alternative non-parametric test for ranking two samples (Kim and Kim, 1996). The null hypothesis of the Wilcoxon rank-sum test is typically interpreted as equal medians instead of equal means. The two populations have the same distribution with the same median, which is another way to conceptualize the null. If evidence is found that one distribution is shifted to the left or right of the other, the null hypothesis will be rejected. Rejecting the null proves that the medians of the two populations are different because we assume that our distributions are equal. This study investigates the statistically significant difference between the MFO and MFOS algorithms by computing the rank-sum of any two samples of the 30 iterations.
Particularly, an algorithm is pondered as statistically substantial if the
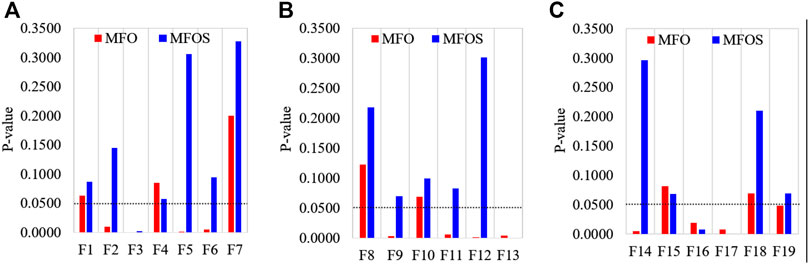
FIGURE 4. Wilcoxon rank-sum test’s comparison of MFO and MFOS algorithms for (A) unimodal functions, (B) multimodal functions, and (C) composite functions.
The MFOS evolutionary algorithm is programmed to enhance the lower bounds of DNA coding sets with
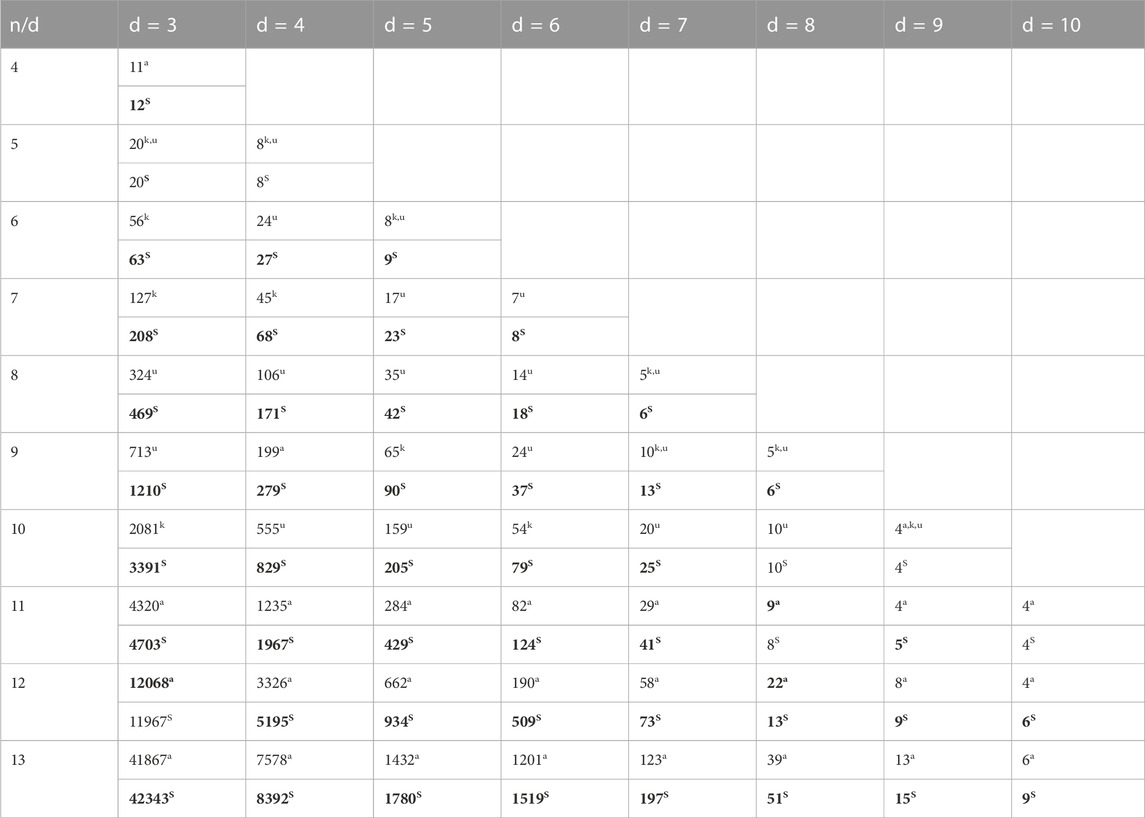
TABLE 3. Lower bounds’ comparison of the MFOS algorithm with KMVO (Cao et al., 2020a), DMVO (Cao et al., 2020b), and Altruistic algorithm (Limbachiya et al., 2018) for
New lower bounds reported by the MFOS outperformed other algorithms, shown in Table 3. We analyzed the previous three studies’ lower bounds and then compared our lower bounds with the one with the highest lower bound. For example, at n = 8 and d = 3, the lower bounds of the Altruistic algorithm are 289, KMVO has 319, DMVO obtained 324, and our work achieved 469. Therefore, we compared MFOS with the one with the highest lower bound (DMVO). While few coding sets are on the same previous level, i.e., MFOS has the same sets as KMVO and DMVO when n = 5 and d = 3,4, and n = 11 and d = 10 with an Altruistic algorithm. Similarly, few lower bounds are reported with fewer coding sets as the number of sequence lengths (n) increased. For example, MFOS lower bounds were reduced by 0.83% at n = 12 and d = 3, and 11.11% at n = 11 and d = 8, compared to the Altruistic algorithm. However, with an average of 52.28%, the proposed algorithm improved the lower bound coding sets compared with that of the d = 5. Meanwhile, compared with KMVO and DMVO algorithms in the same state (n = 6–13 and d = 5), the MFOS algorithm’s lower bounds are 12–35% higher than the KMVO and 12–28% higher than the DMVO.
These considerable improvements in MFOS are strengthened by adopting Levy flight and OBL mutation strategies. This strategic method accredits the MFOS algorithm with fast convergence and stronger exploration abilities, enabling it to jump out of the local optima to secure itself in the optimal global solution. In conclusion, the proposed MFOS algorithm considerably acquired a large number of lower-bound DNA-coding sets compared to the benchmark algorithm and designed the conditions to store larger files in the DNA storage system.
Regardless of these substantial developments, the fact that the consecutive repetition of subsequences unaffected with
In contrast, the coding set in a particular Hamming distance is also increased and decreased. For example, in d = 3, 21.13% of lower bounds increased and 11.71% decreased, which is insufficient for DNA data storage construction. It is probably due to the decrement of the MFOS algorithm candidate sets, which decrees the number of appropriate sequences. It indicates there is still room to construct more robust DNA codes without decreasing the lower bounds. For instance, if the candidate sets are increased, n = 10 and d = 7, MFOS can deliver larger sequences with improved lower bounds.
We have illustrated Figure 5 to compare lower-bound improvements for
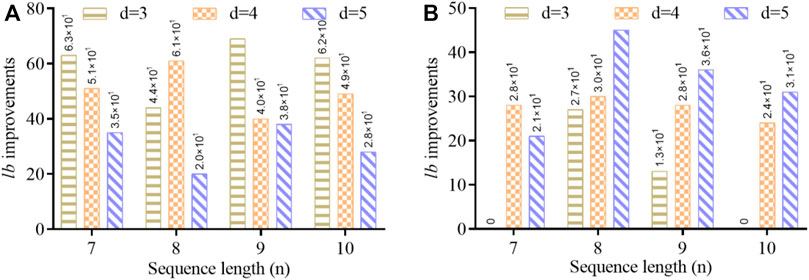
FIGURE 5. Comparison of improved lower bounds (lb) with different sequence lengths based on (A) Table 3 and (B) Table 4.
TABLE 5. DNA coding sets received at
The advancement in the lower bounds is directly favorable to the improvements in DNA coding rates (
where
The empirical analysis of Table 3 revealed that the MFOS algorithm acquired almost the same coding rate with shorter sequence lengths
Figure 6 compares the DNA-coding rate based on the standard error mean (SEM) for d = 3. The SEM measures how precise the new sample is as the probability of the existing sample. It is used to statistically estimate the interval of the DNA code rate between our new codes with previous codes. Figure 6A presents the coding rate of Table 3 based on

FIGURE 6. DNA-coding rate comparison at d = 3 using standard error mean based on (A) Table 3 and (B) Table 4.
Hence, these analytical results determined that shorter sequences can also gain the same DNA storage performance as longer sequences. Consequently, shorter sequences would easily reduce the cost and make it easier to synthesize with more stable conditions. The increased lower bounds in the given coding sets signify the reduction of the SS in the DNA sequences, which helped the proposed approach to avoid the non-specific hybridization errors. These results emphasize the improvement of lower bounds for the further advancement of density-based DNA data storage.
The temperature variance of DNA codes analytically evaluates the rationality of the newly introduced constraint. In DNA coding, half of the double-stranded DNAs split into single-stranded DNAs during the denaturation process (Sager and Stefanovic, 2006) by the melting temperature (
As the main objective of this work was to generate a DNA sequence with shorter sequences, an experiential thermodynamic test was performed to authenticate the DNA sequences. The experiential parameters of primer concentration are set at
Computationally optimized DNA storage algorithms have uncertainty for DNA code stability as required by the DNA synthesis and sequencing process. We, therefore, applied mutation strategies to enhance the optimization efficiency by improving the lower bounds, which allowed us to construct stable DNA codes with the minimum hybridization errors. We synergized a bioengineering-based evolutionary approach with the MFOS algorithm and RC coding constraints to construct more stable and robust codes for DNA storage. The results presented in Figures 3, 4 indicate the MFOS’s competence, faster convergence, and better optimization efficiency than previous algorithms. The improved heuristic algorithm is practiced to generate the optimized DNA code words with the GC-content, Hamming distance, no-runlength constraints, and improved 12–28% lower bounds coding sets than the prior algorithm (DMVO), as revealed in Table 3. In addition, the RC constraint with MFOS meaningfully enhanced the coding rate in 50% of the lower bounds at the same constraints compared with the existing work (Table 4). It attained effective coding rates with shorter sequences by avoiding the SS and enhancing DNA storage density and stability. Consequently, our approach’s shorter sequences can help reduce errors during DNA synthesis and sequencing. Thus, storing a larger file in a shorter DNA sequence is feasible due to the improved lower bounds and coding rates of DNA coding sets. Eventually, comparing temperature variances (
In the future, the DNA codes generated by the MFOS algorithm can be assessed under more strict constraints, i.e., hairpin structure or triplet-based unpaired constraints (Zhu et al., 2021). As the constraints are strict, the DNA-coding set will be smaller and have a higher density of DNA data storage codes. Similarly, various lower bounds and coding rates are still captivating to be enhanced for more stable DNA codes. Additionally, the constructed coding sets by the proposed approach can be used to design an end-to-end DNA data storage system (Takahashi et al., 2019).
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
AR, QJ, and QQ conceived and designed the methodology. AR conducted the experiments and prepared the original manuscript. QJ and QQ supervised the project. QQ, YW, JD, and XH analyzed and validated the theoretical results. AR and QJ reviewed the final draft.
This work is supported by the National Key Research and Development Program of China under fund numbers 2021YFF1200100, 2021YFF1200104, 2020YFA0909100, and 2021YFF1201700.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2023.1158337/full#supplementary-material
1http://clipart-library.com/clipart/horse-clip-art-9.htm
Aboluion, N., Smith, D. H., and Perkins, S. (2012). Linear and nonlinear constructions of DNA codes with Hamming distance d, constant GC-content and a reverse-complement constraint. Discrete Math. 312 (5), 1062–1075. doi:10.1016/j.disc.2011.11.021
Cannon, J. B., Fieker, C., and Steel, A. K. (2011). Handbook of Magma functions. Available online: https://www.math.uzh.ch/sepp/magma-2.20.4-cr/HandbookVolume09.
Cao, B., Zhao, S., Li, X., and Wang, B. (2020). K-means multi-verse optimizer (KMVO) algorithm to construct DNA storage codes. Ieee Access 8, 29547–29556. doi:10.1109/access.2020.2970838
Cao, B., Li, X., Zhang, X., Wang, B., Zhang, Q., and Wei, X. (2020). Designing uncorrelated address constrain for DNA storage by DMVO algorithm. IEEE/ACM Trans. Comput. Biol. Bioinforma. 19, 866–877.
Cao, B., Zhang, X., Cui, S., and Zhang, Q. (2022). Adaptive coding for DNA storage with high storage density and low coverage. npj Syst. Biol. Appl. 8 (1), 23. doi:10.1038/s41540-022-00233-w
Chee, Y. M., and Ling, S. (2008). Improved lower bounds for constant GC-content DNA codes. IEEE Trans. Inf. Theory 54, 391–394. doi:10.1109/tit.2007.911167
Church, G. M., Gao, Y., and Kosuri, S. (2012). Next-generation digital information storage in DNA. Science 337 (6102), 1628. doi:10.1126/science.1226355
Deng, L., Wang, Y., Noor-A-Rahim, M., Guan, Y. L., Shi, Z., Gunawan, E., et al. (2019). Optimized code design for constrained DNA data storage with asymmetric errors. Ieee Access 7, 84107–84121. doi:10.1109/access.2019.2924827
Dinis, T. B. V., Sousa, F., and Freire, M. G. (2020). Insights on the DNA stability in aqueous solutions of ionic liquids. Front. Bioeng. Biotechnol. 8, 547857. doi:10.3389/fbioe.2020.547857
Dong, W., Kang, L., and Zhang, W. (2017). Opposition-based particle swarm optimization with adaptive mutation strategy. Soft Comput. 21 (17), 5081–5090. doi:10.1007/s00500-016-2102-5
Emary, E., Zawbaa, H. M., Ghany, K. K. A., hassanien, A. E., and Parv, B. (2015). “Firefly optimization algorithm for feature selection,” in Proceedings of the 7th Balkan Conference on Informatics Conference, Craiova, Romania, September 2015 (Association for Computing Machinery), Article 26.
Erlich, Y., and Zielinski, D. (2017). DNA Fountain enables a robust and efficient storage architecture. Science 355 (6328), 950–954. doi:10.1126/science.aaj2038
Grass, R. N., Heckel, R., Puddu, M., Paunescu, D., and Stark, W. J. (2015). Robust chemical preservation of digital information on DNA in silica with error-correcting codes. Angew. Chemie-International Ed. 54 (8), 2552–2555. doi:10.1002/anie.201411378
Heckel, R., Mikutis, G., and Grass, R. N. (2019). A characterization of the DNA data storage channel. Sci. Rep. 9 (1), 9663. doi:10.1038/s41598-019-45832-6
Heidari, A. A., Mirjalili, S., Faris, H., Aljarah, I., Mafarja, M., and Chen, H. (2019). Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 97, 849–872. doi:10.1016/j.future.2019.02.028
Kim, D. H., and Kim, Y. C. (1996). Wilcoxon signed rank test using ranked-set sample. Korean J. Comput. Appl. Math. 3 (2), 235–243. doi:10.1007/bf03008904
King, O. D. (2003). Bounds for DNA codes with constant GC-content. Electron. J. Comb. 10 (1). doi:10.37236/1726
Li, M., Wu, J., Dai, J., Jiang, Q., Qu, Q., Huang, X., et al. (2021). A self-contained and self-explanatory DNA storage system. Sci. Rep. 11 (1), 18063. doi:10.1038/s41598-021-97570-3
Li, X., Wei, Z., Wang, B., and Song, T. (2021). Stable DNA sequence over close-ending and pairing sequences constraint. Front. Genet. 12, 644484. doi:10.3389/fgene.2021.644484
Limbachiya, D., Gupta, M. K., and Aggarwal, V. (2018). Family of constrained codes for archival DNA data storage. Ieee Commun. Lett. 22 (10), 1972–1975. doi:10.1109/lcomm.2018.2861867
Lu, M., wang, M., Qiang, W., Cui, J., Wang, Y., Huang, X., et al. (2023). Towards high-density storage of text and images into DNA by the “Xiao-Pang” codec system. Sci. China Life Sci. doi:10.1007/s11427-022-2252-0
Mirjalili, S., Mirjalili, S. M., and Lewis, A. (2014). Grey Wolf optimizer. Adv. Eng. Softw. 69, 46–61. doi:10.1016/j.advengsoft.2013.12.007
Mirjalili, S., Mirjalili, S. M., and Hatamlou, A. (2016). Multi-verse optimizer: A nature-inspired algorithm for global optimization. Neural Comput. Appl. 27 (2), 495–513. doi:10.1007/s00521-015-1870-7
Mirjalili, S. (2015). Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowledge-Based Syst. 89, 228–249. doi:10.1016/j.knosys.2015.07.006
Organick, L., Ang, S. D., Chen, Y. J., Lopez, R., Yekhanin, S., Makarychev, K., et al. (2018). Random access in large-scale DNA data storage. Nat. Biotechnol. 36 (3), 242–248. doi:10.1038/nbt.4079
Rasool, A., Qu, A., Jiang, Q., and Wang, Y. (2022). “A strategy-based optimization algorithm to design codes for DNA data storage system,” in Algorithms and Architectures for Parallel processing (Cham: Springer International Publishing), 284–299.
Rasool, A., Qu, Q., Wang, Y., and Jiang, Q. (2022). Bio-constrained codes with neural network for density-based DNA data storage. Mathematics 10 (5), 845. doi:10.3390/math10050845
Sager, J., and Stefanovic, D. (2006). “Designing nucleotide sequences for computation: A survey of constraints,” in DNA computing (Berlin, Heidelberg: Springer Berlin Heidelberg).
Song, W., Cai, K., Zhang, M., and Yuen, C. (2018). Codes with run-length and GC-content constraints for DNA-based data storage. Ieee Commun. Lett. 22 (10), 2004–2007. doi:10.1109/lcomm.2018.2866566
Song, L. F., Deng, Z. H., Gong, Z. Y., Li, L. L., and Li, B. Z. (2021). Large-Scale de novo Oligonucleotide Synthesis for Whole-Genome Synthesis and Data Storage: Challenges and Opportunities. Front. Bioeng. Biotechnol. 9, 689797. doi:10.3389/fbioe.2021.689797
Song, L., Geng, F., Gong, Z. Y., Chen, X., Tang, J., Gong, C., et al. (2022). Robust data storage in DNA by de Bruijn graph-based de novo strand assembly. Nat. Commun. 13 (1), 5361. doi:10.1038/s41467-022-33046-w
Takahashi, C. N., Nguyen, B. H., Strauss, K., and Ceze, L. (2019). Demonstration of end-to-end automation of DNA data storage. Sci. Rep. 9 (1), 4998. doi:10.1038/s41598-019-41228-8
Wang, Z. J., Zhan, Z. H., Lin, Y., Yu, W. J., Wang, H., Kwong, S., et al. (2020). Automatic niching differential evolution with contour prediction approach for multimodal optimization problems. Ieee Trans. Evol. Comput. 24 (1), 114–128. doi:10.1109/tevc.2019.2910721
Wang, P. H., Mu, Z., Sun, L., and Wang, B. (2022). Hidden addressing encoding for DNA storage. Front. Bioeng. Biotechnol. 10, 916615. doi:10.3389/fbioe.2022.916615
Xiaoru, L. L. G., and Ling, G. (2021). Combinatorial constraint coding based on the EORS algorithm in DNA storage. PLoS ONE 16 (7), e0255376. doi:10.1371/journal.pone.0255376
Yang, A. M., Zhang, W., Wang, J., Yang, K., Han, Y., and Zhang, L. (2020). Review on the application of machine learning algorithms in the sequence data mining of DNA. Front. Bioeng. Biotechnol. 8, 1032. doi:10.3389/fbioe.2020.01032
Yazdi, S. M. H. T., Gabrys, R., and Milenkovic, O. (2017). Portable and error-free DNA-based data storage. Sci. Rep. 7 (1), 5011. doi:10.1038/s41598-017-05188-1
Yim, A. K.-Y., Yu, A. C. S., Li, J. W., Wong, A. I. C., Loo, J. F. C., Chan, K. M., et al. (2014). The essential component in DNA-based information storage system: Robust error-tolerating module. Front. Bioeng. Biotechnol. 2, 49. doi:10.3389/fbioe.2014.00049
Yin, Z., Ye, C. M., and Wen, M. (2010). Research on DNA encoding design constraint by minimal free energy. Comput. Eng. Appl. 46 (12), 25–27.
Zhang, L., Xu, X., Zhou, C., Ma, M., and Yu, Z. (2011). “An improved differential evolution algorithm for optimization problems,” in Advances in computer science, intelligent system and environment (Berlin, Heidelberg: Springer Berlin Heidelberg).
Zhu, C. X., Liu, X., Li, Y., Ma, S., Wang, M., and You, T. (2021). Hairpin DNA assisted dual-ratiometric electrochemical aptasensor with high reliability and anti-interference ability for simultaneous detection of aflatoxin B1 and ochratoxin A. Biosens. Bioelectron. 174, 112654. doi:10.1016/j.bios.2020.112654
Keywords: biocomputing, DNA coding sets, bioconstrained codes, MFO, DNA data storage
Citation: Rasool A, Jiang Q, Wang Y, Huang X, Qu Q and Dai J (2023) Evolutionary approach to construct robust codes for DNA-based data storage. Front. Genet. 14:1158337. doi: 10.3389/fgene.2023.1158337
Received: 07 February 2023; Accepted: 02 March 2023;
Published: 20 March 2023.
Edited by:
Ka-Chun Wong, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Yasser Youssef, University of Oklahoma, United StatesCopyright © 2023 Rasool, Jiang, Wang, Huang, Qu and Dai. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingshan Jiang, cXMuamlhbmdAc2lhdC5hYy5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.