Zhao Yang
C. Mary Schooling
Man Ki Kwok- 1School of Public Health, Li Ka Shing Faculty of Medicine, The University of Hong Kong, Hong Kong, China
- 2Graduate School of Public Health and Health Policy, City University of New York, New York, NY, United States
Selection bias is increasingly acknowledged as a limitation of Mendelian randomization (MR). However, few methods exist to assess this issue. We focus on two plausible causal structures relevant to MR studies and illustrate the data-generating process underlying selection bias via simulation studies. We conceptualize the use of control exposures to validate MR estimates derived from selected samples by detecting potential selection bias and reproducing the exposure–outcome association of primary interest based on subject matter knowledge. We discuss the criteria for choosing the control exposures. We apply the proposal in an MR study investigating the potential effect of higher transferrin with stroke (including ischemic and cardioembolic stroke) using transferrin saturation and iron status as control exposures. Theoretically, selection bias affects associations of genetic instruments with the outcome in selected samples, violating the exclusion-restriction assumption and distorting MR estimates. Our applied example showing inconsistent effects of genetically predicted higher transferrin and higher transferrin saturation on stroke suggests the potential selection bias. Furthermore, the expected associations of genetically predicted higher iron status on stroke and longevity indicate no systematic selection bias. The routine use of control exposures in MR studies provides a valuable tool to validate estimated causal effects. Like the applied example, an antagonist, decoy, or exposure with similar biological activity as the exposure of primary interest, which has the same potential selection bias sources as the exposure–outcome association, is suggested as the control exposure. An additional or a validated control exposure with a well-established association with the outcome is also recommended to explore possible systematic selection bias.
Highlights
What is Already Known on this Subject?
• Mendelian randomization (MR) provides unconfounded estimates, but is particularly vulnerable to selection bias because of the small magnitude of genetic estimates.
• Negative controls provide helpful tools to detect residual confounding, selection, and measurement bias in conventional epidemiological studies but often lack specificity in the type of bias they detect.
What this Adds to What is Known?
• Given genetics are a lifelong exposure, a key source of selection bias in MR studies is missing people from the same underlying birth cohorts as the original population who die before recruitment, which may violate the exclusion-restriction assumption and distort the MR estimates.
• The use of control exposures that have the same potential selection bias sources as the exposure–outcome association of interest can detect potential selection bias and validate MR estimates.
• The estimated exposure–outcome association is more credible if this result is robust to potential selection bias and reproducible by using the relevant control exposures based on subject matter knowledge.
What is the Implication, What Should Change Now?
• Systematic selection bias may occur particularly when the genetic variants affect survival and the outcome of interest or a competing risk of that outcome affects survival; interpretation of MR estimates should be cautious.
• The routine use of control exposures could add more credibility to MR estimates.
Introduction
Mendelian randomization (MR) uses genetic variants as a natural experiment in observational studies to investigate potential causal effects of modifiable risk factors on health outcomes (Davey Smith and Ebrahim, 2003). MR is often conducted in two homogeneous study populations, i.e., two-sample MR (Burgess et al., 2015). MR is thought to be robust to the confounding that often occurs in conventional observational studies due to the random allocation of genetic endowment at conception being used as a proxy for the exposure (Burgess et al., 2012; Davies et al., 2018). Currently, MR is a popular approach for assessing causality (Sekula et al., 2016). However, MR estimate rests on stringent assumptions, as illustrated using directed acyclic graphs (DAGs) in Figures 1A,B (Davey Smith and Ebrahim, 2003; Lawlor et al., 2008).
• IV1 (the relevance assumption): the genetic variant is robustly associated with the exposure of interest;
• IV2 (the independence assumption): the genetic variant is not associated with confounders that bias the exposure–outcome association;
• IV3 (the exclusion-restriction assumption): the genetic variant affects the health outcome only via its effect on the exposure.
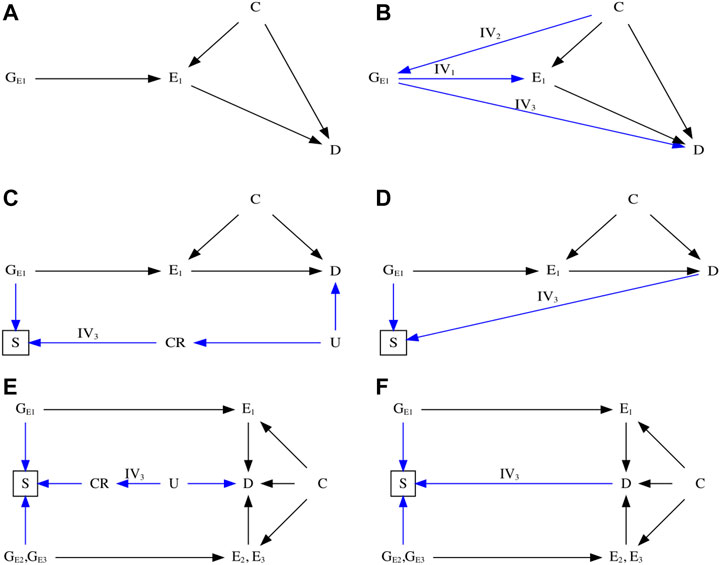
FIGURE 1. Directed acyclic graph (DAG) illustrating Mendelian randomization (MR). (A) DAG illustrating an ideal scenario of an MR study. (B) DAG illustrating the three instrumental assumptions (Davey Smith and Ebrahim, 2003)—IV1: Relevance (Burgess et al., 2015); IV2: Independence (Burgess et al., 2012); IV3: Exclusion restriction. (C) DAG illustrating potential biased pathway with selection bias in the presence of competing risks that share substantial etiological factors with the outcome. (D) DAG illustrating potential biased pathway with selection bias in the unrepresentative selected samples. (E) DAG illustrating an MR study using control exposures to detect potential selection bias in the presence of competing risks. (F) DAG illustrating an MR study using control exposures to detect potential selection bias in the unrepresentative selected samples. E1: the primary exposure of interest; E2 and E3: the control exposures; C: the confounder that associates with both the exposure and outcome; D: the outcome; CR: the competing risks; U: the unmeasured and shared confounders of the competing risks and the outcome; GE1, GE2, and GE3: genetic variants that are strongly associated with the exposure of primary interest and the control exposures.
Notably, aside from IV1 that can be empirically verified using the F-statistic (Staiger and Stock, 1997; Bowden et al., 2016a), IV2 and IV3 are typically harder to justify. Hence, violations of these assumptions can occur, leading to misleading conclusions. Of these, selection bias is increasingly acknowledged as distorting MR estimates in the selected populations investigated (Nitsch et al., 2006; VanderWeele et al., 2014; Canan et al., 2017; Vansteelandt et al., 2018a; Vansteelandt et al., 2018b; Munafò et al., 2018; Munafò and Smith, 2018; Gkatzionis and Burgess, 2019; Smit et al., 2019; Schooling et al., 2020) and has largely focused on bias arising from selection on exposure (Vansteelandt et al., 2018a; Vansteelandt et al., 2018b; Munafò et al., 2018; Gkatzionis and Burgess, 2019; Smit et al., 2019).
Genetic studies are usually carefully designed to avoid selecting sample on genetic make-up and phenotypes. Generally, selection bias occurs in an MR study when the sample in the original genome-wide association study (GWAS) are selected conditional on survival until study recruitment on genotype of interest in the presence of prior death from the outcome or competing risks of the outcome (Figure 1C), especially in the original outcome GWAS (Schooling et al., 2020). The problem is the time lag between genetic randomization at conception and recruitment of participants into the GWAS. Participants diagnosed with or dead from the outcome or a competing risk of the outcome are not recruited into the outcome GWAS, which attenuates or reverses MR estimates for harmful exposures, because people who have already died of their harmful genetic endowment and people who have died of the outcome or a competing risk of the outcome are missing. As such, selection bias may create a spurious genetic variant–outcome association by opening the backdoor path from genetic instruments to the outcome of interest, violating the IV3 assumption.
For example, previous observational studies showed that higher transferrin binds to circulating iron and influences iron status, which may further cause iron-deficiency anemia and increase the risk of stroke (Chang et al., 2013; Marniemi et al., 2005; Gillum et al., 1996). However, a recent MR study reported that lower iron status also appeared to protect against stroke (van der et al., 2005; Gill et al., 2018), especially cardioembolic stroke (Gill et al., 2018). An increasingly acknowledged explanation is selection bias, possibly due to the presence of competing risks [e.g., coronary artery disease (Gill et al., 2017), hypercholesterolemia (Gill et al., 2019), chronic kidney disease (Fishbane et al., 2009), skin infections (Gill et al., 2019), liver disorders (e.g., hepatitis C) (Shan et al., 2005), and rheumatoid arthritis (Yuan and Larsson, 2020)] caused by the shared confounders (e.g., socioeconomic position, lifestyle, and health status), affecting survival of the underlying population (Camaschella, 2015; McLean et al., 2009), as shown in Figure 2. For instance, people with competing risks, such as coronary artery disease, tend to die earlier than those with stroke in Western settings (Kesteloot and Decramer, 2008; Menotti et al., 2019; Diseases and Injuries, 2020). As such, people vulnerable to these competing risks with higher iron status may die before study recruitment, leaving more “healthier” participants in the study and inducing biased estimates.
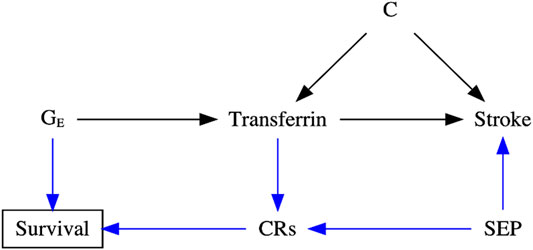
FIGURE 2. Directed acyclic graph (DAG) illustrating the possible data-generating process underlying selection bias in the transferrin–stroke association due to missing people in the presence of competing risks (CRs, e.g., coronary artery disease) caused by the shared confounder [e.g., socioeconomic position (SEP)] of stroke and CRs in two-sample Mendelian randomization settings. C: the unmeasured confounder of the transferrin–stroke association.
Several statistical methods have been proposed to detect and eliminate selection bias in MR studies, most of which focus on bias arising from selection on exposure (Bareinboim and Pearl, 2012; Arnold and Ercumen, 2016; Hemani et al., 2017; Tchetgen Tchetgen and Wirth, 2017; Vansteelandt et al., 2018a; Brumpton et al., 2020; Zhao et al., 2020; Sanderson et al., 2021; Wang and Han, 2021), which is generally thought to have limited effects. However, selection on genetic endowment and outcome or competing risk of the outcome is more pervasive (Schooling et al., 2020) and can have larger effects. One approach that has not been considered is the use of a “negative control,” which has been widely used in laboratory science for decades to help detect problems with the experimental method (Arnold and Ercumen, 2016). In epidemiological studies, a formal approach has been described in detail and suggested as a means of detecting residual confounding, selection bias, and measurement bias (Lipsitch et al., 2010; Arnold et al., 2016). Recently, negative control outcomes, defined as sharing identical confounders with the exposure–outcome association but not associated with the exposure, have been proposed to detect potential population stratification in MR studies (Sanderson et al., 2021). Other approaches include summary data-based MR [SMR, e.g., MR robust adjusted profile score (MR-RAPS)] (Zhao et al., 2020; Wang and Han, 2021), two-sample MR Steiger method (Hemani et al., 2017), and three-sample MR (Zhao et al., 2019), in which the selection procedure of genetic instrument (e.g., winner’s curse) is considered a form of selection bias (Wang and Han, 2021). However, such a situation is different from the scenario where the original outcome GWAS is missing people from the same underlying population (birth cohorts) as those included, some of whom have already died from the instrument and some of whom have already died from the outcome or a competing risk of the outcome, as shown in Figures 1C,D.
In this study, as an extension of negative control outcomes, we advance the use of control exposures to validate MR estimates that might be susceptible to such selection bias. We focus on plausible causal structures relevant to MR studies and illustrate how to validate MR estimates using control exposures through a real example investigating the potential association of transferrin with stroke (including ischemic and cardioembolic stroke). This association is thought to be particularly vulnerable to selection bias, especially among older populations, because transferrin affects survival and stroke is open to competing risk from IHD (Schooling et al., 2020; Yang et al., 2021). We further discuss the criteria for choosing the control exposures and the limitations of this approach.
Methods
Figures 1C,D show DAGs for MR with selection bias caused by sample selection. In the presence of competing risks (Figure 1C), the selected samples may have a lower risk of developing the phenotype [e.g., the outcome (D)] because the GWAS is missing people with genetic vulnerability to earlier death and people who have died from a disease that shares causes (e.g., U) with the phenotype. As such, the backdoor pathway directly linking GE1 to D will be reopened in the selected samples if the instruments affect survival, i.e., have allele frequencies that differ from the underlying population (e.g., birth cohort). This situation violates the IV3 assumption and distorts MR estimates, which can attenuate or reverse the true association or create a spurious association. The small effect sizes of genetic associations (Park et al., 2011; Global Burden of Disease, 2020) make them particularly vulnerable to perturbation by such bias (Schooling et al., 2020). In the absence of competing risks (Figure 1D), the phenotype (e.g., D) risk and instruments’ frequencies may vary because of selecting on genetic instruments and outcome, which generates unrecoverable selection bias.
To clearly illustrate the data-generating process underlying selection bias due to missing people from the original birth cohorts who formed the underlying population through death before study recruitment, we conducted extensive simulation studies. Details are presented in the Supplementary Material. Briefly, we induced selection bias by selecting study participants as survivors to study recruitment. We assumed that the survival of the underlying population was influenced by the genetic instruments GE1, exposure E1, outcome D, confounder C of the exposure–outcome association, or the unmeasured confounder U mediated by competing risks CR. We used the relative hazard (i.e., hazard ratio) per-unit change in either GE1, E1, C, D, or U to quantify their effects on the survival, as shown in Supplementary Figure S1. As such, the impact of selection bias induced by the survival status of the underlying population until study recruitment was governed by hazard ratio of per-unit change in either GE1, E1, C, D, or U. Then, we induced selection bias in two-sample MR by having instruments determining survival to recruitment and outcome of interest affecting survival to recruitment. Details of the simulation study are in the Supplementary Material, along with the corresponding R scripts.
Figure 3 and Supplementary Figure S1 show the impact of selection bias arising from selecting samples conditioning on genetic instruments G and outcome D, with no effects of either exposure E1 or the shared confounder U mediated by competing risks on survival of the underlying population (i.e., birth cohort) based on simulation studies. More details have been presented in Supplementary Material S1. As expected, selecting samples conditioning on genetic instruments G and outcome D of interest induces selection bias, with its impacts varying depending on the relative hazard of G and D on survival of the underlying population. Given summary statistics obtained from the original exposure and outcome GWASs, it seems not easy to recover the true causal estimate from the observed MR estimates in two-sample MR settings due to the essence of missing people before the recruitment of the original GWASs.
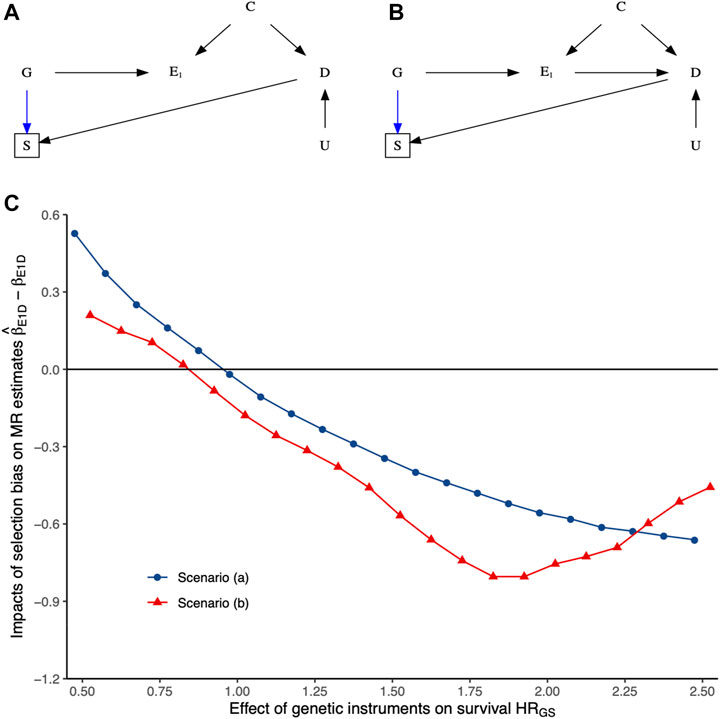
FIGURE 3. The impacts of selection bias (i.e.,
Validating MR Estimates by Detecting Selection Bias and Reproducing Associations of Interest Using Control Exposures
To explore selection bias, we reproduce a condition that does not involve the hypothesized causal mechanism but involves the same potential selection bias sources in the original MR study. We introduce an antagonist or decoy of E1 as the control exposure E2, mimicking a natural experiment, because E2 acts as an endogenous intervention of E1. Moreover, E2 effects on survival would be nearly identical to E1, as depicted in Figures 1E,F, but has an opposite impact on D from E1. If such an E2 exists, then any consistent effects of E1 and E2 on D would be mainly due to selection bias rather than study design. That is, the consistent effects of E1 and E2 on D could indicate potential selection bias. Otherwise, the estimated causal effects derived from the selected samples are robust to selection bias. Moreover, an intuitive interpretation herein is that the E1–D association is credible and reproducible by using a relevant control exposure E2 because of the known relationship between E1 and E2.
We can extend the selection of E2 by using exposure with similar biological activity as E1 because they are also likely to share the same potential selection bias sources and have similar or even the same effects on D. This idea is widely applied in developing pharmaceutical products [Food and Drug A (2014). Bioa, 2014; Committee for Medicinal P, 2010]. If such an E2 exists, then any inconsistent effects of E1 and E2 on D would be mainly caused by potential selection bias. Conversely, consistent results of E1 and E2 on D would validate the estimated effects. In other words, these estimated effects derived from the selected samples are less likely to be affected by selection bias. Even if selection bias exists, its impact would be limited. It would not extend to reverse the causal direction or distort the estimated effect far away from the truth. Notably, the use of such kinds of control exposures does not require a null or well-established association between the control exposure E2 and D.
Issue of Systematic Selection Bias
However, this method might still fail to detect selection bias if systematic selection bias exists, especially when E1 and E2 are selected from the same GWAS. In such a case, it might distort both the E1–D and E2–D associations similarly, such as reversing the estimated E1–D and E2–D associations simultaneously. To handle this situation, we introduced an additional negative (or positive) control E3 with the same potential selection bias sources concerning the E1–D association or identified a validated control exposure (E2) that had a clear association with D to triangulate the estimated effects. As such, any associations of E3/E2 with D would indicate potentially systematic selection bias. Otherwise, the estimated effects derived from the selected samples are likely to be robust to selection bias and reproducible.
Choosing Control Exposures
Control exposures could be used to detect potential selection bias and validate MR estimates. To this end, it might be necessary to specify the criteria for choosing the control exposures E2 and/or E3 as follows.
1) The control exposure E2 should have the same potential selection bias sources (e.g., affecting survival in the underlying population) as E1 on D. For example, using antagonist, decoy, or an exposure with similar biological activity as E2, such a criterion is approximately satisfied;
2) To explore potentially systematic selection bias, an additional control exposure (E3) with the same potential selection bias sources as E1 on D or a validated control exposure E2 should have a well-established association with D.
We recommend choosing E1, E2, and/or E3 from different GWASs to minimize potentially systematic selection bias. If such E2 and E3 exist, then the estimated effects of E1, E2, and E3 on D can be used to detect potential selection bias and triangulate the causal estimates. The estimated E1–D association would be more credible because it is robust to potential selection bias and can be reproducible using a relevant control exposure E2 based on subject matter knowledge.
An Applied Example
To illustrate, we investigated the association of higher transferrin (i.e., E1) with stroke (including ischemic and cardioembolic stroke), with transferrin saturation as a control exposure E2 and iron status as a positive control exposure E3. We selected transferrin saturation as the control exposure E2 because it measures circulating iron and reflects the proportion of transferrin occupied by iron (Wish, 2006). Biologically, transferrin saturation is inversely associated with transferrin but positively associated with iron status. Furthermore, iron deficiency, reflected by lower transferrin saturation and higher transferrin, causes anemia and reduces lifespan directly or via competing risks [e.g., stroke (23), Figure 2] (McLean et al., 2009; Camaschella, 2015). Consequently, the associations of transferrin saturation and iron status with stroke are open to similar potential selection bias as the transferrin-stroke association. Hence, transferrin saturation and iron status are control exposures here. As such, any consistent transferrin–stroke and transferrin saturation–stroke associations (especially in the same causal direction) indicate potential selection bias. In addition, any null iron status–stroke association suggests the presence of systematic selection bias due to its clear associations with stroke and longevity (Gill et al., 2018; Daghlas and Gill, 2021); particularly, the iron status-longevity association is less likely to subject to selection bias (Andersen et al., 2012).
We selected independent (r2 < 0.01) genetic instruments mimicking effects of transferrin (MR-base id: ieu-a-1052), transferrin saturation (MR-base id: ieu-a-1051), and iron status (MR-base id: ieu-a-1049) from the MR-base at a genome-wide significance
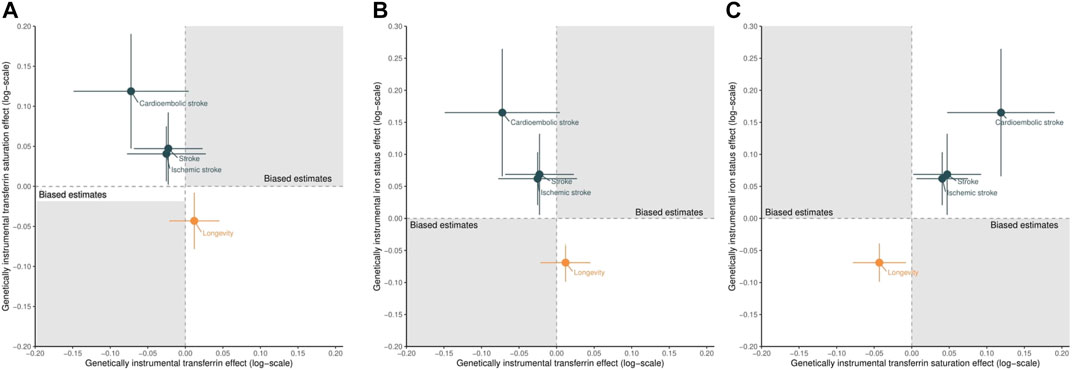
FIGURE 4. Scatter plots of the estimated effects of genetically predicted higher transferrin versus higher transferrin saturation (A), higher transferrin versus higher iron status (B), and higher transferrin saturation versus higher iron status (C) on stroke (including ischemic and cardioembolic stroke) and longevity. Points located in the gray area indicate the presence of selection bias.
We applied the identified instruments to publicly available GWAS of European descent of stroke (40,585 cases and 406,111 controls), ischemic stroke (34,217 cases and 406,111 controls), and cardioembolic stroke (7,193 cases and 406,111 controls) (Timmers et al., 2019). Supplementary Table S1 presents a detailed summary of the included studies. We extracted summary statistics for stroke (MR-base id: ebi-a-GCST005838), ischemic stroke (MR-base id: ebi-a-GCST005834), and cardioembolic stroke (MR-base id: ebi-a-GCST006910) from MR-base (Hemani et al., 2018). Supplementary Table S2 lists genetic associations of the included instruments associated with stroke.
We assessed the associations of genetically predicted transferrin, transferrin saturation, and iron status with stroke using the Wald ratio (i.e., the ratio of the genetic outcome effect estimate and the corresponding genetic exposure effect estimate) or the inverse-variance weighted average of the Wald ratio estimates with random effects (Burgess et al., 2013). We assumed that all these associations were linear and homogeneous (Lawlor et al., 2008). We reported Cochran’s Q-statistic to detect potential heterogeneity. We conducted sensitivity analyses using the weighted median (Bowden et al., 2016b), MR-Egger (Bowden et al., 2015), and MR-RAPS(40) to address the potential unknown pleiotropy statistically. We also reported the MR-Egger intercept and its SE with p-value as an indicator of potential pleiotropy. Two-sided p-values at the Bonferroni-corrected threshold of 0.05/3 (for three exposures) = 0.017 were considered statistically significant. P-values between 0.017 and 0.05 were reported as nominal. Data involving these exemplars were publicly available, so it does not require ethical approval.
Results
Up to 11 genetic instruments were used for transferrin (mean concentration 2.1 g/L and SD 0.43 g/L), 7 instruments for transferrin saturation (mean percentage 29.9% and SD 11.0%), and 5 instruments for iron status (mean concentration 18.4 μmol/L and SD 5.6 μmol/L). The F-statistics of instruments for transferrin ranged from 32.4 to 1,296.1, for transferrin saturation ranged from 35.6 to 808.5, and for iron status was 37.8 to 346.7, suggesting weak instrument bias to be less likely.
Figure 4 shows the scatter plot of the estimated effects of genetically predicted higher transferrin versus higher transferrin saturation (A), higher transferrin versus higher iron status (B), and higher transferrin saturation versus higher iron status (C) on stroke (including ischemic and cardioembolic stroke) and longevity, with full details presented in Supplementary Table S3. Genetically predicted higher transferrin was associated with a lower risk of stroke (Figures 4A,B), although these protective effects did not reach nominal significance (p < 0.05). Conversely, genetically predicted higher transferrin saturation was nominally associated with higher risk of stroke (Figures 4A,C). Such results suggest that the observed transferrin–stroke association is open to selection bias, possibly due to the missing people from the original GWAS of stroke because they died before recruitment from the genetic predictors of iron, an iron-related condition, stroke, or a competing risk of stroke, which attenuated the true association (Figure 2).
In addition, as expected (Gill et al., 2018; Daghlas and Gill, 2021), genetically predicted higher iron status was associated with increased stroke and reduced longevity, as shown in Figures 4B,C and Supplementary Table S3. Finally, the consistent effects of higher transferrin saturation and higher iron status on stroke and longevity further triangulated our conclusions. Even if selection bias exists, its impact on the transferrin saturation–stroke and iron status–stroke associations would be limited or at least could not reverse the observed associations or biased them to the null. These results support the advantages of using control exposures.
Discussion
This paper advances the use of control exposures based on subject matter knowledge in MR studies to triangulate the estimated causal effects vulnerable to selection bias. The potential mechanisms underlying selection bias in MR lies in the re-opened backdoor pathway from genetic instruments to the outcome of interest in the selected samples. It violates the IV3 assumption and distorts the MR estimates. The applied example demonstrates that MR is vulnerable to selection bias because of missing data from sample selection (Figures 1, 3), which is unlikely to be missing at random, so requires modeling of the missing data process to recover the estimates (Mohan and Pearl, 2021). Our proposal provides a valuable approach to assessing credible MR estimates in the presence of selection bias from selection of survivors.
Furthermore, the control exposures introduced in the proposal inherit properties similar to those of negative or positive control exposures used in the conventional observational studies but provide a more intuitive and clinically meaningful interpretation of the estimated effects (Lipsitch et al., 2010; Shi et al., 2020; Sanderson et al., 2021). Choosing antagonists, decoys, or exposures with similar biological activity as the control exposures based on subject matter knowledge may facilitate its application in MR studies. Systematic selection bias distorting both the exposure–outcome and control exposure–outcome associations, in a similar or even the same way, may exist, resulting in inconclusive or misleading conclusions. However, an additional or a validated control exposure with a clear association with the outcome provides another tool to triangulate the estimated effects. Notably, it is possible to use a single control exposure in the proposal solely to validate the MR estimates, especially when E1, E2, and E3 are selected from different GWASs.
Despite the strengths of the proposal in validating MR estimates, limitations exist. First, the proposal only detects potential selection bias but fails to address it. The impact of selection bias on summary statistics obtained from the original GWAS might vary due to the small fraction of heritability explained by genetic variants and the small effect size of the genetic associations (Greenland, 2003; Freedman et al., 2004; Park et al., 2011; Schooling, 2019). Thus, the proposal might fail to detect its small effect on MR estimates. Nonetheless, routinely applying control exposures still adds more credibility to MR estimates. Second, the proposal inherits properties of the conventional MR; limitations such as the stringent instrumental assumptions remain (Davey Smith and Ebrahim, 2003; Smith and Ebrahim, 2004; Lawlor et al., 2008). However, recent advances in MR provide more tools to alleviate or even eliminate these limitations (Ye et al., 2019; Zhao et al., 2020; Liu et al., 2021). Third, choosing control exposures that have the same potential selection bias sources as the exposure–outcome association of interest or a clear association with the outcome might be difficult in practice, further limiting its application.
Conclusion
Routinely using control exposures in MR studies provides a helpful tool to validate estimated causal effects that are vulnerable to potential selection bias in the selected samples.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
All authors contributed to the study conception and design. Material preparation was performed by ZY. The first draft of the article was written by ZY and all authors commented on previous versions of the article. All authors read and approved the final article.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2021.729326/full#supplementary-material
Abbreviations
CR, competing risks; DAG, directed acyclic graph; GWAS, genome-wide association study; IV, instrumental variable; MR, Mendelian randomization.
References
Andersen, P. K., Geskus, R. B., de Witte, T., and Putter, H. (2012). Competing Risks in Epidemiology: Possibilities and Pitfalls. Int. J. Epidemiol. 41 (3), 861–870. doi:10.1093/ije/dyr213
Arnold, B. F., Ercumen, A., Benjamin-Chung, J., and Colford, J. M. (2016). Brief Report. Epidemiology 27 (5), 637–641. doi:10.1097/EDE.0000000000000504
Arnold, B. F., and Ercumen, A. (2016). Negative Control Outcomes. JAMA 316 (24), 2597–2598. doi:10.1001/jama.2016.17700
Bareinboim, E., and Pearl, J. (2012). Controlling Selection Bias in Causal Inference. Artificial Intelligence and Statistics (PMLR), 100–108.
Benyamin, B., Esko, T., Esko, T., Ried, J. S., Radhakrishnan, A., Vermeulen, S. H., et al. (2014). Novel Loci Affecting Iron Homeostasis and Their Effects in Individuals at Risk for Hemochromatosis. Nat. Commun. 5, 4926. doi:10.1038/ncomms5926
Bowden, J., Del Greco M, F., Minelli, C., Davey Smith, G., Sheehan, N. A., and Thompson, J. R. (2016). Assessing the Suitability of Summary Data for Two-Sample Mendelian Randomization Analyses Using MR-Egger Regression: the Role of the I2 Statistic. Int. J. Epidemiol. 45 (6), 1961–1974. doi:10.1093/ije/dyw220
Bowden, J., Davey Smith, G., and Burgess, S. (2015). Mendelian Randomization with Invalid Instruments: Effect Estimation and Bias Detection through Egger Regression. Int. J. Epidemiol. 44 (2), 512–525. doi:10.1093/ije/dyv080
Bowden, J., Davey Smith, G., Haycock, P. C., and Burgess, S. (2016). Consistent Estimation in Mendelian Randomization with Some Invalid Instruments Using a Weighted Median Estimator. Genet. Epidemiol. 40 (4), 304–314. doi:10.1002/gepi.21965
Brumpton, B., Sanderson, E., Heilbron, K., Hartwig, F. P., Harrison, S., Vie, G. A., et al. (2020). Avoiding Dynastic, Assortative Mating, and Population Stratification Biases in Mendelian Randomization through Within-Family Analyses. Nat. Commun. 11 (1), 3519. doi:10.1038/s41467-020-17117-4
Burgess, S., Butterworth, A., Malarstig, A., and Thompson, S. G. (2012). Use of Mendelian Randomisation to Assess Potential Benefit of Clinical Intervention. BMJ 345, e7325. doi:10.1136/bmj.e7325
Burgess, S., Butterworth, A., and Thompson, S. G. (2013). Mendelian Randomization Analysis with Multiple Genetic Variants Using Summarized Data. Genet. Epidemiol. 37 (7), 658–665. doi:10.1002/gepi.21758
Burgess, S., Scott, R. A., Scott, R. A., Timpson, N. J., Davey Smith, G., and Thompson, S. G. (2015). Using Published Data in Mendelian Randomization: a Blueprint for Efficient Identification of Causal Risk Factors. Eur. J. Epidemiol. 30 (7), 543–552. doi:10.1007/s10654-015-0011-z
Camaschella, C. (2015). Iron-deficiency Anemia. N. Engl. J. Med. 372 (19), 1832–1843. doi:10.1056/NEJMra1401038
Canan, C., Lesko, C., and Lau, B. (2017). Instrumental Variable Analyses and Selection Bias. Epidemiology 28 (3), 396–398. doi:10.1097/EDE.0000000000000639
Chang, Y.-L., Hung, S.-H., Ling, W., Lin, H.-C., Li, H.-C., and Chung, S.-D. (2013). Association between Ischemic Stroke and Iron-Deficiency Anemia: a Population-Based Study. PLoS One 8 (12), e82952. doi:10.1371/journal.pone.0082952
Committee for Medicinal Products for Human U (2010). Guideline on the Investigation of Bioequivalence. London: European Medicines Agency, 1–27.
Daghlas, I., and Gill, D. (2021). Genetically Predicted Iron Status and Life Expectancy. Clin. Nutr. 40 (4), 2456–2459. doi:10.1016/j.clnu.2020.06.025
Davey Smith, G., and Ebrahim, S. (2003). 'Mendelian Randomization': Can Genetic Epidemiology Contribute to Understanding Environmental Determinants of Disease?*. Int. J. Epidemiol. 32 (1), 1–22. doi:10.1093/ije/dyg070
Davies, N. M., Holmes, M. V., and Davey Smith, G. (2018). Reading Mendelian Randomisation Studies: a Guide, Glossary, and Checklist for cliniciansPMCPMC6041728 Interests and Declare that We Have No Competing Interests. BMJ 362, k601. doi:10.1136/bmj.k601
Diseases, G. B. D., and Injuries, C. (2020). Global burden of 369 Diseases and Injuries in 204 Countries and Territories, 1990-2019: a Systematic Analysis for the Global Burden of Disease Study 2019. Lancet 396 (10258), 1204–1222. doi:10.1016/S0140-6736(20)30925-9
Fishbane, S., Pollack, S., Feldman, H. I., and Joffe, M. M. (2009). Iron Indices in Chronic Kidney Disease in the National Health and Nutritional Examination Survey 1988-2004. Cjasn 4 (1), 57–61. doi:10.2215/CJN.01670408
Food, Drug A (2014). Bioavailability and Bioequivalence Studies Submitted in NDAs or INDs—General Considerations (Draft Guidance). Silver Spring (MD): Food and Drug Administration.
Freedman, M. L., Reich, D., Penney, K. L., McDonald, G. J., Mignault, A. A., Patterson, N., et al. (2004). Assessing the Impact of Population Stratification on Genetic Association Studies. Nat. Genet. 36 (4), 388–393. doi:10.1038/ng1333
Gill, D., Benyamin, B., Moore, L. S. P., Monori, G., Zhou, A., Koskeridis, F., et al. (2019). Associations of Genetically Determined Iron Status across the Phenome: A Mendelian Randomization Study. Plos Med. 16 (6), e1002833. PMCPMC6586257 following competing interests: LSPM has consulted for bioMerieux (2014), DNAelectronics (2015-2018), Dairy Crest (2017-2018), and Pfizer (2018) and has received research grants from Leo Pharma (2016) and educational support from Eumedica (2016-2017). All other authors have no competing interest to declare. doi:10.1371/journal.pmed.1002833
Gill, D., Del Greco M., F., Walker, A. P., Srai, S. K. S., Laffan, M. A., and Minelli, C. (2017). The Effect of Iron Status on Risk of Coronary Artery Disease. Arterioscler Thromb. Vasc. Biol. 37 (9), 1788–1792. doi:10.1161/ATVBAHA.117.309757
Gill, D., Monori, G., Tzoulaki, I., and Dehghan, A. (2018). Iron Status and Risk of Stroke. Stroke 49 (12), 2815–2821. doi:10.1161/STROKEAHA.118.022701
Gillum, R. F., Sempos, C. T., Makuc, D. M., Looker, A. C., Chien, C.-Y., and Ingram, D. D. (1996). Serum Transferrin Saturation, Stroke Incidence, and Mortality in Women and Men: The NHANES I Epidemiologic Followup Study. Am. J. Epidemiol. 144 (1), 59–68. doi:10.1093/oxfordjournals.aje.a008855
Gkatzionis, A., and Burgess, S. (2019). Contextualizing Selection Bias in Mendelian Randomization: How Bad Is it Likely to Be. Int. J. Epidemiol. 48 (3), 691–701. doi:10.1093/ije/dyy202
Global Burden of Disease Collaborative Network (2020). Global Burden of Disease Study 2019 (GBD 2019) Results. Seattle, United States: Institute for Health Metrics and Evaluation IHME. Available at: http://ghdx.healthdata.org/gbd-results-tool (Accessed August 18, 2021).
Greenland, S. (2003). Quantifying Biases in Causal Models: Classical Confounding vs Collider-Stratification Bias. Epidemiology 14 (3), 300–306. doi:10.1097/01.ede.0000042804.12056.6c
Hemani, G., Zheng, J., Elsworth, B., Wade, K. H., Haberland, V., Baird, D., et al. (2018). The MR-Base Platform Supports Systematic Causal Inference across the Human Phenome. Elife 7, 7. doi:10.7554/eLife.34408
Hemani, G., Tilling, K., and Davey Smith, G. (2017). Orienting the Causal Relationship between Imprecisely Measured Traits Using GWAS Summary Data. Plos Genet. 13 (11), e1007081. doi:10.1371/journal.pgen.1007081
Kesteloot, H., and Decramer, M. (2008). Age at Death from Different Diseases: the Flemish Experience during the Period 2000-2004. Acta Clinica Belgica 63 (4), 256–261. doi:10.1179/acb.2008.047
Lawlor, D. A., Harbord, R. M., Sterne, J. A. C., Timpson, N., and Davey Smith, G. (2008). Mendelian Randomization: Using Genes as Instruments for Making Causal Inferences in Epidemiology. Statist. Med. 27 (8), 1133–1163. doi:10.1002/sim10.1002/sim.3034
Lipsitch, M., Tchetgen Tchetgen, E., and Cohen, T. (2010). Negative Controls. Epidemiology 21 (3), 383–388. doi:10.1097/EDE.0b013e3181d61eeb
Liu, Z., Ye, T., Sun, B., Schooling, M., and Tchetgen, E. T. (2021). On Mendelian Randomisation Mixed-Scale Treatment Effect Robust Identification (MR MiSTERI) and Estimation for Causal Inference. medRxiv 2020, 20204420. doi:10.1101/2020.09.29.20204420
Marniemi, J., Alanen, E., Impivaara, O., Seppänen, R., Hakala, P., Rajala, T., et al. (2005). Dietary and Serum Vitamins and Minerals as Predictors of Myocardial Infarction and Stroke in Elderly Subjects. Nutr. Metab. Cardiovasc. Dis. 15 (3), 188–197. doi:10.1016/j.numecd.2005.01.001
McLean, E., Cogswell, M., Egli, I., Wojdyla, D., and de Benoist, B. (2009). Worldwide Prevalence of Anaemia, WHO Vitamin and Mineral Nutrition Information System, 1993-2005. Public Health Nutr. 12 (4), 444–454. doi:10.1017/S1368980008002401
Menotti, A., Puddu, P. E., Tolonen, H., Adachi, H., Kafatos, A., and Kromhout, D. (2019). Age at Death of Major Cardiovascular Diseases in 13 Cohorts. The Seven Countries Study of Cardiovascular Diseases 45-year Follow-Up. Acta Cardiologica 74 (1), 66–72. doi:10.1080/00015385.2018.1453960
Mohan, K., and Pearl, J. (2021). Graphical Models for Processing Missing Data. J. Am. Stat. Assoc. 116 (534), 1023–1037. doi:10.1080/01621459.2021.1874961
Munafò, M. R., Tilling, K., Taylor, A. E., Evans, D. M., and Davey Smith, G. (2018). Collider Scope: when Selection Bias Can Substantially Influence Observed Associations. Int. J. Epidemiol. 47 (1), 226–235. doi:10.1093/ije/dyx206
Munafò, M., and Smith, G. D. (2018). Biased Estimates in Mendelian Randomization Studies Conducted in Unrepresentative Samples. JAMA Cardiol. 3 (2), 181. doi:10.1001/jamacardio.2017.4279
Nitsch, D., Molokhia, M., Smeeth, L., DeStavola, B. L., Whittaker, J. C., and Leon, D. A. (2006). Limits to Causal Inference Based on Mendelian Randomization: A Comparison with Randomized Controlled Trials. Am. J. Epidemiol. 163 (5), 397–403. doi:10.1093/aje/kwj062
Park, J.-H., Gail, M. H., Weinberg, C. R., Carroll, R. J., Chung, C. C., Wang, Z., et al. (2011). Distribution of Allele Frequencies and Effect Sizes and Their Interrelationships for Common Genetic Susceptibility Variants. Proc. Natl. Acad. Sci. 108 (44), 18026–18031. doi:10.1073/pnas.1114759108
Sanderson, E., Richardson, T. G., Hemani, G., and Davey Smith, G. (2021). The Use of Negative Control Outcomes in Mendelian Randomization to Detect Potential Population Stratification. Int. J. Epidemiol. doi:10.1093/ije/dyaa288
Schooling, C. M. (2019). Biases in GWAS – the Dog that Did Not Bark. bioRxiv, 709063. doi:10.1101/709063
Schooling, C. M., Lopez, P. M., Yang, Z., Zhao, J. V., Au Yeung, S. L., and Huang, J. V. (2020). Use of Multivariable Mendelian Randomization to Address Biases Due to Competing Risk before Recruitment. Front. Genet. 11, 610852. doi:10.3389/fgene.2020.610852
Sekula, P., Del Greco M, F., Pattaro, C., and Köttgen, A. (2016). Mendelian Randomization as an Approach to Assess Causality Using Observational Data. Jasn 27 (11), 3253–3265. doi:10.1681/ASN10.1681/asn.2016010098
Shan, Y., Lambrecht, R. W., and Bonkovsky, H. L. (2005). Association of Hepatitis C Virus Infection with Serum Iron Status: Analysis of Data from the Third National Health and Nutrition Examination Survey. Clin. Infect. Dis. 40 (6), 834–841. doi:10.1086/428062
Shi, X., Miao, W., and Tchetgen, E. T. (2020). A Selective Review of Negative Control Methods in Epidemiology. Curr. Epidemiol. Rep., 1–13. doi:10.1007/s40471-020-00243-4
Smit, R. A. J., Trompet, S., Dekkers, O. M., Jukema, J. W., and le Cessie, S. (2019). Survival Bias in Mendelian Randomization Studies. Epidemiology 30 (6), 813–816. doi:10.1097/EDE.0000000000001072
Smith, G. D., and Ebrahim, S. (2004). Mendelian Randomization: Prospects, Potentials, and Limitations. Int. J. Epidemiol. 33 (1), 30–42. doi:10.1093/ije/dyh132
Staiger, D., and Stock, J. H. (1997). Instrumental Variables Regression with Weak Instruments. Econometrica 65 (3), 557–586. doi:10.2307/2171753
Tchetgen Tchetgen, E. J., and Wirth, K. E. (2017). A General Instrumental Variable Framework for Regression Analysis with Outcome Missing Not at Random. Biom 73 (4), 1123–1131. doi:10.1111/biom.12670
Timmers, P. R., Mounier, N., Lall, K., Fischer, K., Ning, Z., Feng, X., et al. (2019). Genomics of 1 Million Parent Lifespans Implicates Novel Pathways and Common Diseases and Distinguishes Survival Chances. Elife 8, 8. doi:10.7554/eLife.39856
van der, D. L., Grobbee, D. E., Roest, M., Marx, J. J. M., Voorbij, H. A., and van der Schouw, Y. T. (2005). Serum Ferritin Is a Risk Factor for Stroke in Postmenopausal Women. Stroke 36 (8), 1637–1641. doi:10.1161/01.STR.0000173172.82880.72
VanderWeele, T. J., Tchetgen Tchetgen, E. J., Cornelis, M., and Kraft, P. (2014). Methodological Challenges in Mendelian Randomization. Epidemiology 25 (3), 427–435. doi:10.1097/EDE.0000000000000081
Vansteelandt, S., Dukes, O., and Martinussen, T. (2018). Survivor Bias in Mendelian Randomization Analysis. Biostatistics 19 (4), 426–443. doi:10.1093/biostatistics/kxx050
Vansteelandt, S., Walter, S., and Tchetgen Tchetgen, E. (2018). Eliminating Survivor Bias in Two-Stage Instrumental Variable Estimators. Epidemiology 29 (4), 536–541. doi:10.1097/EDE.0000000000000835
Wang, K., and Han, S. (2021). Effect of Selection Bias on Two Sample Summary Data Based Mendelian Randomization. Sci. Rep. 11 (1), 7585. doi:10.1038/s41598-021-87219-6
Wish, J. B. (2006). Assessing Iron Status: beyond Serum Ferritin and Transferrin Saturation. Cjasn 1 (1 Suppl. l), S4–S8. doi:10.2215/CJN.01490506
Yang, Z., Schooling, C. M., and Kwok, M. K. (2021). Genetic Evidence on the Association of Interleukin (IL)-1-mediated Chronic Inflammation with Airflow Obstruction: A Mendelian Randomization Study. COPD: J. Chronic Obstructive Pulm. Dis. 18 (4), 432–442. doi:10.1080/15412555.2021.1955848
Ye, T., Shao, J., and Kang, H. (2019). Debiased Inverse-Variance Weighted Estimator in Two-Sample Summary-Data Mendelian Randomization. Ann. Stat. 49 (4), 2079–2100. doi:10.1214/20-AOS2027
Yuan, S., and Larsson, S. (2020). Causal Associations of Iron Status with Gout and Rheumatoid Arthritis, but Not with Inflammatory Bowel Disease. Clin. Nutr. 39 (10), 3119–3124. doi:10.1016/j.clnu.2020.01.019
Zhao, Q., Wang, J., Hemani, G., Bowden, J., and Small, D. S. (2020). Statistical Inference in Two-Sample Summary-Data Mendelian Randomization Using Robust Adjusted Profile Score. Ann. Statist 48 (3), 1742–1769. doi:10.1214/19-AOS1866
Keywords: causal estimates, control exposures, Mendelian randomization, reproducible, selection bias
Citation: Yang Z, Schooling CM and Kwok MK (2021) Credible Mendelian Randomization Studies in the Presence of Selection Bias Using Control Exposures. Front. Genet. 12:729326. doi: 10.3389/fgene.2021.729326
Received: 23 June 2021; Accepted: 01 November 2021;
Published: 24 November 2021.
Edited by:
Miguel E. Rentería, QIMR Berghofer Medical Research Institute, AustraliaReviewed by:
Huaizhen Qin, University of Florida, United StatesSantiago Diaz-Torres, The University of Queensland, Australia
Copyright © 2021 Yang, Schooling and Kwok. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Man Ki Kwok, bWFnZ2lla0Boa3UuaGs=