
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Genet., 15 June 2021
Sec. Statistical Genetics and Methodology
Volume 12 - 2021 | https://doi.org/10.3389/fgene.2021.682638
This article is part of the Research TopicCurrent Status and Future Challenges of Biobank Data AnalysisView all 6 articles
 Wenjian Bi1,2,3*
Wenjian Bi1,2,3* Seunggeun Lee4*
Seunggeun Lee4*With the advances in genotyping technologies and electronic health records (EHRs), large biobanks have been great resources to identify novel genetic associations and gene-environment interactions on a genome-wide and even a phenome-wide scale. To date, several phenome-wide association studies (PheWAS) have been performed on biobank data, which provides comprehensive insights into many aspects of human genetics and biology. Although inspiring, PheWAS on large-scale biobank data encounters new challenges including computational burden, unbalanced phenotypic distribution, and genetic relationship. In this paper, we first discuss these new challenges and their potential impact on data analysis. Then, we summarize approaches that are scalable and robust in GWAS and PheWAS. This review can serve as a practical guide for geneticists, epidemiologists, and other medical researchers to identify genetic variations associated with health-related phenotypes in large-scale biobank data analysis. Meanwhile, it can also help statisticians to gain a comprehensive and up-to-date understanding of the current technical tool development.
With the advances in genotyping technologies and electronic health records (EHRs), large biobanks genotype and extensively phenotype hundreds of thousands of individuals (Greely, 2007; Häyrinen et al., 2008; De Souza and Greenspan, 2013; Nielsen et al., 2018; Wolford et al., 2018; Beesley et al., 2019). For example, UK Biobank is a national and international health resource that collected whole-genome scale genetic data, thousands of complex traits and exposures from ICD billing codes, web surveys, and lab measurements on ∼500,000 individuals (Fry et al., 2017; Bycroft et al., 2018; Canela-Xandri et al., 2018). Other population-based biobanks include All of Us (All of Us Research Program Investigators., 2019), Biobank Japan (BBJ; Nagai et al., 2017), China Kadoorie Biobank (Chen et al., 2011), Nord-Trøndelag Health Study (HUNT) (Krokstad et al., 2013) et al. These datasets can be great resources to identify and validate genetic associations on a genome-wide and even a phenome-wide scale.
Phenome-wide association studies (PheWAS) utilize large numbers of measured phenotypes and can explore the associations between one genetic variant and the entire phenome (Denny et al., 2010). Benefit from the large sample size and extensive traits in analysis, PheWAS in biobanks have the potential to discover novel associations for translational and clinical research, including to construct risk prediction models for complex diseases and phenotypes (Fritsche et al., 2018; Torkamani et al., 2018), to identify the causal effect of exposures and drugs (Verbanck et al., 2018), and to identify drug targets and repurposing (Lam et al., 2017; Pushpakom et al., 2019).
To date, several PheWAS have been performed on biobank data (Roden et al., 2010; Bush et al., 2016). More than thousands of phenotypes have been analyzed at the variant level (Elliott et al., 2018; Zhou et al., 2018; Jiang et al., 2019), gene level (Zhao et al., 2020; Zhou et al., 2020), and pathway level (Dutta et al., 2021). Recently, web-based tools, such as PheWeb (Gagliano Taliun et al., 2020), were developed for visualizing, navigating and sharing the analysis results. All these efforts enable us to provide important insights into many aspects of human genetics and biology. However, due to huge computational burden, unbalanced phenotypic distribution, and genetic relatedness among individuals, PheWAS on large-scale biobank data urgently require more efficient and accurate algorithms.
In this paper, we review challenges in biobank data analysis and regression approaches to addressing these challenges with the goal of providing a practical guidance to statisticians, epidemiologists, and other medical researchers. In section “Statistical and Computational Challenges in Biobank Data Analysis and Approaches to Addressing Them,” we discuss statistical and computational challenges of genome-wide association studies (GWAS) and PheWAS on large-scale biobank data. In section “Scalable and Robust Association Testing Methods,” we summarize recently developed scalable and robust regression approaches. In section “Phenome-Wide Biobank Data Analysis Results and Phewebs,” we introduce existing phenome-wide analyses results. In section “Future Challenges,” we mention potential future challenges which require more advanced methods and tools.
In this section, we give a brief discussion about statistical and computational challenges in large-scale biobank data analysis and useful strategies to address these challenges (see Table 1).
Increasing sample size contributes to more statistical power to identify novel marginal genetic effects and gene-environment interaction (G × E) effects. Meanwhile, it also results in a larger computational burden, which should be carefully handled. In GWAS, most regression approaches include covariates such as age, sex, and top SNP-derived principal components (PCs) to adjust for. Wald and likelihood ratio tests require fitting full models and thus both genetic and covariate effects are simultaneously estimated for all variants. If the number of covariates is large, it will take a substantial amount of time. For example, suppose that 20 covariates were adjusted to fit a standard logistic model, as the sample size increases from 5,000 to 500,000, the computation time increases from 0.02 to 2.55 s. If projected to a PheWAS with 10 million genetic variants and 100 phenotypes, the corresponding computation time increases from 238.3 CPU days to 80.8 CPU years (see Figure 1). Hence, in a large-scale PheWAS, it is not practical to use Wald and likelihood ratio tests even if multiple CPU cores are used for parallel computation.
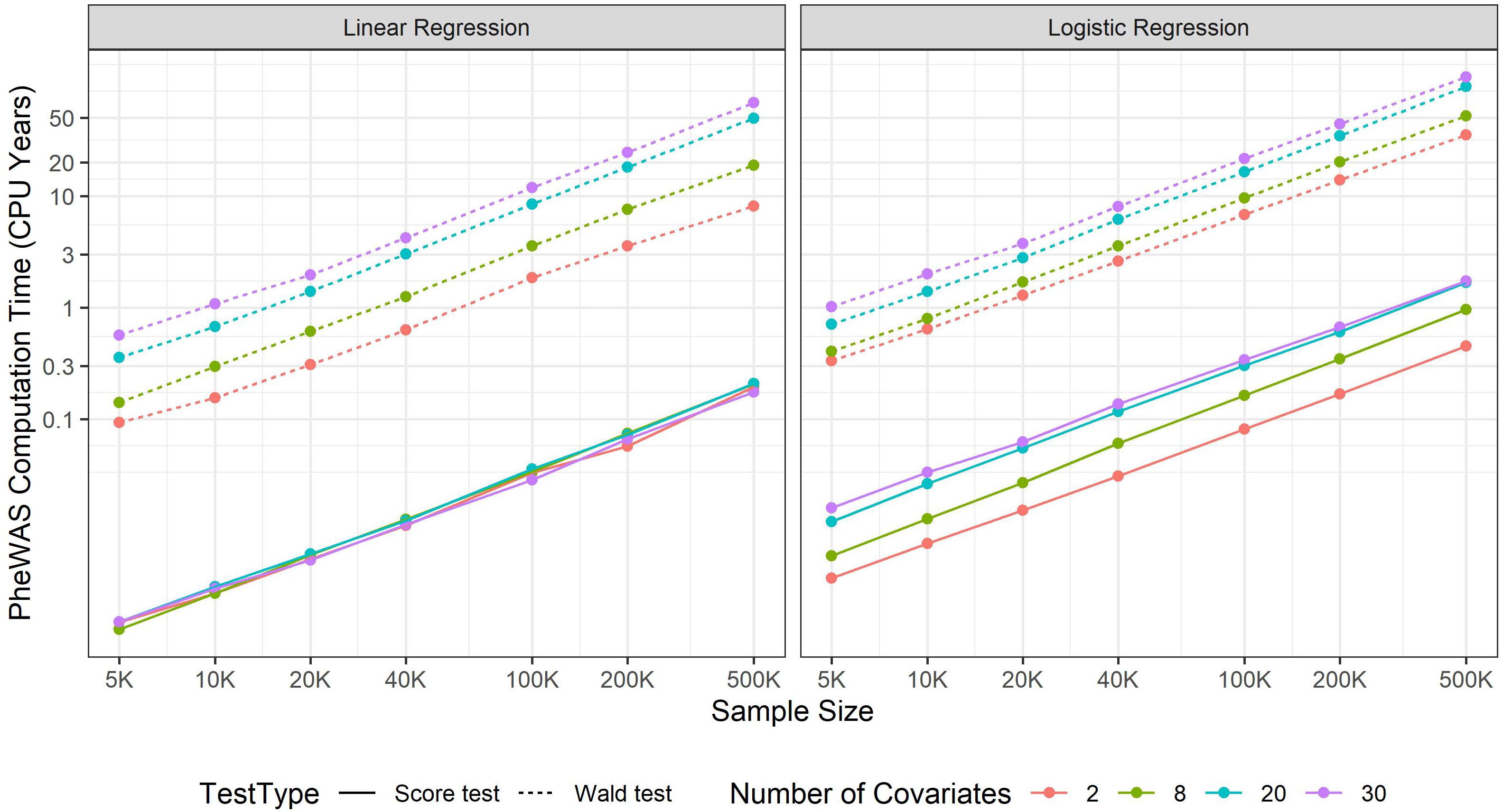
Figure 1. PheWAS computation time. The computation time is evaluated at CPU core of Intel i7-7700T 2.90GHz and then projected to a phenome-wide association studies including 100 balanced binary phenotypes and 10 million variants.
In contrast to Wald and likelihood ratio tests, score test does not require fitting the full model. Score test contains two steps: (1) fitting a model under the null hypothesis; (2) calculating score statistics and p values for each variant (see Figure 2). When testing marginal genetic effects, the null hypotheses for all variants are the same. Hence, across a genome-wide analysis, score test only requires fitting one null model, which greatly reduces the computation time. Recently, many scalable methods based on score test have been developed to analyze quantitative traits (Zhou and Stephens, 2012; Loh et al., 2015; Jiang et al., 2019), binary traits (Zhou et al., 2018, 2020), time-to-event data (Bi et al., 2020; Dey et al., 2020; He and Kulminski, 2020), and ordinal categorical data (Bi et al., 2021).
Score test is successful in reducing computation time since it avoids duplicated computation to adjust for covariates. This strategy can also be applied to other cases. Recently, scalable methods were proposed for a genome-wide G × E analysis (Bi et al., 2019; Wang et al., 2020). When testing G × E effect, the null model should include marginal genetic effect. Hence, different genetic variants correspond to different null models and the regular score test is not scalable in a large-scale biobank data analysis. Instead of fitting a null model including both covariate and marginal genetic effects, the new methods fit a covariates-only model in Step 1 and then use matrix projection to adjust for the marginal genetic effect in Step 2. Because only one covariates-only model fitting is required for a genome-wide analysis, this strategy can greatly reduce the computation time. However, the matrix projection approach might be inaccurate if the marginal genetic effect is large. To balance the computational efficiency and accuracy, SPAGE (Bi et al., 2019) uses a hybrid strategy as follows. If the marginal genetic effect is small or moderate (e.g., p value > 5e-3), the matrix projection is used. Otherwise, regular approaches are used to test the marginal G × E effect.
For most of the population-based biobanks, individuals are recruited following a cohort study design, that is, a representative sub-population of the source population are recruited (Beesley et al., 2019). For example, UK Biobank invited all residents aged 40–69 who lived within 25 miles of one of their 22 assessment centers to participate (Bycroft et al., 2018). Due to no stratified sampling, the proportion of rare conditions in biobanks could be very low. For example, in the UK Biobank data, most binary phenotypes based on PheCodes (1,431 out of 1,688; 84.8%) have a case-control ratio lower than 1:100 (Zhou et al., 2018). The unbalanced phenotypic distribution would cause an inflation of type I error rates.
Based on a penalized likelihood function, the Firth’s approach can correct the first-order asymptotic bias of parameter estimates (Firth, 1993). Firth bias correction likelihood ratio test is well calibrated and robust for testing low frequency and rare variants in unbalanced studies (Ma et al., 2013). However, the exact Firth’s method still lacks computational efficiency because it involves fitting the full model (Dey et al., 2017). Recently, Rounak et al. proposed a fast genotype odds ratios estimation in which Firth’s penalty was adjusted (Dey and Lee, 2019). REGENIE also used an approximate Firth regression in which covariate effects were incorporated through an offset term (Mbatchou et al., 2021). These strategies reduce the number of predictors and thus are scalable in GWAS.
If the phenotypic distribution is unbalanced, the underlying null distribution of score test statistics could be highly skewed. Thus, regular normal distribution approximation often fails since only the first two cumulants (i.e., mean and variance) are used (Dey et al., 2017). As an alternative approach, saddlepoint approximation (SPA) uses the entire cumulant-generating function (CGF) to estimate the null distribution, which considerably improve type I error rate control (Daniels, 1954; Jensen, 1995). Recently, SPA is attracting more attention in GWAS and PheWAS (Dey et al., 2017; Zhou et al., 2018, 2020; Bi et al., 2019; Zhao et al., 2020). Extensive simulation studies and real data analysis suggest that SPA greatly outperforms the regular methods especially when testing low-frequency variants. Although more accurate, SPA takes more time than the regular normal distribution approximation. Using the fact that many elements of the genotypes are zeroes (i.e., homozygous major genotypes), the computation of SPA can be speeded up through a partial normal approximation (Dey et al., 2017; Bi et al., 2021). Another strategy is to use SPA only if the normalized score statistics is far away from 0 (e.g., >2), and to use the regular normal distribution approximation otherwise (Dey et al., 2017; Bi et al., 2020).
For SPA, one important step is to estimate CGF of the score test statistic, S, under the null hypothesis, i.e., K(t) = log(EH0(etS)). When analyzing binary or ordinal categorical traits, the score test statistic is the sum of multiple random variables, each of which follows a Bernoulli distribution (Dey et al., 2017; Bi et al., 2019, 2021). Hence, the CGF can be explicitly expressed. However, in certain cases, the CGF cannot be expressed in a closed form, which limits the use of SPA. Recently, an empirical SPA approach was used to estimate the CGF (Bi et al., 2020). This approach has been successfully applied to time-to-event data analysis. Since the empirical SPA approach does not rely on the theoretical expression of CGF, it can be used to analyze other complex traits.
As sample sizes continue to increase, many biobanks contain a large proportion of individuals with genetic relatedness. For example, in Nord Trøndelag Health Study (HUNT) (Krokstad et al., 2013), around 81% of the individuals have at least a third degree relative that is also in the study. If not carefully addressed, the genetic relatedness can inflate type I error rates. Including SNP-derived PCs as covariates can relieve it to a certain degree but is not accurate enough. During the past decade, efficient mixed model approaches have emerged as promising solutions (Kang et al., 2010; Zhou and Stephens, 2012; Loh et al., 2015; Zhou et al., 2018; Bi et al., 2021).
Using genome-wide genetic data, the genetic relatedness among individuals can be characterized by a genetic relationship matrix (GRM) (Astle and Balding, 2009; Aguilar et al., 2011). The off-diagonal elements in GRM are close to the kinship coefficients between two individuals. In addition to the fixed effects of covariates, a random effect is included to account for the genetic relatedness. The random effect is assumed following a multivariate normal distribution with a covariance matrix of GRM. For mixed model approaches, the SNP-derived PCs can also be included as covariates to better adjust population stratification (Zhang and Pan, 2015). Mixed model approaches have been proposed to analyze quantitative trait (Kang et al., 2010; Zhou and Stephens, 2012; Loh et al., 2015), binary trait (Zhou et al., 2018, 2020), time-to-event data (Dey et al., 2020; He and Kulminski, 2020), and ordinal categorical data (Bi et al., 2021).
It is technically challenging to apply mixed model approaches in large-scale data. For example, the memory storage of the GRM is O(n2), where n is the sample size. Suppose that sample size n = 408, 961 (white British participants in UK Biobank), then it takes 669 Gb of memory to store the GRM given a float-precision format. Instead of precomputing a GRM and then storing it into the memory, an alternative approach is to store the raw genotype (used to construct GRM) into a bitwise binary vector and then load it when in usage (Loh et al., 2015). Suppose that m = 93,511 variants are used to calculate GRM, the memory usage can be reduced to 9.56 GB. Another computational challenge is to fit the model under the null hypothesis which requires either performing spectral decomposition on GRM or calculating the inverse of the n × n matrices, both require O(n3) calculation. Instead, a linear system solver, such as the preconditional conjugate gradient (PCG) approach can be used to provide scalable computation, which requires O(mn1.5) (Kaasschieter, 1988). PCG is easily parallelizable, so parallel computing libraries, such as OpenMP (Dagum and Menon, 1998) and RcppParallel (Allaire et al., 2018), can be used to fully utilize the available CPU cores as many as possible.
Although scalable to analyze hundreds of thousands of individuals, the mixed model approaches using full (dense) GRM are still computationally intensive. A straightforward approach is to use a sparse GRM in which values less than a pre-given cutoff (e.g., <0.05) were set to 0 (Jiang et al., 2019; Bi et al., 2021). This approach can substantially reduce computation time and memory usage. However, using sparse GRM can be less powerful than using full GRM since the sparse GRM cannot incorporate polygenic effects (Jiang et al., 2019).
When analyzing a candidate variant, the variants in linkage disequilibrium with it (including the candidate variant itself) should not be used to construct GRM to avoid modeling effects twice (Yang et al., 2014). To avoid the proximal contamination, leave one chromosome out (LOCO) scheme is used in linear mixed model approaches (Lippert et al., 2011; Yang et al., 2014; Loh et al., 2015). For binary trait, sensitivity analyses suggested that the proximal contaminations in GWAS for diseases with low prevalence is not as substantial as for more common diseases and thus LOCO scheme might not be required (Zhou et al., 2018).
Instead of the mixed effect model framework, a fixed effect model with a penalty can be used to account for genetic relatedness. A recent developed REGENIE (Mbatchou et al., 2021) used two-step ridge regressions to calculate predictors from genetic data and then used linear and logistic regression to associate quantitative and binary traits with genetic variants. Compared to mixed effect model approaches, fixed effect model approaches can be faster and needs a smaller amount of memory. Although shown to perform similarly as BOLT-LMM (Loh et al., 2015) and SAIGE (Zhou et al., 2018) when applying to UK Biobank, it is not clear whether the genetic relatedness can be well characterized by the fixed effect model if the participants are in a highly related or in a multiethnic cohort study.
In this section, we introduce regression methods that are scalable and robust in large-scale biobank data analysis (see Table 2). We let G denote the genotype of genetic variant and X denote the confounding covariates. The corresponding coefficients are βG and βX, respectively. For mixed models, we let Φ denote GRM, σ denote variance component, b denote the random effect and assume that b follows a multivariate normal distribution N(0,σΦ). The trait of interest is denoted as Y.
Linear regression is the most widely used approach when the trait of interest is measured quantitatively. When analyzing unrelated individuals, the regular linear model is
where ϵ is an error term that is usually assumed normally and independently distributed. The test of null hypothesis H0:βG = 0 is implemented in several tools including GCTA (Yang et al., 2011), plink (Chang et al., 2015), et al. To adjust for the genetic relatedness, additional random effect b should be included and the LMM (Kang et al., 2010; Zhou and Stephens, 2012) is
BOLT-LMM (Loh et al., 2015) proposed to compactly store the genotype used to construct a full GRM Φ in memory and applied PCG to efficiently fit the null mixed model. fastGWA (Jiang et al., 2019) used sparse GRM to further reduce the computation time and memory usage. If the distribution of quantitative trait is highly skewed, inverse-normal transformation is commonly used to convert the raw quantitative trait.
For complex disease research, individuals are usually divided into two groups: the cases (Y = 1) or the controls (Y = 0). Logistic model and logistic mixed model can model the dependence of a binary trait on covariates and genetic variants as below.
In the presence of population stratification, applying LMMs to binary traits can lead to incorrect type I error rates, particularly when the population groups have heterogeneous case-control ratios (Chen et al., 2016). This is because LMM assumes that the variance of the binary trait is constant and does not change with the mean (Jarque and Bera, 1980). Based on the logistic mixed model, Chen et al. (2016) developed a score test called GMMAT. GMMAT uses penalized quasi-likelihood (Breslow and Clayton, 1993) and average information restricted maximum likelihood algorithm (Gilmour et al., 1995) to fit the null mixed model. However, GMMAT package requires storing a precalculated GRM, which takes huge amount of memory when sample size is very large (e.g., >100,000). In addition, it cannot control type I error rates when case-control ratio is unbalanced. To address these challenges, SAIGE method applied computational strategies as in BOLT-LMM to avoid storing GRM and used SPA for testing (Zhou et al., 2018). Recently, more optimized tools have been developed to increase the computational performance of SAIGE (Zheng and Davis, 2020).
Ordinal categorical trait is an extension of binary trait to measure more conditions. It is widely used in surveys, questionnaires, and tests to measure human behaviors, satisfaction, and preferences (Agresti, 2003). For example, hedonic scale of liking ranging from “extremely dislike” to “extremely like” was widely used to measure preferences (Bi et al., 2021). Although usually coded as numeric values, the ordinal categorical data is different from quantitative trait since the values cannot characterize the underlying scale well (Agresti, 2003).
Suppose that Y = 1, 2, J is to denote an ordinal categorical phenotype with J ordinal conditions. Recently, proportional odds logistic mixed model (POLMM) (Bi et al., 2021) has been used to model the ordinal categorical phenotype as follows
where νj = Pr(Y ≤ j|X, G, b) is the cumulative probability of the phenotype Y ≤ j and ϵ: ϵ1 < … < ϵJ = ∞ were used to categorize the data. POLMM supports both full (dense) GRM and sparse GRM when fitting the null model and is scalable to analyze biobanks with hundreds of thousands of individuals. In addition, POLMM uses SPA and thus is robust when testing low-frequency and rare variance even if the phenotypic distribution is highly unbalanced (Bi et al., 2021).
Time-to-event data is unique because the outcome of interest is not only whether an event occurred, but also when the event occurred (Altman and Bland, 1998). In medical studies, time-to-event data were often used to characterize outcomes such as death and cancer progression (Tolles and Lewis, 2016). Another unique feature of the time-to-event data is censoring, that is, not all subjects experience the event by the end of the follow-up period. With the increasing use of EHRs and biobanks for genetics research, time-to-event data analysis is becoming more common in genetic studies of human diseases (Huang et al., 2009; Kapoor et al., 2014).
Cox proportional hazard (PH) model is widely used to analyze time-to-event data (Cox, 1972). The Cox PH model specifies the hazard function λ(t) for the failure time associated with genotype and covariates as below.
where λ0(t) is a baseline hazard function. R package gwasurvivr (Rizvi et al., 2018) was developed to perform genome-wide survival analysis. To increase the computational efficiency, gwasurvivr first fits null model with βG = 0 and then uses the parameter estimates as initial points when testing variants. Since gwasurvivr is based on a Wald test, it is still not scalable when the sample size is large (>100,000). Recently, a fast and accurate method called SPACox was proposed to use an empirical SPA to calibrate p values (Bi et al., 2020). SPACox is based on a score test and is more robust to analyze low-frequency and rare variants, especially when the event rate is moderate or low.
If random effect is included to adjust for genetic relatedness, the corresponding mixed model (i.e., frailty model) is
Existing methods such as COXMEG (He and Kulminski, 2020) and GATE (Dey et al., 2020) are scalable in large-scale GWAS. When fitting the null model, COXMEG supports sparse GRM and GATE supports both full and sparse GRM. In addition, GATE uses SPA to calibrate p values, which makes it more powerful and robust to analyze low-frequency and rare variants.
Gene-environment interaction (G × E) plays an important role in the etiology of many complex traits (Gauderman et al., 2017; McAllister et al., 2017). For a binary trait Y, the full logistic model for G × E is as follows.
where E is environmental factor and G × E is the interaction term. One strategy to reduce computation time is to test both marginal and interaction effects of G: βG = βG × E = 0, which share the same null hypothesis in the entire genome and hence can greatly reduce computation time if the score test is used. However, since the marginal genetic effect is usually larger than the G × E effect, the association identified by the joint test is mostly driven by the marginal genetic effect, which is not the major interest in a G × E study.
Software packages such as CGEN (Bhattacharjee et al., 2010) and GxEScan (Gauderman et al., 2013) have been developed for a genome-wide G × E analysis. Since these tools mainly implement the Wald test, the computation burden is still very high in a large-scale biobank data analysis. To improve the efficiency, several two-step approaches have been proposed (Kooperberg and LeBlanc, 2008; Murcray et al., 2008). These methods compute screening p values to test marginal genetic associations (i.e., βG = 0) or the dependency between E and G. Then, the variants with significant screening p values are selected to test G × E effect in the next step. In addition to the single-variant tests, various set-based methods have been proposed to test G × E effect (Chen et al., 2014; Lin et al., 2016; He et al., 2017b; Su et al., 2017). These methods jointly test variants in a particular gene or functional region to increase power for low-frequency and rare variants.
Recently, more efficient approaches have been proposed for genome-wide G × E analysis (Bi et al., 2019; Wang et al., 2020). Instead of fitting a null model, these methods fit a covariates-only model and then use matrix projection to calculate score statistics and p values. SPAGE (Bi et al., 2019) uses SPA to calibrate p values and thus is more robust even if the case-control ratio is unbalanced. MAGEE (Wang et al., 2020) is a set-based method which is developed based on mixed model and can identify associations between an aggregate variant set and environmental exposures on quantitative and binary traits.
When testing for low-frequency and rare variants, the statistical power of single-variant based association tests is usually low. Region-based approaches can boost power by evaluating association for multiple variants in a biologically relevant region, such as gene (Wu et al., 2011; Lee et al., 2012a,b, 2013, 2014; Ionita-Laza et al., 2013). Burden tests collapse rare variants into genetic scores and are powerful when a large proportion of variants are causal and the effects are in the same direction (Morgenthaler and Thilly, 2007; Li and Leal, 2008). Variance-component testing approaches, such as SKAT, test variance of genetic effects and are more powerful in the presence of variants with different effect directions or a small fraction of causal variants (Pan, 2009; Neale et al., 2011; Wu et al., 2011). Combined tests, such as SKAT-O (Lee et al., 2012a,b) and ACAT (Liu et al., 2019) methods, can combine burden and variance-component tests and are more robust in different scenarios.
R package SKAT is a useful generic tool for region-based rare variant analysis. Besides the original Burden, SKAT, and SKAT-O methods, features including efficient resampling (ER) (Lee et al., 2016), combined test of common and rare variants (Ionita-Laza et al., 2013), and X chromosome test (Ma et al., 2015) are also supported. To control for unbalanced case-control ratio, Zhao et al. proposed robust region-based association approaches. The robust approaches use SPA and ER to calibrate p values and can control type I error rates when the case-control ratio is unbalanced (Zhao et al., 2020). SMMAT is an extension of GMMAT into the region-based association analysis (Chen et al., 2019). SMMAT can adjust for genetic relatedness but is not applicable when the sample size is large or the case-control ratio is unbalanced. SAIGE-Gene (Zhou et al., 2020) can incorporate a full GRM to account for genetic relatedness and is scalable and accurate to analyze hundreds of thousands of individuals. Recently, integrative region-based association approaches were proposed to incorporate multiple functional annotations of genetic variation (He et al., 2017a; Li et al., 2020). If the variant risk status can be predicted by functional annotations, these approaches can significantly improve power.
In this section, we highlight existing phenome-wide analyses results. The usage of PheWeb facilitates the sharing and organizing of genetic association results.
• Oxford Brain Imaging Genetics (BIG) Server version 2.0 can browse GWAS results for UK Biobank Brain Imaging Phenotypes and other traits/diseases. The primary source included results from 3,144 GWAS of Brain Imaging Derived Phenotypes (IDPs) measured on 9,707 participants of the UK Biobank study. Currently, the server has loaded more GWAS results including the GWAS results of ∼ 2,000 phenotypes in the UK Biobank processed by Ben Neale1.
• The Michigan Genomics Initiative (MGI) is a collaborative research effort among physicians, researchers, and patients at the University of Michigan (U-M). Since most of the PheWAS are based on UK Biobank, the PheWAS data analysis based on MGI is an important supplementary although its sample size (∼40,000) is less than UK Biobank2.
• The BBJ project has collected around 200,000 individuals with diseases cases consisting of 47 various diseases. These subjects were recruited from 12 medical institutes in Japan. The analysis results of total 244 phenotypes including both binary and quantitative traits have been released3.
• SAIGE method can better control type I error rates when the case-control ratio is unbalanced. Using SAIGE, GWAS on 1403 ICD-based traits were performed based on the White British participants of the UK Biobank4.
• POLMM is an extension of SAIGE on ordinal categorical data analysis. PheWAS of 258 ordinal categorical phenotypes on UK Biobank has been conducted, in which 150 phenotypes are to describe food and other health-related preferences5.
• Based on the fastGWA method, PheWAS was applied to 2,173 traits on 456,422 array-genotyped as well as 49,960 whole-exome-sequenced individuals of European ancestry in the UK Biobank. Since linear mixed model approaches were used to analyze binary traits and ordinal categorical data, the PheWAS only analyze variants with MAF > 0.016.
• Using the robust SKAT-O approach for binary phenotypes, a total of 18,360 genes were analyzed based on 45,596 independent European samples across 791 binary phenotypes with at least 50 cases. The PheWAS are based on UK Biobank 50K exome data processed by FE pipeline7.
• PathWeb displays results for associations between over 10,000 pathways (gene-sets) and phenotypes derived from ICD billing codes of White British participants of the UK Biobank. GWAS summary-statistics obtained using SAIGE for 1,403 binary phenotypes derived from ICD billing codes have been used in the analysis8.
The recent success in methodology development has greatly facilitated the large-scale biobank data analysis on a genome-wide and phenome-wide scale. In the future, it is expected that more comprehensive information, in terms of both genome and phenome, will be collected and shared through the continuously upgrading biobanks. The rapid development of biobanks provides a basis for precision health and medicine. Meanwhile, it also brings new challenges, which requires more advanced methods and tools. Here we list some of these challenges.
The current biobanks usually recruit half million participants. In the future, we are likely to encounter biobanks with millions of and even tens of millions of participants. For example, All of US biobank in US aims to recruit 1 million individuals and UK announced a plan to recruit 5 million individuals (Scott et al., 2019). The increase of sample size asks for more computational time and memory usage, which should be carefully addressed in terms of methodology and software implement.
In the coming decades, whole genome sequencing (WGS) will replace GWAS chips and become the most widely used genotyping platform. Since WGS can accurately identify and genotype rare variants, more scalable and powerful strategies and methods to evaluate rare variant associations in whole genome are increasingly needed. The evolving availability of new technologies will provide us with rich multi-omics data resources. Effectively incorporating additional information, such as epigenetics, is also important to boost powers and to increase interpretability in WGS studies.
In the past decades, GWAS mainly focus on univariate phenotypes, that is, the phenotype of interest has only one variable. Recently, multivariate and high dimensional phenotypes are increasingly available. For example, longitudinal data track the same sample and collect repeated observations at different time points. Image phenotypes, such as Magnetic Resonance Imaging (MRI) of brain and other organs, are collected to better diagnose and treat diseases. Developing scalable and robust methods to appropriately analyze these complex phenotypes is important to fully utilize these data.
The current phenome-wide analyses are mainly to test single phenotype and then look at the association patterns across phenome. This strategy does not utilize the correlation and causal relationship between phenotypes. Effectively aggregating associations in large numbers of phenotypes can boost statistical powers and gain better phenome-wide understanding. Existing joint tests of multiple phenotypes include MultiPhen (O’Reilly et al., 2012), MANOVA (Stephens, 2013), USAT (Ray et al., 2016), and Multi-SKAT (Dutta et al., 2019). Some of the methods developed for non-human data, such as GPWAS (Liang et al., 2020) for plant genetics, also can be used. In addition, when analyzing multiple phenotypes, the imputation of missing data will be important since removing individuals with at least one missing phenotype will greatly reduce the sample size.
Population structure and family relatedness are major confounders in genetic association studies. The recently proposed mixed effect and fixed effect models are usually applied to individuals from the same ancestry group, as it isn’t clear whether they can accurately analyze multiethnic individuals. Meta-analysis is commonly applied to combine analysis results from different ancestry groups, but it may need more research if individuals of different ancestry groups are related. For admixed population, specialized approach is needed to construct GRM, such as a method using individual specific allele frequency, but scalable mixed model to use this type of GRM is under-developed (Thornton et al., 2012). As biobanks recruit individuals from diverse populations, it would be important to identify and develop optimal methods and tools to analyze multiethnic and admixed individuals.
The emergence of biobanks allows researchers to explore extensive associations between genetic variants and thousands of complex traits. In this paper, we discussed statistical and computational challenges in large-scale biobank data analysis and reviewed available methods and tools to address these challenges. In addition, we also briefly introduced possible challenges in the future. Benefit from the continuous biobanking efforts to connect genome-wide variants and phenome-wide traits, several PheWAS have been performed and it is expected that more PheWAS results will be available in the coming decade. Scalable and robust statistical approaches will certainly play an essential role in the success. In addition, developing user-friendly software that makes full use of the computing capacity is also important.
WB and SL conceived the study and drafted the manuscript. Both authors contributed to the article and approved the submitted version.
This research was supported by NIH grants R01-HG008773 (WB), and Brain Pool Plus (BP+, Brain Pool+) Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (2020H1D3A2A03100666, SL).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Aguilar, I., Misztal, I., Legarra, A., and Tsuruta, S. (2011). Efficient computation of the genomic relationship matrix and other matrices used in single-step evaluation. J.Anim. Breed. Genet. 128, 422–428. doi: 10.1111/j.1439-0388.2010.00912.x
All of Us Research Program Investigators. (2019). The “All of Us” research program. N. Engl. J. Med. 381, 668–676.
Allaire, J. J., François, R., Ushey, K., Vandenbrouck, G., and Geelnard, M. (2018). RcppParallel: Parallel Programming Tools for ‘Rcpp’. R Package Version 4.4. 2.
Astle, W., and Balding, D. J. (2009). Population structure and cryptic relatedness in genetic association studies. Stat. Sci. 24, 451–471.
Beesley, L. J., Salvatore, M., Fritsche, L. G., Pandit, A., Rao, A., Brummett, C., et al. (2019). The emerging landscape of health research based on biobanks linked to electronic health records: existing resources, statistical challenges, and potential opportunities. Stat. Med. 39, 773–800.
Bhattacharjee, S., Chatterjee, N., and Wheeler, W. (2010). CGEN: An R Package for Analysis of Case-Control Studies in Genetic Epidemiology.
Bi, W., Fritsche, L. G., Mukherjee, B., Kim, S., and Lee, S. (2020). A fast and accurate method for genome-wide time-to-event data analysis and its application to UK biobank. Am. J. Hum. Genet. 107, 222–233. doi: 10.1016/j.ajhg.2020.06.003
Bi, W., Zhao, Z., Dey, R., Fritsche, L. G., Mukherjee, B., and Lee, S. (2019). A fast and accurate method for genome-wide scale phenome-wide G × E analysis and its application to UK Biobank. Am. J. Hum. Genet. 105, 1182–1192. doi: 10.1016/j.ajhg.2019.10.008
Bi, W., Zhou, W., Dey, R., Mukherjee, B., Sampson, J. N., and Lee, S. (2021). Efficient mixed model approach for large-scale genome-wide association studies of ordinal categorical phenotypes. Am. J. Hum. Genet. 108, 825–839. doi: 10.1016/j.ajhg.2021.03.019
Breslow, N. E., and Clayton, D. G. (1993). Approximate inference in generalized linear mixed models. J. Am. Stat. Assoc. 88, 9–25.
Bush, W. S., Oetjens, M. T., and Crawford, D. C. (2016). Unravelling the human genome–phenome relationship using phenome-wide association studies. Nat. Rev. Genet. 17:129. doi: 10.1038/nrg.2015.36
Bycroft, C., Freeman, C., Petkova, D., Band, G., Elliott, L. T., Sharp, K., et al. (2018). The UK Biobank resource with deep phenotyping and genomic data. Nature 562:203.
Canela-Xandri, O., Rawlik, K., and Tenesa, A. (2018). An atlas of genetic associations in UK Biobank. Nat. Genet. 50, 1593–1599.
Chang, C. C., Chow, C. C., Tellier, L. C. A. M., Vattikuti, S., Purcell, S. M., and Lee, J. J. (2015). Second-generation PLINK: rising to the challenge of larger and richer datasets. Gigascience 4:7.
Chen, H., Huffman, J. E., Brody, J. A., Wang, C., Lee, S., Li, Z., et al. (2019). Efficient variant set mixed model association tests for continuous and binary traits in large-scale whole-genome sequencing studies. Am. J. Hum. Genet. 104, 260–274. doi: 10.1016/j.ajhg.2018.12.012
Chen, H., Meigs, J. B., and Dupuis, J. (2014). Incorporating gene-environment interaction in testing for association with rare genetic variants. Hum. Hered. 78, 81–90.
Chen, H., Wang, C., Conomos, M. P., Stilp, A. M., Li, Z., Sofer, T., et al. (2016). Control for population structure and relatedness for binary traits in genetic association studies via logistic mixed models. Am. J. Hum. Genet. 98, 653–666. doi: 10.1016/j.ajhg.2016.02.012
Chen, Z., Chen, J., Collins, R., Guo, Y., Peto, R., Wu, F., et al. (2011). China Kadoorie Biobank of 0.5 million people: survey methods, baseline characteristics and long-term follow-up. Int. J. Epidemiol. 40, 1652–1666.
Cox, D. R. (1972). Regression models and life-tables. J. Royal Stat. Soc. Ser. B Method 34, 187–202.
Dagum, L., and Menon, R. (1998). OpenMP: an industry standard API for shared-memory programming. IEEE Comput. Sci. Eng. 5, 46–55.
De Souza, Y. G., and Greenspan, J. S. (2013). Biobanking past, present and future: responsibilities and benefits. AIDS 27, 303–312.
Denny, J. C., Ritchie, M. D., Basford, M. A., Pulley, J. M., Bastarache, L., Brown-Gentry, K., et al. (2010). PheWAS: demonstrating the feasibility of a phenome-wide scan to discover gene-disease associations. Bioinformatics 26, 1205–1210. doi: 10.1093/bioinformatics/btq126
Dey, R., and Lee, S. (2019). Technical note: efficient and accurate estimation of genotype odds ratios in biobank-based unbalanced case-control studies. bioRxiv [Preprint] doi: 10.1101/646018
Dey, R., Schmidt, E. M., Abecasis, G. R., and Lee, S. (2017). A fast and accurate algorithm to test for binary phenotypes and its application to PheWAS. Am. J. Hum. Genet. 101, 37–49. doi: 10.1016/j.ajhg.2017.05.014
Dey, R., Zhou, W., Kiiskinen, T., Havulinna, A., Elliott, A., Karjalainen, J., et al. (2020). An efficient and accurate frailty model approach for genome-wide survival association analysis controlling for population structure and relatedness in large-scale biobanks. bioRxiv [Preprint] doi: 10.1101/2020.10.31.358234
Dutta, D., Scott, L., Boehnke, M., and Lee, S. (2019). Multi-SKAT: general framework to test for rare-variant association with multiple phenotypes. Genet. Epidemiol. 43, 4–23. doi: 10.1002/gepi.22156
Dutta, D., VandeHaar, P., Fritsche, L. G., Zöllner, S., Boehnke, M., Scott, L. J., et al. (2021). A powerful subset-based method identifies gene set associations and improves interpretation in UK Biobank. Am. J. Hum. Genet. 108, 669–681. doi: 10.1016/j.ajhg.2021.02.016
Elliott, L. T., Sharp, K., Alfaro-Almagro, F., Shi, S., Miller, K. L., Douaud, G., et al. (2018). Genome-wide association studies of brain imaging phenotypes in UK Biobank. Nature 562, 210–216. doi: 10.1038/s41586-018-0571-7
Firth, D. (1993). Bias reduction of maximum likelihood estimates. Biometrika 80, 27–38. doi: 10.1093/biomet/80.1.27
Fritsche, L. G., Gruber, S. B., Wu, Z., Schmidt, E. M., Zawistowski, M., Moser, S. E., et al. (2018). Association of polygenic risk scores for multiple cancers in a phenome-wide study: results from the Michigan Genomics Initiative. Am. J. Hum. Genet. 102, 1048–1061.
Fry, A., Littlejohns, T. J., Sudlow, C., Doherty, N., Adamska, L., Sprosen, T., et al. (2017). Comparison of sociodemographic and health-related characteristics of UK Biobank participants with those of the general population. Am. J. Epidemiol. 186, 1026–1034.
Gagliano Taliun, S. A., VandeHaar, P., Boughton, A. P., Welch, R. P., Taliun, D., Schmidt, E. M., et al. (2020). Exploring and visualizing large-scale genetic associations by using PheWeb. Nat. Genet. 52, 550–552. doi: 10.1038/s41588-020-0622-5
Gauderman, W. J., Mukherjee, B., Aschard, H., Hsu, L., Lewinger, J. P., Patel, C. J., et al. (2017). Update on the state of the science for analytical methods for gene-environment interactions. Am. J. Epidemiol. 186, 762–770. doi: 10.1093/aje/kwx228
Gauderman, W. J., Zhang, P., Morrison, J. L., and Lewinger, J. P. (2013). Finding novel genes by testing G x E interactions in a genome-wide association study. Genet. Epidemiol. 37, 603–613. doi: 10.1002/gepi.21748
Gilmour, A. R., Thompson, R., and Cullis, B. R. (1995). Average information REML: an efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51, 1440–1450. doi: 10.2307/2533274
Greely, H. T. (2007). The uneasy ethical and legal underpinnings of large-scale genomic biobanks. Annu. Rev. Genomics Hum. Genet. 8, 343–364.
Häyrinen, K., Saranto, K., and Nykänen, P. (2008). Definition, structure, content, use and impacts of electronic health records: a review of the research literature. Int. J. Med. Inform. 77, 291–304.
He, L., and Kulminski, A. M. (2020). Fast algorithms for conducting large-scale gwas of age-at-onset traits using cox mixed-effects models. Genetics 215, 41–58.
He, Z., Xu, B., Lee, S., and Ionita-Laza, I. (2017a). Unified sequence-based association tests allowing for multiple functional annotations and meta-analysis of noncoding variation in metabochip data. Am. J. Hum. Genet. 101, 340–352. doi: 10.1016/j.ajhg.2017.07.011
He, Z., Zhang, M., Lee, S., Smith, J. A., Kardia, S. L. R., Roux, V. D., et al. (2017b). Set-based tests for the gene–environment interaction in longitudinal studies. J. Am. Stat. Assoc. 112, 966–978.
Huang, Y.-T., Heist, R. S., Chirieac, L. R., Lin, X., Skaug, V., Zienolddiny, S., et al. (2009). Genome-wide analysis of survival in early-stage non-small-cell lung cancer. J. Clin. Oncol. 27, 2660–2667. doi: 10.1200/JCO.2008.18.7906
Ionita-Laza, I., Lee, S., Makarov, V., Buxbaum, J. D., and Lin, X. (2013). Sequence kernel association tests for the combined effect of rare and common variants. Am. J. Hum. Genet. 92, 841–853.
Jarque, C. M., and Bera, A. K. (1980). Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 6, 255–259. doi: 10.1016/0165-1765(80)90024-5
Jiang, L., Zheng, Z., Qi, T., Kemper, K. E., Wray, N. R., Visscher, P. M., et al. (2019). A resource-efficient tool for mixed model association analysis of large-scale data. Nat. Genet. 51, 1749–1755
Kaasschieter, E. F. (1988). Preconditioned conjugate gradients for solving singular systems. J. Comput. Appl. Math. 24, 265–275.
Kang, H. M., Sul, J. H., Service, S. K., Zaitlen, N. A., Kong, S.-Y., Freimer, N. B., et al. (2010). Variance component model to account for sample structure in genome-wide association studies. Nat. Genet. 42, 348–354. doi: 10.1038/ng.548
Kapoor, M., Wang, J.-C., Wetherill, L., Le, N., Bertelsen, S., Hinrichs, A. L., et al. (2014). Genome-wide survival analysis of age at onset of alcohol dependence in extended high-risk COGA families. Drug Alcohol Depend. 142, 56–62.
Kooperberg, C., and LeBlanc, M. (2008). Increasing the power of identifying gene× gene interactions in genome-wide association studies. Genet. Epidemiol. 32, 255–263.
Krokstad, S., Langhammer, A., Hveem, K., Holmen, T. L., Midthjell, K., Stene, T. R., et al. (2013). Cohort profile: the HUNT study. Norway. Int. J. Epidemiol. 42, 968–977. doi: 10.1093/ije/dys095
Lam, M., Trampush, J. W., Yu, J., Knowles, E., Davies, G., Liewald, D. C., et al. (2017). Large-scale cognitive GWAS meta-analysis reveals tissue-specific neural expression and potential nootropic drug targets. Cell Rep. 21, 2597–2613.
Lee, S., Abecasis, G. R., Boehnke, M., and Lin, X. (2014). Rare-variant association analysis: study designs and statistical tests. Am. J. Hum. Genet. 95, 5–23. doi: 10.1016/j.ajhg.2014.06.009
Lee, S., Emond, M. J., Bamshad, M. J., Barnes, K. C., Rieder, M. J., Nickerson, D. A., et al. (2012a). Optimal unified approach for rare-variant association testing with application to small-sample case-control whole-exome sequencing studies. Am. J. Hum. Genet. 91, 224–237.
Lee, S., Fuchsberger, C., Kim, S., and Scott, L. (2016). An efficient resampling method for calibrating single and gene-based rare variant association analysis in case–control studies. Biostatistics 17, 1–15.
Lee, S., Teslovich, T. M., Boehnke, M., and Lin, X. (2013). General framework for meta-analysis of rare variants in sequencing association studies. Am. J. Hum. Genet. 93, 42–53.
Lee, S., Wu, M. C., and Lin, X. (2012b). Optimal tests for rare variant effects in sequencing association studies. Biostatistics 13, 762–775.
Li, B., and Leal, S. M. (2008). Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am. J. Hum. Genet. 83, 311–321.
Li, X., Li, Z., Zhou, H., Gaynor, S. M., Liu, Y., Chen, H., et al. (2020). Dynamic incorporation of multiple in silico functional annotations empowers rare variant association analysis of large whole-genome sequencing studies at scale. Nat. Genet. 52, 969–983. doi: 10.1038/s41588-020-0676-4
Liang, Z., Qiu, Y., and Schnable, J. C. (2020). Genome–phenome wide association in maize and arabidopsis identifies a common molecular and evolutionary signature. Mol. Plant 13, 907–922. doi: 10.1016/j.molp.2020.03.003
Lin, X., Lee, S., Wu, M. C., Wang, C., Chen, H., Li, Z., et al. (2016). Test for rare variants by environment interactions in sequencing association studies. Biometrics 72, 156–164.
Lippert, C., Listgarten, J., Liu, Y., Kadie, C. M., Davidson, R. I., and Heckerman, D. (2011). FaST linear mixed models for genome-wide association studies. Nat. Methods 8, 833–835.
Liu, Y., Chen, S., Li, Z., Morrison, A. C., Boerwinkle, E., and Lin, X. (2019). Acat: a fast and powerful p value combination method for rare-variant analysis in sequencing studies. Am. J. Hum. Genet. 104, 410–421.
Loh, P. R., Tucker, G., Bulik-Sullivan, B. K., Vilhjalmsson, B. J., Finucane, H. K., Salem, R. M., et al. (2015). Efficient Bayesian mixed-model analysis increases association power in large cohorts. Nat. Genet. 47, 284–290. doi: 10.1038/ng.3190
Ma, C., Blackwell, T., Boehnke, M., and Scott, L. J. (2013). Recommended joint and meta-analysis strategies for case-control association testing of single low-count variants. Genet. Epidemiol. 37, 539–550. doi: 10.1002/gepi.21742
Ma, C., Boehnke, M., Lee, S., and Go, T. D. I. (2015). evaluating the calibration and power of three gene-based association tests of rare variants for the X chromosome. Genet. Epidemiol. 39, 499–508.
Mbatchou, J., Barnard, L., Backman, J., Marcketta, A., Kosmicki, J. A., Ziyatdinov, A., et al. (2021). Computationally efficient whole-genome regression for quantitative and binary traits. Nat. Genet. doi: 10.1038/s41588-021-00870-7 [Epub ahead of print].
McAllister, K., Mechanic, L. E., Amos, C., Aschard, H., Blair, I. A., Chatterjee, N., et al. (2017). Current challenges and new opportunities for gene-environment interaction studies of complex diseases. Am. J. Epidemiol. 186, 753–761. doi: 10.1093/aje/kwx227
Morgenthaler, S., and Thilly, W. G. (2007). A strategy to discover genes that carry multi-allelic or mono-allelic risk for common diseases: a cohort allelic sums test (CAST). Mutat. Res. 615, 28–56.
Murcray, C. E., Lewinger, J. P., and Gauderman, W. J. (2008). Gene-environment interaction in genome-wide association studies. Am. J. Epidemiol. 169, 219–226.
Nagai, A., Hirata, M., Kamatani, Y., Muto, K., Matsuda, K., Kiyohara, Y., et al. (2017). Overview of the BioBank Japan Project: study design and profile. J. Epidemiol. 27, S2–S8.
Neale, B. M., Rivas, M. A., Voight, B. F., Altshuler, D., Devlin, B., Orho-Melander, M., et al. (2011). Testing for an unusual distribution of rare variants. PLoS Genet 7:e1001322. doi: 10.1371/journal.pgen.1001322
Nielsen, J. B., Thorolfsdottir, R. B., Fritsche, L. G., Zhou, W., Skov, M. W., Graham, S. E., et al. (2018). Biobank-driven genomic discovery yields new insight into atrial fibrillation biology. Nat. Genet. 50, 1234–1239. doi: 10.1038/s41588-018-0171-3
O’Reilly, P. F., Hoggart, C. J., Pomyen, Y., Calboli, F. C. F., Elliott, P., Jarvelin, M.-R., et al. (2012). MultiPhen: joint model of multiple phenotypes can increase discovery in GWAS. PLoS One 7:e34861. doi: 10.1371/journal.pone.0034861
Pan, W. (2009). Asymptotic tests of association with multiple SNPs in linkage disequilibrium. Genet. Epidemiol. 33, 497–507.
Pushpakom, S., Iorio, F., Eyers, P. A., Escott, K. J., Hopper, S., Wells, A., et al. (2019). Drug repurposing: progress, challenges and recommendations. Nat. Rev. Drug Discov. 18, 41–58.
Ray, D., Pankow, J. S., and Basu, S. (2016). USAT: a Unified Score-based Association Test for Multiple Phenotype-Genotype Analysis. Genet. Epidemiol. 40, 20–34. doi: 10.1002/gepi.21937
Rizvi, A. A., Karaesmen, E., Morgan, M., Wang, J., Preus, L., Sovic, M., et al. (2018). gwasurvivr: an R package for genome-wide survival analysis. Bioinformatics 35, 1968–1970. doi: 10.1093/bioinformatics/bty920
Roden, D. M., Masys, D. R., Crawford, D. C., Wang, D., Pulley, J. M., Denny, J. C., et al. (2010). PheWAS: demonstrating the feasibility of a phenome-wide scan to discover gene–disease associations. Bioinformatics 26, 1205–1210.
Scott, R. H., Fowler, T. A., and Caulfield, M. (2019). Genomic medicine: time for health-care transformation. Lancet 394, 454–456.
Stephens, M. (2013). A unified framework for association analysis with multiple related phenotypes. PLoS One 8:e65245. doi: 10.1371/journal.pone.0065245
Su, Y.-R., Di, C.-Z., and Hsu, L. (2017). A unified powerful set-based test for sequencing data analysis of GxE interactions. Biostatistics 18, 119–131.
Thornton, T., Tang, H., Hoffmann, T. J., Ochs-Balcom, H. M., Caan, B. J., and Risch, N. (2012). Estimating kinship in admixed populations. Am. J. Hum. Genet. 91, 122–138. doi: 10.1016/j.ajhg.2012.05.024
Torkamani, A., Wineinger, N. E., and Topol, E. J. (2018). The personal and clinical utility of polygenic risk scores. Nat. Rev. Genet. 19, 581–590.
Verbanck, M., Chen, C.-Y., Neale, B., and Do, R. (2018). Detection of widespread horizontal pleiotropy in causal relationships inferred from Mendelian randomization between complex traits and diseases. Nat. Genet. 50, 693–698.
Wang, X., Lim, E., Liu, C.-T., Sung, Y. J., Rao, D. C., Morrison, A. C., et al. (2020). Efficient gene–environment interaction tests for large biobank-scale sequencing studies. Genet. Epidemiol. 44, 908–923. doi: 10.1002/gepi.22351
Wolford, B. N., Willer, C. J., and Surakka, I. (2018). Electronic health records: the next wave of complex disease genetics. Hum. Mol. Genet. 27, R14–R21. doi: 10.1093/hmg/ddy081
Wu, M. C., Lee, S., Cai, T., Li, Y., Boehnke, M., and Lin, X. (2011). Rare-variant association testing for sequencing data with the sequence kernel association test. Am. J. Hum. Genet. 89, 82–93.
Yang, J., Lee, S. H., Goddard, M. E., and Visscher, P. M. (2011). GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88, 76–82. doi: 10.1016/j.ajhg.2010.11.011
Yang, J., Zaitlen, N. A., Goddard, M. E., Visscher, P. M., and Price, A. L. (2014). Advantages and pitfalls in the application of mixed-model association methods. Nat. Genet. 46, 100–106.
Zhang, Y., and Pan, W. (2015). Principal component regression and linear mixed model in association analysis of structured samples: competitors or complements? Genet. Epidemiol. 39, 149–155. doi: 10.1002/gepi.21879
Zhao, Z., Bi, W., Zhou, W., VandeHaar, P., Fritsche, L. G., and Lee, S. (2020). UK Biobank Whole-Exome Sequence Binary Phenome Analysis with Robust Region-Based Rare-Variant Test. Am. J. Hum. Genet. 106, 3–12. doi: 10.1016/j.ajhg.2019.11.012
Zheng, X., and Davis, J. W. (2020). SAIGEgds—an efficient statistical tool for large-scale PheWAS with mixed models. Bioinformatics 37, 728–730. doi: 10.1093/bioinformatics/btaa731
Zhou, W., Nielsen, J. B., Fritsche, L. G., Dey, R., Gabrielsen, M. E., Wolford, B. N., et al. (2018). Efficiently controlling for case-control imbalance and sample relatedness in large-scale genetic association studies. Nat. Genet. 50, 1335–1341. doi: 10.1038/s41588-018-0184-y
Zhou, W., Zhao, Z., Nielsen, J. B., Fritsche, L. G., LeFaive, J., Gagliano Taliun, S. A., et al. (2020). Scalable generalized linear mixed model for region-based association tests in large biobanks and cohorts. Nat. Genet. 52, 634–639. doi: 10.1038/s41588-020-0621-6
Keywords: phenome-wide association studies, electronic health records-EHR, saddlepoint approximation, biobank data analysis, unbalanced phenotypic distribution, genetic relatedness, mixed model approaches
Citation: Bi W and Lee S (2021) Scalable and Robust Regression Methods for Phenome-Wide Association Analysis on Large-Scale Biobank Data. Front. Genet. 12:682638. doi: 10.3389/fgene.2021.682638
Received: 18 March 2021; Accepted: 17 May 2021;
Published: 15 June 2021.
Edited by:
Chuhsing Kate Hsiao, National Taiwan University, TaiwanReviewed by:
Zhikai Liang, University of Minnesota Twin Cities, United StatesCopyright © 2021 Bi and Lee. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wenjian Bi, d2VuamlhbmJAdW1pY2guZWR1; Seunggeun Lee, bGVlNzgwN0BzbnUuYWMua3I=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.