Xiong Yang1
Xumin Ni
Shuhua Xu- 1Key Laboratory of Computational Biology, Chinese Academy of Sciences (CAS) and Max Planck Society (MPG) Partner Institute for Computational Biology, Shanghai Institute of Nutrition and Health, University of Chinese Academy of Sciences, Chinese Academy of Sciences, Shanghai, China
- 2Department of Mathematics, School of Science, Beijing Jiaotong University, Beijing, China
- 3Institute of Applied Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, China
- 4School of Life Science and Technology, ShanghaiTech University, Shanghai, China
- 5Center for Excellence in Animal Evolution and Genetics, Chinese Academy of Sciences, Kunming, China
- 6Henan Institute of Medical and Pharmaceutical Sciences, Zhengzhou University, Zhengzhou, China
- 7Collaborative Innovation Center of Genetics and Development, Fudan University, Shanghai, China
Background: Population admixture is a common phenomenon in humans, animals, and plants, and it plays a very important role in shaping individual genetic architecture and population genetic diversity. Inference of population admixture, however, is very challenging and typically relies on in silico simulation. We are aware of the lack of a computerized tool for such a purpose. A simulator capable of generating data under various complex admixture scenarios would facilitate the study of recombination, linkage disequilibrium, ancestry tracing, and admixture dynamics in admixed populations. We described such a simulator here.
Results: We developed a forward-time simulator (AdmixSim) under the standard Wright Fisher model. It can simulate the following admixed populations: (1) multiple ancestral populations; (2) multiple waves of admixture events; (3) fluctuating population size; and (4) admixtures of fluctuating proportions. Analysis of the simulated data by AdmixSim showed that our simulator can quickly and accurately generate data resembling real-world values. We included in AdmixSim all possible parameters that would allow users to modify and simulate any kind of admixture scenario easily, so it is very flexible. AdmixSim records recombination break points and traces of each chromosomal segment from different ancestral populations, with which users can easily perform further analysis and comparative studies with empirical data.
Conclusions: AdmixSim facilitates the study of population admixture by providing a simulation framework with the flexible implementation of various admixture models and parameters.
Background
Demographic history, together with natural selection, resulted in population differentiation especially in different continental populations. Nevertheless, the population admixture that has occurred over the past few millennia shaped the face of the modern world. Population isolations and migrations have been common phenomena through the history of anatomically modern humans. Hundreds of admixture events have been inferred in the recent 4,000 years in human history (Hellenthal et al., 2014), which plays an important role in shaping the genetic diversity of modern humans. The study of population admixture will shed light on the human genetic history, and has many implications in medical research. However, inferring population admixture relies heavily on simulations. In silico simulation is useful in testing population genetic models, studying recombination, assessing linkage disequilibrium, tracking ancestry, and evaluating admixture dynamics in admixed populations. Many forward- and backward-time simulators (Hudson, 2002; Guillaume and Rougemont, 2006; Liang et al., 2007; Hernandez, 2008; Chen et al., 2009; Hoban et al., 2011) have been developed in recent years. Some backward-time simulators (most of which are coalescent-based), for example, ms (Hudson, 2002), can simulate population admixtures in simple scenarios. However, it is very difficult or even impossible to simulate an admixed population with a fluctuating population size or fluctuating gene flow generation after generation. Some forward-time simulators, for example, SFS_CODE (Hernandez, 2008), can also simulate admixtures in simple scenarios, but they suffer from the same problems as coalescent-based simulators. To our knowledge, there is no simulator that focuses on simulating and tracking the dynamics of recombination and ancestry in admixed populations, and allowing change population size and gene flow generation after generation.
Implementation
A Generalized Admixture Model
Population admixture occurs when gene flow moves from ancestral populations either continuously or discontinuously. To render the modeling of population admixture more general, we can model this process generation by generation, in which, if the admixed population does not receive further gene influx in a particular generation, we set the strength of gene flow to 0. A given admixed population with K (K > 1) ancestral populations formed T (T > 0) generations ago can be fully modeled by a K × T matrix M. The rows (i) refers to the ancestral populations and the columns (j) refers to the generations. mij in M denotes the strength of gene flow from the jth ancestral population at ith generation, where mij fulfills two requirements: (1) 0 ≤ mij ≤ 1; and (2) ∑mij = 1 when i = 1.
Simulation Process
Because novel mutations and selections have negligible impacts on shaping the genetic diversity of a recent admixed population on the whole genome scale, we disregarded mutations and selections in our simulation here. Recombination is modeled as a Poison process along the chromosome (chromosomal end is ignored) with rate 1 (unit in Morgan). At a specific generation, i, the size of the admixed population is N, and the rate of gene flow from the jth ancestral population is mij, we generate individuals in the current generation by two steps.
1) For gene flow from the jth ancestral population, we randomly sample N×mij individuals from the jth ancestral population and repeat this procedure for all the gene flow events in the current generation, and the rest of the individuals are randomly sampled from the admixed population in the previous generation;
2) With the sample pool generated in step 1, we randomly choose two individuals in the pool, then randomly choose one chromosome from one individual. We pair and recombine it with the one randomly chosen in another individual to form a new chromosome pair. We repeat these procedures until N individuals are generated.
Individuals are generated using the two steps generation by generation. At the end of the simulation, n individuals are randomly sampled; and the start and end positions and the ancestry of each chromosome segment are recorded. The haplotypes for each individual are also recorded for further study.
Results
A previous study established the theoretical distribution of the length of the ancestral chromosomal segment (LACS) under an HI model (Jin et al., 2014). It is not difficult to test the performance of our simulator. Under the HI model, the distribution of LACS from the ancestral population with ancestry contribution m is (1-m)Te−(1−m)Tx. Here, we simulated an admixed population with constant N = 5,000, admixed 100 generations ago, following the HI model, in which ancestral population 1 contributes 25% of the total ancestry. As expected, the distribution of LACS simulated (dots) matches the theoretical distribution of LACS (dashed line) well for ancestries from both ancestral populations 1 and 2 (Figure 1).
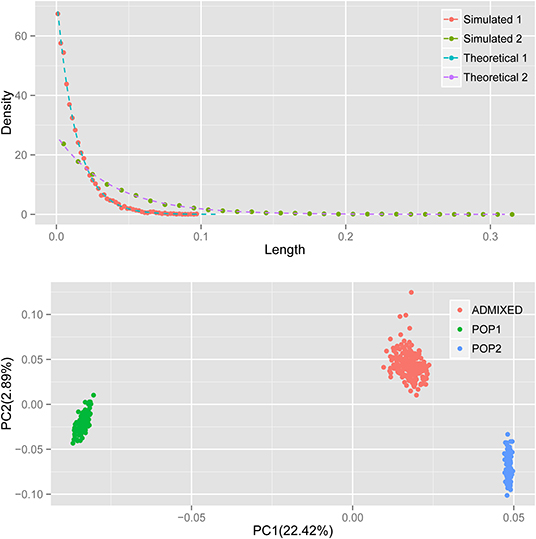
Figure 1. The distribution of LACS and PCA of the simulated data. Top: red and green dots denote the distribution of LACS from ancestral population 1 and ancestral population 2; blue and purple dashed lines are the theoretical distributions of LACS derived from (1-m)Te−(1−m)Tx, where m is the ancestry contribution of that ancestral population and T is the generation since admixture. Bottom: green and blue dots denote the individuals from ancestral populations, and the red dots denote individuals in the admixed population.
Principal component analysis (PCA) with smartpca (Patterson et al., 2006; Price et al., 2006) shows that first principal component (PC) separates ancestral population 1 and ancestral population 2, just as expected and usually observed in real data. Simulated individuals from the two ancestral populations cluster within their own groups, and the admixed individuals cluster between two ancestral populations along PC1 (Figure 1). Because ancestral population 2 contributes more to the admixed population, the distance between individual from admixed population and individual from ancestral population 2 is much closer than that from ancestral population 1 to the admixed individuals. All these results observed in the simulated data resembled what can be observed in real data, which indicates our simulator does generate correct datasets that resemble the real one.
In the results of the ADMIXTURE analysis (Alexander et al., 2009) of the simulated data, we can clearly observe the assignment of ancestries of the admixed individuals: blue represents ancestry from ancestral population 1 and green represents ancestry from ancestral population 2. The contributions from ancestral population 1 were found to vary from 18 to 30% (Supplementary Figure 1), which also resembles what was observed in real data.
The time complexity of AdmixSim is O(L), O(N), and O(T2). In theory, the running time of AdmixSim is linearly determined by the chromosome length (L) and the population size (N) simulated; and quadratic depends on the generations since admixture (T). Benchmark tests are carried on a laptop with an Intel CoreTM Duo CPU @ 2.0 GHz, 2 Gb RAM, and Ubuntu 12.04 32-bit operation system. Running time is recorded by Linux command time, and the user time is collected and compared. Each time, only one parameter is allowed to be variable. For example, to assess the impact of generation since admixture on running time, we ran a series of tests in which generation ranges from start to end, increased by 1 step size each time. The details of the parameter settings for each test can be found in Table 1. The results show that the AdmixSim runs very fast even with large population size, and the running time shows a trend as expected (Figure 2).
Table 1. Detailed parameters of benchmark test.
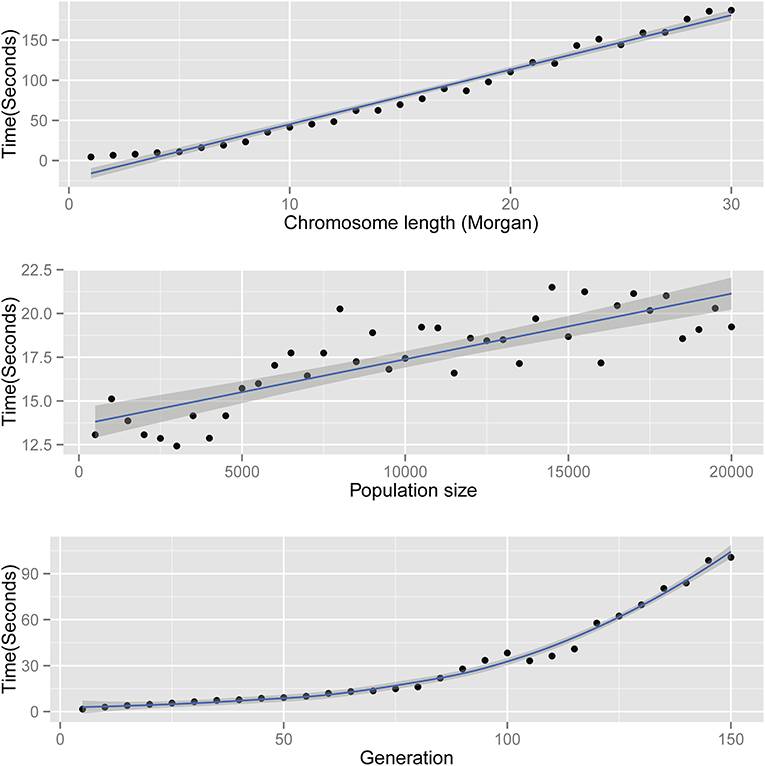
Figure 2. Running time of AdmixSim. Top: running time versus chromosome length simulated; middle: running time vs. population size simulated; and bottom: running time vs. generation since admixture.
Conclusions
Here, we developed a fast and flexible simulator suitable for modeling various and complex scenarios involving population admixture. This system can simulate an admixed population under several sets of conditions: (1) multiple ancestral populations; (2) multiple waves of admixture events; (3) fluctuating population sizes; and (4) fluctuating admixture proportions. With the AdmixSim, the user can not only easily simulate an admixed population under the three typical admixture models, i.e., hybrid isolation (HI) model, gradual admixture (GA) model, and continuous gene flow (CGF) model as described in previous studies (Jin et al., 2012), but also simulate admixed populations with more complex scenarios, for example, three-way admixture with multiple waves of gene flow. In several recent studies, we have applied this simulator to generate simulation data under many of population admixture scenarios, such as GA model, CGF model, and multiple-wave admixture model (Ni et al., 2016, 2018, 2019; Feng et al., 2017). The distribution of ancestral segments based on simulated data matched well with the theoretical distribution, which showed the reliability and power of our simulator. This simulator will facilitate the study of population admixture and greatly help us to understand the processes of human migration, admixture, and evolution, which provides further insight into both evolutionary and medical studies of human genetic diversity.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author/s.
Author Contributions
SX conceived the study. XY designed and implemented the AdmixSim with contribution from XN, WG, and YZ. XY and SX wrote the manuscript. XY, XN, and WG analyzed the time complexity and the performance of the simulator with contribution from KY. All authors read and approved the final manuscript.
Funding
This study was supported by the National Science Fund for Distinguished Young Scholars (31525014), the National Natural Science Foundation of China (NSFC) Grant No. (32030020, 91731303, 31771388, 31961130380, 31900418, 32041008, and 11801027), the Strategic Priority Research Program (XDB38000000) and Key Research Program of Frontier Sciences (QYZDJ-SSW-SYS009) of the Chinese Academy of Sciences (CAS), the UK Royal Society-Newton Advanced Fellowship (NAF\R1\191094), the National Key Research and Development Program (2016YFC0906403), the Shanghai Municipal Science and Technology Major Project (2017SHZDZX01), and the Fundamental Research Funds for the Central Universities (2020RC001).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank LetPub (www.letpub.com) for its linguistic assistance during the preparation of the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fgene.2020.601439/full#supplementary-material
Supplementary Figure 1. ADMIXTURE analysis of simulated data. Blue and green denote two ancestral components and the admixed individuals show combination of the ancestries from two ancestral populations.
Supplementary Text 1. Tutorials for AdmixSim.
Abbreviations
CGF, Continuous gene flow; GA, Gradual admixture; HI, Hybrid isolation; LACS, Length of ancestral chromosomal segment; PCA, Principal component analysis; PC, Principal component.
References
Alexander, D. H., Novembre, J., and Lange, K. (2009). Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 19, 1655–1664. doi: 10.1101/gr.094052.109
Chen, G. K., Marjoram, P., and Wall, J. D. (2009). Fast and flexible simulation of DNA sequence data. Genome Res. 19, 136–142. doi: 10.1101/gr.083634.108
Feng, Q., Lu, Y., Ni, X., Yuan, K., Yang, Y., Yang, X., et al. (2017). Genetic history of xinjiang's uyghurs suggests bronze age multiple-way contacts in eurasia. Mol. Biol. Evol. 34, 2572–2582. doi: 10.1093/molbev/msx177
Guillaume, F., and Rougemont, J. (2006). Nemo: an evolutionary and population genetics programming framework. Bioinformatics 22, 2556–2557. doi: 10.1093/bioinformatics/btl415
Hellenthal, G., Busby, G. B., Band, G., Wilson, J. F., Capelli, C., Falush, D., et al. (2014). A genetic atlas of human admixture history. Science 343, 747–751. doi: 10.1126/science.1243518
Hernandez, R. D. (2008). A flexible forward simulator for populations subject to selection and demography. Bioinformatics 24, 2786–2787. doi: 10.1093/bioinformatics/btn522
Hoban, S., Bertorelle, G., and Gaggiotti, O. E. (2011). Computer simulations: tools for population and evolutionary genetics. Nat Rev Genet. 13, 110–122. doi: 10.1038/nrg3130
Hudson, R. R. (2002). Generating samples under a wright-fisher neutral model of genetic variation. Bioinformatics 18, 337–338. doi: 10.1093/bioinformatics/18.2.337
Jin, W., Li, R., Zhou, Y., and Xu, S. (2014). Distribution of ancestral chromosomal segments in admixed genomes and its implications for inferring population history and admixture mapping. Eur. J. Hum. Genet. 22, 930–937. doi: 10.1038/ejhg.2013.265
Jin, W., Wang, S., Wang, H., Jin, L., and Xu, S. (2012). Exploring population admixture dynamics via empirical and simulated genome-wide distribution of ancestral chromosomal segments. Am. J. Hum. Genet. 91, 849–862. doi: 10.1016/j.ajhg.2012.09.008
Liang, L., Zollner, S., and Abecasis, G. R. (2007). GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics 23, 1565–1567. doi: 10.1093/bioinformatics/btm138
Ni, X., Yang, X., Guo, W., Yuan, K., Zhou, Y., Ma, Z., et al. (2016). Length distribution of ancestral tracks under a general admixture model and its applications in population history inference. Sci. Rep. 6:20048. doi: 10.1038/srep26367
Ni, X., Yuan, K., Liu, C., Feng, Q., Tian, L., Ma, Z., et al. (2019). MultiWaver 2.0: modeling discrete and continuous gene flow to reconstruct complex population admixtures. Eur. J. Hum. Genet. 27, 133–139. doi: 10.1038/s41431-018-0259-3
Ni, X., Yuan, K., Yang, X., Feng, Q., Guo, W., Ma, Z., et al. (2018). Inference of multiple-wave admixtures by length distribution of ancestral tracks. Heredity 121, 52–63. doi: 10.1038/s41437-017-0041-2
Patterson, N., Price, A. L., and Reich, D. (2006). Population structure and eigenanalysis. PLoS Genet. 2:e190. doi: 10.1371/journal.pgen.0020190
Keywords: simulation, population admixture, genetic ancestry, Wright Fisher model, admixture model
Citation: Yang X, Yuan K, Ni X, Zhou Y, Guo W and Xu S (2020) AdmixSim: A Forward-Time Simulator for Various Complex Scenarios of Population Admixture. Front. Genet. 11:601439. doi: 10.3389/fgene.2020.601439
Received: 01 September 2020; Accepted: 29 October 2020;
Published: 03 December 2020.
Edited by:
Fernanda Rodrigues-Soares, Universidade Federal do Triângulo Mineiro, BrazilReviewed by:
Giordano Bruno Soares-Souza, Bio Bureau Biotechnology, BrazilGilderlanio Santana Araújo, Federal University of Pará, Brazil
Copyright © 2020 Yang, Yuan, Ni, Zhou, Guo and Xu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shuhua Xu, xushua@picb.ac.cn