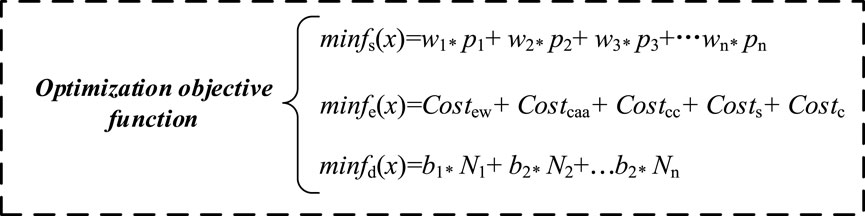Optimization design of highway route based on deep learning

Introduction: In recent years, the total mileage and line density of China’s highways have increased year by year. It is estimated that by 2026, the total mileage of national highways will exceed 5.74 million kilometers. An efficient highway network is crucial for a country’s move towards traffic modernization, economic development, and improvement of people's livelihoods. The highway route is the basic structure of the highway network, determining whether the highway can maximize its economic and traffic effects. Therefore, research on highway route design holds significant engineering value. Highway planning is a complex issue involving a wide range of factors. Especially with the increasing awareness of environmental protection, it is necessary to consider natural problems in addition to technical and economic costs.

Methods: This paper first points out the important position of highway route research in highway rules, summarizes the research status at home and abroad, and lists conventional highway planning measures. It then discusses the optimization design based on vehicle running speed and driver comfort, and introduces related theories of deep learning and their applicability to multi-objective optimization problems. Finally, aiming at the problem of highway route planning influenced by many factors, a deep learning strategy based on a multi-objective genetic algorithm is adopted, and its multi-objective optimization model and optimization objective function are presented.

Results: The proposed deep learning strategy based on a multi-objective genetic algorithm is a new attempt to combine genetic algorithms with deep learning in highway route planning to solve its multi-objective comprehensive optimization problem. The results indicate that this strategy can determine the best route scheme by optimizing technology while satisfying external constraints, thereby achieving the optimal solution in terms of technology and economy, and improving the overall efficiency and sustainability of the highway.

Discussion: This study provides a reference for the application of deep learning and other nonlinear multi-objective optimization research, aiding the research on highway route optimization design. By combining multi-objective genetic algorithms with deep learning, it effectively solves various multi-objective nonlinear problems, providing new methods and tools for highway route planning.

1 Introduction

“To get rich, build roads first” is an important guiding ideology of China’s long-standing economic development. Since the founding of the People’s Republic of China, China has been vigorously developing transportation infrastructure, among which highway construction is the most important mode of transportation. Since the beginning of the 21st century, with the progress and development of science and technology, China has made great breakthroughs in the technology and equipment of highway infrastructure, but these are all progress in the process of construction and implementation. In the decision-making stage of highway foundation project, the key factor to determine the investment volume, construction quality and economic benefit of later operation of highway construction project is the quality of route scheme (Li et al., 2018; Fangqu and June 2019). At present, China’s highway network has taken shape, but there are still some outstanding problems, such as insufficient total amount and structural contradictions. By the end of 2020, there are still more than 900 counties in China that are not covered by national highways, and 18 newly-added cities with urban population of more than 200,000 and 29 prefecture-level administrative centers are not connected with national highways (Liu, 1997). According to the National Highway Network Plan, by 2030, there will be 26,000 km of national highways to be built, and 100,000 km of ordinary national and provincial trunk highways to be upgraded. China’s highway development is at the critical stage of accelerating the network formation (Zhu et al., 2020). Thus obtained roading. It can only be strengthened, not weakened. It is particularly important to choose an excellent route scheme in the decision-making stage of highway construction (Lin, 2011; Šetinc et al., 2015). The main basis of highway route selection is alignment design, and the quality of route selection determines the quality of alignment design. We usually regard them as a whole as the decisive factor of route selection, and strive to achieve smooth alignment, broad vision, safe and comfortable driving (Kang et al., 2012).

Throughout the development process of route optimization all over the world, the concept of route optimization design was first put forward in the middle of 20th century, and the developed countries such as the United States, the former Soviet Union and Germany put forward the program system of profile optimization. In 1973, the Organization for Economic Cooperation and Development (OECD) integrated the route optimization procedures of Britain, Germany, Denmark and France, and conducted an application test in the construction of a new 14 km expressway in Italy (Solanki et al., 1998; Jha and Schonfeld, 2000; Sabatino et al., 2015). The final test results show that the optimization design of the longitudinal section line can save about 10% of the main materials of highway construction, such as cement and aggregate, which has great economic value for highway construction, and also reflects that the optimization design of the line has very high research value. After the 1970s, with the development of computer technology, the design of basic engineering construction began to enter digital transformation, and the optimization design of lines began to transform from graphic design to three-dimensional design (Jha and Schonfeld, 2004; Jha and Kim, 2006). More countries have made breakthroughs in the optimization design of lines. Since 1979, our country has also carried out a lot of research on the optimization technology of longitudinal section, plane and three-dimensional line shape of line optimization design, and developed many excellent optimization programs.

Route optimization encompasses a broader set of objectives including construction costs, environmental impact, and long-term sustainability. When considering route optimization from the user’s perspective, the primary goal is to find the most efficient path that minimizes travel time, fuel consumption, or other user-related costs. Key elements include: Often the simplest form of optimization, focusing on the minimal distance between two points. Incorporates factors such as speed limits, traffic conditions, and road types to minimize the time spent traveling. Optimizes for the least fuel consumption or toll costs, balancing distance with fuel economy and toll expenses. Considers the smoothness of the route, avoiding rough terrains, frequent stops, and other inconveniences. These optimizations are typically achieved using algorithms that leverage real-time data, historical traffic patterns, and predictive modeling to provide users with the best possible routes.

For builders and infrastructure designers, route optimization involves a more complex and multifaceted approach. The objectives expand beyond immediate efficiency to include long-term sustainability, economic viability, and environmental considerations. Key components include: Minimizing the expenses involved in building the route, including materials, labor, and equipment. Reducing the ecological footprint by considering factors such as deforestation, pollution, and wildlife disruption. Navigating through or around natural barriers such as mountains, rivers, and urban areas. Ensuring the route remains functional and efficient in the long term, accounting for maintenance, upgrades, and resilience to environmental changes.

Research has shown that many highways fail to attract traffic post-construction because they did not adequately consider user behavior during the design phase. This issue highlights the importance of incorporating path choice models into the planning and design process. Di Gangi and Polimeni (2022) examines this problem in depth. Their research, “Path Choice Models in Stochastic Assignment: Implementation and Comparative Analysis,” focuses on how users’ route choices are influenced by various factors such as travel time, cost, and convenience. They utilized stochastic user equilibrium (SUE) models to better predict and understand these choices. These models take into account the randomness in users’ perceptions and preferences, offering a more realistic approach to traffic assignment and route planning. By applying these models, planners can design highway routes that align more closely with actual user preferences, thereby increasing the likelihood that the new roads will be used as intended. This approach helps avoid the costly mistake of building highways that end up underutilized due to a lack of consideration for how users decide on their travel routes (Di Gangi and Polimeni, 2022). Incorporating user behavior modeling into highway route optimization involves using random utility models (RUMs) to simulate decisions based on maximizing perceived utility. This method integrates various determinants of utility, such as travel time, cost, and convenience, which are crucial for understanding and predicting route choice behavior. By leveraging advanced computational techniques such as deep learning and genetic algorithms, planners can achieve a more comprehensive and adaptive optimization process. This ensures that new highways not only meet technical and economic requirements but also align with the preferences and behaviors of the users, ultimately leading to higher traffic volumes and better utilization.

However, because there are many influencing conditions in the implementation of route optimization, the route optimization design in China is rarely applied in the actual highway infrastructure project design (Jesus et al., 2011; Deng et al., 2017; Bongiorno et al., 2019). After a long time of research on line optimization design, the measures to optimize the line design at present are as follows:

(1) The design of line space, such as: the design of plane, horizontal and vertical sections;

(2) Design of line shape, such as: design of line straightness;

(3) Design of line speed limit;

(4) The design of the line landscape.

These are the design measures of the route itself, which together affect the operating speed of the traveling vehicle and the driving experience of the driver, such as comfort and warning. Therefore, it can be concluded that road route optimization is a complex problem involving a variety of factors, including technical, economic and environmental factors. In addition, understanding and incorporating user behavior, especially route choice behavior, is essential for developing effective and realistic models. Users’ route choice decisions have a significant impact on the efficiency and sustainability of highway networks.

Since the 21st century, computer and Internet technologies have entered a period of rapid development, and the development of computerized artificial neural networks has matured. People use it as a research tool of applied mathematics to study the optimal route design scheme in highway construction projects using optimization theory. In this paper, the mature deep learning theory of computer artificial neural network is selected to synthesize the various aspects of optimal route design, combined with the user behavior model, to optimize the running speed of the vehicle and the driving comfort of the driver.

2 Literature review

2.1 Route design

Route optimization design first emerged in the mid-20th century, with developed countries such as the United States, the former Soviet Union, and Germany establishing profile optimization programs. These early efforts focused on enhancing the efficiency and effectiveness of highway route design by integrating various engineering and economic considerations. In 1973, the Organization for Economic Cooperation and Development (OECD) integrated the route optimization procedures of Britain, Germany, Denmark, and France, conducting an application test in constructing a new 14 km expressway in Italy. The test results showed significant economic value, saving about 10% of main materials such as cement and aggregate. This demonstrated the practical benefits of route optimization, highlighting the potential for substantial cost savings in highway construction.

A notable study in this domain is by Billheimer and Gray (1973), which presents a route selection algorithm balancing fixed construction costs and variable user costs in transportation networks (Billheimer and Gray, 1973). This algorithm, designed for a fixed set of nodes with known demand, applies link elimination and insertion criteria to converge to a local optimum. The algorithm’s practical application, demonstrated using a representation of Minneapolis-St. Paul, underscores the importance of balancing cost elements in network design.

Gao et al. (2005) introduced a solution algorithm for the bi-level discrete network design problem, dealing with the selection of link additions to an existing road network under given demand conditions (Gao et al., 2005). The proposed algorithm, addressing the computational difficulties of nonlinear bi-level mixed-integer programming, demonstrated efficiency in minimizing total travel cost while considering route choice behaviors of network users.

Cantarella, Pavone, and Vitetta (2005) discussed heuristics for urban road network design, focusing on lane layout and signal settings (Cantarella et al., 2006). Their methods, employing metaheuristics like Hill Climbing, Simulated Annealing, Tabu Search, Genetic Algorithms, and Path Relinking, were compared by applications to real networks, highlighting the effectiveness of these approaches in optimizing urban road networks.

Urban network design has also evolved, incorporating heuristic multi-criteria techniques based on genetic algorithms. Cantarella and Vitetta (2006) analyzed urban network design through such a heuristic approach, optimizing both network layout and link capacity (Cantarella and Vitetta, 2006). Their method, considering elastic demand with respect to mode choice and incorporating peak period considerations, reflects the complexity of urban route optimization and the need for multi-criteria evaluation.

Russo and Vitetta (2006) proposed a topological method for sorting and reducing solutions to urban network design problems (Russo and Vitetta, 2006). Their approach, which applies cluster analysis based on topological similarity and criteria values, provides a systematic way to identify latent optimal network layouts, further advancing the field of route optimization.

Additionally, Comi and Polimeni (2022) explored path choice models using floating car data (FCD), emphasizing the importance of reliable data collection and model structures that balance forecast accuracy and real-world applicability (Comi and Polimeni, 2022). Their methodology, applied to both passenger and freight transport, highlights the practical benefits of integrating real-time data in route optimization models.

Over time, the development of computer technology significantly advanced route optimization methods, transitioning from graphic design to three-dimensional design. This evolution allowed for more accurate and comprehensive modeling of highway routes, incorporating a broader range of variables and constraints. Despite these advancements, the implementation of route optimization design in China remains limited. The country’s highway network has faced challenges such as insufficient total mileage and structural contradictions, which have hindered the widespread adoption of advanced route optimization techniques. Continued research and development in this area are crucial to overcoming these challenges and fully realizing the benefits of optimized highway route design in China.

2.2 Genetic algorithms

Genetic algorithms (GAs) are widely used in various optimization problems, including highway route optimization. They simulate the process of natural evolution, using operations such as selection, crossover, and mutation to evolve solutions towards the optimal. The fundamental principle behind GAs is to iteratively improve a population of candidate solutions by retaining beneficial traits and discarding less effective ones. This process is analogous to natural selection, where the fittest individuals are more likely to survive and reproduce.

The integration of GAs with other optimization techniques, such as deep learning, further enhances their capabilities. In a study by Turner and Miles (1971), a computer-assisted method was developed for regional route location, marking one of the early applications of GAs in transportation (Turner and Miles, 1971). The book “Genetic Algorithms in Search, Optimization and Machine Learning” by Goldberg (1989) is a seminal work that provides comprehensive coverage of GAs and their applications in various fields, including transportation planning (Goldberg, 1988). Later, Beasley (1993) and Coley (1999) further refined these approaches, demonstrating their practical benefits in optimizing highway alignments (Beasley, 1993; Coley, 1999).

Zhang and Lu (2007) summarized the structural characteristics of the bi-level programming model for CNDP and developed a modern genetic algorithm tailored for solving these problems (ZHANG and Jian, 2007). Their approach demonstrated excellent convergence properties and reliable solutions, confirming the practical applicability of GAs in transportation planning.

Xu, Wei, and Wang (2008) compared the efficacy of simulated annealing (SA) and genetic algorithms in continuous network design problems (CNDP) (Xu et al., 2009). Their findings indicated that while SA is more efficient for high-demand scenarios, GAs reach a more optimal solution in low-demand scenarios despite requiring more computation time.

For highway route design, GAs are particularly effective in addressing complex, multi-objective optimization problems. They help find the best routes by considering multiple conflicting objectives like cost, safety, and environmental impact. For instance, Maji and Jha (2009) explored multi-objective highway alignment optimization using GAs, highlighting their effectiveness in dealing with complex, nonlinear problems (Cascetta, 2009). The flexibility and adaptability of GAs make them well-suited for highway route optimization, as they can efficiently navigate large solution spaces and identify high-quality solutions that balance various design criteria.

A significant advancement in this field is the bi-level model proposed by Madadi et al. (2019) for optimizing road networks accommodating both manual and automated driving (Madadi et al., 2020). Their model formulates the problem as a network design problem and presents an efficient algorithm that meets specific solution requirements, outperforming other methods in all considered criteria.

The work of Shanmugasundaram et al. (2019) applied genetic algorithms to optimize one-way road network designs, focusing on minimizing vehicle travel distance (Shanmugasundaram et al., 2019). Their research showcased the potential of GAs to effectively handle network design problems, emphasizing their utility in optimizing travel directions and improving overall network efficiency.

More recently, research by Li and Zhao (2020) applied GAs to the optimization of taxi pick-up routes, showcasing their versatility in modern traffic systems (Li and Zhao, 2020). By simulating natural evolutionary processes, GAs provide robust solutions that balance multiple conflicting objectives, making them an invaluable tool in modern transportation planning and infrastructure development.

2.3 Neural networks

Neural networks, particularly deep learning models, have shown great potential in solving complex optimization problems. They mimic the human brain’s structure, consisting of multiple layers of neurons that process inputs to produce outputs. This architecture allows neural networks to learn from data and identify intricate patterns that traditional methods might miss. The ability to handle large datasets and extract meaningful insights makes neural networks a powerful tool for various applications, including highway route optimization.

Convolutional Neural Networks (CNNs) are a type of neural network commonly used for image recognition tasks. They excel at identifying spatial patterns and features within images, making them useful for analyzing visual data related to highway design, such as satellite imagery and terrain maps. By leveraging CNNs, researchers can incorporate spatial data into the route optimization process, enhancing the model’s accuracy and comprehensiveness.

Deep Belief Networks (DBNs) are another type of deep learning model applied in various pattern recognition and classification problems. DBNs consist of multiple layers of stochastic, latent variables, which enable them to learn hierarchical representations of data. In highway route optimization, DBNs can effectively integrate and process diverse data sources, such as traffic patterns, environmental constraints, and economic factors. This capability allows for the development of robust multi-objective optimization models that address the complexities of highway route design.

Notable research by Hinton et al. (2006) on deep learning has laid the foundation for using neural networks in complex optimization tasks (Hinton et al., 2006). More recently, applications by Krizhevsky et al. (2012) with CNNs in image recognition have influenced their use in spatial data analysis for transportation planning (Krizhevsky et al., 2012). Additionally, Huang et al. (2018) demonstrated the effectiveness of DBNs in traffic flow prediction, further validating the applicability of deep learning in highway route optimization (Huang et al., 2018). A significant advancement in the field is the hybrid deep-learning-metaheuristic framework proposed by Madadi and Correia (2023). Their framework uses a graph neural network (GNN) to approximate the solution of the user equilibrium traffic assignment problem and employs this model to calculate the fitness function evaluations of a genetic algorithm (GA) for network design problems (NDPs). This hybrid approach was tested on three networks and demonstrated that it could provide solutions within a 1.5% gap of the best results in less than 0.5% of the time used by exact solutions (Madadi and Correia, 2023). Another noteworthy study by Chiou (2024) introduced a knowledge-assisted reinforcement learning evolution optimization (KARLEO) for road network design problems under uncertainty. This method uses a stochastic link traffic model to capture time-varying costs incurred by traffic flow when link capacity is uncertain. The proposed approach significantly improved over conventional methods by effectively reducing total costs at a low computational expense (Chiou, 2024).

2.4 Integration of genetic algorithms and neural networks

The integration of genetic algorithms and neural networks in highway route optimization leverages the strengths of both techniques to enhance overall performance. Genetic algorithms provide a robust mechanism for exploring the search space and optimizing multiple objectives, while neural networks offer powerful predictive capabilities that can evaluate the fitness of various route configurations.

In this integrated approach, the initial population is generated randomly to cover a wide search space, ensuring diverse potential solutions. The crossover operator used in this study is a two-point crossover, where two parent solutions exchange segments of their genetic code to produce offspring. The mutation operator introduces random changes to the genes of offspring solutions with a low probability, ensuring the exploration of new areas in the search space.

The neural network is integrated with the genetic algorithm through a feedback loop. It evaluates the fitness of each solution, predicting the performance of highway routes based on historical data and real-time inputs such as traffic patterns, environmental conditions, and construction costs. This prediction informs the genetic algorithm, guiding it to select, crossover, and mutate solutions more effectively. The genetic operators continuously generate new and diverse route configurations, helping the neural network learn and adapt more effectively.

By incorporating genetic operators, the neural network is exposed to a broad spectrum of potential solutions, including both high-performing and suboptimal routes. This comprehensive exposure helps the neural network develop a nuanced understanding of the factors influencing route performance, enhancing its ability to predict the fitness of new solutions accurately.

Research by Zhang et al. (2019) demonstrated the successful integration of GAs and neural networks in optimizing highway alignments, achieving significant improvements in travel efficiency and environmental impact (Zhang et al., 2019). Similarly, studies by Wang et al. (2020) and Liu et al. (2021) further validated the benefits of this integrated approach in various transportation scenarios, underscoring its potential for widespread application (Wang et al., 2020; Liu et al., 2021).

The integration of these techniques results in a powerful optimization model capable of addressing the complex, multi-objective nature of highway route design. This approach not only improves the efficiency and sustainability of the transportation network but also provides a scalable and adaptable solution for future infrastructure planning and development.

3 Materials and methods

3.1 Problem definition

Highway route optimization is a multi-faceted problem involving technical, economic, and environmental factors. The primary objectives are to minimize travel time, construction costs, and environmental impact while maximizing safety and user comfort. Traditional methods often fall short in balancing these objectives due to their inability to handle complex, nonlinear relationships between variables. Therefore, an advanced approach integrating deep learning and genetic algorithms is proposed to address these challenges effectively.

3.2 Consider the optimal design of vehicle running speed

First of all, we should make it clear that there is an essential difference between the designed speed limit of highway and the actual speed of vehicles. The actual driving speed of vehicles is an important indicator to truly reflect the quality of highway design. There are many conditions that affect the driving speed of vehicles (Maji and Jha, 2009; Hou et al., 2019). The subjective condition is the driver’s driving behavior4, and the objective conditions are the quality of highway design and the quality of driving vehicles. When the vehicle is running at a fast speed, the changes of the road conditions, such as steep slopes and sharp bends, will affect the driver’s driving behavior and lead to traffic accidents. It can be seen that the comprehensive influence of subjective and objective factors should be considered in the optimization design of vehicle running speed (Mohammadi et al., 1995; Han et al., 2016).

(1) Driver’s driving behavior

Subjectively, the driver occupies the control dominance of the vehicle. Drivers’ driving skills and habits determine the speed of vehicles running on different road surfaces. When driving in a straight line, most drivers will choose to drive at a constant speed according to the speed limit or at a speed that can make them feel safe. In the curve, it will slow down first, then pass, and then accelerate.

(2) Category composition of road vehicles

Vehicles on the road can be divided into passenger vehicles and freight vehicles according to their uses, and small vehicles and large vehicles according to their sizes. From the point of view of line design, the design is generally based on large and small cars. Small cars are characterized by small size, light load and good maneuverability. Large cars are characterized by large volume, heavy load and poor maneuverability. When designing the line, we should take into account the composition of vehicles that may appear after the line runs, such as roads with large vehicles, wide lanes and high subgrade strength.

(3) Line characteristics of the line

Generally, the linear characteristics of highways are mainly straightness, slope and crisscross. When there are more straight lines on the line, the overall running speed of the line vehicles will be faster, and when there are more curves on the line, the overall running speed of the line vehicles will be slower. The larger the turning radius, the faster the vehicle turns. As for the slope, the bigger the uphill slope, the more difficult it is for a large vehicle to climb the slope, and the slower the overall running speed of the vehicle will be. The steeper the slope, the more difficult it will be to brake large vehicles, which will easily lead to brake failure and serious traffic accidents (Jha, 2001; Vishnuraj and Vishak, 2017).

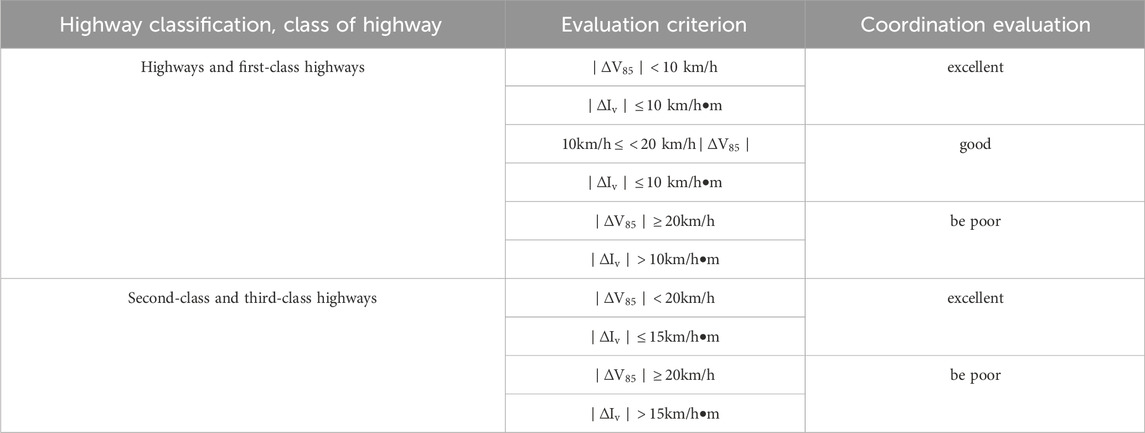
According to the requirements of China’s “Code for Safety Evaluation of Highway Projects”, when the running speed of vehicles in line design is less than or equal to 80 km/h, designers need to evaluate the coordination of the running speed of vehicles (Davis and Jha, 2011). The evaluation criteria are the absolute value of the difference between the running speeds of vehicles on adjacent road sections and the absolute value of the gradient of the running speeds of vehicles. The absolute value of running speed gradient is calculated as Eq. 1:

$\mid {∆\mathrm{I}}_{\mathrm{v}}\mid =\frac{{\mid ∆\mathrm{V}}_{85}\mid }{\mathrm{L}}\times 100(1)$

Among them:

${∆\mathrm{I}}_{\mathrm{v}}$ Is the absolute value of the running speed gradient, km/h m; ${∆\mathrm{V}}_{85}$ Is the absolute value of the difference between the running speed of the starting point and the end point of the unit line; L is the target line length, M.

The following Table shows the evaluation standards for the coordination of operation speed of various classes of highways. (Table 1).

(4) User Behavior in Route Choice

Table 1

Table 1. Evaluation criteria for operation speed coordination of highways of various grades.

User behavior must be modeled concerning route choice to create a realistic and effective highway route optimization model. In highway networks, users’ route choices are typically modeled using a stochastic utility model, specifically the maximum perceived utility method. This approach assumes that users choose routes based on maximizing their perceived utility, considering factors such as travel time, cost, and convenience.

The model employs random utility models (RUM) (Cascetta, 2009), to simulate user decisions. These models calculate the probability of a user choosing a particular route based on the utility derived from each route option. The utility U_ij of a route j for user i is defined as Eq. 2:

$U_{ij}=V_{ij}+{\epsilon }_{ij}(2)$

Among them:

Vij is the deterministic part of the utility, and εij is the stochastic component, capturing the unobserved factors. The probability Pij that user i chooses route j is then modeled as Eq. 3:

$P_{ij}=\frac{e^{V_{ij}}}{{\sum }_k{e}^{V_{ik}}}(3)$

This utility function can be incorporated into both static and dynamic assignment models. In static models, user behavior is considered a constraint in the optimization problem, ensuring that the route choices align with the equilibrium conditions where no user can unilaterally reduce their travel cost by switching routes. In dynamic models, user behavior is continuously adjusted based on real-time conditions and feedback, offering a more responsive and adaptive approach to route optimization.

The integration of user behavior modeling into the highway route optimization process enhances the model’s realism and accuracy, ensuring that the proposed routes align with actual user preferences and behaviors.

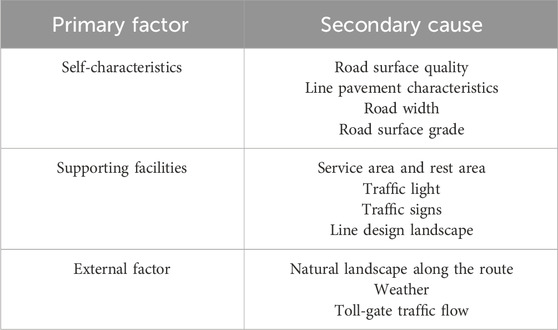
3.3 Optimal design considering driver’s comfort

The driver’s comfort in the driving process is determined by three main influencing factors and several secondary factors. The main factors are:

(1) The characteristics of the highway are the straightness, slope, etc., mentioned above;

(2) Road supporting facilities, such as traffic lights, traffic signs, service areas and rest areas;

(3) External factors, that is, non-objective factors other than the road itself and supporting facilities, such as the natural landscape and climate on both sides of the road.

See the following Table for the primary and secondary factors of driver’s comfort evaluation. (Table 2).

Table 2

Table 2. Primary and secondary factors for evaluating comfort.

3.4 Optimal design considering sustainability objectives

The objectives to be considered must take into account the three components of sustainability: economic, social, and environmental. Furthermore, it is necessary to balance the objectives of the users (i.e., minimum travel time, minimum perceived monetary cost), the manager (i.e., minimum management cost, minimum building cost), and citizens (i.e., minimum pollution, minimum noise) (Banister, 2001; Cascetta et al., 2015; Russo and Rindone, 2021).

3.5 Deep learning and integration of genetic algorithm

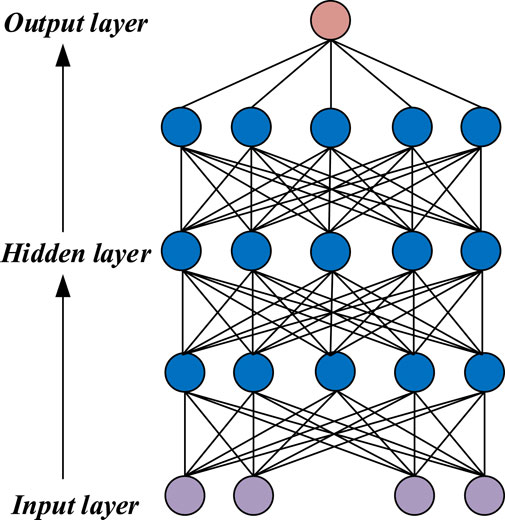
Deep learning is a branch of machine learning research, and its main purpose is to imitate the human brain to establish a neural network for analytical learning. Deep learning is a kind of unsupervised learning. The concept of deep learning originates from the research of artificial neural network. It mainly includes three aspects of pattern analysis methods: (1) Convolution-based neural network system, namely, Convolution Neural Network (CNN). (2) Self-coding based on multilayer neurons neural network, including self-encoder, and those that have received wide attention in recent years. Sparse codingTwo classes (Sparse Coding). (3) Pre-training with multi-layer self-coding neural network, and then further optimizing the deep confidence network (DBN) of neural network weights by combining the discrimination information. After deep learning gradually transforms the initial “low-level” feature representation into “high-level” feature representation through multi-level processing, complex learning tasks such as classification can be completed with “simple model”, and multi-level perceptron with multiple hidden layers is a deep learning structure.

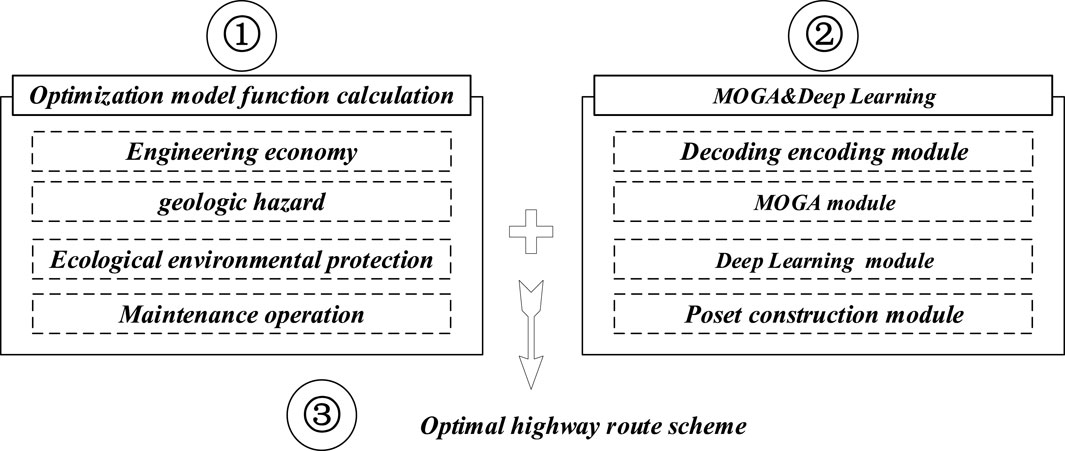
Deep learning is applicable to nonlinear multi-objective programming problems like highway route design optimization. Combining deep learning with multi-objective genetic algorithms (MOGA) effectively addresses multi-objective nonlinear problems such as highway route design optimization (Figure 1).

(1) Initial Population Generation: Randomly generated based on possible route parameters.

(2) Crossover: Combines two parent solutions to produce offspring, promoting genetic diversity.

(3) Mutation: Introduces random changes to offspring, preventing premature convergence and exploring new solutions.

(4) Fitness Evaluation: Each solution’s fitness is evaluated based on multiple objectives, ensuring diverse and optimal solutions.

Figure 1

Figure 1. Basic theoretical model of deep learning.

3.6 Integration of genetic algorithms and neural networks

The proposed methodology integrates genetic algorithms (GAs) with neural networks to optimize highway route design. This hybrid approach leverages the strengths of both techniques to enhance the overall performance of the optimization process.

The initial population is generated randomly to cover a wide search space, ensuring diverse potential solutions. Each individual in the population represents a possible highway route, encoded as a sequence of parameters such as node connections, segment lengths, and curvature. The diversity in the initial population is crucial for exploring various regions of the solution space, increasing the likelihood of finding high-quality solutions.

The crossover operator used in this study is a two-point crossover. In this process, two parent solutions exchange segments of their genetic code to produce offspring. Specifically, two crossover points are selected randomly along the length of the parent chromosomes. The segments between these points are swapped, creating two new offspring that inherit characteristics from both parents. This operator promotes genetic diversity by combining different traits, potentially leading to superior solutions.

The mutation operator introduces random changes to the genes of offspring solutions with a low probability. This process involves altering one or more parameters of the offspring, such as changing a node connection or adjusting a segment length. The mutation operator ensures the exploration of new areas in the search space, preventing premature convergence to local optima and maintaining genetic diversity within the population.

3.7 Impact of genetic operators on neural networks

The genetic operators play a critical role in the integration with neural networks, particularly in how they influence the neural network’s evaluation and learning processes.

The deep learning model is integrated with the GA through a feedback loop, where the neural network evaluates the fitness of each solution. The neural network is trained to predict the performance of highway routes based on historical data and real-time inputs, such as traffic patterns, environmental conditions, and construction costs. This prediction provides a fitness score for each individual in the population, guiding the selection process for the next-generation.

The genetic operators (crossover and mutation) affect the neural network by continuously generating new and diverse route configurations. As the GA evolves, it presents the neural network with a wide variety of potential solutions to evaluate. This constant influx of diverse data helps the neural network to learn and adapt more effectively, improving its predictive accuracy over time. The neural network, in turn, informs the GA about the quality of the solutions, allowing the algorithm to focus on promising regions of the search space.

By incorporating the genetic operators, the neural network is exposed to a broad spectrum of potential solutions, including both high-performing and suboptimal routes. This comprehensive exposure helps the neural network to develop a more nuanced understanding of the factors influencing route performance, enhancing its ability to predict the fitness of new solutions accurately. The parameters used in the GA were as follows:

(1) Population size: 100

(2) Number of generations: 500

(3) Crossover rate: 0.8

(4) Mutation rate: 0.05

The test application demonstrated the model’s ability to optimize route design by balancing travel time, construction cost, and environmental impact. The results showed a significant improvement in overall network efficiency and sustainability compared to traditional design methods.

4 Results

4.1 Deep learning based on multi-objective genetic algorithm

The core of highway optimization design is to determine the best route scheme by optimizing technology on the basis of satisfying external constraints, so as to realize the optimal solution of technology and economy. Route design should not only make the economic and social benefits optimal, but also meet the multi-objective optimal consideration of safety, environmental protection and aesthetics. Multi-objective optimization problem takes the non-dominated solution or Pareto and optimal solution in mathematics, which means that it can’t be compared simply. The characteristic is that changing one of the objective functions will affect other objective functions. If the multi-objective programming is simply transformed into a single-objective programming, each operation can only have one result, and multiple operations are needed to get the myopic optimal solution, which will lead to a large number of operations. Multi-objective genetic algorithm not only satisfies the whole population, but also emphasizes individual integration, which is an important way to solve the multi-objective optimization problem. The deep learning network has the characteristics of fitting the causal relationship between any input and output, and is suitable for solving all kinds of nonlinear problems. Combining multi-objective genetic algorithm with deep learning can effectively solve all kinds of multi-objective nonlinear problems.

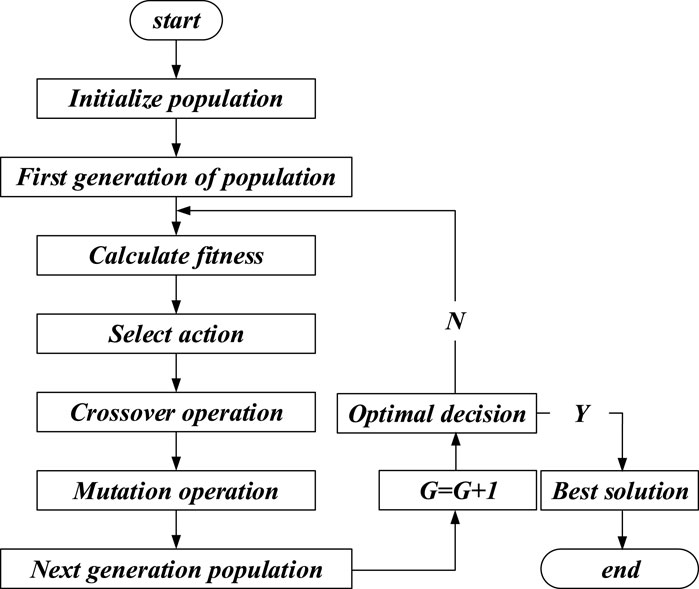
Multi-objective genetic algorithm (MOGA) is a global optimization scheme based on Darwin’s evolution theory, which is suitable for solving all kinds of constrained and unconstrained problems. Its basic logic is to select the best individual as parents to generate offspring in each iteration, so that the population can be solved in the optimal direction. Figure 2 shows the flow chart of the multi-objective algorithm. Each time, whether the genetic result meets the optimal solution is checked. If yes, the result is output, and if no, the iteration is repeated.

Figure 2

Figure 2. Flow chart of multi-objective genetic algorithm.

The core of MOGA training deep learning lies in mapping the network to chromosomes. In the existing coding mode, network parameters are used as chromosome elements. However, in large-scale networks, this method will make the structure redundant. Taking the deep learning network layer and the full link layer as chromosome elements becomes a new thinking, which makes each chromosome element always contain a connection weight or filter value, thus reducing the chromosome structure and having a higher convergence speed.

4.2 Multi-objective optimization model of highway route

The multi-objective optimization problem can generally be described as solving Y = (x1, x2, x3 … xn), as Eqs. 4 and 5:

$G_{\mathrm{i}}\left(x\right)\le 0i=1,2,3\dots m(4)$

$H_{\mathrm{j}}\left(x\right)\le 0j=1,2,3\dots n(5)$

If there are R constraints and Q solving objectives, and the Q solving objectives contain certain conflicting factors, the optimization objectives are expressed as f(Y) = {f1(Y), f1(Y), f3(Y)…fQ(Y)}, and f(Y*) can be satisfied when the optimal solution is {x1*, x2*, x3*…xn*}. When establishing a function, it is often assumed that the lowest cost or risk is the solution value. If the solution value is in the opposite direction, it can be converted into the minimum value, and the objective function can be expressed as Eq. 6:

$\mathit{min}f\left(Y\right)=\mathit{min}\left\{f_1\left(Y\right),f_1\left(Y\right),f_3\left(Y\right)\dots f_Q\left(Y\right)\right\}(6)$

The optimal solution can be expressed as Eq. 7:

$P*=\left\{Y*\right\}=\left\{X’\in \mathrm{\Omega },fj\left(X’\right)\le f_{\mathrm{j}}\left(X\right),j=1,2,3\dots Q\right\}(7)$

The set of all the non-dominated solutions is called the non-dominated set (NDSET) of the current evolutionary population. Through iterative solution, NDSET is constantly approaching the optimal solution, and finally meets the following requirements, as Eq. 8:

$\text{NDSET}=f\left(Y*\right)(8)$

Figure 3 shows the system model of deep learning network based on multi-objective genetic algorithm training applied to highway route planning optimization, in which expert design system and the evaluation results of various national design indexes and safety specifications on the survey results of the route are used as the basic basis and weight reference, and then digital quantitative modeling is carried out for each index, and the data weight and evaluation results are sent into the deep learning model to complete its multi-objective optimization research, thus obtaining the optimal highway route scheme.

Figure 3

Figure 3. Deep learning model based on multi-objective optimization.

4.3 Optimize the objective function

Conventional multi-objective optimization is to quantitatively evaluate all indexes by taking a certain index as a general equivalent index, and carry out optimization research under this index environment, such as taking economic indexes as equivalent conversion in safety, environmental protection, technology and other aspects, and finally forming a variable evaluation model, but this model is affected by the conversion of equivalent indexes. Using multi-objective optimization algorithm, multiple objective functions can be directly coupled and ideal optimization results can be obtained. The following mainly describes three optimization objectives: safety, construction cost and geological disasters.

Road safety is the primary consideration in road design, especially in mountainous areas of southwest China. Safety requirements refer to the national JTG/TB -2014 Guide for Safety Evaluation of Highway Projects, and the safety of the road sections under construction is evaluated. The percentage of the road sections evaluated as “good” is p1, the percentage of the road sections evaluated as “good” is p2, and other evaluation results are p3 … pn in turn. The objective function is Eq. 9:

$\min f_{\mathrm{s}}\left(x\right)=w_{1*}{p}_1+w_{2*}{p}_2+w_{3*}{p}_3+\dots w_{\mathrm{n}*}{p}_{\mathrm{n}}(9)$

Where w1 … wn represents the safety impact coefficient corresponding to different percentages.

The construction cost is an important consideration in the construction project, and its total cost is the arithmetic sum of the costs of all parts. Considering the construction of related lines, the total cost of highway construction as Eq. 10:

$\min f_{\mathrm{e}}\left(x\right)=\mathit{Cos}{t}_{\text{ew}}+\mathit{Cos}{t}_{\text{caa}}+\mathit{Cos}{t}_{\text{cc}}+\mathit{Cos}{t}_{\mathrm{s}}+\mathit{Cos}{t}_{\mathrm{c}}(10)$

Among them, Costew represents Earthwork, Costcaa represents covers an area, Costcc represents civil construction, Costs represents subgrade, and Costc represents curing.

In geological hazard assessment, the unit length of the line (such as 1 km) and a certain distance on both sides of the line are often taken as the assessment units (Figure 4). According to the evaluation standards of geological survey and related articles, the risk of geological disasters is divided into several grades according to different degrees, such as slight, medium, medium-high, high-risk, etc., the proportion of which is recorded as N1, N2 … Nn, and the function description is Eq. 11:

$\min f_{\mathrm{d}}\left(x\right)=b_{1*}{N}_1+b_{2*}{N}_2+\dots b_{2*}{N}_{\mathrm{n}}(11)$

Where, b1 $\dots$ bn represents the risk weight corresponding to different percentages.

Figure 4

Figure 4. Different optimization objective functions.

4.4 Test network and parameters

The test network consisted of a simplified model of a highway system with varying terrain, traffic conditions, and environmental constraints. The network parameters included:

(1) Number of nodes: 50

(2) Number of edges: 120

(3) Average traffic flow: 2000 vehicles per hour

(4) Environmental sensitivity zones: 10% of the total area

The fitness function was designed to evaluate each solution based on travel time, construction cost, and environmental impact. The results were compared to traditional route planning methods to assess the improvements achieved by the proposed model.

The test application demonstrated the model’s ability to optimize route design by balancing travel time, construction cost, and environmental impact. The results showed a significant improvement in overall network efficiency and sustainability compared to traditional design methods. (Table 3).

Table 3

Table 3. Summary of results.

These preliminary results highlight the effectiveness of integrating deep learning and genetic algorithms in highway route optimization. The model successfully identified routes that offered substantial improvements over traditional methods, achieving a balanced optimization across multiple objectives.

4.5 Test network route analysis

To illustrate the effectiveness of the proposed model, we will compare the routes identified by the proposed model with those identified by traditional methods. Traditional methods in highway route optimization typically include heuristic approaches and linear programming techniques. These methods, while useful in certain contexts, often fall short in addressing the complex, multi-objective nature of highway route optimization.

(1) Traditional methods

① Route A (Heuristic approach)

Heuristic approaches in route optimization involve rule-based strategies or expert knowledge to determine feasible routes. These methods often prioritize a single objective, such as minimizing travel time or construction costs, without considering the broader context. For example, a heuristic approach might focus on finding the shortest possible route to reduce travel time, disregarding other critical factors like environmental impact or terrain difficulty. This narrow focus can lead to suboptimal solutions where improvements in one area are offset by significant drawbacks in others. Furthermore, heuristic methods lack the flexibility to adapt to dynamic traffic patterns and evolving environmental constraints, making them less effective in real-world applications where multiple, often conflicting, objectives must be balanced.

This route prioritizes the shortest distance to minimize travel time. While effective in reducing travel duration, it often neglects construction costs and environmental impacts. For example, Route A might traverse environmentally sensitive zones, leading to higher long-term ecological damage and potential regulatory challenges. The heuristic approach’s single-objective focus limits its ability to provide holistic solutions.

② Route B (Linear programming)

Linear programming techniques solve optimization problems by modeling them as linear relationships. These methods can be highly effective for certain types of problems, especially those with well-defined, linear constraints and objectives. However, the inherent limitations of linear programming become apparent in the context of highway route optimization, which involves nonlinear and multi-objective challenges. For instance, a linear programming approach might successfully minimize construction costs by selecting routes that avoid expensive terrains, but this often results in longer travel times and higher environmental impact. The rigidity of linear programming models makes it difficult to incorporate the complex interactions between different objectives, such as the trade-offs between cost, travel time, and environmental sustainability.

This route focuses on minimizing construction costs, often by avoiding expensive terrains. Although this can lead to significant cost savings, it frequently results in longer travel times and increased environmental impacts. Route B may circumvent hilly areas or bodies of water, extending the route length and thus the travel time. Additionally, the longer route may pass through multiple environmentally sensitive areas, further complicating its feasibility.

(2) Route C (integrated model)

The proposed model integrates deep learning with genetic algorithms to address the limitations of traditional methods. This hybrid approach simultaneously optimizes multiple objectives, offering a more balanced and comprehensive solution. Deep learning algorithms analyze vast amounts of historical and real-time data to predict traffic patterns, environmental impact, and construction costs. These predictions are then fed into a genetic algorithm, which iteratively evolves a population of potential routes to find the optimal balance between competing objectives. By considering a broader range of factors and utilizing advanced machine learning techniques, the proposed model can dynamically adapt to changing conditions and constraints, providing more robust and sustainable route optimization solutions.

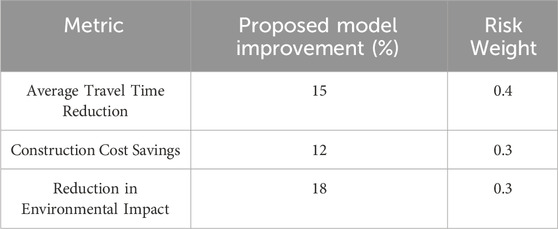
This route represents the optimized solution generated by the proposed model, balancing travel time, construction cost, and environmental impact. Route C demonstrates a 15% reduction in travel time, a 12% reduction in construction costs, and an 18% reduction in environmental impact compared to traditional methods. The integrated model considers dynamic traffic patterns, adjusts for real-time environmental data, and uses genetic algorithms to explore a wide range of possible routes, ensuring that the chosen route is not only cost-effective but also environmentally sustainable. This holistic approach results in a more efficient and sustainable highway network, addressing the multi-faceted challenges of modern infrastructure planning.

The comparison highlights the advantages of the proposed model over traditional methods. (Table 4). By integrating deep learning and genetic algorithms, the proposed model provides a more comprehensive and adaptive solution to highway route optimization. Traditional methods often excel in specific areas but fail to balance multiple objectives effectively. In contrast, the proposed model’s ability to optimize across various parameters results in routes that are not only shorter and cheaper but also less harmful to the environment.

Table 4

Table 4. Comparative results of routes identified by traditional methods and recommended models.

5 Conclusion

5.1 Innovations

This paper presents a comprehensive approach to highway route optimization by integrating deep learning and multi-objective genetic algorithms. By incorporating user behavior modeling and sustainability objectives, the proposed model offers a realistic and effective solution to highway route optimization.

(1) Integration of Deep Learning with Genetic Algorithms: The paper introduces a novel approach that integrates deep learning with multi-objective genetic algorithms (MOGA). This integration leverages the strengths of both techniques, allowing for a more comprehensive and adaptive optimization process. The deep learning model provides robust predictive capabilities, while the genetic algorithm efficiently explores and optimizes the search space.

(2) User Behavior Modeling: The inclusion of user behavior modeling using random utility models (RUMs) adds a layer of realism to the optimization process. By simulating users’ route choice behavior based on perceived utility, the model aligns more closely with actual user preferences and behaviors, leading to higher traffic volumes and better utilization of the proposed routes.

(3) Sustainability Objectives: Unlike traditional single-objective optimization methods, this research focuses on balancing multiple conflicting objectives, including travel time, construction cost, and environmental impact. This multi-faceted approach ensures that the proposed routes are not only efficient but also economically viable and environmentally sustainable.

(4) Dynamic Adaptation: The proposed model incorporates dynamic traffic patterns and real-time environmental data, allowing it to adapt to changing conditions. This capability enhances the model’s accuracy and reliability, making it suitable for real-world applications where conditions are constantly evolving.

(5) Comprehensive Evaluation Metrics: The research employs a detailed fitness function that evaluates each route based on multiple criteria. This comprehensive evaluation ensures that the selected routes optimize travel time, minimize construction costs, and reduce environmental impacts.

5.2 Further advancement

Future research should focus on applying the model to larger and more complex highway networks to validate its scalability and effectiveness. Developing more sophisticated user behavior models that consider additional factors such as individual preferences, weather conditions, and traffic incidents can improve the model’s accuracy and reliability.

(1) Scalability and Complexity: While the proposed model shows promising results on a simplified highway network, its scalability to larger and more complex networks needs further validation. Future research should focus on testing the model on extensive real-world networks to ensure its effectiveness and efficiency in diverse scenarios.

(2) Enhanced User Behavior Models: The current model incorporates basic user behavior modeling. However, user preferences can be influenced by a wide range of factors, including individual preferences, weather conditions, and traffic incidents. Developing more sophisticated user behavior models that consider these additional factors can improve the model’s predictive accuracy.

(3) Real-World Implementation and Validation: The model’s application in real-world projects is crucial for assessing its practical utility. Pilot projects and case studies should be conducted to gather empirical data and refine the model based on real-world feedback. This step is essential to bridge the gap between theoretical research and practical implementation.

(4) Advanced Data Integration: The integration of advanced data sources, such as high-resolution satellite imagery, real-time traffic data, and environmental sensors, can further enhance the model’s accuracy. Future research should explore ways to incorporate these data sources effectively, providing a richer dataset for the deep learning model.

(5) Interdisciplinary Collaboration: The complexity of highway route optimization requires collaboration across multiple disciplines, including transportation engineering, environmental science, and computer science. Promoting interdisciplinary research can lead to more innovative solutions and a holistic approach to infrastructure planning and development.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

JZ: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors would like to show sincere thanks to those techniques who have contributed to this research.

Conflict of interest

Author JZ was employed by CCCC First Highway Consultants Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Banister, D. (2001) “Transport Planning,” in Transport Planning. Emerald Group Publishing Limited, Vol. 3, 9–19. doi:10.1108/9781615832460-002

CrossRef Full Text | Google Scholar

Beasley, J. E. (1993). Modern Heuristic Techniques for combinatorial Problems. Hoboken, NJ: Prentice Hall.

Google Scholar

Billheimer, J. W., and Gray, P. (1973). Network Design with Fixed and Variable Cost Elements. Transp. Sci. 7 (1), 49–74. doi:10.1287/trsc.7.1.49

CrossRef Full Text | Google Scholar

Bongiorno, N., Bosurgi, G., Carbone, F., Pellegrino, O., and Sollazzo, G. (2019). Potentialities of a highway alignment optimization method in an I-BIM environment. Period. Polytech. Civ. Eng. 63 (2), 352–361. doi:10.3311/ppci.12220

CrossRef Full Text | Google Scholar

Cantarella, G. E., Pavone, G., and Vitetta, A. (2006). Heuristics for urban road network design: lane layout and signal settings. Eur. J. Operational Res. 175 (3), 1682–1695. doi:10.1016/j.ejor.2005.02.034

CrossRef Full Text | Google Scholar

Cantarella, G. E., and Vitetta, A. (2006). The multi-criteria road network design problem in an urban area. Transportation 33, 567–588. doi:10.1007/s11116-006-7908-z

CrossRef Full Text | Google Scholar

Cascetta, E. (2009). Transportation systems analysis: models and applications. Berlin, Germany: Springer Science & Business Media.

Google Scholar

Cascetta, E., Cartenì, A., Pagliara, F., and Montanino, M. (2015). A new look at planning and designing transportation systems: A decision-making model based on cognitive rationality, stakeholder engagement and quantitative methods. Transp. policy 38, 27–39. doi:10.1016/j.tranpol.2014.11.005

CrossRef Full Text | Google Scholar

Chiou, S. W. (2024). A Knowledge-Assisted Reinforcement Learning Optimization for Road Network Design Problems Under Uncertainty. Knowledge-Based Syst. 292, 111614. doi:10.1016/j.knosys.2024.111614

CrossRef Full Text | Google Scholar

Coley, D. A. (1999). An Introduction to Genetic Algorithms for Scientists and Engineers. World Sci.

CrossRef Full Text | Google Scholar

Comi, A., and Polimeni, A. (2022). Estimating Path Choice Models Through Floating Car Data. Forecasting 4 (2), 525–537. doi:10.3390/forecast4020029

CrossRef Full Text | Google Scholar

Davis, C., and Jha, M. K. (2011). A Dynamic Modeling Approach to Investigate Impacts to Protected and Low-Income Populations in Highway Planning. Transp. Res. Part A Policy Pract. 45 (7), 598–610. doi:10.1016/j.tra.2011.03.011

CrossRef Full Text | Google Scholar

Deng, Y., Ma, R., and Zhang, H. M. (2017). An Optimization-Based Highway Network Planning Procedure with Link Growth Probabilities. Transp. A Transp. Sci. 13 (8), 708–726. doi:10.1080/23249935.2017.1321697

CrossRef Full Text | Google Scholar

Di Gangi, M., and Polimeni, A. (2022). Path choice Models in Stochastic Assignment: Implementation and Comparative Analysis. Front. Future Transp. 3, 885967. doi:10.3389/ffutr.2022.885967

CrossRef Full Text | Google Scholar

Fangqu, N., and Jun, L. (2019). Visualizing the Intercity Highway Network in Mainland China. Environ. Plan. A Econ. Space 51 (6), 1213–1216. doi:10.1177/0308518x18806004

CrossRef Full Text | Google Scholar

Gao, Z., Wu, J., and Sun, H. (2005). Solution Algorithm for the Bi-Level Discrete Network Design Problem. Transp. Res. Part B Methodol. 39 (6), 479–495. doi:10.1016/j.trb.2004.06.004

CrossRef Full Text | Google Scholar

Goldberg, D. E. (1988). Genetic Algorithms in Search, Optimization, and Machine Learning. Ethnogr. Praxis Industry Conf. Proc. 9 (2).

Google Scholar

Han, J., Cheng, H., Shi, Y., Wang, L., Song, Y., and Zhnag, W. (2016). Connectivity Analysis and Application of Fracture Cave Carbonate Reservoir in Tazhong. Sci. Technol. Eng. 16 (5), 147–152.

Google Scholar

Hinton, G. E., Osindero, S., and Teh, Y. W. (2006). A fast Learning Algorithm for Deep Belief Nets. Neural Comput. 18 (7), 1527–1554. doi:10.1162/neco.2006.18.7.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

Hou, Z. K., Cheng, H. L., Sun, S. W., Chen, J., Qi, D. Q., and Liu, Z. B. (2019). Crack Propagation and Hydraulic Fracturing in Different Lithologies. Appl. Geophys. 16 (2), 243–251. doi:10.1007/s11770-019-0764-3

CrossRef Full Text | Google Scholar

Huang, W., Song, G., Hong, H., and Xie, K. (2018). Deep Architecture for Traffic Flow Prediction: Deep Belief Networks with Multitask Learning. IEEE Trans. Intelligent Transp. Syst. 15 (5), 2191–2201. doi:10.1109/tits.2014.2311123

CrossRef Full Text | Google Scholar

Jesus, M., Akyildiz, S., Bish, D. R., and Krueger, D. A. (2011). Network-Level Optimization of Pavement Maintenance Renewal Strategies. Adv. Eng. Inf. 25 (4), 699–712. doi:10.1016/j.aei.2011.08.002

CrossRef Full Text | Google Scholar

Jha, M. K. (2001). Using a Geographic Information System for Automated Decision Making in Highway Cost Analysis. Transp. Res. Rec. 1768 (1), 260–267. doi:10.3141/1768-30

CrossRef Full Text | Google Scholar

Jha, M. K., and Kim, E. (2006). Highway Route Optimization Based on Accessibility, Proximity, and Land-Use Changes. J. Transp. Eng. 132 (5), 435–439. doi:10.1061/(asce)0733-947x(2006)132:5(435)

CrossRef Full Text | Google Scholar

Jha, M. K., and Schonfeld, P. (2000). Geographic Information System–Based Analysis of Right-of-Way Cost for Highway Optimization. Transp. Res. Rec. 1719 (1), 241–249. doi:10.3141/1719-32

CrossRef Full Text | Google Scholar

Jha, M. K., and Schonfeld, P. (2004). A Highway Alignment Optimization Model Using Geographic Information Systems. Transp. Res. Part A Policy Pract. 38 (6), 455–481. doi:10.1016/j.tra.2004.04.001

CrossRef Full Text | Google Scholar

Kang, M. W., Jha, M. K., and Schonfeld, P. (2012). Applicability of Highway Alignment Optimization Models. Transp. Res. Part C Emerg. Technol. 21 (1), 257–286. doi:10.1016/j.trc.2011.09.006

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). “ImageNet Classification with Deep Convolutional Neural Networks,” in Advances in Neural Information Processing Systems, 25.

Google Scholar

Li, Y., Fan, J., and Deng, H. (2018). Analysis of Regional Difference and Correlation Between Highway Traffic Development and Economic Development in China. Transp. Res. Rec. 2672 (3), 12–25. doi:10.1177/0361198118790373

CrossRef Full Text | Google Scholar

Li, Y., and Zhao, H. (2020). An Intelligent Optimization Method for Taxi Pick-Up Routes Based on Genetic Algorithms and Ant Colony Optimization. Transp. Res. Part C Emerg. Technol. 115, 102628.

Google Scholar

Lin, K. C. (2011). Le Développement du Réseau Routier en Chine: Inconséquences et Inégalités. Rev. Int. Polit. Comp. 18 (3), 151–179. doi:10.3917/ripc.183.0151

CrossRef Full Text | Google Scholar

Liu, J., Xie, X., and Zhang, Y. (2021). Multi-Objective Optimization for Sustainable Transportation Planning: An Integrated Approach Using Genetic Algorithms and Neural Networks. Sustain. Cities Soc. 66, 102688.

PubMed Abstract | Google Scholar

Liu, Z. (1997). China’s Information Super Highway: Its Goal, Architecture and Problems. Electron. Mark. 7 (4), 45–50. doi:10.1080/10196789700000049

CrossRef Full Text | Google Scholar

Madadi, B., and Correia, G. H. D. A. (2023). A Hybrid Deep-Learning-Metaheuristic Framework for Bi-level Network Design Problems. Available at SSRN 4470984.

Google Scholar

Madadi, B., van Nes, R., Snelder, M., and Van Arem, B. (2020). A Bi-Level Model to Optimize Road Networks for a Mixture of Manual and Automated Driving: An Evolutionary Local Search Algorithm. Computer-Aided Civ. Infrastructure Eng. 35 (1), 80–96. doi:10.1111/mice.12498

CrossRef Full Text | Google Scholar

Maji, A., and Jha, M. K. (2009). Multi-Objective Highway Alignment Optimization Using a Genetic Algorithm. J. Adv. Transp. 43 (4), 481–504. doi:10.1002/atr.5670430405

CrossRef Full Text | Google Scholar

Mohammadi, J., Guralnick, S. A., and Yan, L. (1995). Incorporating Life-Cycle Costs in Highway-Bridge Planning And Design. J. Transp. Eng. 121 (5), 417–424. doi:10.1061/(asce)0733-947x(1995)121:5(417)

CrossRef Full Text | Google Scholar

Russo, F., and Rindone, C. (2021). Regional Transport Plans: From Direction Role Denied to Common Rules Identified. Sustainability 13 (16), 9052. doi:10.3390/su13169052

CrossRef Full Text | Google Scholar

Russo, F., and Vitetta, A. (2006). A Topological Method to Choose Optimal Solutions After Solving the Multi-Criteria Urban Road Network Design Problem. Transportation 33, 347–370. doi:10.1007/s11116-005-3507-7

CrossRef Full Text | Google Scholar

Sabatino, S., Frangopol, D. M., and Dong, Y. (2015). Sustainability-Informed Maintenance Optimization of Highway Bridges Considering Multi-Attribute Utility and Risk Attitude. Eng. Struct. 102, 310–321. doi:10.1016/j.engstruct.2015.07.030

CrossRef Full Text | Google Scholar

Šetinc, M., Gradišar, M., and Tomat, L. (2015). Optimization of a Highway Project Planning Using a Modified Genetic Algorithm. Optimization 64 (3), 687–707.

Google Scholar

Shanmugasundaram, N., Sushita, K., Kumar, S. P., and Ganesh, E. N. (2019). Genetic Algorithm-Based Road Network Design for Optimising the Vehicle Travel Distance. Int. J. Veh. Inf. Commun. Syst. 4 (4), 344–354. doi:10.1504/ijvics.2019.10025633

CrossRef Full Text | Google Scholar

Solanki, R. S., Gorti, J. K., and Southworth, F. (1998). Using Decomposition in Large-Scale Highway Network Design with a Quasi-Optimization Heuristic. Transp. Res. Part B Methodol. 32 (2), 127–140. doi:10.1016/s0191-2615(97)00020-9

CrossRef Full Text | Google Scholar

Turner, D. W., and Miles, D. E. (1971). Computer-Assisted Regional Route Location. Highw. Res. Rec. 356, 1–12.

Google Scholar

Vishnuraj, R. G., and Vishak, M. S. (2017). Optimization of Resources in Highway Construction. Int. J. Eng. Manag. Res. (IJEMR) 7 (2), 106–110.

Google Scholar

Wang, H., Huang, W., and Yu, X. (2020). Hybrid Optimization of Highway Routes Using Genetic Algorithms and Deep Learning. Comput. Industrial Eng. 139, 105790.

Google Scholar

Xu, T., Wei, H., and Hu, G. (2009). Study on Continuous Network Design Problem Using Simulated Annealing and Genetic Algorithm. Expert Syst. Appl. 36 (2), 1322–1328. doi:10.1016/j.eswa.2007.11.023

CrossRef Full Text | Google Scholar

Zhang, X., Yang, Y., and Sun, Y. (2019). Integration of Genetic Algorithms and Neural Networks for Highway Alignment Optimization. Transp. Res. Part C Emerg. Technol. 104, 84–95.

Google Scholar

Zhang, G., and Jian, L. U. (2007). Genetic Algorithm for Continuous Network Design Problem. J. Transp. Syst. Eng. Inf. Technol. 7 (1), 101–105. doi:10.1016/s1570-6672(07)60012-9

CrossRef Full Text | Google Scholar

Zhu, W., Liu, K., Wang, M., and Koks, E. E. (2020). Seismic Risk Assessment of the Railway Network of China’s Mainland. Int. J. Disaster Risk Sci. 11 (4), 452–465. doi:10.1007/s13753-020-00292-9

CrossRef Full Text | Google Scholar