- Chair of Automatic Control Engineering, Technical University of Munich, Munich, Germany
Motion planning algorithms for automated vehicles need to assess the intended behavior of other Traffic Participants (TPs), in order to predict the likely future trajectory of TPs and plan the motion consequently. Information resulting from several sources, like sensors, must be gathered and combined into a reliable estimate of the intended behavior of TPs. Such estimates must be sufficiently steady and quantify the inherent uncertainty around the assessment. We present a novel information fusion algorithm to combine information from different sources into a coherent and reliable estimate. To explicitly account for the uncertainty of estimates, we leverage the Belief Function Theory and evaluate and handle possible disagreements between estimates individually provided by the sources. The algorithm is flexible and can also handle sources that do not discern between some of the considered behaviors and are only capable of assessing the probability of unions or clusters of different behaviors. We discuss the strengths of the approach through simulations in SUMO, comparing it to the Interactive Multiple Model algorithm.
1 Introduction
The automated driving field has recently seen incredible progress and autonomous vehicles are nowadays capable of dealing with complex situations. Especially in urban automated driving, handling interaction with traffic participants (TPs) is complicated, as it requires predicting their future motion. Connected and Automated Vehicles (CAVs) alleviate the task, as they share information making other CAVs aware of the future intention. However, although the share of CAVs on roads is expected to quickly increase, for a significant amount of time traffic will still mainly be characterized by human-driven vehicles, whose future motion is unknown because of the lack of communication. Moreover, also in the long term, automated vehicles will continue to have to deal with the presence of non-communicating TPs, such as cyclists and pedestrians, who should be given special attention as vulnerable road users.
In control-based autonomous driving schemes such as Model Predictive Control, the future behavior of the automated vehicle is optimized, accounting for the future moves of the other TPs, whose future motion must, therefore, be predicted. Several common approaches to infer the expected future motion of the other TPs rely on running prediction models starting from the current position and velocity of TPs. The design of.such prediction models is a challenging task, as they have to consider both the dynamics of TPs and their internal objective, depending on the driving style and on the maneuver being executed Lefevre et al. (2014). Tuning the prediction model depending on the maneuver being executed or even the selection of different prediction models depending on the traffic situation requires an online assessment of the behavior of TPs.
The intention driving the behavior of a given TP, whether it is another vehicle, a cyclist, or a pedestrian, can be estimated based on information collected from onboard sensors, cameras, and radars along the road and from intelligent infrastructures communicating with automated vehicles. The past trajectory of each TP can be analyzed and candidate behaviors ranked evaluating a measure of similarity with respect to properly designed models representing different situations Tran and Firl (2014). In Woo et al. (2017), a lane change detection mechanism is introduced, relying on phase models of lane changes. However, phase models for lane changes are required, thus the method does not generalize well. In Carvalho et al. (2014), the Interacting Multiple Model (IMM) algorithm is used to estimate the intended trajectory of target vehicles. However, the variability of the estimation is not considered and the estimation might suddenly and repetitively change if none of the considered models perfectly matches the dynamics, making the estimate unreliable. Berclaz et al. (2011) proposes an efficient multiple-object tracking algorithm based on the K-shortest paths optimization, which is applied to track pedestrians who walk possibly producing occlusions. Notably, Bewley et al. (2016) introduced SORT, an online multi-object tracking algorithm based on the Kalman filter, which was further improved in Wojke et al. (2017). Neural networks have also been extensively used for pedestrian tracking, see, for example, Zhao and Thorpe (2000); Song et al. (2021). Further motion tracking algorithms are mentioned in the surveys Moeslund et al. (2006); Gerónimo et al. (2010). Furthermore, heuristics and other non-vision or radar-based sources, e.g., traffic statistics, can provide a bias useful to categorize the behavior of TPs.
After the intended behavior of TPs has been recognized, the future motion of vehicles and vulnerable road users can be predicted as in Deo et al. (2018). Moreover, the authors in Xin et al. (2018) present a long short-term memory network for long-horizon trajectory prediction, relying on identified intended maneuvers of the TPs. In addition, in Ding and Shen (2019) a two-level vehicle prediction framework is introduced, in which the second block consists of an optimization-based prediction method relying on the prior identification of the intended vehicle maneuver. Further motion prediction models are discussed in the recent survey Ghorai et al. (2022). Then, the predicted trajectories and their estimated probabilities can be passed on to the motion planner of the automated vehicle accounting for the multiple possible future motions of TPs depending on their probability, as, e.g., in our recent work Benciolini et al. (2023).
However, when different sources or multiple motion tracking algorithms are used to infer the probability candidate behaviors of TPs, a multitude of estimates of the probabilities of candidate behaviors are produced, which might differ. Thus, the information provided by the several sources must be combined and gathered in a coherent estimate. One main challenge in combining different behavior estimations lies in handling the inherent uncertainty around the information provided by each source and in their possible discord. Furthermore, the resulting overall estimation of the behavior of TPs should be made as stable and reliable as possible and the reliability of the provided information should be explicitly quantified. Assessing the reliability of the provided estimation is especially important to allow motion planners to subsequently take action to address the uncertainty and to avoid aggressive decisions until the estimation is reliable enough, particularly when interacting with vulnerable users. Finally, combining non-homogeneous individual estimations is challenging. For example, some of the sources might not discern between some of the candidate behaviors and estimate their probability separately, but rather only assign probability to their unions, that is, that either of them will occur. Examples of sensors only capable of assigning belief mass to the union of singletons can be found in Jøsang (2019a) for genetic mutation detection application and in Milisavljevic and Bloch (2003) for mine detection.
In this work, we rely on Belief Function Theory (BFT) to combine information resulting from different sources in a reliable way, explicitly accounting for the uncertainty around the estimate. BFT has been utilized to account for the reliability of the information in a safe reinforcement learning framework in our previous works Zhou et al. (2020, 2021), and for grid-based mapping and tracking in our previous works Tanzmeister et al. (2014); Tanzmeister and Wollherr (2017). In Wu et al. (2002), BFT is utilized for sensor fusion, through the Dempster-Shafer evidence combination rule and an improved evidence combination rule that weighs sensors. However, conflict among observations is not dealt with and thus additional observations always render the result more certain, even when they do not agree with each other. Several conflict detection mechanisms were proposed in Martin (2019), which, however, do not consider the uncertainty of the sources, which is to some extent unreasonable. A conflict-handling mechanism called Uncertainty Maximization has been presented in Jøsang (2019b), transferring part of the belief masses to the uncertainty independently of the degree of conflict, which, depending on the application, is also unreasonable for small conflicts.
We provide a two-step algorithm to combine the information about the behavior of TPs provided by multiple sources in a consistent and reliable estimate using BFT. At first, a modification of the Dempster-Shafer rule is used to gather the information collected by several sources independently during the last sampling time. Sensors estimating the probability of unions of events instead of the probabilities of singletons can also be adopted. Furthermore, we design a new conflict-handling mechanism taking the reliability of the information provided by each source into account. Then, the information is fused with the estimate from the previous iteration, giving steadiness to the framework. We compare our approach with the IMM algorithm Genovese (2001) through numerical simulations in SUMO Krajzewicz et al. (2002). The proposed approach is well suited to combine the information obtained by different sources to estimate the future trajectory of TPs handling conflicts in the estimation through the notion of uncertainty. For this reason, the approach leads to improved safety when automated vehicles need to interact with non-communicating TPs, such as human-driven vehicles and vulnerable users like cyclists and pedestrians.
The remainder of the paper is organized as follows. An overview of the proposed approach is given in Section 2. Remarks on BFT and the formal definition of opinions and possible generation mechanisms are given in Section 3, whereas the steps of the belief processing mechanism and their properties are outlined in Section 4. Simulation results and an outlook for future research are given in Section 5, whereas conclusive remarks Section in 6.
2 Overview of the approach
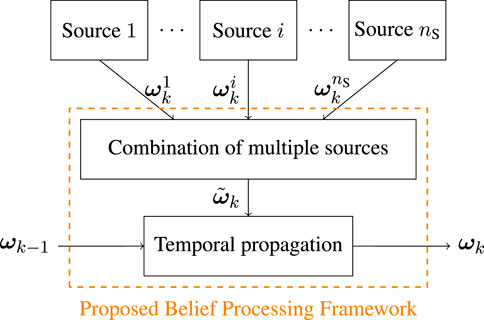
The information flow considered in this work is repeated in parallel for each TP separately. The procedure can be divided into three parts, namely, generation of opinions, multi-source information fusion, and temporal belief distribution propagation. The scheme of information handling is represented in Figure 1. Our focus is combining information with a view to assessing the behavior of TPs, but the method is not limited to this specific application.
At first, information is collected from each source independently. This step happens outside and independently of our belief processing algorithm. Based on new data, at each time step k, nS opinions
Secondly, independently-generated opinions are combined, gathering the information resulting from the current time step. An agreement between individual estimations provided by different sources is found, based on the last samples available, reporting possible changes in the behavior. The processing of individual estimations is independent of how opinions are generated. Observe that the combined opinion is not just an average of the estimated probabilities from every separated source. Rather, opinions are merged considering the uncertainty of each of them, weighing in more sources that provide more reliability. Furthermore, an assessment of the uncertainty of the combined estimate is also provided, so that several independent but coherent opinions reduce the overall level of uncertainty, whereas possible disagreement is treated through a mechanism outlined in Section 4.1. The combined opinion is labeled
Finally, to propagate the estimation over time, the combined opinion-gathering information from the current time step
In this work, singletons and individual probabilities represent different behaviors of TPs, resulting in different expected future trajectories. As a possible purpose of providing such an estimate, we refer to the motion planning problem using predictive controllers. Therein, an estimation of the probabilities of several candidate future trajectories of TPs allows us to optimize with respect to different outcomes depending on their probabilities, as in our previous work Benciolini et al. (2023). Nevertheless, the algorithm for information handling is potentially general and applicable for other purposes.
Remark 1. Our algorithm provides a reliable combined estimate of the probability of the currently intended behavior of traffic participants, which is suitable to be used to predict future maneuvers or future trajectories (given the intended maneuver). However, such (potential) prediction module is not part of our algorithm, whose output is the combined estimate of the probabilities of candidate behaviors.
3 Opinions
In this section, we rigorously define the concept of opinion and explain how opinions can be obtained from data. Then, Section 4 outlines the mechanism to combine opinions. Depending on the application, different definitions of opinion are possible. The aim of our approach is to combine different sources of information explicitly assessing and handling the inherent uncertainty stemming from incomplete information and from relying on approximated models. Each event or singleton is associated with a possible behavior or maneuver of the TP, determining a (nominal) future trajectory.
In order to quantitatively take the uncertainty into account, rather than the Bayesian probability framework we employ Belief Function Theory Shafer (1976). Probabilities assigned to events are called belief masses. In the following, we assume that the sources of information provide estimations on the probability of the N outcomes possibly independently of a clear mathematical model. Therefore, the considered estimates of probabilities are in fact subjective probabilities Kahneman and Tversky (1972).
Definition 1. An opinion is the vector
where scalars b1, … , bM, μ ≥ 0 are the belief masses. Opinions are 1-norm unit vectors, i.e.,
A major difference of BFT compared to Bayesian probability is that probability can be assigned not only to each singleton event but also to the union of several singletons Srivastava (2011). Thus, the number of considered belief masses can be larger than the number of singleton events, i.e., M ≥ N, since, different belief masses can refer to non-mutually-exclusive events. This allows more flexibility in the information handling, considering that some sources of information might not be able to distinguish between different singleton events, and thus only assess the probability of their union. Furthermore, μ is the belief mass assigned to the union of all singletons and is called uncertainty Jøsang (2019b). Variable μ gives an additional degree of freedom to quantify the epistemic uncertainty, e.g., assessing the reliability of the information carried by the other belief masses. Uncertainty μ is understood as the belief mass of the whole outcome set, that is, the probability of any of the considered outcomes to occur. Since it represents the gap between the sum of the belief masses of the considered events and 1, the uncertainty is a measure of the inaccuracy of the information, representing the belief mass that cannot be allocated and anyhow further specified yet. Thus, μ is inversely proportional to the subjective confidence in the opinion.
Remark 2. Belief masses b1, … , bM are not probabilities, since they do not add up to one and are referred also to as unions of singletons. Nevertheless, standard probabilities are obtained for example, equally dividing probabilities of unions between all considered events. In doing so, also the belief mass of uncertainty must be equally split among all events.
3.1 Example of opinion generation
In this section, an example of opinion generation for a TP motion estimation application is given, to clarify how belief masses and uncertainty can be estimated from data. As previously mentioned, the opinion generation takes place upstream of our method and is not part of it, thus this section serves as a purely explanatory example. Any other opinion generation mechanism resulting in opinions in the form (1) is suitable.
We consider a set of candidate behaviors or maneuvers, each determining a (nominal) future trajectory, and propose an opinion generation mechanism based on the lateral y-position of a TP measured by a noisy sensor. For each considered candidate behavior, let yi, i = 1, … , N be the y-position of the nominal trajectory realizing the behavior. Furthermore, for every candidate behavior, we assume that the variance
then rescaling masses
Then, to assess the uncertainty of the probabilities obtained from (3), we consider the perturbation of the distribution of
where
Finally, the opinion is obtained as
that is, rescaling the probabilities from (3) given the quantified uncertainty. Depending on the source of information, a similar approach can be used to generate other opinions.
Remark 3. The same procedure applied to the longitudinal velocity of a TP approaching an intersection would not be able to discern between a right and a left turn. Indeed, in both cases, the expected longitudinal speed profile would be the same, as it is reasonable to imagine that a vehicle needs to slow down in a similar way when approaching the intersection. In this case, it is more reasonable to estimate the belief mass of proceeding straight and of a turn, without further specifying the direction of the turn. This is the reason why the proposed algorithm admits sources that specify the belief masses of unions of singletons, allowing more flexibility.Additionally, non-sensor sources can be included, for example, using statistics of the recorded traffic. Belief masses can be set proportionally to the statistical frequency of each behavior, and the uncertainty can be determined based on the variance of the recorded data. In this case, the resulting opinion is independent of the current behavior of a TP but rather constitutes a bias, which can be included in the information fusion.
Remark 4. Independently of the opinion generation mechanism, the choice of the set of candidate behaviors plays a crucial role, as previously discussed in Benciolini et al. (2023). However, should a TP execute a maneuver that does not belong in the set of considered behaviors, the uncertainty component would increase, signalizing that none of the considered modes can be reliably trusted.
Remark 5. In this work, a discrete set of candidate intended behaviors is considered. Nevertheless, in practice the possible future trajectories of TPs are infinite. Although this is undoubtedly a limitation of the approach, the N candidate trajectories are to be intended as nominal trajectories each representing a cluster of similar future motions, as our algorithm aims to return the probability of high-level behaviors. Once the high-level behavior has been recognized (and fixed), an appropriate model can be fit to estimate the precise parameters describing the motion of the TP, thus yielding a refined prediction of the future trajectory. However, the prediction module to forecast the exact future positions of the TPs is not included in our algorithm, which is intended to estimate the probability of candidate high-level behaviors. For such purposes, a discrete set of candidate nominal trajectories is sufficient.
4 Combination of opinions
In this section, we outline the two steps composing the proposed belief processing algorithm, consisting of the combination of information from multiple sources and of the temporal propagation.
4.1 Combination of multiple sources
Here we introduce the first opinion combination mechanism. The aim is to gather the whole information collected at the current iteration, that is, merge opinions
Remark 6. In the following formulation of the algorithm, we assume independence of the nS sources. When some of the considered sources are dependent, they should be combined into a single opinion upstream of our algorithm, so that the input to the algorithm consists of nS independently generated beliefs. Alternatively, the algorithm can be adapted to handle dependent sources along the lines of Denoeux (2006).To combine the most recent opinions generated by different sources of information, we use a revised version of Dempster’s rule of combination Srivastava (2011) allowing the combined opinion to only consist of singletons and of the union of all singletons. Opinions are iteratively combined two at a time. We assume possibly heterogeneous sources of information, thus opinions might, in general, consider different unions of singletons. Given two opinions ωA and ωB, the new belief masses for all singletons i = 1, … , N and the overall uncertainty are obtained as
where
Theorem 1. The combined uncertainty
Proof. The proof is given in Appendix A.As a result, the more opinions are considered, the smaller the uncertainty of the combination is, following the idea that more independent sources make the information more reliable. However, this effect might also be undesirable, if the sources of information contradict one another. For this reason, we add a conflict detection mechanism, that reassigns part of the belief mass to the uncertainty of the combined opinion
where bA and bB contain all belief masses of the opinions but the uncertainty component, i.e.,
As for any two given sources i, j the conflict is 0 ≤ Ci,j ≤ 1, so is also the coefficient in brackets in (8a). As a result, the adjusted belief masses
4.2 Temporal propagation
After combining the information collected through different sources in the current time step, the combined opinion is mixed with the information collected up to the previous step. The aim of this second combination is the temporal propagation of the information, allowing the detection of patterns that are revealed over multiple steps. At the same time, providing a stable and reliable estimate preventing large fluctuations between consecutive time steps is of primary concern. Therefore, we adopt the Weighted Belief Fusion (WBF) operator Jøsang (2019b).
Opinion
Observe that from (9), if one of the two opinions is certain (μ = 0), then the result coincides with that one, that is the other one is neglected and uncertainty is also set to zero. If both opinions are certain but indicate different beliefs, then ωk is set to the completely uncertain opinion, to signal that the information is completely unreliable.
In general, the resulting opinion is obtained as a weighted average of the two opinions, accounting for each of them depending on its uncertainty. Moreover, in this case, uncertainty does not necessarily decrease and, for example, the combination of two identical opinions results in the same opinion as an output, leaving the level of uncertainty unchanged. Indeed, WBF can be adopted under the assumption of dependent sources, thus additional sources do not necessarily result in additional evidence Jøsang (2019b).
5 Simulation results
In this section, we showcase the belief processing algorithm through numerical simulations in SUMO Krajzewicz et al. (2002). SUMO is a widely used open-source traffic simulation environment to validate and compare algorithms in urban and highway environments, providing a microscopic simulation platform that includes models of different modes of transportation, including pedestrians, bicycles, and vehicles, providing a realistic representation of traffic dynamics.
We consider two scenarios involving processing information provided by different sources to estimate the intended maneuver executed by a vehicle approaching an intersection and a pedestrian. We consider both the case in which sources provide coherent individual estimations and the case with conflict among sources. We compare our BFT-based algorithm with the IMM algorithm. The IMM algorithm consists of one Kalman Filter for every candidate behavior, and estimates from each filter are combined depending on the estimated probability, accounting for possible switches between behaviors occurring between consecutive time steps.
In the simulations, the BFT-based algorithm combines opinions generated by three sources: a sensor for the lateral position applying the procedure presented in Section 3; a sensor for the longitudinal velocity also applying the procedure from Section 3; a constant opinion representing traffic statistics. The IMM algorithm is implemented along the lines of (Benciolini et al., 2023; Section IV-B), but considering as measurements the lateral position and the longitudinal velocity. The motion of both the vehicle and the pedestrian is realized using the TraCI library in SUMO and noisy measurements are used in both estimation frameworks.
5.1 Uncertain behavior of a vehicle
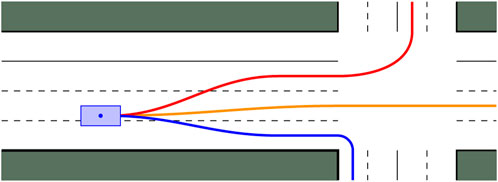
In the first simulation, a vehicle approaches an intersection on a three-lane road and is detected by sensors of an automated vehicle position on the same road, behind. Alternatively, the lateral position and the longitudinal speed of the vehicle could be measured by sensors placed on the infrastructure at the intersection and communicated to connected vehicles. Finally, the traffic statistics representing the third opinion, as mentioned above, are assumed to be available from an online server. The candidate intended behaviors are: A) right turn, B) proceed straight, C) left turn, see Figure 2. In reality a larger number of candidate behaviors could be included, so as to differentiate among multiple rates for the lane change and the turn, for example. However, a few considerations concerning the choice of multiple candidate behaviors representing relatively similar future motions arise, as discussed in (Benciolini et al., 2023; Section VII). For simplicity, in the following, we consider only three candidate behaviors, each intended as representative of a cluster of possible trajectories.
The vehicle exhibits ambiguous behavior as it approaches the intersection, possibly simulating a distracted driver. The vehicle stays in the center lane, as to proceed straight, but not at the center, rather proceeds irregularly and a little to the right of the lane, close to the edge. Thus, the opinion based on the lateral position regards going straight as the most likely maneuver, although the belief mass of a right turn maneuver is non-negligible, see Figure 3A. Furthermore, the vehicle slows down, therefore the opinion based on the longitudinal velocity tends to give a higher belief mass to the turn maneuver, see Figure 3B. This behavior is the union of the left and of the right turn maneuvers, that are not distinguishable considering the longitudinal velocity. Finally, the BFT algorithm includes a constant bias
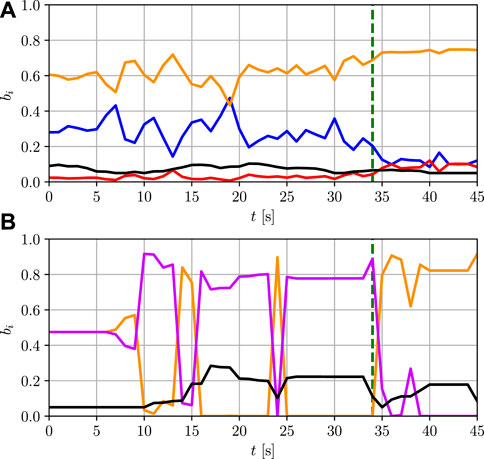
FIGURE 3. Opinions generated by different sources. (A): Opinion generated from lateral position measurements: right turn (blue), proceed straight (orange), left turn (red), uncertainty (black). (B): Opinion generated from longitudinal velocity measurements: turn (purple), proceed straight (orange), uncertainty (black). The vertical line in green represents the moment in which the vehicle reaches the intersection and proceeds straight.
The result of the estimation for the two frameworks is presented in Figure 4A and Figure 4B, respectively. While the vehicle is still approaching the intersection and showing ambiguous behavior, the opinions produced by the three sources are conflicting. The combination provided by our BFT-based algorithm generally assigns the relative highest belief to the proceed straight maneuver, which is altogether to be considered the most likely. However, the uncertainty is very high, quantitatively expressing that a reliable estimate cannot be extracted from the current data. Therefore, a motion planner based on the BFT estimate might make use of the uncertainty information to use caution while the intention of this TP is not clear and the prediction could not be reliable. However, once the vehicle actually reaches the intersection, the conflict between sources is resolved and the belief mass of the proceed straight maneuver gradually increases and the uncertainty decreases. Conversely, the IMM estimation is extremely noisy and shows large and repetitive fluctuations even between consecutive time steps, since none of the models can consistently explain the data. Moreover, confidence oscillates between right turn and left turn, whereas the proceed straight maneuver only emerges as dominant when the vehicle reaches the intersection. As a matter of fact, the IMM considers the dynamics of the model, thus the irregular behavior is repeatedly interpreted as the beginning of a turning maneuver. The IMM estimation is not reliable enough to be used for the prediction of TP future trajectories.
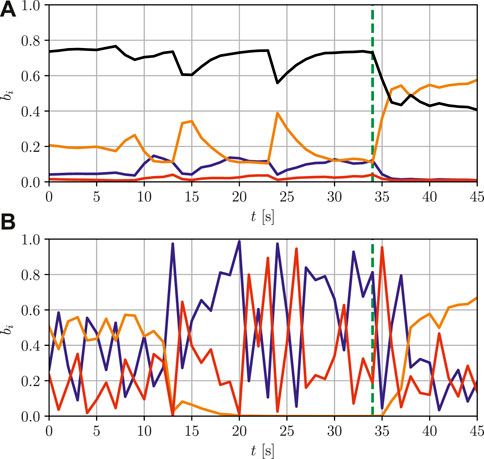
FIGURE 4. Probability estimate produced by the two frameworks: right turn (blue), proceed straight (orange), left turn (red), uncertainty (black). (A): Combined opinion generated by the BFT-based algorithm. (B): Probabilities estimated by the IMM. The vertical line in green represents the moment in which the vehicle reaches the intersection and proceeds straight.
The IMM does not explicitly quantify probability uncertainty, rather model mismatches result in large estimation variance for the state estimate, which, depending on the application, might be impractical. Moreover, different sensors are included in the IMM algorithm as different outputs of the model. Thus, the handling of the degree of uncertainty of different sources in the IMM is restricted to specifying different statistical properties of the disturbances in the underlying models. However, such statistical properties can not be straightforwardly adapted online depending on the data collected over time, thus the IMM algorithm is less suited to cope with sources with different reliability. Furthermore, any conflict between the information provided by each sensor is not explicitly addressed and reflects in large fluctuations in the estimate yielded at consecutive time steps.
5.2 Clear behavior of a pedestrian
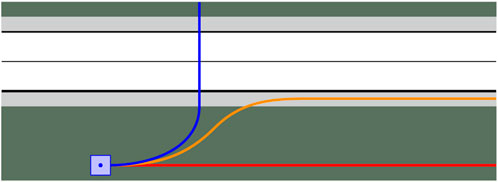
In the second simulation, the two frameworks are compared in estimating the intended behavior of a pedestrian, initially located on the grass in the vicinity of the road. Also this scenario assumes that the position and speed of the pedestrian are detected by sensors of the intelligent infrastructure on the side of the road or by sensors of an automated vehicle on the street, moving from left to right, that may potentially cross the path of the pedestrian. The three candidate behaviors are: A) remain on the grass, B) move to the sidewalk, C) jaywalk, see Figure 5. For this simulation, both the BFT-based algorithm and the IMM collect measurements of the lateral velocity, rather than of the lateral position. Furthermore, the bias is set to
The results of the estimation for the two frameworks are presented in Figure 6A and Figure 6B, respectively. Despite being discouraged by the bias opinion, the BFT algorithm quickly recognizes that the pedestrian wants to jaywalk. The two sensor-based opinions generate coherent estimates, thus the uncertainty of the combination is mainly due to partially contradicting measurements, because of the noise, and due to conflicts with the bias opinion. The latter, however, has a large uncertainty, being based on statistics. Therefore, the conflict handling mechanism introduced in Section 4.1 does not severely affect the estimation and the uncertainty of the combined estimate is considerably smaller than in the previous simulation. Finally, the IMM also promptly recognizes that the pedestrian will jaywalk. However, due to the lack of the uncertainty component in the estimate, model mismatches and noisy measurements result in considerably large fluctuations in the estimated probabilities, requiring post-processing of the estimate to smooth the results.
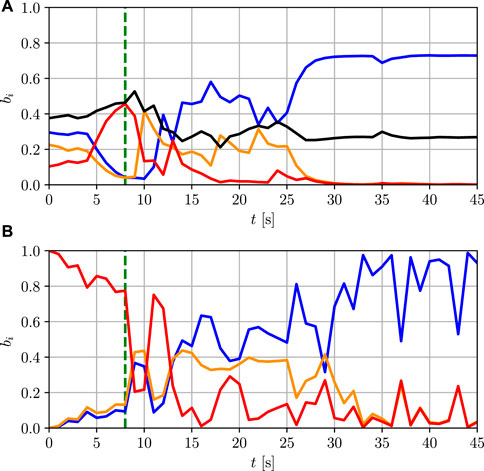
FIGURE 6. Probability estimate produced by the two frameworks: grass (red), sidewalk (orange), jaywalking (blue), uncertainty (black). (A): Combined opinion generated by the BFT-based algorithm. (B): Probabilities estimated by the IMM. The vertical line in green represents the moment in which the pedestrian starts moving toward the road.
Observe that in practice the pedestrian might cross the road at different locations. To account for this, further candidate trajectories could be included, each considering a different crossing location. Furthermore, once the most likely nominal crossing location has been recognized, an ad hoc model could be fit, so that the exact crossing location over a continuous range can be identified, instead of relying only on a few nominal candidate locations.
5.3 Belief function theory-based safety constraints
In this section, we briefly discuss how the estimate produced by this algorithm can be applied to the design of collision avoidance safety constraints. In Benciolini et al. (2023), we have proposed an algorithm to iteratively estimate the probability of several candidate trajectories of TPs using the IMM algorithm. Then, probabilistic safety constraints are designed in a Stochastic Model Predictive Control fashion, that is, requiring collisions to be avoided at least with a specified probability. For each candidate trajectory, the specified level of probability for constraint satisfaction is directly computed from the estimated probability for that specific trajectory. Thus, only those future TP trajectories currently considered sufficiently likely are taken into consideration in the planning of the future motion of the automated vehicle. In doing so, we refrain from excessive conservatism that would occur if all candidate future trajectories of TPs were considered at all times. Nevertheless, none of the candidate future trajectories is permanently excluded and each candidate might be considered in future sampling times if the estimate of the TP behavior changed.
In such a framework, the probability estimates for each candidate behavior play a major role. On the one hand, probability estimates must be adapted iteratively depending on the most recently collected data. On the other hand, too sudden and repetitive variations in the estimated probabilities make the safety constraints for the automated vehicle inconsistent among consecutive steps, causing problems in the motion planning for the automated vehicle. Therefore, the probability estimates provided by the algorithm presented in this paper are well-suited, since inconsistencies between estimates are dealt with using the concept of uncertainty and the final estimates are more steady over time. Moreover, the uncertainty parameter might be used to enforce additional safety constraints for the automated vehicle, designed to prevent aggressive maneuvers from being taken if the motion of the TPs is not clearly recognizable yet.
Differently, with minor adaptations of the presented algorithm, the quantification of the probability of unions of candidate trajectories could be maintained also in the final opinion provided by the algorithm, that is, after the temporal propagation outlined in Section 4.2. Then, the additional information might be used to enforce additional safety constraints for the automated vehicle, designed to prevent aggressive maneuvers from being taken if the motion of the TPs is not clearly recognizable yet. Similarly, since the uncertainty expresses the reliability of the estimation, some of the constraints related to currently unlikely future trajectories could be tightened depending on the estimated uncertainty, in order not to exclude possible future trajectories that currently seem unlikely due to insufficient information. The discussion on the design of safety constraints based on BFT is worth a separate discussion, which we will address in a separate publication.
6 Conclusion
We presented a novel information fusion algorithm to combine information resulting from multiple sources in a coherent and steady estimation of the behavior of TPs. By leveraging BFT, an explicit quantification of the uncertainty of the estimates is provided, representing the reliability of the information. At first, opinions provided by independent sources during the last time step are combined, evaluating and handling possible conflicts. Then, the information is propagated over time, giving steadiness to the estimate, which is suitable to be used as a basis for a motion planning algorithm. Sources that cannot discern between all considered individual behaviors, but rather assess the probability of unions of singletons can also be included. We discussed the advantages through numerical simulations in SUMO and compared the performances with the IMM algorithm.
The proposed algorithm allows great flexibility and is well suited to combining information from possibly inconsistent sources. When the different sources provide individual estimates of the intended behavior of TPs that do not match, the degree of conflict is evaluated and part of the belief mass is transferred to the uncertainty parameter. Other estimation mechanisms that do not address possible contradictions among the information provided by different sources, like the IMM, tend to produce inconsistent results over consecutive sampling times, making the overall combined estimate unreliable and therefore unfit for practical application. Furthermore, by propagating the estimation over time, sudden variations in the estimate probabilities are attenuated. This aspect is especially important when human TPs are considered, as sudden contradictory movements for a short time are often encountered due to distraction. The temporal propagation results in an estimate which is less sensitive to sudden but short changes in the motion and which is steadier over time. Nevertheless, if changes in the motion of TPs persist for a longer time, eventually the estimate will reflect them, as desirable. Finally, the estimate provided by our algorithm incorporates a quantitative, though subjective, measure of the reliability of the information contained, which motion planning algorithms can take advantage of.
In future extensions of the approach presented in this work, the temporal correlation between the opinions generated by sources over time and the impact on the combined estimate should be investigated, as this aspect is not accounted for in the present formulation.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
TB initiated the idea for the paper and is responsible for the design of the algorithm, the discussion of the properties, the conceptualization of the simulations, and discussion of the results, and the drafting of the manuscript. XZ contributed to the design of the algorithm and to the discussion of its properties, and is responsible for the implementation of the simulations. DW and ML contributed to the conception of the research project and to the critical revision of the manuscript. All authors contributed to the article and approved the submitted version.
Funding
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) with the project number 490649198.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Benciolini, T., Wollherr, D., and Leibold, M. (2023). Non-conservative trajectory planning for automated vehicles by estimating intentions of dynamic obstacles. IEEE Trans. Intelligent Veh. 8, 2463–2481. doi:10.1109/tiv.2023.3234163
Berclaz, J., Fleuret, F., Turetken, E., and Fua, P. (2011). Multiple object tracking using K-shortest paths optimization. IEEE Trans. Pattern Analysis Mach. Intell. 33, 1806–1819. doi:10.1109/tpami.2011.21
Bewley, A., Ge, Z., Ott, L., Ramos, F., and Upcroft, B. (2016). “Simple online and realtime tracking,” in 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, September 25-28, 2016.
Carvalho, A., Gao, Y., Lefevre, S., and Borrelli, F. (2014). “Stochastic predictive control of autonomous vehicles in uncertain environments,” in 12th International Symposium on Advanced Vehicle Control, TUAT, Japan, September 2014.
Denoeux, T. (2006). “The cautious rule of combination for belief functions and some extensions,” in 2006 9th International Conference on Information Fusion, Florence, Italy, 10-13 July 2006.
Deo, N., Rangesh, A., and Trivedi, M. M. (2018). How would surround vehicles move? A unified framework for maneuver classification and motion prediction. IEEE Trans. Intelligent Veh. 3, 129–140. doi:10.1109/tiv.2018.2804159
Ding, W., and Shen, S. (2019). “Online vehicle trajectory prediction using policy anticipation network and optimization-based context reasoning,” in 2019 International Conference on Robotics and Automation (ICRA), Montreal, Canada, 24 May 2019.
Genovese, A. F. (2001). The interacting multiple model algorithm for accurate state estimation of maneuvering targets. JOHNS HOPKINS Apl. Tech. Dig.
Gerónimo, D., López, A. M., Sappa, A. D., and Graf, T. (2010). Survey of pedestrian detection for advanced driver assistance systems. IEEE Trans. Pattern Analysis Mach. Intell.
Ghorai, P., Eskandarian, A., Kim, Y.-K., and Mehr, G. (2022). State estimation and motion prediction of vehicles and vulnerable road users for cooperative autonomous driving: A survey. IEEE Trans. Intelligent Transp. Syst. 23, 16983–17002. doi:10.1109/tits.2022.3160932
Jøsang, A. (2019a). “Belief mosaics of subjective opinions,” in International Conference on Information Fusion (FUSION), Ottawa, ON, Canada, July 2-5, 2019.
Kahneman, D., and Tversky, A. (1972). Subjective probability: A judgment of representativeness. Cogn. Psychol. 3, 430–454. doi:10.1016/0010-0285(72)90016-3
Krajzewicz, D., Hertkorn, G., Feld, C., and Wagner, P. (2002). SUMO (simulation of urban MObility). Open-Source Traffic Simul.
Lefevre, S., Vasquez, D., and Laugier, C. (2014). A survey on motion prediction and risk assessment for intelligent vehicles. Robomech J. 1, 1. doi:10.1186/s40648-014-0001-z
Martin, A. (2019). “Conflict management in information fusion with belief functions,” in Information quality in information fusion and decision making. Editors É. Bossé, and G. L. Rogova (Cham: Springer International Publishing). Information Fusion and Data Science.
Milisavljevic, N., and Bloch, I. (2003). Sensor fusion in anti-personnel mine detection using a two-level belief function model. IEEE Trans. Syst. Man, Cybern. Part C 33, 269–283. doi:10.1109/tsmcc.2003.814034
Moeslund, T. B., Hilton, A., and Krüger, V. (2006). A survey of advances in vision-based human motion capture and analysis. Comput. Vis. Image Underst. 104, 90–126. doi:10.1016/j.cviu.2006.08.002
Reineking, T. (2014). “Belief functions: theory and algorithms,”. Ph.D. thesis (Bremen, Germany: Universität Bremen).
Shafer, G. (1976). A mathematical theory of evidence. New Jersey, United States: Princeton University Press.
Song, X., Chen, K., Li, X., Sun, J., Hou, B., Cui, Y., et al. (2021). Pedestrian trajectory prediction based on deep convolutional LSTM network. IEEE Trans. Intelligent Transp. Syst. 22, 3285–3302. doi:10.1109/tits.2020.2981118
Srivastava, R. P. (2011). An introduction to evidential reasoning for decision making under uncertainty: bayesian and belief function perspectives. Int. J. Account. Inf. Syst. 12, 126–135. doi:10.1016/j.accinf.2010.12.003
Tanzmeister, G., Thomas, J., Wollherr, D., and Buss, M. (2014). “Grid-based mapping and tracking in dynamic environments using a uniform evidential environment representation,” in IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, May - 7 June 2014.
Tanzmeister, G., and Wollherr, D. (2017). Evidential grid-based tracking and mapping. IEEE Trans. Intelligent Transp. Syst., 1–14. doi:10.1109/tits.2016.2608919
Tran, Q., and Firl, J. (2014). “Online maneuver recognition and multimodal trajectory prediction for intersection assistance using non-parametric regression,” in 2014 IEEE Intelligent Vehicles Symposium (IV), Anchorage, AK, United States, June 4-7, 2023.
Wojke, N., Bewley, A., and Paulus, D. (2017). “Simple online and realtime tracking with a deep association metric,” in 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, September 17-20, 2017.
Woo, H., Ji, Y., Kono, H., Tamura, Y., Kuroda, Y., Sugano, T., et al. (2017). Lane-change detection based on vehicle-trajectory prediction. IEEE Robotics Automation Lett. 2, 1109–1116. doi:10.1109/lra.2017.2660543
Wu, H., Siegel, M., Stiefelhagen, R., and Yang, J. (2002). “Sensor fusion using Dempster-Shafer theory [for context-aware HCI],” in IEEE Instrumentation and Measurement Technology Conference, Anchorage, AK, USA, 21-23 May 2002.
Xin, L., Wang, P., Chan, C.-Y., Chen, J., Li, S. E., and Cheng, B. (2018). “Intention-aware long horizon trajectory prediction of surrounding vehicles using dual LSTM networks,” in 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, Hawaii, USA, November 2018.
Zhao, L., and Thorpe, C. (2000). Stereo- and neural network-based pedestrian detection. IEEE Trans. Intelligent Transp. Syst. 1, 148–154. doi:10.1109/6979.892151
Zhou, Z., Oguz, O. S., Leibold, M., and Buss, M. (2020). A general framework to increase safety of learning algorithms for dynamical systems based on region of attraction estimation. IEEE Trans. Robotics 36, 1472–1490. doi:10.1109/tro.2020.2992981
Zhou, Z., Oguz, O. S., Leibold, M., and Buss, M. (2021). Learning a low-dimensional representation of a safe region for safe reinforcement learning on dynamical systems. IEEE Trans. Neural Netw. Learn. Syst. 34, 2513–2527. doi:10.1109/tnnls.2021.3106818
Appendix: Proof of theorem 1
Proof. We show that
Then, since from (2)
that is, the uncertainty of the combined opinion is upper bounded by the uncertainty of each individual opinion.
Keywords: information fusion, trajectory estimation, estimate combination, uncertainty handling, belief function theory
Citation: Benciolini T, Zhang X, Wollherr D and Leibold M (2023) Information fusion for online estimation of the behavior of traffic participants using belief function theory. Front. Future Transp. 4:1216527. doi: 10.3389/ffutr.2023.1216527
Received: 04 May 2023; Accepted: 09 August 2023;
Published: 29 August 2023.
Edited by:
Felix Antreich, Aeronautics Institute of Technology (ITA), BrazilReviewed by:
Noah Goodall, Virginia Transportation Research Council, United StatesOmar García Crespillo, German Aerospace Center (DLR), Germany
Copyright © 2023 Benciolini, Zhang, Wollherr and Leibold. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tommaso Benciolini, dC5iZW5jaW9saW5pQHR1bS5kZQ==
 Tommaso Benciolini
Tommaso Benciolini Xuhui Zhang
Xuhui Zhang Dirk Wollherr
Dirk Wollherr Marion Leibold
Marion Leibold