
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Future Transp., 16 June 2022
Sec. Connected Mobility and Automation
Volume 3 - 2022 | https://doi.org/10.3389/ffutr.2022.915219
This article is part of the Research TopicTransport Demand Management in the Era of App-influenced MobilityView all 4 articles
With advances in digitization and automation, autonomous mobility on demand services have the potential to disrupt the future mobility system landscape. Ridepooling services in particular can both decrease land consumption by reducing the need for parking and increase transportation efficiency by increasing the average vehicle occupancy. Nevertheless, because ridepooling services require a sufficient user base for pooling to take effect, their performance can suffer if multiple operators offer such a service and must split the demand. This study presents a simulation framework for evaluating the impact of competition and cooperation among multiple ridepooling providers. Two different kinds of interaction via a broker platform are compared with the base cases of a single monopolistic operator and two independent operators with divided demand. In the first, the broker presents trip offers from all operators to customers (similar to a mobility-as-a-service platform), who can then freely choose an operator. In the second, a regulated broker platform can manipulate operator offers with the goal of shifting the customer-operator assignment from a user equilibrium towards a system optimum. To model adoptions of the service design depending on the different interaction scenario, a game setting is introduced. Within alternating turns between operators, operators can adapt parameters of their service (fleet size and objective function) to maximize profit. Results for a case study based on Manhattan taxi data, show that operators generate the highest profit in the broker setting while operating the largest fleet. Additionally, pooling efficiency can nearly be maintained compared to a single operator. The regulated competition benefits not only operators (profit) and cities (increased pooling efficiency), but customers also experience higher service rate, though they need to accept slightly increased waiting and travel time due to increased pooling efficiency. Contrarily, when users can decide freely, the lowest pooling efficiency and operator profit is observed.
With the increased availability of mobile internet, mobility-on-demand (MOD) services have become increasingly popular over the last decade. In times of urbanization, they can represent an alternative to private vehicles that offers a similar convenience. MOD services result in a higher temporal utilization of vehicles which, if replacing private vehicle trips, can potentially free up urban space that would otherwise be used for parking. Furthermore, ridepooling services have the potential to increase the average vehicle occupancy during trips, thereby resulting in more spatially efficient utilization of the road. The probability of finding and pooling similar trips increases with demand density. Therefore, the pooling potential increases with the scale of supply and demand. As a consequence, fragmentation of the ridepooling market into multiple independent competitors can be expected to decrease the efficiency of each competitor. Mobility-as-a-service (MaaS) platforms represent a possibility to break the stark independence of competitors, as offers from multiple mobility service providers are collected in one place for travelers.
Compared to current MOD services, automation can change the cost structure significantly (Bösch et al., 2018). When these cost reductions from the fleet operation with autonomous vehicles are translated into cheaper fares for users, disruptions to the transportation systems as we know them are possible in the form of massive modal shifts and system utilization. Hence, city authorities are confronted with the questions of whether and how autonomous mobility-on-demand (AMOD) systems and competition between multiple providers should be regulated.
This paper studies how interaction between AMOD operators can counteract the effects of competition and fragmentation. To this end, the concept of an AMOD broker is introduced which is a (possibly regulated) platform—similar to a MaaS platform—for multiple AMOD operators. As illustrated in Figure 1), the broker collects trip offers from multiple AMOD providers and forwards them to the customers. In addition, the broker can be regulated to adapt the offers to align the platform with city goals. The adaptation can range from sorting the offers in a certain order or manipulating prices, to the suppression of certain offers which are in conflict with city goals. The effect of the regulating measures can be compared with moving the dynamic traffic assignment from a user equilibrium towards the system optimum.
The goal of this study is to compare different types of AMOD provider interaction and their impact on the providers. More specifically, we investigate the following scenarios with the help of simulations: a monopolistic AMOD service, independent AMOD providers, and the two forms of broker systems (unregulated and fully regulated).
Several studies deal with the operation of AMOD fleets and its impacts. Even without pooling, a single AV can replace a significant number of private vehicles (Fagnant et al., 2015) or carsharing vehicles (Dandl and Bogenberger, 2019). Optimization of request and repositioning assignments based on demand estimations can further improve fleet performance (Hyland and Mahmassani, 2018; Hörl et al., 2019b; Dandl et al., 2019c). However, without pooling, these vehicle reductions only affect stationary traffic, i.e., parking space. To observe improvements to traffic flow, ridepooling is required (Engelhardt et al., 2019a; Ruch et al., 2020). The optimization of ridepooling assignments is a challenging problem, which can be addressed with graph-based approaches (Santi et al., 2014; Alonso-Mora et al., 2017) and heuristics based on them (Simonetto et al., 2019; Hyland and Mahmassani, 2020). For ridepooling services, positive scaling properties, i.e., a higher efficiency for higher levels of demand, are observed in both analytical and simulation models (Tachet et al., 2017; Bilali et al., 2020). Two effects play into this scaling behavior for ridepooling systems: 1) a higher density of vehicles means that the approach becomes shorter (similarly to in the ridehailing case), and 2) the probability of finding trips that can be matched with only minor detours increases with demand.
These operational studies assume a fixed exogenous demand, and the problem is to serve this demand as efficiently as possible. To study the impact of AMOD on transportation systems, the integration of AMOD into demand models is necessary. Open-source software packages like SimMobility (Nahmias-Biran et al., 2020; Oke et al., 2020), MATSim (Hörl et al., 2019a; Kaddoura et al., 2020), Polaris (Gurumurthy et al., 2020), and mobiTopp (Wilkes et al., 2021), as well as commercial software solutions already have capabilities to model AMOD supply and demand interactions. Most of these demand models utilize a pre-day assignment of AMOD demand, be it by iterative learning or a mode choice model. Wilkes et al. (2021) developed a within-day mode choice model, which is based on real-time information of the fleet and thereby relevant for modeling MaaS platforms.
Most of the previously mentioned references study a single AMOD operator; a generalization to multiple independent operators has been implemented in Dandl et al. (2019a), and an operator with multiple service offers (hailing and pooling with different vehicle sizes) was investigated in Atasoy et al. (2015); Liu et al. (2019). For ridehailing, the impact of multiple AMOD operators in the same market is analyzed with a theoretical model by Séjournè et al. (2018) and data-driven models with simulation by Kondor et al. (2022). Séjournè et al. (2018) show that demand patterns are crucial when it comes to the division of the market and find two phases. The first is denoted “fragmentation resilient” and describes a system where the price of sharing the market decreases with the size of the market; in the other phase, denoted “fragmentation affected”, a division of the market generates much higher costs regardless of the size of the market because empty vehicle repositioning is required to balance supply and demand. Kondor et al. (2022) derived a mathematical equation for the cost of non-coordinated market fragmentation and run simulations to find the coefficients for various cities. For ridepooling, Pandey et al. (2019) analyzed three models of multi-company market models—competitive, cooperative, and centralized—and derived approaches to address the resulting problems with linear assignment problems.
There are several studies examining the even more complex market dynamics for multiple ridehailing services with drivers. For instance, Jiang and Zhang (2018) study the effect of “double-apping” in a (human driven) ridehailing market with two competitors, where both drivers and customers have the possibility to use both ridehailing apps. They observed that users and drivers can benefit, but without any contract or guarantee that the other ridehailing provider will do the same, a ridehailing operator does not benefit from drivers serving customers of both providers. Qian and Ukkusuri (2017) study the competition between a traditional taxi and a ridehailing provider in a game, where passengers are the leaders and the two mobility providers are the followers. They find that fleet size and pricing policy significantly impact the outcome. In another study, Xi et al. (2021) propose a “name-your-own-price auction” in a MaaS platform, where travelers and a wide range of mobility service providers (with ridehailing being one of them) can submit a bid. They also use a leader-follower formulation, with the MaaS platform being the leader and the mobility service providers and the travelers being the followers.
AMOD providers do not just compete against each other. They can compete with, but also complement public transport, depending on their service designs. In most demand models, AMOD systems are treated as a separate competing mode. Positive and negative effects mainly depend on the number of users that are attracted from private vehicle or public transport modes. Additionally, AMOD systems can be utilized as feeder systems to increase intermodality and improve public transport (Liang et al., 2016; Wen et al., 2018). To avoid competition, AMOD routes can also be restricted/designed to complement the existing public transport system (Dandl et al., 2019b), or AMOD and public transport can be designed jointly (Pinto et al., 2019). With a growing market share of today’s MOD services, negative externalities of user-centric ridehailing can be observed (Henao and Marshall, 2019; Schaller, 2021). Therefore, the regulation of MOD (Li et al., 2019; Zhang and Nie, 2019)—with part of the focus on the regulatory protection of drivers—and of AMOD services (Simoni et al., 2019; Dandl et al., 2021; Mo et al., 2021) is becoming increasingly relevant. Simoni et al. (2019) study various congestion pricing models in the presence of an AMOD system. Dandl et al. (2021) consider an AMOD ridepooling service which is regulated such that it cannot offer guaranteed single-passenger rides. Moreover, they introduce a regulatory tri-level framework optimizing a congestion-based road toll, parking fees, public transport frequency, and an AMOD fleet limit, where the reaction of an AMOD provider to changed regulatory settings is taken into account. Mo et al. (2021) investigate how regulatory measures like fleet size limitations and public transport subsidies can steer the competition between AMOD and line-based public transport. The equilibrium state is found with an iterative approach, in which the AMOD operator is updated every iteration—representing a day—and the public transport service every month. These time scales should reflect the frequencies with which AMOD and public transport operators are likely to modify their service.
A collaboration of mobility services can help to create a better combined service offer, which could reduce private vehicle ownership and be beneficial to the service providers. MaaS platforms are one form of such collaboration. Typically, they at least collect information of multiple providers, offer the possibility to book mobility services, and provide a common method for payment (Smith and Hensher, 2020). The design and possible regulation of a MaaS platform, e.g., by pricing and bundling of services, can affect user decisions (Feneri et al., 2020) and ultimately help in reaching sustainability objectives (Muller et al., 2021).
This paper contributes several new aspects to the literature. While most previous studies focused on the ridehailing market, this paper evaluates the losses resulting from fragmented ridepooling demand. Moreover, the effects of different interactions between multiple operators and a central platform are compared. The potential benefits of a broker which selects between the offers of different providers, thereby representing the most extreme form of regulation on this platform, is examined and compared to a platform where customers select the offers by themselves. To the authors knowledge, this is the first study that additionally evaluates the adoption of the service design to optimize the operators profit for a given interaction scenario within a game setting. The case study shows the significant impact that fleet size and the operator objectives have on the level of service and overall transportation system.
This section describes the agent-based simulation environment, which is used to study different operator interactions. First, the simulation’s agents and process flow are introduced, and the representation of different AMOD operators is explained. Then, the operator module with the task to assign customers to vehicles is described in detail. Lastly, an iterative simulation to model possible service adaptations to the studied operator interactions (independent, unregulated and regulated broker) in addition to a monopolistic operator is presented.
The simulation environment consists of three or four main agents: 1) customers, who request trips from AMOD operator(s) and choose their travel mode; 2) operators, who provide the mobility service by operating a fleet of vehicles with the tasks to create mobility offers for customer requests and fulfill these offers in case customers accept them; 3) vehicles controlled and dispatched by an operator which specifies which, where, and in which sequence customers have to be picked up and dropped off; and 4) a broker, which makes decisions to regulate the platform in the broker scenarios.
Customer and vehicle agents move on a network G = (N, E) with nodes N and edges E connecting these nodes. A customer request is defined by the tuple
In so-called interaction scenarios, this study distinguishes several decision processes defining which specific operator is booked by a customer. The four different interaction scenarios implemented in this study are as follows:
1) Single Operator: In this scenario, only a single monopolistic AMOD operator is offering a ridepooling service, and therefore no interaction between operators is implemented. Customers requesting a trip from this operator always book a trip if they receive an offer, and if not, they leave the system unserved.
2) Independent Operators: In this scenario, multiple AMOD operators are offering a ridepooling service, but no direct interaction between them is assumed. Customers only request a trip from one of these operators, and they always book a trip if they receive an offer from this operator. If they don’t receive an offer, they leave the system unserved. From the simulation point of view, this scenario is equivalent to the Single Operator scenario, but with the demand for AMOD being split between the operators.
3) User Decision: In this scenario, multiple AMOD operators are offering the mobility service over a central platform, here referred to as a “broker”. Instead of interacting directly with one of the operators, customers request a trip from the broker, which forwards the request to each of the operators. The operators then each send an offer to the broker, which presents these options to the customer. The customer then chooses the offer with the highest user utility ϕuser (ui,o). If the broker does not receive an offer from either of the operators, the customer leaves the system unserved. A flowchart of this scenario is shown in Figure 2.
4) Broker Decision: In this scenario, multiple AMOD operators are also offering the mobility service via a central broker. Customers send their requests to the broker, which then forwards them to each of the operators, who send their offers back to the broker. In contrast to the User Decision scenario, however, rather than allowing the customer to choose their preferred offer, the broker chooses the offer which it deems best for the transportation system by evaluating the highest system utility ϕbroker (si,o). Therefore, a broker decision aims towards a system-optimal state, whereas the user decision reflects a quasi-user optimal scenario. A flowchart of this scenario is shown in Figure 2.
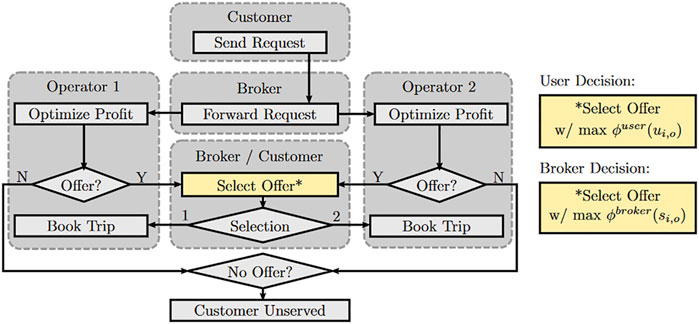
FIGURE 2. Flowchart of the User Decision and Broker Decision scenarios. The only difference between the scenarios is the criteria used to choose an offer, highlighted in yellow.
The main tasks of each operator are 1) to create offers for customers (or a broker) which serves as their basis to decide for or against the service, 2) to assign and schedule its vehicles to customers who have booked their service, and 3) distribute idle vehicles according to expected demand by assigning repositioning tasks.
The assignment of customers to vehicles and their corresponding schedules is modeled as a solution of a dynamic vehicle routing problem. With the set of vehicles Vo of operator o, we define a schedule ψk (v, Rγ) as the kth feasible permutation of stops for vehicle v ∈ Vo serving the subset of requests Rγ ⊂ Ro of all currently active requests Ro, i.e., all customers that are either 1) in-vehicle, 2) waiting for or in the process of pick-up, or 3) waiting for a response by the operator. Hereby, stops refer to origin and destination locations of requests in Rγ where boarding and alighting processes of the corresponding customers are performed. In this study, a schedule is called feasible if.
1. each customer is picked up before being dropped off,
2. at no point in time the number of on-board passengers exceeds the vehicle capacity cv,
3. each customer i ∈ Rγ has been or is scheduled to be picked up before a maximum waiting time
4. the in-vehicle travel time of each customer i ∈ Rγ is not increased by more than Δ compared to the direct travel time between
To compare different schedules, each schedule ψk (v, Rγ) is rated by an objective function ρα which we define in this study by
FIGURE 3. Sketch showing the influence of
Within the simulation, customers can request trips in every simulation time step of 60 s. Depending on the scenario, the customers or the broker decide for or against the service depending on the respective offers sent by the operators. In this study, an immediate decision process is assumed, i.e., the operators are informed that a customer is either booking a trip or declines an offer before the next customer request is considered.
In most cases, it is not meaningful to use global optimization to create an offer for a new customer requests. First, performing a global optimization for the ridepooling assignment problem is computationally very demanding. Additionally, many of the requests will be declined by the customers when they choose to book with the competing operator. Therefore, each time a new customer requests a trip in the offer phase, a heuristic is applied to find an initial solution for the assignment problem. This initial solution is used to create an offer. If the customer books the service, the solution (schedule) is assigned to the vehicle, otherwise the solution is discarded. Every 60 s, after all customer requests in one time step have been processed, a global re-optimization is performed for all currently scheduled or on-board requests. The two steps (offer creation, global re-optimization) are described in more detail in the following.
In the offer phase, an insertion heuristic is applied to find the initial solution from which the offer is created. In this heuristic, new feasible vehicle schedules are constructed by inserting customers into the currently assigned vehicle schedules. Because a schedule can only be feasible if this new customer can be picked up within
For re-optimizing the vehicle schedules once all new customers within the current simulation step have been processed, an algorithm based on that of (Alonso-Mora et al., 2017) is applied in this study. A high level description of the implementation is presented here, and the reader is referred to (Engelhardt et al., 2019b) for details. The idea of the algorithm is to find all feasible schedules first and solve an Integer Linear Problem (ILP) to assign these schedules afterwards. Since an exhaustive search is intractable for the ridepooling assignment problem, a guided search is applied which exploits the fact that most combinations of vehicles serving a set of requests are infeasible due to time constraints (if sufficiently strict).
Thereby, a V2RB (vehicle-to-request-bundle) Ψ(v, Rγ) is defined as the set of all feasible permutations k of schedules of vehicle v serving Rγ with
being the objective function value of this V2RB.
The guided search can be divided into the following three steps: In a first step, all feasible vehicle-customer combinations are searched. These combinations are defined as feasible for all vehicles theoretically able to reach the origin of the customer request within
Once all feasible V2RBs are created, the following ILP can be solved to assign the V2RBs:
Equation 4 selects the schedules with cost
To adjust the spatial distribution of vehicles for upcoming demand, a repositioning strategy is applied periodically. Every Trepo, a parameter-free rebalancing strategy based on (Pavone et al., 2012) is applied. After estimating available vehicles and expected demand for each taxi zone, a minimum transportation problem, which aims to minimize the travel costs to reach some zone supply and demand balance constraints, is solved.
The different interaction scenarios introduced in the beginning of this section describe different external environments in which the operators offer their service. Depending on these environments operators will adapt their service design to maximize profit. In this study, the adaptation of the service of the operators is modeled as a turn-based game (illustrated in Figure 4). Each operator starts with specific service parameters based on the scenario without interaction. In each turn, one operator has the active role, while the other one has the passive role. These roles are exchanged every turn. The active operator explores different sets of service parameters (with exhaustive search), while the service parameters of the passive operator remain constant. At the end of each turn, the active operator adopts the service parameters that resulted in the highest profit.
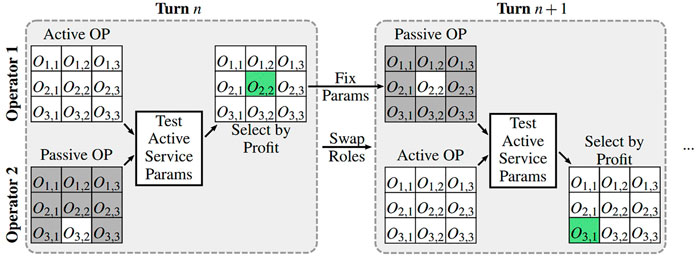
FIGURE 4. Illustration of the game. Operators take turns playing the “active” role. In each turn, the active operator tests all of its possible service parameters Ok,l against the passive operator’s fixed parameters. The parameters that bring the highest effective profit for the active operator are then used in the next turn, where the roles are reversed.
The profit P is calculated by the difference of revenue R and costs C after each simulation.
with Cserved being the set of all served customers,
To optimize this profit P for only a few days of simulation, operators would choose small fleets to increase overall vehicle utilization (including off-peak times). However, the service rate would suffer strongly leading to an unreasonable large number of customers that have to be rejected. Since such an unreliable service is improbable to survive on the long run, another term penalizing the number of requests, which did not receive an offer NC,no (within the given service quality constraints) during the simulation, should be considered. Hence, we define the effective profit Peff to be maximized within the game:
Thereby, pno is a penalty cost for each request without offer. pno and f will be determined within calibration simulations in the results section.
Alternating turns with operators maximizing their effective profit are repeated until equilibrium is reached. All operators adopting the same parameter set is one of the equilibrium states the game can converge in. In this case no operator has an advantage in changing their parameter sets anymore. Generally, it is not guaranteed to find such equilibrium states. Depending on the overall setting, it is for example feasible that operators with different market penetrations and therefore different fleet sizes also reflect a stable system. Nevertheless, it turns out that as long as certain symmetries between the operators are assumed as described in the following case study, these symmetric equilibrium states can be found in all scenarios tested.
We test the model on a case study for the publicly available taxi data set of Manhattan, NYC. The simulation inputs are described in the following.
Figure 5 shows the street network and the operating area of the simulated ridepooling services. All operators offer the service in the same operating area in this study. The street network G = (N, E) has been extracted from OpenStreetMap data using the Python library OSMnx (Boeing, 2017). Initially, edge travel times are assigned according to free flow speeds from the OpenStreetMap data. In order to replicate realistic travel times, edge travel times are scaled after every 15 min simulation time according to actual trip travel times within the NYC taxi trip data. Shortest (travel time) paths are computed using a combination of the classical Dijkstra algorithm and preprocessing origin-destination node pairs in lookup tables.
As demand for the ride pooling service, NYC taxi trips that are starting and ending within the operating area of Manhattan are used. Trip requests are created for the week from 2018/11/11 to 2018/11/18. Trip origins and destinations are matched onto the closest intersection nodes that are only connected to roads with classes “living street”, “residential”, “primary”, “secondary”, and “tertiary”. Presumably defective trip records with average travel times below 1 m/s or above 30 m/s are removed from the data set. Overall 1,511,476 trips remain in the data set. To decrease overall computational time, this set is subsampled to generate the requests for the ridepooling services: For each trip a random number between [0, 1] is drawn. If this random number is smaller than 0.1, the trip is transferred into the set of ridepooling requests resembling a 10% market penetration of the simulated ridepooling services. Using different random seeds, three set of request sets are generated and used within the simulations.
The rebalancing algorithm is called every Trepo = 15 min. Demand and supply forecasts are aggregated to the corresponding taxi zones. For simplicity, trip forecasts, i.e., the average number of incoming and outgoing trips within a time interval of 15 min per zone, are created by counting the overall trips in the data and multiplying the counts with the market penetration of 10%. In the case of multiple operators sharing the demand, it is assumed that all operators rebalance the vehicle fleet based on the same spatio-temporal forecast distribution. Therefore the average counts are additionally divided by the number of operators.
Further details on network and trip data processing can be found in (Syed et al., 2021).
We evaluate a system with a maximum of two ridepooling operators. It is assumed in this study that both operators offer a similar service quality. Namely, the operators use vehicles with maximum traveler capacity cv = 4. Additionally, they only offer trips to customers that do not exceed 1) a maximum waiting time of
With respect to the different interaction scenarios, the inputs for these scenarios are the following:
1) Single Operator: A single operator with the specified attributes serves the whole demand.
2) Independent Operators: The demand is split evenly between two operators. Each customer can only request a trip from the corresponding assigned operator.
3) User Decision: The broker forwards customer requests to both operators. In case a customer i receives offers from both operators, the decision to book with operator oi is made based on the evaluation of
with the arrival time
4) Broker Decision: The broker requests trips for the customers from each operator. In this study, the system costs are measured by the additional driven distance to accommodate a new request. Hence, in case the broker receives offers from both operators, the decision to book customer i with operator oi is made based on the evaluation of
with the additional driving distance δdi,o required for operator o to serve customer i.
The parameters defining the objective function for each operator are set to
The goal of the game is to model operators’ adaptation of their service within different environments (interaction scenarios) to maximize their profit. While there are many different parameters for operators to adapt, in this study we allow the operators 1) to change their fleet size and 2) to modify their objective function for assigning offers and vehicle plans. Fleet sizes Nv can be changed initially in steps of 20 vehicles around the initial fleet size to be defined in the following calibration step. In the “Single Operator” scenario, one operator has to serve double the amount of requests; hence, fleet size step sizes are doubled accordingly. Possible parameter options
Once an equilibrium with the initial parameter step sizes can be observed, the step sizes for fleet size and objective parameters are decreased for the remaining steps of the game to increase the resolution quality of the equilibrium state. Thereby, parameter steps are adopted by halving the step size, setting the currently found optimum within the new parameter table to be observed. This procedure is repeated until no clear symmetric equilibrium can be found anymore, which is interpreted as the maximum solution quality possible with respect to stochastic variations within the simulations. In the conducted simulations, alternating jumps between neighbouring cells in the parameter table are observed indicating the best possible resolution quality of the optimal parameter set.
Parameters for calculating the costs in Eq. 7, i.e., the fix cost per vehicle Cv and the distance-dependent cost cdis, are set to 25€per day and cdis = 0.25€/km, respectively, according to (Bösch et al., 2018).
The fare f to calculate the profit in Eq. 7 and the penalty cost for requests without offer pno, which are required to calculate the effective profit in Eq. 10, will be determined within calibration simulations in the next chapter.
In this section, results of the simulations are presented. Firstly, the calibration is described to determine the initial fleet size as well as the parameters pno and f. Secondly, the results after performing the game are presented and lastly, fleet key performance indicators (KPIs) are compared before and after the game and between the different interaction scenarios.
Since the envisioned autonomous ridepooling services are not yet operating, the values for f and pno cannot be found empirically. Instead, we use the interaction scenario of two independent operators as calibration scenario, where we choose 90% served customers as a target service rate. Conducting simulations for fleet sizes ranging from 75 to 250 reveals 190 vehicles are needed for each operator to achieve this service rate. The distance dependent fare f is chosen to create a break even profit using 190 vehicles resulting in f = 43 ct/km (see blue curve in Figure 6). The goal of calibrating the penalty cost parameter pno for unserved requests is to create a maximum for effective profit Peff at the target service rate of 90%. A value of pno = 46 ct accomplishes this target (see orange curve in Figure 6) and is used for further simulations.
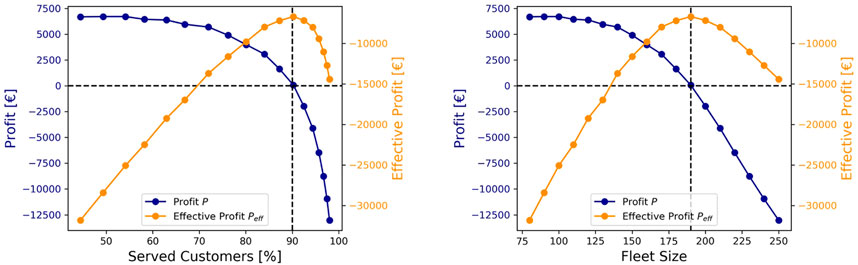
FIGURE 6. Calibration of break even fare and unserved customer penalty. The break even fare is chosen to achieve 0 € Profit at 90% served customers, while the unserved customer penalty is set to result in a maximum for the Effective Profit at 90% served customers as shown in the left figure. 190 vehicles are needed for each operator to served 90% customers as depicted in the right figure.
Figure 7 shows the development of operator service parameters over the course of the game for the broker scenario. Within each turn, the active operator explores 6 by 6 different possibilities for fleet size and objective function parameters, respectively, while the parameters of the passive operator remain fixed. During the course of the game the differences between neighboring explored parameter possibilities (in the region of the optimum in the rougher grid) become smaller to increase accuracy. This is illustrated by grey fields in Figure 7 as yet unexplored combinations. After each turn, the active operator takes over the parameter set resulting in the highest effective profit indicated by the orange boxes. For all interaction scenarios an equilibrium can be observed by no later than 6 turns. As indicated in Figure 7 no clear symmetric equilibrium is observed after increasing the step accuracy, which is also the case for the user decision interaction scenario. Instead alternating jumps between neighbouring cells are observed, which can likely be attributed to the dynamic and stochastic nature of the agent-based simulation model. In the shown example of the broker scenario, simulations until turn 10 reveal alternating jumps within the cells (Fleet Size = 210 veh,
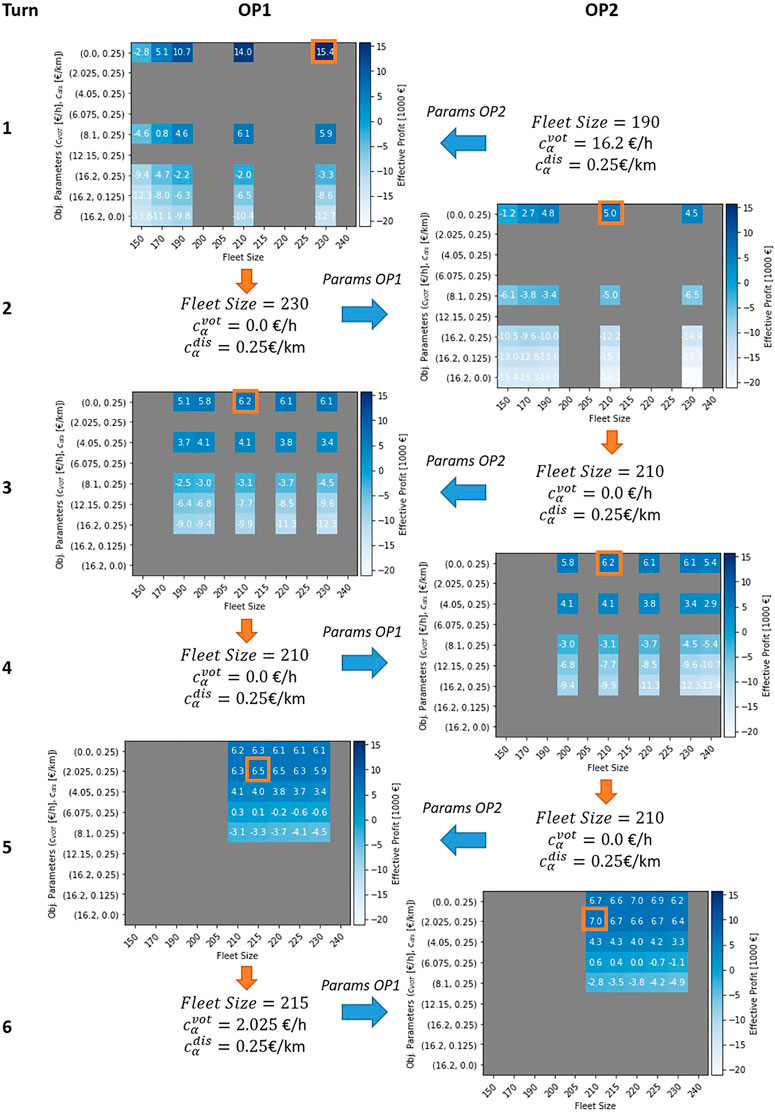
FIGURE 7. Illustration of the development of operator parameters over the course of the game for the broker interaction scenario. Blue arrows indicate parameter settings of the passive operator. Orange arrows indicate the parameter selection resulting in the highest effective profit of the active operator. A first equilibrium can be observed at turn 4, when OP2 adjusts its parameters to the same parameters as OP1. After turn 6 alternating behavior is revealed once the step size is decreased further in turn 5.
Table 1 shows operator parameters before and after the game. Initially all operators start with a fleet size of 190 vehicles, or 380 vehicles in the case of a single operator, and an objective function parameterized by
Figure 8 shows the fraction of served requests before and after the game for each interaction scenario. In all cases around 90% of all requests could be served as targeted within the calibration. Before the game the overall fleet size in the system is set the same for all interaction scenarios to illustrate the price of non-coordination. Therefore, most customers could be served within a single monopolistic operator setting, because the fleet can be controlled most efficiently having full access to all customers. On the contrary, with completely independent operators fewest customers can be served before the game due to effects of market fragmentation. Because customers have access to both operators and can choose the other operator in case the first cannot serve them, in the broker and user decision scenarios the fraction of served customers lies in between. After the game, the single operator decreases its fleet size resulting in the lowest fraction of served customers. Most customers are served in the broker decision scenario because operating larger vehicle fleets is profitable in this case indicating an advantage also for customers in this regulated scenario.
In Figure 9 the effective profit and the actual profit before and after the game is illustrated. Before the game the effective profit is dominated by the penalty for unserved customers resulting—similar to Figure 8 — in the highest value for the single operator and the lowest one for independent operators. The highest combined actual profit can be obtained within the broker decision scenario. The operator assignment process of selecting the operator with the lowest additional driven distance is here in line with the distance-dependent operating cost. The profit for independent operators is close to zero because this scenario is chosen in the calibration step to define the break even fare.
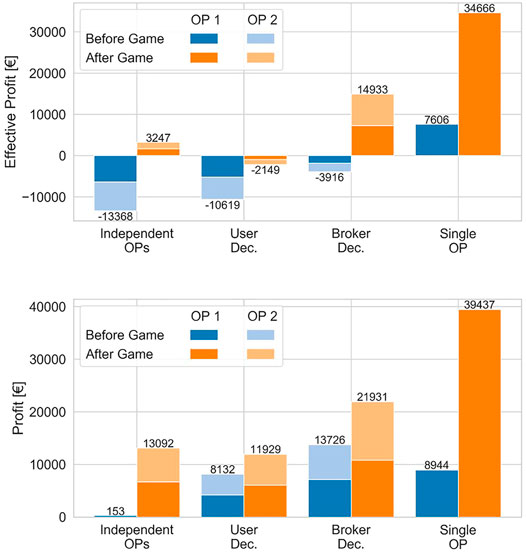
FIGURE 9. Effective Profit (top) and Profit (bottom) before and after the game for the different interaction scenarios.
After the game, operators could increase their effective as well as their actual profit in all interaction scenarios. The highest gain is obtained for the single operator who could decrease both fixed costs by decreasing fleet size and distance-dependent costs by changing the objective to select shorter routes without losing many customers by competition. The smallest gain is observed in the user decision case. Because of pressure due to competition, operators have to focus on assigning routes with low waiting and detour time for customers which results in a trade-off to higher fleet mileage and therefore in higher costs. Within all scenarios with more than one operator, operators achieve most actual as well as effective profit in the broker decision setting after the game. On the one hand, assigning customers to operators with the smallest additional driven distance is equal to the option that produces the lowest costs for the operator. On the other hand operators can additionally change their objective to putting more focus on assigning short routes without the market pressure from customers deciding for fastest trips.
The effectiveness of pooling can be measured by the relative saved distance rsd, which is plotted in Figure 10 and defined by
with the direct distance
Lastly, Figure 11 shows customer waiting and detour times. Before the game the average relative detour per customer is rather low indicating few pooled trips, in line with the evaluation of the relative saved distance of Figure 10. While the change in customer waiting times comparing before and after the game are minor in all scenarios, a large increase in detour times can be observed especially in the single operator and broker decision scenario. In these scenarios also the relative saved distance increases most, showing the trade-off between customer travel time and efficiency of sharing rides. Nevertheless, the average relative detour of up to 15% is still acceptable as it is limited by constraints to 40%. Comparing the scenarios after the game, the lowest customer waiting and detour times can be observed for the user decision scenario. Here, customers pick offers with the smallest waiting and travel times while operators additionally put more focus on assigning routes that minimize these parameters.
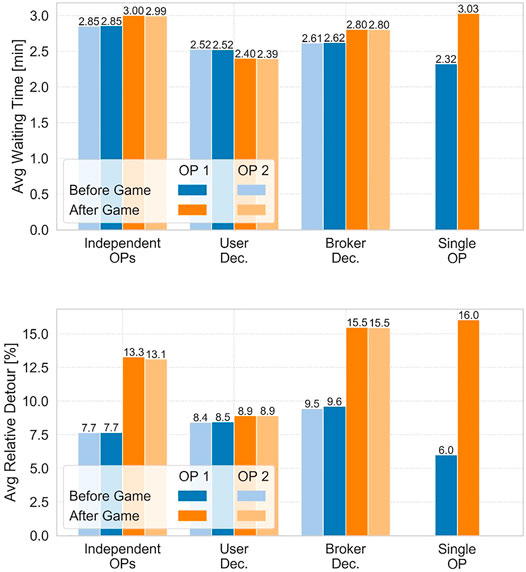
FIGURE 11. Customer waiting time (top) and relative detour time (bottom) before and after the game for the different interaction scenarios.
This study evaluates and quantifies the negative operational impacts of fragmenting AMOD ridepooling demand. Moreover, the concept of an AMOD broker is introduced to counteract these negative aspects. Two extreme forms of this broker, in which 1) the broker only collects the offers of multiple operators and the user selects the operator, and 2) the broker selects the operator better suited from a system viewpoint, are evaluated in a case study for taxi trips in Manhattan, NYC. The evaluation is performed with agent-based simulations in a static setting with constant fleet size and operator parameters, as well as in a game setting allowing the operators to adapt their service to maximize profit.
After operators adopted their service parameters in the game setting, the cumulative AMOD fleet size increased to 390 vehicles in the user decision scenario and 420 vehicles in the broker decision scenarios, compared to 310 vehicles in the single-operator system. These increased fleet sizes correspondingly resulted in higher service-rates when competition is present. In most interaction scenarios, operators increase their weight on minimizing fleet mileage to save costs. Only in the scenario where customers choose their AMOD service, operators are forced to offer trips with fast customer arrival times to succeed in competition. Correspondingly, in the user decision scenario pooling efficiency measured by the relative saved distance is reduced by around 14% compared to a single-operator system. This result indicates, that operators might prioritize offering non-shared trips when competition based on customer decision is present. Contrarily, the broker successfully shifts the operators objectives to decrease fleet mileage resulting in only 2% in relative saved distance loss compared to the single-operator system. Due to the correlation of fleet mileage and operating costs, most profit could be made when the broker regulates the competition of multiple operators.
All in all, it can be observed that regulating the broker platform can be beneficial for everyone: the transportation system has to supply fewer driven kilometers, the operators can save operational costs, thereby offsetting the fixed costs of adding more vehicles to the fleet, and, at the same time, less users have to be rejected from the AMOD services. While users also experience slightly increased waiting and especially travel time due to increased pooling efficiency, the maximum increase is limited by time constraints which are assumed to be accepted by users of a ridepooling service.
Several open questions have to be addressed before a real-world application makes sense:
1. Who should operate a broker platform?
2. How will users respond to a platform making the decision for them about which AMOD provider serves them?
3. Are the shown financial benefits enough motivation for AMOD providers to join a broker, or will municipalities have to enforce it?
The components of the broker objective could be more sophisticated than just additional driven distance, and additionally have to be traceable, i.e., allow a live tracking of fleet KPIs. The complexity of operating such platform is rather high and might be challenging for municipalities. However, as the broker objective and regulations should be aligned with public goals, a private platform provider at least should be paid for and commissioned by municipalities. To avoid cherry-picking, the AMOD services should likely receive a certain level-of-service/share of served request goal, e.g., by adding penalties for requests for which they make no offer. Moreover, an integration into existing public transportation services will be studied in the future.
With respect to the second question, behavioral studies have to be employed. In addition to the extreme regulatory measure of the broker choosing the AMOD operator, some intermediary levels of regulation can be studied in future work, in which the broker does not impose the choice of operator, but rather merely manipulates the offers (e.g., fares) to influence traveler behavior. Within this context, the symmetry between AMOD service levels should also be relaxed. That is, a broker should also be able to make valuable decisions in case one operator offers a service with high customer convenience, higher fares and lower occupancy compared to a service with the opposite strategy. To quantify such systems, more advanced mode choice models will be required.
When demand is modeled as price-sensitive, it also makes sense to integrate competitive pricing into the game framework. Moreover, the effect of different repositioning strategies can affect results significantly. It will be interesting to evaluate whether users benefit from competition as trade-offs are likely: users likely experience cheaper fares from competitive pricing, but might also suffer from lower service quality due to reduced ridepooling efficiency resulting from market fragmentation. Moreover, future work could also include studies with more than two operators. Asymmetric service design or even strongly asymmetric initial conditions can hint at whether the AMOD market will steer towards monopolies or a shared market with broker platforms. Nevertheless, the applied game framework might not be suited to investigate asymmetric final operator states. Therefore, the application limits of the current game setting have to be studied, and possibly, new methods have to be developed to study these effects.
Publicly available datasets were analyzed in this study. This data can be found here: https://www1.nyc.gov/site/tlc/about/tlc-trip-record-data.page.
Study conception and design: RE, PM, FD, and KB; data collection: RE, PM; analysis and interpretation of results: RE, PM, and FD; draft manuscript preparation: RE, PM, and FD. All authors reviewed the results and approved the final version of the manuscript.
The German Federal Ministry of Transport and Digital Infrastructure provides funding through the project “EasyRide” with grant number 16AVF2108H. The authors remain responsible for all findings and opinions presented in the paper.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Alonso-Mora, J., Samaranayake, S., Wallar, A., Frazzoli, E., and Rus, D. (2017). On-demand High-Capacity Ride-Sharing via Dynamic Trip-Vehicle Assignment. Proc. Natl. Acad. Sci. U.S.A. 114, 462–467. doi:10.1073/pnas.1611675114
Atasoy, B., Ikeda, T., Song, X., and Ben-Akiva, M. E. (2015). The Concept and Impact Analysis of a Flexible Mobility on Demand System. Transp. Res. Part C Emerg. Technol. 56, 373–392. doi:10.1016/j.trc.2015.04.009
Bilali, A., Engelhardt, R., Dandl, F., Fastenrath, U., and Bogenberger, K. (2020). Analytical and Agent-Based Model to Evaluate Ride-Pooling Impact Factors. Transp. Res. Rec. 2674, 1–12. doi:10.1177/0361198120917666
Bösch, P. M., Becker, F., Becker, H., and Axhausen, K. W. (2018). Cost-based Analysis of Autonomous Mobility Services. Transp. Policy 64, 76–91. doi:10.1016/j.tranpol.2017.09.005
Boeing, G. (2017). Osmnx: New Methods for Acquiring, Constructing, Analyzing, and Visualizing Complex Street Networks. Comput. Environ. Urban Syst. 65, 126–139. doi:10.1016/j.compenvurbsys.2017.05.004
Dandl, F., and Bogenberger, K. (2019). Comparing Future Autonomous Electric Taxis with an Existing Free-Floating Carsharing System. IEEE Trans. Intell. Transp. Syst. 20, 2037–2047. doi:10.1109/TITS.2018.2857208
Dandl, F., Bogenberger, K., and Mahmassani, H. S. (2019a). “Autonomous Mobility-On-Demand Real-Time Gaming Framework,” in 2019 6th International Conference on Models and Technologies for Intelligent Transportation Systems (MT-ITS), Cracow, Poland, June 5-7, 2019 (IEEE), 1–10. doi:10.1109/MTITS.2019.8883286
Dandl, F., Grueber, B., Friese, H., and Bogenberger, K. (2019b). Design and Simulation of a Public-Transportation-Complimentary Autonomous Commuter Shuttle. Transp. Res. Proc. 41, 240–250. doi:10.1016/j.trpro.2019.09.043
Dandl, F., Hyland, M., Bogenberger, K., and Mahmassani, H. S. (2019c). Evaluating the Impact of Spatio-Temporal Demand Forecast Aggregation on the Operational Performance of Shared Autonomous Mobility Fleets. Transportation 46, 1975–1996. doi:10.1007/s11116-019-10007-9
Dandl, F., Engelhardt, R., Hyland, M., Tilg, G., Bogenberger, K., and Mahmassani, H. S. (2021). Regulating Mobility-On-Demand Services: Tri-level Model and Bayesian Optimization Solution Approach. Transp. Res. Part C Emerg. Technol. 125, 103075. doi:10.1016/j.trc.2021.103075
Engelhardt, R., Dandl, F., Bilali, A., and Bogenberger, K. (2019a). “Quantifying the Benefits of Autonomous On-Demand Ride-Pooling: A Simulation Study for Munich, germany,” in 2019 22nd IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, New Zealand, October 27-30, 2019 (IEEE), 2992–2997. doi:10.1109/ITSC.2019.8916955
Engelhardt, R., Dandl, F., and Bogenberger, K. (2019b). Speed-up Heuristic for an On-Demand Ride-Pooling Algorithm. Ithaca, New York: arXiv. doi:10.48550/arXiv.2007.14877
Fagnant, D. J., Kockelman, K. M., and Bansal, P. (2015). Operations of Shared Autonomous Vehicle Fleet for Austin, Texas, Market. Transp. Res. Rec. 2563, 98–106. doi:10.3141/2536-12
Feneri, A.-M., Rasouli, S., and Timmermans, H. J. P. (2020). Modeling the Effect of Mobility-As-A-Service on Mode Choice Decisions. Transp. Lett. 12, 1–8. doi:10.1080/19427867.2020.1730025
Frei, C., Hyland, M., and Mahmassani, H. S. (2017). Flexing Service Schedules: Assessing the Potential for Demand-Adaptive Hybrid Transit via a Stated Preference Approach. Transp. Res. Part C Emerg. Technol. 76, 71–89. doi:10.1016/j.trc.2016.12.017
Gurumurthy, K. M., de Souza, F., Enam, A., and Auld, J. (2020). Integrating Supply and Demand Perspectives for a Large-Scale Simulation of Shared Autonomous Vehicles. Transp. Res. Rec. 2674, 181–192. doi:10.1177/0361198120921157
Henao, A., and Marshall, W. E. (2019). The Impact of Ride-Hailing on Vehicle Miles Traveled. Transportation 46, 2173–2194. doi:10.1007/s11116-018-9923-2
Hörl, S., Balac, M., and Axhausen, K. W. (2019a). “Dynamic Demand Estimation for an Amod System in Paris,” in IEEE Intelligent Vehicle Symposium, Paris, France, June 09-12 , 2019. doi:10.1109/IVS.2019.8814051
Hörl, S., Ruch, C., Becker, F., Frazzoli, E., and Axhausen, K. W. (2019b). Fleet Operational Policies for Automated Mobility: A Simulation Assessment for Zurich. Transp. Res. Part C Emerg. Technol. 102, 20–31. doi:10.1016/j.trc.2019.02.020
Hyland, M., and Mahmassani, H. S. (2018). Dynamic Autonomous Vehicle Fleet Operations: Optimization-Based Strategies to Assign Avs to Immediate Traveler Demand Requests. Transp. Res. Part C Emerg. Technol. 92, 278–297. doi:10.1016/j.trc.2018.05.003
Hyland, M., and Mahmassani, H. S. (2020). Operational Benefits and Challenges of Shared-Ride Automated Mobility-On-Demand Services. Transp. Res. Part A Policy Pract. 134, 251–270. doi:10.1016/j.tra.2020.02.017
Jiang, W., and Zhang, L. (2018). Evaluating the Effects of Double-Apping on the Smartphone-Based E-Hailing Service: A Simulation-Based Study. IEEE Access 6, 6654–6667. doi:10.1109/ACCESS.2018.2797207
Kaddoura, I., Leich, G., and Nagel, K. (2020). The Impact of Pricing and Service Area Design on the Modal Shift towards Demand Responsive Transit. Proc. Comput. Sci. 170, 807–812. doi:10.1016/j.procs.2020.03.152
Kondor, D., Bojic, I., Resta, G., Duarte, F., Santi, P., and Ratti, C. (2022). The Cost of Non-coordination in Urban On-Demand Mobility. Sci. Rep. 12, 4669. doi:10.1038/s41598-022-08427-2
Li, S., Tavafoghi, H., Poolla, K., and Varaiya, P. (2019). Regulating Tncs: Should Uber and Lyft Set Their Own Rules? Transp. Res. Part B Methodol. 129, 193–225. doi:10.1016/j.trb.2019.09.008
Liang, X., Correia, G. H. d. A., van Arem, B., and van Arem, B. (2016). Optimizing the Service Area and Trip Selection of an Electric Automated Taxi System Used for the Last Mile of Train Trips. Transp. Res. Part E Logist. Transp. Rev. 93, 115–129. doi:10.1016/j.tre.2016.05.006
Liu, Y., Bansal, P., Daziano, R., and Samaranayake, S. (2019). A Framework to Integrate Mode Choice in the Design of Mobility-On-Demand Systems. Transp. Res. Part C Emerg. Technol. 105, 648–665. doi:10.1016/j.trc.2018.09.022
Mo, B., Cao, Z., Zhang, H., Shen, Y., and Zhao, J. (2021). Competition between Shared Autonomous Vehicles and Public Transit: A Case Study in singapore. Transp. Res. Part C Emerg. Technol. 127, 103058. doi:10.1016/j.trc.2021.103058
Muller, M., Park, S., Lee, R., Fusco, B., and Correia, G. H. d. A. (2021). Review of Whole System Simulation Methodologies for Assessing Mobility as a Service (Maas) as an Enabler for Sustainable Urban Mobility. Sustainability 13, 5591. doi:10.3390/su13105591
Nahmias-Biran, B.-h., Oke, J. B., Kumar, N., Lima Azevedo, C., and Ben-Akiva, M. (2020). Evaluating the Impacts of Shared Automated Mobility On-Demand Services: An Activity-Based Accessibility Approach. Transportation 48, 1613. doi:10.1007/s11116-020-10106-y
Oke, J. B., Akkinepally, A. P., Chen, S., Xie, Y., Aboutaleb, Y. M., Azevedo, C. L., et al. (2020). Evaluating the Systemic Effects of Automated Mobility-On-Demand Services via Large-Scale Agent-Based Simulation of Auto-dependent Prototype Cities. Transp. Res. Part A Policy Pract. 140, 98–126. doi:10.1016/j.tra.2020.06.013
Pandey, V., Monteil, J., Gambella, C., and Simonetto, A. (2019). On the Needs for Maas Platforms to Handle Competition in Ridesharing Mobility. Transp. Res. Part C Emerg. Technol. 108, 269–288. doi:10.1016/j.trc.2019.09.021
Pavone, M., Smith, S. L., Frazzoli, E., and Rus, D. (2012). Robotic Load Balancing for Mobility-On-Demand Systems. Int. J. Robotics Res. 31, 839–854. doi:10.1177/0278364912444766
Pinto, H. K. R. F., Hyland, M. F., Mahmassani, H. S., and Verbas, İ. Ö. (2019). Joint Design of Multimodal Transit Networks and Shared Autonomous Mobility Fleets. Transp. Res. Proc. 38, 98–118. doi:10.1016/j.trpro.2019.05.007
Qian, X., and Ukkusuri, S. V. (2017). Taxi Market Equilibrium with Third-Party Hailing Service. Transp. Res. Part B Methodol. 100, 43–63. doi:10.1016/j.trb.2017.01.012
Ruch, C., Lu, C., Sieber, L., and Frazzoli, E. (2020). Quantifying the Efficiency of Ride Sharing. IEEE Trans. Intell. Transp. Syst. 22, 5811–5816. doi:10.1109/TITS.2020.2990202
Santi, P., Resta, G., Szell, M., Sobolevsky, S., Strogatz, S. H., and Ratti, C. (2014). Quantifying the Benefits of Vehicle Pooling with Shareability Networks. Proc. Natl. Acad. Sci. U.S.A. 111, 13290–13294. doi:10.1073/pnas.1403657111
Schaller, B. (2021). Can Sharing a Ride Make for Less Traffic? Evidence from Uber and Lyft and Implications for Cities. Transp. Policy 102, 1–10. doi:10.1016/j.tranpol.2020.12.015
Séjournè, T., Samaranayake, S., and Banerjee, S. (2018). The Price of Fragmentation in Mobility-On-Demand Services. Proc. ACM Meas. Anal. Comput. Syst. 2, 1–26. doi:10.1145/3224425
Simonetto, A., Monteil, J., and Gambella, C. (2019). Real-time City-Scale Ridesharing via Linear Assignment Problems. Transp. Res. Part C Emerg. Technol. 101, 208–232. doi:10.1016/j.trc.2019.01.019
Simoni, M. D., Kockelman, K. M., Gurumurthy, K. M., and Bischoff, J. (2019). Congestion Pricing in a World of Self-Driving Vehicles: An Analysis of Different Strategies in Alternative Future Scenarios. Transp. Res. Part C Emerg. Technol. 98, 167–185. doi:10.1016/j.trc.2018.11.002
Smith, G., and Hensher, D. A. (2020). Towards a Framework for Mobility-As-A-Service Policies. Transp. Policy 89, 54–65. doi:10.1016/j.tranpol.2020.02.004
Syed, A. A., Dandl, F., Kaltenhäuser, B., and Bogenberger, K. (2021). Density Based Distribution Model for Repositioning Strategies of Ride Hailing Services. Front. Future Transp. 2, 13. doi:10.3389/ffutr.2021.681451
Tachet, R., Sagarra, O., Santi, P., Resta, G., Szell, M., Strogatz, S. H., et al. (2017). Scaling Law of Urban Ride Sharing. Sci. Rep. 7, 42868. doi:10.1038/srep42868
Wen, J., Chen, Y. X., Nassir, N., and Zhao, J. (2018). Transit-oriented Autonomous Vehicle Operation with Integrated Demand-Supply Interaction. Transp. Res. Part C Emerg. Technol. 97, 216–234. doi:10.1016/j.trc.2018.10.018
Wilkes, G., Engelhardt, R., Briem, L., Dandl, F., Vortisch, P., Bogenberger, K., et al. (2021). Self-regulating Demand and Supply Equilibrium in Joint Simulation of Travel Demand and a Ride-Pooling Service. Transp. Res. Rec. 2675, 226–239. doi:10.1177/0361198121997140
Xi, H., Aussel, D., Liu, W., Waller, S. T., and Rey, D. (2021). Single-leader Multi-Follower Games for the Regulation of Two-Sided Mobility-As-A-Service Markets. Ithaca, New York: arXiv. doi:10.48550/arXiv.2106.02151
Keywords: ridepooling, mobility-on-demand, competition, cooperation, agent-based simulation
Citation: Engelhardt R, Malcolm P, Dandl F and Bogenberger K (2022) Competition and Cooperation of Autonomous Ridepooling Services: Game-Based Simulation of a Broker Concept. Front. Future Transp. 3:915219. doi: 10.3389/ffutr.2022.915219
Received: 07 April 2022; Accepted: 19 May 2022;
Published: 16 June 2022.
Edited by:
Neema Nassir, The University of Melbourne, AustraliaReviewed by:
Shaopeng Zhong, Dalian University of Technology, ChinaCopyright © 2022 Engelhardt , Malcolm , Dandl and Bogenberger . This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roman Engelhardt , cm9tYW4uZW5nZWxoYXJkdEB0dW0uZGU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.