Evaluation of forest loss data using fractal algorithms: case study Eastern Carpathians–Romania

Logging causes the fragmentation of areas with direct implications for hydrological processes, landslides, or habitats. The assessment of this fragmentation process plays an important role in the planning of future logging, reconstruction, and protection measures for the whole ecosystem. The methodology used includes imaging techniques applying two fractal indices: the Fractal Fragmentation Index (FFI) and the Fractal Fragmentation and Disorder Index (FFDI). The results showed the annual evolution and disposition of deforested areas. Only 3% of deforestation resulted in the fragmentation and splitting of forest plots. The remaining 97% resulted in the reduction of existing compact stands without fragmentation. The method has many advantages in quantifying the spatial evolution of forests, estimating the capture of carbon emissions and establishing sustainability of bird and animal habitats. The analysis took place in the Eastern Carpathians, in Romania, in the time period of 2001–2022.

1 Introduction

Deforestation and forest fragmentation are interrelated processes that have significant impacts on ecosystems. Logging reduces forest cover, while fragmentation divides the remaining forest into smaller, isolated patches, altering the landscape and affecting biodiversity (Taubert et al., 2018; Liu et al., 2019). Deforestation and selective logging significantly increase the ratio of forest edge to area and the number of forest fragments, with edge effects extending deep into the remaining forest areas, leading to ecological consequences such as reduced genetic diversity, altered pollinator interactions, and different environmental conditions (Broadbent et al., 2008). Fragmentation affects the genetic and demographic structure of plant populations. It can lead to reduced genetic diversity, altered pollinator interactions and changes in environmental conditions due to edge effects (Honnay et al., 2005). Remote sensing technologies, which provide critical insight into the conservation status of habitats and structural changes within forested landscapes over time, have become a key tool in the analysis of forest fragmentation (Wulder, 1998). Remote sensing data was used by different researchers for the analysis of deforestation and forest fragmentation (Saunders et al., 1991; Nagendra et al., 2003; Biradar et al., 2005; Echeverría et al., 2011; Sahana et al., 2015, 2018). It allows for the efficient mapping of large areas by providing a precise and relevant collection of digital data at multiple scales. Forest fragmentation often occurs over large areas that are difficult to monitor using field-based methods alone (García-Gigorro and Saura, 2005; Carranza et al., 2014; Ganivet and Bloomberg, 2019). Forest fragmentation caused by deforestation is a major problem in natural landscapes, with significant consequences for terrestrial eco-systems (Echeverria et al., 2006; Taubert et al., 2018; Fischer et al., 2021; Slattery and Fenner, 2021; Ma et al., 2023). The relationship between deforestation and flooding is a critical area of study with significant implications for environmental management, economic activity, and human well-being (Angelsen and Kaimowitz, 1999). Previous studies have shown a significant correlation between deforestation and flood risk in affected regions (Bradshaw et al., 2007; Danáčová et al., 2020; Fazel-Rastgar, 2020; Peptenatu et al., 2020; Posada-Marín and Salazar, 2022; Hou et al., 2023). The process of forest fragmentation alters the structure and functions of these ecosystems, reducing their ability to regulate water flows and prevent flooding (Cramer and Hobbs, 2002; National Research Council, 2008; Hurtado-Pidal et al., 2022). Deforestation can affect hydrological services such as flood control, which is essential for preventing natural disasters and maintaining ecological balance (Bradshaw et al., 2007). As a result, forest fragmentation increases land vulnerability to flooding and amplify its impacts on human communities and infrastructure (Randhir and Erol, 2013; Renó et al., 2016). In developing countries, where the economic and human toll of floods can be devastating, this relationship is particularly pronounced. Loss of forested areas impacts liquid runoff on slopes (rapid flooding, accelerated land erosion, etc.) as well as loss of biodiversity. Such a study can contribute to the development of the institutional and regulatory framework for forest sector activity and sustainable management of forest resources. The preponderance of evidence supports the importance of forest conservation in flood risk management, although there is some debate about the impact of deforestation on major flood events (Chang et al., 2009; Dijk et al., 2009; Brookhuis and Hein, 2016; Tan-Soo et al., 2016).

Short-winged birds are particularly vulnerable to the effects of forest fragmentation. Because of their limited ability to move through gaps between woodlots in search of mates and food, many species accustomed to living deep in forests are exposed to predators in fragmented forests (Weeks et al., 2023). Conflicts between humans and wildlife intensify when the migration routes of certain species (wild boar, bears) are destroyed. Wild animals see human-altered landscapes, such as farms and towns, as another part of their original natural habitat (Betts et al., 2022).

The loss of carbon sequestration capacity through deforestation is a major contributor to accelerating climate change. Trees absorb carbon dioxide from the air and release it when they are felled (Tong et al., 2020). In addition, evapotranspiration, the process by which water is recycled to the atmosphere through leaf evaporation and plant root transpiration, is decreased when forests are cleared with a direct consequence through increased air temperature (Li et al., 2020).

The EU Deforestation Regulation (EUDR), which aims to tackle the urgent problems of greenhouse gas emissions and biodiversity loss, confirms the desire of governments to adopt a more cautious attitude towards forests Regulation (EU) 2023/1115 of the European Parliament and of the Council of 31 May 2023 on the making available on the Union market and the export from the Union of certain commodities and products associated with deforestation and forest degradation and repealing Regulation (EU) No 995/2010. Green Deal: EU agrees law to fight global deforestation and forest degradation driven by EU production and consumption (2022, December 6). European Commission. In this research we aim to analyze the dynamics of forest fragmentation through fractal imaging and examine the spatial processes of deforestation using the Fractal Fragmentation Index (FFI) (Andronache et al., 2016) and Fractal Fragmentation and Disorder Index (FFDI) indices (Peptenatu et al., 2023). These indices have demonstrated their utility in previous studies analyzing the evolution of forested areas (Einzmann et al., 2017; Andronache et al., 2019; Diaconu et al., 2019).

2 Materials and methods

2.1 Study area and data

The Eastern Carpathians (Figure 1) are the eastern part of the large mountain segments of the Carpathian Mountains range, with a wide variety of geological rocks, geophysical, geological, and morphological features, elevations, and degree of forestation.

Figure 1

Figure 1. Location of the research area.

On the Romanian territory, they are generally oriented NW–SE, representing 55% of the country’s mountainous area. They are fragmented by numerous watercourses and depressions. Their present appearance dates to the second part of the Quaternary, with the warming of the climate that produced the melting of the glaciers on the highest peaks.

Petrographically, these mountains have as geological bedrocks a strip of crystalline rocks in the central part, sedimentary rocks in the eastern part and volcanic rocks in the west. However, the average altitude is a little lower, about 950 m, the maximum altitude being 2,303 m. The Rodna Mountains, the most striking feature of the relief is the parallelism of the peaks.

The climate is zoned by both altitude and the length and width of the mountain range. The average annual air temperature is between +6°C and −2°C and rainfall ranges from 800 mm to 1,200–1,400 mm per year.

The Eastern Carpathians are distinguished by a large extension of spruce and mixed forests (fir, spruce, and beech) representing 40% of Romania’s forest heritage. This area was chosen because many local communities engage in logging activities, floods caused by rivers that drain the mountainous area and the existence of fauna biodiversity that is pressured by human intervention (Paveluc et al., 2021; Crişan et al., 2023; Andronache, 2024).

2.2 Methodology

Fractals are conceptual objects displaying structures at all spatial scales, with a scale-dependent self-similarity (Mandelbrot, 1983; Al Saadi and Badr, 2024). The shape of fractals cannot be rectified, consisting of an infinite sequence of clusters within clusters. In rectifiable objects, increasingly accurate measurements based upon successive scale reductions lead to a series converging to a limit: the true extent of the object.

The fractal concept is also useful for characterizing certain aspects of patch dynamics. The research architecture used in this article is summarized in Figure 2.

Figure 2

Figure 2. Research flowchart.

The final phase of the research, fractal analysis using the FFI and FFDI index, is also structured as follows (Figure 3).

Figure 3

Figure 3. FFI and FFDI research flowchart.

2.2.1 Image preprocessing

The Global Forest Change 2000–2014 database provided by the University of Maryland Department of Geographic Sciences was used to assess the area of deforestation. This database was created by analyzing 654,178 LSTM+ images characterizing global forest surface from 2000 to 2022 (Hansen et al., 2013).

The forest and deforestation maps were extracted in.tiff format with the open-source software QGIS at a resolution of 2,480 × 3,507 pixels. This resolution was chosen because it provides a sufficient level of detail and covers the entire study area for fractal analysis. The analysis started with the reprojection of the Hansen_GFC into the national coordinate reference system Pulkovo 1942(58)/Stereo 70, EPSG: 3844 to obtain metric results. All of the deforestation areas have been extracted using the Raster layer unique values report tool from the QGIS Processing toolbox. This algorithm returns the number and the area of each unique value in each raster layer. In this study it has returned the number of all the pixels and the area in square meters. For the entire Romanian Eastern Carpathians, forested and deforested areas over the 22-year period were analyzed.

The images from 2001 to 2022 and the tree cover image from 2000 (Hansen et al., 2013) were converted to binary using Fiji/ImageJ2 2.14.0/1.54f java 1.8.0_322 [64-bit] (Schindelin et al., 2012; Schneider et al., 2012; Schindelin et al., 2015): ‘Image – Adjust – Threshold’ function with a range of [0, >0]. The binary images of cumulative loss were obtained by adding the loss area image from 2002 to the loss area image from 2001 for the 2001–2002 image, using Image Calculator from Fiji/ImageJ2. Similarly, the deforested area image from 2003 was added to the cumulative loss image from 2001 to 2002 for the 2001–2003 image. This iterative process continued, and the deforested area image from 2022 was added to the cumulative loss image from 2020 to 2021 for the 2001–2022 period (Figure 4).

Figure 4

Figure 4. Dynamics of tree cumulative loss areas in the Eastern Carpathians from 2001 to 2022.

The tree cover image for 2001 was extracted from the tree cover image of 2000, using the loss for 2001. The tree cover image for 2002 was obtained by extracting the cumulative loss image for 2001–2002 from the tree cover image of 2001. This iterative process continued until the tree cover image for 2022 was obtained by extracting the cumulative loss image for 2001–2021 from the tree cover image for 2021 (Figure 5).

Figure 5

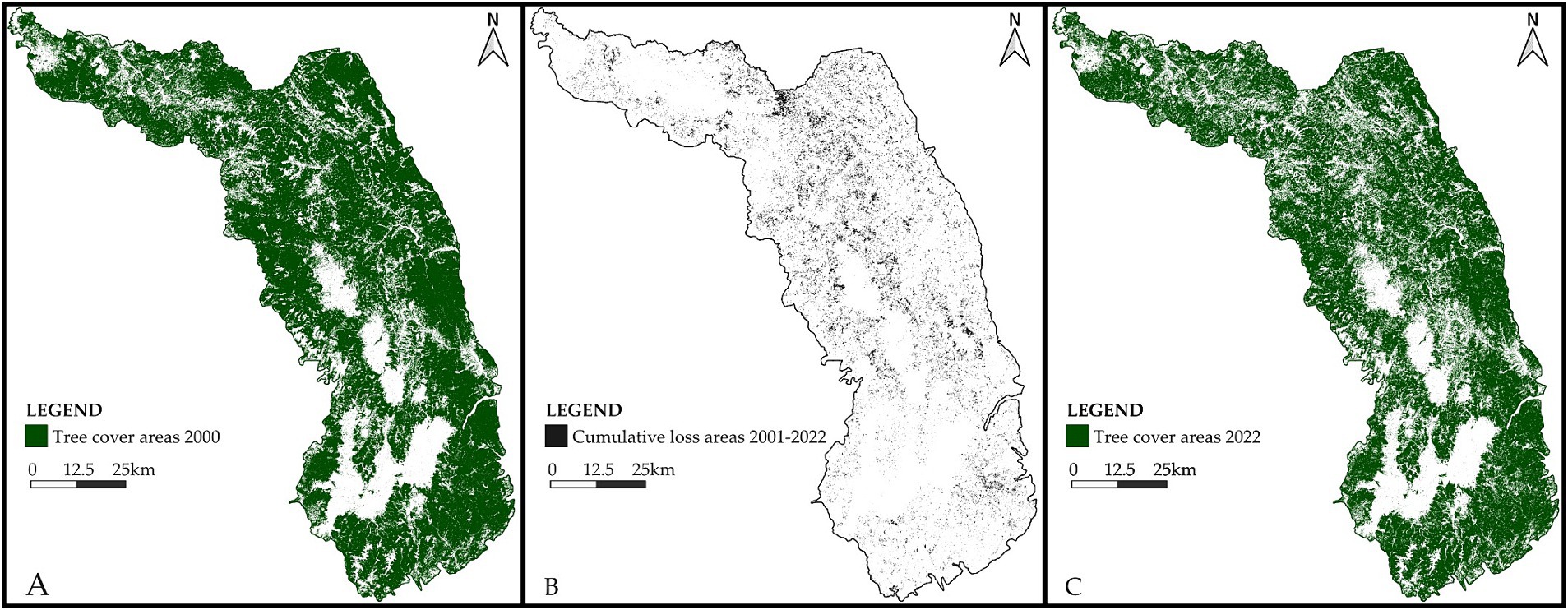
Figure 5. Dynamics of tree cover areas in the Eastern Carpathians from 2000 (A) to 2022 (C), in green. The image on the center (B) displays in black the cumulative loss areas between 2001 and 2022.

Particle analysis is a technique used to count and measure the characteristics of objects or particles in a digital image. It can determine the number, size, shape, distribution, and other properties of particles present in the image. Fiji/ImageJ2 software was used for this analysis.

Fractal fragmentation index (FFI). The Fractal Fragmentation Index (FFI) is a fractal index that estimates the degree of fragmentation or compaction of objects filling a space, as well as the deviation of each object’s shape from a geometrical Euclidean shape (Andronache et al., 2016). The FFI is calculated using multi-scale fractal techniques and the following Equation (1):

$\begin{array}{ll}\mathrm{F}\mathrm{F}\mathrm{I}=D_A-D_P=\underset{\epsilon \to 0}{lim}\left(\frac{logN\left(\epsilon \right)}{log\frac{1}{\epsilon }}\right)-\underset{\epsilon \to 0}{lim}\left(\frac{log{N}^{\prime }\left(\epsilon \right)}{log\frac{1}{\epsilon }}\right)& (1)\end{array}$

where, FFI the Fractal Fragmentation Index, D_A is box counting fractal dimension of areas (forest patches in this paper) and D_P is the box counting fractal dimension of the perimeters of those areas; ε represents the size of the boxes used in the analysis; log N(ε) represents the number of contiguous and non-overlapping boxes required to cover the object area(s), and log N′(ε) represents the number of contiguous and non-overlapping boxes required to cover only the object perimeter(s). According to the equation: FFI = 0, FFI is 0 (D_A = D_P) when the image is completely fragmented. FFI is 1 (D_A = 2, D_P = 1) when a single object is being analyzed and it has an Euclidian form (for example, a square). Therefore, the images with FFI = 0 are perfectly fragmented images and those with FFI = 1 are perfectly compact. In practice, those situations are rare, FFI having values situated between 0 and 1. As the image gets more fragmented, the FFI will start to tend towards 0. The reverse is true and as the image gets more compact, the FFI will start to tend towards 1. When the dynamics of a process or phenomena is analyzed, FFI helps with understanding the trend of fragmentation by reducing its value in time or compaction by raising its value in time the fractal entities being analyzed are very small, their contour cannot be extracted effectively, therefore D_A = D_P; (0 > FFI < 1).

FFI provides a global view of fragmentation across the whole image, which allows a comprehensive analysis of the spatial distribution of fractal objects. This indicator is insensitive to small artifacts, such as isolated or residual pixels, which may occur during image binarization. This provides a more accurate and reliable analysis of fragmentation.

Fractal fragmentation and disorder index (FFDI). The Fractal Fragmentation and Disorder Index is a fractal index that uses multi-scale fractal techniques to estimate the degree of fragmentation/compaction and spatial disorder of objects that fill a space (Peptenatu et al., 2023). The FFDI is derived from both the FFI (Andronache et al., 2016) and the Information Dimension (D₁) (Baker and Gollub, 1996). Like the FFI, it differentiates spatial organization patterns. It is calculated using Equation (2).

$\begin{array}{l}\mathrm{FFDI}=D_1\left(1-\mathrm{F}\mathrm{F}\mathrm{I}\right)=\left(\underset{\epsilon \to 0}{lim}{\displaystyle \sum }_{i=1}^{N\left(\epsilon \right)}\frac{m_i\left(\epsilon \right)log\left(m_i\left(\epsilon \right)\right)}{log\left(\epsilon \right)}\right)\\ \left(1-\left(\underset{\epsilon \to 0}{lim}\left(\frac{logN\left(\epsilon \right)}{log\frac{1}{\epsilon }}\right)-\underset{\epsilon \to 0}{lim}\left(\frac{log{N}^{\prime }\left(\epsilon \right)}{log\frac{1}{\epsilon }}\right)\right)\right)\end{array}\text{ (2)}$

where m_i = M_i/M, M_i is the number of points in the ith box, M is the total number of points of the object, ε is the size of the boxes, N(ε) is the number of contiguous and non-overlapping boxes required to cover the area of the object(s) and N′(ε) represents the number of contiguous and non-overlapping boxes required to cover only the perimeter of the object(s).

In this definition, 1-FFI is used because FFI = 0 indicates fragmentation and FFI = 1 indicates compaction (Andronache et al., 2016).

The FFDI range is between 0 and 2. The maximum value of FFDI approaches 2 when objects are strongly disordered and fragmented, whereas the lowest value approaches 0 when objects are weakly disordered and compact.

FFI can be used to discern patterns and identify thresholds in the spatial distribution of the objects under analysis, thus providing a better understanding of the structure and evolution of the system under study. The index can be used to analyze the dynamics of fragmentation over time and the influence of different factors on it. This allows to monitor and evaluate changes in the spatial distribution of the analyzed objects in an efficient and detailed way.

FFI can provide a global picture of fragmentation when the analyzed image includes several objects, but can also provide a local picture when the analyzed image includes only one object. FFDI is only a global analysis.

FFI and FFDI have been implemented as an open-source plugin for ImageJ2/Fiji within the ComsystanJ package (Ahammer et al., 2023). This plugin can be downloaded from https://comsystan.github.io/comsystanj/ or from GitHub at https://github.com/comsystan/comsystanj/tags. FFI and FFDI were intended for use exclusively with binary images.

For the fractal analysis, three image stacks were initially created, one stack for loss areas with 22 images, each image corresponding to 1 year from 2001 to 2022. A second stack for cumulative loss areas also with 22 images for the same period and a third stack for tree cover with 23 images, each image corresponding to 1 year from 2000 to 2022. Each stack was imported into ComsystanJ, and the “Fractal Fragmentation Indices” plugin was applied. The maximum number of boxes was set to its maximum value (# boxes = 10), and the values for regression min and regression max were set to 1 and 10, respectively.

Conventional GIS methods and techniques for cartographic representation of information as well as Word and Excel packages for information representation and editing were used in the research and data representation.

3 Results

The analysis of the loss areas showed that the tree cover of the Eastern Carpathians decreased by 201,077.4218 ha, from 2,327,594.44 ha in 2000 to 2,126,517.01 ha in 2022, which is a decrease of 8.6%. The most intensive deforestation occurred in 2003 (3,117.05 ha) and 2007 (23,135.51 ha).

During the analyzed period, a total of 74,902 forest patches were cleared, with an average of 3,405 patches per year. The highest number of patches occurred in 2007 (6,679), while the lowest was in 2003 (1,461). Between 2001 and 2022, 74,902 forest patches were deforested, resulting in 31,710 cumulative patches. Of these loss forest patches, 58% disappeared due to merging, leading to the fragmentation and disorder of compact forest areas. During this period, 2,262 new forest patches appeared due to fragmentation, representing a 17% increase in patches (from 10,851 in 2000 to 13,113 in 2022). Only 3% of deforestation resulted in the creation of new forest patches. The remaining 97% led to the reduction of compact forest areas without fragmentation, by deforestation occurring in isolated forest patches.

The trends in tree cover and deforestation changes from 2001 to 2022 are shown in Figure 6.

Figure 6

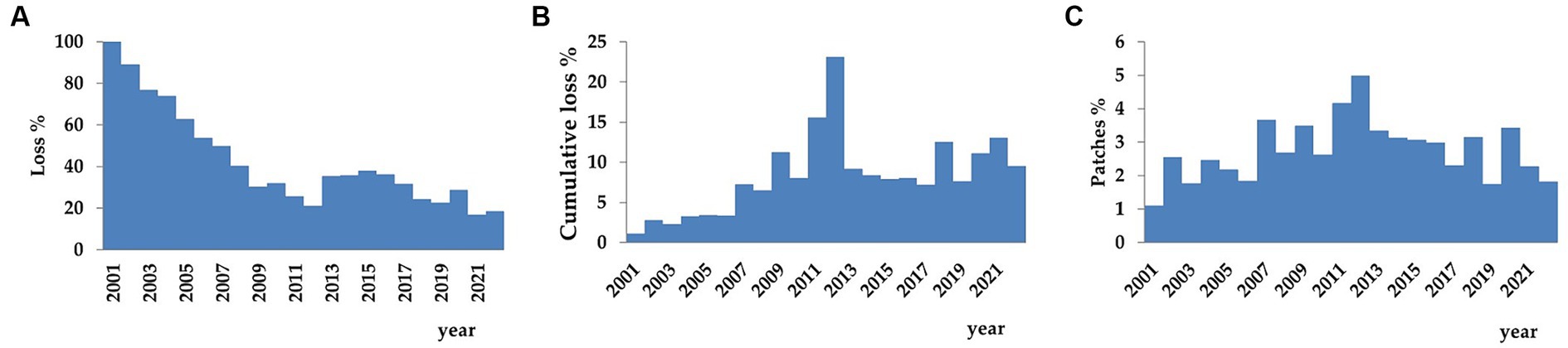
Figure 6. Analysis of change evolution in Eastern Carpathian Forests between 2001 and 2022: Trends in the percentage occupied by new loss (A), new cumulative loss patches (B), and tree cover patches (C).

From 2001 to 2012, there was a downward trend in the percentage of new patches of cumulative loss resulting from new loss events, as shown in Figure 6A. However, after 2012, although the downward trend continued, there were some years where the percentage of new patches of cumulative loss increased compared to the previous year, specifically in 2010, 2014–2015, 2020, and 2022. The most significant decrease was observed in 2003 compared to 2002 (−12%), while the most significant increase was observed in 2013 compared to 2012 (13%). Between 2002 and 2007, 50–89% of loss patches resulted in new patches of cumulative loss, indicating that deforestation mostly occurred in isolation. In contrast, deforestation occurred more in continuation of pre-existing losses in the years 2012, 2018–2019, and 2021–2022, as only between 17 and 25% of loss patches resulted in new patches of cumulative loss.

Furthermore, there is a trend towards an increase in the percentage of tree cover patches due to new patches of cumulative loss, which is more pronounced during the period of 2001–2012 (refer to Figure 6B). There were some exceptions where there were decreases in the years 2010, 2017, 2019, and 2022 compared to their preceding years. Like the previous situation, the largest increase was in 2018 compared to 2017 (5.32%), while the largest decrease was in 2013 compared to 2012 (−14%). Between 2001 and 2006, de-forestation only slightly fragmented the tree cover, with new patches of cumulative loss generating new patches of tree cover at a rate of 1.1–3.4%. However, in more recent years (2009, 2011–2012, 2018, and 2020–2022), as deforestation continued from pre-existing clearings, the fragmentation of tree cover into more patches increased significantly, with new patches of cumulative loss resulting in new patches of tree cover at a rate of 11.2–23.1%.

Regarding the percentage of tree cover patches resulting from new patches of cumulative loss (Figure 6C), there is a trend of yearly increase during the period 2001–2012, followed by a slight trend of decrease after 2013. Prior to 2012, deforestation led to a greater fragmentation of tree cover, with deforestation occurring in a more disorderly manner. However, after 2013, deforestation occurred more in continuation of previous clearings, but also over isolated small patches of tree cover. Two distinct patterns have been identified in the data. The largest increase occurred in 2007 compared to 2006 (1.82%), while the largest decrease occurred in 2013 compared to 2012 (−1.64%). Between 2001 and 2022, new loss patches generated new patches of tree cover in only 1.2–2.2% of cases, with higher values of 3.2–5% recorded in 2007, 2009, and 2011–2015, as well as in 2020.

In the case of loss areas, deforestation averaged between 2.13 ha/patch in 2003 and 3.46 ha/patch in 2007, while cumulative loss areas increased from 2.19 ha/patch in 2001 to 6.44 ha/patch in 2022. Conversely, tree cover areas decreased from 214.51 ha/patch in 2000 to 162.17 ha/patch (Figure 7).

Figure 7

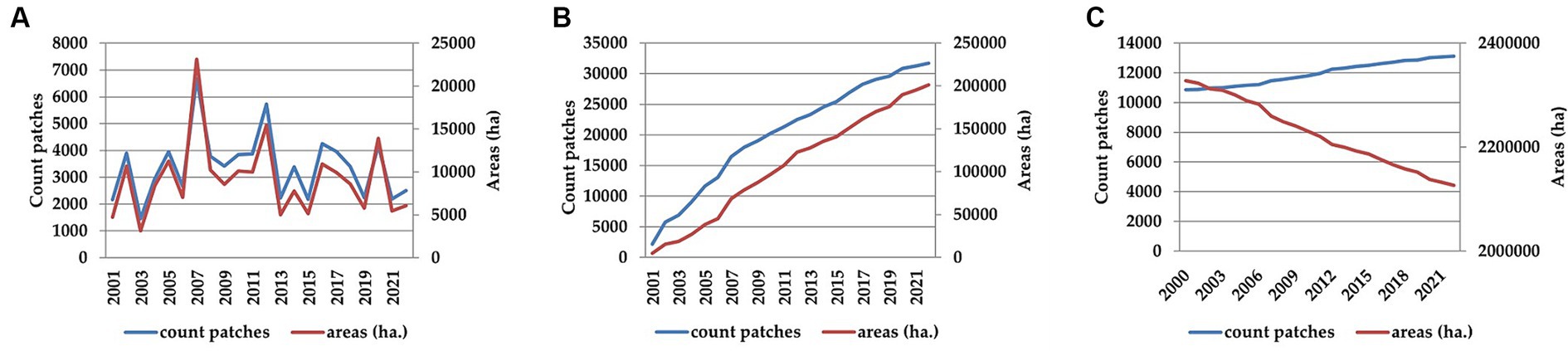
Figure 7. Relationship between area and number of patches for loss areas (A), cumulative loss areas (B) and tree cover (C).

Figure 7 illustrates the relationship between areas and number of patches for loss areas (Figure 7A), cumulative loss areas (Figure 7B) and tree cover (Figure 7C). Figures 7A,B show a dependence between deforested areas and the number of patches for loss and cumulative loss areas. However, as forest area decreases due to forest loss, it fragments, leading to an increase in the number of forest patches.

The analysis of loss and cumulative loss areas between 2001 and 2022 indicates that deforested patches are small and heterogeneously distributed spatially (Figures 8A,B).

Figure 8

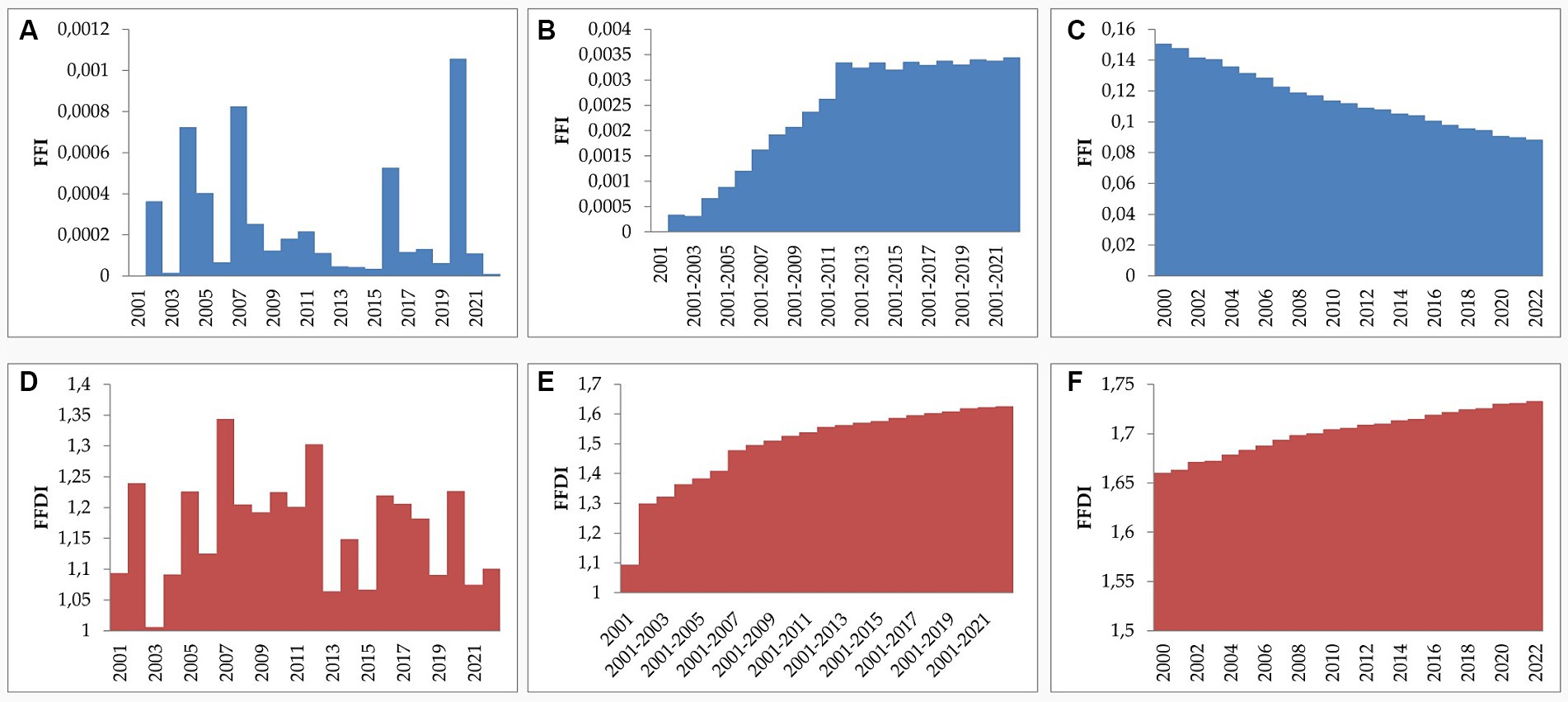
Figure 8. Dynamics of deforestation patterns and forest fragmentation in Eastern Carpathian forests from 2000 to 2022 (A-C) fractal fragmentation index of (A) loss, (B) cumulative loss, (C) tree cover; (D-F) fractal fragmentation and index of (D) loss, (E) cumulative loss, (F) tree cover.

Deforestation was slightly more compact in 2004, 2007, and 2020 (Figure 8A). The same pattern is observed for cumulative loss, with FFI increasing from 0 in 2001 to 0.003 from 2001 to 2022 (Figure 8B). A trend towards forest compaction was observed between 2001 and 2012, despite disorderly deforestation during the same period (Figure 8C). As deforestation occurs chaotically and in small, fragmented, rarely interconnected patches (Andronache et al., 2016), FFI values are very low, making this index unsuitable for differentiation between years. To tackle this issue, we employed FFDI, which measures the level of disorder in deforested areas (Figures 8D–F). FFDI peaked in 2007, a year marked by extensive, fragmented, and disorderly deforestation (Pintilii et al., 2017). The lowest FFDI value was observed in 2003, during a period of reduced deforestation and a much more orderly spatial distribution (Figure 8D). Over 22 years of continuous deforestation, the FFDI increased by 33%, indicating increasingly fragmented forests (Figure 8E). The analysis of deforestation effects on tree cover revealed continuous forest fragmentation, with FFI decreasing by 41% between 2000 and 2022 (Figure 8C). This ongoing forest fragmentation also led to spatial disorder of forest patches, as indicated by FFDI estimating a 4% increase in forest fragmentation and disorder (Figure 8F).

Figures 9A–C illustrate the correlation between the count of patches and FFDI. In all three analyses (loss, cumulative loss, and tree cover), the fragmentation and disorder of these patches increase as the number of deforested patches increases.

Figure 9

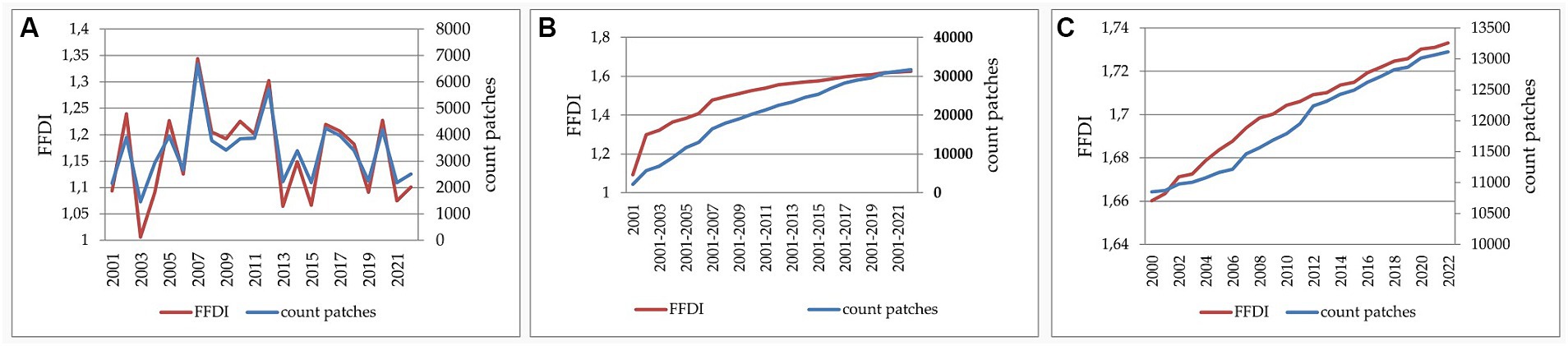
Figure 9. Correlation between count of patches and forest fragmentation disorder index (FFDI) in Eastern Carpathian forests, for: (A) loss, (B) cumulative loss and (C) tree cover patches.

The analysis showed that a significant amount of deforestation occurred during the studied period, resulting in a total loss of 76,205 forest patches, averaging 3,464 patches per year. The highest number of patches was observed in 2007, indicating significant deforestation activity, while the lowest was observed in 2003.

4 Discussion

The proposed methodology has proven to be relevant for identifying areas where major land use changes have occurred in a short time. The research is part of a series of analyses that looked at the structured impact of forest loss on the ecosystem (Andronache et al., 2016; Einzmann et al., 2017; Andronache et al., 2019; Diaconu et al., 2019; Peptenatu et al., 2023) and local economies (Pintilii et al., 2017).

The importance of this analysis methodology lies in the rapidity with which it provides information on how the woody mass on slopes has been exploited, and consequently on the potential impact on run-off coefficients on slopes and the degree of habitat fragmentation. The need for such research is highlighted in numerous studies (Clarke and Schweizer, 1991; Imaizumi et al., 2008; Zhang et al., 2020; Zhao et al., 2021).

FFDI revealed patterns of forest fragmentation and disorder over time, with FFDI values gradually increasing over the studied period, indicating increasingly fragmented forests. Figures 9A–C support this trend, indicating a positive correlation between the count of deforested patches and FFDI across different analyses (loss, cumulative loss, and tree cover).

The research has shown that the FFI–FFDI pair is advantageous for analyzing forest fragmentation. Both FFI and FFDI are useful for analyzing tree cover fragmentation and disorder. However, FFDI yielded better results for the analysis of loss and cumulative loss.

The results highlight the complex dynamics of deforestation and its implications for forest fragmentation and spatial disorder. Effective forest management strategies are important to mitigate fragmentation and preserve forest ecosystems. Detail analyses allow for better understanding of the factors that determine forest loss and are relevant methods to assist decision making in the silvic and biodiversity sectors. As such, silvic code could be completed with mechanisms that monitor resources and exploitation process of wood.

Our findings reveal ongoing forest fragmentation as a result of deforestation, accompanied by an increase in their spatial disorder. This fragmentation and disorder may contribute to heightened flood risk in the affected regions. Fragmented and disorderly forests may lose their ability to regulate water flows and mitigate flood risk, exacerbating land vulnerability to extreme precipitation events. Therefore, it is essential to understand and appropriately manage forest fragmentation and disorder processes to reduce the risk of flooding and protect human communities and infrastructure.

The evaluation methodology of forest fragmentation does not have a relevant correspondent that permits validating indices. It must be mentioned that analyzed image resolution and synoptic situations may lower the accuracy of data and generate errors. Another limitation of the FFI analysis is that it is calculated for the whole picture without providing information on regional variations. A scale limitation is another general problem in image analysis, with a single pixel as the smallest scale and the whole image size as the largest scale. In addition, natural objects are also intrinsically limited in scaling due to the finite size of their structural units. Our study has some limitations that must be addressed. The images used, with a spatial resolution of 30 m, allowed us to capture only a coarser picture of forest patterns. The use of more detailed images would resolve this restriction and thus improve FFI or LCFD accuracies.

The main disadvantage of FFI is that this index does not differentiate patterns where the component objects are extremely small so that the edges cannot be extracted, or where the objects completely occupy the space. The FFDI was also designed to overcome these limitations by further quantifying the information entropy in the image using the Information Dimension. FFDI provides a clearer differentiation in the categorization of synthetic images and in real applications.

Both FFI and FFDI have the disadvantage of only analyzing binary images. Initial preprocessing of binary images, such as binarization and noise removal, can influence the results of fractal analysis and must be carefully managed. Depending on the threshold chosen, binarization may introduce analytical bias; however, this effect can be further investigated and could be corrected by incorporating a scaling relationship or using FFI or FFDI as a relative index for comparing different patterns or states of the system, rather than as an absolute measure of fragmentation or fragmentation and de-ordering.

Furthermore, the interpretation of fractal analysis results can be influenced by the scale at which measurements are made, and an inappropriate choice of scale can lead to misinterpretations (Ciobotaru et al., 2019; Tarko et al., 2020).

In Romania, the economic pressure on the silvic fund has risen after 1990 at the same time when external commerce of logs became more permissive (Tronicke and Lück, 2023). The legislative regulations from that moment led to a rise in fragmentation due to authorized and unauthorized logging on surfaces covered in forest (Knorn et al., 2012; Iordăchescu and Vasile, 2022). In the field, this is identified with great difficulty, but when using remote sensing technologies this becomes more accessible and accurate.

Speaking of limitations, the resolution of satellite images significantly influences the calculated values of the Fractal Fragmentation Index (FFI) and Fractal Fragmentation and Disorder Index (FFDI). High resolution images provide more detailed information, which can lead to a more accurate fractal analysis of forest fragmentation. Lower resolution images may miss fine details, resulting in an underestimation of fragmentation metrics. In this study, to avoid this problem, all images analyzed were converted to the same resolution.

Converting grayscale images into binary images, a necessary step for fractal analysis, involves selecting a binarization threshold. An inappropriate threshold can either hide critical details or introduce noise, thus affecting the values of FFDI or other fractal metrics. It is important to note that the FFI is relatively insensitive to this bias, since isolated, noise-like pixels do not influence the final result. However, to minimize bias for FFDI or other binary fractal analysis metrics, future research should consider using adaptive binarization techniques that adjust based on local image features. In the situation of our study, there was no need for adaptive binarization because the images in the Global Forest Change database only provide information about the presence or absence of forests or deforestation.

The scale at which fractal analysis is performed can significantly affect the interpretation of FFI and FFDI. Analysis at different spatial scales can reveal different aspects of forest fragmentation. Analyses at small scales may reveal detailed patterns of fragmentation, while analyses at large scales may show broader trends. Future studies should conduct multi-scale analyses to capture both fine and coarse details of fragmentation. A hierarchical approach, analyzing data at different scales, can provide a comprehensive understanding of forest fragmentation.

5 Conclusion

Deforestation occurred through various mechanisms during this period. These mechanisms included the emergence of new loss areas, continuation of deforestation in previously lost areas, or the merging of two previously lost areas into a single loss area.

A notable finding is that 57% of loss patches disappeared due to merging, leading to the fragmentation and disorder of compact forest areas. This highlights the impact of deforestation on the spatial structure of forest landscapes.

The analysis identified the creation of new forest patches due to fragmentation, representing a 17% increase over the studied period. However, only 3% of deforestation resulted in the creation of new forest patches, indicating that most deforestation led to the reduction of compact forest areas without fragmentation.

Trends in tree cover changes and deforestation patterns were demonstrated. From 2001 to 2012, there was a downward trend in the percentage of new patches of cumulative loss, followed by fluctuations in subsequent years. Deforestation tended to occur more in continuation of pre-existing losses in recent years, rather than as isolated events.

The fractal indicators used offer the possibility to quantify the reduction in forest area in a fast and highly accurate way. If the limitations of the methodology are taken into account in this process, it can be widely used at least at the level of forested areas.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DD: Conceptualization, Supervision, Validation, Writing – original draft, Writing – review & editing. IA: Conceptualization, Data curation, Formal analysis, Software, Validation, Writing – original draft. AG: Investigation, Writing – original draft. TB: Formal analysis, Writing – review & editing. AB: Investigation, Software, Validation, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahammer, H., Reiss, M. A., Hackhofer, M., Andronache, I., Radulovic, M., Labra-Spröhnle, F., et al. (2023). ComsystanJ: a collection of Fiji/ImageJ2 plugins for nonlinear and complexity analysis in 1D, 2D and 3D. PLoS One 18:e0292217. doi: 10.1371/journal.pone.0292217

Crossref Full Text | Google Scholar

Al Saadi, J., and Badr, L. (2024). Fractal dimension, lacunarity, and Shannon entropy of self-assembled macroscopic copper dendrites. Front. Phys. 12:1278781. doi: 10.3389/fphy.2024.1278781

Crossref Full Text | Google Scholar

Andronache, I. (2024). Analysis of forest fragmentation and connectivity using fractal dimension and succolarity. Land 13:138. doi: 10.3390/land13020138

Crossref Full Text | Google Scholar

Andronache, I. C., Ahammer, H., Jelinek, H. F., Peptenatu, D., Ciobotaru, A.-M., Draghici, C. C., et al. (2016). Fractal analysis for studying the evolution of forests. Chaos Solit. Fractals 91, 310–318. doi: 10.1016/j.chaos.2016.06.013

Crossref Full Text | Google Scholar

Andronache, I., Marin, M., Fischer, R., Ahammer, H., Radulovic, M., Ciobotaru, A.-M., et al. (2019). Dynamics of forest fragmentation and connectivity using particle and fractal analysis. Sci. Rep. 9:12228. doi: 10.1038/s41598-019-48277-z

Crossref Full Text | Google Scholar

Angelsen, A., and Kaimowitz, D. (1999). Rethinking the causes of deforestation: lessons from economic models. World Bank Res. Obs. 14, 73–98. doi: 10.1093/WBRO/14.1.73

Crossref Full Text | Google Scholar

Baker, G. L., and Gollub, J. P. (1996). Chaotic dynamics: an introduction. 2nd Edn. Cambridge, United Kingdom: Cambridge University Press.

Google Scholar

Betts, M. G., Yang, Z., Hadley, A. S., Smith, A. C., Rousseau, J. S., Northrup, J. M., et al. (2022). Forest degradation drives widespread avian habitat and population declines. Nat. Ecol. Evol. 6, 709–719. doi: 10.1038/s41559-022-01737-8

Crossref Full Text | Google Scholar

Biradar, C. M., Saran, P. L., Raju, N., and Roy, P. S. (2005). Forest canopy density stratification: how relevant is biophysical spectral response modeling approach? Geocarto Int. 20, 15–21. doi: 10.1080/10106040508542332

Crossref Full Text | Google Scholar

Bradshaw, C. J. A., Sodhi, N. S., Peh, K. S.-H., and Brook, B. W. (2007). Global evidence that deforestation amplifies flood risk and severity in the developing world. Glob. Change Biol. 13, 2379–2395. doi: 10.1111/j.1365-2486.2007.01446.x

Crossref Full Text | Google Scholar

Broadbent, E., Asner, G., Keller, M., Knapp, D., Oliveira, P., and Silva, J. (2008). Forest fragmentation and edge effects from deforestation and selective logging in the Brazilian Amazon. Biol. Conserv. 141, 1745–1757. doi: 10.1016/J.BIOCON.2008.04.024

Crossref Full Text | Google Scholar

Brookhuis, B., and Hein, L. (2016). The value of the flood control service of tropical forests: a case study for Trinidad. Forest Policy Econ. 62, 118–124. doi: 10.1016/J.FORPOL.2015.10.002

Crossref Full Text | Google Scholar

Carranza, M., Frate, L., Acosta, A., Hoyos, L., Ricotta, C., and Cabido, M. (2014). Measuring forest fragmentation using multitemporal remotely sensed data: three decades of change in the dry Chaco. Eur. J. Remote Sens. 47, 793–804. doi: 10.5721/EuJRS20144745

Crossref Full Text | Google Scholar

Chang, H., Franczyk, J., and Kim, C. (2009). What is responsible for increasing flood risks? The case of Gangwon Province, Korea. Nat. Hazards 48, 339–354. doi: 10.1007/S11069-008-9266-Y

Crossref Full Text | Google Scholar

Ciobotaru, A.-M., Andronache, I., Ahammer, H., Radulovic, M., Peptenatu, D., Pintilii, R.-D., et al. (2019). Application of fractal and gray-level co-occurrence matrix indices to assess the forest dynamics in the curvature Carpathians—Romania. Sustain. For. 11:6927. doi: 10.3390/su11246927

Crossref Full Text | Google Scholar

Clarke, K. C., and Schweizer, D. M. (1991). Measuring the fractal dimension of natural surfaces using a robust fractal estimator. Cartogr. Geogr. Inf. Syst. 18, 37–47. doi: 10.1559/152304091783805617

Crossref Full Text | Google Scholar

Cramer, V. A., and Hobbs, R. J. (2002). Ecological consequences of altered hydrological regimes in fragmented ecosystems in southern Australia: impacts and possible management responses. Austral Ecol. 27, 546–564. doi: 10.1046/j.1442-9993.2002.01215.x

Crossref Full Text | Google Scholar

Crişan, V.-E., Dincă, L., Bragă, C., Murariu, G., Tupu, E., Mocanu, G. D., et al. (2023). The configuration of Romanian Carpathians landscape controls the volume diversity of Picea abies (L.) stands. Land 12:406. doi: 10.3390/land12020406

Crossref Full Text | Google Scholar

Danáčová, M., Földes, G., Labat, M. M., Kohnová, S., and Hlavčová, K. (2020). Estimating the effect of deforestation on runoff in small mountainous basins in Slovakia. Water 12:3113. doi: 10.3390/w12113113

Crossref Full Text | Google Scholar

Diaconu, D., Andronache, I., Pintilii, R. D., Bretcan, P., Simion, A. G., Draghici, C.-C., et al. (2019). Using fractal fragmentation and compaction index in analysis of the deforestation process in Bucegi mountains group, Romania. Carpathian J. Earth Environ. Sci. 14, 431–438. doi: 10.26471/cjees/2019/014/092

Crossref Full Text | Google Scholar

Dijk, A., Noordwijk, M., Calder, I., Bruijnzeel, S., Schellekens, J., and Chappell, N. (2009). Forest–flood relation still tenuous – comment on ‘Global evidence that deforestation amplifies flood risk and severity in the developing world’ by Bradshaw, C.J.A.; Sodi, N.S.; Peh, K.S.-H.; Brook, B.W. Glob. Change Biol. 15, 110–115. doi: 10.1111/j.1365-2486.2008.01708.x

Crossref Full Text | Google Scholar

Echeverria, C., Coomes, D., Salas, J., Rey-Benayas, J. M., Lara, A., and Newton, A. (2006). Rapid deforestation and fragmentation of Chilean temperate forests. Biol. Conserv. 130, 481–494. doi: 10.1016/j.biocon.2006.01.017

Crossref Full Text | Google Scholar

Echeverría, C., Newtonb, A., Nahuelhualc, L., Coomesd, D., and Benayase, J. M. (2011). How landscapes change: integration of spatial patterns and human processes in temperate landscapes of southern Chile. Appl. Geogr. 32, 822–831. doi: 10.1016/j.apgeog.2011.08.014

Crossref Full Text | Google Scholar

Einzmann, K., Immitzer, M., Böck, S., Bauer, O., Schmitt, A., and Atzberger, C. (2017). Windthrow detection in European forests with very high-resolution optical data. Forests 8:21. doi: 10.3390/f8010021

Crossref Full Text | Google Scholar

Fazel-Rastgar, F. (2020). Contribution of deforestation to severe flooding in southeast parts of the Caspian Sea: a case study with NDVI analysis. J. Extr. Even. 7:2050008. doi: 10.1142/S2345737620500086

Crossref Full Text | Google Scholar

Fischer, R., Taubert, F., Müller, M. S., Groeneveld, J., Lehmann, S., Wiegand, T., et al. (2021). Accelerated forest fragmentation leads to critical increase in tropical forest edge area. Sci. Adv. 7:eabg7012. doi: 10.1126/sciadv.abg7012

Crossref Full Text | Google Scholar

Ganivet, E., and Bloomberg, M. (2019). Towards rapid assessments of tree species diversity and structure in fragmented tropical forests: a review of perspectives offered by remotely-sensed and field-based data. For. Ecol. Manag. 432, 40–53. doi: 10.1016/j.foreco.2018.09.003

Crossref Full Text | Google Scholar

García-Gigorro, S., and Saura, S. (2005). Forest fragmentation estimated from remotely sensed data: is comparison across scales possible? For. Sci. 51, 51–63. doi: 10.1093/FORESTSCIENCE/51.1.51

Crossref Full Text | Google Scholar

Hansen, M. C., Potapov, P. V., Moore, R., Hancher, M., Turubanova, S. A., Tyukavina, A., et al. (2013). High-resolution global maps of 21st-century forest cover change. Science 342, 850–853. doi: 10.1126/science.1244693

Crossref Full Text | Google Scholar

Honnay, O., Jacquemyn, H., Bossuyt, B., and Hermy, M. (2005). Forest fragmentation effects on patch occupancy and population viability of herbaceous plant species. New Phytol. 166, 723–736. doi: 10.1111/J.1469-8137.2005.01352.X

Crossref Full Text | Google Scholar

Hou, Y., Wei, X., Zhang, M., Creed, I. F., McNulty, S. G., and Ferraz, S. F. B. (2023). A global synthesis of hydrological sensitivities to de-forestation and forestation. For. Ecol. Manag. 529:120718. doi: 10.1016/j.foreco.2022.120718

Crossref Full Text | Google Scholar

Hurtado-Pidal, J., Acero Triana, J. S., Aguayo, M., Link, O., Valencia, B. G., Espitia-Sarmiento, E., et al. (2022). Is forest location more important than forest fragmentation for flood regulation? Ecol. Eng. 183:106764. doi: 10.1016/j.ecoleng.2022.106764

Crossref Full Text | Google Scholar

Imaizumi, F., Sidle, R., and Kamei, R. (2008). Effects of forest harvesting on the occurrence of landslides and debris flows in the steep terrain of central Japan. Earth Surf. Process. Landf. 33, 827–840. doi: 10.1002/ESP.1574

Crossref Full Text | Google Scholar

Iordăchescu, G., and Vasile, M. (2022). Forests of fear: illegal logging, criminalization, and violence in the Carpathian Mountains. Ann. Am. Assoc. Geogr. 113, 2108–2125. doi: 10.1080/24694452.2023.2209631

Crossref Full Text | Google Scholar

Knorn, J., Kuemmerle, T., Radeloff, V. C., Szabo, A., Mindrescu, M., Keeton, W. S., et al. (2012). Forest restitution and protected area effectiveness in post-socialist Romania. Biol. Conserv. 146, 204–212. doi: 10.1016/j.biocon.2011.12.020

Crossref Full Text | Google Scholar

Li, Y., Piao, S. L., Chen, A. P., Ciais, P., and Li, L. Z. X. (2020). Local and teleconnected temperature effects of afforestation and vegetation greening in China. Natl. Sci. Rev. 7, 897–912. doi: 10.1093/nsr/nwz132

Crossref Full Text | Google Scholar

Liu, J., Coomes, D., Gibson, L., Hu, G., Liu, J., Luo, Y., et al. (2019). Forest fragmentation in China and its effect on biodiversity. Biol. Res. 94, 1636–1657. doi: 10.1111/brv.12519

Crossref Full Text | Google Scholar

Ma, J., Li, J., Wu, W., and Liu, J. (2023). Global forest fragmentation change from 2000 to 2020. Nat. Commun. 14:3752. doi: 10.1038/s41467-023-39221-x

Crossref Full Text | Google Scholar

Mandelbrot, B. B. (1983). The fractal geometry of nature, vol. 51. 3rd Edn. New York: W. H. Freeman and Company, 286–287.

Google Scholar

Nagendra, H., Southworth, J., and Tucker, C. (2003). Accessibility as a determinant of landscape transformation in Western Honduras: linking pattern and process. Landsc. Ecol. 18, 141–158. doi: 10.1023/A:1024430026953

Crossref Full Text | Google Scholar

National Research Council (2008). Hydrologic effects of a changing forest landscape. Washington, D.C.: National Academies Press.

Google Scholar

Paveluc, L. E., Pintilie, A. M., Hutanu, E., and Grozavu, A. (2021). A comparative analysis of historical flood events (post-1990) in the Trebeș-Negel representative basin for eastern Carpathians and Subcarpathians transition zone. Carpathian J. Earth Environ. Sci. 16, 31–46. doi: 10.26471/cjees/2021/016/153

Crossref Full Text | Google Scholar

Peptenatu, D., Andronache, I., Ahammer, H., Radulovic, M., Costanza, J. K., Jelinek, H. F., et al. (2023). A new fractal index to classify forest fragmentation and disorder. Landsc. Ecol. 38, 1373–1393. doi: 10.1007/s10980-023-01640-y

Crossref Full Text | Google Scholar

Peptenatu, D., Grecu, A., Simion, A. G., Gruia, K. A., Andronache, I., Draghici, C. C., et al. (2020). “Deforestation and frequency of floods in Romania” in Water resources management in Romania. eds. A. M. Negm, G. Romanescu, and M. Zeleňáková (Springer International Publishing: Cham), 279–306.

Google Scholar

Pintilii, R.-D., Andronache, I., Diaconu, D. C., Dobrea, R. C., Zeleňáková, M., Fensholt, R., et al. (2017). Using fractal analysis in modeling the dynamics of forest areas and economic impact assessment: Maramureș County, Romania, as a case study. Forests 8:25. doi: 10.3390/f8010025

Crossref Full Text | Google Scholar

Posada-Marín, J. A., and Salazar, J. F. (2022). River flow response to deforestation: contrasting results from different models. Water Secur. 15:100115. doi: 10.1016/j.wasec.2022.100115

Crossref Full Text | Google Scholar

Randhir, T. O., and Erol, A. (2013). Emerging threats to forests: resilience and strategies at system scale. Am. J. Plant Sci. 4, 739–748. doi: 10.4236/ajps.2013.43A093

Crossref Full Text | Google Scholar

Renó, V., Novo, E., and Escada, M. (2016). Forest fragmentation in the lower Amazon floodplain: implications for biodiversity and ecosystem service provision to riverine populations. Remote Sens. 8:886. doi: 10.3390/rs8110886

Crossref Full Text | Google Scholar

Sahana, M., Hong, H., Liu, J., and Zhu, A. (2018). Assessing deforestation susceptibility to forest ecosystem in Rudraprayag district, India using fragmentation approach and frequency ratio model. Sci. Total Environ. 627, 1264–1275. doi: 10.1016/j.scitotenv.2018.01.290

Crossref Full Text | Google Scholar

Sahana, M., Sajjad, H., and Ahmed, R. (2015). Assessing spatio-temporal health of forest cover using forest canopy density model and forest fragmentation approach in Sundarban reserve forest, India. Model. Earth Syst. Environ. 1, 2–10. doi: 10.1007/s40808-015-0043-0

Crossref Full Text | Google Scholar

Saunders, D. A., Hobbs, R. J., and Margules, C. R. (1991). Biological consequences of ecosystem fragmentation: a review. Conserv. Biol. 5, 18–32. doi: 10.1111/j.1523-1739.1991.tb00384.x

Crossref Full Text | Google Scholar

Schindelin, J., Arganda-Carreras, I., Frise, E., Kaynig, V., Longair, M., Pietzsch, T., et al. (2012). Fiji: an open-source platform for biological-image analysis. Nat. Methods 9, 676–682. doi: 10.1038/nmeth.2019

Crossref Full Text | Google Scholar

Schindelin, J., Rueden, C. T., Hiner, M. C., and Eliceiri, K. W. (2015). The ImageJ ecosystem: an open platform for biomedical image analysis. Mol. Reprod. Dev. 82, 518–529. doi: 10.1002/mrd.22489

Crossref Full Text | Google Scholar

Schneider, C. A., Rasband, W. S., and Eliceiri, K. W. (2012). NIH image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675. doi: 10.1038/nmeth.2089

Crossref Full Text | Google Scholar

Slattery, Z., and Fenner, R. (2021). Spatial analysis of the drivers, characteristics, and effects of forest fragmentation. Sustain. For. 13:3246. doi: 10.3390/su13063246

Crossref Full Text | Google Scholar

Tan-Soo, J., Adnan, N., Ahmad, I., Pattanayak, S., and Vincent, J. (2016). Econometric evidence on forest ecosystem services: deforestation and flooding in Malaysia. Environ. Resour. Econ. 63, 25–44. doi: 10.1007/S10640-014-9834-4

Crossref Full Text | Google Scholar

Tarko, A., Tsendbazar, N. E., de Bruin, S., and Bregt, A. K. (2020). Influence of image availability and change processes on consistency of land transformation interpretations. Int. J. Appl. Earth Obs. Geoinform. 86:102005. doi: 10.1016/j.jag.2019.102005

Crossref Full Text | Google Scholar

Taubert, F., Fischer, R., Groeneveld, J., Lehmann, S., Müller, M. S., Rödig, E., et al. (2018). Global patterns of tropical forest fragmentation. Nature 554, 519–522. doi: 10.1038/nature25508

Crossref Full Text | Google Scholar

Tong, X., Brandt, M., Yue, Y., Ciais, P., Rudbeck Jepsen, M., Penuelas, J., et al. (2020). Forest management in southern China generates short term extensive carbon sequestration. Nat. Commun. 11:129. doi: 10.1038/s41467-019-13798-8

Crossref Full Text | Google Scholar

Tronicke, J., and Lück, E. (2023). “Multi-scale analysis and interpretation of multi-method geophysical data sets” in Advances in on- and offshore archaeological prospection: proceedings of the 15th international conference on archaeological prospection (Kiel: Kiel University Publishing), 439–442.

Google Scholar

Weeks, T. L., Betts, M. G., Pfeifer, M., Wolf, C., Banks-Leite, C., Barbaro, L., et al. (2023). Climate-driven variation in dispersal ability predicts responses to forest fragmentation in birds. Nat. Ecol. Evol. 7, 1079–1091. doi: 10.1038/s41559-023-02077-x

Crossref Full Text | Google Scholar

Wulder, M. (1998). Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters. Prog. Phys. Geogr. 22, 449–476. doi: 10.1177/030913339802200402

Crossref Full Text | Google Scholar

Zhang, X., Song, J., Wang, Y., Deng, W., and Liu, Y. (2020). Effects of land use on slope runoff and soil loss in the loess plateau of China: a meta-analysis. Sci. Total Environ. 755:142418. doi: 10.1016/j.scitotenv.2020.142418

Crossref Full Text | Google Scholar

Zhao, M., Boll, J., and Brooks, E. (2021). Evaluating the effects of timber harvest on hydrologically sensitive areas and hydrologic response. J. Hydrol. 593:125805. doi: 10.1016/j.jhydrol.2020.125805

Crossref Full Text | Google Scholar