Competition and density dependence in arid mountain forest stands: revealing the complex process from spatial patterns

Understanding the spatial patterns and interaction of trees is crucial for exploring forest dynamics. However, limited research has explored the spatial pattern and interactions between adult trees and their offspring population in arid mountain forest ecosystems. We investigated the spatial distribution and interaction of recruitment, survival, and mortality at different size classes in the Populus davidiana forest in the Luoshan Mountains (Ningxia, China), to gain insights into its stand dynamics. (1) This demonstrated the characteristic shift from an aggregated to random distribution as seedlings grew and developed into adult trees. (2) The adult trees exhibited strong positive and weak negative spatial associations with seedlings and saplings, respectively, with an increasing spatial scale, yet both stages underwent stark transitions from negative (1–15 m scales) to positive (> 20 m scale) associations. (3) Generally, the closer the individual trees were to each other, the greater the negative impact of neighboring trees on the size of an individual tree. (4) Additionally, adult trees strongly increased the risk of seedling mortality across the spatial scale of 0–50 m. (5) Live seedlings were less than the dead ones around dead seedlings. There was a stronger aggregation of dead seedlings than live seedlings. Moreover, the density-dependent mortality in our study rejected the random mortality hypothesis. In summary, these results suggest that spatial separation occurs between dead and live seedlings of P. davidiana. Under adult trees, negative dependence plays an important role in the arid mountain forest recruitment. Our findings will contribute to the restoration and conservation of arid mountain forests and provide theoretical support for forest management.

Introduction

The patterns and scales of tree distribution influence forest structure and dynamics through complex interactions involving crown architecture differences between species (Haq et al., 2023), soil properties (Waheed et al., 2022), water availability constraints on tree height (Klein et al., 2015), disturbance effects (Zhang et al., 2022), and the integration of dynamics across various spatial scales within forest ecosystems (Mitchell et al., 2023). Changing spatial patterns can strengthen or weaken interactions within and among tree populations, and between them and their environment (Kuehne et al., 2018). Several empirical studies have found that spatial patterns significantly influence forest recruitment rates (Yang et al., 2008; Hai et al., 2014; Rendenieks et al., 2022). In a forest, the spatial arrangement of different-sized stems within tree populations can influence competition for resources, which, in turn, affects tree growth and mortality rates (Beyns et al., 2021). In particular, stem aggregation or dispersion could explain the certain spatial processes observed (e.g., density dependence, thinning, and predation) in a forest through spatial point pattern analysis (Nguyen et al., 2022; Salas-Eljatib et al., 2022; Muñoz-Gallego et al., 2023).

The spatial point pattern analysis is a fundamental tool for exploring the spatial processes and patterns of an ecosystem (Illian et al., 2008). In a spatial point pattern analysis, every single tree can be considered a point (Ripley, 1976), which allows the estimate of the spatial distribution of individual trees mapped in a given area (Diggle, 2003; Wiegand and Moloney, 2004; Illian et al., 2008; Law et al., 2009; Wiegand and Moloney, 2014). Therefore, by analyzing spatial point patterns, we may infer certain properties or behaviors of related or underlying spatial processes involved (Baddeley et al., 2015; Xin et al., 2022). However, different ecological mechanisms and processes such as competition and disturbance may result in the same spatial patterns (Detto and Muller-Landau, 2013). Exploring the underlying ecological dynamics that drive these spatial patterns remains a significant challenge in ecology.

In forest stands, density dependence is an important mechanism that could change the spatial distribution of trees (Piao et al., 2013; Kuang et al., 2017; Miao et al., 2018; Ma et al., 2024). As the density of recruits increases beyond the maximum threshold that the environment can support, resource competition occurs. Thereafter, negative density dependence leads to a lower probability of survival close to parent trees. For instance, in pure Norway spruce forests in Switzerland, the small dead trees tend to gather close to large trees, and this aggregation effect decreases as the distance increases (Bianchi et al., 2021). A study of Japanese larch forests revealed that density dependence did not play a role, and the further away seedlings were from the seed tree, the greater their survival rates (Im et al., 2023). However, in tropical mountain rainforests, the densities of saplings and small and medium trees increased and then decreased with the distance from old-growth trees, which exhibited a consistent pattern of density dependence (Miao et al., 2018). In Barro Colorado Island forests, the research found a high probability of recruitment in the vicinity of adult trees of other species (Condit et al., 1992). Consequently, further research is needed to investigate whether density dependence is consistent across different forest stands and under various environmental conditions.

Arid mountain forests harbor a significant proportion of global biodiversity, acting as reservoirs for diverse species and providing essential ecosystem services such as soil protection and habitat creation (Zhang et al., 2023). In this study, we aimed to examine the arid mountain forest ecosystem of the Luoshan Mountains in Ningxia, northwest China, situated in the transitional zone between grassland and desert. The forest stands in this area are dominated by Qinghai spruce (Picea crassifolia), Chinese pine (Pinus tabulaeformis), and Aspen (Populus davidiana) (Liang, 2018). P. davidiana, a common pioneer species that emerges in the aftermath of human disturbances, is known to function as effective sites for seedling recruitment (Bouchard et al., 2018). Unlike P. crassifolia and P. tabulaeformis (seedlings from seed germination), P. davidiana reproduces asexually through root sprouting, and this method can result in more dense individual trees around adult trees. We aimed to investigate how the spatial correlation of different sizes distributes in P. davidiana stands in this arid mountain forest. We also sought to determine whether there is density dependence between recruits and adult trees, and if the death of seedlings is random or density-dependent? Therefore, we aimed to answer these questions from five perspectives.

1 We use the univariate O-ring statistic O₁₁(r) under the heterogeneous Poisson null model to analyze whether the spatial distributions of various P. davidiana size classes transition from an aggregated pattern to a uniform or random pattern. As tree sizes increase, stems should exhibit more regular spatial patterns at small scales, due to self-thinning resulting from competition (Salas-Eljatib et al., 2022).

2 Then, by using the bivariate O-ring statistic O₁₂(r) under an antecedent condition null model (Wiegand and Moloney, 2004), we could analyze the spatial associations among different size classes. The antecedent condition null model conveys the relationships between living adult trees and saplings or seedlings (Wiegand et al., 1999), enabling us to examine the influence of adult trees upon seedlings and saplings across a range of spatial scales.

3 The mark-correlation functions could quantify the similarity or dissimilarity between neighboring trees in terms of their attributes (such as size, height, and biomass). Researchers can identify patterns of positive or negative associations among tree attributes at different spatial scales. Positive correlations indicate that similar tree attributes tend to cluster together, while negative correlations suggest a tendency for dissimilar attributes to be spatially segregated. By using mark-correlation functions k_m1m1(r) under the independent marking null model, we could test the similarity of two neighboring trees separated by distance (Illian et al., 2008; Wiegand and Moloney, 2014).

4 The trivariate random labeling null model enables the study of how an extra (previous) pattern affects the processes associated with a distinctly identified pattern (Holík et al., 2021). Within this method, pairs of points are chosen based on a set distance r, with the initial point originating from the primary pattern (adult tree) and the subsequent point from another clearly defined pattern (whether the seedlings and saplings are dead or alive). The cumulative non-normalized r-mark correlation function C^cum_.,m2 based on a trivariate random labeling null model was applied to examine the impact of living adult trees on seedling mortality (Wiegand, 2014).

5 We aimed to test the random mortality hypothesis, which posits that individual mortality events occur randomly in space (Wang et al., 2019). According to this hypothesis, spatial correlations between individual mortality events should not be observed, and the mortality of adjacent individual trees should not increase in response to neighborhood density. In contrast, we propose that the spatial positioning of individual trees may have an impact on the mortality of its neighboring trees. To test this alternative hypothesis, we employed the g12, g22-g11, and g2, 1 + 2-g1, 1 + 2 functions under the random labeling null model (Stoyan and Stoyan, 1994; Raventós et al., 2010; Wiegand and Moloney, 2014).

Methods

Study area

The study area is located in the Luoshan National Nature Reserve in the arid region of central Ningxia, China (37°11′–37°25′ N, 106°04′–106°24′ E). Since the Luoshan Mountains of the reserve are located within the ecotone between grassland and desert biomes, they provide a variety of species in this ecosystem. The reserve protects the arid mountain forest ecosystems (Picea crassifolia, Pinus tabulaeformis, and Populus davidiana) in Ningxia, northwest China. The elevation spans from1560.0 m to 2624.5 m in the study area, with an average annual temperature of 8.8°C, annual precipitation ranging from 151.4 to 485.4 mm, and annual evaporation of 2,325 mm (Liang, 2018).

Data collection

In October 2022, a 100-m × 100-m plot (1 ha) was set up in a forest stand dominated by P. davidiana in the Luoshan National Nature Reserve. The geocoordinates of each tree were recorded using the real-time kinematic (RTK) GPS (Hi-Target, D8 VR, China), along with the measurements of their diameter of breast height (DBH) and seedling basal diameter, as well as their status (live or dead). A total of 6,830 individual trees were surveyed in the plot (see Figure 1). Based on the size of P. davidiana, the conspecific individual trees in the sampled population were divided into three size classes as a proxy of growth stages: seedling, DBH ≤ 6 cm; sapling, 6 cm < DBH ≤ 15 cm; and adult tree, DBH > 15 cm.

Figure 1

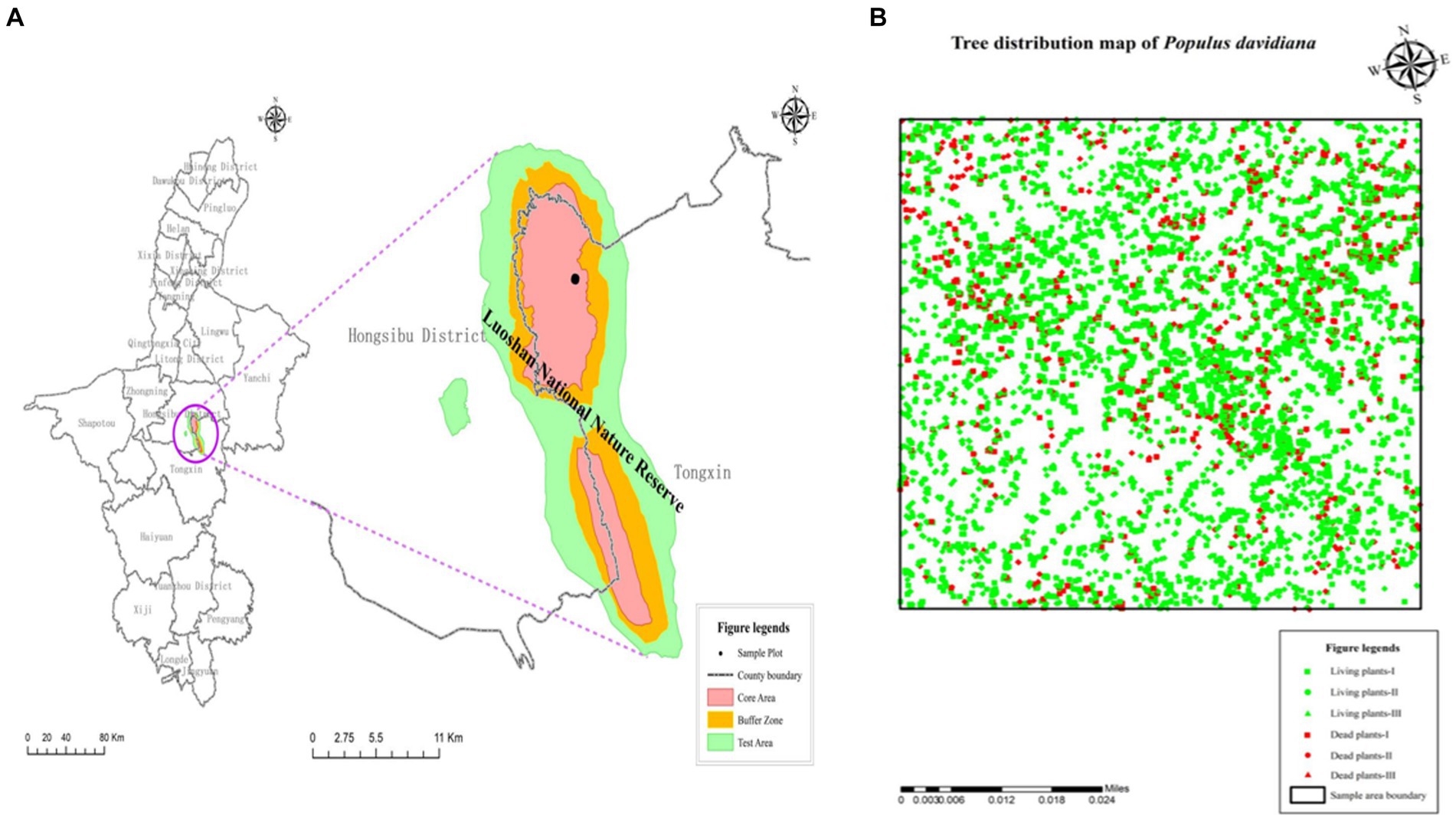
Figure 1. Location of the 1-ha sample plot (A) and distribution of Populus davidiana tree stems (B) living plants—I: living seedlings; living plants—II: living saplings; living plants—III: living adult trees; dead plants—I: dead seedlings; dead plants—II: dead saplings; dead plants—III: dead adult trees.

Data analysis

Ripley’s K or L function is a method used to analyze the spatial patterns of species in a circle of radius r centered at one point (Wiegand and Moloney, 2004; Getzin et al., 2006). However, as the radius increases, it includes information from all smaller scales, which can confound effects at large scales with those at small scales (Condit et al., 2000; Wiegand and Moloney, 2004; George et al., 2006). In contrast, O-ring statistics replaces circles with rings and uses the mean number of neighboring trees in a ring of radius r and ring width around an individual, isolating specific distance classes (Stoyan and Stoyan, 1994; Wiegand and Moloney, 2004). This allows for the analysis of spatial patterns deriving from ecological processes easily and intuitively. O-ring statistics includes both univariate and bivariate statistics, with univariate statistics used for analyzing the spatial pattern of one object and bivariate statistics used for analyzing the spatial association of two objects (Wiegand and Moloney, 2004).

Analysis 1

In our research, we utilized the univariate O-ring statistic O₁₁(r) to examine the spatial distribution patterns of the size classes. To determine the basic null model for the univariate O-ring statistic, we first visualized the stem distribution of trees at different size classes. If there was no evidence of strong clustering (indicated by clearly visible clusters in the pattern), we chose complete spatial randomness (CSR) as the null model, which assumes that the spatial distribution of a given species is completely random and devoid of underlying biological processes (Ebert et al., 2016). However, the pattern was heterogeneous (e.g., only distributed in part of the plot) (Velázquez et al., 2016), therefore, we chose the heterogeneous Poisson null model as an alternative to CSR. For univariate point patterns, O₁₁(r) inside the envelope indicates a random distribution of trees at scale r; while O₁₁(r) above the envelope’s upper bound indicates clumping and O₁₁(r) below the envelope’s lower bound indicates regularity.

Analysis 2

For the bivariate O-ring statistic, we hypothesized that higher-size classes would inhibit the recruitment and growth of lower ones, but that lower-size classes would not affect higher ones. An antecedent condition null model randomizes the locations of the lower-size classes while keeping the locations of the higher ones constant (Cipriotti and Aguiar, 2005). Therefore, we utilized the bivariate pairwise correlation function O₁₂(r) to analyze the spatial associations between different-sized individual trees of P. davidiana under the antecedent condition null model. In the correlation analysis, when O₁₂(r) is inside the envelope, there is no significant correlation between the two size classes at scale r; when O₁₂(r) is above the envelope’s upper bound, the two size classes have a significant positive correlation at scale r; when O₁₂(r) is below the envelope’s lower bound, the two size classes showed a significant negative correlation at scale r (Wiegand and Moloney, 2004).

Analysis 3

In addition to point pattern locations, other information called “mark” such as the tree size can be analyzed. We choose an independent marking null model, which randomly shuffles the marks over all trees; thus, means sizes are independent of individual locations (Wiegand and Moloney, 2014). The influence of neighboring trees’ size on individual growth could be analyzed using mark-correlation functions k_m1m1(r) (Stoyan and Stoyan, 1994). When the k_m1m1(r) > 1, it indicates that two trees have a larger size than average when they are nearby (positive correlation); conversely, when k_m1m1(r) < 1, it means that individual trees tend to have a smaller size (negative correlation), and if k_m1m1(r) = 1, there is no significant correlation between individual trees (Illian et al., 2008; Wiegand and Moloney, 2014).

Analysis 4

Trivariate random labeling is useful for testing how an additional antecedent pattern influences the processes for producing marks in a qualitatively marked pattern (Wiegand, 2014). We calculated the cumulative non-normalized r-mark correlation function C^cum_.,m2 to estimate the proportion of dead seedlings among all seedlings that are located within a distance r of adult trees. This summary function explores the effect of an antecedent focal pattern (i.e., adult trees) on the process that distributes a qualitative mark (i.e., live as type 1 and dead as type 2) on a second pattern (i.e., seedlings). When the C^cum_.,m2 (r) > 1, this indicates that adult trees increase the mortality of seedlings; conversely, when C^cum_.,m2 (r) < 1, adult trees tend to increase the survival proportion, and if C^cum_.,m2 (r) = 1, there is no mortality impact of seedlings coming from adult trees. Therefore, the influence of adult trees on the mortality of seedlings could be investigated by using cumulative non-normalized r-mark correlation function C^cum_.,m2.

Analysis 5

The test of the random mortality hypothesis under the random labeling null model.

1 Testing the spatial aggregation of live and dead trees.

g₂₁(r) may be used to statistically analyze spatial patterns of tree survival and mortality (Goreaud and Pélissier, 2003). g₂₁(r) falls below a simulation envelope when there are fewer dead neighboring trees at distance r from an arbitrary live tree than expected under the random labeling null model (Goreaud and Pélissier, 2003). This means that live and dead seedlings tend to be negatively correlated at distance r (i.e., segregated). Conversely, dead seedlings are considered positively correlated with dead seedlings when g₂₁(r) lies above the envelope.

Furthermore, the function g₂₁(r)-g₂₂(r) is applied to explore if the live seedlings around dead seedlings have the same density as the dead seedlings around the dead ones at scale r (g₂₁(r)-g₂₂(r) = 0). If g₂₁(r)-g₂₂(r) > 0, it indicates that the neighborhood density of live seedlings around dead seedlings outnumbers the dead seedlings around dead seedlings. If g g₂₁(r)-g₂₂(r) < 0, it suggests that there are fewer live seedlings than dead seedlings around the dead seedlings.

2 Comparing the clustering of live and dead trees.

The univariate functions g₂₂ and g₁₁ under the random labeling null model can show the clustering of dead (type 2) and live (type 1) seedlings, respectively. In this study, we examine which of those two clusters is denser by using the function g₂₂-g₁₁. If g₂₂-g₁₁ falls above the envelope, it indicates dead trees are more clustered than surviving ones, and vice versa if g₂₂-g₁₁ falls below the envelope.

3 Testing for density-dependent mortality of seedlings.

We employed the statistic g_2,1 + 2-g_1,1 + 2 to assess density-dependent mortality effects (Miao et al., 2018). This g_2,1 + 2-g_1,1 + 2 function compares the density of dead and live seedlings (1 + 2) around dead seedlings (pattern 2) and their density around live seedlings (pattern 1). Under the random labeling null model, the expected value is zero. However, under density-dependent mortality, we expect dead seedlings to occur more often in areas with high live seedlings density (i.e., g_2,1 + 2-g_1,1 + 2 > 0).

Programita 2018 software was used to run every spatial two-dimensional coordinate analysis. For this purpose, the spatial scale was set to 0–50 m in the plot (step size: 1 m). In total, 199 Monte Carlo random simulations were performed to generate the 95% confidence envelopes; the goodness-of-fit (GoF) test was used to assess the ability of the null models to reflect the data (Loosmore and Ford, 2006). Both SPSS 25 and Excel 2007 were used for the statistical analysis of the data, while two other programs such as ArcGIS10.0 and Origin 2021 were used to graph the spatial trends found.

Results

Testing for environmental heterogeneity from spatial patterns of trees

As shown in Figure 2, the spatial Poisson distribution after removing environmental heterogeneity revealed that P. davidiana seedlings and saplings were aggregated at the smallest scale of 1 m and were then transitioned to a random distribution as the spatial scale increased (Figures 2A,B). Adult trees had a random distribution across all spatial scales investigated (0–50 m) (Figure 2C). This demonstrated the characteristic shift of aggregated distribution to random distribution with greater tree size.

Figure 2

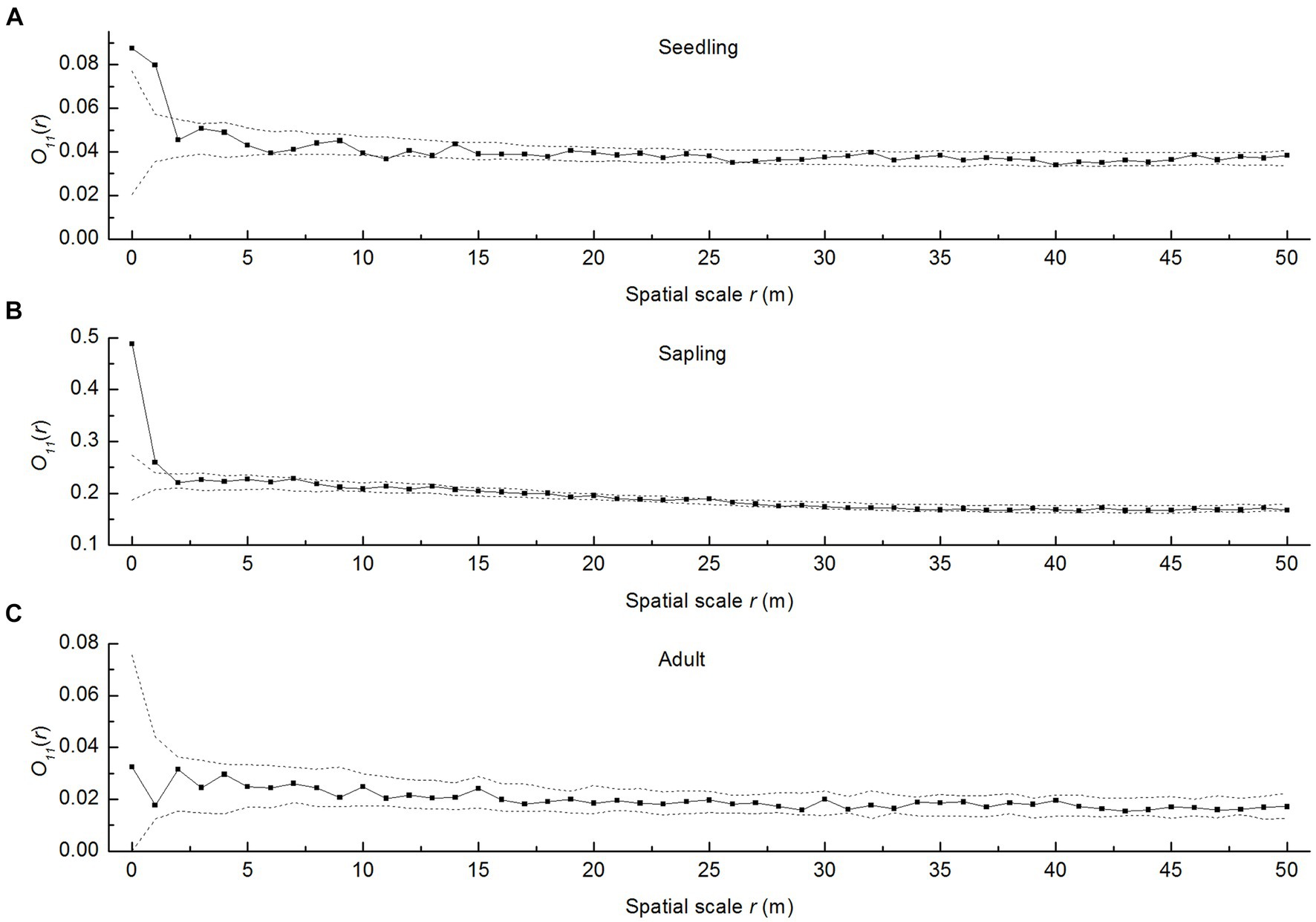
Figure 2. Spatial patterns of P. davidiana seedlings, saplings, and adult trees under the heterogeneous Poisson model. The solid lines indicate obtained values for the ring statistic O₁₁(r); dashed lines indicate the upper and lower limits of the 95% simulation envelope for the heterogeneous Poisson null model. The points above an envelope indicate a cluster pattern, the points within an envelope indicate spatial independence, and the points below an envelope indicate a segregation pattern, (A) the seedlings of Populus davidiana; (B) the saplings of P. davidiana; (C) the adult trees of P. davidiana.

Influence of adult trees on seedlings and saplings

Overall, the curve evidently above the upper envelope (Figure 3A) indicated that adult trees were positively correlated with seedlings at all spatial scales examined. However, adult trees and saplings were negatively correlated at scales of 1–14 m, beyond which their relationship was random (Figure 3B). Saplings and seedlings displayed a significant negative correlation at scales of 1–14 m, which shifted to a positive correlation beyond 20 m (Figure 3C). These results showed the existence of significant spatial differences and scale dependence in the spatial distribution of P. davidiana saplings and seedlings.

Figure 3

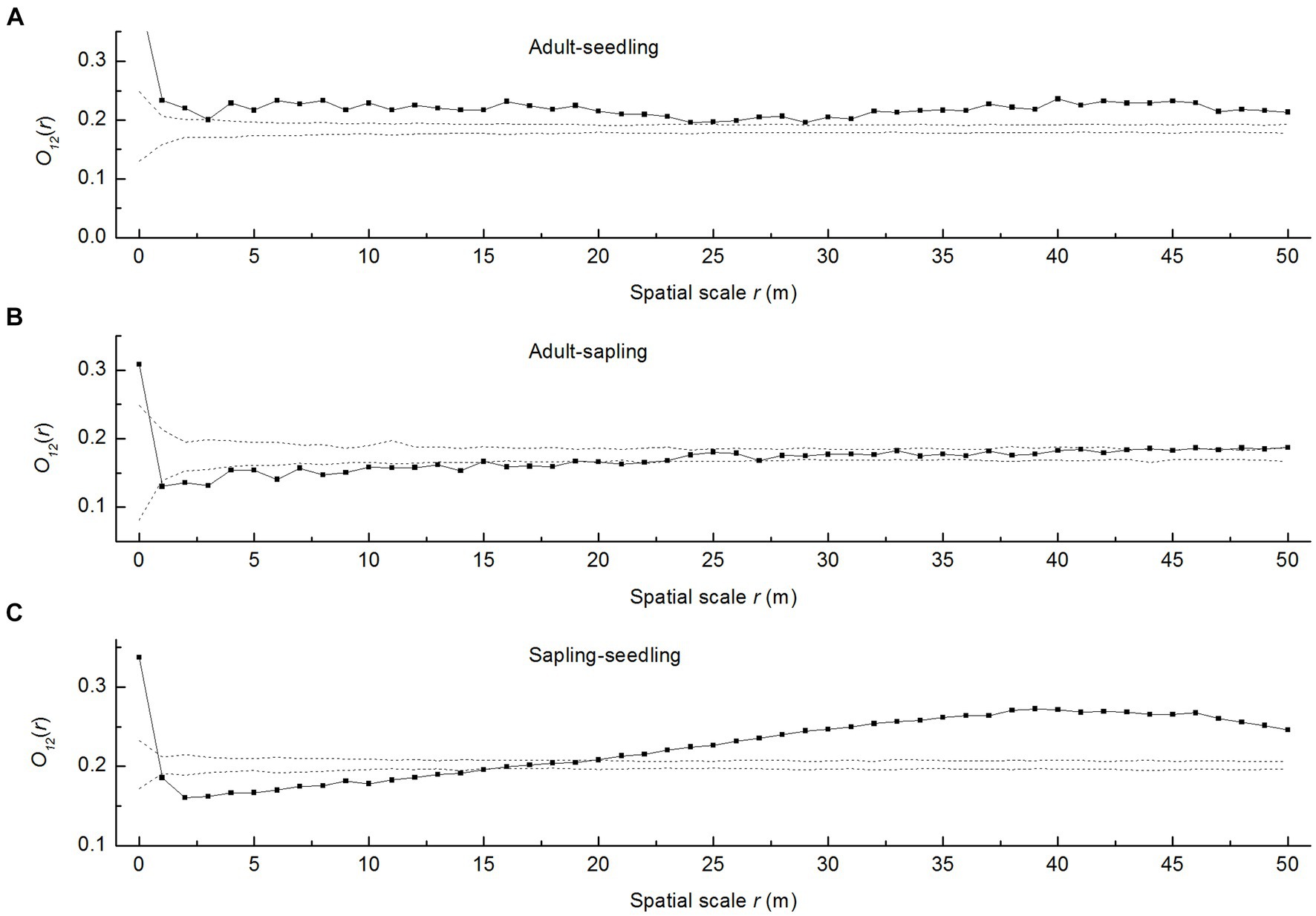
Figure 3. Spatial associations of P. davidiana adult trees, seedlings, and saplings. The solid lines indicate ring statistics O₁₂(r); dotted lines indicate the upper and lower limits of the 95% simulation envelope of the heterogeneous Poisson null model. The points lying above the upper envelope indicate positive associations, the points lying between the envelopes indicate spatial independence, and the points lying below the lower envelope indicate negative associations, (A) Spatial association of adult trees to seedlings (B) Spatial association of adult trees to saplings (C) Spatial association of saplings to seedlings.

Mark-correlation function analysis

According to the mark-correlation functions k_m1m1(r), the resulting trend of k_m1m1(r) was below 1, indicating a significant negative correlation across scales of 0–50 m (Figure 4A), but this correlation diminished with increasing scale. This showed that P. davidiana trees were smaller in size than the average size around neighboring living trees. The closer the spatial distance between individual trees, the greater the negative impact on their size.

Figure 4

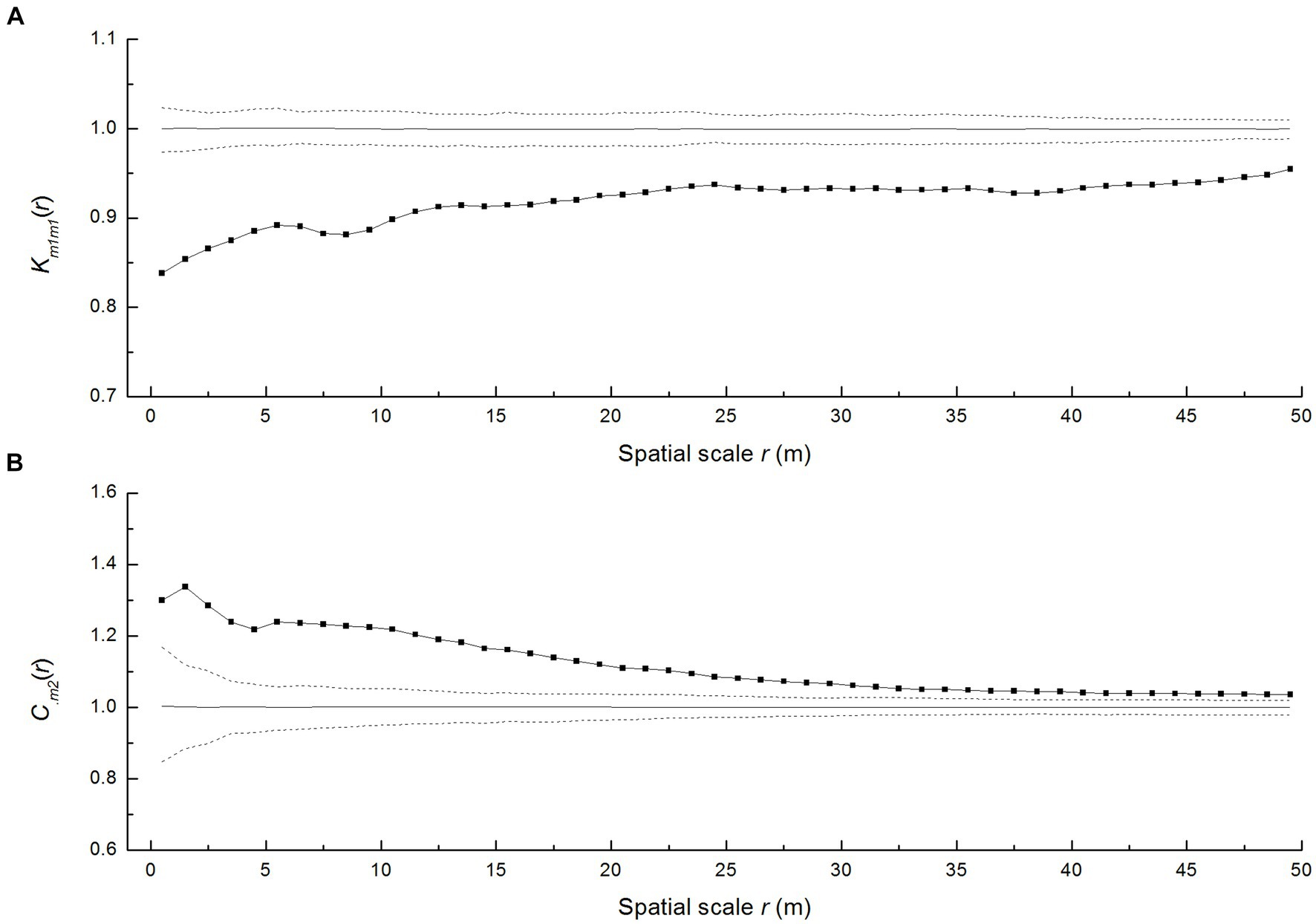
Figure 4. (A) Univariate mark function k_m1m1(r) of P. davidiana and (B) trivariate random labeling on the mark-correlation function C_.m2 of P. davidiana. The solid line indicates the empirical curve, the gray line indicates the expected value under the random labeling null model, and the dashed lines indicate the limits of 199 Monte Carlo simulation envelopes.

The impact of adult trees on seedling mortality was evaluated using the non-normalized r-mark correlation function C^cum_.,m2 under the trivariate random labeling null model. It revealed that adult trees augment the risk of seedling mortality at almost all distances (Figure 4B).

As shown in Figure 5A, the g₂₁ trend indicated that the spatial association was mostly random between live and dead seedlings in the studied P. davidiana population. According to the results for the g₂₁-g₁₁ function—testing whether the number of dead seedlings around live seedlings exceeds that around dead seedlings—there were fewer live seedlings near dead seedlings than dead seedlings around the dead ones (Figure 5B), suggesting the aggregation of the latter. Furthermore, the g₂₂-g₁₁ trend also showed a stronger aggregation for dead seedlings than for live seedlings (Figure 5C). In most spatial scale r, g_2,1 + 2-g_1,1 + 2 > 0 convinced density-dependent mortality (Figure 5D), while rejecting the random mortality hypothesis.

Figure 5

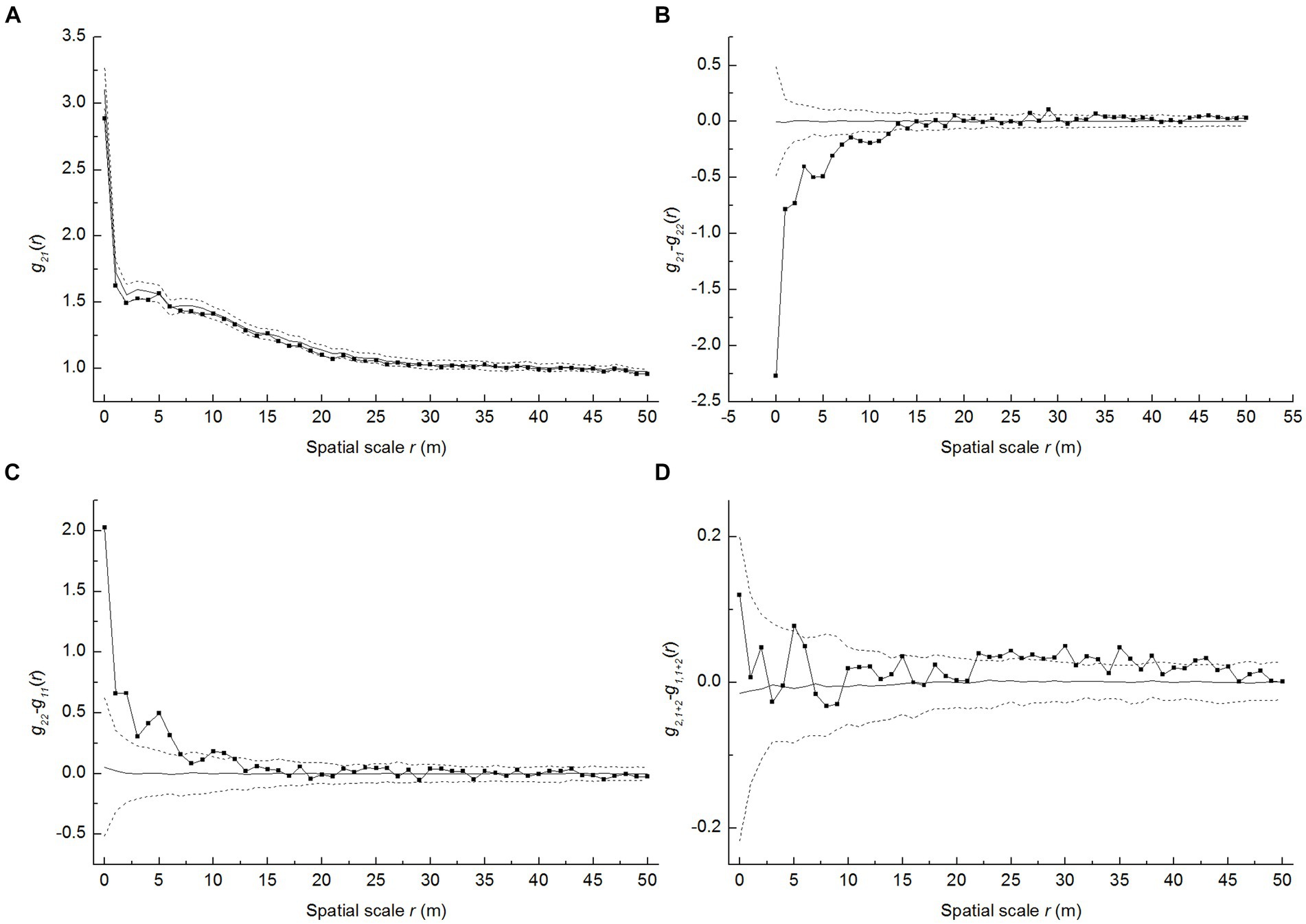
Figure 5. Spatial analysis of random mortality of P. davidiana seedlings. The solid line indicates the empirical curve, the gray line indicates the expected value under the random labeling null model, and the dashed lines indicate the limits of 199 Monte Carlo simulation envelopes, (A) g21 function of live and dead seedlings; (B) g21-g11 function of live and dead seedlings; (C) g21-g22 function of live and dead seedlings (D) g2,1+2-g1,1+2 function of live and dead seedlings.

Discussion

For Analysis1, our comparison of the spatial distributions O₁₁(r) of different-sized Populus davidiana trees is consistent with earlier findings of Miao et al. (2009) and lends further support to the hypothesis that tree population’s spatial distribution transitions from aggregated to random through ontogeny in most temperate forests.

Based on the spatial association results of O₁₂(r), we found a high positive correlation between conspecific adult trees and seedlings (Analysis 2). This is easily explained because P. davidiana seedlings originate from root sprouts of reproductive individual trees and are therefore expected to exhibit strong positive spatial correlations with these adult trees (Qin and Shangguan, 2006). However, for Analysis 3, as the seedlings grow and recruit into saplings, the stem density-related limitations and greater competition for the resource (i.e., light, water, and nutrient) strongly influenced the distance and size of individual trees, especially asymmetrically vis-à-vis taller neighboring trees (Figure 4A). Therefore, at a spatial position away from adult trees (1-14 m in our result, Figure 3B), seedlings tend to have a better potential to reach the sapling stage (Shao et al., 2011; Gao et al., 2014), which, in turn, enhances their prospects for adult recruitment into the canopy.

To explore the possible reasons for seedling mortality of P. davidiana, we hypothesized that it was the outcome of an excessively high local density, leading to intense intraspecific competition and self-thinning effects (Analysis 4 and Analysis 5). Although g₂₁ did not detect a significant negative spatial correlation between dead and live seedlings, the function g_2,1 + 2-g_1,1 + 2 > 0 indicated that the mortality of seedlings was density-dependent (Figure 5D). As a result of high-density seedlings from root sprouting, P. davidiana adult trees showed a positive association with seedlings (Figure 3A). Therefore, the seedling mortality is density dependent due to the presence of adult trees. The results from C^cum_.,m2 evidenced that adult trees contribute to a higher risk of seedling mortality that nonetheless declines with distance (Figure 4B). As seedlings were negatively correlated with saplings at both medium and small spatial scales, the initially high density of seedlings may have led to higher post-dispersal mortality risks faced by P. davidiana at the stage when its individual trees are most vulnerable. Thus, the closer the seedlings are to an adult tree, the stronger the negative conspecific impact in the form of higher mortality (Liang et al., 2016).

The g₂₁-g₂₂ and g₂₂-g₁₁ functions together discover the dead seedlings that emerged more cluster around dead ones and depart with live seedlings (Figures 5B,C). For P. davidiana, its dead seedlings display higher aggregation than the surviving seedlings, which rejected the random mortality hypothesis. However, we did not investigate why having an excessive density of seedlings makes them prone to die off in a clustered spatial pattern. Additionally, we did not know the maximum density limit that causes mortality at the seedling. Seedling mortality is a result of a complex causes. At different scales, different dominant causes lead to their death. For instance, forest research on negative density-dependent dynamics in trees has confirmed that local high densities of the progeny of the same species could lead to disproportionately high levels of seedling mortality caused by soil pathogens (Janzen-Connell hypothesis) (Liu et al., 2007). Such a negative density-dependent feedback driven by the soil microbial community is actually common and ecologically important in many temperate tree species (Packer and Clay, 2000; Liang et al., 2016; Jevon et al., 2020). Moreover, Yamazaki et al. (2009) found that vertebrate herbivores (mainly rodents) were the major cause of mortality for large-seeded tree species, whereas the disease was most important for small-seeded species. Therefore, further investigation is needed on where and how the density impacts seedling mortality in arid mountain forests.

Conclusion

The spatial patterns of trees in an arid region, such as the Luoshan Mountains in China, are influenced by plant competition. To gain insights into the stand dynamics and guide regeneration strategies, we investigated the spatial distribution of individual trees at different growth stages (sizes) in P. davidiana forest in the Luoshan Mountains.

Spatial point pattern analysis confirmed that the spatial distribution of individual trees shifted from an aggregated distribution to random distribution as seedlings grew and developed into adult trees. Additionally, we found that more seedlings emerged around adult trees while high seedlings’ mortality happened in clusters. Further research is arguably needed to elucidate the causes of P. davidiana mortality, and the close relationship between its adult trees, seedling density, and seedling mortality was prominent in this arid mountain forest.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JuY: Conceptualization, Funding acquisition, Project administration, Software, Writing – original draft, Writing – review & editing. JiY: Funding acquisition, Resources, Writing – review & editing. GW: Investigation, Methodology, Visualization, Writing – review & editing. XL: Conceptualization, Project administration, Resources, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was funded by Ningxia Rural and Development Projects (2023BEG02039) and (2021BEG02009).

Acknowledgments

The authors would like to thank Jiajing Li and Hu Yang for their contributions to data collection and field inventory. We greatly thank Julian Norghauer for editing the manuscript. Special thanks to Raquel Muñoz-Gallego for providing function interpretation and software guidance.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baddeley, A., Rubak, E., and Turner, R. (2015). Spatial point patterns: methodology and applications with R-London. New York: Chapman and Hall/CRC Press.

Google Scholar

Beyns, R., Bauman, D., and Drouet, T. (2021). Fine-scale tree spatial patterns are shaped by dispersal limitation which correlates with functional traits in a natural temperate forest. J. Veg. Sci. 32:e13070. doi: 10.1111/jvs.13070

Crossref Full Text | Google Scholar

Bianchi, E., Bugmann, H., Hobi, M. L., and Bigler, C. (2021). Spatial patterns of living and dead small trees in subalpine Norway spruce forest reserves in Switzerland. For. Ecol. Manag. 494:119315. doi: 10.1016/j.foreco.2021.119315

Crossref Full Text | Google Scholar

Bouchard, H., Guittonny, M., and Brais, S. (2018). Early recruitment of boreal forest trees in hybrid poplar plantations of different densities on mine waste rock slopes. For. Ecol. Manag. 429, 520–533. doi: 10.1016/j.foreco.2018.07.003

Crossref Full Text | Google Scholar

Cipriotti, P. A., and Aguiar, M. R. (2005). Effects of grazing on patch structure in a semi-arid two-phase vegetation mosaic. J. Veg. Sci. 16, 57–66. doi: 10.1111/j.1654-1103.2005.tb02338.x

Crossref Full Text | Google Scholar

Condit, R., Ashton, P. S., Baker, P., Bunyavejchewin, S., Gunatilleke, S., Gunatilleke, N., et al. (2000). Spatial patterns in the distribution of tropical tree species. Science 288, 1414–1418. doi: 10.1126/science.288.5470.1414

Crossref Full Text | Google Scholar

Condit, R. S. T. R., Hubbell, S. P., and Foster, R. B. (1992). Recruitment near conspecific adults and the maintenance of tree and shrub diversity in a neotropical forest. Am. Nat. 140, 261–286. doi: 10.1086/285412

PubMed Abstract | Crossref Full Text | Google Scholar

Detto, M., and Muller-Landau, H. C. (2013). Fitting ecological process models to spatial patterns using Scalewise variances and moment equations. Am. Nat. 181, E68–E82. doi: 10.1086/669678

PubMed Abstract | Crossref Full Text | Google Scholar

Diggle, P. (2003) Statistical analysis of spatial point patterns, 2nd. London: Arnold.

Google Scholar

Ebert, A., Brito Da Costa, R., and Brondani, G. E. (2016). Spatial distribution pattern of Mezilaurus itauba (Meins.) Taub. Ex mez. In a seasonal forest area of the southern Amazon, Brazil. IForest (Viterbo) 9, 497–502. doi: 10.3832/ifor1427-008

Crossref Full Text | Google Scholar

Gao, L. S., Zhao, X. H., Wang, X. M., and Zhang, C. Y. (2014). Sexual differences in climatic response of dioecious Populus davidiana tree. Ying Yong Sheng Tai Xue Bao 25, 1863–1869.

PubMed Abstract | Google Scholar

George, L. W. P., Miller, B. P., and Enright, N. J. (2006). A comparison of methods for the statistical analysis of spatial point patterns in plant ecology. Plant Ecol. 181, 59–82. doi: 10.1007/s11258-006-9133-4

Crossref Full Text | Google Scholar

Getzin, S., Dean, C., He, F., Trofymow, J. A., Wiegand, K., and Wiegand, T. (2006). Spatial patterns and competition of tree species in a Douglas-fir chronosequence on Vancouver Island. Ecography 29, 671–682. doi: 10.1111/j.2006.0906-7590.04675.x

Crossref Full Text | Google Scholar

Goreaud, F., and Pélissier, R. (2003). Avoiding misinterpretation of biotic interactions with the intertype K12-function: population independence vs. random labelling hypotheses. J. Veg. Sci. 14, 681–692. doi: 10.1111/j.1654-1103.2003.tb02200.x

Crossref Full Text | Google Scholar

Hai, N. H., Wiegand, K., and Getzin, S. (2014). Spatial distributions of tropical tree species in northern Vietnam under environmentally variable site conditions. J. For. Res. 25, 257–268. doi: 10.1007/s11676-014-0457-y

Crossref Full Text | Google Scholar

Haq, S. M., Rashid, I., Waheed, M., and Khuroo, A. A. (2023). From forest floor to tree top: partitioning of biomass and carbon stock in multiple strata of forest vegetation in Western Himalaya. Environ. Monit. Assess. 195:812. doi: 10.1007/s10661-023-11376-6

PubMed Abstract | Crossref Full Text | Google Scholar

Holík, J., Janík, D., and Adam, D. (2021). Light can modify density-dependent seedling mortality in a temperate forest. J. Veg. Sci. 32:e12992. doi: 10.1111/jvs.12992

Crossref Full Text | Google Scholar

Illian, J., Penttinen, A., and Stoyan, H. (2008). Statistical analysis and modelling of spatial point patterns. Chichester: John Wiley & Sons Ltd.

Google Scholar

Im, C., Chung, J., Kim, H. S., Chung, S., and Yoon, T. K. (2023). Are seed dispersal and seedling establishment distance- and/or density-dependent in naturally regenerating larch patches? A within-patch scale analysis using an eigenvector spatial filtering approach. For. Ecol. Manag. 531:120763. doi: 10.1016/j.foreco.2022.120763

Crossref Full Text | Google Scholar

Jevon, F. V., Record, S., Grady, J., Lang, A. K., Orwig, D. A., Ayres, M. P., et al. (2020). Seedling survival declines with increasing conspecific density in a common temperate tree. Ecosphere 11:e03292. doi: 10.1002/ecs2.3292

Crossref Full Text | Google Scholar

Klein, T., Randin, C., and Korner, C. (2015). Water availability predicts forest canopy height at the global scale. Ecol. Lett. 18, 1311–1320. doi: 10.1111/ele.12525

PubMed Abstract | Crossref Full Text | Google Scholar

Kuang, X., Zhu, K., Yuan, Z., Lin, F., Ye, J., Wang, X., et al. (2017). Conspecific density dependence and community structure: insights from 11 years of monitoring in an old-growth temperate forest in Northeast China. Ecol. Evol. 7, 5191–5200. doi: 10.1002/ece3.3050

Crossref Full Text | Google Scholar

Kuehne, C., Weiskittel, A., Pommerening, A., and Wagner, R. G. (2018). Evaluation of 10-year temporal and spatial variability in structure and growth across contrasting commercial thinning treatments in spruce-fir forests of northern Maine, USA. Ann. For. Sci. 75, 1–12. doi: 10.1007/s13595-018-0697-7

Crossref Full Text | Google Scholar

Law, R., Illian, J., Burslem, D., Gratzer, G., Gunatilleke, C. V. S., and Gunatilleke, I. A. U. N. (2009). Ecoogical information from satial patterns of plants: insights from point process theory. J. Ecol. 97, 616–628. doi: 10.1111/j.1365-2745.2009.01510.x

Crossref Full Text | Google Scholar

Liang, Z. (2018). Variation pattern of physicochemical properties along altitudes of Luoshan Mountain in Ningxia-world. J. For. 7, 19–31. doi: 10.12677/wjf.2018.71004

Crossref Full Text | Google Scholar

Liang, M., Liu, X., Gilbert, G. S., Zheng, Y., Luo, S., Huang, F., et al. (2016). Adult trees cause density-dependent mortality in conspecific seedlings by regulating the frequency of pathogenic soil fungi. Ecol. Lett. 19, 1448–1456. doi: 10.1111/ele.12694

PubMed Abstract | Crossref Full Text | Google Scholar

Liu, D., Kelly, M., Gong, P., and Guo, Q. (2007). Characterizing spatial–temporal tree mortality patterns associated with a new forest disease. For. Ecol. Manag. 253, 220–231. doi: 10.1016/J.FORECO.2007.07.020

Crossref Full Text | Google Scholar

Loosmore, N. B., and Ford, E. D. (2006). Statistical inference using the g or K point pattern spatial statistics. Ecology 87, 1925–1931. doi: 10.1890/0012-9658(2006)87[1925:SIUTGO]2.0.CO;2

Crossref Full Text | Google Scholar

Ma, R., Li, J., Guo, Y., Wang, B., Xiang, W., Li, D., et al. (2024). Recruitment dynamics in a tropical karst seasonal rain forest: revealing complex processes from spatial patterns. For. Ecol. Manag. 553:121610. doi: 10.1016/j.foreco.2023.121610

Crossref Full Text | Google Scholar

Miao, N., Liu, S. R., Shi, Z. M., Yu, H., and Liu, X. L. (2009). Spatial patterns of dominant tree species in sub-alpine Betula-Abies forest in West Sichuan of China. Ying Yong Sheng Tai Xue Bao 20, 1263–1270.

PubMed Abstract | Google Scholar

Miao, N., Xu, H., Moermond, T. C., Li, Y., and Liu, S. (2018). Density-dependent and distance-dependent effects in a 60-ha tropical mountain rain forest in the Jianfengling mountains, Hainan Island, China: spatial pattern analysis. For. Ecol. Manag. 429, 226–232. doi: 10.1016/j.foreco.2018.07.013

Crossref Full Text | Google Scholar

Mitchell, J. C., Kashian, D. M., Chen, X., Cousins, S., Flaspohler, D., Gruner, D. S., et al. (2023). Forest ecosystem properties emerge from interactions of structure and disturbance. Front. Ecol. Environ. 21, 14–23. doi: 10.1002/fee.2589

Crossref Full Text | Google Scholar

Muñoz-Gallego, R., Wiegand, T., Traveset, A., and Fedriani, J. M. (2023). From seed dispersal service to reproductive collapse: density-dependent outcome of a palm–mammal interaction. Oikos 2023:e10002. doi: 10.1111/oik.10002

Crossref Full Text | Google Scholar

Nguyen, V. A. T., Blardoni, F., Manh, H. B., Schlicht, R., and Wagner, S. (2022). Disentangling the regeneration niche of Vatica odorata (Griff.) Symington using point pattern analysis. Ecologies 3, 336–360. doi: 10.3390/ecologies3030026

Crossref Full Text | Google Scholar

Packer, A., and Clay, K. (2000). Soil pathogens and spatial patterns of seedling mortality in a temperate tree. Nature (London) 404, 278–281. doi: 10.1038/35005072

PubMed Abstract | Crossref Full Text | Google Scholar

Piao, T., Comita, L. S., Jin, G., and Kim, J. H. (2013). Density dependence across multiple life stages in a temperate old-growth forest of Northeast China. Oecologia 172, 207–217. doi: 10.1007/s00442-012-2481-y

PubMed Abstract | Crossref Full Text | Google Scholar

Qin, J., and Shangguan, Z. (2006). Physiological-ecological effects of Populus davidiana--Quercus liaotungensis mixed forest in Ziwuling forest area. Ying Yong Sheng Tai Xue Bao 17, 972–976.

PubMed Abstract | Google Scholar

Raventós, J., Wiegand, T., and Luis, M. D. (2010). Evidence for the spatial segregation hypothesis: a test with nine-year survivorship data in a Mediterranean shrubland. Ecology 91, 2110–2120. doi: 10.1890/09-0385.1

PubMed Abstract | Crossref Full Text | Google Scholar

Rendenieks, Z., Liepa, L., and Nikodemus, O. (2022). Spatial patterns and species composition of new forest areas present challenges for forest management in Latvia. For. Ecol. Manag. 509:120097. doi: 10.1016/j.foreco.2022.120097

Crossref Full Text | Google Scholar

Ripley, B. D. (1976). The second-order analysis of stationary point processes. J. Appl. Probab. 13, 255–266. doi: 10.2307/3212829

Crossref Full Text | Google Scholar

Salas-Eljatib, C., Riquelme-Alarcón, J., Donoso, P. J., Ponce, D., and Soto, D. P. (2022). Analysing changes in spatial point patterns: A proposal using data from a forest thinning experiment. For. Ecosyst. 9, 878–887. doi: 10.1016/j.fecs.2022.100081

Crossref Full Text | Google Scholar

Shao, F. L., Yu, X. X., Song, S. M., and Zhao, Y. (2011). Spatial structural characteristics of natural Populus davidiana - Betula platyphylla secondary forest. Ying Yong Sheng Tai Xue Bao 22, 2792–2798.

PubMed Abstract | Google Scholar

Stoyan, D., and Stoyan, H. (1994). Fractals, random shapes and point fields. Methods of geometrical gtatistics. - Chichester, Wiley.

Google Scholar

Velázquez, E., Martínez, I., Getzin, S., Moloney, K. A., and Wiegand, T. (2016). An evaluation of the state of spatial point pattern analysis in ecology. Ecography 39, 1042–1055. doi: 10.1111/ecog.01579

Crossref Full Text | Google Scholar

Waheed, M., Arshad, F., Majeed, M., Fatima, S., Mukhtar, N., Aziz, R., et al. (2022). Community structure and distribution pattern of Woody vegetation in response to soil properties in semi-arid Lowland District Kasur Punjab, Pakistan. Land 11:2145. doi: 10.3390/land11122145

Crossref Full Text | Google Scholar

Wang, Q., Chi, X., Tang, Z., and Jiang, M. (2019). Analysing tree–neighbourhood interactions in ecotones of montane evergreen and deciduous forests in China. J. Veg. Sci. 30, 654–663. doi: 10.1111/jvs.12737

Crossref Full Text | Google Scholar

Wiegand, T. (2014). User manual for the Programita software., Germany.

Google Scholar

Wiegand, T., and Moloney, K. A. (2004). Rings, circles, and null-models for point pattern analysis in ecology. Oikos 104, 209–229. doi: 10.1111/j.0030-1299.2004.12497.x

Crossref Full Text | Google Scholar

Wiegand, T., and Moloney, K. (2014). Handbook of spatial point-pattern analysis in ecology-USA. Boca Raton, FL: Chapman and Hall/CRC Press.

Google Scholar

Wiegand, T., Moloney, K. A., Naves, J., and Knauer, F. (1999). Finding the missing link between landscape structure and population dynamics: a spatially explicit perspective. Am. Nat. 154, 605–627. doi: 10.1086/303272

PubMed Abstract | Crossref Full Text | Google Scholar

Xin, H., Jackson, T., Cao, Y., Zhang, H., Lin, Y., and Shenkin, A. (2022). Spatial pattern analysis of forest trees based on the vectorial mark. J. For. Res. 33, 1301–1315. doi: 10.1007/s11676-021-01417-6

Crossref Full Text | Google Scholar

Yamazaki, M., Iwamoto, S., and Seiwa, K. (2009). Distance- and density-dependent seedling mortality caused by several diseases in eight tree species co-occurring in a temperate forest. Plant Ecol. 201, 181–196. doi: 10.1007/s11258-008-9531-x

Crossref Full Text | Google Scholar

Yang, J., He, H. S., and Shifley, S. R. (2008). Spatial controls of occurrence and spread of wildfires in the Missouri Ozark highlands. Ecol. Appl. 18, 1212–1225. doi: 10.1890/07-0825.1

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, Y., Tariq, A., Hughes, A. C., Hong, D., Wei, F., Sun, H., et al. (2023). Challenges and solutions to biodiversity conservation in arid lands. Sci. Total Environ. 857:159695. doi: 10.1016/j.scitotenv.2022.159695

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, M., Wang, J., and Kang, X. (2022). Spatial distribution pattern of dominant tree species in different disturbance plots in the Changbai Mountain. Sci. Rep. 12:14161. doi: 10.1038/s41598-022-18621-x

PubMed Abstract | Crossref Full Text | Google Scholar