Timeseries partitioning of ecosystem respiration components in seasonal, non-tropical forests; comparing literature derived coefficients with evaluation at two contrasting UK forest sites

Introduction: Understanding carbon flows within ecosystems is key to quantifying the impacts of land-use change in the climate. However, while the net exchange of CO₂ between the ecosystem and atmosphere indicates global warming potentials, partitioning into individual flux components is needed to understand sinks and sources, residence times, and sensitivities to land-use impacts. Scaling from research site to region requires modelling evaluated against in situ measurements, but there is often a mismatch between outputs of process models (e.g., soil heterotrophic respiration (Rh)) and site-measured parameters (e.g., total soil surface respiration (Rs) or whole ecosystem respiration (Re)).

Methods: This study took a literature review approach to determine fractional coefficients for estimating Rh from Re or Rs and considered whether these fractions differed across a year in seasonal forests, where relative contributions of root respiration might be expected to vary between growing and dormant seasons. Compiled timeseries data were grouped by forest type (broadleaf, needleleaf, and mixed), and coefficients for a fraction of each component (Rs or Re) that Rh represented were calculated using two approaches, namely a simple annual mean value over all months and individual monthly means. These coefficients were then used to estimate Rh separately from higher-level fluxes (Re from eddy covariance and Rs from soil chambers), measured concurrently at two UK forest sites, and compared to Rh estimated from the same datasets using previously published generic coefficients as well as to concurrently measured Rh and Re.

Results: Both approaches resulted in much closer convergence of the two separate estimates of Rh (derived from Re or Rs) than previously published coefficients, particularly for Rh/Re coefficients that had previously been measured under peatland blanket bog rather than forest.

Discussion/Conclusion: This result suggests that land cover is an important factor in determining the relative contribution of heterotrophic respiration to higher-level fluxes and that the coefficients used would ideally be derived from studies on similar ecosystems.

1 Introduction

Quantifying the inward and outward fluxes of carbon dioxide (CO₂) for ecosystems is key to determining the climate impacts of land-use systems and changes within them. While measurements of net ecosystem exchange (NEE) with the atmosphere, such as from the eddy covariance (ECo) method (Baldocchi, 2003), can estimate the impacts of a site on atmospheric CO₂ (and associated global warming potentials), partitioning of these net fluxes into individual components (e.g., soil surface emissions) is needed to understand the dynamics of particular pools. Beyond information on local-scale impacts, the compilation and synthesis of such flux-partitioned studies may be used to provide key information, and validation datasets, for process-based soil organic matter models. Model output can then be applied spatially to scale up from the local to the regional or global scale. However, where soil models typically output specific component fluxes, such as soil heterotrophic respiration (Rh), field-based studies typically capture these components only in combination with integrated, higher-level fluxes. For example, ECo studies [from which a range of data repositories are freely available (Valentini, 2003; Friend et al., 2007; Sabbatini et al., 2018)] measure NEE (subsequently partitioned into photosynthetic uptake (GPP) and whole ecosystem respiration (Re)), which is the sum of all above and below ground sources of CO₂. Soil surface chamber-based studies (e.g., Pumpanen et al., 2004; Rochette and Hutchinson, 2005) typically report total soil surface respiration (Rs), which is the sum of below ground heterotrophic (Rh) and autotrophic (Ra) root-derived respiration (plus any litter decomposition or plant respiration where these are present on the soil surface within chamber collars), although some will use isolation methods to capture these components separately (Hanson et al., 2000; Kuzyakov, 2006). Wiant (1967) defined root-derived respiration as including all respiration derived from the organic compounds originating directly from plants, which includes the respiration of mycorrhizal fungi and microbial decomposition of root exudates and dead root tissue. We also use the term root-derived respiration to make this distinction clear.

The derivation, and provision in the literature, of generic coefficients to estimate Rh from the most widely available datasets (Re or Rs) would greatly improve the potential for these datasets to be used in model evaluation. Subke et al. (2006) provided a literature review of chamber flux partitioning studies and reported values for Rh as a fraction of Rs across a wide range of land cover types and climate zones from 97 studies. Jian et al. (2022) expanded this greatly to 880 studies (including 256 temperate/boreal forest sites) using the global soil respiration database (SRDB-V5) (Jian et al., 2021), although they are primarily concerned with predicting global distributions and report only a single global mean value for Ra/Rs (0.42). Notably, neither study investigates relative component contributions as a function of time of year. It is possible that the contribution of Ra in particular (and therefore potentially the relative contribution of Rh) to both Rs and Re will vary substantially between growing and dormant periods in a seasonal climate (Hanson et al., 1993, 2000; Flattery et al., 2018). Hanson et al. (2000) reported, from their literature review, a wide range of Ra/Rs (from 0.1 to 0.9), dependent on vegetation type and time of year, with a mean annual value of 0.46 for forest soils (n = 37) (therefore, Rh/Rs = 0.54). However, they caution against assuming this value for every month of the year because Ra contribution to Rs is commonly greater during the growing season compared to the dormant season, a conclusion supported by Heinemeyer et al. (2012) in their multi-year flux partitioning study. Hanson et al. (2000) insisted, in their recommendations, that studies of the components of soil respiration must “involve repeated measurements throughout an annual cycle”. It may not necessarily follow, though, that the relative contributions of Ra and Rh to a dynamic Rs would change since Rh is also likely to be lower during the dormant season due to reduced microbial activity in colder soils (Curiel Yuste et al., 2007).

In the ECOSSE soil process model (Smith et al., 2010), and others such as RothC (Smith et al., 1997), the CO₂ flux output specifically estimates soil Rh, presenting a challenge when validating results against either ECo-derived respiration data (Re) or unpartitioned soil chamber flux data (Rs). Some studies (Khalil et al., 2013, 2016) have used separate process models (e.g., DNDC, DAYCENT) run with the same site data to estimate the relative contributions of individual respiration components comprising the measured Re, then adjusting as appropriate before evaluating ECOSSE output of estimated Rh. However, this approach is computationally intensive and assumes that the other process models have themselves correctly partitioned Re. Flattery et al. (2018) preferred to validate ECOSSE output of Rh against soil chamber Rs measurements due to the difficulties in estimating Rh from ECo-derived Re at their site. However, they made no attempt to partition their chamber Rs into its components and noted that the match was at its worst during the growing season, as might be expected due to increased root-derived respiration. Other studies (Abdalla et al., 2014; Dondini et al., 2016) have relied on generic coefficients for estimating Rh from Re, derived from a study by Hardie et al. (2009). These studies assume fractional (Rh/Re) values specific to time periods within the year. However, while the Hardie et al. (2009) values provide a pragmatic approach, they were measured within a single study under a specific European upland peatland ecosystem (blanket bog dominated by Sphagnum spp., Calluna vulgaris, and Eriophorum vaginatum). Transferring these coefficients to very different vegetation systems, such as forests, is likely to result in significant errors in the estimation of Rh from Re due to very different plant inputs (litter quality, root exudates, and turnover rates) and decomposition characteristics. For further evaluation against soil chamber data (at sites where direct measurements of the individual components were not available), Dondini et al. (2016) used vegetation-specific single annual coefficients based on Subke et al. (2006) literature review to estimate Rh/Rs. Overall, this mismatch between process model output parameters and datasets commonly available for validation remains a substantial challenge in assessing the reliability of up-scaled spatial modelling.

Our current study aims to address this knowledge gap of how to derive Rh from more commonly available datasets, specifically for forest systems in seasonal, non-tropical climates, and consider whether component contributions are specific to the time of year. The aim of this study was achieved by compiling literature-based coefficients to estimate the contribution of Rh to both Rs and Re at a monthly timestep across the year and comparing to using a simple annual mean across all months. Due to the scarcity of available timeseries datasets, rather than splitting into training and validation datasets, we assess the performance of these coefficients and compare them to those previously published, by investigating how consistently Rh is estimated separately from Re and Rs measured concurrently in two contrasting UK forest stands (upland evergreen needleleaf on peaty soil and lowland deciduous broadleaf on mineral soil). We make the assumption that independent estimates of Rh (derived from two distinct measurement techniques, Re from ECo and Rs from soil chambers) at the same site in the same period should converge around a true value if the derivation coefficients are to be considered reliable. Finally, we compare our estimate of Rh as a fraction of Re to two rare datasets, where these fractions were concurrently measured for multiple years in deciduous broadleaf forest stands.

2 Methods

2.1 Datasets

A Web of Science (Web of Science Core Collection. © Copyright Clarivate 2023) search was carried out with the term “forest CO₂ respiration partitioning,” which resulted in 465 research articles (including 20 research reviews), 16 conference proceedings, three book chapters, and two early access articles. These results were then manually searched for timeseries of partitioned respiration fluxes (Rh/Rs, Rs/Re, Rh/Re) and filtered to exclude tropical climates following allocation to climatic zones within the Koppen–Geiger climate classification (Peel et al., 2007) using the “kgc” package (Bryant et al., 2017) in R (R Core Team, 2022). Climate zones included in the study are given in Table 1. Where data were only provided as graphs (rather than data tables), data values were extracted digitally using the “digitize” package in R (Poisot, 2011). For datasets where only Ra is provided, Rh is calculated based on Equation 1.

Table 1

Table 1. Time series studies included in the derivation of partitioning coefficients.

Additional chamber-based soil flux datasets were made available within the Netzero+ project.¹ These came from two forest sites in England maintained by UK Forest Research²: Harwood (55°13′0” N / 2°1′31” W), a second rotation evergreen needleleaf (ENF) (Picea sitchensis) plantation on high carbon, cambic stagnohumic gley soil (Xenakis et al., 2021), and Alice Holt (51°9′13” N / 0°51′30” W), a deciduous broadleaf (DBF) (Quercus robur/Quercus petrea) dominated woodland (Wilkinson et al., 2016) on a surface water gley soil. Total soil respiration (Rs) data from Harwood were available from February 2015 to December 2020 and are referred to here as Harwood 2020. Data from Alice Holt were available from two separate studies, one timeline from April 2008 to December 2010 (Alice Holt 2010), where soil chambers in plots (with roots either included or excluded) were monitored concurrently to provide Rh and Rs (Heinemeyer et al., 2012), and another from May 2013 to October 2020 (Alice Holt 2020), where only Rs was measured (unpublished data). Data from Harwood 2020 and Alice Holt 2020 were supplied as individual sampling event results (typically one or two times per month). To create a continuous monthly timeseries, the mean flux rate of all sampling within each month was summed into a monthly total flux [no account was made of possible diurnal biases due to time-of-day sampling (Heinemeyer et al., 2011)], with fractional relationships between fluxes calculated at this monthly timestep. Chamber data from Alice Holt 2010 were provided at a daily timestep; therefore, fractional relationships were calculated at this daily timestep before being averaged to monthly means.

Eddy covariance data were also supplied by Harwood and Alice Holt, measured concurrent to the chamber studies, gapfilled to continuous timeseries, and partitioned into gross photosynthetic uptake (GPP) and ecosystem respiration (Re) following the Fluxnet standard approach (Reichstein et al., 2005), providing validation datasets for Rs/Re from Alice Holt 2020 and Harwood 2020. The concurrent measurements of ECo-derived Re and both Rh and Rs during the Alice Holt 2010 study also made it possible to derive a monthly timeseries of Rh/Re for this period at that site. Only one literature study (Brændholt et al., 2018), measuring within a Fagus sylvatica-dominated woodland (DBF), was found to provide a similar timeseries of Rh (using soil chambers on trenched plots) measured concurrently with Re (from ECo), allowing an estimate of monthly Rh/Rs (this dataset here subsequently referred to as Braendholt 2018). Due to this limited data availability, our coefficients for Rh/Re were solely derived from the other measured fractions using Equation 4, while the Alice Holt 2010 and Braendholt 2018 datasets were reserved as validation data to compare to the derived values for DBF.

2.2 Respiration components

Rh – heterotrophic soil respiration.

Ra – autotrophic soil respiration (root-derived respiration).

Rs – total soil surface respiration (Rh + Ra).

Re – total ecosystem respiration (Rs + above ground autotrophic respiration and decomposition of plant litter).

Where studies only presented Ra as a fraction of Rs, Rh was calculated as the residual:

$\begin{array}{ll}Rs-Ra=Rh& (1)\end{array}$

Three fractional relationships were considered:

Soil surface respiration as a fraction of ecosystem respiration shown below Equation 2.

$\begin{array}{ll}Rs/\mathrm{R}\mathrm{e}& (2)\end{array}$

Soil heterotrophic respiration as a fraction of total soil respiration shown below Equation 3.

$\begin{array}{ll}Rh/Rs& (3)\end{array}$

Soil heterotrophic respiration as a fraction of ecosystem respiration shown below Equation 4.

$\begin{array}{ll}Rh/\mathrm{R}\mathrm{e}=Rs/\mathrm{R}\mathrm{e}xRh/\mathrm{R}\mathrm{e}& (4)\end{array}$

2.3 Data analysis

Literature data were grouped into forest type (evergreen needleleaf (ENF), deciduous broadleaf (DBF), and mixed forest (MF)) and fractional ratio (Rs/Re and Rh/Rs) with coefficients for each fraction derived either as the mean fraction for each month of the year across all datasets in each group (monthly means) or as single value coefficients derived as the annual mean over all months for each ratio and forest type (annual mean).

Comparisons of these two coefficient sets were made to the performance of the previously published approach, which we refer to here as Hardie/Subke (Abdalla et al., 2014; Dondini et al., 2016), using their coefficients for seasonal three-month blocks for Rh/Re (Dec–Feb = 0.59, Mar–May = 0.525, Jun–Aug = 0.46, and Sep–Nov = 0.525) from the ECo data combined with single annual coefficients (Rh/Rs [ENF] = 0.56, Rh/Rs [DBF] = 0.59) for the soil chamber data based on a mean annual value for each forest type (excluding tropical systems) from Subke et al. (2006). A performance test was carried out by estimating Rh independently from ECo (Re) and chamber (Rs) datasets at Harwood (ENF) and Alice Holt (DBF) and investigating how closely these separate estimates of Rh within each forest type converged when estimated using each of the three coefficient sets (monthly means, annual mean, and Hardie/Subke).

Comparisons between the two Rh estimates from each site were made using major axis regression (rather than ordinary least squares due to uncertainties in both axes) using the R package “lmodel2” (Legendre, 2018) and the index of agreement (d) (Willmott, 1981) using the R package “hydroGOF” (Zambrano-Bigiarini, 2020). The equation for this index of agreement is provided in Supplementary Equation S1, and is a standardised measure of the degree of model prediction error, which varies from 0 to 1 (with 1 being the perfect match). Due to both estimates of Rh being “simulated” in this case, a mean value of d was calculated, using each estimate of Rh (from ECo or Chambers) as the observed or simulated value in turn. Prior to analysis, the data were checked for normality of distribution with the Shapiro–Wilk test for bi-variate distribution (Shapiro and Wilk, 1965) using the “mvnormtest” package in R (Jarek, 2012) and subsequently transformed to normality using a Box-Cox power transform with the “car” package (Fox and Weisberg, 2019).

For the initial statistical analyses, the Alice Holt 2010, Alice Holt 2020, and Harwood 2020 primary datasets are excluded from coefficient derivation (due to the conflict of using data in both training and validation). However, due to the limited number of datasets in each forest type and respiration fraction group, these three datasets are subsequently included in the derivation and presentation of the final generic coefficients (Table 2, monthly means and Supplementary Table S2, annual mean), with a subsequent re-analysis of the convergence of the two estimates of Rh (Supplementary Table S1).

Table 2

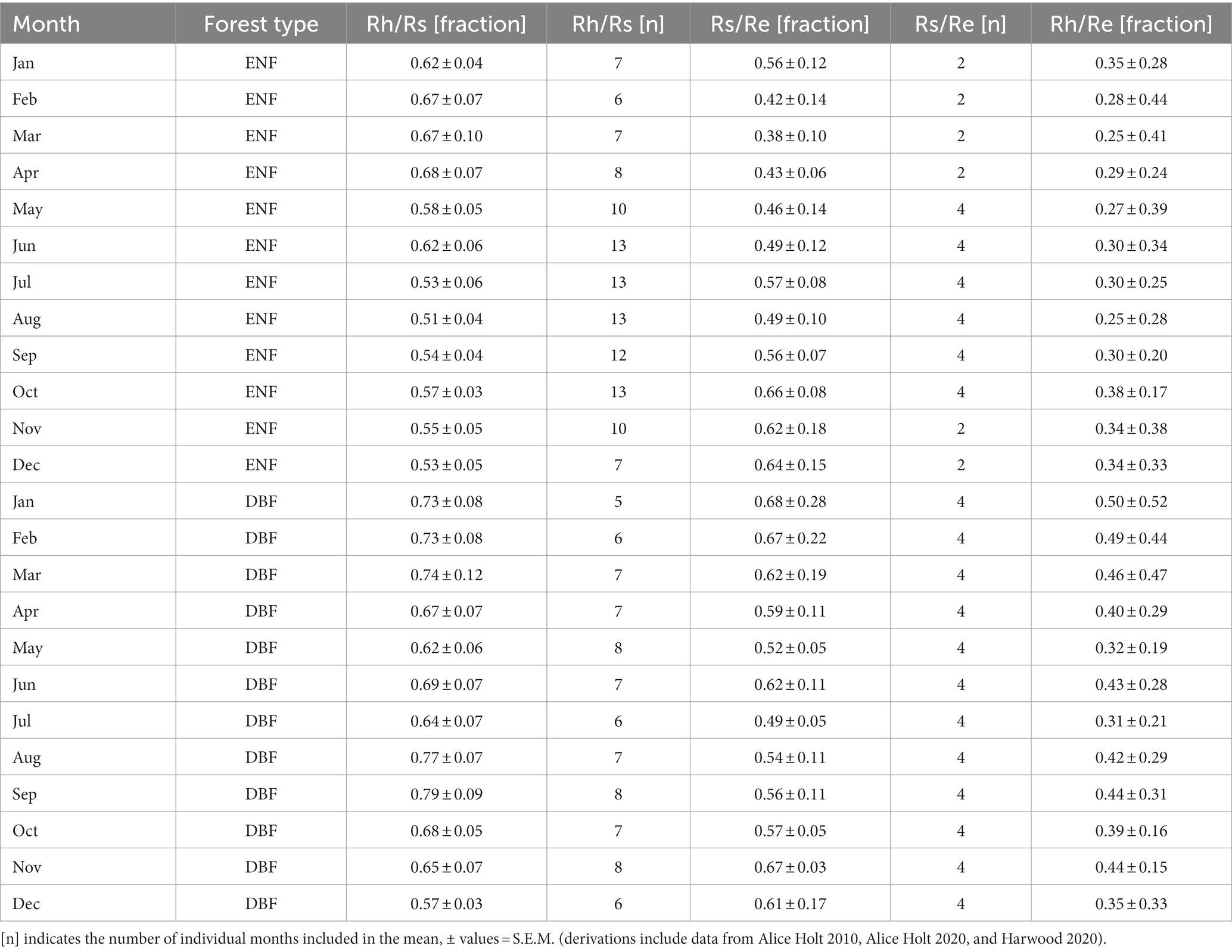
Table 2. Monthly means literature-derived values for fractional relationships between respiration components (Rs = soil surface respiration, Re = ecosystem respiration, and Rh = heterotrophic respiration) for individual months of the year, grouped by forest type (DBF = deciduous broadleaf forest and ENF = evergreen needleleaf forest).

3 Results

Following filtering, 21 studies were found to provide timeseries partitioning for ecosystem or soil respiration in seasonal, non-tropical forests (with some studies providing datasets from more than one site/forest type) across three forest types (ENF, DBF, and MF) and two fractional relationships (Rs/Re, Rh/Rs). Only four of the studies (Yuste et al., 2005; Wu et al., 2006; Ferréa et al., 2012; Ma et al., 2019) provided datasets from mixed forests (ENF + DBF); of these the Ferréa et al. (2012) forest was dominated by deciduous oak so was allocated to DBF, while the remaining three were discounted from further analysis due to the absence of additional validation data for MF. Consequently, a total of 29 individual timeseries datasets were used in the coefficient derivation across the two forest types and fractions (including our primary data from the Alice Holt and Harwood sites). References for individual datasets included in the coefficient derivation, along with their associated forest types, age class, latitude, climatic zone, and measurement technique under which they were studied, are presented in Table 1.

There were nearly three times as many chamber-based datasets providing the components of Rs (Rh and/or Ra) as ECo + chambers reporting Rs as a fraction of Re (21 vs. 8) and 17 datasets for ENF compared to 12 for DBF. Figure 1 shows monthly timeseries for individual studies grouped into forest type and fraction. Of the 29 datasets, 12 provided only partial coverage of an entire year (<12 monthly values) and one (Giasson et al., 2013) provided single values for each three-month block of the year. Figure 2 shows the monthly means (along with their standard errors) across all datasets for each forest type and fraction; the contribution of Rs to Re tended to be greater during the dormant season (Nov–Mar) than during the growing season (Apr–Oct) for both forest types, though standard errors were large and overlapped throughout most of the year.

Figure 1

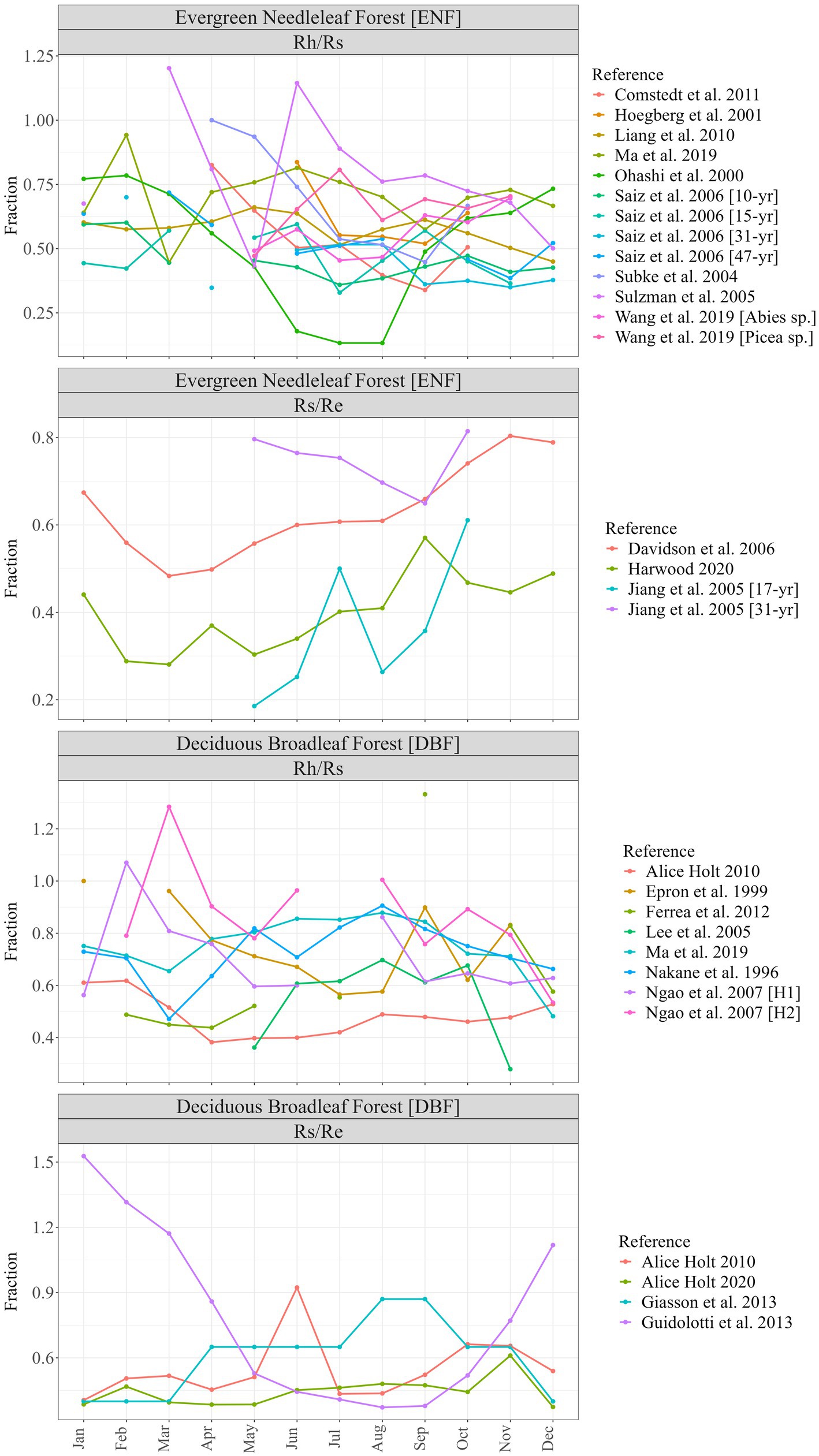
Figure 1. Individual study timeseries of respiration fractional relationships grouped by forest type (ENF, evergreen needleleaf forest; DBF, deciduous broadleaf forest) and ratio (Rh/Rs, heterotrophic respiration as fraction of total soil respiration; Rs/Re, total soil respiration as a fraction of ecosystem respiration) from the literature review including additional data from Harwood and Alice Holt (see Table 1).

Figure 2

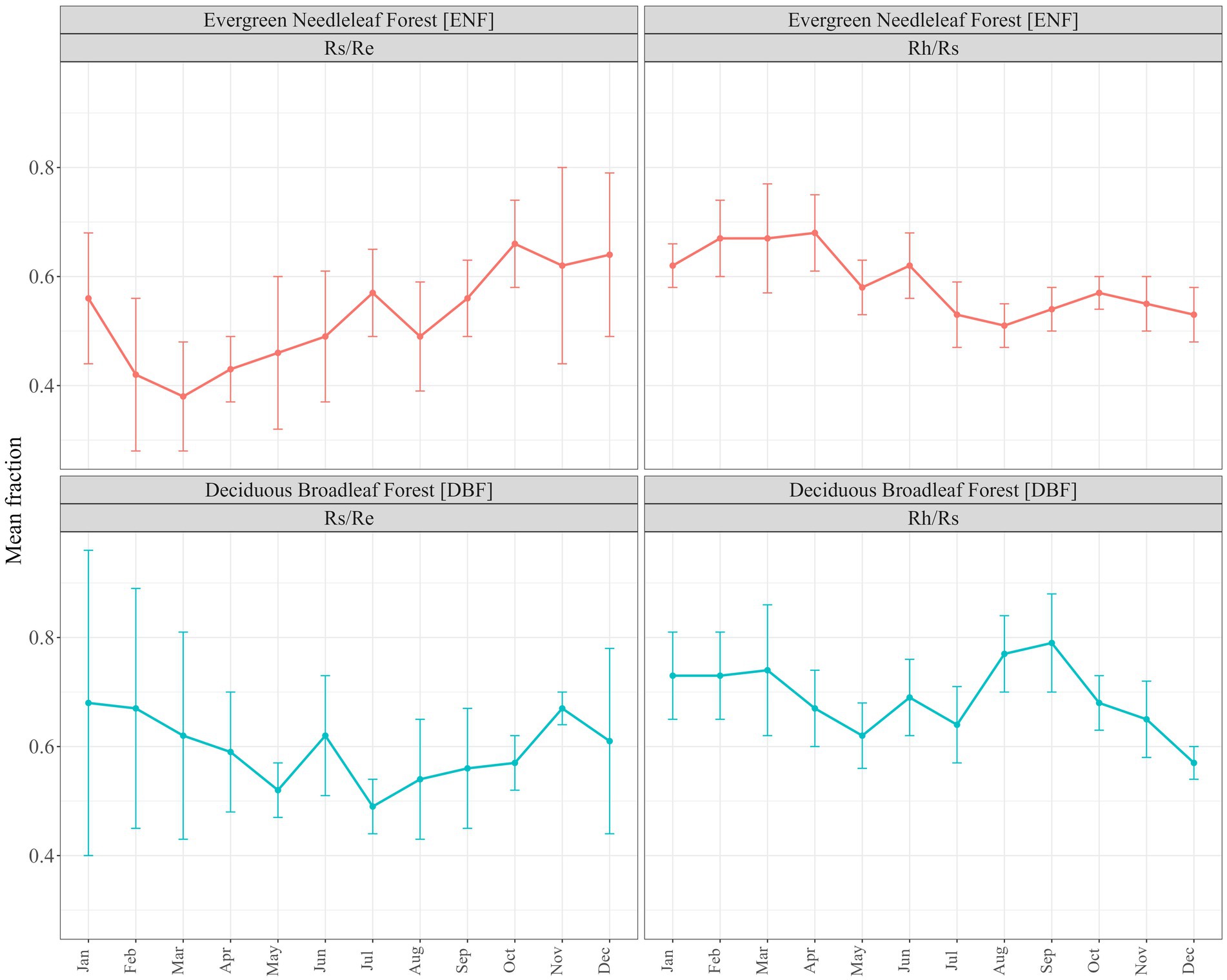
Figure 2. Mean monthly respiration fractions, by forest type (ENF, evergreen needleleaf forest; DBF, deciduous broadleaf forest) and ratio (Rh/Rs, heterotrophic respiration as fraction of total soil respiration; Rs/Re, total soil respiration as a fraction of ecosystem respiration) compiled from literature review and including additional data from Harwood and Alice Holt. Error bars show S.E.M.

Literature-derived coefficients (annual mean and monthly means) for the estimation of Rh from Re (ECo) and Rs (chambers) both resulted in improved convergence of the two estimates at both of our validation sites, compared to the Hardie/Subke approach (Table 3). The d values improved from 0.54 (ENF) and 0.64 (DBF) to >0.7 for both approaches, with annual mean the best fit for both ENF (0.75) and DBF (0.76). Figure 3 shows the results of estimating Rh from both Rs and Re over the monthly timeseries at each of our sites (Harwood and Alice Holt) compared to the originally measured fluxes, using the monthly means coefficients (derived without the inclusion of the Alice Holt and Harwood data). Convergence of the two independent estimates of Rh following all three of our approaches (including error bars) is shown in Supplementary Figure S1.

Table 3

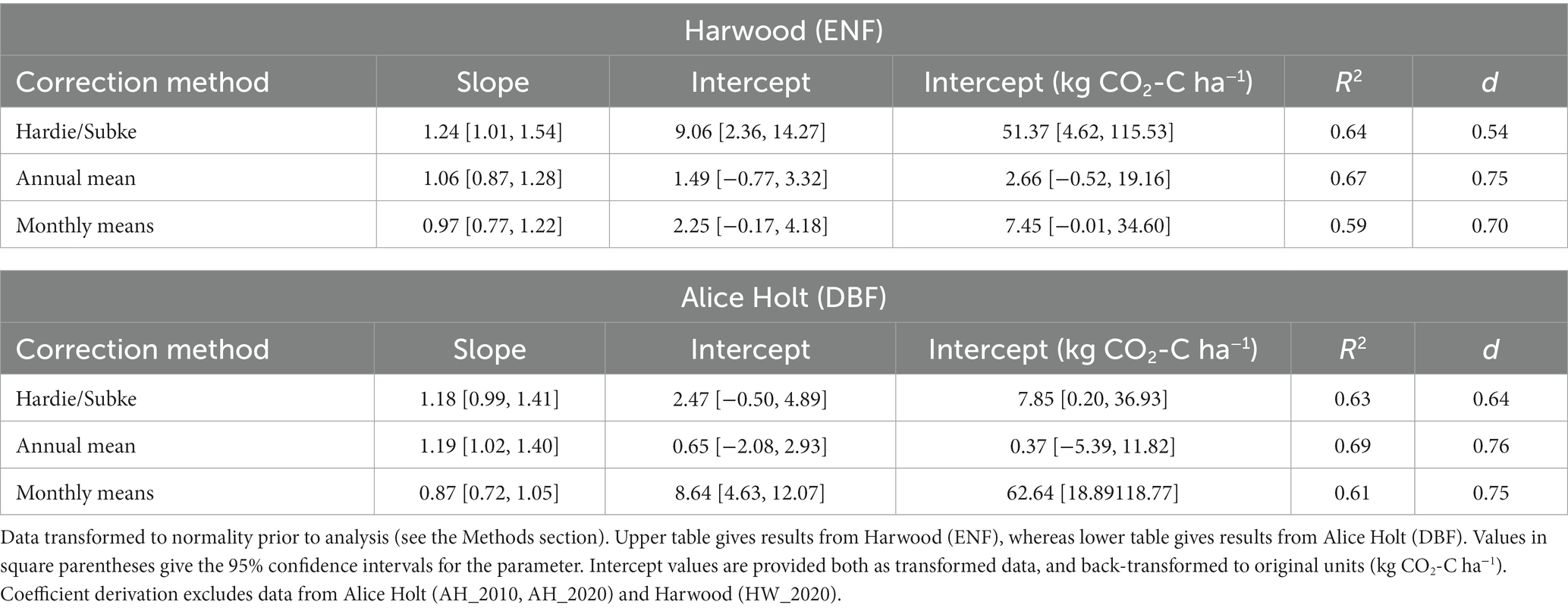
Table 3. Major axis regression coefficients and index of agreement (d) between Rh estimated from ECo (Re) and soil chamber (Rs) data measured independently at each site using each of the three literature-derived coefficient sets (Hardie/Subke, annual mean, and monthly means).

Figure 3

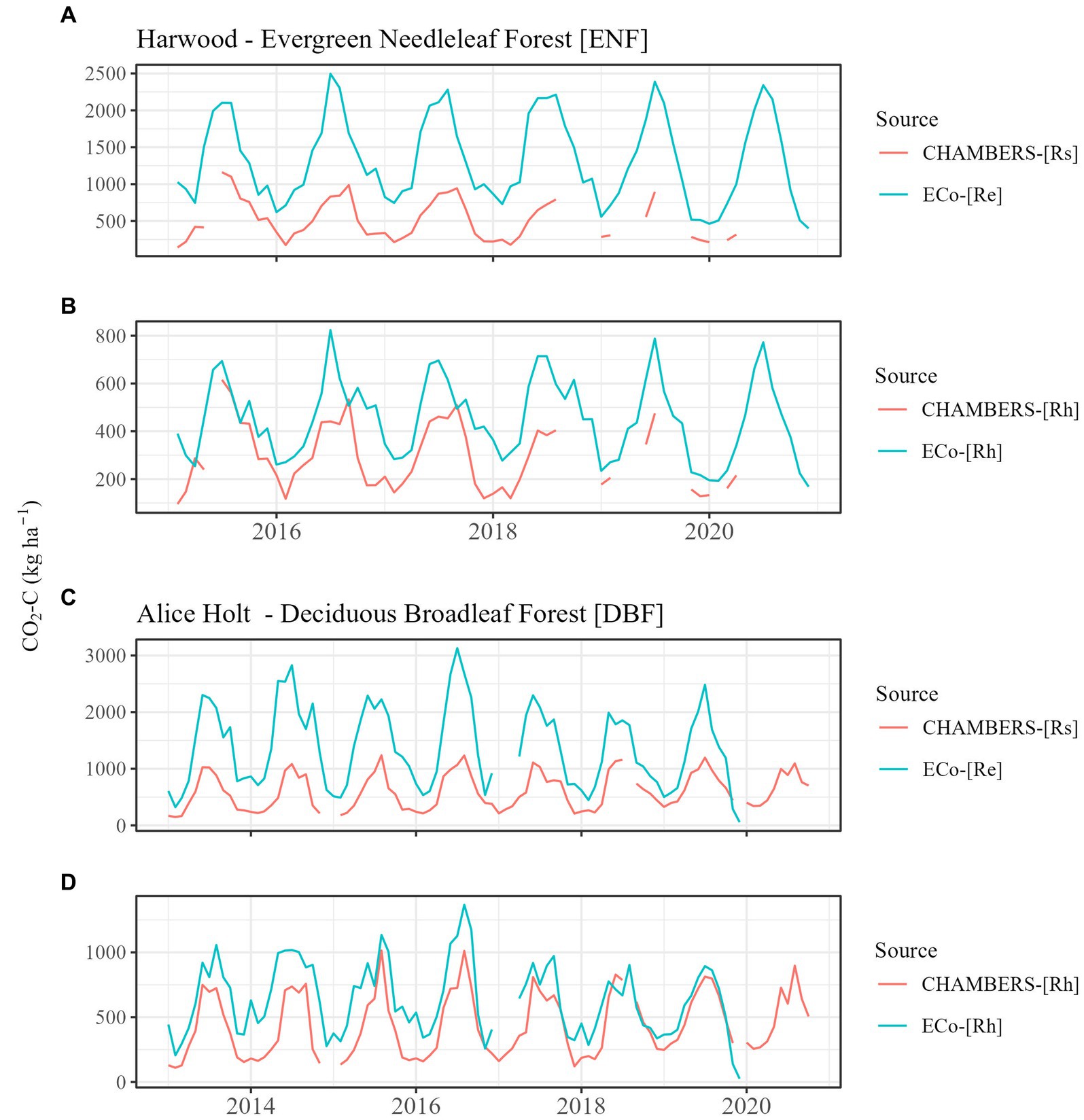
Figure 3. Comparison between chamber (CHAMBERS) and eddy covariance (ECo) original measured fluxes at Harwood evergreen needleleaf forest (plot A) and Alice Holt deciduous broadleaf forest (plot C) and subsequently adjusted to Rh (plots B,D) using monthly means literature-derived coefficients (excluding Alice Holt and Harwood data in this derivation). Rh, heterotrophic respiration; Rs, total soil respiration; and Re, ecosystem respiration.

From the major axis regression, annual mean gave the largest R2 (0.67) for ENF, however monthly means had the best slope fit (0.97) although the confidence intervals of both encompassed the perfect 1:1 fit, in contrast to Hardie/Subke which did not, and had the poorest slope fit. The intercept for the monthly means fit was greater than that for the annual mean (2.25 vs. 1.49), though the 95% confidence intervals (CIs) for both contained zero. Again, this is in contrast to Hardie/Subke, which had the largest intercept (9.06) and confidence intervals which did not cross zero (Table 3 provides intercept values back-transformed to original units (kg CO₂-C ha⁻¹) for all model fits).

For DBF, the slope fit was better for monthly means compared to the annual mean (0.87 vs. 1.19) and captured the 1:1 slope within its CIs, which the annual mean did not. In this instance, Hardie/Subke performed slightly better than the annual mean with a slope of 1.18 and CIs that did cross 1:1. However, the annual mean had the greatest R² (0.69) of the three, a much smaller intercept (0.65) and tighter confidence intervals than the other two approaches. Intercept CIs for both Hardie/Subke and annual mean crossed zero, whereas monthly means, with the largest intercept (8.64), did not.

As might be expected, the Alice Holt and Harwood data inclusion in the coefficient derivation improved the convergence of the two Rh estimates at each site with “d” values increasing to >0.80 for both the annual mean and monthly means approaches. The relative performance of both approaches changed slightly, whereas monthly means resulted in the best slope fit for both ENF and DBF when excluding these data, including them resulted in annual mean having the best slope fit for ENF with monthly means performing best for intercept and R². The relative performance for DBF between the two approaches remained unchanged. Results of the statistical analysis repeated with the inclusion of these data in the coefficient derivation are presented in Supplementary Table S1.

Fractional coefficients (and associated standard errors) for each component partition from the monthly means approach (Figure 2) are presented in Table 2. For the annual mean, Rh as a fraction of Rs (Rh/Rs) was larger for the DBF dataset than ENF (0.69 ± 0.07 vs. 0.59 ± 0.06) as was Rs/Re (0.60 ± 0.12 vs. 0.52 ± 0.11). Combining these two values to estimate Rh/Re (Equation 4) suggested that DBF has a greater contribution of heterotrophic respiration to total ecosystem respiration (0.41 ± 0.3) than ENF (0.3 ± 0.31); these coefficients are presented in Supplementary Table S3.

The monthly means-derived coefficients (Equation 4) for monthly Rh/Re fractions (see Table 2) for DBF fell between the fractions available from the two validation sites, where these parameters were measured (Alice Holt 2010 and Braendholt 2018). The derived coefficients compared to these two sites individually are shown in Figure 4, with Alice Holt 2010 showing a smaller fraction for Rh/Re in all months and Braendholt 2018 being larger in all months except January. Error bars associated with the monthly means-derived fractions were large, however, and covered both validation datasets in all months except October, where Braendholt 2018 was substantially greater. This positioning somewhere between the two datasets was also evident in a comparison between the measured mean annual values, with Braendholt 2018 (0.55 ± 0.04) more than two times the value for Alice Holt 2010 (0.26 ± 0.02). When compared to the mean of these two sites at the monthly timestep (Supplementary Figure S2), the derived coefficients matched more closely, with error bars overlapping in all months and very similar annual means (validation sites mean = 0.4 ± 0.04, derived coefficients = 0.41 ± 0.3).

Figure 4

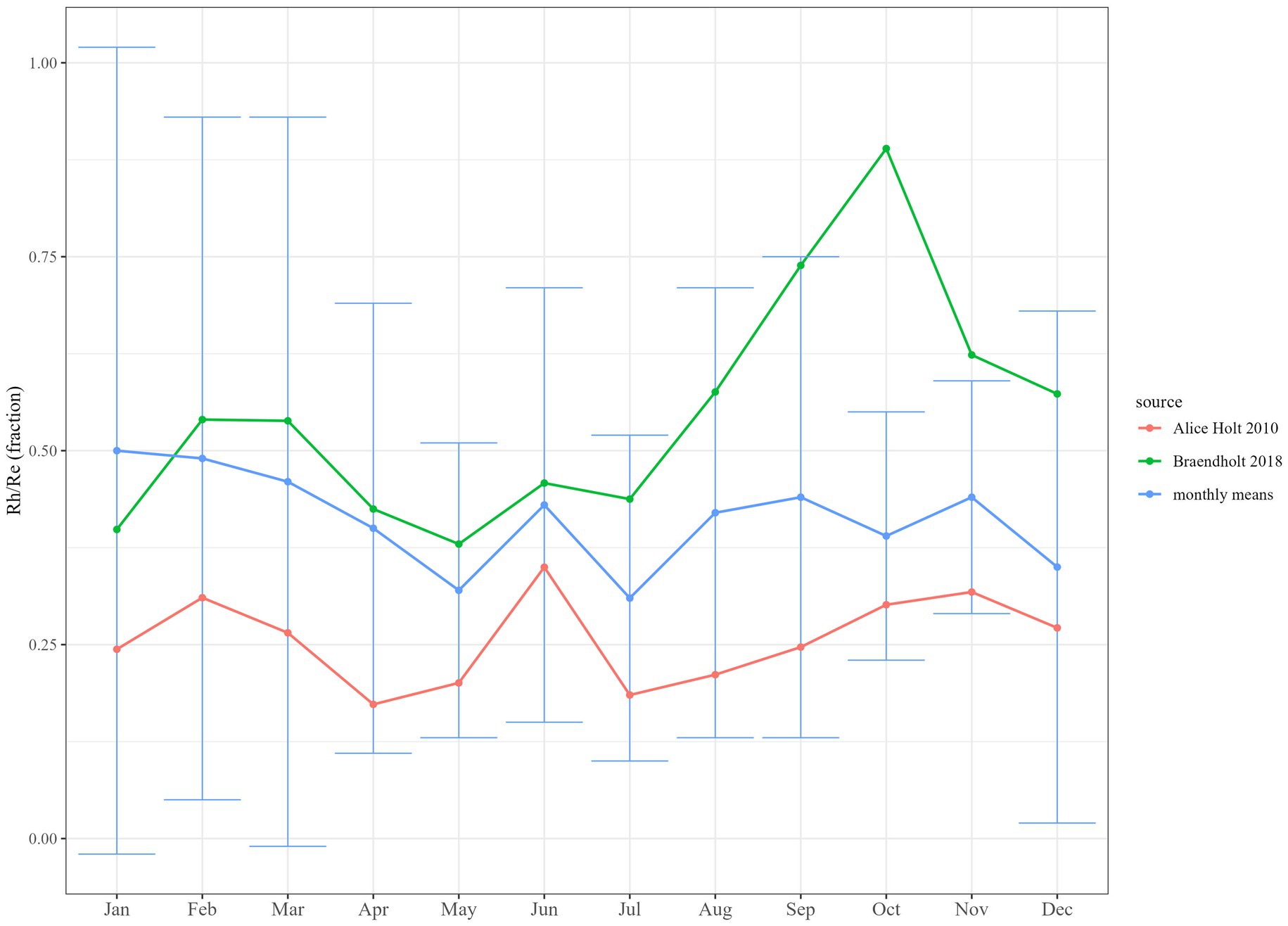
Figure 4. Comparison between monthly means literature-derived coefficients for deciduous broadleaf forest (DBF) and site measurements (Alice Holt 2010 and Braendholt 2018) of soil heterotrophic respiration (Rh) as a fraction of ecosystem respiration (Re). Error bars show S.E.M.

4 Discussion

In this study, we have presented literature-based coefficients to partition forest ecosystem CO₂ fluxes into their component contributions for individual months of the year, along with mean annual values. These coefficients relate specifically to evergreen needleleaf and deciduous broadleaf forests in seasonal, non-tropical climates. It is possible that different species mixtures and age classes within a forest category (e.g., within DBF) might produce differences in flux fractions that would be greater than the difference between forest categories (i.e., ENF vs. DBF); however, a thorough examination of this is beyond the scope of this study (and likely the available data). This study aimed to produce mean timeseries coefficients that can be easily matched to existing data repositories (such as Fluxnet³ or ICOS⁴), which class forest types in these terms (ENF, DBF, and MF) or literature summaries such as Subke et al. (2006) which do the same.

While there are many studies presenting short-term intermittent monitoring of forest soil CO₂ flux from chambers, few of them do so across entire or multiple years, and fewer still provide complete (or even partial) timeseries of partitioning into individual components (Rh and Ra). Similarly, there are many studies in the literature presenting timeseries of ecosystem-scale forest respiration (Re) from ECo, but fewer with concurrent chamber measurements to separate soil surface flux (Rs) and, to the best of our knowledge, only one study further partitioned Rs measurements to estimate Rh as a fraction of Re for individual months of the year. This scarcity of datasets precluded a thorough validation of our derived coefficients against independent data (i.e., separation into training vs. validation datasets) and led to our approach of using these coefficient sets to independently estimate Rh as a fraction of Re and Rs from our own ECo and chamber data. We then used the statistics of the subsequent convergence of these two independent estimates of the same parameter to investigate the performance of our derived coefficients, and compared them to a previously published approach. While this may not be ideal, we present this here as a pragmatic approach given these data limitations.

Some studies in our compilation (Epron et al., 1999; Subke et al., 2004; Sulzman et al., 2005; Ngao et al., 2007; Ferréa et al., 2012; Guidolotti et al., 2013) present results for some months that may be conceptually invalid (i.e., Rh/Rs > 1, or Rs/Re > 1), this may be explained by measurements for these individual components being taken at different scales and locations within the same study. For example: Rs from small, ground-level chambers being compared to Re from above-canopy, large spatial-scale ECo systems, which can lead to such discrepancies when the individual component represents the majority of the overall flux (e.g., soil respiration being the dominant ecosystem flux during the dormant season). It might have been considered appropriate to correct all such values to 1 for these individual months (e.g., when Rs/Re > 1, Rs = Re), but it was decided to incorporate the values as they were extracted from the individual studies. It should further be noted that the vast majority of the literature data values for this study were extracted directly from published graphs rather than data tables (see Table 1); this process was carried out with manual calibration of axes and pinpointing of datapoints within each individual graph using the R digitize package (Poisot, 2011). While great care was taken to ensure this was as accurate as possible, there will inevitably be some unquantified error associated with this process, which will subsequently be incorporated into our coefficient estimates.

While it is not possible to compare our results directly to other timeseries partitioning due to the scarcity of datasets, we can compare the annual means derived from our timeseries compilation to values reported in other studies. For Rh as a fraction of Rs (chamber-based studies), the review by Subke et al. (2006) suggests a mean annual value of 0.59 ± 0.03 for DBF (excluding tropical climates), which is substantially lower than the annual mean for the same forest type across our monthly timeseries at 0.69 ± 0.07. ENF values were much closer at 0.56 ± 0.02 than our mean annual value of 0.59 ± 0.06 (± S.E.M). The review by Hanson et al. (2000) suggested a generic value for forest Rh/Rs rather lower than these at 0.54, while the review by Jian et al. (2022) suggested a global generic value for root contribution to total soil respiration at 0.42, which would suggest a value of 0.58 for Rh. Our results reflect the suggestion in Subke et al. (2006) that DBF contributes relatively more Rh to Rs (and therefore to Re) than ENF, though our difference was greater. This greater Rh/Rs fraction in DBF might be explained by differences in both litter quality and mineralisation rates. DBF litter is generally more decomposable than ENF due to lower lignin and greater nutrient (particularly potassium and phosphate) content (Krishna and Mohan, 2017), with mineralisation rates generally being higher in their associated higher pH, macro- and micro-fauna-based (i.e., earthworms and bacteria) soil saprotrophic systems than the more acidic, fungal-based soils typically associated with ENF (Růžek et al., 2021). However, despite the literature support for our results suggesting that mineralisation rates (and therefore, potentially, the Rh/Rs fraction) may be greater for DBF than ENF, our associated standard errors were overlapping between the two forest types, suggesting that these differences, in our results at least, may not be statistically significant. More datasets and careful consideration of the independence of individual datasets within studies would be needed to investigate these relationships thoroughly (particularly where individual datasets were collected from forest sites very close together from the same species under different age classes) [e.g., Saiz et al. (2006) or Jiang et al. (2005)].

Jian et al. (2022) reported that differences in climate conditions were more significant than the ecosystem type in determining the relative contribution of roots to soil respiration. Whether the lack of significant differences between ecosystem types in predicting their root contribution to soil respiration (and therefore Rh/Rs) holds for the soil heterotrophic respiration contribution to whole ecosystem respiration (Rh/Re) is not considered in these review papers. However, the very large difference in our estimate for forests (mean across ENF and DBF) at 0.36 compared to a mean of 0.53 in Hardie et al. (2009) moss-based peatland study, and the much-improved convergence of our separate estimates of Rh, suggests that it is inadvisable to use values measured under very different ecosystems (e.g., using moss-dominated peat moorland coefficients for forests in our case) for this fraction at least. This conclusion is again supported by the Subke et al. (2006) review, which shows Rh/Rs values across nine different ecosystems ranging from 0.36 for shrubland to 0.85 for peatland.

Again, there are too few studies in our compilation to draw firm conclusions about intra-annual trends for fractional contributions within our groups, particularly in the chamber data partitioning, or to suggest more sophisticated model fits to the data beyond taking simple means for each month. As shown in Figure 2, there were no clearly apparent seasonal trends in the monthly distribution of our fraction coefficients, though intra-annual variability was very evident. This aspect might suggest that month-to-month environmental/climatic variability (and associated microbial activity and response to photosynthates) had a greater impact than seasonal trends in the relative contribution of individual fluxes. Furthermore, with so few studies in each forest-type/respiration fraction grouping, it is possible that inconsistencies in partitioning methodology between studies will also be a significant factor, with individual studies being more or less successful in the separation of component fluxes. For example, results from an individual site, which had been confounded by artefacts of chamber collar insertions impacting root-derived fluxes (Heinemeyer et al., 2011), may exert a strong influence on the mean value for a particular fraction within its group. Additionally, with any root exclusion experiment (by whatever means), there will be an unavoidable impact on soil hydrology and, therefore, microbial activity with impacts being more significant under particular environmental conditions. Even where care is taken not to interrupt soil water flows (e.g., through using root exclusion meshes), the absence of active roots will reduce transpiration rates and impact oxygen availability, which could potentially reduce heterotrophic CO₂ emissions (Gomez et al., 2016). A similar impact on Rh might be assumed in year-to-year rainfall variation, similarly impacting soil hydrology generally at a given site. How this would affect our conclusions around the relative contribution of Rh to Rs is, though, unclear, as the same reduction in soil oxygen availability might concurrently reduce tree biological activity and, therefore, Ra (Joseph et al., 2020). The lack of clear seasonal trends was reflected in our estimation of Rh using our fractional coefficients; while the monthly means timeseries coefficients performed better than annual mean in some statistical parameters (notably the slopes of the regression between the two estimates of Rh), they were not an unequivocal improvement (Table 3; Supplementary Figure S1), though both clearly performed better than the Hardie/Subke approach. A more thorough investigation of intra- versus inter-annual variability, such as that provided in Heinemeyer et al. (2012), is largely outside the scope of this current study, though, where the aim is to provide simple generic forest-type coefficients for partitioning.

Values for soil heterotrophic respiration as a fraction of forest ecosystem respiration, Rh/Re, were particularly lacking in the literature, with only one published study (Brændholt et al., 2018) found to provide this as a monthly timeseries for a seasonal forest (in this case from within DBF). We were able to add to this with the Alice Holt 2010 dataset, also collected within DBF, due to the availability of eddy covariance data being collected concurrently with the root exclusion experiment at the same site. Absolute estimates of monthly Rh/Re fractions between these two datasets were substantially different, with the Brændholt et al. (2018) being double those at Alice Holt and with a notable spike in the autumn months (Figure 4; Supplementary Figure S2), as might be expected from a seasonal input of leaf litter in these months (captured in the chamber collars) and a decline in above and below ground autotrophic respiration. Although the Alice Holt 2010 collars also incorporated leaf litter, they did not exhibit such a clear autumn increase in the contribution of Rh to Re. Despite both being collected from deciduous broadleaf forests, the stands contained different tree species and were at different latitudes (Alice Holt 2010: Quercus spp. in Southern England, Braendholt 2018: Fagus sylvatica in Denmark). So ecosystem temporal behaviour might be expected to differ due to climate and tree specific interactions, and there is also the possibility of methodological artefacts in these data. As conceded by Brændholt et al. (2018), there was the possibility that decomposing root material in the trenched plots was contributing to the estimate of Rh and increasing its estimated contribution to Rs and, therefore, to estimates of Rh/Re. Also, mycorrhizal respiration may not have been completely excluded in the Brændholt 2018 Rh dataset (with monthly cutting to only 25-cm depth), which may have added to the estimated contribution, in both absolute terms and variability. In Alice Holt’s 2010 study (Heinemeyer et al., 2012), care was taken to permanently exclude mycorrhizal respiration and to limit root decomposition effects in their measurements of Rh (the mycorrhrizal contribution to Rs was measured separately in their study), which would lower fluxes and their variability. When we sum the values for heterotrophic and mycorrhizal respiration for Alice Holt 2010, the estimates of Rh/Re become much closer to our literature-derived values and correspondingly to the Brændholt et al. (2018) values (Supplementary Figure S3), supporting the suggestion that studies less rigorous than the Heinemeyer et al. (2012) approach may have been incorporating some level of mycorrhizal respiration in their estimates of Rh.

5 Conclusion

The coefficients we present here, based on a combination of literature review and our own primary data, represent a substantial improvement on the previously published method for estimating soil heterotrophic respiration (Rh) from total soil (Rs) or ecosystem respiration (Re) for seasonal, non-tropical forest ecosystems. Our results show that ecosystem-specific coefficients are important in estimating these components and that using “global” literature values, or values estimated under very different ecosystems, may not be reliable. Furthermore, while there was little difference between the performance of the monthly and annual mean coefficient sets, the slightly improved slope fit in the monthly means approach suggests that these should be preferred to an annual mean when estimating Rh over timeseries of higher-level CO₂ fluxes. However, the limited number of available studies in the literature (almost non-existent for the estimation of Rh from measured Re), particularly under mixed forests, highlights a need for more, and targeted, studies to further improve the estimates for the components of ecosystem-specific CO₂ fluxes and their relative contributions over time.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JoM: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Writing – original draft. AnH: Data curation, Writing – review & editing. JaM: Funding acquisition, Writing – review & editing. GX: Data curation, Investigation, Writing – review & editing. MB: Data curation, Investigation, Writing – review & editing. MW: Data curation, Investigation, Writing – review & editing. AsH: Funding acquisition, Project administration, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was supported by UK Research and Innovation and the Biotechnology and Biological Research Council through the Strategic Priorities Fund for Greenhouse Gas Removal. NetZeroPlus: Sustainable Treescapes Demonstrator and Decision Tools (Netzeroplus.ac.uk), Grant number BB/V011588/1. The Alice Holt 2010 soil flux data were collected as part of a Natural Environment Research Council (NERC grants: F14/G6/105 & NE/C513550/1) funded project Centre for Terrestrial Carbon Dynamics.

Acknowledgments

The authors would like to thank Prof. Jo Smith at Aberdeen University for comments and suggestions on an early draft, and special thanks to Edward Eaton for assisting with running the Alice Holt site and contributing to the soil flux measurements. We are further grateful to the Forestry Commission, UK, for funding both the Alice Holt and Harwood long-term research sites.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2024.1352527/full#supplementary-material

Footnotes

1. ^https://netzeroplus.ac.uk/

2. ^https://www.forestresearch.gov.uk/

3. ^https://fluxnet.org/

4. ^https://www.icos-cp.eu/

References

Abdalla, M., Hastings, A., Bell, M., Smith, J., Richards, M., Nilsson, M., et al. (2014). Simulation of Co2 and attribution analysis at six European peatland sites using the Ecosse model. Water Air Soil Pollut. 225, 1–14. doi: 10.1007/s11270-014-2182-8

Crossref Full Text | Google Scholar

Baldocchi, D. D. (2003). Assessing the eddy covariance technique for evaluating carbon dioxide exchange rates of ecosystems: past, present and future. Glob. Chang. Biol. 9, 479–492. doi: 10.1046/j.1365-2486.2003.00629.x

Crossref Full Text | Google Scholar

Brændholt, A., Ibrom, A., Larsen, K. S., and Pilegaard, K. (2018). Partitioning of ecosystem respiration in a beech forest. Agric. For. Meteorol. 252, 88–98. doi: 10.1016/j.agrformet.2018.01.012

Crossref Full Text | Google Scholar

Bryant, C., Wheeler, N., Rubel, F., and French, R. (2017). Kgc: Koeppen-Geiger climatic zones. R package version 1.0.0.2. Available at: https://Cran.R-project.org/package=kgc.

Google Scholar

Comstedt, D., Boström, B., and Ekblad, A. (2011). Autotrophic and heterotrophic soil respiration in a Norway spruce forest: estimating the root decomposition and soil moisture effects in a trenching experiment. Biogeochemistry 104, 121–132. doi: 10.1007/s10533-010-9491-9

Crossref Full Text | Google Scholar

Curiel Yuste, J., Baldocchi, D., Gershenson, A., Goldstein, A., Misson, L., and Wong, S. (2007). Microbial soil respiration and its dependency on carbon inputs, soil temperature and moisture. Glob. Chang. Biol. 13, 2018–2035. doi: 10.1111/j.1365-2486.2007.01415.x

Crossref Full Text | Google Scholar

Davidson, E. A., Richardson, A., Savage, K., and Hollinger, D. (2006). A distinct seasonal pattern of the ratio of soil respiration to total ecosystem respiration in a spruce-dominated forest. Glob. Chang. Biol. 12, 230–239. doi: 10.1111/j.1365-2486.2005.01062.x

Crossref Full Text | Google Scholar

Dondini, M., Richards, M. I., Pogson, M., Mccalmont, J., Drewer, J., Marshall, R., et al. (2016). Simulation of greenhouse gases following land-use change to bioenergy crops using the Ecosse model: a comparison between site measurements and model predictions. GCB Bioenergy 8, 925–940. doi: 10.1111/gcbb.12298

Crossref Full Text | Google Scholar

Epron, D., Farque, L., Lucot, E., and Badot, P.-M. (1999). Soil Co2 efflux in a beech forest: the contribution of root respiration. Ann. For. Sci. 56, 289–295. doi: 10.1051/forest:19990403

Crossref Full Text | Google Scholar

Ferréa, C., Zenone, T., Comolli, R., and Seufert, G. (2012). Estimating heterotrophic and autotrophic soil respiration in a semi-natural forest of Lombardy, Italy. Pedobiologia 55, 285–294. doi: 10.1016/j.pedobi.2012.05.001

Crossref Full Text | Google Scholar

Flattery, P., Fealy, R., Fealy, R. M., Lanigan, G., and Green, S. (2018). Simulation of soil carbon efflux from an arable soil using the Ecosse model: need for an improved model evaluation framework? Sci. Total Environ. 622–623, 1241–1249. doi: 10.1016/j.scitotenv.2017.12.077

PubMed Abstract | Crossref Full Text | Google Scholar

Fox, J., and Weisberg, S., (2019). An {R} companion to applied regression, Third Edition. Thousand Oaks Ca: Sage. Available at: https://socialsciences.mcmaster.ca/jfox/Books/Companion/.

Google Scholar

Friend, A. D., Arneth, A., Kiang, N. Y., Lomas, M., Ogee, J., Rödenbeck, C., et al. (2007). Fluxnet and modelling the global carbon cycle. Glob. Chang. Biol. 13, 610–633. doi: 10.1111/j.1365-2486.2006.01223.x

Crossref Full Text | Google Scholar

Giasson, M. A., Ellison, A. M., Bowden, R. D., Crill, P. M., Davidson, E. A., Drake, J. E., et al. (2013). Soil respiration in a northeastern us temperate forest: a 22-year synthesis. Ecosphere 4, 1–28. doi: 10.1890/Es13.00183.1

Crossref Full Text | Google Scholar

Gomez, J., Vidon, P., Gross, J., Beier, C., Caputo, J., and Mitchell, M. (2016). Estimating greenhouse gas emissions at the soil–atmosphere interface in forested watersheds of the us northeast. Environ. Monit. Assess. 188, 295–216. doi: 10.1007/s10661-016-5297-0

PubMed Abstract | Crossref Full Text | Google Scholar

Guidolotti, G., Rey, A., D'andrea, E., Matteucci, G., and De Angelis, P. (2013). Effect of environmental variables and stand structure on ecosystem respiration components in a Mediterranean beech forest. Tree Physiol. 33, 960–972. doi: 10.1093/treephys/tpt065

PubMed Abstract | Crossref Full Text | Google Scholar

Hanson, P., Edwards, N., Garten, C. T., and Andrews, J. (2000). Separating root and soil microbial contributions to soil respiration: a review of methods and observations. Biogeochemistry 48, 115–146. doi: 10.1023/A:1006244819642

Crossref Full Text | Google Scholar

Hanson, P., Wullschleger, S., Bohlman, S., and Todd, D. (1993). Seasonal and topographic patterns of forest floor Co2 efflux from an upland oak forest. Tree Physiol. 13, 1–15. doi: 10.1093/treephys/13.1.1

PubMed Abstract | Crossref Full Text | Google Scholar

Hardie, S., Garnett, M., Fallick, A., Ostle, N., and Rowland, A. (2009). Bomb-14C analysis of ecosystem respiration reveals that peatland vegetation facilitates release of old carbon. Geoderma 153, 393–401. doi: 10.1016/j.geoderma.2009.09.002

Crossref Full Text | Google Scholar

Heinemeyer, A., Di Bene, C., Lloyd, A., Tortorella, D., Baxter, R., Huntley, B., et al. (2011). Soil respiration: implications of the plant-soil continuum and respiration chamber collar-insertion depth on measurement and modelling of soil Co2 efflux rates in three ecosystems. Eur. J. Soil Sci. 62, 82–94. doi: 10.1111/j.1365-2389.2010.01331.x

Crossref Full Text | Google Scholar

Heinemeyer, A., Wilkinson, M., Vargas, R., Subke, J.-A., Casella, E., Morison, J. I., et al. (2012). Exploring the "overflow tap" theory: linking forest soil co 2 fluxes and individual mycorrhizosphere components to photosynthesis. Biogeosciences 9, 79–95. doi: 10.5194/bg-9-79-2012

Crossref Full Text | Google Scholar

Hoègberg, P., Nordgren, A., Buchmann, N., Taylor, A. F., Ekblad, A., Hoègberg, M. N., et al. (2001). Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature 411, 789–792. doi: 10.1038/35081058

PubMed Abstract | Crossref Full Text | Google Scholar

Jarek, S. (2012). Mvnormtest: normality test for multivariate variables. R package version. 0.1-9. Available at: https://Cran.R-project.org/package=mvnormtest.

Google Scholar

Jian, J., Frissell, M., Hao, D., Tang, X., Berryman, E., and Bond-Lamberty, B. (2022). The global contribution of roots to total soil respiration. Glob. Ecol. Biogeogr. 31, 685–699. doi: 10.1111/geb.13454

Crossref Full Text | Google Scholar

Jian, J., Vargas, R., Anderson-Teixeira, K., Stell, E., Herrmann, V., Horn, M., et al. (2021). A restructured and updated global soil respiration database (Srdb-V5). Earth Syst. Sci. Data 13, 255–267. doi: 10.5194/essd-13-255-2021

Crossref Full Text | Google Scholar

Jiang, L., Shi, F., Li, B., Luo, Y., Chen, J., and Chen, J. (2005). Separating rhizosphere respiration from total soil respiration in two larch plantations in northeastern China. Tree Physiol. 25, 1187–1195. doi: 10.1093/treephys/25.9.1187

PubMed Abstract | Crossref Full Text | Google Scholar

Joseph, J., Gao, D., Backes, B., Bloch, C., Brunner, I., Gleixner, G., et al. (2020). Rhizosphere activity in an old-growth forest reacts rapidly to changes in soil moisture and shapes whole-tree carbon allocation. Proc. Natl. Acad. Sci. 117, 24885–24892. doi: 10.1073/pnas.2014084117

PubMed Abstract | Crossref Full Text | Google Scholar

Khalil, M. I., Abdalla, M., Lanigan, G., Osborne, B., and Müller, C. (2016). Evaluation of parametric limitations in simulating greenhouse gas fluxes from Irish arable soils using three process-based models. Agric. Sci. 7, 503–520. doi: 10.4236/as.2016.78051

Crossref Full Text | Google Scholar

Khalil, M., Richards, M., Osborne, B., Williams, M., and Müller, C. (2013). Simulation and validation of greenhouse gas emissions and Soc stock changes in arable land using the Ecosse model. Atmos. Environ. 81, 616–624. doi: 10.1016/j.atmosenv.2013.09.038

Crossref Full Text | Google Scholar

Krishna, M., and Mohan, M. (2017). Litter decomposition in forest ecosystems: a review. Energy Ecol. Environ. 2, 236–249. doi: 10.1007/s40974-017-0064-9

Crossref Full Text | Google Scholar

Kuzyakov, Y. (2006). Sources of Co2 efflux from soil and review of partitioning methods. Soil Biol. Biochem. 38, 425–448. doi: 10.1016/j.soilbio.2005.08.020

Crossref Full Text | Google Scholar

Lee, M. S., Nakane, K., Nakatsubo, T., and Koizumi, H. (2005). The importance of root respiration in annual soil carbon fluxes in a cool-temperate deciduous forest. Agric. For. Meteorol. 134, 95–101. doi: 10.1016/j.agrformet.2005.08.011

Crossref Full Text | Google Scholar

Legendre, P. (2018). _lmodel2: Model Ii Regression_. R package version 1.7–3. Available at: https://Cran.R-project.org/package=lmodel2.

Google Scholar

Liang, N., Hirano, T., Zheng, Z. M., Tang, J., and Fujinuma, Y. (2010). Soil Co₂ efflux of a larch forest in northern Japan. Biogeosciences 7, 3447–3457. doi: 10.5194/bg-7-3447-2010

Crossref Full Text | Google Scholar

Ma, M. Z., Zang, Z. H., Xie, Z. Q., Chen, Q. S., Xu, W. T., Zhao, C. M., et al. (2019). Soil respiration of four forests along elevation gradient in northern subtropical China. Ecol. Evol. 9, 12846–12857. doi: 10.1002/ece3.5762

PubMed Abstract | Crossref Full Text | Google Scholar

Nakane, K., Kohno, T., and Horikoshi, T. (1996). Root respiration rate before and just after clear-felling in a mature, deciduous, broad-leaved forest. Ecol. Res. 11, 111–119. doi: 10.1007/Bf02347678

Crossref Full Text | Google Scholar

Ngao, J., Longdoz, B., Granier, A., and Epron, D. (2007). Estimation of autotrophic and heterotrophic components of soil respiration by trenching is sensitive to corrections for root decomposition and changes in soil water content. Plant Soil 301, 99–110. doi: 10.1007/s11104-007-9425-z

Crossref Full Text | Google Scholar

Ohashi, M., Gyokusen, K., and Saito, A. (2000). Contribution of root respiration to total soil respiration in a Japanese cedar (Cryptomeria japonica D. Don) artificial forest. Ecol. Res. 15, 323–333. doi: 10.1046/j.1440-1703.2000.00351.x

Crossref Full Text | Google Scholar

Peel, M. C., Finlayson, B. L., and Mcmahon, T. A. (2007). Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 11, 1633–1644. doi: 10.5194/hess-11-1633-2007

Crossref Full Text | Google Scholar

Poisot, T. (2011). The digitize package: extracting numerical data from scatterplots. R J. 3:25. doi: 10.32614/RJ-2011-004

Crossref Full Text | Google Scholar

Pumpanen, J., Kolari, P., Ilvesniemi, H., Minkkinen, K., Vesala, T., Niinistö, S., et al. (2004). Comparison of different chamber techniques for measuring soil Co2 efflux. Agric. For. Meteorol. 123, 159–176. doi: 10.1016/j.agrformet.2003.12.001

Crossref Full Text | Google Scholar

R Core Team (2022). R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available at: https://www.R-project.org/.

Google Scholar

Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., et al. (2005). On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm. Glob. Chang. Biol. 11, 1424–1439. doi: 10.1111/j.1365-2486.2005.001002.x

Crossref Full Text | Google Scholar

Rochette, P., and Hutchinson, G. L. (2005). Measurement of soil respiration in situ: chamber techniques. Micrometeorol. Agric. Syst. 47, 247–286. doi: 10.2134/agronmonogr47.c12

Crossref Full Text | Google Scholar

Růžek, M., Tahovská, K., Guggenberger, G., and Oulehle, F. (2021). Litter decomposition in European coniferous and broadleaf forests under experimentally elevated acidity and nitrogen addition. Plant Soil 463, 471–485. doi: 10.1007/s11104-021-04926-9

Crossref Full Text | Google Scholar

Sabbatini, S., Mammarella, I., Arriga, N., Fratini, G., Graf, A., Hörtnagl, L., et al. (2018). Eddy covariance raw data processing for Co2 and energy fluxes calculation at Icos ecosystem stations. Int. Agrophys. 32, 495–515. doi: 10.1515/intag-2017-0043

Crossref Full Text | Google Scholar

Saiz, G., Byrne, K. A., Butterbach-Bahl, K., Kiese, R., Blujdea, V., and Farrell, E. P. (2006). Stand age-related effects on soil respiration in a first rotation Sitka spruce chronosequence in Central Ireland. Glob. Chang. Biol. 12, 1007–1020. doi: 10.1111/j.1365-2486.2006.01145.x

Crossref Full Text | Google Scholar

Shapiro, S., and Wilk, M. (1965). An analysis of variance test for normality (complete samples). Biometrika 52, 591–611. doi: 10.1093/biomet/52.3-4.591

Crossref Full Text | Google Scholar

Smith, J., Gottschalk, P., Bellarby, J., Richards, M., Nayak, D., Coleman, K., et al. (2010). Model to estimate carbon in organic soils–sequestration and emissions (Ecosse). Carbon 45, 193–205. doi: 10.3354/cr00902

Crossref Full Text | Google Scholar

Smith, P., Smith, J., Powlson, D., Mcgill, W., Arah, J., Chertov, O., et al. (1997). A comparison of the performance of nine soil organic matter models using datasets from seven long-term experiments. Geoderma 81, 153–225. doi: 10.1016/S0016-7061(97)00087-6

Crossref Full Text | Google Scholar

Subke, J.-A., Hahn, V., Battipaglia, G., Linder, S., Buchmann, N., and Cotrufo, M. F. (2004). Feedback interactions between needle litter decomposition and rhizosphere activity. Oecologia 139, 551–559. doi: 10.1007/s00442-004-1540-4

PubMed Abstract | Crossref Full Text | Google Scholar

Subke, J.-A., Inglima, I., and Francesca Cotrufo, M. (2006). Trends and methodological impacts in soil Co2 efflux partitioning: a metaanalytical review. Glob. Chang. Biol. 12, 921–943. doi: 10.1111/j.1365-2486.2006.01117.x

Crossref Full Text | Google Scholar

Sulzman, E. W., Brant, J. B., Bowden, R. D., and Lajtha, K. (2005). Contribution of aboveground litter, belowground litter, and rhizosphere respiration to total soil Co2 efflux in an old growth coniferous forest. Biogeochemistry 73, 231–256. doi: 10.1007/s10533-004-7314-6

Crossref Full Text | Google Scholar

Valentini, R. (ed.). (2003). “Euroflux: an integrated network for studying the long-term responses of biospheric exchanges of carbon, water, and energy of European forests” in Fluxes of carbon, water and energy of European forests, vol. 163 (Berlin, Heidelberg: Springer Berlin Heidelberg)

Google Scholar

Wang, J., Wang, G., Fu, Y., Chen, X., and Song, X. (2019). Short-term effects of nitrogen deposition on soil respiration components in two alpine coniferous forests, southeastern Tibetan plateau. J. For. Res. 30, 1029–1041. doi: 10.1007/s11676-018-0678-6

Crossref Full Text | Google Scholar

Wiant, H. V. (1967). Has the contribution of litter decay to forest" soil respiration" been overestimated? J. For. 65, 408–409. doi: 10.1093/jof/65.6.408

Crossref Full Text | Google Scholar

Wilkinson, M., Crow, P., Eaton, E. L., and Morison, J. I. (2016). Effects of management thinning on co 2 exchange by a plantation oak woodland in South-Eastern England. Biogeosciences 13, 2367–2378. doi: 10.5194/bg-13-2367-2016

Crossref Full Text | Google Scholar

Willmott, C. J. (1981). On the validation of models. Phys. Geogr. 2, 184–194. doi: 10.1080/02723646.1981.10642213

Crossref Full Text | Google Scholar

Wu, J. B., Guan, D. X., Wang, M., Pei, T. F., Han, S. J., and Jin, C. J. (2006). Year-round soil and ecosystem respiration in a temperate broad-leaved Korean pine forest. For. Ecol. Manag. 223, 35–44. doi: 10.1016/j.foreco.2005.10.055

Crossref Full Text | Google Scholar

Xenakis, G., Ash, A., Siebicke, L., Perks, M., and Morison, J. I. (2021). Comparison of the carbon, water, and energy balances of mature stand and clear-fell stages in a British Sitka spruce forest and the impact of the 2018 drought. Agric. For. Meteorol. 306:108437. doi: 10.1016/j.agrformet.2021.108437

Crossref Full Text | Google Scholar

Yuste, J. C., Nagy, M., Janssens, I., Carrara, A., and Ceulemans, R. (2005). Soil respiration in a mixed temperate forest and its contribution to total ecosystem respiration. Tree Physiol. 25, 609–619. doi: 10.1093/treephys/25.5.609

Crossref Full Text | Google Scholar

Zambrano-Bigiarini, M., (2020) Hydrogof: Goodness-of-fit functions for comparison of simulated and observed hydrological time series R package version 0.4–0. Available at: https://github.com/hzambran/hydrogof.

Google Scholar