
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. For. Glob. Change, 24 April 2024
Sec. Forest Management
Volume 7 - 2024 | https://doi.org/10.3389/ffgc.2024.1261310
This article is part of the Research TopicDynamics of Asia's and Australasia's forests in a changing worldView all 22 articles
 Zhuizhui Guan1,2
Zhuizhui Guan1,2 Qingbin Zhang1
Qingbin Zhang1 Tiaozi Xu2
Tiaozi Xu2 Dong Chen2
Dong Chen2 Yizeng Lu3
Yizeng Lu3 Qingjun Han3
Qingjun Han3 Ningning Li3
Ningning Li3 Wenjun Ma4
Wenjun Ma4 Junhui Wang4
Junhui Wang4 Yan Su2
Yan Su2 Jiyue Li2
Jiyue Li2 Quan Qiu2*
Quan Qiu2* Qian He2*
Qian He2*The development and morphology of branches, a crucial step in producing high-quality large-diameter lumber, may be influenced by fertilization. The response of branch attributes to different fertilization regimes, however, is still poorly understood. The Catalpa bungei plantations, which had been growing for 6 years in northern China, were chosen to study how various fertilization measures affected branch attributes. The two fertilization techniques used were hole fertilization (HF) and water and fertilizer integration (WF), with no fertilization (CK) as a control. The quantity, density, morphology (e.g., diameter, length, and angle), and position (e.g., height and orientation) of branches, and organ biomass of 18 standard trees (total of 516 branches) were investigated. The results demonstrated a considerable increase in tree height, diameter at breast height (DBH), canopy ratio, branch quantity, and organ biomass following the addition of fertilizer. Both the maximum branch diameter and the number of branches rose with fertilization. Following fertilization, the number of branches rose by 16% (HF) and 28% (WF) compared to non-fertilized trees, while the maximum branch diameter increased by 3.5% (HF) and 17.3% (WF), respectively. WF led to an increase in the number of branches and largest branch diameter in comparison to CK and HF. The length, angle, and diameter of branches, however, were not affected significantly by different fertilization treatments. There were roughly equal amounts of branches in four orientations. The mixed-model analysis revealed that the number of branches was positively correlated with branch density and tree height. The branch diameter increased with the increase of branch length and angle. The branch length was negatively correlated with branch height and angle. The branch angle showed a larger angle at the bottom of the canopy. Tree height plus diameter at breast height combined, or just the diameter at breast height indicator alone, can both reliably predict the total biomass of trees. The branch models created in this research may offer some theoretical backing for understanding the crown dynamics of valuable tree species in northern China.
The vigor and yield of trees are directly determined by the size, composition, and morphology of the tree canopy (Hein et al., 2007; Newton et al., 2012). The first-order branch, a vital component of the crown, mainly serves as the backbone of the tree. The crown shape is primarily determined by the length and spatial layout of the first-order branch. The evaluation and selection of appropriate management measures are potentially more accurate and biologically realistic via the quantitative simulation of the quantity, size, distribution, and growth of first-order branches, which can accurately forecast canopy dynamics, tree growth, and wood quality (Hein, 2008; Danescu et al., 2015; Wang et al., 2016, 2018).
Numerous studies have explored the branch attributes of various tree species, and, the majority of reports focus mostly on the linear and nonlinear models (Li, 2004; Liu et al., 2008; Courbet et al., 2012). For example, the branch models (e.g., diameter, length, angle, and number) are constructed directly with stand variables (e.g., site and density), tree variables (e.g., diameter at breast height, tree height, and crown length), as well as branch depth (Maguire et al., 1999; Courbet et al., 2007). These models have a high level of accuracy. The collinearity problem must be taken into account since variable components may autocorrelate. Furthermore, the model’s forest interpretation is subpar (Hein et al., 2007; Jiang et al., 2012). Actually, the fundamental data used in forest management may follow a hierarchical pattern. As an illustration, consider the following categorization system: the stand covers the sample plot, the plot covers the sample tree, and the sample tree covers the branch (Wang et al., 2015, 2017, 2018). Therefore, the errors can not satisfy the assumption of independent distribution due to the situations of ‘plot effect’ or ‘tree effect’ in traditional modeling. As a result of the random selection of plots and trees, at least three effects should be included in the random errors (i.e., plots, trees, and branches).
The theoretical model (such as the nonlinear model) serves as the foundation for the mixed effect model. The fact that there is nesting in the data means that the mixed effects model can only be applied under this condition. The goal of mixed linear models, as opposed to general linear models, is to introduce random effects to create a better model for data interpretation. The theoretical model’s parameters are updated to include the variable factors that have a meaningful relationship with the dependent variables. The model parameters that were built have strong ecological or forest implications (Gao et al., 2014). The mixed-effect models specify several covariance structures to describe the pertinent error scenario in order to reduce the error correlation and heterogeneity caused by the hierarchical structure data, increase the predictive power of models and illuminate the origin of variance components (Li and Tang, 2010).
In recent years, mixed models have been extensively utilized in forest investigation, such as diameter at breast height (Lei et al., 2009; Li, 2011), tree height (Fang and Bailey, 2001; Calegario et al., 2005), wood volume (Jiang et al., 2011), stem form (Jiang and Liu, 2011), and stand basal area (Li and Tang, 2010). Meredieu et al. (1998) established the length and angle models of Pinus nigra branches using a linear mixed model. Similarly, Beaulieu et al. (2011) developed the branch models of Pinus banksiana after considering the random impacts of the block, plot, and individual tree. Wang et al. (2018) created the generalized linear mixed models of live and dead branch numbers for Betula alnoides plantations. Dong et al. (2013) predicted the size of first-order branches for Pinus koraiensis forests based on mixed-effect models. All of the relevant reports show that the mixed models outweigh traditional regression techniques when modeling the branch properties.
Until now, research has focused primarily on the effects of planting density (Wang et al., 2015, 2017), stand thinning (Weiskittel et al., 2007; Jia et al., 2021), and pruning (Pinkard, 2002; Wang and Zeng, 2016) on branch development, whereas reports on the effects of different fertilization regimes on branch attributes are scarce. Fertilization can regulate the growth of trees, which in turn can indirectly affect branch development. Chen (2020) discovered that various fertilization methods might drastically alter the branch diameter and length for seven-year-old Tectona grandis clones. Moreover, Briggs et al. (2008) noted that fertilizer intake had an impact on the branch diameter of coastal Douglas-fir plantings. As a result, we used the commercially valuable tree species Catalpa bungei originated from northern China as an example to investigate the effects of various fertilization measures, including water and fertilizer integration, hole fertilization, and no fertilization as a control, on branch attributes and tree biomass through branch dissection. The objectives of this study are addressed: First, create the mixed models that predict the quantity, diameter, angle, length of the branches, and tree biomass, respectively; second, explore whether the various fertilization regimes have an impact on the branch attributes. The hypothesis put forth in this study is that fertilization will, on the one hand, increase the biomass of trees, as well as the diameter and length of their branches, and will also significantly affect the branching angle of those branches; on the other hand, the branching properties of branches will be affected differently by different fertilization regimes. The findings of this study can be used to theoretically support branch development forecasts in broad-leaved trees in North China.
The study plots are situated in the Jujube Preservation Warehouse in Zhangqiu District, Shandong Province, China (36°25′-37°09′ N, 117°10′-117°35′ E). The research regions experience a moderate monsoon climate. The yearly average temperature is 12.8°C, with a maximum monthly temperature in July of 27.2°C and a minimum in January of-3.2°C. There is an average of 600.8 mm of precipitation, 2647.6 h of sunshine, and 192 days without frost throughout the entire year. The growing seasons of C. bungei forests last 130–150 days from May to September.
In March 2017, we established a pure forest with a row spacing of 3 × 4 m using a 2-year-old C. bungei clone (“9–1”). The total planting area was 0.8 ha with a total of 18 plots (384 m2 for each plot), and 45 trees (5 rows × 9 columns) were planted in each plot. Since the planting of the trees, no tending had been done. After planting, C. bungei trees had an average height of 4.2 m and diameter at breast height (DBH) of 4.0 cm. Immediately following afforestation, the chemical composition of the soil was assessed, including its pH (7.67), organic matter content (19.64 g/kg), total nitrogen (0.91 g/kg), total phosphorus (0.53 g/kg), total potassium (16.70 g/kg), alkaline hydrolyzed nitrogen (81.88 mg/kg), available phosphorus (32.10 mg/kg), and available potassium (176.82 mg/kg). The majority of the soil in the area is brown loam.
Beginning in May 2018, we selected 9 plots at random and fertilized them as part of a split-plot experiment. Existing fertilization techniques included hole fertilization (HF) and water and fertilizer integration (WF), with no fertilization acting as a control. The HF approach was applied based on the previously fertilized forests of C. bungei (unpublished). The WF method was alluded to as being derived from the fertilization of fruits and crops in the agricultural ecosystem. Three plots were randomly selected for each fertilization treatment, and the distance between plots was around 6–8 m.
Early in May 2018, fertilization studies were carried out, with WF and HF applying the same quantity of fertilizers each year. In the first year, N (24 g/tree), P2O5 (8 g/tree), and K2O (16 g/tree) were applied as fertilizers. Subsequently, the annual amount of fertilizers increased by 20% compared to the previous year. Every year in May, HF applied all of the fertilizers at once. We excavated a hole, with a size of 20 cm in diameter and 30 cm in depth in the south and north of each tree. Then the fertilizers were equally divided into 2 parts and placed into the holes. No water was added after covering the soil. WF divided its annual fertilizers into 12 portions that were distributed equally. Starting on May 1st, we fertilized once every 10 days. The fertilizers were correctly delivered close to the roots after being dissolved in 1000 L of water using an intelligent drip irrigation system (HN-BXE, Huinong Automation Corporation, China). Potassium sulfate was employed as the potassium fertilizer and urea as the nitrogen fertilizer for HF and WF. Calcium superphosphate was utilized as a phosphate fertilizer for HF, whereas ammonium dihydrogen phosphate was used for WF. All Fertilizers were purchased on the Taobao website. The temperature and precipitation data from the nearby meteorological station for the years 2017 through 2022 were displayed in Supplementary Figure S1.
The standard tree represents the average level of trees in each sample plot, including their average height and DBH. Two standard trees were felled in each plot, and a total of 18 trees and 516 branches were collected in November 2021. In short, 6 trees were felled in each of the three treatments. The DBH and crown width (CW) were measured before being cut down. The tree height (TH) and the height of the crown base (HCB) were determined after felling. All branches (except dead branches) were dissected from the crown base to the top. The branch height (BH) (2.30–9.13 m), diameter (BD) (6.21–94.05 mm), angle (BA) (6.3–92.8°), length (BL) (0.45–5.10 m), orientation (BO) (0–355°), number of branches (NB) (20–39 branches), and density of the branches (DB) (3–6 branches·m−1) were measured.
The DBH was the diameter of the trunk at 1.3 m. The CW was the mean of the east–west and north–south projections of the canopy. The TH was the vertical distance from the bottom to the top of the tree. The HCB was the vertical distance from the bottom of the trunk to the crown base. The BH was the vertical distance from the base of the branch to the bottom of the trunk. The BD was the diameter at the base of the branch. The BA was the insertion angle between the branch and trunk pith. The BL was the distance between the base and the tip of the branch. The DB was the ratio of branch number to crown length. In addition, the trees were divided into the individual organ, including stems, branches, leaves, and roots. All of the roots were dug up with an excavator, and any soil that was left on top of the roots was then removed with a brush. The fresh weight of each organ was determined. Then, a small portion of each organ was collected, taken back to the laboratory at low temperature, and dried for water content determination.
The biomass was the difference between the fresh weight and water content of the organ. The total biomass of the tree was the sum of trunks, branches, leaves, and roots. The differences in branch attributes or organ biomass in different fertilization regimes were compared using a one-way analysis of variance (ANOVA) and Tukey’s honestly significant difference test (Tukey’s HSD). Since the data for the branch attributes of the investigated trees had a hierarchical structure, linear mixed-effects models (Equations 1 and 2) were used to assess the significance of variations in treatment for branch attributes at the tree and branch level.
Where y was observed value; μ was the overall mean; ϑF was the effect of fertilization regimes; φp, φpt, and φptbr were the random effects for plot (p), tree (t), and branch (br), respectively.
The restricted maximum likelihood estimation (REML) was employed in the mixed-model analysis, and Tukey’s HSD was utilized to conduct multiple range tests between treatments. Generalized linear mixed models (GLMM) were utilized for count variables (e.g., branch number) in the model-building process, and linear mixed models (LMM) were used for continuous variables (e.g., BD and BL). The following approaches were used to model the branch attributes. The multiple linear regression models were initially run for dependent variables with all pertinent independent variables to select potential factors. The prospective factors with statistical significance, a reasonable ecological explanation, and a variance inflation factor (VIF) that was not greater than three were then used to construct the mixed effects models. All of the above candidate and random components (such as plot and tree effects) were then evaluated using likelihood ratio tests (LRT) when a mixed effects model was constructed using the REML. Factors at a significance level of 0.05 were incorporated into models. Generalized linear models (GLM) or linear models (LM) were replaced in the absence of any discernible random factors. Lastly, the models were updated using the previously selected fixed and random components, and the best-fit models were picked from a range of variance functions primarily based on model simplicity and the Akaike Information Criterion (AIC).
Model performance was evaluated using the root mean squared error (RMSE), which was determined for each model on the original data scale. In the case of GLM, the predictive power R2 was calculated as the squared correlation between observations and predictions. The marginal R2 (Rm2, only the fixed effects) and conditional R2 (Rc2, including the fixed and random effects) were measured for LMM. The associations between the dependent and all independent variables were expressed using simulation plots built on the fitting models. All statistical analyses and model building were performed using SPSS 25.0 for Windows (IBM-SPSS Inc., Chicago, IL, United States) (Table 1).
The fertilizing regimes had minimal impact on the HCB and CD but markedly increased the TH, DBH, and CR (Table 2). The DBH grew by 7.8 and 19.5% and the TH increased by 1.9 and 8.2% for HF and WF in comparison to CK, respectively. HF and WF produced greater stems, branches, leaves, roots, and total biomass than CK (Table 3). WF dramatically enhanced the total biomass of each organ compared to other fertilizing methods. WF increased the stem biomass by 45.9%, branch biomass by 59.8%, leaf biomass by 63.8%, root biomass by 37.7%, and total biomass by 48.3% compared to CK, respectively. The rank of organ biomass in three fertilization regimes was: stem > root > branch > leaf. The fertilization techniques did not, however, have a significant impact on the allocation proportion of organ biomass.
Amongst the three fertilization regimes, there was a noticeable difference in the total number of branches within the crown (Table 4). Most branches were in WF, and the fewest were in CK. Branch density did not considerably vary in response to fertilization regimes. The amount and percentage of branches at the four orientations for each fertilization treatment did not differ noticeably (Table 5). Thus, the four orientations of the branches within the crown were distributed roughly equally.

Table 5. The branch quantity at four orientations of Catalpa bungei undergoing three fertilization regimes.
Fertilization regimes had no discernible effect on the diameter, length, and angle of the C. bungei branches (Table 4). WF dramatically increased the biggest branch diameter compared to CK and HF. The height of the largest branch in WF was dramatically lowered than CK and HF.
The number of branches (NB) was strongly correlated with the density of branches (DB), fertilization regimes (FR), and tree height (TH) (Equation 3). Parameter estimates, standard errors, and statistical significance of the intercepts and predictors of the equation were displayed in Table 6.
The NB increased with the increase of DB (Figure 1A) and TH (Figure 1B). The NB under fertilization was higher than CK, and the NB in WF was larger than HF. A larger percentage of the overall variation was explained by the model (R2 = 0.804). The accuracy of the model was likewise great (RMSE = 1.150).
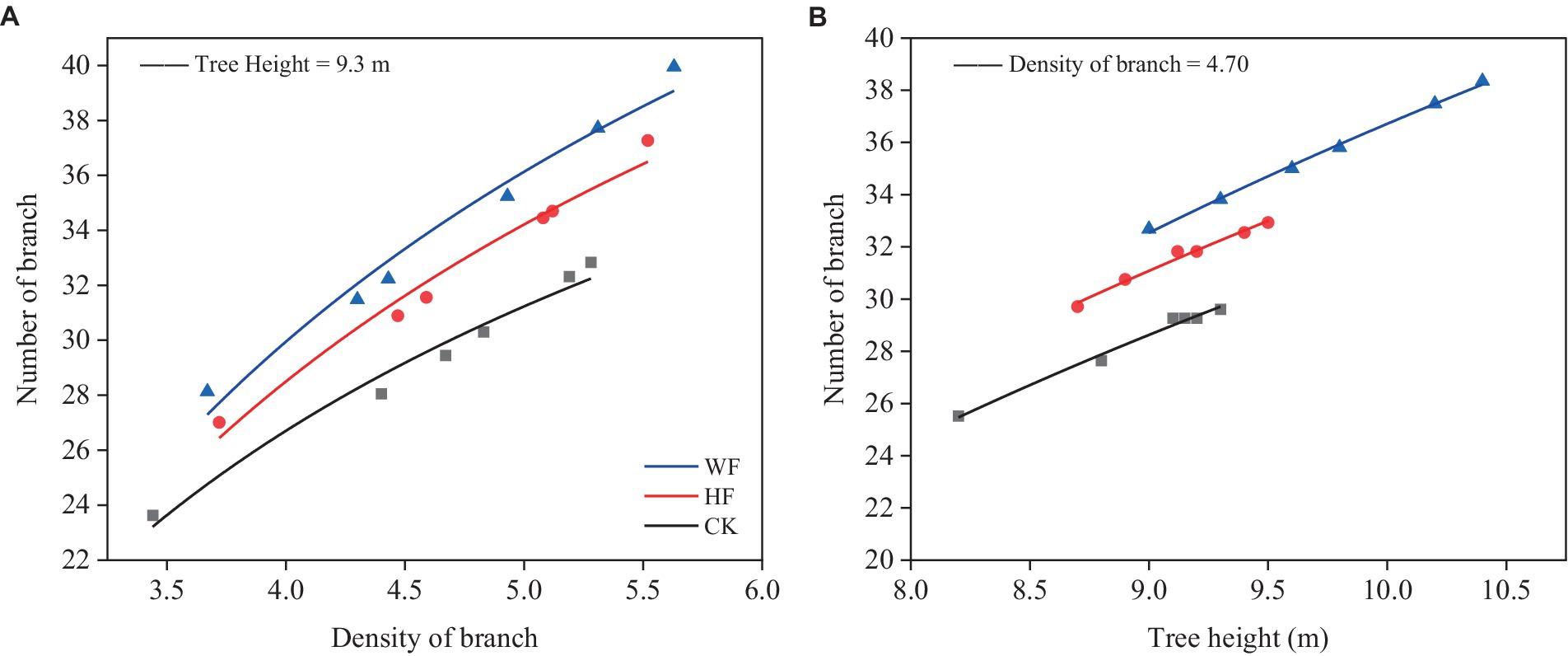
Figure 1. Relationships between branch number and branch density (A) and tree height (B). The abbreviations were referred to Table 1.
Branch diameter (BD) was closely associated with branch length (BL) and angle (BA) (Equation 4). Parameter estimates, standard errors, and statistical significance of the intercepts, fixed and random effects of the equation were presented in Table 6.
Branch diameter was positively correlated with branch length (Figure 2A) and angle (Figure 2B). Branch length had a higher impact on branch diameter than branch angle across the whole range of our dataset under consideration. The current model had a modestly low level of precision (RMSE = 9.300 mm), and it only adequately explained about 40% of the overall variance (Rm2 = 0.363, Rc2 = 0.370).
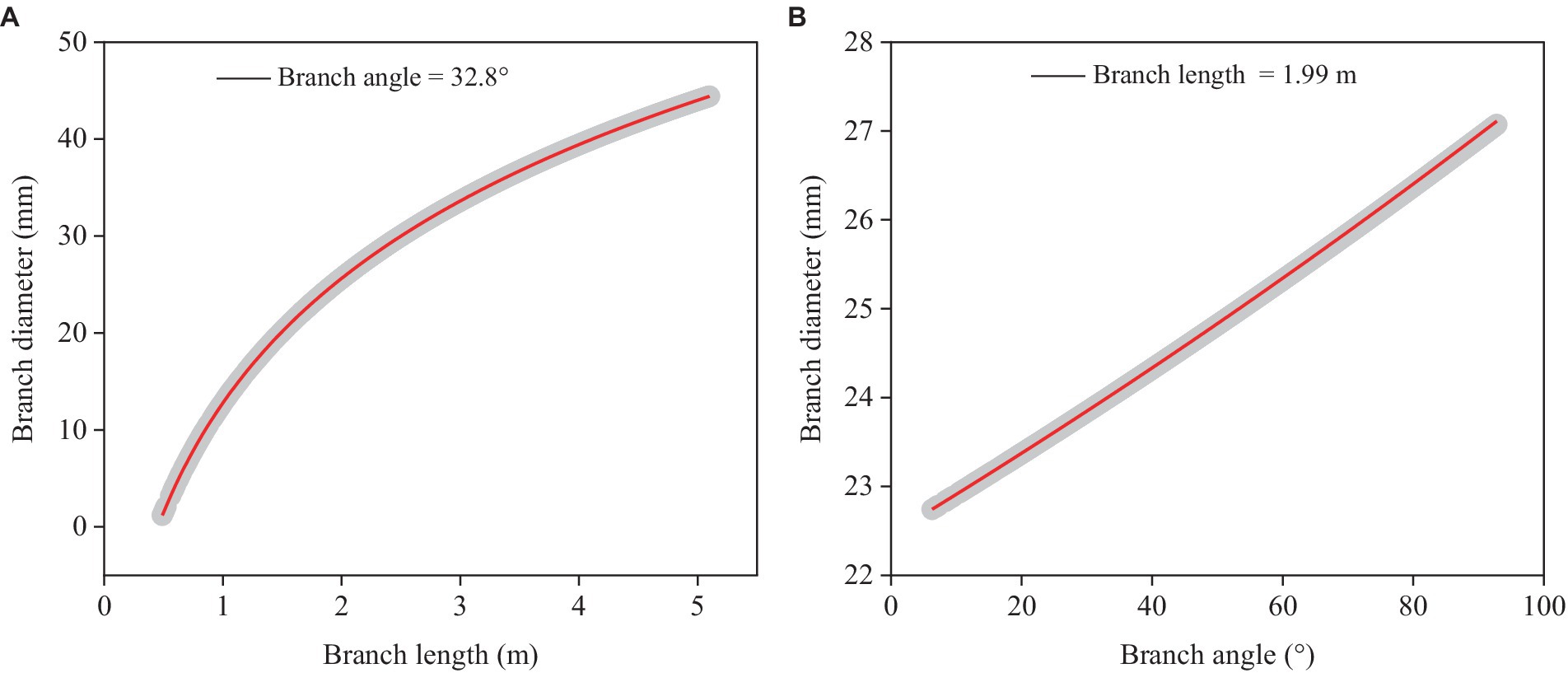
Figure 2. Simulated plots (red lines) based on the model (Equation 4) for predicting branch diameter with 95% confidence intervals (gray shadow). (A) Relationships between predicted branch diameter and branch length based on the mean branch angle. (B) Relationships between predicted branch diameter and branch angle based on the mean branch length.
The model showed that branch length (BL) was significantly correlated with branch diameter (BD), height (BH), and angle (BA) (Equation 5).
Across the whole range of the datasets we gathered, branch length increased as branch diameter did (Figure 3A), but it decreased when branch height and angle did (Figures 3B,C). Branch height and angle were less influential factors in determining branch length than branch diameter. The current model performed well in terms of prediction accuracy (RMSE = 0.882 m), accounting for around 50% of the overall variance (Rm2 = 0.453, Rc2 = 0.457).
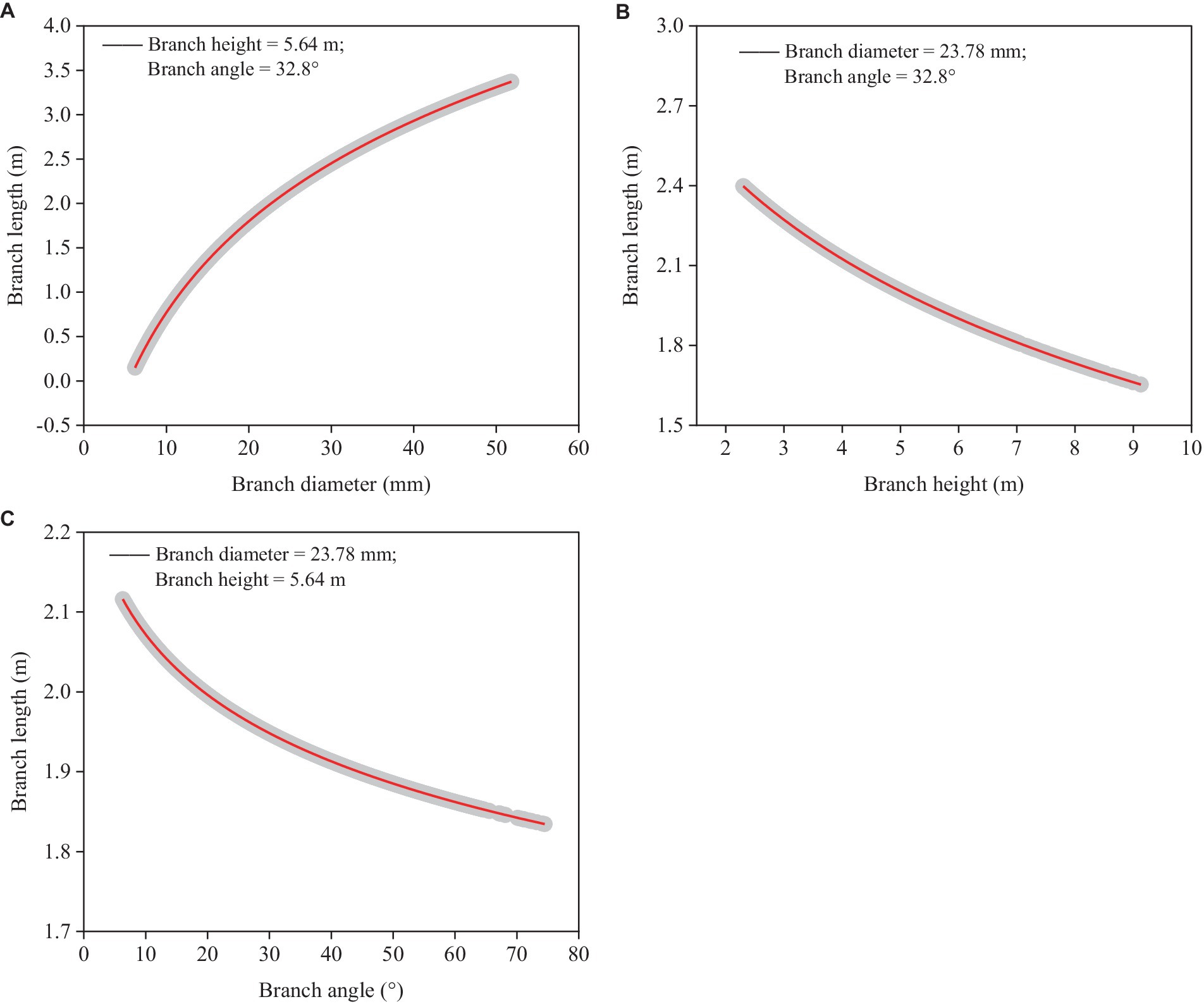
Figure 3. Simulated plots (red lines) based on the model (Equation 5) for predicting branch length with 95% confidence intervals (gray shadow). (A) Relationships between predicted branch length and branch diameter based on the mean branch height and angle. (B) Relationships between predicted branch length and branch height based on the mean branch diameter and angle, and (C) Relationships between predicted branch length and branch angle based on the mean branch diameter and height.
In our study, branch angle was significantly correlated with branch height (BH), diameter (BD), and length (BL) (Equation 6).
The branch angle increased as branch diameter increased (Figure 4B), but it reduced when branch height (Figure 4A) and length (Figure 4C) increased. The influence of branch diameter on branch angle was stronger than that of branch height and length across the entire range of our investigated datasets. The model had a good level of precision (RMSE = 5.8°), and it described a significant amount of the overall variation (Rm2 = 0.717, Rc2 = 0.723).
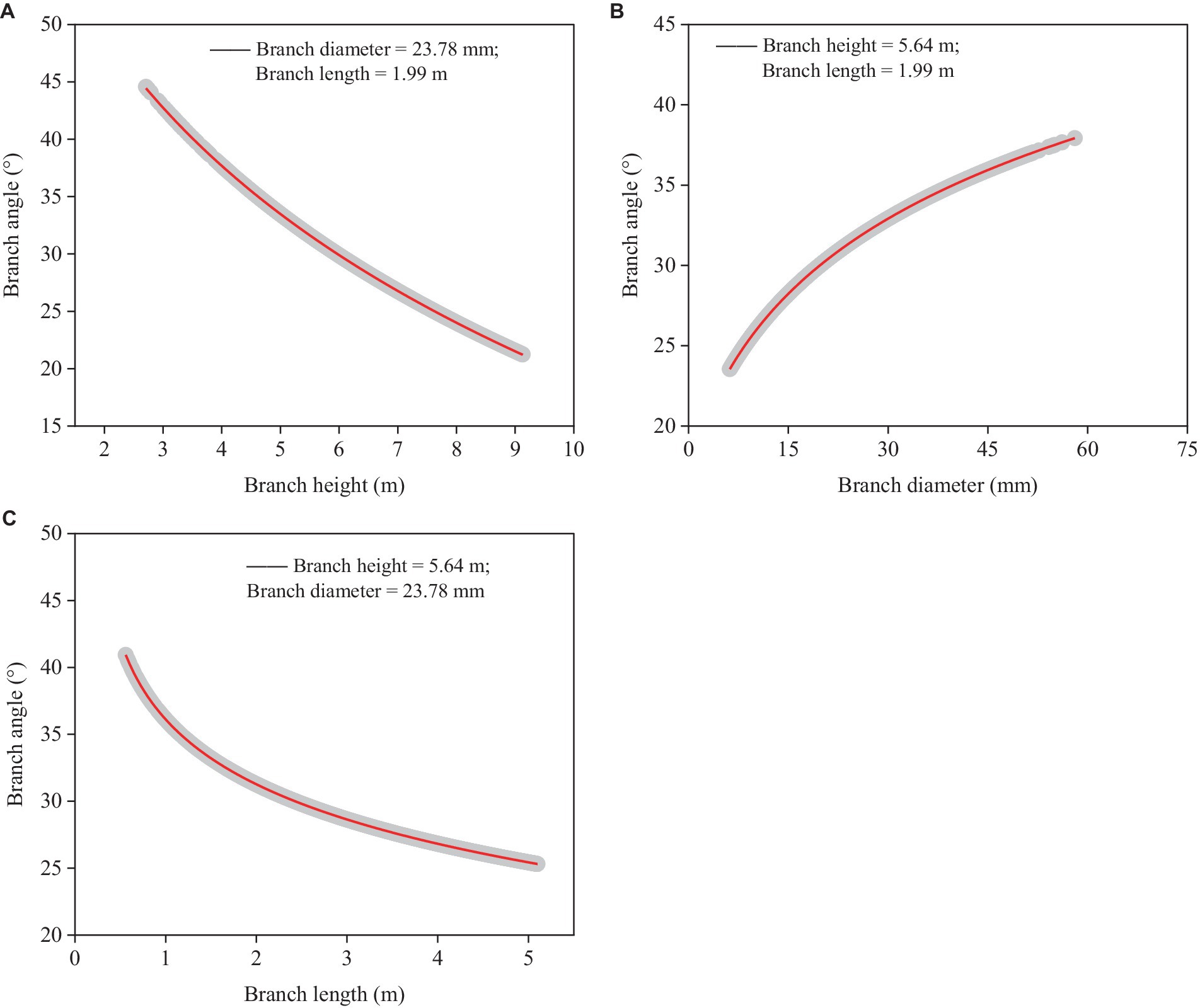
Figure 4. Simulated plots (red lines) based on the model (Equation 6) for predicting branch angle with 95% confidence intervals (gray shadow). (A) Relationships between predicted branch angle and branch height based on the mean branch diameter and length. (B) Relationships between predicted branch angle and branch diameter based on the mean branch height and length, and (C) Relationships between predicted branch angle and branch length based on the mean branch diameter and height.
We developed the models that combined individual tree biomass and growth parameters such as tree height, DBH, crown width, and so on, and discovered that a single index (DBH) or two indexes (H and DBH) can better predicted biomass, with adj-R2 reaching 0.95 (Table 7). The models of H-TB, CW-TB, and H:DBH-TB with adj-R2 only ranging from 0.34 to 0.53 had lower predictive ability for TB.
Our results showed that fertilization regimes (i.e., WF and HF) significantly increased the tree height, DBH, and organ biomass in the C. bungei forests compared to no fertilization. The fertility of the soil and availability of nutrients needed for plant growth are improved through soil fertilization (Tumushime et al., 2019; Yang and Karban, 2019; Li et al., 2021). In this study, the WF forests had greater tree growth and organ biomass than the HF forests did. Tree absorption and utilization for liquid fertilizer were superior to solid fertilizer, producing more biomass in the WF forests (Ma et al., 2019; Guan et al., 2022). The forest serves as a massive biomass carbon reservoir while also conserving water. Thus, WF forests may be recommended in terms of exhibiting greater water conductivity and carbon storage capabilities. Moreover, the DBH-TB model stated that it was possible to compute the total biomass of trees fairly quickly and efficiently, saving both time and labor, by precisely determining the DBH value.
The H:D (i.e., TH: DBH) and crown ratio (i.e., CR) can be generally used as the indicators of tree vigor. The findings on the Scots pine and Norway spruce demonstrated that greater tree vigor increased the number of branches in a whorl (Kellomäki and Tuimala, 1981; Hein et al., 2007). Similarly, our results also indicated that fertilizer input obviously improved the CR and branch quantity compared to non-fertilizer added. Furthermore, WF considerably increased the tree height and crown ratio compared to HF, which may result in an increase in branch number. However, our study was not partly in line with the reports on Tectona grandis, where the number of total branches was proved to be not affected by fertilization (Chen, 2020). Weiskittel et al. (2007) also found that the branch numbers of the coastal Douglas-fir were not related to the fertilizer input. But, instead, our results seemed to be in agreement with observations of a positive relationship between the number of branches and height growth in Norway spruce (Colin and Houllier, 1992; Klang and Ekö, 1999), and our study showed that fertilization increased the annual height growth of the stem. Another finding in our study was that the branch quantity in the WF forests was higher than that in the HF forests. These differences in the above studies might originate from the differences in fertilizer types, duration, and frequency in different fertilization regimes. In addition, the varying results among studies may also be potentially attributable to differences in soil attributes and species morphology/physiology.
The fertilized trees exhibited bigger crowns than the control trees due to their enhanced height and branch growth. The competition for light, thus, may be more intense in WF and HF stands. The base of the green crown was, however, lower in WF and HF forests than in non-fertilized forests, but the difference was small. This indicated that light limitations had not resulted in increased branch mortality at the bottom of the canopy in WF and HF stands. The fact that there were fewer living branches at the bottom of the canopy in control stands was probably the effect of low nutrient availability in non-fertilized stands.
Branch characteristics, such as branch diameter, length, and angle, control the crown architecture and have a substantial impact on stem growth and knot development (Hein et al., 2008; Forrester et al., 2012; Nelson et al., 2014). Our investigation found that fertilization schedules only increased the diameter of the largest branch but had no discernible impacts on the mean diameter and length of the branches. The results were partly different from the previous reports on Tectona grandis (Chen, 2020), Pseudotsuga menziesii (Briggs et al., 2008), as well as Picea abies (Mäkinen et al., 2001). These reports all concluded that fertilization had a positive effect on the branch size. Branch diameter was directly correlated with the age and size of the trees. The C. bungei species under investigation was young (i.e., 6 years old), hence the influence of fertilization on branch growth was not fully reflected. As a tree ages, the effect of fertilization on mean branch diameter would progressively become apparent; however, for the largest branch in the crown, as branches with large diameters were also longer, competition effects between trees first became apparent on the larger branches. Furthermore, the position of the main branch on the stem is crucial to forest managers since it may shed with serious knot-related issues. Fertilization decreased the height of the biggest branch in the current study. That is to say, trees in the fertilization stands gave lower branches a preference for nutrients, which facilitated their rapid growth. Hence, pruning at the appropriate time improves the quality of the wood at the most desirable stem portion (e.g., below 6 m in the stem).
The angle at which the branches are attached to the stem has a significant impact on the wood’s quality and the shape of the crown (Kantola and Mäkelä, 2004). On a particular tree, the factors of gravity, light availability, and reaction wood production dominate in determining branch angle. Also, the social position of the trees in the stand can significantly affect the branch angle (Maguire et al., 1994; Weiskittel et al., 2007). Hence, branch position inside the crown and branch diameter had a major role in determining branch angle in this study. The models used in the current study demonstrated that as branch height fell near the crown base, branch angles became flatter.
Steep branch angles can prolong the time that branch stubs are occluded, which can result in severe wood defects including discoloration and knots (Hein, 2008; Danescu et al., 2015; Wang et al., 2015). In this study, fertilization did not seem to have much of an impact on the mean branch angle. The results had also been acknowledged by studies on Picea abies (Mäkinen et al., 2001) and Tectona grandis (Chen, 2020). However, research on Scots pine had indicated that branch angle was only marginally correlated with site fertility and stand structure (Mäkinen and Uusvaara, 1992). These different results might be properly explained by their differences in age, branching habits of species, and other compound effects. In our study, The tree-level variance component of the mixed model explained a moderate part of the total variation in branch angle, i.e., branch angles within a tree were correlated and the between-tree differences could not be completely explained by the fixed tree or stand variables. This may be the effect of the moderate heritability of the branch angle (Haapanen et al., 1997).
The development of crown branches is influenced by a variety of factors, including site characteristics, stand density, management techniques, and tree growth potential. However, due to the limitations – a young stand age and a small number of sample trees – the models given are not suitable for widespread application. The impact of other aspects must also be taken into account while creating a large-scale model. A future study based on more extensive data from various geographic regions is required to create models that might be broadly utilized.
Tree branches develop inconsistently at every age stage. The competition between branches for water, light, and nutrients intensifies as trees get older, which leads to natural pruning and inevitable disruption of the branch indexes. Furthermore, the size of knots as well as the diameter, angle, and length of branches are significantly influenced by stand density. In the future, research on the development of large-diameter timber without knots in C. bungei plantations could focus on the importance of reasonable afforestation density and appropriate tending measures.
This study looked into the effects of several fertilization methods on the branch properties and tree growth. The biomass and development of C. bungei stands were positively impacted by fertilization. Water and fertilizer integration produced greater biomass and growth in comparison to hole fertilization. The number of live branches at age 6 years was greater on trees that had received HF and WF fertilization. Certain branch characteristics, like diameter, length, and angle, were not discovered to be significantly more sensitive to various fertilization regimes. Only the size and height of the largest branch, which was typically concerned with the quality of the wood at the lower stem section, were related to fertilization. With a high prediction accuracy and a clear understanding of the relationships and influencing variables between branch attributes, the mixed effect models of branches (including number, diameter, angle, and length) developed in this work might be utilized to forecast the dynamic evolution of the C. bungei crown. The established models could serve as a guide for producing high-quality wood from other valuable tree species in northern China.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.
ZG: Writing – original draft, Writing – review & editing. QZ: Conceptualization, Writing - original draft. TX: Conceptualization, Writing – original draft. DC: Data curation, Methodology, Writing – review & editing. YL: Formal analysis, Project administration, Writing – review & editing. QHa: Funding acquisition, Resources, Writing – review & editing. NL: Investigation, Software, Writing – review & editing. WM: Resources, Visualization, Writing – review & editing. JW: Resources, Visualization, Writing – review & editing. YS: Methodology, Supervision, Writing – review & editing. JL: Writing – review & editing. QQ: Writing – review & editing. QHe: Writing – review & editing.
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The research was supported by the National Key Research and Development Program of China (2017YFD0600604 and 2017YFD060060404).
The author thanks QH for her assistance in experimental design and revise. We also thank the Guangdong Key Laboratory for Innovative Development and Utilization of Forest Plant Germplasm, College of Forestry and Landscape Architecture, South China Agricultural University.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2024.1261310/full#supplementary-material
Beaulieu, E., Schneider, R., Berninger, F., Ung, C., and Swift, D. E. (2011). Modeling jack pine branch characteristics in eastern Canada. Forest Ecol. Manag. 262, 1748–1757. doi: 10.1016/j.foreco.2011.06.054
Briggs, D. G., Kantavichai, R., and Turnblom, E. C. (2008). Effect of precommercial thinning followed by a fertilization regime on branch diameter in coastal United States Douglas-fir plantations. Can. J. For. Res. 38, 1564–1575. doi: 10.1139/X07-199
Calegario, N., Daniels, R. F., Maestri, R., and Neiva, R. (2005). Modeling dominant height growth based on nonlinear mixed-effects model: a clonal Eucalyptus plantation case study. Forest Ecol. Manag. 204, 11–21. doi: 10.1016/j.foreco.2004.07.051
Chen, T. (2020). Effects of Planting Density and Fertilization on the Growth and Branch Development of Teak (Tectona grandis L.f.) Clones. Dissertation. Chinese Academy of Forestry, Beijing.
Colin, F., and Houllier, F. (1992). Branchiness of Norway spruce in northeastern France: predicting the main crown characteristics from usual tree measurements. Ann. Sci. For. 49, 511–538. doi: 10.1051/forest:19920506
Courbet, F., Hervé, J., Klein, E. K., and Colin, F. (2012). Diameter and death of whorl and interwhorl branches in atlas cedar (Cedrus atlantica Manetti): a model accounting for acrotony. Ann. Forest Sci. 69, 125–138. doi: 10.1007/s13595-011-0156-1
Courbet, F., Sabatler, S., and Guédon, Y. (2007). Predicting the vertical location of branches along atlas cedar stem (Cedrus atlantica Manetti) in relation to annual shoot length. Ann. Forest Sci. 64, 707–718. doi: 10.1051/forest:2007051
Danescu, A., Ehring, A., Bauhus, J., Albrecht, A., and Hein, S. (2015). Modelling discoloration and duration of branch occlusion following green pruning in Acer pseudoplatanus and Fraxinus excelsior. Forest Ecol. Manag. 335, 87–98. doi: 10.1016/j.foreco.2014.09.027
Dong, L., Liu, Z., Li, F., and Jiang, L. (2013). Primary branch size of Pinus koraiensis plantation: a prediction based on linear mixed effect model. Chin. J. Appl. Ecol. 24, 2447–2456. doi: 10.13287/j.1001-9332.2013.0490
Fang, Z., and Bailey, R. L. (2001). Nonlinear mixed effects modeling for slash pine dominant height growth following intensive silvicultural treatments. For. Sci. 47, 287–300. doi: 10.1046/j.1439-0329.2001.00240.x
Forrester, D. I., Collopy, J. J., Beadle, C. L., and Baker, T. G. (2012). Interactive effects of simultaneously applied thinning, pruning and fertiliser application treatments on growth, biomass production and crown architecture in a young Eucalyptus nitens plantation. Forest Ecol. Manag. 267, 104–116. doi: 10.1016/j.foreco.2011.11.039
Gao, Z., Wang, X., Li, H., and Zhang, P. (2014). An optimal model of the Cunninghamia lanceolata branch diameter in Fujian Province. J. Northeast Forest. Univ. 42, 23–27. doi: 10.13759/j.cnki.dlxb.20140721.018
Guan, Z., Lu, Q., Lin, Y., Lin, D., Lu, Y., Han, Q., et al. (2022). Spatial variations and pools of non-structural carbohydrates in young Catalpa bungei undergoing different fertilization regimes. Front. Plant Sci. 13:1010178. doi: 10.3389/fpls.2022.1010178
Haapanen, M., Velling, P., and Annala, M. (1997). Progeny trial estimates of genetic parameters for growth and quality traits in scots pine. Silva Fenn. 31, 3–12. doi: 10.14214/sf.a8506
Hein, S. (2008). Knot attributes and occlusion of naturally pruned branches of Fagus sylvatica. Forest Ecol. Manag. 256, 2046–2057. doi: 10.1016/j.foreco.2008.07.033
Hein, S., Makinen, H., Yue, C., and Kohnle, U. (2007). Modelling branch characteristics of Norway spruce from wide spacings in Germany. Forest Ecol. Manag. 242, 155–164. doi: 10.1016/j.foreco.2007.01.014
Hein, S., Weiskittel, A. R., and Kohnle, U. (2008). Branch characteristics of widely spaced Douglas-fir in South-Western Germany: comparisons of modelling approaches and geographic regions. Forest Ecol. Manag. 256, 1064–1079. doi: 10.1016/j.foreco.2008.06.009
Jia, W., Luo, T., and Li, F. (2021). Branch density model for Pinus koraiensis plantation based on thinning effects. J. Beijing Forest. Univ. 43, 10–21. doi: 10.12171/j.1000−1522.20200057
Jiang, L., Du, S., and Li, F. (2011). Simulation of Larix gmelinii tree volume growth based on random effect. Chin. J. Appl. Ecol. 22, 2936–2969. doi: 10.13287/j.1001-9332.2011.0414
Jiang, L., Li, F., and Zhang, R. (2012). Modeling branch diameter with linear mixed effects for Dahurian larch. For. Res. 25, 464–469. doi: 10.13275/j.cnki.lykxyj.2012.04.013
Jiang, L., and Liu, R. (2011). A stem taper model with nonlinear mixed effects for Dahurian larch. Sci. Silvae Sinicae 19, 338–341. doi: 10.3724/SP.J.1011.2011.00338
Kantola, A., and Mäkelä, A. (2004). Crown development in Norway spruce [Picea abies (L.) karst.]. Trees 18, 408–421. doi: 10.1007/s00468-004-0319-x
Kellomäki, S., and Tuimala, A. (1981). Effect of stand density on branchiness of young scots pine. Folia Forestalia 478, 1–27.
Klang, F., and Ekö, P. (1999). Tree properties and yield of Picea abies planted in shelterwoods. Scand. J. Forest Res. 14, 262–269. doi: 10.1080/02827589950152782
Lei, X., Li, Y., and Xiang, W. (2009). Individual basal area growth model using multi-level linear mixed model with repeated measures. Sci. Silvae Sinicae 45, 74–79. doi: 10.1007/978-1-4020-9623-5_5
Li, C. (2011). Using random intercept effects in DBH increment model of individual trees for fir plantation. J. Beijing Forest. Univ. 33, 7–12. doi: 10.13332/j.1000-1522.2011.04.022
Li, C., and Tang, S. (2010). The basal area model of mixed stands of Larix olgensis, Abies nephrolepis and Picea jezoensis based on nonlinear mixed model. Sci. Silvae Sinicae 36, 474–477. doi: 10.3724/SP.J.1238.2010.00474
Li, F. (2004). Modeling crown profile of Larix olgensis trees. Sci. Silvae Sinicae 32, 105–127. doi: 10.1016/j.jce.2003.10.003
Li, Y., Liu, X., Fang, H., Shi, L., Yue, X., and Yang, Q. (2021). Exploring the coupling mode of irrigation method and fertilization rate for improving growth and water-fertilizer use efficiency of young mango tree. Sci. Hortic Amsterdam 286:110211. doi: 10.1016/j.scienta.2021.110211
Liu, Z., Shu, Y., and Li, F. (2008). Modeling for primary branch length and branch diameter of Mongolian scots pine trees. Bull. Botanical Res. 28, 244–247.
Ma, F., Liu, Y., Cui, J., Fan, H., Lu, Y., and Li, M. (2019). Review on the research progress of water and fertilizer integration. Xinjiang Agric. Sci. 56, 183–192. doi: 10.6048/j.issn.1001-4330.2019.01.022
Maguire, D. A., Johnston, S. R., and Cahill, J. (1999). Predicting branch diameters on second-growth Douglas-fir from tree-level descriptors. Can. J. For. Res. 29, 1829–1840. doi: 10.1139/x99-147
Maguire, D. A., Moeur, M., and Bennett, W. S. (1994). Models for describing basal diameter and vertical distribution of primary branches in young Douglas-fir. Forest Ecol. Manag. 63, 23–55. doi: 10.1016/0378-1127(94)90245-3
Mäkinen, H., Saranpää, P., and Linder, S. (2001). Effect of nutrient optimization on branch characteristics in Picea abies (L.) karst. Scand. J. For. Res. 16, 354–362. doi: 10.1080/02827580120345
Mäkinen, H., and Uusvaara, O. (1992). Effect of Fertilization on the Branchiness and the Wood Quality of Scots Pine. The Finnish Forest Research Institute, Folia Forestalia.
Meredieu, C., Colin, F., and Hervé, J. (1998). Modelling branchiness of Corsican pine with mixed-effect models (Pinus nigra Arnold ssp. laricio (Poiret) Maire). Ann. Forest Sci. 55, 359–374. doi: 10.1051/forest:19980307
Nelson, A. S., Weiskittel, A. R., and Wagner, R. G. (2014). Development of branch, crown, and vertical distribution leaf area models for contrasting hardwood species in Maine, USA. Trees 28, 17–30. doi: 10.1007/s00468-013-0926-5
Newton, M., Lachenbruch, B., Robbins, J. M., and Cole, E. C. (2012). Branch diameter and longevity linked to plantation spacing and rectangularity in young Douglas-fir. Forest Ecol. Manag. 266, 75–82. doi: 10.1016/j.foreco.2011.11.009
Pinkard, E. A. (2002). Effects of pattern and severity of pruning on growth and branch development of pre-canopy closure Eucalyptus nitens. Forest Ecol. Manag. 157, 217–230. doi: 10.1016/S0378-1127(00)00647-2
Tumushime, I., Vogel, J. G., Minor, M. N., and Jokela, E. J. (2019). Effects of fertilization and competition control on tree growth and C, N, and P dynamics in a loblolly pine plantation in north Central Florida. Soil Sci. Soc. Am. J. 83, 242–251. doi: 10.2136/sssaj2018.08.0289
Wang, C., Hein, S., Zhao, Z., Guo, J., and Zeng, J. (2016). Branch occlusion and discoloration of Betula alnoides under artificial and natural pruning. Forest Ecol. Manag. 375, 200–210. doi: 10.1016/j.foreco.2016.05.027
Wang, C., Tang, C., Hein, S., Guo, J., Zhao, Z., and Zeng, J. (2018). Branch development of five-year-old Betula alnoides plantations in response to planting density. Forests 9:42. doi: 10.3390/f9010042
Wang, C., and Zeng, J. (2016). Research advances in forest tree pruning. World Forest. Res. 29, 65–70. doi: 10.13348/j.cnki.sjlyyj.2016.03.006
Wang, C., Zeng, J., Hein, S., Zhao, Z., Guo, J., and Zeng, J. (2017). Crown and branch attributes of mid-aged Betula alnoides plantations in response to planting density. Scand. J. Forest Res. 32, 679–687. doi: 10.1080/02827581.2016.1261936
Wang, C., Zhao, Z., Hein, S., Zeng, J., Schuler, J., Guo, J., et al. (2015). Effect of planting density on knot attributes and branch occlusion of Betula alnoides under natural pruning in southern China. Forests 6, 1343–1361. doi: 10.3390/f6041343
Weiskittel, A. R., Maguire, D. A., and Monserud, R. A. (2007). Modeling crown structural responses to competing vegetation control, thinning, fertilization, and Swiss needle cast in coastal Douglas-fir of the Pacific northwest, USA. Forest Ecol. Manag. 245, 96–109. doi: 10.1016/j.foreco.2007.04.002
Keywords: Catalpa bungei, fertilization, mixed-effects models, branch attributes, wood quality, integration of water and fertilizer
Citation: Guan Z, Zhang Q, Xu T, Chen D, Lu Y, Han Q, Li N, Ma W, Wang J, Su Y, Li J, Qiu Q and He Q (2024) Modeling branch attributes and biomass for Catalpa bungei plantations under various fertilization regimes. Front. For. Glob. Change. 7:1261310. doi: 10.3389/ffgc.2024.1261310
Received: 19 July 2023; Accepted: 11 April 2024;
Published: 24 April 2024.
Edited by:
Manfred J. Lexer, University of Natural Resources and Life Sciences Vienna, AustriaReviewed by:
Muhammad Ishtiaq, Mirpur University of Science and Technology, PakistanCopyright © 2024 Guan, Zhang, Xu, Chen, Lu, Han, Li, Ma, Wang, Su, Li, Qiu and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qian He, aGVxaWFuQHNjYXUuZWR1LmNu; Quan Qiu, cXFpdUBzY2F1LmVkdS5jbg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.