Integrating wildfire resistance and environmental concerns into a sustainable forest ecosystem management approach

This research aims at presenting landscape management planning methods to help stakeholders select forest ecosystem management plans that may address concerns with wildfire risk and with the environmental impacts of clearcuts. Specifically, we develop mixed integer programming models for spatial optimization that incorporate a wildfire resistance index as well as constraints on the size of clearcut openings. The former is used to enforce a minimum level of resistance to wildfire while the latter limits the size of openings, in each period of the planning horizon. Timber volume even flow is another concern that is also taken into account. This research is applied to the Zonas de Intervenção Florestal (ZIF) de Paiva and de Entre-Douro e Sousa (ZIF_VS) which are located in northwestern Portugal.

1. Introduction

The forest sector plays a key role in the Portuguese economy and society. Nonetheless, its structural weaknesses have been highlighted recently by the occurrence of catastrophic wildfires. Traditional approaches that focus on forest products such as timber or cork to achieve desirable income levels should be extended to consider the provision of a wider range of ecosystem services. Ecosystem management planning approaches emerge as a viable alternative (Brockerhoff et al., 2017; Li et al., 2022). Nevertheless, acknowledging the complex temporal and spatial interactions involved in the provision of ecosystem services is a challenge (Bennet and Balvanera, 2007; Kuuluvainen, 2009) and calls for innovative decision support tools (Segura et al., 2014; Marto et al., 2018). Wildfires are natural disturbances that have an impact on the composition, structure, and functioning of ecosystems, as well as on nutrient cycling and carbon storage (Bowman et al., 2009). Human activities such as land-use changes and fire suppression as well as climate change have modified the frequency, intensity, and spatial distribution of fires, leading to significant impacts on biophysical systems and human communities. Portugal has strongly felt the effect of the dramatic wildfires of 2017. With climate change, and based on current trends, large and severe fires as well as longer fire seasons are more likely to occur (Halofsky et al., 2020). The reader is referred to Marques et al. (2011) for the characterization of wildfires in Portugal as well as to Garcia-Gonzalo et al. (2012), Marques et al. (2012), and Botequim et al. (2013) for the discussion of wildfire risk and damage models in this country. Recognizing the role of fire in forest ecosystems and implementing sustainable management practices may help to ensure the long-term resilience of ecosystems and communities in fire-prone regions. Thus, the sustainability forest ecosystem management must rely on effective wildfire management.

The integration of wildfire risk in forest management planning in Portugal has been addressed by previous research (Ferreira et al., 2015; Marques et al., 2017). Ferreira et al. (2015) used a wildfire resistance index to facilitate that integration. This index considers the flammability of individual stands as well as landscape features that may impact fire spread from one given stand to its neighbors (e.g., stand spatial configuration, edge between stands, and relative slope position). Bettinger (2010) and Chung (2015) reviewed recent research targeting the integration of wildfire risk into forest management. Adding fire-related metrics to the objective function (Thompson et al., 2000; González et al., 2005; Kim et al., 2009; González-Olabarria and Pukkala, 2011; Troncoso et al., 2016) and to constraints (Acuna et al., 2010; Ferreira et al., 2015) are common modeling approaches to achieve that integration.

Large contiguous harvested areas (clearcuts) may be harmful for forest management as they may have a negative impact on the provision of ecosystem services (e.g., Malchow-Moller et al., 2004). Frequently, in order to limit the detrimental consequences on the stands, restrictions on the area of the clearcuts are imposed (McDermott et al., 2010). The literature reports the use of several approaches to represent and solve this adjacency problem (Nelson and Brodie, 1990; Hof and Joyce, 1992; Lockwood and Moore, 1993; Borges and Hoganson, 2000; McDill et al., 2002, 2016; Constantino et al., 2008; Goycoolea et al., 2009; Borges et al., 2016; Constantino and Martins, 2018; Yoshimoto and Asante, 2018). Portuguese law (DR n. 82/2021) states that “In afforestation, reforestation, and forest conversion actions, monospecific and even stands (same species, with the same age) cannot have a continuous surface area >50 ha.” Despite the progress in integrating wildfire risk in forest management planning and in solving adjacency problems, there is little research bringing together both issues (e.g., Troncoso et al., 2016). This remains a challenge for forest management model building and model solving.

This research addresses this gap by developing a forest management planning mixed integer program that integrates a wildfire risk indicator, product even flow constraints, and adjacency constraints. The first is used to target minimum levels of landscape resistance to wildfires. The second and the third address is concerned with the sustainability of product flows and with the environmental impacts of clearcuts, respectively. The integer program includes further a soil erosion indicator. Contrarily to former research (e.g., Troncoso et al., 2016), we do not consider the Unit Restriction Model (Murray, 1999) in which two adjacent stands cannot be harvested in the same period. This research considers rather the Area Restriction Model (ARM) (Murray, 1999) to represent adjacency. This approach is more general and may accommodate typical forest management planning contexts where stands have varying sizes. It enables to harvest two or more adjacent stands in the same period unless the combined area is greater than the maximum opening size. This innovative forest management planning integer program is applied for demonstration purposes to the Zona de Intervenção Florestal (ZIF) de Paiva and de Entre-Douro e Sousa (ZIF_VS), a 14,765 ha forested landscape located in northwestern Portugal.

2. Materials and methods

2.1. Case study

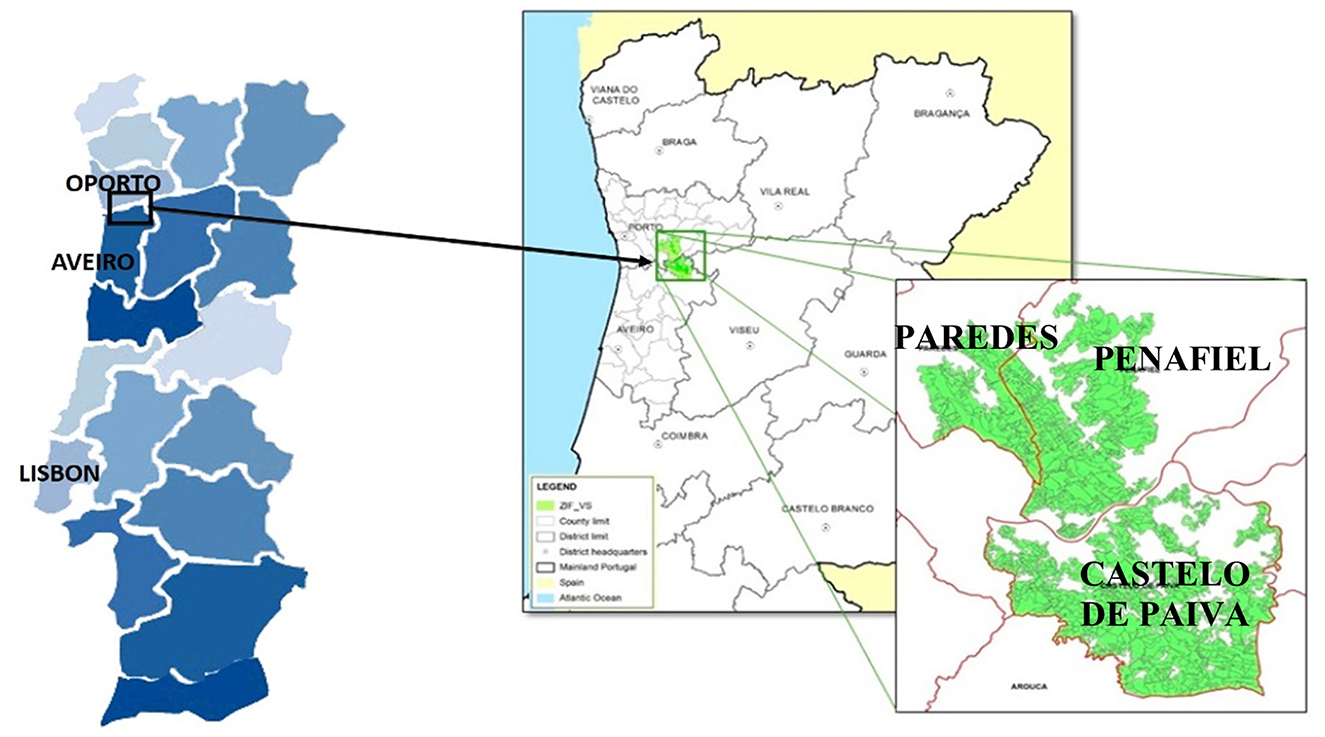
The case study area includes Zonas de Intervenção Florestal (ZIF) de Paiva and de Entre-Douro e Sousa (ZIF_VS) located in northwestern Portugal, 100 km from Oporto in a rural area with a Mediterranean climate with an Atlantic influence. ZIF_VS is a forested landscape that extends over 14,765 ha and encompasses three counties: Penafiel, Castelo de Paiva, and Paredes (Figure 1). In 2017, nearly 47% of the ZIF_VS area got burned. Recent remote sensing information and field inventory data led to the classification of the landscape into 1,345 stands, of which 1,272 and 73 are pure and mixed, respectively (Table 1). The former may be occupied by maritime pine, eucalyptus, chestnut, cork oak, or pedunculate oak. The latter includes two species, maritime pine and eucalyptus.

FIGURE 1

Figure 1. ZIF_VS location in Northwest Portugal.

TABLE 1

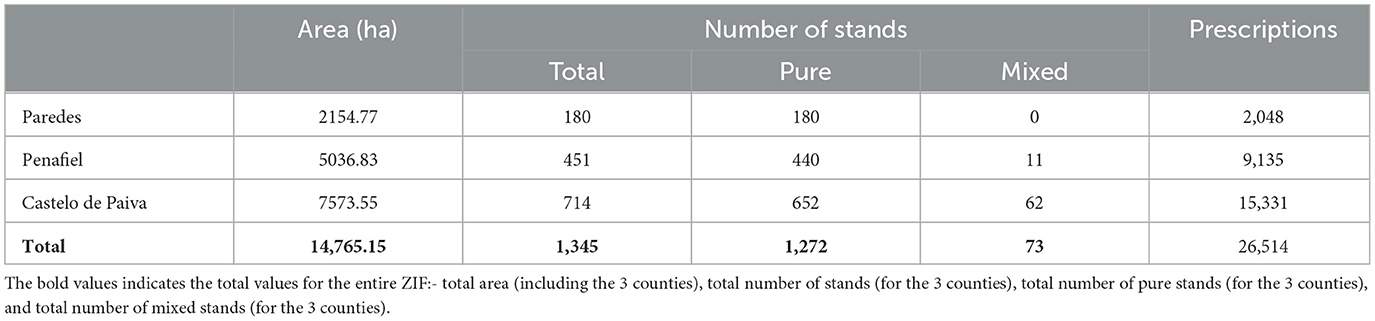
Table 1. Distribution of area, number of stands and prescriptions within the three counties of ZIF_VS.

In this research, we considered a planning horizon of 90 years divided into nine periods of 10 years each. We simulated a total of 26,514 prescriptions to manage the 1,345 stands (Table 1). These prescriptions involve the possibility of species conversion. They were afterward combined with different fuel treatment scenarios (0-, 1-, 5-, 10-, or 15-years periodicity) leading to a total of 5 ^* 26,514 = 132,570 stand-level management possibilities.

The simulation of prescriptions encompassed the corresponding projection of forest conditions and outcomes with species-specific growth and yield models (e.g., Paulo and Tomé, 2006; Tomé et al., 2006; Almeida et al., 2010; Nunes et al., 2011; Botequim et al., 2015; Gómez-García et al., 2015). Eucalyptus, pine, chestnut, and oak stands are even aged. The prescriptions assumed that at the end of a rotation, the stand is regenerated by a plantation. In the case of cork oak, since there is no final harvest, the growth and yield simulator (Paulo and Tomé, 2006) assumes that natural regeneration replaces the trees removed over the planning horizon. Stand-level prescriptions encompass the option of species conversion. The latter may take place after a clearcut and complies with policy constraints to eucalyptus plantation (Law no. 77/2017). The generation of prescriptions took further into account the suitability of the site to species conversion. The values of indicators that measure the provision of other ecosystem services, e.g., soil erosion and biodiversity, were estimated using the approaches described by Botequim et al. (2021) and Rodrigues et al. (2021), respectively. Net present value (NPV) was computed using constant prices and with a real discount rate of 3%.

2.2. Wildfire resistance index

A wildfire resistance index developed by Ferreira et al. (2015) was used to measure the forest stands' vulnerability to wildfires. This index takes into account wildfire occurrence and damage probability models developed for forest species in Portugal (e.g., Garcia-Gonzalo et al., 2012; Marques et al., 2012; Botequim et al., 2013). This index recognizes that the vulnerability (resistance) of a stand may be affected by the flammability of the neighboring stands. For instance, fuel treatments in a stand impact its flammability as well as its vulnerability (resistance) to wildfires. They thus impact the probability of a neighboring stand burning because of the wildfires spreading from the former to the latter stand. Thus, the wildfire resistance index considers the specific resistance of a stand and a correction factor of that resistance that is measured according to the resistance of its neighbors. An adjusted resistance is thus computed for each stand i, in each period t, according to the following equations:

$r{a}_{it}=r_{it}+(1-w_i){\displaystyle \sum _{sϵV(i)}{\alpha }_{is}(r{a}_{st}-r_{it}),\forall i,\forall t}$

where ra_it is the adjusted resistance, which ranges from 0 to 1, r_it is the specific resistance of stand i, V(i) is the set of neighbors of stand i, (1−w_i) is the weight given to the impact of the neighbors on the resistance of stand i, with (1−w_i) ϵ [0, 1], depending on the shape and dimension of stand i. α_is reflects the probability of a fire that occurs in stand s to spread to stand i, taking into consideration the relative position, the common borders, and the kind of paths between stands i and s. For more details, the reader is referred to Ferreira et al. (2015).

2.3. Clearcut area constraints

In this research, we impose a maximum clearcut area (A_max). Considering the Portuguese law, this was set at 50 ha. Therefore, a feasible clearcut is a continuous harvested area that does not exceed A_max. We consider that two stands are adjacent if they share an edge, whichever their size is. The generation of the clearcut constraints was made using the Path formulation (Martins et al., 1999; McDill et al., 2002; Murray and Weintraub, 2002). The path formulation encompasses the definition of clusters. A cluster is a set of contiguous stands. If the total area of the cluster is greater than A_max, it is considered an unfeasible cluster. A minimal unfeasible cluster is an unfeasible cluster such that if any of its stands is removed, the resulting cluster or clusters are feasible (Figure 2). The path formulation guarantees that the maximum number of stands in a cluster that are harvested in the same period is equal to the total number of stands minus one at the most, i.e., Card(C)-1, where Card(C) corresponds to the total number of stands in cluster C.

FIGURE 2

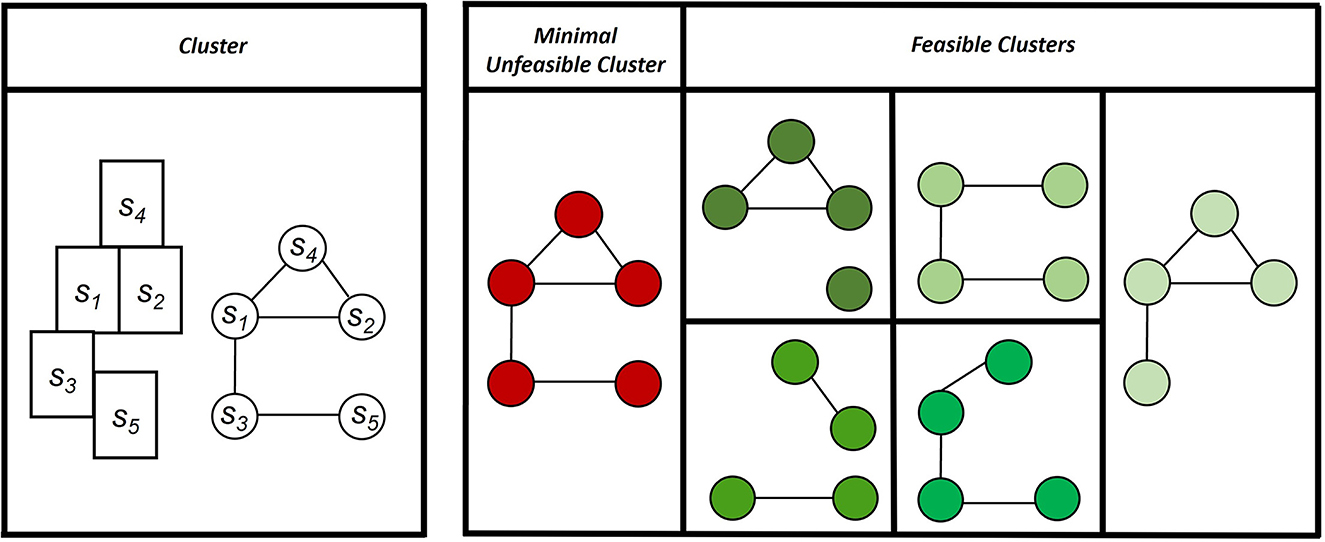
Figure 2. Example of a cluster that is unfeasible if its total area is greater than A_max. It is a minimal unfeasible cluster if, when removing any of its stands, the remaining clusters (in green on the right) are feasible.

In this research, mixed stands are treated for simulation purposes as two independent stands, s_A and s_B (pine and eucalyptus). Specifically, our approach generates two sets of prescriptions for the mixed stands, one set for each species. Nevertheless, for adjacency purposes, the mixed stand is treated as a single stand. Thus, we defined three different sets: S, B_s, and I. S is the set of all current stands; B_s is the set that includes either stand s (if s is pure) or the two component parts (s_A and s_B) of stand s (if s is mixed); and I is the set that includes all pure stands and all component parts of mixed stands. Thus,

$B_s=\{\begin{array}{l}\left\{s\right\},ifsisapurestand\\ \{s_A,s_B\},ifsisamixedstand\end{array},sϵS$

2.4. The mixed integer programming model

The mixed integer programming (MIP) model used to define the decision space chooses a prescription to be implemented in each stand over the planning horizon. The values of the ecosystem products and services derive from the landscape management plan found by the model. Thus, the MIP model intends to find the management policy to be followed in the landscape that may enhance its resistance to wildfires while guaranteeing a limit on the clearcut areas. This is done by defining a minimum level for the wildfire resistance index and a maximum opening size in each planning period. The MIP model enforces a timber even flow policy. It is described as follows:

Sets and indexes:

S, set of all current stands;

I, set of all pure stands and all two component parts of all mixed stands;

P, set of fuel treatment schedules (i.e., 0, 1, 5, 10, or 15 years);

J_i,set of prescriptions that may be implemented in stand i, with i ϵ I;

E, set of forest species. E = {Ec, Pb, Ct, Sb, Qr, Rp}, where Ec = eucalyptus, Pb = pine, Ct = chestnut, Sb = cork oak, Qr = pedunculated oak, Rp = riparian};

T, set of periods of the planning horizon. T = {1, …, T} and T corresponds to the total number of planning periods (in this case, T = 9 periods of 10 years each);

X, set of minimal unfeasible clusters;

s, stand, with s ϵ S;

i, pure stand or the component part of a mixed stand. with i ϵ I;

j, prescription that may be assigned to stand i, with j ϵ J_i;

p, periodicity of shrub cleaning that may be assigned to stand i, with p ϵ P;

e, forest species, with e ϵ E;

t, planning period, with t ϵ T;

Parameters:

v_ijte, timber volume of species e in period t, that results from assigning prescription j to stand i;

A_i, area of stand i, in hectares; A_F= $\sum _{iϵS}{A}_i$;

RES_t, minimum value defined for the landscape wildfire resistance in period t, with RES_t ϵ [0,1];

ra_ijte, adjusted resistance index for stand i, in period t, when prescription j is adopted considering species e;

λ, maximum variation allowed over a target level for the volume of timber harvested in each period;

Card(^*), corresponds to the cardinality of set ^*;

$c{r}_{ij}^t=\{\begin{array}{c}1,ifstandi\left(iϵI\right)ismanagedbyprescriptionj\\ andthereisaclearcutinperiodt\\ \\ 0,otherwise\end{array}$

Variables:

$x_{ijp}=\{\begin{array}{c}1,ifstandiismanagedbyprescriptionjandis\\ chosenpforfueltreatment\\ \\ 0,otherwise\end{array}$

$y_i^t=\{\begin{array}{l}1,ifstandi\left(iϵI\right)isclearcutinperiodt\\ 0,otherwise\end{array}$

$z_s^t=\{\begin{array}{c}1,ifstands\left(sϵS\right)isclearcutinperiodt\\ 0,otherwise\end{array}$

W, is a target volume for the timber harvested in each period. The model will find this value (Martins et al., 2014);

Vol_t, total amount of timber volume harvested in period t;

RA_it, adjusted resistance index reached for stand i in period t.

MIP model:

$\begin{array}{ll}\text{Max }/\text{Min }\text{Z }& (1)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{jϵJ_i}{\displaystyle \sum _{pϵP}{x}_{ijp}=1,iϵI}}& (2)\end{array}$

$\begin{array}{ll}{y}_i^t={\displaystyle \sum _{jϵJ_i}{\displaystyle \sum _{pϵP}c{r}_{ij}^t{x}_{ijp},iϵI,tϵT}}& (3)\end{array}$

$\begin{array}{ll}{z}_s^t\ge {\displaystyle \sum _{iϵB_s}{y}_i^t+\left(1-Card\left(B_s\right)\right)\text{},sϵS,tϵT}& (4)\end{array}$

$\begin{array}{ll}{z}_s^t\le y_i^t,iϵB_s,sϵS,tϵT& (5)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{sϵC}{z}_s^t}\le Card\left(C\right)-1,CϵX,tϵT& (6)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{iϵI}{\displaystyle \sum _{jϵJ_i}{\displaystyle \sum _{pϵP}{\displaystyle \sum _{eϵE}{v}_{ijte}{x}_{ijp}=Vo{l}_t,tϵT}}}}& (7)\end{array}$

$\begin{array}{l}Vo{l}_t\ge \left(1-\lambda \right)W,tϵT\\ Vo{l}_t\le \left(1+\lambda \right)W,tϵT& (8)\end{array}$

$\begin{array}{ll}{\displaystyle \sum _{jϵJ_i}{\displaystyle \sum _{pϵP}{\displaystyle \sum _{eϵE}r{a}_{ijte}{x}_{ijp}=R{A}_{it},iϵS,tϵT}}}& (9)\end{array}$

$\begin{array}{ll}\frac{{\displaystyle {\sum }_{iϵI}{A}_{i}R{A}_{it}}}{A_F}\ge RE{S}_t,tϵT& (10)\end{array}$

$x_{ijp},y_i^t,z_s^t,ϵ\left\{0,1\right\}\text{},iϵS,jϵJ_i,pϵP$

Equation (1) expresses the objective function, which can change according to the objectives related to different ecosystem forest products and services that are considered as a priority. Equation (2) ensure that one and only one management alternative prescription with one and only one fuel treatment periodicity is assigned to each stand. Equation (3) computes the value of variables $y_i^t$, saying that stand I is harvested or not in period t according to the prescription chosen by the model for the stand. Equations (4, 5) compute the value of variables $z_s^t$ that are either 1 or 0 even if stand s is harvested or is not harvested in period t, respectively. If stand s is a mixed stand, the variable z is only equal to 1 if the two parts of the stand are harvested simultaneously in the same period or, in other words, if the stand is completely harvested. Equation (6) requires that the total number of harvested stands in a minimal unfeasible cluster is less than or equal to the number of stands of that of cluster minus one. This will guarantee that the maximum area defined for a clearcut, in each period, is not overcome. Equation (7) defines the volume of timber harvested in each planning period, while Equation (8) states that the volume of timber harvested is between 1 – λ and 1 + λ times the average value defined in the model (W). The maximum difference between the volumes of timber harvested over the planning horizon is thus 2 λ times than average. Equation (9) computes the adjusted wildfire resistance of each stand in each period. In order to address wildfire risk concerns, a minimum value for the forest-wide adjusted wildfire resistance is defined in Equation (10). The levels of the adjusted resistance indicator in each period are computed as the weighted average of its stands' adjusted wildfire resistance, where the weights correspond to the stands' area. Rather than imposing a minimum value for the adjusted resistance in each period t, one could consider another variable U standing for that resistance in all periods of the planning horizon. In this case, Equation (10) would be replaced by Equation (11).

$\begin{array}{ll}\frac{{\displaystyle {\sum }_{iϵI}{A}_{i}R{A}_{it}}}{A_F}\ge U,tϵT.& (11)\end{array}$

The model computes the net present value, the total timber volume, and cork weight harvested as well as the total erosion over the 9–10-years planning periods (Table 2). It computes further the ending inventory volume. These variables as well as the minimum wildfire resistance (U) may be selected to define the objective function as discussed in the next section.

TABLE 2

Table 2. Management objectives.

3. Results

The MIP model was implemented with the algebraic language IBM ILOG CPLEX Optimization Studio, version 20.1, in a computer-i7, 2600 central processing unit, 3.40 GHz with 32 GB of random access memory.

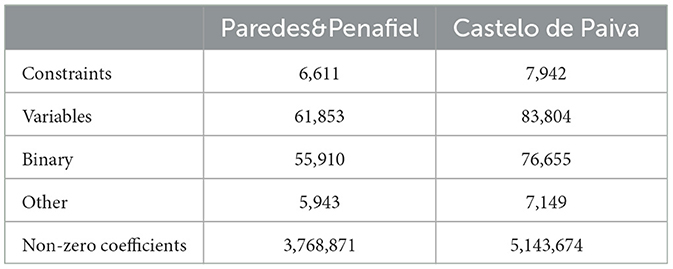
Due to the complexity of the problem and the corresponding computational constraints, we decomposed the ZIF_VS master problem into two subproblems: Paredes&Penafiel and Castelo de Paiva. These subproblems represent subregions of ZIF_VS that are separated by the Douro River. Thus, they do not share adjacent stands. First, we ran the model without adjacency constraints (Equation 6). The model found feasible solutions to run with and without the imposition of a minimum level for wildfire resistance despite the need for different computational capacity for each subproblem. Castelo de Paiva is the largest subproblem (Tables 1, 3) and, consequently, demanded higher RAM capacity. Specifically, the solution of the Castelo de Paiva subproblem required servers with 32 GB of RAM.

TABLE 3

Table 3. MIP model size for the subproblems Paredes&Penafiel and Castelo de Paiva.

We report results for the two subproblems without adjacency constraints considering several objective functions (Table 4). There are no feasible solutions if we consider λ <0.3 and 0.35 in Paredes&Penafiel and Castelo de Paiva, respectively. Moreover, when a minimum level for wildfire forest resistance in each period is imposed, it is also not possible to reach feasible solutions if that level is above 0.9 and 0.8 in Castelo de Paiva and Paredes&Penafiel, respectively.

TABLE 4

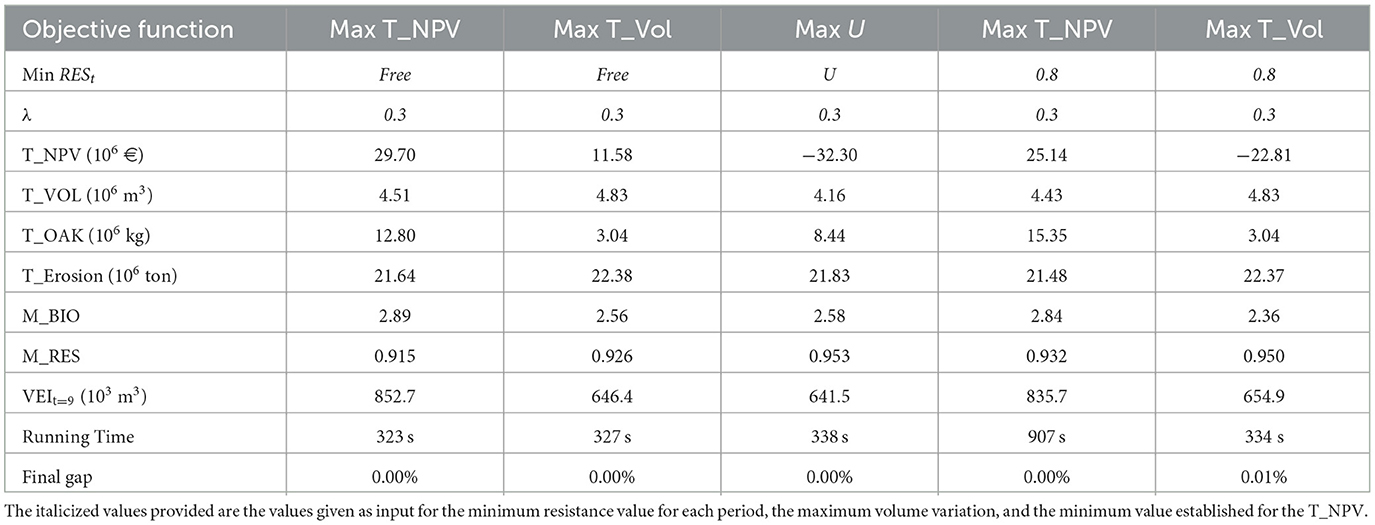
Table 4. Solutions to the Paredes&Penafiel subproblems without adjacency constraints demanding or not a minimum resistance level in each period.

The results show that defining a minimum level for resistance or maximizing the resistance may have a huge impact on the economic objectives, namely, in the NPV (Tables 4, 5). These scenarios deliver high negative values for NPV that translate the effort made in wildfire prevention measures, specifically, with shrub cleanings, which become more frequent and consequently overall more costly. The decision-makers must be aware that to guarantee sustainability and a more resistant forest, it is necessary to acknowledge its impact on short-term profitability. To avoid such dramatic economic results, it is possible to add to the MIP model constraints to demand a minimum value for NPV so that the losses are not so significant. A compromise solution between the extreme previous scenarios may be achieved if the NPV is maximized and a minimum level of resistance is required. For both Castelo de Paiva and Paredes&Penafiel, this was the solution that took more running time (513 and 907 s, respectively).

TABLE 5

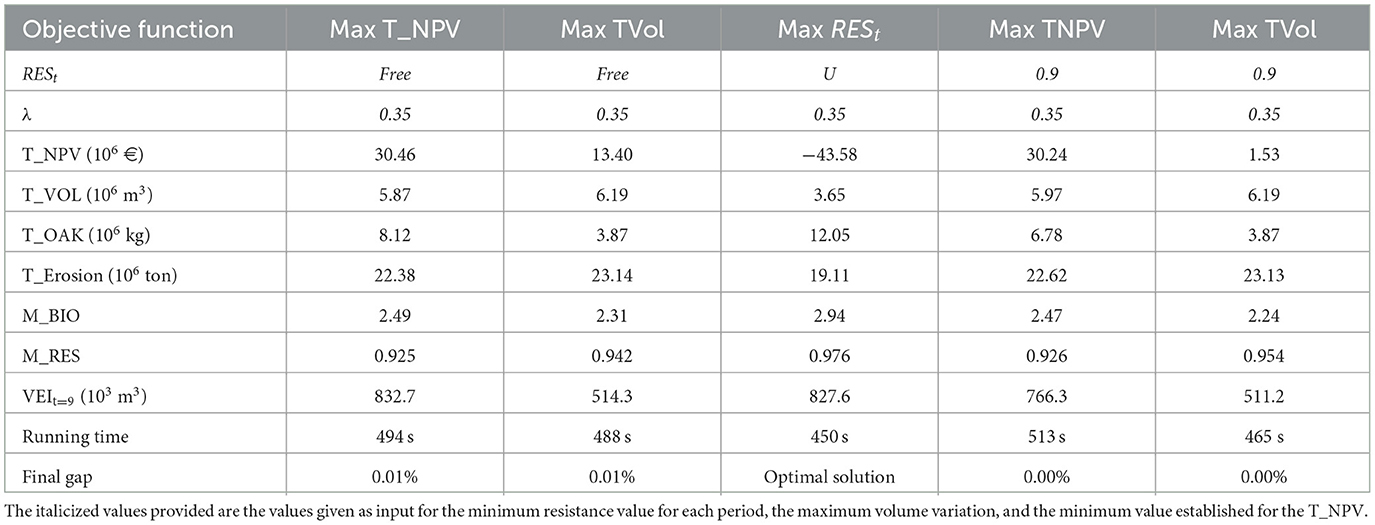
Table 5. Solutions to the Castelo de Paiva subproblem without adjacency constraints demanding or not a minimum resistance level in each period.

As would be expected, when the models address concerns with the landscape vulnerability to wildfires, higher levels are reached for wildfire forest resistance. Although the mean values for resistance in the other scenarios are not very low, there is no consistency across planning periods when stand-level species conversions are more frequent in the first and second periods. Conversions lead to clearcuts and, counterintuitively, as shown in Stone et al. (2008), and timber harvesting may also contribute to lower resistance levels in those periods.

For all the achieved solutions, the gap (the variation between the upper bound and the solution reached by the model) takes on low values.

In Paiva, the differences between the solutions obtained for the maximization of the NPV with no constraints on vulnerability to wildfires or with a minimum resistance level are not so distinct. However, the scenario of maximization of resistance also leads to a high negative value for NPV.

When bringing together the solutions to both subproblems, it is possible to observe substantial differences in the level of resistance for the whole forest across runs. If the objective function addresses financial concerns, e.g., by maximizing the NPV, the model ignores vulnerability to wildfires, and the achieved resistance level for the forest is much lower than in the case of the scenario of maximizing the minimum resistance level in each period (Figure 3).

FIGURE 3

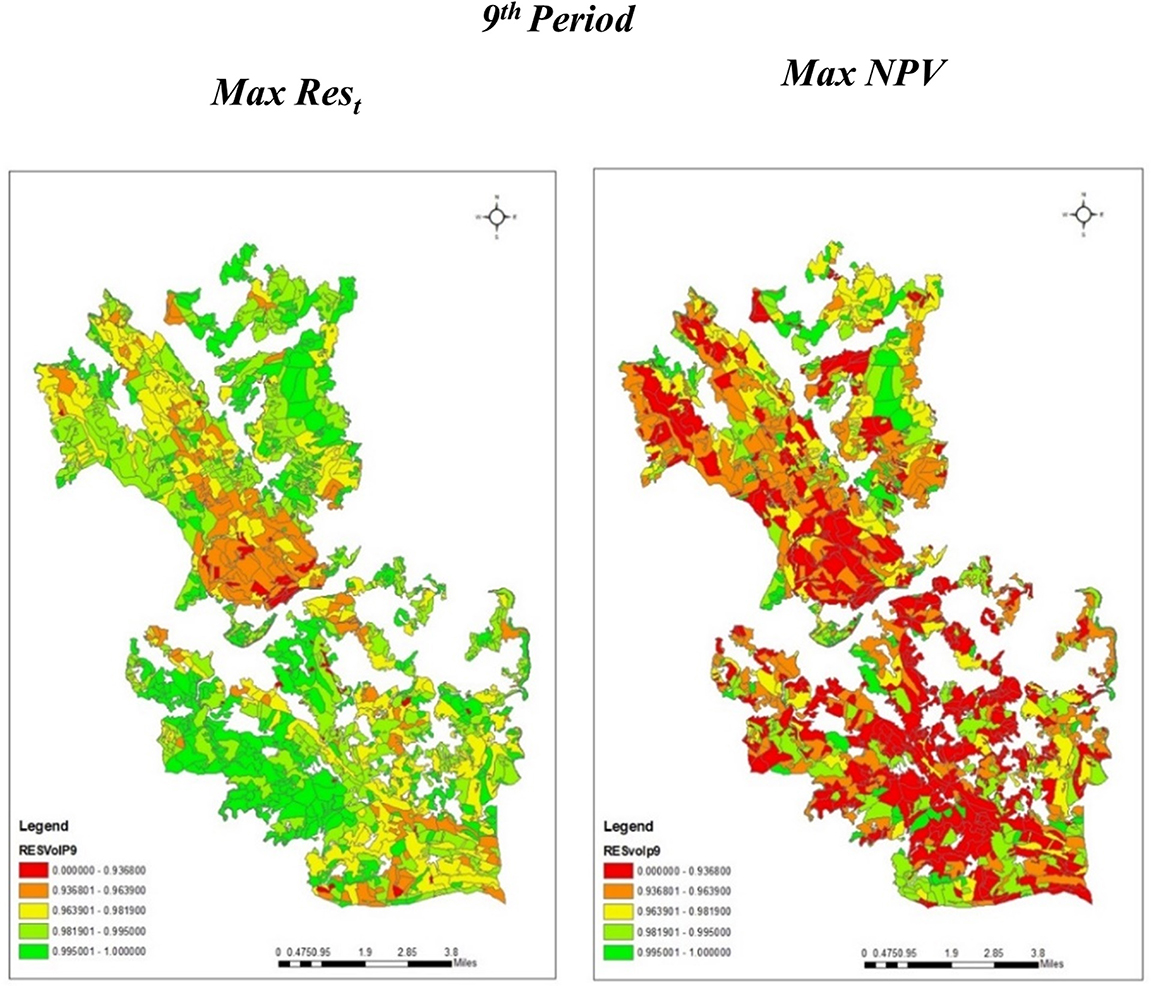
Figure 3. Resistance level achieved in the ninth period for ZIF_VS when different objective functions are considered: maximization of the minimum resistance level in each period or maximization of NPV without resistance concerns. Green stands are more resistant stands, whereas red stands are less-resistant stands.

In order to include the adjacency constraints in the model, it was necessary to generate the minimal unfeasible clusters for each region (Paredes&Penafiel and Castelo de Paiva). This required several days of running time. After including adjacency constraints in the model, the problem became even more difficult to solve. The number of constraints and variables increased substantially. Specifically, the number of constraints in the case of Paredes&Penafiel and Paiva got increased by 43- and 54-fold, respectively. The number of variables in the case of Paredes&Penafiel and Castelo de Paiva increased approximately by 46 and 40%, respectively. Model building considered the exact number of minimal unfeasible clusters in the case of Paiva. Nevertheless, in the case of Paredes&Penafiel, specific clusters, called as barrier clusters, were used to build the model. Barrier clusters are feasible clusters that encompass two stands: one of the most frequent stands in the set of minimal unfeasible clusters and another adjacent stand. This option was due to the existence of many adjacent stands with small areas to include in several elements of the set of clusters. Barrier clusters were then considered in the model as they were minimal unfeasible clusters. Using barrier clusters encompassing these specific stands in the set of minimal unfeasible clusters prevents the simultaneous clearcut in the same period and makes it no longer mandatory to consider all minimal unfeasible clusters (Table 6). This was influential to reduce the number of minimal unfeasible clusters.

TABLE 6

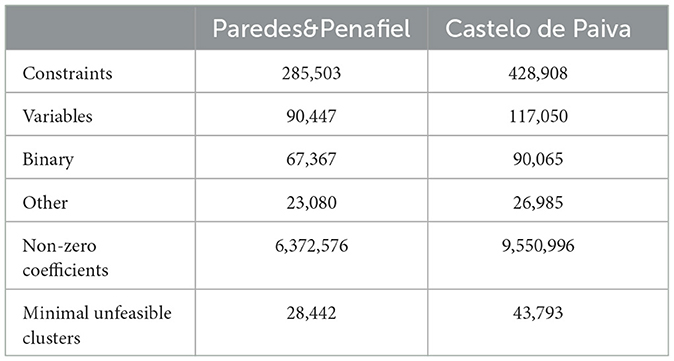
Table 6. MIP model size in the case of the Paredes&Penafiel and Castelo de Paiva subproblems with adjacency constraints.

The addition of constraints on a clearcut area introduces new issues in the solution process. In some minimal unfeasible clusters, the prescriptions available to manage all of its stands only included clearcuts in the same period(s). Therefore, there are stands that have to be left without an assigned prescription, as otherwise constraints would be violated in that (those) period(s) (Figure 4). Thus, the equal sign in constraints (2) had to be replaced by the less than or equal sign in order to reach a feasible solution. Basically, this stands for the listing of a “do nothing” prescription in those stands. In Paredes&Penafiel, when the NPV is maximized with no constraints on the level of resistance, there are 125 out of 620 stands assigned to a “do nothing” prescription, whereas this number decreases to 76 stands if a minimum resistance is prescribed. In the other scenarios, there are between 11 and 12% of management units with an implicit assignment of a “do nothing” prescription (Table 7). In Castelo de Paiva, when maximizing the minimum resistance level, 31 management units are implicitly assigned a “do nothing” prescription. In all the other optimization scenarios, more than 100 management units (in a total of 714) are assigned this “do nothing” prescription (Table 8).

FIGURE 4

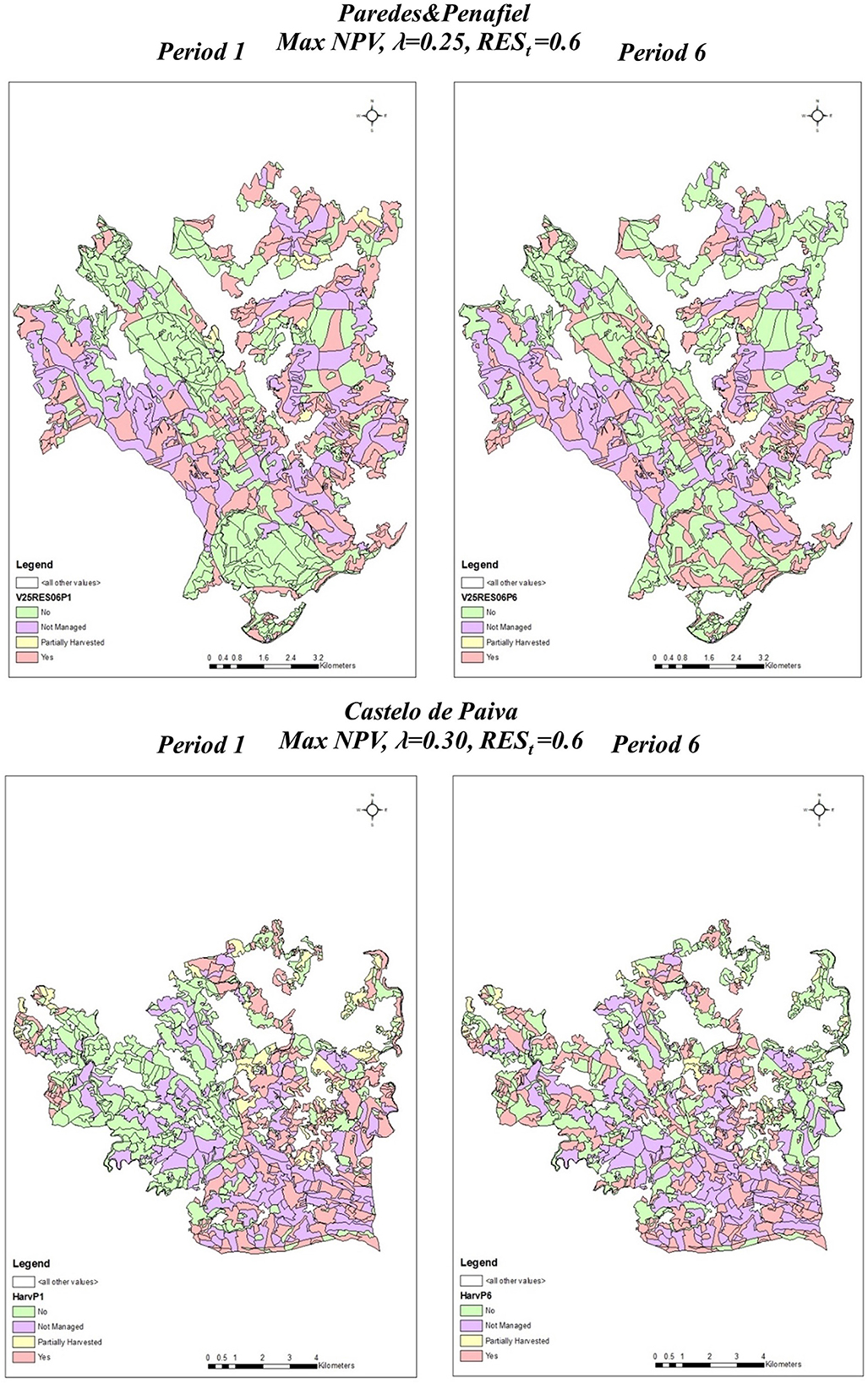
Figure 4. Maps of Paredes&Penafiel and Castelo Paiva for solutions achieved by the MIP model encompassing timber volume, resistance, and constraints on the clearcut area for periods 1 and 6.

TABLE 7

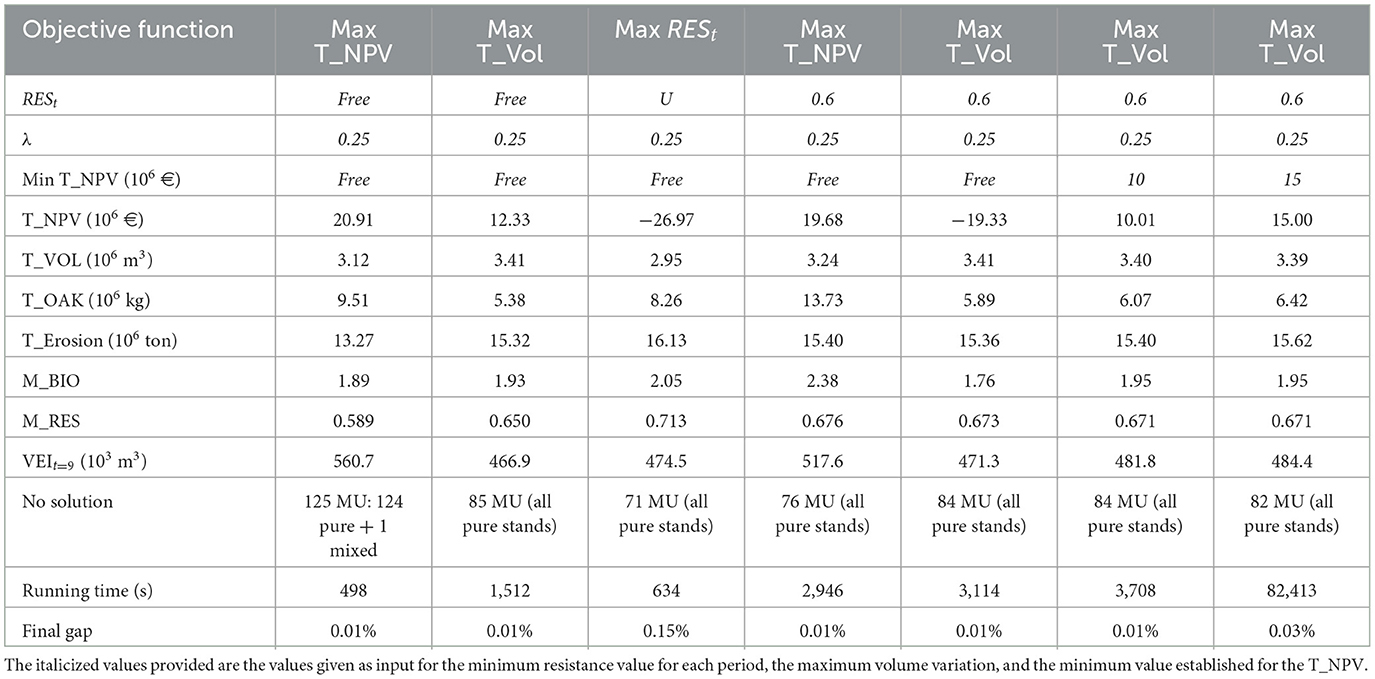
Table 7. Results for Paredes&Penafiel, considering different objective functions for the MIP model, imposing a maximum variation of 25% in timber flows between different periods and demanding or not a minimum resistance level for each period, with adjacency constraints.

TABLE 8

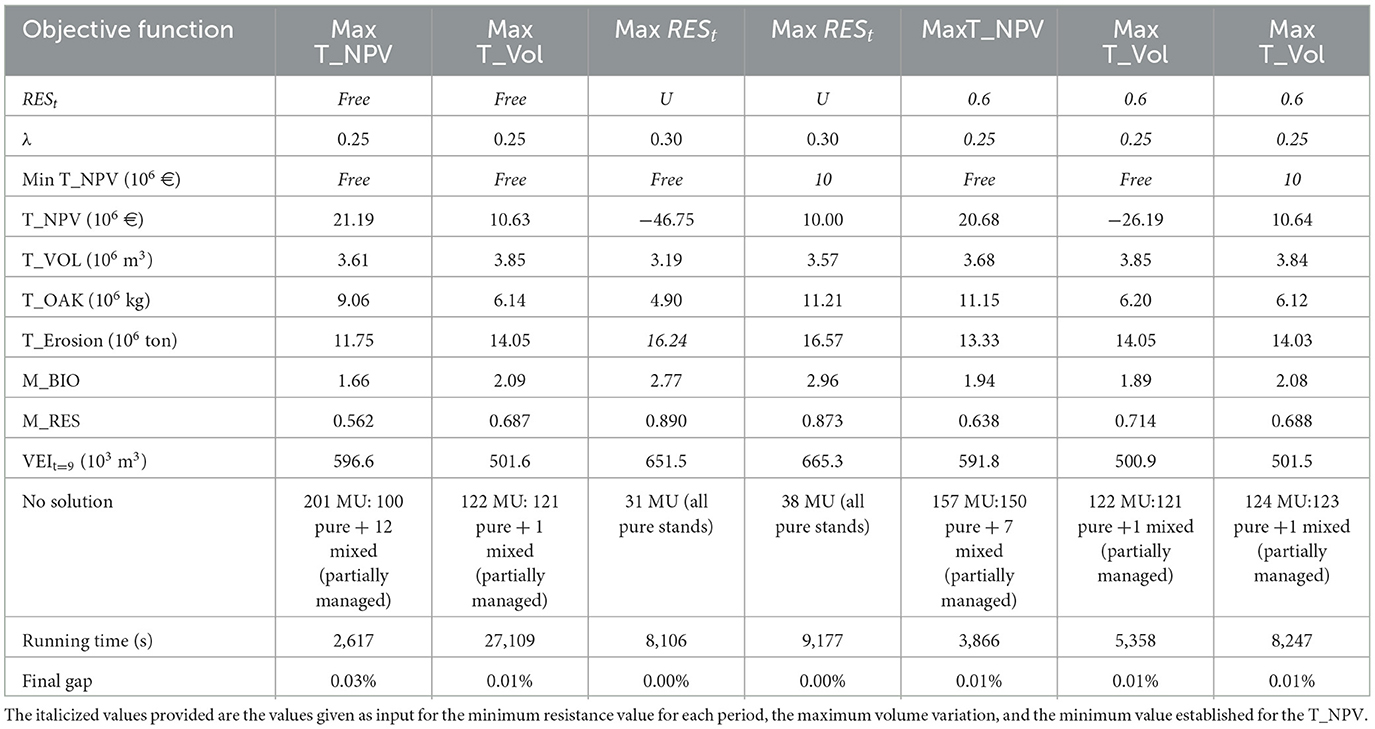
Table 8. Results for Castelo de Paiva, considering different objective functions for the MIP model, imposing a maximum variation of 30% in timber flows between different periods and demanding or not a minimum resistance level for each period, with adjacency constraints.

When comparing the scenarios that maximize NPV in Paredes&Penafiel, the results show that if a minimum resistance level is considered there is an improvement in several objectives: the average resistance is 0.676, the mean for biodiversity also increases to 2.38, and there is further an increase in the total values of timber volume and extracted cork which will balance the costs of a higher number of shrub cleanings. This contributes to a positive NPV. Nevertheless, the running time also increases substantially from 498 s to 2,946 s (Table 7).

In Castelo Paiva, the solutions achieved for the maximization of NPV with or without a minimum resistance level are again similar in terms of the objective function value. However, there is an increase in the computational effort. Moreover, if a minimum level for resistance is required the model finds higher values for timber volume, cork, biodiversity, and resistance objectives. It assigns active prescriptions to 557 out of 714 management units. This number decreases to 513 stands if there is no constraint on resistance (Table 8).

The highest values of the mean of both biodiversity and resistance objectives across planning periods are achieved with the maximization of the minimum value for wildfire resistance in each period (2.77 and 0.890, respectively). This scenario also provides active prescriptions for more management units (only 31 without solution) but at the price of an excessive negative value for NPV (Table 8).

In Castelo de Paiva, it was possible to find solutions with a variability of timber flows between different periods under 30% under several scenarios. Nevertheless, when maximizing wildfire resistance, only solutions with 30% of regularity of timber volume were reached.

Solutions targeting a minimum level of total NPV in scenarios with and without adjacency constraints were also developed for both regions. As the minimum level for NPV increases, the model proposes less expensive plans, while still guaranteeing the minimum level of fire resistance (Tables 7–10). To reach some of these solutions, the computational effort increased significantly. For instance, when a minimum level of 15 million euros was imposed for Castelo Paiva, it was impossible to reach a solution within running daytime (Tables 7, 8).

TABLE 9

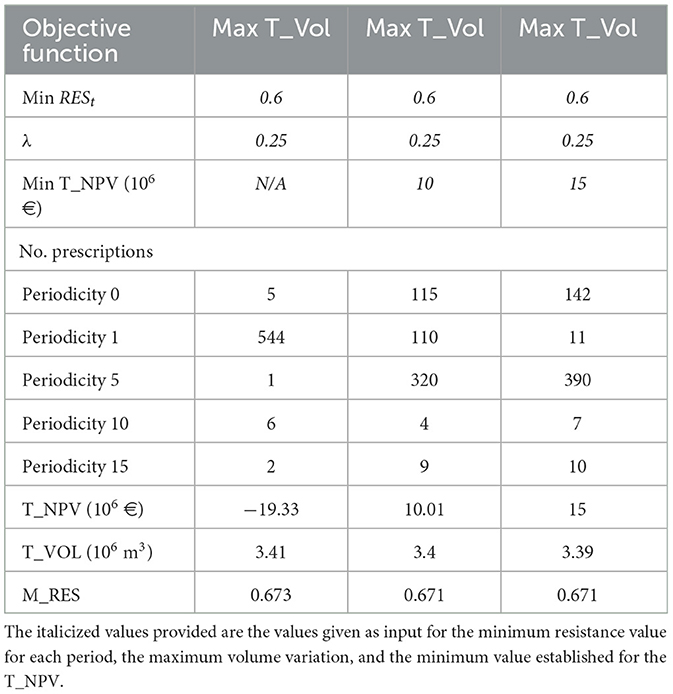
Table 9. Results for Paredes&Penafiel, with adjacency constraints, considering the maximization of volume as objective function for the MIP model, imposing a maximum variation of 25% in timber flows between different periods and demanding minimum levels for resistance and NPV.

TABLE 10

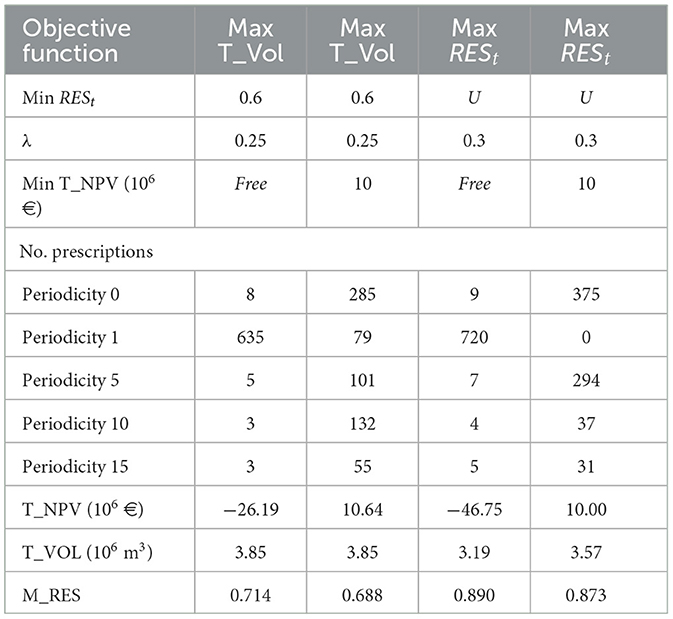
Table 10. Results for Castelo de Paiva, with adjacency constraints, considering the maximization of resistance or volume as objective functions for the MIP model, demanding minimum levels for resistance and NPV.

The predominant species in the suggested management plans change when a minimum value is demanded for NPV. When maximizing total volume in Paredes&Penafiel, the model proposes often to convert pine and eucalyptus mixed stands as well as pure eucalyptus stands to pine in order to reach the imposed resistance levels. This is highlighted by the decrease in the eucalyptus area in periods 1 and/or 2. In solutions targeting minimum NPV values, most prescriptions that maintain cleanings with periodicity of 1 year are assigned to eucalyptus stands (Figure 5). In Castelo de Paiva, when maximizing wildfire resistance, eucalyptus stands are converted into pine, cork oak, and chestnuts, thus increasing too the cork production. In this study, expensive plans including shrub cleanings with periodicity of 1 year are totally replaced by policies that encompass larger periodicities (Figure 6).

FIGURE 5

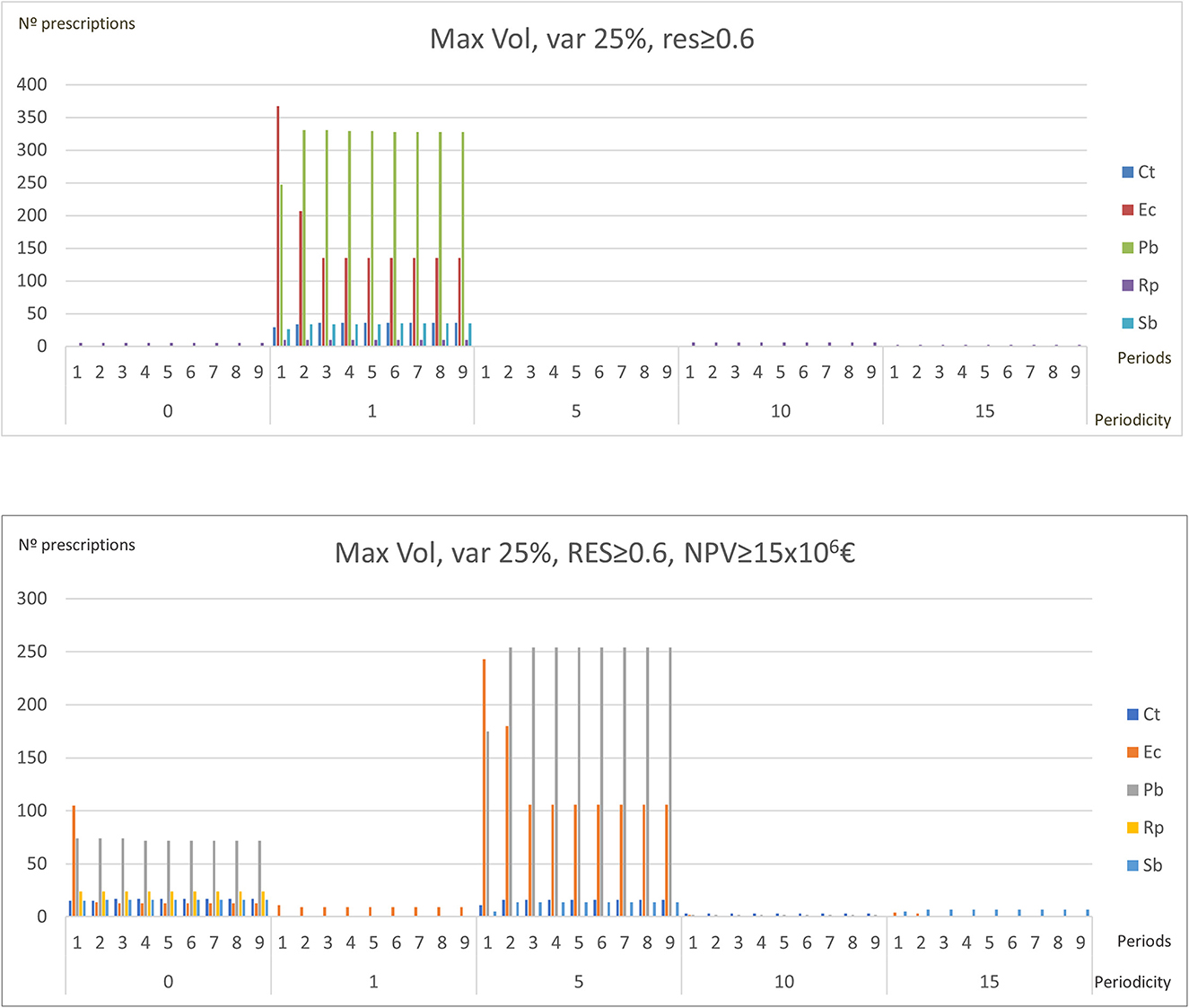
Figure 5. Differences in species and shrub cleanings periodicities of the management plans of Paredes&Penafiel when a minimum level of NPV is or is not imposed.

FIGURE 6

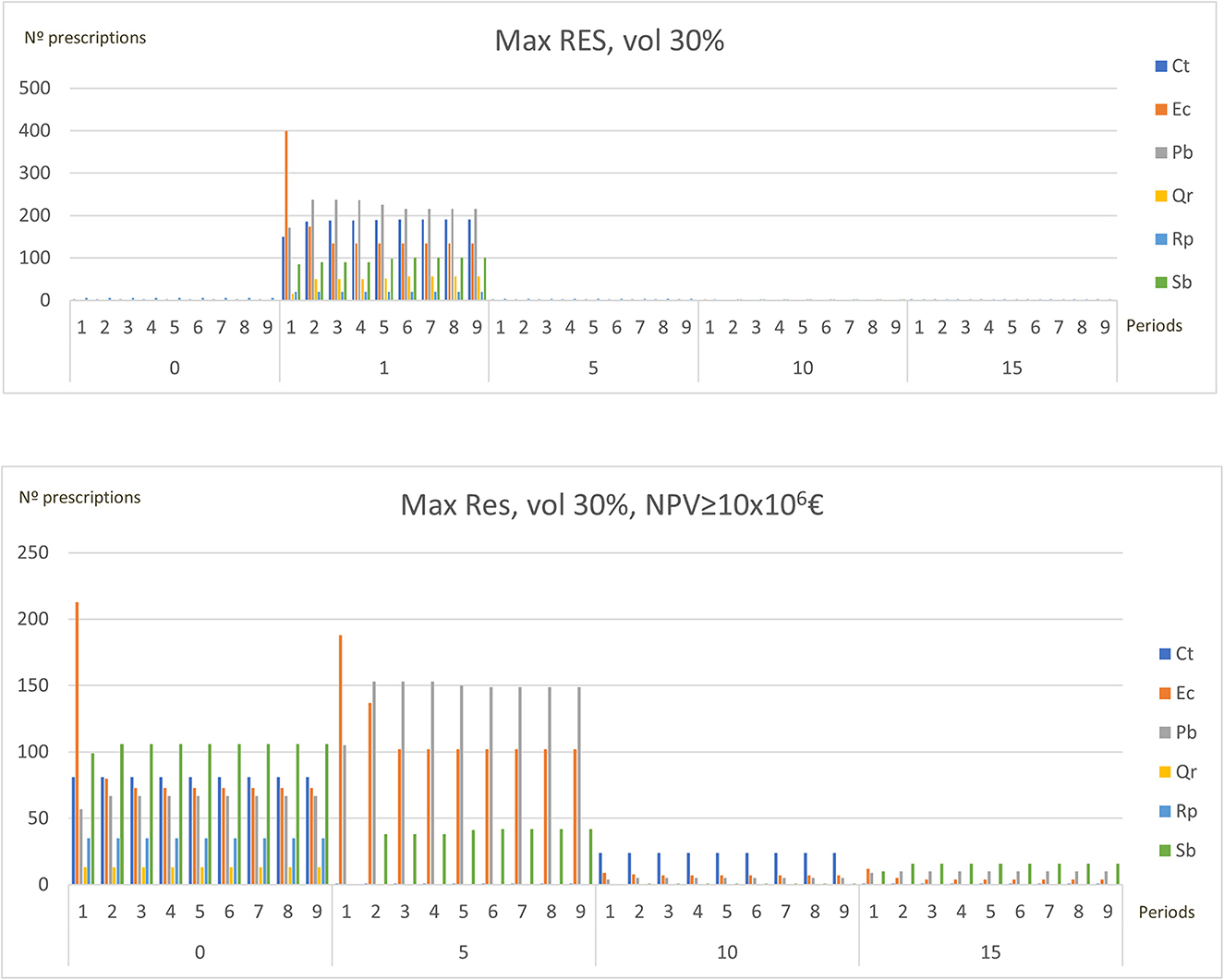
Figure 6. Differences in species and shrub cleanings periodicities of the management plans of Castelo Paiva when a minimum level of NPV is or is not imposed.

Solving problems with adjacency constraints requires additional computational effort (Tables 7, 8). The number of minimum infeasible clusters −43,793 and over 100,000 in the case of Castelo de Paiva and Paredes&Penafiel, respectively—contributes to the computational complexity and solution time. The barrier cluster approach used in this research helped to address computational constraints by reducing the number of minimal unfeasible clusters used by the model for Paredes&Penafiel. Twelve barrier clusters were considered in the case of this region in order to avoid the violation of constraints on the clearcut area.

4. Discussion

A forested landscape is a spatial patchwork of stands. The introduction of spatial details, relationships, and conditions is key for the effectiveness of forest management planning (Hof and Joyce, 1992; Weintraub and Murray, 2006). The problem of designing a landscape that is more resistant to wildfires is harder to solve considering the whole region. In order to provide solutions, it was necessary to split the region into two subproblems: Paredes&Penafiel and Castelo de Paiva. These subproblems represent subregions that are separated by the Douro River; thus, adjacency constraints between them are naturally satisfied. First, the model only considered volume and wildfire resistance constraints. In the second phase, clearcut area constraints were also included. To satisfy these constraints, minimal unfeasible clusters were defined which made the problem even more difficult to solve. Nevertheless, solutions were achieved after some hours of running time. Another possibility was to solve the path formulation with only one sufficiently meaningful subset of constraints by branch-and-cut. This procedure could start without constraints (5) which were being applied to the incomplete model throughout the enumeration tree when they were violated by integer solutions of the node subproblems. This approach was already proposed by Martins et al. (2022) to solve the ARM problem, without fire concerns, for the Zonas de Intervenção Florestal de Paiva and de Entre-Douro e Sousa using data prior to the 2017 fires.

Adjacency constraints consider the location and arrangement of forest stands in management plans to improve the representation of forest ecosystems and their ecological processes. Some previous studies have shown that incorporating spatial constraints in forest management plans can enhance biodiversity conservation (e.g., Bettinger et al., 1997; Watson et al., 2018), carbon sequestration and timber production (e.g., Bixby et al., 2019; Deng et al., 2022). Given that, in our study, the model was not able to provide a solution for all management units in order to satisfy spatial constraints, it was not possible to measure the improvement in such values. Concerning both wildfire risk and harvest adjacency constraints in forest management planning, and taking simulated fires into account, Troncoso et al. (2016) concluded that the inclusion of a threat index in the objective function produces timber harvest schedules that are better in terms of total volume harvested than those produced using an objective function that does not include potential fire loss measures.

In this problem, there was a substantial number of minimal unfeasible clusters with slightly more than 50 hectares. Alternative methods of using minimal unfeasible clusters and barrier clusters may be explored to determine their impact on solutions. Additionally, adjacency constraints may further allow to address species diversity in stands of the same minimal unfeasible clusters and growth development stages.

The solutions presented in this research were generated considering a single objective function. Another possibility might be to consider a Pareto frontier multi-objective optimization approach in order to assist forest stakeholders in a posteriori trade-off analysis (Marques et al., 2021a,b). Different weights or priorities to each objective, based on a priori information, could be used. Nevertheless, as argued by Borges et al. (2017), Pareto frontier approaches may be more effective as they do not require the elicitation of preferences and weights before stakeholders are aware of the tradeoffs between ecosystem services.

5. Conclusion

This research set out to develop a spatial optimization mixed integer programming model through the simultaneous introduction of a fire resistance index and clearcut area constraints. The former addressed concerns about the vulnerability of the forested landscape to wildfires in each management period. The latter avoids openings that can be harmful to neighboring stands due to various factors such as erosion and wind. Concerns related to volume even flow over the planning horizon were also addressed.

The results give insights into the importance of prevention wildfire measures, namely, shrub cleanings, to reach a more resilient forest. These are costly and have a substantial impact on income. The extreme scenarios presented in this study may be balanced by including constraints that limit the effort supported by decision-makers, namely, by imposing minimum values for economic indicators objectives.

Future studies will analyze the effect on solutions of considering alternative ways of using minimal unfeasible clusters as well as barrier clusters. It will further explore the potential of integrating this approach with Pareto frontier methods to support a posteriori trade-off analysis by forest stakeholders.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The presented study was partially supported by National Funding from FCT—Fundação para a Ciência e a Tecnologia, under the projects: UIDB/00239/2020, UIDB/04561/2020, and UIDB/04674/2020. Open access publication was funded by the project UIDB/00239/2020 of the Forest Research Centre (CEF) and LA/P/0092/2020 of Associated Laboratory TERRA. This study also has received funding from the projects H2020-MSCA-RISE-2020/101007950, with the title DecisionES—Decision Support for the Supply of Ecosystem Services under Global Change, funded by the Marie Curie International Staff Exchange Scheme, H2020-LC-GD-2020-3/101037419, with the title FIRE-RES—Innovative technologies and socio-ecological-economic solutions for fire resilient territories in Europe, funded by the EU Horizon 2020—Research and Innovation Framework Programme. The study was also partially supported by national funds through the FCT—Fundação para a Ciência e a Tecnologia, I.P. in the scope of Norma Transitória—DL57/2016/CP1382/CT15 and also received funding from the project MODFIRE—A multiple criteria approach to integrate wildfire behavior in forest management planning with the reference PCIF/MOS/0217/2017.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Acuna, M. A., Palma, C. D., Cui, W., Martell, D. L., and Weintraub, A. (2010). Integrated spatial fire and forest management planning. Can. J. For. Res. 40, 2370–2383. doi: 10.1139/X10-151

CrossRef Full Text | Google Scholar

Almeida, A. M., Tomé, J., and Tomé, M. (2010). Development of a system to predict the evolution of individual tree mature cork caliber over time. For. Ecol. Manag, 260, 1303–1314. doi: 10.1016/j.foreco.2010.07.017

CrossRef Full Text | Google Scholar

Bennet, E. M., and Balvanera, P. (2007). The future of production systems in a globalized world. Front. Ecol. Environ. 5, 191–198. doi: 10.1890/1540-9295(2007)5191:TFOPSI2.0.CO

CrossRef Full Text | Google Scholar

Bettinger, P. (2010). An overview of methods for incorporating wildfires into forest planning models. Int. J. Math. Comput. For. Nat. Resour. Sci. 2, 43–52. Available online at: http://mcfns.net/index.php/Journal/article/view/MCFNS.2-43/MCFNS_2%3A43-52

Google Scholar

Bettinger, P., Sessions, J., and Boston, K. (1997). Using Tabu search to schedule timber harvests subject to spatial wildlife goals for big game. Ecol. Modell. 94, 111–123. doi: 10.1016/S0304-3800(96)00007-5

CrossRef Full Text | Google Scholar

Bixby, J. J., Hoganson, H. M., and Wei, Y. (2019). Potential gains from spatially-explicit coordinated planning between two large public ownerships in Minnesota. For. Ecosyst. 6, 11. doi: 10.1186/s40663-019-0176-0

CrossRef Full Text | Google Scholar

Borges, J. G., and Hoganson, H. M. (2000). Structuring a landscape by forestland classification and harvest scheduling spatial constraints. For. Ecol. Manage. 130, 269–275. doi: 10.1016/S0378-1127(99)00180-2

CrossRef Full Text | Google Scholar

Borges, J. G., Marques, S., Garcia-Gonzalo, J., Rahman, A. U., Bushenkov, V., Sottomayor, M., et al. (2017). A multiple criteria approach for negotiating ecosystem services supply targets and forest owners' programs. For. Sci. 63, 49–61. doi: 10.5849/FS-2016-035

CrossRef Full Text | Google Scholar

Borges, P., Martins, I., Bergseng, E., Eid, T., and Gobakken, T. (2016). Effects of site productivity on forest harvest scheduling subject to green-up and maximum area restrictions. Scand. J. For. Res. 31, 507–516. doi: 10.1080/02827581.2015.1089931

CrossRef Full Text | Google Scholar

Botequim, B., Bugalho, M., Rodrigues, A. R., Marques, S., Marto, M., Borges, J. G., et al. (2021). Combining tree species composition and understory coverage indicators and optimization techniques to address concerns with landscape-level biodiversity. Land 10, 126. doi: 10.3390/land10020126

CrossRef Full Text | Google Scholar

Botequim, B., Garcia-Gonzalo, J., Marques, S., Ricardo, A., Borges, J., Tomé, M., et al. (2013). Developing wildfire risk probability models for Eucalyptus globulus stands in Portugal. iForest 16, 217–227. doi: 10.3832/ifor0821-006

CrossRef Full Text | Google Scholar

Botequim, B., Zubizarreta-Gerendiain, A., Garcia-Gonzalo, J., Silva, A., Marques, S., Fernandes, P. M., et al. (2015). A model of shrub biomass accumulation as a tool to support management of Portuguese forests. iForest 8, 114–125. doi: 10.3832/ifor0931-008

CrossRef Full Text | Google Scholar

Bowman, D. M., Balch, J. K., Artaxo, P., Bond, W. J., Cochrane, M. A., D'Antonio, C. M., et al. (2009). Fire in the earth system. Science 324, 481–484. doi: 10.1126/science.1163886

PubMed Abstract | CrossRef Full Text | Google Scholar

Brockerhoff, E. G., Barbaro, L., Castagneyrol, B., Forrester, D. I., Gardiner, B., Gonzalez-Olabarria, J. R., et al. (2017). Forest biodiversity, ecosystem functioning and the provision of ecosystem services. Biodivers. Conserv. 26, 3005–3035. doi: 10.1007/s10531-017-1453-2

CrossRef Full Text | Google Scholar

Chung, W. (2015). Optimizing fuel treatments to reduce wildland fire risk. Curr. For. Rep. 1, 44–51. doi: 10.1007/s40725-015-0005-9

CrossRef Full Text | Google Scholar

Constantino, M., and Martins, I. (2018). Branch-and-cut for the forest harvest scheduling subject to clearcut and core area constraints. Eur. J. Oper. Res. 265, 723–734. doi: 10.1016/j.ejor.2017.07.060

CrossRef Full Text | Google Scholar

Constantino, M., Martins, I., and Borges, J. G. (2008). A new mixed-integer programming model for harvest scheduling subject to maximum area restrictions. Oper. Res. 56, 542–551. doi: 10.1287/opre.1070.0472

CrossRef Full Text | Google Scholar

Deng, W., Xiang, W., Ouyang, S., Hu, Y., Chen, L., Zeng, Y., et al. (2022). Spatially explicit optimization of the forest management tradeoff between timber production and carbon sequestration. Ecol. Indic. 142, 109193. doi: 10.1016/j.ecolind.2022.109193

CrossRef Full Text | Google Scholar

Ferreira, L., Constantino, M., Borges, J. G., and Garcia-Gonzalo, J. (2015). Addressing wildfire risk in a landscape-level scheduling model. An application in Portugal. For. Sci. 61, 266–277. doi: 10.5849/forsci.13-104

CrossRef Full Text | Google Scholar

Garcia-Gonzalo, J., Zubizarreta-Gerendiain, A., Ricardo, A., Marques, S., Botequim, B., Borges, J. G., et al. (2012). Modelling wildfire risk in pure and mixed forest stands in Portugal. German J. For. Res. 183, 238–248. Available online at: http://hdl.handle.net/10174/9780

Google Scholar

Gómez-García, E., Crecente-Campo, F., Anta, M. B., and Diéguez-Aranda, U. (2015). A disaggregated dynamic model for predicting volume, biomass and carbon stocks in even-aged pedunculate oak stands in Galicia (NW Spain). Eur. J. For. Res. 134, 569–583. doi: 10.1007/s10342-015-0873-3

CrossRef Full Text | Google Scholar

González, J. R., Palahi, M., and Pukkala, T. (2005). Integrating fire risk considerations in forest management planning in Spain - a landscape level perspective. Landsc. Ecol. 20, 957–970. doi: 10.1007/s10980-005-5388-8

CrossRef Full Text | Google Scholar

González-Olabarria, J. R., and Pukkala, T. (2011). Integrating fire risk considerations in landscape-level forest planning. For. Ecol. Manage. 261, 278–287. doi: 10.1016/j.foreco.2010.10.017

CrossRef Full Text | Google Scholar

Goycoolea, M., Murray, A., Vielma, J., and Weintraub, A. (2009). Evaluating approaches for solving the area restriction model in harvest scheduling. For. Sci. 55, 149–165. Available online at: https://academic.oup.com/forestscience/article/55/2/149/4604425

Google Scholar

Halofsky, J. E., Peterson, D. L., and Harvey, B. J. (2020). Changing wildfire, changing forests: the effects of climate change on fire regimes and vegetation in the Pacific Northwest, USA. Fire Ecol. 16, 4. doi: 10.1186/s42408-019-0062-8

CrossRef Full Text | Google Scholar

Hof, J. G., and Joyce, L. A. (1992). Spatial optimization for wildlife and timber in managed forest ecosystems. For. Sci. 38, 489–508.

Google Scholar

Kim, Y.-H., Bettinger, P., and Finney, M. A. (2009). Spatial optimization of the pattern of fuel management activities and subsequent effects on simulated wildfires. Eur. J. Oper. Res. 197, 253–65. doi: 10.1016/j.ejor.2008.05.025

CrossRef Full Text | Google Scholar

Kuuluvainen, T. (2009). Forest management and biodiversity conservation based on natural ecosystem dynamics in Northern Europe: the complexity challenge. Ambio 38, 309–315. doi: 10.1579/08-A-490.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, T., Xiong, K., Yang, S., Liu, H., Qin, Y., Wang, Z., et al. (2022). Progress and prospects of forest ecological asset research. Sustainability 14, 395. doi: 10.3390/su14010395

CrossRef Full Text | Google Scholar

Lockwood, C., and Moore, T. (1993). Harvest scheduling with spatial constraints: a simulated annealing approach. Can. J. For. Res. 23, 468–478. doi: 10.1139/x93-065

CrossRef Full Text | Google Scholar

Malchow-Moller, N., Strange, N., and Thorsen, B. J. (2004). Real-options aspects of adjacency constraints. For. Policy Econ. 6, 261–270. doi: 10.1016/j.forpol.2004.03.002

CrossRef Full Text | Google Scholar

Marques, M., Reynolds, K. M., Marto, M., Lakicevic, M., Caldas, C., Murphy, P. J., et al. (2021a). Multicriteria decision analysis and group decision-making to select stand-level forest management models and support landscape-level collaborative planning. Forests 12, 399. doi: 10.3390/f12040399

CrossRef Full Text | Google Scholar

Marques, S., Borges, J. G., Garcia-Gonzalo, J., Moreira, F., Carreiras, J., Oliveira, M., et al. (2011). Characterization of wildfires in Portugal. Eur J Forest Res 130, 775–784. doi: 10.1007/s10342-010-0470-4

CrossRef Full Text | Google Scholar

Marques, S., Botequim, B., Garcia-Gonzalo, J., Borges, J. G., Tomé, M., and Oliveira, M. (2012). Assessing wildfire risk probability in Pinus pinaster Ait. stands in Portugal. For. Syst. 21, 111–120. doi: 10.5424/fs/2112211-11374

CrossRef Full Text | Google Scholar

Marques, S., Bushenkov, V., Lotov, A., and Borges, G. J. (2021b). Building pareto frontiers for ecosystem services tradeoff analysis in forest management planning integer programs. Forests 12, 1244. doi: 10.3390/f12091244

CrossRef Full Text | Google Scholar

Marques, S., Marto, M., Bushenkov, V., McDill, M., and Borges, J. (2017). Addressing wildfire risk in forest management planning with multiple criteria decision making methods. Sustainability 9, 298. doi: 10.3390/su9020298

CrossRef Full Text | Google Scholar

Martins, I., Constantino, M., and Borges, J. G. (1999). “Forest management models with spatial structure constraints,” in Working paper2/1999, Centro de Investigação Operacional, Faculdade de Ciências, Lisbon, Portugal.

Google Scholar

Martins, I., Marques, S., Marques, M., and Marto, M. (2022). Optimizing harvest scheduling with clearcut size constraints in long planning: a case study. (under review).

Google Scholar

Martins, I., Ye, M., Constantino, M., Fonseca, M. C., and Cadima, J. (2014). Modelling target volume flows in forest harvest scheduling subject to maximum area restrictions. Top 22, 343–362. doi: 10.1007/s11750-012-0260-x

CrossRef Full Text | Google Scholar

Marto, M., Reynolds, K. M., Borges, J. G., Bushenkov, V., and Marques, S. (2018). Combining decision support approaches for optimizing the selection of bundles of ecosystem services. Forests 9, 438. doi: 10.3390/f9070438

CrossRef Full Text | Google Scholar

McDermott, C., Cashore, B., and Kanowski, P. (2010). Global Environmental Forest Policies: An International Comparison, 1st edn. Routledge. doi: 10.4324/9781849774925

CrossRef Full Text | Google Scholar

McDill, M., Tóth, S., Rachel St. John, R., Braze, J., and Stephanie A. Rebain, S. (2016). Comparing model I and model II formulations of spatially explicit harvest scheduling models with maximum area restrictions. For. Sci. 62, 28–37. doi: 10.5849/forsci.14-179

CrossRef Full Text | Google Scholar

McDill, M. E., Rebain, S. A., and Braze, J. (2002). Harvest scheduling with area-based adjacency constraints. For. Sci. 48, 631–642. doi: 10.1093/forestscience/48.4.631

CrossRef Full Text | Google Scholar

Murray, A. (1999). Spatial restrictions in harvest scheduling. For. Sci. 45, 45–52. doi: 10.1093/forestscience/45.1.45

CrossRef Full Text | Google Scholar

Murray, A. T., and Weintraub, A. (2002). Scale and unit specification influences in harvest scheduling with maximum area restrictions. Fo. Sci. 48, 779–789. doi: 10.1093/forestscience/48.4.779

CrossRef Full Text | Google Scholar

Nelson, J. D., and Brodie, J. D. (1990). Comparison of a random search algorithm and mixed integer programming for solving area-based forest plans. Can. J. For. Res. 20, 934–942. doi: 10.1139/x90-126

CrossRef Full Text | Google Scholar

Nunes, L., Patrício, M., Tomé, J., and Tomé, M. (2011). Modeling dominant height growth of maritime pine in Portugal using GADA methodology with parameters depending on soil and climate variables. Ann. For. Sci. 68, 311–323. doi: 10.1007/s13595-011-0036-8

CrossRef Full Text | Google Scholar

Paulo, J. A., and Tomé, M. (2006). Equações para Estimação do Volume e Biomassa de Duas Espécies de Carvalhos: Quercus suber e Quercus ilex. Publicações GIMREF—RC1/2006; Departamento de Engenharia Florestal, Instituto Superior de Agronomia: Lisboa, Portugal, 2006, 21. Available online at: http://hdl.handle.net/10400.5/1730A (accessed January 10, 2023).

Google Scholar

Rodrigues, A. R., Marques, S., Botequim, B., Marto, M., and Borges, J. G. (2021). Forest management for optimizing soil protection: a landscape-level approach. For. Ecosyst. 8, 50. doi: 10.1186/s40663-021-00324-w

CrossRef Full Text | Google Scholar

Segura, M., Ray, D., and Maroto, C. (2014). Decision support systems for forest management: a comparative analysis and assessment. Comput. Electron. Agric. 101, 55–67. doi: 10.1016/j.compag.2013.12.005

CrossRef Full Text | Google Scholar

Stone, C., Hudak, A., and Morgan, P. (2008). “Forest harvest can increase subsequent forest fire severity,” in Proceedings of the Second International Symposium on Fire Economics, Planning, and Policy: A Global View. PSW-GTR-208 (A. González-Cabán Technical Coordinator). (Albany, CA: USDA Forest Service, Pacific Southwest Research Station), 525–534.

Google Scholar

Thompson, W. A., Vertinsky, I. I., Schreier, H, and Blackwell, B.A. (2000). Using forest fire modelling in multiple use forest management planning. For. Ecol. Manag. 134, 163–176. doi: 10.1016/S0378-1127(99)00255-8

CrossRef Full Text | Google Scholar

Tomé, M., Oliveira, T., and Soares, P. (2006). O modelo GLOBULUS 3.0 - dados e equações.” Available online at: https://www.repository.utl.pt/handle/10400.5/1760 (accessed March 15, 2022).

Google Scholar

Troncoso, J. J., Weintraub, A., and Martell, D. L. (2016). Development of a threat index to manage timber production on flammable forest landscapes subject to spatial harvest constraints. Inf. Syst. Oper. Res. 54, 262–281. doi: 10.1080/03155986.2016.1197543

CrossRef Full Text | Google Scholar

Watson, J. E. M., Evans, T., Venter, O., Williams, B., Tulloch, A., and Stewart, C. The exceptional value of intact forest ecosystems. Nat. Ecol. Evol. 2, 599–610. (2018). doi: 10.1038/s41559-018-0490-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Weintraub, A., and Murray, A. (2006). Review of combinatorial problems induced by spatial forest harvesting planning. Discret. Appl. Math. 154, 867–879. doi: 10.1016/j.dam.2005.05.025

CrossRef Full Text | Google Scholar

Yoshimoto, A., and Asante, P. (2018). A new optimization model for spatially constrained harvest scheduling under area restrictions through maximum flow problem. For. Sci. 64, 392–406. doi: 10.1093/forsci/fxy006

CrossRef Full Text | Google Scholar