Predicting the global fundamental climate niche of lodgepole pine for climate change adaptation

The widely used species-occurrence-based models that predict the realized climate niche of plants can be too restrictive and do not reflect among-population variation in assessing climate change impact and guiding assisted migration for adaptation to future climates. To mitigate this deficiency, this study built a fundamental climate niche model for lodgepole pine (Pinus contorta Dougl. ex Loud.) based on 20-year tree height from wide-ranging provenance trials as a case study. The model was built through comparisons and optimizations of two candidate models, universal response function (URF) and universal transfer function (UTF), with linear and linear mixed-effect forms, against varying sample sizes based on the comprehensive provenance trials. We found that URF and UTF models had similar performances, while URF models were more straightforward in identifying optimal provenances for planting sites. Linear mixed-effect models did not show clear advantages over linear models in our case but prevented including additional predictors, which are often critical. We selected the linear model of URF and predicted the fundamental climate niche of lodgepole pine on a global scale and revealed a great potential of using this species for climate change adaptation beyond its native distribution, representing a significant step in forest genecology. Our study presented a new approach for assisted migration at the species and the population levels to optimize adaptation and productivity under a changing climate.

1. Introduction

Climate change is causing a mismatch between the climate that trees are historically adapted to and the climate that the trees will experience in the future at both the species and population levels (Guisan and Thuiller, 2005; Aitken et al., 2008). Such a mismatch will result in maladaptation of the trees, thereby causing compromised health and forest ecosystems functions. Assessments of such impacts, assisted migration, and assisted gene-flow (Aitken and Whitlock, 2013) have been proposed to help trees in alignment with a changing climate (Hodgins and Moore, 2016), mitigating the negative impacts of climate change. Climate niche models (CNMs), often more broadly called species distribution models (SDMs), have been widely used to predict tree species’ climate niches and project their shift under future climate conditions. Such information has been used as a scientific basis for assessing the impact of climate change and developing forest adaptation strategies, including assisted migration. Most CNMs are species occurrence data-based correlative models and predict a species’ realized climate niche (Pearson and Dawson, 2003; Rehfeldt et al., 2006; Wang et al., 2016b).

Climate is often the dominant factor that defines a forest species distribution. In the context of a changing climate, it is assumed that other environmental conditions defining a species ecological niche continue to stay relatively stable. Thus a species’ climate niche, reflecting the climatic aspect of an ecological niche (Pearson and Dawson, 2003), is widely used for assessing climate change impact on forest trees. The realized climate niche of a species represents a set of climate conditions within which the species naturally occurs. It is affected by limiting factors, such as inter-species competition, interactions with other organisms, dispersal limitations, and human impact (Woodward and Williams, 1987; Morgenstern, 2011). When none of these limiting factors are present, the full range of the climate conditions that a species can occupy and use is defined as fundamental climate niche, which can be considered as the climate component of Hutchinson’s (1957) fundamental niche. Thus, a species’ realized climate niche does not reflect the species’ full range of potential habitat. Using a realized climate niche for assessing the impact of climate change and for assisted migration may be too restrictive or unnecessarily conservative, as trees may still survive outside its realized climate niche while still within its fundamental climate niche, and especially most of the factors limiting the realized climate niche do not apply in plantations (Gray et al., 2011). Therefore, by predicting the fundamental climate niche within which a species can survive, for ecologically or economically important species, can better assess climate change impact on forest’s health and survival. Knowing a species’ fundamental climate niche is also necessary to support assisted migration and genetic conservation (Pecchi et al., 2019). Furthermore, in order to optimize climate matching at the population level (Aitken and Whitlock, 2013), the among-population variation that reflects local adaptation within a species should also be considered to facilitate assisted gene-flow (DeMarche et al., 2019).

In provenance trials, populations are tested over a wide range of climatic conditions under controlled environments, so most of the factors limiting the realized climate niche are excluded and fundamental climate niche can be determined (Booth et al., 1988). Using provenance data, a climate-based population response function can be built based on the relationship between population’s growth and test sites’ climate conditions. A population response function can predict not only the population’s quantitative performance (or productivity) but also the range of climatic conditions within which the population can grow, which represents the fundamental climate niche of the population (Booth, 2017; Chakraborty et al., 2019). Integration of response functions of individual populations based on systematically designed comprehensive provenance trials provides the possibility to model the fundamental climate niche at the species level while reflecting the among-population variation.

The Illingworth (1978) lodgepole pine provenance trials is one of the most comprehensive common garden experiments. They comprise 60 test sites covering a wide range of climate conditions and 140 provenances spanning the entire species distribution. The universal response function (URF) developed by Wang et al. (2010) was based on the Illingworth provenance trials and integrated response functions of individual populations. It has the potential to predict the fundamental climate niche of the species. The URF is a multiple linear regression model, which uses both test site (environmental) and provenance (genetic) climate effects and their interactions to predict the performance of any population planted at any site. The potential of using the URF as a candidate model to predict the fundamental climate niche has been demonstrated in predicting the performance of Douglas-fir introduced to Europe (Chakraborty et al., 2015, 2019). By representing among-population genetic variation and predicting growth potential, URFs may provide more accurate and informative predictions of the climate niche and growth potential of a species than widely used CNMs when comprehensive provenance trials available. In addition, URFs can also be used for assisted migration at the population level (Aitken and Whitlock, 2013; DeMarche et al., 2019).

Provenance trials often have a small number of test sites, which limits the use of the URF. For provenance trials with limited number of test sites and inconsistent planting years, Leites et al. (2012) proposed a linear mixed-effect model. This model integrated individual transfer functions to predict populations’ response to climate transfer distance (climate transfer distance = climate of test site − climate of provenance) (Matyas, 1994). This mixed model includes population climate transfer distance, provenance climate, and their interactions as fixed effects, with test site and provenance as random effects. As the model can predict the performance of any population with any transfer distance (Leites et al., 2012), it also has the potential to predict the fundamental climate niche of a species. To distinguish their model from individual transfer functions, we refer to their model as a “universal transfer function” (UTF) in this study. In linear mixed-effect model, random effects take statistical correlation into account; they are capable of explaining data dependency and hierarchy (Gałecki and Burzykowski, 2013), displaying variation sources, and improving model prediction accuracy (Sáenz-Romero et al., 2017). Even though random effects cannot be used in prediction for new locations, their inclusion in a model is expected to improve the fixed effects’ coefficients (Faraway, 2016) and possibly result in improved prediction accuracy over a standard linear model (Weigel et al., 1991). Both the URF and UTF are based on linear and quadratic polynomial functions as the bell-shaped response to each climate variable fits well to the climate niche definition (Pearson and Dawson, 2003).

The lodgepole pine (Pinus contorta Dougl. ex Loud.) has probably the widest range of environmental tolerance of all conifers in Western North America. In its native range, it grows from the Pacific Coast to the Rocky Mountains from 64° N in Yukon Territory to 31° N in Baja California at elevations <3,900 m. Due to the lodgepole pine’s physiological characteristics, such as drought-tolerance, fire-dependence, and rapid juvenile growth (Murray, 1983), this species is important in delivering ecosystem services and provisioning services in Western North America. Economically, it has a key role in the pulp and lumber industries in British Columbia. Ecologically, it can protect the watersheds and provide habitats for many animal species. Outside of its native habitat, lodgepole pine has been successfully introduced to many temperate regions for commercial or conservation purposes (Richardson, 1998). The comprehensive provenance trials for the lodgepole pine in British Columbia provides ideal materials for comparisons between the URF and the UTF and build the fundamental CNM of this species. The global inventory derived from publications and research facilities, including the areas with a successful introduction, can be used to validate the predictions of a fundamental CNM. Thus, lodgepole pine is an ideal species for a case study to develop the fundamental climate niche of a forest tree species.

The objectives of this study were to: (1) compare model performances between the two candidate models URF and UTF; (2) evaluate the contribution of random effects to model prediction accuracy with different sample sizes; and (3) build a final model to predict the spatial distribution of fundamental climate niche of lodgepole pine on a global range using local provenances (i.e., local populations) and optimal provenances that have the highest growth potential for each test site under the current and the future climates.

2. Materials and methods

2.1. Vegetation data

The Illingworth provenance trials were established by the British Columbia Ministry of Forests, Canada, in 1974. Seeds were collected from 140 populations that range from southern California (34° N latitude) to central Yukon (64° N latitude) (Supplementary Figure 1A). Trees of these populations were planted at 60 test sites throughout the interior of the province of British Columbia using an unbalanced experimental design (Supplementary Figure 1B), with most populations planted at 30–40 of the total test sites (Illingworth, 1978; Wang et al., 2010; McLane et al., 2011). Both population and test sites were selected using a stratified random sampling method. Within each site, a randomized complete block design was used, with one nine-tree square plot of each provenance planted in each of two blocks at 3 × 3 m spacing. The provenance trials were measured for height at 5, 10, 15, 20, and 32 years old. Due to the damage by mountain pine beetle, the number of test sites was substantially reduced before the 32-year-old measurement (from 57 to 42). Thus, we used the 20-year height as a proxy for this species’ growth potential and fitness. After excluding missing values, we used 4,583 observations from 138 populations and 57 test sites as our full data. Each observation in our data represented a population’s average height at a specific test site.

The existing worldwide occurrence data of lodgepole pine were used to validate models’ prediction performance. They were collected from recorded public observations from the Global Biodiversity Information Facility (GBIF.org, 2021), publications about introducing lodgepole pine test trials that were mostly done in Europe and Asia (Ackzell et al., 1994; Elfving et al., 2001; Tilki and Ugurlu, 2008; Fedorkov and Gutiy, 2017), and inventory of lodgepole pine as invasive species that is concentrated in Southern Hemisphere (Brockerhoff and Kay, 1998; Peña et al., 2008).

2.2. Climate data

Climate variables for the test sites and provenances were generated from ClimateNA (version 6.40) (Wang et al., 2016a), a software package that uses a combination of bilinear interpolation and dynamic local elevation adjustment approaches to downscale climate data from various sources into scale-free point data. It also uses the scale-free data as a baseline to downscale historical and future climate variables for individual years and period between 1901 and 2100. The package includes three Representative Concentration Pathways (RCP 2.6, RCP 4.5, and RCP 8.5) from 15 general circulation models (GCMs) of the Coupled Model Intercomparison Project (CMIP5) included in the IPCC Fifth Assessment Report (Pachauri and Mayer, 2015). All 23 available annual climate variables for the reference period 1961–1990 were used for model fitting to match the provenance period (Supplementary Table 1). For spatial predictions of the fundamental climate niche of lodgepole pine within its native range (Western North America) for the current climate (1961–1990 normal), we generated climate variables in raster format at the spatial resolution of 4 × 4 km. For the current climate (1961–1990 normal) on the global scale, we generated climate variables in raster format at the spatial resolution of 10 × 10 km, covering the entire world using the algorithms in ClimateNA. The ensembles of 15 GCMs included in ClimateNA for greenhouse gas emission scenarios RCP 4.5 at the same spatial resolution was used for projecting the distribution of fundamental climate niche for the future climate in 2041–2070 (as referred to as the 2050s). The spatial resolution of 10 × 10 km was selected for global prediction to balance between the map details and file size.

2.3. Statistical analysis

All statistical analyses were conducted using RStudio (R Core Team, 2020), with package “lme4” was used for linear mixed-effect model building (Bates et al., 2014), package “blockCV” used for spatial block cross-validation (Valavi et al., 2018).

2.3.1. Universal response functions

The linear model of URF is expressed as:

$Y_{ij}=b_0+b_1{X}_i+b_2{X}_i^2+b_3{X}_j+b_4{X}_j^2+b_5{X}_i^{\text{k}}{X}_j^{\text{k}}+e_{ij}(1)$

where Y_ij is the observed 20-year height of the provenance i at the test site j; X_i is one or more climate variables of the provenance i; X_j is one or more climate variables of the test site j; $X_i^{\text{k}}{X}_j^{\text{k}}$ are the first and second order interactions between the X_i and X_j, where k equals 1 or 2; e_ij is the residual; and b₀–b₅ are the intercept and coefficients to be determined.

The linear mixed-effect model of URF (URF_m) is:

$Y_{ij}=(b_0+r_{1i}+r_{2j})+(b_1+r_{3j}+r_{4\text{i}})X_j+b_2{X}_j^2+(b_3+r_{5j}+r_{6i})X_i$

$+b_4{X}_i^2+b_5{X}_i{X}_j+e_{ij}(2)$

where r₁–r₆ are the random effects with other terms remaining the same as in Equation 1. Random effects adjust the model’s intercept and the various slopes for the fixed effects.

2.3.2. Universal transfer functions

The linear model of the UTF included provenance climate and climate transfer distance (climate transfer distance = climate of test site − climate of provenance) as predictors. It is written as:

$Y_{id}=b_0+b_1{X}_{\text{i}}+b_2{X}_{\text{i}}^2+b_3{X}_{id}+b_4{X}_{id}^2+b_5{X}_i{X}_{id}$

$+b_5{X}_i^{\text{k}}{X}_{id}^{\text{k}}+e_{id}(3)$

where Y_id is the observed 20-year height of the provenance i with the transfer distance d; X_i is one or more climate variables of the provenance i; X_id is the climate transfer distance of the population i; $X_i^{\text{k}}{X}_{id}^{\text{k}}$ are the first and second order interactions between the X_i and X_id, where k equals to 1 or 2; e_id is the residual; and b₀– b₅ are the intercept and coefficients to be determined.

The linear mixed-effect model of UTF (UTF_m) is:

$Y_{id}=(b_0+r_{1i}+r_{2id})+(b_1+r_{3id}+r_{4\text{i}})X_{id}+b_2{X}_{id}^2$

$+(b_3+r_{5id}+r_{6i})X_i+b_4{X}_i^2+b_5{X}_i{X}_{id}+e_{id}(4)$

where X_i X_id is the interaction between X_i and X_id; r₁–r₆ are the random effects. All other terms remaining the same as in Equation 3.

2.3.3. Candidate models’ selection and validation

The URF’s original model is a standard linear model with only fixed effects, while the UTF is a linear mixed-effect model with both fixed and random effects. We built URFs and UTFs in both standard linear models and linear mixed-effect models for thorough comparisons. We first built models with one climate variable, namely simple regression models, as was done for the UTF in the original report (Leites et al., 2012), then added more climate variables to improve the model-fit when appropriate (i.e., when additional variables were significant) and possible (i.e., linear mixed-effect models were able to converge). The selection of the first climate variable was based on each variables’ importance on explaining variance for the 20-year tree height, which was determined by each climate variable’s R² independently. The selection of the subsequent climate variable was based on how well the simple regression model’s R² can be improved.

All linear mixed-effect models were fitted by maximum likelihood (method = ML), with fixed effects identical to their paralleled linear model. We included population-level and study site-level random effects following Leites et al. (2012). However, our attempt at using the same random effect structure as the original model failed to converge. Thus, we adjusted random terms for each linear mixed-effect model to converge and determined final random terms based on the combination of AIC, Loglik, and R² values. AIC and Loglik were used to consider models’ marginal likelihood, and R² was used for evaluating models’ capability in explaining variance for the response variable.

There were several possible forms for each model type, and the final candidate model for each model type was determined based on R² and AIC values through stepwise model selection process that started with considering all linear and quadratic interactions between each climatic variable for test site and provenance. The terms that were not significant (p-value < 0.05) were eliminated step-by-step.

To compare the prediction accuracy for extrapolation of the linear and linear mixed-effect models, fivefold spatial block cross-validations (sbCV) were performed for each final candidate model. In order to better correspond to the extent of the Illingworth provenance trials of lodgepole pine, 14 blocks were created, and each block’s size was 300 km × 300 km. These blocks were assigned randomly to the training and testing folds. Due to the unbalance spatial distribution of test sites across British Columbia, the sbCV was repeated ten times to reduce the bias. Prediction errors (i.e., RMSE) and R² values resulted from the sbCV were averaged for each model as the metrics (Tables 1, 2).

TABLE 1

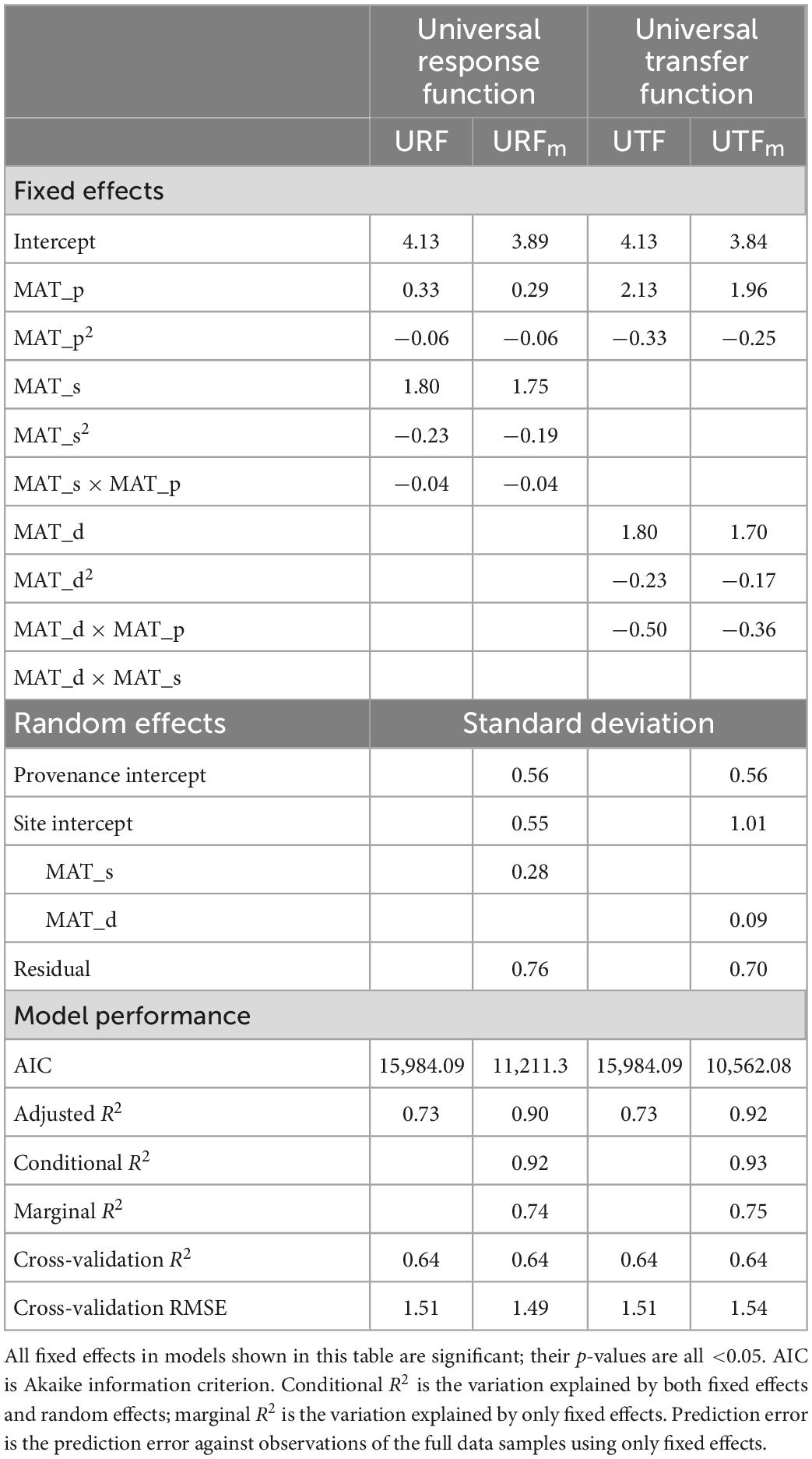
Table 1. Parameter estimates and model performance statistics for universal response function (URF), universal transfer functions (UTF), and their mixed-effect models (URF_m and UTF_m) with a single climate variable, mean annual temperature for test site (MAT_s), provenance (MAT_p), and transfer distance (MAT_d = MAT_s − MAT_p).

TABLE 2

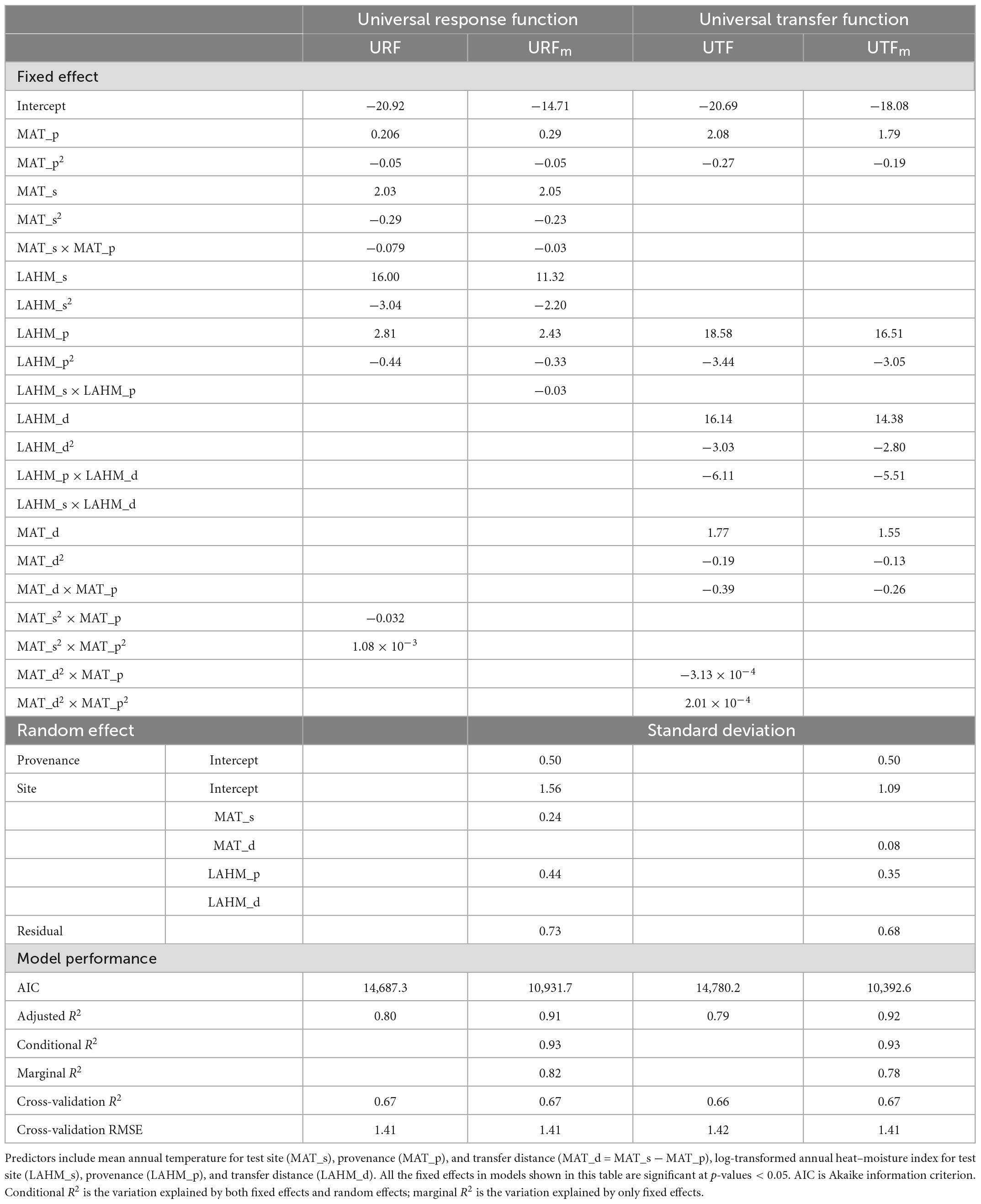
Table 2. Parameter estimates and model performance statistics for multiple regression universal response function (URF), universal transfer functions (UTF), and their mixed-effect models (URF_m and UTF_pdm).

2.3.4. Testing model effectiveness with varying sample sizes

In order to test model effectiveness with small sample sizes, we also built URFs and UTFs in both linear and linear mixed-effect models with varying sample sizes through a series of subsets of the full dataset to predict the full dataset against the observations for validation. The size of the subset samples varied from 14 (10%) to 138 (100%) for the number of provenances, from 6 (10%) to 57 (100%) for test sites. The test was repeated 50 times, and the averages and ranges of prediction error were compared. These comparisons were performed only with single variable models since the linear mixed-effect models could not converge with many of the subset samples for multiple regression models.

2.4. Predictions of the fundamental climate niche

A final model for the prediction of the fundamental climate niche was selected based on the model comparisons between URFs and UTFs, linear and linear mixed-effect models, and simple regression and multiple regression models. We predicted the fundamental climate niche based on 20-year tree height. Our rationale was that trees must be able to achieve a certain level of growth for an environment to be considered within the fundamental climate niche. As lodgepole pine is a forest tree species, we arbitrarily defined the areas with predicted tree height greater than three meters as being considered within the fundamental climate niche of the species and the areas with predicted tree height greater than five meters as productive areas.

The current spatial distribution of the fundamental climate niche of lodgepole pine was predicted with the climate variables in a raster format covering the entire world for the current normal period 1961–1990. We projected the spatial distribution of fundamental climate niche using both local and optimal provenances for the future period 2050s based on the climate change scenarios RCP 4.5, where optimal provenances were identified through partial derivatives of climate variables at provenance following Wang et al. (2010) steps. Changes in 20-year height growth potential from the current to the 2050s were also calculated. As the fundamental climate niche may be distributed far beyond its current distribution, the local provenances here referred to the provenances from a climate that matched the current climate within the species distribution rather than geographically local provenances.

3. Results

3.1. Simple regression models

Of all the 23 annual climate variables tested, mean annual temperature (MAT) was found to be the most important variable for building both URFs and UTFs according to the importance analysis of annual climate variables (Supplementary Table 1). Thus, mean annual temperature for test site (MAT_s) and provenance (MAT_p) were used to build the URFs. For UTFs, MAT_p, and population transfer distance in mean annual temperature (MAT_d) were used to build the UTFs.

The linear models (URF and the UTF) showed the same prediction accuracy across all metrics (R², cross-validation R², and cross-validation RMSE) despite using different predictors (Table 1). However, the inclusion of the interaction term in UTF increased the R² from 0.66 to 0.73, but in URF, the interaction term only increased R² from 0.72 to 0.73, indicating that the inclusion of the interaction term in the UTF model was more critical (10.6% in terms of R² value) than that in the URF model (0.9%).

All the linear mixed-effect models (URF_m and UTF_m) had a better fit than their corresponding linear models, with a larger adjusted R² (by about 23%) (Table 1) due to the contributions of random effects in the mixed models. The ability of random effects to improve model accuracy was also noticeable in mixed models’ conditional R² and marginal R² (Table 1). However, all linear models and linear mixed-effect models had the same cross-validation R² and similar cross-validation RMSE values. The linear models’ cross-validation RMSE values are slightly lower than UTF_m but slightly higher than URF_m, which indicated that random effects did not improve model prediction accuracy in cross-validation.

Despite having the same (or almost the same for the mixed models) performances between the URFs and UTFs tested, the response surfaces of URFs and UTFs represent different meanings as they used different predictors. Using the linear models of URF and UTF as an example shown in Figure 1, the URF had explicit test site climate (MAT_s) and provenance climate (MAT_p) as predictors, while the UTF did not have an explicit test site climate.

FIGURE 1

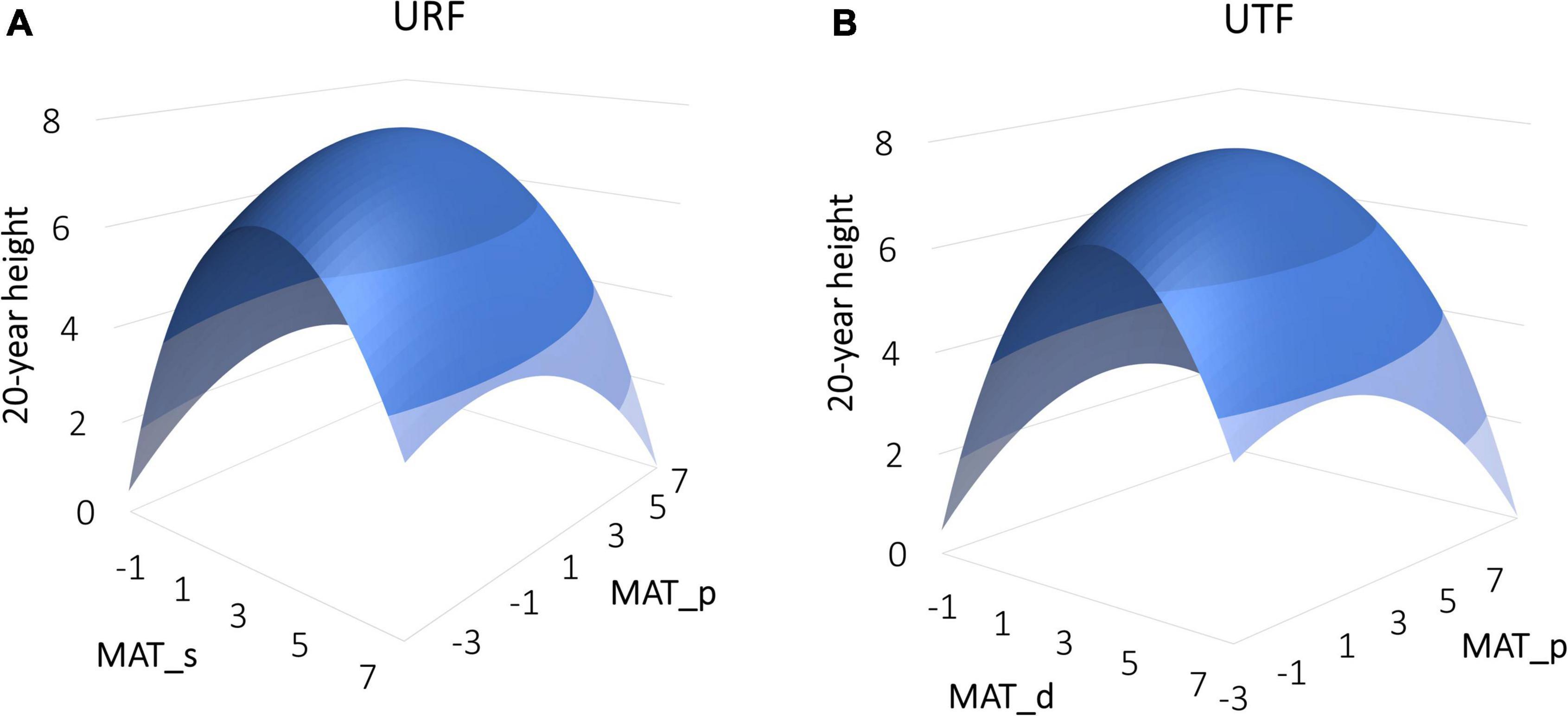
Figure 1. Response surfaces of 20-year tree height of lodgepole pine to climate predicted by a simple regression universal response function (URF) (A) and universal transfer function (UTF) (B). The URF is fitted with mean annual temperature for test site (MAT_s) and provenance (MAT_p), while the UTF is fitted with climate transfer distance (MAT_d = MAT_s – MAT_p) and provenance (MAT_p).

3.2. Simple regression models with varying sample sizes

Prediction errors were high with a large variation across the 50 repeated runs when sample sizes were small (number of test sites <20 or number of populations <50) (Figure 2). Model performances were improved and stabilized with increased sample size for all models, reaching the lowest prediction error at the sample size of 30 test sites and 80 populations. Although the linear mixed-effect models of URF (URF_m) and UTF (UTF_m) showed slightly lower prediction errors when the sample sizes were very small, they did not show clear advantages in predictions of the full dataset compared to their linear counterparts.

FIGURE 2

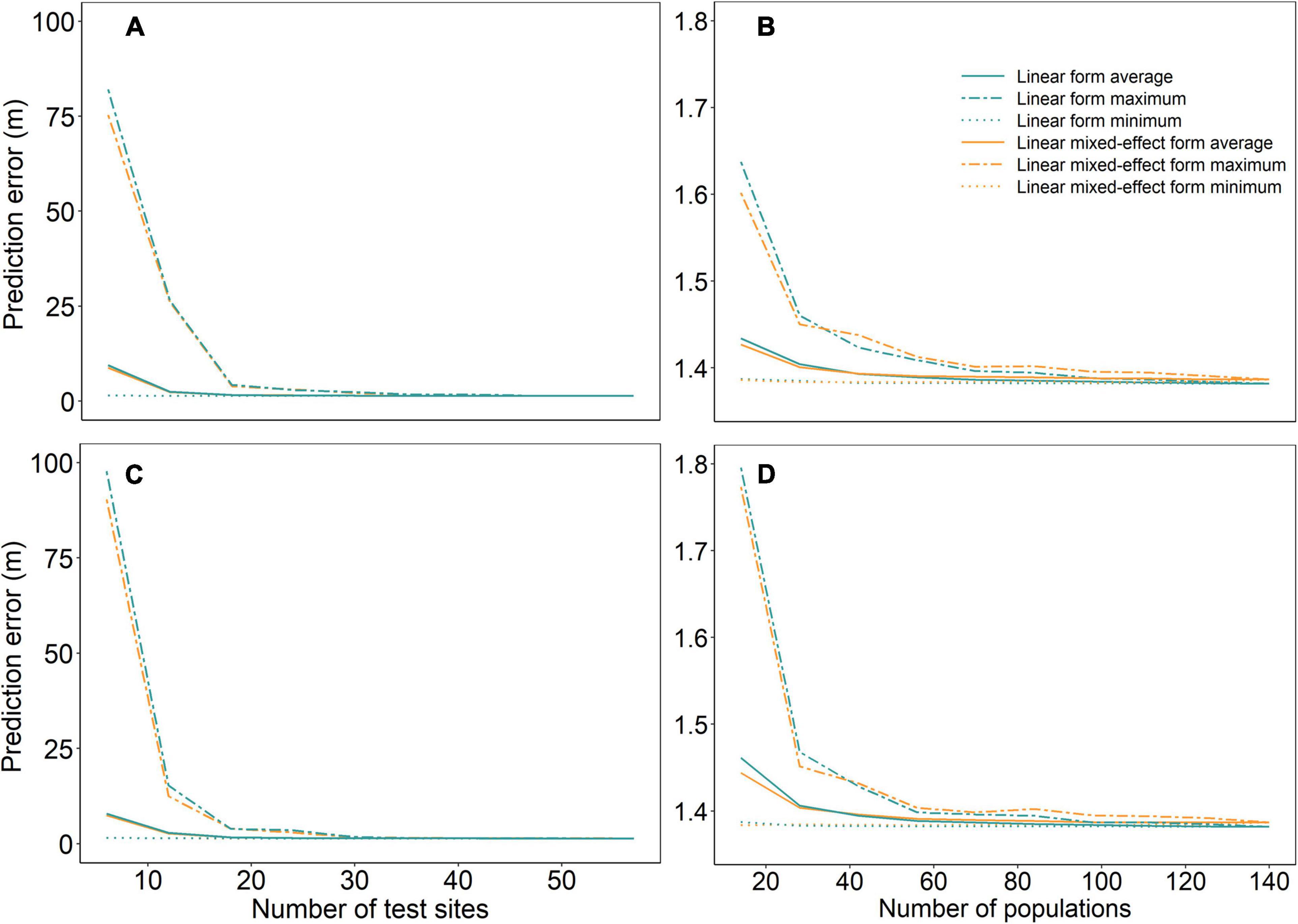
Figure 2. Prediction errors of linear and linear mixed-effect URFs (A,B) and UTFs (C,D) with varying numbers of test sites and populations. Panels (A,C) are for a varying number of test sites, and panels (B,D) for a varying number of populations. The dash line, solid line, and dotted line represent maximum, mean, and minimum values of prediction errors, respectively, resulting from 50 repeated runs with bootstrap samples for each sample size.

3.3. Multiple regression models

The log-transformed annual heat-moisture index [LAHM = log (MAT + 10)/(MAP/1,000)] was found to be the second most important climate variable for both URFs and UTFs. As shown in Tables 1, 2, all models with the climate variables MAT and LAHM showed improved performances over their corresponding single variable models. R² values increased from 0.73 to 0.80 for the linear models and from a range of 0.75–0.78 to 0.78–0.82 for the marginal R² values of the mixed models. There was no change in the conditional R² values of the mixed models.

Similar to single variable models, all linear models had lower R² than their corresponding linear mixed-effect models. All models have similar cross-validation R² and cross-validation RMSE values, except that URF_m’s cross-validation RMSE is about 9% higher than the rest.

3.4. The final model

For the model selection, we first dropped the linear mixed-effect models as they showed no clear advantage in model predictions but introduced a serious challenge in model-fitting. Between the linear URF and UTF, with the same performance, we chose the URF because of its explicit use of site and provenance climates. The multiple regression URF was then selected as the final URF (fURF) (Table 2). The fURF explained 80% of the total variation in 20-year tree height among test sites and provenances.

Compared to the simple regression model, the fURF not only improved model prediction accuracy evaluated by cross-validation (Tables 1, 2) but also made the predicted fundamental climate niche more realistic based on its spatial pattern (Figure 3). For the spatial distribution of 20-year tree height predicted by the URF with MAT only, the most productive areas were located in southern Alberta and Saskatchewan, which was clearly unrealistic and misleading. In contrast, the productive areas in the spatial distribution of 20-year tree height predicted by the final multiple regression model matched well with our expectations.

FIGURE 3

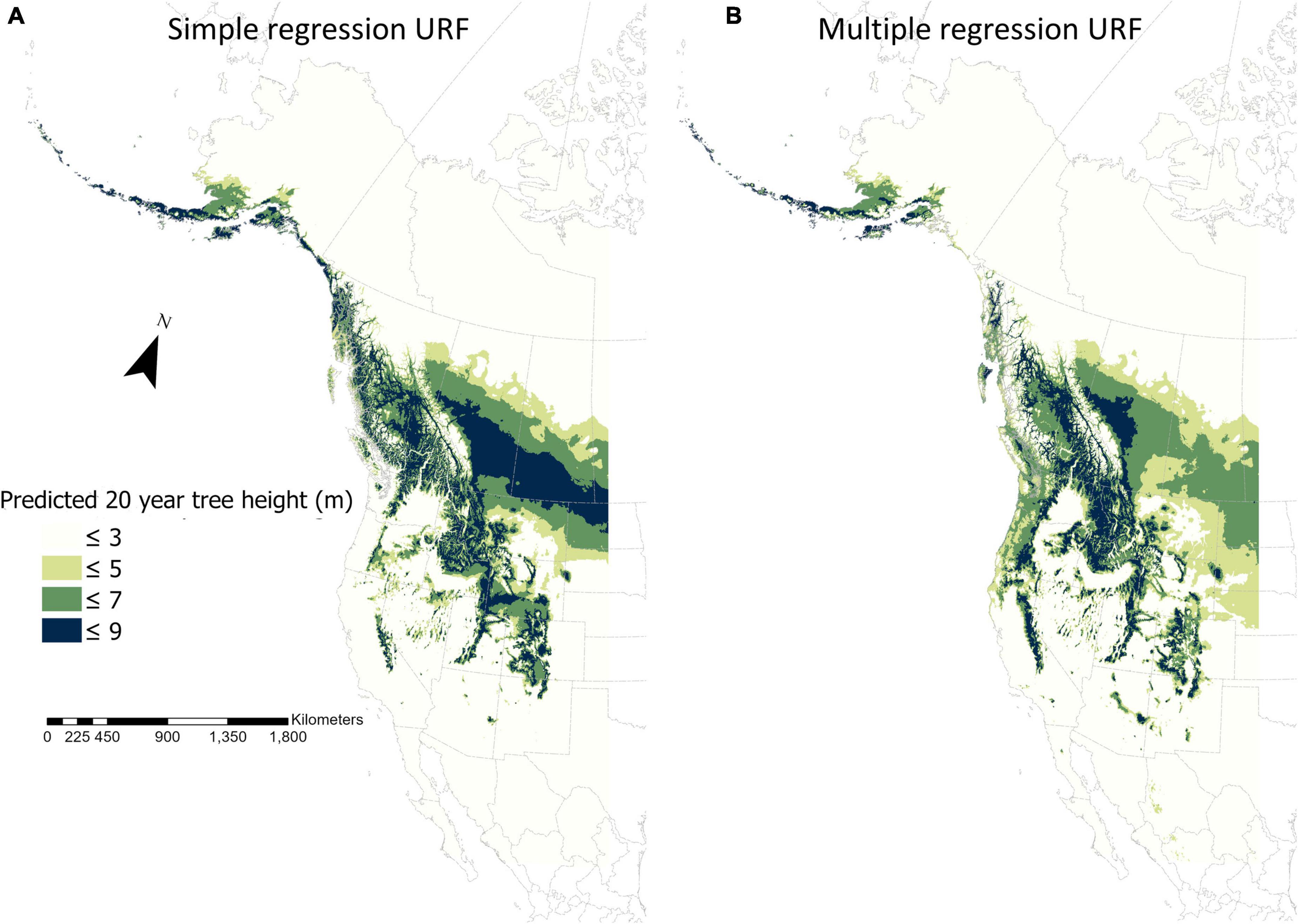
Figure 3. Spatial distributions of the fundamental climate niche of lodgepole pine (Pinus contorta) in Western North America in current climate predicted by a simple regression universal response function (A) and the final universal response function with multiple variables (B). The spatial resolution is 4 × 4 km. The climate variables for the simple regression and the final universal response functions are listed in column of “URF” in Table 1 and column “URF” in Table 2, respectively.

3.5. Predictions of spatial distributions of the fundamental climate niche for the current and the future climates

The fundamental climate niche predicted using the fURF for lodgepole pine was widely distributed across the globe (Figure 4A). The predicted climate niche was concentrated between 30° and 60° latitude in the North Hemisphere through North America and Eurasia. On the continent of North America, the niche ranged from the Maritime zone of Alaska on the west coast to Newfoundland and Nova Scotia on the east coast. It covered lodgepole pine’s native habitat in the west of Canada and the United States and extended to the Great Lakes region along the US-Canada border. In Eurasia, the niche ranged from Iceland and countries around the North Sea and Baltic Sea in Europe, passed through central Russia and Kazakhstan and extended eastward to coastal and island areas in East Asia. Moreover, it covered central to northeast China, Korea, and Japan. The fundamental climate niche was also predicted in the Southern Hemisphere with small and scattered distributions. It appeared on the west coast of South America, especially in Peru and Southern Chile, and on the southeast coast of Australia, as well as in New Zealand. High productivity areas were mostly located on the western sides of the Rocky Mountains in Western North America, the Great Lakes region on the east coast, northern Europe around the Baltic Sea, northeast of China, and northern Japan. The predicted current spatial distribution of fundamental climate niche matched well with both the reported natural distribution in Western North America (Little, 1971) and observations from the areas where the species has been introduced globally (Figure 4A), with only 863 out of the total 15,854 occurrence points were located outside of the current fundamental climate niche (i.e., 94.6% of the observations are located within the current distribution of fundamental climate niche).

FIGURE 4

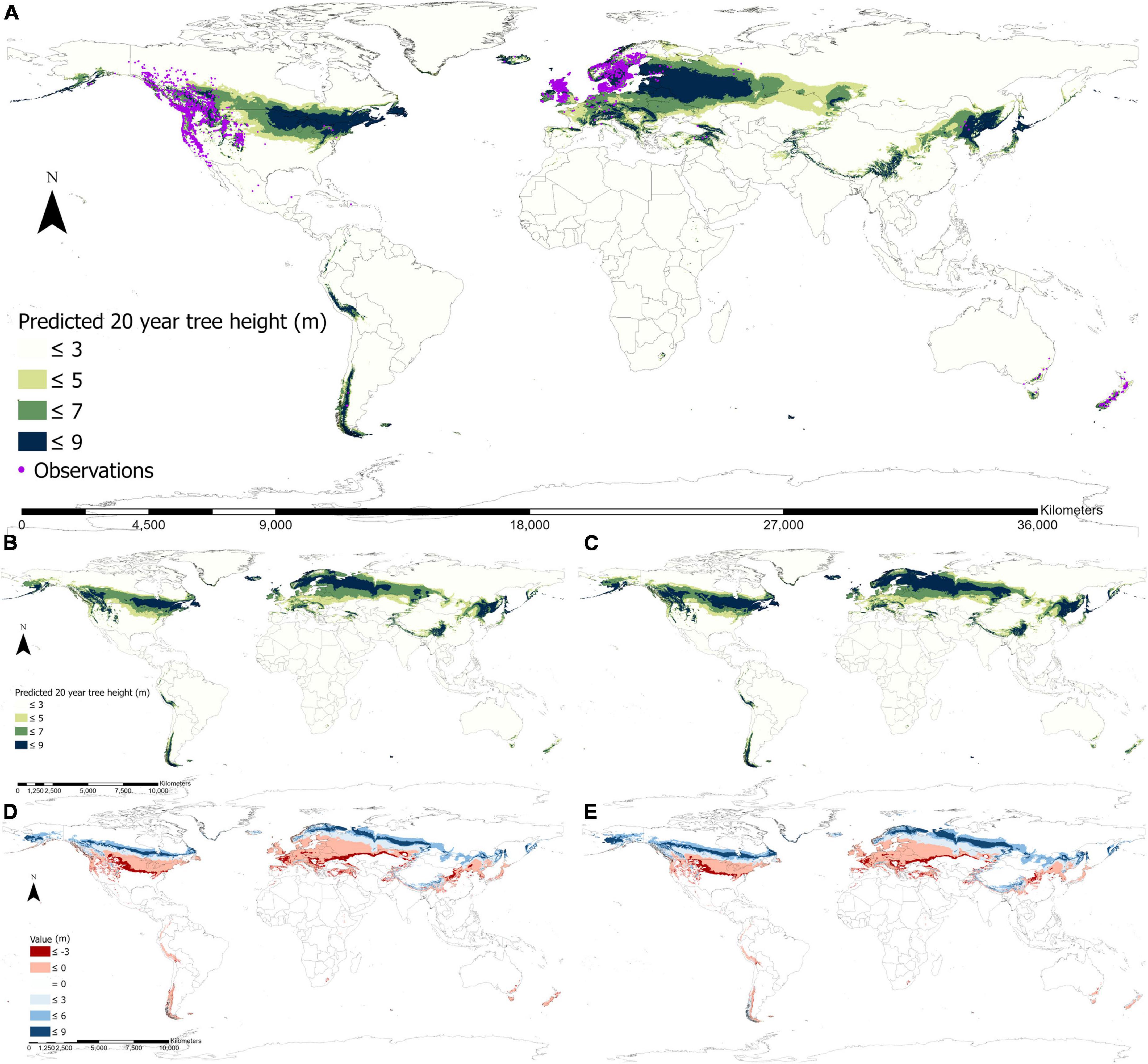
Figure 4. Global distributions of the fundamental climate niche of lodgepole pine predicted by the final universal response function (fURF) for the current and the 2050s climates. The current fundamental climate niche distribution overlaid with the observed occurrence of lodgepole pine worldwide (A), where each dot represents a single occurrence point. Potential growth performances (represented by 20-year height) by the 2050s with emission scenario RCP 4.5 using climatically local (B), and optimal provenances (C). Differences in the performance between the two future projections (B,C) and the current are shown in panels (D,E), respectively.

The global distribution of the fundamental climate niche and the potential growth performance were projected to shift northward and expand for the future climate period 2050s with the climate change scenarios RCP 4.5 (Figures 4B, C) using climatically local (Figure 4B) and optimal provenances (Figure 4C). If local provenances were used, the fundamental climate niche (>3 m) and the productive area (>5 m) were projected to increase by 16 and 14%, respectively. If optimal provenances were used for each planting site, such increases would be much greater (28% for niche expansion and 29% for productive areas). For future projections, an increase in productivity in the colder region and a decrease in the warmer region was noticeable worldwide (Figure 4). The overall trend of shifting to colder regions for the fundamental climate niche distribution was particularly obvious in northern North America, northern Europe, northern Asia, the Himalaya region, and southern Chile.

Using optimal provenances could considerably enhance productivity and broaden the extent of the spatial distribution of the fundamental climate niche. Such improvement was especially distinct in Alaska, central China, and southern Chile (Figures 4B, C). A substantial loss in productivity was projected to occur on the west coast of North America, central to eastern North America, southern Europe, northeastern Asia, Australia, and New Zealand by the 2050s. Using optimal provenances would considerably reduce such losses and increase potential productivity in the colder regions.

4. Discussion

4.1. Transfer function vs. response function

Whether to include site climate or climatic transfer distance is the primary difference between Wang et al.’s (2010) URF and Leites et al.’s (2012) UTF if random effects are not considered. Our results indicated that the two models had exactly the same performance (Table 1); however, the interaction term in the UTF model played a more important role (>10%) than that in the URF model (<1%). Such contrast is probably because of the direct use of provenance climate and site climate in URF, which makes it possible to explicitly predict the performance of a population from a specific provenance planted at a specific test site. While transfer distance in the UTF confounds site and provenance effects, the interaction term makes it provenance-specific (Leites et al., 2012), thus making it more critical to include the interaction term in the model. This also explains the poor model accuracy in general transfer functions (Matyas and Yeatman, 1992; Carter, 1996; Rehfeldt et al., 1999), where observations were pooled, resulting in the absence of the difference in transfer effect among provenances.

Despite the same performance of the URF and UTF models, explicitly using site and provenance climate in the URF has a clear advantage over the UTF. Climate effects can be directly visualized in terms of provenance and test site climate in a URF (as shown in Figure 1A). Thus, it is straightforward to perceive the predictive performance of any population at any planting site in a URF, while it requires an additional step to convert a transfer distance to a specific site in a UTF. In addition, transfer distance does not distinctly represent the environmental effect, as it is a combination of site and provenance effects. Being explicit in both site and provenance also enables an important feature of the URF; it can identify the optimal provenance for any planting locations through the first-order derivative function from the URF (Wang et al., 2010). This feature has been used to identify optimal provenances for Douglas-fir in Europe (Chakraborty et al., 2015) and for white pine and black spruce in Ontario, Canada (Yang et al., 2015). It was also applied to assess the level of local adaptation of Chinese thuja populations based on the difference in growth potential between using the optimal and local provenances (Hu et al., 2019).

4.2. Linear vs. linear mixed-effect models

Linear regression is used in URF models (Wang et al., 2010) and traditional transfer functions (Matyas, 1994; Carter, 1996; Rehfeldt et al., 1999). Adding random effects to a linear model helps explain the variations between groups that are not explained by fixed effects and may result in less biased coefficients for fixed terms when samples are over-represented from a population (Faraway, 2016). Thus, including random effects may also make the model more effective in handling smaller sample sizes as expected by Leites et al. (2012). In this study, we found that a substantial amount of variation can be explained by the random effects from the error term of the corresponding linear models, which improves the model accuracy (from 0.74–0.75 to 0.92–0.93 in R²). However, such an improvement on R² does not necessarily indicate a significantly better predictive power for new data points, as only fixed effects in the linear mixed-effect model are used for predicting new subjects, such as spatial predictions and future climates. Our results showed similar performance for the mixed and linear models in cross-validations when only fixed effects were used (Tables 1, 2). The models built with varying sample sizes showed that mixed models performed slightly better than linear models with very small sample sizes, which aligns with previous studies (Figure 2). However, such differences were insignificant, and linear models showed better stability as the sample size increased. In addition, mixed models built with small sample sizes often failed to converge. Thus, no advantages of using a linear mixed-effect model were observed to deal with small samples in our case. Furthermore, the inclusion of random effects increases model complexity and makes convergence in model fitting a challenge, often resulting in linear mixed-effect models that are fitted with only a single climate variable (Leites et al., 2012; Sáenz-Romero et al., 2017). Thus, whether to include random effects or additional climate variables has been a tradeoff. As we found no significant advantages of including random effects in our models, such a tradeoff becomes unnecessary in our case. On the other hand, we found that including additional climate variables is critical not only to improving the model performance (R², cross-validation R², and cross-validation RMSE) (Tables 1, 2), but also to making the spatial distribution of the fundamental climate niche of lodgepole pine more realistic (Figure 3) (not reflected by statistics), as lodgepole pine’s high productivity area is located along the Rocky Mountains (Wang et al., 2006, 2010). Even in the case of a relatively high R² value (0.73), the model with a single climate variable predicted the most productive areas being located in prairie land in Canada, which is misleading. This is consistent with previous studies in building response functions for individual lodgepole pine populations (Wang et al., 2006) and transfer function for Douglas-fir (Clair et al., 2019).

4.3. Application of fundamental climate niche for assisted migration and assisted gene flow

A species’ realized climate niche predicted based on species occurrence data is limited by inter-species competition, physical barriers, historical events, and human impact (Aitken et al., 2008) and does not reflect growth potential. Thus, the realized climate niche could be too restrictive for assisted migration in plantation forestry, which is not affected by those limiting factors. The fundamental climate niche predicted based on tree height would provide a full range of potentially suitable areas for assisted migration and quantify climate change impact on forest growth. In this study, the spatial distribution of the fundamental climate niche predicted by our URF model was far beyond the current species range (Little, 1971).

The predictions outside the native range highly matched the areas with the successful introduction of this species worldwide. As a fast-growing and drought-resistant forest species, lodgepole pine was introduced to many countries in the 20th century, such as in North-West Russia (Fedorkov and Gutiy, 2017), Eastern Turkey (Tilki and Ugurlu, 2008), Northeast China (Zhou et al., 2007), Northern Europe (Elfving et al., 2001), Chile (Peña et al., 2008), Southeast Australia (Richardson et al., 1994), and New Zealand (Brockerhoff and Kay, 1998). It outperformed native species Pinus sylvestris by 30–40% in Norway and Sweden (Pötzelsberger et al., 2020). Similarly, lodgepole pine was also introduced to Northeast China through provenance trials for ecosystem restoration (Zhou et al., 2007). Our predictions also aligned with these records well (Figure 4). Locations that did not match our predictions are mainly in Northern British Columbia, Yukon Territory, and Northern Switzerland (Figure 4). This is likely due to the extreme slow height growth (<1 m for 20 years) at some of the northern test sites. Overall, these results suggest a robust prediction of the fundamental climate niche global distribution for lodgepole pine using the URF and reveal a tremendous potential for assisted migration of this species globally.

The spatial distribution of the fundamental climate niche of lodgepole pine and its shift under future climates (Figure 4A) provides a basis for assessing the impact of climate change on this species in terms of habitat suitability and growth potential at both the species and population levels. The size of the fundamental climate niche distribution was projected to increase by 16% by the 2050s under the climate change scenario RCP4.5, suggesting an even greater potential for planting lodgepole pine worldwide. Although considered invasive in many countries, this species may play an important role in forest adaptation to future climates and carbon sequestration to mitigate climate change. It could be particularly important to serve as an alternative tree species in ecosystems with a limited choice of coniferous species and regions where local conifers have been projected to have substantially contracted distributions in future climates, such as in Europe (Pötzelsberger et al., 2020) and China (Zhou et al., 2007).

The URF reflects both the genetic effect of populations (or local adaptation) and the environmental effect of planting sites (or phenotypic plasticity) on growth potential. Thus, the URF-based fundamental CNM is important for forest operational practice, such as assisted migration at the species level mentioned above and assisted gene flow at the population level (Aitken and Whitlock, 2013). The URF’s ability to identify optimal provenances for planting sites is particularly useful for adaptive forest management under a changing climate. We found that using optimal provenances could substantially mitigate the negative impact of climate change on both the size of the spatial distribution of fundamental climate niche and growth potential within the fundamental climate niche of this species (Figure 4).

Despite the clear advantages of the URF-based fundamental CNMs, it requires comprehensive provenance trials to build such a model. Such a requirement is likely to prevent URF’s application to many species with a small scale of provenance trials. However, comprehensive provenance trials are available for a number of important forest tree species, such as black spruce and white pine (Yang et al., 2015), Douglas-fir (Chakraborty et al., 2019), Chinese thuja (Hu et al., 2019), White spruce (Risk et al., 2021), and Norway spruce. There also have been efforts for sharing and integrating provenance trials across European countries (Trees4Future, 2022), which have been making comprehensive provenance trials available for more forest tree species. It can also serve as a guideline for provenance trial design in the future. Thus, our URF-based fundamental climate niche modeling approach provides a good potential for application to some other major forest tree species to facilitate assisted migration at both species and population levels for optimal adaptation to climate change.

5. Conclusion

In this study, we developed a fundamental CNM for a forest species after thoroughly comparing two potential candidate models based on the comprehensive provenance trials for lodgepole pine. Our results suggested the linear URF with multiple climate variables to be the final model. With this model, we predicted the fundamental climate niche of lodgepole pine on the global scale and projected its shift under a future climate using local and optimal seed sources, which is the first time for forest tree species. These projections demonstrated the potential of assisted migration at the species level and assisted gene-flow at the population level.

Data availability statement

Data supporting this research are available from the BC Ministry of Forest Land and Natural Resources, with permission obtained from a provincial government data sharing agreement, and are not accessible to the public. Request for data access can be made by contacting research scientist Greg O’Neill (greg.oneill@gov.bc.ca). The code generated during this study is available on GitHub (https://github.com/YueruZ/provenance-based-models) and will be permanently archived on Zenodo, DOI: 10.5281/zenodo.5809708.

Author contributions

TW conceived the idea and supervised the project. YZ processed the data, performed the analysis, and carried out data visualization. TW and YZ interpreted the result and drafted the manuscript. Both authors contributed to the article and approved the submitted version.

Funding

Funding for this study was provided by the Natural Sciences and Engineering Research Council of Canada to TW (RGPIN-2018-04643).

Acknowledgments

We thank the Ministry of Forests for providing the provenance data. We appreciate Dr. Gregory A. O’Neill’s insightful comments on a previous version of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2023.1084797/full#supplementary-material

References

Ackzell, L., Elfving, B., and Lindgren, D. (1994). Occurrence of naturally regenerated and planted main crop plants in plantations in boreal Sweden. For. Ecol. Manag. 65, 105–113. doi: 10.1016/0378-1127(94)90162-7

CrossRef Full Text | Google Scholar

Aitken, S., and Whitlock, M. (2013). Assisted gene flow to facilitate local adaptation to climate change. Annu. Rev. Ecol. Evol. Syst. 44, 367–388. doi: 10.1146/annurev-ecolsys-110512-135747

CrossRef Full Text | Google Scholar

Aitken, S., Yeaman, S., Holliday, J., Wang, T., and Curtis-McLane, S. (2008). Adaptation, migration or extirpation: Climate change outcomes for tree populations: Climate change outcomes for tree populations. Evol. Appl. 1, 95–111. doi: 10.1111/j.1752-4571.2007.00013.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2014). Fitting linear mixed-effects models using lme4 [Internet]. arXiv [Preprint]. doi: 10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Booth, T. (2017). Assessing species climatic requirements beyond the realized niche: Some lessons mainly from tree species distribution modelling. Clim. Chang. 145, 259–271. doi: 10.1007/s10584-017-2107-9

CrossRef Full Text | Google Scholar

Booth, T., Nix, H., Hutchinson, M., and Jovanic, T. (1988). Niche analysis and tree species introduction. For. Ecol. Manag. 23, 47–59. doi: 10.1016/0378-1127(88)90013-8

CrossRef Full Text | Google Scholar

Brockerhoff, E., and Kay, M. (1998). Prospects and risks of biological control of Wilding Pinus contorta in New Zealand. N. Z. Plant Prot. 51, 216–223. doi: 10.30843/nzpp.1998.51.11656

CrossRef Full Text | Google Scholar

Carter, K. (1996). Provenance tests as Indicators of growth response to climate change in 10 north temperate tree species. Can. J. For. Res. 26, 1089–1095. doi: 10.1139/x26-120

CrossRef Full Text | Google Scholar

Chakraborty, D., Schueler, S., Lexer, M., and Wang, T. (2019). Genetic trials improve the transfer of Douglas-fir distribution models across continents. Ecography 42, 88–101. doi: 10.1111/ecog.03888

CrossRef Full Text | Google Scholar

Chakraborty, D., Wang, T., Andre, K., Konnert, M., Lexer, M., Matulla, C., et al. (2015). Selecting populations for non-analogous climate conditions using universal response functions: The case of douglas-fir in central Europe. PLoS One 10:e0136357. doi: 10.1371/journal.pone.0136357

PubMed Abstract | CrossRef Full Text | Google Scholar

Clair, J., Howe, G., and Kling, J. (2019). The 1912 Douglas-Fir heredity study: Long-term effects of climatic transfer distance on growth and survival. J. For. 118, 1–13. doi: 10.1093/jofore/fvz064

CrossRef Full Text | Google Scholar

DeMarche, M., Doak, D., and Morris, W. (2019). Incorporating local adaptation into forecasts of species’ distribution and abundance under climate change. Glob. Chang. Biol. 25, 775–793. doi: 10.1111/gcb.14562

PubMed Abstract | CrossRef Full Text | Google Scholar

Elfving, B., Ericsson, T., and Rosvall, O. (2001). The introduction of lodgepole pine for wood production in Sweden — a review. For. Ecol. Manag. 141, 15–29. doi: 10.1016/S0378-1127(00)00485-0

CrossRef Full Text | Google Scholar

Faraway, J. (2016). Extending the linear model with R: Generalized linear, mixed effects and nonparametric regression models, second edition, 2nd Edn. New York, NY: Chapman and Hall/CRC, 413. doi: 10.1201/9781315382722

CrossRef Full Text | Google Scholar

Fedorkov, A., and Gutiy, L. (2017). Performance of lodgepole pine and Scots pine in field trials located in north-west Russia. Silva Fenn. 51:1692. doi: 10.14214/sf.1692

CrossRef Full Text | Google Scholar

Gałecki, A., and Burzykowski, T. (2013). “Linear mixed-effects model,” in Linear mixed-effects models using R: A step-by-step approach [internet], eds A. Gałecki and T. Burzykowski (New York, NY: Springer), 245–273. doi: 10.1007/978-1-4614-3900-4_13

CrossRef Full Text | Google Scholar

GBIF.org (2021). GBIF occurrence download. Copenhagen: Global Biodiversity Information Facility.

Google Scholar

Gray, L., Gylander, T., Mbogga, M., Chen, P. Y., and Hamann, A. (2011). Assisted migration to address climate change: Recommendations for aspen reforestation in western Canada. Ecol. Appl. 21, 1591–1603. doi: 10.1890/10-1054.1

CrossRef Full Text | Google Scholar

Guisan, A., and Thuiller, W. (2005). Predicting species distribution: Offering more than simple habitat models. Ecol. Lett. 8, 993–1009. doi: 10.1111/j.1461-0248.2005.00792.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hodgins, K., and Moore, J. (2016). Adapting to a warming world: Ecological restoration, climate change, and genomics. Am. J. Bot. 103, 590–592. doi: 10.3732/ajb.1600049

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, X., Mao, J., El-Kassaby, Y., Jia, K., Jiao, S., Zhou, S., et al. (2019). Local adaptation and response of platycladus orientalis (l.) franco populations to climate change [Internet]. Basel: Multidisciplinary Digital Publishing Institute. doi: 10.3390/f10080622

CrossRef Full Text | Google Scholar

Hutchinson, G. (1957). Concluding remarks. Cold Spring Harb. Symp. Quant. Biol. 22, 415–427. doi: 10.1101/SQB.1957.022.01.039

CrossRef Full Text | Google Scholar

Illingworth, K. (1978). “Study of lodgepole pine genotype-environment interaction in BC,” in Proc The IUFRO joint meeting of working parties, S2-02-06 lodgepole pine provenances, (Vancouver, BC: British Columbia Ministry of Forests, Information Services Branch), 151–158.

Google Scholar

Leites, L., Robinson, A., Rehfeldt, G., Marshall, J., and Crookston, N. (2012). Height-growth response to climatic changes differs among populations of Douglas-fir: A novel analysis of historic data. Ecol. Appl. 22, 154–165. doi: 10.1890/11-0150.1

CrossRef Full Text | Google Scholar

Little, E. Jr. (1971). Atlas of United States trees, Volume 1: Conifers and important hardwoods. Washington, DC: U.S. Department of Agriculture, Forest Service. doi: 10.5962/bhl.title.130546

PubMed Abstract | CrossRef Full Text | Google Scholar

Matyas, C. (1994). Modeling climate change effects with provenance test data. Tree Physiol. 14, 797–804. doi: 10.1093/treephys/14.7-8-9.797

PubMed Abstract | CrossRef Full Text | Google Scholar

Matyas, C., and Yeatman, C. (1992). Effect of geographical transfer on growth and survival of jack pine (Pinus banksiana Lamb.) populations. Silvae Genet. 41, 370–376.

Google Scholar

McLane, S., Daniels, L., and Aitken, S. (2011). Climate impacts on lodgepole pine (Pinus contorta) radial growth in a provenance experiment. For. Ecol. Manag. 262, 115–123. doi: 10.1016/j.foreco.2011.03.007

CrossRef Full Text | Google Scholar

Morgenstern, M. (2011). Geographic variation in forest trees: Genetic basis and application of knowledge in silviculture. Vancouver, BC: UBC Press, 224.

Google Scholar

Murray, M. (1983). Lodgepole pine: Regeneration and management. Gen Tech Rep PNW-GTR-157. Portland, OR: US Department of Agriculture, Forest Service, Pacific Northwest Research Station, 53. doi: 10.2737/PNW-GTR-157

CrossRef Full Text | Google Scholar

Pachauri, R., and Mayer, L. (2015). “Intergovernmental panel on climate change,” in Climate change 2014: Synthesis report, eds Core Writing Team, R. K. Pachauri and L. A. Meyer (Geneva: Intergovernmental Panel on Climate Change), 151.

Google Scholar

Pearson, R., and Dawson, T. (2003). Predicting the impacts of climate change on the distribution of species: Are bioclimate envelope models useful? Glob. Ecol. Biogeogr. 12, 361–371. doi: 10.1046/j.1466-822X.2003.00042.x

CrossRef Full Text | Google Scholar

Pecchi, M., Marchi, M., Burton, V., Giannetti, F., Moriondo, M., Bernetti, I., et al. (2019). Species distribution modelling to support forest management. A literature review. Ecol. Model. 411:108817. doi: 10.1016/j.ecolmodel.2019.108817

CrossRef Full Text | Google Scholar

Peña, E., Hidalgo, M., Langdon, B., and Pauchard, A. (2008). Patterns of spread of Pinus contorta Dougl. ex Loud. invasion in a Natural Reserve in southern South America. For. Ecol. Manag. 256, 1049–1054. doi: 10.1016/j.foreco.2008.06.020

CrossRef Full Text | Google Scholar

Pötzelsberger, E., Spiecker, H., Neophytou, C., Mohren, F., Gazda, A., and Hasenauer, H. (2020). Growing non-native trees in european forests brings benefits and opportunities but also has its risks and limits. Curr. For. Rep. 6, 339–353.

Google Scholar

R Core Team (2020). R: A language and environment for statistical computing [Internet]. Vienna: R Foundation or Statistical Computing.

Google Scholar

Rehfeldt, G., Crookston, N., Warwell, M., and Evans, J. (2006). Empirical analyses of plant-climate relationships for the Western United States. Int. J. Plant Sci. 167, 1123–1150. doi: 10.1086/507711

CrossRef Full Text | Google Scholar

Rehfeldt, G., Tchebakova, N., and Barnhardt, L. (1999). Efficacy of climate transfer functions: Introduction of Eurasian populations of Larix into Alberta. Can. J. For. Res. 29, 1660–1668. doi: 10.1139/x99-143

CrossRef Full Text | Google Scholar

Richardson, D. (1998). Forestry trees as invasive aliens. Conserv. Biol. 12, 18–26. doi: 10.1046/j.1523-1739.1998.96392.x

CrossRef Full Text | Google Scholar

Richardson, D., Williams, P., and Hobbs, R. (1994). Pine invasions in the Southern Hemisphere: Determinants of spread and invadability. J. Biogeogr. 21:511. doi: 10.2307/2845655

CrossRef Full Text | Google Scholar

Risk, C., McKenney, D., Pedlar, J., and Lu, P. (2021). A compilation of North American tree provenance trials and relevant historical climate data for seven species. Sci. Data 8:29. doi: 10.1038/s41597-021-00820-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Sáenz-Romero, C., Lamy, J., Ducousso, A., Musch, B., Ehrenmann, F., Delzon, S., et al. (2017). Adaptive and plastic responses of Quercus petraea populations to climate across Europe. Glob. Chang. Biol. 23, 2831–2847. doi: 10.1111/gcb.13576

PubMed Abstract | CrossRef Full Text | Google Scholar

Tilki, F., and Ugurlu, C. (2008). Performance of Pinus contorta Dougl. Ex. Loud. Provenances at three sites in Eastern Turkey. World Appl. Sci. J. 3, 875–878.

Google Scholar

Trees4Future (2022). Trees4Future Network [Internet]. TF4. Available online at: http://www.trees4future.eu/ (accessed February 6, 2022).

Google Scholar

Valavi, R., Elith, J., Lahoz-Monfort, J., and Guillera-Arroita, G. (2018). blockCV: An R package for generating spatially or environmentally separated folds for k-fold cross-validation of species distribution models [Internet]. bioRxiv [Preprint]. doi: 10.1111/2041-210X.13107

CrossRef Full Text | Google Scholar

Wang, T., Hamann, A., Yanchuk, A., O’Neill, G., and Aitken, S. (2006). Use of response functions in selecting lodgepole pine populations for future climates: Lodgepole pine populations for future climates. Glob. Chang. Biol. 12, 2404–2416. doi: 10.1111/j.1365-2486.2006.01271.x

CrossRef Full Text | Google Scholar

Wang, T., O’Neill, G., and Aitken, S. (2010). Integrating environmental and genetic effects to predict responses of tree populations to climate. Ecol. Appl. 20, 153–163. doi: 10.1890/08-2257.1

CrossRef Full Text | Google Scholar

Wang, T., Wang, G., Innes, J., Nitschke, C., and Kang, H. (2016b). Climatic niche models and their consensus projections for future climates for four major forest tree species in the Asia–Pacific region. For. Ecol. Manag. 360, 357–366. doi: 10.1016/j.foreco.2015.08.004

CrossRef Full Text | Google Scholar

Wang, T., Hamann, A., Spittlehouse, D., and Carroll, C. (2016a). Locally downscaled and spatially customizable climate data for historical and future periods for North America. PLoS One 11:e0156720. doi: 10.1371/journal.pone.0156720

PubMed Abstract | CrossRef Full Text | Google Scholar

Weigel, K., Gianola, D., Tempelman, R., Matos, C., Chen, I., Wang, T., et al. (1991). Improving estimates of fixed effects in a mixed linear model. J. Dairy Sci. 74, 3174–3182. doi: 10.3168/jds.S0022-0302(91)78503-2

CrossRef Full Text | Google Scholar

Woodward, F., and Williams, B. (1987). Climate and plant distribution at global and local scales. Vegetatio 69, 189–197. doi: 10.1007/BF00038700

CrossRef Full Text | Google Scholar

Yang, J., Pedlar, J., McKenney, D., and Weersink, A. (2015). The development of universal response functions to facilitate climate-smart regeneration of black spruce and white pine in Ontario, Canada. For. Ecol. Manag. 339, 34–43. doi: 10.1016/j.foreco.2014.12.001

CrossRef Full Text | Google Scholar

Zhou, S., Chen, J., Jiao, S., Liu, Y., Zhang, J., Yu, A., et al. (2007). Introduction test and ISSR analysis of Pinus contorta in semi-dry region of Jilin Province, China.pdf. Jilin For. Sci. Technol. 36, 1–27.

Google Scholar