Review and Synthesis of Estimation Strategies to Meet Small Area Needs in Forest Inventory

Small area estimation is a growing area of research for making inferences over geographic, demographic, or temporal domains smaller than those in which a particular survey data set was originally intended to be used. We aimed to review a body of literature to summarize the breadth and depth of small area estimation and related estimation strategies in forest inventory and management to-date, as well as the current state of terminology, methods, concerns, data sources, research findings, challenges, and opportunities for future work relevant to forestry and forest inventory research. Estimation methodologies explored include direct, indirect, and composite estimation within design-based and model-based inference bases. A variety of estimation methods in forestry have been applied to extensive multi-resource inventory systems like national forest inventories to increase the precision of estimates on small domains or subsets of the overall populations of interest. To avoid instability and large variances associated with small sample sizes when working with small area domains, forest inventory data are often supplemented with information from auxiliary sources, especially from remote sensing platforms and other geospatial, map-based products. Results from many studies show gains in precision compared to direct estimates based only on field inventory data. Gains in precision have been demonstrated in both project-level applications and national forest inventory systems. Potential gains are possible over varying geographic and temporal scales, with the degree of success in reducing variance also dependent on the types of auxiliary information, scale, strength of model relationships, and methodological alternatives, leaving considerable opportunity for future research and growth in small area applications for forest inventory.

1. Introduction

The frequency and sophistication of statistical methods in forest inventory have grown steadily since their earliest adoption by forest researchers, with an overall goal of providing information of sufficiently high quality to inform decision-making (Schumacher, 1945). One ongoing trend involves the use of data collected as a part of broad regional or national forest inventories to produce estimates for areas smaller than the surveys were originally designed to address (Magnussen et al., 2014). This trend reflects a situation described by W. A. Fuller in a plenary presentation delivered to a 1998 workshop on Environmental Monitoring Surveys Over Time hosted by the University of Washington, Seattle (Fuller, 1999):

“The client will always require more than is specified at the design stage. For example, the client will explain that they require estimates only at the regional or national level and then, when data are available, ask for county estimates.”

While the quotation cites a typical circumstance, many situations arise in forest resource assessment where stakeholders recognize that data from multiple sources and scales could be leveraged to give improved estimates for increasingly small subsets of survey populations—whether based on geographic areas, time periods, or demographic subsets of larger populations from which sample data were collected.

One means of addressing this need is through small area estimation (SAE), a set of statistical methods aimed at providing estimates of parameters of interest for population subsets known as small area domains, typically by linking information from auxiliary sources with sample observations gathered over a larger population that encompasses multiple small area domains. A small area in this case can be described as any geographic, temporal, or categorical domain for which an established approach for direct estimation does not provide adequate precision (Rao and Molina, 2015). Usual quantities of interest include finite population parameters such as area totals or means, especially where tolerances for estimator accuracy have been specified as a part of the sample design. Domains in SAE are typically subsets of larger survey populations, such as those found in regional or national economic, health, or agricultural surveys focused on multiple attributes of interest (Schreuder et al., 1993). These surveys may involve decades of repeated sampling and data collection targeting dozens of attributes, or be limited to a single attribute observed at just one point in time.

SAE methods seek to improve the precision of estimates for small area domains of interest (DOI) using data observed from other domains to increase the amount of sample information available, an approach often described as “borrowing strength.” The indirect (i.e., outside-of-domain) data are generally linked to small area DOI through one or more auxiliary variables and a model relationship that holds across multiple domains. In this sense, the domain (d) direct data (y ∈ d) are linked to the indirect data (y ∉ d) via a model relationship involving the auxiliary data (x) and corresponding observations of y. In the example Fuller (1999) described, counties of interest are the small area domains, with the sample data collected in a specific county serving as its source of direct information. Sample observations from surrounding areas—including other counties—are the source of indirect data. In a national forest inventory (NFI) application consistent with Fuller's example both y ∈ d and y ∉ d would be collected on observational units selected by statistical sampling. Auxiliary information to construct a model for y ~ x might come from remote sensing or other geospatial data sets separate from the NFI sample observations, or from other sources including surveys of forest landowners, agencies, or enterprises that keep records of timber harvesting, tree-planting, or other management-related activities. Other arrangements and sources of information are possible, but the overall pattern of direct, indirect, and auxiliary information, and a model y ~ x is present in most SAE applications (Rao, 2008).

Methods now widely associated with SAE largely appeared in technical literature beginning in the 1970s to address needs for increased accuracy when estimating for small area domains within population, social-economic, and public health surveys (Federal Committee on Statistical Methodology, 1993). Since then, SAE has been adopted in applications aimed at estimating incomes (Fay and Herriot, 1979), census groupings, and crop areas (Battese et al., 1988), among others. Methods for SAE have continued to develop over time as new statistical and computational tools have become available, together with widespread availability and cost-effectiveness of modern data sets. Remote sensing technologies such as satellite imagery or aerial laser scanning (ALS) have played a key role in accelerating the application of SAE methodologies to forest inventory settings (Pfeffermann, 2002, 2013; Sugasawa and Kubokawa, 2020; Coulston et al., 2021).

Interest in applying SAE across disciplines has grown over time but most applications in forest inventory began to appear in published work over the past several decades (Burk and Ek, 1982; Anderson and Breidenbach, 2007; Breidenbach et al., 2010; Goerndt et al., 2011). SAE reduces forest inventory estimator errors for small area domains, offering an efficient and cost-effective option for reducing uncertainty compared to increasing sampling intensity by installing additional forest-inventory field plots (Magnussen et al., 2014). SAE techniques have been used to enhance precision of NFI-derived estimates (Breidenbach and Astrup, 2012; Frank et al., 2020), in forest stand inventories (Ver Planck et al., 2018), and from surveys of wood processors or commercial landowner inventories (Green et al., 2020; Coulston et al., 2021), but are not limited to those uses (Affleck and Gregoire, 2015). The ability of SAE to increase estimator precision in small areas where data are otherwise too sparse to satisfy tolerance specifications makes it attractive for applications in forest inventory (Guldin, 2021). For example, the Norwegian NFI has employed national canopy height maps from aerial remote sensing as auxiliary data sources since about 2010 to address needs for better local information in producing municipal forest statistics and forest-management related inventories (Astrup et al., 2019; Breidenbach et al., 2020). SAE has been used with forest inventory data from the U.S. Department of Agriculture Forest Service Forest Inventory and Analysis (FIA) program to generate estimates of forest attributes in small areas such as biofuel supply areas around co-firing power plants (Goerndt et al., 2019). In forests where field plots can be precisely referenced to high-quality geospatial auxiliary data (e.g., ALS), SAE can provide increased precision of estimates for arbitrarily small spatial areas—accounting for spatial correlations in sample data when warranted—even where no direct sample data lie within some DOI (Babcock et al., 2018; Pascual et al., 2018). Current research aims to combine forest biomass data from field plots with canopy-height measurements from the NASA GEDI spaceborne lidar platform and other remotely-sensed auxiliary information in a SAE framework, signaling the first efforts to obtain global scale forest biomass estimates in an inferential framework (Patterson et al., 2019).

While the potential value of SAE for use in forest inventory and monitoring is high, the number of applications reported in technical literature to date is relatively small. A main objective of this work is to provide an overview of published findings of small area applications in forest inventory including relevant considerations for their implementation in other, perhaps novel, settings. An underlying goal is to provide a backdrop of SAE-related concepts and terminology, as the clear and consistent use of statistical language is important to wider adoption of these tools in future work. A further objective is to provide clarification, without a heavy emphasis on mathematical statistics, where ample terminology and notation can pose challenges to those interested in pursuing small area applications, possibly for the first time. We begin in Section 2 with background on relevant statistical paradigms of design- and model-based inference relevant to SAE, including an important extension of design-based inference known as model-assisted estimation. Section 3 presents terminology for direct and indirect estimators along with an overview of composite estimators used in a majority of SAE methods classified as either unit-level or area-level methods. In Section 4, we summarize key findings of published SAE research in forestry, with synthesis and comparison to design-based approaches including model-assisted estimation. Section 4 also includes some discussion of variance estimators in small-area inventory applications along with emerging topics in SAE. We conclude in Section 5 with some take-home findings of the work.

2. Background

2.1. Design-Based Estimators

The design-based framework for inference from statistical sampling is a pillar of many SAE procedures, especially area-level estimators that will be discussed in Section 3.3 below. Sampling is likely familiar to most forest inventory specialists as it provides the basis for establishing statistical properties of estimators in well-designed inventories (Shiver and Borders, 1996; Gregoire and Valentine, 2007; Thompson, 2012). The sample design assigns probabilities to population units (e.g., plots, trees, etc.) in the sampling frame for being selected in a particular random draw from a finite population, with the overall probability of any unit being included in a sample determined from its selection probability in the context of the sampling scheme. While the attributes of each unit—whether sampled or not—are treated as fixed quantities, randomness in design-based methods arises through the process of sampling. Gregoire (1998) explained this detail stating, “in the design-based framework, the population is regarded as fixed whereas the sample is regarded as a realization of a stochastic process.” Design-based methods rely on the randomization distribution of sampling and possible estimates that could be obtained by following the sample design and its implementation in the sampling scheme. A key consequence is the lack of reliance on mathematical assumptions of how elements in the population are distributed, or of model relationships assumed about how two or more variables in the population are related (Sterba, 2009).

The usual goal of design-based sampling and subsequent estimation is to obtain reliable estimates of finite population parameters in an inferential framework. In forest inventories, population totals, means, or proportions for various attributes of interest are typical subjects of estimation. No assumptions about the underlying structure or distributions of population units being surveyed are required for valid inference in the design-based framework. Design-based estimators compatible with their sample designs are design-unbiased, meaning the expected value of the estimator over all possible samples equals the true population parameter being estimated. It follows that design-based estimators are design consistent, such that, “both the design bias and the variance go to zero as the sample size increases” (Skinner and Wakefield, 2017).

The Horvitz-Thompson (H-T) estimator is a design-based estimator widely used in forest inventory and introduced in many texts starting with simple random sampling. Any finite population total for attribute y can be estimated using the H-T estimator

$\begin{array}{ll}{\widehat{\tau }}_y={\displaystyle \sum _{iϵs}}\frac{y_i}{{\pi }_i}& (1)\end{array}$

where ${\widehat{\tau }}_y$ is the estimated population total, s denotes the set of observed values in the sample, y_i is the observed value of attribute y on the i^th sample unit, and π_i is the probability that y_i is included in s. In this form design-based estimators rely entirely on observed sample data and sample design weights, i.e., the inclusion probabilities in the denominator of Equation (1), to estimate an attribute of interest. Standard errors of an estimate require pairwise joint inclusion probabilities P(y_i ∩ y_j) (i ≠ j), calculated as the product of π_i and π_j when random sampling is from non-overlapping population units. Thus, the inference base for H-T estimator makes use of properties of the sample design such as a sampling scheme that draws samples according to design weights, independence of sample observations, and sampling distribution properties including applicability of Student's t-distribution and the Central Limit Theorem (Sterba, 2009). Sampling methods relying on a design-based framework do so largely for its desirable properties of unbiasedness and asymptotic consistency, often sought in inventory settings. These methods, however, rely on direct data—values of y observed directly by sampling from the population of interest—which can be expensive to obtain. Any need for estimates on small subsets of the population will likely result in a need for increased sampling intensity and additional expense (Fuller, 1999).

2.2. Model-Assisted Estimators

Models can be used within a design-based framework to improve estimates in what are often called model-assisted estimators (Särndal et al., 1992; McConville et al., 2017, 2020). Like the H-T estimator (Equation 1), model-assisted estimators are direct estimators in that they rely on values of y only from population DOI. One example is post-stratification which has formed the basis of forest inventory estimation strategies in the U.S. for many decades (Bechtold and Patterson, 2005). Among the simplest model-assisted estimators are linear combinations of auxiliary variables x – either univariate or multivariate – available for all sampled units and having known population means (μ_x) or totals (τ_x). Using the H-T estimator (1), the model-assisted estimator can be written as in Stahl et al. (2016)

$\begin{array}{ll}{\widehat{\tau }}_y^{MA}={\displaystyle \sum _{i\in U}}\widehat{y_i}+{\displaystyle \sum _{i\in s}}\frac{y_i-\widehat{y_i}}{{\pi }_i}& (2)\end{array}$

where ${\widehat{\tau }}_y^{MA}$ is the estimated model-assisted population total for attribute y, U denotes the (universal) set of all population units, and predicted values are obtained from a model, i.e., $\widehat{y_i}=m(x_i)$, oftentimes a linear regression model. The first term on the right-hand side of Equation (2) requires at least that population totals τ_x for all predictors are known, while the second summand is a H-T estimator of sample deviations from model-predicted values, which should be positive if the model underpredicts for y∈s and negative if the model overpredicts.

Särndal et al. (1992) presented an unbiased estimator for the variance of Equation (2) when the coefficients of a linear model m are known constants, an application known as the difference estimator. The difference estimator is design-based because both the estimator ${\widehat{\tau }}_y^{MA}$ and it's estimated variance are unbiased over all possible samples due to the sample design. Thus, although ${\widehat{\tau }}^{MA}$ is a design-based estimator, the phrase “model-assisted” is used to indicate that a model relationship is involved in the estimation of τ.

The regression estimator, or generalized regression estimator (GREG) is based on the same form as Equation (2) in cases where ŷ is predicted from a regression model. GREG has been applied in forest inventory solutions that include post-stratification, ratio estimators, LASSO, ridge, and elastic-net regressions (Stehman, 2009; McConville et al., 2020). Extensions using non-linear, semiparametric, and non-parametric predictive modeling techniques have also been demonstrated in forest inventory applications (Opsomer et al., 2007; Tipton et al., 2013; Kangas et al., 2016). Although taking the same form as the difference estimator, as distinguished by Särndal et al. (1992), the linear predictor m(x) in GREG consists of a regression model y = xβ fit to paired sample values of x and y. Some authors distinguish between the difference estimator and GREG as either external or internal, respectively, based on the sources of information from which their coefficients are derived (Kangas et al., 2016; Stahl et al., 2016). Still within the realm of direct, model-assisted estimators, the term modified GREG is used to distinguish models where coefficients are derived using data outside the population of interest (Rao and Molina, 2015). For GREG to be approximately design-unbiased, sample inclusion probabilities for x and y are used in a weighted-least-squares fit of the model to sample observations. Inclusion probabilities are also used in an approximate variance formulation for the GREG estimator detailed by Särndal et al. (1992, ch. 6). Confidence intervals can be reliably constructed for these estimators, but are usually used for major domains as their variance can be large or unstable in domains having small sample sizes (Särndal, 1984; Lehtonen and Veijanen, 2009). We note that design-based approaches including H-T and model-assisted estimation are sometimes categorized as SAE (see Figure 2.1 in Rahman and Harding, 2017; Hill et al., 2021); however, they are often used where interest lies in only a single population domain, such as in the methods demonstrated by McConville et al. (2020) for estimating forest attributes in a single county in Utah, USA.

2.3. Model-Based Estimators

A second pillar of many SAE procedures is the model-based framework for inference, which we introduce here as being distinct from a purely design-based framework, including model-assisted estimators described in Section 2.2. In model-based estimation, univariate or multivariate statistical models are formulated to establish the basis for assigning probabilities to observed data, for characterizing probabilistic relationships between variables, or for both. Unlike the fixed-quantity view of population units in design-based estimation, model-based approaches treat observable units in a population as realizations or instances of random variables that underlie the observable population. For this reason these conceptual models of population variables and their statistical distributions are sometimes referred to as “superpopulation models” but are just as often simply called models (Gregoire, 1998; Skinner and Wakefield, 2017).

Model-based estimators can be useful when random sampling is impractical, or when assigning inclusion probabilities to sample observations requires some assumption about the statistical or spatial distributions of population units (e.g, Radtke and Bolstad, 2001). Sterba (2009) emphasized the utility of model-based estimators in surveys where selection probabilities were unknown, particularly in some forms of non-random sampling. Perhaps most important in the context of this review, models serve an important purpose in providing a statistical link between sample observations of y and auxiliary data x, to make use of auxiliary information in ways that increase the precision of parameter estimates. The parameters of interest in forest inventory likely include population totals or means; additionally, parameters of the models themselves, such as regression parameters or ratios linking auxiliary and sample data may be of interest (Gregoire, 1998). Model-based methodology includes many tools to assist with identifying best models to fit data, to estimate parameters and standard errors for model predictors, and to adopt complex models and analyze more complex data structures than might be possible from sampling alone (Rao and Molina, 2015). While the complex and expansive nature of model-based methodologies leads to a wide array of SAE techniques that make use of models, they place a somewhat greater burden on analysts to adequately address model selection, goodness of fit, or checking of model assumptions—all model concepts that would not be required in design-based approaches.

3. Terminology and Methods

In Sections 2.1–2.3, estimation was presented as a means of obtaining reliable information about population parameters of interest—either for fixed finite populations or underlying model superpopulations—along with rationale for making statistical inferences under design-based and model-based paradigms. In moving to settings where the goal involves making reliable estimates for subsets or domains of interest within broader populations, the presentation will be expanded to include ideas and terminology better suited to the purposes and practice of SAE.

3.1. Direct, Indirect, and Composite Estimators

Apart from the design- and model-based modes of inference introduced above, estimators in general can be described as being either direct, indirect, or composite in nature, depending on the sources of information they make use of. Domain-direct estimates use observed values y_i only from sample units in a particular domain, i.e., i∈s_d. Domain-specific totals can be estimated directly as

$\begin{array}{ll}{\widehat{\tau }}_d^{DIR}={\displaystyle \sum _{iϵs_d}}{w}_i{y}_i& (3)\end{array}$

where DIR indicates that $\widehat{\tau }$ is a direct estimator, and d denotes the domain of interest. Substituting w_i = 1/π_i in Equation 3 shows how the H-T estimator (Equation 1) serves as the domain-direct estimator when data are restricted to sample units selected in domain d, i.e., when i ∈ s_d. The benefit of direct domain estimation is that no explicit model assumptions are required (cf. Sterba, 2009), and sampling weights can be used, allowing for design-unbiased estimates. A fundamental concern of SAE is that direct estimation often leads to unacceptably large or unstable standard errors for domains with small sample sizes (n_d). Additionally, no direct estimates are possible for domains having no sampled units, i.e., when n_d = 0.

Indirect domain estimation seeks to remedy the direct domain estimator's shortcoming of large variance when n_d is small by increasing the “effective sample size” using information outside of the domain of interest together with a statistical model (Rao and Molina, 2015, pg. 35). The indirect approach is manifest in what is often called a synthetic estimator, e.g.,

$\begin{array}{ll}{\widehat{\tau }}_d^{SYN}={\tau }_{xd}^{\prime }\widehat{\beta }& (4)\end{array}$

which gives the indirect or synthetic estimate (Schaible, 1993) of the total for the d^th small area domain, with domain d auxiliary total τ_xd, and regression coefficients $\widehat{\beta }$ estimated from (x, y) data sampled across the entire population to borrow strength for estimating on d. Benefits of the synthetic estimator are that it can allow for estimates to be made in non-sampled units, and likely has a smaller variance than direct domain estimates, especially where n_d is small. However, Equation (4) as given does not account for between-domain heterogeneity and thus can be biased for specific domains. Additionally the indirect estimator does not necessarily trend toward the unknown domain total τ_d as n_d increases.

Not all synthetic estimators are regression models, but the example in Equation (4) was chosen to illustrate some additional details. First, when the coefficients are estimated only from data sampled in the domain of interest, i.e., when $\widehat{\beta }$ in Equation (4) is replaced by ${\widehat{\beta }}_d$, the estimator is considered to be a model-assisted (GREG) estimator having design-based properties for inference. The same is true when the regression model is fit using sample observations weighted by their design weights using weighted least squares (Särndal et al., 1992; McConville et al., 2020, Section 6.4). Second, a synthetic estimator's inference base may depend on assumptions about its model form being correct, and whether its parameters estimated from one set of domains are suitable for making predictions for other domains. As with any estimator, care should be taken to verify what conditions must be met to satisfy the inference base for GREG.

The synthetic estimator can be used in concert with the direct domain estimator to create a composite estimator that balances the strengths and weaknesses of direct and indirect estimators (Rao and Molina, 2015):

$\begin{array}{ll}{\widehat{\tau }}_d^{COMP}={\gamma }_d{\widehat{\tau }}_d^{DIR}+(1-{\gamma }_d){\widehat{\tau }}_d^{SYN}& (5)\end{array}$

The weighted average of the direct and indirect estimators comprises the composite estimator ${\widehat{\tau }}_d^{COMP}$, where ${\widehat{\tau }}_d^{DIR}$ is a direct estimator, e.g., (3), ${\widehat{\tau }}_d^{SYN}$ is an indirect estimator, e.g., (4), and γ_d ∈ [0, 1] is a domain-specific weighting factor, also known as a shrinkage factor. An optimal solution for minimum $MSE({\widehat{\tau }}_d^{COMP})$ can be formulated as ${\widehat{\gamma }}_d=MSE({\widehat{\tau }}_d^{SYN})/(MSE({\widehat{\tau }}_d^{SYN})+MSE({\widehat{\tau }}_d^{DIR}))$ (Rao and Molina, 2015, Section 3.3.1). For the optimal solution, as n_d gets large or when $MSE({\widehat{\tau }}_d^{DIR})$ is small, ${\widehat{\gamma }}_d$ tends toward 1, moving the composite estimator toward ${\widehat{\tau }}_d^{DIR}$ and its favorable properties of unbiasedness and consistency. Similarly ${\widehat{\tau }}_d^{COMP}$ tends toward the synthetic estimator when n_d is small or $MSE({\widehat{\tau }}_d^{DIR})$ is large. Most SAE approaches favor the composite estimator for its ability to balance the unbiasedness and precision of direct and indirect estimators, respectively, while allowing for flexibility in the choice and formulation of direct estimators and synthetic models.

3.2. Unit Level SAE

Unit-level SAE employs synthetic models that operate at the scale of observational or sample units in the population, typically field plots in forest inventory applications. The synthetic model in a unit-level estimator is used to predict ŷ on all population units in a domain d, regardless of how many (or whether) sample data for y were observed in that domain. Predictors from auxiliary variables x and the model relationship y~x provide the means of generating predictions for ŷ∈d. Here x is either known for every unit in d or known in aggregate, as in a case where a domain-specific mean for x, denoted ${\bar{x}}_d$, is known. In either case, paired values of (x, y) are observed on sampled units across the broader population, i.e., the indirect data, and used to fit or train a synthetic model. Errors in the synthetic model predictions are partitioned into two components (see Rao and Molina, 2015, model 4.3.1). A domain-specific error v_d is attributed to synthetic model variance that applies equally to all y∈d, and within-domain residual errors e_di—independent of v_d—that apply to individual sample units y_i; i ∈ d.

The unit-level composite estimator developed by Battese et al. (1988, hereafter BHF) is an excellent example from which to study unit-level SAE, as the data and models the authors used to demonstrate the application are integrated into the R “sae” package (Molina and Marhuenda, 2015). BHF used the nested-error linear regression model

$y_{di}=x_{di}^{\prime }\beta +v_d+e_{di};d=1,\dots ,D;i=1,\dots ,n_d.$

to estimate crop areas for corn and soybeans in Iowa, using USDA Statistical Reporting Service field survey data from 1978 as direct observations of y, and Landsat 2 multispectral scanner (57 x 79 m) raster imagery as auxiliary information for x. Unit-level approaches rely on matching individual sample unit observations to the auxiliary data; thus, the satellite image pixels in BHF were assigned to corresponding 250-ha (1 sq. mile) field survey units (BHF called the units “segments”)—about 555 raster cells per segment. The aggregated Landsat and field survey data formed (x, y) pairs for 37 sampled segments in a population of D = 12 counties, with each county treated as a small-area domain of interest. The BHF synthetic model used a response y = sample segment area (ha) growing corn, in a linear regression model with an intercept and two predictors x₁ = Landsat pixels classified as corn and x₂ = pixels classified as soybeans, with $\sum _{d\in D}{n}_d=37$ observed segments.

Using their synthetic model, similar to Equation (4), BHF were able to predict domain means for corn area per segment in counties as

$\begin{array}{ll}{\widehat{\mu }}_d={\bar{x}}_d^{\prime }\widehat{\beta }+{\widehat{v}}_d& (6)\end{array}$

with ${\bar{x}}_d$ calculated from all segments in county d, using Landsat pixel class counts of a given crop in each segment (see Table 1, Battese et al., 1988). By estimating $\widehat{\beta }$ as fixed effects and ${\widehat{v}}_d$ as random effects using mixed linear regression modeling, BHF obtained the empirical best linear unbiased predictor (EBLUP) of domain-specific means ${\widehat{\mu }}_d^{EBLUP}={\bar{x}}_d^{\prime }\widehat{\beta }+{\widehat{v}}_d$, a key contribution of their work because of the favorable properties of the EBLUP.

Goerndt et al. (2013, Equation 5) and Costa et al. (2009, Equation 13) presented the BHF unit-level nested error EBLUP in the form of a composite estimator with domain-level, i.e., county-level estimates obtained from direct and synthetic regression estimates weighted as

$\begin{array}{ll}{\widehat{\mu }}_d^{EBLUP}=\left(\frac{{\widehat{\sigma }}_v^2}{{\widehat{\sigma }}_v^2+\frac{{\widehat{\sigma }}_e^2}{n_d}}\right){\widehat{\mu }}_d^{DIR}+\left(1-\frac{{\widehat{\sigma }}_v^2}{{\widehat{\sigma }}_v^2+\frac{{\widehat{\sigma }}_e^2}{n_d}}\right){\bar{x}}_d^{\prime }\widehat{\beta }& (7)\end{array}$

where ${\widehat{\mu }}_d^{DIR}$ is a sample-direct estimate of the mean y for small area domain d and $\widehat{\beta }$ is the vector of fixed effects regression coefficients obtained by linear mixed modeling with domain-specific random effects. The term ${\sigma }_v^2$ in Equation (7) denotes the variance among domain random effects $v_d~{N}(0,{\sigma }_v^2)$, and ${\sigma }_e^2$ as the residual variance of population units—the variance unaccounted for by the EBLUP—within domains, i.e., $e_{di}~{N}(0,{\sigma }_e^2)$. This assumption assigns a single residual variance to all domains, with ${\sigma }_e^2$ estimated from the full set of sample residuals. As when using optimal shrinkage weights ${\widehat{\gamma }}_d$ in Equation (5), the weights in Equation (7) ensure that as the domain-specific direct estimator variance gets small, such as when n_d is large, the EBLUP tends toward ${\widehat{\mu }}_d^{DIR}$.

Unit-level paired (x, y) data typically provide an information-rich means of linking indirect data from broad and extensive populations to specific domains of interest. Further, when y is observed by non-random sampling, the model-based properties of the composite estimator support approximate and asymptotic inference bases where direct estimation alone would not. Efforts should be made to verify the veracity of the underlying statistical model and stochastic processes, especially when data collection employs stratification, clustering, or disproportionate sampling among some elements of the population (Sterba, 2009). In applications involving large data sets the computational requirements of unit-level analyses can be demanding, especially when objectives include the validation of variance estimates approximated by Taylor series linearization or when using resampling procedures to estimate variance components (Prasad and Rao, 1990; González-Manteiga and Morales, 2008). Computationally demanding synthetic models can also pose challenges for SAE, but software advances have made steady gains in providing tools to address such challenges (McRoberts et al., 2007). As with any model-based inference approach, customary steps involving model selection, goodness-of-fit, and checking other assumptions are important in unit-level SAE. In cases where influential points, heteroscedastic error variances, or non-independence of residuals present problems, developments have been made to help overcome limitations of the BHF approach (Babcock et al., 2015; Breidenbach et al., 2018).

3.3. Area Level SAE

Unlike unit-level approaches, area-level SAE employs synthetic models that operate at the scale of subpopulation domains, rather than individual sample or observational units. As a consequence, auxiliary data do not need to be paired one-to-one with individual sample observations. Instead, domain-direct estimates (e.g., ${\widehat{\tau }}_d^{DIR}$ or ${\widehat{\mu }}_d^{DIR}$) are paired with domain-specific observations, such as domain means or totals of x ∈ d, which we denote as x_d. The paired domain data $({ŷ}_d^{DIR},x_d)$ are then used to develop regression models or train other types of synthetic models for use in SAE. Rao and Molina (2015, model 4.2.5) presented a regression-based area-level model

$\begin{array}{ll}{\widehat{y}}_d^{DIR}={x^{\prime }}_d\beta +b_d{\psi }_d+{ϵ}_d& (8)\end{array}$

where ψ_d are domain-specific model errors and ϵ_d are errors due to sampling on the domain-direct estimates that appear on the left-hand side in Equation (8). In the basic area-level model, Rao and Molina (2015) explain that b_d are domain specific positive constants set to b_d = 1 in the model presented by Fay and Herriot (1979), which, for direct estimates of domain totals can be expressed as

$\begin{array}{ll}{\widehat{\tau }}_d^{FH}={x^{\prime }}_d\beta +{\psi }_d+{ϵ}_d& (9)\end{array}$

Fay-Herriot (F-H) models (Fay and Herriot, 1979) like the one shown in Equation (9) are often synonymous with area-level SAE, as they have seen considerable use in area-level applications since their introduction. An EBLUP derived from the F-H model, expressed as a composite estimator having a form similar to Equation (5) shows the roles of direct and synthetic estimators

$\begin{array}{ll}{\widehat{\tau }}_d^{FH}=\left({\widehat{\gamma }}_d\right){\widehat{\tau }}_d^{DIR}+\left(1-{\widehat{\gamma }}_d\right){x^{\prime }}_d\widehat{\beta }& (10)\end{array}$

with weights ${\widehat{\gamma }}_d={\widehat{\sigma }}_{{\psi }_d}^2/({\widehat{\sigma }}_{{\psi }_d}^2+{\sigma }_{{ϵ}_d}^2)$ composed as the model variance relative to the total variance. A difference in the shrinkage weights' formulations for Equations (7) and (10) is that ${\sigma }_{{ϵ}_d}^2$ in Equation (10) is assumed to be known, but typically specified as the variance estimated from sample observations y ∈ d. Wang and Fuller (2003) developed a modified area-level estimator that accounts for the empirical estimation of domain-direct variances, which has been demonstrated in forest inventory applications (Magnussen et al., 2017). Similar to the unit-level model, $\widehat{\beta }$ in Equation (10) is a vector of fixed-effects coefficients from a linear mixed model having domain-specific random effects. As in Equation (7) the F-H EBLUP tends toward the direct estimator when the direct variance is low, and toward the synthetic estimator when the direct variance is high. Because the synthetic estimator in the F-H model operates on subpopulation domains, the same aggregated measures x_d from the auxiliary data that were used in estimating the regression coefficients are also used in predicting ${\widehat{\tau }}_d^{FH}$ in Equation (10). In contrast, the unit-level EBLUP uses an aggregated measure such as ${\bar{x}}_d$ in Equation (7), despite the model coefficients having been estimated using observed x (and y) values from individual sample units.

In applications framed in a geographic context, such as forest inventories, where field plot observations are often paired to auxiliary data from remote sensing, area level modeling obviates the need for highly accurate plot coordinates, and can be used when there is a degree of misalignment between plots and auxiliary data (Goerndt et al., 2011). This concern is highly relevant when the protection of confidential information prevents the release of exact coordinates of sampled locations to unauthorized personnel. Instead, only direct linkage to a specific domain is needed for each plot. This also facilitates using sample units that possess indistinct sampling boundaries, such as where linear transects or variable-radius plots are used in field sampling (Ver Planck et al., 2018). This method also tends to require less processing time which lends itself to analysis involving very large datasets.

3.4. Other SAE Methods

In addition to the aforementioned model forms, there are other methods which serve as alterations or variations of the above model types and as such are not mutually exclusive from them. Such methods include Bayes methods, and nearest neighbor models which are worthy of particular mention due to their use in forestry SAE (McRoberts, 2012; Babcock et al., 2018; Ver Planck et al., 2018). Bayesian methods, both empirical Bayes (EB) and hierarchical Bayes (HB) offer some advantages over their frequentest counterparts such as being able to model different target variable types such as binary or count data (He and Sun, 2000). HB also gives posterior distributions of the small area parameters, and can therefore avoid relying on unrealistic asymptotic assumptions (Pfeffermann, 2013). Bayesian methods offer flexibility in specifying spatial structures such as spatially correlated random effects (Wang et al., 2018).

Nearest neighbor techniques offer a similar set of benefits for SAE, for example, where estimators for categorical, binary, or count variables are involved. They are non-parametric in that no distributional assumptions regarding response or predictor variables are necessary, which has proven useful when multivariate auxiliary information is used to construct synthetic models. Nearest neighbor models can also accommodate correlated sample and auxiliary data that may arise in spatial or temporal domains (McRoberts et al., 2007; McRoberts, 2012).

4. Applications in Forest Inventory

We now turn to selected examples related to SAE in forest inventory from published research (Table 1). Note that in Table 1, we exclude a large body of literature employing post-stratification, a widely-used model-assisted estimation technique. Instead we aim to focus on estimators less-commonly used in existing forest inventory production processes. Post-stratification notwithstanding, model-assisted estimators including GREG were among the most widely-used and earliest-adopted methods for increasing estimator precision using models to link auxiliary information from remote-sensing with field sample data. As such, we elected to include a number of model-assisted applications in our example references, even though some of the selected examples do not involve “small area” domains as the term is often used in SAE (Table 1).

TABLE 1

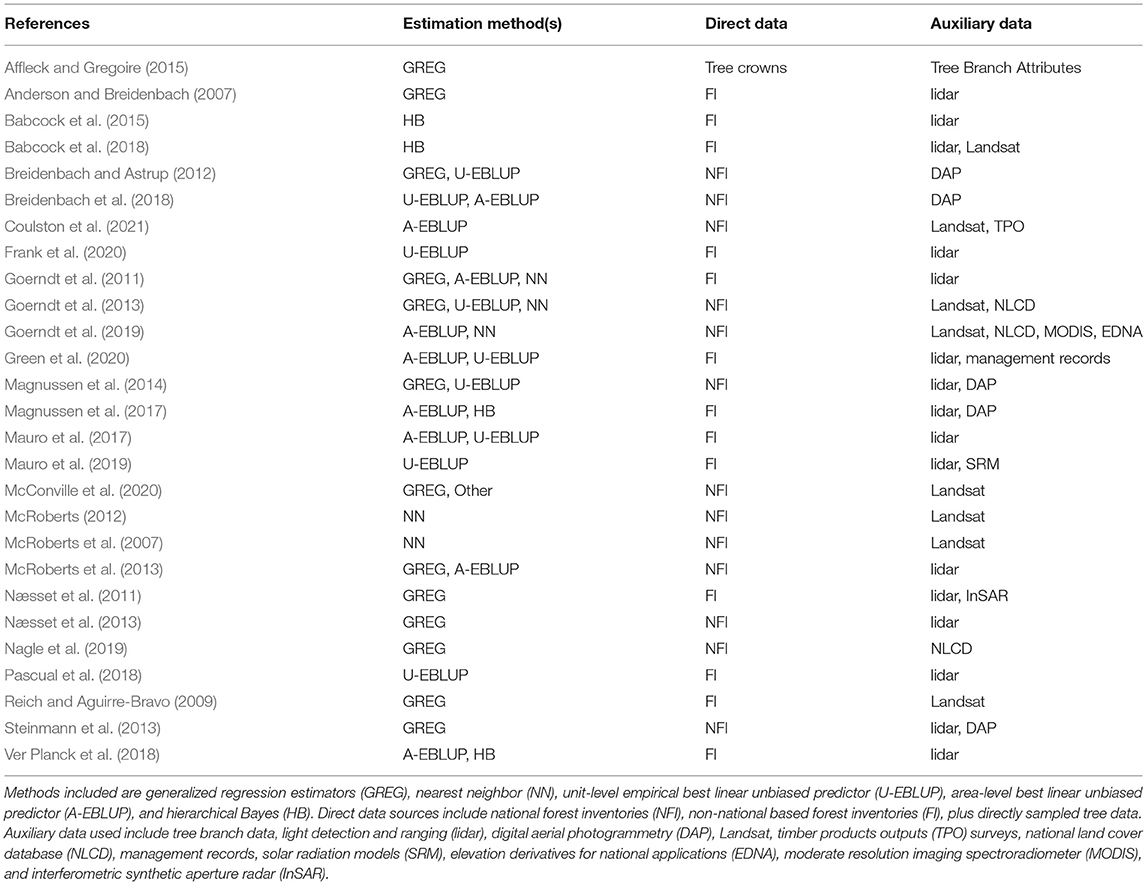
Table 1. Table of selected studies using SAE-related methods in forest inventory with methods and data used.

Among the reasons authors have given for adopting model-assisted estimators was the need to ensure design-based inference in large, multi-resource sample designs (Reich and Aguirre-Bravo, 2009; Næsset et al., 2011). Others cited the need for precise estimation in small area domains nested within broader population surveys as a motivating factor (Goerndt et al., 2011; McRoberts, 2012; Magnussen et al., 2014). A few noted that consistency and additivity of estimates from small areas nested within larger domains were motivating concerns (Reich and Aguirre-Bravo, 2009; Nagle et al., 2019). Others noted the need for sample survey organizations to conduct generic inference, i.e., to make compatible estimates of all forest attributes simultaneously by using the same model to define survey weights (Opsomer et al., 2007; Johnson et al., 2008; McConville et al., 2020). Nearly all research referenced in Table 1 reported the potential for increased efficiency in estimating forest inventory attributes as a reason for pursuing the work, with the high cost of increasing field sample sizes frequently noted as an operational constraint.

Lidar and digital aerial photogrammetry (DAP) were major data sources used as auxiliary information, with some authors using lidar or DAP point cloud metrics, e.g., height percentiles or pulse return densities aggregated to unit or area levels, and others using canopy height models (CHM) processed from point cloud data (Steinmann et al., 2013; Babcock et al., 2015). Field plots in forest inventories were the primary source of directly-sampled observations, with more than half of the selected studies using NFI or other land-management agency field sample observations, and most others using plots installed for management or research purposes, such as on state, university, private, or public experimental and working forests (Anderson and Breidenbach, 2007; Mauro et al., 2017; Green et al., 2020).

Several studies aimed to examine and augment existing estimation frameworks in forest inventory settings to address potential violations in underlying assumptions. Examples include accounting for heteroscedasticity of variance in synthetic model residuals and spatial or temporal autocorrelation among measurements on observational units or areas of interest (Babcock et al., 2018; Breidenbach et al., 2018; Ver Planck et al., 2018; Mauro et al., 2019). Estimating the change of forest attributes over time with SAE methods was demonstrated successfully by Mauro et al. (2019) and by Coulston et al. (2021), both of which used repeated measurements from forest field plots in their work.

Multiple studies applying one or both unit-level and area-level EBLUP-based SAE appear in Table 1. The choice of adopting unit- or area-level SAE in forest inventory applications can depend on limitations of sample or auxiliary data sets, for instance, where georeferencing inaccuracies introduce significant errors in pairing field observations to remotely-sensed or other geospatial data sets, e.g., maps (Næsset et al., 2011; Green et al., 2020). Similar challenges in pairing field data to remote-sensing can occur where plot designs and raster layers are incompatible, such as when variable radius field plots (i.e., angle gauge sampling) are used, or when field plot sizes are small compared to the pixel size in available auxiliary data sources (Goerndt et al., 2011; Ver Planck et al., 2018; Temesgen et al., 2021). Although area-level estimators are flexible to accommodate situations where precise georeferencing is impractical, a trade-off may arise due to the loss of information from aggregating unit-level observations to domain- or area-level scales; further, aggregating sample observations also reduces effective numbers of observations available for synthetic model development (Magnussen et al., 2017).

When georeferencing enables pairing of auxiliary and sample data, sampled units can all serve as (x, y) observations for fitting or training synthetic models. The models can then be used to make predictions on raster cells or other spatial units that correspond to unobserved population units (Babcock et al., 2018; Frank et al., 2020). It follows that unit-level SAE estimators can be used to map predictions or estimates at finer spatial resolutions than area-level methods, the latter of which allow for mapping SAE predictions only at domain levels. Another potential advantage of the unit-level approach is the ability to define arbitrary spatial domains subsequent to sampling without necessarily losing substantial power of inference (Pascual et al., 2018). Gains in efficiency between unit-level and area-level SAE methods have been compared in multiple studies, generally confirming the potential for greater gains from unit-level approaches (Mauro et al., 2017; Breidenbach et al., 2018).

4.1. Gains Over Direct Estimation

4.1.1. Model-Assisted Estimation

Model-assisted estimators have proven to reduce estimator errors considerably, e.g., when measured by the relative efficiency of a model-assisted estimator compared to its simplest direct counterpart—often characterized as simple random sampling—cf. Equations (2) and (3)

$\begin{array}{ll}RE=\frac{Var({\widehat{\tau }}_y^{MA})}{Var({\widehat{\tau }}_y^{DIR})}& (11)\end{array}$

McRoberts et al. (2013) demonstrated substantial variance reduction 100%(1−RE) = 84% using a non-linear regression-based model-assisted estimator of growing stock volume per unit area in a 1,300 km² study area in southeastern Norway. The gains corresponded to over sixfold increase in apparent sample size, calculated as RE⁻¹. Aerial lidar (0.7 pulses m^-2) served as the auxiliary data, with direct observations from n = 145 NFI-type (200 m²) field plots over the study area. They noted similar variance reduction (82%) using the same method to estimate growing stock volume over a one-half partition of the study area represented by n = 69 field plots, thus demonstrating how sample data from a larger area can be used to increase the precision of estimates in a smaller area (McRoberts et al., 2013).

Model-assisted estimation has been demonstrated to increasing precision in multiple population sub-domains including Breidenbach and Astrup (2012), who tested GREG as a model-assisted estimator in a similar sized study area in Norway divided into 14 municipalities, each having from 1 to 35 NFI sample plots of a total n = 145. They noted gains in precision were smaller and more variable than McRoberts et al. (2013), with RE ranging from 0.35 to 0.87 in eight municipalities having n_d≥ 6. They concluded that sample sizes n_d <6 in the other six municipalities gave unstable estimates, a finding similar to Næsset et al. (2011). Their data revealed that despite GREG's limitation in areas with small n_d, its estimates deviated from sample-direct design-based estimates by less than half as much as synthetic model estimates alone, a result consistent with the design-unbiased property of GREG in the model-assisted framework. Næsset et al. (2013) observed consistent improvement in precision of estimates of aboveground forest biomass using GREG with aerial lidar auxiliary data in model-assisted two-stage sampling. Their gains were greatest (RE = 0.125) for all cover classes combined (n = 632), and only slightly more modest 0.09 ≤ RE ≤ 0.20 for individual age and productivity classes, all of which had class-specific sample sizes n_c≥46.

Reduced RMSE of synthetic model estimates when compared to direct estimator variance has been demonstrated in a number of applications involving the pairing of ALS and NFI-type field sample data (Næsset et al., 2011; Järnstedt et al., 2012; Nord-Larsen and Schumacher, 2012; Kotivuori et al., 2016; Nilsson et al., 2017; Novo-Fernandez et al., 2019). A variety of synthetic modeling approaches have been tested including parametric and non-parametric regression modeling, Random Forests and other ensemble predictive models, and nearest-neighbor imputation, often with a goal of identifying suitable auxiliary data sources for estimating forest biophysical attributes (Latifi et al., 2010; Popescu et al., 2011; Bright et al., 2012; Rahlf et al., 2014). A common theme in these studies is the direct examination of synthetic model prediction errors (e.g., using cross validation) without formulating the models in a design-based or composite modeling framework to mitigate potential synthetic estimator bias (cf. McRoberts et al., 2013; Irulappa-Pillai-Vijayakumar et al., 2019; McConville et al., 2020). In model-assisted applications the usual goal is to increase the precision of population-level estimates, and less often to produce estimates for domains that divide a larger population into small areas where direct estimator instability can be a concern. Where investigated, model-assisted estimators were able to reduce small area uncertainties considerably, within limits of direct-data sampling intensity and the strength of model relationships involving indirect and auxiliary data (Breidenbach and Astrup, 2012).

4.1.2. Unit-Level SAE

Research comparing unit-level SAE to model-assisted estimators has shown that gains in precision are generally greater for unit-level EBLUPS than model-assisted estimates (e.g., GREG) primarily when direct-domain sample sizes are small. In directly comparing unit-level EBLUPs to model-assisted GREG estimates, Breidenbach and Astrup (2012) noted an average $\overline{RE}=0.86$, meaning unit-level SAE MSEs were lower than direct estimate variances by an additional 14%, on average, compared to GREG. Not all EBLUP MSEs were smaller than those computed for GREG. Comparisons showed greatest gains in five of six municipalities having 6 ≤ n_d ≤ 17, but smaller—even negative—gains ($\overline{RE}=0.93$ and 1.15) were noted in two municipalities having n_d≥29. Such findings indicate that unit-level EBLUPS may not have as clear of an advantage over GREG in reducing estimator variance when domain sample sizes are relatively large; nonetheless, even when n_d was relatively large, EBLUP performance was not much worse than model-assisted regression estimates (Breidenbach and Astrup, 2012). EBLUPS showed considerable stability across the range from 1 ≤ n_d ≤ 35 compared to GREG, with unit-level SAE relative errors ranging from just [7.0, 12.4] % compared to a range of [0.6, 25.4] % for GREG, even with three municipalities having n_d = 1 excluded for the GREG results since their errors could not be calculated (Breidenbach and Astrup, 2012). Magnussen et al. (2014) reported virtually identical gains for model-assisted and unit-level EBLUP estimates (both $\overline{RE}=0.49$) when compared to direct volume per hectare estimates for forest districts in Switzerland. The near identical results may have been related to comparatively large average sample sizes ${\bar{n}}_d=79$ across the D = 108 Swiss forest districts.

Of the studies listed in Table 1 that compared unit-level EBLUPs to domain-direct estimates, the largest variance reductions noted ($\overline{RE}=0.03$) were in a study of forest volume in Burgos Province, Spain, made up of D = 54 stands in an area covering about 13.65 km² (Pascual et al., 2018). The same authors reported more modest gains ($\overline{RE}=0.50$) in a 3 km² management area having D = 6 stands near Cercedilla, Spain. The authors attributed the greater gains at Burgos as being due to the lower sampling intensity there (about 0.5 %) compared to a 4 % sampling intensity at the Cercedilla site (Pascual et al., 2018). Large gains were reported for unit-level volume EBLUPs ($\overline{RE}=0.09$) tested by Mauro et al. (2017) in an area roughly 8 km². A high degree of positive skewness was evident in the distribution of n_d across domains, with roughly 30% of map unit domains having n_d ≤ 2 despite ${\bar{n}}_d=10.3$ across D = 64 map units having any sample observations (Mauro et al., 2017). In estimating volume change in D = 24 stands experimentally manipulated for three levels of forest structural diversity, Mauro et al. (2019) reported unit-level gains ($\overline{RE}=0.71$) for 7-year volume change estimates. The sample design relied on 1 remeasured plot per 8 ha on a systematic grid, for a sparse but narrow range of domain-direct sample sizes, with 3 ≤ n_d ≤ 10 and ${\bar{n}}_d=6.3$ (Mauro et al., 2019). Breidenbach et al. (2018) reported greater efficiencies $\overline{RE}=0.43$ and $\overline{RE}=0.28$ compared to direct estimate variances, with the latter result including a formulation that accounted for heteroskedasticity of variance in synthetic model residuals.

By artificially reducing sample sizes from the available n = 680 NFI plots across D = 12 county-sized domains for estimating Oregon Coast Range forest volumes, Goerndt et al. (2013) demonstrated diminishing efficiency gains with increasing n_d in unit-level EBLUPS from $\overline{RE}=0.41$ (n = 136), to $\overline{RE}=0.57$ (n = 204), to $\overline{RE}=0.71$ (n = 272). They also found that alternative unit-level composite estimators calculated with smoothed variances performed well in terms of increased precision and low apparent biases in unit-level SAE (Costa et al., 2003; Goerndt et al., 2013). The alternative estimators employed multiple linear regression, as well as nearest neighbor and gradient-nearest-neighbor imputation in synthetic models to achieve balances between bias and precision of SAE (Ohmann and Gregory, 2002).

4.1.3. Area-Level SAE

A number of studies have shown area-level SAE precision gains for timber volume or biomass compared to sample-direct estimates. Breidenbach et al. (2018), for example, reported a reduction in overall standard error from 32.7 m³ha⁻¹ for direct volume estimates compared to F-H area-level RMSE of 23.1 m³ha⁻¹ ($\overline{RE}$ = 0.50). A nearly identical gain in efficiency ($\overline{RE}$ = 0.50) was reported by Goerndt et al. (2011) for volume estimates in forest stands treated as small area domains with intentionally-reduced sample sizes between 2 ≤ n_d ≤ 4. Relative gains tended to be less when the simulated small n_d were increased by factors of two and three, with no gains for larger sample size increases. Despite finding modest gains when n_d was large, area-level EBLUPS were demonstrably superior—in terms of RE and lack of apparent biases—to two synthetic estimators and two composite James-Stein type estimators tested (James and Stein, 1961; Goerndt et al., 2011). In testing area-level SAE with counties as small-area domains, a composite estimator similar to F-H showed $0.43\le \overline{RE}\le 0.91$ over a 20-state region of the northeastern U.S. (Goerndt et al., 2019). In the same study a composite estimator based on a non-parametric nearest-neighbor (NN) synthetic model showed slightly less gain in efficiency than the F-H type approach. Despite this, Goerndt et al. (2019) indicated the NN approach may have lower model bias and they cautioned against potential biases in model-based estimators, pointing out the need for thorough checking of model assumptions to ensure validity of model-based inferences.

The pattern of decreasing gains in efficiency with increasing n_d was also noted by Mauro et al. (2017), who reported an average $\overline{RE}$ = 0.48 over D = 84 management areas (domains), while no gain ($\overline{RE}$ = 1.13) was noted in 14 of the domains having n_d≥25 sample plots (cf. Goerndt et al., 2011, 2019). Green et al. (2020) noted average $\overline{RE}$ = 0.79 in F-H estimates of timber volume across D = 40 stands, with little or no efficiency gains in stands where direct estimates were already quite precise (relative standard errors <10%). Greater gains ($\overline{RE}\approx 0.35$) were noted in stands having direct relative standard errors >25%. Findings such as these indicate that where domain-direct estimates are already quite precise, as in cases where n_d is large or variation within domains is inherently low, F-H type estimators may exhibit a limited ability to further increase precision over domain-direct estimates.

Magnussen et al. (2017) reported $\overline{RE}$ ranging from 0.44 to 0.77 in four study areas in Spain, Norway, Switzerland, and Germany, using a modification of F-H that treats domain-specific variances as estimates rather than known constants (Wang and Fuller, 2003). In the same study they found greater gains $0.28\le \overline{RE}\le 0.34$ by including a non-stationary spatial correlation process in an area-level composite estimator which accounted for the spatial covariance structure in model residuals (Chandra et al., 2012, 2015). In a third approach Magnussen et al. (2017) used the HB approach of Datta and Mandal (2015) to obtain efficiency gains intermediate ($0.27\le \overline{RE}\le 0.81$) compared to their baseline—specifying empirically estimated variances—and non-stationary spatial F-H approaches. The Bayesian approach demonstrated several advantages related to estimated posterior distributions for specific domains, especially when the random-effect variance was largely attributable to a small number of domains from the larger population (Magnussen et al., 2017). Coulston et al. (2021) evaluated the performance of area-level F-H models including a simultaneous autoregressive (SAR) model of residual spatial correlation among domains in estimating forest removals, noting the spatial model improved efficiency of estimates at scales of individual counties, but not at the scale of larger survey regions encompassing groups of 12-20 counties each in the southeastearn United States. Ver Planck et al. (2018) compared F-H gains with no accounting for spatial autocorrelation ($\overline{RE}=0.23$) to a conditionally-autoregressive (CAR) F-H model that further reduced estimator variance ($\overline{RE}=0.19$), noting that the CAR model performance was generally greater in domains (stands) sharing boundaries with high numbers (> 10) of neighboring stands. The non-stationary spatial process (Chandra et al., 2012) may improve upon simpler CAR and SAR modeling approaches, as it employs a distance-weighted measure of correlation among domains rather than a simple binary model based on domain adjacency. Spatial models provide a promising tool for future applications of area-level SAE that account for non-trivial spatial correlations among small area domains likely to be realistic in many forest inventory applications (Finley et al., 2011; Magnussen et al., 2017).

4.1.4. Unit Level vs. Area Level SAE

Although area-level EBLUPS have shown clear gains in efficiency over direct estimates in forest inventory SAE applications, still greater gains have been demonstrated using unit-level approaches when suitable data are available and model assumptions are met (Breidenbach et al., 2016, 2018). In comparing both approaches to direct estimates of forest volume, Mauro et al. (2017) observed halving of variance ($\overline{RE}$ = 0.48) and ten-fold reduction ($\overline{RE}$ = 0.09) for area-level and unit-level estimates, respectively. A notable feature in the study was the large proportion—slightly more than half—of the 84 stand groupings defined as small area domains containing n_d ≤ 6 field plots, linking greatest gains in efficiency to domains having relatively small n_d. Their unit-level results achieved variance reductions among the largest of any reported in forest inventory literature (Mauro et al., 2017; Pascual et al., 2018). By comparison, Breidenbach et al. (2018) reported $\overline{RE}=0.50$ (see Section 4.1.3) for area-level and $\overline{RE}=0.28$ (see Section 4.1.2) for unit-level estimators applied to a common data set. Their domain-direct sample sizes were also small [4 ≤ n_d ≤ 7], so the source of differential gains between the two studies' unit-level estimators may be related to other factors including the strength of the synthetic model relationships, which we weren't able to compare between the two studies (Mauro et al., 2017; Breidenbach et al., 2018). A distinct barrier to achieving large gains in efficiency with unit-level SAE, especially compared to area-level approaches, is the ability to accurately georeference field plots and spatial auxiliary data sources. Green et al. (2020) noted this as a possible reason for the lack of gains in their unit-level models compared to area-level SAE.

4.2. Variance Estimation

Variances for model coefficients and estimates of finite-population parameters for design-based direct or model-assisted estimates (Sections 2.1 and 2.2) are in most cases calculable using commercially available statistical software packages (Molina and Marhuenda, 2015; Breidenbach, 2018; McConville et al., 2018; Hill et al., 2021). Other variance estimators are documented in research literature in sufficient detail to facilitate calculation with scientific programming software (McRoberts, 2012; Mandallaz et al., 2013; Babcock et al., 2015; Magnussen et al., 2017; Mauro et al., 2017; Frank et al., 2020). In design-based model-assisted estimators, variance calculations exist in closed form for some estimators such as GREG, or as approximations for others including ratio estimators (Särndal et al., 1992; Breidenbach and Astrup, 2012; Mandallaz, 2013; Magnussen et al., 2018). Because variance calculations often require accounting for non-independence of observations or heteroskedasticity of residuals, or where algorithmic synthetic models such as non-parametric or nearest-neighbor modeling are employed, iterative methods can be used to estimate approximate variances, even where closed-form solutions exist when model assumptions allow for them (McRoberts et al., 2007). Numerical approaches, such as leave-one-out cross validation or parametric bootstrap estimation have proven useful in variance estimation, although care must be taken to ensure that bootstrap data-generating mechanisms are aligned with error correlation structures and distributional assumptions.

Standard errors of domain-direct estimates are required inputs for FH and other area-based SAE, which can pose a problem when n_d is insufficient to give stable variance estimates (Särndal, 1984; Breidenbach and Astrup, 2012). A solution for such applications is the use of generalized variance estimators (Valliant, 1987; Wolter, 2007; Goerndt et al., 2013; Coulston et al., 2021). Generalized variance functions tend to give variance estimates that are highly dependent on n_d, e.g., Coulston et al. (2021), which may differ from direct variance estimates in domains having sufficient sampling intensity to produce stable standard errors.

Closed form solutions typically do not exist for variance estimation for SAE composite estimators, e.g., when domain-level estimates are obtained as EBLUPs (Fay and Herriot, 1979; Battese et al., 1988; Rao and Molina, 2015). Variance of EBLUPs is assessed by mean squared errors (MSE) rather than standard errors to distinguish EBLUPS from design-unbiased estimators. The MSEs are routinely calculated in SAE software as additive combinations of terms representing uncertainties associated with (a) prediction of random effects, (b) estimation of regression model coefficients, and (c) estimation of the random-effect variance, i.e., the variance among small-area domains (Prasad and Rao, 1990). Alternatives involving parametric bootstrap variance estimation are employed in some applications, as are variances determined from posterior distributions in Bayesian analyses (Prasad and Rao, 1990; Babcock et al., 2015; Molina and Marhuenda, 2015).

4.3. Emerging Applications

Bayesian methods have been applied to SAE across disciplines for several decades (Morris, 1983; Ghosh and Rao, 1994), with recent applications in forest inventory settings as well (e.g., Finley et al., 2011). Babcock et al. (2018) used HB to estimate aboveground biomass with coupled auxiliary data from Landsat and lidar, to resolve incomplete coverage of remote sensing data. Of the HB models they tested, one incorporating spatial random effects with lidar as auxiliary data led to $0.33\le \overline{RE}\le 0.51$ across their 4 areas of interest. By incorporating coregionalization and adding tree cover derived from Landsat to complement incomplete lidar coverage, the range of $\overline{RE}$ decreased to $0.16\le \overline{RE}\le 0.35$. Ver Planck et al. (2018) also saw success in formulating the F-H approach in a HB framework to increase precision of aboveground biomass SAE over direct estimates ($\overline{RE}=0.23$). Further improvement was demonstrated by adding conditional autoregressive random effects to account for spatial correlation ($\overline{RE}=0.80$), with the autoregressive model giving greater gains in precision in domains that shared boundaries with larger numbers of neighbors (Ver Planck et al., 2018). Adding a spatial random effect did not always lead to greater predictive performance, however, as shown by Babcock et al. (2015), who attributed modest to negative gains ($0.83\le \overline{RE}\le 1.27$) to possible overfitting.

Estimating population parameters for multiple attributes of interest is an important concern in forest inventory applications ranging from local-scale stand assessments to regional and national multi-resource inventories (Babcock et al., 2013; Lochhead et al., 2018). Multivariate F-H and spatial F-H approaches have been developed and incorporated into statistical software, but their application to forest inventory has been limited (Molina and Marhuenda, 2015; Benavent and Morales, 2016). While multiple domain-specific estimates can be obtained using SAE in separate modeling procedures for each attribute, doing so fails to maintain logical consistencies among estimates, and overlooks potential gains in efficiency that may otherwise be realized by accounting for cross-attribute correlations (Mauro et al., 2017; Coulston et al., 2021). Generic inference in model-assisted design-based estimation affords consistency in multivariate estimates, but may come at a cost of increased standard errors in attributes uncorrelated or weakly correlated with selected auxiliary variables (McConville et al., 2020). Nearest-neighbor approaches have been used successfully in multivariate forest inventory settings, including multivariate model-assisted estimation to improve estimator efficiencies while preserving consistency among estimates (Chirici et al., 2016; McRoberts et al., 2017). Hierarchical Bayesian multivariate methods for SAE have been demonstrated for both unit-level and area-level settings suitable for forest inventory applications (Datta et al., 1998; Arima et al., 2017). Recent advances have also increased computational efficiencies for Bayesian analyses that can be applied to multivariate SAE involving very large data sets, expanding opportunities for further advances in this area (Finley et al., 2015, 2017; Datta et al., 2016; Babcock et al., 2018).

Another development in SAE applications for forest inventory aims at modeling sample and observational units at a level approaching that of individual trees rather than forest plots or larger subpopulation domains (Næsset, 2002; Mauro et al., 2016). Frank et al. (2020) tested a semi-individual tree (s-ITC) model approach—analogous to a unit-level approach—by segmenting tree crowns in lidar point clouds and delineating s-ITC units around them. Compared to a unit-level approach the s-ITC model showed a $\overline{RE}=1.04$ for volume, $\overline{RE}=0.71$ for basal area, $\overline{RE}=1.38$ for stem density, and $\overline{RE}=0.48$ for quadratic mean diameter. Despite attaining similar precision as plot-based unit-level EBLUPs for volume estimates at the population level, the s-ITC approach showed potential for its increased spatial resolution and ability to estimate population parameters more closely related to individual trees, such as mean diameter (Frank et al., 2020).

Applications of enhanced estimators such as model-assisted and SAE are not limited to cases where estimates per unit of land area are needed. Affleck and Gregoire (2015) compared estimation of crown biomass using randomized branch sampling to provide sample data for GREG. In their examination of a univariate estimator, model-assisted estimation led to improvement in the precision of estimates across a range of simulated sample sizes in randomized branch sampling (n = 5, 10, 20 and $\overline{RE}=0.54$, 0.71, and 0.97, respectively), although the authors cautioned against the possible trade-off between precision and design-unbiasedness (Affleck and Gregoire, 2015). Gains in precision were not limited to one sampling scheme. Increased precision was also seen for n = 5 based on other branch sampling methods: probability proportional to size sampling ($\overline{RE}=0.94$), simple random sampling ($\overline{RE}=0.28$), and stratified random sampling ($\overline{RE}=0.28$). The potential gains in biomass estimation at the tree level demonstrates how SAE may prove a useful tool in other contexts than estimating forest inventory attributes for small geographic areas.

5. Conclusions

Small area estimation (SAE) is a growing area of research in forest inventory owing largely to its ability to support model-based inference in small area domains lacking sufficient sample data to provide stable estimates using purely design-based estimation. A variety of modeling techniques can be employed in the SAE framework with linear mixed modeling among the most widely used to-date. A unifying requirement is the use of auxiliary data that allows estimators to both borrow strength from indirect sample data that co-vary with auxiliary observations and to provide auxiliary population parameters as predictors in synthetic models for composite estimation. The availability of large data sets like those collected in NFIs, along with increasingly available auxiliary data such as DAP, ALS, satellite remote-sensing, or other digital map products has made SAE of particular interest to forest inventory specialists. Increases in precision from SAE can provide efficient alternatives to sample intensification when insufficient sample data are available to meet needed tolerances for estimator error.

The examples summarized here demonstrate potential benefits of SAE, along with some limitations researchers have encountered in applying evolving model-assisted design-based estimators or composite estimators that lie within unit-level or area-level SAE frameworks. As with any model-based approaches considerable attention should be paid to model assumptions including distributional assumptions for residuals, correct model form (e.g., linear vs. non-linear), careful selection of model predictors, and accounting for correlation structures among synthetic model residuals. Challenges may arise from a lack of correspondence between sample and auxiliary data such as when precise pairing of (x, y) observations is impractical, or when auxiliary data are unavailable for specific areas or time periods of interest. Consideration of alternative approaches including design-based and model-assisted estimation, area-level, or unit-level (model-based) SAE is needed to ensure suitability of methods given inferential needs. Many topics for further research have been identified in the literature reviewed here, pointing out opportunities for future improvement in forest inventory applications of SAE. Although no tool can address needs in all circumstances, methods like those reviewed here provide flexible, efficient alternatives to reduce the need for sample intensification in many cases and to meet tolerance specifications in others at reduced cost by increasing estimator efficiency.

Author Contributions

GD, PR, and JC: conception, design, and outline. GD and PR: literature review and document drafts. JC, PG, BW, and GM: reviewed drafts, provided corrections and revisions, discussion of needed changes, additions, and redesign. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by USDA Forest Service Southern Research Station and Virginia Tech Department of Forest Resources and Environmental Conservation, Joint Venture Agreement 20-JV-11330145-074. Sponsorship of research into improving estimation of timber damage in tropical storms in the southeastern United States. Funds from the Virginia Tech Library paid for open-access fees.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Affleck, D. L. R., and Gregoire, T. G. (2015). Generalized and synthetic regression estimators for randomized branch sampling. Forestry 88, 599–611. doi: 10.1093/forestry/cpv027

CrossRef Full Text | Google Scholar

Anderson, H. E., and Breidenbach, J. (2007). “Statistical properties of mean stand biomass estimators in a LIDAR-based double sampling forest survey design,” in Proceedings of the ISPRS Workshop on Laser Scanning and SilviLaser (Espoo), 8–13.

Google Scholar

Arima, S., Bell, W. R., Datta, G. S., Franco, C., and Liseo, B. (2017). Multivariate fay-herriot bayesian estimation of small area means under functional measurement error. J. R. Stat. Soc. Ser. A Stat Soc. 180, 1191–1209. doi: 10.1111/rssa.12321

CrossRef Full Text | Google Scholar

Astrup, R., Rahlf, J., Bjorkelo, K., Debella-Gilo, M., Gjertsen, A.-K., and Breidenbach, J. (2019). Forest information at multiple scales: development, evaluation and application of the Norwegian forest resources map SR16. Scand. J. Forest Res. 34, 484–496. doi: 10.1080/02827581.2019.1588989

CrossRef Full Text | Google Scholar

Babcock, C., Finley, A. O., Andersen, H.-E., Pattison, R., Cook, B. D., Morton, D. C., et al. (2018). Geostatistical estimation of forest biomass in interior Alaska combining Landsat-derived tree cover, sampled airborne lidar and field observations. Remote Sens. Environ. 212, 212–230. doi: 10.1016/j.rse.2018.04.044

CrossRef Full Text | Google Scholar

Babcock, C., Finley, A. O., Bradford, J. B., Kolka, R., Birdsey, R., and Ryan, M. G. (2015). LiDAR based prediction of forest biomass using hierarchical models with spatially varying coefficients. Remote Sens. Environ. 169, 113–127. doi: 10.1016/j.rse.2015.07.028

CrossRef Full Text | Google Scholar

Babcock, C., Matney, J., Finley, A. O., Weiskittel, A., and Cook, B. D. (2013). Multivariate spatial regression models for predicting individual tree structure variables using lidar data. IEEE J. Select. Top. Appl. Earth Observat. Remote Sens. 6, 6–14. doi: 10.1109/JSTARS.2012.2215582

CrossRef Full Text | Google Scholar

Battese, G. E., Harter, R. M., and Fuller, W. A. (1988). An error-components model for prediction of county crop areas using survey and satellite data. J. Am. Stat. Assoc. 83, 10. doi: 10.1080/01621459.1988.10478561

CrossRef Full Text | Google Scholar

Bechtold, W. A., and Patterson, P. L. (2005). The Enhanced Forest Inventory and Analysis Program - National Sampling Design and Estimation Procedures. Technical report. U.S. Department of Agriculture, Forest Service, Southern Research Station.

Google Scholar

Benavent, R., and Morales, D. (2016). Multivariate Fay-Herriot models for small area estimation. Comput. Stat. Data Anal. 94, 372–390. doi: 10.1016/j.csda.2015.07.013

CrossRef Full Text | Google Scholar

Breidenbach, J. (2018). JoSAE: Unit-Level and Area-Level Small Area Estimation. Comprehensive R Archive Network. Available online at: https://CRAN.R-project.org/package=JoSAE (accessed February 28, 2022).

Google Scholar

Breidenbach, J., and Astrup, R. (2012). Small area estimation of forest attributes in the Norwegian National Forest Inventory. Eur. J. Forest Res. 131, 1255–1267. doi: 10.1007/s10342-012-0596-7

CrossRef Full Text | Google Scholar

Breidenbach, J., Granhus, A., Hylen, G., Eriksen, R., and Astrup, R. (2020). A century of National Forest Inventory in Norway-informing past, present, and future decisions. Forest Ecosyst. 7, 46. doi: 10.1186/s40663-020-00261-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Breidenbach, J., Magnussen, S., Rahlf, J., and Astrup, R. (2018). Unit-level and area-level small area estimation under heteroscedasticity using digital aerial photogrammetry data. Remote Sens. Environ. 212, 199–211. doi: 10.1016/j.rse.2018.04.028

CrossRef Full Text | Google Scholar

Breidenbach, J., McRoberts, R. E., and Astrup, R. (2016). Empirical coverage of model-based variance estimators for remote sensing assisted estimation of stand-level timber volume. Remote Sens. Environ. 173, 274–281. doi: 10.1016/j.rse.2015.07.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Breidenbach, J., Nothdurft, A., and Kandler, G. (2010). Comparison of nearest neighbour approaches for small area estimation of tree species-specific forest inventory attributes in central Europe using airborne laser scanner data. Eur. J. Forest Res. 129, 833–846. doi: 10.1007/s10342-010-0384-1

CrossRef Full Text | Google Scholar

Bright, B. C., Hicke, J. A., and Hudak, A. T. (2012). Estimating aboveground carbon stocks of a forest affected by mountain pine beetle in Idaho using lidar and multispectral imagery. Remote Sens. Environ. 124, 270–281. doi: 10.1016/j.rse.2012.05.016

CrossRef Full Text | Google Scholar

Burk, T. E., and Ek, A. R. (1982). Application of empirical Bayes/James-Stein procedures to simultaneous estimation problems in forest inventory. Forest Sci. 28, 753–771.

Google Scholar

Chandra, H., Salvati, N., and Chambers, R. (2015). A spatially nonstationary Fay-Herriot model for small area estimation. J. Surv. Stat. Methodol. 3, 109–135. doi: 10.1093/jssam/smu026

CrossRef Full Text | Google Scholar

Chandra, H., Salvati, N., Chambers, R., and Tzavidis, N. (2012). Small area estimation under spatial nonstationarity. Comput. Stat. Data Anal. 56, 2875–2888. doi: 10.1016/j.csda.2012.02.006

CrossRef Full Text | Google Scholar

Chirici, G., Mura, M., McInerney, D., Py, N., Tomppo, E. O., Waser, L. T., et al. (2016). A meta-analysis and review of the literature on the k-nearest neighbors technique for forestry applications that use remotely sensed data. Remote Sens. Environ. 176, 282–294. doi: 10.1016/j.rse.2016.02.001

CrossRef Full Text | Google Scholar

Costa, A., Satorra, A., and Ventura, E. (2003). “An empirical evaluation of small area estimators,” in Economics Working Papers 674 (Barcelona: Department of Economics and Business, Pompeu Fabra University). Available online at: https://ideas.repec.org/p/upf/upfgen/674.html

Google Scholar

Costa, A., Satorra, A., and Ventura, E. (2009). On the performance of small-area estimators: fixed vs. random area parameters. Sort 33, 85–104. Available online at: http://dmle.icmat.es/pdf/SORT_2009_33_01_04.pdf (accessed February 28, 2022).

Google Scholar

Coulston, J. W., Green, P. C., Radtke, P. J., Prisley, S. P., Brooks, E. B., Thomas, V. A., et al. (2021). Enhancing the precision of broad-scale forestland removals estimates with small area estimation techniques. Forestry Int. J. Forest Res. 94, 427–441. doi: 10.1093/forestry/cpaa045

CrossRef Full Text | Google Scholar

Datta, A., Banerjee, S., Finley, A. O., and Gelfand, A. E. (2016). Hierarchical nearest-neighbor gaussian process models for large geostatistical datasets. J. Am. Stat. Assoc. 111, 800–812. doi: 10.1080/01621459.2015.1044091

PubMed Abstract | CrossRef Full Text | Google Scholar

Datta, G. S., Day, B., and Maiti, T. (1998). Multivariate bayesian small area estimation: an application to survey and satellite data. Sankhya Indian J. Stat. Ser. A 60, 344–362.

Google Scholar

Datta, G. S., and Mandal, A. (2015). Small area estimation with uncertain random effects. J. Am. Stat. Assoc. 110, 1735–1744. doi: 10.1080/01621459.2015.1016526

CrossRef Full Text | Google Scholar

Fay, R. E., and Herriot, R. A. (1979). Estimates of income for small places: An application of James-Stein procedures to census data. J. Am. Stat. Assoc. 74, 269–277. doi: 10.1080/01621459.1979.10482505

CrossRef Full Text | Google Scholar

Federal Committee on Statistical Methodology (1993). Indirect Estimators in Federal Programs. Technical report, Office of Management and Budget, Washington, DC.

Google Scholar

Finley, A. O., Banerjee, S., and MacFarlane, D. W. (2011). A hierarchical model for quantifying forest variables over large heterogeneous landscapes with uncertain forest areas. J. Am. Stat. Assoc. 106, 31–48. doi: 10.1198/jasa.2011.ap09653

PubMed Abstract | CrossRef Full Text | Google Scholar

Finley, A. O., Banerjee0, S., Zhou, Y., Cook, B. D., and Babcock, C. (2017). Joint hierarchical models for sparsely sampled high-dimensional lidar and forest variables. Remote Sens. Environ. 190, 149–161. doi: 10.1016/j.rse.2016.12.004

CrossRef Full Text | Google Scholar

Finley, A. O., Bsnerjee, S., and Gelfand, A. E. (2015). spBayes for large univariate and multivariate point-referenced spatio-temporal data models. J. Stat. Softw. 63, 1–28. doi: 10.18637/jss.v063.i13

CrossRef Full Text | Google Scholar

Frank, B., Mauro, F., and Temesgen, H. (2020). Model-based estimation of forest inventory attributes using Lidar: a comparison of the area-based and semi-individual tree crown approaches. Remote Sens. 12, 2525. doi: 10.3390/rs12162525

CrossRef Full Text | Google Scholar

Fuller, W. A. (1999). Environmental surveys over time. J. Agric. Biol. Environ. Stat. 4, 331–354. doi: 10.2307/1400493

CrossRef Full Text | Google Scholar

Ghosh, M., and Rao, J. N. K. (1994). Small area estimation: an appraisal. Stat. Sci. 9, 55–76. doi: 10.1214/ss/1177010647

CrossRef Full Text | Google Scholar

Goerndt, M. E., Monleon, V. J., and Temesgen, H. (2011). A comparison of small-area estimation techniques to estimate selected stand attributes using LiDAR-derived auxiliary variables. Can. J. Forest Res. 41, 1189–1201. doi: 10.1139/x11-033

CrossRef Full Text | Google Scholar

Goerndt, M. E., Monleon, V. J., and Temesgen, H. (2013). Small-area estimation of county-level forest attributes using ground data and remote sensed auxiliary information. Forest Sci. 59, 536–548. doi: 10.5849/forsci.12-073

CrossRef Full Text | Google Scholar

Goerndt, M. E., Wilson, B. T., and Aguilar, F. X. (2019). Comparison of small area estimation methods applied to biopower feedstock supply in the Northern U.S. region. Biomass Bioenergy 121, 64–77. doi: 10.1016/j.biombioe.2018.12.008

CrossRef Full Text | Google Scholar

González -Manteiga, W., and Morales, D. (2008). Bootstrap mean squared error of small-area EBLUP. J. Stat. Comput. Simul. 78, 443–462. doi: 10.1080/00949650601141811

CrossRef Full Text | Google Scholar

Green, P. C., Burkhart, H. E., Coulston, J. W., and Radtke, P. J. (2020). A novel application of small area estimation in loblolly pine forest inventory. Forestry Int. J. Forest Res. 93, 444–457. doi: 10.1093/forestry/cpz073

CrossRef Full Text | Google Scholar

Gregoire, T., and Valentine, H. (2007). Sampling Strategies for Natural Resources and the Environment. Boca Raton, FL: Chapman and Hall/CRC. doi: 10.1201/9780203498880

PubMed Abstract | CrossRef Full Text | Google Scholar

Gregoire, T. G. (1998). Design-based and model-based inference in survey sampling: appreciating the difference. Can. J. Forest Res. 28, 1429–1447. doi: 10.1139/x98-166

CrossRef Full Text | Google Scholar

Guldin, R. W. (2021). A systematic review of small domain estimation research in forestry during the twenty-first century from outside the United States. Front. Forests Glob. Change 4, 695929. doi: 10.3389/ffgc.2021.695929

CrossRef Full Text | Google Scholar

He, Z., and Sun, D. (2000). Hierarchical Bayes estimation of hunting success rates with spatial correlations. Biometrics 56, 360–367. doi: 10.1111/j.0006-341X.2000.00360.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, A., Massey, A., and Mandallaz, D. (2021). The R package forestinventory: design-based global and small area estimations for multiphase forest inventories. J. Stat. Softw. 97, 1–40. doi: 10.18637/jss.v097.i04

CrossRef Full Text | Google Scholar

Irulappa-Pillai-Vijayakumar, D. B., Renaud, J.-P., Morneau, F., McRoberts, R. E., and Vega, C. (2019). Increasing precision for french forest inventory estimates using the k-nn technique with optical and photogrammetric data and model-assisted estimators. Remote Sens. 11, 991. doi: 10.3390/rs11080991

CrossRef Full Text | Google Scholar

James, W., and Stein, C. (1961). “Estimation with quadratic loss,” in Fourth Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, ed J. Neyman (Berkeley, CA: University of California Press), 361–379.

Google Scholar

Järnstedt, J., Pekkarinen, A., Tuominen, S., Ginzler, C., Holopainen, M., and Viitala, R. (2012). Forest variable estimation using a high-resolution digital surface model. ISPRS J. Photogrammetry Remote Sens. 74, 78–84. doi: 10.1016/j.isprsjprs.2012.08.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, A. A., Breidt, F. J., and Opsomer, J. D. (2008). Estimating distribution functions from survey data using nonparametric regression. J. Stat. Theory Pract. 2, 419–431. doi: 10.1080/15598608.2008.10411884

PubMed Abstract | CrossRef Full Text | Google Scholar

Kangas, A., Myllymäki, M., Gobakken, T., and Næsset, E. (2016). Model-assisted forest inventory with parametric, semiparametric, and nonparametric models. Can. J. Forest Res. 46, 855–868. doi: 10.1139/cjfr-2015-0504

CrossRef Full Text | Google Scholar

Kotivuori, E., Korhonen, L., and Packalen, P. (2016). Nationwide airborne laser scanning based models for volume, biomass and dominant height in Finland. Silva Fennica 50, 1567. doi: 10.14214/sf.1567

CrossRef Full Text | Google Scholar

Latifi, H., Nothdurft, A., and Koch, B. (2010). Non-parametric prediction and mapping of standing timber volume and biomass in a temperate forest: application of multiple optical/LiDAR-derived predictors. Forestry 83, 395–407. doi: 10.1093/forestry/cpq022

CrossRef Full Text | Google Scholar

Lehtonen, R., and Veijanen, A. (2009). “Chapter 31: Design-based methods of estimation for domains and small areas,” in Handbook of Statistics, ed C. R. Rao (Amsterdam: Elsevier), 219–249. doi: 10.1016/S0169-7161(09)00231-4

CrossRef Full Text | Google Scholar

Lochhead, K., LeMay, V., Bull, G., Schwab, O., and Halperin, J. (2018). Multivariate estimation for accurate and logically consistent forest-attributes maps at macroscales. Can. J. Forest Res. 48, 345–359. doi: 10.1139/cjfr-2017-0221

CrossRef Full Text | Google Scholar

Magnussen, S., Mandallaz, D., Breidenbach, J., Lanz, A., and Ginzler, C. (2014). National forest inventories in the service of small area estimation of stem volume. Can. J. Forest Res. 44, 1079–1090. doi: 10.1139/cjfr-2013-0448

CrossRef Full Text | Google Scholar

Magnussen, S., Mauro, F., Breidenbach, J., Lanz, A., and Kändler, G. (2017). Area-level analysis of forest inventory variables. Eur. J. Forest Res. 136, 839–855. doi: 10.1007/s10342-017-1074-z

CrossRef Full Text | Google Scholar

Magnussen, S., Nord-Larsen, T., and Riis-Nielsen, T. (2018). Lidar supported estimators of wood volume and aboveground biomass from the Danish National Forest Inventory (2012–2016). Remote Sens. Environ. 211, 146–153. doi: 10.1016/j.rse.2018.04.015

CrossRef Full Text | Google Scholar

Mandallaz, D. (2013). Design-based properties of some small-area estimators in forest inventory with two-phase sampling. Can. J. Forest Res. 43, 441–449. doi: 10.1139/cjfr-2012-0381

CrossRef Full Text | Google Scholar

Mandallaz, D., Breschan, J., and Hill, A. (2013). New regression estimators in forest inventories with two-phase sampling and partially exhaustive information: a design-based Monte Carlo approach with applications to small-area estimation. Can. J. Forest Res. 43, 1023–1031. doi: 10.1139/cjfr-2013-0181

CrossRef Full Text | Google Scholar

Mauro, F., Molina, I., Garcia-Abril, A., Valbuena, R., and Ayuga-Tellez, E. (2016). Remote sensing estimates and measures of uncertainty for forest variables at different aggregation levels. Environmetrics 27, 225–238. doi: 10.1002/env.2387

CrossRef Full Text | Google Scholar

Mauro, F., Monleon, V. J., Temesgen, H., and Ford, K. R. (2017). Analysis of area level and unit level models for small area estimation in forest inventories assisted with LiDAR auxiliary information. PLoS ONE 12, e0189401. doi: 10.1371/journal.pone.0189401

PubMed Abstract | CrossRef Full Text | Google Scholar

Mauro, F., Ritchie, M., Wing, B., Frank, B., Monleon, V., Temesgen, H., et al. (2019). Estimation of changes of forest structural attributes at three different spatial aggregation levels in Northern California using multitemporal LiDAR. Remote Sens. 11, 923. doi: 10.3390/rs11080923

CrossRef Full Text | Google Scholar

McConville, K., Tang, B., Zhu, G., Cheung, S., and Li, S. (2018). mase: Model-Assisted Survey Estimation. Comprehensive R Archive Network. Available online at: https://cran.r-project.org/package=mase (accessed February 28, 2022).

Google Scholar

McConville, K. S., Breidt, F. J., Lee, T. C. M., and Moisen, G. G. (2017). Model-assisted survey regression estimation with the Lasso. J. Surv. Stat. Methodol. 5, 131–158. doi: 10.1093/jssam/smw041

PubMed Abstract | CrossRef Full Text | Google Scholar

McConville, K. S., Moisen, G. G., and Frescino, T. S. (2020). A tutorial on model-assisted estimation with application to forest inventory. Forests 11, 244. doi: 10.3390/f11020244

CrossRef Full Text | Google Scholar

McRoberts, R. E. (2012). Estimating forest attribute parameters for small areas using nearest neighbors techniques. Forest Ecol. Manage. 272, 3–12. doi: 10.1016/j.foreco.2011.06.039

CrossRef Full Text | Google Scholar

McRoberts, R. E., Chen, Q., and Walters, B. F. (2017). Multivariate inference for forest inventories using auxiliary airborne laser scanning data. Forest Ecol. Manage. 401, 295–303. doi: 10.1016/j.foreco.2017.07.017

CrossRef Full Text | Google Scholar

McRoberts, R. E., Næsset, E., and Gobakken, T. (2013). Inference for lidar-assisted estimation of forest growing stock volume. Remote Sens. Environ. 128, 268–275. doi: 10.1016/j.rse.2012.10.007

CrossRef Full Text | Google Scholar

McRoberts, R. E., Tomppo, E. O., Finley, A. O., and Heikkinen, J. (2007). Estimating areal means and variances of forest attributes using the k-Nearest Neighbors technique and satellite imagery. Remote Sens. Environ. 111, 466–480. doi: 10.1016/j.rse.2007.04.002

CrossRef Full Text | Google Scholar

Molina, I., and Marhuenda, Y. (2015). sae: An R package for small area estimation. R J. 7, 81–98. doi: 10.32614/RJ-2015-007

CrossRef Full Text | Google Scholar

Morris, C. N. (1983). Parametric empirical bayes inference: theory and applications. J. Am. Stat. Assoc. 78, 47–55. doi: 10.1080/01621459.1983.10477920

CrossRef Full Text | Google Scholar

Næsset, E. (2002). Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 80, 88–99. doi: 10.1016/S0034-4257(01)00290-5

CrossRef Full Text | Google Scholar

Næsset, E., Gobakken, T., Bollandss, O. M., Gregoire, T. G., Nelson, R., and Sthl, G. (2013). Comparison of precision of biomass estimates in regional field sample surveys and airborne LiDAR-assisted surveys in Hedmark County, Norway. Remote Sens. Environ. 130, 108–120. doi: 10.1016/j.rse.2012.11.010

CrossRef Full Text | Google Scholar

Næsset, E., Gobakken, T., Solberg, S., Gregoire, T. G., Nelson, R., Stahl, G., et al. (2011). Model-assisted regional forest biomass estimation using LiDAR and InSAR as auxiliary data: A case study from a boreal forest area. Remote Sens. Environ. 115, 3599–3614. doi: 10.1016/j.rse.2011.08.021

CrossRef Full Text | Google Scholar

Nagle, N. N., Schroeder, T. A., and Rose, B. (2019). A regularized raking estimator for small-area mapping from forest inventory surveys. Forests 10, 1045. doi: 10.3390/f10111045

CrossRef Full Text | Google Scholar

Nilsson, M., Nordkvist, K., Jonzan, J., Lindgren, N., Axensten, P., Wallerman, J., et al. (2017). A nationwide forest attribute map of Sweden predicted using airborne laser scanning data and field data from the national forest inventory. Remote Sens. Environ. 194, 447–454. doi: 10.1016/j.rse.2016.10.022

CrossRef Full Text | Google Scholar

Nord-Larsen, T., and Schumacher, J. (2012). Estimation of forest resources from a country wide laser scanning survey and national forest inventory data. Remote Sens. Environ. 119, 148–157. doi: 10.1016/j.rse.2011.12.022

CrossRef Full Text | Google Scholar

Novo-Fernandez, A., Barrio-Anta, M., Recondo, C., Camara-Obregon, A., and Lopez-Sanchez, C. A. (2019). Integration of national forest inventory and nationwide airborne laser scanning data to improve forest yield predictions in north-western Spain. Remote Sens. 11, 1693. doi: 10.3390/rs11141693

CrossRef Full Text | Google Scholar

Ohmann, J. L., and Gregory, M. J. (2002). Predictive mapping of forest composition and structure with direct gradient analysis and nearest- neighbor imputation in coastal Oregon, USA. Can. J. Forest Res. 32, 725–741. doi: 10.1139/x02-011

CrossRef Full Text | Google Scholar

Opsomer, J. D., Breidt, F. J., Moisen, G. G., and Kauermann, G. (2007). Model-assisted estimation of forest resources with generalized additive models. J. Am. Stat. Assoc. 102, 400–409. doi: 10.1198/016214506000001491

CrossRef Full Text | Google Scholar

Pascual, C., Mauro, F., Abril, A. G., and Manzanera, J. A. (2018). “Applications of ALS (Airborne Laser Scanning) data to forest inventory. Experiences with pine stands from mountainous environments in Spain,” in IOP Conference Series-Earth and Environmental Science (Voronezh), 1–12. doi: 10.1088/1755-1315/226/1/012001

CrossRef Full Text | Google Scholar

Patterson, P. L., Healey, S. P., Stahl, G., Saarela, S., Holm, S., Andersen, H. E., et al. (2019). Statistical properties of hybrid estimators proposed for GEDI-NASA's global ecosystem dynamics investigation. Environ. Res. Lett. 14, 065007. doi: 10.1088/1748-9326/ab18df

CrossRef Full Text | Google Scholar

Pfeffermann, D. (2002). Small area estimation–New developments and directions. Int. Stat. Rev. 70, 125–143. doi: 10.1111/j.1751-5823.2002.tb00352.x

CrossRef Full Text | Google Scholar

Pfeffermann, D. (2013). New important developments in small area estimation. Stat. Sci. 28, 40–68. doi: 10.1214/12-STS395

CrossRef Full Text | Google Scholar

Popescu, S. C., Zhao, K., Neuenschwander, A., and Lin, C. (2011). Satellite lidar vs. small footprint airborne lidar: comparing the accuracy of aboveground biomass estimates and forest structure metrics at footprint level. Remote Sens. Environ. 115, 2786–2797. doi: 10.1016/j.rse.2011.01.026

CrossRef Full Text | Google Scholar

Prasad, N., and Rao, J. N. K. (1990). The estimation of the mean squared error of small-area estimators. J. Am. Stat. Assoc. 85, 163–171. doi: 10.1080/01621459.1990.10475320

CrossRef Full Text | Google Scholar

Radtke, P., and Bolstad, P. (2001). Laser point-quadrat sampling for estimating foliage height profiles in broad-leaved forests. Can. J. Forest Res. 31, 410–418. doi: 10.1139/x00-182

CrossRef Full Text | Google Scholar

Rahlf, J., Breidenbach, J., Solberg, S., Næsset, E., and Astrup, R. (2014). Comparison of four types of 3d data for timber volume estimation. Remote Sens. Environ. 155, 325–333. doi: 10.1016/j.rse.2014.08.036

CrossRef Full Text | Google Scholar

Rahman, A., and Harding, A. (2017). Small Area Estimation and Microsimulation Modeling. Boca Raton, FL: CRC Press. doi: 10.1201/9781315372143

CrossRef Full Text | Google Scholar

Rao, J. N. K. (2008). Some methods for small area estimation. Rivista Internazionale di Scienze Sociali 116, 387–405. Available online at: http://www.jstor.org/stable/41625216 (accessed February 28, 2022).

Google Scholar

Rao, J. N. K., and Molina, I. (2015). Small Area Estimation, 2nd Edn. Hoboken, NJ: John Wiley & Sons, Inc. doi: 10.1002/9781118735855

CrossRef Full Text | Google Scholar

Reich, R. M., and Aguirre-Bravo, C. (2009). Small-area estimation of forest stand structure in Jalisco, Mexico. J. Forest. Res. 20, 285–292. doi: 10.1007/s11676-009-0050-y

CrossRef Full Text | Google Scholar

Särndal, C.-E., Swensson, B., and Wretman, J. (1992). Model Assisted Survey Sampling. New York, NY: Springer Science & Business Media. doi: 10.1007/978-1-4612-4378-6

CrossRef Full Text | Google Scholar

Särndal, C. E. (1984). Design-consistent versus model-dependent estimation for small domains. J. Am. Stat. Assoc. 79, 624–631. doi: 10.1080/01621459.1984.10478089

CrossRef Full Text | Google Scholar

Schaible, W. L. (1993). “Indirect estimators: definition, characteristics, and recommendations,” in Proceedings of the Survey Research Methods Section (San Francisco, CA: American Statistical Association), 1–10.

Google Scholar

Schreuder, H. T., Gregoire, T. G., and Wood, G. B. (1993). Sampling Methods for Multiresource Forest Inventory. New York, NY: John Wiley & Sons.

Google Scholar

Schumacher, F. X. (1945). Statistical method in forestry. Biometr. Bull. 1, 29–32. doi: 10.2307/3001954

CrossRef Full Text | Google Scholar

Shiver, B., and Borders, B. (1996). Sampling Techniques for Forest Resource Inventory. New York, NY: Wiley.

Google Scholar

Skinner, C., and Wakefield, J. (2017). Introduction to the design and analysis of complex survey data. Stat. Sci. 32, 165–175. doi: 10.1214/17-STS614

CrossRef Full Text | Google Scholar

Stahl, G., Saarela, S., Schnell, S., Holm, S., Breidenbach, J., Healey, S. P., et al. (2016). Use of models in large-area forest surveys: comparing model-assisted, model-based and hybrid estimation. Forest Ecosyst. 3, 5. doi: 10.1186/s40663-016-0064-9

CrossRef Full Text | Google Scholar

Stehman, S. V. (2009). Model-assisted estimation as a unifying framework for estimating the area of land cover and land-cover change from remote sensing. Remote Sens. Environ. 113, 2455–2462. doi: 10.1016/j.rse.2009.07.006

CrossRef Full Text | Google Scholar

Steinmann, K., Mandallaz, D., Ginzler, C., and Lanz, A. (2013). Small area estimations of proportion of forest and timber volume combining Lidar data and stereo aerial images with terrestrial data. Scand. J. Forest Res. 28, 373–385. doi: 10.1080/02827581.2012.754936

CrossRef Full Text | Google Scholar

Sterba, S. K. (2009). Alternative model-based and design-based frameworks for inference from samples to populations: from polarization to integration. Multivariate Behav. Res. 44, 711–740. doi: 10.1080/00273170903333574

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugasawa, S., and Kubokawa, T. (2020). Small area estimation with mixed models: a review. Jpn. J. Stat. Data Sci. 3, 693–720. doi: 10.1007/s42081-020-00076-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Temesgen, H., Mauro, F., Hudak, A. T., Frank, B., Monleon, V., Fekety, P., et al. (2021). Using Fay-Herriot models and variable radius plot data to develop a stand-level inventory and update a prior inventory in the western cascades, or, united states. Front. Forests Glob. Change 4:745916. doi: 10.3389/ffgc.2021.745916

CrossRef Full Text | Google Scholar

Thompson, S. K. (2012). Sampling, 3rd Edn. Hoboken, NJ: John Wiley &Sons. doi: 10.1002/9781118162934

CrossRef Full Text | Google Scholar

Tipton, J., Opsomer, J., and Moisen, G. (2013). Properties of endogenous post-stratified estimation using remote sensing data. Remote Sens. Environ. 139, 130–137. doi: 10.1016/j.rse.2013.07.035

CrossRef Full Text | Google Scholar

Valliant, R. (1987). Generalized variance functions in stratified two-stage sampling. J. Am. Stat. Assoc. 82, 499–508. doi: 10.1080/01621459.1987.10478454

CrossRef Full Text | Google Scholar

Ver Planck, N. R., Finley, A. O., Kershaw, J. A., Weiskittel, A. R., and Kress, M. C. (2018). Hierarchical Bayesian models for small area estimation of forest variables using LiDAR. Remote Sens. Environ. 204, 287–295. doi: 10.1016/j.rse.2017.10.024

CrossRef Full Text | Google Scholar

Wang, J., and Fuller, W. A. (2003). The mean squared error of small area predictors constructed with estimated area variances. J. Am. Stat. Assoc. 98, 716–723. doi: 10.1198/016214503000000620

CrossRef Full Text | Google Scholar

Wang, X., Berg, E., Zhu, Z., Sun, D., and Demuth, G. (2018). Small area estimation of proportions with constraint for national resources inventory survey. J. Agric. Biol. Environ. Stat. 23, 509–528. doi: 10.1007/s13253-018-0329-6

CrossRef Full Text | Google Scholar

Wolter, K. M. (2007). Introduction to Variance Estimation. Statistics for Social and Behavioral Sciences, 2nd Edn. New York, NY: Springer. doi: 10.1007/978-0-387-35099-8_15

CrossRef Full Text | Google Scholar