
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. For. Glob. Change, 21 December 2020
Sec. Forest Soils
Volume 3 - 2020 | https://doi.org/10.3389/ffgc.2020.550884
This article is part of the Research TopicChanges in Forest Ecosystem NutritionView all 25 articles
Root exudation of citrate is discussed as mechanism to mobilize P from the soils' solid phase. Microbial processes can mitigate the mobilization efficiency of citrate. Due to higher microbial activity in topsoils compared to subsoils, we hypothesized a lower mobilization efficiency of exuded citrate in topsoils than in the subsoils. As a model system we used microdialysis (MD) probes and we followed diffusive fluxes of citrate from the perfusate into the soil and of phosphate from the soil into the dialysate in three soil horizons (Oa, Ah, Bw) of a Fagus sylvatica L. stand Cambisol. Three different MD perfusates with a KCl background concentration have been used: control, 1, and 3 mmol L−1 citric acid. Fluxes have been measured after 24, 48, and 144 h. The high-citrate perfusate increased the cumulative 144 h P-influx by a factor of 8, 13, and 113 in the Oa, Ah, and Bw horizon, respectively. With the high-citrate treatment, P mobilization efficiency decreased over time, whereas for the low citrate, P mobilization efficiency had a maximum at day 2. Minimum P mobilization efficiency of citrate was 1:25,000 mol phosphate per mol citrate in the Oa horizon between days 2 and 6, and maximum was 1:286 in the Bw-horizon during day 2. An increasing citrate efflux over time indicated an increasing sink term for citrate in the soil due to microbial decay or immobilization processes. Cumulative phosphate influx could be fitted to cumulative citrate efflux and soil horizon in a logarithmic model explaining 87% of the variability. For the first time, we could follow the localized P-uptake with citrate exudation over several days. Cumulative citrate efflux as the main control of P-mobilization has been barely discussed yet, however, it could explain some gaps in the role of carboxylates in the rhizosphere. Batch experiments are not capable to elucidate microscale dynamic competition for phosphate and carboxylates. MD is a promising tool for spatially explicit investigation of phosphate–citrate exchange, since such detailed insights in are not possible with batch experiments. In combination with the analysis of microbial properties, this technique has a huge potential to identify mobilization processes in soils as induced by citrate.
Of all nutrients, phosphorus has the highest discrepancy between the concentrations in leaf dry mass and soil solution. The relation of both, Degryse et al. (2009) calls it “concentration factor,” easily exceeds 105 in which case the uptake of phosphorus in 1 kg of dry leaf mass based on soil-water mass flow would require a water volume of 10 m3 that is difficult to imagine. Reasons are not only small P stocks in many forest soils (Lang et al., 2017) but also the high affinity of P to the soil solid phase (Schachtman et al., 1998; Hinsinger et al., 2011). Therefore, root systems had to develop efficient strategies to sustain the required leaf-P concentrations. First, they possess high-affinity carriers that virtually deplete the soil solution against huge concentration gradients between soil solution and root cells (Schachtman et al., 1998; Scheerer et al., 2019). Second, they associate with mycorrhizal fungi (Bucher, 2007; Zavišić et al., 2018) or form specialist root systems, such as cluster roots (Lambers et al., 2015). Third, they change the chemical environment of the rhizosphere by emitting mobilizing substances either themselves or in association with microorganisms (Hinsinger, 2001; Richardson et al., 2011).
One group of such substances intensely discussed in this context are carboxylates, i.e., anions of organic acids, such as oxalate, malate, and citrate (Jones, 1998; Richardson et al., 2011; Gerke, 2015). Carboxylates can increase P-mobility by ligand exchange on oxidic surfaces, and by dissolution of metal-P complexes and subsequent chelating of the cationic species of Ca, Fe, or Al. This helps keeping orthophosphates in solution. By decreasing the pH the solubility of metal-P complexes is increased (Barrow et al., 2018). Also, P bound in oxide-organic surfaces is well-mobilized by carboxylates. Renella et al. (2007) reported a strong increase of phosphatase activity by stimulation of microbial activity due to carboxylate exudation. It is well-documented that these effects can increase plant uptake. However, the mechanisms of P mobilization in the root–soil interface by carboxylates are still not fully clear (Richardson et al., 2011; Gerke, 2015). In this context, it has to be considered that microbial decay of carboxylates reduces their half life to a few hours (van Hees et al., 2002; Oburger et al., 2009). By this way microorganisms possibly hamper mobilization of P by carboxylate exudation (Barrow et al., 2018).
Most experimental data of carboxylate-based P mobilization was provided by batch experiments (e.g., Fox and Comerford, 1992; Gerke et al., 2000; Oburger et al., 2009), in some cases including suppression of biotic activity (Henintsoa et al., 2017; Barrow et al., 2018). The assessment of P mobilization in these experiments is mainly based on equilibrium conditions and does not consider depletion of soil solution by roots and dynamic replenishment by the solid phase. To improve the shortcoming of routine methods, Menezes-Blackburn et al. (2016) used diffusive gradient in thin film extraction (DGT). However, citric and oxalic acid had to be added in one single dose that was equilibrated with the soil–water mixture. This method is still far from typical rhizosphere processes. An experimental alternative to DGT that allows the constant release of carboxylates from a spatially discrete source like a root surface is microdialysis (MD). MD is based on highly miniaturized flow-through membranes that enrich soil solutes in the dialysate and release perfusate-solutes by diffusion. Various MD applications in soil science are listed in the comprehensive review of Buckley et al. (2020). The applicability of this dynamic extraction technique for soil phosphate including the effect of citric acid has been shown first by Demand et al. (2017). McKay Fletcher et al. (2019) measured the short-time dynamic of citrate release on P absorption to parameterize a rhizosphere model. As mentioned above, a comprehensive process description of the interaction between carboxylate exudation and P absorption is challenging. However, MD experiments simulate P mobilization by exudating fine root better than other infinite-sink extraction methods (Brackin et al., 2017; Demand et al., 2017; McKay Fletcher et al., 2019).
The aim of our study was to track for the first time absorption of the phosphate by MD probes with and without exudation of citric acid over several days. Citric acid turned out to be one of the most efficient rhizosphere carboxylates to mobilize phosphorus (Wang et al., 2008; Gerke, 2015). Furthermore, P-concentration in citric acid batch extracts of soil samples is regarded as a reasonable proxy for the foliar nutrition status of central European forest trees (Fäth et al., 2019) and it is the base of several P-mobilizing studies (e.g., Gerke, 2015; Barrow et al., 2018).
In the soil environment, citric acid is subject to fast microbial degradation and when it is supplied continuously it can stimulate the microbial community (Renella et al., 2007). Therefore, we hypothesized a decreasing P-mobilizing efficiency during continuous citrate exudation. van Hees et al. (2002) reported a strong decline in citrate mineralization with soil depth and decreasing SOM. Based on their observations, we expected the strongest decrease in citrate P-mobilizing efficiency over time in the SOM-rich topsoil and the lowest decrease in the deeper mineral soil.
Another aim of this study was to calculate an exudation efficiency as the molar ratio between citrate efflux and net gain of P from the MD flux data. This relation would be an important aspect to assess the plant's costs of P acquisition (Raven et al., 2018).
Soil samples have been collected in a beech-forest (Fagus sylvatica L.) in the Rhön mountains close to the town of Bad Brückenau, northern Bavaria/Germany. The soil developed on periglacial layers of basalt rock, and is classified as dystric sceletic Cambisol (hyperhumic, loamic) (FAO, 2015). We sampled the Oa, Ah, and Bw horizons. The site belongs to the core sites of the priority research program “Ecosystem nutrition” on forest-P nutrition and is the site with the highest phosphorus stocks (Lang et al., 2017). Altitude is 809 m a.s.l., mean annual temperature is 5.8°C, and precipitiation 1,031 mm/year. Properties of the sampled soil horizons are listed in Table 1.
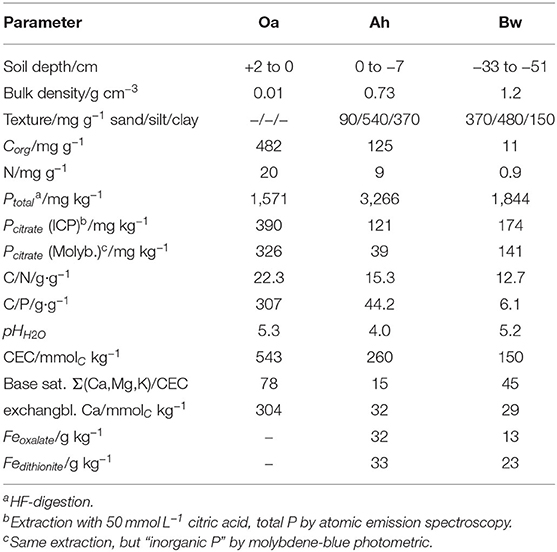
Table 1. Characteristics of the sampled soil horizons (Lang et al., 2017).
Soil samples have been prevented from drying and have been stored at 4°C. Within 1 week after sampling field-fresh soil material has been homogenized by passing through a 2 mm sieve. Homogenization leveled the expected small-scale heterogeneity of the samples without inducing strong effects on P-mineralization processes (Bünemann et al., 2016). Round plastic containers (200 cm3, diameter 9 cm, height 4 cm) for the MD experiments have been used. The containers have been filled to a predefined height with a soil mass involving field moisture and organic matter to achieve a bulk density of 0.52, 0.9, and 1.0 g cm−3 for Oa, Ah, and Bw, respectively. The final water content has been adjusted to 85% water-filled pore space. This is a compromise between ensuring a capillary continuum at the membrane surface and leaving a sufficient air-filled porosity to avoid P-mobilization caused by reduction of Fe and Mn-oxides. Furthermore, the experimental setup limited the maximum diffusion distance to the fully oxygenated air to 2 cm, which makes reductive Fe-mobilizing unlikely.
The microdialysis extractions of the soil samples followed the proceeding described in Demand et al. (2017). We used CMA 20 Elite concentric MD probes (CMA Microdialysis AB, Kista, Sweden) equipped with a polyarylethersulfone (PAES) membrane with 20 kDa molecular cutoff. The membrane cylinder had 0.52 mm diameter and 10 mm vertical length. Fluid transport through the probes was achieved by a 24 channel peristaltic pump (Ismatec IPC-N 24, Cole Partner GmbH, Wertheim, Germany) with a minimum rotor speed of 0.11 min−1. The recommended pump tubes for minimum flow rates turned out to be not stable enough to produce a constant flow over more than 12 h. The longlife tubing (PharMed Ismaprense SC0323, Cole Partner GmbH, Wertheim, Germany) was not available with a minimum diameter smaller than 0.64 mm. Because this was not adequate to achieve the targeted low flow rate of 3 μL min−1 by constant rotation, we used the pumps in intermittent mode with 2.6 s pumping and 17.4 s pause corresponding to a nominal flow rate of 3.22 μL min−1. The actual flow rates through the MD-probes with these settings were around 3 μL min−1 but varied slightly between pumps and probes. Furthermore, pump rate increased when not all 24 rotors of a pump were used. Therefore, we monitored the flux rates during the experiments for calculation of efflux and influx data. To minimize losses of perfusate when MD probes were in contact with the non-saturated soil, a push-pull technique (Li et al., 2008) has been used. This technique is based on forcing fluid flow of both, perfusate and dialysate by mounting transport tubes on the coupled rotors of the multi-channel peristaltic pump. Perfusate loss has been monitored by comparing the soil mass before and after the MD extractions. The setup is outlined in Figure 1.
Tubing and probes have been conditioned by pumping deionized water through the system for 16 h. Setup and probes have then been tested for P recovery with a perfusate of 15 mmol−1 KCl at the flow rate setting of 3.22 μ L min−1 in a stirred 0.84 μ mol L−1 phosphate solution over 20 h. In this experiment, P recovery varied between 5 and 15% with a median of 10.8%. This was only half the recovery observed by Demand et al. (2017) with a similar setup, but with a 10 times higher phosphate concentration in the outer medium.
Three different perfusates have been applied. Demand et al. (2017) demonstrated the strong effect of the ionic strength of the perfusate on P recovery. Therefore, we used a 15 mmol−1 KCl solution as the control perfusate and as the base electrolyte for the two citric acid treatments with 1 and 3 mmol L−1 addition of citrate anions as citric acid monohydrate (C6H8O7·H2O).
For the soil experiments 6 MD probes have been inserted into the soil within one plastic container. This left a 10 cm2 free space around each probe to avoid interference during the extraction time. Before sampling of dialysates, the probes have been flushed for 3 min with 23 μ L min−1 to remove air bubbles. Dialysates have been sampled over 6 d separately for three subsequent periods: 0–24, 24–48, and 48–144 h. Temperature was kept constant at 15°C. With the three horizons and three perfusates, in total nine treatments have been tested. For each treatment, six individual dialysates of MD probes have been sampled (plus six extra replications for the control in Bw), yielding in total 180 dialysates. Actual flow rates were determined based on the weight of the sampled dialysate divided by perfusion time. Concentrations of phosphate, citrate, and chloride have been analyzed to calculate rates of absorption from and release into the soil. Average exchange between MD membrane and soil has been calculated from the change of concentration between dialysates and perfusates multiplied by the respective flow rate. The loss of perfusate into the soil samples was around 5%, but reached up to 20% in the Bw horizon. Because the soil samples could only be weighted at the end of the experiment and not together with each dialysate vial, a quantitative consideration of this term is not yet possible. For future experiments, we will foresee separate perfusate vials allowing to track the perfusate loss.
Phosphate in the dialysate has been analyzed with the molybdenum-blue method by using a continuous flow analyzer (SAN Plus, Skalar Analytical B.V., The Netherlands) equipped with a 50 cm extended light-path cell (Zhang and Chi, 2002). Limit of detection was around 7 nmol L−1, limit of quantification around 20 nmol L−1 based on the 95% confidence limit of a 5-point calibration. Citrate and chloride concentrations have been analyzed with capillary-zone electrophoresis (Agilent Technologies, Waldbronn, Germany) according to the procedure of Göttlein and Blasek (1996).
From the molar relation of the citrate-increased P-influx and the related citrate efflux, we calculated an efficiency term (Equation 1):
with Ecit the efficiency of citrate to mobilize P, QP the molar influx of P with citrate in the perfusate (+cit) and without (−cit), and Qcit the molar efflux of citrate. Qcit is the product of the dialysate-flow rate and the difference between perfusate and dialysate concentration of citrate. Statistics have been calculated with R-statistics version 3.5.0 (R Core Team, 2018). The observed fluxes (Table 2, Figure 2) and citrate P-mobilization efficiencies (Figure 3) have been tested with robust 2-way analyses of variance (anova) from the R-statistics package WRS (Mair and Wilcox, 2020). We used the function t2way to reveal significant effects of soil horizon and citrate treatment on the cumulative fluxes (Table 2). For the fluxes over time (Figure 2) and for the mobilization efficiency (Figure 3), we used the mixed-anova function bwsplit to reveal significant effects of sampling time and citrate treatment. In this anova, the differences between sampling times have been regarded as within-subject effects (repeated measurements on individual probes) and the citrate treatment as between-subject (group) effect. Additionally, we reported in the graphics the approximated 95% confidence limits of the median (McGill et al., 1978) to facilitate the localization of significant differences. We based the regression of P-influx over citrate efflux on a log-log model of the medians as a robust approach. With these transformations, we achieved a normal distribution of the P-influx data (Shapiro-test). In the error estimation, this aggregation is considered by the strong reduction of the number of degrees of freedom. The model formula was:
with ΣQP and Σ − QCit the cumulated molar fluxes of phosphate and the opposite flux of citrate, I0, IHor, S0, and SHor the intercept and the slope. Both are composed of a basic term (subscript “0”) that covers the Oa horizon and a further additive term of slope and intercept (subscript “hor”) that covers the modifications for Ah and Bw horizon.
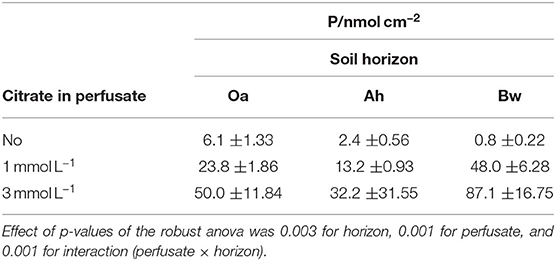
Table 2. Cumulative phosphate influx (medians ±95% confidence limits) into MD probes during 6 days (144 h).
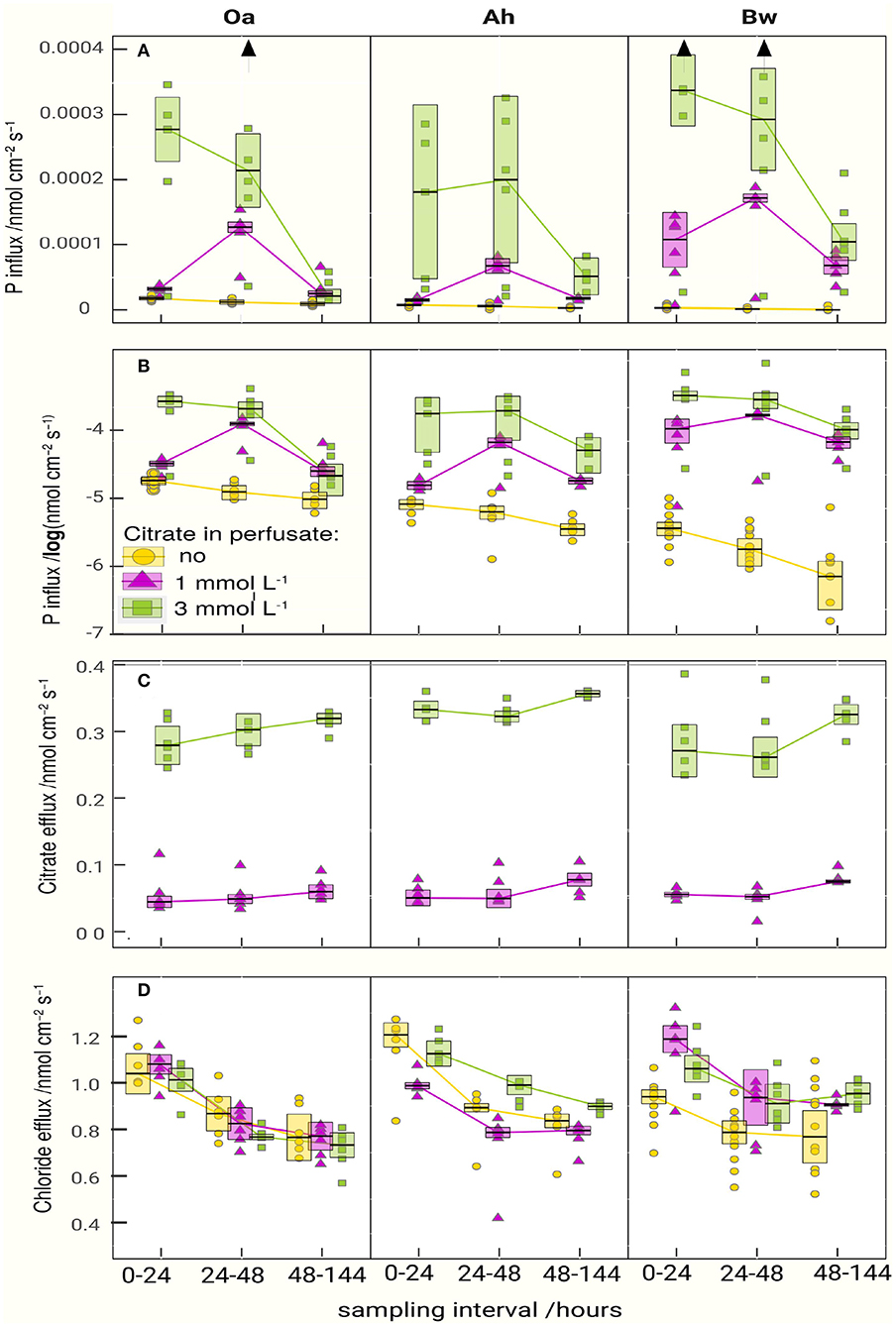
Figure 2. Fluxes of phosphate (A,B), citrate (C), and chloride (D) between soil and microdialysis probes. The boxes represent the approximated 95% confidence limit of the median (anova statistics is presented in Table 3). The lines are connecting medians indicating the temporal pattern. For the phosphate influx, the plot is repeated with logarithmic scaling in (B) to highlight the gradation of the P-absorption between control and citrate treatments. Vertical arrows in the upper graph symbolize outliers beyond the maximum axis value.
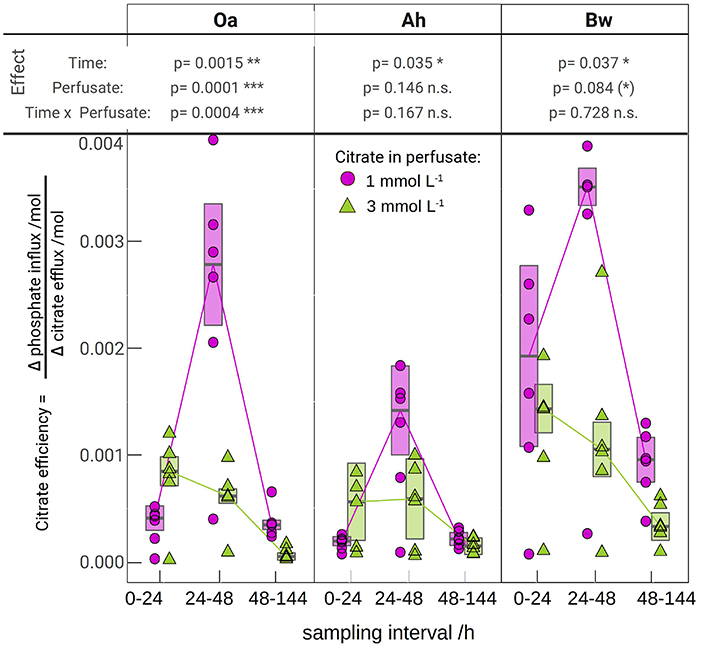
Figure 3. The molar efficiency of citrate to release phosphate, calculated as the ratio of flux changes between the respective citrate perfusate and the control (Equation 1). The lines are connecting medians indicating the temporal pattern. The error bars limit the approximated 95% confidence limits of the medians, the tabled p-values come from a robust mixed 2-way anova (c.f. that was applied separately for each soil horizon. Significance of p-values is symbolized by: (*) < 0.1, * < 0.05, ** < 0.01, *** < 0.001).
P-influx of MD depended on the citrate concentration of the perfusate. Maximum cumulative 144 h influx (Table 2) without citrate was in the Oa horizon and minimum in the Bw-subsoil. With the high-citrate perfusate, the ranking changed and maximum influx was in the Bw horizon. There was an interaction between the effects of citrate concentration of perfusate and time (Figures 2A,B, Table 3). With the control and the high-citrate treatment P influx decreased continuously over time, while for the low-citrate treatment P influx reached a maximum after 48 h. By trend, both citrate treatments produced highest P influx for the samples of the Bw subsoil, whereas with the control P-influx decreased with soil depth from Oa to the Bw. The highest relative P-mobilization effect of citrate was observed for samples of the Bw horizon between 48 and 144 h where the median of P influx raised from 6.9E-7 (control) to 1.05E-4 nmol cm−2 s−1 (high citrate), i.e., by a factor of 157. The continuous decrease of P influx over time with the control is in agreement with a depletion of the probe environment by diffusion with or without first-order desorptive replenishment.
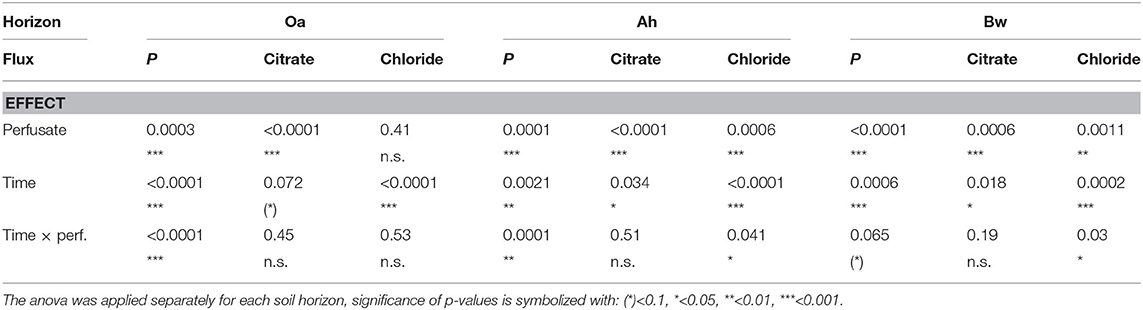
Table 3. Comparison of fluxes reported in Figure 2: p-values of the robust 2-way mixed anova considering within-subject effects (repeated measurement of probes over time) and between-subject effects (perfusates).
Cumulative P-influx (Table 2) of both citrate treatments did not reflect the gradation of the batch-citrate extractable P in Table 1 neither for the molybdenum active part, nor the total P in the citrate extract. Maximum concentration of batch-citrate extractable P was found in the Oa horizon and minimum in the Ah: On a volume base it was for total citrate-extractable P [Pcit (ICP)] 195, 108, and 174 μg cm−3, and for inorganic [Pcit (Molyb.)] 163, 35, and 141 μg cm−3 in Oa, Ah, and Bw, respectively. This does not correlate to the clear maximum of MD-P influx in the Bw horizon. The minimum of batch-extractable P in the Ah horizon coincides only with the MD influx of low citrate but not with the high citrate perfusate where MD-P influx of the Ah horizon was close to that of the Oh horizon.
In all horizons and all perfusates efflux of chloride (Figure 2D) decreased strongly from day 1 to 2 followed by a constant efflux or a further decrease to day 3–6. Final Cl− efflux was only 70–90% of that of day 1. This pattern can easily be attributed to a transient diffusion process of an ion that does not interact with the solid phase and approaches a steady-state efflux. Citrate efflux (Figure 2C), in contrast, increased over time with all treatments and horizons (for the Oa horizon, the p-value is 0.072, Table 3; in this case, we have to classify the increase as tendency). Horizon-specific effects could not be revealed.
Figure 3 shows the calculated efficiencies of citrate efflux to mobilize P according to Equation (1). Individual MD-probe observations have been used for P-influx [QP, (+cit)] of the citrate treatments and the respective citrate efflux (Qcit). The median of the control P-influx of the respective horizon, perfusate, and time has been used for the term QP, (−cit). The highest P yield for a given citrate efflux was observed in the Bw horizon with low citrate at day 2 with 0.0035 mol·mol−1, i.e., 286 citrate molecules were needed to harvest one additional phosphate. Lowest efficiency was observed in the Oa horizon with high-citrate treatment between 48 and 144 h with 0.00004 mol·mol−1 or 25.000 citrate molecules needed for one additional phosphate. Efficiency of the high-citrate treatment decreased progressively from day 1 to 3–6, whereas low-citrate treatment showed a maximum efficiency during day 2.
The plot of the cumulated phosphate absorption over cumulated citrate efflux (Figure 4) exhibits a logarithmic trend and could be fitted by a regression model (Equation 2). The coefficients of the model are listed in Table 4. In the plot three sections along the x-axis can be distinguished: Points left of the drawn ellipse stem only from the low citrate treatment, points right of ellipse only from the high citrate treatment. Points within the ellipse come from both treatments equally and form a smooth transition between the citrate treatments. P-influx after 144 h of low-citrate efflux was virtually the same as P-influx of 24 h of high-citrate efflux. This can also be expressed in terms of citrate efficiency (Equation 1). The 24 h efficiency of high-citrate treatment has been taken directly from Figure 3, and the 144 h efficiency of the low-citrate treatment has been calculated from the cumulative fluxes of phosphate and citrate. In the Oa horizon, the 144 h low and the 24 h high efficiency were 0.001 and 0.00084, respectively, in the Ah 0.00055 and 0.00051, and in the Bw 0.0021 and 0.0014 mol mol−1. In neither of the three horizons, the 144 h low and the 24 h high P-efficiencies revealed significant differences (Wilcoxon rank test). The close similarity of the efficiencies in the soil horizons are notable insofar that the major control of P mobilization by citrate was the cumulated efflux of citrate and that this was independent of time or citrate concentration.
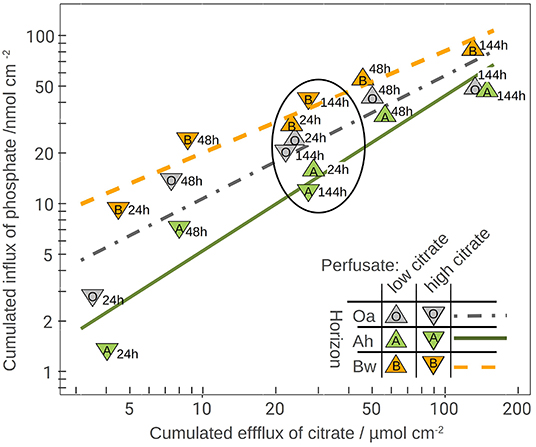
Figure 4. Phosphate influx over citrate efflux together with the logarithmic model fitting (model parameters in Table 4). The numbers right of the symbols are the time in hours. The ellipse highlights the overlapping results of both perfusate-citrate concentrations where the values of the low citrate treatment cover 144 h efflux and those of the high-citrate treatment only 24 h.
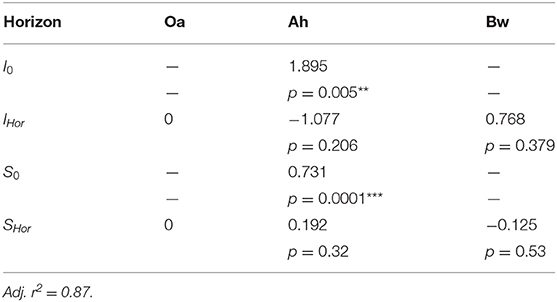
Table 4. Coefficients of the regression model of cumulated P-influx over cumulated citrate efflux (Equation 2 displayed in Figure 4), with p-values of coefficients: **<0.01, ***<0.001.
Citrate efflux from the MD probes into the soil increased P influx into the MD probes. Beyond that, the specific time patterns of P-influx and citrate efflux during the 6-days experiment merit specific analysis. The volume of soil that is influenced by the activity of a living root is defined as rhizosphere with a radius in the μm-range up to cm (Hinsinger et al., 2009). The radius of an “MD-rhizosphere” is limited by the modification of solute concentrations that can also trigger modifications of biotic activity. The efflux from the perfusate increased concentrations of K+, Cl−, and citrate in the solution surrounding the MD-probe. For an ion that does not interact with the solid phase, such as Cl−, a transient growth of the dispersal volume together with flattened concentration gradients near the MD membrane can be expected. In our results, this was reflected by the decreasing diffusional loss of Cl− with time (Figure 2). The efflux characteristics of Cl are crucial for our interpretations since it is an ion that hardly interacts with microbes or the solid phase. Chloride reveals the typical efflux pattern dominated by diffusion. Though we can assume the same transport physics for citrate and Cl anions, the development of citrate efflux over time is completely different. We observed a decreasing Cl efflux over time, but an increasing citrate efflux. Diffusion of solutes revealing a stronger interaction to the solid phase than Cl would slow down in a similar way. A solute depletion by first-order kinetics (adsorption, precipitation) or Michaelis–Menten kinetics would delay a saturation, but never lead to an increase of diffusional loss over time. Precipitation of citrate by polyvalent cations can neither explain increasing diffusional loss since this process would follow zero-order kinetics, resulting in constant citrate efflux, nor it can be explained by citrate adsorption, since this would cause decreasing citrate efflux over time. The most obvious explanation for increasing efflux is microbial decay or metabolization of citrate with increasing rates after begin of efflux. In the following, we summarize evidence from literature supporting this assumption. In soils, citrate is easily metabolized or degraded by microorganisms and reveals short half life of only up to some hours (Jones, 1998; van Hees et al., 2002). This would not cause increasing efflux rates into the MD environment as long as the microbial citrate sink is controlled by constant concentration-dependent kinetics. Several models of citrate concentration around exuding roots are based on decay constants (Geelhoed et al., 1999; Schnepf et al., 2012; McKay Fletcher et al., 2019). When parametrized with literature-based decay constants these models yield a radius of 0.1 and 0.4 cm around the exuding surface where citrate concentrations approach zero. In these models, citrate efflux decreases over time. This type of citrate efflux characteristics was observed by McKay Fletcher et al. (2019) in a 20 h MD experiment. However, the assumption of constant rates of concentration-dependent citrate decay in the rhizosphere is questionable. Fujii et al. (2012) observed an increase of Michaelis–Menten parameters of carboxylate decay in the rhizosphere vs. bulk soil.
Here it has to be emphasized that carboxylate exudation by actual roots is a dynamic process insofar, that the efflux is concentrated at the rather short-living root tip (Canarini et al., 2019). This means a root grows toward a soil spot devoid of an active root and often with higher availability of water or nutrients. There, it begins to exude, e.g., citrate, an easily available additional energy source for microorganisms that will stimulate the microbial community. Root exuded low-molecular organic acids exert a particularly strong rhizosphere priming effect (Renella et al., 2007; Keiluweit et al., 2015; Shahzad et al., 2015), which describes a microbial carbon mineralization in the rhizosphere that releases more CO2 than could be expected from the amount of exudates (Kuzyakov, 2002). Modification of the microbial community is an important trait of the rhizosphere (Hinsinger et al., 2011; Kaiser et al., 2011). Therefore, it is unlikely that biotic activity in the rhizosphere as well as in the vicinity of a MD probe in a living soil remains unchanged during hours and days following the emergence of a local citrate source. In contrast to first-order processes, a microbial stimulation counteracts a saturation and can cause an increasing diffusional efflux of citrate. In our experiments, diffusional efflux of citrate increased by a factor up to 1.57 within 6 days. This factor is also the minimum estimate of increased decay in the direct vicinity of the MD membrane. This is evident from the physics of diffusion: An increase of efflux needs a proportional lowering of the citrate concentration directly at the membrane surface. The actual increase of the rate of microbial decay was nevertheless higher by an unknown factor, because a part of the initial diffusion efflux was not used solely by microbes, but contributed to a transient adsorption by the solid phase near the membrane (Gerke et al., 2000).
We hypothesized a stronger effect of microbial citrate consumption on P-mobilization in the topsoil horizons rich in SOM. This would have been supported by a stronger increase of citrate efflux with time in the Oa and Ah horizon than in the Bw horizon, but for this effect there is no direct evidence in the results. Overall, the data do not allow a detailed analysis of the rising citrate efflux over time. Furthermore, without additional data on soil respiration conclusions on time patterns of microbial stimulation remain speculative. As shown by Stenström et al. (1998), the delay and the further trend of soil respiration after stimulation by added substrate depend on the composition of the microbial community with members whose population grow and others that only increase their metabolism in response to an addition of easily available substrate. The authors found that increase in soil respiration by growing microbial populations is stronger, but begins later than increased substrate mineralization by a non-growing population.
Generally, it is assumed that microbial decay of citrate lowers its efficiency to mobilize phosphate (Geelhoed et al., 1999; Barrow et al., 2018) because microbial loss reduces citrate concentrations responsible for P-mobilization processes, such as ligand exchange, surface reactions, or chelating of Fe. We hypothesized therefore an increasing efficiency of citrate to mobilize phosphate with decreasing SOM as a proxy for microbial activity and thereby citrate decay according to van Hees et al. (2002). In accordance with our hypothesis, we observed uniformly higher mobilizing efficiencies of citrate in the Bw horizon than in the topsoil (Oa and Ah horizon). Independently of a priming by citrate in the MD vicinity a higher density of potentially citrate consuming microorganisms would lower the citrate concentration in the soil solution and additionally could compete with the MD membranes for mobilized phosphate.
We parametrized a regression model that explains 87% of the total variation of phosphate influx into the MD probes solely based on the cumulative citrate efflux and the soil horizon (Table 4). The model is thus independent of time and citrate concentration in the perfusate. The logarithmic trend implies a decreasing marginal benefit of citrate exudation for phosphate mobilization. Until now, cumulative efflux has barely been discussed as the main control of P-mobilization by citrate. Results supporting the relevance of cumulative efflux of carboxylates were obtained by Fox et al. (1990). The authors applied one single dose of oxalate to a soil sample and extracted soil solution after 12 h and compared the results to sequential extractions after applying smaller doses over several days. They obtained congruent curves of P yield plotted over the cumulative amount of added oxalate. Though the authors did not discuss the mechanisms that cause this phenomenon, they emphasized the important ecological role of small, but continuous release of carboxylates mobilizing strongly adsorbed solutes like Al or P.
Most existing studies of P mobilization by carboxylates focus on equilibrium concentration as controlling factor (Hinsinger, 2001), probably because batch extraction is a common approach and equilibrium coefficients allow a straightforward implementation of numeric models. In contrast, McKay Fletcher et al. (2019) related the P mobilization potential of citrate efflux in an MD experiment to the efflux rate of citrate. However, their results do not contradict our findings because the experiments were limited to 20 h. Low efflux rates need to be observed with extended exposure times. Citrate efficiencies plotted in Figure 3 indicate that there exists, however, a threshold of cumulated citrate efflux to mobilize P. With the high-citrate treatment we observed a strong decrease of mobilization efficiency over time. The extremely low phosphate extra yield in the Oa horizon after 48 h of citrate efflux implies high costs of phosphate mobilization. With low citrate efflux initial mobilizing efficiency, however, was low and not until the second day it reached a marked peak to decrease again during the period between day 3 and 6. This is not in compliance with the logarithmic model in Figure 4, which implies a continuous decrease of the specific efficiency: The more citrate was released, the lower its ability to mobilize additional P. In the logarithmic fit, the reduced initial low-citrate efficiency is reflected by the systematically negative residuals of the 24 h low-citrate observations in Figure 4.
Gerke et al. (2000) described a threshold of citrate concentration on the solid phase implying also a minimum dissolved citrate concentration where the dissolved phosphate concentration begins to increase. In the dynamic MD extraction, such a sharp threshold cannot be expected, but with low citrate concentrations in solution, a stronger competition between phosphate mobilization and other processes of citrate immobilization is probable (Jones and Brassington, 1998). Filling up the most selective citrate adsorption positions in the direct vicinity of the membrane can therefore explain the delayed maximum efficiency in case of low citrate. A similar effect could be hypothesized for selective microbial uptake of phosphate around the membranes. In the high-citrate treatment, this possible threshold is masked by the high amount of exuded citrate in the first 24 h, which is close to the 144 citrate efflux of the low-citrate treatment. With the experimental data of our study, a quantitative limitation of the scope of the logarithmic model is not yet possible. For the lower threshold, a high-citrate efflux has to be tested with reduced time steps.
Adsorption/desorption characteristics of citrate and phosphate are mostly non-linear (Gerke et al., 2000), i.e., at low concentrations a higher fraction is bound to the solid phase. When only desorption from the solid phase is considered, phosphate mobilization independently of the applied citrate concentration is therefore remarkable. Possibly, processes of P mobilization are much more diverse than those included in the established quantitative models. Kinetics of obviously relevant rhizosphere processes, such as stepwise P release from supramolecular SOM structures by citrate (Clarholm et al., 2015) or the absorption of “leftover” P of SOM-mineralization triggered by the priming effect of citrate (Renella et al., 2007; Dijkstra et al., 2013) is difficult to quantify. A further validation of cumulative carboxylate efflux as major control of P-mobilization needs application of a wider variation of efflux rates and an overlapping of resulting efflux over several points in time. This should be amended by quantification of citrate-triggered change of soil respiration. If cumulative efflux proved to be a generalizable control of P mobilization, a discussion of the underlying mechanisms would be needed.
Because MD-influx originates from an unknown volume, it cannot be converted directly to batch extracted P. A distance-weighted distribution of the P-influx can only be obtained by parametrizing models with diffusion, adsorption, and decay data (Schnepf et al., 2012; McKay Fletcher et al., 2019). Nevertheless, MD P-influx data of our three soil horizons did not reflect the differences and ranking of phosphate mobilized with citrate-batch extraction (Table 1). Because our experiments yielded the first quantitative data on P-absorption of a citric acid exuding membrane in soil environment over several days, a direct reference to existing studies is not available. One important difference to batch experiments is the MD membrane acting as an additional sink for dissolved P that competes with chelating species, adsorbing surfaces (Barrow, 2017), and microbial uptake (Schneider et al., 2017). In such a far-from equilibrium dynamic, each single interacting citrate molecule can mobilize a phosphate whose fate is determined by the spatial arrangement of sinks and the diffusion speed (McKay Fletcher et al., 2020). The probability of a dissolved P to reach the MD surface decreases by both diffusion time and the number of opportunities to be re-immobilized. Therefore, the competetiveness of the MD surfaces strongly increases with decreasing distance between the place of mobilization and the absorbing membrane. As Raynaud et al. (2008) illustrated by modeling spatial interaction of rhizosphere processes, it could be beneficial for a root when the concentration of a mobilizing solute around a root drops in a narrow radius because this decreases the share of the mobilized nutrients that are lost for the exuding root.
MD assesses far-from equilibrium dynamics that cannot be modeled with equilibrium constants involving instantaneous exchange. By leveling desorption/adsorption kinetics and the microscale-spatial distribution of both exchanging surfaces and microorganisms, an equilibrium experiment can barely reflect the specific low-distance competetiveness of an absorbing membrane. Furthermore, the standard citrate extraction procedure applied for the values in Table 1 is based on a concentration of 50 mmol L−1 of citrate, which is much higher than we induced directly at the membrane surface.
A critical point of our study are the absolute concentrations we applied. Carboxylate concentrations in the rhizosphere are generally higher than in the bulk soil (Jones, 1998; Fujii et al., 2012). There is an evidence of increased carboxylate exudation when roots grow in soils with limited P availability (Hoffland et al., 1989) including European beech (De Feudis et al., 2016). However, citrate concentrations of 1 mmol L−1 or more are barely observed in soil solution (Except in the vicinity of specialist root structures, such as cluster roots; Lambers et al., 2015). In topsoil solutions of beech stands, Shen et al. (1996) measured citrate concentrations below 1 μmol L−1. In bulk soil solutions citrate concentrations solution rarely exceed 50 μmol L−1 (Jones, 1998), in forest floor of coniferous stands they may approach 500 μmol L−1 (van Hees et al., 2005a).
Though soil-solution sampling in the rhizosphere is challenging (Luster et al., 2009), it is assumed that natural concentrations of citrate are lower than those applied in most experiments (Hinsinger, 2001). From the existing data of low rhizosphere concentrations and low exudation rates, Richardson et al. (2011) recognize only a “modest” evidence that organic anion release of non-cluster root plants can improve P nutrition. Maximum concentrations in our experiment were directly at the membrane–soil contact zone. They can be easily estimated due to the low membrane thickness and its high porosity (Demand et al., 2017), where the diffusional flux causes a marginal gradient. Therefore, concentrations at the outer membrane surface were close to the perfusate of 1, respectively 3 mmol L−1.
The point-like membrane-surface concentration is not equal to a rhizosphere concentration that is always defined on a volume base. Until now rhizosphere concentration measurements are limited in the spatial resolution to 1–2 mm (Fujii et al., 2012) or in case of micro-suction cups to 1 cm (Dessureault-Rompré et al., 2006). As mentioned above, the localized exudation of this easily degradable organic carbon causes very steep concentration gradients around the sources approaching zero within an mm range. Reliable data of exudation rates of individual tree roots are scarce (Preece and Peñuelas, 2016; Oburger and Jones, 2018). By relating mineralization kinetics and the concentrations in bulk-soil solution, van Hees et al. (2005b) calculated soil-mass related production rates of citrate for podzolic forest soils between 0.4 and 600 nmol g−1day−1. Considering the fast mineralization, van Hees et al. (2005a) assumed turnover rates up to 80 day−1 for the dissolved part and 10 day−1 for total carboxylates including the adsorbed part. These high turnover rates require a permanent replenishment of the soil solution. Roots play an important role in this replenishment (Nguyen, 2003). However, both time and spot of exudation of carboxylates in root systems can be highly localized (Hinsinger et al., 2011; Canarini et al., 2019). This means until now we do not know the maximum citrate concentrations directly at exuding root tips. There are furthermore scaling challenges because potentially an important part of phosphate is mobilized in pores with diameters below 10 μm, which are barely accessible to microscopic concentration measurements. Though it would be desirable to extend the range of citrate concentrations in the MD-experiments toward lower values, existing information on efflux rates of root citrate does not exclude the local occurrence of high concentrations directly at the root surface or in individual pores in direct contact to the membrane surface.
Following phosphate influx into MD probes and synchronous efflux of citrate over several days yielded novel insights into soil P-mobilization. A surprising result was the rather complex patterns of P-influx modified by time, soil-horizon, and perfusate concentration that could be aggregated in a logarithmic model. This model predicts cumulated phosphate influx by the cumulated citrate efflux independently of time and efflux rate. We conclude therefore that processes other than sorption/desorption or precipitation/solution control the mobilization efficiency of exuded citrate in soil. Our data are consistent with the assumption that in this context microbial decomposition or immobilization processes are central. Our data also show that in soils with high concentrations of adsorbed phosphate, the exudation of citrate in the subsoil is more beneficial for the plant roots' P uptake than in the SOM-rich topsoil. The logarithmic character of the model implies a decreasing marginal benefit of citrate exudation, which can probably be related to stimulation of microbial activity by citrate and an increasing distance between mobilization of phosphate and membrane uptake. Both effects lower the competitiveness of the uptaking membrane to other processes. In order to deepen our knowledge of P-mobilization by carboxylates, the presented MD approach should be amended with (a) lower citrate efflux rates but longer observation time, (b) analyses of soil microbial activity with high time resolution, and (c) on-site use of spatial MD grids. Our results confirm that the developed advancement of MD application is promising for the identification of P mobilization processes in soils mediated by plant roots but also indicate still open questions regarding this issue. Nevertheless, we agree with Brackin et al. (2017) who called the MD method “Roots-eye view.”
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
HS-K contributed to the experimental design and data analysis and wrote the major part of the manuscript. CL contributed to the experimental design, carried out respectively supervised the experiment, and did the data analysis. FL conceptualized the project, wrote the funding application, and contributed to the manuscript. All authors contributed to the article and approved the submitted version.
The project was funded by the German Research Foundation (DFG, GZ: LA 1398/12-2 AOBJ: 632054).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The authors gratefully acknowledge A. Thiemann, C. Gabriel, and M. P. Haas who carefully conducted experiments and analyses.
Barrow, N. (2017). The effects of pH on phosphate uptake from the soil. Plant Soil 410, 401–410. doi: 10.1007/s11104-016-3008-9
Barrow, N., Debnath, A., and Sen, A. (2018). Mechanisms by which citric acid increases phosphate availability. Plant Soil 423, 193–204. doi: 10.1007/s11104-017-3490-8
Brackin, R., Atkinson, B. S., Sturrock, C. J., and Rasmussen, A. (2017). Roots-eye view: using microdialysis and microCT to non-destructively map root nutrient depletion and accumulation zones. Plant Cell Environ. 40, 3135–3142. doi: 10.1111/pce.13072
Bucher, M. (2007). Functional biology of plant phosphate uptake at root and mycorrhiza interfaces. New Phytol. 173, 11–26. doi: 10.1111/j.1469-8137.2006.01935.x
Buckley, S., Brackin, R., Jämtgård, S., Näsholm, T., and Schmidt, S. (2020). Microdialysis in soil environments: current practice and future perspectives. Soil Biol. Biochem. 143:107743. doi: 10.1016/j.soilbio.2020.107743
Bünemann, E. K., Augstburger, S., and Frossard, E. (2016). Dominance of either physicochemical or biological phosphorus cycling processes in temperate forest soils of contrasting phosphate availability. Soil Biol. Biochem. 101, 85–95. doi: 10.1016/j.soilbio.2016.07.005
Canarini, A., Kaiser, C., Merchant, A., Richter, A., and Wanek, W. (2019). Root exudation of primary metabolites: mechanisms and their roles in plant responses to environmental stimuli. Front. Plant Sci. 10:157. doi: 10.3389/fpls.2019.00420
Clarholm, M., Skyllberg, U., and Rosling, A. (2015). Organic acid induced release of nutrients from metal-stabilized soil organic matter-the unbutton model. Soil Biol. Biochem. 84, 168–176. doi: 10.1016/j.soilbio.2015.02.019
De Feudis, M., Cardelli, V., Massaccesi, L., Bol, R., Willbold, S., Cocco, S., et al. (2016). Effect of beech (Fagus sylvatica L.) rhizosphere on phosphorous availability in soils at different altitudes (central Italy). Geoderma 276, 53–63. doi: 10.1016/j.geoderma.2016.04.028
Degryse, F., Smolders, E., Zhang, H., and Davison, W. (2009). Predicting availability of mineral elements to plants with the DGT technique: a review of experimental data and interpretation by modelling. Environ. Chem. 6, 198–218. doi: 10.1071/EN09010
Demand, D., Schack-Kirchner, H., and Lang, F. (2017). Assessment of diffusive phosphate supply in soils by microdialysis. J. Plant Nutr. Soil Sci. 180, 220–230. doi: 10.1002/jpln.201600412
Dessureault-Rompré, J., Nowack, B., Schulin, R., and Luster, J. (2006). Modified micro suction cup/rhizobox approach for the in-situ detection of organic acids in rhizosphere soil solution. Plant Soil 286, 99–107. doi: 10.1007/s11104-006-9029-z
Dijkstra, F. A., Carrillo, Y., Pendall, E., and Morgan, J. A. (2013). Rhizosphere priming: a nutrient perspective. Front. Microbiol. 4:216. doi: 10.3389/fmicb.2013.00216
FAO (Ed.). (2015). World Reference Base for Soil Resources 2014, Update 2015: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps. World Soil Resources Reports. Rome: FAO.
Fäth, J., Kohlpaintner, M., Blum, U., Göttlein, A., and Mellert, K. H. (2019). Assessing phosphorus nutrition of the main european tree species by simple soil extraction methods. For. Ecol. Manag. 432, 895–901. doi: 10.1016/j.foreco.2018.10.007
Fox, T., and Comerford, N. (1992). Influence of oxalate loading on phosphorus and aluminum solubility in spodosols. Soil Sci. Soc. Am. J. 56, 290–294. doi: 10.2136/sssaj1992.03615995005600010046x
Fox, T., Comerford, N., and McFee, W. (1990). Kinetics of phosphorus release from spodosols: effects of oxalate and formate. Soil Sci. Soc. Am. J. 54, 1441–1447. doi: 10.2136/sssaj1990.03615995005400050038x
Fujii, K., Aoki, M., and Kitayama, K. (2012). Biodegradation of low molecular weight organic acids in rhizosphere soils from a tropical montane rain forest. Soil Biol. Biochem. 47, 142–148. doi: 10.1016/j.soilbio.2011.12.018
Geelhoed, J., Van Riemsdijk, W., and Findenegg, G. (1999). Simulation of the effect of citrate exudation from roots on the plant availability of phosphate adsorbed on goethite. Eur. J. Soil Sci. 50, 379–390. doi: 10.1046/j.1365-2389.1999.00251.x
Gerke, J. (2015). The acquisition of phosphate by higher plants: effect of carboxylate release by the roots. A critical review. J. Plant Nutr. Soil Sci. 178, 351–364. doi: 10.1002/jpln.201400590
Gerke, J., Beißner, L., and Römer, W. (2000). The quantitative effect of chemical phosphate mobilization by carboxylate anions on P uptake by a single root. I. The basic concept and determination of soil parameters. J. Plant Nutr. Soil Sci. 163, 207–212. doi: 10.1002/(SICI)1522-2624(200004)163:2<207::AID-JPLN207>3.0.CO;2-P
Göttlein, A., and Blasek, R. (1996). Analysis of small volumes of soil solution by capillary electrophoresis. Soil Sci. 161, 705–715. doi: 10.1097/00010694-199610000-00007
Henintsoa, M., Becquer, T., Rabeharisoa, L., and Gerard, F. (2017). Geochemical and microbial controls of the effect of citrate on phosphorus availability in a ferralsol. Geoderma 291, 33–39. doi: 10.1016/j.geoderma.2016.12.020
Hinsinger, P. (2001). Bioavailability of soil inorganic P in the rhizosphere as affected by root-induced chemical changes: a review. Plant Soil 237, 173–195. doi: 10.1023/A:1013351617532
Hinsinger, P., Bengough, A. G., Vetterlein, D., and Young, I. M. (2009). Rhizosphere: biophysics, biogeochemistry and ecological relevance. Plant Soil 321, 117–152. doi: 10.1007/s11104-008-9885-9
Hinsinger, P., Brauman, A., Devau, N., Gérard, F., Jourdan, C., Laclau, J.-P., et al. (2011). Acquisition of phosphorus and other poorly mobile nutrients by roots. Where do plant nutrition models fail? Plant Soil 348:29. doi: 10.1007/s11104-011-0903-y
Hoffland, E., Findenegg, G. R., and Nelemans, J. (1989). Solubilization of rock phosphate by rape: II. Local root exudation of organic acids as response to P-starvation. Plant Soil 113, 161–165. doi: 10.1007/BF02280176
Jones, D., and Brassington, D. (1998). Sorption of organic acids in acid soils and its implications in the rhizosphere. Eur. J. Soil Sci. 49, 447–455. doi: 10.1046/j.1365-2389.1998.4930447.x
Jones, D. L. (1998). Organic acids in the rhizosphere–a critical review. Plant Soil 205, 25–44. doi: 10.1023/A:1004356007312
Kaiser, C., Fuchslueger, L., Koranda, M., Gorfer, M., Stange, C. F., Kitzler, B., et al. (2011). Plants control the seasonal dynamics of microbial N cycling in a beech forest soil by belowground C allocation. Ecology 92, 1036–1051. doi: 10.1890/10-1011.1
Keiluweit, M., Bougoure, J. J., Nico, P. S., Pett-Ridge, J., Weber, P. K., and Kleber, M. (2015). Mineral protection of soil carbon counteracted by root exudates. Nat. Clim. Change 5, 588–595. doi: 10.1038/nclimate2580
Kuzyakov, Y. (2002). Factors affecting rhizosphere priming effects. J. Plant Nutr. Soil Sci. 165, 382–396. doi: 10.1002/1522-2624(200208)165:4<382::AID-JPLN382>3.0.CO;2-#
Lambers, H., Martinoia, E., and Renton, M. (2015). Plant adaptations to severely phosphorus-impoverished soils. Curr. Opin. Plant Biol. 25, 23–31. doi: 10.1016/j.pbi.2015.04.002
Lang, F., Krüger, J., Amelung, W., Willbold, S., Frossard, E., Bünemann, E. K., et al. (2017). Soil phosphorus supply controls P nutrition strategies of beech forest ecosystems in central europe. Biogeochemistry 136, 5–29. doi: 10.1007/s10533-017-0375-0
Li, Z., Hughes, D., Urban, J. P., and Cui, Z. (2008). Effect of pumping methods on transmembrane pressure, fluid balance and relative recovery in microdialysis. J. Membr. Sci. 310, 237–245. doi: 10.1016/j.memsci.2007.10.051
Luster, J., Göttlein, A., Nowack, B., and Sarret, G. (2009). Sampling, defining, characterising and modeling the rhizosphere—the soil science tool box. Plant Soil 321, 457–482. doi: 10.1007/s11104-008-9781-3
Mair, P., and Wilcox, R. (2020). Robust statistical methods in R using the WRS2 package. Behav. Res. Methods 52, 464–488. doi: 10.3758/s13428-019-01246-w
McGill, R., Tukey, J. W., and Larsen, W. A. (1978). Variations of box plots. Am. Stat. 32, 12–16. doi: 10.1080/00031305.1978.10479236
McKay Fletcher, D., Shaw, R., Sánchez-Rodríguez, A., Daly, K., Van Veelen, A., Jones, D., et al. (2019). Quantifying citrate-enhanced phosphate root uptake using microdialysis. Plant Soil. doi: 10.1007/s11104-019-04376-4. [Epub ahead of print].
McKay Fletcher, D. M., Ruiz, S., Dias, T., Petroselli, C., and Roose, T. (2020). Linking root structure to functionality: the impact of root system architecture on citrate-enhanced phosphate uptake. New Phytol. 227, 376–391. doi: 10.1111/nph.16554
Menezes-Blackburn, D., Paredes, C., Zhang, H., Giles, C. D., Darch, T., Stutter, M., et al. (2016). Organic acids regulation of chemical-microbial phosphorus transformations in soils. Environ. Sci. Technol. 50, 11521–11531. doi: 10.1021/acs.est.6b03017
Nguyen, C. (2003). Rhizodeposition of organic C by plants: mechanisms and controls. Agronomie 23, 375–396. doi: 10.1051/agro:2003011
Oburger, E., and Jones, D. L. (2018). Sampling root exudates-mission impossible? Rhizosphere 6, 116–133. doi: 10.1016/j.rhisph.2018.06.004
Oburger, E., Kirk, G. J., Wenzel, W. W., Puschenreiter, M., and Jones, D. L. (2009). Interactive effects of organic acids in the rhizosphere. Soil Biol. Biochem. 41, 449–457. doi: 10.1016/j.soilbio.2008.10.034
Preece, C., and Peñuelas, J. (2016). Rhizodeposition under drought and consequences for soil communities and ecosystem resilience. Plant Soil 409, 1–17. doi: 10.1007/s11104-016-3090-z
R Core Team (2018). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.
Raven, J. A., Lambers, H., Smith, S. E., and Westoby, M. (2018). Costs of acquiring phosphorus by vascular land plants: patterns and implications for plant coexistence. New Phytol. 217, 1420–1427. doi: 10.1111/nph.14967
Raynaud, X., Jaillard, B., and Leadley, P. W. (2008). Plants may alter competition by modifying nutrient bioavailability in rhizosphere: a modeling approach. Am. Nat. 171, 44–58. doi: 10.1086/523951
Renella, G., Landi, L., Valori, F., and Nannipieri, P. (2007). Microbial and hydrolase activity after release of low molecular weight organic compounds by a model root surface in a clayey and a sandy soil. Appl. Soil Ecol. 36, 124–129. doi: 10.1016/j.apsoil.2007.01.001
Richardson, A. E., Lynch, J. P., Ryan, P. R., Delhaize, E., Smith, F. A., Smith, S. E., et al. (2011). Plant and microbial strategies to improve the phosphorus efficiency of agriculture. Plant Soil 349, 121–156. doi: 10.1007/s11104-011-0950-4
Schachtman, D. P., Reid, R. J., and Ayling, S. M. (1998). Phosphorus uptake by plants: from soil to cell. Plant Physiol. 116, 447–453. doi: 10.1104/pp.116.2.447
Scheerer, U., Netzer, F., Bauer, A., and Herschbach, C. (2019). Measurements of 18O-Pi uptake indicate fast metabolism of phosphate in tree roots. Plant Biol. 21, 565–570. doi: 10.1111/plb.12922
Schneider, K. D., Voroney, R. P., Lynch, D. H., Oberson, A., Frossard, E., and Bünemann, E. K. (2017). Microbially-mediated P fluxes in calcareous soils as a function of water-extractable phosphate. Soil Biol. Biochem. 106, 51–60. doi: 10.1016/j.soilbio.2016.12.016
Schnepf, A., Leitner, D., and Klepsch, S. (2012). Modeling phosphorus uptake by a growing and exuding root system. Vadose Zone J. 11:vzj2012.0001. doi: 10.2136/vzj2012.0001
Shahzad, T., Chenu, C., Genet, P., Barot, S., Perveen, N., Mougin, C., et al. (2015). Contribution of exudates, arbuscular mycorrhizal fungi and litter depositions to the rhizosphere priming effect induced by grassland species. Soil Biol. Biochem. 80, 146–155. doi: 10.1016/j.soilbio.2014.09.023
Shen, Y., Ström, L., Jönsson, J. Å., and Tyler, G. (1996). Low-molecular organic acids in the rhizosphere soil solution of beech forest (Fagus sylvatica L.) cambisols determined by ion chromatography using supported liquid membrane enrichment technique. Soil Biol. Biochem. 28, 1163–1169. doi: 10.1016/0038-0717(96)00119-8
Stenström, J., Stenberg, B., and Johansson, M. (1998). Kinetics of substrate-induced respiration (SIR): theory. Ambio 27, 35–39. doi: 10.1080/010503998420630
van Hees, P. A., Jones, D. L., Finlay, R., Godbold, D. L., and Lundström, U. S. (2005a). The carbon we do not see—the impact of low molecular weight compounds on carbon dynamics and respiration in forest soils: a review. Soil Biol. Biochem. 37, 1–13. doi: 10.1016/j.soilbio.2004.06.010
van Hees, P. A., Jones, D. L., and Godbold, D. L. (2002). Biodegradation of low molecular weight organic acids in coniferous forest podzolic soils. Soil Biol. Biochem. 34, 1261–1272. doi: 10.1016/S0038-0717(02)00068-8
van Hees, P. A., Jones, D. L., Nyberg, L., Holmström, S. J., Godbold, D. L., and Lundström, U. S. (2005b). Modelling low molecular weight organic acid dynamics in forest soils. Soil Biol. Biochem. 37, 517–531. doi: 10.1016/j.soilbio.2004.08.014
Wang, Y., He, Y., Zhang, H., Schroder, J., Li, C., and Zhou, D. (2008). Phosphate mobilization by citric, tartaric, and oxalic acids in a clay loam ultisol. Soil Sci. Soc. Am. J. 72, 1263–1268. doi: 10.2136/sssaj2007.0146
Zavišić, A., Yang, N., Marhan, S., Kandeler, E., and Polle, A. (2018). Forest soil phosphorus resources and fertilization affect ectomycorrhizal community composition, beech P uptake efficiency, and photosynthesis. Front. Plant Sci. 9:463. doi: 10.3389/fpls.2018.00463
Keywords: forest soil, microdialysis, rhizosphere, carboxylates, microbial citrate attenuation
Citation: Schack-Kirchner H, Loew CA and Lang F (2020) The Cumulative Amount of Exuded Citrate Controls Its Efficiency to Mobilize Soil Phosphorus. Front. For. Glob. Change 3:550884. doi: 10.3389/ffgc.2020.550884
Received: 10 April 2020; Accepted: 26 October 2020;
Published: 21 December 2020.
Edited by:
Andreas Schindlbacher, Austrian Research Centre for Forests (BFW), AustriaReviewed by:
Lukas Kohl, University of Helsinki, FinlandCopyright © 2020 Schack-Kirchner, Loew and Lang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Helmer Schack-Kirchner, aGVsbWVyLnNjaGFjay1raXJjaG5lckBzb2lsLnVuaS1mcmVpYnVyZy5kZQ==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.