What We Know About Stemflow's Infiltration Area

Van Stan, John T.; Allen, Scott T.

doi:10.3389/ffgc.2020.00061

MINI REVIEW article

Front. For. Glob. Change, 27 May 2020

Sec. Forest Hydrology

Volume 3 - 2020 | https://doi.org/10.3389/ffgc.2020.00061

What We Know About Stemflow's Infiltration Area

A commentary has been posted on this article:

Response: Commentary: What We Know About Stemflow's Infiltration Area
1. Read general commentary
Commentary: What We Know About Stemflow's Infiltration Area
1. Read general commentary

$\nJohn T. Van Stan II,$ John T. Van Stan II^1,2^*

Scott T. Allen³

¹Applied Coastal Research Laboratory, Georgia Southern University, Savannah, GA, United States
²Department of Geology and Geography, Georgia Southern University, Statesboro, GA, United States
³Department of Geology and Geophysics, University of Utah, Salt Lake City, UT, United States

A portion of precipitation drains to the surface down plant stems, as “stemflow.” Although per observations to date, stemflow rarely represents >2% of gross precipitation in forests, it can result in larger water fluxes to near-stem soils that are hypothetically more important to roots. The ecohydrological importance of stemflow is often predicated upon assumptions about how it infiltrates into near-stem soils. Our objective is to review the small number of studies over the ~140 years of stemflow research that have quantified its infiltration area (i.e., soil surface area over which stemflow spreads while infiltrating). We found several empirical descriptions of stemflow infiltration areas inferred from disparate approaches, and we discuss that evidence in the context of dominant assumptions and conceptualizations (i.e., equating infiltration area to basal area or estimations based on assumed soil conductivity metrics). However, we conclude that a more empirical understanding of stemflow infiltration is needed before we quantify or qualify stemflow's influence from its assumed infiltration rate. Toward this goal, we provide a critical discussion of two methods (stable isotopes and dye tracing) that seem most promising for quantifying stemflow infiltration area.

Introduction

Precipitation is redistributed by forest canopies into spatiotemporally heterogeneous patterns at the forest floor. This redistribution, however, is not always random and can involve the routing of water to specific places: notably, large canopy areas can capture and drain precipitation to the tree stem and down to nearby soils as stemflow (Tanaka et al., 1996; Metzger et al., 2019). This stemflow generation is highly variable across forest species and storm characteristics, but rarely exceeds 2% of the precipitation inputs to a forest (Carlyle-Moses et al., 2018; Van Stan and Gordon, 2018). Nonetheless, for over a century, researchers have argued that these small amounts of stemflow can be remarkably important if canopies funnel water such that it preferentially infiltrates around the stem base (Riegler, 1881; Pressland, 1973; Carlyle-Moses et al., 2018). This process is often quantified per “funneling ratios” (F; Herwitz, 1986):

\begin{array}{l} F = \frac{S_{T}}{P {\cdot I}_{T}} & (1) \end{array}

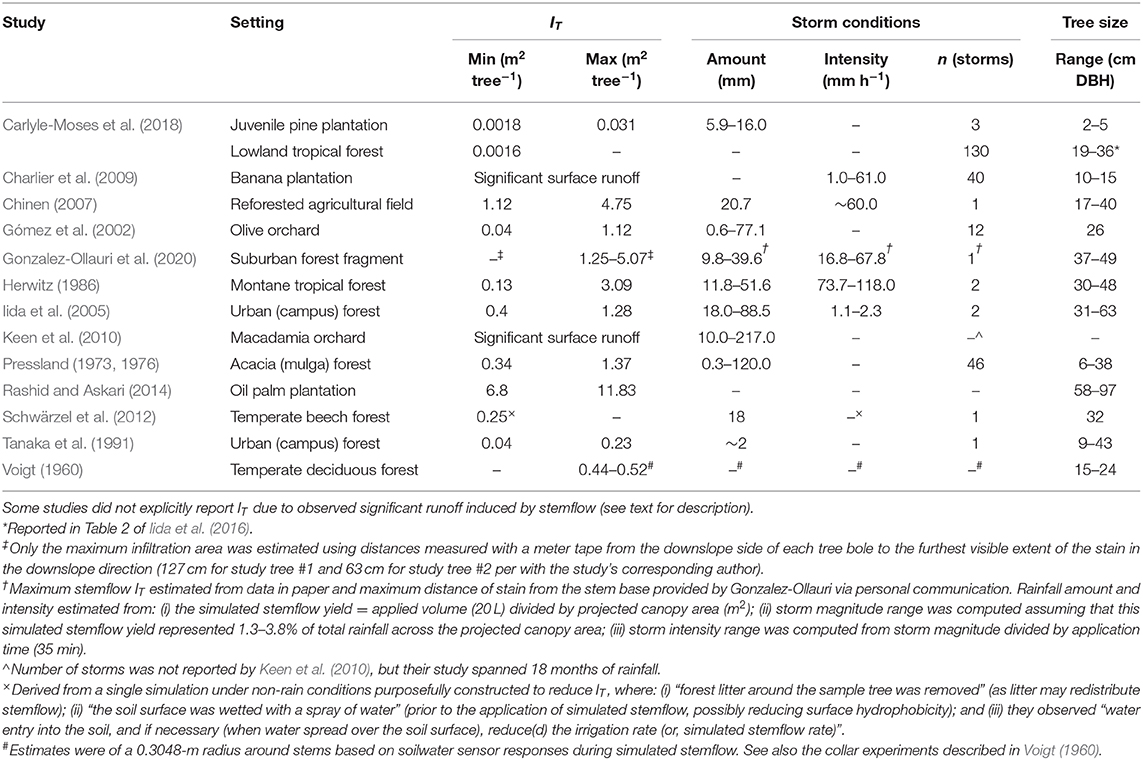
where S_T is stemflow volume (L tree⁻¹), P is depth (mm) of gross rainfall or throughfall to be compared with S_T, and I_T is infiltration area (m² tree⁻¹), often assumed equal to stem basal area (m²) (Figure 1a: Herwitz, 1986). For F > 1, stem cross sectional areas receive more precipitation due to contributions of the tree crown than equivalent areas of open ground. However, the area of soil that water actually infiltrates into is unlikely to equal stem basal area. This is because stemflow water presumably infiltrates both vertically and laterally around the stem perimeter (Figure 1b; Gómez et al., 2002); perhaps at discrete locations receiving distinct stemflow rivulets (Figure 1c; Imamura et al., 2017). As early as the mid-twentieth century, (Voigt, 1960) simulated stemflow and observed soilwater responses that led him to conclude that stemflow infiltrated within 0.3 m of the stem base (i.e., I_T values that are substantially larger than the trees' basal areas).

FIGURE 1

Figure 1. Conceptualizations of stemflow infiltration area (I_T), (a) represented as a function of stem basal area (Herwitz, 1986), (b) assumed equal to the minimum area around the stem that could transmit stemflow inputs (Gómez et al., 2002), (c) inferred from localized stemflow pathways given assumed saturated conductivity rates (Imamura et al., 2017; Carlyle-Moses et al., 2018), (d) inferred empirically from photographed, video-recorded, and scour-based observations (this study, from scarce empirical observations in Table 1), and (e) example photograph of infiltrating stemflow (note that this is a planted tree with artificial surface cover). (f₁,f₂) When a gap is present between the stem base and soils, it is reasonable to think that substantial stemflow infiltration may occur immediately beside the stem. Alternatively, (g) litter scour marks suggest large stemflow infiltration areas or (h) wide root bases may provide physical impediments to infiltration and, thus, we would expect infiltration areas to be larger (photos by authors).

Although Herwitz's (1986) equation for F employs the concept of I_T, it was not intended to be a literal representation of how stemflow infiltrates, and recent work acknowledges that the F metric requires a more realistic I_T parameter (Carlyle-Moses et al., 2018). A more realistic I_T parameter is needed to more precisely understand the effects of stemflow on individual trees (which requires considering where that stemflow infiltrates and to where it flows, e.g., to roots, into the soil matrix, or through macropores). A benefit of continuing to use the basal-area F is that values exist for a wide variety of shrub and tree species around the globe which can permit size-standardized cross-site comparisons (Levia and Germer, 2015; Van Stan and Gordon, 2018). Another benefit is that, when predicting stemflow volumes where stemflow is not measured, species- and size-specific F values measured elsewhere could be used to predict stemflow yields in stands where only basal areas and precipitation inputs are known.

TABLE 1

Table 1. Stemflow infiltration areas (I_T) reported from previous work.

Published observations that explicitly describe the size of I_T are scarce; however, there are pieces of evidence that suggest I_T is larger, 10⁻¹-10¹ m² (Voigt, 1960; Pressland, 1973, 1976; Herwitz, 1986; Tanaka et al., 1991; Gómez et al., 2002; Iida et al., 2005; Chinen, 2007; Charlier et al., 2009; Keen et al., 2010; Schwärzel et al., 2012; Rashid and Askari, 2014; Gonzalez-Ollauri et al., 2020), than the areas assumed elsewhere, e.g., 10⁻⁴-10⁻¹ m² (Iida et al., 2016; McKee and Carlyle-Moses, 2017; Carlyle-Moses et al., 2018). Studies have described stemflow infiltration pathways that include large “fingers” spreading outward from stems (Figures 1d,e; Chinen, 2007; Rashid and Askari, 2014), or large areas of runoff (Charlier et al., 2009; Keen et al., 2010). Here we review those previous observations and discuss how they may conflict with assumed infiltration areas, demonstrating the potential for inferential errors regarding how stemflow moves through the critical zone [i.e., as localized intense infiltration that percolates deeply at stems (Carlyle-Moses et al., 2018), as diffuse infiltration around stems (Voigt, 1960), or as surface runoff (Keen et al., 2010)]. To be clear, we recognize that stemflow fluxes can be larger at the surface than open rainfall or mean throughfall for certain ecosystems, and we do not disregard stemflow's potential ecological relevance. However, given that claims about stemflow's ecohydrological relevance are often predicated upon assumptions about its (small) infiltration area (Riegler, 1881; Carlyle-Moses et al., 2018), we believe it is important to critically review the scarce measurements that are useful in constraining such assumptions.

Estimating Stemflow Infiltration Areas (I_T)

Estimates of I_T have been made from various types of observations: post-storm litter marks caused by infiltration excess (Tanaka et al., 1991; Iida et al., 2005; Rashid and Askari, 2014); post-storm soil scour marks originating at the stem (Tanaka et al., 1991; Chinen, 2007); video recordings during storms (Cattan et al., 2009; Charlier et al., 2009; Keen et al., 2010); simulated stemflow during dry periods (Voigt, 1960; Schwärzel et al., 2012); in-storm measurement of the infiltration ring itself (Pressland, 1973, 1976; Gómez et al., 2002); dye tests (Spencer and van Meerveld, 2016; Imamura et al., 2017; Carlyle-Moses et al., 2018; Gonzalez-Ollauri et al., 2020); and estimates based on site-specific stemflow and near-stem infiltration rates (de Ploey, 1982; Herwitz, 1986; Gómez et al., 2002; Carlyle-Moses et al., 2018). Marks due to litter relocation and soil scour are difficult to interpret quantitatively, because these areas do not represent mean I_T for an individual storm, nor do they represent the maximum I_T for any given storm (although these I_T estimates are typically the largest areas reported: Table 1). They likely underestimate maximum I_T per storm, because they only represent the area where stemflow runoff mobilized the greatest leaf biomass or had flow velocities great enough to incise channels into the sediments. Stemflow simulations have rarely been done (Schwärzel et al., 2012; Spencer and van Meerveld, 2016; Gonzalez-Ollauri et al., 2020; Guo et al., 2020), and only one of these studies explicitly reported an I_T observation (Schwärzel et al., 2012)—which likely represents a minimum I_T (see footnotes in Table 1). Altogether, we found 11 infiltration areas reported or able to be estimated based on available data, and an additional 2 studies which reported runoff (Table 1).

Others have computed expected infiltration areas. I_T in forests has been estimated through dividing mean stemflow rate per tree, S_r (L tree⁻¹ h⁻¹) by the saturated hydraulic conductivity of the soil surface, K_sat (mm h⁻¹):

\begin{array}{l} I_{T} = \frac{S_{r}}{K_{s a t}} . & (2) \end{array}

This equation (modified from Carlyle-Moses et al., 2018), assumes that so long as inferred K_sat > S_r, stemflow will immediately infiltrate. At the stand scale, where stems often occupy 0.1–1% of forests (Hall, 2003), and with a recommended range of inferred K_sat = 100 to >1,000 mm h⁻¹ (Carlyle-Moses et al., 2018), this assumption yields stemflow infiltration area estimates that are a much smaller fraction of ground area (10⁻⁴-10⁰% of plot area; Carlyle-Moses et al., 2018). Carlyle-Moses et al. (2018) showed that this can lead to I_T values that are smaller than that of basal areas (i.e., <1% of basal area ha⁻¹); thus, the resulting F can be orders of magnitude higher than those reported using basal area as the assumed infiltration area. For example, stand-scale F in a lowland tropical forest site increases from 4.6 (per basal area) to 151.8 (per eq. 2), suggesting that the <1% of rainfall that becomes stemflow results in a “mean depth of stemflow infiltration >15,000% of the (open) precipitation” (Carlyle-Moses et al., 2018)! While this conceptualization of stemflow as a ring (or partial ring) around stems is physically more accurate than representations of I_T on basal area (Figure 1), the inferred intensity of stemflow inputs into soils around stems would be exaggerated if I_T is systematically underestimated by Equation (2). On the other hand, given the sometimes-observable gap between stems and soils (Figures 1f₁,f₂), we speculate that infiltration areas may sometimes be much smaller than would be predicted as a function of soil conductivity if these gaps extend deeper into the subsurface to facilitate flow along coarse roots (e.g., Schwärzel et al., 2012; Spencer and van Meerveld, 2016). Ultimately, existing stemflow infiltration data do not yet support generalizations about I_T.

From all estimation methods the reported range of I_T is 0.04–11.83 m² tree⁻¹, across various storm conditions and trees with diameters of 6–97 cm (Table 1). Some sites in (Table 1) did not report an I_T value as they directly observed runoff (Charlier et al., 2009; Keen et al., 2010). Spencer and van Meerveld (2016) did not report an I_T, but described finding dyed stemflow as much as 40 cm away from the stem (in the top 10 cm of soil). The complex patterns of the infiltration reported by Spencer and van Meerveld (2016) did not permit I_T estimation (but see mapped dye cross sections provided in the figures and supplement). Gonzalez-Ollauri et al. (2020) also did not report an I_T, but photographs of the soils after the dye tests, in Figure 1b of Gonzalez-Ollauri et al. (2020), show ellipse-shaped stained surface soils downslope (likely due to surface runoff) under natural simulated stemflow rates. If the Gonzalez-Ollauri et al. (2020) basal-area F values (0.1 to >9.0) are divided by the observed I_T in (Table 1), the revised range of F decreases to 0.0–1.6. It has been claimed that I_T “values in the range of 1 to 2 m² (tree⁻¹) are almost always associated with extreme precipitation conditions,” specifically, intense rainfall rates (Carlyle-Moses et al., 2018). However, I_T > 1 m² tree⁻¹ has been reported under low rainfall intensities, 1–2 mm h⁻¹ (Iida et al., 2005), and for a small storm, ~2.0 mm (Tanaka et al., 1991 in Iida et al., 2005). In fact, Iida et al. (2005) provide photographs of litter marks showing I_T = 0.4–1.3 m² tree⁻¹ under non-extreme precipitation conditions (again, note that litter marks may not represent the maximum I_T). It is important to note that existing I_T estimates are mostly from agricultural, urban or managed plantation settings, leaving I_T in natural forests under-researched.

Challenges in Estimating Stemflow Infiltration Area (I_T)

To integrate stemflow processes into broader hydrological and ecological models and conceptual frameworks, I_T estimates need to be further constrained by empirical data. Misrepresentations of I_T could result in errors in estimating the role of stemflow in surface runoff and erosion (Cattan et al., 2009; Charlier et al., 2009; Keen et al., 2010) and deep recharge via concentrated infiltration into a small area (Voigt, 1960). Even a seemingly straightforward assumption, that stemflow will infiltrate so long as S_r is less than an inferred K_sat, can underestimate I_T to a degree such that it results in significant differences in the resulting/expected hydrological process. For example, significant surface erosion can be attributed to stemflow intensities exceeding infiltration capacities and flowing laterally. Keen et al. (2010) estimated substantial stemflow-related runoff and erosion carried away 3.8 t ha⁻² y⁻¹ of soils, a phenomenon that may be overlooked if too-small infiltration areas were assumed.

Regarding S_r, one must take care to include the input of throughfall (mm h⁻¹) within the area defined by I_T, which can range from being small, <10% (Fathizadeh et al., 2014), to significant augmentations to stemflow rates, >30% (Gómez et al., 2002). Stemflow can also “splash” from the bark as it flows to the surface, especially on rough bark, thereby expanding the soil surface area over which stemflow is distributed. For example, Voigt (1960) showed that much of stemflow splashes off of stems, up to 0.5 m away, dramatically widening the radius of influence and potential stemflow infiltration area. As I_T likely varies with rainfall rate, the augmentation of S_r by throughfall and stemflow splash over these varying areas will also vary with rainfall rate. Since I_T is estimated at the sub-plot scale, estimates of additional local throughfall inputs will require knowledge of the large spatiotemporal variability of throughfall (Zimmermann and Zimmermann, 2014). If much of stemflow splashes from stems before reaching the soil surface, then it would also need to percolate through the litter layer, a storage that may intercept, spatially redistribute, and buffer stemflow (Gerrits and Savenije, 2011; Van Stan and Gordon, 2018).

Regarding inferred K_sat, there are multiple factors that can result in differences between inferred K_sat and actual infiltrability. Firstly, topsoils are likely unsaturated when stemflow first contacts the surface and, in order to infiltrate, stemflow will need to displace air in the soil pores (Horton, 1933; Linden and Dixon, 1976). The entrapment of air by infiltrating waters is particularly relevant, having been reported to reduce infiltration by 60% (e.g., Jelinkova et al., 2011); its representation remains challenging (Beven, 2018; Guo and Lin, 2018). Soil hydrophobicity may also reduce infiltrability of stemflow, as its patterns are variable in space and time (Doerr and Ritsema, 2006). Water repellency appears to be present in surface soils of all major textural types at vegetated sites, even when undisturbed (Doerr et al., 2006; de Jonge et al., 2009; Goebel et al., 2011) and can develop during inter-storm dry periods (Ferreira et al., 2016; Gimbel et al., 2016). Even given favorable circumstances at the soil surface, other vertical factors can alter stemflow's capability to infiltrate: for example, K_sat may vary significantly with soil depth and laterally (Herwitz, 1986). Alternatively, structural anomalies (e.g., gaps between soils and stems) could dramatically enhance soils infiltrability and reduce I_T.

Finally, near-stem belowground volume can be mostly occupied by large roots (Ryan and McGarity, 1983; Clemente et al., 2005), where root:soil cross-sectional area ratio decreases laterally with distance from the stem (Abdi and Deljouei, 2019; Moresi et al., 2019), hypothetically causing much of stemflow entering soils to be physically forced to move laterally. For example, researchers often describe beech (Fagus sylvatica, L. and F. grandifolia, Ehrh.) trees as having very high stemflow rates (Gersper and Holowaychuk, 1971; Falkengren-Grerup, 1989; Germer et al., 2012; Van Stan and Gordon, 2018), due to their smooth bark (e.g., Van Stan et al., 2016), but they also have wide, flared bases with roots extending laterally (Figure 1h) that complicate any assumptions about how those stemflow waters would infiltrate. Thus, the level of disagreement between I_T predicted from inferred K_sat and S_r and real-world observations might be substantial and problematic. Consistent occurrence of stemflow runoff has also been video recorded in a banana plantation (Cattan et al., 2009) and modeled (Charlier et al., 2009). Indeed, Charlier et al. (2009) opted to use a “stemflow function (that) allowed runoff to be simulated for rainfall intensities lower than the K_sat measured at the soil surface.” Similar stemflow-induced erosion has been observed in other settings besides forests, like beneath corn and sorghum under simulated rainfall (Bui and Box, 1992). Importantly, we lack a broad, fundamental understanding of stemflow's subsurface interactions at the very start of infiltration: e.g., what is the shape and size of I_T? How is it controlled by surface cover, topography or root architecture?

How to Detect Stemflow Infiltration Areas

Problematically, most of our few examples where infiltration areas have been measured are qualitative or anecdotal [see section on “Estimating stemflow infiltration areas (I_T)”] and mostly not in natural forests (Table 1) and, thus, do not necessarily capture what we would expect to occur in forests. Systematic measurements of infiltration areas are needed to improve our process-level understanding of how stemflow infiltration affects (plant-available) soil-water. Moreover, characterizing those infiltration areas is a first step toward using those infiltration areas in calculations of F (as proposed by Carlyle-Moses et al., 2018).

Dye tracers have long been used to trace infiltration processes, but in this case, dye would have to be exclusively applied to stemflow. This has been done through artificially producing stemflow [e.g., using a backpack sprayer (Spencer and van Meerveld, 2016; Gonzalez-Ollauri et al., 2020)]; however, extensive excavation is required to measure dye infiltration patterns, limiting the possibility for replication. Furthermore, dye tends to mostly provide qualitative information on where stemflow is infiltrating; it is not a conservative tracer and cannot be used to quantify how much stemflow reaches any specific area. Dye, however, does provide evidence related to the testing of the “double-funneling” hypothesis (Spencer and van Meerveld, 2016), that stemflow is not only concentrated from the canopy to the stems, but that it is also preferentially funneled to roots (Johnson and Lehmann, 2006).

Stable isotope tracers are another option for discerning where stemflow infiltrates. While isotopic differences between throughfall and stemflow can be large for individual events, those differences are inconsistent in magnitude and sign (Allen et al., 2017); whereas throughfall may be isotopically heavier than stemflow in one event, the opposite may be true of the next event. Considering this type of variability and the long residence times of soil-water (i.e., reflecting many previous events), it is unlikely that stemflow could be reliably discerned from throughfall in soils (e.g., Snelgrove et al., 2020). Alternatively, applying deuterated water as a tracer spike could provide an unambiguous signal that allows for quantitatively determining the fractions of new stemflow in mixtures across the subsurface. After applying the artificial stemflow, soils could be sampled at various depths and distances from the stem base to not only estimate I_T but also the shape of the stemflow infiltration plume. Although this soil sampling can be less destructive than the excavations done after dye tests, the soil disturbance still limits the possibility for replication. Challenges include generating artificial stemflow in realistic conditions (i.e., during storms) and at realistic rates (Gonzalez-Ollauri et al., 2020; Guo et al., 2020). Nonetheless, a microcontroller could be used to automatically generate realistic stemflow rates by drawing from a reservoir of deuterated water. Future work could apply these more realistic stemflow rates and dynamics directly to tree stems using dyes as well. Using either of these approaches involves the challenge of distinguishing between the effects of how the water is input (i.e., as throughfall or rainfall vs. stemflow) from the effect of the soils (i.e., near-stem soils vs. those less affected by roots).

Conclusions

Stemflow can play relevant roles in the coupled hydrology, biogeochemistry, and ecology of vegetated ecosystems; however, its role hinges upon its infiltration area (I_T), and we found little empirical evidence to constrain estimates of that infiltration area. In consideration of how little is known about I_T, we suggest that little is also known about stemflow's relevance to subsurface processes. These conceptual unknowns do not discount the potential relevance of stemflow to vegetated ecosystems; instead, they justify research opportunities. Future research should seek to address the unknowns that limit our understanding of stemflow's impacts and interactions across vegetated ecosystems. One of these needs is clearly a better understanding of how and where stemflow infiltrates. Addressing this knowledge gap will not only give funneling ratio metrics physical meaning, but may provide a more empirical signal to direct future investigations of stemflow's relevance and role in ecohydrological processes.

Author Contributions

JV conceived the study. JV and SA reviewed, compiled, and analyzed the past literature. Both authors also equally contributed to the manuscript writing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors gratefully acknowledge the constructive reviews of Doug P. Aubrey at the Savannah River Ecology Lab and Kevin E. Mueller at Cleveland State University.

References

Abdi, E., and Deljouei, A. (2019). Seasonal and spatial variability of root reinforcement in three pioneer species of the Hyrcanian forest. Austrian J. Soil Sci. 136, 175–198.

Google Scholar

Allen, S. T., Keim, R. F., Barnard, H. R., McDonnell, J. J., and Renée Brooks, J. (2017). The role of stable isotopes in understanding rainfall interception processes: a review. Wiley Interdiscip. Rev. Water 4:e1187. doi: 10.1002/wat2.1187

PubMed Abstract | CrossRef Full Text | Google Scholar

Beven, K. (2018). A century of Denial: preferential and nonequilibrium water flow in soils, 1864–1984. Vadose Zo. J. 17, 1–17. doi: 10.2136/vzj2018.08.0153

MINI REVIEW article

What We Know About Stemflow's Infiltration Area

Introduction

Estimating Stemflow Infiltration Areas (IT)

Challenges in Estimating Stemflow Infiltration Area (IT)

How to Detect Stemflow Infiltration Areas

Conclusions

Author Contributions

Conflict of Interest

Acknowledgments

References

Estimating Stemflow Infiltration Areas (I_T)

Challenges in Estimating Stemflow Infiltration Area (I_T)