
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Evol. Neurosci. , 23 June 2010
Volume 2 - 2010 | https://doi.org/10.3389/fnevo.2010.00007
Some numerical knowledge, such as the immediate recognition of small quantities, is observed in animals. The development of arithmetical abilities found in man’s evolution as well as in child’s development represents a long process following different stages. Arithmetical abilities are relatively recent in human history and are clearly related with counting, i.e., saying aloud a series of number words that correspond to a collection of objects. Counting probably began with finger sequencing, and that may explain the 10-base found in most numerical systems. From a neuropsychological perspective, there is a strong relationship between numerical knowledge and finger recognition, and both are impaired in cases of left posterior parietal damage (angular or Gerstmann’s syndrome). Writing numbers appeared earlier in human history than written language. Positional digit value is clearly evident in Babylonians, and around 1,000 BC the zero was introduced. Contemporary neuroimaging techniques, specifically fMRI, have demonstrated that the left parietal lobe, particularly the intraparietal sulcus, is systematically activated during a diversity of tasks; other areas, particularly the frontal lobe, are also involved in processing numerical information and solving arithmetical problems. It can be conjectured that numerical abilities continue evolving due to advances in mathematical knowledge and the introduction of new technologies.
Calculation abilities have followed a long process from the initial quantification systems up to modern algebra, geometry, and physics. Some rudimentary numerical concepts are observed in animals, and there is no question that pre-historic man used some quantification. However, the ability to represent quantities, the development of a numerical system, and the use of arithmetical operations are found only in old civilizations.
This paper reviews the evolution of calculation abilities, including numerosity and counting in non-human animals, calculation abilities in primitive and modern humans, and links between language and number concepts throughout human history. In addition, the paper reviews contemporary studies of the neurological substrates of numerical abilities and discusses the implications of technological advances with regard to continued evolution of these abilities.
The origin of mathematical concepts can be traced to sub-human species. Throughout recent history different reports have argued that animals (horses, rats, dogs, chimpanzees, dolphins, and even birds) can use numerical concepts and perform arithmetical operations. Some of these reports represent evident charlatanry directed to the general public. Some others, however, are rigorous and highly controlled scientific studies (e.g., Rugani et al., 2009 ).
There is, in general, agreement that some rudimentary numerical concepts are observed in animals. These basic numerical skills can be considered as the real origin of the calculation abilities found in contemporary man. For instance, pigeons can be trained to peck a specific number of times on a board, and rats can be trained to press a lever a certain amount of times to obtain food (Koehler, 1951 ; Mechner, 1958 ; Capaldi and Miller, 1988 ). It could be conjectured that pigeons and rats can count, at least up to a certain quantity; that is, they can recognize how many times a motor act – to peck on a board or to press a lever – has been repeated. Whether or not this behavior can really be interpreted as counting is nonetheless questionable. However, this behavior is observed, at least after a long and painstaking training. Nonetheless, these animal responses (to peck or to press the lever) are not precise but just approximate. In other words, when the rat is required to press the lever seven times, the rat presses it about seven times (i.e., 5, 6, 7, 8 times). As Dehaene (1997) emphasizes, for an animal, 5 plus 5 does not make 10, but only about 10. According to him, such fuzziness in the internal representation of numbers prevents the emergence of exact numerical arithmetical knowledge in animals. Using highly controlled and sophisticated designs, it has been pointed out that chimpanzees can even use and add simple numerical fractions (e.g., 1/2 + 1/4 = 3/4) (Woodruff and Premack, 1981 ). These observations support the assumption that some quantity concepts can be found in different animals.
Counting (or rather, approximately counting) motor responses is just a motor act as is walking or running. “Counting” lever pressings is not very different from estimating the effort (e.g., number of steps or general motor activity) required in going from one point to another. Counting in such a case could be linked to some proprioceptive and kinesthetic information.
In the human brain Kansaku et al. (2006) identified a network of areas involved in enumerating small numbers of auditory, visual, and somatosensory stimuli, and in enumerating sequential movements of hands and feet, in the bilateral premotor cortex, presupplementary motor area, posterior temporal cortex, and thalamus. The most significant consistent activation across sensory and motor counting conditions was observed in the lateral premotor cortex. Lateral premotor activation was not dependent on movement preparation, stimulus presentation timing, or number word verbalization. Furthermore, movement counting, but not sensory counting, activated the anterior parietal cortex.
Not only chimpanzees, but also rats and many other animals, can distinguish numerosity (i.e., global quantification); for instance, they prefer a bowl containing a larger number of nutritive elements (such as chocolates or pellets) when selecting between two bowls containing different amounts (Davis and Perusse, 1988 ). It may be conjectured that global quantification (numerosity perception) and counting (at least the approximate counting of motor responses) represent kinds of basic calculation abilities found at the animal level. Rats prefer a bowl containing 20 pellets to a bowl containing only 10 pellets; however, they do not prefer a bowl containing 20 pellets to a bowl containing 21 pellets. Obviously, numerosity perception is related to the size and shape of the visual image projected to the retina. It can be assumed that 20 pellets in a bowl result in a larger and more complex retinal image than 10 pellets. But the visual image corresponding to 20 pellets is difficult to distinguish from the visual image corresponding to 21 pellets.
Chimpanzees are capable of various forms of numerical competence, including some correspondence constructions (that is, comparing two collections of elements) for low quantities (Premack, 1976 ; Davis and Perusse, 1988 ). Most likely, these numerical abilities also existed in pre-historic man. Homo sapiens antecessors may have been capable of using correspondence constructions in some social activities, such as food sharing. It has been proposed that Homo habilis (ancestor of Homo erectus, living about 2.3 million to 1.4 million years ago) needed to use correspondence constructions when butchering large animal carcasses (Parker and Gibson, 1979 ). Distributing pieces of a divided whole (e.g., prey) into equal parts required the ability to construct one-to-one correspondences. Probably, Paleolithic man was able to match the number of objects in different groups and, eventually, the number of objects in a collection with the number of items in some external cue system, e.g., fingers or pebbles (incidentally, calculus means pebbles).
The immediate recognition of certain small quantities is found not only in animals, but also in small children. Animals and children can readily distinguish one, two, or three objects (Fuson, 1988 ; Wynn, 1990 , 1992 ; Cook and Cook, 2009 ). Antell and Keating (1983) observed that newborn infants were able to discriminate among visual stimulus arrays consisting of few a dots. It was found that infants were able to discriminate between small numbers (2 versus 3) but not for larger sets. This ability for discriminating and also representing and remembering small numbers of items has also been reported by other authors (e.g., Starkey and Cooper, 1980 ). Interestingly, evoked potentials at 3 months are already capable of marking changes in the nature and number of a set of objects, and these activation changes relate to the parietal lobe (Dehaene and Dehaene-Lambertz, 2009 ). Noteworthy, in normally developing children and adults, the increase in arithmetic competence is associated with shift of activation from frontal brain areas to parietal areas. A shift of activation is also observed within the parietal lobe from the intraparietal sulci to the left angular gyrus; experts’ arithmetic proficiency depends on a more extended activation than the network found in beginners. In expert individuals with solid, extensive mathematical training, specific brain activation changes are also observed (Zamarian et al., 2009 ).
Oneness, twoness, and threeness seemingly are basic perceptual qualities that our brain can distinguish and process without counting. It can be conjectured that when pre-historic humans began to speak, they may have been able to name only the numbers one, two, and three, corresponding to specific perceptions. To name them was probably no more difficult than naming any other sensory attribute (Dehaene, 1997 ). Of note, all world languages can count up to three, even though three may represent “many”, “several”, or “a lot” (Hurford, 1987 ). “One” is obviously the unit, the individual (the speaker may also be “one”). “Two” conveys the meaning of “another” (for example, in English and also in Spanish, “second” is related with the verb “to second” and the adjective “secondary”). “Three” may be a residual form of “a lot”, “beyond the others”, or “many” (for example, “troppo”, which in Italian means “too much”, is seemingly related with the word three -tre). In the original Indo-European language, spoken perhaps some 15000–20000 years ago, apparently the only numbers were “one”, “one and another” (two), and “a lot”, “several”, or “many” (three) (Dehaene, 1997 ). Interestingly, in some contemporary languages, two different plurals are found: a plural for small quantities (usually two, sometimes three and four) and a second plural for larger quantities; for instance, in Russian, “one house” is “odin dom”, “two, three, or four houses” is “dva, tri, cheterye doma” but “five houses” is “pyat domov”.
Of note, in different world languages, the word “one” does not have any apparent relationship with the word “first”; and the word “two” is also not related with the word “second”. “Three” may sometimes, but not always, hold some relationship with “third”. Beyond three, ordinals are clearly associated with cardinal numbers. The conclusion is obvious: for small quantities (one, two, three), cardinals and ordinals must have a different origin. For larger quantities, ordinal numbers are derived from cardinals. As a matter of fact, one/first and two/second correspond to different conceptual categories.
It may be speculated that for pre-historic man the first person and the second person in a line (or the first animal and the second animal during hunting, or other similar concepts) do not seem to be related with the number one and the number two. For small children “first” has the meaning of “initial” (e.g., “I go first”) whereas “second” is related to “later” or “after” (e.g., “you go second”). These words have a temporal and also spatial meaning, but not an evident numerical meaning. The association between “one” and “first”, and “two” and “second” seems a relatively advanced process in the development of numerical concepts. That is, the numerical meaning of “first” and “second” seems to appear after its temporal and spatial meaning. The association between ordinals and cardinals becomes evident only for larger quantities (more than three) and seems to represent a later acquisition in human evolution and the complexization of numerical concepts. Moreover, in many contemporary languages (e.g., the Huitoto language, spoken by the Huitoto Indians in the Amazonian jungle 1 ) there are no ordinal numbers. For “first”, the Huitoto language uses “the beginning”; to express “second” the word “another” is used.
Arithmetical abilities are clearly related with counting. Counting – not simply recording the approximate amount of motor responses required for obtaining reinforcement, but actually saying aloud a series of number words that correspond to a collection of objects – is relatively recent in human history. Counting also occurs relatively late in child development. In human history, as well as in child development, counting using number words begins with sequencing the fingers (i.e., using a correspondence construction) (Hitch et al., 1987 ). The name of the finger and the corresponding number can be represented using the very same word (that means the very same word is used for naming the thumb and the number one; the very same word is used to name the index finger and the number two, etc.). The fingers [and toes; as a matter of fact, many languages such as Spanish use a single word (dedo) to name both the fingers and toes] are usually sequenced in a particular order. This strategy represents a basic procedure found in different ancient and contemporary cultures around the world (LevyBruhl, 1910/1947 ; Cauty, 1984 ; Klein and Starkey, 1987 ; Dansilio, 2008 ). Interestingly, it has been demonstrated that children with low arithmetical skills also present a finger misrepresentation on the Draw-a-Person test (Pontius, 1989 ). This observation has been confirmed in different cultural groups. By the same token, difficulty in recognizing and naming the fingers represents a reliable predictor of developmental dyscalculia (Kaufmann, 2008 ).
Taking a typical example as an illustration, the Colombian Sikuani or Guahibo Amazonian jungle Indians 2 count in the following way: the person (an adult when counting or a child when learning to count) places his/her left hand in supination; to point to number one, the right index points to the left little finger, which is then bent (Queixalos, 1989 ). The order followed in counting is always from the little finger to the index. To point to number five, the hand is turned and the fingers opened; for six, both thumbs are joined, the left fingers are closed, and the right opened; they are opened one after the other for seven, eight, nine and ten. Between 11 and 20, the head points to the feet and the sequence is re-initiated. The lexicon used is:
1: kae (the unit, one)
2: aniha-behe (a pair, both)
3: akueyabi
4: penayanatsi (accompanied; that is, the fingers together)
5: kae-kabe (one hand)
Numbers from six to nine, are formed with “one hand and (a certain number) of fingers”. Ten becomes “two hands”:
6: kae-kabe kae-kabesito-nua (one hand and one finger)
7: kae-kabe anih-akabesito-behe (one hand and a pair of fingers)
10: anih-akabe-behe (two hands)
“Two hands” is maintained between 10 and 20. Toes (taxawusito) are added between 11 and 14; and “one foot” (kaetaxu) is used in 15. Twenty is “two hands together with two feet”:
11: aniha-kabe-behe kae-taxuwusito (two hands and one toe)
12: aniha-kabe-behe aniha-tuxuwusito-behe (two hands and two toes)
15: aniha-kabe-behe kae-taxu-behe (two hands and one foot)
16: aniha-kae-behe kae-taxu-behe kaetaxuwusito (two hands, one foot, and one toe)
20: aniha-kabe-behe aniha-taxu-behe (two hands and two feet)
Fingers are named according to their order in counting (as mentioned above, counting begins always with the little finger of the left hand). The Sikuani language possesses number words only up to three (kae, aniha-behe, akueyabi). Four (penayanatsi = accompanied, together) represents a correspondence construction. Strictly speaking, the Sikuani language counts only up to three. From four to twenty, they use a correspondence construction, not really counting; and for higher quantities, they resort to a global quantification.
Sometimes not only the fingers (and toes) but also other body segments may be used in counting: the wrist, the shoulders, the knees, etc. (Levy-Bruhl, 1910/1947 ; Cauty, 1984 ; Dansilio, 2008 ). However, sequencing the fingers (and toes) represents the most universal procedure in counting. Some languages (e.g., some Mayan dialects and Greenland Eskimo) use the same word to denote the number 20 (that is, “all the fingers and all the toes”) and “a person”.
In different Amerindian languages, for higher than 10 or 20 figures, most often “many” is used (global quantification principle) (Cauty, 1984 ; Ifrah, 2000 ). Or, they can refer to other people’s hands (correspondence construction) (e.g., thirty-five might be something like “my two hands, my two feet, my father’s two hands, my father’s one foot”). As mentioned, “twenty” sometimes becomes something like “one person”, a sort of higher order numeral. It is interesting to note that in some contemporary languages (like English and Spanish) “one” means the unit, but it is also used as a sort of indefinite personal pronoun. In English and Spanish we can also use “one” as synonymous with “myself”. Twenty is found to be the base number in the Mayan numerical system (Swadesh, 1967 ; Cauty, 1984 ). In many contemporary languages, a 10 and/or 20 base is evident.
“Digit” (from Latin digitus) means both number and finger. The correspondence construction between numbers and fingers is evident. Latin number notation was originally Etruscan (Turner, 1984 ) and referred (as in other languages) to the fingers. One, two, and three were written simply by making vertical strokes. In four, the Latin system resorts to a simplification. Originally, four was written IIII, but later on it became IV. Five (V) represented the whole hand with the arm bent (that is, all the fingers of the hand), and ten (X) the two arms crossed.
From a neuropsychological perspective, a strong relationship between numerical knowledge, finger gnosis, and even lateral (right–left) knowledge is evident (Ardila and Rosselli, 2002 ; Kaufmann, 2008 ). Finger agnosia (and probably right–left discrimination disturbances) could be interpreted as a restricted form of autotopagnosia (inability to recognize or localize the various body parts) (Ardila et al., 1989 , 2000 ).
It is not surprising to find that a decimal (or vigesimal, i.e., with a base of 20) system has been most often developed. Simultaneously or very close in time, decimal systems appeared in different countries (Sumer, Egypt, India, and Crete). Different symbols were used to represent 1, 10, 100, and 1000 (Childe, 1936 ; Dansilio, 2008 ).
There is, however, an interesting and intriguing exception: Sumerian and later Babylonians (about 2,000 BC) developed not only a decimal but also a sexagesimal system: a symbol represented 60 or any 60-multiple and another different symbol represented the number 10 and any 10-multiple. Thus, for example, the number 173 was then represented: 2 × 60 (the symbol for 60 repeated twice) + 5 × 10 (the symbol for 10 repeated five times) + 3 (a symbol for units repeated three times). A base of 60 has remained for some contemporary time measures (e.g., minutes and seconds). Twelve is also frequently maintained as a “second-order” unit (e.g., a dozen). Evidently, 60 results from “five times twelve”. Five obviously is “one hand”, and the question becomes, where does 12 come from? What are the two additional units? It might be speculated that 12 means the 10 fingers plus the two feet – or even the two elbows or the two shoulders or the two knees (individuality of components is easier to appreciate in the hands than in the feet). But this is only speculation, although it is feasible according to our knowledge about counting procedures used in different cultural groups (Levy-Bruhl, 1910/1947 ; Ifrah, 2000 ; Dansilio, 2008 ).
Maya Indians developed a similar system, but had 20 as a base (Leon-Portilla, 1986 ). They used different symbols to represent 20, 400 (20 × 20), and 8000 (20 × 20 × 20) (Cauty, 1984 ).
Thus, reviewing the history of numerical concepts, it is found that world languages developed a base 10 (10 fingers) or 20 (10 fingers plus 10 toes) or even five (five fingers) to group quantities. In some contemporary languages a residual 20-base can be found (e.g., in French 80 can be “four twenties”). In many contemporary languages, different words are used between 1 and 10. Between 10 and 20, the numerical systems usually become irregular, unpredictable, and idiosyncratic. From 20 onward, numbers are formed simply with the words “twenty plus one”, “twenty plus two”, etc. Some contemporary languages still use a five-base in counting. For instance, in the Amerindian language Tanimuca in South America 3 , speakers count up to five. Between five and 10, numbers are “five one”, “five two”, and so on.
Writing numbers appeared earlier in history than writing language. Some cultures (e.g., Incas) developed a number representing system, but not a language representing system (Swadesh, 1967 ). As mentioned before, “calculus” means pebble. Pebbles, marks, knots, or any other element were used as a correspondence construction to record the number of elements (people, cows, fishes, houses, etc). In Sumer, the first number writing system has been found (about 3,000 BC) (Childe, 1936 ; Ifrah, 2000 ): Instead of using pebbles, fingers, or knots, it was simpler just to make a mark (a stroke or a point) on the floor, on a tree branch, or on a board if one wanted to keep the record. In Egypt, India and later in Crete, a similar system was developed: units were represented by a conventional symbol (usually a stroke) repeated several times to mean a digit between one and nine; a different symbol was used for 10 and 10-multiples.
Positional digit value is clearly evident in Babylonians, and around 1,000 BC the zero was introduced. Positional value and zero are also evident in Maya Indians (Leon-Portilla, 1986 ). Egyptians and Babylonians commonly used fractions. Small fractions (1/2, 1/3, and 1/4) are relatively simple numerical concepts, and even chimpanzees can be trained to use small fractions (Woodruff and Premack, 1981 ).
As pointed out, recognition of individual marks or elements up to three is easy: It represents an immediate perception readily recognizable. Beyond three, the number of marks (strokes or dots) usually has to be counted and errors are more likely. Furthermore, it is rather time-consuming and cumbersome to be constantly counting marks. Interestingly, the different digit notational systems always represent one, two and three with strokes (or points, or any specific mark). In other words, the numbers one, two and three are written making one, two or three strokes. But beyond these figures, digit writing may give way to other strategies. In our Arabic digit notation system, “one” is a vertical line whereas two and three were originally horizontal lines that became tied together by being handwritten (Ifrah, 2000 ). This observation may be related with the inborn ability to perceptually recognize up to three elements. Beyond three, errors become progressively more likely. Perceptually distinguishing eight and nine strokes is not as easy as distinguishing between two and three strokes. The introduction of a different representation for quantities over three was a useful and practical simplification.
The numerical system, along with measurement units, were developed departing from the body dimensions (fingers, hands, arm, steps, etc.). This tendency to use the human body not only to count but also as measure units is still observed in some contemporary measurement units (e.g., foot).
Adding, subtracting, multiplying and dividing were possible in the Egyptian system, but of course, following procedures quite different from those procedures we currently use. Egyptians based multiplication and division on the “duplication” and “halving” method (Childe, 1936 ). Interestingly, this very same procedure (duplicating and halving quantities) is also observed in illiterate people when performing arithmetical operations. Thus, to multiply 12 × 18 in the Egyptian system the following procedure was followed:
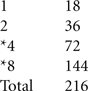
(The number 18 is duplicated one or several times, and the amounts corresponding to 12 (4 + 8 in this example) are selected and summed up: 72 + 144 = 216. To divide, the inverse procedure was used. Therefore, the procedure used to divide 19 by 8 would be:

That is, 2 + 4 + 8 (2 + 1/4 + 1/8), which is 2.375
In brief, different steps were followed in the development of arithmetical abilities: representing quantities, initially as correspondence constructions (i.e., one mark represents one element), later new marks were added to represent larger quantities (usually 10); providing a positional value to the marks; using fractions; and computing quantities (adding and subtracting; and later multiplying and dividing).
Since primary acalculia (a basic defect in computational ability) was initially described by Henschen (1925) it has been associated with left posterior parietal damage (e.g., Mazzoni et al., 1990 ; Ardila et al., 2000 ; Mayer et al., 2003 ). Furthermore, it was suggested that different cerebral pathways are responsible for processing rote numerical knowledge (e.g., multiplication tables) and semantic knowledge of numerical quantities. Dehaene and Cohen (1997) have proposed that a left subcortical network contributes to the storage and retrieval of rote verbal arithmetical facts, whereas an inferior parietal network is dedicated to the mental manipulation of numerical quantities.
Neuroimaging techniques (e.g., fMRI) have been used to analyze the pattern of brain activity during diverse calculation tasks. It has been demonstrated that different brain areas are active during arithmetical tasks, but the specific pattern of brain activity depends on the particular type of task that is used. At minimum, the following brain areas become activated during calculation: the upper cortical surface and anterior aspect of the left middle frontal gyrus (Burbaud et al., 1995 ); the supramarginal and angular gyrus (bilaterally) (Rueckert et al., 1996 ); the left dorsolateral prefrontal and premotor cortices, Broca’s area, and the inferior parietal cortex (Burbaud et al., 1999 ); and the left parietal and inferior occipitotemporal regions (lingual and fusiform gyri) (Rickard et al., 2000 ). The diversity of brain areas involved in arithmetical processes supports the assumption that calculation ability represents a multifactor skill, including verbal, spatial, memory, body knowledge, and executive function abilities (Ardila and Rosselli, 2002 ). Dehaene et al. (2004) , however, proposed that regardless of the diversity of areas that become active during arithmetical tasks, the human ability for arithmetic is associated with activation of very specific brain areas, in particular, the intraparietal sulcus. Neuroimaging studies with humans have demonstrated that the intraparietal sulcus is systematically activated during a diversity of number tasks and could be regarded as the most crucial brain region in the understanding and use of quantities (Ashkenazi et al., 2008 ). These observations have been supported using brain electrostimulation (Roux et al., 2009 ). Other brain areas, such as the precentral area and the inferior prefrontal cortex, are also activated when subjects engage in mental calculations. RoSca (2009) has proposed that there exists a fronto–parieto–subcortical circuit responsible for complex arithmetic calculations and that procedural knowledge relies on a visuo-spatial sketchpad that contains a representation of each sub-step of the procedure.
Traditionally, calculation defects have been associated with posterior left parietal damage (Henschen, 1925 ; Boller and Grafman, 1983 ), and frequently included in the so-called Gerstmann’s (or angular gyrus) syndrome. Symptoms of Gerstmann’s syndrome (acalculia with agraphia, disorders in right-left orientation, and finger agnosia) (Gerstmann, 1940 ) can be found during direct cortical stimulation in the angular gyrus region (Roux et al., 2003 ). Using fMRI, it has been observed that the left angular gyrus is not only involved in arithmetic tasks requiring simple fact retrieval, but may show significant activations as a result of relatively short training of complex calculation (Delazer et al., 2003 ).
Colvin et al. (2005) investigated numerical abilities in a split-brain patient using experiments that examined the hemispheres’ abilities to make magnitude comparisons. One experiment examined the ability to enumerate sets of stimuli, and another two experiments required judgments about two concurrently presented stimuli that were either identically coded (i.e., two Arabic numerals, two number words, or two arrays of dots) or differently coded (e.g., an Arabic numeral and a number word). Both hemispheres were equally able to enumerate stimuli and make comparisons between numerical representations regardless of stimuli coding. However, the left hemisphere was more accurate than the right when the task involved number words.
Cohen et al. (2000) reported a patient with a lesion in the left perisylvian area who showed a severe impairment in all tasks involving numbers in a verbal format, such as reading aloud, writing to dictation, or responding verbally to questions of numerical knowledge. In contrast, her ability to manipulate non-verbal representation of numbers, i.e., Arabic numerals, was comparatively well preserved. This observation supports the proposal that language and calculation disorders can be dissociated (Basso et al., 2000 ). Some authors have assumed that language and numerical concepts are differently organized in the brain and follow distinct developmental patterns in children (Gelman and Butterworth, 2005 ). Other authors have suggested that calculation and language are mediated by partially different and also partially overlapped brain systems (Baldo and Dronkers, 2007 ). Semenza et al. (2006) have emphasized that calculation and language usually share the same hemisphere.
In summary, diverse brain areas are activated during the performance of different arithmetical tasks, although contemporary evidence suggests that the intraparietal sulcus seems to the play the most crucial role. During the learning of new calculation abilities, additional brain areas become involved and the specific pattern of brain activity depends on the particular type of test that is used. It can be assumed that during human history, the development of new numerical abilities was correlated with the involvement of new brain areas during the performance of progressively more complex numerical tasks.
Arithmetical abilities and number representation have existed for only some 5000–6000 years. Most likely, during the Stone-Age, only simple counting up to three and, of course, “bigger” and “smaller” (magnitude judgment) concepts were present. Global quantification is observed at the pre-human level. Correspondence constructions allowed increasing the amount of numbers to be used. The most immediate correspondence construction is performed with the fingers. Finger knowledge and counting represent, to a certain extent, the same cognitive ability, as is still evident in some contemporary languages, such as Sikuani.
Counting, finger gnosis, and even lateral spatial knowledge may present a common historical origin. Seemingly, calculation abilities were derived from finger sequencing. Number representation and arithmetical operations are observed only since some 5000–6000 years ago. Currently, calculation abilities are rapidly evolving due to the introduction of modern technology and resulting cognitive demands. Right-left discrimination (as well as the use of other spatial concepts) most likely was present in pre-historic man, because requirements of spatial abilities may have been very high, even higher than in contemporary man (Hours, 1982 ; Ardila and Ostrosky, 1984 ; Ardila, 1993 ). Rightleft discrimination and finger gnosis are strongly interdependent, and even they can be interpreted as components of the autotopagnosia syndrome. It seems, in consequence, that there is a rationale for finding a common brain activity for finger gnosis, calculation, and right-left discrimination (and in general, spatial knowledge mediated by language) (Ardila and Rosselli, 2002 ).
Contemporary neuroimaging techniques, specifically fMRI, have demonstrated that the left parietal lobe, particularly the intraparietal sulcus is systematically activated during a diversity of number tasks; other areas, particularly the frontal lobe, are also involved in processing numerical information and solving arithmetical problems. Also, it has been suggested that there exists a fronto–parieto–subcortical circuit responsible for complex arithmetic calculations and procedural knowledge.
It can be conjectured that numerical abilities continue evolving due to advances in mathematical knowledge and the introduction of new technologies; for instance, instead of writing numbers down on paper and applying certain computational rules, we more often require the ability to use a pocket calculator or a computer program. Doubtless, computation ability is evolving in a new direction. Brain representation of calculation may be taking a new direction, and even the acalculia syndrome may present different clinical manifestations.
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Antell, S. E., and Keating, D. (1983). Perception of numerical invariance by neonates. Child Dev. 54, 695–701.
Ardila, A., Concha, M., and Rosselli, M. (2000). Angular gyrus syndrome revisited: acalculia, finger agnosia, right-left disorientation, and semantic aphasia. Aphasiology 14, 743–754.
Ardila, A., Lopez, M. V., and Solano, E. (1989). “Semantic aphasia reconsidered,” in Brain Organization of Language and Cognitive Processes, eds A. Ardila and F. Ostrosky-Solis (New York: Plenum Publishing Company), 77–193.
Ardila, A., and Ostrosky, F. (1984). “Some final remarks,” in The Right Hemisphere: Neurology and Neuropsychology, eds A. Ardila and F. Ostrosky-Solis (London: Gordon and Breach Science Publishers), 265–273.
Ashkenazi, S., Henik, A., Ifergane, G., and Shelef, I. (2008). Basic numerical processing in left intraparietal sulcus (IPS) acalculia. Cortex 44, 439–448.
Baldo, J. V., and Dronkers, N. F. (2007). Neural correlates of arithmetic and language comprehension: a common substrate? Neuropsychologia 45, 229–235.
Basso, A., Burgio, F., and Caporali, A. (2000). Acalculia, aphasia and spatial disorders in left and right brain-damaged patients. Cortex 36, 265–280.
Boller, F., and Grafman, J. (1983). Acalculia: Historical development and current significance. Brain Cogn. 2, 205–223.
Burbaud, P., Camus, O., Guehl, D., Bioulac, B., Caille, J. M., and Allard, M. (1999). A functional magnetic resonance imaging study of mental subtraction in human subjects. Neurosci. Lett. 273, 195–199.
Burbaud, P., Degreze, P., Lafon, P., Franconi, J. M., Bouligand, B., Bioulac, B., Caille, J. M., and Allard, M. (1995). Lateralization of prefrontal activation during internal mental calculation: a functional magnetic resonance imaging study. J. Neurophysiol. 74, 2194–2200.
Capaldi, E. J., and Miller, D. J. (1988). Counting in rats: its functional significance and the independent cognitive processes that constitute it. J. Exp. Psychol. Anim. Behav. Process 14, 3–17.
Cohen, L., Dehaene, S., Chochon, F., Lehericy, S., and Naccache, L. (2000). Language and calculation within the parietal lobe: a combined cognitive, anatomical and fMRI study. Neuropsychologia 38, 1426–1440.
Colvin, M. K., Funnell, M. G., and Gazzaniga, M. S. (2005). Numerical processing in the two hemispheres: studies of a split-brain patient. Brain Cogn. 57, 43–52.
Cook, J. L., and Cook, G. (2009). Child development: Principles and perspectives. Boston: Pearson Allyn and Bacon.
Dansilio, S. (2008). Los trastornos del cálculo y el procesamiento del número. Montevideo: Prensa Médica Latinoamericana.
Davis, H., and Perusse, R. (1988). Numerical competence in animals: Definitional issues, current evidence and a new research agenda. Behav. Brain Sci. 11, 561–615.
Dehaene, S. (1997). The Number Sense. How the Mind Creates Mathematics. New York: Oxford University Press.
Dehaene., S., and Cohen, L. (1997). Cerebral pathways for calculation: double dissociation between rote verbal and quantitative knowledge of arithmetic. Cortex 33, 219–250.
Dehaene, S., and Dehaene-Lambertz, G. (2009). Neuro-imagerie cognitive: phylogenèse et ontogenèse. Bull. Acad. Natl. Med. 193, 883–889.
Dehaene, S., Molko, N., Cohen, L., and Wilson, A. J. (2004). Arithmetic and the brain. Curr. Opin. Neurobiol. 14, 218–224.
Delazer, M., Domahs, F., Bartha, L., Brenneis, C., Lochy, A., Trieb, T., and Benke, T. (2003). Learning complex arithmetic-an fMRI study. Brain Res. Cogn. Brain Res. 18, 76–88.
Gelman, R., and Butterworth, B. (2005). Number and language: how are they related? Trends Cogn. Sci. (Regul. Ed.) 9, 6–10.
Gerstmann, J. (1940). The syndrome of finger agnosia, disorientation for right and left, agraphia and acalculia. Arch. Neurol. Neurochir. Psychiatr. 44, 398–408.
Henschen, S. E. (1925). Clinical and anatomical contributions on brain pathology. Arch. Neurol. Psychiatry 13, 226–249.
Hitch, G., Cundick, J., Haughey, M., Pugh, R., and Wright, H. (1987). “Aspects of counting in children’s arithmetics,” in Cognitive Processes in Mathematics eds J. A. Sloboda and D. Rogers (Oxford: Clearendon Press), 26–41.
Ifrah, G. (2000). The Universal History of the Numbers. New York: Wiley. Available at: indian-cultures.com/Cultures/huitoto.html. Retrieved December 17, 2009; indian-cultures.com/Cultures/guahibo.html. Retrieved December 17, 2009.
Kansaku, K., Johnson, A., Grillon, M. L., Garraux, G., Sadato, N., and Hallett, M. (2006). Neural correlates of counting of sequential sensory and motor events in the human brain. Neuroimage 31, 649–660.
Klein, A., and Starkey, P. S. (1987). “The origins and development of numerical cognition: A comparative analysis,” in Cognitive Processes in Mathematics, eds J. A. Sloboda and D. Rogers (Oxford: Clearendon Press), 1–25.
Leon-Portilla, M. (1986). Tiempo y Realidad en el Pensamiento Maya [Time and reality in Maya thinking]. México: Universidad Nacional Autónoma de México.
Levy-Bruhl, L. (1910/1947). Las Funciones Mentales en las Sociedades Inferiores [Mental functions in lower societies]. Buenos Aires: Lautaro.
Mayer, E., Reicherts, M., Deloche, G., Willadino-Braga, L., Taussik, I., Dordain, M., Van der Linden, M., and Annoni, J. M. (2003). Number processing after stroke: anatomoclinical correlations in oral and written codes. J. Int. Neuropsychol. Soc. 9, 899–912.
Mazzoni, M., Pardossi, L., Cantini, R., Giornetti, V., and Arena, R. (1990). Gerstmann’s syndrome: a case report. Cortex 25, 459–468.
Mechner, F. (1958). Probability relations within response sequences under ratio reinforcement. J. Exp. Anal. Behav. 1, 109–121.
Parker, S. T., and Gibson, K. H. (1979). A developmental model for the evolution of language and intelligence in early hominids. Behav. Brain Sci. 2, 367–408.
Pontius, A. A. (1989). Color and spatial error in block design in stone-age Auca Indians: Ecological underuse of occipital-parietal system in men and of frontal lobes in women. Brain Cogn. 10, 54–75.
Queixalos, F. (1989). Numeración tradicional Sikuani. [Traditional Sikuani numbering] Glotta, 3, 28–31.
Rickard, T. C., Romero, S. G., Basso, G., Wharton, C., Flitman, S., and Grafman, J. (2000). The calculating brain: An fMRI Study. Neuropsychologia 38, 325–335.
RoSca, E. C. (2009). Arithmetic procedural knowledge: a cortico-subcortical circuit. Brain Res. 1302, 148–156.
Roux, F. E., Boetto, S., Sacko, O., Chollet, F., and Tremoulet, M. (2003). Writing, calculating, and finger recognition in the region of the angular gyrus: a cortical stimulation study of Gerstmann syndrome. J. Neurosurg. 99, 716–727.
Roux, F. E., Boukhatem, L., Draper, L., Sacko, O., and Démonet, J. F. (2009). Cortical calculation localization using electrostimulation. J. Neurosurg. 110, 1291–1299.
Rueckert, L., Lange, N., Partiot, A., Appollonio, I., Litvan, I., Le Bihan, D., and Grafman, J. (1996). Visualizing cortical activation during mental calculation with functional MRI. Neuroimage 3, 97–103.
Rugani, R., Fontanari, L., Simoni, E., Regolin, L., and Vallortigara, G. (2009). Arithmetic in newborn chicks. Proc. Biol. Sci. 276, 2451–2460.
Semenza, C., Delazer, M., Bertella, L., Granà, A., Mori, I., Conti, F. M., Pignatti, R., Bartha, L., Domahs, F., Benke, T,, and Mauro, A. (2006). Is math lateralized on the same side as language? Right hemisphere aphasia and mathematical abilities. Neurosci. Lett. 406, 285–288.
Swadesh, M. (1967). El Lenguage y La Vida Humana [Language and human life]. México: Fondo de Cultura Económica.
Turner, R. (1984). The Great Cultural Tradition. The Foundation of Civilization. New York: McGraw-Hill.
Woodruff, G., and Premack, D. (1981). Primitive mathematical concepts in the chimpanzee: Proportionality and numerosity. Nature 293, 568–570.
Wynn, K. (1992). Children’s acquisition of the number words and counting system. Cogn. Psychol. 24, 220–251. Available at: www.ethnologue.com/show_family.asp?subid=931–916 .
Keywords: calculation abilities, numerical knowledge, calculation origins, brain evolution
Citation: Ardila A (2010) On the evolution of calculation abilities. Front. Evol. Neurosci. 2:7. doi: 10.3389/fnevo.2010.00007
Received: 25 January 2010;
Paper pending published: 01 March 2010;
Accepted: 07 June 2010;
Published online: 23 June 2010
Edited by:
J. M. Davis, University of Georgia, USA; University of Macau, ChinaReviewed by:
Anthony Dugbartey, University of Victoria, CanadaCopyright: © 2010 Ardila. This is an open-access article subject to an exclusive license agreement between the authors and the Frontiers Research Foundation, which permits unrestricted use, distribution, and reproduction in any medium, provided the original authors and source are credited.
*Correspondence: Alfredo Ardila, Department of Communication Sciences and Disorders, NHS 431B, Florida International University, Miami, FL 33182, USA. e-mail:YXJkaWxhYUBmaXUuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.