A sociohydrological model for evaluating the drought resilience of indigenous and modern dryland irrigation systems in Sri Lanka

Over the millennia, indigenous small tanks (small reservoirs or ponds) have served to store rainwater and surface runoff to irrigate drylands. However, despite their significance, small tanks have been gradually abandoned in drylands over the past decades to expand cultivable areas under modern agricultural interventions, such as dam reservoirs and canal systems. Sole reliance on modern water interventions has intensified freshwater stress and rendered dryland agriculture vulnerable to droughts. Herein, we present a sociohydrological model incorporating the concept of human salience (i.e., attention accorded by farmers based on actual and perceived reservoir water availability and rainfall) and access to small tanks to simulate farmer decisions on cultivation area. By applying the model to a centrally managed modern irrigation system and a quasi-decentralized indigenous irrigation system in the Mahaweli H irrigation scheme of the Sri Lankan dry zone for the 2010–2020 period, we calibrated farmer perception levels to show that indigenous system farmers perceive a significantly low rainfall threshold indicating greater adaptability to dry conditions. Sensitivity of perception levels to cultivation area demonstrate that modern system farmers have an 18% higher dependency on reservoir water availability compared to indigenous farmers when deciding cultivation area. This stark dependency on reservoir water availability of modern system farmers is rooted in lack of accessibility to small tanks, a feature that enhance drought resilience of farmers in the indigenous system. While providing quantifiable insights, this comparative assessment underscores the importance of critically evaluating the efficacy of decentralized indigenous small tanks in current water resource investments.

1 Introduction

The escalating demand for food production driven by socio-economic trends has necessitated global agricultural land expansion (Ramankutty et al., 2018; Winkler et al., 2021) and drylands are not exempt from this development (Wang et al., 2023). Although drylands are limited in soil moisture due to high aridity (low precipitation and high evaporation), they cover about half of the earth’s surface and provide ecosystem services to inhabited nearly third of the world population (Millennium Ecosystem Assessment, 2005; Reynolds et al., 2007). Over the last century, drylands have expanded and it is projected to continue the expansion in this century due to changes in aridity (Huang et al., 2017). According to the United Nations (2011), an estimated 25% of drylands are used to irrigated and rainfed farming, where Lewin et al. (2024) predict to experience current dryland natural habitat conversion due to anthropogenic interventions including agricultural expansion. Meanwhile, already critical state of water scarcity in drylands are expected to exacerbate with less rainfall and increased temperature due to climate change, which increases the vulnerability of dryland agriculture (Ahmed et al., 2022; IUCN, 2019; Thomas, 2008). Hence, sustainable agricultural water management interventions in drylands are imperative to confront drought and enhance resilience (Chander et al., 2019; Ward, 2016).

Throughout the history of human civilization, the majority of dryland agriculture has depended on irrigation (Angelakιs et al., 2020). Notable examples of indigenous irrigation systems invented by early societies in drylands could include ancient irrigation canals in Egypt and Mesopotamia (Koç, 2018), Qanat systems in Middle East (Nasiri and Mafakheri, 2015), small tank (pond) cascade systems in South Asia (Panabokke et al., 2002) and Acequia systems in Spain and its colonies (Martos-Rosillo et al., 2019). Such systems have demonstrated intrinsic drought resilience attributes by storing rainfall and runoff to provide irrigation water in dry seasons (Bebermeier et al., 2017; Srivastava and Chinnasamy, 2022), enhancing hydrological connectivity between surface and ground water (Fernald et al., 2015; Wickramasinghe and Nakamura, 2024) and fostering interaction between human and water systems that highlight community values (Gunda et al., 2018).

The Sri Lankan dry zone, the target area in this study is recognized in global dryland classifications, specifically within the dry sub-humid category (Maestre et al., 2021). This region still demonstrates a unique example of resilient indigenous water management practices. These integrate locally managed small tank systems within the large dam irrigation systems, linking small tanks to dam reservoir to supply water for a wider area of farmlands and human settlements (Abeywardana et al., 2018; Brohier, 1937). The sustained communities in these irrigation and domestic water supply systems symbolize human–water interactions from both the total environmental and historical perspectives (Jayasena et al., 2021). Such interlinked systems are polycentric because of their ability to function on different scales and in different spaces adding redundancy and diversity to the system (Carlisle and Gruby, 2019; Yu et al., 2020). The quasi-decentralized nature (a combination of large-scale water resources and distributed local capacities) can increase the flexibility of the system in managing extreme events under accelerating climate change (Gilrein et al., 2019). However, during the past few decades, dryland agriculture has been boosted by centrally managed irrigation systems, including large dam reservoirs and water diversion projects (Chen et al., 2016; Liu et al., 2013; Müller and Hettige, 1995). Such expansion of agricultural lands and canal systems have caused the destruction and abandonment of existing decentralized small tank systems in Sri Lanka and other countries, resulting in unified modern irrigation systems that rely solely on remote freshwater supply (Li et al., 2023; Zubair, 2005).

Although modern irrigation interventions are promising in the short term, a growing body of evidence has shown that they are associated with unintended secondary consequences resulting in unsustainable outcomes (Di Baldassarre et al., 2018; Gohari et al., 2013; Madani and Mariño, 2009). One particular development is the reservoir effect, a typical sociohydrological phenomenon in which overreliance on reservoirs increases vulnerability and reduce drought resilience (Di Baldassarre et al., 2018). This situation calls for a new agenda to integrate small, distributed water infrastructure into dam reservoirs for resilience development (IWMI, 2021). While decentralized irrigation techniques such as water harvesting from small tanks (or ponds and small reservoirs) are well-studied (Bebermeier et al., 2017; Birner et al., 2010; Geekiyanage and Pushpakumara, 2013; Wisser et al., 2010), how integrating distributed local water storages to dam reservoirs can increase drought resilience remains limited in conceptualization and quantification. Yet the impacts of integrated locally managed small storages to dam reservoirs, such as those indigenous water management systems observed in Sri Lankan dry zone, present and important contribution to the resilience of agricultural water interventions.

As recent modeling approaches have adopted holistic socio-hydrological frameworks which effectively account for the interaction between human and water systems (Sivapalan, 2015), here we present a sociohydrological model to simulate cultivation area and apply it to a quasi-decentralized indigenous and a centralized modern irrigation system in Sri Lankan dry zone to discuss drought resilience comparatively. Our model integrated the concept of human salience, which describes in cognitive dimensions as the process by which individuals prioritize and respond to incoming information based on their existing expectations. These expectations are shaped by the interaction of situational and societal contexts, as well as the individual’s long-term memory and cognitive frameworks (Schmid and Günther, 2016). In our approach, we defined farmer salience as the perceived adequacy of water availability for cultivation. Here we incorporate an average farmers’ perceived seasonal reservoir water availability and rainfall levels as their expectations with observed reservoir water availability and rainfall to conceptualize farmer salience to decide cultivation area. Finally, we quantify farmers’ perceived reservoir water availability threshold and rainfall threshold levels for both irrigation systems by calibrating model parameters using historical data from 2010 to 2020. We utilize these perceived levels and their sensitivity on deciding cultivation area as a proxy to unravel their dependency on water resources, which is crucial for assessing drought resilience. The findings of this study can inform policymakers to better tailor effective agricultural water interventions for enhancing drought resilience in drylands, while protecting indigenous water systems.

2 Materials and methods

2.1 Study area

In this study, the proposed sociohydrological model is applied and validated using the Mahaweli H irrigation scheme in the dry zone of Sri Lanka. Yoda Ela (YE) is an indigenous irrigation water system built in 459 AD that supplies water from the Kalawewa Reservoir to downstream farmlands while feeding small tanks along the way (Brohier, 1937). The capacity to store water in a series of interconnected irrigation tanks in Yoda Ela provides farmers with the flexibility to withdraw water when required (Panapitiya et al., 2008). The small tanks in this quasi-decentralized system were abandoned in some reaches in the 1970s in favor of expanding land to grow rice under a centralized modern irrigation canal named New Jaya Ganga (NJG) (Fernando, 1980), which relies on remote fresh water where Kalawewa reservoir inflow was increased with transbasin water diversion.

At present, both modern and indigenous irrigation systems function separately, where water is withdrawn through separate sluices from the Kalawewa Reservoir (Figure 1). In the modern New Jaya Ganga system, mainly irrigation water from reservoir is directly supplied to farmlands. In contrast, farmers withdraw water from small tanks and small tanks are fed by the reservoir water in the indigenous Yoda Ela system. Characteristics of both irrigation systems are shown in Table 1, details of small tanks connected to Yoda Ela canal are given in Supplementary Table S1 and the schematic representation of water management is shown in Figure 2. Farmers in both systems are involved in rice cultivation in two rainy seasons, namely, Maha (October–March), the wet season, and Yala (April–September), the dry season. The region has faced severe agricultural droughts during the last few decades, particularly in the Yala season (Alahacoon and Amarnath, 2022), resulting in increased freshwater consumption and vulnerability to rice cultivation.

Figure 1

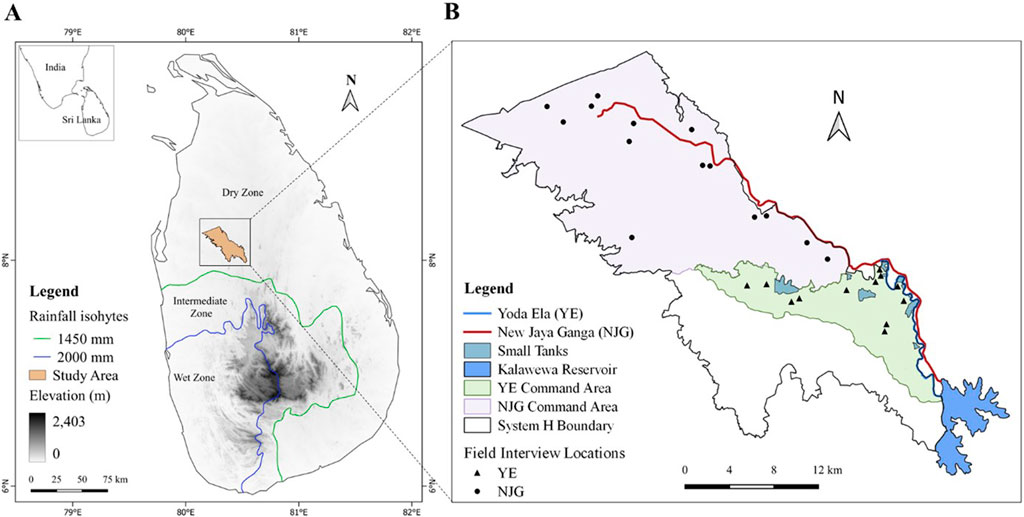
Figure 1. Study area information. (A) The site location in Sri Lankan dry zone. (B) Coexisting quasi-decentralized indigenous Yoda Ela and centralized modern New Jaya Ganga systems in the Mahaweli System H irrigation scheme.

Table 1

Table 1. Characteristics of two irrigation systems. Data was obtained from WMS, MASL and (Wickramasinghe and Nakamura, 2024).

Figure 2

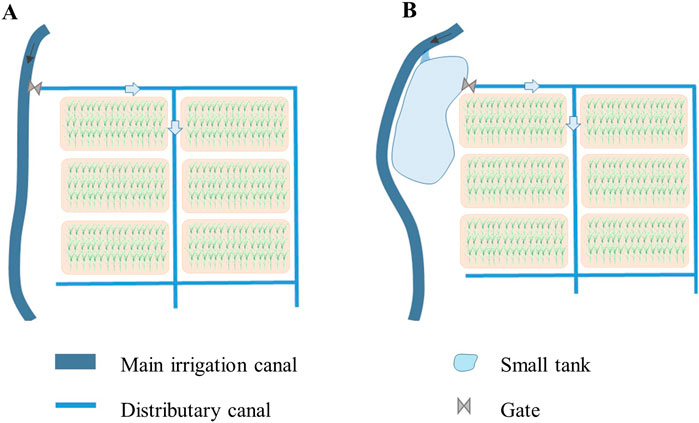
Figure 2. Different irrigation water management styles. (A) Direct reservoir water conveyance to the farmland in the centralized modern system and (B) is the quasi-decentralized indigenous water management system where reservoir water first supplied to the small tank and farmers withdraw water from the small tank.

According to historical Kalawewa Reservoir water supply data obtained from seasonal summary reports of the Water Management Secretariat of the Mahaweli Authority of Sri Lanka (WMS, MASL), the modern system (NJG) shows a higher actual water withdrawals from reservoir than planned (Figure 3). This is in contrast to the behavior of the indigenous system (YE), which demonstrates a balance between the predicted and actual water withdrawals from the reservoir. Such high dependency on remote freshwater irrigation makes farming more vulnerable to extreme weather events in the modern system. Thus, the Mahalweli H irrigation scheme represents a case study to evaluate the impact of integrated small tanks to dam reservoir on farmer drought resilience.

Figure 3

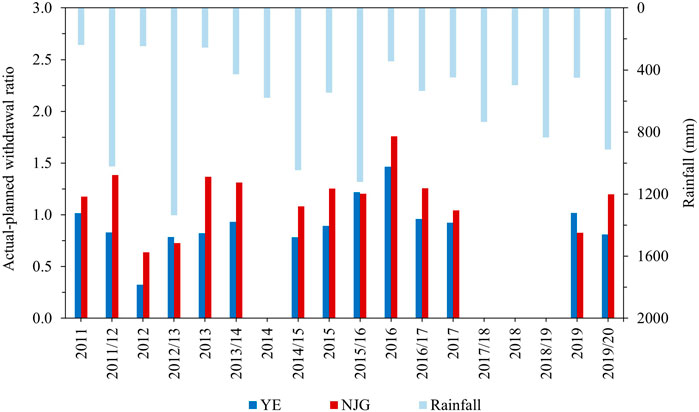
Figure 3. Comparison of actual and planned reservoir withdrawals between modern New Jaya Ganga (NJG) and indigenous Yoda Ela (YE) irrigation systems during the Yala (dry) and Maha (wet) seasons. The Y-axis represents the withdrawal ratio (unitless), where values greater than 1 indicate higher withdrawals than planned and values below 1 indicate lower withdrawals than planned. The X-axis denotes irrigation seasons: Yala (April–September) is labeled with a single year (e.g., “2011” for Yala 2011), while Maha (October–March) spans two calendar years and is labeled accordingly (e.g., “2011/12” for Maha 2011–12). Data were unavailable for the 2014 Yala, 2017/18 Maha, 2018 Yala, and 2018/19 Maha seasons.

2.2 Conceptualization

The sociohydrological model simulates the interplay among water resources (reservoir storage, rainfall, and small tanks) and determines the cultivation area for modern and indigenous irrigation systems. Primary qualitative data for model development were collected through 37 interviews conducted at the target site between February and March 2024. Farmers, local irrigation managers, and national water-allocation engineers were interviewed. The semi-structured interviews focused on cultivation decision making, water management processes (including water application), and reservoir operations. The interview participants were selected across diverse spatial locations, such as those cultivated under small tanks in Yoda Ela and those who depended directly on the Kalawewa reservoir in New Jaya Ganga.

To translate seasonal hydrological conditions (i.e., reservoir storage and rainfall) to farmer responses (deciding cultivation area), we apply the concept of human salience, which is defined as a cognitive process of assessing incoming information based on existing expectations of individuals, which are shaped by long term memory based cognitive context, situational and social contexts (Schmid and Günther, 2016). In our model, farmer salience is defined as the perceived adequacy of water availability to support cultivation. Based on long term cultivation experiences, farmers have developed their own perception (expectation) thresholds on reservoir water availability and rainfall to decide cultivation area. We utilize actual and perceived seasonal reservoir water availability and rainfall values to conceptualize farmer salience and consequently decide cultivation area. Modelling farmer salience is explained in detail in Section 2.2.2.

At the target site, the irrigation authority first announces cultivation plans to both systems prior to the season, based on their internal weather predictions. In parallel, farmers in both systems observe reservoir storage and rainfall as the main influences in determining their cultivation area based on salience levels. In the indigenous system, small tanks provide flexibility to farmers, which can compensate for the balance cultivation area if available reservoir and rainfall water is perceived to be inadequate. The proposed sociohydrological model consists of sub-models of reservoir storage, cultivation area, and irrigation water demand, and is linked to account for feedback between subsystems (Figure 4).

Figure 4

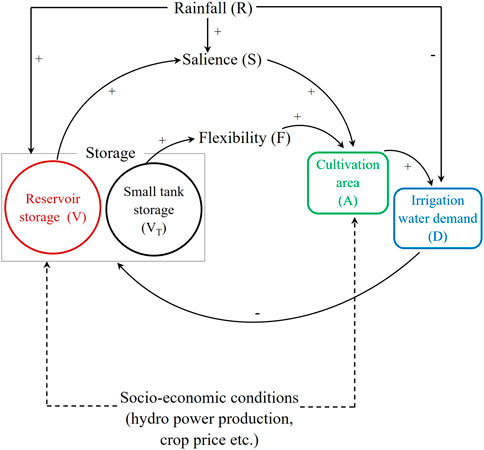
Figure 4. Causal loop diagram of the relationships among reservoir storage (red), cultivation area (green), irrigation water demand model (blue) and small tank storage (black). Here, salience refers to the perceived adequacy of water availability for deciding the cultivation area, whereas flexibility generated by small tank storage compensates to balance cultivation area. Solid arrows denote direct influence and dashed arrows demonstrate indirect effects.

2.2.1 Reservoir storage sub-model

In the case study, both the modern and indigenous systems withdraw water from the same reservoir using separate sluices. Our model explicitly determines a seasonal water balance for each system. A season equals to 6 months for a given cultivation year (October–March for the Maha season and April–September for the Yala season). For the considered irrigation canal system, the model assumes that the water supply is sourced from reservoir storage (including inflow), rainfall, and small tank storage. The model utilizes the observed reservoir storage, inflow from diversions, spillage, and total other allocations (total water allocation to other canal systems except the considered system) as seasonal inputs for the water balance calculation. For simplicity, the catchment inflow and evaporation losses were included within the diversion inflow component by conducting a preliminary water balance. For a given isolated system, the reservoir storage at the end of the season V_t+1 (m³) is calculated using Equation 1 as follows:

$V_{t+1}=V_t+Q_I-Q_A-Q_S-Q_O(1)$

where V_t (m³) is the reservoir storage at the beginning of the season, Q_I (m³) is the total observed seasonal reservoir inflow, Q_A (m³) is the observed other total allocation, Q_S (m³) is the observed seasonal spill flow, and Q_O (m³) is the seasonal reservoir outflow to the considered irrigation system through the sluice. Since reservoir storage cannot exceed its physical storage capacity, a capping mechanism was applied to ensure consistency with real-world operations. Here, we divided the sluice outflow into agricultural water and environmental flow requirements in the Equation 2 as follows:

$Q_O=Q_E+W(2)$

where Q_E (m³) is the canal environmental flow and W (m³) is the water withdrawal for water supply to the irrigation system (Equation 3). Because both irrigation systems finally rely on the reservoir for their net irrigation water demand, we estimated the irrigation withdrawals by employing reservoir operational rules. The model simulates withdrawal using linear hedging, which is used to reduce the risk of severe shortages by imposing conservation, although storage and inflow remain available (Shih and ReVelle, 1994; You and Cai, 2008).

$W=\left\{\begin{array}{l}\frac{V_t+Q_I-Q_A-Q_S}{k_h}if{V}_t+Q_I-Q_A-Q_S<k_{h}D\\ D\text{\hspace{0.17em}otherwise\hspace{0.5em}}\end{array}\right.(3)$

where D (m³) is the seasonal irrigation water demand of the irrigation system and k_h is the slope of the hedging release function. When k_h is equal to 1, the standard operation policy is replicated, in which the demand is always met until water is available in the reservoir. When k_h exceeds 1, withdrawals are reduced if the available water is below k_hD (Cancelliere et al., 1998). A visualized explanation of the standard operation policy and hedging policy is provided in Supplementary Figure S1 and application of the hedging policy to simulate seasonal reservoir operation as explained in Equation 3 is visualized in Supplementary Figure S2.

Canal environmental flow (Q_E) was calculated based on a water budget approach in which fixed allocation volumes were provided (Granco et al., 2019). This method prioritizes satisfying human demands, and establishes limits based on the percentage of natural inflow, and does not directly satisfy downstream ecological demands (Stein et al., 2022). Based on this mechanism, we calculated the canal environmental flow as a percentage of the remaining reservoir storage after satisfying the irrigation demands. This assumption was verified through interviews with water managers. To support in understanding the behavior of Equation 4, a visual plot illustrating their functionality is provided in Supplementary Figure S3.

$Q_E=\left\{\begin{array}{l}{e}_n\left(V_t+Q_I-Q_A-Q_S-W\right)\text{ if }{V}_t+Q_I-Q_A-Q_S>k_{h}D\\ 0\text{\hspace{0.17em}else }\end{array}\right.(4)$

where e_n is the environmental flow factor of the remaining storage.

2.2.2 Cultivation area sub-model

Field interviews revealed that, as the cultivation season approaches, farmers begin to monitor rainfall—either visually or referring to weather reports 1 month prior to the established season’s starting month (April or October). At the onset of the season, the management authority declares the start of cultivation and initiates transbasin water diversion to the reservoir. From this point onward, farmers not only continue observing rainfall but also begin assessing reservoir storage and inflows. Farmers at different locations along the main canal (head, mid and tail) initiate sowing at different times. The sowing activities are guided by farmers’ perceived adequacy of available water for cultivation (i.e., salience) and sowing is primarily conducted within the first four months and rarely initiated during the final two months of the season.

To represent this observed behaviour in the model, we conceptualize a representative average farmer, whose seasonal cultivation response is determined by the saliency level. Here it is assumed to be a homogeneous farming community within the irrigation system, where all farmers respond similarly, without explicitly accounting for variations in farm size or socio-economic conditions. First, we estimate the cropping intensity (percentage of cultivation area from the available land) of an average farmhold. In our model, farmer remains flexible in initiating cultivation within the first four months, adjusting their decisions based on perceived water adequacy. Since exact sowing times are unknown, we estimate farmers’ cultivation behavior retrospectively by assessing cumulative hydraulic conditions (reservoir inflow and rainfall) over this period. Salience, representing perceived water adequacy, is computed as a single retrospective assessment after four months and determines the cropping intensity of this average farmer and then it is scaled up to the command area to reflect the total cultivation area of the irrigation system.

Until the fourth month of the season, the conceptualized average farmer asses cumulative reservoir water availability V_s (m³) and cumulative rainfall R_S (mm) as key sources of information to develop their salience levels are given in Equations 5, 6:

$V_S=V_{t=0}+{\displaystyle \sum _{t=0}^3}{Q}_t(5)$

$R_S={\displaystyle \sum _{t=-1}^3}{R}_t(6)$

where Q_t (m³) is the monthly observed reservoir inflow (includes catchment inflow and transbasin diversions) and R_t (mm) is the monthly observed rainfall. As farmers assess adequacy of reservoir and rainfall conditions separately during the decision-making period, we first explicitly modeled farmer salience to the cumulative reservoir water availability (V_s), termed reservoir salience (S_V), and to cumulative rainfall (R_S) as rainfall salience (S_R).

We conceptualized the growth of S_V and S_R as arising from the interplay between dynamic growth promotion (reservoir water availability and rainfall) and inhibiting forces (land constraints). Farmers’ perception of water adequacy is highly influenced by their perceived thresholds on reservoir water availability and rainfall, which developed by their past experience and other social contexts. This determines how sensitive farmers are to changes in water availability, influencing their cultivation decisions. As positive feedback mechanisms commence, growth accelerates, and eventually limiting factors cause growth to taper off. Consequently, each of these farmer salience growths often follow an S-shaped curve, ranging from 0 (no attention when water availability is far below the perceived threshold) to 1 (full attention when water availability exceeds the threshold). To represent this phenomena mathematically, we deployed the well-known logistic function of Verhulst in Equations 7, 8, as it is the simplest mathematical function capable of reproducing the S-curve (Bacaër, 2011; Kucharavy and De Guio, 2011).

$S_V=\frac{1}{1+e^{-k_v\left(V_S-v_C\right)}}(7)$

$S_R=\frac{1}{1+e^{-k_r\left(R_S-r_C\right)}}(8)$

where V_s (m³) is the cumulative reservoir water availability in the cultivation period, v_C (m³) is the perceived threshold reservoir water availability, k_v is the storage curve steepness, R_S (mm) is the cumulative rainfall during the monitoring period, r_c (mm) is the perceived threshold rainfall, and k_r is the rainfall curve steepness. The perceived threshold value in the logistic growth curve determines the inflection point at which the perceived adequacy of water availability shifts to accelerate or decelerate. A higher threshold value indicates a higher level of reservoir water availability or rainfall is required to observe significant farmer salience. Curve steepness indicates the rate of function transition from low to high saliency around the threshold. The steeper the curve, the more rapidly the salience response changes once the threshold is reached, whereas a gentle slope indicates farmers gradually adjust salience responses.

In practice, neither rainfall nor reservoir storage alone fully determines farmer behavior; rather, it is their interaction that shapes decision-making. If either reservoir storage or rainfall is low in a given season, farmers’ willingness to cultivate decreases significantly. To capture this interdependence and measure overall perceived adequacy of water availability on cultivation, we define integrated saliency (S) in Equation 9, calculated as the product of reservoir saliency (S_V) and rainfall saliency (S_R).

$S{=S}_V\times S_R(9)$

Here, a value of S close to 0 indicates extremely low perceived adequacy of water availability, suggesting less motivation to cultivation. Whereas a value close to 1 suggests higher perceived adequacy of water availability with highly favorable conditions for cultivation. Based on the overall perceived adequacy of water availability, the conceptualize average farmer determines the cropping intensity. Finally, the calculated seasonal cropping intensity for this average farmhold is then scaled up to the command area of the irrigation system to obtain seasonal cultivation area A (m²) of the irrigation system as in Equation 10:

$A=a_c\left[S+\left(1-S\right)F\right](10)$

where a_c (m²) is the command area of the system and F is the flexibility generated by the small tank system connected to the reservoir. As Panapitiya et al. (2008) argued, with the stationary nature of the water supply from small tanks adding the benefit of flexibility, this conceptualization allows small tanks to compensate for lower overall farmer saliency in water-scarce periods in a nonlinear manner. This agrees well with the argument of Gilrein et al. (2019) that decentralized infrastructure systems can increase flexibility owing to their small scale. In this study, flexibility is conceptualized in Equations 11, 12 as a function of seasonal small tank storage and the average farmer access to small tanks as follows:

$V_T=a_{T}R\lambda (11)$

$F=\frac{V_T}{v}\left(1-r\right)(12)$

where V_T (m³) is the total seasonal storage of the small tank system, a_T (m²) is the total surface area of small tanks, R (mm) is the observed seasonal rainfall and λ is the model parameter representing net inflow of seasonal rainfall to the small tank cascade system. v (m³) is the maximum storage of the small tank cascade system, and r is the normalized distance of an average farmer to the small tank cascade system.

2.2.3 Irrigation water demand sub-model

Irrigation water demand was calculated using a crop water requirement sub-model. Field interviews with farmers and irrigation managers revealed that during the Maha (wet) season, almost all farmers typically cultivated rice, as water was sufficiently available. This can change in the Yala (dry) season, during which the rice cultivation area is reduced compared to Maha season, and other field crops are introduced as the perceived water availability is low. However, rice is the main crop cultivated by most Sri Lankan farmers because of its role as a staple food, cultural attachment, lower input cost and care during the growing period than other crops, easy market access, market stability, and strong institutional support (Burchfield and Poterie, 2018). Therefore, in this model, for simplicity in the calculation of crop water requirements, we neglected crop diversification, limiting to a single crop, which was rice. The seasonal crop water requirement was calculated using the single-crop coefficient method proposed by the FAO (Allen et al., 1998) in Equation 13 as follows:

${ET}_c={\displaystyle \sum _{i=0}^3}{k}_{c,i}{d}_i{ET}_0(13)$

where ET_c (mm) is the crop evapotranspiration (crop water requirement), i is the growth stage of the crop, k_c is the crop coefficient, d (days) is the length of the crop growth stage, and ET₀ (mmday⁻¹) is the reference crop evapotranspiration. The model considers 105 days (seeds to maturity) of rice cultivation (Water Management Secretariat, 2022) and the relevant growth stages and corresponding k_c values were obtained from local irrigation guidelines (Ponrajah, 1984), as shown in Table 2.

Table 2

Table 2. Growth stages and crop coefficients.

Up on deciding cultivation area in Section 2.2.2, it was assumed that cultivation period may differ within the season. Therefore, this sub-model uses the seasonal average ET₀ value to calculate crop evapotranspiration, replicating the seasonal behavior of the irrigation system. The average ET₀ was calculated using the relevant daily reference evapotranspiration data obtained from the U.S. Geological Survey (Hobbins et al., 2023). Model accounts for water requirement for land preparation, farmer efficiency in water application, available water from rainfall, and small tanks storage. We assumed that, at the start of each season, small tank storage is to be zero and all the accumulated water throughout the season is fully consumed by farmers. Then, the seasonal field irrigation water requirement, FIR (m³), is calculated using Equation 14 as follows:

$FIR=\left\{\begin{array}{l}\left(\frac{{ET}_c+l_p}{e_a}\right)A-P_e-V_T\text{ if }\left(\frac{{ET}_c+l_p}{e_a}\right)>P_e+V_T\\ 0\text{ else }\end{array}\right.(14)$

where l_p (mm) is the water depth required for land preparation, e_a (%) is the water application efficiency to the farmland, ET_c (mm) is the crop evapotranspiration (crop water requirement), A (m²) is the seasonal total cultivation area, V_T (m³) is the total seasonal storage of the small tank system and P_e (mm) is the effective seasonal rainfall calculated using Equation 15 according to local guidelines (Ponrajah, 1984):

$P_e=\left\{\begin{array}{l}0.67\left(R-150\right)\text{if }R>150\\ 0\text{\hspace{0.17em}else }\end{array}\right.(15)$

where R (mm) is seasonal rainfall.

Finally, the seasonal irrigation water demand D (m³) from the reservoir was calculated using the systems water conveyance efficiency (e_c) as in Equation 16. e_c considers the overall efficiency of water transmission through different levels (main, branch, and field canals).

$D=\frac{FIR}{e_c}(16)$

After integrating the sub-models, this sociohydrological model simulates the cultivation area, water withdrawals, and reservoir storage at seasonal time steps. Each season spans 6 months, where farmers engage in cultivation across two rainy seasons: April to September and October to March. The model is applied to both modern and indigenous irrigation systems, covering the period from 2010 to 2020.

2.3 Model parameterization

We fit the cultivation area, reservoir storage, and reservoir water outflow modules, as explained in the conceptualization to the historical dataset of our modern and indigenous irrigation systems separately. The parameterization process aimed to accurately represent historical data by ensuring that the simulated outputs closely matched the observed patterns in both systems and to understand unique characteristics of each irrigation system. We specified reservoir initial storage as the first observed storage and set boundary conditions from observed data to fit above parameters to each of the irrigation system.

When dealing with complex systems, such as socio-hydrological models, equifinality, having more than one set of parameters that equally results in good model performance, must be avoided (Beven and Freer, 2001; Kelleher et al., 2017). A promising approach to overcome this problem and achieve robust model performance is to adopt multivariable optimization (Koltsida and Kallioras, 2022; Sirisena et al., 2020). Here, we used the cultivation area, reservoir storage, and reservoir outflow variables for model calibration and employed the Nash–Sutcliffe Efficiency (NSE) as a multivariable objective function, assigning equal weights to each variable. Finally, the automatic Dual-Annealing optimization algorithm, implemented in Scipy library (available at https://github.com/scipy/scipy/blob/main/scipy/optimize/_dual_annealing.py) within the Python ecosystem was used to fit the social and hydrological parameters for each irrigation system by maximizing the multivariable NSE between the model and observed data.

During automatic optimization, the algorithm proposes a value for the parameter constrained by the user-defined range values. The parameter ranges were obtained from local reports, irrigation guidelines, and field interviews. For example, in Ponrajah’s (1984) local irrigation guideline, it is assumed 7-inch water depth for land preparation (l_p) and 55%–60% for application efficiency (e_a) of water applying in general. In previous studies and local estimates, it is used system conveyance efficiency (e_c) for modern and indigenous systems as 60% and 70% respectively (Wickramasinghe and Nakamura, 2024). Regarding the normalized distance of an average farmer to the small tank system (r), we assumed that farmers in the modern system do not have access to small tanks (i.e., r equals to 1), whereas up to 80% of farmers in the indigenous system benefit from them (i.e., r between 0.2 and 1). This information was retrieved from interviews with farmers and irrigation managers in both systems. However, discussions with farmers and irrigation managers revealed that water requirements for land preparation and environmental flow release vary considerably across seasons. To replicate uncertainty and these observations, we set ranges for each parameter, as shown in Table 3. Additionally, water requirement for land preparation (l_p) and the environmental flow factor of the remaining storage (e_n) were calibrated seasonally to distinguish between Maha and Yala seasons, to improve model accuracy. Model calibration was carried out in 50 iterations, with each iteration consisting of 1000 simulation runs suggesting best parameter set for each iteration. For a given parameter cluster, we select the median as the representative optimal value, as it best represents the cluster centroid. The observed values of the seasonal cultivation area, reservoir storage, and reservoir outflow for each irrigation system were retrieved from the Water Management Secretariat of the Mahaweli Authority of Sri Lanka.

Table 3

Table 3. Model calibration information.

2.4 Quantifying relative dependency using sensitivity analysis

It is crucial to understand the relative importance of different parameters in influencing model outcomes (farmer cropping intensity). This will lead to informing key drivers of system dynamics and consequently prioritizing management interventions. Sensitivity analysis allows the identification of the parameters that have the greatest influence on the model output. We thus conducted a sensitivity analysis for the parameters using Soboĺ’s (1993) global sensitivity analysis method, which was developed based on the concept of variance decomposition. This method enables the calculation of the first order (direct effect) and the total order (interaction effect) sensitivity of each parameter. The total order calculation estimates include the effect of the interaction of a parameter with other parameters on the model output (Saltelli et al., 2010). This popular global sensitivity analysis technique has been widely applied to parameter sensitivity analysis in hydrological studies (Chen et al., 2021; Wang and Solomatine, 2019; Zhang et al., 2013). In this study, we used the open-source Sensitivity Analysis Library (SALib) in Python (available at https://github.com/SALib/SALib) to perform the Sobol sensitivity analysis. By specifying parameter ranges as outlined in Table 3, all parameters are varied simultaneously over the entire parameter space, enabling the simultaneous assessment of the relative contributions of each individual parameter and their interactions to the output variability. Through 2000 unique parameter combinations, we calculated the total order parameter sensitivity (S_T) of a parameter to the representative farmers’ cropping intensity variability. Based on how much each parameter contributes to model variability, we measure relative dependency of cropping intensity on each parameter using Equation 17.

$D_p=\frac{S_{T,p}}{{\sum }_{p=1}^n{S}_{T,p}}\times 100(17)$

where D_p (%) is the relative dependency of cropping intensity on parameter p, S_T,p is the total order parameter sensitivity of parameter p, and n is the number of parameters.

2.5 Scenario analysis

If small tanks are converted into cultivable land or if they are abandoned under modern irrigation expansion projects, the increased water demand must be met by additional reservoir withdrawals. This can be replicated in the model by changing farmer access to small tanks. To evaluate how farmer accessibility to small tanks contributes to changing farmers’ dependency on reservoir in deciding cultivation area, we conduct a scenario-based Sobol sensitivity analysis by systematically fixing the normalized distance to small tanks (r) at different levels and analyzing its impact on the sensitivity of other key parameters in the indigenous system. Since there is no variation in the normalized distance, direct parameter influence and interactions it had with other parameters in the original sensitivity analysis will be zero. This could lead to increased or decreased sensitivity of other parameters to model variability, depending on how strongly they were interacting with normalized distance. Fixing normalized distance allows us to isolate how other parameters behave without its influence, while our model is able to measure the contribution of small tanks to cropping intensity variability via the model parameter related to small tanks storage (λ). Finally, we observed relative dependency (D_p) of cropping intensity on perceived threshold reservoir water availability (v_c), rainfall (r_c) and small tank storage parameter (λ) under different small tank access levels (r).

3 Results and discussion

3.1 Different farmer perceptions in modern and indigenous irrigation systems

The sociohydrological model uses a modern centralized (NJG) and an indigenous quasi-decentralized (YE) irrigation system in Sri Lankan dry zone to provide an overview of how farmers weigh on different factors on deciding the cultivation area. Farmers in the NJG system solely depend on reservoir water, while farmers in the YE have access to small tank water in addition to reservoir water. Table 3 summarizes the fitted parameters for each irrigation system and Figure 5 shows the quantified goodness-of-fit of the modelled cultivation area, reservoir storage, and reservoir outflow for the historical time series of the modern and indigenous irrigation systems at seasonal (6 months) intervals. The model exhibited satisfactory performance across both irrigation systems after parameter optimization, achieving an NSE ≥ 0.6 for all variables except reservoir outflow to the indigenous irrigation system (Figure 5F). The disparity may have been caused by the assumption of zero small tank storage at the beginning of each season. In addition, seasonal reservoir outflow to the irrigation system can vary based on downstream demands and reservoir water availability, whereas our assumptions were fixed across seasons. Nevertheless, Figure 5F successfully reproduced the general trend of reservoir outflow, particularly during most drought years.

Figure 5

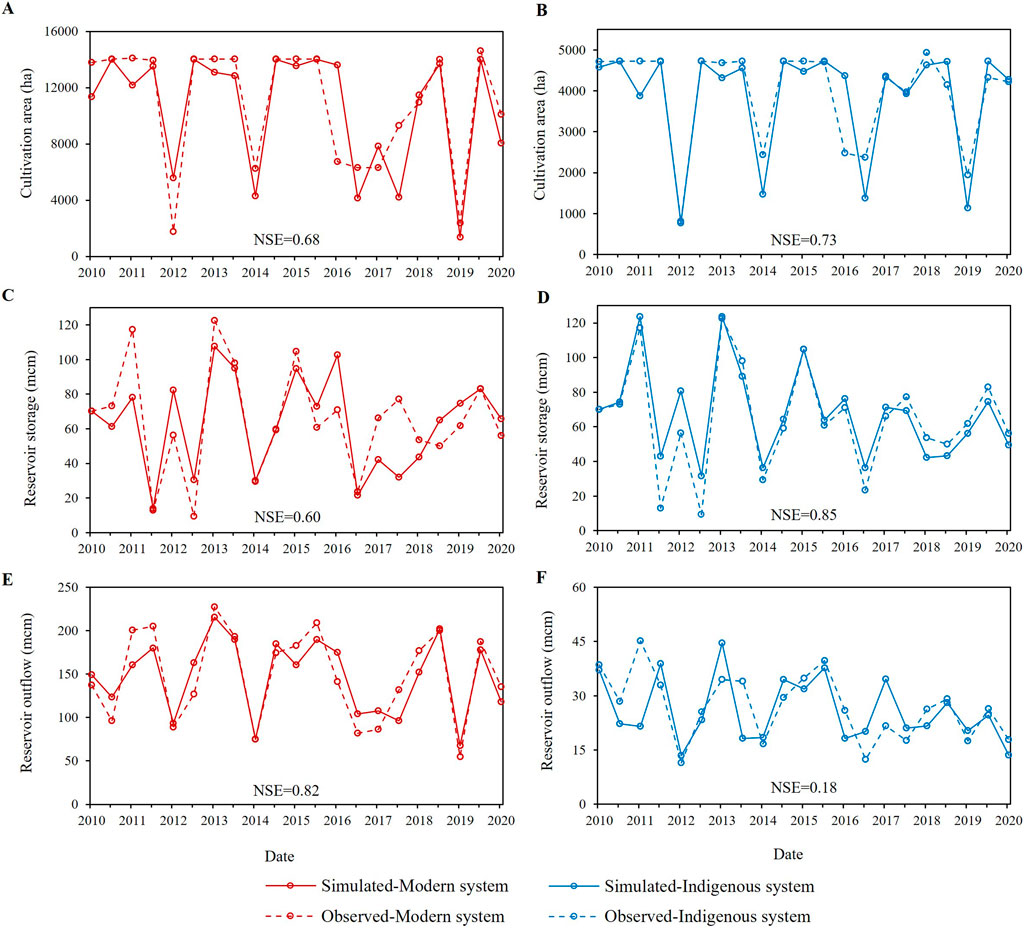
Figure 5. Observed and simulated variables in the reproduction of reservoir operations for each system including goodness-of-fit metric (NSE): Cultivation area of the (A) modern and (B) indigenous system, reservoir storage when simulating the (C) modern and (D) indigenous system, and reservoir outflow for the (E) modern and (F) indigenous system. In the x-axis, labeled years represent dry seasons, whereas the intermediate points represent wet seasons.

According to Table 3, an average farmer in the modern system perceives a higher threshold reservoir water availability and rainfall (v_c = 228 mcm, r_c = 232 mm) compared to a farmer in the indigenous system (v_c = 218 mcm, r_c = 100 mm). Although both systems have closer perceived threshold reservoir water availability values, the perceived rainfall threshold is significantly high among modern system farmers. To further explain, we quantified integrated farmer salience (S) by using calibrated parameters and shown in Figure 6. It shows the integrated farmer salience (S) heat maps for the two systems, which illustrates how critical inputs of reservoir water availability, and rainfall interact with farmer perceptions to develop perceived adequacy of water availability for cultivation. In the modern system (Figure 6A), when rainfall reaches its perceived threshold, salience gradually increases in response to reservoir water availability. However, once reservoir water availability exceeds its perceived threshold, salience increases sharply around the rainfall threshold. This suggests that farmers in the modern system rely more on reservoir storage for cultivation decision-making, while showing high rainfall requirement to trigger cultivation. In contrast, farmers in the indigenous system (Figure 6B) exhibit a sharp increase in salience in response to reservoir water availability once observed rainfall reaches its perceived threshold. Notably, their response to rainfall differs from that of modern system farmers. When reservoir water availability exceeds its perceived threshold, salience increases gradually around its much lower perceived rainfall threshold compared to modern system farmers, indicating that indigenous system farmers are more comfortable to start cultivation with lower rainfall. This distinction highlights key differences in drought resilience—farmers in the indigenous system appears more adaptable to rainfall variability, while the modern system remains more rigidly dependent on reservoir storage.

Figure 6

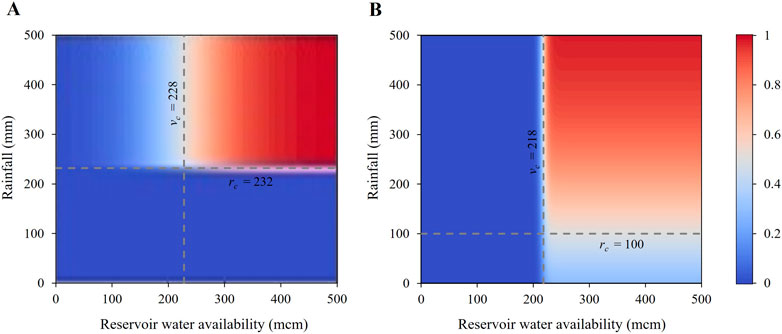
Figure 6. Integrated farmer salience of an average farmer in the (A) modern and (B) indigenous system. The color scale indicates salience values, with blue representing low salience (0) and red representing maximum salience (1). Dash lines represent calibrated perceived threshold values.

Farmers’ perceptions of rainfall and reservoir water availability act as mental benchmarks in decision making. Such human perceptions may shaped by past experience of rainfall, reservoir operations, community influence and institutional policies (Hubertus et al., 2023; Plakandaras et al., 2025; Simelton et al., 2013). In sociohydrological models, capturing these perceptions helps to bridge the gap between hydrological realities and human decision-making, leading to more realistic simulations of agricultural dynamics (Elshafei et al., 2014). Our sociohydrological modelling approach aligns with acknowledging that historical experiences shape farmer’s decisions by incorporating fixed perceived threshold values for rainfall and reservoir water availability, which influence cultivation choices based on past water availability and irrigation reliability. Previous researchers also have incorporated such time invariant parameters in dynamic sociohydrological models (Di Baldassarre et al., 2015). Knowing the extent of perception levels of environmental conditions can support the adaptation of farmers for extreme events such as droughts (Howe et al., 2014). Policymakers can use these values to propose realistic system specific strategies. For example, in this case study, introducing supplementary irrigation methods, soil moisture retention techniques or promoting drought-tolerant crops can enhance modern system farmers’ confidence to cultivate with lower water conditions while reducing perceived threshold of rainfall and reservoir water availability in long term. On the other hand, implementing policies like imposing water restrictions without considering such farmer perception levels can lead to resistance and aligning policies with these thresholds ensure they are more likely to be adopted by local farmers.

3.2 Reservoir dependency on deciding cropping intensity

We further investigated how average farmers’ cropping intensity is dependent upon each of the input parameters using relative dependency values, which measured based on total order sensitivity indices (sensitivity indices are shown in Supplementary Figure S4). Figure 7A demonstrates relative dependency of cropping intensity on each parameter for a modern system farmer, where dependency on perceived threshold reservoir water availability (v_c) is 70%, and dependency on perceived threshold rainfall (r_c) is 23%. However, in the indigenous system (Figure 7B), small tank system parameters moderated the behaviour. However, perceived threshold reservoir water availability (v_c) remained as the top contributor for the cropping intensity with 52% and small tank storage parameters ranked in second as normalized access parameter (r) with 16% and pond storage factor (λ) with 16%. While perceived threshold rainfall (r_c) accounted for 11% of the cropping intensity variability.

Figure 7

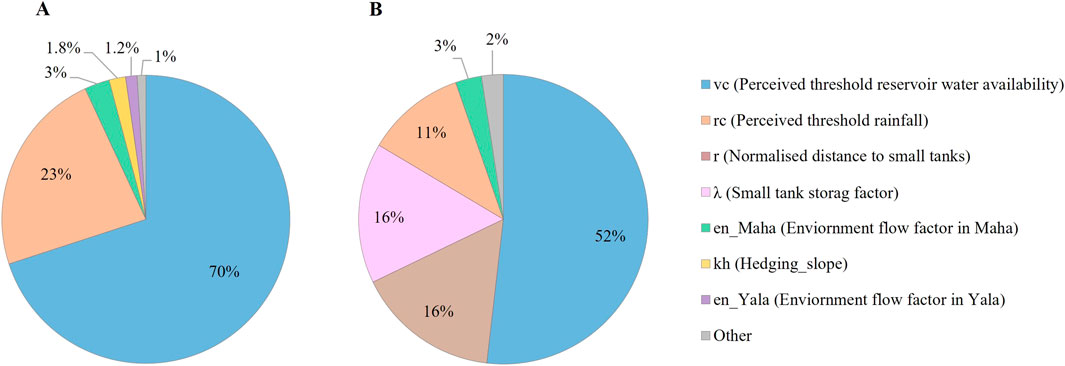
Figure 7. Relative dependency of cropping intensity on different parameters, where (A) represents a modern system farmer and (B) represents an indigenous system farmer. Information on other parameters for both systems is shown in Supplementary Figure S5.

Based on the relative dependency analysis results, the perceived threshold for reservoir water availability has the highest impact on farmers’ cropping intensity variation, which indicates farmers in both systems critically evaluate reservoir water conditions in deciding cultivation. This is confirmed by the site information that farmers in both systems initiate sowing after only the management authority announced the reservoir water issuing dates. Our quantification demonstrates that cropping intensity dependency on perceived threshold reservoir water availability is 18% higher, whereas cropping intensity dependency on perceived rainfall is 12% higher in a modern system farmer compared to an indigenous farmer. This indicates that modern system farmers not only perceive higher reservoir water availability and rainfall but also rely more on it when making cropping decisions compared to indigenous system farmers.

This stronger dependency on reservoir water availability suggests that modern system farmers are more influenced by centralized reservoir operations, whereas indigenous system’s lower dependency on reservoir water availability and diversified reliance on other water sources, point to a more polycentric resilience strategy. Therefore, relative dependency results in this study emphasize resilience-enhancing principles for infrastructure-dependent systems, where incorporating polycentric attributes, such as redundancy and flexibility, through a combination of large-scale centralized infrastructure and decentralized capacities strengthens ability to cope with changing weather conditions (Garcia et al., 2022; Yu et al., 2020). Our simulation results support the call of IWMI (2021) for a new agenda to integrate small, distributed water infrastructure into dam reservoirs to overcome reservoir over-reliance and reduce potential vulnerability in drought periods. In parallel studies, it is proposed that reactivating traditional small water bodies (ponds) for irrigation could decrease the water footprint of rice production and reduce freshwater consumption (Li et al., 2023) and conjunctive use of canals and ponds in rice irrigation to support the optimum use of scarce water in dry regions (Noory et al., 2019).

3.3 Impact of small tanks accessibility on reservoir dependency

The scenario analysis presented for the indigenous system in Figure 8 demonstrates a sharp decline in the cropping intensity dependency on pond storage (λ) from 66% to 0%, when the distance to small tanks (r) increases from 0 to 1. Meanwhile, the relative dependency of cropping intensity variability on perceived reservoir water availability (v_c) shows a steeper increase from 25% to 78%, whereas the relative dependency on rainfall perception threshold (r_c) increases at a slower rate from 6% to 14%. This suggests that cropping intensity is mostly dominated by the reservoir water availability, while rainfall is always a factor but does not compensate for a lack of small tank access as effectively as reservoir storage.

Figure 8

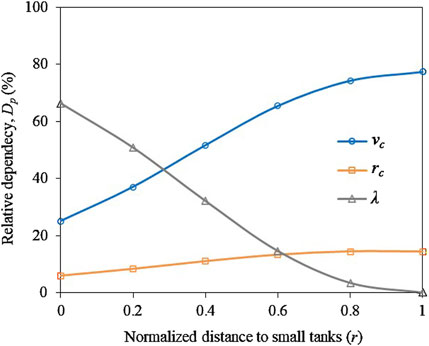
Figure 8. Scenario analysis. How the changes in normalized average distance to small tanks in the indigenous system affect cropping intensity dependency on perceived threshold reservoir water availability (v_c), perceived rainfall threshold (r_c), and small tank storage (λ). Here, normalized average distance of 0 indicates full access to small tanks, whereas 1 indicates no access to small tanks. Higher relative dependency value indicate greater dependency of cropping intensity on the respective parameter.

These findings highlight the critical role of small tanks in buffering farmers from over-reliance on dam reservoirs. As a result, targeted water management interventions, such as preserving and rehabilitating small tank networks, can help to reduce the vulnerability of farmers to fluctuations in reservoir water levels, particularly in drylands where reservoir water availability is uncertain. If small tanks are converted into cultivable land, the increased water demand must be met by additional reservoir withdrawals and this trade-off can be evaluated by suggesting optimal conditions using our scenario analysis. In Figure 8, increasing cultivable land demonstrates by increasing farmer normalized distance to small tanks (r). Here, r ≈ 0.4 appears to be the transition zone where reservoir dependency starts increasing sharply. Keeping r ≤ 0.4 (i.e., at least 60% of lands have access to small tanks) would ensure moderate dependence on reservoir on deciding cropping intensity while retaining the buffering capacity of small tanks. As the Sri Lankan dry zone is home to millennia-old traditional small tanks that continue to function as vital components of local water management, a lack of knowledge of their resilient attributes can lead them to be demolished and overlooked in favor of expanding cultivable land using modern agricultural interventions, as has occurred in post-colonial land colonization projects (Panapitiya et al., 2008; Zubair, 2005). Although the legacy of dam reservoirs can, in some cases, exacerbate water crises during droughts (Di Baldassarre et al., 2021), the development of large dam reservoirs and water transfer infrastructure remains a top priority in the fight against water scarcity, not only in Sri Lanka (Birendra et al., 2023) but also in other developing countries located in tropical and semi-tropical regions (Biswas and Tortajada, 2001; Wheeler et al., 2020). Hence, the insights that this study provides on integrating indigenous systems to modern irrigation systems are highly important to avoid water users being trapped in unintended consequences.

4 Conclusion

Over the past few decades, dryland agriculture has expanded with centrally managed modern irrigation infrastructure (dam reservoirs, canals, and diversions), contributing to rising global food demand. This expansion has prompted the destruction of decentralized indigenous irrigation systems (small tanks and ponds) in many nations, resulting modern irrigation systems to heavily rely on remote freshwater. However, locally managed small storages integrated to dam reservoirs, such as those indigenous water management systems present and important contribution to the resilience of dryland agriculture. Yet, it remains elusive in conceptualization and quantification of how integrating distributed local water storages to dam reservoirs can increase drought resilience in dryland agriculture.

This study presents a sociohydrological model to simulate farmers’ cropping intensity dependency on water sources and apply it to indigenous and modern irrigation systems in Sri Lankan dry zone to discuss drought resilience comparatively. Our assessment integrates farmers’ perception levels on reservoir water availability and rainfall as well as access to small tanks to conceptualize their seasonal cropping intensity. By calibrating farmer perception levels, first we have shown here, particularly indigenous system farmers’ expectation on rainfall to initiate cultivation is significantly lower than that of modern system farmers. This shows a greater adaptability of indigenous farmers to dry conditions indicating drought resilient attributes. Second, by quantifying the relative dependency of cropping intensity variability on water sources, our simulation demonstrates that modern-system farmers have an 18% higher dependency on reservoir water availability and a 12% higher dependency on rainfall compared to indigenous farmers. Third, our conceptualization shows that reservoir dependency is sharply increased by abandoning small tanks. These confirm that integrating small tanks significantly reduce farmers being over-reliance on dam reservoir, which in turn reduce vulnerability to reservoir depletions induced by droughts or reduced transbasin diversions.

In our conceptualization, we came across several assumptions. We assumed that an average farmer would always cultivate rice, given the hydrological conditions, regardless of the season. However, in Yala (dry season), farmers may reduce their rice cultivation area and diversify it by cultivating other field crops. In addition to hydrological conditions, other factors such as market conditions and institutional decisions may also influence indirectly to farmers’ decision making in cultivation areas (Weerahewa et al., 2010) and crop types. Difference in farmers’ authority to access the water source (water management in small tanks and modern canal) and farmers’ social behavior also can be investigated. As the early steps, this approach considered uniform perceived threshold hydrological conditions across wet and dry seasons and future work can focus on season-specific dynamic perceived thresholds. Nevertheless, our comparative assessment provides a framework to capture not only sociohydrological dynamics in perception-based decision making and evaluate drought resilience, but also it suggests policy insights to agricultural water management in drylands.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics statement

Ethical approval was not required for the studies involving humans because ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

RW: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Writing–original draft, Writing–review and editing. SN: Conceptualization, Formal Analysis, Funding acquisition, Supervision, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article This research was financially supported by a Japanese Government Scholarship (Monbukagakusho: MEXT) and JST-Mirai Program, Grant Number JPMJMI24I1, Japan.

Acknowledgments

The authors wish to thank the officials in the Resident Project Managers Office and farmers from Mahaweli System H for providing support in conducting the field interviews. We also thank the Water Management Secretariat Office of the Mahaweli Authority of Sri Lanka for providing historical data for model parametrization. Finaly, we thank the reviewers for their valuable comments and suggestions, which improved the clarity and content of this manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2025.1535598/full#supplementary-material

References

Abeywardana, N., Bebermeier, W., and Schütt, B. (2018). Ancient water management and governance in the dry zone of Sri Lanka until abandonment, and the influence of colonial politics during reclamation. Water 10 (12), 1746. doi:10.3390/w10121746

CrossRef Full Text | Google Scholar

Ahmed, M., Hayat, R., Ahmad, M., ul-Hassan, M., Kheir, A. M. S., ul-Hassan, F., et al. (2022). Impact of climate change on dryland agricultural systems: a review of current status, potentials, and further work need. Int. J. Plant Prod. 16 (3), 341–363. doi:10.1007/s42106-022-00197-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Alahacoon, N., and Amarnath, G. (2022). Agricultural drought monitoring in Sri Lanka using multisource satellite data. Adv. Space Res. 69 (11), 4078–4097. doi:10.1016/j.asr.2022.03.009

CrossRef Full Text | Google Scholar

Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). Crop evapotranspiration - guidelines for computing crop water requirements - FAO Irrigation and drainage paper 56. Rome: Food and Agriculture Organization of the United Nations.

Google Scholar

Angelakιs, A., Zaccaria, D., Krasilnikoff, J., Salgot, M., Bazza, M., Roccaro, P., et al. (2020). Irrigation of world agricultural lands: evolution through the millennia. Water 12 (5), 1285. doi:10.3390/w12051285

CrossRef Full Text | Google Scholar

Bacaër, N. (2011). A short history of mathematical population dynamics. London: Springer. doi:10.1007/978-0-85729-115-8

CrossRef Full Text | Google Scholar

Bebermeier, W., Meister, J., Withanachchi, C., Middelhaufe, I., and Schütt, B. (2017). Tank cascade systems as a sustainable measure of watershed management in South Asia. Water 9 (3), 231. doi:10.3390/w9030231

CrossRef Full Text | Google Scholar

Beven, K., and Freer, J. (2001). Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology. J. Hydrol. 249 (1–4), 11–29. doi:10.1016/S0022-1694(01)00421-8

CrossRef Full Text | Google Scholar

Birendra, K. C., Rohan, P., Prasad, P. V., Bart, E. S., and Krishna, P. (2023). “Key approaches of water resources development and management in Sri Lanka. In R. Ragab (chair),” in 25th ICID International Congress on Irrigation and Drainage, Visakhapatnam (Vizag), Andhra Pradesh State, India

Google Scholar

Birner, R., McCarthy, N., Robertson, R., Waale, D., and Schiffer, E. (2010). “Increasing access to irrigation: lessons learned from investing in small reservoirs in Ghana,” in Workshop on agricultural services, decentralization, and local governance. Accra, Ghana.

Google Scholar

Biswas, A. K., and Tortajada, C. (2001). Development and large dams: a global perspective. Int. J. Water Resour. Dev. 17 (1), 9–21. doi:10.1080/07900620120025024

CrossRef Full Text | Google Scholar

Brohier, R. L. (1937). The inter-relation of groups of ancient reservoirs and channels in Ceylon. J. Ceylon Branch R. Asiat. Soc. G.B. Irel. 34 (90), 64–85.

Google Scholar

Burchfield, E. K., and Poterie, A. T. D. L. (2018). Determinants of crop diversification in rice-dominated Sri Lankan agricultural systems. J. Rural. Stud. 61, 206–215. doi:10.1016/j.jrurstud.2018.05.010

CrossRef Full Text | Google Scholar

Cancelliere, A., Ancarani, A., and Rossi, G. (1998). Susceptibility of water supply reservoirs to drought conditions. J. Hydrologic Eng. 3 (2), 140–148. doi:10.1061/(ASCE)1084-0699(1998)3:2(140)

CrossRef Full Text | Google Scholar

Carlisle, K., and Gruby, R. L. (2019). Polycentric systems of governance: a theoretical model for the commons. Policy Stud. J. 47 (4), 927–952. doi:10.1111/psj.12212

CrossRef Full Text | Google Scholar

Chander, G., Reddy, T. Y., Kumar, S., Padmalatha, Y., Reddy, S., Adinarayana, G., et al. (2019). Low-cost interventions for big impacts in dryland production systems. Arch. Agron. Soil Sci. 65 (9), 1211–1222. doi:10.1080/03650340.2018.1560426

CrossRef Full Text | Google Scholar

Chen, J., Shi, H., Sivakumar, B., and Peart, M. R. (2016). Population, water, food, energy and dams. Renew. Sustain. Energy Rev. 56, 18–28. doi:10.1016/j.rser.2015.11.043

CrossRef Full Text | Google Scholar

Chen, Y., Liu, G., Huang, X., Chen, K., Hou, J., and Zhou, J. (2021). Development of a surrogate method of groundwater modeling using gated recurrent unit to improve the efficiency of parameter auto-calibration and global sensitivity analysis. J. Hydrol. 598, 125726. doi:10.1016/j.jhydrol.2020.125726

CrossRef Full Text | Google Scholar

Di Baldassarre, G., Mazzoleni, M., and Rusca, M. (2021). The legacy of large dams in the United States. Ambio 50 (10), 1798–1808. doi:10.1007/s13280-021-01533-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Di Baldassarre, G., Viglione, A., Carr, G., Kuil, L., Yan, K., Brandimarte, L., et al. (2015). Debates—perspectives on socio-hydrology: capturing feedbacks between physical and social processes. Water Resour. Res. 51 (6), 4770–4781. doi:10.1002/2014wr016416

CrossRef Full Text | Google Scholar

Di Baldassarre, G., Wanders, N., AghaKouchak, A., Kuil, L., Rangecroft, S., Veldkamp, T. I. E., et al. (2018). Water shortages worsened by reservoir effects. Nat. Sustain. 1 (11), 617–622. doi:10.1038/s41893-018-0159-0

CrossRef Full Text | Google Scholar

Elshafei, Y., Sivapalan, M., Tonts, M., and Hipsey, M. R. (2014). A prototype framework for models of socio-hydrology: identification of key feedback loops and parameterisation approach. Hydrology Earth Syst. Sci. 18 (6), 2141–2166. doi:10.5194/hess-18-2141-2014

CrossRef Full Text | Google Scholar

Fernald, A., Guldan, S., Boykin, K., Cibils, A., Gonzales, M., Hurd, B., et al. (2015). Linked hydrologic and social systems that support resilience of traditional irrigation communities. Hydrol. Earth Syst. Sci. 19 (1), 293–307. doi:10.5194/hess-19-293-2015

CrossRef Full Text | Google Scholar

Fernando, A. D. N. (1980). Major ancient irrigation works of Sri Lanka. J. Sri Lanka Branch R. Asiat. Soc. 22, 1–24.

Google Scholar

Garcia, M., Yu, D., Park, S., Yousefi Bahambari, P., Mohajer Iravanloo, B., and Sivapalan, M. (2022). Weathering water extremes and cognitive biases in a changing climate. Water Secur. 15, 100110. doi:10.1016/j.wasec.2022.100110

CrossRef Full Text | Google Scholar

Geekiyanage, N., and Pushpakumara, D. K. N. G. (2013). Ecology of ancient tank cascade systems in island Sri Lanka. J. Mar. Isl. Cult. 2 (2), 93–101. doi:10.1016/j.imic.2013.11.001

CrossRef Full Text | Google Scholar

Gilrein, E. J., Carvalhaes, T. M., Markolf, S. A., Chester, M. V., Allenby, B. R., and Garcia, M. (2019). Concepts and practices for transforming infrastructure from rigid to adaptable. Sustain. Resilient Infrastruct. 6 (3–4), 213–234. doi:10.1080/23789689.2019.1599608

CrossRef Full Text | Google Scholar

Gohari, A., Eslamian, S., Mirchi, A., Abedi-Koupaei, J., Massah Bavani, A., and Madani, K. (2013). Water transfer as a solution to water shortage: a fix that can Backfire. J. Hydrol. 491, 23–39. doi:10.1016/j.jhydrol.2013.03.021

CrossRef Full Text | Google Scholar

Granco, G., Heier Stamm, J. L., Bergtold, J. S., Daniels, M. D., Sanderson, M. R., Sheshukov, A. Y., et al. (2019). Evaluating environmental change and behavioral decision-making for sustainability policy using an agent-based model: a case study for the Smoky Hill River Watershed, Kansas. Sci.Total Environ. 695, 133769. doi:10.1016/j.scitotenv.2019.133769

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunda, T., Turner, B., and Tidwell, V. (2018). The influential role of sociocultural feedbacks on community-managed irrigation system behaviors during times of water stress. Water Resour. Res. 54 (4), 2697–2714. doi:10.1002/2017wr021223

CrossRef Full Text | Google Scholar

Hobbins, M., Dewes, C., and Jansma, T. (2023). Global reference evapotranspiration for food-security monitoring (ver. 2.1, April 2024), distributed by U.S. Geological Survey. doi:10.5066/P9IIQMV1

CrossRef Full Text | Google Scholar

Howe, P. D., Thaker, J., and Leiserowitz, A. (2014). Public perceptions of rainfall change in India. Clim. Change 127 (2), 211–225. doi:10.1007/s10584-014-1245-6

CrossRef Full Text | Google Scholar

Huang, J., Li, Y., Fu, C., Chen, F., Fu, Q., Dai, A., et al. (2017). Dryland climate change: recent progress and challenges. Rev. Geophys. 55 (3), 719–778. doi:10.1002/2016RG000550

CrossRef Full Text | Google Scholar

Hubertus, L., Groth, J., Teucher, M., and Hermans, K. (2023). Rainfall changes perceived by farmers and captured by meteorological data: two sides to every story. Reg. Environ. Change 23 (2), 75. doi:10.1007/s10113-023-02064-9

CrossRef Full Text | Google Scholar

IUCN (2019). Drylands and climate change.

Google Scholar

IWMI (2021). Storing water: a new integrated approach for resilient development. Stockholm, Sweden: Global Water Partnership and International Water Management Institute.

Google Scholar

Jayasena, H., Rathnayake, R., Chandasena, M., and Ranathunga, B. (2021). A classic example of urban-rural linkages through ancient Yoda Ela in Srilanka - symbiosis of total environment on efficient water management. Larhyss J. 47, 59–82.

Google Scholar

Kelleher, C., McGlynn, B., and Wagener, T. (2017). Characterizing and reducing equifinality by constraining a distributed catchment model with regional signatures, local observations, and process understanding. Hydrol. Earth Syst. Sci. 21 (7), 3325–3352. doi:10.5194/hess-21-3325-2017

CrossRef Full Text | Google Scholar

Koç, C. (2018). The past and present of irrigation services in Turkey. Agric. Res. 7 (4), 480–489. doi:10.1007/s40003-018-0332-8

CrossRef Full Text | Google Scholar

Koltsida, E., and Kallioras, A. (2022). Multi-variable SWAT model calibration using satellite-based evapotranspiration data and streamflow. Hydrology 9 (7), 112. doi:10.3390/hydrology9070112

CrossRef Full Text | Google Scholar

Kucharavy, D., and De Guio, R. (2011). Application of S-shaped curves. Procedia Eng. 9, 559–572. doi:10.1016/j.proeng.2011.03.142

CrossRef Full Text | Google Scholar

Lewin, A., Murali, G., Rachmilevitch, S., and Roll, U. (2024). Global evaluation of current and future threats to drylands and their vertebrate biodiversity. Nat. Ecol. and Evol. 8 (8), 1448–1458. doi:10.1038/s41559-024-02450-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Zhuang, Y., Liu, H., Wang, Z., Zhang, F., Lv, M., et al. (2023). Enhancing rice production sustainability and resilience via reactivating small water bodies for irrigation and drainage. Nat. Commun. 14 (1), 3794. doi:10.1038/s41467-023-39454-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, J., Zang, C., Tian, S., Liu, J., Yang, H., Jia, S., et al. (2013). Water conservancy projects in China: achievements, challenges and way forward. Glob. Environ. Change 23 (3), 633–643. doi:10.1016/j.gloenvcha.2013.02.002

CrossRef Full Text | Google Scholar

Madani, K., and Mariño, M. A. (2009). System dynamics analysis for managing Iran’s Zayandeh-Rud river basin. Water Resour. manage. 23 (11), 2163–2187. doi:10.1007/s11269-008-9376-z

CrossRef Full Text | Google Scholar

Maestre, F. T., Benito, B. M., Berdugo, M., Concostrina-Zubiri, L., Delgado-Baquerizo, M., Eldridge, D. J., et al. (2021). Biogeography of global drylands. New Phytol. 231 (2), 540–558. doi:10.1111/nph.17395

PubMed Abstract | CrossRef Full Text | Google Scholar

Martos-Rosillo, S., Ruiz-Constán, A., González-Ramón, A., Mediavilla, R., Martín-Civantos, J. M., Martínez-Moreno, F. J., et al. (2019). The oldest managed aquifer recharge system in Europe: new insights from the Espino recharge channel (Sierra Nevada, southern Spain). J. Hydrology 578, 124047. doi:10.1016/j.jhydrol.2019.124047

CrossRef Full Text | Google Scholar

Millennium Ecosystem Assessment (2005). Ecosystems and human well-being: Synthesis. Washington, DC: Island Press.

Google Scholar

Müller, H. P., and Hettige, S. T. (1995). The blurring of a vision, the mahaweli: its social, economic, and political Implications. Sri Lanka, Sarvodaya: Book Pub. Services.

Google Scholar

Nasiri, F., and Mafakheri, M. S. (2015). Qanat water supply systems: a revisit of sustainability perspectives. Environ. Syst. Res. 4 (1), 13. doi:10.1186/s40068-015-0039-9

CrossRef Full Text | Google Scholar

Noory, H., Deyhool, M., and Mirzaei, F. (2019). A simulation-optimization model for conjunctive Use of canal and pond in irrigating Paddy fields. Water Resour. manage. 33 (3), 1053–1068. doi:10.1007/s11269-018-2166-3

CrossRef Full Text | Google Scholar

Panabokke, C. R., Sakthivadivel, R., and Weerasinghe, A. D. (2002). Small tanks in Sri Lanka: Evolution, present status, and issues. Colombo, Sri Lanka: International Water Management Institute.

Google Scholar

Panapitiya, M., Senivirathne, L. P., and Hewadewa, S. K. (2008). Rehabilitation Programmes of large scale irrigation projects—an Opportunity to alter the farmers’ role in irrigation water management. Eng. J. Inst. Eng. Sri Lanka 41 (1), 17. doi:10.4038/engineer.v41i1.7080

CrossRef Full Text | Google Scholar

Plakandaras, V., Khadim, F. K., Kazana, V., Anagnostou, E., and Bagtzoglou, A. C. (2025). Unveiling farmers’ perceptions: a citizen science and machine learning approach to exploring drivers in the adequacy and fairness of water systems. Environ. Res. Commun. 7 (2), 025008. doi:10.1088/2515-7620/ada1ac

CrossRef Full Text | Google Scholar

Ponrajah, A. J. P. (1984). Design of irrigation headworks for small catchments. Colombo: Department of Irrigation.

Google Scholar

Ramankutty, N., Mehrabi, Z., Waha, K., Jarvis, L., Kremen, C., Herrero, M., et al. (2018). Trends in global agricultural land Use: implications for environmental Health and food Security. Annu. Rev. Plant Biol. 69 (1), 789–815. doi:10.1146/annurev-arplant-042817-040256

PubMed Abstract | CrossRef Full Text | Google Scholar

Reynolds, J. F., Smith, D. M. S., Lambin, E. F., Turner, B. L., Mortimore, M., Batterbury, S. P. J., et al. (2007). Global Desertification: Building a science for dryland development. Science 316 (5826), 847–851. doi:10.1126/science.1131634

PubMed Abstract | CrossRef Full Text | Google Scholar

Saltelli, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M., and Tarantola, S. (2010). Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 181 (2), 259–270. doi:10.1016/j.cpc.2009.09.018

CrossRef Full Text | Google Scholar

Schmid, H.-J., and Günther, F. (2016). Toward a unified socio-cognitive framework for salience in Language. Front. Psychol. 7, 1110. doi:10.3389/fpsyg.2016.01110

PubMed Abstract | CrossRef Full Text | Google Scholar

Shih, J., and ReVelle, C. (1994). Water-supply operations during drought: Continuous hedging rule. J. Water Resour. Plann. Manage. 120 (5), 613–629. doi:10.1061/(ASCE)0733-9496(1994)120:5(613)

CrossRef Full Text | Google Scholar

Simelton, E., Quinn, C. H., Batisani, N., Dougill, A. J., Dyer, J. C., Fraser, E. D. G., et al. (2013). Is rainfall really changing? Farmers’ perceptions, meteorological data, and policy implications. Clim. Dev. 5 (2), 123–138. doi:10.1080/17565529.2012.751893

CrossRef Full Text | Google Scholar

Sirisena, T. A. J. G., Maskey, S., and Ranasinghe, R. (2020). Hydrological model calibration with Streamflow and remote sensing based evapotranspiration data in a data poor basin. Remote Sens. 12 (22), 3768. doi:10.3390/rs12223768

CrossRef Full Text | Google Scholar

Sivapalan, M. (2015). Debates—perspectives on socio-hydrology: changing water systems and the “tyranny of small problems”—socio-hydrology. —Socio-hydrology 51 (6), 4795–4805. doi:10.1002/2015wr017080

CrossRef Full Text | Google Scholar

Soboĺ, I. M. (1993). Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 4, 407–413.

Google Scholar

Srivastava, A., and Chinnasamy, P. (2022). Tank cascade system in Southern India as a traditional surface water infrastructure: a review. Rural Technol. Dev. Deliv., 179–199. doi:10.1007/978-981-19-2312-8_15

CrossRef Full Text | Google Scholar

Stein, E. D., McClain, M. E., Sengupta, A., Grantham, T. E., Zimmerman, J. K. H., and Yarnell, S. M. (2022). “Allocations and environmental flows,” in Water resources allocation and agriculture. Editors J. Rouillard, C. Babbitt, E. Challies, and J.-D. Rinaudo (London: IWA Publishing), 49–62. doi:10.2166/9781789062786_0049

CrossRef Full Text | Google Scholar

Thomas, R. J. (2008). Opportunities to reduce the vulnerability of dryland farmers in Central and West Asia and North Africa to climate change. Agric. Ecosyst. and Environ. 126 (1–2), 36–45. doi:10.1016/j.agee.2008.01.011

CrossRef Full Text | Google Scholar

United Nations (2011). Global drylands: a UN systems-Wide report.

Google Scholar

Wang, A., and Solomatine, D. P. (2019). Practical experience of sensitivity analysis: Comparing six methods, on three hydrological models, with three performance Criteria. Water 11 (5), 1062. doi:10.3390/w11051062

CrossRef Full Text | Google Scholar

Wang, H., Liu, Y., Wang, Y., Yao, Y., and Wang, C. (2023). Land cover change in global drylands: a review. Sci. Total Environ. 863, 160943. doi:10.1016/j.scitotenv.2022.160943

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, C. (2016). Improved agricultural water management for Africa’s drylands. Chicago, IL: World Bank Publications.

Google Scholar

Water Management Secretariat (2022). Crop calendar (in Sinhala). Sri Lanka: Mahaweli Authority of Sri Lanka.

Google Scholar

Weerahewa, J., Kodithuwakku, S. S., and Ariyawardana, A. (2010). “Case study #7-11: the fertilizer subsidy program in Sri Lanka,” in Food policy for developing countries: case studies. Editors P. Pinstrup-Andersen,, and F. Cheng, 1–12. Available online at: https://hdl.handle.net/1813/55709.

Google Scholar

Wheeler, K. G., Jeuland, M., Hall, J. W., Zagona, E., and Whittington, D. (2020). Understanding and managing new risks on the nile with the Grand Ethiopian Renaissance dam. Nat. Commun. 11 (1), 5222. doi:10.1038/s41467-020-19089-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Wickramasinghe, R., and Nakamura, S. (2024). Evaluation of the drought resilience of indigenous irrigation water systems: a case study of dry zone Sri Lanka. Environ. Res. Commun. 6 (3), 035003. doi:10.1088/2515-7620/ad2a90

CrossRef Full Text | Google Scholar

Winkler, K., Fuchs, R., Rounsevell, M., and Herold, M. (2021). Global land use changes are four times greater than previously estimated. Nat. Commun. 12 (1), 2501. doi:10.1038/s41467-021-22702-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Wisser, D., Frolking, S., Douglas, E. M., Fekete, B. M., Schumann, A. H., and Vörösmarty, C. J. (2010). The significance of local water resources captured in small reservoirs for crop production – a global-scale analysis. J. Hydrol. 384 (3–4), 264–275. doi:10.1016/j.jhydrol.2009.07.032

CrossRef Full Text | Google Scholar

You, J., and Cai, X. (2008). Hedging rule for reservoir operations: 1. A theoretical analysis. Water Resour. Res. 44 (1), 2006WR005481. doi:10.1029/2006WR005481

CrossRef Full Text | Google Scholar

Yu, D. J., Schoon, M. L., Hawes, J. K., Lee, S., Park, J., Rao, P. S. C., et al. (2020). Toward general principles for resilience engineering. Risk Anal. 40 (8), 1509–1537. doi:10.1111/risa.13494

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, C., Chu, J., and Fu, G. (2013). Sobol′’s sensitivity analysis for a distributed hydrological model of Yichun River Basin, China. J. Hydrol. 480, 58–68. doi:10.1016/j.jhydrol.2012.12.005

CrossRef Full Text | Google Scholar

Zubair, L. (2005). Modernisation of Sri Lanka’s traditional irrigation systems and sustainability. Sci. Technol. Soc. 10 (2), 161–195. doi:10.1177/097172180501000201

CrossRef Full Text | Google Scholar