- 1Aquanty Inc., Waterloo, ON, Canada
- 2Department of Earth and Environmental Sciences, University of Waterloo, Waterloo, ON, Canada
- 3Bayer AG, Monheim, Germany
Introduction: Plant protection products (PPPs) such as pesticides and herbicides are experiencing increased use worldwide. In the context of PPP authorization and registration, water exposure assessments (drinking water and aquatic exposure) use numerical modeling to simulate relevant hydrological processes and exposure pathways. A common practice for estimating PPP leaching to groundwater, PPP loading onto surface water via tile drainage, or PPP transport via runoff utilizes multiple one-dimensional models, each representing a separate exposure pathway. Separate analysis of individual exposure pathways can result in disparate assumptions being made that represent relative worst-case scenarios for each pathway, rather than an integrated reasonable worst-case scenario for all pathways.
Methods: The interplay between PPP degradation, leaching to groundwater, transport in tile drainage, and runoff is well-suited for simulation using an integrated surface–subsurface hydrologic and chemical fate and transport model. This study presents functionality added to HydroGeoSphere (HGS), a three-dimensional, fully integrated, surface–subsurface hydrologic model. HGS was verified against other recognized models: PRZM, HYDRUS, PEARL, PELMO, and MACRO. Added features include automatic irrigation, non-linear adsorption, temperature and soil water content-dependent degradation, and solute uptake by plant roots.
Results and Discussion: HGS results for leaching of PPP mass to groundwater showed the highest correlation, lowest error, and lowest bias relative to PEARL model results. Simulation of macropore flow to tile drains in HGS produced an intermittent tile drain flow in summer that resulted in generally lower peak effluent concentrations compared to the MACRO model. Simulation of runoff in HGS produced a higher total runoff compared to the PRZM model, attributed to lower evapotranspiration in HGS. Use of the integrated HGS model resulted in a greater agreement in water balance components relative to using multiple models to simulate individual hydrologic pathways.
1 Introduction
Sustainable development goals adopted by United Nations Member States in 2015 (UNGA, 2015) include alleviation of hunger, access to clean water, and responsible agricultural production. These goals are at the nexus of the use of plant protection products (PPPs) to improve crop production while simultaneously reducing the potential for negative effects on drinking water and the aquatic environment. Plant protection products are herbicides, insecticides, and fungicides used in agriculture to protect crops from pests and disease. In some of the largest agricultural regions worldwide (the United States, Australia, Canada, and the European Union), PPP sales and active ingredient registrations show a stable or slightly increasing trend through nominally the last 10 years (Eurostat, 2022; Maino et al., 2023; PMRA, 2023), while among low-to-middle income countries, PPP use is increasing steadily (Shattuck et al., 2023). Signatory countries to the UN Convention on Biodiversity have committed to decreasing the risks associated with PPP contaminants in the environment to half by 2030 (CBD, 2022). In light of PPP usage trends that are stable or increasing, improved evaluation of risks to drinking water and the environment, as well as mitigation of those risks, can potentially be realized through increased rigor of PPP exposure assessment. Reliable assessment of the risks associated with PPP application requires concentrations in the environment to be known or estimated and then compared to potential effect thresholds. In the context of PPP authorization, water exposure assessments (drinking water and aquatic exposure) use numerical modeling software to simulate relevant hydrological processes (USEPA, 2023). Models are validated and approved by regulatory authorities and thus provide a benchmark for any new model that might be used for the same purpose (European Commission, 2014).
Leaching of PPPs and their degradates to groundwater (GW) is of concern for direct human or animal consumption of well water (Squillace et al., 2002; Bexfield et al., 2021), as well as transport during groundwater–surface water (GW–SW) exchange (Hintze et al., 2020). Direct loading of surface water (SW) bodies occurs via aerial drift, tile drainage, and runoff with potential resultant effects on aquatic receptors (Kladivko et al., 2001; Silburn, 2023). Increased recognition of the occurrence and persistence of PPPs in the water environment has resulted in an increasing need to improve scientific rigor when modeling the potential fate and transport of PPPs to GW or SW (Gassmann, 2021; Jorda et al., 2021; Pietrzak, 2021). Use of fate and transport modeling as part of the environmental exposure assessment is one tool that serves to inform the environmental risk to GW and SW receptors associated with particular PPP products or active ingredients (Holmes et al., 2009).
The interplay between PPP degradation, leaching to GW, transport in tile drainage, and runoff is well-suited for simulation using an integrated surface–subsurface hydrology and the chemical fate and transport model (Gatel et al., 2019). A common practice for estimating PPP leaching to GW, PPP loading onto SW via tile drainage, or PPP transport via runoff utilizes multiple one-dimensional (1D) models, each representing a separate exposure pathway (FOCUS, 2001; European Commission, 2014). Separate analysis of individual exposure pathways can result in disparate assumptions being made that represent relative worst-case scenarios for each pathway, rather than an integrated reasonable worst-case scenario for all pathways. Additionally, modeling of exposure pathways in multiple models can limit interpretations of overlapping or interrelated hydrological processes. Inherently dependent hydrological processes, such as deep percolation to GW, tile drainage, and surface runoff, can be simulated in a single integrated surface–subsurface hydrologic model while maintaining water and pesticide mass balance. HydroGeoSphere (HGS) is a three-dimensional (3D), fully integrated surface–subsurface hydrological modeling platform (Brunner and Simmons, 2012; Kurtz et al., 2017; Aquanty, 2024), with a tightly coupled formulation (Barthel and Banzaf, 2016). HGS is a flexible fully integrated GW–SW and chemical fate and transport model that supports many conceptualizations of hydrological settings using physically realistic boundary conditions and contaminant source geometries; as such, it is not solely a PPP transport model but a modeling platform well-suited to PPP fate and transport modeling. The general flow formulation of HGS includes variably saturated 3D flow using Richards’ equation and the two-dimensional (2D) depth-averaged surface flow using the diffusive-wave approximation of the Saint-Venant shallow water flow equation. HGS is designed to simulate the entire terrestrial water cycle, with a surface boundary condition driven by precipitation and potential evapotranspiration. Actual evapotranspiration is calculated internally in HGS by accounting for soil moisture effects on soil evaporation and plant transpiration and includes open water evaporation.
The HGS model has been successfully benchmarked for variably saturated subsurface and overland flow against several other integrated hydrologic models (Maxwell et al., 2014; Koch et al., 2016; Kollet et al., 2017). In the 2017 flow benchmarking study, HGS produced results indicative of the model ensemble norm for surface flow depth, ponding, and saturated and unsaturated zone storage dynamics. Recent applications of HGS for subsurface water flow include simulation of dynamics of infiltration and vadose zone storage in a karst aquifer using a dual-permeability approach by Bresinsky et al. (2023), quantification of percolation to GW with a fluctuating water table by Gong et al. (2023), and dynamics of GW–SW flow reversals between small surface water bodies and their connected aquifer by Steidl et al. (2023). Previous modeling of agri-chemical fate and transport in GW using HGS has included the simulation of a soluble, non-sorbing hypothetical PPP similar to 2-methyl-4-chlorophenoxyacetic acid, bentazone, metam sodium, clopyralid, and nitrate by Lutz et al. (2013), and of sulfonamide antibiotics by Park et al. (2016). Viscosity effects of liquid manure infiltration into macroporous soil were simulated using HGS by Frey et al. (2012), and variable density effects of saline GW intrusion were simulated using HGS by Paldor et al. (2022). HGS has been used to model tile drainage in several studies using different approaches, ranging from using a single porous medium with seepage nodes to model flow only (de Schepper et al., 2017; Hwang et al., 2019) to dual domain flow representing the soil matrix and macropores including nutrient transport to a discrete tile drain network (Frey et al., 2016).
The overarching objective of this work is to develop a physics-based, 3D, fully integrated chemical fate and transport model for simulating PPP loading on GW and SW and improve PPP mass balance accounting in exposure assessment through the use of a single model that can be used to track water and PPP mass. Toward achieving this objective, the fate and transport routines of the HGS model have been updated to include the addition of non-linear chemical adsorption in both the soil matrix and macropore domains, implementation of temperature and soil moisture-dependent chemical degradation in both the soil matrix and macropore domains, and solute uptake by plant roots. To enhance HGS application in an agricultural setting, automatic irrigation via modeled water content has been added. This manuscript documents the verification of the new HGS functionality against other widely accepted models used for the simulation of PPP leaching to GW. Following verification of subsurface fate and transport functionality, PPP transport to tile drains in macroporous soils is demonstrated, as well as runoff generation.
2 Methods
Upgrades to the capability of HGS to simulate PPP fate and transport in soil and runoff were guided by the existing functionality of multiple separate hydrologic models used for PPP fate and transport simulation in the European Union regulatory context. The PEARL (Leistra et al., 2001) and PELMO (Klein, 2020) models are used within the European Union’s FOrum for the Co-ordination of pesticide models and their USe (FOCUS) framework for the simulation of predicted environmental concentrations of PPPs in GW (European Commission, 2014). The MACRO model (Larsbo and Jarvis, 2003) is used within the FOCUS framework to simulate transport of PPPs through macroporous soils to surface water via tile drainage, and the PRZM model (Suarez, 2005) is used to simulate PPP loading to surface water via runoff (Young and Fry, 2019), including both dissolved substances and those adhered to eroded sediment (FOCUS, 2001).
Following guidance on the use of recommended numerical models, the FOCUS GW and SW working groups developed a set of standard scenarios that can be used to evaluate predicted environmental concentrations of PPPs in GW and SW (FOCUS, 2001; European Commission, 2014). The FOCUS scenarios include a set of test substances that are a suite of regulator-accepted and industry-utilized scenarios that have been previously used for model sensitivity analysis by FOCUS (European Commission, 2014), model intercomparison by FOCUS (2001), and model verification by others, as was conducted by Diamantopoulos et al. (2017) with the HYDRUS model (Šimůnek et al., 2012). The FOCUS scenarios were used in the current study for the verification of the HGS model to simulate PPP leaching to GW and demonstrate PPP transport to tile drains and runoff generation.
2.1 Model formulation
2.1.1 Added functionality for irrigation
The HGS model simulates 3D variably saturated subsurface flow in porous media using Richards’ equation and solute transport using the advection–dispersion equation and has been under development from early work by Therrien and Sudicky (1996) to present. In addition to simulating flow in variably saturated uniform porous media, HGS also includes optional subsurface flow domains: discrete fractures, wells, tile drains, and a dual domain for simulating flow and transport in macroporous soils or fractured media (Aquanty, 2024). Of the FOCUS GW models, PEARL and PELMO, the subsurface flow functionality of HGS most closely resembles that of the Richards’ equation-based PEARL model, rather than the soil moisture capacitance formulation of the PELMO model.
The FOCUS version of the PEARL model FOCUSPEARL (Berg et al., 2019) includes an automated irrigation scheme. The FOCUS GW leaching scenarios include irrigation for some of the location and crop combinations. Therefore, irrigation triggered by soil matric potential was added to HGS to better align with the irrigation scheme within FOCUSPEARL. The new irrigation functionality in HGS applies irrigation over a user-specified duration defined by a table of irrigation depths and soil matric potentials. The drier the soil is, the more irrigation water is added. Irrigation occurs only during the user-specified growing season, and irrigation events can be restricted to occur at fixed time intervals defined by a recurrence interval, e.g., one irrigation event per week.
2.1.2 Added functionality for subsurface PPP fate and transport
The numerical models within the FOCUS framework for modeling PPP fate and transport in soil, namely, PEARL (Leistra et al., 2001), PELMO (Klein, 2020), MACRO (Larsbo and Jarvis, 2003), and PRZM (Suarez, 2005), include soil moisture and temperature-dependent PPP degradation. PPP degradation rates increase with an increase in soil moisture and temperature. New functionality was added to HGS to incorporate soil moisture and temperature-dependent degradation of PPPs for both dissolved and adsorbed phases. Modifications made to the degradation coefficient formulation, including temperature and saturation dependence (Equations 1, 2, respectively), and the inclusion of non-linear adsorption (Equation 3) were updates made to the pre-existing HGS functionality that included non-temperature and non-saturation-dependent degradation and linear adsorption. Therefore, only the updates to the degradation and adsorption formulations are given here, and the reader is referred to Frey et al. (2016) for the governing equations for reactive transport in the soil matrix and macropore domains in HGS for parent and daughter species. The first-order degradation coefficient, λS [T−1], dependent on soil water saturation is given by
where αS [T−1] is the degradation coefficient determined at reference volumetric soil water content, θr [L3 L−3]; while θw [L3 L−3] is the simulated water content, and
The first-order degradation coefficient dependent on temperature, λT [T−1], is calculated using a modified form of the Arrhenius equation:
where αT [T−1] is the degradation coefficient determined at reference temperature Tr [K], Tb is the bulk soil temperature [K], Ea [M L2 N−1 T−2] is the activation energy of the reaction, and R is the universal gas constant [M L2 N−1 K−1 T−2]. An analytical solution to the heat conduction equation was used to calculate the 1D subsurface temperature profile (Schilling et al., 2019), wherein the surface soil temperature boundary condition is user-specified, typically taken to be the average daily air temperature, and the temperature boundary condition at depth is typically taken to be the long-term average air temperature. Degradation is implemented in HGS for straight and branched decay chains.
Numerical models used for modeling PPP fate and transport in the FOCUS framework, namely, PEARL (Leistra et al., 2001), PELMO (Klein, 2020), MACRO (Larsbo and Jarvis, 2003), and PRZM (Suarez, 2005), include the non-linear Freundlich adsorption isotherm. The non-linear Freundlich adsorption isotherm formulation was added to HGS, which relates the amount of adsorbate in equilibrium, X [M M−1], to the solute concentration, C [M L−3], via the empirical relationship:
where KF is the Freundlich adsorption capacity [L3 M−1], C0 [M L−3] is the reference concentration, and n [-] is the Freundlich exponent.
The solution distribution coefficient, K′ [L3 M−1], (Equation 4) is defined as the slope of the non-linear Freundlich isotherm:
PPP mass, M [M], uptake by plant roots has been incorporated into HGS via plant transpiration water flux, qtrans [L3 T−1] (Equation 5), according to Briggs et al. (1982). The mass flux rate for uptake via plant roots is therefore given as
where fT [-] is the transpiration stream concentration factor. Plant uptake is typically less than mass available in the plant solution (Leistra et al., 2001); therefore, fT ≤ 1 and is typically specified as 0.5 for ionic species (European Commission, 2014).
2.1.3 Macropore flow and transport to tile drains
PPP transport, following application on an agricultural field, via infiltration through soil macropores and then into tile drainage and ultimately into surface water is one of the transport pathways of concern in the FOCUS framework. The methodology employed in the FOCUS (2001) framework utilizes the MACRO (Larsbo and Jarvis, 2003) 1D, dual-permeability model to simulate the preferential flow through a high hydraulic conductivity macropore domain using the kinematic wave approach (Germann, 1985), connected with a lower hydraulic conductivity soil matrix domain. The dual-permeability, variably saturated 3D flow solution in HGS solves two coupled Richards’ equations for both the macropore and matrix domains. HGS supports both a common node and dual node approach. The dual node approach, used here, calculates explicit exchange fluxes between the two model domains. For simulating water flow and solute exchange between the two domains, HGS employs the formulation of Gerke and van Genuchten (1993). Dual domain solute transport is simulated in both HGS (Frey et al., 2012; Frey et al., 2016) and MACRO (Larsbo and Jarvis, 2003) using the advection dispersion equation in both models.
Tile drainage in the 1D MACRO model assumes a fully penetrating seepage surface, such as a ditch or highly permeable backfill above the tile drain (Larsbo and Jarvis, 2003). Lateral flow from saturated soil layers to the ditch or tile drain is simulated in MACRO using seepage potential theory (Leeds-Harrison et al., 1986). Tile drainage can be simulated in HGS using two approaches, where one simulates flow and transport in discrete subsurface 1D linear tile drain elements (De Schepper et al., 2015) and the second approach utilizes drain nodes to extract water from the model under saturated conditions at the depth of tile installation (Boico et al., 2023), used for modeling herein.
2.1.4 Runoff generation
HGS utilizes a globally implicit control-volume finite element approach with adaptive time stepping and OpenMP parallelization (Hwang et al., 2014) to solve a coupled set of equations that includes diffusive wave approximation to the 2D depth-averaged Saint-Venant equation for overland flow and 1D Manning’s equation for the open channel flow (Aquanty, 2024). Partitioning of rainfall into runoff is simulated implicitly in HGS based on the infiltrability of the subsurface, which can result in either saturation-excess or infiltration-excess overland flow being generated. The soil moisture saturation level and hydraulic conductivity of the subsurface influence whether rainfall will infiltrate or run off.
Runoff generation mechanisms in agricultural settings are controlled by surface attributes including vegetation cover, macro and microtopography, and subsurface conditions such as hydraulic conductivity and soil moisture levels (Appels et al., 2016; Sittig et al., 2020). The effect of topography on runoff generation at multiple scales has been demonstrated using HGS simulations, including wetlands, coastal areas, and upland agricultural landscapes (Frei et al., 2012; Amado et al., 2016; Frey et al., 2021; Paldor et al., 2022). Rain event-induced runoff was separated into rainfall-excess overland flow (13%) and exfiltration-induced overland flow (87%) using HGS by Chen et al. (2023), thus demonstrating the model’s ability to quantify mixing of surface and subsurface water in runoff. Transport of PPPs in surface water in HGS currently includes dissolved species only. Advection and diffusion of solutes are simulated both to and from the surface and subsurface domains.
2.2 Verification of PPP leaching to GW
An objective of this study was to verify the new chemical fate and transport functionality added to HGS by using the FOCUS GW scenarios. Soil water balance and PPP leaching to GW simulated using HGS were compared against leaching results from the PEARL, PELMO, and HYDRUS models after Diamantopoulos et al. (2017), for the nine FOCUS GW scenarios summarized in Table 1. Although the HYDRUS model is not currently included within the FOCUS framework, it has been widely applied to simulate PPP fate and transport in soils (Boivin et al., 2006; Cheviron and Coquet, 2009; Köhne et al., 2009; Anlauf et al., 2018). The nine FOCUS GW sites are distributed across the European Union and were estimated to be representative of 65% of the arable area of 27 member states, as of 2014 (European Commission, 2014). The FOCUS GW leaching scenarios span a range of crops and associated parameterized model inputs that effect plant water uptake (e.g., time varying leaf area index [LAI], root growth, and maximum root depth), as well as the timing of planting and PPP application.
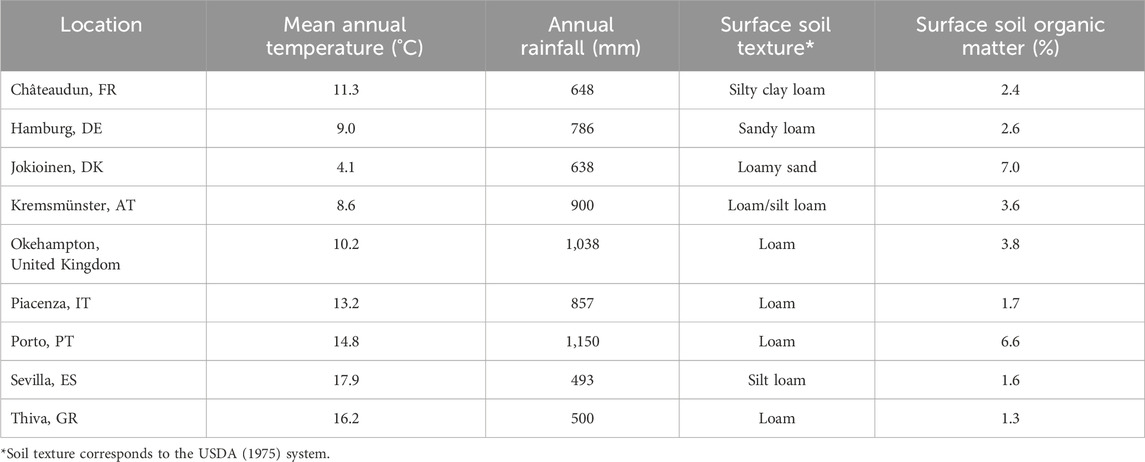
Table 1. Summary of the nine groundwater scenario locations: climate, soil texture, and soil organic matter, after FOCUS (2000).
The HGS models used for the simulation of PPP leaching to GW were constructed as 1D soil column models comprising a single 1-m square quadrilateral element in the horizontal plane and vertically discretized in uniform 1-cm increments. Modeled soil column depths were 4.5 m, except for the Sevilla model which was 6.0 m deep. HGS model parameterization for the porous media was specified from each FOCUS GW scenario (European Commission, 2014), including soil layering, saturated hydraulic conductivity, saturated volumetric water content, and van Genuchten (1980) soil hydraulic parameters. A potato crop was selected for HGS model verification to align with the methodology of Diamantopoulos et al. (2017). Growth stage timing, maximum LAI, and maximum rooting depth were aligned with the FOCUS scenarios and were used to generate daily LAI and root depth time series for input into the HGS models.
Daily rainfall was applied to the top boundary of the HGS models using FOCUS meteorological datasets for a 20-year period taken from the 1971 to 1996 interval, including a six-year spin-up period. Irrigation was generated internally by HGS in response to soil matric potential for the five FOCUS scenarios that include irrigation: Châteaudun, FR; Piacenza, IT; Porto, PT; Sevilla, ES; and Thiva, GR. Daily potential evapotranspiration (PET) was applied using FOCUS daily reference evapotranspiration for each scenario, which was then internally partitioned into plant transpiration and soil evaporation by HGS using partitioning coefficients based on the method of Kristensen and Jensen (1975). Actual transpiration calculated by HGS is a function of soil matric potential and is calculated using the method of Feddes et al. (1978), whereby transpiration is maximum across a user-specified matric potential range, and then progressively decreases under excessively wet or dry conditions. Soil evaporation is maximum under wet soil conditions and progressively decreases to zero as soil dries, according to user-specified matric potential thresholds, following Allen et al. (1998).
No flow lateral boundary conditions were used in both the surface and subsurface model domains. The bottom boundary conditions were scenario-dependent, as per the HYDRUS models developed by Diamantopoulos et al. (2017). The free drainage boundary condition in HGS is a direct analog to the free drainage boundary condition in HYDRUS, while the specified head boundary condition in HGS is similar to the time varying pressure head boundary condition in HYDRUS. The fluid transfer boundary condition in HGS has the most similarity to the deep drainage boundary condition in HYDRUS and was used for five of the scenarios. The fluid transfer boundary condition in HGS is a flux boundary that is controlled by a user-specified hydraulic conductivity and a reference head value applied over a user-specified distance from the boundary, while the deep drainage boundary condition in HYDRUS uses the water table position and two empirical parameters to define the flux across the boundary. Details of the FOCUS GW model inputs and bottom boundary conditions are included in Supplementary Material.
Four test substances and associated fate and transport parameter values are prescribed in the FOCUS framework for use in model verification. The four test substances were originally developed by the FOCUS GW working group to demonstrate a range of leaching sensitivity across the suite of scenarios (European Commission, 2014). The four test substances and their description are given in Table 2.
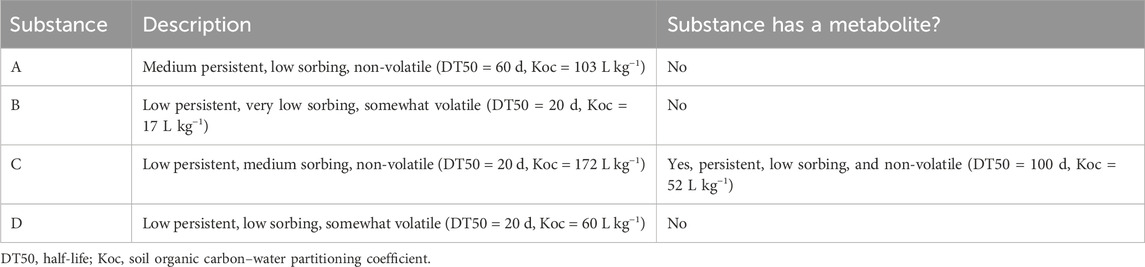
Table 2. Summary of FOCUS groundwater leaching test substances after European Commission (2014).
A 1D analytical heat conduction model is used in HGS to calculate the vertical soil profile temperature of the bulk porous medium to account for the temperature dependence of PPP degradation (Aquanty, 2024). The thermal diffusivity for calculation of the soil temperature profile was set to 4.0 × 10−7 m2 s−1 for all scenarios. For each site, the surface boundary condition for the analytical heat conduction model was taken to be equal to the daily air temperature provided in the FOCUS scenarios, while the background soil temperature at depth was taken to be equal to the 20-year average air temperature.
The dispersion length was set to 0.05 m for all FOCUS GW leaching scenario models, and the molecular diffusion coefficient in water was set to 4.98 × 10−10 m2 s−1. For soil moisture-dependent PPP degradation (Equation 1), the reference soil moisture saturation was specified at −10 kPa for all soils and the shape parameter was set to 0.7 for all substances, as recommended in European Commission (2014). For temperature-dependent degradation, a reference temperature of 20°C and an activation energy of 65.4 kJ mol−1 were used in Equation 2. Depth dependency of PPP degradation is included as per the FOCUS framework, which specifies that the degradation rate coefficient is maximum in the plough layer (Ap) and is multiplied by a factor of 0.5 for the layer (B) immediately below the plough layer, by a factor of 0.3 for the subsequent layer (C), and by a factor of 0.0 below 1.0 m depth (European Commission, 2014). The specification of the Freundlich adsorption isotherm in HGS (Equation 3) used a reference concentration of 1 mg L−1, with a Freundlich exponent of n = 0.9 and the adsorption capacity, KF as the product of Koc and the soil organic carbon content specified for each soil in each FOCUS scenario. The transpiration stream concentration factor for PPP uptake by plant roots was not used for the GW leaching scenarios, to be consistent with the methodology of Diamantopoulos et al. (2017), with which the HGS results are compared. Test PPPs were applied to the HGS models at the soil surface as a specified mass flux of 1 kg ha−1. All test substances (A, B, C, and D) were applied 1 day before crop emergence.
2.3 Demonstration of surface water pathway modeling
Within the FOCUS framework, simulation of PPP transport to surface water (FOCUS, 2001) is prescribed separately from that for GW(European Commission, 2014). Two models are used for the two PPP transport pathways to SW. For simulation of PPP transport off-field via tile drains, the dual permeability MACRO model is specified by FOCUS, while for simulating PPP transport off-field in runoff, the PRZM model is specified. Comparisons are made here between HGS results and the output from the MACRO and PRZM models for a single FOCUS scenario for each model. The comparison between FOCUS model results (MACRO and PRZM) against HGS model results is intended to serve as a demonstration of the current HGS functionality and identify future HGS model development requirements.
FOCUS (2001) SW scenarios cover a range of climate, landscape, land use, and cropping characteristics. To demonstrate the HGS model for SW PPP loading applications, one tile drainage scenario was selected—site D4 in Skousbo, DK—and one runoff scenario was selected—site R3 in Ozzano, Bologna, IT. The basis for selection of these two scenarios was their locations in Northern (D4) and Southern Europe (R3), respectively, thereby representing very broad continental trends in agricultural runoff and drainage. Summary details for the surface water loading scenarios are contained in Supplementary Material.
2.3.1 Tile drainage scenario construction
The FOCUS Surface Water Scenarios Help software program (SWASH) serves as a graphical user interface for the MACRO and PRZM models for FOCUS simulations and includes climate inputs, hydraulic parameters, a database of PPP properties, PPP application timing, and a means to run the suite of FOCUS SW loading scenarios (European Comission, 2024). The SWASH program (SWASH v5.3, Berg et al. (2015)) was used to generate the MACRO tile drainage model for the D4 scenario with a potato crop.
An HGS tile drainage model was constructed for the FOCUS D4 SW loading scenario to demonstrate HGS tile drainage with PPP fate and transport modeling functionality in macroporous soils. The D4 scenario simulation period comprises 7 years and 4 months (1979–1985), with the first 6 years being a model spin-up period, followed by a 16-month analysis period (FOCUS, 2001).
Flow to agricultural tile drains is primarily a 2D process with predominantly vertical infiltration into soil macropores and lateral flow toward the drain (Gerke et al., 2013). The HGS model domain was constructed 5-m wide, which is half of the 10-m tile drain spacing specified in the D4 scenario, thereby taking advantage of symmetry about the midline between tile drains. The thickness of the soil column was set at 1.8 m, with the tile drain at 1.2-m depth, as per the D4 scenario. Surface topography was constructed to be typical of potato ridge and a furrow cropping system with ridges 0.15-m high, 0.3-m top width, and an inter-ridge spacing of 1 m (Schock et al., 2013). A surface slope of 1% was applied in the direction of the furrows, which is within the 0.5%–2% range of surface slope for the D4 scenario. The HGS model domain was discretized into rectangular prism elements of 0.05 m on each side, which were deformed within the Ap layer below the furrows to a thickness of 0.025 m to accommodate the difference in furrow topography, with a uniform 0.01-m thick layer of elements added at the soil surface. A dual permeability formulation was used to represent a fast-flowing macropore domain coupled with a slow-flowing soil matrix domain. A cross section through the HGS tile drain model is illustrated in Figure 1.
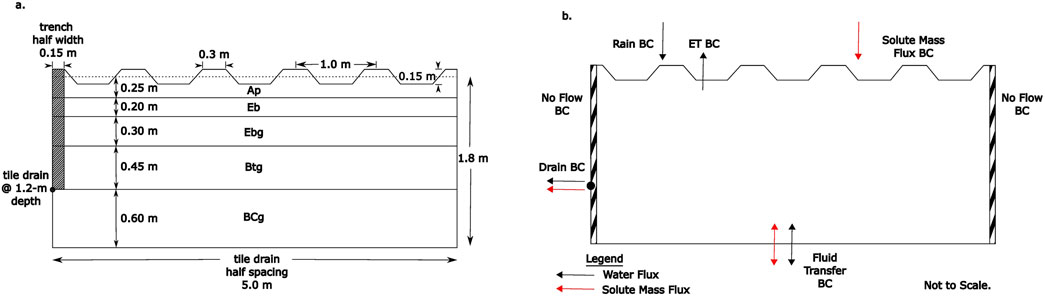
Figure 1. Cross section through the HGS tile drain model for the FOCUS surface water D4 scenario, (A) showing model geometry, layering, and (B) boundary conditions (BCs).
The vertical profile was subdivided into five soil layers, according to the D4 scenario. The three middle layers were further subdivided for specification of depth-dependent PPP degradation parameters, for a total of eight property layers. Since not all the parameters required for HGS input were given in the D4 tile drainage scenario, some equivalencies were estimated. The bulk saturated hydraulic conductivity from the D4 scenario MACRO model input was split into a saturated macropore and matrix hydraulic conductivity for HGS by assuming a fixed macropore fraction of 2% for the macroporous soil layers above the tile drain depth, which was decreased to 0.1% below the tile drain depth. Unsaturated soil hydraulic parameters, using the van Genuchten (1980) formulation for the HGS model’s soil matrix, were calculated using the Rosetta pedotransfer model (Zhang and Schaap, 2017). Percent sand, silt, and clay; wilting point; and bulk density from the D4 scenario were used as input to Rosetta. Macropore hydraulic properties used in the HGS model followed the van Genuchten (1980) formulation and were taken from Frey et al. (2016). Matrix and macropore hydraulic properties used for HGS model input are included in Supplementary Material.
There is no direct guidance in FOCUS (2001) for building 2D or 3D models of tile drainage, such as with HGS. Therefore, some assumptions were required with respect to constructing the D4 tile drainage scenario in HGS. In MACRO, tile drains are assumed to be laid in a trench of highly permeable backfill material (Larsbo and Jarvis, 2003). The highly permeable backfill assumption enables simulation of tile drainage by 1D models, such as MACRO (FOCUS, 1997). To enable comparison of results between the HGS and MACRO models, it was convenient to adopt a similar conceptualization of a well-drained trench in the HGS model. Therefore, a trench backfilled with disturbed, well-drained soils was included in the HGS model to be fully penetrating to just below the tile drain depth (Figure 1). In HGS, the assumption of well-drained soils in the trench required a higher macropore domain hydraulic conductivity than the corresponding undisturbed soil, which is a reasonable assumption. The resultant minimum bulk saturated hydraulic conductivity used for the Ebg and Btg layers of trench backfill material was 80 mm h−1, which is a factor of 10 greater than that of the undisturbed Ebg layer and a factor of 80 greater than that of the undisturbed Btg layer.
Daily rainfall plus irrigation for a potato crop (as a single rainfall time series) was specified for the D4 scenario, as provided in the FOCUS meteorological forcing data. PET calculated by MACRO was used as input to HGS to facilitate an inter-model comparison of water balance components. In the HGS model, a third-type bottom boundary condition was used, which is similar to the “percolation as a function of water table height” boundary condition used in the MACRO model.
Crop growth was included in the HGS model through specification of time-varying LAI and root depth based on crop growth stages from the D4 scenario. The substance properties used in the HGS model were for FOCUS (2001) Test Substance I, a very low sorbing (Koc = 17 L kg−1), low persistence (DT50 = 6 d), and moderately volatile PPP, as recommended for a potato crop from the FOCUS test protocol. A single application per year of Test Substance I was applied at a rate of 3 kg ha−1 to the soil surface. Due to the high degree of sensitivity of peak tile drain effluent concentrations to flushing caused by rainfall events, the FOCUS framework includes a set of rules for PPP application timing relative to rainfall. For the D4 potato scenario, the target date for spring PPP application is the crop emergence date minus 1 day, which results in a target application date of 22 May. The pesticide application timing calculator (PAT) within the SWASH program was used to generate the PPP application dates for both the MACRO and HGS models. The basis of the PAT search algorithm is to apply the PPP on days without excessive rainfall but to have an appreciable amount of rainfall in the days following application. The initial rules that the PAT calculator attempts to satisfy are that there should be at least 10 mm of rainfall in the 10 days following application and less than 2 mm of rain per day for a 5-day period centered on the application day (FOCUS, 2001). In the model runs, the application date ranged from 14 days prior to 1 day prior to the target date (22 May) for the seven annual PPP applications.
The soil surface boundary conditions for the analytical heat conduction model were assumed to be equal to the daily air temperature provided in the FOCUS D4 scenario, with the background temperature at depth taken to be the 7-year average (1979–1985) of the daily air temperature.
2.3.2 Runoff scenario construction
The SWASH software program was used to generate the PRZM model for the R3 (Bologna, IT) runoff scenario. An HGS model was constructed to demonstrate the utility of a physics-based approach for runoff generation, through comparison to the PRZM model. Currently, the HGS model does not include a specific scheme for mixing shallow PPP-laden soil water with surface runoff nor does HGS include soil erosion and sediment transport of adhered chemicals. Therefore, in lieu of comparing PPP transport in runoff between HGS and PRZM, a comparison of runoff generated by both models was made using the R3 scenario with a potato crop to demonstrate similarities and differences between the physics-based approach to runoff generation in HGS and the empirically based runoff generation in PRZM. Surface runoff generation in HGS is primarily controlled by the infiltrability of the subsurface, which controls whether infiltration excess or saturation excess overland flow is produced by the model. Runoff is generated in PRZM using the empirically based Natural Resources Conservation Service (NRCS) curve number (CN) approach (Suarez, 2005). The CN approach was originally conceptualized for watershed-scale, event-based streamflow estimation (Garen and Moore, 2005). CNs tabulated for four hydrologic soil groups are adjusted for land use, soil hydrologic condition, and agricultural practice (Suarez, 2005). The CN tabulated in PRZM is the CN for average antecedent soil moisture conditions and is subsequently adjusted for soil moisture by linear interpolation between a range of values using PRZM’s modeled soil moisture (Young and Fry, 2020).
The HGS model surface represents ridge and furrow microtopography, typical of potato cropping, from one ridge centerline to another at a spacing of 1 m (Figure 2). The HGS model comprised four soil layers (Ap1, Ap2, Bk, and C) to a depth of 1.6 m. Node spacing was 0.05 m in the horizontal directions, with node spacing 0.01 m and 0.04 m for the top two rows in the vertical direction and 0.05 m, thereafter, to the bottom of the model. The FOCUS R3 location has a surface slope terraced to 5%, which was applied to the HGS model along the direction of the furrows. Surface slope is not an input to the curve number method used in the 1D PRZM runoff model (Suarez, 2005).
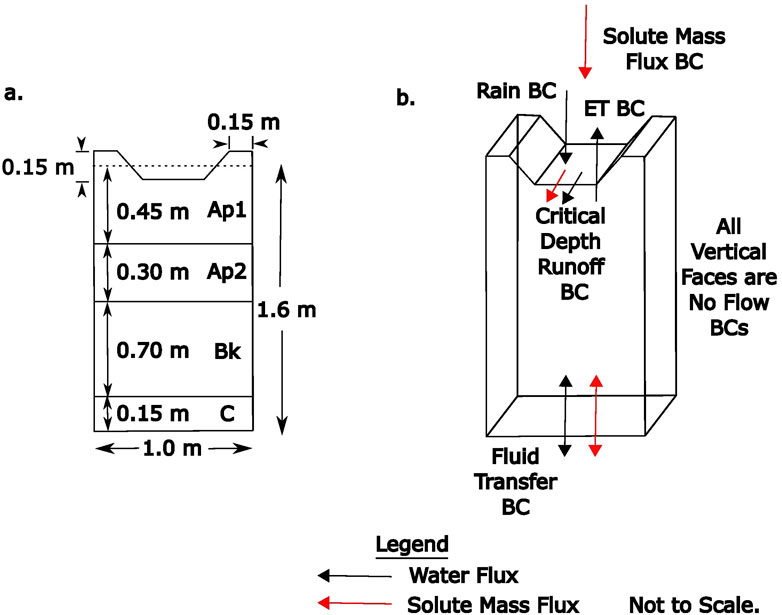
Figure 2. Cross section through the HGS runoff model for the FOCUS surface water R3 potato scenario, (A) showing model geometry, layering, and (B) boundary conditions (BCs).
The CN method used in PRZM generates runoff in relation to rainfall, initial abstraction, and soil moisture (Equation 6) (NRCS, 2004):
where Q [L] is runoff, P [L] is rainfall, S [L] is the potential maximum soil moisture retention, and Ia [L] is initial abstraction before runoff begins. S is related to the CN by S = 1,000/CN – 10, and within PRZM, Ia is set to 0.2 S. The CN method lumps interception, early infiltration, and surface depression storage into the Ia term (NRCS, 2004), while in contrast, HGS models these processes separately. This presented a challenge to parameterize HGS and PRZM in a similar way; however, some equivalencies were developed to aid in HGS parameterization. Canopy interception was set to zero in HGS as it was in PRZM, according to FOCUS (2001). Therefore, the initial abstraction term was conceptually reduced to include only two processes: early infiltration and surface depression storage. Within HGS, it was necessary to only parameterize the surface depression storage process because the infiltration process is handled separately through hydraulic parameterization of the model subsurface. The bare furrow in the HGS runoff model was assumed to be similar to the fallow condition in the PRZM model, with a CN of 91, which resulted in a calculated initial abstraction of 5 mm. An equivalent surface depression storage in HGS can therefore be assumed to be ≤5 mm. HGS parameterizes surface depression storage through a term called “rill storage,” which uses a parabolic representation for surface depressions (Aquanty, 2024). In the demonstration run, a rill storage of 4 mm was assumed, which corresponds to an initial abstraction depth of 3.15 mm of water. Additional parameterization of the HGS surface domain was completed by using a Manning’s roughness coefficient of 0.1, adopted from the PRZM model input.
Additional parameterization of the HGS subsurface domain was required since the PRZM model is a soil water capacitance model (i.e., a tipping bucket) and does not include hydraulic parameters used for the discretized form of Richards’ equation in HGS, including saturated hydraulic conductivity and the van Genuchten (1980) parameters for variably saturated soils. Soil texture (% sand, % silt, and % clay) is provided for the FOCUS surface water scenarios and was used as an input to the Rosetta pedotransfer function model (Zhang and Schaap, 2017) to generate estimates of saturated hydraulic conductivity. Additional supplemental information provided by FOCUS for the R3 scenario included field capacity and wilting point as percentage of water content by volume and bulk density, which were used as inputs to Rosetta to produce estimates of the van Genuchten parameters.
Daily rainfall plus irrigation (as a single rainfall time series) and potential evaporation for a potato crop were specified for the R3 scenario for 6 years (1975–1980), as provided in the FOCUS meteorological forcing data. Crop growth was included in the HGS model through specification of time-varying LAI and root depth based on crop growth stages from the FOCUS R3 scenario for a potato crop. As per FOCUS (2001), the analysis year for the R3 scenario with spring PPP application was 1980, which was the final year of the simulation. In the HGS model, a third-type bottom boundary condition was used for the subsurface domain, and the surface boundary conditions were no flow on the upslope side, no flow along the two ridges, and critical depth on the downslope side, as illustrated in Figure 2.
3 Results and discussion
3.1 Verification of soil moisture-controlled irrigation
An example comparison of HGS water balance components for a 20-year simulation period (first 6 years removed as spin up) is shown for the FOCUS Châteaudun GW scenario in Figure 3 and is compared to values from the PEARL model output of Diamantopoulos et al. (2017). In addition to 648 mm of average annual precipitation, average annual irrigation simulated using HGS for Châteaudun was 204 mm, compared to 198 mm from PEARL. Average annual combined soil evaporation and plant transpiration simulated using HGS for Châteaudun was 612 mm compared to 637 mm for PEARL. The net result was an average annual bottom outflow simulated using HGS for Châteaudun of 244 mm compared to 210 mm from PEARL. Bar charts of annual water balance components for the other eight FOCUS GW scenarios are included in Supplementary Material.
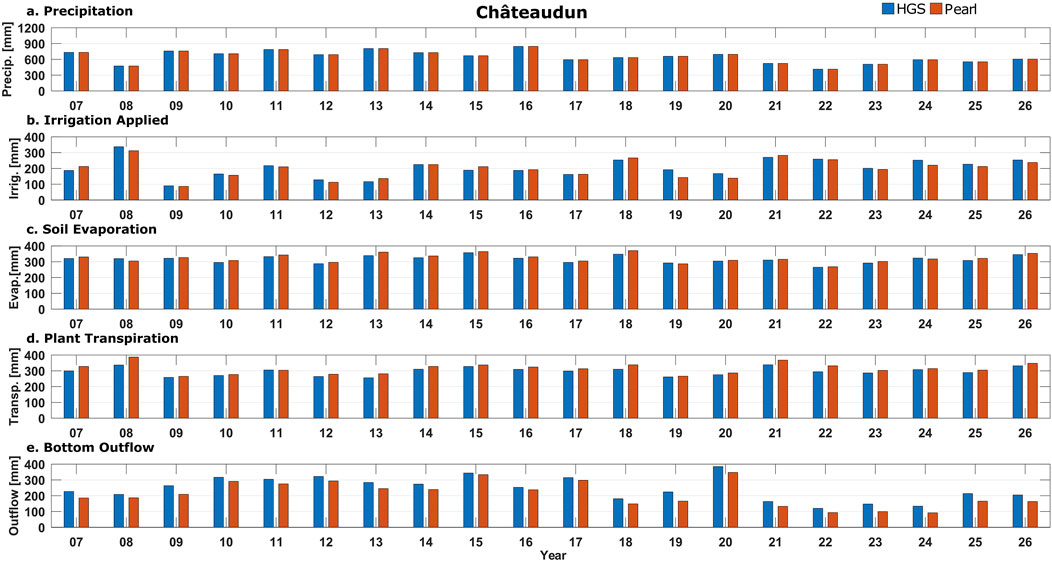
Figure 3. Comparison of annual water balance components between the HGS and PEARL models for a 20-year period for the FOCUS Châteaudun groundwater scenario with a potato crop: precipitation (A), irrigation applied (B), soil evaporation (C), plant transpiration (D), and bottom outflow (E). PEARL model results after Diamantopoulos et al. (2017).
Irrigation is a specified requirement for the potato test crop for five of the more southerly locations out of the nine FOCUS scenarios (Châteaudun, FR; Piacenza, IT; Porto, PT; Sevilla, ES; and Thiva, GR). Climatic variability resulted in varied crop requirements for irrigation to supplement rainfall for the five irrigated scenarios. Soil moisture-controlled irrigation results produced using HGS were compared to irrigation values from the irrigated FOCUS GW scenarios from PEARL produced by Diamantopoulos et al. (2017). Annual soil moisture-controlled irrigation simulated using HGS is biased high relative to PEARL by 54 mm on average for the ensemble of five FOCUS scenarios shown in Figure 4A and summarized in Table 3. A high degree of sensitivity was noted in the annual irrigation amounts calculated by HGS relative to the pressure head trigger used (data not shown). In HGS, the depth of irrigation water was applied based on a user-specified table of soil matric potentials. The HGS-simulated annual irrigation totals were within a similar range to irrigation amounts reported for the FOCUS scenarios modeled using PELMO, reported by European Commission (2014) (data not shown). Therefore, it was decided that further attempt to calibrate the HGS irrigation scheme to the PEARL model results was not justified. The positive bias in the HGS modeled irrigation amounts is offset by higher evaporation (41 mm on average) in the HGS results compared to PEARL, resulting in generally lower bias (5.8 mm on average) for the model bottom outflow shown in Figure 4B. Given the relatively low bias between the bottom outflow of both models, the irrigation scheme implemented in HGS appears to function sufficiently well.
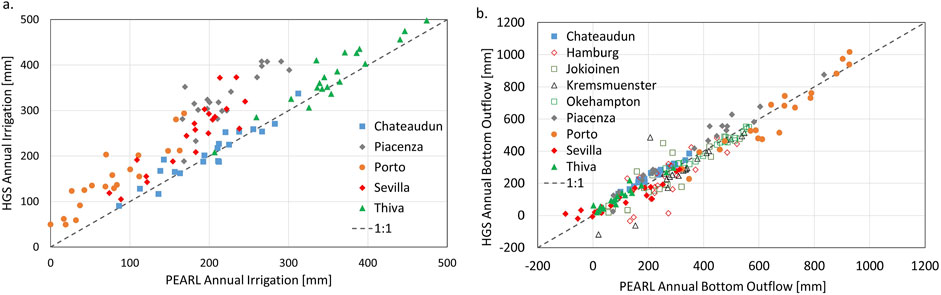
Figure 4. Crossplot of simulated moisture-controlled irrigation (A) and bottom outflow (B) simulated using HGS and PEARL models for the FOCUS groundwater scenarios. PEARL model results after Diamantopoulos et al. (2017). Irrigated sites are indicated with filled symbols, while non-irrigated sites have unfilled symbols.
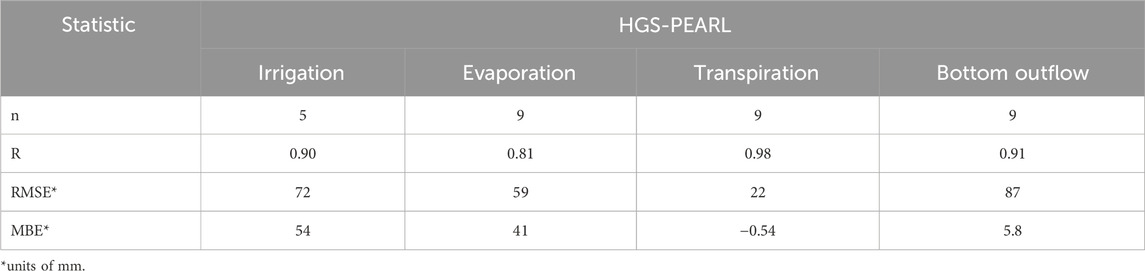
Table 3. Summary of statistics for the comparison of simulated water balance components for a 20-year period for HGS vs. PEARL model results for the FOCUS groundwater scenarios with a potato crop.
3.2 Verification of PPP leaching to groundwater
HGS results for leaching to GW for four test substances in the Châteaudun GW scenario for a potato crop are compared to HYDRUS, PEARL, and PELMO results after Diamantopoulos et al. (2017) in Figure 5. Mass flux comparison plots for the other eight FOCUS GW scenarios are included in Supplementary Material.
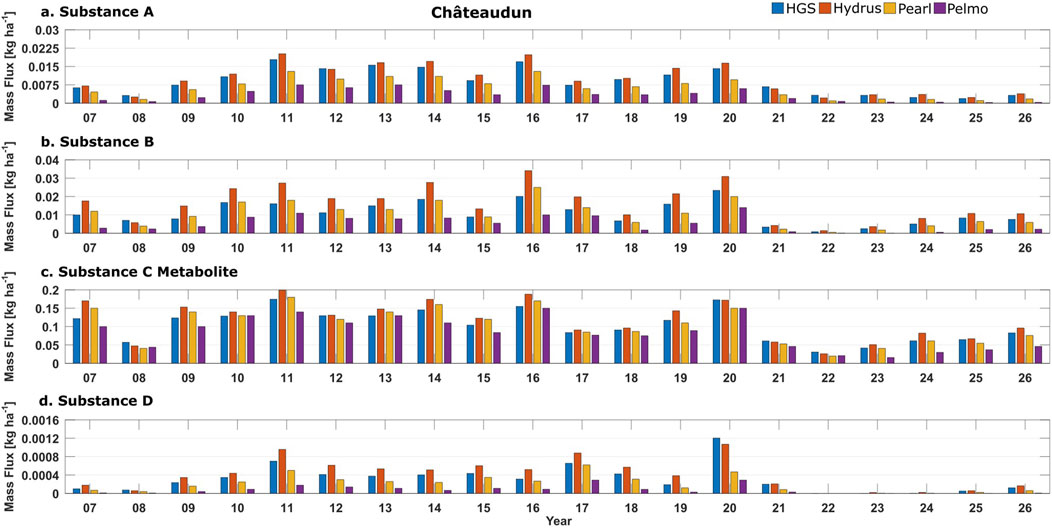
Figure 5. Comparison of annual PPP mass flux to groundwater for the FOCUS Châteaudun potato crop scenario simulated using HGS, HYDRUS, PEARL, and PELMO models for test substances: A (A), B (B), C-Metabolite (C), and D (D). HYDRUS, PEARL, and PELMO model results after Diamantopoulos et al. (2017).
Statistics comparing modeled annual mass leached from the four models and four test substances are given in Table 4. Crossplots of simulated annual PPP mass leached for the nine FOCUS GW scenarios are included in Supplementary Material. Of the three models’ results, the PEARL results for annual mass of PPP leached to GW show the highest degree of linear correlation with HGS, Pearson correlation coefficient (R) = 0.94 to 0.96, across the four test substances, which is higher than the correlation for the two FOCUS models, PEARL vs. PELMO, which has R = 0.84 to 0.92 across the four test substances in Table 4. Additionally, the degree of spread, as quantified by the root mean squared error (RMSE), and the mean bias error (MBE) are both the lowest for HGS vs. PEARL, in comparison to HYDRUS and PELMO. Although HGS mass leaching results for some individual scenarios show higher bias relative to PEARL results compared to other scenarios, the aggregate MBE is lower in magnitude than for PEARL vs. PELMO for test substances A, B, and D but is larger for C-metabolite. Overall, the PPP fate and transport functionality of HGS, including the newly added non-linear sorption and PPP degradation as a function of temperature and soil moisture content, is satisfactorily verified against the three other models across the four test substances.
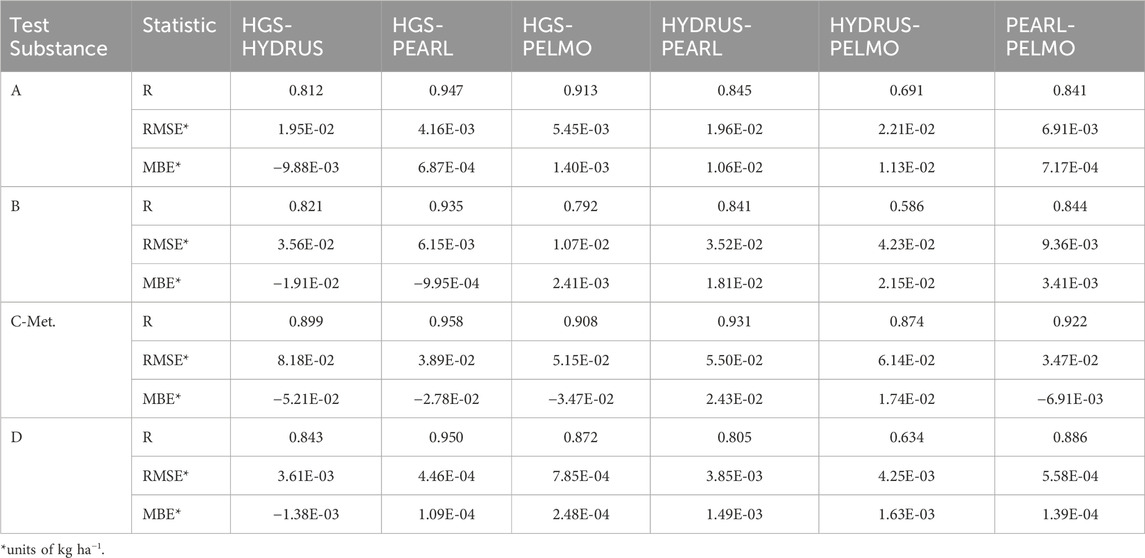
Table 4. Summary statistics for the comparison of simulated annual mass of PPP leached to groundwater for nine FOCUS groundwater scenarios for a 20-year period for HGS, HYDRUS, PEARL, and PELMO model results.
3.3 Demonstration of PPP transport via tile drains
Due to differences in the dimensionality between HGS (3D) and MACRO (1D), the comparison of HGS results to MACRO should not be interpreted as a model verification in a strict sense; however, the comparison of tile drainage and PPP transport in HGS to the MACRO results does provide indication of the HGS model capability. As per the guidance of the FOCUS framework, mass balance analysis for PPP mass transported via tile drainage was conducted over the final 16 months of the 7-year simulation, while the preceding 6-year period was regarded as the model spin up. The inclusion of the spin-up period allows buildup of PPP residues between annual application intervals, as may be expected to occur in a repetitional agricultural setting (FOCUS, 2001). HGS and MACRO water balance results for the FOCUS SW D4 potato scenario (Skousbo, DK) for the final year of the simulation (1 May 1985 to April 30, 1986) are given in Table 5. Rainfall + irrigation applied to the two models was essentially identical. Of the remaining water balance components listed in Table 5, percolation, runoff, and storage change show differences between HGS and MACRO on the order of 1% or less when normalized by the rainfall + irrigation total. The two largest differences between the HGS and MACRO results were for AET and tile drain flow. The excess AET in the HGS model results was approximately offset by a lower tile drain flow. If this comparison is extended to the AET subcomponents, plant transpiration accounted for 87% of the difference, soil evaporation accounted for 24%, surface evaporation accounted for 0.2%, and canopy evaporation accounts for −11%. The exact reason for lower plant transpiration in the MACRO model results relative to HGS is unclear.
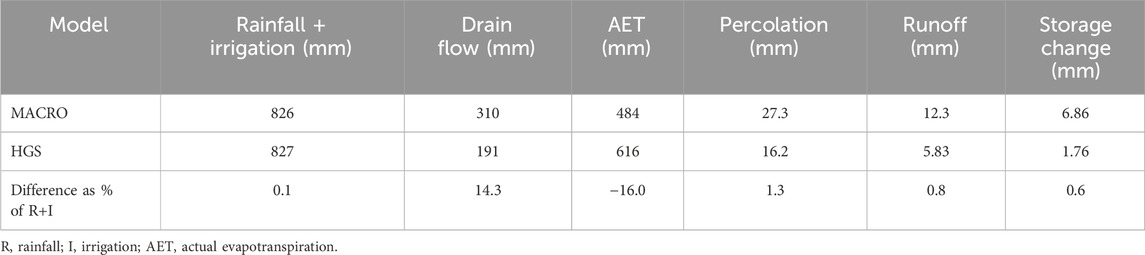
Table 5. Water balance components for the FOCUS surface water D4 potato scenario for HGS and MACRO model runs for analysis year: 1 May 1985 to 30 April 1986.
During the winter period with negligible evapotranspiration, tile drain flows between HGS and MACRO were very similar, as shown in Figure 6A. During summer months, the effect of higher transpiration in HGS vs. MACRO resulted in periods of low to no tile drain flow from HGS, while the MACRO flows showed high response to periods of rain + irrigation. A higher tile drain flow in MACRO during spring and summer resulted in mass flushing of Test Substance I in summer that did not occur in HGS until fall. The delay of mass flushing in HGS until fall allowed additional time for degradation to reduce mass in the soil profile, thereby reducing the magnitude of the mass flux rates shown in Figure 6B, and in the peak concentrations shown in Figure 6C. Fall and winter tile drain mass flux and concentrations in the tile drain effluent were higher in HGS compared to MACRO, likely due to two processes; one is the mass flushing in MACRO through summer, which depleted the soil column of mass, and the second is the delay in HGS mass flushing, which resulted in deeper penetration of Test Substance I in the soil profile below the degradation extinction depth of 0.5 m. Penetration of mass below the depth of degradation resulted in elevated mass flushing and elevated tile drain concentrations through the winter period in the HGS results.
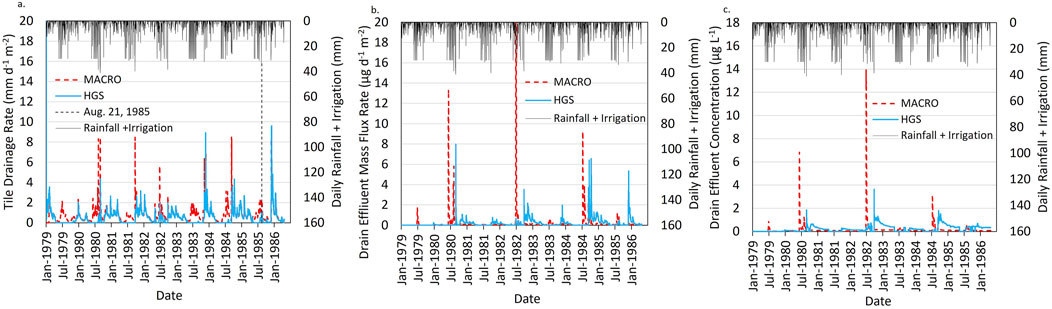
Figure 6. Comparison of HGS and MACRO modelling results for the FOCUS surface water D4 scenario as implemented with a potato crop: (A) tile drainage rate, (B) drain effluent mass flux rate for Test Substance I, and (C) tile drainage effluent Test Substance I concentration. For panel (B), mass flux axis was truncated to show additional detail. The peak mass flux rate for MACRO on 29 June 1982 was 78 μg d−1 m−2.
Mass balance results for the Test Substance I for the final 16 months of the HGS and MACRO tile drainage simulations are given in Table 6. The largest differences between mass balance components between the two models are for the plant uptake and mass degraded. A higher plant uptake simulated in HGS was offset by lower degradation. Plant uptake of Test Substance I in MACRO was 83% lower than that of HGS, for the 16-month period. The lower plant uptake of Test Substance I in MACRO was at least partly attributable to the lower calculated transpiration, which was 64% lower in MACRO than in HGS. The remainder of the difference in plant uptake between the two models may be a result of differences between the models with respect to the domain (matrix or macropore), from where transpiration water is drawn. In HGS, transpiration water is drawn exclusively from the matrix domain (Aquanty, 2024), while in MACRO, at least part of the transpiration stream is drawn from the macropore domain (Larsbo and Jarvis, 2003). The dynamics of Test Substance I concentrations in the MACRO macropore domain would be expected to be more variable than in the soil matrix, thereby introducing a potential difference between the two models’ results.
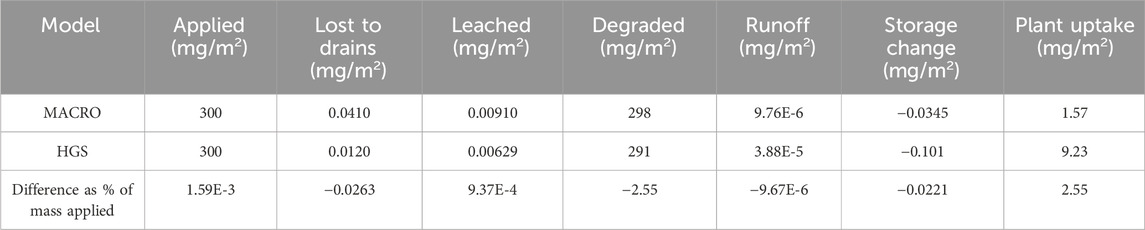
Table 6. Mass balance comparison for Test Substance I between HGS and MACRO for the FOCUS surface water D4 potato scenario for the 16-month period: 1 January 1985 to 30 April 1986.
For the D4 potato scenario, Test Substance I was applied uniformly across the top of the HGS model. A cross section of Test Substance I concentrations is plotted in Figure 7 for the date of the summer high-flow event on 21 August 1985. It is notable that the higher Test Substance I concentrations occurred below the bottoms of the furrows, compared to below the ridges, at approximately 0.5-m depth, which is the depth below which no further degradation occurs in the model. This sequence of high and low concentrations laterally across the model demonstrates the effect of the interaction of the 2D flow field developed below the ridge and furrow microtopography. Higher infiltration rates occurred below the furrows, akin to the mechanism of depression-focused recharge (Berthold et al., 2004; Wiebe et al., 2023) but on a smaller scale. The increased rate of flow below the furrows transported PPP mass deeper than under the ridges. Since degradation was specified in the model to decrease with depth, less mass is degraded below the furrows than below the ridges. These higher Test Substance I residual concentrations below the furrows demonstrate that PPP application directly to the potato ridges could reduce mass leaching to depth and into the tile drains. Precision application of PPPs shows potential to reduce losses to the water environment (GW or SW) by targeting application to a smaller footprint, such as to individual plants or rows of plants (Zanin et al., 2022). Thereby, less PPP is applied where it is not readily effective. Precision PPP application is increasing in practice (Anastasiou et al., 2023), and thereby, the need for fate and transport models to simulate PPP application scenarios that are fundamentally 2D or 3D in geometry can also be expected to increase for exposure assessments.
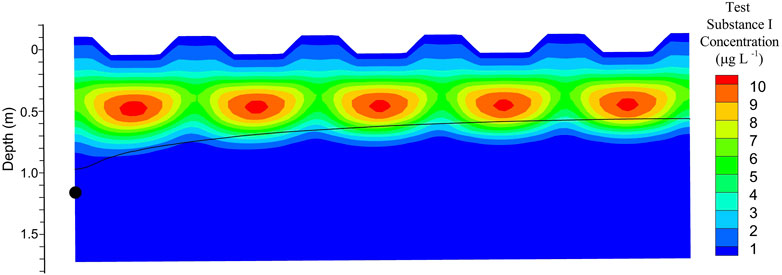
Figure 7. Cross section through the FOCUS surface water D4 scenario, as implemented in HGS with a potato crop, showing simulated Test Substance I concentrations within the porous media (micropore) domain in μg L−1 on 21 August 1985 with the water table position (black line). The tile drain position is indicated with a black circle. The depth scale is approximate.
3.4 Demonstration of surface runoff generation
Surface runoff generated in HGS was compared to runoff generated using the PRZM model for the FOCUS SW R3 scenario with a potato crop (Bologna, IT). Runoff is generated in HGS as either infiltration or saturation excess runoff, depending on soil moisture and variably saturated hydraulic conductivity at the time of a rainfall event. For the PRZM model, runoff behavior is a function of general field conditions, namely, land use, cover treatment, hydrologic condition, and hydraulic soil group, with modifications made to the CN based on the antecedent soil moisture condition prior to rainfall (Suarez, 2005; Young and Fry, 2020). Insights into the differences in runoff generated between HGS and PRZM can be gleaned from examination of the major water balance components for the R3 scenario, for the 1980 analysis year in Table 7. The parameterization scheme for soil hydraulic parameters used in HGS (saturated hydraulic conductivity and the variably saturated hydraulic parameters of the van Genuchten (1980) formulation) resulted in similar annual percolation rates of 189 mm and 169 mm for PRZM and HGS, respectively. The largest difference in the subsurface water balance occurred in AET, calculated in HGS as 545 mm, compared to 635 mm in PRZM. The ET parameters used in the HGS R3 scenario were adopted directly from the HGS models used for the FOCUS GW scenarios. Minor differences in annual water storage between HGS and PRZM were observed, which is to be expected, given the difference in model flow formulation between the Richards’ equation-based HGS model and the soil water capacitance-based PRZM model. The net effect on the annual water balance was that for the 1980 analysis year, HGS produced a higher simulated runoff of 231 mm compared to 110 mm for PRZM, a difference of 121 mm, 90 mm of which was attributed to lower modeled AET in the HGS model. The daily PET time series input to both models was equal to the pan evaporation multiplied by a pan factor of 0.9, with annual PET for 1980 of 739 mm, given in Table 7. No attempt was made to adjust the PET input to HGS.
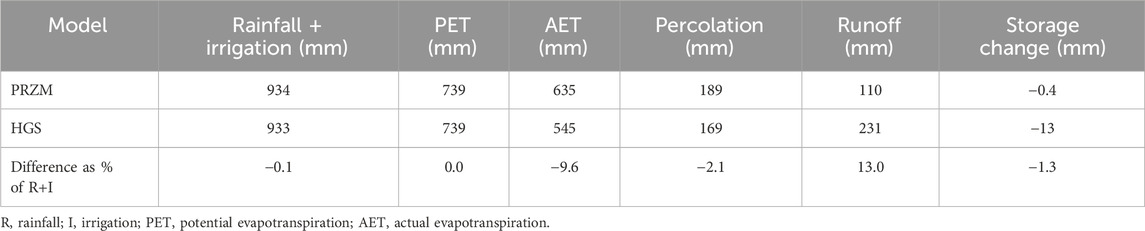
Table 7. Water balance components for the FOCUS surface water R3 potato scenario for HGS and PRZM models for 1980.
The PRZM AET formulation is soil moisture-based (Suarez, 2005; Young and Fry, 2020) not matric potential-based, as used in HGS (Aquanty, 2024). PRZM does not parameterize a matric potential-based root water uptake function, such as that of Feddes et al. (1978), commonly implemented in Richards’ equation-based models such as HGS (Aquanty, 2024), HYDRUS (Šimůnek et al., 2012), and PEARL (Leistra et al., 2001). Therefore, given the differences in flow and AET formulations between PRZM and HGS, it is not surprising that the calculated AET values are substantially different between them. The verification of transpiration values calculated with HGS against the HYDRUS and PEARL models (Table 3) lends credence to the robustness of the AET formulation used in HGS. Therefore, if AET calculated in HGS was biased low and runoff was biased high relative to PRZM, it is likely that the ET formulation in PRZM was the source of the discrepancy and not the AET calculation within HGS. This relatively large difference in runoff generated between the tipping bucket-style model (PRZM) and the Richards’ equation-based model with Feddes’ root water uptake function (HGS) highlights the benefits of calculating infiltration and runoff using a single physics-based model, such as HGS. The use of multiple hydrologic models with different numerical formulations to calculate PPP leaching to GW and PPP transport in runoff can lead to discrepancies in the major water balance components, which then contribute to differences in solute mass partitioning to GW and SW pathways. A hydrologic model cannot reasonably be expected to capture surface–subsurface interactions that are not adequately included in its model formulation (Ebel and Loague, 2006). Therefore, there exists a strong use-case for the unification of PPP fate and transport to GW and SW within a single modeling platform to avoid misallocation of PPP mass to GW or SW or vice versa.
The frequency of runoff events was nearly identical between HGS and PRZM, shown in Figure 8, resulting from a close match between depression storage modeled in HGS and the initial abstraction term in PRZM. Differences in the runoff magnitude between the HGS and PRZM models show some seasonal trends. Differences were generally smaller outside of the growing season, reflecting less of an influence of the discrepancy between AET calculated by the two models.
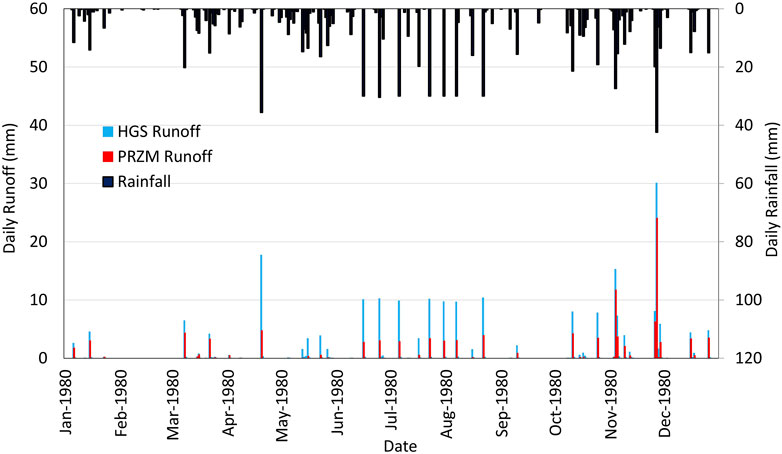
Figure 8. Daily runoff simulated by HGS and PRZM for the FOCUS surface water R3 potato scenario with a potato crop for the analysis year 1980.
4 Conclusion and future work
New irrigation, soil adsorption, and chemical degradation functionality were added to the HGS 3D fully integrated, surface–subsurface hydrological model. The added functionality has been verified for simulated leaching of PPPs to GW for a suite of four test substances using nine geographically based scenarios across the EU from the FOCUS GW framework (European Commission, 2014). HGS model functionality for PPP transport to SW has been demonstrated using two FOCUS (2001) SW scenarios: one for tile drainage and one for runoff generation. HGS results for a 2D cross-sectional dual permeability model produced reasonable tile drain flows, mass fluxes, and concentrations compared to the MACRO model. Runoff generation in HGS was demonstrated through comparison to the PRZM model, which highlighted the role that subsurface hydrologic conditions play in the generation of runoff, along with the calculation of AET.
Fate and transport modeling of PPP leaching to GW, SW via tile drainage, or transport via runoff is commonly simulated with multiple 1D models, each representing a separate exposure pathway. Inherently dependent hydrological processes such as deep percolation to GW, tile drainage, and surface runoff can be simulated in a single 3D, fully integrated, surface–subsurface HGS model while maintaining water and solute mass balance closure. One-dimensional models, as commonly used for exposure assessments, are also not capable of evaluating complex 2D or 3D PPP application geometries or the effects of multidimensional flow on subsurface PPP concentrations. PPP exposure assessment for GW and SW via the tile drainage pathway can now be extended from the use of uncoupled 1D models to the 3D, fully integrated HGS model, with a goal of reducing total mass of PPP in the water environment through precision application. Thus, HGS models can demonstrate that PPP effectiveness is maintained, while environmental risks to GW and SW are decreased. Recognition of the potential role for 3D PPP fate and transport modeling in the regulatory area has long been present (European Commission, 2014). However, noted lack of modeling technology has limited application of 3D models as potential exposure assessment tools. The verification of HGS for PPP fate and transport modeling against existing models should serve to increase the confidence for the use of HGS in a regulatory context. The implications of this verification of the reactive transport functionality of HGS for PPP fate and transport in soil and GW are not limited to the simulation of PPPs. HGS can be applied to other chemicals of concern with reactive transport properties compatible with the new HGS formulations for chemical adsorption and degradation.
Current limitations in the functionality of HGS to simulate PPP fate and transport relative to the FOCUS GW and SW models include a lack of vapor phase and sediment transport. For the current suite of FOCUS test substances used to verify HGS results for leaching of PPPs to GW, the lack of vapor phase transport did not appear to appreciably affect the HGS results. Future work should investigate the potential implications of vapor phase transport on environmental concentrations of PPPs in GW or SW. The robust physics of subsurface flow and runoff generation and verified PPP fate processes paves the way for continued development of HGS functionality, such as the incorporation of PPP subsurface partitioning to surface runoff and transport of PPPs adhered to eroded sediment.
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://zenodo.org/records/13119195.
Author contributions
MC: conceptualization, data curation, formal analysis, investigation, methodology, validation, visualization, writing–original draft, and writing–review and editing. SF: conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, validation, visualization, and writing–review and editing. KM: methodology, software, and writing–review and editing. H-TH: methodology, software, and writing–review and editing. RZ: conceptualization, funding acquisition, project administration, and writing–review and editing. KH: conceptualization, funding acquisition, project administration, and writing–review and editing. SB: conceptualization, project administration, and writing–review and editing. ES: conceptualization and writing–review and editing.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study, including publishing, was financially supported by Bayer AG, who helped develop the scope of the research and provided valuable feedback on preparation of the manuscript.
Acknowledgments
The authors express their appreciation to Diamantopoulos et al. (2017) who graciously shared their HYDRUS, PEARL, and PELMO modeling results with the authors.
Conflict of interest
Authors MC, SF, KM, H-TH, SB, and ES were employed by Aquanty Inc. Authors RZ and KH were employed by Bayer AG.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2024.1505480/full#supplementary-material
Abbreviations
AET, actual evapotranspiration; CN, curve number; DT50, half-life; FOCUS, FOrum for the Co-ordination of pesticide models and their USe; GW, groundwater; Koc, soil organic carbon-water partitioning coefficient; LAI, leaf area index; NRCS, Natural Resources Conservation Service; PET, potential evapotranspiration; PPP, plant protection product; SW, surface water.
References
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). “Crop evapotranspiration: guidelines for computing crop water requirements,” in FAO irrigation and drainage paper 56 (Rome, Italy: Food and Agriculture Organization of the United Nations).
Amado, A. A., Politano, M., Schilling, K., and Weber, L. (2016). Investigating hydrologic connectivity of a drained prairie pothole region wetland complex using a fully integrated, physically-based model. Wetlands 38, 233–245. doi:10.1007/s13157-016-0800-5
Anastasiou, E., Fountas, S., Voulgaraki, M., Psiroukis, V., Koutsiaras, M., Kriezi, O., et al. (2023). Precision farming technologies for crop protection: a meta-analysis. Smart Agric. Technol. 5, 100323. doi:10.1016/j.atech.2023.100323
Anlauf, R., Schaefer, J., and Kajitvichyanukul, P. (2018). Coupling HYDRUS-1D with ArcGIS to estimate pesticide accumulation and leaching risk on a regional basis. J. Environ. Manag. 217, 980–990. doi:10.1016/j.jenvman.2018.03.099
Appels, W. M., Bogaart, P. W., and van der Zee, S. E. A. T. M. (2016). Surface runoff in flat terrain: how field topography and runoff generating processes control hydrological connectivity. J. Hydrology 534, 493–504. doi:10.1016/j.jhydrol.2016.01.021
Aquanty (2024). HydroGeoSphere theory manual. Waterloo, ON, Canada: Version 2653. Available at: https://aquanty-artifacts-public.s3.amazonaws.com/hgs/hydrosphere_theory.pdf (Accessed March 8, 2024).
Barthel, R., and Banzhaf, S. (2016). Groundwater and surface water interaction at the regional-scale – a review with focus on regional integrated models. Water Resour. Manage 30, 1–32. doi:10.1007/s11269-015-1163-z
Berg, F. van den, Beltman, W. H. J., Adriaanse, P. I., de Jong, A., and te Roller, J. A. (2015). SWASH manual 5.3, user’s guide version 5. The statutory research tasks unit for nature and the environment. Wageningen, Netherlands: WOT Natuur and Milieu, 58. WOT-technical report 36. Available at: https://edepot.wur.nl/352934
Berg, F. van den, Tiktak, A., van Kraalingen, D. W. G., and Boesten, J. J. T. I. (2019). User manual for FOCUSPEARL version 5.5.5. The statutory research tasks unit for nature and the environment. Wageningen, Netherlands: WOT Natuur and Milieu, 76. WOT-technical report 164.
Berthold, S., Bentley, L. R., and Hayashi, M. (2004). Integrated hydrogeological and geophysical study of depression-focused groundwater recharge in the Canadian prairies. Water Resour. Res. 40. doi:10.1029/2003WR002982
Bexfield, L. M., Belitz, K., Lindsey, B. D., Toccalino, P. L., and Nowell, L. H. (2021). Pesticides and pesticide degradates in groundwater used for public supply across the United States: occurrence and human-health context. Environ. Sci. Technol. 55, 362–372. doi:10.1021/acs.est.0c05793
Boico, V. F., Therrien, R., Fleckenstein, J. H., Nogueira, G., Iversen, B. V., and Petersen, R. J. (2023). 3D surface–subsurface modeling of a bromide tracer test in a macroporous tile-drained field: improvements and limitations. Soil Sci. Soc Amer J 87, 462–484. doi:10.1002/saj2.20537
Boivin, A., Šimůnek, J., Schiavon, M., and Van Genuchten, M.T. (2006). Comparison of pesticide transport processes in three tile-drained field soils using HYDRUS-2D. Vadose Zone J. 5, 838–849. doi:10.2136/vzj2005.0089
Bresinsky, L., Kordilla, J., Engelhardt, I., Livshitz, Y., and Sauter, M. (2023). Variably saturated dual-permeability flow modeling to assess distributed infiltration and vadose storage dynamics of a karst aquifer – the Western Mountain Aquifer in Israel and the West Bank. J. Hydrology X 18, 100143. doi:10.1016/j.hydroa.2022.100143
Briggs, G. G., Bromilow, R. H., and Evans, A. A. (1982). Relationships between lipophilicity and root uptake and translocation of non-ionised chemicals by barley. Pestic. Sci. 13, 495–504. doi:10.1002/ps.2780130506
Brunner, P., and Simmons, C. T. (2012). HydroGeoSphere: a fully integrated, physically based hydrological model. Groundwater 50, 170–176. doi:10.1111/j.1745-6584.2011.00882.x
Chen, X., Yu, Z., Yi, P., Aldahan, A., Hwang, H.-T., and Sudicky, E. A. (2023). Disentangling runoff generation mechanisms: combining isotope tracing with integrated surface/subsurface simulation. J. Hydrology 617, 129149. doi:10.1016/j.jhydrol.2023.129149
Cheviron, B., and Coquet, Y. (2009). Sensitivity analysis of transient-MIM HYDRUS-1D: case study related to pesticide fate in soils. Vadose Zone J. 8, 1064–1079. doi:10.2136/vzj2009.0023
Convention on Biological Diversity (CBD) (2022). “Kunming-montreal global biodiversity framework,” in Decision Adopted by the Conference of the Parties to the Convention of Biological Diversity. Fifteenth meeting – Part II, Montreal, Canada. Available at: https://www.cbd.int/doc/decisions/cop-15/cop-15-dec-04-en.pdf (Accessed December 19, 2022).
De Schepper, G., Therrien, R., Refsgaard, J. C., and Hansen, A. L. (2015). Simulating coupled surface and subsurface water flow in a tile-drained agricultural catchment. J. Hydrology 521, 374–388. doi:10.1016/j.jhydrol.2014.12.035
De Schepper, G., Therrien, R., Refsgaard, J. C., He, X., Kjaergaard, C., and Iversen, B. V. (2017). Simulating seasonal variations of tile drainage discharge in an agricultural catchment. Water Resour. Res. 53, 3896–3920. doi:10.1002/2016WR020209
Diamantopoulos, E., Šimůnek, J., Oberdörster, C., Hammel, K., Jene, B., Schröder, T., et al. (2017). Assessing the potential exposure of groundwater to pesticides: a model comparison. Vadose Zone J. 16, 1–13. doi:10.2136/vzj2017.04.0070
Ebel, B. A., and Loague, K. (2006). Physics-based hydrologic-response simulation: seeing through the fog of equifinality. Hydrol. Process. 20, 2887–2900. doi:10.1002/hyp.6388
European Commission (EC) (2014). Assessing potential for movement of active substances and their metabolites to ground water in the EU. Rep. FOCUS Ground Water Work Group, EC Document Reference Sanco/13144/2010 Version 3, 613. Available at: https://esdac.jrc.ec.europa.eu/public_path/projects_data/focus/gw/NewDocs/focusGWReportOct2014.pdf
European Commission (EC) (2024). SWASH (website). Brussels, Belgium: Joint Research Centre, European Soil Data Centre. Available at: https://esdac.jrc.ec.europa.eu/projects/swash (Accessed March 1, 2024).
Eurostat (2022). “Pesticide sales,”. Luxembourg: European Commission. Available at: https://ec.europa.eu/eurostat/databrowser/view/aei_fm_salpest09/default/table?lang=en (Accessed on February 23, 2024).
Feddes, R. A., Kowalik, P. J., and Zaradny, H. (1978). Simulation of field water use and crop yield. Wiley, 188.
FOCUS (1997). Surface water models and EU registration of plant protection products. Final report of the work of the regulatory modelling working group on surface water models of FOCUS. Eur. Comm. Doc. 6476/VI/96. Available at: https://esdac.jrc.ec.europa.eu/public_path/projects_data/focus/docs/sw_en_6476VI96_24Feb1997.pdf.
FOCUS (2000). FOCUS groundwater scenarios in the EU review of active substances. Report of the FOCUS Groundwater Scenarios Working Group. EC Doc. Ref. Sanco/321/2000 rev.2, 202pp. Available at: https://esdac.jrc.ec.europa.eu/public_path/projects_data/focus/gw/docs/Generic_guidance_forV1_1.pdf
FOCUS (2001). FOCUS surface water scenarios in the EU evaluation process under 91/414/EEC. Report of the FOCUS working group on surface water scenarios. EC Doc. Ref. SANCO/4802/2001-rev.2 Version 1.4 (May 2015). Available at: https://esdac.jrc.ec.europa.eu/public_path/projects_data/focus/sw/docs/Generic%20FOCUS_SWS_vc1.4.pdf (Accessed on May, 2015).
Frei, S., Knorr, K. H., Peiffer, S., and Fleckenstein, J. H. (2012). Surface micro-topography causes hot spots of biogeochemical activity in wetland systems: a virtual modeling experiment. J. Geophys. Res. 117. doi:10.1029/2012JG002012
Frey, S. K., Hwang, H.-T., Park, Y.-J., Hussain, S. I., Gottschall, N., Edwards, M., et al. (2016). Dual permeability modeling of tile drain management influences on hydrologic and nutrient transport characteristics in macroporous soil. J. Hydrology 535, 392–406. doi:10.1016/j.jhydrol.2016.01.073
Frey, S. K., Miller, K., Khader, O., Taylor, A., Morrison, D., Xu, X., et al. (2021). Evaluating landscape influences on hydrologic behavior with a fully-integrated groundwater – surface water model. J. Hydrology 602, 126758. doi:10.1016/j.jhydrol.2021.126758
Frey, S. K., Rudolph, D. L., Lapen, D. R., and Ball Coelho, B. R. (2012). Viscosity dependent dual-permeability modeling of liquid manure movement in layered, macroporous, tile drained soil. Water Resour. Res. 48. doi:10.1029/2011WR010809
Garen, D. C., and Moore, D. S. (2005). Curve number hydrology in water quality modelling: uses, abuses and future directions. J. Am. Water Resour. Assoc. 41, 377–388. doi:10.1111/j.1752-1688.2005.tb03742.x
Gassmann, M. (2021). Modelling the fate of pesticide transformation products from plot to catchment scale — state of knowledge and future challenges. Front. Environ. Sci. 9, 717738. doi:10.3389/fenvs.2021.717738
Gatel, L., Lauvernet, C., Carluer, N., Weill, S., Tournebize, J., and Paniconi, C. (2019). Global evaluation and sensitivity analysis of a physically based flow and reactive transport model on a laboratory experiment. Environ. Model. and Softw. 113, 73–83. doi:10.1016/j.envsoft.2018.12.006
Gerke, H. H., Dusek, J., and Vogel, T. (2013). Solute mass transfer effects in two-dimensional dual-permeability modeling of bromide leaching from a tile-drained field. Vadose Zone J. 12, 1–21. doi:10.2136/vzj2012.0091
Gerke, H. H., and Van Genuchten, M. T. (1993). A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 29, 305–319. doi:10.1029/92WR02339
Germann, P. F. (1985). Kinematic wave approach to infiltration and drainage into and from soil macropores. Trans. ASAE 28, 745–0749. doi:10.13031/2013.32331
Gong, C., Cook, P. G., Therrien, R., Wang, W., and Brunner, P. (2023). On groundwater recharge in variably saturated subsurface flow models. Water Resour. Res. 59, e2023WR034920. doi:10.1029/2023WR034920
Hintze, S., Glauser, G., and Hunkeler, D. (2020). Influence of surface water – groundwater interactions on the spatial distribution of pesticide metabolites in groundwater. Sci. Total Environ. 733, 139109. doi:10.1016/j.scitotenv.2020.139109
Holmes, K. J., Graham, J. A., McKone, T., and Whipple, C. (2009). Regulatory models and the environment: practice, pitfalls, and prospects. Risk Anal. 29, 159–170. doi:10.1111/j.1539-6924.2008.01186.x
Hwang, H.-T., Park, Y.-J., Frey, S. K., Callaghan, M. V., Berg, S. J., Lapen, D. R., et al. (2019). Efficient numerical incorporation of water management operations in integrated hydrosystem models: application to tile drainage and reservoir operating systems. J. Hydrology 575, 1253–1266. doi:10.1016/j.jhydrol.2019.03.098
Hwang, H.-T., Park, Y.-J., Sudicky, E. A., and Forsyth, P. A. (2014). A parallel computational framework to solve flow and transport in integrated surface–subsurface hydrologic systems. Environ. Model. and Softw. 61, 39–58. doi:10.1016/j.envsoft.2014.06.024
Jorda, H., Huber, K., Kunkel, A., Vanderborght, J., Javaux, M., Oberdörster, C., et al. (2021). Mechanistic modeling of pesticide uptake with a 3D plant architecture model. Environ. Sci. Pollut. Res. 28, 55678–55689. doi:10.1007/s11356-021-14878-3
Kladivko, E. J., Brown, L. C., and Baker, J. L. (2001). Pesticide transport to subsurface tile drains in humid regions of North America. Crit. Rev. Environ. Sci. Technol. 31, 1–62. doi:10.1080/20016491089163
Klein, M. (2020). “PELMO (pesticide leaching model), user manual. Version 5.00,” in Fraunhofer institute for molecular biology and applied Ecology. Germany: Schmallenberg.
Koch, J., Cornelissen, T., Fang, Z., Bogena, H., Diekkrüger, B., Kollet, S., et al. (2016). Inter-comparison of three distributed hydrological models with respect to seasonal variability of soil moisture patterns at a small forested catchment. J. Hydrology 533, 234–249. doi:10.1016/j.jhydrol.2015.12.002
Köhne, J. M., Köhne, S., and Šimůnek, J., 2009. A review of model applications for structured soils: b Pesticide transport. Journal of Contaminant Hydrology 104, 36–60. doi:10.1016/j.jconhyd.2008.10.003
Kollet, S., Sulis, M., Maxwell, R. M., Paniconi, C., Putti, M., Bertoldi, G., et al. (2017). The integrated hydrologic model intercomparison project, IH-MIP2: a second set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 53, 867–890. doi:10.1002/2016WR019191
Kristensen, K. J., and Jensen, S. E. (1975). A model for estimating actual evapotranspiration from potential evapotranspiration. Hydrol. Res. 6, 170–188. doi:10.2166/nh.1975.0012
Kurtz, W., Lapin, A., Schilling, O. S., Tang, Q., Schiller, E., Braun, T., et al. (2017). Integrating hydrological modelling, data assimilation and cloud computing for real-time management of water resources. Environ. Model. and Softw. 93, 418–435. doi:10.1016/j.envsoft.2017.03.011
Larsbo, M., and Jarvis, N. (2003). MACRO 5.0. A model of water flow and solute transport in microporous soil, Technical Description. Emergo: Swedish University of Agricultural Sciences, Department of Soil Sciences, Division of Environmental Physics. 6 Report.
Leeds-Harrison, P. B., Shipway, C. J. P., Jarvis, N. J., and Youngs, E. G. (1986). The influence of soil macroporosity on water retention, transmission and drainage in a clay soil. Soil Use Manag. 2, 47–50. doi:10.1111/j.1475-2743.1986.tb00678.x
Leistra, M., van der Linden, A. M. A., Boesten, J. J. T. I., Tiktak, A., and Berg, F. van den. (2001). PEARL model for pesticide behaviour and emissions in soil-plant system: description of the processes in FOCUS PEARL v 1.1.1. Bilthoven, National Institute of Public Health and the Environment. Wageningen, Alterra, Green World Res. RIVM Rep. 711401009/Alterra-rapport 013, 116. Available at: https://edepot.wur.nl/26563
Lutz, S. R., Van Meerveld, H. J., Waterloo, M. J., Broers, H. P., and Van Breukelen, B. M. (2013). A model-based assessment of the potential use of compound-specific stable isotope analysis in river monitoring of diffuse pesticide pollution. Hydrol. Earth Syst. Sci. 17, 4505–4524. doi:10.5194/hess-17-4505-2013
Maino, J. L., Thia, J., Hoffmann, A. A., and Umina, P. A. (2023). Estimating rates of pesticide usage from trends in herbicide, insecticide, and fungicide product registrations. Crop Prot. 163, 106125. doi:10.1016/j.cropro.2022.106125
Maxwell, R. M., Putti, M., Meyerhoff, S., Delfs, J., Ferguson, I. M., Ivanov, V., et al. (2014). Surface-subsurface model intercomparison: a first set of benchmark results to diagnose integrated hydrology and feedbacks. Water Resour. Res. 50, 1531–1549. doi:10.1002/2013WR013725
Natural Resources Conservation Service (NRCS) (2004). National engineering handbook Part 630: hydrology, chapter 10: estimation of direct runoff from storm rainfall. Washington DC: Natural Resources Conservation Service, United States Department of Agriculture.
Paldor, A., Stark, N., Florence, M., Raubenheimer, B., Elgar, S., Housego, R., et al. (2022). Coastal topography and hydrogeology control critical groundwater gradients and potential beach surface instability during storm surges. Hydrol. Earth Syst. Sci. 26, 5987–6002. doi:10.5194/hess-26-5987-2022
Park, J. Y., Ruidisch, M., and Huwe, B. (2016). Transport of sulfonamide antibiotics in crop fields during monsoon season. Environ. Sci. Pollut. Res. 23, 22980–22992. doi:10.1007/s11356-016-7465-8
Pest Management Regulatory Agency (2023). Pest control product sales report for 2021. Ottawa, ON: Health Canada. Available at: https://www.canada.ca/en/health-canada/services/consumer-product-safety/reports-publications/pesticides-pest-management/corporate-plans-reports/pest-control-products-sales-report.html.
Pietrzak, D. (2021). Modeling migration of organic pollutants in groundwater — review of available software. Environ. Model. and Softw. 144, 105145. doi:10.1016/j.envsoft.2021.105145
Schilling, O. S., Park, Y., Therrien, R., and Nagare, R. M. (2019). Integrated surface and subsurface hydrological modeling with snowmelt and pore water freeze–thaw. Groundwater 57, 63–74. doi:10.1111/gwat.12841
Schock, C. C., Wang, F., Flock, R., Eldredge, E., Pereira, A., and Klauzer, J. (2013). “Drip irrigation guide for potatoes,” in Sustainable agriculture techniques. Corvallis, OR: Oregon State University. Extension Service. EM 8912, Revised Jan. 2013.
Shattuck, A., Werner, M., Mempel, F., Dunivin, Z., and Galt, R. (2023). Global pesticide use and trade database (GloPUT): new estimates show pesticide use trends in low-income countries substantially underestimated. Glob. Environ. Change 81, 102693. doi:10.1016/j.gloenvcha.2023.102693
Silburn, D. M. (2023). Pesticide extraction from soil into runoff under a rainfall simulator. Soil Res. 61, 468–483. doi:10.1071/SR22115
Šimůnek, J., van Genuchten, M.T., and Šejna, M. (2012). The HYDRUS software package for simulating two- and three-dimensional movement of water, heat, and multiple solutes in variably-saturated porous media. Technical manual, Version 2.0. Prague, Czech Republic: PC Progress.
Sittig, S., Sur, R., Baets, D., and Hammel, K. (2020). Consideration of risk management practices in regulatory risk assessments: evaluation of field trials with micro-dams to reduce pesticide transport via surface runoff and soil erosion. Environ. Sci. Eur. 32, 86. doi:10.1186/s12302-020-00362-1
Squillace, P. J., Scott, J. C., Moran, M. J., Nolan, B. T., and Kolpin, D. W. (2002). VOCs, pesticides, nitrate, and their mixtures in groundwater used for drinking water in the United States. Environ. Sci. Technol. 36, 1923–1930. doi:10.1021/es015591n
Steidl, J., Gliege, S., Semiromi, M. T., and Lischeid, G. (2023). Groundwater flow reversal between small water bodies and their adjoining aquifers: a numerical experiment. Hydrol. Process. 37, e14890. doi:10.1002/hyp.14890
Suarez, L. A. (2005). PRZM-3, A model for predicting pesticide and nitrogen fate in the crop root zone and unsaturated zones: user manual for release 3.12.2. National exposure research laboratory. Athens, GA: U.S. Environmental Protection Agency.
Therrien, R., and Sudicky, E. A. (1996). Three-dimensional analysis of variably-saturated flow and solute transport in discretely-fractured porous media. J. Contam. Hydrology 23, 1–44. doi:10.1016/0169-7722(95)00088-7
United Nations General Assembly (UNGA) (2015). “Transforming our world: the 2030 agenda for sustainable development,” in Resolution adopted by the general assembly. Seventieth session. New York, USA. Available at: https://documents.un.org/doc/undoc/gen/n15/291/89/pdf/n1529189.pdf (Accessed October 21, 2015).
United States Department of Agriculture (USDA) (1975). “Soil taxonomy. A basic system of soil classification for making and interpreting soil surveys,” in Agriculture handbook no. 436. Soil conservation Service (Washington DC: USDA).
United States Environmental Protection Agency (USEPA) (2023). Models for pesticide risk assessment. Available at: https://www.epa.gov/pesticide-science-and-assessing-pesticide-risks/models-pesticide-risk-assessment#aquatic (Accessed April 11, 2024).
van Genuchten, M. T. (1980). A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44 (5), 892–898. doi:10.2136/sssaj1980.03615995004400050002x
Walker, A. (1974). A simulation model for prediction of herbicide persistence. J. Environ. Qual. 3, 396–401. doi:10.2134/jeq1974.00472425000300040021x
Wiebe, A. J., Menkveld, P. G., and Rudolph, D. L. (2023). Quantifying seasonal, depression focused recharge in the context of public supply well vulnerability. Hydrol. Process. 37, e14938. doi:10.1002/hyp.14938
Young, D. F., and Fry, M. M. (2019). Field-scale evaluation of pesticide uptake into runoff using a mixing cell and a non-uniform uptake model. Environ. Model. and Softw. 122, 104055. doi:10.1016/j.envsoft.2017.09.007
Young, D. F., and Fry, M. M. (2020). “PRZM5, A model for predicting pesticides in runoff, erosion, and leachate,” in Rev. B. Office of pesticide programs. Washington DC: U.S. Environmental Protection Agency.
Zanin, A. R. A., Neves, D. C., Teodoro, L. P. R., Da Silva Júnior, C. A., Da Silva, S. P., Teodoro, P. E., et al. (2022). Reduction of pesticide application via real-time precision spraying. Sci. Rep. 12, 5638. doi:10.1038/s41598-022-09607-w
Keywords: pesticide, three-dimensional, reactive transport, HydroGeoSphere, agricultural water, green water
Citation: Callaghan MV, Frey SK, Miller K, Hwang H-T, Zolfaghari R, Hammel K, Berg SJ and Sudicky EA (2024) Development of a fully integrated hydrological fate and transport model for plant protection products: incorporating groundwater, tile drainage, and runoff. Front. Environ. Sci. 12:1505480. doi: 10.3389/fenvs.2024.1505480
Received: 02 October 2024; Accepted: 18 November 2024;
Published: 09 December 2024.
Edited by:
Jahangeer Jahangeer, University of Nebraska-Lincoln, United StatesReviewed by:
Michael Tso, United Kingdom Centre for Ecology and Hydrology (UKCEH), United KingdomJiangjiang Zhang, Hohai University, China
Copyright © 2024 Callaghan, Frey, Miller, Hwang, Zolfaghari, Hammel, Berg and Sudicky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michael V. Callaghan, bWNhbGxhZ2hhbkBhcXVhbnR5LmNvbQ==
 Michael V. Callaghan
Michael V. Callaghan Steven K. Frey
Steven K. Frey Killian Miller1
Killian Miller1