Numerical modeling the impacts of increasing groundwater pumping upon discharge decline of the BL Spring located in Xilin Gol League in east inner Mongolia, China

Spring discharge decline induced by increasing groundwater pumping under the background of increasing water demand for agricultural, industrial, and domestic utilizations has been recognized as a significant geo-environmental issue which poses a great threat to springshed eco-environmental safety. In this study, numerical approach was utilized and a series of 3D groundwater flow models based on the MODFLOW module were developed to simulate current-stage and future trends of spring discharges under the impacts of increasing groundwater pumping due to the rapid development of tourism in the BL spring located in Xilin Gol League in east Inner Mongolia (China), for the purpose of understanding the responses of spring discharges to various groundwater pumping scenarios in future. Simulation results indicated that: (1) spring discharge has reduced from 201.4 m³/d to 193.7 m³/d (reduction ratio of 3.80%) under current-stage pumping scheme; (2) the spring-discharge-affected zone is 2.025 km² under current-stage pumping scheme and groundwater pumping within this zone contributes to spring discharge decline; (3) impact of the pumping well located nearest to the BL spring is the most significant while impact of the pumping well located farthest to the BL spring is negligible; and (4) spring discharge would reduce 25%, 50%, 75%, and 100% if total pumping rate of the seven abstraction wells would increase from 45.8 m³/d (current-stage pumping scheme) to 297.7, 586.2, 888.5, and 1,176 m³/d, respectively. The outcome of this study can provide useful references for advising sustainable groundwater exploitation strategies to meet the requirement of groundwater supply under the premise of spring discharge management and eco-environmental protection.

Highlight

• This paper describes numerical modeling of the impacts of increasing groundwater pumping rates on spring discharge decline.

• A linear relationship between spring discharge and groundwater pumping rate is demonstrated.

• Reaching an equilibrium between increasing groundwater pumping rate and spring discharge decline is important to maintain springshed eco-environmental safety.

1 Introduction

Spring which provides a natural drainage pathway for groundwater discharge is considered as an obvious observable indicator inferring the status of groundwater systems, and is recognized as one of the important components in hydrological cycle (Batelaan et al., 2003; Mechal et al., 2017). From hydrological and hydrogeological perspectives, spring discharge can be affected by climate change (e.g., changing precipitation/evaporation/temperature regimes) and anthropogenic activities (e.g., groundwater pumping, coals/mines dewatering) (Frisbee et al., 2013; Work, 2020; Meyers et al., 2022; Gai et al., 2023). Due to population growth and economic development, groundwater supply for agricultural, industrial, and domestic utilizations increased in many populated areas worldwide, while groundwater over-exploitation and/or coals/mines dewatering resulted in declining or even diminishing of spring discharge in those areas (Musgrove et al., 2010; Filippini et al., 2024). For long-term management and protection of spring discharge, the fundamental task is to quantitatively investigate historical and current-stage as well as predict future trends of spring discharge for deeper understanding the impacts of climate change and anthropogenic activities upon spring discharge (Nolin et al., 2023).

To date, two approaches have been seen frequently used to quantitively evaluate climate change and anthropogenic activities impacts upon spring discharge, that is, physical-based method and data-driven method (Li et al., 2023). Physical-based method based on numerical modeling approach has been demonstrated to be the most important and effective predictive tool available for simulating hydrological and hydrogeological processes and predicting how spring discharge might respond to climate change and anthropogenic activities (Rooij et al., 2013; Aamery et al., 2021). In recent years, fruitful research upon changing trends of spring discharge were conducted based on numerical modeling approach. For example, Scanlon et al. (2003) conducted a case study regarding modeling regional groundwater flow and spring discharge of the Barton Springs (Texas, United States), and comparisons between simulation results and field investigations indicated that numerical modeling tool can fairly accurately simulate the temporal variation of spring discharge; Duran and Gill (2021) developed a MODFLOW-USG model to assess the dynamics of groundwater flow field in a small-scale watershed feeding the Manorhamilton Spring (located in county Leitrim, Ireland), and the developed model turned out that a good agreement between the monitored and simulated spring discharge with high simulation accuracy had been achieved; Xu and Hu (2021) developed numerical models based on field investigated data to quantify the understanding of hydrogeological processes in the Woodville Karst Plain in northern Florida, United States; Li et al. (2022) developed a MODFLOW-CFP model to evaluate the maximum groundwater pumping rate of those extraction wells closed to the BL Sping, and found that groundwater extraction rate cannot exceed 0.69 m³/s for ensuring continuous flow of the Jinan Spring (Jinan, China); Other similar modeling studies included, but were not limited to, Doummar et al. (2012), Doummar et al. (2018), Chang et al. (2019), Chen (2021). Unlike the physical-based method, data-driven method based on machine learning approach was emerged with the development of artificial intelligence recently by predicting spring discharge through historical discharge data (capturing the relationship between input and target variables and identifying the inherent patterns concealed in the time-series data) without understanding the underlying physical properties used in physical-based method (Cerqueira et al., 2019; Bai and Tahmasebi, 2023). Data-driven method utilizes water balance elements as model input (e.g., precipitation, infiltration, seepage, pumping, etc.), and modeling methods include, but are not limited to, multiple linear regression (Shi et al., 2015), support vector machine (Barzegar et al., 2018), K-Nearest Neighbor (Rahmati et al., 2019), random forest (Rahmati et al., 2019; Sezen et al., 2019; Wang et al., 2018), etc. However, data-driven method as a novel approach still has many deficiencies, such as its disadvantages of focusing on the relationships between time series while ignoring spatial dependence (Frederik et al., 2018), requiring large amounts of historical monitoring data for searching for inherent patterns, and incapability of predicting hydrological dynamics in those watersheds with stable hydrological conditions (Zhou and Zhang, 2023).

For effective management of spring discharge and better protection of springshed eco-environment, it is very important and necessary to understand the impacts of climate change and anthropogenic activities upon spring discharge (Dass et al., 2021). In this study, a baseline model (based on the MODFLOW module) was developed and calibrated to simulate current-stage groundwater flow and spring discharge, and a series of predictive models (based on the MODFLOW module) were developed to predict future trends of spring discharge on a basis of the baseline model as well as multiple scenarios regarding various groundwater pumping schemes, aiming at quantitatively evaluating the negative effects of increasing groundwater pumping on spring discharge decline. To the best knowledge of the authors, this research is the first effort to unravel the relationships between spring discharge and pumping rate for determination of the “equilibrium” between tourism development and eco-environment protection of the BL spring located in Xilin Gol League in east Inner Mongolia (China), and simulation results can be used to analyze the maximum groundwater withdrawal rate to meet the requirement of groundwater supply under the premise of maintaining a certain level of spring discharge.

2 Overview of study area

The study area is the BL spring located in Xilin Gol League in east Inner Mongolia, China (shown in Figure 1A). The study area used to be a sparsely-populated area far away from cities, agricultural lands and industrial areas while spring discharge remained stable under its natural conditions (approximately 200 m³/d all over 1 year). With the rapid development of tourism since 2017, several hotels and restaurants were implemented to host visitors and seven groundwater pumping wells were installed to ensure water supply for domestic utilizations (see Figure 1A of these pumping wells’ locations), while a slow decline of spring discharge has been seen based on monitoring data since 2019.

Figure 1

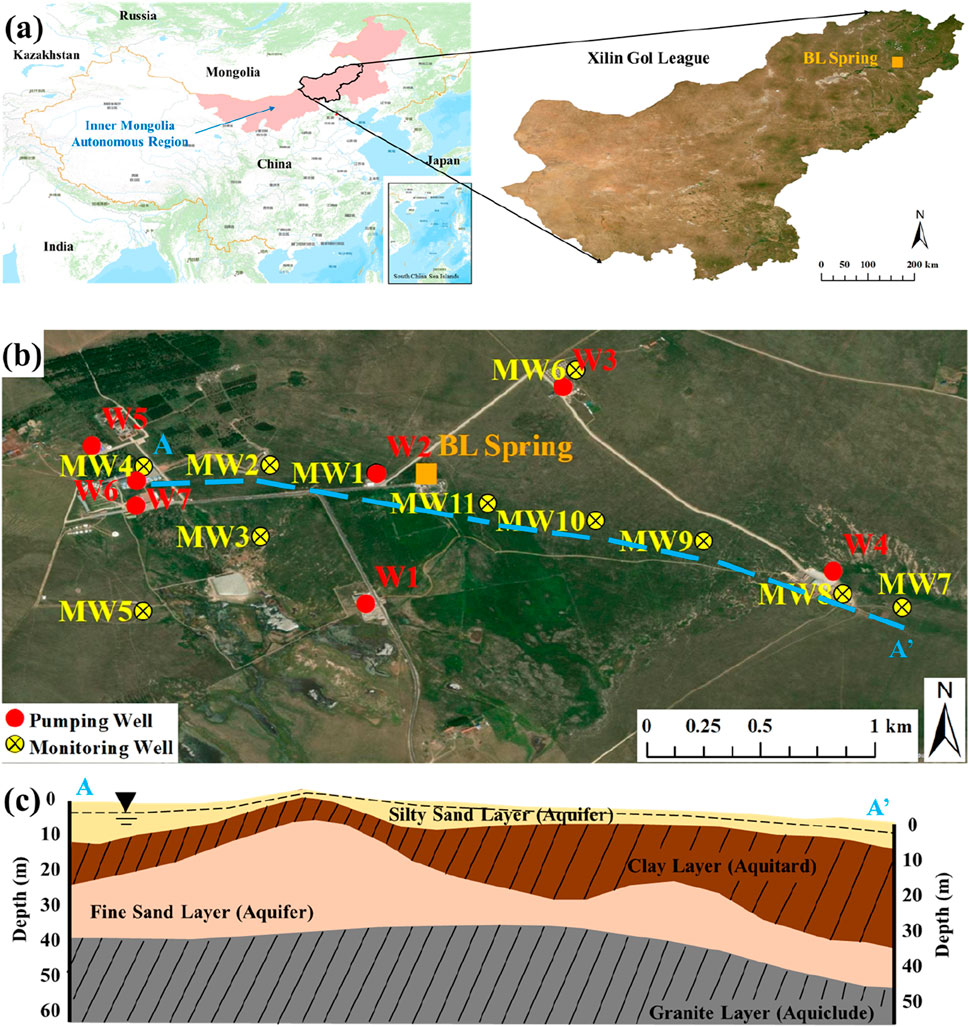
Figure 1. (A) Location of the BL Spring; (B) Locations of the pumping wells and monitoring wells adjacent to the BL Spring; (C) Hydrogeological formations of the cross-section A-A’.

2.1 Hydro-climatic conditions

The study area is in the temperate continental climate region featuring with short and windy springs, short and wet summers, short and moderate falls, and long and dry winters: annual-average temperature ranges from −7.4°C to 8.6°C with the highest temperature in July (average temperature 19.9°C) and the lowest temperature in January (average temperature −22.3°C); annual-average rainfall is 320.9 mm (>70% rainfall occurs in the wet season from June to August) and annual-average evaporation is 1,542.7 mm. The Wulagai River (endorheic river with its depth 0.2–0.8 m and maximum flowrate 17.6 m³/d) and its main tributary the Seyeleji River are located approximately 25 km far away from the study area (Xilin Gol League’s Water Resources Bulletin, http://www.xilinhaote.gov.cn/xilinhaote/2023-08/04/article_2023080410460750025.html).

2.2 Hydrogeological conditions

Based on borehole data, the sedimentary deposits of the hydrogeological formations can be classified into four layers including, from top to bottom, the silty sand layer, the clay layer, the fine sand layer, and the granite layer. The silty sand layer’s (Holocene series) thickness is varied from 3.4 to 15.2 m, and groundwater stored within this layer is unconfined with water table depth ranging from 0 to 4.5 m (water table elevation ranging from 903.0 to 908.7 m); the clay layer’s (Pleistocene series) thickness is varied from 8.9 to 27.1 m, and this layer is considered as an aquitard with relatively low hydraulic conductivity; The fine sand layer’s (Pliocene series) thickness is varied from 10.4 to 31.6 m, and groundwater stored within this layer is confined or semi-confined; The granite layer’s (Miocene series) thickness is greater than 120 m (upper bound elevation ranging from 854.1 to 867.5 m), and this layer is considered as an aquiclude which limits groundwater downward migration to deeper zones. Hydrogeological parameters such as hydraulic conductivity, porosity, specific yield, and specific storage of the silty sand layer, clay layer, and fine sand layer (see Supplementary Table S1) were determined by hydrogeological experiments such as pumping tests. The hydrogeological formations of cross-section A-A’ (see Figure 1A for its location within the study area) were visualized in Figure 1B.

2.3 Spring water source

Based on historical data before 2017, spring discharge was under “steady-state” condition since it remained unchanged in monthly-scale and annual-scale, and spring water temperature always stayed around 5°C throughout the year, indicating that spring water should be yielded from the confined aquifer (fine sand layer). For the sake of determination of whether spring water is yielded from the unconfined aquifer (silty sand layer) or the confined aquifer (fine sand layer), water quality of the spring discharge, the silty sand layer, and the fine sand layer were analyzed, and the Piper diagram and the Gibbs diagram were plotted for comparison of water quality between spring discharge and the silty sand layer, as well as water quality between spring discharge and the fine sand layer. Note that groundwater samples from spring outlet and the monitoring wells of MW2 (fine sand layer), MW4 (silty sand layer), MW5 (silty sand layer), MW6 (fine sand layer), MW8 (fine sand layer), and MW11 (fine sand layer) were collected twice in 2023 (April and October), and the mean values were shown in Supplementary Table S2.

Based on water quality data in Supplementary Table S2, the piper diagram and the Gibbs diagram were plotted as shown in Supplementary Figures S1A, B, respectively. From Supplementary Figure S1A, it can be observed that water quality of spring discharge (dark grey square symbol located within the purple eclipse) and the monitoring wells of MW2, MW6, MW8, and MW11 in the fine sand layer were similar (Cl—Ca), while water quality of spring discharge and the monitoring wells of MW4 and MW5 in the silty sand layer were different (HCO₃—Ca), indicating that spring water is primarily yielded from the fine sand layer; From Supplementary Figure S1B, it can be observed that water quality of spring discharge (red star symbol located within the red eclipse) and the monitoring wells of MW2, MW6, MW8, and MW11 in the fine sand layer were attributed to water-rock interactions, while water quality of the monitoring wells of MW4 and MW5 in the silty sand layer were different, which further demonstrated that spring water is yielded from the fine sand layer.

2.4 Data sources

Discrete groundwater levels were gained from monitoring wells located adjacent to the BL Spring, and were interpolated to delineate groundwater level contours for representing regional-scale groundwater flow fields. Precipitation and evapotranspiration data were gained from weather station, and groundwater pumping rate as well as the amount of groundwater consumption were gained from water resources bulletin promulgated by the local government.

The top elevations of the upmost layer were assigned land surface elevations gained from the Shuttle Radar Topography Mission (SRTM) data which were used to generate digital elevation data with a resolution of 3 arc-seconds (https://www.usgs.gov/centers/eros/science/usgs-eros-archive-digital-elevation-shuttle-radar-topography-mission-srtm-non), and the bottom elevations of each layer were assigned based on the thickness of each hydrogeological formation.

Hydrogeological parameters including hydraulic conductivity, specific yield, and specific storage of various layers were yielded from in-situ pumping tests.

3 Numerical modeling

A 3D numerical groundwater flow model (the baseline model) was developed based on hydro-climatical and hydrogeological data and calibrated against observed groundwater levels to simulate current-stage spring discharge. Based on the developed/calibrated baseline model, a series of 3D numerical groundwater flow models (the predictive models) were developed to simulate future trends of spring discharge under various groundwater pumping scenarios, and the simulated spring discharges of the baseline model and predictive models were compared for the purpose of quantitatively evaluating pumping effects on spring discharge.

3.1 Simulation code

The MODFLOW module which was one of the most frequently-used numerical simulation tool that has been successfully applied to many cases studies worldwide was selected, and the Groundwater Vistas software which has been demonstrated to be one of the most useful graphical-user-interface and data pre- and post-processor was utilized for implementing and calibrating numerical models. The governing equation of the MODFLOW module which was used to simulate groundwater flow is:

$\frac{\partial }{\partial x}\left(K_x\frac{\partial H}{\partial x}\right)+\frac{\partial }{\partial y}\left(K_y\frac{\partial H}{\partial y}\right)+\frac{\partial }{\partial z}\left(K_z\frac{\partial H}{\partial z}\right)+W=S_s\frac{\partial H}{\partial t}$

where: $H$ is groundwater level elevation [L]; $K_x{,K}_y{,K}_z$ are hydraulic conductivity in the x-, y-, and z- directions [LT^-1]; $W$ is source/sink [T^-1]; $S_s$ is specific storage [L^-1]; and $t$ is time [T].

3.2 Model domain

The model domain (see Figure 2A) of the baseline model and the predictive models was determined based on current-stage regional-scale groundwater flow field (Xilin Gol League’s Water Resources Bulletin, http://www.xilinhaote.gov.cn/xilinhaote/2023-08/04/article_2023080410460750025.html) that model boundaries were either parallel or perpendicular to the groundwater level contours (the fine sand layer). The model domain covers an area approximately 106 km², and the silty sand layer, the clay layer, and the fine sand layer were included.

Figure 2

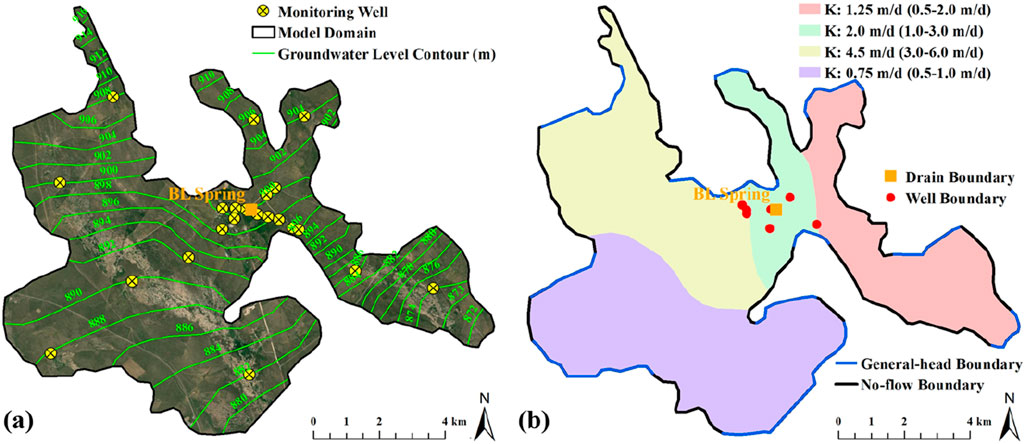
Figure 2. (A) Model domain; (B) Spatial variation of general-head boundary and no-flow boundary as well as horizontal hydraulic conductivity zones in the fine sand layer.

3.3 Hydrogeological parameters

Hydrogeological parameters of the baseline model and the predictive models included, but were not limited to, hydraulic conductivity, porosity, specific yield and specific storage. Based on the results from pumping tests (see Supplementary Table S1), horizontal hydraulic conductivity of the silty sand layer and the clay layer were assigned constant values of 5 m/d and 0.0005 m/d, while spatial variation of horizontal hydraulic conductivity of the fine sand layer were interpolated and switched to zoned values as shown in Figure 2B. Vertical anisotropy (the ratio of vertical/horizontal hydraulic conductivity) was assumed to be 0.1. Porosity, specific yield, and specific storage of the silty sand layer and the fine sand layer were designated based on the values in Supplementary Table S1. Note that the values of these hydrogeological parameters were slightly adjusted during model calibration processes for better model performance.

3.4 Boundary and initial conditions

Boundary conditions of the baseline model and the predictive models were implemented based on hydrological and hydrogeological conditions of each hydrostratigraphic unit. General-head boundary and no-flow boundary were assigned to lateral boundaries (referred to the eastern, western, southern, and northern boundaries), while recharge/evaporation boundary and no-flow boundary were assigned to vertical boundaries (referred to the top and bottom boundaries). The general-head boundary was assigned to the lateral boundaries that are parallel to groundwater level contours to represent groundwater inflow/outflow at model boundary (see Figure 2B), while the no-flow boundary was assigned to the lateral boundaries that are perpendicular to groundwater level contours to represent zero groundwater flux into/out of model boundary (see Figure 2B); the recharge boundary and evaporation boundary were assigned to the top boundary of the top layer, while the no-flow boundary was assigned to the bottom boundary of the bottom layer. The spatial variation of recharge rate (representing infiltration from precipitation) was estimated based on the spatial variation of precipitation (recharge rate specified as a net flux of 5% of precipitation), while the spatial variation of evaporation was estimated based on the spatial variation of potential evaporation with extinction depth limit of 4 m.

Current-stage groundwater level contours (see Figure 2A) were utilized to represent initial heads of the baseline model, and spatial variation of groundwater levels simulated by the baseline model were utilized to represent initial heads of the predictive models.

3.5 Sources and sinks

Sources and sinks of the baseline model and the predictive models mainly include infiltrated rainwater (annual rainfall 320.9 mm with infiltration/rainfall ratio assumed to be 0.1), evaporation (annual evaporation 1,542.7 mm), groundwater pumping (seven wells 45.8 m³/d in total with single well 6.54 m³/d) and spring discharge (calculated by the developed model). The recharge boundary and the evaporation boundary were assigned to the upper bound of the top layer to represent infiltrated rainwater and evaporation. The well boundary was assigned to the fine sand layer to represent groundwater pumping (see Figure 2B). The drain boundary was assigned to the fine sand layer to represent spring discharge (see Figure 2B). The spring discharge was affected by the differences between potentiometric level and land surface elevation, and was calculated automatically during MODFLOW simulation period by multiplying the differences between potentiometric level and land surface elevation by conductance coefficient. Note that the conductance coefficient was used to represent head loss of spring discharge from subsurface conduits to land surface, and its value was assigned to be 100 m²/d based on empirical value.

3.6 Spatial-temporal discretization

Spatially, the model domain of the baseline model and the predictive models was horizontally divided into 260 rows and 299 columns (with a cell size of 50 m × 50 m) and vertically divided into 3 layers with Layers 1, 2, and 3 representing the silty sand layer, the clay layer, and the fine sand layer, respectively. Land surface elevations were assigned to the top elevations of Layer 1, while the bottom elevations of Layers 1, 2, and 3 were assigned based on the thickness of each hydrogeological formation (see Figure 1B). Temporally, the baseline model was steady-state which simulated current-stage spring discharge, the predictive models were transient and the simulation periods were set 10 years with 10 stress periods (1 year per stress period) and 120 time steps (1 month per time step).

4 Results and discussion

4.1 Model calibration

The baseline model was calibrated using the trial-and-error method by gradually adjusting the values of horizontal hydraulic conductivity and vertical anisotropy within a reasonable range, aiming at matching the simulated groundwater levels with the observed groundwater levels from the 22 monitoring wells (see Figure 2A) to a satisfactory degree.

The scatter diagram showing the goodness of fit between the simulated and observed groundwater levels was shown in Supplementary Figure S2. After calibration, the Nash-Sutcliffe efficiency coefficient reaches 0.95, and the simulated spring discharge (193.7 m³/d) was very closed to the monitored value (192.6 m³/d), indicating that the implementation of the baseline model (e.g., boundary and initial conditions, hydrogeological parameters, spatial and temporal discretization, etc.) was appropriate and the predictive models developed based on the baseline model were reliable.

4.2 Simulation results of the baseline model

4.2.1 Spring discharge

The simulated water table of the silty sand layer and potentiometric level of the fine sand layer were shown in Figures 3A,B, respectively. It can be observed from Figure 3A that water table in the northwest was highest while in the southeast was lowest, indicating that groundwater flow in the silty sand layer is from northwest to southeast. It can also be observed from Figure 3B that potentiometric level in the northwest was highest while in the southeast was lowest, indicating that groundwater flow in the fine sand layer is from northwest to southeast. In addition, it can be observed from Figures 3A,B that the silty sand layer’s groundwater flow at the spring location was diverged whereas the fine sand layer’s groundwater flow at the spring location was converged, which further demonstrated that spring water source is yielded from the fine sand layer. Note that potentiometric level is higher than water table, revealing that the overlying silty sand layer may receive upward recharge from the fine sand layer.

Figure 3

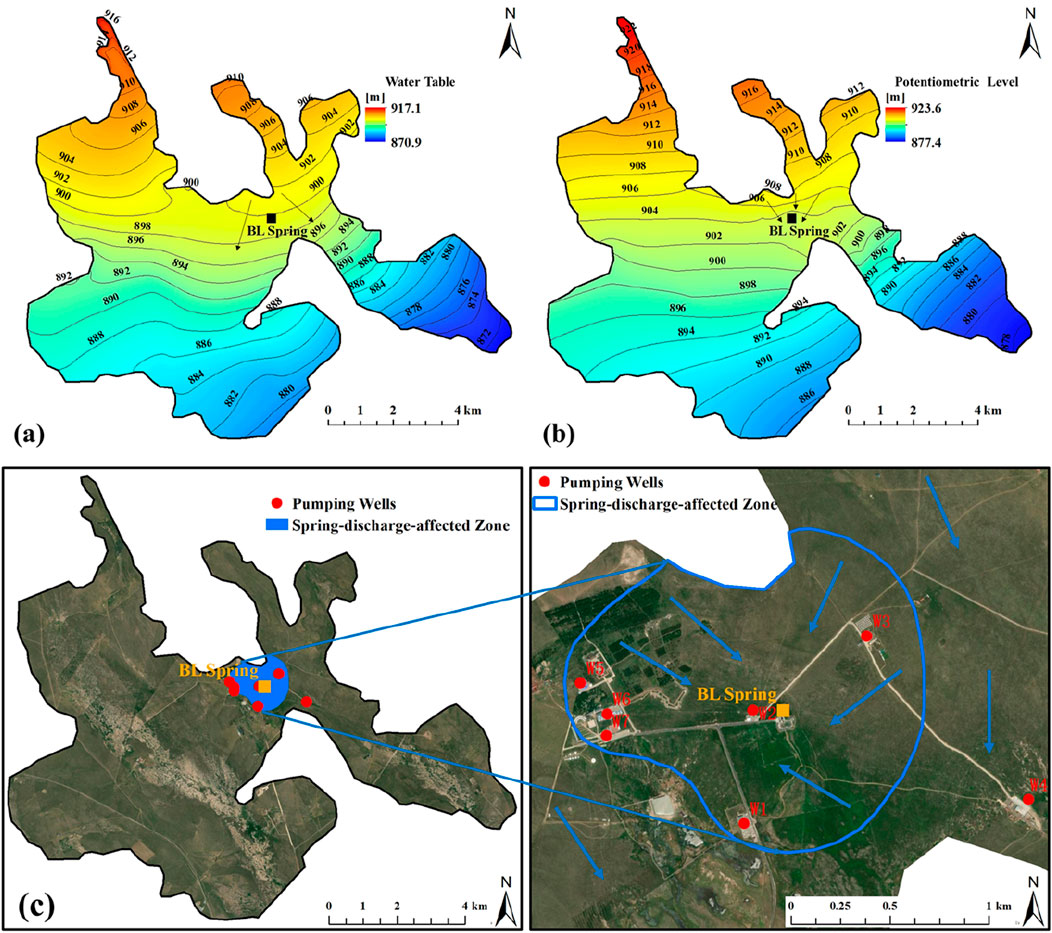
Figure 3. (A) Spatial variation of water table of the silty sand layer; (B) Spatial variation of potentiometric level of the fine sand layer; (C) Location of the spring-discharge-affected zone under current-stage pumping scheme.

The simulated spring discharge was 193.7 m³/d, which was very closed to the monitored value (192.6 m³/d). To quantitatively assess the impacts of current-stage pumping scheme upon spring discharge, nine pumping scenarios (Scenarios 0–8) were implemented as described in Supplementary Table S3. Scenario 0 represented the “natural stage” without groundwater pumping; Scenarios 1, 2, 3, 4, 5, 6, and 7 represented single-well pumping scheme (only one well was active (pumping rate 6.54 m³/d) while the other six wells were inactive (pumping rate 0 m³/d)); and Scenario 8 represented the current-stage pumping scheme (same with the baseline model that pumping rate 45.8 m³/d in total with single well 6.54 m³/d).

With respect to Scenarios 0, 1, 2, 3, 4, 5, 6, 7, and 8, the spring discharge was simulated to be 201.4, 200.0, 198.4, 200.4, 201.4, 200.9, 200.7, 200.6, and 193.7 m³/d, indicating a reduction of 1.4, 3.0, 1.0, 0, 0.5, 0.7, and 0.8 m³/d when only Well #1, #2, #3, #4, #5, #6, and #7 is active and a reduction of 7.7 m³/d when all wells are active in comparison to the “natural stage” spring discharge of 201.4 m³/d. It can be seen that: 1) current-stage pumping scheme can affect spring discharge with a reduction ratio of 3.80%; 2) single pumping of Well #1, #2, #3, #5, #6, and #7 can affect spring discharge with a reduction ratio of 0.70%, 1.49%, 0.50%, 0.25%, 0.35%, 0.40%, respectively; 3) the impact of Well #2 pumping on spring discharge decline is the most significant in that the distance of Well #2 to spring is the nearest; and 4) the impact of Well #4 pumping on spring discharge decline is negligible in that the distance of Well #4 to spring is the farthest.

4.2.2 Spring-discharge-affected zone

Based on the simulated groundwater flowlines of the fine sand layer, the spring-discharge-affected zone where groundwater flow directions headed to the BL spring was visualized in Figure 3C. It can be seen that Wells #1, #2, #3, #5, #6, and #7 are located within the spring-discharge-affected zone, whereas Well #4 is located outside the spring-discharge-affected zone. Under current-stage pumping scheme, the area of the spring-discharge-affected zone was calculated to be 2.025 km², and the farthest distance from the BL spring to the boundary of this zone was measured to be 1.12 km.

Since Well #4 is located outside the spring-discharge-affected zone, groundwater abstraction from Well #4 may not affect spring discharge. Since Well #1, Well #3, Well #5, Well #6, and Well #7 were located adjacent to the boundary of the spring-discharge-affected zone, the impacts of groundwater pumping from these five abstraction wells were relatively small. Since Well #2 is located adjacent to the BL Spring, the impacts of groundwater abstraction at Well #2 were significant.

4.3 Simulation results of the predictive models

To assess the impacts of increasing groundwater pumping due to the rapid development of tourism on spring discharge, a series of predictive models were implemented by adjusting the values of pumping rates of the Well boundary condition of the developed and calibrated baseline model. Twelve groundwater pumping scenarios (Scenarios 9–20) regarding twelve pumping rates which represented various pumping schemes in future were applied to the twelve predictive models (see Supplementary Table S4). Note that: 1) Scenario 0 represented the “natural stage” without groundwater pumping; 2) Scenario 8 represented the current-stage pumping scheme (same with the baseline model); and 3) Scenarios 9–20 represented the situations of groundwater pumping rates being 2, 4, 6, 7.5, 8, 10, 12, 15, 19.4, 20, 25, and 25.7 times of the current-stage pumping rate (45.8 m³/d). Note that the length of the stress period of each predicted model was set 10 years. The simulated potentiometric levels of the fine sand layer with respect to Scenarios 9–20 were visualized in Figures 4A–L, respectively. It can be observed from Figures 4A–L that local-scale groundwater flow field and potentiometric level contours began to change and groundwater depression zones started to form with an increasing groundwater pumping rate.

Figure 4

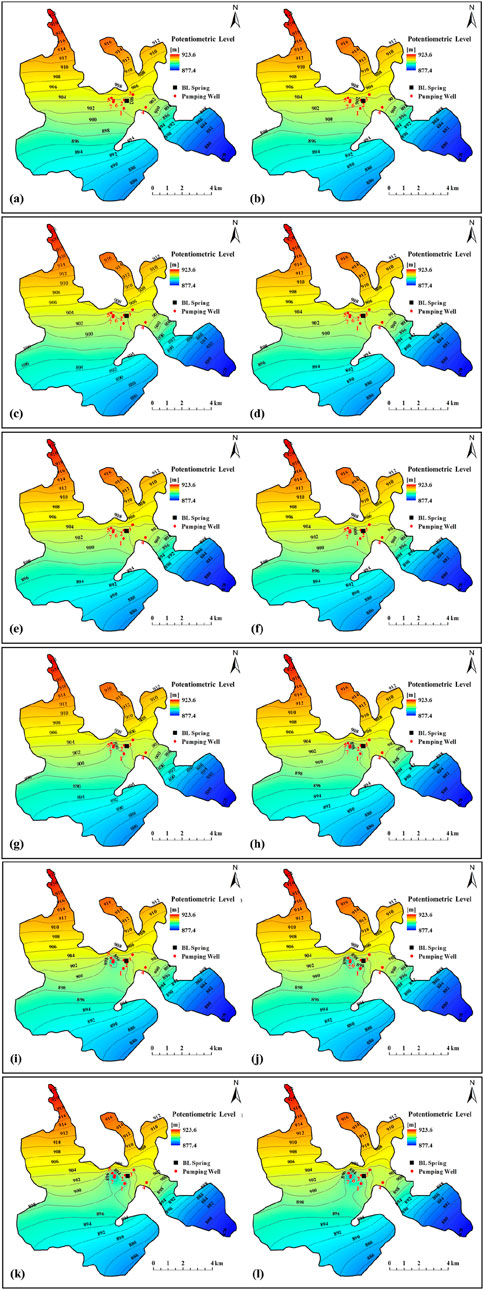
Figure 4. Groundwater flow field and potentiometric level contours of the fine sand layer: (A) Scenario 9; (B) Scenario 10; (C) Scenario 11; (D) Scenario 12; (E) Scenario 13; (F) Scenario 14; (G) Scenario 15; (H) Scenario 16; (I) Scenario 17; (J) Scenario 18; (K) Scenario 19; (L) Scenario 20.

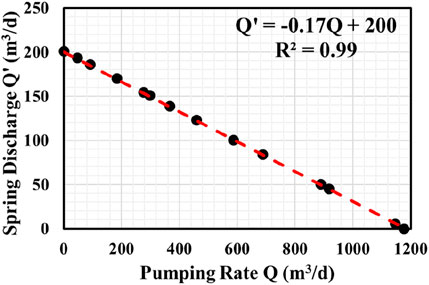
With respect to Scenarios 9–20, the spring discharge was simulated to be 185.9, 170.2, 154.5, 151.1, 138.9, 123.2, 100.7, 84.0, 50.4, 45.0, 5.8, and 0 m³/d, indicating a reduction of 15.5, 31.2, 46.9, 50.3, 62.5, 78.2, 100.7, 117.4, 151.0, 156.4, 195.6, and 201.4 m³/d in comparison to the “natural stage” spring discharge of 201.4 m³/d. It can be seen that: 1) a 1, 3, 5, 7, 9, 14, 19, and 24 times increase of pumping rate in future comparison to the current-stage pumping rate would result in a spring discharge decline of 7.7%, 15.5%, 23.3%, 31.0%, 38.8%, 58.3%, 77.1%, and 97.1%, respectively; and 2) the spring discharge would reduce 25%, 50%, 75%, and 100% if future pumping rate would increase from 45.8 m³/d (current-stage pumping scheme) to 297.7, 586.2, 888.5, and 1,176 m³/d, respectively.

Based on the simulation results of various spring discharges (Q’) with respect to different pumping rates (Q), a linear relationship between Q’ and Q was yielded (shown in Figure 5). Note that the fitting coefficient R² was calculated to be 0.99, indicating that the linear relationship between Q’ and Q was reasonable. The fitting equation can be used to estimate spring discharge if groundwater pumping rate is decided. As mentioned above, several hotels and restaurants were implemented to host visitors and groundwater pumping rate increased significantly with the rapid development of tourism since 2017, because groundwater served as the sole source of water supply in this region. Although the recent rapid development of tourism has raised local tax and boosted local GDP, degradation of local eco-environment such as reduction of spring discharge has paid the price. Hence, it is very important and necessary to reach an “equilibrium” between economic growth and eco-environment degradation. In other words, it is imperative to determine the maximum groundwater withdrawal rate under the premise of protecting spring discharge to a certain degree. The yielded fitting equation can serve as a useful tool for water resources managers to make reasonable plans of groundwater exploitation to meet the requirements of increasing groundwater supply due to rapid development of tourism while maintaining spring discharge at a reasonable level in the meanwhile.

Figure 5

Figure 5. Relationship between spring discharge Q’ and pumping rate Q.

4.4 Uncertainty analysis

Uncertainties mainly included, but were not limited to: uncertainties of model parameters, uncertainties of simulation models, uncertainties of values assigned to boundary conditions, and uncertainties of monitoring data.

Under the circumstances of the complexity of groundwater systems (e.g., heterogeneity), hydrogeological parameters such as hydraulic conductivity, specific yield, and specific storage determined from the limited borehole pumping tests might not be representative of regional-scale hydrogeological conditions. Besides, empirical values were assigned to the hydrological parameters of recharge coefficient (infiltration/rainfall ratio) and evaporation extinction depth. Unrealistic expectations and inappropriate implementation of hydrogeological and hydrological parameters may result in uncertainties of model parameters.

Real groundwater systems are complicated while limited borehole data may not be able to unravel the complex variation of hydrogeological conditions precisely, resulting in uncertainties of conceptual model. Numerical model solvers are usually optimized and adjusted for achievements of reasonable computation time and cost, causing computation error especially in local-scale groundwater levels and flowrates, resulting in uncertainties of numerical model.

Uncertainty of model results from boundary conditions was largely yielded from uncertainties of head values assigned to the GHB boundary. The head values assigned to the GHB boundary were determined by groundwater level contours interpolated from the monitoring wells, whereas inaccurate head values assigned to the GHB boundary may sacrifice the accuracy of model output.

Systematic errors and random errors exist unavoidably during data collection and management procedures (e.g., sampling, measurement, recording, digitization, archiving, etc.), resulting in uncertainties of monitoring data.

4.5 Future work

The performance of the baseline model and the predictive models require improvements. The most effective and efficient approach is to gather more groundwater level measurements for increasing the accuracy of conceptual model design and parameterization. It is highly expected that a real-time monitoring network of groundwater levels and spring discharges would be implemented in future for more comprehensive simulation of the long-term variation of spring discharges under the impacts of climate change and anthropogenic activities.

5 Conclusion

Recently, spring discharge decline due to groundwater exploitation has been recognized as a significant issue posing a great threat to eco-environmental safety. In this study, numerical approach was utilized and 3D groundwater flow models based on the MODFLOW module were developed to simulate current-stage and future spring discharges under the impacts of increasing groundwater pumping due to the rapid development of tourism in the BL spring located in Xilin Gol League in east Inner Mongolia (China).

Simulation results indicated that: 1) spring discharge has reduced from 201.4 m³/d to 193.7 m³/d (reduction ratio of 3.80%) under current-stage pumping scheme; 2) the area of the spring-discharge-affected zone is 2.025 km² and the farthest distance from the BL spring to the boundary of this zone is 1.12 km under current-stage pumping scheme; 3) the impact of Well #2 (located nearest to the BL spring) pumping on spring discharge decline is the most significant while the impact of Well #4 (located farthest to the BL spring and outside the spring-discharge-affected zone) pumping is negligible; and 4) spring discharge would reduce 25%, 50%, 75%, and 100% if future pumping rate would increase from 45.8 m³/d (current-stage pumping scheme) to 297.7, 586.2, 888.5, and 1,176 m³/d, respectively.

The outcome of this study can provide a useful reference for long-term planning and management of sustainable groundwater exploitation under the premise of spring discharge management and springshed eco-environmental protection in the BL spring and other springs in the vicinities in east Inner Mongolia, China.

Data availability statement

The datasets presented in this article are not readily available because Data can be provided upon request. Requests to access the datasets should be directed to aHhpYW8wNzE2QDE2My5jb20=.

Author contributions

HX: Conceptualization, Data curation, Investigation, Methodology, Software, Validation, Visualization, Writing–original draft, Writing–review and editing. YY: Conceptualization, Supervision, Writing–review and editing. QL: Data curation, Validation, Writing–review and editing. YZ: Data curation, Writing–review and editing, Funding acquisition, Investigation, Methodology. XL: Data curation, Writing–review and editing, Visualization. FX: Data curation, Writing–review and editing, Funding acquisition, Supervision. YJ: Conceptualization, Writing–review and editing, Project administration.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported by the Yangtze River Joint Phase II Program (No. 2022-LHYJ-02-0509-05) and Fundamental Research Funds for the Central Public Interest Scientific Institution (2023YSKY30).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author disclaimer

The opinions, findings and conclusions expressed in this manuscript were those of the author(s) and not necessarily those of the funding agencies.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2024.1400569/full#supplementary-material

References

Aamery, N. A., Adams, E., Fox, J., Husic, A., Zhu, J., Gerlitz, M., et al. (2021). Numerical model development for investigating hydrologic pathways in shallow fluviokarst. J. Hydrology 593, 125844. doi:10.1016/j.jhydrol.2020.125844

CrossRef Full Text | Google Scholar

Bai, T., and Tahmasebi, P. (2023). Graph neural network for groundwater level forecasting. J. Hydrology 616, 128792. doi:10.1016/j.jhydrol.2022.128792

CrossRef Full Text | Google Scholar

Barzegar, R., Moghaddam, A. A., Deo, R., Fijani, E., and Tziritis, E. (2018). Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 621, 697–712. doi:10.1016/j.scitotenv.2017.11.185

PubMed Abstract | CrossRef Full Text | Google Scholar

Batelaan, O., De Smedt, F., and Triest, L. (2003). Regional groundwater discharge: phreatophyte mapping, groundwater modelling and impact analysis of land-use change. J. Hydrology 275 (1-2), 86–108. doi:10.1016/s0022-1694(03)00018-0

CrossRef Full Text | Google Scholar

Cerqueira, V., Torgo, L., and Soares, C. (2019). Machine learning vs statistical methods for time series forecasting: size matters. Comput. Res. Repos. doi:10.48550/arXiv.1909.13316

CrossRef Full Text | Google Scholar

Chang, Y., Wu, J., Jiang, G., Liu, L., Reimann, T., and Sauter, M. (2019). Modelling spring discharge and solute transport in conduits by coupling CFPv2 to an epikarst reservoir for a karst aquifer. J. Hydrology 569, 587–599. doi:10.1016/j.jhydrol.2018.11.075

CrossRef Full Text | Google Scholar

Chen, X. (2021). A study of effects of reduction of submarine groundwater discharge on thermal habitats for manatee in a spring-fed estuary using a laterally averaged hydrodynamic model. Ecol. Model. 456, 109653. doi:10.1016/j.ecolmodel.2021.109653

CrossRef Full Text | Google Scholar

Dass, B., Abhishek Sen, S., Bamola, V., Sharma, A., and Sen, D. (2021). Assessment of spring flows in Indian Himalayan micro-watersheds – a hydro-geological approach. J. Hydrology 598, 126354. doi:10.1016/j.jhydrol.2021.126354

CrossRef Full Text | Google Scholar

Doummar, J., Kassem, A. H., and Gurdak, J. J. (2018). Impact of historic and future climate on spring recharge and discharge based on an integrated numerical modelling approach: application on a snow-governed semi-arid karst catchment area. J. Hydrology 565, 636–649. doi:10.1016/j.jhydrol.2018.08.062

CrossRef Full Text | Google Scholar

Doummar, J., Sauter, M., and Geyer, T. (2012). Simulation of flow processes in a large-scale karst system with an integrated catchment model (Mike She) – identification of relevant parameters influencing spring discharge. J. Hydrology 426–427, 112–123. doi:10.1016/j.jhydrol.2012.01.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Duran, L., and Gill, L. (2021). Modeling spring flow of an Irish karst catchment using Modflow-USG with CLN. J. Hydrology 597, 125971. doi:10.1016/j.jhydrol.2021.125971

CrossRef Full Text | Google Scholar

Filippini, M., Segadelli, S., Dinelli, E., Failoni, M., Stumpp, C., Vignaroli, G., et al. (2024). Hydrogeological assessment of a major spring discharging from a calcarenitic aquifer with implications on resilience to climate change. Sci. Total Environ. 913, 169770. doi:10.1016/j.scitotenv.2023.169770

PubMed Abstract | CrossRef Full Text | Google Scholar

Frederik, K., Daniel, K., Claire, B., Karsten, S., and Mathew, H. (2018). Rainfall-runoff modelling using long short-term memory (LSTM) networks. Hydrology Earth Syst. Sci. 22 (11), 6005–6022. doi:10.5194/hess-22-6005-2018

CrossRef Full Text | Google Scholar

Frisbee, M. D., Phillips, F. M., White, A. F., Campbell, A. R., and Liu, F. (2013). Effect of source integration on the geochemical fluxes from springs. Appl. Geochem. 28, 32–54. doi:10.1016/j.apgeochem.2012.08.028

CrossRef Full Text | Google Scholar

Gai, Y., Wang, M., Wu, Y., Wang, E., Deng, X., Liu, Y., et al. (2023). Simulation of spring discharge using graph neural networks at Niangziguan Springs, China. J. Hydrology 625, 130079. doi:10.1016/j.jhydrol.2023.130079

CrossRef Full Text | Google Scholar

Li, C., Xing, L., Dong, Y., Pen, Y., Xing, X., Li, C., et al. (2022). Numerical simulation and protection of the dynamic change of Jinan karst spring based on coupling of seepage and conduit flow. Heliyon 8, e10428. doi:10.1016/j.heliyon.2022.e10428

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Zhou, Y., Cheng, J., and Yao, H. (2023). Delay-aware karst spring discharge prediction. J. Hydrology 626, 130250. doi:10.1016/j.jhydrol.2023.130250

CrossRef Full Text | Google Scholar

Mechal, A., Birk, S., Dietzel, M., Leis, A., Winkler, G., Mogessie, A., et al. (2017). Groundwater flow dynamics in the complex aquifer system of Gidabo River Basin (Ethiopian Rift): a multi-proxy approach. Hydrogeology J. 25 (2), 519–538. doi:10.1007/s10040-016-1489-5

CrossRef Full Text | Google Scholar

Meyers, Z. P., Rademacher, L. K., Frisbee, M. D., and Warix, S. R. (2022). Extending classical geochemical weathering studies through the mountain block: the effect of increasing scale on geochemical evolution in the Sierra Nevada (CA). Chem. Geol. 598, 120831. doi:10.1016/j.chemgeo.2022.120831

CrossRef Full Text | Google Scholar

Musgrove, M., Stern, L. A., and Banner, J. L. (2010). Springwater geochemistry at Honey Creek State Natural Area, central Texas: implications for surface water and groundwater interaction in a karst aquifer. J. Hydrology 388, 144–156. doi:10.1016/j.jhydrol.2010.04.036

CrossRef Full Text | Google Scholar

Nolin, A. F., Girardin, M. P., Adamowski, J. F., Barzegar, R., Boucher, M. A., Tardif, J. C., et al. (2023). Observed and projected trends in spring flood discharges for the Upper Harricana River, eastern boreal Canada. J. Hydrology Regional Stud. 48, 101462. doi:10.1016/j.ejrh.2023.101462

CrossRef Full Text | Google Scholar

Rahmati, O., Choubin, B., Fathabadi, A., Coulon, F., Soltani, E., Shahabi, H., et al. (2019). Predicting uncertainty of machine learning models for modelling nitrate pollution of groundwater using quantile regression and UNEEC methods. Sci. Total Environ. 688, 855–866. doi:10.1016/j.scitotenv.2019.06.320

PubMed Abstract | CrossRef Full Text | Google Scholar

Rooij, R., Perrochet, P., and Graham, W. (2013). From rainfall to spring discharge: coupling conduit flow, subsurface matrix flow and surface flow in karst systems using a discrete–continuum model. Adv. Water Resour. 61, 29–41. doi:10.1016/j.advwatres.2013.08.009

CrossRef Full Text | Google Scholar

Scanlon, B. R., Mace, R. E., Barrett, M. E., and Smith, B. (2003). Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrology 276, 137–158. doi:10.1016/s0022-1694(03)00064-7

CrossRef Full Text | Google Scholar

Sezen, C., Bezak, N., Bai, Y., and ˇSraj, M. (2019). Hydrological modelling of karst catchment using lumped conceptual and data mining models. J. Hydrology 576, 98–110. doi:10.1016/j.jhydrol.2019.06.036

CrossRef Full Text | Google Scholar

Shi, H. J., Qi, X., and Jin, H. (2015). Prediction of karst groundwater level based on R Language, taking Jinci Spring Basin as an example. Appl. Mech. Mater. 730, 230–234. doi:10.4028/www.scientific.net/amm.730.230

CrossRef Full Text | Google Scholar

Wang, X., Liu, T., Zheng, X., Peng, H., Xin, J., and Zhang, B. (2018). Short-term prediction of groundwater level using improved random forest regression with a combination of random features. Appl. Water Sci. 8 (125), 1–12. doi:10.1007/s13201-018-0742-6

CrossRef Full Text | Google Scholar

Work, K. (2020). Not just an arid landscape problem: springflow declines in a region with high rainfall. Limnologica 82, 125766. doi:10.1016/j.limno.2020.125766

CrossRef Full Text | Google Scholar

Xu, Z., and Hu, B. X. (2021). Decadal exploration of karst hydrogeology in the Woodville Karst Plain (WKP): a review of field investigation and modeling development. J. Hydrology 594, 125937. doi:10.1016/j.jhydrol.2020.125937

CrossRef Full Text | Google Scholar

Zhou, R., and Zhang, Y. (2023). Linear and nonlinear ensemble deep learning models for karst spring discharge forecasting. J. Hydrology 627, 130394. doi:10.1016/j.jhydrol.2023.130394

CrossRef Full Text | Google Scholar