Adaptive selection of members for convective-permitting regional ensemble prediction over the western Maritime Continent

A common issue faced by the downscaled regional ensemble prediction systems is the under-dispersiveness of the ensemble forecasts, often attributed to the lack of spread under the initial conditions from the global ensemble. In this study, a novel method that adopts an adaptive approach to selecting global ensemble members for regional downscaling has been developed. Instead of using a fixed set of pre-selected global ensemble members, the adaptive selection performs a sampling algorithm and selects the global ensemble members, which maximizes a fractions skill score (FSS)-based displacement between ensemble members. The method is applied to a convective-permitting ensemble prediction system over the western Maritime Continent, referred to as SINGV-EPS. SINGV-EPS has a grid spacing of 4.5 km and is a 12-member ensemble that is driven by the European Centre for Medium-Range Weather Forecasts (ECMWF) 51-member global ensemble. Month-long trials were conducted in June 2020 to assess the impact of adaptive selection on the ensemble forecast spread and rainfall verification scores. In both fixed pre-selection and adaptive selection experiments, SINGV-EPS was still under-dispersive. However, adaptive selection improved the ensemble spread and reduced the root-mean-square error (RMSE) of the ensemble mean in wind, temperature, and precipitation fields. Further verification of the rainfall forecasts showed that there was a reduction in the Brier score and a higher hit rate in the relative operating characteristic (ROC) curve for all rainfall thresholds when adaptive selection was applied. Additionally, the ensemble mean forecasts from adaptive selection experiments are more accurate beyond 24 h, with a higher FSS for all rainfall thresholds and neighborhood lengths. These results suggest that the adaptive selection is superior to the fixed pre-selection of global ensemble members for downscaled regional ensemble prediction.

1 Introduction

Singapore is situated in Southeast Asia, a region often affected by heavy rainfall that can lead to floods and landslides. While the prediction of heavy rainfall in this tropical region by atmospheric models is beneficial for flood planning, it is extremely challenging due to complex interactions of deep convection with the large-scale motions and underlying air–sea interactions. Local land–sea breeze circulations, surface heating during the day, and delayed rainfall response to deep convection (Mori et al., 2004; Yamanaka, 2016) play a significant role in governing the diurnal cycle in this region (Yang and Slingo, 2001). High-resolution numerical weather prediction (NWP) systems still struggle to accurately predict the location, intensity, and spatio-temporal extent of rainfall associated with deep convection.

The accuracy of NWP forecasts can be restricted by (i) initial condition errors: an inaccurate representation of the initial atmospheric state due to, for example, a lack of observations and/or limitations of data assimilation; (ii) model errors: errors in the model formulation arising from the need to discretize the atmospheric governing equations and conduct crude parameterization of the unresolved physical processes. For regional NWP, another source of error arises from the lateral boundary conditions. These errors are difficult to quantify as they evolve spatially and temporally. In a chaotic atmospheric system, they can grow exponentially, leading to large forecast uncertainties. Over Southeast Asia, which is dominated by deep convection and highly non-linear, these uncertainties are particularly large, and it is not trivial to estimate them.

The probabilistic approach using convective-permitting ensembles attempts to provide an estimate of the forecast uncertainty (Gebhardt et al., 2008; Schwartz et al., 2010; Schwartz et al., 2014; Clark et al., 2011; Migliorini et al., 2011; Clark et al., 2016; Cafero et al., 2019; Porson et al., 2020). These ensemble prediction systems typically have a grid spacing that is less than 5 km, which allows convective parametrizations to be switched off, or reduced, as deep convection starts to be resolved explicitly by the dynamical core of the atmospheric model, thus reducing the parametrization-related biases (Weusthoff et al., 2010; Ferret et al., 2021 and references therein). Due to the increasing computing power, many operational centers have implemented and run various types of convective-permitting ensemble prediction systems (Clark et al., 2011; Bouttier et al., 2012; Schumacher et al., 2013; Schumacher and Clark, 2014; Hagelin et al., 2017; Zhang, 2018; Frogner et al., 2019; Porson et al., 2020; Ono et al., 2021; Wastl et al., 2021). These systems differ in terms of the number of ensemble members and the approach to capturing the various sources of uncertainties. Despite providing useful forecast guidance, many operational centers and studies report an issue with under-dispersiveness of the ensemble (Buizza et al., 2005; Raftery et al., 2005; Hohenegger et al., 2008; Gebhardt et al., 2011; El-Ouartassy et al., 2022; Lakatos et al., 2023; Manikanta et al., 2023), where the spread of the ensemble members is too small to fully capture the forecast uncertainty.

Typically, convective-permitting ensemble prediction systems are downscaled using the initial and boundary conditions from a global ensemble. However, the convective-permitting ensemble often has fewer members than the global ensemble because of higher computational costs in running convective-permitting ensemble forecasts. Therefore, the driving global ensemble members need to be chosen somehow. Existing approaches include using a fixed selection of a subset of the global ensemble to drive the convective-permitting ensemble, assuming each ensemble member represents an equally likely outcome. However, this pre-selection limits the range of the resulting probability distribution function and may not fully capture the uncertainty under initial conditions originating from the global ensemble. Instead, an adaptive approach may be adopted when selecting the members to better represent the uncertainty in the global ensemble.

In collaboration with the United Kingdom Met Office, Meteorological Service Singapore has implemented a basic convective-permitting ensemble prediction system over Singapore and the surrounding region, referred to as SINGV-EPS (Porson et al., 2019). Preliminary investigations showed that SINGV-EPS also suffers from under-dispersiveness, assessed by comparing the ensemble spread with the corresponding root-mean-square error (RMSE) of the ensemble mean (Fortin et al., 2014). The main aim of this study is to obtain the optimal spread from the reduced number of global ensemble members driving SINGV-EPS, which should lead to improvements in the spread–error relationship of the SINGV-EPS forecasts. We explore an approach that uses an adaptive selection of members so that at each forecast time, different members are selected, such that the ‘displacement’ between the selected ensemble members is optimized. We focus solely on uncertainties arising from the specification of initial and boundary conditions; sensitivity experiments using perturbed model physics were also conducted, but results are omitted because that is not the focus of this paper. We attempt to answer the following questions in this study:

1. How does the spread/uncertainty of SINGV-EPS change when the ECMWF members are adaptively selected?

2. How does the change in spread/uncertainty impact the forecast skill of SINGV-EPS?

The remainder of the article is organized as follows: the details and description of experiments are discussed in Section 2. The data used for the analysis and evaluation methods are discussed in Section 3. The results are discussed in Section 4. The summary and conclusions are presented in Section 5.

2 Experiment setup

2.1 SINGV-EPS description

SINGV-EPS is downscaled using the initial and lateral boundary conditions from the European Centre for Medium-Range Weather Forecasts (ECMWF) global model ensemble analysis and forecast (0.2° horizontal resolution; ∼18 km, with 137 vertical levels), operating on a 364 × 342 horizontal grid with a grid spacing of 4.5 km and 80 vertical levels over the western Maritime Continent (see Figure 1A for domain). It spans from 94.75° to 109.35°E and 5°S to 8.05°N. It is initialized twice a day at 00:00 UTC and 12:00 UTC, with forecast lead times up to 36 h. The dynamical core is based on the Met Office Unified Model framework, which solves a non-hydrostatic, deep atmosphere equation set using semi-implicit, semi-Lagrangian time stepping methods. The formulation of SINGV-EPS is based on a regional ensemble version referred to as MOGREPS-UK (Hagelin et al., 2017). However, SINGV-EPS uses a different science configuration, including differing parametrization scheme settings, compared to MOGREPS-UK. SINGV-EPS uses a tropical configuration, while MOGREPS-UK uses a midlatitude configuration. The main differences are discussed in Bush et al. (2020)—the first Regional Atmosphere and Land configuration tailored for the tropical region (RAL1-T).

FIGURE 1

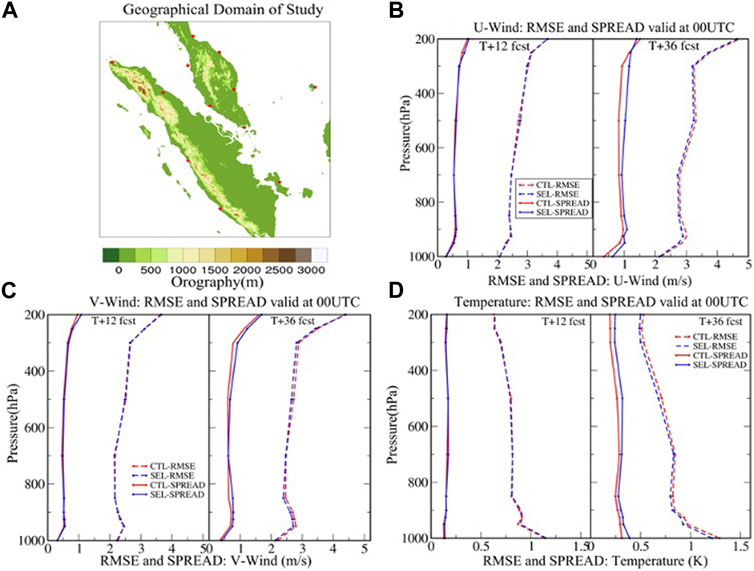
FIGURE 1. (A) Geographical domain of interest showing the terrain elevation (m; contours) and the distribution of 12 radiosonde locations used for verification (red); the vertical profile of ensemble spread and RMSE of the ensemble mean for 12-h (T + 12) and 36-h forecasts (T + 36) of (B) zonal wind, (C) meridional wind, and (D) temperature fields.

SINGV-EPS does not implement additional ensemble perturbations apart from the initial and lateral boundary perturbations inherited from the global ECMWF ensemble (Buizza and Palmer, 1995; Buizza et al., 1999; Palmer et al., 2009; Leutbecher et al., 2017), which uses an ensemble of data assimilation approaches to generate ensemble perturbations. The global ECMWF ensemble contains 51 members (50 members and 1 control), and SINGV-EPS currently uses a pre-selection of 12 members (11 members and 1 control).

2.2 Adaptive selection of ensemble members

As mentioned in Section 1, it is possible to adopt an adaptive approach in selecting members to better represent the uncertainty under initial conditions. This can be achieved by applying a sampling approach based on the fractions skill score (FSS; Gilleland et al., 2020; Roberts, N., 2008; Roberts and Lean, 2008; Skok, G., 2015; Skok and Roberts, 2016; Skok and Roberts, 2018). FSS compares two gridded fields and measures the degree of correspondence as a function of the spatial scale. The forecast and observation fields are re-gridded and converted into binary fields based on the values in each grid cell being higher or lower than a certain threshold. A neighborhood length N (number of grid cells) is defined and used to convert regularly gridded fields into fractions based on the number of grid cells within neighborhoods of size N × N have cell values exceeding the threshold. FSS is then expressed as

${FSS}_{\left(N\right)}=1-\frac{{MSE}_{\left(N\right)}}{{MSE}_{\left(N\right)ref}},(1)$

where

${MSE}_{\left(N\right)}=\frac{1}{N_x{N}_y}{\displaystyle \sum _{i=1}^{N_x{N}_y}}{\left[O_{\left(N\right)i,j}-M_{\left(N\right)i,j}\right]}^2(2)$

and

${MSE}_{\left(N\right)ref}=\frac{1}{N_x{N}_y}\left[{\displaystyle \sum _{i=1}^{N_x{N}_y}}{\left[O_{\left(N\right)i,j}^2+M_{\left(N\right)i,j}^2\right]}^2\right].(3)$

Here, MSE is the mean square error, MSE_(N) is the MSE between the observed and modeled fractions, and MSE_(N)ref is the maximum possible error from the two fields. O_(N) and M_(N) are the fields of fractions for neighborhood length N for observations and models, respectively; N_x and N_y are the numbers of neighborhoods in the full domain along the longitude and latitude axes, respectively. FSS is usually computed for a series of varying neighborhood sizes (L) and differing thresholds.

FSS can be used to estimate spatial agreement between ensemble member pairs for different neighborhood sizes, thereby providing an overall measure of spatial ensemble agreement for different neighborhood sizes from all member–member comparisons (Dey et al., 2014). The method selected to adopt here uses FSS as a direct measure of spatial distance. Following the approach of Skok (2015), Skok and Roberts (2016), and Skok and Roberts (2018), the proxy for the spatial distance ($d$) between two fields of a variable (e.g., precipitation) is expressed as

$d=\left(1-FSS\right).\left(2L+1\right),(4)$

where L is an odd number representing the neighborhood radius in model grid points that defines the neighborhood size $\left(2L+1\right)$ used to calculate FSS. Here, we introduce a novel approach which uses this formula and applies it to atmospheric fields (instead of precipitation fields) to select the ensemble members. Note that this approach has been modified slightly from that of Skok and Roberts (2018) who recommended an approach that accounts for overlapping features to provide a more accurate absolute distance measure. However, since we are interested in relative distances rather than absolute distances, the overlap extension is not deemed essential. For each ensemble member (the $i\text{th}$ member), we perform the following steps to compute the total displacement ${\overline{d}}_i^{tot}$:

(i) For a two-dimensional atmospheric field (e.g., surface zonal wind) from the ECMWF global ensemble member ($i^{\text{th}}$ member) analysis (but also could be from forecasts), the 50th percentile value of the field is used as the threshold; the grid points are assigned ones or zeroes depending on the value being higher or lower than the threshold. Naturally, 50% of the grid points would carry a value of one. These values would be associated with prominent features within the atmospheric field (since adjacent grid points tend to have similar values in a smooth atmospheric field and tend to cluster).

(ii) FSS is calculated for the $i^{\mathit{th}}$ ensemble member with respect to the remaining ensemble members, so FSS is a function of two ensemble indexes ($FS{S}_{i,j}$).

(iii) Using Eq. 4, the displacement $d_{i,j,L}$ is computed for different neighborhood lengths ($L$ being the neighborhood radius as defined previously; 1, 3, and 5 grid points), where the distance between each grid point is 20 km. The use of three different neighborhood lengths enables greater discrimination when calculating the distances. This is necessary because the low percentile (50%) creates good spatial agreement even at the grid scale due to the high (50%) coverage. It means that FSS = 0.5 just by random chance. Hence, the approach of calculating the distance when FSS ∼0.5 (Skok and Roberts, 2018) would often be limited to the grid scale in this setup (i.e., $L=0$; no application of neighbourhooding), which would not account for displacement associated with grid points exceeding the threshold that do not overlap. The use of additional neighborhood lengths accounts for the non-overlapping grid points.

(iv) The displacement $d_{i,j,L}$ is composited first over all ensemble member comparisons ($ith$ member to other ensemble members; $N_{ens}-1$ since $d_{i,i,L}$ is excluded from the composition) and then over different neighborhood lengths ($N_L$), ${\overline{d}}_i=\frac{{\displaystyle {\sum }^{N_L}}{\displaystyle {\sum }^{\left(N_{ens}-1\right)}}{d}_{i,j,L}}{N_L\left(N_{ens}-1\right)}$.

(v) The mean displacement ${\overline{d}}_i$ is computed for each of the four variables: surface (first model level) zonal wind, meridional wind, air temperature, and specific humidity, and the total displacement ${\overline{d}}_i^{tot}$ is computed by summing ${\overline{d}}_i$ across variables. Given that tropical convection is sensitive to near-surface dynamical fields, we expect that the selection of these four variables for the sampling algorithm would subsequently result in a larger impact on the forecasted precipitation field.

After repeating for all ensemble members, the ensemble members are then ranked according to ${\overline{d}}_i^{tot}$. The control is always included, together with the first eight ensemble indexes (with the smallest displacement), and the last three ensemble indexes (with the largest displacement) are the selected subset of 12 members used to drive SINGV-EPS. There is no strict requirement to select the first eight and last three ensemble indexes; thus, the aforementioned setup was selected based on sensitivity experiments.

2.3 Simulation period

We conducted month-long simulations in June 2020 using SINGV-EPS. June typically occurs as the transition month between the inter-monsoon period and the southwest monsoon period for Singapore, so late afternoon thunderstorms are common due to the convective heating over land and relatively near-surface lighter winds throughout the domain. This allows for sufficient events within the month to compute precipitation verification statistics (Section 4). The forecasts are initialized at 12:00 UTC (8 p.m. local time), and we discard the first 12 h of the forecast due to spin-up. SEL and CTL refer to experiments using SINGV-EPS with and without adaptive selection of members, respectively.

3 Data and methods

3.1 Radiosonde observations

Daily wind and temperature data from 00:00 UTC radiosonde profiles in June 2020 have been used for verification. The data are available from approximately 12 locations scattered around Sumatra and the Malaysian Peninsula (Figure 1A). Although they are sparsely distributed within the domain of interest, the radiosondes are still useful for comparison with vertical profiles of SINGV-EPS forecasts, particularly over land.

3.2 ERA5 reanalysis

ERA5 (reference) is a fifth-generation ECMWF global atmospheric retrospective reanalysis dataset available from 1959, with a horizontal resolution of 0.25° × 0.25°. The data on 6-hourly instantaneous wind and temperature have been used to evaluate model forecast errors. The model forecasts have been interpolated into the reanalysis grid for verification. While ERA5 may not be able to represent the winds associated with high-resolution, local storms in the tropics (Campos et al., 2022), it is still the best available dataset over the Southeast Asia region (Bell et al., 2021) for verifying domain-wide fields.

3.3 GPM-IMERG rainfall

The Global Precipitation Measurement Mission (GPM) is a joint mission between NASA and JAXA, which provides next-generation rainfall products (Hou et al., 2008). The rainfall product obtained from the Integrated Multi-satellitE Retrievals for GPM (Final; GPM-IMERG HHv06B; Huffman et al., 2019) has been used for the verification of precipitation forecasts. The spatial resolution and temporal resolution of GPM-IMERG data are 0.1 and 30 min, respectively. Several studies have evaluated the quality of the GPM product over different regions. Some have highlighted an underestimation of heavy rainfall events and rainfall over oceanic regions (Kahn and Maggioni, 2019; Tan et al., 2019). For the Maritime Continent region, studies have shown that GPM is a reliable satellite-derived precipitation dataset, e.g., during the Malaysian flood event in 2014–2015 (Tan et al., 2019) and in representing the diurnal variation in rainfall over Singapore (De Silva et al., 2021).

4 Results and discussion

4.1 Ensemble spread and RMSE: horizontal wind, temperature, and rainfall

It is a common practice to compare the ensemble spread and RMSE of the ensemble mean. For a perfectly reliable and large ensemble, the two quantities should be approximately the same (Leutbecher and Palmer, 2008). As mentioned previously, SINGV-EPS was found to be severely under-dispersive, partly due to the simplicity of its initial implementation. Figures 1B, C display the 12-h forecasts of zonal and meridional wind RMSE values with respect to radiosonde observations, and the corresponding ensemble spread, averaged over 30 forecasts in June 2020. We note that the ensemble spread of the 12-h forecasts from CTL and SEL is virtually indistinguishable, with negligible differences except those higher than 300 hPa. The RMSE values from CTL and SEL are also similar. Comparing the ensemble spread and RMSE of the 12-h forecasts, the RMSE value is notably larger than its ensemble spread, indicating severe under-dispersiveness of SINGV-EPS. For longer lead times (36-h forecasts), we note that there is an increase in the ensemble spread and a reduction in RMSE when adaptive selection is applied. The results are similar for temperature; the application of adaptive selection resulted in an increase in the ensemble spread and a reduction in RMSE for 36-h forecasts (Figure 1D). The improvement in spread and reduction in RMSE for zonal wind, meridional wind, and temperature fields are statistically insignificant at the 12-h lead time but significant at the 90% confidence level at the 36-h lead time for zonal winds and temperature fields (not shown).

Next, we assess the spatial distributions of RMSE with respect to ERA5 reanalysis and ensemble spread for 500-hPa zonal winds of the 36-h forecasts. Figures 2A–D show that the ensemble spread in the 36-h forecasts is too small compared to RMSE over the full SINGV-EPS domain for both CTL and SEL. The higher values of RMSE are observed over Sumatra and off the eastern coast of the Malay Peninsula. However, the ensemble spread appears somewhat uniform (less than 3 m/s) in both experiments. Figure 2E shows domain-averaged RMSE, ensemble spread, and spread–error ratio from CTL and SEL as a function of forecast lead time. We note that SINGV-EPS is under-dispersive (spread–error ratio less than 1) within the 12–36-h forecast lead time window since the ensemble spread increases at roughly the same rate as RMSE during this window. However, as the lead time increases, the difference in ensemble spread and RMSE between SEL and CTL becomes more pronounced; the use of adaptive selection in SEL clearly improves the ensemble spread and reduces RMSE of the ensemble mean. The improvement in the ensemble spread for 850-hPa zonal winds is statistically insignificant at 12-h forecast lead time but significant at the 90% confidence level at longer lead times (18 h and beyond). The reduction in RMSE is statistically insignificant at the 12-h and 18-h forecast lead times but significant at the 85% confidence level for longer lead times (24 h and beyond; not shown). These results were similar for 500-hPa meridional winds and precipitation forecasts verified against GPM data (Supplementary Figures S1, S2). In the following Section 4, we focus on the verification of precipitation forecasts since it has a closer relationship with deep convection and a high impact on the weather in the region.

FIGURE 2

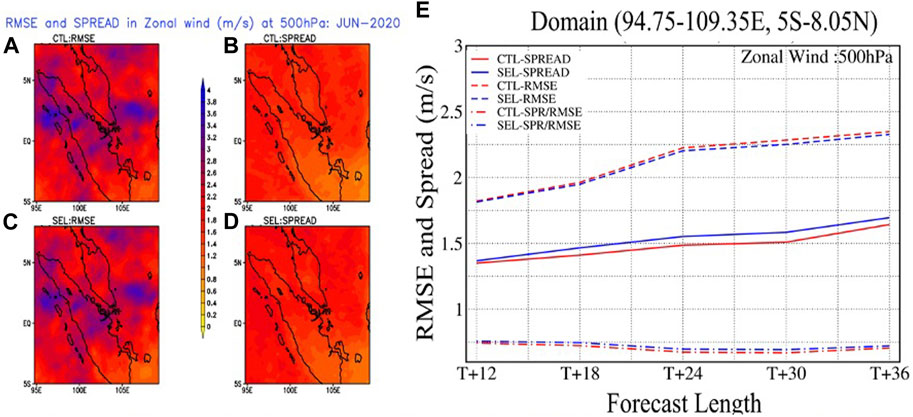
FIGURE 2. Spatial variation in ensemble spread and RMSE of the ensemble mean for 36-h forecasts of 500 hPa zonal wind for (A, B) CTL and (C, D) SEL; and (E) time evolution of domain-averaged ensemble spread (SPREAD), root-mean-square error of ensemble mean (RMSE), and spread–error ratio (SPR/RMSE).

4.2 Probabilistic forecast verification

4.2.1 Brier score

The Brier score (BS; Brier, 1950) measures the average squared difference of the forecast probability of an event and the actual outcome (0 if absent; 1 if present). A smaller BS value implies that the forecast probabilities match closer to the observed outcomes obtained from observations. Figure 3 shows that there is generally an increase in BS with lead time across all four thresholds, indicating a deterioration in ensemble forecast skill with lead time. This result is not surprising since the forecast errors are expected to increase with lead time in a chaotic atmospheric system. The difference of SEL and CTL is more apparent for lower thresholds of rainfall and is only clear after a lead time of 30 h for higher rainfall thresholds. The smaller BS value in SEL compared to that in CTL suggests that applying adaptive selection in SINGV-EPS can improve the ensemble-derived forecast probability products. The reduction in BS is statistically significant at the 90% confidence level at longer forecast lead times (30 h and beyond) for rainfall thresholds of 1 and 2 mm/6 h (not shown).

FIGURE 3

FIGURE 3. Brier score for rainfall (RF) threshold exceeding 1, 2, 4, and 8 mm/6 h for forecasts from CTL (red) and SEL (blue) as a function of forecast lead time.

4.2.2 Relative operating characteristic curve

ROC represents the efficiency of a forecast system in which the hit rate (HR) is plotted as a function of the false alarm rate (FAR). It highlights the capability of an ensemble prediction system to distinguish occurrences and non-occurrences (Buizza et al., 2005). An ROC curve that bows toward the top left corner (larger area under the ROC curve; AUC) indicates that HR is high and FAR is low, which is desirable. A curve aligned along the diagonal indicates that there is no distinction between HR and FAR, and therefore, the model has no skill. Typically, a model is considered skillful if the AUC value is larger than 0.5 (Mason and Graham, 1999). Figure 4A shows that the ROC curve derived from 36-h forecasts from SEL (for an accumulated rainfall threshold of 2 mm/6 h) bows closer to the top left corner compared to that from CTL. The improvement in ROC is statistically significant at the 90% confidence level for the 36-h forecast (not shown). Figure 4B shows that forecasts from both CTL and SEL are skillful, but in general, the AUC value for CTL is smaller than that for SEL across all lead times and rainfall thresholds. It implies that HR is higher and FAR is lower in the ensemble forecasts when adaptive selection is applied in SINGV-EPS.

FIGURE 4

FIGURE 4. (A) Relative operating characteristic (ROC) curve for rainfall (RF) thresholds exceeding 2 mm/6 h for 36-h forecasts from CTL (red) and SEL (blue); (B) area under the curve (AUC) for rainfall thresholds exceeding 1, 2, 4, and 8 mm/6 h as a function of forecast lead time.

4.3 Deterministic forecast verification

Apart from performing probabilistic forecast verification of the ensemble, the ensemble mean rainfall forecast skill is also further evaluated using FSS (Roberts and Lean, 2008). It varies from 0 (worst) to 1 (best) with respect to a reference dataset (usually an observational dataset). Typically, a forecast is considered skillful if the FSS value is larger than 0.5. The FSS value of the ensemble forecast mean from CTL and SEL have been computed with respect to GPM data (accumulated 6-h rainfall). Figures 5A–D show the FSS value for different lead times and thresholds as a function of increasing neighborhood length. We note that the FSS value is larger than 0.5 for rainfall thresholds of 1 and 2 mm at all lead times across all neighborhood lengths in CTL and SEL. The FSS value does not differ substantially between CTL and SEL when the forecast lead time is shorter. However, at longer lead times (beyond 24 h), the ensemble mean forecasts from SEL are more accurate, with a higher FSS value at all rainfall thresholds and neighborhood lengths. This suggests that the application of adaptive selection in SINGV-EPS led to an improvement in the ensemble mean rainfall forecast.

FIGURE 5

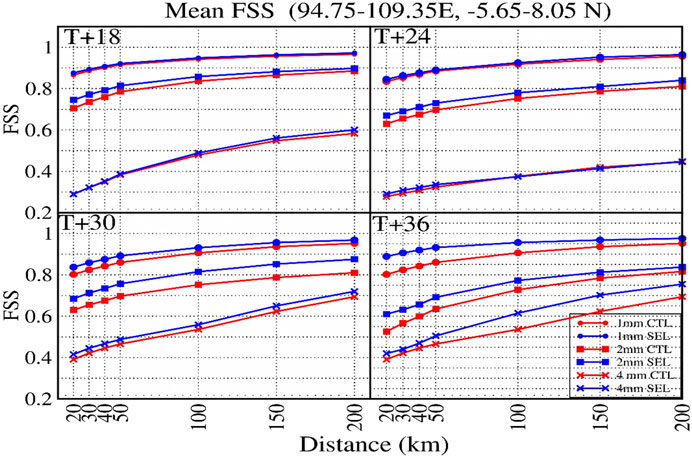
FIGURE 5. Mean fractions skill (FSS) score of 18-h, 24-h, 30-h, and 36-h forecasts from CTL (red) and SEL (blue) for rainfall thresholds exceeding 1, 2, and 4 mm/6 h as a function of the FSS spatial scale (in km).

5 Summary

In this study, we test a novel method of adaptively selecting global ensemble members to drive a regional convective-permitting ensemble prediction system over the western Maritime Continent, referred to as SINGV-EPS. In the control experiment, SINGV-EPS is downscaled using the first 11 odd-numbered global ensemble members (plus the control member), while in the adaptive selection experiment, the 11 global ensemble members (plus the control member) are selected based on a displacement-based algorithm to improve the spread of the initial conditions of SINGV-EPS and therefore the spread in the forecasts. The experiments were conducted in June 2020, a period where convection activity is prevalent. The results are summarized as follows:

(a) A comparison of SINGV-EPS forecasts with radiosonde observations and ERA5 reanalysis data showed that SINGV-EPS is under-dispersive. Applying adaptive selection increased the ensemble spread and reduced the RMSE values of the ensemble mean for zonal wind, meridional wind, and temperature fields. This difference becomes more pronounced for longer forecast lead times, shown for up to 36 h.

(b) A comparison of SINGV-EPS forecasts with satellite-derived precipitation showed that applying adaptive selection also improved the ensemble forecasts of precipitation. With adaptive selection, the Brier score was reduced for all rainfall thresholds, particularly for longer lead times. The relative operating characteristic curve had a larger deviation from a discriminant with no skill, indicating that the ensemble forecasts had a higher hit rate and lower false alarm rate for all rainfall thresholds. The fractions skill score of the ensemble mean was also larger when adaptive selection was applied. This was consistent across all rainfall thresholds, spatial scales, and lead times.

Future research will focus on addressing the inherent under-dispersiveness in SINGV-EPS, through sensitivity studies either with initial and boundary condition perturbations, model physics perturbations, or other post-processing techniques, such as bias correction methods. To this end, various methods used in Tenant (2015), McCabe et al. (2016), and Porson et al. (2020) may be suitable candidates for testing. Further work is currently underway to perform centering of SINGV-EPS on a deterministic high-resolution data assimilation analysis, which should complement the efforts to improve the dispersiveness of the ensemble.

Data availability statement

The ERA5 data and GPM data used in this study are freely available upon registration of their respective websites. The convective ensemble model forecast data are based on the Unified Model framework. The Met Office Unified Model is available for use under license. For further information on how to apply for a license, visit https://www.metoffice.gov.uk/research/modelling-systems/unified-model. Requests to access the datasets should be directed to https://gpm.nasa.gov/data, https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-pressure-levels?tab=overview.

Author contributions

KS: conceptualization, formal analysis, methodology, validation, visualization, and writing–original draft. JL: funding acquisition, methodology, and writing–review and editing. AP: conceptualization, software, supervision, and writing–review and editing. KC: formal analysis, validation, visualization, and writing–review and editing. NR: investigation, methodology, supervision, and writing–review and editing. DoB: data curation, resources, software, and writing–review and editing. HZ: funding acquisition, project administration, supervision, and writing–review and editing. DaB: funding acquisition, project administration, supervision, and writing–review and editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This research has been supported by the National Environment Agency—Singapore.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2023.1281265/full#supplementary-material

References

Bell, B., Hersbach, H., Simmons, A., Berrisford, P., Dahlgren, P., Horányi, A., et al. (2021). The ERA5 global reanalysis: preliminary extension to 1950. Q. J. R. Meteorological Soc. 147, 4186–4227. doi:10.1002/qj.4174

CrossRef Full Text | Google Scholar

Bouttier, F., Vié, B., Nuissier, O., and Raynaud, L. (2012). Impact of stochastic physics in a convection-permitting ensemble. Mon. Weather Rev. 140, 3706–3721. doi:10.1175/MWR-D-12-00031.1

CrossRef Full Text | Google Scholar

Brier, W. V. (1950). Verification of forecasts expressed in terms of probability. Mon. Weather Rev. 78, 1–3. doi:10.1175/1520-0493(1950)078<0001:vofeit>2.0.co;2

CrossRef Full Text | Google Scholar

Buizza, R., Hollingsworth, A., Lalaurette, F., and Ghelli, A. (1999). Probabilistic predictions of precipitation using the ECMWF ensemble prediction system. Weather Forecast 14, 168–189. doi:10.1175/1520-0434(1999)014<0168:PPOPUT>2.0.CO;2

CrossRef Full Text | Google Scholar

Buizza, R., Houtekamer, P. L., Pellerin, G., Toth, Z., Zhu, Y., and Wei, M. (2005). A comparison of the ECMWF, MSC, and NCEP global ensemble prediction systems. Mon. Weather Rev. 133, 1076–1097. doi:10.1175/MWR2905.1

CrossRef Full Text | Google Scholar

Buizza, R., and Palmer, T. N. (1995). The singular-vector structure of the atmospheric global circulation. J. Atmos. Sci. 52, 1434–1456. doi:10.1175/1520-0469(1995)052<1434:TSVSOT>2.0.CO;2

CrossRef Full Text | Google Scholar

Bush, M., Allen, T., Bain, C., Boutle, I., Edwards, J., Finnenkoetter, A., et al. (2020). The first Met Office unified model–JULES regional atmosphere and land configuration, RAL1. Geosci. Model. Dev. 13, 1999–2029. doi:10.5194/gmd-13-1999-2020

CrossRef Full Text | Google Scholar

Cafaro, C., Frame, T. H. A., Methven, J., Roberts, N., and Bröcker, J. (2019). The added value of convection-permitting ensemble forecasts of sea breeze compared to a Bayesian forecast driven by the global ensemble. Q. J. R. Meteorological Soc. 145, 1780–1798. doi:10.1002/qj.3531

CrossRef Full Text | Google Scholar

Campos, R. M., Gramcianinov, C. B., de Camargo, R., and da Silva Dias, P. L. (2022). Assessment and calibration of ERA5 severe winds in the atlantic ocean using satellite data. Remote Sens. (Basel) 14, 4918. doi:10.3390/rs14194918

CrossRef Full Text | Google Scholar

Clark, A. J., Kain, J. S., Stensrud, D. J., Xue, M., Kong, F., Coniglio, M. C., et al. (2011). Probabilistic precipitation forecast skill as a function of ensemble size and spatial scale in a convection-allowing ensemble. Mon. Weather Rev. 139 (5), 1410–1418. doi:10.1175/2010MWR3624.1

CrossRef Full Text | Google Scholar

Clark, P., Roberts, N., Lean, H., Ballard, S. P., and Charlton-Perez, C. (2016). Convection-permitting models: a step-change in rainfall forecasting. Mater. Apps 23, 165–181. doi:10.1002/met.1538

CrossRef Full Text | Google Scholar

Da Silva, N. A., Webber, B. G. M., Matthews, A. J., Feist, M. M., Stein, T. H. M., Holloway, C. E., et al. (2021). Validation of GPM IMERG extreme precipitation in the maritime continent by station and radar data. Earth Space Sci. 8, 1738. doi:10.1029/2021EA001738

CrossRef Full Text | Google Scholar

Dey, S. R. A., Leoncini, G., Roberts, N. M., Plant, R. S., and Migliorini, S. (2014). A spatial view of ensemble spread in convection permitting ensembles. Mon. Weather Rev. 142, 4091–4107. doi:10.1175/MWR-D-14-00172.1

CrossRef Full Text | Google Scholar

El-Ouartassy, Y., Korsakissok, I., Plu, M., Connan, O., Descamps, L., and Raynaud, L. (2022). Combining short-range dispersion simulations with fine-scale meteorological ensembles: probabilistic indicators and evaluation during a ⁸⁵ Kr field campaign. Atmos. Chem. Phys. 22, 15793–15816. doi:10.5194/acp-22-15793-2022

CrossRef Full Text | Google Scholar

Ferrett, S., Frame, T. H. A., Methven, J., Holloway, C. E., Webster, S., Stein, T. H. M., et al. (2021). Evaluating convection-permitting ensemble forecasts of precipitation over Southeast Asia. Weather Forecast 36, 1199–1217. doi:10.1175/WAF-D-20-0216.1

CrossRef Full Text | Google Scholar

Fortin, V., Abaza, M., Anctil, F., and Turcotte, R. (2014). Why should ensemble spread match the RMSE of the ensemble mean? J. Hydrometeorol. 15, 1708–1713. doi:10.1175/JHM-D-14-0008.1

CrossRef Full Text | Google Scholar

Frogner, I. L., Andrae, U. L. F., Bojarova, J., Callado, A., Escribà, P. A. U., Feddersen, H., et al. (2019). HarmonEPS—the HARMONIE ensemble prediction system. Weather Forecast 34, 1909–1937. doi:10.1175/WAF-D-19-0030.1

CrossRef Full Text | Google Scholar

Gebhardt, C., Theis, S., Krahe, P., and Renner, V. (2008). Experimental ensemble forecasts of precipitation based on a convection-resolving model. Atmos. Sci. Lett. 9, 67–72. doi:10.1002/asl.177

CrossRef Full Text | Google Scholar

Gebhardt, C., Theis, S., Paulat, M., and Bouallègue, Z. B. (2011). Uncertainties in COSMO-DE precipitation forecasts introduced by model perturbations and variation of lateral boundaries. Atmos. Res. 100, 168–177. doi:10.1016/j.atmosres.2010.12.008

CrossRef Full Text | Google Scholar

Gilleland, E., Skok, G., Brown, B. G., Casati, B., Dorninger, M., Mittermaier, M. P., et al. (2020). A novel set of geometric verification test fields with application to distance measures. Mon. Weather Rev. 148, 1653–1673. doi:10.1175/MWR-D-19-0256.1

CrossRef Full Text | Google Scholar

Hagelin, S., Son, J., Swinbank, R., McCabe, A., Roberts, N., and Tennant, W. (2017). The Met Office convective-scale ensemble, MOGREPS-UK. Q. J. R. Meteorological Soc. 143, 2846–2861. doi:10.1002/qj.3135

CrossRef Full Text | Google Scholar

Hohenegger, C., Walser, A., Langhans, W., and Schär, C. (2008). Cloud-resolving ensemble simulations of the August 2005 Alpine flood. Q. J. R. Meteorological Soc. 134, 889–904. doi:10.1002/qj.252

CrossRef Full Text | Google Scholar

Hou, A. Y., Skofronick-Jackson, G., Kummerow, C. D., and Shepherd, J. M. (2008). “Global precipitation measurement,” in Precipitation: advances in measurement, estimation and prediction (Berlin, Heidelberg: Springer Berlin Heidelberg), 131–169. doi:10.1007/978-3-540-77655-0_6

CrossRef Full Text | Google Scholar

Huffman, G. J., Bolvin, D. T., and Nelkin, E. J. (2019). Integrated multi-satellitE Retrievals for GPM (IMERG) technical documentation. NASA/GSFC Code, 612, 69.

Google Scholar

Khan, S., and Maggioni, V. (2019). Assessment of level-3 gridded global precipitation mission (GPM) products over oceans. Remote Sens. (Basel) 11, 255. doi:10.3390/rs11030255

CrossRef Full Text | Google Scholar

Lakatos, M., Lerch, S., Hemri, S., and Baran, S. (2023). Comparison of multivariate post-processing methods using global ECMWF ensemble forecasts. Q. J. R. Meteorological Soc. 149, 856–877. doi:10.1002/qj.4436

CrossRef Full Text | Google Scholar

Leutbecher, M., Lock, S., Ollinaho, P., Lang, S. T. K., Balsamo, G., Bechtold, P., et al. (2017). Stochastic representations of model uncertainties at ECMWF: state of the art and future vision. Q. J. R. Meteorological Soc. 143, 2315–2339. doi:10.1002/qj.3094

CrossRef Full Text | Google Scholar

Leutbecher, M., and Palmer, T. N. (2008). Ensemble forecasting. J. Comput. Phys. 227, 3515–3539. doi:10.1016/j.jcp.2007.02.014

CrossRef Full Text | Google Scholar

Manikanta, V., Nikhil Teja, K., Das, J., and Umamahesh, N. V. (2023). On the verification of ensemble precipitation forecasts over the Godavari River basin. J. Hydrol. (Amst) 616, 128794. doi:10.1016/j.jhydrol.2022.128794

CrossRef Full Text | Google Scholar

Mason, S. J., and Graham, N. E. (1999). Conditional probabilities, relative operating characteristics, and relative operating levels. Weather Forecast. 14, 713–725. doi:10.1175/1520-0434(1999)014<0713:CPROCA>2.0.CO;2

CrossRef Full Text | Google Scholar

McCabe, A., Swinbank, R., Tennant, W., and Lock, A. (2016). Representing model uncertainty in the Met Office convection-permitting ensemble prediction system and its impact on fog forecasting. Q. J. R. Meteorological Soc. 142, 2897–2910. doi:10.1002/qj.2876

CrossRef Full Text | Google Scholar

Migliorini, S., Dixon, M., Bannister, R., and Ballard, S. (2011). Ensemble prediction for nowcasting with a convection-permitting model—I: description of the system and the impact of radar-derived surface precipitation rates. Tellus A Dyn. Meteorology Oceanogr. 63, 468. doi:10.1111/j.1600-0870.2010.00503.x

CrossRef Full Text | Google Scholar

Mori, S., Jun-Ichi, H., Tauhid, Y. I., Yamanaka, M. D., Okamoto, N., Murata, F., et al. (2004). Diurnal land–sea rainfall peak migration over sumatera island, Indonesian maritime continent, observed by TRMM satellite and intensive rawinsonde soundings. Mon. Weather Rev. 132, 2021–2039. doi:10.1175/1520-0493(2004)132<2021:DLRPMO>2.0.CO;2

CrossRef Full Text | Google Scholar

Ono, K., Kunii, M., and Honda, Y. (2021). The regional model-based mesoscale ensemble prediction system, MEPS, at the Japan meteorological agency. Q. J. R. Meteorological Soc. 147, 465–484. doi:10.1002/qj.3928

CrossRef Full Text | Google Scholar

Palmer, T. N., Buizza, R., Doblas-Reyes, F., Jung, T., Leutbecher, M., Shutts, G. J., et al. (2009). 598 stochastic parametrization and model uncertainty. Available at: http://www.ecmwf.int/publications/.

Google Scholar

Porson, A. N., Carr, J. M., Hagelin, S., Darvell, R., North, R., Walters, D., et al. (2020). Recent upgrades to the Met Office convective-scale ensemble: an hourly time-lagged 5-day ensemble. Q. J. R. Meteorological Soc. 146, 3245–3265. doi:10.1002/qj.3844

CrossRef Full Text | Google Scholar

Porson, A. N., Hagelin, S., Boyd, D. F. A., Roberts, N. M., North, R., Webster, S., et al. (2019). Extreme rainfall sensitivity in convective-scale ensemble modelling over Singapore. Q. J. R. Meteorological Soc. 145, 3004–3022. doi:10.1002/qj.3601

CrossRef Full Text | Google Scholar

Raftery, A. E., Gneiting, T., Balabdaoui, F., and Polakowski, M. (2005). Using bayesian model averaging to calibrate forecast ensembles. Mon. Weather Rev. 133, 1155–1174. doi:10.1175/MWR2906.1

CrossRef Full Text | Google Scholar

Roberts, N. (2008). Assessing the spatial and temporal variation in the skill of precipitation forecasts from an NWP model. Meteorol. Appl. 15, 163–169. doi:10.1002/met.57

CrossRef Full Text | Google Scholar

Roberts, N. M., and Lean, H. W. (2008). Scale-selective verification of rainfall accumulations from high-resolution forecasts of convective events. Mon. Weather Rev. 136, 78–97. doi:10.1175/2007MWR2123.1

CrossRef Full Text | Google Scholar

Schumacher, R. S., and Clark, A. J. (2014). Evaluation of ensemble configurations for the analysis and prediction of heavy-rain-producing mesoscale convective systems. Mon. Weather Rev. 142, 4108–4138. doi:10.1175/MWR-D-13-00357.1

CrossRef Full Text | Google Scholar

Schumacher, R. S., Clark, A. J., Xue, M., and Kong, F. (2013). Factors influencing the development and maintenance of nocturnal heavy-rain-producing convective systems in a storm-scale ensemble. Mon. Weather Rev. 141, 2778–2801. doi:10.1175/MWR-D-12-00239.1

CrossRef Full Text | Google Scholar

Schwartz, C. S., Kain, J. S., Weiss, S. J., Xue, M., Bright, D. R., Kong, F., et al. (2010). Toward improved convection-allowing ensembles: model physics sensitivities and optimizing probabilistic guidance with small ensemble membership. Weather Forecast 25, 263–280. doi:10.1175/2009WAF2222267.1

CrossRef Full Text | Google Scholar

Schwartz, C. S., Romine, G. S., Smith, K. R., and Weisman, M. L. (2014). Characterizing and optimizing precipitation forecasts from a convection-permitting ensemble initialized by a mesoscale ensemble Kalman filter. Wea. Forecast. 29, 1295–1318. doi:10.1175/WAF-D-13-00145.1

CrossRef Full Text | Google Scholar

Skok, G. (2015). Analysis of Fraction Skill Score properties for a displaced rainband in a rectangular domain. Meteorol. Appl. 22, 477–484. doi:10.1002/met.1478

CrossRef Full Text | Google Scholar

Skok, G., and Roberts, N. (2016). Analysis of Fractions Skill Score properties for random precipitation fields and ECMWF forecasts. Q. J. R. Meteorological Soc. 142, 2599–2610. doi:10.1002/qj.2849

CrossRef Full Text | Google Scholar

Skok, G., and Roberts, N. (2018). Estimating the displacement in precipitation forecasts using the <scp>Fractions Skill Score</scp>. Q. J. R. Meteorological Soc. 144, 414–425. doi:10.1002/qj.3212

CrossRef Full Text | Google Scholar

Tan, J., Huffman, G. J., Bolvin, D. T., and Nelkin, E. J. (2019). Diurnal cycle of IMERG V06 precipitation. Geophys Res. Lett. 46, 13584–13592. doi:10.1029/2019GL085395

CrossRef Full Text | Google Scholar

Tennant, W. (2015). Improving initial condition perturbations for MOGREPS-UK. Q. J. R. Meteorological Soc. 141, 2324–2336. doi:10.1002/qj.2524

CrossRef Full Text | Google Scholar

Wastl, C., Wang, Y., Atencia, A., Weidle, F., Wittmann, C., Zingerle, C., et al. (2021). C-LAEF: convection-permitting limited-area ensemble forecasting system. Q. J. R. Meteorological Soc. 147, 1431–1451. doi:10.1002/qj.3986

CrossRef Full Text | Google Scholar

Weusthoff, T., Ament, F., Arpagaus, M., and Rotach, M. W. (2010). Assessing the benefits of convection-permitting models by neighborhood verification: examples from MAP D-PHASE. Mon. Weather Rev. 138, 3418–3433. doi:10.1175/2010MWR3380.1

CrossRef Full Text | Google Scholar

Yamanaka, M. D. (2016). Physical climatology of Indonesian maritime continent: an outline to comprehend observational studies. Atmos. Res. 178–179, 231–259. doi:10.1016/j.atmosres.2016.03.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, G.-Y., and Slingo, J. (2001). The diurnal cycle in the tropics. Mon. Weather Rev. 129, 784–801. doi:10.1175/1520-0493(2001)129<0784:TDCITT>2.0.CO;2

CrossRef Full Text | Google Scholar

Zhang, X. (2018). Application of a convection-permitting ensemble prediction system to quantitative precipitation forecasts over southern China: preliminary results during SCMREX. Q. J. R. Meteorological Soc. 144, 2842–2862. doi:10.1002/qj.3411

CrossRef Full Text | Google Scholar