- 1College of Resources and Environment, University of Chinese Academy of Sciences, Beijing, China
- 2Yanshan Earth Key Zone and Surface Flux Observation and Research Station, University of Chinese Academy of Sciences, Beijing, China
- 3China Institute of Geo-Environment Monitoring, Beijing, China
- 4Observation and Research Station of Geological Hazard in Sichuan Yaan, Ministry of Natural Resources, Ya’an, Sichuan, China
- 5Technology Innovation Center for Geohazard Monitoring and Risk Early Warning, Ministry of Natural Resources, Beijing, China
Time series Autoregressive Integrated Moving Average (ARIMA) model is often used in landslide prediction and forecasting. However, few conditions have been suggested for the application of ARIMA models in landslide displacement prediction. This paper summarizes the distribution law of the tangential angle in different time periods and analyzes the landslide displacement data by combining wavelet transform. It proposes an applicable condition for the ARIMA model in the field of landslide prediction: when the landslide deformation is in the initial deformation to initial acceleration stage, i.e., the tangential angle of landslide displacement is less than 80°, the ARIMA model has higher prediction accuracy for 24-h landslide displacement data. The prediction results are RMSE = 4.52 mm and MAPE = 2.39%, and the prediction error increases gradually with time. Meanwhile, the ARIMA model was used to predict the 24-h displacements from initial deformation to initial acceleration deformation for the landslide in Guangna Township and the landslide in Libian Gully, and the prediction results were RMSE = 1.24 mm, MAPE = 1.34% and RMSE = 5.43 mm, MAPE = 1.67%, which still maintained high accuracy and thus verified this applicable condition. At the same time, taking the landslide of Libian Gully as an example, the ARIMA model was used to test the displacement prediction effect of the landslide in the Medium-term acceleration stage and the Imminent sliding stage (the tangential angle of landslide displacement is 80° and 85°, respectively). The relative error of displacement data prediction in the Medium-term acceleration stage is within 3%, while the relative error of the prediction value in the Imminent sliding stage is more than 3%, and the error gradually increases with time. This demonstrates that the relative error of the ARIMA model in landslide prediction and forecasting is within 3%. The relative error of the prediction value in the Imminent sliding stage is above 3%, and the error increases gradually with time. Meanwhile, the prediction results are analyzed and it is concluded that the increase in prediction time and tangential angles are the main reasons for the increase in error. The applicable conditions proposed in this study can provide a reference for the application of ARIMA model in landslide prediction and forecast.
1 Introduction
Landslide is a natural disaster that occurs worldwide. It has the characteristics of uneven distribution in space and time and often poses a great threat to human production and life. As one of the core research topics of geological disaster prevention and mitigation, the prediction and forecasting of landslide disasters is also recognized as a world-class problem by scholars at home and abroad (Alimohammadlou et al., 2013; Boyd et al., 2021; Wu et al., 2023). Due to the complexity and uncertainty of landslide activities, the success rate of landslide prediction is still very low. Therefore, studying the temporal prediction and forecasting of landslide hazards is of great theoretical and practical significance. Landslides can be triggered by various factors (such as human influence or geological deformation), and such geological hazards often occur in special geological environments or in conjunction with other hazards, such as earthquakes (Yin et al., 2016; Liu et al., 2019; Zhang et al., 2021; Luo et al., 2022; Zhong et al., 2022). However, the most common cause of landslides is changes in groundwater levels due to prolonged precipitation and human activities (Xu et al., 2012; Haque et al., 2016; Ahmed, 2021).
At present, there are two aspects to landslide prediction and forecasting: temporal and spatial. In the field of landslide prediction and forecasting research, the recognized starting point for landslide time forecasting research began in the 1960s, when the Japanese scholar Saito (1969) proposed an empirical formula for landslide forecasting based on creep theory. He established an accelerated creep equation to predict landslides through displacement monitoring curves. Since then, a large number of landslide time forecasting models have been generated, including statistical forecasting models (Miao et al., 2017; Huang et al., 2021) and nonlinear forecasting models based on machine learning (Li et al., 2018; Niu, 2020; Wang et al., 2022b; Fu et al., 2022; Jiang et al., 2022), among others.
In landslide real-time monitoring, various types of automated monitoring equipment (including fractometer, GNSS, deep displacement, etc.) produce a series of time-related displacement monitoring data. Due to the influence of various external or internal factors, the monitoring equipment collects the data discretely. The discrete wavelet transform can extract the real deformation information to a certain extent by noise reduction and filtering of the original monitoring data of landslides (Khandelwal et al., 2015; Huang et al., 2016; Li et al., 2017; Sun et al., 2021). Li et al. (2019) performed wavelet analysis on GPS-monitored cumulative displacements of Shuping and Baijiabao landslides in the Three Gorges Reservoir area, China, to decompose the displacement time series into low-frequency and high-frequency components in order to solve the problem of non-stationary characteristics. At the same time, during the acquisition of landslide displacement information, data acquisition can be interrupted due to equipment failure or other reasons. This can result in discontinuity in the acquired displacement data, meaning that the displacement data may have different intervals. For time series ARIMA models, having equal time intervals of data is necessary to capture the information in the time series (Calheiros et al., 2015; Pranolo et al., 2022). Therefore, cubic spline interpolation is used to preprocess the landslide displacement data, ensuring that the landslide data have equal time intervals in the time series (Allil et al., 2021). Zhang et al. (2018) introduced two spline interpolation methods to correct and resample the data during the conversion from angle to displacement in the landslide physical modeling tests conducted to study the structural damage of landslides, and the test results were highly consistent with the actual deformation of the landslide model. Li et al. (2021) selected the South Slope Landslide of West Open Pit Mine in Liaoning Province, Northeast China, and the Huangsi Landslide in Gansu Province, Northwest China, as study cases, and proposed a short-term forecasting of landslides (STFL) model by summarizing the displacement data after preprocessing such as cubic spline interpolation and smoothing of the noisy data from the missing data and using it as the input parameter of the model, which realizes a new method that has good reliability and accuracy in landslide prediction.
As a type of statistical forecasting model, the time series Autoregressive Integrated Moving Average (ARIMA) model is known for its remarkable predictive accuracy and flexibility in representing several different types of time series, and it is often used in the field of landslide prediction forecasting (Zhang, 2003; Aggarwal et al., 2020). Singh et al. (2022) were the first to use Sentinel-1A data in the Darjeeling-Sikkim Himalayan region to select potential landslide risk areas and predict landslide displacement and deformation in those areas using an ARIMA model for interannual simulation. Fayaz et al. (2022) used ARIMA prediction models to predict surface temperature and precipitation in the Himalayan region. They determined the weights and critical thresholds of each parameter through field surveys and laboratory tests to give the probability of landslide events in the study area. They also produced hazard level maps for the probability of landslides in each month. Luo et al. (2023) developed a new hybrid model that incorporates the local mean decomposition (LMD), innovations state space models for exponential smoothing (ETS), and the temporal convolutional network (TCN). This proposed model, based on over 10 years of long-term time series monitoring GPS data, was evaluated using a selected case study—the Baijiabao landslide in the Three Gorges Reservoir area of China (TGRA). The proposed model was compared to the ARIMA, support vector regression (SVR), and long short-term memory neural network (LSTM) models. The results indicated that the ARIMA model was suitable for univariate forecasting. Kavoura et al. (2020) analyzed the long-term ground displacements of three of the most famous historical landslide areas in western Greece based on inclinometer data and used an ARIMA model to characterize the specific kinematics of the landslides and to model the kinematic evolution. Wang et al. (2022a) used slope deformation data obtained by interferometric synthetic aperture radar (InSAR) to build a combined LSTM-ARIMA model, obtaining results with higher accuracy than either single model. A major limitation is that ARIMA models assume a linear form of the data of interest, which makes them inappropriate for complex nonlinear time series modeling. Linear models cannot estimate complex nonlinear problems when the prediction horizon is long (Aggarwal et al., 2020). At present, the ARIMA model is mainly applied in the field of landslide prediction and forecasting on annual and monthly time scales and long time series. However, the application of ARIMA model in the field of landslide displacement prediction on hourly time scales is less common, and there is no established applicable condition.
In this research, an applicable condition of the ARIMA model in the field of landslide displacement prediction is proposed and validated based on on-site deformation data at short time intervals. This provides a reference for the application of the ARIMA model in landslide prediction.
2 Case study
In this study, we first use the deformation data of the Qingshui River landslide to propose applicable conditions for the ARIMA model in the field of landslide prediction and forecasting. We verify the proposed conditions with data from the Libiangou landslide and explore the prediction effect of the ARIMA model in the short-term proslide stage of landslides.
The Qingshui River landslide is located in Maoan Village, Sansheng Town, Beibei District, Chongqing of China, on the east flank of the Longwangdong backslope. Figure 1D displays an overview of the Qingshui River landslide. The general topography slopes from southeast to northwest, with the elevation at the bottom of the slope being 573 m and the elevation at the top of the hill being about 651m, resulting in a total height difference of about 78 m. The landslide plane is shaped like a “lap chair”. The rear part of the landslide is gentle terrain, and the left and right side boundaries are located at the foot of the slope. Additionally, there are more buffer ditches at the left and right side boundaries of the lower and middle parts of the landslide. The entire landslide is 78 m in height, 121 m long, and 150 m across, with an average thickness of about 3 m, a landslide area of 1.02 × 104 m2, and a volume of about 3.57 × 104 m³. It is a shallow surface mound landslide with a main sliding direction of 317°. The type of landslide is a small, shallow, earthy slope composed of powdered clay mudstone. The slip zone is made up of powdered clay sandwich gravel, and the slip surface is located at the rock-soil contact surface with a slip bed made of mudstone. The rock yield is 298°∠71°. The main threat to the landslide area is the safety of 19 households and 57 people. The landslide is a small soil landslide, pushed landslide with a tongue-shaped plane. In recent years, the deformation has mainly been concentrated in the middle and rear parts, with pulling cracks and seams measuring 1–5 m long and 1–5 mm wide. Locally, there is a downward deviation of 1–10 mm, and the trees on the slope are skewed.

FIGURE 1. (A) Qingshui River landslide(red point) is located at 29°54′41″N, 106°39′21″E(Chongqing, China); Guangna Township landslide(red point) is located at 32°19′32″N, 107°27′15″E(Sichuan, China); Libian Gully landslide(red point) is located at 32°46′45″N, 110°8′40″E(Hubei, China). (B) Overview of the Qingshui River landslide. (C) Overview of the Guangna Township landslide. (D) Overview of the Libian Gully landslide.
The Guangna Township Landslide is located in Group 2, Mengzi Village, Guangna Township, Tongjiang County, Bazhong City, with geographic coordinates of 107°14′46 “E, 31°50′48 “N. The overall slope is about 24°, and the main slide direction is 340°. The longitudinal length of the slide is about 100 m, and the horizontal width is about 50 m. The overall slope of the landslide is about 24°, the main slip direction is 340°, the longitudinal length of the landslide is about 100 m, the transverse width is about 50 m, the area is about 5000 m2, the average thickness of the slide is about 1–2 m, the scale of the landslide is about 1.0 × 104 m³, it is a small earthy landslide, and the material composition of the landslide is pulverized clay, with looser structure and the content of debris is about 5%.
The Libian Gully landslide is located in Shagou Village, Hujiaying Township, Yunyang District, Shiyan City, Hubei Province of China. Figure 1C displays an overview of the Libian Gully landslide. The landslide underwent initial deformation in July 2003, with the central ground uplift and a deformation range of about 100 m2. The slip body experiences many small-scale collapse slides, with creep slip phenomena occurring every rainy season. Under the influence of strong or continuous rainfall, the slide body may undergo large-scale destabilization and sliding damage.
The on-site monitoring data of the landslides are obtained from the China Geological Disaster Monitoring and Early Warning Information System. Among, the monitoring system for the Qingshuihe landslide is operated by the 208 Hydrogeological Engineering Geological Team of the Chongqing Geological and Mineral Exploration and Development Bureau, the Guangna Township landslide is monitored by the 283rd Brigade of the Sichuan Nuclear Industry Geological Bureau, and the Libiangou landslide is monitored by the Hubei Provincial Geological and Environmental General Station. Displacement data for the three landslides are available on the website (Supplementary Material).
3 Materials and methods
3.1 Application of ARIMA model
A time series is a collection of data gathered at specific intervals, and an appropriate analytical model is created based on the unique nature of the data to predict potential future values of the series. The time series of cumulative landslide displacement is often non-stationary, and the ARIMA model is a commonly used model for dealing with non-stationary time series. The ARIMA model transforms a non-stationary time series into a stationary one, and then regresses the dependent variable on its lagged value, the current value of the random error term, and only the lagged value. The ARIMA model comprises the moving average process (MA), autoregressive process (AR), autoregressive moving average process (ARMA), and the ARIMA process. Specifically, if the time series yt can be smoothed by d differences to obtain Wt = Δdyt (i.e., yt ∼ I(d)), then Wt is a smooth series (i.e., Wt ∼ I(0)), and the ARIMA(p, q) model can be formulated as follows:
The ARIMA (p, q) model after the d-order difference is called ARIMA(p, d, q), where p is the autoregressive order, q is the moving average order, and et is the white noise process. When d = 1, the above equation can be written as:
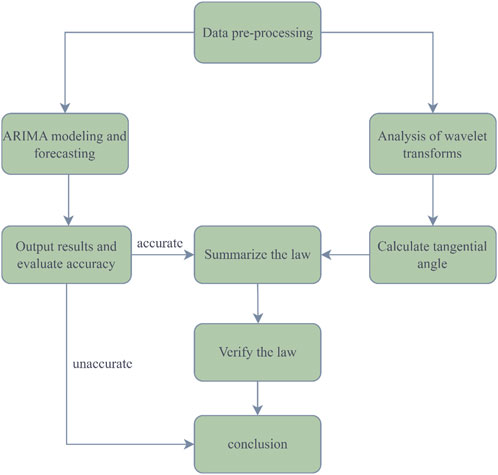
In this study, the application of ARIMA model is divided into the following steps: (1) preprocessing the data; (2) modeling and predicting the data using the ARIMA model; (3) classifying the stage of landslide deformation by wavelet transform analysis; (4) calculating the tangential angle of landslides in the study area with high prediction accuracy of the ARIMA model; (5) summarizing the law of the distribution of the tangential angle; (6) verifying the law; (7) drawing conclusions. The framework of this study is shown in Figure 2.
3.2 Parameters for landslide prediction
Currently, landslide prediction studies are often analyzed from both qualitative and quantitative perspectives. From the qualitative point of view, the severity of precipitation and the nature of the soil, among others, are influences that are often considered (Guzzetti et al., 2020; Prancevic et al., 2020; Li et al., 2022). Among them, the physical mechanisms of soil properties are relatively complex, involving thermodynamic mechanisms of geotechnical particle movement and the influence of permeable water flow (Deng et al., 2020; Bai et al., 2021b). Furthermore, the content of heavy metals in soil is also a key variable. The interaction between heavy metals in soil and the soil itself often leads to anomalies in soil heavy metal content in areas where landslides occur. Therefore, the content of heavy metals in soil can serve as a criterion for predicting landslide hazards (Bai et al., 2021a; Anda et al., 2021). However, qualitative analyses generally cannot be quantified accurately. Therefore, landslide susceptibility mapping (LSM) is often used to express the degree of risk of landslide hazards in a certain area (Zhang et al., 2022b; Li et al., 2022).
Correspondingly, the primary objective of landslide prediction in quantitative terms is to simulate and predict landslide displacement data using prediction models, establish threshold criteria, and ultimately achieve accurate landslide forecasting (Kirschbaum et al., 2010; Fan et al., 2019a; Yang et al., 2019; Guzzetti et al., 2020; Zhang et al., 2022c). The landslide displacement prediction is a key component of early warning systems that emphasizes the ease of access, quantification, and reliability of displacement monitoring data (Du et al., 2013; Manconi and Giordan, 2015; Liu et al., 2018; Yan et al., 2021). Global Navigation Satellite System (GNSS) technology is an effective and direct method in landslide evolution analysis, which can be used to monitor the surface displacement of landslides (Lian et al., 2014; Li et al., 2017; Huang et al., 2022). The displacement data can be recorded to form displacement monitoring curves, which are the core of the evaluation of landslide stability and its trend. It is also the key parameter to realize the accurate early warning of a landslide (Pecoraro et al., 2019; Ju et al., 2020). The monitoring curve is the basis for deformation evolution stage determination, and the monitoring curve of the accelerative deformation stage is the basis for landslide early warning. For landslide prediction and forecasting, it is crucial to delineate different stages of landslide hazard evolution and provide different warning information according to different stages (Li et al., 2016). The current study generally divides the landslide hazard evolution into the following three stages: initial deformation, constant deformation, and accelarative deformation stages (Xu et al., 2008; Zhang et al., 2022a). In this paper, the tangential angle is primarily used as the basis for dividing landslide deformation stages. The accelerated deformation stages are further subdivided into the initial acceleration stage, the medium-term acceleration stage, and the imminent sliding stage, based on previous studies on three-stage landslides (Fan et al., 2019b; Chen et al., 2023; Tan et al., 2023).
For judging the stage of landslide deformation development, the tangential angle is a common statistical quantity that can be used to further classify the deformation stage of landslides from a quantitative perspective, enabling early warning. Currently, a specific division of landslide warning level is made based on the tangential angle, where if the tangential angle is greater than 45°, the landslide deformation enters the initial acceleration deformation stage; if the tangential angle is greater than 80°, the landslide deformation enters the medium-term acceleration deformation stage; if the tangential angle is greater than 85°, the landslide deformation enters the imminent sliding deformation stage (Xu et al., 2009). Therefore, the key to the successful realization of the proslide warning lies in the accurate calculation of the tangential angle. For calculating the tangential angle, the displacement-time curve’s different coordinate scales and the fluctuation correction of the measured data over time must be considered. According to the definition of the improved tangential angle (Xu et al., 2009):
Among them:
Where
As can be seen from Eqs 3, 4, calculating the average deformation rate
4 Results
4.1 Qingshui River landslide displacement prediction
The ARIMA model was tested with monitoring data from the Qingshui River landslide. Figure 3A displays the hourly cumulative displacement change data of the Qingshui River landslide from 10:00:00 on 14 August 2021, to 09:00:00 on 28 September 2021. As shown in Figure 3A, the change trend of the cumulative displacement-time curve of the Qingshui River landslide is smooth, and the deformation of the landslide is not very violent and does not belong to the “step” category landslides. Therefore, the Qingshui River landslide is used as the main research object to explore the applicability conditions of the ARIMA model in landslide prediction and forecasting, in order to determine its suitability for such purposes.
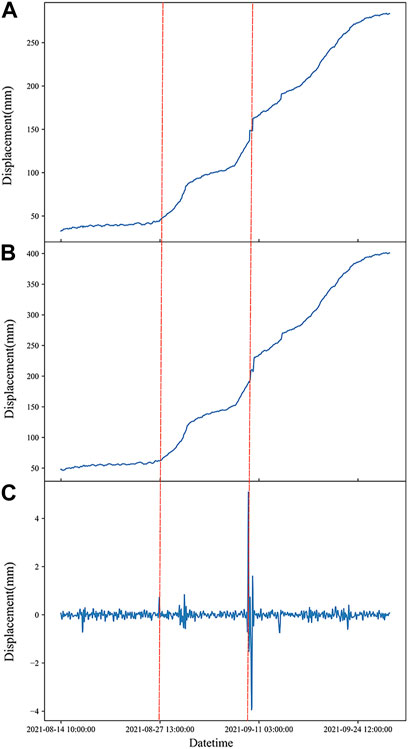
FIGURE 3. (A) Original signal of wavelet transform of landslide displacement in Qingshui River. (B) Low-frequency signal of wavelet transform of landslide displacement in Qingshui River. (C) High-frequency signal of wavelet transform of landslide displacement in Qingshui River.
After preprocessing the original displacement data using the cubic spline interpolation method, the wavelet transform is applied to extract both the high-frequency and low-frequency signals from the displacement data. The high-frequency signal fluctuation (red line) in Figure 3C serves as the dividing point for the uniform deformation phase. Subsequently, the exact time of the constant deformation phase in the original data is determined, enabling the calculation of the rate of change during this phase. Based on this, the qualitative description is expressed quantitatively, and the tangential angle is calculated for each time period. Statistical analysis is then conducted on the range of values for all the tangential angles. This helps reveal the distribution pattern of the improved tangential angle for the Qingshui River landslide displacement at different time intervals, as depicted in Figure 4A.
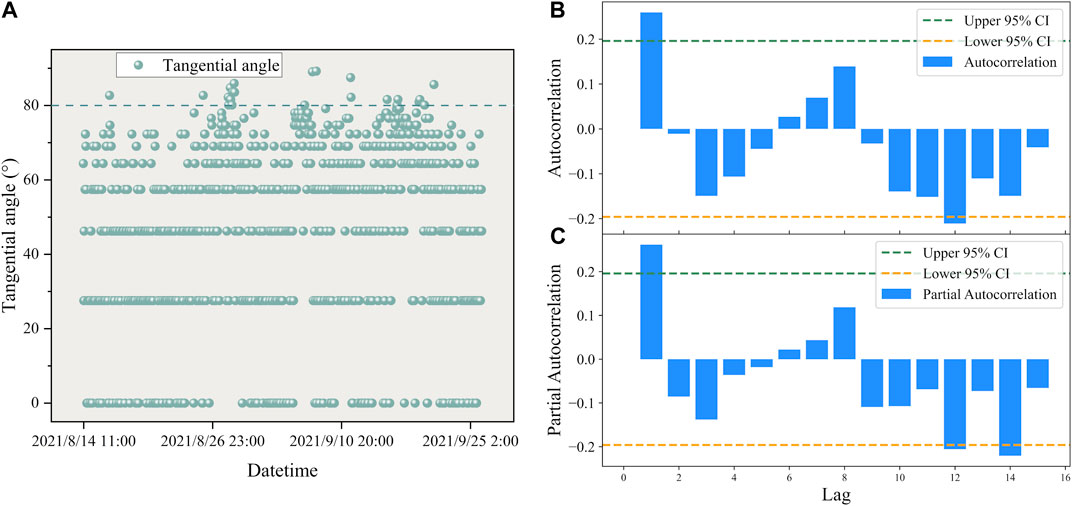
FIGURE 4. (A) The distribution of tangential angles with respect to time in the Qingshui River landslide. (B) ARIMA model autocorrelation plot of the Qingshui River landslide. (C) ARIMA model partial autocorrelation plot of the Qingshui River landslide.
From Figure 4A, it can be seen that the tangential angles of the deformation of the Qingshui River landslide in each time period are roughly distributed in the interval from 0° to 80°, indicating the initial deformation to the initial acceleration deformation stage of the landslide. This suggests that the Qingshui River landslide is currently relatively stable in deformation, making it suitable for prediction using the ARIMA model. A total of 100 displacement data points from 10:00:00 on 14 August 2021, to 13:00:00 on 18 August 2021, are taken as training samples for the model and inputted into the ARIMA model for modeling.
Figure 4B depicts the autocorrelation plot of the ARIMA model for the Qingshui River landslide. The autocorrelation function (ACF) is used to compute the correlation of the time series with itself, describing the degree of correlation between the current value of the series and its past values. Figure 4B includes the coefficients, upper and lower confidence limits. The horizontal axis represents the number of delays and the vertical axis represents the autocorrelation coefficient. The ACF plot is truncated at order q and the partial autocorrelation function (PACF) plot is trailing, and the ARMA model can be reduced to the MA(q) model. If both ACF and PACF plots are trailing, the most significant order (minimum) in PACF and ACF plots can be combined as p and q values. If the ACF and PACF plots are both truncated, a higher differential can be chosen, or the ARMA model is not suitable. Based on Figure 4B, the parameter q of this model is judged to be 1.
Figure 4C shows the partial autocorrelation plot, which uses the partial autocorrelation function (PACF) to find the correlation between the residuals and the next lag value, instead of the correlation between the lag and the current value as with the ACF plot. The PACF plot is truncated at order p, while the ACF plot is trailing, and the ARMA model can be reduced to an AR(P) model. If both the ACF and PACF plots are trailing, the most significant order (minimum) in the PACF and ACF plots can be combined as the p and q values. If both plots are truncated, a higher differential can be chosen or the ARMA model may not be suitable. According to Figure 4C, the present model parameter p is judged to be 1. Thus, the construction of this model is completed as ARIMA(1,1,1).
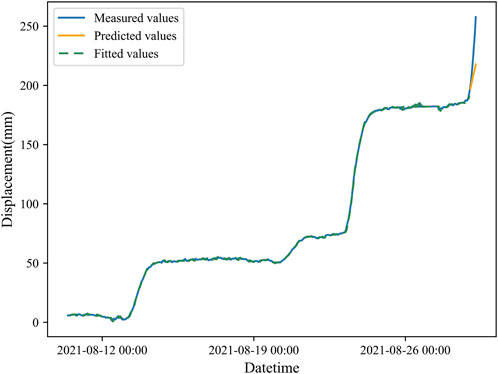
Using the constructed ARIMA(1,1,1) model, forecasts were made and plotted for the last 24 h of data, starting from the data at 14:00:00 on 18 August 2021, and the following results were obtained:
Figure 5A shows the fitting of the ARIMA(1,1,1) model to the displacement data of the Qingshui River landslide, along with the predicted values. The generated data are evaluated using model residuals, and the root mean square error (RMSE) and mean absolute percentage error (MAPE) are used as evaluation metrics. The residuals of the ARIMA model for the Qingshui River landslide are shown in Figures 5B, C, respectively.
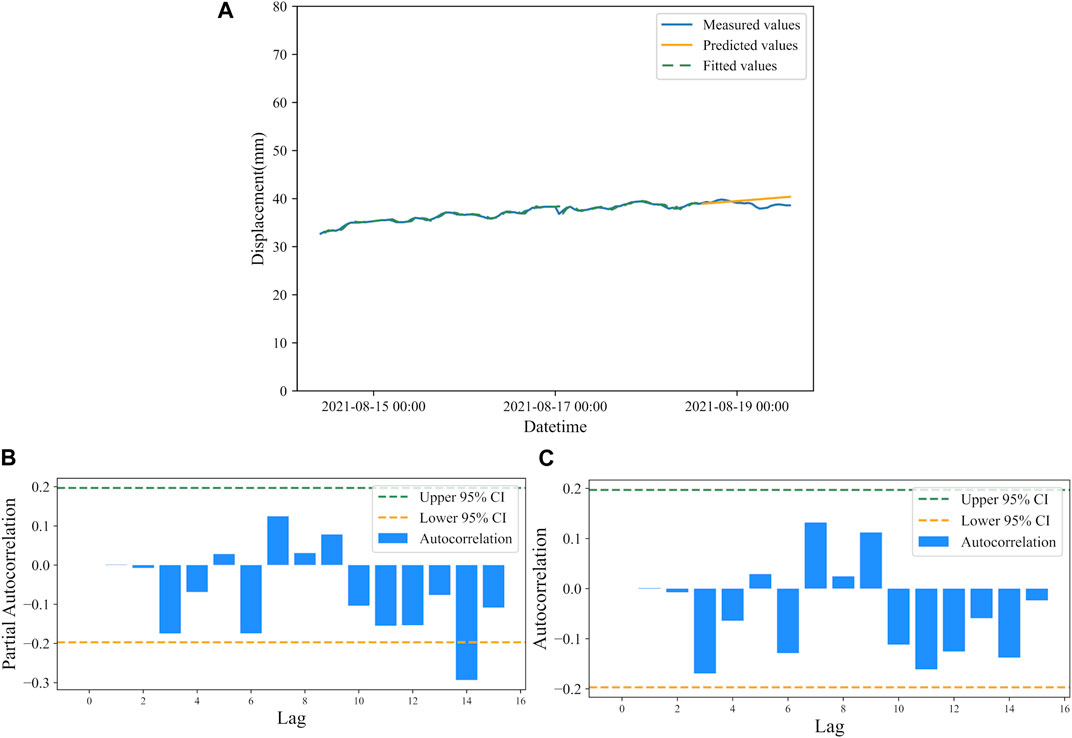
FIGURE 5. (A) Displacement prediction by ARIMA model of Qingshui River landslide. (B) Residual autocorrelation of ARIMA model for the Qingshui River landslide. (C) Residual partial autocorrelation of ARIMA model for the Qingshui River landslide.
If all the correlation coefficients fall within the dashed lines, then the autoregressive model (AR) and moving average model (MA) residuals are considered as white noise series. It is required for the time series that the model residuals are white noise series. In both plots, the residuals at the top order are mostly within the confidence interval, which is consistent with the white noise assumption.
According to the predicted results, RMSE is 4.52 mm and the MAPE is 2.39%. With an R2 value of 0.96, the model fits well. Based on the numerical distribution of the tangential angle of the Qingshui River landslide in different time periods, we conclude that the prediction of landslide deformation displacement is good for the distribution of tangential angles below 80°, which corresponds to the initial deformation to initial acceleration stage. The prediction error will gradually increase with the passage of time.
4.2 Validation of landslide displacement prediction laws
Utilizing the laws obtained from predicting the Qingshui River landslide, the ARIMA model was applied to forecast landslides in Guangna Township and Libian Gully, serving to validate the established applicable conditions.
The overall trend of the landslide in Guangna Township and the landslide in Libian Gully as well as the wavelet analysis are shown in Figure 6. From the overall trend shown in Figure 6D, the cumulative displacement of the landslide fluctuated to a certain extent on 13 August 2021 and 22 August 2021. The deformation of the landslide entered the accelerative deformation phase and returned to stability after a certain period of time. Finally, on 28 August 2021, a violent deformation occurred, indicating that the landslide destabilized. From the available data of the landslide cumulative displacement and warning information records, the warning time of the measuring cumulative displacement device at the landslide was 08:00:00 on 29 August 2021, when the accumulated displacement value was 286.4 mm and the warning level was 0. This study mainly focuses on the time before the occurrence of the landslide, and uses the ARIMA model to predict the cumulative displacement of the landslide to achieve the purpose of early warning. The first step is to extract the deformation characteristics of the displacement-time curve of the landslide in Libian Gully and the landslide in Guangna Township using the discrete wavelet transform.
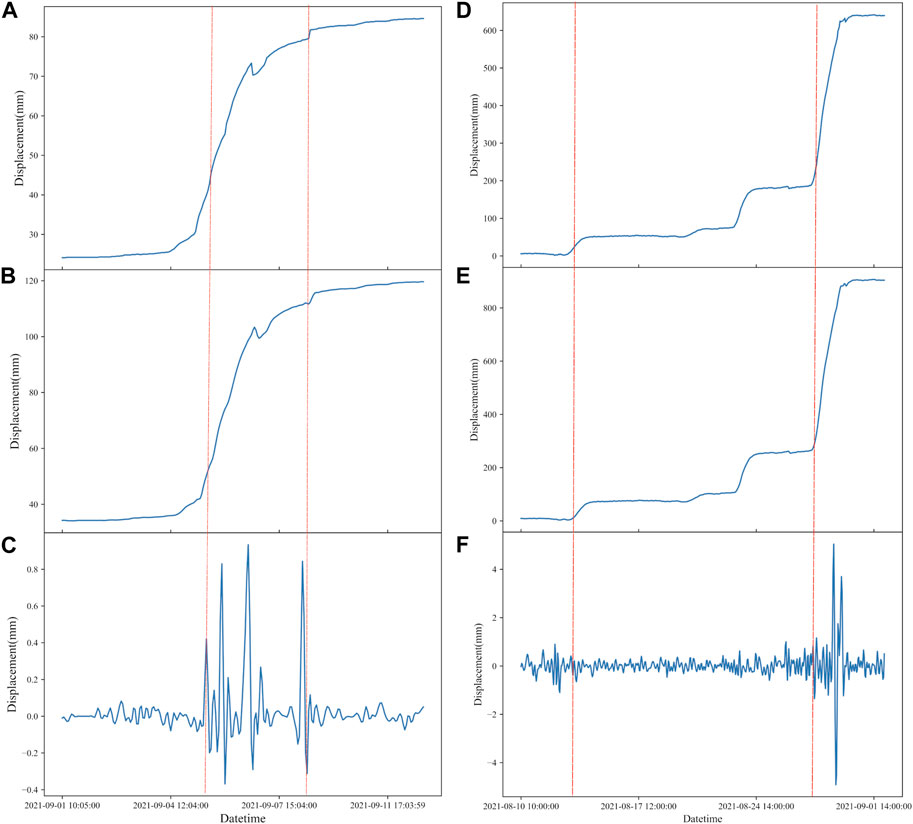
FIGURE 6. (A) Original signal of wavelet transform of landslide displacement in Guangna Township. (B) Low-frequency signal of wavelet transform of landslide displacement in Guangna Township. (C) High-frequency signal of wavelet transform of landslide displacement in Guangna Township. (D) Original signal of wavelet transform of landslide displacement in Libian Gully. (E) Low-frequency signal of wavelet transform of landslide displacement in Libian Gully. (F) High-frequency signal of wavelet transform of landslide displacement in Libian Gully.
After preprocessing the original displacement data using the cubic spline interpolation method, the wavelet transform is applied to extract both the high-frequency and low-frequency signals from the displacement data. The high-frequency signal fluctuation (red line) in Figures 6C, F serve as the dividing point for the uniform deformation phase of Guangna Township landslide and Libian Gully landslide. Subsequently, the exact time of the constant deformation phase in the original data is determined, enabling the calculation of the rate of change during this phase.
The tangential angle data for different time periods of displacement was calculated according to the constant deformation cut-off point of the time period at the red line. The training sample time period used to validate the predictions selected for the landslide in Guangna Township is from 19:05 on 2 September 2021 to 1:04 on 7 September 2021, and the distribution of the landslide tangential angle data for this time period is calculated as shown in Figure 7A. The training sample time period used to validate the predictions selected for the landslide in Libian Gully is from 10:00 on 10 August 2021 to 10:00 on 20 August 2021, and the distribution of the landslide tangential angle data for this time period is calculated as shown in Figure 8A.
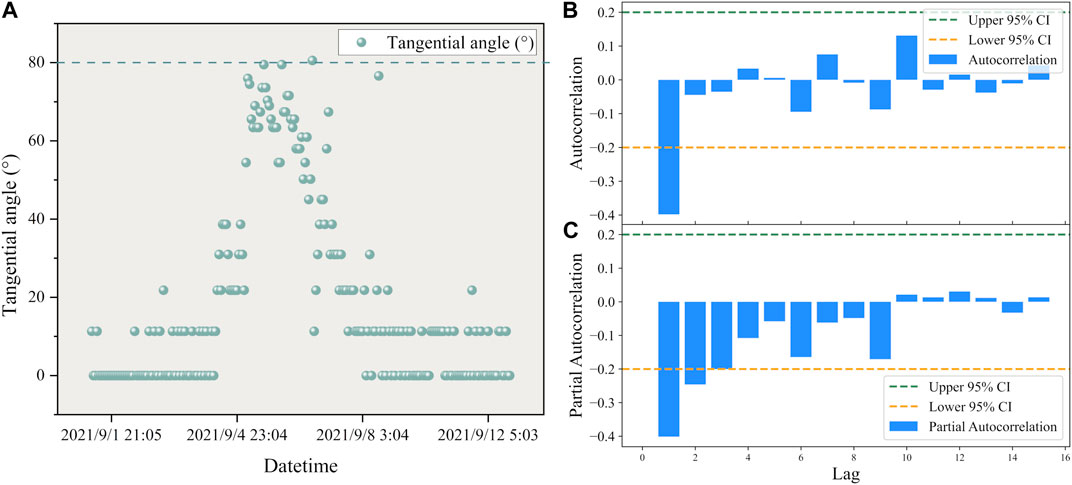
FIGURE 7. (A) The distribution of tangential angles with respect to time in the Guangna Township landslide. (B) ARIMA model autocorrelation plot of the Guangna Township landslide. (C) ARIMA model partial autocorrelation plot of the Guangna Township landslide.
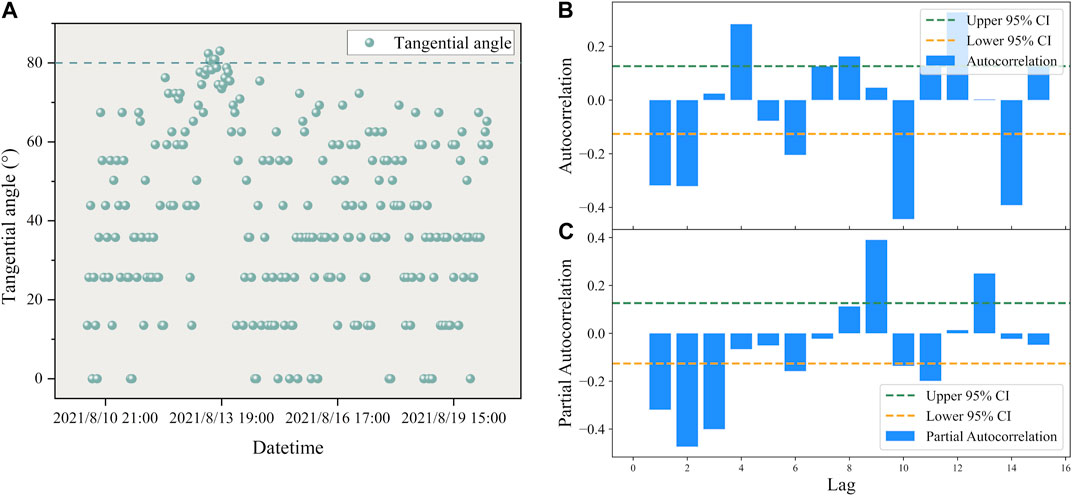
FIGURE 8. (A) The distribution of tangential angles with respect to time in the Libian Gully landslide. (B) ARIMA model autocorrelation plot of the Libian Gully landslide. (C) ARIMA model partial autocorrelation plot of the Libian Gully landslide.
From Figure 7A and Figure 8A, it can be observed that the tangential angles of the training samples from the Guangna Township and Libian Gully landslides are primarily distributed within the range of 0°–80°. This alignment with the previously mentioned condition indicates that the landslides are in the developmental stage between initial deformation and initial acceleration deformation. Subsequently, separate ARIMA models for displacement prediction were developed in the two study areas.
According to Figures 7B, C, and combined with parameter optimization theory, the ARIMA model established for landslide displacement prediction in Guangna Township is ARIMA(1,2,1). The model was also used to predict displacement data for a total of 24 time steps over 24 h, and the results are shown in Figure 9A, and the residuals of the ARIMA model for the Libian Gully landslide are shown in Figures 9B, C, respectively.
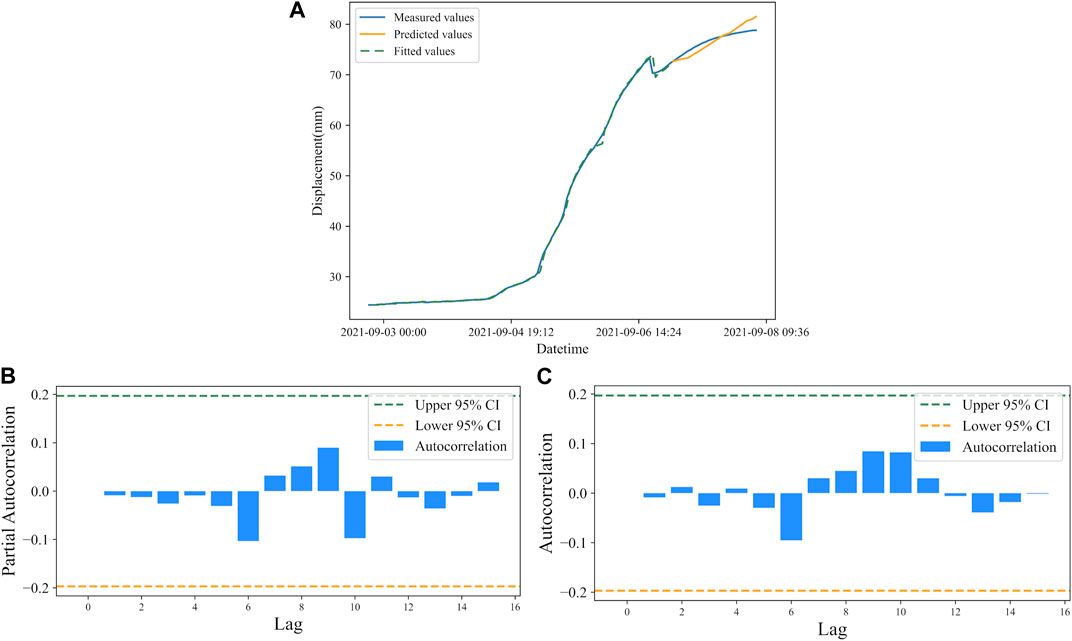
FIGURE 9. (A) Displacement prediction by ARIMA model of Guangna Township landslide. (B) Residual autocorrelation of ARIMA model for the Guangna Township landslide. (C) Residual partial autocorrelation of ARIMA model for the Guangna Township landslide.
According to the predicted results, the RMSE is 1.24 mm, and the MAPE is 1.34%. The error between the predicted and measured values of the model is small, the error float is small, and the R2 is 0.99, at the same time, the model residuals are all within the 95% confidence interval, indicating a good model fit.
According to Figures 8B, C, and combined with parameter optimization theory, the ARIMA model established for landslide displacement prediction in Libian Gully is ARIMA(3,2,2). The model was also used to predict displacement data for a total of 24 time steps over 24 h, and the results are shown in Figure 10A, and the residuals of the ARIMA model for the Libian Gully landslide are shown in Figures 10B, C, respectively.
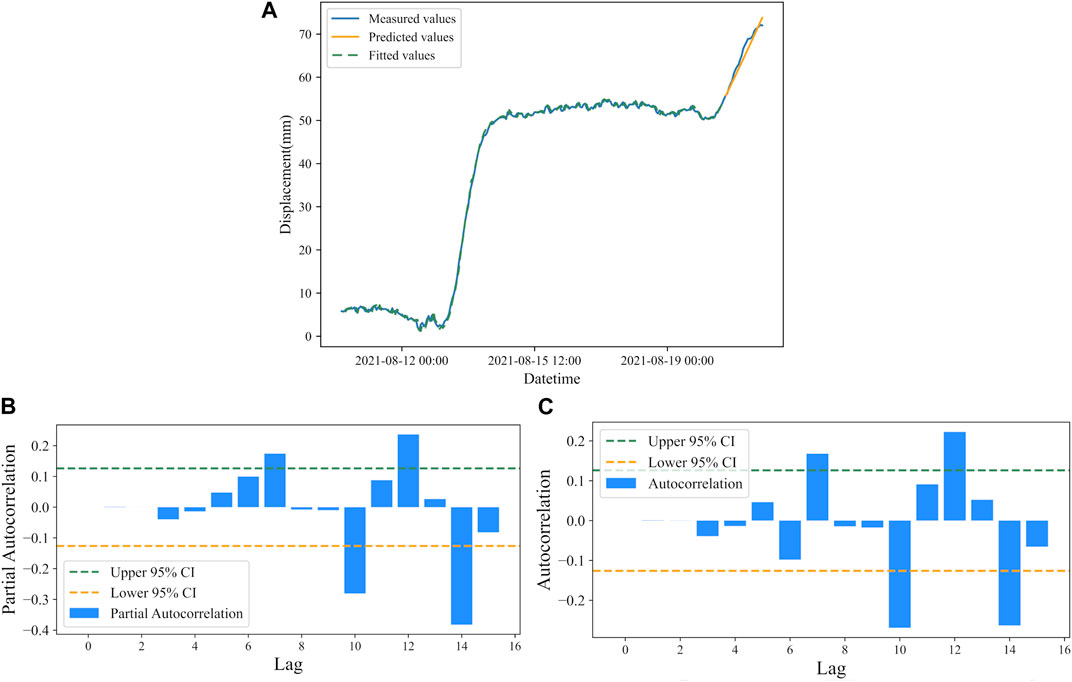
FIGURE 10. (A) Displacement prediction by ARIMA model of Libian Gully landslide. (B) Residual autocorrelation of ARIMA model for the Libian Gully landslide. (C) Residual partial autocorrelation of ARIMA model for the Libian Gully landslide.
According to the predicted results, The RMSE is 5.43 mm, and the MAPE is 1.67%. The error between the predicted and measured values of the model is small, the error float is small, and the R2 is 0.99, at the same time, the model residuals are all within the 95% confidence interval, indicating a good model fit.
Table 1 demonstrates the accuracy evaluation indexes of the ARIMA model for predicting three different landslides. The prediction accuracies of the landslide in Guangna Township and the landslide in Libian Gully verify the conclusion that the ARIMA model has high prediction accuracy in the interval from the initial deformation to the initial acceleration deformation stage (tangential angle less than 80°) of landslide deformation.

TABLE 1. Evaluation of the accuracy of ARIMA model for displacement prediction at three landslides Table.
4.3 Displacement prediction of landslides at high tangential angles
This study further explores the application of the ARIMA model in the acceleration stage and proslide stage (i.e., tangential angle of 80° and 85° or more, respectively) of landslide deformation, based on the Libian Gully landslide. A total of 422 time periods data from 10:00:00 on 10 August 2021 to 23:00:00 on 28 August 2021, in this test area were used as modeling data and predicted using the ARIMA(3,2,2) model. The prediction results are shown in Figure 11.
Figure 11 represents the raw data plot, model fitted values, and model predicted values of this time series model. The last point of the initial acceleration deformation was predicted by using the proximate moment of the landslide occurrence at 22:00:00 on 28 August 2021, with a cumulative displacement of 190.4 mm as the last point of the initial accelerated deformation. The displacement data will be predicted in hours h, from 23:00:00 on 28 August 2021, and the subsequent 7 h displacement data will be predicted and compared with the original data as follows:
From Table 2, it can be seen that the predicted landslide displacement data for the 7-h time period from 22:00:00 on 28 August 2021 has a tangential angle of 80–85° for the first 2 h (medium-term acceleration stage), and above 85° for 3–7 h (imminent sliding). In the medium-term acceleration stage of landslide deformation, i.e., from 1–2 h when the prediction starts, the predicted displacement values are all smaller than the actual measured values, and the relative error is within 3%. However, in the imminent sliding stage of landslide deformation, i.e., from 3 to 7 h, the displacement prediction values are all smaller than the actual measured values, but the relative error gradually increases, reaching 9.66% at the fifth hour and 15.51% at the seventh hour. This indicates that when the ARIMA model is used to predict the displacement values of the landslide in the imminent sliding stage, the relative error gradually increases with the increase of prediction time.
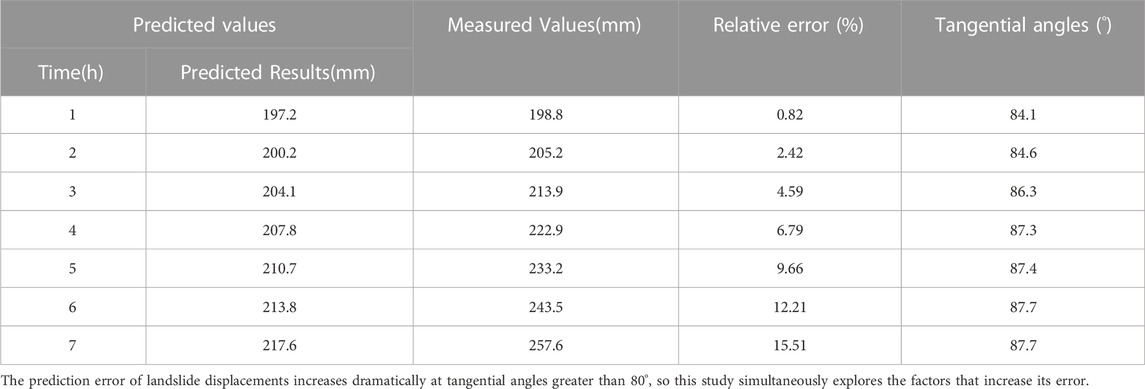
TABLE 2. Evaluation of displacement prediction accuracy in the medium-term acceleration and imminent sliding phases of the Libian Gully landslide.
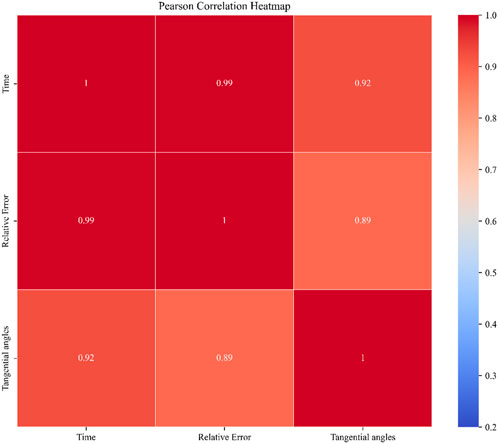
Figure 12 shows the Pearson Correlation Heatmap of the Libian Gully landslide for each variable at a tangential angle greater than 80°. This figure illustrates the relationship between the prediction step (Time), Relative Error, and Tangential angles, from which it can be seen that Tangential angles and Time are the main factors for the increase in Relative Error. It is hypothesized that this is due to the nonlinear mechanics of the landslide, which increases the prediction error dramatically.
5 Discussion
This study summarizes an applicable condition of the ARIMA model in the field of landslide displacement prediction. However, the results are mainly data-driven, and data acquisition is challenging and filled with uncertainty. The selection of training samples and the division of landslide deformation stages also pose difficulties due to changing sampling intervals. Moreover, in cases where the landslide tangential angle is greater than 80°, the prediction accuracy of the ARIMA model will rapidly decrease with an increase in the prediction step. This is due to the influence of the nonlinear mechanics of landslides (Liu et al., 2014). A combination model can be used to adjust the proportion of different models through weighting, thereby improving prediction accuracy and enhancing the model’s generalization ability (David et al., 2016). On the other hand, when the landslide tangential angle is less than 80°, the ARIMA model exhibits higher accuracy in predicting landslide displacement, which holds significant importance for the long-term prediction of landslide evolution stages.
6 Conclusion
In conclusion, this study has successfully identified an applicable condition for the use of the ARIMA model in predicting landslide displacement. The results demonstrate that the ARIMA model exhibits higher prediction accuracy when the landslide deformation is in the initial deformation to initial acceleration stage, characterized by tangential angles of displacement less than 80°. The predicted displacement values for 24-h intervals during this stage have been shown to yield a RMSE of 4.52 mm and a MAPE of 2.39%, indicating a high level of accuracy. This finding has been validated through predictions on different landslide instances, such as the cases of Guangna Township and Libian Gully, which yielded consistent results.
However, it is important to acknowledge the data-driven nature of these results, alongside the inherent challenges and uncertainties associated with data acquisition. The selection of training samples, the division of landslide deformation stages, and the influence of changing sampling intervals present obstacles that could impact the model’s accuracy. Furthermore, the study highlights that when the landslide tangential angle exceeds 80°, the accuracy of the ARIMA model diminishes significantly due to the influence of nonlinear mechanics inherent to landslides. To enhance prediction accuracy and generalize the model, future research could explore combination models that adjust the proportion of different models through weighting. This approach has been previously shown to improve predictive capabilities and overall model performance. Moreover, the study underscores the importance of the identified applicable condition for the long-term prediction of landslide evolution stages when tangential angles are below 80°.
Overall, this research not only contributes an empirically derived applicable condition for ARIMA model utilization in landslide displacement prediction but also sheds light on the challenges and potential directions for future enhancements in landslide prediction methodologies.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
ZW provided the ideas and framework for this study, including the methodology and theoretical studies presented in the paper, and wrote the paper. JT, SH, and YW conducted the initial reading and provided critiques of the first draft of the paper. AZ, JW, and WW assisted with data processing and analysis for the paper. SH, ZF, AL, and BH provided the test site and raw data, including the geographic location of the landslide, the geographic profile of the landslide, and sensor data, among others. All authors contributed to the article and approved the submitted version.
Funding
This work is supported by the Key R&D Program of the Ministry of Science and Technology of China, “Research and Development of Beidou Integrated System for Geological Disaster Monitoring and Early Warning in Complex Mountainous Areas” (2021YFC3000505).
Acknowledgments
Thanks to the China Institute of Geo-Environment Monitoring for providing the displacement data of the landslides in Libian Gully, Guangna Township and Qingshui River.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2023.1249743/full#supplementary-material
References
Aggarwal, A., Alshehri, M., Kumar, M., Alfarraj, O., Sharma, P., Pardasani, K. R. J. C., et al. (2020). Landslide data analysis using various time-series forecasting models. Comput. Electr. Eng. 88, 106858. doi:10.1016/j.compeleceng.2020.106858
Ahmed, B. J. L. (2021). The root causes of landslide vulnerability in Bangladesh. Landslides 18, 1707–1720. doi:10.1007/s10346-020-01606-0
Alimohammadlou, Y., Najafi, A., and Yalcin, A. J. C. (2013). Landslide process and impacts: A proposed classification method. Catena 104, 219–232. doi:10.1016/j.catena.2012.11.013
Allil, R., Lima, L. A. C., Allil, A. S., and Werneck, M. M. (2021). FBG-based inclinometer for landslide monitoring in tailings dams. Ieee Sensors J. 21, 16670–16680. doi:10.1109/jsen.2021.3081025
Anda, M., Purwanto, S., Suryani, E., Husnain and Muchtar, , and Muchtar, (2021). Pristine soil property and mineralogy as the strategic rehabilitation basis in post-earthquake-induced liquefaction, tsunami and landslide in Palu, Indonesia. Catena 203, 105345. doi:10.1016/j.catena.2021.105345
Bai, B., Jiang, S., Liu, L., Li, X., and Wu, H. (2021a). The transport of silica powders and lead ions under unsteady flow and variable injection concentrations. Powder Technol. 387, 22–30. doi:10.1016/j.powtec.2021.04.014
Bai, B., Zhou, R., Cai, G. Q., Hu, W., and Yang, G. C. (2021b). Coupled thermo-hydro-mechanical mechanism in view of the soil particle rearrangement of granular thermodynamics. Comput. Geotechnics 137, 104272. doi:10.1016/j.compgeo.2021.104272
Boyd, J., Chambers, J., Wilkinson, P., Peppa, M., Watlet, A., Kirkham, M., et al. (2021). A linked geomorphological and geophysical modelling methodology applied to an active landslide. Landslides 18, 2689–2704. doi:10.1007/s10346-021-01666-w
Calheiros, R. N., Masoumi, E., Ranjan, R., and Buyya, R. (2015). Workload prediction using ARIMA model and its impact on cloud applications' QoS. Ieee Trans. Cloud Comput. 3, 449–458. doi:10.1109/tcc.2014.2350475
Chen, Z., Huang, G., Xie, W., Zhang, Y., and Wang, L. (2023). GNSS real-time warning technology for expansive soil landslide-A case in ningming demonstration area. Remote Sens. 15, 2772. doi:10.3390/rs15112772
David, M., Ramahatana, F., Trombe, P.-J., and Lauret, P. J. S. E. (2016). Probabilistic forecasting of the solar irradiance with recursive ARMA and GARCH models. Sol. Energy 133, 55–72. doi:10.1016/j.solener.2016.03.064
Deng, Y., Yan, S. X., Scaringi, G., Liu, W., and He, S. M. (2020). An empirical power density-based friction law and its implications for coherent landslide mobility. Geophys. Res. Lett. 47. doi:10.1029/2020gl087581
Du, J., Yin, K. L., and Lacasse, S. (2013). Displacement prediction in colluvial landslides, three Gorges reservoir, China. Landslides 10, 203–218. doi:10.1007/s10346-012-0326-8
Fan, X. M., Xu, Q., Alonso-Rodriguez, A., Subramanian, S. S., Li, W. L., Zheng, G., et al. (2019a). Successive landsliding and damming of the jinsha river in eastern tibet, China: Prime investigation, early warning, and emergency response. Landslides 16, 1003–1020. doi:10.1007/s10346-019-01159-x
Fan, X. M., Xu, Q., Liu, J., Subramanian, S. S., He, C. Y., Zhu, X., et al. (2019b). Successful early warning and emergency response of a disastrous rockslide in Guizhou province, China. Landslides 16, 2445–2457. doi:10.1007/s10346-019-01269-6
Fayaz, M., Meraj, G., Khader, S. A., and Farooq, M. J. E. C. (2022). ARIMA and SPSS statistics based assessment of landslide occurrence in western Himalayas. Environ. Challenges 9, 100624. doi:10.1016/j.envc.2022.100624
Fu, L., Zhang, Q., Wang, T., Li, W., Xu, Q., and Ge, D. (2022). Detecting slow-moving landslides using InSAR phase-gradient stacking and deep-learning network. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.963322
Guzzetti, F., Gariano, S. L., Peruccacci, S., Brunetti, M. T., Marchesini, I., Rossi, M., et al. (2020). Geographical landslide early warning systems. Earth-Science Rev. 200, 102973. doi:10.1016/j.earscirev.2019.102973
Haque, U., Blum, P., Da Silva, P. F., Andersen, P., Pilz, J., Chalov, S. R., et al. (2016). Fatal landslides in europe. Landslides 13, 1545–1554. doi:10.1007/s10346-016-0689-3
Huang, C., Cao, Y., Zhou, L. J. C., and Mathematics, A. (2021). Application of optimized GM (1, 1) model based on EMD in landslide deformation prediction. Comput. Appl. Math. 40, 261–321. doi:10.1007/s40314-021-01658-5
Huang, F., Yin, K., Zhang, G., Gui, L., Yang, B., and Liu, L. (2016). Landslide displacement prediction using discrete wavelet transform and extreme learning machine based on chaos theory. Environ. Earth Sci. 75, 1376. doi:10.1007/s12665-016-6133-0
Huang, G. W., Wang, D., Du, Y., Zhang, Q., Bai, Z. W., and Wang, C. (2022). Deformation feature extraction for GNSS landslide monitoring series based on robust adaptive sliding-window algorithm. Front. Earth Sci. 10. doi:10.3389/feart.2022.884500
Jiang, S., Liu, H., Lian, M., Lu, C., Zhang, S., Li, J., et al. (2022). Rock slope displacement prediction based on multi-source information fusion and SSA-DELM model. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.982069
Ju, N. P., Huang, J., He, C. Y., Van Asch, T. W. J., Huang, R. Q., Fan, X. M., et al. (2020). Landslide early warning, case studies from Southwest China. Eng. Geol. 279, 105917. doi:10.1016/j.enggeo.2020.105917
Kavoura, K., Konstantopoulou, M., Depountis, N., and Sabatakakis, N. (2020). Slow-moving landslides: Kinematic analysis and movement evolution modeling. Environ. Earth Sci. 79, 130. doi:10.1007/s12665-020-8879-7
Khandelwal, I., Adhikari, R., and Verma, G. (2015). Time series forecasting using hybrid ARIMA and ANN models based on DWT decomposition. Procedia Comput. Sci. 48, 173–179. doi:10.1016/j.procs.2015.04.167
Kirschbaum, D. B., Adler, R., Hong, Y., Hill, S., and Lerner-Lam, A. (2010). A global landslide catalog for hazard applications: Method, results, and limitations. Nat. Hazards 52, 561–575. doi:10.1007/s11069-009-9401-4
Li, B. H., Liu, K., Wang, M., He, Q., Jiang, Z. Y., Zhu, W. H., et al. (2022). Global dynamic rainfall-induced landslide susceptibility mapping using machine learning. Remote Sens. 14, 5795. doi:10.3390/rs14225795
Li, C., Zhu, J., Wang, B., Jiang, Y., Liu, X., and Zeng, P. (2016). Critical deformation velocity of landslides in different deformation phases. Chin. J. Rock Mech. Eng. 35, 1407–1414. doi:10.13722/j.cnki.jrme.2015.1548
Li, H. J., Xu, Q., He, Y. S., and Deng, J. H. (2018). Prediction of landslide displacement with an ensemble-based extreme learning machine and copula models. Landslides 15, 2047–2059. doi:10.1007/s10346-018-1020-2
Li, Y. Y., Huang, J. S., Jiang, S. H., Huang, F. M., and Chang, Z. L. (2017). A web-based GPS system for displacement monitoring and failure mechanism analysis of reservoir landslide. Sci. Rep. 7, 17171. doi:10.1038/s41598-017-17507-7
Li, Y. Y., Sun, R. L., Yin, K. L., Xu, Y., Chai, B., and Xiao, L. L. (2019). Forecasting of landslide displacements using a chaos theory based wavelet analysis-Volterra filter model. Sci. Rep. 9, 19853. doi:10.1038/s41598-019-56405-y
Li, Z., Cheng, P., and Zheng, J. (2021). Prediction of time to slope failure based on a new model. Bull. Eng. Geol. Environ. 80, 5279–5291. doi:10.1007/s10064-021-02234-1
Lian, C., Zeng, Z. G., Yao, W., and Tang, H. M. (2014). Extreme learning machine for the displacement prediction of landslide under rainfall and reservoir level. Stoch. Environ. Res. Risk Assess. 28, 1957–1972. doi:10.1007/s00477-014-0875-6
Liu, K., Li, H., Li, Y., and Wang, J. (2019). Landslide distribution pattern in the Himalayan subduction zone based on Mw 7.8 earthquake in Nepal. Acta Geol. Sin. 93, 2666–2677. doi:10.3969/j.issn.0001-5717.2019.10.018
Liu, Y., Qin, Z. M., Hu, B. D., and Feng, S. (2018). State fusion entropy for continuous and site-specific analysis of landslide stability changing regularities. Nat. Hazards Earth Syst. Sci. 18, 1187–1199. doi:10.5194/nhess-18-1187-2018
Liu, Z., Shao, J., Xu, W., Chen, H., and Shi, C. (2014). Comparison on landslide nonlinear displacement analysis and prediction with computational intelligence approaches. Landslides 11, 889–896. doi:10.1007/s10346-013-0443-z
Luo, L., Pei, X., Zhong, C., Yang, Q., Fan, X., Zhu, L., et al. (2022). Multi-temporal landslide inventory-based statistical susceptibility modeling associated with the 2017 M-w 6.5 jiuzhaigou earthquake, sichuan, China. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.858635
Luo, W., Dou, J., Fu, Y., Wang, X., He, Y., Ma, H., et al. (2023). A novel hybrid LMD-ETS-TCN approach for predicting landslide displacement based on GPS time series analysis. Remote Sens. 15, 229. doi:10.3390/rs15010229
Manconi, A., and Giordan, D. (2015). Landslide early warning based on failure forecast models: The example of the Mt. de La saxe rockslide, northern Italy. Nat. Hazards Earth Syst. Sci. 15, 1639–1644. doi:10.5194/nhess-15-1639-2015
Miao, S., Hao, X., Guo, X., Wang, Z., and Liang, M. J. A. J. O. G. (2017). Displacement and landslide forecast based on an improved version of Saito’s method together with the Verhulst-Grey model. Arabian J. Geosciences 10, 53–10. doi:10.1007/s12517-017-2838-y
Niu, H. (2020). Smart safety early warning model of landslide geological hazard based on BP neural network. Saf. Sci. 123, 104572. doi:10.1016/j.ssci.2019.104572
Pecoraro, G., Calvello, M., and Piciullo, L. (2019). Monitoring strategies for local landslide early warning systems. Landslides 16, 213–231. doi:10.1007/s10346-018-1068-z
Prancevic, J. P., Lamb, M. P., Mcardell, B. W., Rickli, C., and Kirchner, J. W. (2020). Decreasing landslide erosion on steeper slopes in soil-mantled landscapes. Geophys. Res. Lett. 47. doi:10.1029/2020gl087505
Pranolo, A., Mao, Y. C., Wibawa, A. P., Utama, A. B. P., and Dwiyanto, F. A. (2022). Robust LSTM with tuned-PSO and bifold-attention mechanism for analyzing multivariate time-series. Ieee Access 10, 78423–78434. doi:10.1109/access.2022.3193643
Saito, M. (1969). Forecasting time of slope failure by tertiary creep. Proc. 7th Int. Conf on Soil Mechanics and Foundation Engineering. Mexico City: Citeseer, 677–683.
Singh, S., Raju, A., and Banerjee, S. (2022). Detecting slow-moving landslides in parts of darjeeling-Sikkim himalaya, NE India: Quantitative constraints from PSInSAR and its relation to the structural discontinuities. Landslides 19, 2347–2365. doi:10.1007/s10346-022-01900-z
Sun, M. C., Xu, W. Y., Wang, H. L., Meng, Q. X., Yan, L., and Xie, W. C. (2021). A novel hybrid intelligent prediction model for valley deformation: A case study in xiluodu reservoir region, China. Cmc-Computers Mater. Continua 66, 1057–1074. doi:10.32604/cmc.2020.012537
Tan, W., Wang, Y., Huang, P., Qi, Y., Xu, W., Li, C., et al. (2023). A method for predicting landslides based on micro-deformation monitoring radar data. Remote Sens. 15, 826. doi:10.3390/rs15030826
Wang, X., Li, G., Liu, Y., and Fu, K. (2017). Critical sliding prediction criterion of landslide based on constant deformation rate. Rock Soil Mech. 38, 3670–3679. doi:10.16285/j.rsm.2017.12.035
Wang, Y. K., Tang, H. M., Huang, J. S., Wen, T., Ma, J. W., and Zhang, J. R. (2022b). A comparative study of different machine learning methods for reservoir landslide displacement prediction. Eng. Geol. 298, 106544. doi:10.1016/j.enggeo.2022.106544
Wang, Y., Li, S., and Li, B. (2022a)., 14. Water, 3990. doi:10.3390/w14243990Deformation prediction of cihaxia landslide using InSAR and deep learning
Wu, Z., Deng, M., Chen, G., Liu, Y., Zhang, Q., Guo, L. J. M. S., et al. (2023). Developing a geological disaster monitoring system based on electrical prospecting. Meas. Sci. Technol. 34, 045902. doi:10.1088/1361-6501/aca990
Xu, F., Wang, Y., Du, J., and Ye, J. (2011). Study of displacement prediction model of landslide based on time series analysis. Chin. J. Rock Mech. Eng. 30, 746–751.
Xu, L., Qiao, X., Wu, C., Iqbal, J., and Dai, F. J. N. H. (2012). Causes of landslide recurrence in a loess platform with respect to hydrological processes. Nat. Hazards 64, 1657–1670. doi:10.1007/s11069-012-0326-y
Xu, Q., Tang, M., Xu, K., and Huang, X. (2008). Research on space-time evolution laws and early warning-prediction of landslides. Chin. J. Rock Mech. Eng. 27, 1104–1112. doi:10.13544/j.cnki.jeg.2020-025
Xu, Q., Zeng, Y., Qian, J., Wang, C., and He, C. (2009). Study on a improved tangential angle and the corresponding landslide pre-warning criteria. Geol. Bull. China 28, 501–505. doi:10.3969/j.issn.1671-2552.2009.04.011
Yan, Y., Guo, C., Zhang, Y., Zhang, X., Zheng, Y., Li, X., et al. (2021). Study of the deformation characteristics of the Xiongba ancient landslide based on SBAS-InSAR method,Tibet,China. Acta Geol. Sin. 95, 3556–3570. doi:10.3969/j.issn.0001-5717.2021.11.027
Yang, B. B., Yin, K. L., Lacasse, S., and Liu, Z. Q. (2019). Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 16, 677–694. doi:10.1007/s10346-018-01127-x
Yin, Z., Xu, Y., Chen, H., Sa, L., and Jiang, X. (2016). The development and distribution characteristics of geohazards induced by August 3,2014Ludian earthquake and comparison with jinggu and yingjiang earthquakes. Acta Geol. Sin. 90, 1086–1097. doi:10.3969/j.issn.0001-5717.2016.06.003
Zhang, Y. Q., Tang, H. M., Li, C. D., Lu, G. Y., Cai, Y., Zhang, J. R., et al. (2018). Design and testing of a flexible inclinometer probe for model tests of landslide deep displacement measurement. Sensors 18, 224. doi:10.3390/s18010224
Zhang, G. P. (2003). Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 50, 159–175. doi:10.1016/s0925-2312(01)00702-0
Zhang, S., Jiang, T., Pei, X., Huang, R., Xu, Q., Xie, Y., et al. (2022a). A new forecasting method for failure time of creep landslide based on nonlinear creep behavior and new pre-warning criterion. Front. Earth Sci. 10. doi:10.3389/feart.2022.1018432
Zhang, W. G., Liu, S. L., Wang, L. Q., Samui, P., Chwala, M., and He, Y. W. (2022b). Landslide susceptibility research combining qualitative analysis and quantitative evaluation: A case study of Yunyang county in chongqing, China. Forests 13, 1055. doi:10.3390/f13071055
Zhang, Y., Du, G., Guo, C., Li, X., Ren, S., and Wu, R. (2021). Research on typical geomechanical model of high-position landslides on the Sichuan-Tibet traffic corridor. Acta Geol. Sin. 95, 605–617. doi:10.3969/j.issn.0001-5717.2021.03.001
Zhang, Y. G., Tang, J., Cheng, Y. M., Huang, L., Guo, F., Yin, X. J., et al. (2022c). Prediction of landslide displacement with dynamic features using intelligent approaches. Int. J. Min. Sci. Technol. 32, 539–549. doi:10.1016/j.ijmst.2022.02.004
Keywords: ARIMA model, time series analysis, tangential angles, landslide displacement prediction, wavelet transform
Citation: Wang Z, Tang J, Hou S, Wang Y, Zhang A, Wang J, Wang W, Feng Z, Li A and Han B (2023) Landslide displacement prediction from on-site deformation data based on time series ARIMA model. Front. Environ. Sci. 11:1249743. doi: 10.3389/fenvs.2023.1249743
Received: 29 June 2023; Accepted: 21 August 2023;
Published: 04 September 2023.
Edited by:
Zhuo Chen, Sichuan Agricultural University, ChinaReviewed by:
Bing Bai, Beijing Jiaotong University, ChinaZhi Ding, Zhejiang University City College, China
Luqi Wang, Chongqing University, China
Copyright © 2023 Wang, Tang, Hou, Wang, Zhang, Wang, Wang, Feng, Li and Han. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jiakui Tang, amt0YW5nQHVjYXMuYWMuY24=; Shengshan Hou, aG91c2hlbmdzaGFuQG1haWwuY2dzLmdvdi5jbg==
 Zhao Wang
Zhao Wang Jiakui Tang1,2*
Jiakui Tang1,2*