- 1Institute of Mathematics, Khwaja Fareed University of Engineering & Information Technology, Rahim Yar Khan, Pakistan
- 2Center of Research, Faculty of Engineering, Future University in Egypt New Cairo, New Cairo, Egypt
Environmental pollution has become a major issue in today’s world, and controlling it is crucial for the sustainable development of our planet. Industries play a significant role in environmental pollution, and their impact must be controlled and minimized. In this paper, we present a novel approach, the complex intuitionistic fuzzy ELECTREE method (CIF–ELECTREE), for environmental impact assessment of industries. The method combines the principles of CIF sets and the ELECTREE method to provide a comprehensive and reliable assessment of the environmental impact of industries. The proposed method has been applied to real-world data, and the results obtained demonstrate the effectiveness of the CIF–ELECTREE method in controlling and reducing the environmental impact of industries. The results show that the CIF–ELECTREE method can provide a more accurate assessment of the environmental impact of industries compared to traditional methods. This study contributes to the existing literature by introducing a novel approach for environmental impact assessment and highlights the importance of considering both the uncertainty and vagueness in real-world data for reliable decision making.
1 Introduction
Multi-attribute and multi-criteria decision making plays a crucial role in everyday life as well as in many complex decision-making scenarios. These techniques are used to make informed decisions based on multiple objectives, criteria, and attributes, which helps in taking into account the trade-off between conflicting goals. For example, in personal life, multi-attribute decision making is often used when making choices such as buying a car, choosing a school, or purchasing a home. These decisions require weighing multiple factors such as cost, location, quality, and personal preferences, and therefore, multi-attribute decision making provides a useful framework for making such choices. In business and other organizations, multi-criteria decision making is frequently used in decision-making scenarios such as selecting suppliers, choosing a marketing strategy, or making investment decisions. These decisions often involve multiple objectives that must be considered, such as financial performance, customer satisfaction, and environmental impact. Despite the importance of multi-attribute and multi-criteria decision making, the process of making decisions based on multiple factors is often difficult due to the complexity of the data and the uncertainty surrounding the information. In many cases, the information used in decision making is incomplete, uncertain, and ambiguous, making it difficult to reach a reliable conclusion. Additionally, conflicting criteria and objectives can lead to trade-offs that are difficult to reconcile. To overcome these difficulties, the use of multi-attribute and multi-criteria decision making in the context of fuzzy set theory provides a useful framework for representing and handling uncertainty and ambiguity in decision-making problems. This allows for a more robust and informed decision-making process, taking into account the trade-off between conflicting objectives and criteria.
The process of making decisions is becoming more difficult as a consequence of the ambiguity that exists in the information, particularly when the data are accessible in a crisp form. In order to accomplish this goal, Zadeh invented the fuzzy set (Zadeh et al., 1996), and the philosophy behind fuzzy sets is an important consideration when it comes to making decisions in the face of ambiguity. He devised the membership grade as a defense mechanism against uncertainty. The development of mathematics has reached an all-time high thanks to fuzzy theory, since it is so useful in decision making. Many researchers work on fuzzy theory. For example, fuzzy theory has been used to improve digital mammography (Hassanien and Badr, 2003), play a big role in pharmacology (Sproule et al., 2002), create a system to help make decisions about nitrogen fertilizer (Yu et al., 2018), develop a system for risk assessment (Ebadi and Shahraki, 2010) and audit detection (Chang et al., 2008), and look at the social factors of migrant workers with HIV/AIDS (Kandasamy and Smarandache, 2004). The FSDEs (Jafari et al., 2021) are used in real-world systems such as those found in economics and finance, where the phenomena are tied to randomness and fuzziness as two separate forms of uncertainty. However, there are certain limitations to Zadeh’s fuzzy sets. For example, when there are more than two alternative values to address uncertainty, the method does not function well.
It has been found that intuitionistic fuzzy sets (IFSs), which were first introduced by Atanassov (1986), Atanassov (1989), and Atanassov (1999), are among the best higher-order fuzzy sets for dealing with ambiguity. In situations in which the information at hand is insufficient for the precise definition of an imprecise concept using a traditional fuzzy set, the idea of an IFS can be viewed as an alternative method for defining a fuzzy set. This can be performed by considering the concept of an IFS as an alternative approach to defining a fuzzy set. IFS theory may be thought of as a broader version of the original fuzzy set theory. Consequently, it is anticipated that IFSs might be used to imitate human decision-making processes and other tasks involving human experience and knowledge (Li, 1999; Li, 2003) which are inherently imprecise or unreliable. The idea of ambiguous sets was first described in the work of Gau and Buehrer (1993). Burillo and Bustince (Dengfeng and Chuntian, 2002; Xiao and Pedrycz, 2022) showed that the concepts of IFSs and ambiguous sets are synonymous with one another. Some operations on IFSs were defined by De et al. (2000). Szmidt and Kacprzyk (2000) studied the distances between IFSs. Szmidt and Kacprzyk (1996) and Szmidt and Kacprzyk (1997) considered the use of IFSs for building soft decision-making models with imprecise information. They proposed two solution concepts: the intuitionistic fuzzy core and the consensus winner for group decision making utilizing IFSs.
In terms of membership functions, making crisp sets into fuzzy sets is the same as making a set of integers into a set of real numbers. Changing the range of the membership function from {0, 1} to [0,1] is the same as changing I to R. Obviously, the development of numbers did not stop with the introduction of the real number system. In the past, we started with real numbers and then added complex numbers to their range. As a result, this modification might be the starting point for future work in fuzzy set theory. In the context of fuzzy set theory, a complex fuzzy set is the result of this kind of extension; it is a fuzzy set that differs from other fuzzy sets by having a membership function that accepts values in the complex number range. The theories that have been proposed by Ramot et al. have examined the decision-making problems that arise when using the fuzzy set and its generalizations, which can only deal with the ambiguity and uncertainty present in the data. These cannot account for the differences in data at a given moment. For this reason, Ramot et al. (2002) looked into the CFS, whereby the degree of membership is a complex integer that belongs to a unit disc on a complex plane. A complex fuzzy set (CFS) processes the data in a single set, which is just two dimensions deep. Despite the fact that Nguyen et al. (2000) were the ones to first propose a CFS, Ramot et al.’s conceptual space is more accommodating to decision makers. Over the last several years, the CFS has received a lot of research and media coverage. CFS operations (Zhang et al., 2009), power aggregation operators (Hu et al., 2019), and continuity of complex fuzzy operations (Hu et al., 2018) all had different operation features and distance measures. (Li and Chiang (2012) proposed a method through the use of CFSs for conducting the dual-output forecasting experiments (Xiao et al., 2022) with real-world financial time series, such as the Dow Jones Industrial Average, the Taiwan Stock Exchange Capitalization Weighted Stock Index, and the National Association of Securities Dealers Automated Quotation System.
In light of the significance of similarity measures (SMs), many researchers have recently opted for SMs based on the fuzzy set (FS) (Beg and Ashraf, 2009), CFS (Bi et al., 2019; Xiao, 2020a), and hesitant fuzzy set (HFS) (Xu and Xia, 2011). However, when a decision maker assigns membership grades in the form of groups, the complex values render the existing measures inadequate. In this work, the authors establish a complex intuitionistic fuzzy set (CIFS), a hybrid of the IFS and CFS , to deal with such problems while retaining the benefits of the SMs. Complex-valued membership degrees are presented in a polar form in CIFS theory. When a decision maker is presented with a set of data that only has two dimensions, all of the available theories, including the fuzzy set and CFS, perform admirably.
Benayoun et al. (1966) were the pioneers of the ELECTREE technique. The original inspiration for its core notions of concordance, discordance, and outranking was drawn from practical use cases. In addition, it uses concordance and discordance indices to examine the ordering of options. Energy (Beccali et al., 1998; Xiao, 2022), environment or water management (Ahrens and Kantelhardt, 2009), finance (Doumpos and Zopounidis, 2001), and decision analysis (Almeida, 2005; Xiao, 2020b) are just some of the domains where ELECTREE methodologies have been put to use. We have already shown that the ELECTREE technique, one of the most well-known outranking models, may be used to address the multi-criteria decision making (MCDM) issue. This approach is excellent because of its obvious logic, but it has been used in very little CIFS research. The ELECTREE technique involves contrasting potential solutions head-to-head in light of the decision maker’s own evaluations of the available options. Relationships of concordance, discordance, and superiority are of interest to this methodology. In this study, we provide a novel approach to using the ELECTREE technique in CIF systems, making it possible to solve MCDM issues there. People may use the CIFS to express uncertain scenarios in a decision-making dilemma, and its features are concerned with the degree of membership, the degree of complex membership, the degree of non-membership, the degree of complex non-membership grades, and the intuitionistic index all at once. In the ELECTREE assessment process, decision makers use CFS data with several values rather than a single value, and they are provided CFS data with multiple criteria to choose from.
The rest of the paper is organized as follows: In Section 2 we define some fundamental preliminaries, basic operations, and properties, and the construction of the CIF decision matrix is described. In Section 3, the proposed complex intuitionistic fuzzy ELECTREE method is described briefly along with the algorithm. In Section 4, the case study of the paper is discussed. Last, in Section 6, we discuss the paper’s final findings and conclusions.
2 Preliminaries
Definition 2.1. Suppose we have a finite universal set M such that M = {m1, m2, m3, …mn}; then, an IFS B in M is defined in the following form:
where the functions
Definition 2.2. A set C of the form given below defined upon M universal set is called as the CFS.
where
are the representation of the complex-valued certainty grade generally, which is subset of the unit disc in a complex plane having condition
Definition 2.3. A CIFS W defined on the universal set M is given as follows:
where
2.1 Some basic operations upon the intuitionistic fuzzy set and complex intuitionistic fuzzy set We considered
as the intuitionistic index of the member mk in the set M. This is the degree of indeterminacy membership of the element mk to the set M. It is sure that for each
The operations of the IFS (Atanassov, 1986; Atanassov, 1989; Atanassov, 1999) are given as follows. For every B, C ∈ A-IFS (M),
(1) B ⊂ C if
(2) B = C if B ⊂ C and C ⊂ B.
(3)
(4)
where
Definition 2.4. Let
(1)
(2) H ⊆ W if
(3) H = W if H ⊆ W and W ⊆ H.
(4)
(5) d(H, W) =
2.2 Construction of the complex intuitionistic fuzzy decision matrix
A decision matrix may be used to represent an MCDM problem in which each element represents the evaluation or value of the kth alternative
The decision makers assign a set of grades of importance,
such that
Starting at the beginning of the closed interval
3 ELECTREE methods based on complex intuitionistic fuzzy data
The CIF–ELECTREE technique (with the algorithm) and concordance and discordance sets are introduced in this section. For numerical examples, we will utilize the CIF–ELECTREE method algorithm. Binary outranking relations are used to simulate ELECTREE procedures; the connection is constructed by the decision maker and need not be transitive. Non-dominant alternative partial ordering is enabled by the connection. For each pair of alternatives x and
3.1 Discordance and concordance sets
The ideas of scoring function, accuracy function, and hesitant degree of the CIF value allow us to evaluate many alternatives to their CIF values. When two alternatives have the same score degree, the better option has a higher score degree or a higher accuracy degree. A greater accuracy degree denotes a lower hesitation degree, and a higher score degree denotes a bigger membership degree or a smaller non-membership degree. With the principles of the score function and accuracy function, we categorize various concordance sets as “concordance sets,” medium concordance sets,” and “weak concordance sets.” The discordance set, intermediate discordance set, and weak discordance set are further terms for the many sorts of discordance sets. The score function was developed by Chen and Tan (1994) to measure how well an option meets a decision maker’s needs. Suppose
where L = {l|l = 1, 2, 3, …, n}, a higher degree of accuracy translates to a lower degree of hesitation, a higher score translates to a higher CIF value, and Eq. 10 is more concordant than Eq. 11 or Eq. 12.The midrange concordance set
The hesitancy degree is the main distinction between Eq. 10 and Eq. 11; in the midrange concordance set, the hesitancy degree at the xth alternative with regard to the lth criterion is higher than at the yth alternative with respect to the lth criterion. Thus, Eq. 10 is more quadrant than Eq. 11.The least concordant set is given as follows:
Eq. 11 is more concordant than Eq. 12 because the degree of non-membership at the xth alternative with respect to the lth criteria in the weak concordance set Eq. 12 is greater than the degree of non-membership at the yth alternative with respect to the lth criteria.
The discordance set consists of all criteria where Gx is inferior to Gy. Using the aforementioned principles, the discordance set Bxy can be expressed as follows:
The middle discordant set is defined as follows:
Eq. 13 is more discordant than Eq. 14. The least discordant set is given as follows:
Eq. 14 is more discordant than Eq. 15.
We use the idea of discordant and concordant sets to compute matrices of concordant and discordant and the CIF–ELECTREE technique to calculate the aggregate dominance matrix. We then select the optimal option.
3.2 The complex intuitionistic fuzzy ELECTREE method
The CIF–ELECTREE technique is a combination of the CIFS and ELECTREE methods using evaluation data. The concordant index is a way to figure out the worth of the concordance set of the CIF–ELECTREE method. The concordance index is equal to the sum of the weights for the criteria and relationships in the concordance sets. So, for this paper, the concordance index
where
where the highest possible value of
A certain Gx has lower ratings than an alternative Gy. Here, we provide a formal definition of the discordance index:
where
Here is how we characterize
where
The way to figure out the concordance dominance matrix is based on the idea that the best choice is the one that is closest to the positive ideal solution. This is how the concordance dominance matrix
where
It means how far away each potential option is from the optimum answer. If
where
This describes how to distinguish each alternative from the negative optimum point. For Gx to be preferred over Gy,
The distance from both negative and positive optimal points can be used in the aggregate dominance matrix decision procedure to rank the many possibilities. The definition of the total dominance matrix
where
such that
and
where the best alternative is
The CIF–ELECTREE method is described here as a new MCDM method for making decisions. It combines the CIFS and ELECTREE techniques with assessment data. The algorithm for the suggested method will be built in three separate steps: evaluation, aggregation, and selection. In the assessment phase, decision makers use the CIFS to choose relevant criteria, recognize alternatives (with varying weights assigned to various criteria), and establish a decision matrix based on the assessed data. During the aggregation phase, we use the suggested method to build concordance and discordance dominance matrices by comparing each option to the others to confirm the dominance connection. After that, we calculate a matrix that represents the overall dominant structure. The CIF–ELECTREE technique is used during the selection phase to determine which option is the best and to rank the options in the order of preference.
Algorithm: The CIF–ELECTREE method’s algorithm and decision-making process may be summed up in the following eight phases:
Step (1). We can use evaluation data to build the choice matrix and include input from decision makers in the form of CIF values or comparisons between options. There are three substeps inside this larger phase.
(1) We can select the problem-specific criteria and non-inferior alternatives; various MCDM issues need different criteria. Most criteria may be classified as either subjective or objective. The decision makers find and take into account potential options.
(2) We can obtain a scorecard with relative weights for various factors to consider. With the help of Eq. 7,
(3) Decision makers gather cardinal information and use it to build an CIF decision matrix
Step (2). We can use the scoring function, the accuracy function, and the degree of hesitation of the CIF value to tell the difference between the different concordance and discordance sets. Using Eqs 10–15, we can obtain the chi-squared values Axy,
Step (3). We can determine the matrix
Step (4). Here is how to figure out matrix
Step (5). We can assemble the dominance matrix
Step (6). We can construct the dominant matrix
Step (7). The indices of the dominant matrices of concordance and discordance, defined in Eq. 24 and Eq. 25, respectively, are used to form the aggregate dominant matrix
Step (8). We can pick the optimal solution: the sum of the evaluation’s final values using Eq. 26 and Eq. 27. All possible options are ranked, and the one with the highest score is deemed the best.
4 Case study: the environmental impact of three industries
Introduction: This case study aims to compare the environmental impact of three industries: oil and gas, coal mining, and paper manufacturing. These industries have been selected as they are known to have a significant impact on the environment, and the study will focus on four common criteria: air pollution, water pollution, land degradation, and waste generation.
Oil and gas industry: The oil and gas industry is known to have a significant impact on air pollution, primarily due to the emissions from drilling and transportation. The burning of fossil fuels also contributes to the release of greenhouse gases, which contribute to climate change. In addition, oil spills and leaks can cause water pollution and damage to marine life. The industry also requires large amounts of water for extraction, which can put a strain on local water resources. However, the industry also creates jobs, income, and energy resources that are important for the human economy.
Coal mining industry: The coal mining industry is known to cause land degradation, as the process of extracting coal requires the removal of large areas of land, including forests and wildlife habitats. This can also lead to soil erosion and landslides. The burning of coal also contributes to air pollution and the release of greenhouse gases. The industry also generates large amounts of waste, including coal ash and slurry, which can contaminate water resources.
Paper manufacturing industry: The paper manufacturing industry generates large amounts of waste, including wood waste and chemical by-products. The industry also requires large amounts of water for production, which can put a strain on local water resources. The production of paper also contributes to air pollution, primarily due to the emissions from the burning of fossil fuels used in the production process. The industry also causes deforestation which is one of the major causes of land degradation and loss of biodiversity.
Conclusion: All three industries have a significant impact on the environment, with the oil and gas industry primarily affecting air pollution, the coal mining industry primarily affecting land degradation, and the paper manufacturing industry primarily affecting waste generation. It is important to note that the study is based on the common criteria only, and there are many other factors that should be considered when evaluating the environmental impact of an industry. It is important to find a balance between economic development and environmental protection and to implement sustainable practices in these industries to minimize their impact on the environment.
4.1 Numerical example
Phase (1):
(1) Taking expert advice into account, we consider the four criteria listed as follows: c1(air pollution), c2(water pollution), c3(land degradation), and c4(waste generation) in the problem. As an alternative, we consider the following industries: I1, I2, and I3.
(2) In the end, it is up to the specialists making the decisions to give each factor a subjective value
(3) The specialists making the decisions to give each factor a relative value
Given the CIVF decision-making matrix
Phase (2). Using the outcomes of Steps 1–3, we determine which sets exhibit concordance and which exhibit discordance.
The concordance set compiled using Eq. 10 is given as follows:
where in matrix Axy, the first element of A31 = (3, 3) present in the third (horizontal) row and first (vertical) column represents the simple membership concordant, and the second element represents the complex membership concordant. A11 = (−, −) is empty.
The midrange concordance set compiled using Eq. 11 is given as follows:
The weak concordance set compiled using Eq. 12 is given as follows:
The discordance set compiled using Eq. 13 is given as follows:
The midrange discordance set compiled using Eq. 14 is given as follows:
The least discordance set compiled using Eq. 15 is given as follows:
Phase (3). The concordance matrix
For example,
Phase (4). The disconcordance matrix
For example,
Phase (5). The dominant concordance matrix
Phase (6). The dominant discordance matrix
Phase (7). The aggregate dominant matrix
Phase (8). The best alternative using Step (8) is chosen as follows:
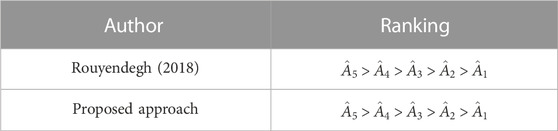
The optimized order of alternatives is given as
5 Comparison analysis
So far, we have compared the suggested technique to the intuitionistic ELECTREE method (Benayoun et al., 1966). We look at the five options
The relative weights of the criteria are given as
The intuitionistic fuzzy decision matrix
The concordance set compiled using Eq. 10 is given as follows:
The midrange concordance set compiled using Eq. 11 is given as follows:
The weak concordance set compiled using Eq. 12 is given as follows:
The discordance set compiled using Eq. 13 is given as follows:
The midrange discordance set compiled using Eq. 14 is given as follows:
The least discordance set compiled using Eq. 15 is given as follows:
The concordance matrix
The disconcordance matrix
The dominant concordance matrix
The dominant discordance matrix
The aggregate dominant matrix
The best alternative using Step (8) is chosen as follows:
The optimized order of alternatives is given as
Table 1 provides a comparison of the final assessments of the suggested approach to those of another technique.
6 Conclusion
In this study, we proposed a CIF–ELECTREE and TODIM method to evaluate the ranking of different alternatives discussed under the available criteria. In the proposed ELECTREE method, for the selection criteria of the optimum alternative, we use the relative weights of the criteria given by the decision makers to construct the discordant and discordant matrices. The complex intuitionistic concept of “fuzzy distance” is used to determine the distance of each point from the positive and negative optimum points. While the CIFS, which is made up of membership and non-membership functions represented by a set of possible values, is a new way to express human uncertainty in everyday life, in this paper, we also propose a new method, called the CIF–TODIM method, for solving MCDM problems with uncertain fuzzy information. The best thing about the CIF–TODIM method is that it can deal with decision-making problems in which CIFEs show how alternatives rank on each criterion while also taking into account how the decision makers (DMs) act psychologically. The proposed complex intuitionistic fuzzy ELECTREE and TODIM methods are effective in dealing with the issues of decision making in ambiguous and complex situations. The proposed approaches are effective as they allow for multi-attribute decision making with multiple criteria and also allow us to visualize the membership grades in dual dimensions (2D). In this study, CIF–ELECTREE and TODIM methods are used along with four criteria to figure out how different sectors affect the environment. In conclusion, the CIF–ELECTREE and TODIM methods have different strengths and can be used in different decision-making situations depending on the issue and the preferences of the person making the decision. However, in the future, researchers may use complex IFSs in fields as different as weather forecasting, fuzzy time series forecasting, and data analysis, in addition to studying how they might be used in MADM.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Ahrens, H., and Kantelhardt, J. (2009). Accounting for farmers’ production responses to environmental restrictions within landscape planning. Land Use Policy 26 (4), 925–934. doi:10.1016/j.landusepol.2008.11.003
Almeida, A. T. (2005). Multicriteria modelling of repair contract based on utility and ELECTRE I method with dependability and service quality criteria. Ann. Operations Res. 138, 113–126. doi:10.1007/s10479-005-2448-z
Atanassov, K. (1986). Intuitionistic fuzzy sets. fuzzy sets Syst. 20 (1), 87–96. doi:10.1016/s0165-0114(86)80034-3
Atanassov, K. T. (1999). Fuzzy sets and systems, intuitionistic fuzzy sets: Theory and applications. New York: Physica-Verlag, Heidel.
Atanassov, K. T. (1989). More on intuitionistic fuzzy sets. Fuzzy sets Syst. 33 (1), 37–45. doi:10.1016/0165-0114(89)90215-7
Beccali, M., Cellura, M., and Ardente, D. (1998). Decision making in planning: The ELECTRE multicriteria analysis approach compared to a FUZZY-SETS methodology. Energy Convers. Manag. 39 (16-18), 1869–1881. doi:10.1016/s0196-8904(98)00053-3
Beg, I., and Ashraf, S. (2009). Similarity measures for fuzzy sets. Appl. Comput. Math. 8 (2), 192–202.
Benayoun, R., Roy, B., and Sussman, B. (1966). Electre: Une m éthode pour guider le choix en présence de points de vue multiples. Note trav. 49, 2–120.
Bi, L., Zeng, Z., Hu, B., and Dai, S. (2019). Two classes of entropy measures for complex fuzzy sets. Mathematics 7 (1), 96. doi:10.3390/math7010096
Chang, S. I., Tsai, C.172.16.32.141F., Shih, D. H., and Hwang, C. L. (2008). The development of audit detection risk assessment system: Using the fuzzy theory and audit risk model. Expert Syst. Appl. 35 (3), 1053–1067. doi:10.1016/j.eswa.2007.08.057
Chen, S. M., and Tan, J. M. (1994). Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy sets Syst. 67 (2), 163–172. doi:10.1016/0165-0114(94)90084-1
De, S. K., Biswas, R., and Roy, A. R. (2000). Some operations on intuitionistic fuzzy sets. Fuzzy sets Syst. 114 (3), 477–484. doi:10.1016/s0165-0114(98)00191-2
Dengfeng, L., and Chuntian, C. (2002). New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions. Pattern Recognit. Lett. 23 (1-3), 221–225. doi:10.1016/s0167-8655(01)00110-6
Deschrijver, G., and Kerre, E. E. (2003). On the relationship between some extensions of fuzzy set theory. Fuzzy sets Syst. 133 (2), 227–235. doi:10.1016/s0165-0114(02)00127-6
Doumpos, M., and Zopounidis, C. (2001). Assessing financial risks using a multicriteria sorting procedure: The case of country risk assessment. Omega 29 (1), 97–109. doi:10.1016/s0305-0483(00)00028-1
Dubois, D., Gottwald, S., Hajek, P., Kacprzyk, J., and Prade, H. (2005). Terminological difficulties in fuzzy set theory—the case of “intuitionistic fuzzy sets”. Fuzzy sets Syst. 156 (3), 485–491. doi:10.1016/j.fss.2005.06.001
Ebadi, M. J., and Shahraki, M. S. (2010). Determination of scale elasticity in the existence of non-discretionary factors in performance analysis. Knowledge-Based Syst. 23 (5), 434–439. doi:10.1016/j.knosys.2010.02.005
Gau, W. L., and Buehrer, D. J. (1993). Vague sets. IEEE Trans. Syst. man, Cybern. 23 (2), 610–614. doi:10.1109/21.229476
Hassanien, A. E., and Badr, A. (2003). A comparative study on digital mamography enhancement algorithms based on fuzzy theory. Stud. Inf. control 12 (1), 21–32.
Hong, D. H., and Choi, C. H. (2000). Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy sets Syst. 114 (1), 103–113. doi:10.1016/s0165-0114(98)00271-1
Hu, B., Bi, L., and Dai, S. (2019). Complex fuzzy power aggregation operators. Math. problems Eng. 2019, 1–7. doi:10.1155/2019/9064385
Hu, B., Bi, L., Dai, S., and Li, S. (2018). Distances of complex fuzzy sets and continuity of complex fuzzy operations. J. Intelligent Fuzzy Syst. 35 (2), 2247–2255. doi:10.3233/jifs-172264
Jafari, H., Malinowski, M. T., and Ebadi, M. J. (2021). Fuzzy stochastic differential equations driven by fractional Brownian motion. Adv. Differ. Equations 2021 (1), 16–17. doi:10.1186/s13662-020-03181-z
Kandasamy, W. V., and Smarandache, F. (2004). Analysis of social aspects of migrant labourers living with HIV/AIDS using Fuzzy Theory and Neutrosophic Cognitive Maps. Hyderabad, Telangana: Infinite Study.
Li, C., and Chiang, T. W. (2012). Complex neurofuzzy ARIMA forecasting—A new approach using complex fuzzy sets. IEEE Trans. Fuzzy Syst. 21 (3), 567–584. doi:10.1109/tfuzz.2012.2226890
Li, D. F. (2003). Fuzzy multiobjective many-person decision makings and games. Beijing: National Defense Industry Press, 138–158.
Li, D. (1999). Fuzzy multiattribute decision-making models and methods with incomplete preference information. Fuzzy Sets Syst. 106 (2), 113–119. doi:10.1016/s0165-0114(97)00272-8
Montero, J., Gómez, D., and Bustince, H. (2007). On the relevance of some families of fuzzy sets. Fuzzy sets Syst. 158 (22), 2429–2442. doi:10.1016/j.fss.2007.04.021
Nguyen, H. T., Kandel, A., and Kreinovich, V. (2000). “Complex fuzzy sets: Towards new foundations,” in Ninth IEEE international conference on fuzzy systems. FUZZ-IEEE 2000 (cat. No. 00CH37063) (New Jersey, United States: IEEE), 2, 1045–1048.
Ramot, D., Milo, R., Friedman, M., and Kandel, A. (2002). Complex fuzzy sets. IEEE Trans. fuzzy Syst. 10 (2), 171–186. doi:10.1109/91.995119
Rouyendegh, B. D. (2018). The intuitionistic fuzzy ELECTRE model. Int. J. Manag. Sci. Eng. Manag. 13 (2), 139–145. doi:10.1080/17509653.2017.1349625
Sproule, B. A., Naranjo, C. A., and Türksen, I. B. (2002). Fuzzy pharmacology: Theory and applications. Trends Pharmacol. Sci. 23 (9), 412–417. doi:10.1016/s0165-6147(02)02055-2
Szmidt, E., and Kacprzyk, J. (2000). Distances between intuitionistic fuzzy sets. Fuzzy sets Syst. 114 (3), 505–518. doi:10.1016/s0165-0114(98)00244-9
Szmidt, E., and Kacprzyk, J. (1997). “Intuitionistic fuzzy sets for more realistic group decision making,” in International conference on transition to advanced market institutions and economies, Warsaw, 430–433.
Szmidt, E., and Kacprzyk, J. (1996). Some remarks on assigning weights to experts in multi-attribute group decision making using intuitionistic fuzzy sets. Notes IFS 2 (1), 43–51. doi:10.7546/nifs.2020.26.3.43-51
Xiao, F., Cao, Z., and Lin, C. T. (2022). “A complex weighted discounting multisource information fusion with its application in pattern classification IEEE Transactions on Knowledge and Data Engineering,” in IEEE transactions on knowledge and data engineering (New York: IEEE).
Xiao, F. (2022). Generalized quantum evidence theory. Appl. Intell., 1–16. doi:10.1007/s10489-022-04181-0
Xiao, F. (2020). Giq: A generalized intelligent quality-based approach for fusing multisource information. IEEE Trans. Fuzzy Syst. 29 (7), 2018–2031. doi:10.1109/tfuzz.2020.2991296
Xiao, F. (2020). On the maximum entropy negation of a complex-valued distribution. IEEE Trans. Fuzzy Syst. 29 (11), 3259–3269. doi:10.1109/tfuzz.2020.3016723
Xiao, F., and Pedrycz, W. (2022). Negation of the quantum mass function for multisource quantum information fusion with its application to pattern classification. IEEE Trans. Pattern Analysis Mach. Intell. 45 (2), 2054–2070. doi:10.1109/tpami.2022.3167045
Xu, Z., and Xia, M. (2011). Distance and similarity measures for hesitant fuzzy sets. Inf. Sci. 181 (11), 2128–2138. doi:10.1016/j.ins.2011.01.028
Yu, D., Xu, Z., and Wang, W. (2018). Bibliometric analysis of fuzzy theory research in China: A 30-year perspective. Knowledge-Based Syst. 141, 188–199. doi:10.1016/j.knosys.2017.11.018
Zadeh, L. A., Klir, G. J., and Yuan, B. (1996). Fuzzy sets, fuzzy logic, and fuzzy systems: Selected papers, 6. Singapore: World Scientific.
Keywords: complex intuitionistic fuzzy set, ELECTREE method, multi-attribute decision making, decision making, CIF–ELECTREE method
Citation: Ashraf S, Ali M, Sohail M and Eldin SM (2023) Assessing the environmental impact of industrial pollution using the complex intuitionistic fuzzy ELECTREE method: a case study of pollution control measures. Front. Environ. Sci. 11:1171701. doi: 10.3389/fenvs.2023.1171701
Received: 22 February 2023; Accepted: 03 May 2023;
Published: 18 May 2023.
Edited by:
Dragan Pamucar, University of Belgrade, SerbiaReviewed by:
Zhenkun Liu, Dongbei University of Finance and Economics, ChinaFuyuan Xiao, Chongqing University, China
Copyright © 2023 Ashraf, Ali, Sohail and Eldin. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Shahzaib Ashraf, c2hhaHphaWIuYXNocmFmQGtmdWVpdC5lZHUucGs=; Sayed M. Eldin, c2F5ZWQuZWxkaW4yMkBmdWUuZWR1LmVn
 Shahzaib Ashraf
Shahzaib Ashraf Mubashar Ali
Mubashar Ali Muhammad Sohail
Muhammad Sohail Sayed M. Eldin
Sayed M. Eldin