
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
REVIEW article
Front. Environ. Sci. , 28 November 2023
Sec. Soil Processes
Volume 11 - 2023 | https://doi.org/10.3389/fenvs.2023.1171194
This article is part of the Research Topic Early-Career Scientists’ Contributions to Soil Processes Research: 2022 View all 7 articles
Soils are increasingly acknowledged as complex systems, with potential non-linear behaviors having important implications for ecosystem and Earth system dynamics, but soil models could improve adoption of analytical tools from the broader interdisciplinary field of complex systems. First- and new-generation soil models formulate many soil pools using first-order decomposition, which tends to generate simpler yet numerous parameters. Systems or complexity theory, developed across various scientific and social fields, may help improve robustness of soil models, by offering consistent assumptions about system openness, potential dynamic instability and distance from commonly assumed stable equilibria, as well as new analytical tools for formulating more generalized model structures that reduce parameter space and yield a wider array of possible model outcomes, such as quickly shrinking carbon stocks with pulsing or lagged respiration. This paper builds on recent perspectives of soil modeling to ask how various soil functions can be better understood by applying a complex systems lens. We synthesized previous literature reviews with concepts from non-linear dynamical systems in theoretical ecology and soil sciences more broadly to identify areas for further study that may help improve the robustness of soil models under the uncertainty of human activities and management. Three broad dynamical concepts were highlighted: soil variable memory or state-dependence, oscillations, and tipping points with hysteresis. These themes represent possible dynamics resulting from existing observations, such as reversibility of organo-mineral associations, dynamic aggregate- and pore hierarchies, persistent wet-dry cycles, higher-order microbial community and predator-prey interactions, cumulative legacy land use history, and social management interactions and/or cooperation. We discuss how these aspects may contribute useful analytical tools, metrics, and frameworks that help integrate the uncertainties in future soil states, ranging from micro-to regional scales. Overall, this study highlights the potential benefits of incorporating spatial heterogeneity and dynamic instabilities into future model representations of whole soil processes, and contributes to the field as a modern synthetic review that connects existing similar ideas across disciplines and highlights their implications for future work and potential findings. Additionally, it advocates for transdisciplinary collaborations between natural and social scientists, extending research into anthropedology and biogeosociochemistry.
Soils represent the basis of recurring civilization (Montgomery, 2007; Nunes et al., 2020; Marris, 2022), and models depicting their structure and dynamics may help improve generalized understanding of their behavior and ecology. New generation models of soil nutrient cycles (Sulman et al., 2018; Zhang et al., 2021) certainly improve on older generation ones (Coleman and Jenkinson, 1996; Powlson et al., 1996; Berardi et al., 2020), adding foci on organic matter stabilization by mineral association that considers the efficiency of microbial degradation (Cotrufo et al., 2013), molecular and pool stochasticity (Sierra et al., 2018; Waring et al., 2020; Azizi-Rad et al., 2021), and increasingly large datasets (Todd-Brown et al., 2022). However, both handling large parameter spaces and making predictions across microbial to global scales remain difficult (Wieder et al., 2015; Vereecken et al., 2016), explaining common decisions to make design tradeoffs between model generality, or qualitative diversity of dynamical output and potential case applications, with numerical precision and realism at a particular scale (e.g., global) (Levins, 1966; Livingtson, 1985). Additionally, the increasing recognition of soil habitat structure for organic matter storage and stability (Cotrufo et al., 2013; Kravchenko A. N. et al., 2019; King, 2020), as well as for community assembly and biodiversity maintenance (Erktan et al., 2017; Charlotte et al., 2022; Schweizer, 2022; Vogel et al., 2022), highlights the potential utility of re-conceptualizing how the soil environment is modeled and formulated (Baveye, 2023). Given the breadth of services that soils offer, adopting modeling strategies that are transferable across soil ecology sub-disciplines (Buchkowski et al., 2017) indeed helps move toward addressing the most general of goals in soil ecology, such as how soil biotic and abiotic spheres or networks interact over time to confer bulk soil properties. Fortunately, an old yet increasingly studied field of complex systems focuses on gaining generalized insights from large multi-component systems, from social and neural networks (Marder and Calabrese, 1996) to oscillating chemical reactions (Epstein et al., 1983; Pacault et al., 1987; Epstein and Showalter, 1996), that offer potentially useful analytical perspectives and strategies for generalizing about how heterogeneous soil environments can behave. This synthesis builds on previous efforts to highlight how soil ecology may benefit from integrating tools and concepts from complex systems (Baveye et al., 2000; Young and Crawford, 2004; Lavelle et al., 2016; Pachepsky and Hill, 2017; Bennett et al., 2019), elaborating on how specific modeling principles may help gain insight into a variety of soil processes in more generalized ways.
Early studies of complex systems tended to include explicitly recognized spatial extent and/or separation among modules (Turing, 1952; Levins, 1969; Mandelbrot, 1983), and others recognized explicit state-dependence or time lags (Rutherford and Do, 1997). Mathematical roots of systems and complexity theory built upon nonlinear dynamics (Lorenz, 1963; Winfree and Strogatz, 1984) and chaos theory (May, 1974; Li and Yorke, 1975; Rogers et al., 2022), which was facilitated by computational technologies allowing simulation. In soil science, early reports on fractal dimensions of particle size distributions also represent narratives working toward scale-invariant descriptions of the physical habitat (Young and Crawford, 1991; Kravchenko et al., 1999), though fractal methods can also be useful in describing non-physical domains. Given how large and complicated some systems can be, analytical research questions have tended to switch focus from valuing the precision of model predictive ability to its generality (Levins, 1966), or how consistent a result is across example systems. This strategy of finding intersecting truths across case studies is already somewhat familiar to research in the form of useful reviews, meta-analyses, and model comparison projects (Sulman et al., 2018), but it can also take a more computational form. More useful analysis metrics for complex models with variable outputs tend to shift from distribution centrality (e.g., median, mean) to variance and/or key single exponents in cases of high skewness. Accordingly, research questions about similar complex systems also benefit in switching from precise future values to the probability of certain types of events occurring at any future time or location, depending on input data. Focusing on variance as output also promotes including realistic inherent variation or randomness as input, known as stochasticity, which has been a necessary part of explaining and reproducing natural time series of experimental populations (Henson et al., 2001). Embracing and allowing for variability in time series also offers the potential to predict and observe temporal autocorrelation in anticipation of critical transitions of tipping points (Scheffer et al., 2012), such as during accelerated soil degradation or restoration, or naturally unpredictable chaotic fluctuations with predictable bounds (Schaffer and Kot, 1985; Hastings et al., 1993), such as in response to human drivers (Berryman and Millstein, 1989).
Key examples across fields of study have become increasingly emblematic of complex systems theory. For example, in geophysics, measuring irregular structures in nature using relative units instead of absolute ones (Mandelbrot, 1983) has widely uncovered power law frequencies of system components sub-sets, famously used in geophysics to study regional earthquake magnitudes (Bak et al., 2002; Christensen et al., 2002). This tool from the fractal geometry branch of mathematics was later applied to ecology, both implicitly (Macarthur and Wilson, 1963) and explicitly (Harte, 1999; Ostling, 2000), as well as to soil structure, including aggregation and porosity, with implications for predator-prey (i.e., invertebrate-microbe) interactions (Baveye et al., 2000). Although current applications of nonlinear dynamical systems principles to soils remain somewhat siloed in geophysics, potential applications to soil ecology remain. Another exemplary analysis tool is re-framing focal metrics from distribution centrality to variance measures, as mentioned above. This shift has advanced understanding of consistent spatial and temporal fluctuations (Taylor, 1961) to focus on sub-module synchronization potential, notably formulated as coupled pendulum dynamics in physics (Kuramoto, 1984), and has recently inspired various applications in ecology, including to predator-prey dynamics on interaction networks (Vandermeer, 2021), dispersal shifts across urban agricultural landscapes (Ong et al., 2020), and to biodiversity collapse broadly. These analytical methods tend to uncover internal consistencies or rules among heterogeneous components that predict relatively new patterns at the whole system level, advancing the specific goal of using theory to advance hypothesis testing, compared to other assumed goals like precision forecasting.
In ecology generally, there appears to be a consensus that micro- and meso-habitats are complex, and indeed natural soil systems are regarded as the most complex habitats we know of. Yet formal modeling frameworks remain relatively simplified, in part due to common statistical limitations and disciplinary influences. For example, Michaelis-Menten kinetics generated a strong biochemical influence on representing soil organic carbon cycling and decomposition, which has over time been modified to be “reversed” to focus on total enzyme production rather than individual catalysis (Schimel and Bennett, 2004), and has maintained wide use as a core model structure for fine-scale carbon and nutrient transformations. This was even applied to population ecology (Volterra, 1928), where population growth equations analogous to enzyme kinetics have been well analyzed to yield technically unstable but noticeably consistent oscillatory dynamics, also observable in soil data empirically (Reijneveld, 2013; Kuzyakov and Zamanian, 2019) and modeled (Wang et al., 2014). Other modeling approaches can also yield counter-intuitive results, which may contradict existing empirical data, or pre-date supporting data from future long-term studies. One case of this was the incorporation of adaptive or environmentally-responsive (i.e., non-linear) enzyme production, also interpretable as emphasizing a positive biological feedback based on phenotypic plasticity, and formulated as a flux- or interaction modification (Ludington, 2022). This early modeling study (Schimel and Weintraub, 2003) predicted, in part contrasting contemporary evidence supporting decomposition as primarily nitrogen-limited while aligning with others, that nitrogen additions to soil would suppress rather than stimulate decomposition, a result that preceded future validating evidence of this from longer-term nitrogen fertilization studies. In this case, a key multiplicative (i.e., non-linear) model term associating organic matter decay with both its current pool size (first-order decay) and also a dynamically-responsive enzyme pool, ultimately improved model generality, specifically across time scales from minutes when proteins turnover to multiple years and seasons. More recently, traditional enzyme kinetic formulations have been generalized to allow multiple enzyme and substrate types (Tang and Riley, 2013), facilitating subsequent tests of scale with bottom-up spatially explicit agent-based models (Allison, 2012; Wang et al., 2019). More broadly, mathematical ecology has provided very interesting insights based on linear stability analysis tools to focus analyses (King and Schaffer, 1999), but recent pursuits have expanded to include what was otherwise considered unstable outcomes, like transient dynamics (Hastings, 2004; Hastings et al., 2018) with implications for introduced species establishment (Armstrong and McGehee, 1976; McGehee and Armstrong, 1977; Wilson and Abrams, 2005; Xiao and Fussmann, 2013). These approaches indeed provided new insight on consistently observable patterns, based on the increasing use and acceptance of graphical analytical methods like cobwebbing following the rise of personal computing and simulation power. Recently, comparable tools and concepts from community ecology have been synthetically presented to potentially help address questions in soil carbon cycling and soil community ecology (Buchkowski et al., 2017).
Accordingly, this perspective now draws from theoretical ecology to further extend recent efforts to integrate complex systems principles into soil sciences (Baveye et al., 2000; Young and Crawford, 2004; Sierra and Müller, 2015; Lavelle et al., 2016; Buchkowski et al., 2017; Pachepsky and Hill, 2017; Bennett et al., 2019), and thereby generalize our understanding of the soil habitat, from micro-to macro-scales, notably embracing persistent variation and heterogeneity as notably critical to fundamental soil processes (O’Leary et al., 2018). The intended audience of this paper is broadly soil scientists and biogeochemists, written from the perspective of mathematical and complexity theoretical ecologists with domain knowledge of soil ecology. The purpose of this paper is two-fold, to: 1) highlight ideas in soil ecology that we believe warrant further exploration and integration in soil models, and 2) discuss some ways (non-exhaustively) that nonlinear soil models can move the field forward. This paper contributes to the field as a modern synthetic review that connects existing similar ideas across disciplines and highlights their implications for future work and potential findings. Specifically, this paper includes non-exhaustive discussion of various aspects of soil research that may benefit from integrating perspectives from other complex systems research: including memory, oscillations, tipping points and hysteresis. Relevant supporting phenomena observed in soils include reversible organo-mineral associations, aggregate- and pore hierarchy and dynamics, persistent wet-dry cycles, multi-year gas fluxes (e.g., respiration) and nutrient availability, higher-order microbial community and predator-prey interactions, and cumulative legacy land use history. Overall, adopting tools from systems and complexity theory primarily offers ways of reducing model structural uncertainties (Bradford et al., 2016), thereby also potentially facilitating model-data integration efforts, for example, by reducing parameter space (Bennett et al., 2019; Migliavacca et al., 2021). Addressing model structural variation and uncertainty represents a fundamental branch of research in mathematical ecology that analogously serves as higher level robustness analysis, offering novel insights into results that are relatively universal vs dependent on formulation details (Weisberg, 2007).
The concept of memory represents a form of self-referential dynamics specifically based on an event occurring at least one time step in the past, also referred to as time lags, which in some real systems can result in hierarchical structures. An example from the field of physics is nuclear fusion, in which heavier atoms with more protons are made not by the instant fusion of many lighter atoms, but the simpler merging of few medium atoms previously built, interestingly, also with an apparent critical drop in stability at higher atomic numbers after iron (Pfützner et al., 2012). This shows not only a hierarchical building process resulting from the dependence of the existence of larger nuclei on past states (i.e., previously formed smaller nuclei), but this also shows related consequences, namely, a skewed distribution of nuclear stability across the spectrum of existing nucleus sizes, where the nuclei of smaller atoms are more tightly bound together than larger ones.
Highly skewed or long-tailed distributions, like the power law family, based on component or module attributes like cluster size, are increasingly recognized as (Gillespie, 2015) properties of complex systems (Clauset et al., 2009; Locey and Lennon, 2016). This contrasts the normal “bell curve” distribution, which is often assumed for classic statistical procedures, from simple averages to within-group variance during linear regression. As a result, observing power laws in data has served as initial support for hypothesizing hierarchical or self-organizing processes, offering a novel path to infer process from pattern. Although various underlying processes can yield similar distributions (Bashkirov and Vityazev, 2000; Curado et al., 2018), observing non-normal distributions may at least help de-emphasize selection-like mechanisms that tend to produce bell curves.
Somewhat surprisingly, the nuclear fusion example parallels soil aggregation almost exactly, where larger aggregates tend to be weaker and less structurally stable than smaller aggregates. In this case soil aggregation is in part affected by the amount of surface area allotted to binding agents, as well as the strengths of the various binding agents themselves, ranging from fine-scale organo-mineral associations to fungal mycelial networks (Tisdall and Oades, 1982). Ultimately, this can be tied back to early discussions of fractal dimension parameters of power law distributions observed in porous media and landscsapes (Burrough, 1981), which simultaneously converged with empirical support for soil aggregation as a hierarchical processes (Tisdall and Oades, 1982), and later exploration (Nortcliff, 1984; Armstrong, 1986; Tyler and Wheatcraft, 1989; Perrier et al., 1996; Assouline et al., 1998). As a result, while perhaps controversial (Baveye et al., 2000; Pachepsky and Hill, 2017), one approach for theoreticians and modelers may be to further attempt the study of simple models (Vitousek et al., 2022) to explore ideas and test underlying hypotheses about the implications of hierarchical structural dynamics for soil properties (Stamati et al., 2013). This may be especially important for processes that remain near impossible to measure empirically (Bennett et al., 2019). Some studies seem to align with this process-based modeling focus (Waring et al., 2020), while others tend to prioritize more output precision after long-term simulation (Coleman and Jenkinson, 1996; Powlson et al., 1996; Cong et al., 2014). Additionally, there is also supporting evidence for various hierarchical processes in soils, including those underlying clay flocculation (Brostow et al., 2007; Cuthbertson et al., 2018), aggregation of solids (Tisdall and Oades, 1982) (mentioned above) as a result of physical mixing (Klaminder et al., 2013) and fungal enmeshment (Rillig and Mummey, 2006) amplified by wet-dry cycles (Denef et al., 2001; Wang et al., 2023), and for pore cluster networks (Quigley and Kravchenko, 2022; Vogel et al., 2022), all of which represent interesting modules of the soil environment to explore with hypotheses about hierarchical structural dynamics and their implications. Specifically, hierarchical aggregation has been previously analyzed by binning all aggregates into either micro- or macroaggregate functional groups, a fractionation that has served as a basic structure for some models specific to solid aggregation (Segoli et al., 2013; Stamati et al., 2013), though it may also be relevant for other soil models, such as ones specific to greenhouse gas production (Kravchenko A. et al., 2019; Wang et al., 2019) or microbial diversity.
Overall, these hierarchical patterns emerging from system-wide memory (i.e., past state-dependence) tend to generally reflect natural solutions for coarser level system limitations. Endogenous solutions to system limits can in some cases be formulated and analyzed as an issue of optimizing information flow (Czaplicka et al., 2013). If applied to modeling soil pore dynamics, for example, this general mechanism or principle could help explain empirical soil pore structure data specifically as a single naturally-resulting geometric solution (stable or temporary/unstable) for a set of constraints. Biological constraints might be microbial cross-feeding rates fueled by metabolite-carrying water flowing through pore networks. Physical constraints could be spatial, such as topsoil depth, and/or temporal, such as growing season length, both of which would affect pore-forming processes including microbial secretions and gas exchange (micro-pores) and invertebrate burrowing activity (macro-pores). Importantly, real soils also have historical constraints, which state where pores have been and intuitively predict where new ones can potentially form, which ultimately holistically frames pore network structures as ongoing solutions, with varying robustness, for both past and present ecological activity. Similarly, hierarchical aggregation of solids may also elongate the effects of environmental changes enough to minimize compositional variance of microbial communities living in the smallest habitat pockets (Rillig et al., 2017; Wilpiszeski et al., 2019). System memory, in the form of iterative structural dynamics, can also be environmentally adaptive, such as when system components are dynamic or continuously dismantled and re-assembled into new yet familiar structures, which range in scope from soil micro-habitats to landscape profiles over months and years. Fine-scale positive feedbacks may help explain the diversity of soil profiles and pedons across and within order-level taxonomic soil classifications (Jenny, 1961; Phillips, 2017). In addition to hierarchies, soil systems’ internal or temporal memory can also be a regular source of heterogeneity that increases uncertainty about how soil behaves. In soils, this hypothesis of increasing heterogeneity along hierarchical trajectories could, for example, predict greater variance in diversity or simply beta diversity among microbial communities observed in macro-aggregates compared to those among micro-aggregates. However, there remains little evidence addressing this topic, although technological advances may facilitate future studies (Bailey et al., 2012).
Studying subsoils and soil depth also represents an axis that integrates soil profile memory and time lags. Often only topsoils (e.g., to 10 or 20 cm depth) are studied due to high nutrient concentrations there, yet subsoil horizons store more total carbon (Hicks Pries et al., 2017) and can influence topsoil microbial activity, ultimately highlighting their relevance to whole profile soil functions. Pedological studies have long recognized that land use history, in addition to the classic five state factors of soils, affects current soil function (Turley et al., 2020), especially tillage and fertilization via changes in soil structure and soil fertility (Weitzman et al., 2022). Additionally, microbes may decompose stable organic matter reserves when new labile organic matter is added, known as soil priming (Kuzyakov, 2006; Bastida et al., 2019; Liu et al., 2020), to which subsoils may be more sensitive (Li M. et al., 2022), and thus overall priming may offset any expected new carbon storage in topsoils. Similarly, a multi-year whole profile warming experiment recently showed that soil overall lost carbon mostly from subsoil even though topsoil accumulated carbon (Soong et al., 2021), suggesting that opposite patterns in subsoils may require re-shaping fundamental understanding of soil systems at the profile and pedon levels. In contrast, subsoils at over 1 m depth in agricultural systems may be better posed to accumulate carbon in the long-term compared to their topsoils, due to existing degradation from deeper tillage and the potential for added fertility from added root inputs by perennial plants with deep roots (Button et al., 2022) and other biological subsoiling methods (Ning et al., 2022). Since soil pedogenesis is now understood to follow complex trajectories (Phillips, 2017), future study of subsoils should help develop explanations for underlying processes simultaneously affecting different soil horizons.
Ideas of memory also relate to group-level patterns and processes which are increasingly reported, alongside individual component-level processes (Kerr and Godfrey-Smith, 2002; Traulsen and Nowak, 2006), and can have important implications for overall soil processes. Cooperation often manifests itself as synchrony among individuals, as in early examples of tree seed masting (Ostfeld et al., 2006; Victor et al., 2016) as well as disease transmission (Ostfeld et al., 2005), with similar principles extended to apply to forests (Filotas et al., 2014) and soil rhizospheres to describe nutrient exchange (Simard et al., 1997) along with mycorrhizal symbioses (van der Heijden and Horton, 2009; Simard et al., 2012). Similarly, population quorum sensing by soil bacteria has affected antibiotic production (Li et al., 2021) and other benefits at critical population sizes (Heilmann et al., 2015) and likely with weak time delays in reciprocity (Alfaro and Sanjuan, 2022), and quorum sensing has also been hypothesized to affect enzyme production with implications for nitrogen cycling (DeAngelis et al., 2008; Wang et al., 2014). Time delays also affecting interactions between partners changing at different rates or temporal scales—like between monthly root turnover and exudation affecting momentary microbial gene expression and predatory grazing below- and aboveground—could affect reciprocity of symbioses in soil. Time delays (or accelerations) may also reflect microbial co-metabolisms, a concept that could be explicitly added to even generalized versions of enzyme kinetic models (Tang and Riley, 2013) as additional multiplicative interactive terms among different enzymes and/or substrates, which could lead to asymmetric or incongruent results between spatially implicit versus explicit models (Allison, 2012), depending on local grid- or global whole matrix-scale analysis (Wang et al., 2019). Ultimately, the combinations of spatial and temporal variation generate the fluctuations that make treating dynamic instability as a somewhat unavoidable and thus inherent property of natural soil systems.
Diel cycles in soil temperature and respiration are commonly observed, yet few studies analyze the implications of natural cycles for modeling soil responses to environmental changes, which in some cases can lead to hysteretic irreversibility (Phillips et al., 2011). Complexity and systems theory offer generalized tools and perspectives to better incorporate variance (i.e., by soil depth) into more generalized models of soil processes. The tendency of a systems perspective to shift analysis toward variance is ultimately more inclusive of a diversity of model outcomes, such as regular oscillations or constrained chaotic fluctuations, and more generally validates informative model outputs that are not precise single point solutions and otherwise considered unstable by linear stability analysis. One method of incorporating variances has been to re-formulate dynamical systems using trigonometric functions, which are unique for producing repeated symmetrical curves, from bounded measures of relative distance from a fixed line segment (Coolidge, 1952). These first principles already reflect modern principles now understood about many complex systems, like relativity and symmetry with modification, which likely increase the generality and applicability of modeled output especially when processes and questions are newly framed and formulated in tractable ways.
Oscillations have been predicted by novel and widely cited model structures in agroecology (Vandermeer and Perfecto, 2017) and soil ecology (Baveye et al., 2018), and supported by empirical data across fine- and coarse scales. At fine scales, soil carbon molecular turnover has been recently proposed to depend on functional group complexity that also hypothesizes spatial modularity or hotspots in activity (Vogel et al., 2014), which could produce oscillations of broader soil properties over time (Lehmann et al., 2020). Spatial structuring also strengthens positive feedbacks in decomposition between exo-enzyme activity and assembly or production, which has influenced some early soil models toward predicting consistent variance, in the form of limit cycles, in soil nutrient availability (Schimel and Weintraub, 2003; Wang et al., 2014). Wet-dry cycle frequency has also been cited as affecting soil aggregate stability and as a determinant of patterns in microbial activity (Evans et al., 2022). Various types of limit cycles have also been a classic prediction of predator-prey models, but are rarely applied to describe soil faunal grazer food webs (Baveye et al., 2000; Buchkowski et al., 2017; Erktan et al., 2020; McCary et al., 2021) especially involving viruses and their traits (Emerson et al., 2018; Trubl et al., 2018). When these low-dimensional ecological models are explicitly extended in space, for example, as metacommunities, a wide variety of mosaic landscapes can be generated with some sensitivity to model formulation or structure (Vandermeer and Yitbarek, 2012; Vandermeer, 2013; Yitbarek and Vandermeer, 2017), suggesting that flexible model structures are likely important for robust understanding of causes and consequences of soil heterogeneity. Spatial explicitness also emphasizes studying dispersal processes among soil modular populations more than internal community dynamics shaped by particular parameterizations, which have been increasingly studied (Chaudhary et al., 2020; Hajian-Forooshani and Vandermeer, 2020; Arellano-Caicedo et al., 2021; Mafla-Endara et al., 2021). Spatial or temporal separation of populations has also inspired other model structures proposing competitive hierarchies resulting in intransitive loops (Vandermeer, 2013; Vandermeer and Jackson, 2018), which is already supported by strong evidence (Kerr et al., 2002; Lozano et al., 2019). Again, this is a case where new and diverse model predictions precede empirical supporting evidence, which ultimately highlights the potential value of general models, with a wide range of output, over precise ones, specifically for more basic than applied research. At coarser scales, soil respiration has also experienced regular variance in magnitude over multiple years, explained by regime shifts among various dominant stages of community-level decomposer activity (Sihi et al., 2016; Melillo et al., 2017). Various soil nutrients have also shown regular oscillations over decades (Reijneveld, 2013), although common statistical analyses remain linear which remains an analytical limitation. Some nutrient oscillations are expected from direct harvests, but if nutrient cycles are coupled (i.e., by microbial metabolisms) while oscillating, unintended and unintuitive synergies or conflicts may emerge, as oscillations align either in- or out of phase (Vandermeer, 2006), leading to either robust, or more likely quickly degrading, soil nutrient availabilities. The appearance and prediction of oscillations among a range of soil variables from both advanced first principles and several empirical studies justifies further study of non-linear models of soil behavior and ecology, with example approaches listed in Table 1. The purpose of this included table is to offer some initial non-exhaustive directions in applying relatively unique model formulations to research topics in soil ecology. Some listed approaches include the use of coupled oscillators to represent heterogeneous reversible priming of organo-mineral associations in soils, and/or represent complex soil food webs to better understand the role of faunal predators on soil nutrient and energy dynamics (Melguizo-Ruiz et al., 2020; McCary et al., 2021; Jiao et al., 2022; Morrissey et al., 2023), as well as the use of meta-population/-community formulations to understand pathogen persistence in soils (Kurkjian, 2019).
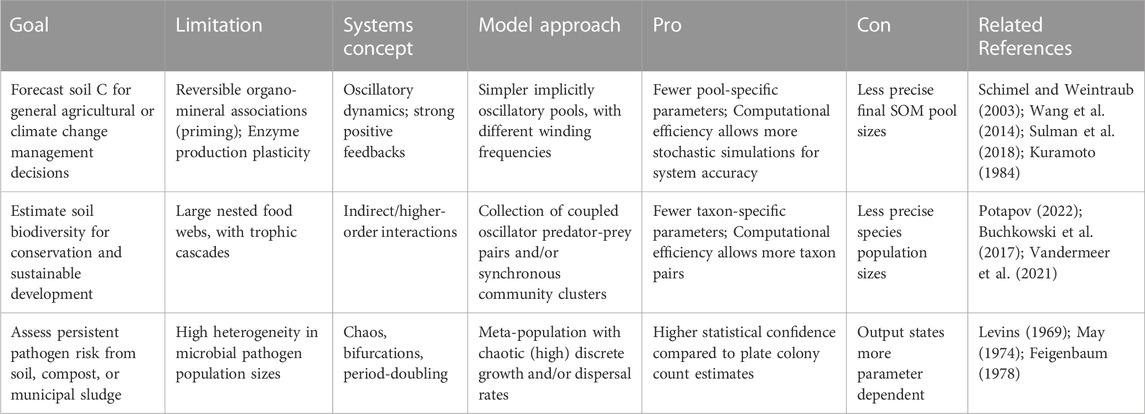
TABLE 1. Example cases where employing modeling strategies based on systems theory could be useful for generalizing about soil ecology and agroecology.
Hysteresis can be framed as a specific kind of non-linear transition and tipping point occurring in soils. Hysteresis is revealed when model stability analyses include outcomes across range of parameters, and underlying component processes also change pace at different speeds (Ong and Vandermeer, 2018). In soils, this occurs with overall water content and its matric pressure, or availability; this is because water always moves through wide pores first regardless of whether the process is drying or wetting, and wide pores have a weaker relationship between these two water variables than in narrow pores, which always mediate water movement second. Here the phenomenon is explained by temporal consistency in process across spatial heterogeneity, which can be another cause of dynamical asymmetry more generally. For example, the relationship between soil temperature and total soil respiration is also hysteretic in that soil respiration responds only after considerable changes in temperature, making respiration stay low as soil warms yet stay high while it cools, even across the same middle temperatures (Riveros-Iregui et al., 2007; Phillips et al., 2011; Zhang et al., 2015), which can also be described as state-dependence or short-term memory for a system. A widely recognized implication of hysteresis is the practical and sometimes permanent (Ong and Vandermeer, 2018) irreversibility of past ecological states, like permanent wilting points for roots under drought, or more internally regulated predator or pest populations.
Soil carbon saturation is a related concept, which is supported by field experiments and models, and is inspiring useful model structures for describing and understanding non-linear processes in soil. Appropriately, the concept of soil carbon saturation has already been formulated and incorporated into new generation soil models like MEMS (Zhang et al., 2021). An early proposed model (Stewart et al., 2007) simulated decadal field data by mixing two pools with different local equilibria: a stable mineral-bound carbon pool that saturates, and a labile pool that mostly decomposes but with no growth limit. This mixed structure produced flexible output—slow linear increases in soil carbon at high concentrations, and quicker but saturating increases at low concentrations—making it more widely applicable and representing a more generalized understanding of long-term soil carbon dynamics.
In contrast, older-generation soil models like CENTURY (Powlson et al., 1996) and RothC (Coleman and Jenkinson, 1996) did not incorporate pool saturation, but instead offered a simpler initial models offering widespread practical use. The relative simplicity of the model structure is broadly observed in the overall linear successive flow from one decomposition pool to the next. Furthermore, each individual pool was formulated to observe first-order decomposition kinetics. While first-order decomposition represents exponential decay, which is curvi-linear over time, the non-linearities and complex dynamics under investigation by systems theory instead stem from multiplicative associations or interactions among dynamic variables. In many cases, multi-pool soil systems tend to be represented with an attempted thoroughness, resulting in a list of coupled equations that influence each other by additive (or subtraction) terms, which usually consist of a key variable multiplied by a corresponding abiotic parameter, which is static relative to carbon or the nutrient of interest (Zhang et al., 2021). This style of formulation acknowledges that soils are complicated habitats, but leaves room to lean into the complexities of the habitat with various nonlinear additions.
Fundamentally, because parameters and dynamic variables in an ordinary differential equation often represent concepts formulated to be operating at relatively distinct time scales, the re-formulation to incorporate multiplicative variable associations can also be interpreted as a change in descriptive timescale. For example, a representative modeling study may test the hypothesis that particulate organic matter and mineral-associated organic matter, even as distinct pools, might each observe transfer rates that could be affected by both its own and the other’s size, within a model time step, rather than between them. More specifically, rather than modeling the primed loss of existing organic matter implicitly in the form of a saturating stable pool, soil priming could be formulated as an interaction modification that implicates the more stable pool’s size back into its incoming transfer rate from the labile pool. Generally, this style of formulation may offer a new class of hypothesis testing, especially for soil processes that are currently difficult to test empirically (Bennett et al., 2019), representing a wider array of model outcomes with just a few key soil descriptor variables, in line with recent qualitative syntheses (Phillips, 2017; Kuzyakov and Zamanian, 2019). Modeling soil systems using tools from complexity theory appears to offer an antidote to the increasingly-large soil simulations that have become more popular, in part alongside increasing computing power in cloud systems. The approach using complexity theory can improve conceptual efficiency by reformulating soil models into fewer modular components with more inter-linked process rates (Lehmann et al., 2020). In this way, soil modeling studies may emerge as useful analyses not only for understanding soils themselves and their management (Angst et al., 2023), but also for aiding other academic disciplines studying complex systems more generally.
Additional recent studies improved generality of understanding by explicitly modeling biological (Craig et al., 2021) and microbial (Wang et al., 2014; Marsland et al., 2020; Pacheco et al., 2021) processes underlying transformation rates, including with saturating enzyme activity (Buchkowski et al., 2017; Van Den Berg et al., 2022). Even more general understanding can be added by expanding similar model structures to describe effects of soil fauna and invertebrates on soil micro-habitats including predatory and dispersive influences on microbial communities (Grandy et al., 2016; Arellano-Caicedo et al., 2021; Creamer et al., 2022). However, integrating models of short-term microbial processes with long-term carbon dynamics remains incomplete (Todd-Brown et al., 2013), in part because they operate on very different timescales. Each model class improves understanding of soil, but for generalized predictions, integrating or coupling models with the fewest explicit dimensions that yield the most diverse qualitative output (Levins, 1966; Lane, 2018) may help at least bound possible outcomes, such as for soil carbon exchange and net storage, or other nutrient cycles (Manzoni and Porporato, 2009). In addition there are many aspects of soil ecology and functioning such as biodiversity maintenance or specific soil pathogen suppression that warrant continued understanding through modeling the soil environment.
Together, several non-linear dynamics or functions among soil variables may then combine to reveal critical transitions (Figure 1). A recent synthesis (Kuzyakov and Zamanian, 2019) revealed many non-linear relationships among key soil variables across several decades, such as between soil bulk density and organic carbon. Their analysis showed distinct phases of pedogenesis, or soil development, under human management, which they termed agro-pedogenesis. Ultimately, they presented a convergence of these processes into an attractor, which they considered to span a narrower range of values for key soil descriptors than would be found under natural pedogenesis. However, underlying non-linearities between the same key soil descriptors, such as bulk density and soil organic carbon, suggest potential future attractor instability and more potential divergence among local pedons, especially under human management. Relatedly, another recent review (Phillips, 2017) highlighted how natural pedogenesis can be described with concepts from non-linear dynamics and complexity theory, notably revealing how pedogenesis can show unstable trajectories, or many possible alternative end states. These studies suggest that while globally, recent anthropedogenesis has converged mostly toward degradation, locally, future anthropedogenesis could still diverge depending on regional management strategies. This inference that helps maintain agro-pedogenesis as a potentially regenerative force for soil fertility, rather than inherently degrading, especially when distinguishing by industrial vs small-scale agricultural land management. Accordingly, a recent global synthesis of soil microbial biomass carbon showed evidence of higher variance in percent change where existing stocks were lower, also showing relative increases in some tropical regions such as the Caribbean (near southeast Ayiti) (Patoine et al., 2022). In this region and others including southern Africa and central Asia, even where soil microbial biomass carbon was lost in sum due to climate changes, land-use change effects on soil microbial biomass carbon were often much closer to positive. This higher variance in soil microbial biomass carbon, in part driven by positive land-use effects, together with global cropland analyses (Padarian et al., 2022), points to a potential for land management to increase soil carbon, rather than necessarily degrade it (Dynarski et al., 2020). These insights highlight that increasing soil carbon globally may still be still feasible especially by sustainable local or regional management coordination.
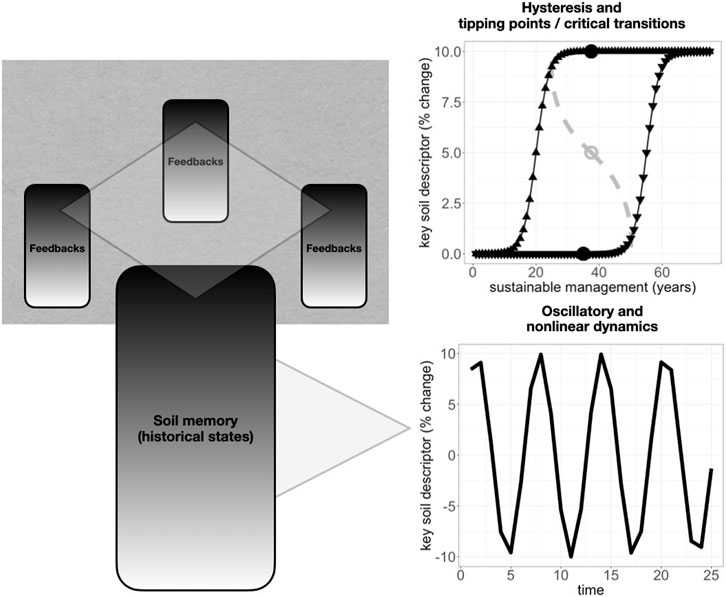
FIGURE 1. Conceptual diagram highlighting (bottom) that past states incorporated down a soil profile, like buried or subsoil horizons that are plowed, primed and nutrient-poor, or instead deeply fertile (black gradient, bottom-left), may induce oscillatory dynamics (bottom-right) in key soil variables, like moisture and microbial biomass, and that (top) similarly continuous feedbacks across many soil profiles and pedons in a landscape (top-left) may produce nonlinear regional patterns including tipping points (top-right) for key soil variables, like soil organic matter, not only during land degradation, but also during coordinated collective management toward regeneration.
Accordingly, even social processes that affect regional land management, such as in agriculture (Newbold et al., 2020), represent a source of uncertainty affecting soil organic matter dynamics. However, for soil ecology, the understanding offered by systems and complexity theory comes less from understanding farmers’ individual decision-making processes, which is still relevant (Mestre et al., 2020), but instead comes from how information spread and collective decision-making processes may affect regional agricultural management regimes and related soil processes. Given the modern corporate food regime (Campbell, 2009; McMichael, 2009) and reliance on plantation land systems (Wolford, 2020), widespread deficit narratives about the ecology of agroecosystems have been somewhat normalized. However, a liberal interpretation of a systems approach to soil ecology, by virtue of normalizing and aiming to integrate hard-to-anticipate critical transitions (Scheffer et al., 2012; Scheffer et al., 2015; Cooper et al., 2020), motivates the vision for a counter-narrative—one that focuses on supporting the world’s small-scale farmers. This results from future global changes to, for example, soil carbon, emerging from the sum of local and regional cooperative efforts toward ecosystem restoration and regenerative agriculture.
Rather than continuing to degrade, regional soil organic matter levels could potentially increase rapidly, assuming most soils are far from carbon (or other nutrient) saturation. This could be directly supported by local social movements that have formed to protect small-scale agriculture and land tenure via local neighboring cooperation and collaborative governance. Studies in Brazil near activity of the landless workers movement, or MST, show that soil fertility is positively associated with the recent adoption of and transition to sustainable land management practices (Stratton et al., 2022) like cover crop diversity, which could also be promoted by stronger social recognition of benefits (Williams et al., 2021). This perspective, together with other studies directly tying soil organic matter to crop yield (Oldfield et al., 2022), ultimately tie soil regeneration to environmental justice issues of land tenure. Integrating socio-ecological processes thus offers an additional means by which key soil variables and anthropedogenesis can show critical non-linear transitions, especially in positive directions, challenging common narratives that depict humans as forces of soil degradation. Some ideas of how social processes affect nutrient cycling have emerged as biogeo-socio-chemistry especially for urban settings (Pataki et al., 2011; Kaushal et al., 2014), and others may help address additional soil ecological dimensions of multi-functionality (Creamer et al., 2022) beyond nutrients like spatial patterns of faunal diversity and soil food web network structures. Recent studies of urban ecology already point to interesting patterns that challenge deficit narratives of societal relationships with local soils and agriculture (Bonilla-Bedoya et al., 2022; Nugent and Allison, 2022; Pindral et al., 2022; Zhang et al., 2022). Novel insights on soil socio-ecological dynamics may help guide how to tailor sustainable development initiatives by individual countries to achieve international soil governance initiatives (Farnese, 2022; García et al., 2022) like through the UN FAO Global Soil Partnership, Global Soil Biodiversity Initiative (Wall et al., 2015), and other working groups generally addressing UN sustainable development goals of combating soil and habitat degradation to enhance ecosystem services via dynamic key soil ecological indicators (Pradhan et al., 2017; Bennich et al., 2020).
In addition to conceptual generality and realism reasons, there are also practical considerations of concern for soil and ecosystem modeling—namely, for data gathering and analysis. For data gathering, the main concern limitation is the collection of fine-resolution time series, for a few reasons. One reason is that detecting curves instead of lines statistically requires a more even distribution of data across focal axes of interpretation. This does not imply a need for long term data over short term data, just higher frequencies of data collection relative to the total study duration; although it is well-established that long-term soil data are rarer and otherwise useful, there are of course still interesting processes in soils occurring with a year and season (Upton et al., 2019). Higher collection frequency is already recognized as important for soil dynamics strongly governed by spatial and temporal hotspots and rare key event frequencies, about nitrous oxide emissions from spatial and temporal hotspots (O’Connell et al., 2022), which in line with the thesis here, is also increasingly recognized as an important feature of complex systems generally. Generally, doing so also highlights the common experimental design trade-off between number of (temporal) groups and replication per group, with non-linear trend detection benefiting from more groups and less replication.
Various example studies showing complex system patterns from empirical data exist in literature from ecology to non-linear geophysics. Observing and tailoring analyses to ‘threshold’ responses is one approach, reported in spatial consideration of predator biocontrol in agro-ecosystems (Vandermeer and Perfecto, 2019), with a supportive model implying underlying chaos (or infinite equilibria) and field observations as one of many possible trajectories. In such cases, implying chaotic dynamics that cannot simultaneously be observed in the field still offers fundamental and flexible understanding of how ecosystems of interest could change under different conditions. Chaos is not elaborated on in this paper, but nonetheless could equally be included as a fundamental, detectable (Toker et al., 2020), and arguably insightful category of even simple model output (Pearce et al., 2020; Rogers et al., 2022). Additional examples of complex patterns arising from empirical studies of soils specifically include focus on soil water hysteresis or characteristic curves (Ji et al., 2016) to explain organic matter decomposition (Ghezzehei et al., 2019), nitrogen availability (Tarquis et al., 2017), or soil respiration from temperature (Phillips et al., 2011), including over time (Mirás-Avalos et al., 2016) as well as overall soil surface micro-roughness (Abban et al., 2017). Complementarily, many theoretical studies of microbial population, community, and resource dynamics involve empirical laboratory approaches using controlled chemostats or successional dilution schemes for culturable taxa, which can manipulate background environmental parameters in multiple directions allowing for observation of hysteretic gaps among overlayed empirical growth curves (Sun et al., 2023). Ultimately, various approaches such as for detecting hysteresis and tipping points converge toward general requirements of varying background conditions across multiple similar high frequency time series, and sub-discipline domain knowledge will be of use for finer details ideally communicated among inter-disciplinary collaborators.
The second set of concerns relate to changes in data analysis, from new empirical or existing model outputs. We have already suggested some relatively unique approaches above, including changing model structural units from one-dimensional to two-variable oscillator units (Kuramoto and Nakao, 2019; Vandermeer et al., 2021), and can add here the study of geometric variation in hysteresis curves, such as from soil water (Mascaro and Vivoni, 2016; Zhao et al., 2020) or similarly in model structure, predator-mediated decomposition (Ong and Vandermeer, 2018). However, there can also be some ways to uncover patterns common to complex systems such as soils by modifying existing approaches. One is reduce parameter uncertainty by focusing more on exploring multiplicative equation terms, rather than assuming simple additive relationships between single variables (and their associated parameters). For example, the very interesting and modern MEMS soil model, that critically highlights the importance of spatial interactions of organic carbon with the fine-scale matrix of soil mineral surfaces, tends to model many separate pools of carbon, with associated decomposition or uptake rates, that represent inter-dependence, but ones that are primarily formulated additively (Robertson et al., 2019 suppl.). A systems-focused analysis, testing ideas from complexity theory, highlights the insight gained from either focusing on parameter sweeps that are associated with multiplicatively interacting variables that are currently implemented and exist, and/or re-formulating two or more equations to into fewer that involve such non-linear terms. Additional strategies can also include model analyses of the relative influences of key variables over time, which is an existing practice (Robertson et al., 2019 Supplementary Figure S5), but not typically at the forefront of hypothesis generation or study presentation. Practically, it is also relevant to acknowledge that this can result in longer computational simulation times, and on the other hand, parameter values for interactive terms become more influential on relevant model output and thus become more important to calibrate, implying that justifying these choices with evidence becomes more important. As modeling methods can also be used primarily for hypothesis testing and model structure piloting, additional modeling strategies include implementing alternative structures to ordinary differential equation sets, an example being agent-based modeling, which is increasingly used in other fields including ecology (Esquivel et al., 2022), but relatively new to soils (Waring et al., 2020). Usefully, there is already some support for these systems analyses in both empirical (Basile et al., 2003) and modeling studies of soils (Zhang et al., 2014); literature is primarily skewed toward soil physics, but tools from physics are increasingly brought into ecology, as those from chemistry have come into ecosystem ecology and biogeochemistry, and is likely fundamental to understanding and advancing the unique field of soil ecology (Erktan et al., 2020). Furthermore, dimension reduction as a model formulation tool can also help reduce model size, and potentially accordingly, also help reduce associated code navigational complexity, learning curves, researcher accessibility, and modeling study reproducibility.
Other concerns include with how to engage with transient dynamics, choosing useful response metrics to show, and subsequent statistical analysis considerations. Transient dynamics are commonly considered as the initial output of a model simulation before reaching equilibrium or steady state, which depending on the time period of interest for analysis, can represent up to 10 or 100 years of changes in soil properties. Traditionally they are excluded from model behavioral analyses, as they usually contain complicated dynamics and technically do not represent “long-term” status of the system. However, if transient dynamics comprise a notable proportion of total simulated time, they are worth considering and analyzing themselves (Hastings et al., 2018; Francis et al., 2021). Here, the research focus is on designing model formulations where there is no single multi-dimensional point to arrive to, but that the complex dynamics of oscillations and large leaps in values or critical transitions are instead the expected outcome, and analyses need to work that. In other words, the non-linear dynamics observable by key soil descriptors discussed here are not transients, but instead dynamic, non-point and geometrically diverse equilibriums (technically considered unstable). Accordingly, one initial strategy, perhaps before changing existing model structures, may be to include some analysis of soil model transient dynamics, to gain intuition on which tend to be key driving variables or sub-pools of soil carbon.
For the concepts highlighted previously in this paper, some concrete tools to analyze useful response metrics include: programming language functions to temporarily store slightly offset or asymmetric data frames to analyze lags among column variables (Li et al., 2022a code for ‘peaks’); calculating lyapunov exponents when descriptor changes are highly variable to check for chaotic equilibrium (Rogers et al., 2022); identifying “critical points” where large transitions occur (Vandermeer, 2021), as well as to identify at which parameter values invisible (i.e., visible when equation set is analytically tractable) “collisions” of phase space (or time series data where time is not an axis) occur (Vandermeer and Yodzis, 1999), which importantly can alter the long-term equilibrium points of original interest (Strogatz and Fox, 2015); and finally calculating the size of hysteretic graphical regions, which may suggest irreversible equilibrium points (Ong and Vandermeer, 2018) under certain realistic parameter combinations.
An ultimate practical consideration for applying a complex systems framework for studying soils building statistical support. The first limitation to this is analyzing and presenting temporal categories as discrete—descretizing time tends to obscure and lower the ability to identify a pattern as non-linear; similar to the previous point about needing higher termporal resolution to better support curvi-linear relationships. The next concern is the ease of use of current implementations of common statistical tests. Currently, linear regressions are relatively simple to run and accessible to learn, as are generalized linear models, linear mixed effects models, and logistic regressions. However, other non-linear regressions, such as generalized and nonlinear mixed effects models can be more error-prone and less easy to run and interpret. As a result, it is not uncommon for researchers to choose simpler statistical tests to run when multiple other test options could also be seen as valid. One work-around is to consider weaker non-parametric tests and focusing on other forms of variance partitioning and determining effect sizes, such as Spearman rank-order correlation, or Kruskal–Wallis with eta-squared effect size calculations when necessary, as non-parametric have more flexible underlying assumptions. These kinds of trade-offs in statistical power when under limited resources for the sake of model exploration (Levins, 1966) may be useful to help advance the soil agroecology toward more new hypothesis-driven research. Ultimately, however, even non-parametric tests maintain some assumptions, such as monotonicity or uni-directionality, which would already be violated by oscillatory relationships, as well as equal variance among groups, which would be violated by mean-variance correlations (Taylor, 1961), all of which remain partial barriers for adoption of complex systems level analyses of soil models. Beyond waiting for new test development, formulation and implementation, and broad acceptance, it has often proved often useful to rely simply on graphical analysis, a type of qualitative analysis analogous to those used in the social sciences, to make wide leaps in new research hypotheses promising to move the field forward.
This synthesis applies a complex systems framework to analyzing key uncertainties about soil processes and habitats, drawing from various analytical tools used across interdisciplinary fields, and presenting how they have and will better address key research questions in the field of soil agroecology. Overall, this paper contributes to the field as a modern synthetic review that connects existing similar ideas across disciplines and highlights their implications for future work and potential findings. Concepts highlighted include soil memory, or legacy effects of management history and past ecological states; oscillations over time, which are observed in many key soil descriptive variables; and, tipping points and hysteresis, when several correlated variables change at different times and/or rates. Together, these three principles should help decrease uncertainty around soil model structures (Bradford et al., 2016) by pointing toward how to improve model generality for key soil processes of interest, such as soil respiration and particulate organic matter storage via occlusion by microbial community byproducts produced during soil aggregation. The complexity perspective on soil agroecology also inspires a positive outlook on the potential feasibility of collective societal solutions to soil degradation crises (Montgomery, 2007; Richter, 2021), by including and better anticipating drastic unexpected changes that often emerge from the combined effects of many interacting processes. Because farms are social-ecological systems, forward steps include collaborating with social sciences, humanities such as history or literature (Schloss and Handelsman, 2007), or non-equilibrium or statistical physics (Bak et al., 2002) including geophysics, to expand and improve the set of potentially useful analytical tools and perspectives needed to inclusively and robustly describe the extreme heterogeneity and complexity of soil habitats.
NM and JV contributed to paper conceptualization, funding acquisition, literature review, conceptual synthesis, and paper organization; NM wrote initial drafts, and NM and JV contributed to later revisions. All authors contributed to the article and approved the submitted version.
This research was supported by the University of Michigan Rackham Merit Fellowship program and NSF DEB Award #1853261.
Thanks to the JV-Perfecto lab for initial organizational feedback, colleagues Kenzo Esquivel and Aidee Guzmán for inviting a conference presentation on the topic, and Jennifer Blesh and Alison E King for initial written draft comments.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Abban, B. K. B., Papanicolaou, A. N., Giannopoulos, C. P., Dermisis, D. C., Wacha, K. M., Wilson, C. G., et al. (2017). Quantifying the changes of soil surface microroughness due to rainfall impact on a smooth surface. Nonlin. Process. Geophys. 24, 569–579. doi:10.5194/npg-24-569-2017
Alfaro, G., and Sanjuan, M. A. F. (2022). Time-dependent effects hinder cooperation on the public goods game. Chaos, Solit. Fractals 160, 112206. doi:10.1016/j.chaos.2022.112206
Allison, S. D. (2012). A trait-based approach for modelling microbial litter decomposition. Ecol. Lett. 15, 1058–1070. doi:10.1111/j.1461-0248.2012.01807.x
Angst, G., Mueller, K. E., Castellano, M. J., Vogel, C., Wiesmeier, M., and Mueller, C. W. (2023). Unlocking complex soil systems as carbon sinks: multi-pool management as the key. Nat. Commun. 14, 2967. doi:10.1038/s41467-023-38700-5
Arellano-Caicedo, C., Ohlsson, P., Bengtsson, M., Beech, J. P., and Hammer, E. C. (2021). Habitat geometry in artificial microstructure affects bacterial and fungal growth, interactions, and substrate degradation. Commun. Biol. 4, 1226. doi:10.1038/s42003-021-02736-4
Armstrong, A. C. (1986). On the fractal dimensions of some transient soil properties. J. Soil Sci. 37, 641–652. doi:10.1111/j.1365-2389.1986.tb00393.x
Armstrong, R. A., and McGehee, R. (1976). Coexistence of species competing for shared resources. Theor. Popul. Biol. 9, 317–328. doi:10.1016/0040-5809(76)90051-4
Assouline, S., Tessier, D., and Bruand, A. (1998). A conceptual model of the soil water retention curve. Water Resour. Res. 34, 223–231. doi:10.1029/97WR03039
Azizi-Rad, M., Chanca, I., Herrera-Ramírez, D., Metzler, H., and Sierra, C. A. (2021). Stochastic and deterministic interpretation of pool models. Glob. Change Biol. 2, 2271–2272. doi:10.1111/gcb.15581
Bailey, V. L., Bilskis, C. L., Fansler, S. J., McCue, L. A., Smith, J. L., and Konopka, A. (2012). Measurements of microbial community activities in individual soil macroaggregates. Soil Biol. Biochem. 48, 192–195. doi:10.1016/j.soilbio.2012.01.004
Bak, P., Christensen, K., Danon, L., and Scanlon, T. (2002). Unified scaling law for earthquakes. Phys. Rev. Lett. 88, 178501. doi:10.1103/PhysRevLett.88.178501
Bashkirov, A. G., and Vityazev, A. V. (2000). Information entropy and power-law distributions for chaotic systems. Phys. A Stat. Mech. its Appl. 277, 136–145. doi:10.1016/S0378-4371(99)00449-5
Basile, A., Ciollaro, G., and Coppola, A. (2003). Hysteresis in soil water characteristics as a key to interpreting comparisons of laboratory and field measured hydraulic properties. Water Resour. Res. 39, 1–12. doi:10.1029/2003WR002432
Bastida, F., García, C., Fierer, N., Eldridge, D. J., Bowker, M. A., Abades, S., et al. (2019). Global ecological predictors of the soil priming effect. Nat. Commun. 10, 3481. doi:10.1038/s41467-019-11472-7
Baveye, P. C. (2023). Ecosystem-scale modelling of soil carbon dynamics: time for a radical shift of perspective? Soil Biol. Biochem. 184, 109112. doi:10.1016/j.soilbio.2023.109112
Baveye, P. C., Otten, W., Kravchenko, A., Balseiro-Romero, M., Beckers, É., Chalhoub, M., et al. (2018). Emergent properties of microbial activity in heterogeneous soil microenvironments: different research approaches are slowly converging, yet major challenges remain. Front. Microbiol. 9, 1929. doi:10.3389/fmicb.2018.01929
Bennett, A. E., Preedy, K., Golubski, A., Umbanhowar, J., Borrett, S. R., Byrne, L., et al. (2019). Beyond the black box: promoting mathematical collaborations for elucidating interactions in soil ecology. Ecosphere 10. doi:10.1002/ecs2.2799
Bennich, T., Weitz, N., and Carlsen, H. (2020). Deciphering the scientific literature on SDG interactions: a review and reading guide. Sci. Total Environ. 728, 138405. doi:10.1016/j.scitotenv.2020.138405
Berardi, D., Brzostek, E., Blanc-Betes, E., Davison, B., DeLucia, E. H., Hartman, M. D., et al. (2020). 21st-century biogeochemical modeling: challenges for Century-based models and where do we go from here? GCB Bioenergy 12, 774–788. doi:10.1111/gcbb.12730
Berryman, A. A., and Millstein, J. A. (1989). Are ecological systems chaotic – and if not, why not? Trends Ecol. Evol. 4, 26–28. doi:10.1016/0169-5347(89)90014-1
Bonilla-Bedoya, S., Ángel Herrera, M., Vaca, A., Salazar, L., Zalakeviciute, R., Mejía, D., et al. (2022). Urban soil management in the strategies for adaptation to climate change of cities in the Tropical Andes. Geoderma 417, 115840. doi:10.1016/j.geoderma.2022.115840
Bradford, M. A., Wieder, W. R., Bonan, G. B., Fierer, N., Raymond, P. A., and Crowther, T. W. (2016). Managing uncertainty in soil carbon feedbacks to climate change. Nat. Clim. Change 6, 751–758. doi:10.1038/nclimate3071
Brostow, W., Pal, S., and Singh, R. P. (2007). A model of flocculation. Mater. Lett. 61, 4381–4384. doi:10.1016/j.matlet.2007.02.007
Buchkowski, R. W., Bradford, M. A., Grandy, A. S., Schmitz, O. J., and Wieder, W. R. (2017). Applying population and community ecology theory to advance understanding of belowground biogeochemistry. Ecol. Lett. 20, 231–245. doi:10.1111/ele.12712
Burrough, P. A. (1981). Fractal dimensions of landscapes and other environmental data. Nature 294, 240–242. doi:10.1038/294240a0
Button, E. S., Pett-Ridge, J., Murphy, D. V., Kuzyakov, Y., Chadwick, D. R., and Jones, D. L. (2022). Deep-C storage: biological, chemical and physical strategies to enhance carbon stocks in agricultural subsoils. Soil Biol. Biochem. 170, 108697. doi:10.1016/j.soilbio.2022.108697
Campbell, H. (2009). Breaking new ground in food regime theory: corporate environmentalism, ecological feedbacks and the “food from somewhere” regime? Agric. Hum. Values 26, 309–319. doi:10.1007/s10460-009-9215-8
Charlotte, V., Laure, V. G., Naoise, N., and Claire, C. (2022). Opportunities and limits in imaging microorganisms and their activities in soil microhabitats. Soil Biol. Biochem. 174, 108807. doi:10.1016/j.soilbio.2022.108807
Chaudhary, V. B., Nolimal, S., Sosa-Hernández, M. A., Egan, C., and Kastens, J. (2020). Trait-based aerial dispersal of arbuscular mycorrhizal fungi. New Phytol. 228, 238–252. doi:10.1111/nph.16667
Christensen, K., Danon, L., Scanlon, T., and Bak, P. (2002). Unified scaling law for earthquakes. Proc. Natl. Acad. Sci. 5 . doi:10.1073/pnas.012581099
Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009). Power-law distributions in empirical data. SIAM Rev. 51, 661–703. doi:10.1137/070710111
Coleman, K., and Jenkinson, D. S. (1996). “RothC-26.3 - a Model for the turnover of carbon in soil,” in Evaluation of soil organic matter models. Editors D. S. Powlson, P. Smith, and J. U. Smith (Berlin, Heidelberg: Springer Berlin Heidelberg), 237–246. doi:10.1007/978-3-642-61094-3_17
Cong, R., Wang, X., Xu, M., Ogle, S. M., and Parton, W. J. (2014). Evaluation of the CENTURY model using long-term fertilization trials under corn-wheat cropping systems in the typical croplands of China. PLoS ONE 9, e95142. doi:10.1371/journal.pone.0095142
Cooper, G. S., Willcock, S., and Dearing, J. A. (2020). Regime shifts occur disproportionately faster in larger ecosystems. Nat. Commun. 11, 1175. doi:10.1038/s41467-020-15029-x
Cotrufo, M. F., Wallenstein, M. D., Boot, C. M., Denef, K., and Paul, E. (2013). The Microbial Efficiency-Matrix Stabilization (MEMS) framework integrates plant litter decomposition with soil organic matter stabilization: do labile plant inputs form stable soil organic matter? Glob. Change Biol. 19, 988–995. doi:10.1111/gcb.12113
Craig, M. E., Mayes, M. A., Sulman, B. N., and Walker, A. P. (2021). Biological mechanisms may contribute to soil carbon saturation patterns. Glob. Change Biol. 27, 2633–2644. doi:10.1111/gcb.15584
Creamer, R. E., Barel, J. M., Bongiorno, G., and Zwetsloot, M. J. (2022). The life of soils: integrating the who and how of multifunctionality. Soil Biol. Biochem. 166, 108561. doi:10.1016/j.soilbio.2022.108561
Curado, E., Nobre, F., and Plastino, A. (2018). Associating an entropy with power-law frequency of events. Entropy 20, 940. doi:10.3390/e20120940
Cuthbertson, A. J. S., Samsami, F., and Dong, P. (2018). Model studies for flocculation of sand-clay mixtures. Coast. Eng. 132, 13–32. doi:10.1016/j.coastaleng.2017.11.006
Czaplicka, A., Holyst, J. A., and Sloot, P. M. A. (2013). Noise enhances information transfer in hierarchical networks. Sci. Rep. 3, 1223. doi:10.1038/srep01223
DeAngelis, K. M., Lindow, S. E., and Firestone, M. K. (2008). Bacterial quorum sensing and nitrogen cycling in rhizosphere soil: bacterial QS and rhizosphere nitrogen cycling. FEMS Microbiol. Ecol. 66, 197–207. doi:10.1111/j.1574-6941.2008.00550.x
Denef, K., Six, J., Bossuyt, H., Frey, S. D., Elliott, E. T., Merckx, R., et al. (2001). Influence of dry-wet cycles on the interrelationship between aggregate, particulate organic matter, and microbial community dynamics. Soil Biol. 13, 1599–1611. doi:10.1016/S0038-0717(01)00076-1
Dynarski, K. A., Bossio, D. A., and Scow, K. M. (2020). Dynamic stability of soil carbon: reassessing the “permanence” of soil carbon sequestration. Front. Environ. Sci. 8, 514701. doi:10.3389/fenvs.2020.514701
Emerson, J. B., Roux, S., Brum, J. R., Bolduc, B., Woodcroft, B. J., Jang, H. B., et al. (2018). Host-linked soil viral ecology along a permafrost thaw gradient. Nat. Microbiol. 3, 870–880. doi:10.1038/s41564-018-0190-y
Epstein, I. R., Kustin, K., De Kepper, P., and Orbán, M. (1983). Oscillating chemical reactions. Sci. Am. 248, 112–123. doi:10.1038/scientificamerican0383-112
Epstein, I. R., and Showalter, K. (1996). Nonlinear chemical dynamics: oscillations, patterns, and chaos. J. Phys. Chem. 100, 13132–13147. doi:10.1021/jp953547m
Erktan, A., Balmot, J., Merino-Martín, L., Monnier, Y., Pailler, F., Coq, S., et al. (2017). Immediate and long-term effect of tannins on the stabilization of soil aggregates. Soil Biol. Biochem. 105, 197–205. doi:10.1016/j.soilbio.2016.11.017
Erktan, A., Rillig, M. C., Carminati, A., Jousset, A., and Scheu, S. (2020). Protists and collembolans alter microbial community composition, C dynamics and soil aggregation in simplified consumer - prey systems, 4961–4980.
Esquivel, K. E., Hesselbarth, M. H. K., and Allgeier, J. E. (2022). Mechanistic support for increased primary production around artificial reefs. Ecol. Appl. 32, e2617. doi:10.1002/eap.2617
Evans, S. E., Allison, S. D., and Hawkes, C. V. (2022). Microbes, memory and moisture: predicting microbial moisture responses and their impact on carbon cycling, 12.
Farnese, P. L. (2022). Soil governance in a pandemic. Soil Secur. 6, 100033. doi:10.1016/j.soisec.2021.100033
Feigenbaum, M. J. (1978). Quantitative universality for a class of nonlinear transformations. J. Stat. Phys. 19, 25–52. doi:10.1007/BF01020332
Filotas, E., Parrott, L., Burton, P. J., Chazdon, R. L., Coates, K. D., Coll, L., et al. (2014). Viewing forests through the lens of complex systems science. Ecosphere 5, 1–23. art1. doi:10.1890/ES13-00182.1
Francis, T. B., Abbott, K. C., Cuddington, K., Gellner, G., Hastings, A., Lai, Y.-C., et al. (2021). Management implications of long transients in ecological systems. Nat. Ecol. Evol. 5, 285–294. doi:10.1038/s41559-020-01365-0
García, S. O., Santillán, V. S., Vivier, V. B., Anglés-Hernánez, M., Pérez, M. E., and Prado, B. (2022). Soil governance and sustainable agriculture in Mexico. Soil Security. 100059. doi:10.1016/j.soisec.2022.100059
Ghezzehei, T. A., Sulman, B., Arnold, C. L., Bogie, N. A., and Berhe, A. A. (2019). On the role of soil water retention characteristic on aerobic microbial respiration. Biogeosciences 16, 1187–1209. doi:10.5194/bg-16-1187-2019
Gillespie, C. S. (2015). Fitting heavy tailed distributions: the powerlaw package. J. Stat. Softw. 64, 1–16. doi:10.18637/jss.v064.i02
Grandy, A. S., Wieder, W. R., Wickings, K., and Kyker-Snowman, E. (2016). Beyond microbes: are fauna the next frontier in soil biogeochemical models? Soil Biol. Biochem. 102, 40–44. doi:10.1016/j.soilbio.2016.08.008
Hajian-Forooshani, Z., and Vandermeer, J. (2020). Spatial structure and pathogen epidemics: the influence of management and stochasticity in agroecosystems. bioRxiv. doi:10.1101/2020.06.19.161810100872
Harte, J., Kinzig, A., and Green, J. (1999). Self-similarity in the distribution and abundance of species. Science 284, 334–336. doi:10.1126/science.284.5412.334
Hastings, A. (2004). Transients: the key to long-term ecological understanding? Trends Ecol. Evol. 19, 39–45. doi:10.1016/j.tree.2003.09.007
Hastings, A., Abbott, K. C., Cuddington, K., Francis, T., Gellner, G., Lai, Y. C., et al. (2018). Transient phenomena in ecology. Science 361, eaat6412. doi:10.1126/science.aat6412
Hastings, A., Hom, C. L., Ellner, S., Turchin, P., and Godfray, H. C. J. (1993). Chaos in ecology: is mother nature a strange attractor? Annu. Rev. Ecol. Sytematics 35, 1–33. doi:10.1146/annurev.es.24.110193.000245
Heilmann, S., Krishna, S., and Kerr, B. (2015). Why do bacteria regulate public goods by quorum sensing? How the shapes of cost and benefit functions determine the form of optimal regulation. Front. Microbiol. 6, 767. doi:10.3389/fmicb.2015.00767
Henson, S. M., Costantino, R. F., Cushing, J. M., Desharnais, R. A., Dennis, B., and King, A. A. (2001). Lattice effects observed in chaotic dynamics of experimental populations. Science 294, 602–605. doi:10.1126/science.1063358
Hicks Pries, C. E., Castanha, C., Porras, R. C., and Torn, M. S. (2017). The whole-soil carbon flux in response to warming. Science 355, 1420–1423. doi:10.1126/science.aal1319
Jenny, H. (1961). Derivation of state factor equations of soils and ecosystems. Soil Sci. Soc. Am. J. 25, 385–388. doi:10.2136/sssaj1961.03615995002500050023x
Ji, W., Lin, M., Biswas, A., Si, B. C., Chau, H. W., and Cresswell, H. P. (2016). Fractal behavior of soil water storage at multiple depths. Nonlin. Process. Geophys. 23, 269–284. doi:10.5194/npg-23-269-2016
Jiao, S., Lu, Y., and Wei, G. (2022). Soil multitrophic network complexity enhances the link between biodiversity and multifunctionality in agricultural systems. Glob. Change Biol. 28, 140–153. doi:10.1111/gcb.15917
Kaushal, S. S., McDowell, W. H., and Wollheim, W. M. (2014). Tracking evolution of urban biogeochemical cycles: past, present, and future. Biogeochemistry 121, 1–21. doi:10.1007/s10533-014-0014-y
Kerr, B., and Godfrey-Smith, P. (2002). Individualist and multi-level perspectives on selection in structured populations. Biol. Philos. 17, 477–517. doi:10.1023/A:1020504900646
Kerr, B., Riley, M. A., Feldman, M. W., and Bohannan, B. J. M. (2002). Local dispersal promotes biodiversity in a real-life game of rock–paper–scissors. Nature 418, 171–174. doi:10.1038/nature00823
King, A. A., and Schaffer, W. M. (1999). The rainbow bridge: Hamiltonian limits and resonance in predator-prey dynamics. J. Math. Biol. 39, 439–469. doi:10.1007/s002850050174
King, A. E., Ali, G. A., Gillespie, A. W., and Wagner-Riddle, C. (2020). Soil organic matter as catalyst of crop resource capture. Front. Environ. Sci. 8, 8. doi:10.3389/fenvs.2020.00050
Klaminder, J., Giesler, R., and Makoto, K. (2013). Physical mixing between humus and mineral matter found in cryoturbated soils increases short-term heterotrophic respiration rates. Soil Biol. Biochem. 57, 922–924. doi:10.1016/j.soilbio.2012.10.038
Kravchenko, A., Otten, W., Garnier, P., Pot, V., and Baveye, P. C. (2019b). Soil aggregates as biogeochemical reactors: not a way forward in the research on soil–atmosphere exchange of greenhouse gases. Glob. Change Biol. 25, 2205–2208. doi:10.1111/gcb.14640
Kravchenko, A. N., Boast, C. W., and Bullock, D. G. (1999). Multifractal analysis of soil spatial variability. Agron. J. 91, 1033–1041. doi:10.2134/agronj1999.9161033x
Kravchenko, A. N., Guber, A. K., Razavi, B. S., Koestel, J., Quigley, M. Y., Robertson, G. P., et al. (2019a). Microbial spatial footprint as a driver of soil carbon stabilization. Nat. Commun. 10, 3121. doi:10.1038/s41467-019-11057-4
Kuramoto, Y., and Nakao, H. (2019). On the concept of dynamical reduction: the case of coupled oscillators.
Kurkjian, H. M. (2019). The Metapopulation Microcosm Plate: a modified 96-well plate for use in microbial metapopulation experiments. Methods Ecol. Evol. 10, 162–168. doi:10.1111/2041-210X.13116
Kuzyakov, Y. (2006). Sources of CO2 efflux from soil and review of partitioning methods. Soil Biol. Biochem. 38, 425–448. doi:10.1016/j.soilbio.2005.08.020
Kuzyakov, Y., and Zamanian, K. (2019). Reviews and syntheses: agropedogenesis – humankind as the sixth soil-forming factor and attractors of agricultural soil degradation. Biogeosciences 16, 4783–4803. doi:10.5194/bg-16-4783-2019
Lane, P. A. (2018). The road before us: have we come to a “fork in the road” in defining complexity? Ecol. Complex. 35, 1–5. doi:10.1016/j.ecocom.2017.07.005
Lavelle, P., Spain, A., Blouin, M., Brown, G., Decaëns, T., Grimaldi, M., et al. (2016). Ecosystem engineers in a self-organized soil: a review of concepts and future research questions. Soil Sci. 181, 91–109. doi:10.1097/SS.0000000000000155
Lehmann, J., Hansel, C. M., Kaiser, C., Kleber, M., Maher, K., Manzoni, S., et al. (2020). Persistence of soil organic carbon caused by functional complexity. Nat. Geosci. 13, 529–534. doi:10.1038/s41561-020-0612-3
Levins, R. (1969). Some demographic and genetic consequences of environmental heterogeneity for biological control. Bull. Entomological Soc. Am. 15, 237–240. doi:10.1093/besa/15.3.237
Li, K., Hajian-Forooshani, Z., Su, C., Perfecto, I., and Vandermeer, J. (2022a). Reduced rainfall and resistant varieties mediate a critical transition in the coffee rust disease. Sci. Rep. 12, 1564. doi:10.1038/s41598-022-05362-0
Li, K., Xu, G., Wang, B., Wu, G., Hou, R., and Liu, F. (2021). The predatory soil bacterium Lysobacter reprograms quorum sensing system to regulate antifungal antibiotic production in a cyclic-di-GMP-independent manner. Commun. Biol. 4, 1131. doi:10.1038/s42003-021-02660-7
Li, M., Meador, T., Sauheitl, L., Guggenberger, G., and Angst, G. (2022b). Substrate quality effects on stabilized soil carbon reverse with depth. Geoderma 406, 115511. doi:10.1016/j.geoderma.2021.115511
Li, T.-Y., and Yorke, J. A. (1975). Period three implies chaos. Am. Math. Mon. 9. doi:10.2307/2318254
Liu, T., Yang, L., Hu, Z., Xue, J., Lu, Y., Chen, X., et al. (2020). Biochar exerts negative effects on soil fauna across multiple trophic levels in a cultivated acidic soil. Biol. Fertil. Soils 56, 597–606. doi:10.1007/s00374-020-01436-1
Livingtson, K. (1985). The dialectical biologist. Richard Levins and richard lewontin. Cambridge, Mass: Harvard University Press.
Locey, K. J., and Lennon, J. T. (2016). Scaling laws predict global microbial diversity. Proc. Natl. Acad. Sci. U. S. A. 113, 5970–5975. doi:10.1073/pnas.1521291113
Lorenz, E. (1963). Deterministic nonperiodic flow. J. Atmos. Sci. 20, 130–141. doi:10.1175/1520-0469(1963)020<0130:dnf>2.0.co;2
Lozano, G. L., Bravo, J. I., Diago, M. F. G., Park, H. B., Hurley, A., Peterson, S. B., et al. (2019). Introducing THOR, a model microbiome for genetic dissection of community behavior. mBio 10, 1–14. doi:10.1128/mBio.02846-18
Ludington, W. B. (2022). Higher-order microbiome interactions and how to find them. Trends Microbiol. S0966842X22000890 30, 618–621. doi:10.1016/j.tim.2022.03.011
Macarthur, R. H., and Wilson, E. O. (1963). An equilibrium theory of insular zoogeography. Evolution 16. doi:10.2307/2407089
Mafla-Endara, P. M., Arellano-Caicedo, C., Aleklett, K., Pucetaite, M., Ohlsson, P., and Hammer, E. C. (2021). Microfluidic chips provide visual access to in situ soil ecology. Commun. Biol. 4, 889. doi:10.1038/s42003-021-02379-5
Manzoni, S., and Porporato, A. (2009). Soil carbon and nitrogen mineralization: theory and models across scales. Soil Biol. Biochem. 41, 1355–1379. doi:10.1016/j.soilbio.2009.02.031
Marder, E., and Calabrese, R. L. (1996). Principles of rhythmic motor pattern generation. Physiol. Rev. 76, 687–717. doi:10.1152/physrev.1996.76.3.687
Marris, E. (2022). A call for governments to save soil. Nature 601, 503–504. doi:10.1038/d41586-022-00158-8
Marsland, R., Cui, W., and Mehta, P. (2020). A minimal model for microbial biodiversity can reproduce experimentally observed ecological patterns. Sci. Rep. 10, 3308. doi:10.1038/s41598-020-60130-2
Mascaro, G., and Vivoni, E. R. (2016). On the observed hysteresis in field-scale soil moisture variability and its physical controls. Environ. Res. Lett. 11, 084008. doi:10.1088/1748-9326/11/8/084008
May, R. M. (1974). Biological populations with nonoverlapping generations: stable points, stable cycles, and chaos. Science 186 (4164), 645–647. doi:10.1126/science.186.4164.645
McCary, M. A., Phillips, J. S., Ramiadantsoa, T., Nell, L. A., McCormick, A. R., and Botsch, J. C. (2021). Transient top-down and bottom-up effects of resources pulsed to multiple trophic levels. Ecology 102, e03197. doi:10.1002/ecy.3197
McGehee, R., and Armstrong, R. A. (1977). Some mathematical problems concerning the ecological principle of competitive exclusion. J. Differ. Equations 23, 30–52. doi:10.1016/0022-0396(77)90135-8
McMichael, P. (2009). A food regime analysis of the “world food crisis.”. Agric. Hum. Values 26, 281–295. doi:10.1007/s10460-009-9218-5
Melguizo-Ruiz, N., Jiménez-Navarro, G., De Mas, E., Pato, J., Scheu, S., Austin, A. T., et al. (2020). Field exclusion of large soil predators impacts lower trophic levels and decreases leaf-litter decomposition in dry forests. J. Anim. Ecol. 89, 334–346. doi:10.1111/1365-2656.13101
Melillo, J. M., Frey, S. D., DeAngelis, K. M., Werner, W. J., Bernard, M. J., Bowles, F. P., et al. (2017). Long-term pattern and magnitude of soil carbon feedback to the climate system in a warming world. Science 358, 101–105. doi:10.1126/science.aan2874
Mestre, M. C. V., Hoey, L., and Vandermeer, J. (2020). Tree management and balancing process among Panamanian farmers. Small-scale For. 19, 541–563. doi:10.1007/s11842-020-09453-6
Migliavacca, M., Musavi, T., Mahecha, M. D., Nelson, J. A., Knauer, J., Baldocchi, D. D., et al. (2021). The three major axes of terrestrial ecosystem function. Nature 598, 468–472. doi:10.1038/s41586-021-03939-9
Mirás-Avalos, J. M., Trigo-Córdoba, E., Da Silva-Dias, R., Varela-Vila, I., and García-Tomillo, A. (2016). Multifractal behaviour of the soil water content of a vineyard in northwest Spain during two growing seasons. Nonlin. Process. Geophys. 23, 205–213. doi:10.5194/npg-23-205-2016
Montgomery, D. R. (2007). Soil erosion and agricultural sustainability. Soil Eros. Agric. Sustain. 104, 13268–13272. doi:10.1073/pnas.0611508104
Morrissey, E. M., Kane, J., Tripathi, B. M., Rion, M. S. I., Hungate, B. A., Franklin, R., et al. (2023). Carbon acquisition ecological strategies to connect soil microbial biodiversity and carbon cycling. Soil Biol. Biochem. 177, 108893. doi:10.1016/j.soilbio.2022.108893
Newbold, T., Tittensor, D. P., Harfoot, M. B. J., Scharlemann, J. P. W., and Purves, D. W. (2020). Non-linear changes in modelled terrestrial ecosystems subjected to perturbations. Sci. Rep. 10, 14051. doi:10.1038/s41598-020-70960-9
Ning, T., Liu, Z., Hu, H., Li, G., and Kuzyakov, Y. (2022). Physical, chemical and biological subsoiling for sustainable agriculture. Soil Tillage Res. 223, 105490. doi:10.1016/j.still.2022.105490
Nortcliff, S. (1984). Spatial analysis of soil. Prog. Phys. Geogr. Earth Environ. 8, 261–269. doi:10.1177/030913338400800205
Nugent, A., and Allison, S. D. (2022). A framework for soil microbial ecology in urban ecosystems. Ecosphere 13. doi:10.1002/ecs2.3968
Nunes, F. C., De Jesus Alves, L., De Carvalho, C. C. N., Gross, E., De Marchi Soares, T., and Prasad, M. N. V. (2020). “Soil as a complex ecological system for meeting food and nutritional security,” in Climate change and soil interactions (Elsevier), 229–269. doi:10.1016/B978-0-12-818032-7.00009-6
O’Connell, C. S., Anthony, T. L., Mayes, M. A., Pérez, T., Sihi, D., and Silver, W. L. (2022). Utilizing novel field and data exploration methods to explore hot moments in high-frequency soil nitrous oxide emissions data: opportunities and challenges. Front. For. Glob. Change 5, 674348. doi:10.3389/ffgc.2022.674348
Oldfield, E. E., Eagle, A. J., Rubin, R. L., Rudek, J., Sanderman, J., and Gordon, D. R. (2022). Crediting agricultural soil carbon sequestration. Science 375, 1222–1225. doi:10.1126/science.abl7991
O’Leary, J., Eastwood, D., Müller, C., and Boddy, L. (2018). Emergent properties arising from spatial heterogeneity influence fungal community dynamics. Fungal Ecol. 33, 32–39. doi:10.1016/j.funeco.2018.02.001
Ong, T. W., Li, K., Lucatero, A., Pak, D., Hawkes, L., Hunter, M., et al. (2020). Taylor made landscapes: using taylor’s law to scale between metapopulations and source-sinks in urban garden space. Front. Sustain. Food Syst. 4, 46. doi:10.3389/fsufs.2020.00046
Ong, T. W. Y., and Vandermeer, J. (2018). Multiple hysteretic patterns from elementary population models. Theor. Ecol. 11, 433–439. doi:10.1007/s12080-018-0376-1
Ostfeld, R., Glass, G., and Keesing, F. (2005). Spatial epidemiology: an emerging (or re-emerging) discipline. Trends Ecol. Evol. 20, 328–336. doi:10.1016/j.tree.2005.03.009
Ostfeld, R. S., Canham, C. D., Oggenfuss, K., Winchcombe, R. J., and Keesing, F. (2006). Climate, deer, rodents, and acorns as determinants of variation in lyme-disease risk. PLoS Biol. 4, e145. doi:10.1371/journal.pbio.0040145
Ostling, A., Harte, J., and Green, J. (2000). Self-similarity and clustering in the spatial distribution of species. Science 290, 671a–671a. doi:10.1126/science.290.5492.671a
Pacault, A., Ouyang, Q., and De Kepper, P. (1987). Bistable and oscillating chemical reactions. J. Stat. Phys. 48, 1005–1016. doi:10.1007/BF01009529
Pacheco, A. R., Osborne, M. L., and Segrè, D. (2021). Non-additive microbial community responses to environmental complexity. Nat. Commun. 12, 2365. doi:10.1038/s41467-021-22426-3
Pachepsky, Y., and Hill, R. L. (2017). Scale and scaling in soils. Geoderma 287, 4–30. doi:10.1016/j.geoderma.2016.08.017
Padarian, J., Minasny, B., McBratney, A., and Smith, P. (2022). Soil carbon sequestration potential in global croplands. PeerJ 10, e13740. doi:10.7717/peerj.13740
Pataki, D. E., Carreiro, M. M., Cherrier, J., Grulke, N. E., Jennings, V., Pincetl, S., et al. (2011). Coupling biogeochemical cycles in urban environments: ecosystem services, green solutions, and misconceptions. Front. Ecol. Environ. 9, 27–36. doi:10.1890/090220
Patoine, G., Eisenhauer, N., Cesarz, S., Phillips, H. R. P., Xu, X., Zhang, L., et al. (2022). Drivers and trends of global soil microbial carbon over two decades. Nat. Commun. 13, 4195. doi:10.1038/s41467-022-31833-z
Pearce, M. T., Agarwala, A., and Fisher, D. S. (2020). Stabilization of extensive fine-scale diversity by ecologically driven spatiotemporal chaos. Proc. Natl. Acad. Sci. U.S.A. 117, 14572–14583. doi:10.1073/pnas.1915313117
Perrier, E., Rieu, M., Sposito, G., and de Marsily, G. (1996). Models of the water retention curve for soils with a fractal pore size distribution. Water Resour. Res. 32, 3025–3031. doi:10.1029/96WR01779
Pfützner, M., Karny, M., Grigorenko, L. V., and Riisager, K. (2012). Radioactive decays at limits of nuclear stability. Rev. Mod. Phys. 84, 567–619. doi:10.1103/RevModPhys.84.567
Phillips, C. L., Nickerson, N., Risk, D., and Bond, B. J. (2011). Interpreting diel hysteresis between soil respiration and temperature. Glob. Change Biol. 17, 515–527. doi:10.1111/j.1365-2486.2010.02250.x
Phillips, J. D. (2017). Soil complexity and pedogenesis. Soil Sci. 182, 117–127. doi:10.1097/SS.0000000000000204
Pindral, S., Kot, R., and Hulisz, P. (2022). The influence of city development on urban pedodiversity. Sci. Rep. 12, 6009. doi:10.1038/s41598-022-09903-5
Potapov, A. M. (2022). Multifunctionality of belowground food webs: resource, size and spatial energy channels. Biol. Rev. 97, 1691–1711. doi:10.1111/brv.12857
Powlson, D. S., Smith, P., and Smith, J. U. (1996). Evaluation of soil organic matter models: using existing long-term datasets. Berlin, Heidelberg: Springer Berlin Heidelberg. doi:10.1007/978-3-642-61094-3
Pradhan, P., Costa, L., Rybski, D., Lucht, W., and Kropp, J. P. (2017). A systematic study of sustainable development goal (sdg) interactions: a systematic study of sdg interactions. Earth’s Future 5, 1169–1179. doi:10.1002/2017EF000632
Quigley, M. Y., and Kravchenko, A. N. (2022). Inputs of root-derived carbon into soil and its losses are associated with pore-size distributions. Geoderma 410, 115667. doi:10.1016/j.geoderma.2021.115667
Reijneveld, J. A. (2013). Unravelling changes in soil fertility of agricultural land in The Netherlands, 240.
Richter, D. D. (2021). Searching for solutions to our soil woes A world without soil: the past, present, and precarious future of the earth beneath our feetjo handelsman yale university press, 2021. 272 pp. Science 374, 1452. doi:10.1126/science.abm4765
Rillig, M. C., Muller, L. A. H., and Lehmann, A. (2017). Soil aggregates as massively concurrent evolutionary incubators. ISME 11, 1943–1948. doi:10.1038/ismej.2017.56
Rillig, M. C., and Mummey, D. L. (2006). Mycorrhizas and soil structure. New Phytol. 171, 41–53. doi:10.1111/j.1469-8137.2006.01750.x
Riveros-Iregui, D. A., Emanuel, R. E., Muth, D. J., McGlynn, B. L., Epstein, H. E., Welsch, D. L., et al. (2007). Diurnal hysteresis between soil CO2 and soil temperature is controlled by soil water content. Geophys. Res. Lett. 34, 1–5. doi:10.1029/2007GL030938
Robertson, A. D., Paustian, K., Ogle, S., Wallenstein, M. D., Lugato, E., and Cotrufo, M. F. (2019). Unifying soil organic matter formation and persistence frameworks: the MEMS model. Biogeosciences 16, 1225–1248. doi:10.5194/bg-16-1225-2019
Rogers, T. L., Johnson, B. J., and Munch, S. B. (2022). Chaos is not rare in natural ecosystems. Nat. Ecol. Evol. 6, 1105–1111. doi:10.1038/s41559-022-01787-y
Rutherford, S. W., and Do, D. D. (1997). Review of time lag permeation technique as a method for characterisation of porous media and membranes. Adsorption 3, 283–312. doi:10.1007/BF01653631
Schaffer, W. M., and Kot, M. (1985). Do strange attractors govern ecological systems? BioScience 35, 342–350. doi:10.2307/1309902
Scheffer, M., Barrett, S., Carpenter, S. R., Folke, C., Green, a. J., Holmgren, M., et al. (2015). Ecosystem collapsed. Science, 8–10. doi:10.1126/science.aaa9484
Scheffer, M., Carpenter, S. R., Lenton, T. M., Bascompte, J., Brock, W., Dakos, V., et al. (2012). Anticipating critical transitions. Science 338, 344–348. doi:10.1126/science.1225244
Schimel, J. P., and Weintraub, M. N. (2003). The implications of exoenzyme activity on microbial carbon and nitrogen limitation in soil: a theoretical model. Soil Biol. Biochem. 35 (04), 549–563. doi:10.1016/S0038-0717(03)00015-4
Schimel, J. P., and Bennett, J. (2004). NITROGEN MINERALIZATION: CHALLENGES OF A CHANGING PARADIGM. Ecology 85, 591–602. doi:10.1890/03-8002
Schloss, P. D., and Handelsman, J. (2007). The last word: books as a statistical metaphor for microbial communities. Annu. Rev. Microbiol. 61, 23–34. doi:10.1146/annurev.micro.61.011507.151712
Schweizer, S. A. (2022). Perspectives from the Fritz-Scheffer Awardee 2021: soil organic matter storage and functions determined by patchy and piled-up arrangements at the microscale. J. Plant Nutr. Soil Sci. Jpln. 202200217, 694–706. doi:10.1002/jpln.202200217
Segoli, M., De Gryze, S., Dou, F., Lee, J., Post, W. M., Denef, K., et al. (2013). AggModel: a soil organic matter model with measurable pools for use in incubation studies. Ecol. Model. 263, 1–9. doi:10.1016/j.ecolmodel.2013.04.010
Sierra, C. A., Hoyt, A. M., He, Y., and Trumbore, S. E. (2018). Soil organic matter persistence as a stochastic process: age and transit time distributions of carbon in soils. Glob. Biogeochem. Cycles 32, 1574–1588. doi:10.1029/2018GB005950
Sierra, C. A., and Müller, M. (2015). A general mathematical framework for representing soil organic matter dynamics. Ecol. Monogr. 85, 505–524. doi:10.1890/15-0361.1
Sihi, D., Gerber, S., Inglett, P. W., and Inglett, K. S. (2016). Comparing models of microbial–substrate interactions and their response to warming. Biogeosciences 13, 1733–1752. doi:10.5194/bg-13-1733-2016
Simard, S. W., Beiler, K. J., Bingham, M. A., Deslippe, J. R., Philip, L. J., and Teste, F. P. (2012). Mycorrhizal networks: mechanisms, ecology and modelling. Fungal Biol. Rev. 26, 39–60. doi:10.1016/j.fbr.2012.01.001
Simard, S. W., Perry, D. A., Jones, M. D., Myrold, D. D., Durall, D. M., and Molina, R. (1997). Net transfer of carbon between ectomycorrhizal tree species in the field. Nature 388, 579–582. doi:10.1038/41557
Soong, J. L., Castanha, C., Hicks Pries, C. E., Ofiti, N., Porras, R. C., Riley, W. J., et al. (2021). Five years of whole-soil warming led to loss of subsoil carbon stocks and increased CO 2 efflux. Sci. Adv. 7, eabd1343. doi:10.1126/sciadv.abd1343
Stamati, F. E., Nikolaidis, Ν. P., Banwart, S., and Blum, W. E. H. (2013). A coupled carbon, aggregation, and structure turnover (CAST) model for topsoils. Geoderma 211–212, 51–64. doi:10.1016/j.geoderma.2013.06.014
Stewart, C. E., Paustian, K., Conant, R. T., Plante, A. F., and Six, J. (2007). Soil carbon saturation: concept, evidence and evaluation. Biogeochemistry 86, 19–31. doi:10.1007/s10533-007-9140-0
Stratton, A. E., Comin, J. J., Siddique, I., Zak, D. R., Dambroz Filipini, L., Rodrigues Lucas, R., et al. (2022). Assessing cover crop and intercrop performance along a farm management gradient. Agric. Ecosyst. Environ. 332, 107925. doi:10.1016/j.agee.2022.107925
Strogatz, S. H., and Fox, R. F. (2015). Nonlinear dynamics and chaos: with applications to physics. Biol. Chem. Eng. 93. doi:10.1063/1.2807947
Sulman, B. N., Moore, J. A. M., Abramoff, R., Averill, C., Kivlin, S., Georgiou, K., et al. (2018). Multiple models and experiments underscore large uncertainty in soil carbon dynamics. Biogeochemistry 141, 109–123. doi:10.1007/s10533-018-0509-z
Sun, X., Han, L., Wang, M., Liu, S., and Shen, Y. (2023). Social exclusion with antisocial punishment in spatial public goods game. Phys. Lett. A 474, 128837. doi:10.1016/j.physleta.2023.128837
Tang, J. Y., and Riley, W. J. (2013). A total quasi-steady-state formulation of substrate uptake kinetics in complex networks and an example application to microbial litter decomposition. Biogeosciences 10, 8329–8351. doi:10.5194/bg-10-8329-2013
Tarquis, A. M., Castellanos, M. T., Cartagena, M. C., Arce, A., Ribas, F., Cabello, M. J., et al. (2017). Scale and space dependencies of soil nitrogen variability. Nonlin. Process. Geophys. 24, 77–87. doi:10.5194/npg-24-77-2017
Tisdall, J. M., and Oades, J. M. (1982). Organic matter and water-stable aggregates in soils. J. Soil Sci. 33, 141–163. doi:10.1111/j.1365-2389.1982.tb01755.x
Todd-Brown, K. E. O., Abramoff, R. Z., Beem-Miller, J., Blair, H. K., Earl, S., Frederick, K. J., et al. (2022). Reviews and syntheses: the promise of big diverse soil data, moving current practices towards future potential. Biogeosciences 19, 3505–3522. doi:10.5194/bg-19-3505-2022
Todd-Brown, K. E. O., Randerson, J. T., Post, W. M., Hoffman, F. M., Tarnocai, C., Schuur, E. A. G., et al. (2013). Causes of variation in soil carbon simulations from CMIP5 Earth system models and comparison with observations. Biogeosciences 10, 1717–1736. doi:10.5194/bg-10-1717-2013
Toker, D., Sommer, F. T., and D’Esposito, M. (2020). A simple method for detecting chaos in nature. Commun. Biol. 3, 11–13. doi:10.1038/s42003-019-0715-9
Traulsen, A., and Nowak, M. A. (2006). Evolution of cooperation by multilevel selection. Proc. Natl. Acad. Sci. U.S.A. 103, 10952–10955. doi:10.1073/pnas.0602530103
Trubl, G., Jang, H. B., Roux, S., Emerson, J. B., Solonenko, N., Vik, D. R., et al. (2018). Soil viruses are underexplored players in ecosystem carbon processing. mSystems 3, 000766. doi:10.1128/msystems.00076-18
Turley, N. E., Bell-Dereske, L., Evans, S. E., and Brudvig, L. A. (2020). Agricultural land-use history and restoration impact soil microbial biodiversity. J. Appl. Ecol. 57, 852–863. doi:10.1111/1365-2664.13591
Tyler, S. W., and Wheatcraft, S. W. (1989). Application of fractal mathematics to soil water retention estimation. SOIL SCIENCE SOCIETY OF AMERICA, 987–996. doi:10.2136/sssaj1989.03615995005300040001x
Upton, R. N., Bach, E. M., and Hofmockel, K. S. (2019). Spatio-temporal microbial community dynamics within soil aggregates. Soil Biol. Biochem. 132, 58–68. doi:10.1016/j.soilbio.2019.01.016
Van Den Berg, N. I., Machado, D., Santos, S., Rocha, I., Chacón, J., Harcombe, W., et al. (2022). Ecological modelling approaches for predicting emergent properties in microbial communities. Nat. Ecol. Evol. 6, 855–865. doi:10.1038/s41559-022-01746-7
van der Heijden, M. G. A., and Horton, T. R. (2009). Socialism in soil? The importance of mycorrhizal fungal networks for facilitation in natural ecosystems. J. Ecol. 12. doi:10.1111/j.1365-2745.2009.01570.x
Vandermeer, J. (2006). Oscillating populations and biodiversity maintenance. Oscillating Populations Biodivers. Maintenance 56, 967–975. doi:10.1641/0006-3568(2006)56[967:opabm]2.0.co;2
Vandermeer, J. (2013). Forcing by rare species and intransitive loops creates distinct bouts of extinction events conditioned by spatial pattern in competition communities. Theor. Ecol. 6, 395–404. doi:10.1007/s12080-012-0175-z
Vandermeer, J. (2021). The meta-Allee effect: a generalization from intermittent metapopulations. Ecol. Complex. 46, 100912. doi:10.1016/j.ecocom.2021.100912
Vandermeer, J., Hajian-Forooshani, Z., Medina, N., and Perfecto, I. (2021). New forms of structure in ecosystems revealed with the Kuramoto model. R. Soc. open Sci. 8, 210122. doi:10.1098/rsos.210122
Vandermeer, J., and Jackson, D. (2018). Stabilizing intransitive loops: self-organized spatial structure and disjoint time frames in the coffee agroecosystem. Ecosphere 9, 17. doi:10.1002/ecs2.2489
Vandermeer, J., and Perfecto, I. (2017). Ecological complexity and agroecosystems: seven themes from theory. Agroecol. Sustain. Food Syst. 41, 697–722. doi:10.1080/21683565.2017.1322166
Vandermeer, J., and Perfecto, I. (2019). Hysteresis and critical transitions in a coffee agroecosystem. Proc. Natl. Acad. Sci. U.S.A. 116, 15074–15079. doi:10.1073/pnas.1902773116
Vandermeer, J., and Yitbarek, S. (2012). Self-organized spatial pattern determines biodiversity in spatial competition. J. Theor. Biol. 300, 48–56. doi:10.1016/j.jtbi.2012.01.005
Vandermeer, J., and Yodzis, P. (1999). Basin boundary collision as a model of discontinuous change in ecosystems. Ecol. Soc. Am. 80 1817–1827. doi:10.1890/0012-9658(1999)080[1817:bbcaam]2.0.co;2
Vereecken, H., Schnepf, A., Hopmans, J. W., Javaux, M., Or, D., Roose, T., et al. (2016). Modeling soil processes: review, key challenges, and new perspectives. Vadose Zone J. 57. doi:10.2136/vzj2015.09.0131
Victor, J. M., Goulet, L. M., Schmidt, K., Linds, W., Episkenew, J.-A., and Goulet, K. (2016). Like braiding sweetgrass: nurturing relationships and alliances in indigenous community-based research. Int. Rev. Qual. Res. 23. doi:10.1525/irqr.2016.9.4.423
Vitousek, P. M., Treseder, K. K., Howarth, R. W., and Menge, D. N. L. (2022). A “toy model” analysis of causes of nitrogen limitation in terrestrial ecosystems. Biogeochemistry 160, 381–394. doi:10.1007/s10533-022-00959-z
Vogel, C., Mueller, C. W., Höschen, C., Buegger, F., Heister, K., Schulz, S., et al. (2014). Submicron structures provide preferential spots for carbon and nitrogen sequestration in soils. Nat. Commun. 5, 2947. doi:10.1038/ncomms3947
Vogel, H., Balseiro-Romero, M., Kravchenko, A., Otten, W., Pot, V., Schlüter, S., et al. (2022). A holistic perspective on soil architecture is needed as a key to soil functions. Eur. J Soil Sci. 73. doi:10.1111/ejss.13152
Volterra, V. (1928). Variations and fluctuations of the number of individuals in animal species living together. ICES J. Mar. Sci. 3, 3–51. doi:10.1093/icesjms/3.1.3
Wall, D. H., Nielsen, U. N., and Six, J. (2015). Soil biodiversity and human health. Nature 528, 69–76. doi:10.1038/nature15744
Wang, B., Brewer, P. E., Shugart, H. H., Lerdau, M. T., and Allison, S. D. (2019). Soil aggregates as biogeochemical reactors and implications for soil – atmosphere exchange of greenhouse gases — a concept. Glob. Chang. Biol. 25, 373–385. doi:10.1111/gcb.14515
Wang, S., Thi Thu Hoang, D., The Luu, A., Mostafa, T., and Razavi, B. S. (2023). Environmental memory of microbes regulates the response of soil enzyme kinetics to extreme water events: drought-rewetting-flooding. Geoderma 437, 116593. doi:10.1016/j.geoderma.2023.116593
Wang, Y. P., Chen, B. C., Wieder, W. R., Leite, M., Medlyn, B. E., Rasmussen, M., et al. (2014). Oscillatory behavior of two nonlinear microbial models of soil carbon decomposition. Biogeosciences 11, 1817–1831. doi:10.5194/bg-11-1817-2014
Waring, B. G., Sulman, B. N., Reed, S., Smith, A. P., Averill, C., Creamer, C. A., et al. (2020). From pools to flow: the PROMISE framework for new insights on soil carbon cycling in a changing world. Glob. Change Biol. 26, 6631–6643. doi:10.1111/gcb.15365
Weisberg, M. (2007). Forty years of “the strategy”: Levins on model building and idealization. Biol. Philos. 21, 623–645. doi:10.1007/s10539-006-9051-9
Weitzman, J. N., Brooks, J. R., Compton, J. E., Faulkner, B. R., Mayer, P. M., Peachey, R. E., et al. (2022). Deep soil nitrogen storage slows nitrate leaching through the vadose zone. Agric. Ecosyst. Environ. 332, 107949. doi:10.1016/j.agee.2022.107949
Wieder, W. R., Allison, S. D., Davidson, E. A., Georgiou, K., Hararuk, O., He, Y., et al. (2015). Explicitly representing soil microbial processes in Earth system models: soil microbes in earth system models. Glob. Biogeochem. Cycles 29, 1782–1800. doi:10.1002/2015GB005188
Williams, T. G., Dressler, G., Stratton, A. E., and Müller, B. (2021). Ecological and financial strategies provide complementary benefits for smallholder climate resilience: insights from a simulation model. E&S 26, art14. art14. doi:10.5751/ES-12207-260214
Wilpiszeski, R. L., Aufrecht, J. A., Retterer, S. T., Sullivan, M. B., Graham, D. E., Pierce, E. M., et al. (2019). Soil aggregate microbial communities: towards understanding microbiome interactions at biologically relevant scales. Appl. Environ. Microbiol. 85, 003244. doi:10.1128/AEM.00324-19
Wilson, W. G., and Abrams, P. A. (2005). Coexistence of cycling and dispersing consumer species: Armstrong and McGehee in space. Am. Nat. 165, 193–205. doi:10.1086/427733
Winfree, A. T., and Strogatz, S. H. (1984). Organizing centres for three-dimensional chemical waves. Nature 311, 611–615. doi:10.1038/311611a0
Wolford, W. (2020). The plantationocene: a lusotropical contribution to the theory. Ann. Am. Assoc. Geogr., 1–18. doi:10.1080/24694452.2020.1850231
Xiao, X., and Fussmann, G. F. (2013). Armstrong – McGehee mechanism revisited: competitive exclusion and coexistence of nonlinear consumers. J. Theor. Biol. 339, 26–35. doi:10.1016/j.jtbi.2013.05.025
Yitbarek, S., and Vandermeer, J. H. (2017). Reduction of species coexistence through mixing in a spatial competition model. Theor. Ecol. 10, 443–450. doi:10.1007/s12080-017-0341-4
Young, I. M., and Crawford, J. W. (1991). The fractal structure of soil aggregates: its measurement and interpretation. J. Soil Sci. 42, 187–192. doi:10.1111/j.1365-2389.1991.tb00400.x
Young, I. M., and Crawford, J. W. (2004). Interactions and self-organization in the soil-microbe complex. Science 304, 1634–1637. doi:10.1126/science.1097394
Zhang, Q., Katul, G. G., Oren, R., Daly, E., Manzoni, S., and Yang, D. (2015). The hysteresis response of soil CO2 concentration and soil respiration to soil temperature. J. Geophys. Res. Biogeosci. 120, 1605–1618. doi:10.1002/2015JG003047
Zhang, Q., Manzoni, S., Katul, G., Porporato, A., and Yang, D. (2014). The hysteretic evapotranspiration-Vapor pressure deficit relation: ET-VPD hysteresis. J. Geophys. Res. Biogeosci. 119, 125–140. doi:10.1002/2013JG002484
Zhang, Y., Lavallee, J. M., Robertson, A. D., Even, R., Ogle, S. M., Paustian, K., et al. (2021). Simulating measurable ecosystem carbon and nitrogen dynamics with the mechanistically defined MEMS 2.0 model. Biogeosciences 18, 3147–3171. doi:10.5194/bg-18-3147-2021
Zhang, Z., Gao, X., Zhang, S., Gao, H., Huang, J., Sun, S., et al. (2022). Urban development enhances soil organic carbon storage through increasing urban vegetation. J. Environ. Manag. 312, 114922. doi:10.1016/j.jenvman.2022.114922
Keywords: complex systems, nonlinear oscillator dynamics, soil system modeling, hysteresis, critical tipping point transition
Citation: Medina N and Vandermeer J (2023) Developing systems theory in soil agroecology: incorporating heterogeneity and dynamic instability. Front. Environ. Sci. 11:1171194. doi: 10.3389/fenvs.2023.1171194
Received: 21 February 2023; Accepted: 06 November 2023;
Published: 28 November 2023.
Edited by:
Joséphine Peigne, Institut Supérieur d’Agriculture Rhône-Alpes, FranceReviewed by:
Bin Wang, Oak Ridge National Laboratory (DOE), United StatesCopyright © 2023 Medina and Vandermeer. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nicholas Medina, bm1lZGluYUB1bWljaC5lZHU=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.