The prioritization of solutions for reducing the influence of climate change on the environment by using the conception of bipolar complex fuzzy power Dombi aggregation operators

This article aims to examine the causes and consequences of climate change on the environment and then prioritize the solution for reducing its influence on the environment under the setting of the bipolar complex fuzzy set (BCFS). Climate change is illustrated by the transformation of wind, temperature, and precipitation; regardless of its natural causes, it is generally connected with human movement and ozone-depleting substances. It is an important task to determine the reasons, effects, and, especially, solutions for reducing the effects of climate change. The prioritization of the solution for reducing the influence of climate change is a multi-attribute decision-making (MADM) dilemma, and for solving such a dilemma, we need a proper MADM technique. Thus, in this study, we first interpreted various aggregation operators (AOs) such as bipolar complex fuzzy (BCF) power Dombi averaging (BCFPDA); BCF power Dombi weighted averaging (BCFPDWA); BCF power Dombi ordered weighted averaging (BCFPDOWA); BCF power Dombi geometric (BCFPDG); BCF power Dombi weighted geometric (BCFPDWG); and BCF power Dombi ordered weighted geometric (BCFPDOWG) and then interpreted an MADM approach based on the invented operators. Furthermore, we studied a numerical example regarding the prioritization of solutions for the reduction of the influence of climate change on the environment and achieved the best solution, i.e., $D_{BCFS-4}=$ ocean and sea protection. Finally, the advantages of this approach are compared with those of other approaches.

1 Introduction

Climate change depicts a transformation under normal circumstances such as precipitation and temperature in a particular region during a certain period. For instance, some centuries ago, a large part of the United States was covered by ice sheets and today, there is a hotter climate with fewer glacial masses. Worldwide climate change alludes to the typical long-haul changes over the whole planet, such as reduction in rain and the rise in temperature, that imply increased ice liquefaction in places such as Greenland, the Arctic, and Antarctica; the rise of ocean levels; the change in blossom and plant-sprouting times; and the contraction of mountains’ icy masses. Researchers have noticed atypical changes. For instance, the planet’s typical temperature has been increasing more rapidly than anticipated in recent years. Some regions face more change in the temperature than others. However, the air temperature of the world near the surface of the earth has increased by two degrees Fahrenheit in the last hundred years. The last 5 years have been the hottest in hundreds of years. Researchers are worried about this warming up. If the climate of the earth keeps heating up, the power of precipitation during tempests, such as tropical storms, will increase and dry spells will intensify. A change of a couple of degrees in the temperature of the whole planet will seriously affect the earth, plants, and animals. There are various solutions for the reduction of the effects of climate change that can help in saving the planet. Falloon et al. (2014)) investigated ensembles and vagueness in climate change influence. Im et al. (2022) discussed climate change and air pollution. Khurshid et al. (2022) studied the influence of climate change on economic development. Dong et al. (2023) used the integrated fuzzy decision technique to study digital green innovation investment project selection of photovoltaic building material enterprises.

MADM can offer the best option among the possible ones. To make the right decisions, various scholars have come up with various possible ideas. Initially, their decisions were modeled on the notion of crisp sets which were headed toward unsatisfactory outcomes and were not applicable in real-life circumstances. Due to the increased complexity of these circumstances, it is difficult for an expert or decision analyst to deal with vague or imprecise information, so experts cannot use the conventional approach to determine the best alternative. Zadeh (1965) proposed a novel model which is a fuzzy set (FS) that is a strong model to handle MADM issues. In FS, the domain element consists of a value between 0 and 1, which is called the grade of satisfaction (GS). The FS model has been used in many areas by numerous scholars (Maiers and Sherif, 1985; Adlassnig, 1986; Rasheed, 2019; Lin et al., 2021). But, in some circumstances, the FS lacks certain information or data due to deficiencies in the model. For example, the FS model cannot express the negative expressions of human beings in real-life issues. Therefore, Zhang (1994) proposed a new model which is a bipolar fuzzy set (BFS), which is a strong model to handle MADM problems that cannot be handled by the FS. In the BFS, a domain element consists of a value between 0 and 1 which is called a positive grade of satisfiability (PGS), and a value between −1 and 0 which is called a negative grade of satisfiability (NGS).

Some shortcomings of the FS model have been discussed previously. Another limitation of the FS model is the lack of a second dimension, i.e., extra fuzzy information. The FS model is unsuccessful in real-life issues where experts need additional fuzzy information or a second dimension. Ramot et al. (2002) proposed a modified model of the FS which is a complex fuzzy set (CFS) that is a great model for handling MADM issues where the second dimension is required. In CFS, an element of the domain consists of a value in a unit disk of a complex plane which is called the grade of satisfaction. Due to the development of the world and the increasing complexities in every situation, it is difficult for an expert or decision analyst to handle information containing ambiguities or inaccuracies. Therefore, experts cannot determine the best alternative with the models discussed previously in numerous real-life circumstances, since each model has its shortcomings; for example, the FS cannot model negative expressions and the second dimension, the BFS cannot model the second dimension, and the CFS cannot model negative expressions. Therefore, Mahmood and Ur Rehman (2022a) combined all these models and formed a new bipolar complex fuzzy set (BCFS) model which is perfect to handle MADM problems which could not be managed by the previous models. In BCFS, an element of the domain consists of a positive grade of satisfiability and a negative grade of satisfiability in a unit square of the complex plane.

1.1 Literature review

Various researchers worked on climate change, for instance, Short and Neckles (1999) investigated the influence of global climate change on seagrass, Kolk and Pinkse (2004) analyzed the market strategies for climate change, Carlton and Jacobson (2013) investigated the climate change and coastal environment, Barnes et al. (2013) studied the influence of climate change on respiratory and allergic diseases, Chevallier et al. (2011) studied the threat of climate change to the environment, Durkalec et al. (2015) investigated the effect of climate change on the environment as a factor of homegrown health, and Dahlmann et al. (2019) analyzed the effect of corporate climate change focusing on environmental implementation. Javadinejad et al. (2021) investigated the factors influencing farmers’ resilience under climate change. Escoriza and Hernandez (2021) studied buffered microclimate determinates. Lo Piccolo and Landi (2021) studied red-leafed species for urban greening in the era of global climate change.

Zhu et al. (2020) studied the influence of climate change under the setting of FS. Zamani et al. (2020) investigated climate change by using the multi-criteria decision-making (MCDM) approach. Chung and Kim (2014) constructed a fuzzy multi-criteria method to rank areas for treating wastewater assuming various climate change situations. Climate change was studied under fuzzy SWAT and TOPSIS approaches by Senent-Aparicio et al. (2017). Deveci et al. (2022) investigated climate change using the fuzzy WASPAS method. A large number of decision-making (DM) approaches investigated by various authors for BFS such as the MCDM technique discussed by Alghamdi et al. (2018), TOPSIS and ELECTRE-I approaches invented by Akram and Arshad (2020), MULTIMOORA technique investigated by Stanujkic et al. (2019), and the VIKOR mechanism established by Alsolame and Alshehri (2020). Numerous researchers have studied graphs in the setting of a BFS such as Rashmanlou et al. (2016), Samanta and Pal (2012), Singh and Kumar (2014), and Akram (2011). Bipolar fuzzy (BF) relations were investigated by Lee and Hur (2019), Yang (2020), and Dudziak and Pe (2010). Several scholars have explored aggregation operators (AOs) for BFS such as Jana et al. (2019a), Wei et al. (2018), and Riaz et al. (2022). The algebraic structures of the BFS were investigated by different authors such as Abughazalah et al. (2022) who investigated serval ideals in BCI algebras in the setting of the BFS, Yiarayong (2021) who studied bipolar fuzzy semigroups, and Senapati (2015) who invented bipolar fuzzy BG sub-algebras. Abdullah et al. (2014) gave the notion of BF soft sets (SSs).

Tamir et al. (2011) studied the notion of CFS in the Cartesian structure. The relations in the setting of CFS were explored by Zhang et al. (2010) and Khan et al. (2021). The AOs for the CFS were discussed by Bi et al. (2019), Bi et al. (2018), and Hu et al. (2019). Ur Rehman and Mahmood (2022) explored similarity measures (SMs) in the environment of the BCFS. Ur Rehman et al. (2022) established an analytical hierarchy process based on the Frank AOs in the setting of the BCFS. Mahmood and Ur Rehman (2022b) explored the MADM mechanism based on the Dombi AOs in the environment of the BCFS. Mahmood et al. (2022a) identified and classified the AOs for BCFS. The Hamacher AOs for the BCF information were diagnosed by Mahmood et al. (2021a). Mahmood et al. (2022b) studied Bonferroni mean operators relying on the BCFS. Mahmood et al. (2022c) researched the bipolar complex fuzzy SS (BCFSS).

1.2 Motivation and advantages

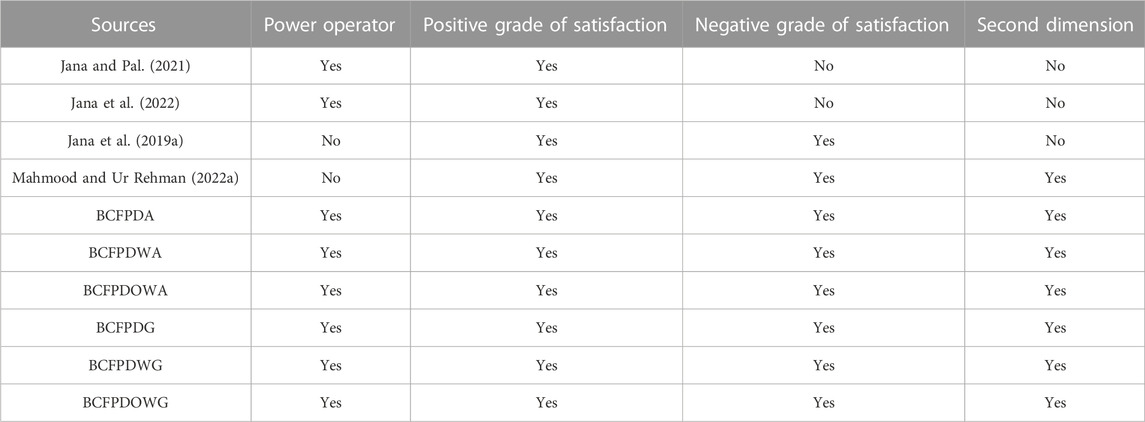
Dombi t-norm and t-conorm operators were first investigated by Dombi (1982). Dombi operators (DOs) have a great facility to work in the assessment of parameters and provide accurate and successful outcomes. Numerous scholars around the world used DOs in many notions (Jana et al., 2019a; Jana et al., 2019b; Khan et al., 2019; Seikh and Mandal, 2021; Jana et al., 2022). In 2001, Yager (2001) proposed the power aggregation operator (PAO) to manage and lessen the impact of important approximation information of certain favoritism decision-makers. Several scholars have used PAOs in various notions such as Jiang et al. (2018), Wei and Lu (2018), Hu et al. (2019), Liu et al. (2021), and Alcantud et al. (2022). The reality is that the BCFS is a perfect model for the management of MADM issues involving ambiguous and uncertain information, and it is the most modified version of the FS. The comparison of the BCFS with a few prevailing notions is shown in Table 1.

TABLE 1

TABLE 1. Comparison of BCFS with certain prevailing theories.

The combination of DOs and PAOs would finish the favoritism of a decision-maker and will make the process more fair and reliable. Until now, there has been no study on the power of Dombi AOs in the setting of the BCFS which means that the experts cannot get the advantages of the parameter of DOs and the PAOs in the environment of the BCFS and would not get a fair result. Motivated by this, in this study, we combined DOs and PAOs in a BCFS environment to obtain the advantages of DOs, PAOs, and BCFS, and we investigated BCFPDA, BCFPDWA, BCFPDOWA, BCFPDG, BCFPDWG, and BCFPDOWG operators and the MADM approach based on these operators. In various situations in the area of environmental science, the decision experts would face the information in the model of the BCFS, and to get better and fair results, they would need the invented operators and the invented MADM approach. Thus, in addition, we studied the prioritization of solutions to reduce the effect of climate change on the environment under the setting of the BCFS. A few precious advantages of the discovered information are as follows.

1. Neglecting the imaginary part in both the positive grade of satisfaction and negative grade of satisfaction in the invented operators, the operator will decrease to the BFS model.

2. Neglecting the negative grade of satisfaction in the invented operators, the operator will decrease to the CFS model.

3. Neglecting the imaginary part in a positive grade of satisfaction and neglecting a negative grade of satisfaction in the invented operators, the operator will decrease to the FS model.

The following Table 2 shows the comparison of the derived work with certain existing operators.

TABLE 2

TABLE 2. Comparison of the derived operators with certain existing operators.

The structure of this article is as follows. In Section 2, we explore some basics about climate change, BCFS, its properties, Dombi t-norm and t-conorm, and PAOs. In Section 3, we have two subsections: we develop the BCF power Dombi-averaging operators in subsection 3.1 and we develop the BCF power Dombi geometric operators in subsection 3.2. In Section 4, we propose an MADM approach in the BCF sets by using the proposed operators and discussing a numerical example. The proficiency and advantages of this study are shown in Section 5, where our approach is compared with those of some works in the literature. The conclusion is presented in Section 6.

2 Preliminaries

Climate change is a worldwide alteration of the climate over an extended period of time. This transformation can occur at both territorial and universal levels. The climate change that is currently occurring poses a great danger to life on this planet. World leaders have reached an important compromise in the Paris Agreement to begin reducing the effects of climate change. At the heart of all climate change agreements is the reduction of fluxes of ozone-depleting substances, which should reach zero quickly. Since seas and plants play an important role in maintaining the climate or environment, that is the inherent capacity of plants and seas will retain carbon dioxide, which would help reduce global warming. Substances that damage the ozone layer allow the sun to shine unrestrictedly on the earth’s surface. Normal ozone-depleting substances ensure a reasonable temperature for life on the planet, instead of artificial gases that produce exceptionally high heat expansion. They prevent its intensity from being reflected into space and disperse it throughout the world. There are several substances that damage the ozone layer. The six gases to be managed by the Paris Agreement are hydrofluorocarbons, methane, sulfur hexafluoride, carbon dioxide, nitrous oxide, and perfluorocarbons. The effects of climate change are as follows:

1. Global warming: Global warming is one of the main impacts of climate change. It is undeniable that the Earth’s temperature is rising rapidly due to human actions such as intensive agriculture, deforestation, over-exploitation, and mining.

2. Air pollution: The vital ozone-depleting substance is not considered an atmospheric pollutant as it does not appear to influence human wellbeing. However, there is a relationship between global warming and climate change as the atmospheric intensity of some air pollutants.

3. Water pollution: Climate change and water pollutants are firmly connected, both in streams, seas, and oceans. This pollution specifically manifests itself through changes in the progressions of different streams, temperature expansion, and the focus of pollutants in the water.

4. Land pollution: Dirt is equally affected by climate change. The land and the climate are affected by human actions; natural resources are exceptionally delicate and, most of the time, are wasted by men.

There are several solutions to reduce and manage the influence of climate change on the environment. In Section 4, we will discuss solutions to climate change.

Definition 1. The model of BCFS is propounded according to Mahmood and Ur Rehman, 2022b:

$D_{BCFS}=\left\{\left(y,\left({{\rm K}}_{D_{BCFS}}^P\left(y\right),{{\rm K}}_{D_{BCFS}}^N\left(y\right)\right)\right)|y\in \mathcal{Y}\right\}=\left\{\left(y,\left(\begin{array}{c}{{\rm K}}_{D_{BCFS}}^{RP}\left(y\right)+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IP}\left(y\right),\\ {{\rm K}}_{D_{BCFS}}^{RN}\left(y\right)+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IN}\left(y\right)\end{array}\right)\right)|y\in \mathcal{Y}\right\}(1)$

where ${{\rm K}}_{D_{BCFS}}^P\left(y\right)$ is considered as PGS and ${{\rm K}}_{D_{BCFS}}^N\left(y\right)$ is considered as NGS and ${{\rm K}}_{D_{BCFS}}^{RP}\left(y\right),{{\rm K}}_{D_{BCFS}}^{IP}\left(y\right)\in \left[0,1\right]$, ${{\rm K}}_{D_{BCFS}}^{RN}\left(y\right),{{\rm K}}_{D_{BCFS}}^{IN}\left(y\right)\in \left[-1,0\right].$ The bipolar complex fuzzy number (BCFN) is portrayed as $D_{BCFS}=\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)=\left({{\rm K}}_{D_{BCFS}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IP},{{\rm K}}_{D_{BCFS}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IN}\right)$.

Definition 2. Consider a BCFN, $D_{BCFS}=\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)=\left({{\rm K}}_{D_{BCFS}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IP},{{\rm K}}_{D_{BCFS}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IN}\right)$, then the following equations provide the scores and accuracy values, respectively (Mahmood et al., 2021a):

$\mathbb{S}\left(D_{BCFS}\right)=\frac{1}{4}\left(2+{{\rm K}}_{D_{BCFS}}^{RP}+{{\rm K}}_{D_{BCFS}}^{IP}-{{\rm K}}_{D_{BCFS}}^{RN}+{{\rm K}}_{D_{BCFS}}^{IN}\right),\mathbb{S}\left(D_{BCFS}\right)\in \left[0,1\right](2)$

$\mathbb{H}\left(D_{BCFS}\right)=\frac{{{\rm K}}_{D_{BCFS}}^{RP}+{{\rm K}}_{D_{BCFS}}^{IP}-{{\rm K}}_{D_{BCFS}}^{RN}-{{\rm K}}_{D_{BCFS}}^{IN}}{4},\mathbb{H}\left(D_{BCFS}\right)\in \left[0,1\right](3)$

Definition 3. (Mahmood et al., 2021a) Consider two BCFNs, $D_{BCFS-1}=\left({{\rm K}}_{D_{BCFS-1}}^P,{{\rm K}}_{D_{BCFS-1}}^N\right)=\left({{\rm K}}_{D_{BCFS-1}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS}-1}^{IP},{{\rm K}}_{D_{BCFS-1}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-1}}^{IN}\right)$ and $D_{BCFS-2}=\left({{\rm K}}_{D_{BCFS-2}}^P,{{\rm K}}_{D_{BCFS-2}}^N\right)=\left({{\rm K}}_{D_{BCFS-2}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-2}}^{IP},{{\rm K}}_{D_{BCFS-2}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-2}}^{IN}\right),$ with $\sigma \ge 0$, then

1. $D_{BCFS-1}\oplus D_{BCFS-2}=\left(\begin{array}{c}{{\rm K}}_{D_{BCFS-1}}^{RP}+{{\rm K}}_{D_{BCFS-2}}^{RP}-{{\rm K}}_{D_{BCFS-1}}^{RP}{{\rm K}}_{D_{BCFS-2}}^{RP}\\ +\mathrm{i}\left({{\rm K}}_{D_{BCFS-1}}^{IP}+{{\rm K}}_{D_{BCFS-2}}^{IP}-{{\rm K}}_{D_{BCFS-1}}^{IP}{{\rm K}}_{D_{BCFS-2}}^{IP}\right),\\ -\left({{\rm K}}_{D_{BCFS-1}}^{RN}{{\rm K}}_{D_{BCFS-2}}^{RN}\right)+\mathrm{i}\left(-\left({{\rm K}}_{D_{BCFS-1}}^{IN}{{\rm K}}_{D_{BCFS-2}}^{IN}\right)\right)\end{array}\right)$

2. $D_{BCFS-1}\otimes D_{BCFS-2}=\left(\begin{array}{c}{{\rm K}}_{D_{BCFS-1}}^{RP}{{\rm K}}_{D_{BCFS-2}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-1}}^{IP}{{\rm K}}_{D_{BCFS-2}}^{IP},\\ {{\rm K}}_{D_{BCFS-1}}^{RN}+{{\rm K}}_{D_{BCFS-2}}^{RN}+{{\rm K}}_{D_{BCFS-1}}^{RN}{{\rm K}}_{D_{BCFS-2}}^{RN}\\ \mathrm{i}\left({{\rm K}}_{D_{BCFS-1}}^{IN}+{{\rm K}}_{D_{BCFS-2}}^{IN}+{{\rm K}}_{D_{BCFS-1}}^{IN}{{\rm K}}_{D_{BCFS-2}}^{IN}\right)\end{array}\right)$

3. $\sigma D_{BCFS-1}=\left(\begin{array}{c}1-{\left(1-{{\rm K}}_{D_{BCFS-1}}^{RP}\right)}^{\sigma }+\mathrm{i}\left(1-{\left(1-{{\rm K}}_{D_{BCFS-1}}^{IP}\right)}^{\sigma }\right),\\ -{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}^{\sigma }+\mathrm{i}\left(-{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}^{\sigma }\right)\end{array}\right)$

4. $D_{BCFS-1}^{\sigma }=\left(\begin{array}{c}{\left({{\rm K}}_{D_{BCFS-1}}^{RP}\right)}^{\sigma }+\mathrm{i}{\left({{\rm K}}_{D_{BCFS-1}}^{IP}\right)}^{\sigma },\\ -1+{\left(1+{{\rm K}}_{D_{BCFS-1}}^{RN}\right)}^{\sigma }+\mathrm{i}\left(-1+{\left(1+{{\rm K}}_{D_{BCFS-1}}^{IN}\right)}^{\sigma }\right)\end{array}\right)$.

Definition 4. The Dombi t-norms and t-conorms for any two real numbers $D_{RN-1}$, $D_{RN-2}$ are interpreted as (Dombi, 1982):

$Dom\left(D_{RN-1},D_{RN-2}\right)=\frac{1}{1+{\left\{{\left(\frac{1-D_{RN-1}}{D_{RN-1}}\right)}^{\alpha }+{\left(\frac{1-D_{RN-2}}{D_{RN-2}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}(4)$

$Do{m}^{*}\left(D_{RN-1},D_{RN-2}\right)=1-\frac{1}{1+{\left\{{\left(\frac{D_{RN-1}}{{1-D}_{RN-1}}\right)}^{\alpha }+{\left(\frac{D_{RN-2}}{1-D_{RN-2}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}(5)$

where $\left(D_{RN-1},D_{RN-2}\right)\in \left[0,1\right]\times \left[0,1\right]$ and $\alpha \ge 1$.

Definition 5. Consider a class of positive numbers, then, the PAO is determined as (Yager, 2001):

$PA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \oplus \\ \mathrm{J}=1\end{array}\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{D}_{BCFS-\mathrm{J}}(6)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ and $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ signify the support among $D_{BCFS-\mathrm{J}}$ and $D_{BCFS-l}$ with the following properties.

1. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\in \left[0,1\right]$

2. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)=\mathit{Sup}\left(D_{BCFS-l},D_{BCFS-\mathrm{J}}\right)$

3. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\ge \mathit{Sup}\left(D_{BCFS-r},D_{BCFS-s}\right)$ if $d\left(D_{BCFS-\mathrm{J}},D_{BCFS-\mathrm{J}}\right)<d\left(D_{BCFS-r},D_{BCFS-s}\right)$, where $d$ is any distance measure among them.

Definition 6. Consider two BCFNs, $D_{BCFS-1}=\left({{\rm K}}_{D_{BCFS-1}}^P,{{\rm K}}_{D_{BCFS-1}}^N\right)=\left({{\rm K}}_{D_{BCFS-1}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS}-1}^{IP},{{\rm K}}_{D_{BCFS-1}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-1}}^{IN}\right)$ and $D_{BCFS-2}=\left({{\rm K}}_{D_{BCFS-2}}^P,{{\rm K}}_{D_{BCFS-2}}^N\right)=\left({{\rm K}}_{D_{BCFS-2}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-2}}^{IP},{{\rm K}}_{D_{BCFS-2}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-2}}^{IN}\right)$, with $\sigma \ge 0$, and the Dombi operation in the setting of the BCFS is portrayed as (Mahmood and Ur Rehman., 2022a):

1. $D_{BCFS-1}\oplus D_{BCFS-2}=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }+{\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{RP}}{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }+{\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{IP}}{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}\right)}^{\alpha }+{\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}\right)}^{\alpha }+{\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)$

2. $D_{BCFS-1}\otimes D_{BCFS-2}=\left(\begin{array}{c}\frac{1}{1+{\left\{{\left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}{{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }+{\left(\frac{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}{{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{1}{1+{\left\{{\left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}{{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }+{\left(\frac{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}{{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}\right)}^{\alpha }+{\left(\frac{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}\right)}^{\alpha }+{\left(\frac{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$

3. $\sigma D_{BCFS-1}=\left(\begin{array}{c}1-\frac{1}{1+{\left\{\sigma {\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{\sigma \left(\frac{{{\rm K}}_{D_{BCFS-1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\sigma \left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{\sigma \left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)$

4. ${\left(D_{BCFS-1}\right)}^{\sigma }=$ $\left(\begin{array}{c}\frac{1}{1+{\left\{\sigma {\left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}{{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{1}{1+{\left\{{\sigma \left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}{{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{\sigma {\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\left(-1+\frac{1}{1+{\left\{\sigma {\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$

3 BCF power Dombi aggregation operators

Here, we have two subsections. In Section 3.1, we propound BCF power Dombi-averaging operators, and in Section 3.2, we propound BCF power Dombi geometric operators. ${\wp }_{\mathcal{w}}=\left({\wp }_{\mathcal{w}-1},{\wp }_{\mathcal{w}-2},\dots ,{\wp }_{\mathcal{w}-n}\right)$ is considered as weight vector (WV) holding that ${\wp }_{\mathcal{w}-\mathrm{J}}\in \left[0,1\right]$ and ${\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}=1$ in the whole article.

3.1 BCF power Dombi-averaging operators

By fusing Dombi and power operators in the environment of BCFNs, here, we are defining BCFPDA, BCFPDWA, and BCFPDOWA operators.

In the following, we derived the BCFPDA operator.

Definition 7. Consider a class of BCFNs, $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, and then, the BCFPDA operator is determined as

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \oplus \\ \mathrm{J}=1\end{array}\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{D}_{BCFS-\mathrm{J}}(7)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ and $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ signify the support among $D_{BCFS-\mathrm{J}}$ and $D_{BCFS-l}$ with the following properties.

1. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\in \left[0,1\right]$

2. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)=\mathit{Sup}\left(D_{BCFS-l},D_{BCFS-\mathrm{J}}\right)$

3. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\ge \mathit{Sup}\left(D_{BCFS-r},D_{BCFS-s}\right)$ if $d\left(D_{BCFS-\mathrm{J}},D_{BCFS-\mathrm{J}}\right)<d\left(D_{BCFS-r},D_{BCFS-s}\right)$, where $d$ is any distance measure among BCF sets.

Theorem 1. After using the BCFPDA operator on the class of BCFNs: $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, we achieve an aggregated value in the form of BCFN

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)(8)$

Proof. First, ${ɧ}_{\mathrm{J}}=\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}$ was substituted in Eq. 8, then Eq. 8 became

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{ɧ}_{\mathrm{J}}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{{ɧ}_{\mathrm{J}}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)(9)$

Next, we must portray that Eq. 9 is held for $n=2$

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2}\right)={ɧ}_1{D}_{BCFS-1}\oplus {ɧ}_2{D}_{BCFS-2},$

and we have

${ɧ}_1{D}_{BCFS-1}=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_1\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right),$

${ɧ}_2{D}_{BCFS-2}=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_2{\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{RP}}{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_2\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{IP}}{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right),$

then, by using part 1 of Definition 6,

${ɧ}_1{D}_{BCFS-1}\oplus {ɧ}_2{D}_{BCFS-2}=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_1\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)\oplus \left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_2{\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{RP}}{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_2\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{IP}}{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)$

$=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }+{ɧ}_2{\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{RP}}{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_1\left(\frac{{{\rm K}}_{D_{BCFS-1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }+{{ɧ}_2\left(\frac{{{\rm K}}_{D_{BCFS-2}}^{IP}}{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}\right)}^{\alpha }+{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_1\left(\frac{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}\right)}^{\alpha }+{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)$

$=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{ɧ}_{\mathrm{J}}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{{ɧ}_{\mathrm{J}}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right).(10)$

Eq. 10 implies that Eq. 9 is valid for $n=2$. Furthermore, we assume that Eq. 9 is valid for $n=\mathbb{Q}$, i.e.,

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-\mathbb{Q}}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right).$

Next, we assume $n=\mathbb{Q}+1$. Then by part 1 of definition 6, we have

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-\mathbb{Q}},D_{BCFS-\mathbb{Q}+1}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)\oplus \left(\begin{array}{c}1-\frac{1}{1+{\left\{{ɧ}_{\mathbb{Q}+1}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{{ɧ}_2\left(\frac{{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{{ɧ}_2\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)$

$=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{ɧ}_{\mathrm{J}}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{{ɧ}_{\mathrm{J}}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{{ɧ}_{\mathrm{J}}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right).$

Eq. 9 is valid for $n=\mathbb{Q}+1$. This completes the proof.Following are the properties which the BCFPDA operator holds.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, BCFPDA operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDA\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right).$ Then,

$D_{BCFS}^{-}\le BCFPDA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

We derived the BCFPDWA operator as follows.

Definition 8. Consider a class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, then the BCFPDWA operator is determined as

$BCFPDWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \oplus \\ \mathrm{J}=1\end{array}\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{D}_{BCFS-\mathrm{J}},(11)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$.

Theorem 2. After using the BCFPDA operator on the class of BCFNs, $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, we achieve an aggregated value in the form of BCFN

$BCFPDWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)(12)$

The properties which the BCFPDWA operator holds are as follows.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, BCFPDWA operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDWA\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right),$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$. Then,

$D_{BCFS}^{-}\le BCFPDWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

We derived the BCFPDOWA operator as follows

Definition 9. Consider a class of BCFNs, $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$; then, the BCFPDOWA operator is determined as

$BCFPDOWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \oplus \\ \mathrm{J}=1\end{array}\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{D}_{BCFS-\eta \left(\mathrm{J}\right)}(13)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ and $\left(\eta \left(1\right),\eta \left(2\right),\dots ,\eta \left(n\right)\right)$ would be the permutations of $\eta \left(\mathrm{J}\right),\mathrm{J}=1,2,\dots ,n$ and $\forall$ $D_{BCFS-\eta \left(\mathrm{J}-1\right)}\ge D_{BCFS-\eta \left(\mathrm{J}\right)}$; $D_{BCFS-\eta \left(\mathrm{J}\right)}$ is the $\mathrm{J}th$ largest element of BCFNs.

Theorem 3. After using the BCFPDOWA operator on the class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, we achieved an aggregated value in the form of BCFN

$BCFPDOWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{\left(\frac{{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RP}}{1-{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}1-\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}\left(\frac{{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IP}}{1-{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ \frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RN}}{\left|{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{-1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}\left(\frac{1+{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IN}}{\left|{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IN}\right|}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\end{array}\right)(14)$

The properties which the BCFPDOWA operator holds are as follows.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, BCFPDOWA operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDOWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDOWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDOWA\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$. Then

$D_{BCFS}^{-}\le BCFPDOWA\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

3.2 BCF power Dombi geometric operators

By fusing the Dombi geometric and power operators in the environment of BCFNs, here, we are defining BCFPDG, BCFPDWG, and BCFPDOWG operators.

We derived the BCFPDG operator as follows.

Definition 10. Consider a class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, then the BCFPDG operator is determined as

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \otimes \\ \mathrm{J}=1\end{array}{\left(D_{BCFS-\mathrm{J}}\right)}^{\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}},(15)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ and $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ signify the support among $D_{BCFS-\mathrm{J}}$ and $D_{BCFS-l}$ with the following properties.

1. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\in \left[0,1\right]$

2. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)=\mathit{Sup}\left(D_{BCFS-l},D_{BCFS-\mathrm{J}}\right)$

3. $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)\ge \mathit{Sup}\left(D_{BCFS-r},D_{BCFS-s}\right)$ if $d\left(D_{BCFS-\mathrm{J}},D_{BCFS-\mathrm{J}}\right)<d\left(D_{BCFS-r},D_{BCFS-s}\right)$, where $d$ is any distance measure among BCF sets.

Theorem 4. After using the BCFPDG operator on the class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n,$we achieve an aggregated value in the form of BCFN

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)(16)$

Proof. First, ${ɧ}_{\mathrm{J}}=\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}$ is substituted in Eq. 16, and then Eq. 16 becomes

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)(17)$

Next, we must portray that Eq. 17 is held for $n=2$

$BCFPDA\left(D_{BCFS-1},D_{BCFS-2}\right)={\left(D_{BCFS-1}\right)}^{{ɧ}_1}\otimes {\left(D_{BCFS-1}\right)}^{{ɧ}_1},$

and by using part 2 of Definition 6, we have:

${\left(D_{BCFS-1}\right)}^{{ɧ}_1}\otimes {\left(D_{BCFS-1}\right)}^{{ɧ}_1}=\left(\begin{array}{c}\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{RP}}{{{\rm K}}_{D_{BCFS-1}}^{RP}}\right)}^{\alpha }+{ɧ}_2{\left(\frac{1-{{\rm K}}_{D_{BCFS-2}}^{RP}}{{{\rm K}}_{D_{BCFS-2}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{1-{{\rm K}}_{D_{BCFS-1}}^{IP}}{{{\rm K}}_{D_{BCFS-1}}^{IP}}\right)}^{\alpha }+{ɧ}_2{\left(\frac{1-{{\rm K}}_{D_{BCFS-2}}^{IP}}{{{\rm K}}_{D_{BCFS-2}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{RN}}\right)}^{\alpha }+{ɧ}_2{\left(\frac{\left|{{\rm K}}_{D_{BCFS-2}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-2}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{ɧ}_1{\left(\frac{\left|{{\rm K}}_{D_{BCFS-1}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-1}}^{IN}}\right)}^{\alpha }+{ɧ}_2{\left(\frac{\left|{{\rm K}}_{D_{BCFS-2}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-2}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right).$

$=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^2{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)(18)$

Equation 18 implies that Eq. 17 is valid for $n=2$. Furthermore, we assume that Eq. 17 is valid for $n=\mathbb{Q}$, i.e.,

$=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$

Next, we assume $n=\mathbb{Q}+1$. Then, by using part 2 of Definition 6, we have

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-\mathbb{Q}},D_{BCFS-\mathbb{Q}+1}\right)=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)\otimes \left(\begin{array}{c}\frac{1}{1+{\left\{{ɧ}_{\mathbb{Q}+1}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{1}{1+{\left\{{ɧ}_{\mathbb{Q}+1}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{ɧ}_{\mathbb{Q}+1}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\left(-1+\frac{1}{1+{\left\{{ɧ}_{\mathbb{Q}+1}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathbb{Q}+1}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$

$=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{ɧ}_{\mathrm{J}}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}+\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^{\mathbb{Q}+1}{ɧ}_{\mathrm{J}}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$

Eq. 17 is valid for $n=\mathbb{Q}+1$. This completes the proof.The properties which the BCFPDG operator holds are as follows.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, BCFPDG operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDG\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$. Then,

$D_{BCFS}^{-}\le BCFPDG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

We derived the following BCFPDWG operator.

Definition 11. Consider a class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, then the BCFPDWG operator is determined as:

$BCFPDWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \otimes \\ \mathrm{J}=1\end{array}{\left(D_{BCFS-\mathrm{J}}\right)}^{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}}(19)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$.

Theorem 5. After using the BCFPDWG operator on the class of BCFNs, $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, we achieve an aggregated value in the form of BCFN

$BCFPDWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)$.(20)

The properties which the BCFPDWG operator holds are as follows.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, the BCFPDWG operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDWG\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$. Then,

$D_{BCFS}^{-}\le BCFPDWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

We introduce the following BCFPDOWG operator.

Definition 12. Consider a class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, then the BCFPDOWG operator is determined as:

$BCFPDOWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\begin{array}{c}n\\ \otimes \\ \mathrm{J}=1\end{array}{\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)}^{\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}}(21)$

where ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ and $\left(\eta \left(1\right),\eta \left(2\right),\dots ,\eta \left(n\right)\right)$ would be the permutations of $\eta \left(\mathrm{J}\right),\mathrm{J}=1,2,\dots ,n$ and $\forall$ $D_{BCFS-\eta \left(\mathrm{J}-1\right)}\ge D_{BCFS-\eta \left(\mathrm{J}\right)}$; $D_{BCFS-\eta \left(\mathrm{J}\right)}$ is the $\mathrm{J}th$ largest element of BCFNs.

Theorem 6. After using the BCFPDOWG operator on the class of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right),\mathrm{J}=1,2,\dots ,n$, we achieve an aggregated value in the form of BCFN

$BCFPODWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=\left(\begin{array}{c}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RP}}{{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{\left(\frac{1-{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IP}}{{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IP}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}},\\ -1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RN}\right|}{1+{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{RN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\\ +\mathrm{i}\left(-1+\frac{1}{1+{\left\{{\displaystyle \sum }_{\mathrm{J}=1}^n\frac{{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n{\wp }_{\mathcal{w}-\mathrm{J}}\left(1+{\rm T}\left(D_{BCFS-\eta \left(\mathrm{J}\right)}\right)\right)}{\left(\frac{\left|{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IN}\right|}{1+{{\rm K}}_{D_{BCFS-\eta \left(\mathrm{J}\right)}}^{IN}}\right)}^{\alpha }\right\}}^{\frac{1}{\alpha }}}\right)\end{array}\right)(22)$

The following are the properties which the BCFPDOWG operator holds.Consider two classes of BCFNs $D_{BCFS-\mathrm{J}}=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right)$ and $D_{BCFS-\mathrm{J}}^{\prime }=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^P,{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^N\right)=\left({{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IP},{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS-\mathrm{J}}^{\prime }}^{IN}\right)$; $\mathrm{J}=1,2,\dots ,n$. Then, BCFPDOWG operators hold the following properties.

1. Idempotency: When all $D_{BCFS-\mathrm{J}}$ are the same, i.e., $D_{BCFS-\mathrm{J}}=D_{BCFS}$, then

$BCFPDOWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)=D_{BCFS}.$

2. Monotonicity: If $D_{BCFS-\mathrm{J}}\le D_{BCFS-\mathrm{J}}^{\prime }\forall \mathrm{J}$, then

$BCFPDWOG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le BCFPDWOG\left(D_{BCFS-1}^{\prime },D_{BCFS-2}^{\prime },\dots ,D_{BCFS-n}^{\prime }\right).$

3. Boundedness: Let $D_{BCFS}^{-}=\left(\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$ and $D_{BCFS}^{+}=\left(\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RP}\right\}+\mathrm{i}\underset{\mathrm{J}}{\max }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IP}\right\},\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{RN}\right\}+\mathrm{i}\underset{\mathrm{J}}{\min }\left\{{{\rm K}}_{D_{BCFS-\mathrm{J}}}^{IN}\right\}\right)$. Then,

$D_{BCFS}^{-}\le BCFPDOWG\left(D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right)\le D_{BCFS}^{+}.$

4 Application

Climate change is detrimental to the environment and the earth’s health. In the previous sections, we have briefly discussed climate change, its effects, and its causes. Now, we consider ways of preventing climate change. There are some solutions to climate change listed as follows:

1. Renewable energies: To reduce climate change, we need to adopt renewable and clean energies such as geothermal, solar, biomass, and wind.

2. Sustainable transportation: For the prevention of climate change, we have to align transportation techniques with ecological needs, and we have to decrease their carbon footprint. It is vital to re-evaluate our vehicle strategies from the planning phase toward eco-friendly transportation.

3. Air pollution prevention: There are numerous strategies to reduce, control, and prevent air pollution, namely, by reducing the use of non-renewable energy sources and restricting industrial and waste outflows. By preventing air pollution, climate change would be reduced.

4. Squander management and reusing: The best way to reduce waste is to fit creative techniques into our utilization designs. The reuse system must also be considered in our usage propensities.

5. Ocean and sea protection: Seas and oceans are the biggest reservoirs of ozone-depleting substances and are an extraordinary emotional support network for life on earth. Presently, it is critical to restrict overfishing and unreasonable constructions in beachfront regions; the utilization of harmless ecosystem elements is advisable.

6. Circular economy: To prevent climate change, we need to use the three “Rs” of the circular economy, i.e., Reduce, Reuse, and Recycle, to collectively reduce our waste and avoid the superfluous creation of new things.

The search for the best solution to climate change is an MADM issue, and for this, we provide an MADM approach.

4.1 MADM method

Let a class of $n$ alternatives $\left\{D_{BCFS-1},D_{BCFS-2},\dots ,D_{BCFS-n}\right\}$ and $m$ attributes $\left\{{\mathcal{Z}}_{AT-1},{\mathcal{Z}}_{AT-2},..,{\mathcal{Z}}_{AT-m}\right\}$ with connected WV ${\wp }_{\mathcal{w}}=\left({\wp }_{\mathcal{w}-1},{\wp }_{\mathcal{w}-2},\dots ,{\wp }_{\mathcal{w}-m}\right)$, satisfying $0\le {\wp }_{\mathcal{w}-\mathrm{J}}\le 1\forall \mathrm{J}$ and ${\displaystyle \sum }_{\mathrm{J}=1}^m{\wp }_{\mathcal{w}-\mathrm{J}}=1$. Then, the structure of the MADM method is explored as follows:

Step 1The information or data presented by the expert in the structure of BCFN was gathered, i.e., $D_{BCFS}=\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)=\left({{\rm K}}_{D_{BCFS}}^{RP}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IP},{{\rm K}}_{D_{BCFS}}^{RN}+\mathrm{i}{{\rm K}}_{D_{BCFS}}^{IN}\right)$, where ${{\rm K}}_{D_{BCFS}}^{RP},{{\rm K}}_{D_{BCFS}}^{IP}\in \left[0,1\right]$, ${{\rm K}}_{D_{BCFS}}^{RN},{{\rm K}}_{D_{BCFS}}^{IN}\in \left[-1,0\right]$, and a decision matrix was built.

Step 2The matrix was normalized to achieve a normalized matrix if the data are cost type by using the following formula

${\mathbb{N}}_{BCFS}=\left\{\begin{array}{cc}\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)& forbenefitsortdata\\ {\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)}^c& forcostsortdata\end{array}\right.(23)$

where ${\left({{\rm K}}_{D_{BCFS}}^P,{{\rm K}}_{D_{BCFS}}^N\right)}^c={\left({{\rm K}}_{D_{BCFS}}^{RP}+\mathfrak{i}{{\rm K}}_{D_{BCFS}}^{IP},{{\rm K}}_{D_{BCFS}}^{RN}+\mathfrak{i}{{\rm K}}_{D_{BCFS}}^{IN}\right)}^c=\left(1-{{\rm K}}_{D_{BCFS}}^{RP}+\mathfrak{i}\left(1-{{\rm K}}_{D_{BCFS}}^{IP}\right),-1-{{\rm K}}_{D_{BCFS}}^{RN}+\mathfrak{i}\left(-1-{{\rm K}}_{D_{BCFS}}^{IN}\right)\right)$. There is no such requirement if the data are benefit type.

Step 3The decision matrix achieved was aggregated after step 2 with the assistance of one of the propounded BCFPDA, BCFPDWA, BCFPDOWA, BCFPDG, BCFPDWG, and BCFPDOWG operators.

Step 4To be able to order the aggregated values of the previous step, the score values were determined with the assistance of Eq. 2. If Eq. 2 showed equal values for any two aggregated values, then one can determine the accuracy values by Eq. 3.

Step 5. Relying on this obtained order, the ranking can be determined.Now, we consider a numerical example regarding the prioritization of solutions to reduce the influence of climate change on the environment.

4.2 Numerical example

Let us consider four solutions to climate change, i.e., $D_{BCFS-1}=Renewableenergy$, $D_{BCFS-2}=Airpollutionprevention$, $D_{BCFS-3}=Circulareconomy$, and $D_{BCFS-4}=OceanandSeaprotection$, and four attributes related to these solutions, i.e., ${\mathcal{Z}}_{AT-1}=Reducingtemperature$, ${\mathcal{Z}}_{AT-2}=Wasteprevention$, ${\mathcal{Z}}_{AT-3}=Regulatetheclimate$, and ${\mathcal{Z}}_{AT-4}=Reducepollutants$. The weight vector considered by the expert linked with attributes is (0.25, 0.25, 0.3, 0.2).

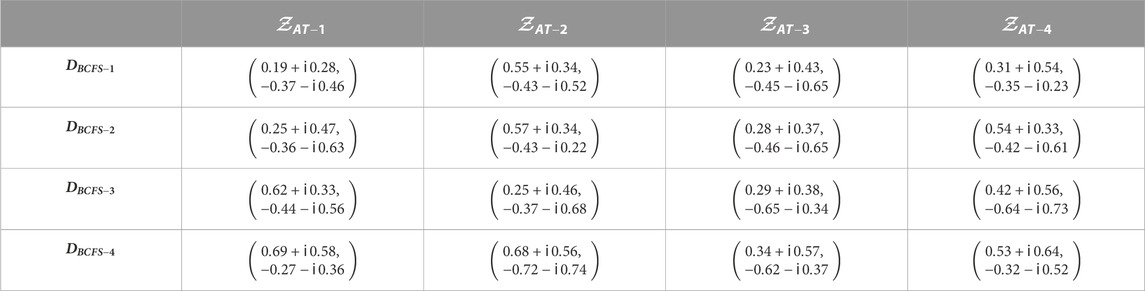
Step 1The data presented by the expert in the model of BCFS are illustrated in Table 3.

TABLE 3

TABLE 3. Data explored by the expert.

Step 2No requirement for normalization.

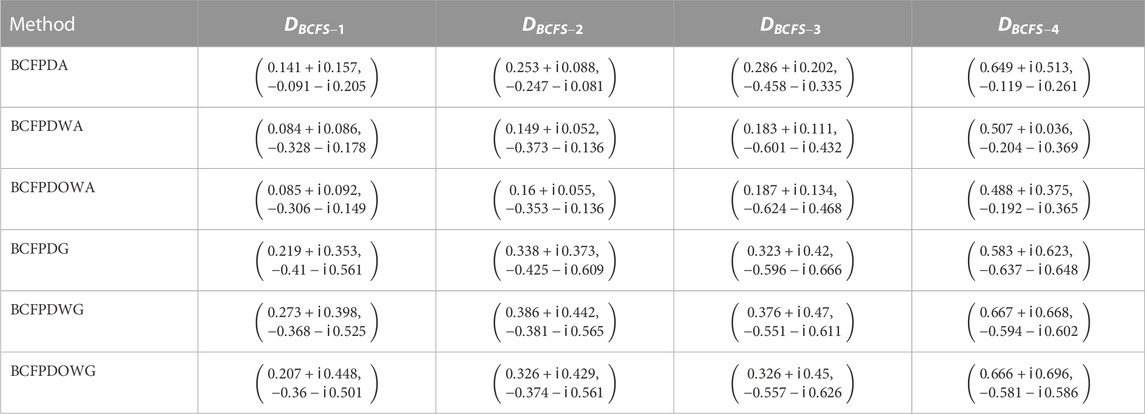
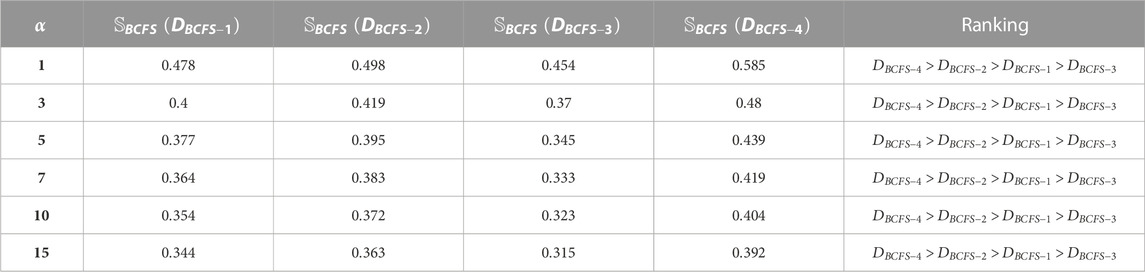
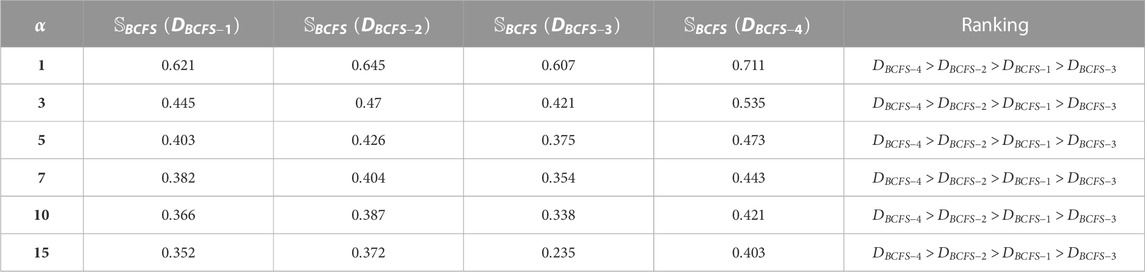
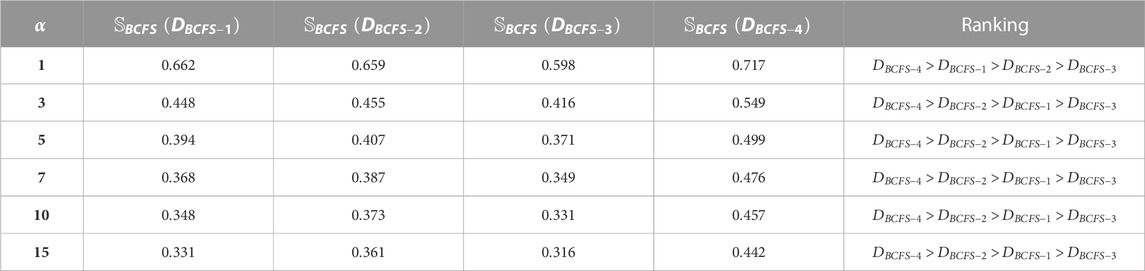
Step 3The decision matrix obtained after step 2 was aggregated with the assistance of the proposed BCFPDA, BCFPDWA, BCFPDOWA, BCFPDG, BCFPDWG, and BCFPDOWG operators, and the outcomes are displayed in Table 4. Furthermore, we used the SM defined by Mahmood and Rehman (Rashmanlou et al., 2016) for support.In Table 4, we present the aggregated outcomes of each alternative. Using BCFPDA, we found the aggregated outcomes as $D_{BCFS-1}=\left(\begin{array}{c}0.141+\mathrm{i}0.157,\\ -0.091-\mathrm{i}0.205\end{array}\right)$, $D_{BCFS-2}=\left(\begin{array}{c}0.253+\mathrm{i}0.088,\\ -0.247-\mathrm{i}0.081\end{array}\right)$, $D_{BCFS-3}=\left(\begin{array}{c}0.286+\mathrm{i}0.202,\\ -0.458-\mathrm{i}0.335\end{array}\right)$, and $D_{BCFS-4}=\left(\begin{array}{c}0.649+\mathrm{i}0.513,\\ -0.119-\mathrm{i}0.261\end{array}\right)$. Using BCFPDWA, we found the aggregated outcomes as $D_{BCFS-1}=\left(\begin{array}{c}0.084+\mathrm{i}0.086,\\ -0.328-\mathrm{i}0.178\end{array}\right)$, $D_{BCFS-2}=\left(\begin{array}{c}0.149+\mathrm{i}0.052,\\ -0.373-\mathrm{i}0.136\end{array}\right)$, $D_{BCFS-3}=\left(\begin{array}{c}0.183+\mathrm{i}0.111,\\ -0.601-\mathrm{i}0.432\end{array}\right)$, and $D_{BCFS-4}=\left(\begin{array}{c}0.507+\mathrm{i}0.036,\\ -0.204-\mathrm{i}0.369\end{array}\right)$. Using BCFPDWA, we found the aggregated outcomes as $D_{BCFS-1}=\left(\begin{array}{c}0.085+\mathrm{i}0.092,\\ -0.306-\mathrm{i}0.149\end{array}\right)$, $D_{BCFS-2}=\left(\begin{array}{c}0.16+\mathrm{i}0.055,\\ -0.353-\mathrm{i}0.136\end{array}\right)$, $D_{BCFS-3}=\left(\begin{array}{c}0.187+\mathrm{i}0.134,\\ -0.624-\mathrm{i}0.468\end{array}\right)$, and $D_{BCFS-4}=\left(\begin{array}{c}0.488+\mathrm{i}0.375,\\ -0.192-\mathrm{i}0.365\end{array}\right)$. Similarly, after using BCFPDG, BCFPDWG, and BCFPDOWG operators, the aggregated outcomes are investigated in Table 4.

TABLE 4

TABLE 4. Aggregated outcomes.

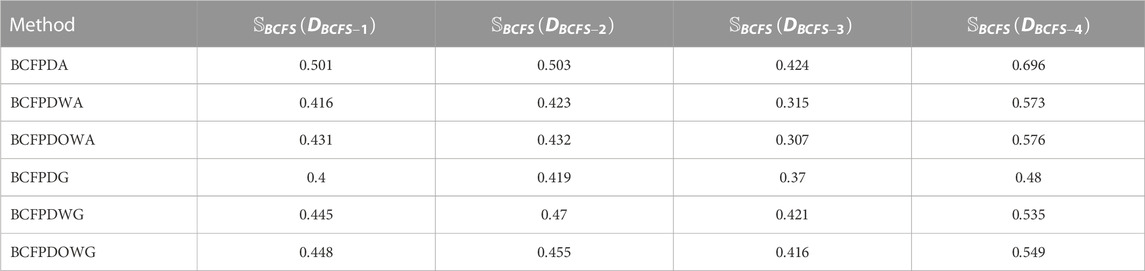
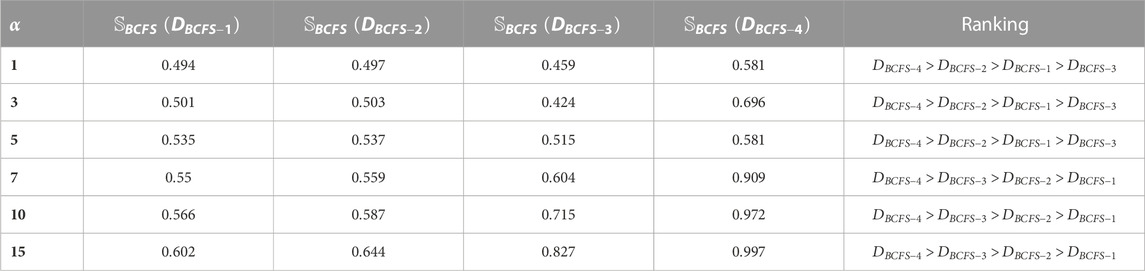
Step 4We achieved the order among the aggregated outcomes by retrieving the score values with the help of Eq. 2, as shown in Table 5.In Table 5, we present the score value of each alternative. By using BCFPDA and Eq. 2, we found the score value of $D_{BCFS-1}=0.501$, $D_{BCFS-2}=0.503$, $D_{BCFS-3}=0.424$, and $D_{BCFS-4}=0.696$. Using BCFPDWA and Eq. 2, we found the score value of $D_{BCFS-1}=0.416$, $D_{BCFS-2}=0.423$, $D_{BCFS-3}=0.315$, and $D_{BCFS-4}=0.573$. Using BCFPDOWA and Eq. 2, we found the score values of $D_{BCFS-1}=0.431$, $D_{BCFS-2}=0.432$, $D_{BCFS-3}=0.307$, and $D_{BCFS-4}=0.576$. Similarly after using BCFPDG, BCFPDWG, and BCFPDOWG operators and Eq. 2, we found the rest of the score values presented in Table 5.

TABLE 5

TABLE 5. Score values of the aggregated outcomes.

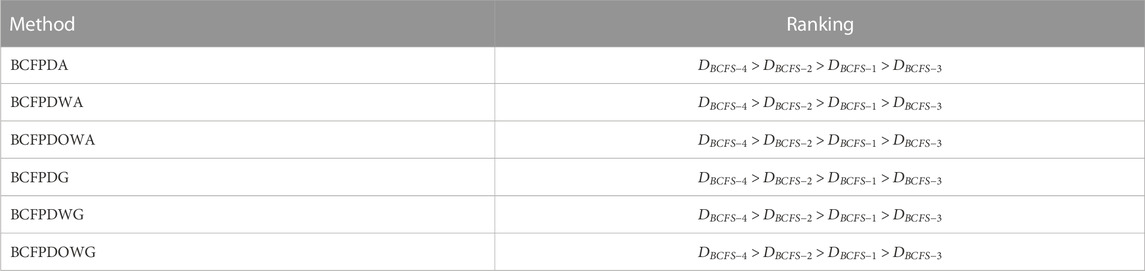
Step 5. Relying on the score values, the ranking is presented in Table 6.From Table 6, we achieved the ranking order by using all the invented operators and keeping the parameter $\alpha =3$; we have $D_{BCFS-4}>D_{BCFS-2}>D_{BCFS-1}>D_{BCFS-3}$ as a ranking order. This means that $D_{BCFS-4}=OceanandSeaprotection$ is the best solution to reduce the influence of climate change on the environment.

TABLE 6

TABLE 6. Ranking order relies on the score values.

4.3 Advantages and limitations

The investigated MADM approach has the advantage of tackling the information in the environment of BCFS, BFS, CFS, and FS. The investigated MADM technique used one of the invented operators in the setting of BCFS and can be reduced to the settings of BFS, CFS, and FS. Thus, the invented MADM approach can also transform into the BFS, CFS, and FS. The invented MADM approach is unable to handle the information in the setting of complex intuitionistic fuzzy sets, bipolar complex intuitionistic fuzzy set, and their generalizations. Furthermore, from the previously discussed numerical example, we noticed that the data of this example are artificial but it is a practical situation from real life. This shows that the interpreted operators and MADM technique would be useful to handle real-life dilemmas in various fields such as computer science and environmental science.

4.4 Sensitivity analysis of $\mathit{\alpha }$

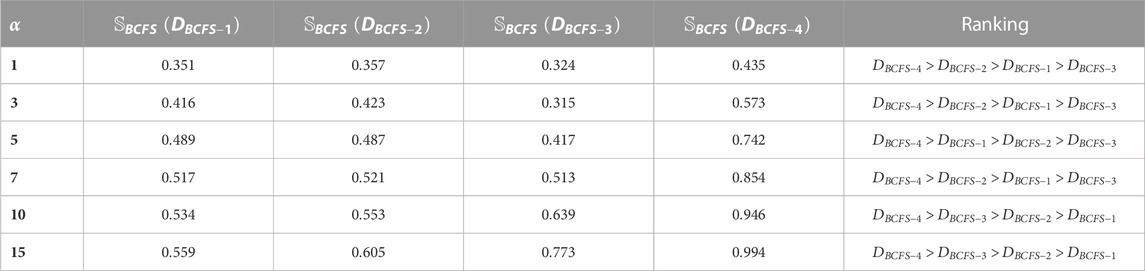
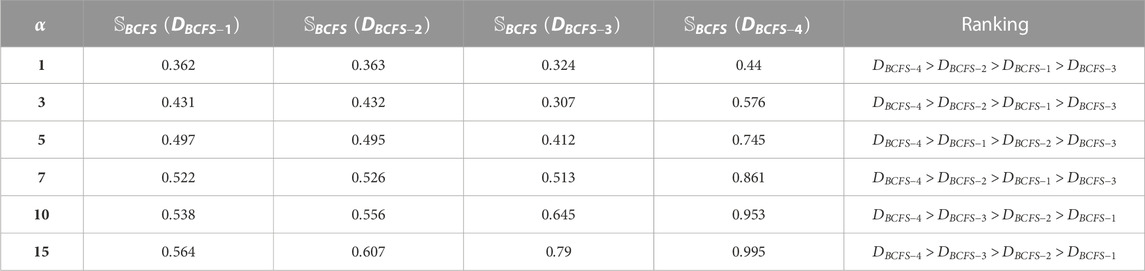
Here, we observed the effect of the parameter $\alpha$ on the result of the DM dilemma by taking various values of $\alpha$. For various arguments of $\alpha$ such as $1,3,5,7,10,$ and $15$, the ranking order and score values determined by each invented operator are described in Tables 7–12.

TABLE 7

TABLE 7. Score values and ranking order for various values of $\alpha$ using the BCFPDA operator.

TABLE 8

TABLE 8. Score values and ranking order for various values of $\alpha$ using the BCFPDWA operator.

TABLE 9

TABLE 9. Score values and ranking order for various values of $\alpha$ using the BCFPDOWA operator.

TABLE 10

TABLE 10. Score values and ranking order for various values of $\alpha$ using the BCFPDG operator.

TABLE 11

TABLE 11. Score values and ranking order for various values of $\alpha$ using the BCFPDWA operator.

TABLE 12

TABLE 12. Score values and ranking order for various values of $\alpha$ using the BCFPDOWA operator.

By using the BCFPDA operator and by putting $\alpha =1,3,$ and $5$, the ranking order is $D_{BCFS-4}>D_{BCFS-2}>D_{BCFS-1}>D_{BCFS-3}$ and by putting the $\alpha =7,10,$ and $15$, the ranking order is $D_{BCFS-4}>D_{BCFS-3}>D_{BCFS-2}>D_{BCFS-1}$, as described in Table 7. By using BCFPDWA and BCFDOWA operators and by putting $\alpha =1,3,$ and $7$, the ranking order becomes $D_{BCFS-4}>D_{BCFS-2}>D_{BCFS-1}>D_{BCFS-3}$. By putting the $\alpha =5$, the ranking order becomes $D_{BCFS-4}>D_{BCFS-1}>D_{BCFS-2}>D_{BCFS-3}$, and by putting the $\alpha =10$ and $15$, the ranking order becomes $D_{BCFS-4}>D_{BCFS-3}>D_{BCFS-2}>D_{BCFS-1}$ as described in Tables 8,9. By using BCFPDG and BCFPDWG operators for all given values of $\alpha$, we achieved the same ranking, which is $D_{BCFS-4}>D_{BCFS-1}>D_{BCFS-2}>D_{BCFS-3}$, interpreted in Tables 10,11. By using the BCFPDOWG operator and by putting $\alpha =1,$ the ranking order is $D_{BCFS-4}>D_{BCFS-1}>D_{BCFS-2}>D_{BCFS-3}$ and by putting the $\alpha =3,5,7,10,$ and $15$, the ranking order becomes $D_{BCFS-4}>D_{BCFS-2}>D_{BCFS-1}>D_{BCFS-3}$ investigated in Table 12. This shows that $D_{BCFS-4}$ is the most common and superb alternative. Furthermore, in the invented DM approach based on the BCFPDA, BCFPDWA, BCFPDOWA, BCFPDG, BCFPDWG, and BCFPDOWG operators, by changing the values of $\alpha$, the related ranking order can be changed. Moreover, we noted that by increasing the values of $\alpha$, the score values based on the aggregated values obtained using BCFPDA, BCFPDWA and BCFPDOWA increased, while by increasing the values of $\alpha$, the score values based on the aggregated values obtained using BCFPDG, BCFPDWG, and BCFPDOWG decreased.

5 Comparison

The research we developed in this article has more advantages and is more effective than the solutions proposed in other articles. To prove this, we apply the data in Table 3 which contains the information on the structure of BCFNs from the works of Jana et al. (2022), Jana et al. (2019a), Mahmood and Ur Rehman. (2022b), and our own. The results are shown in Table 13, and the ranking is in Table 14.

TABLE 13

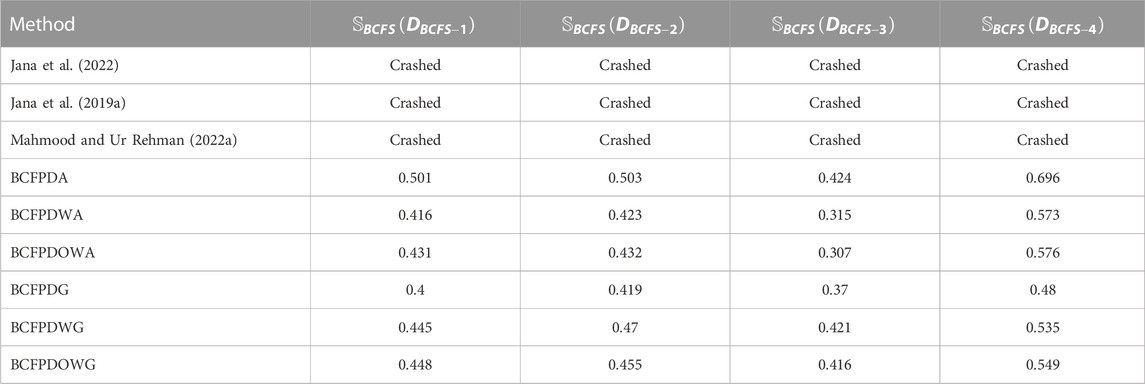
TABLE 13. Score values of the data given in Table 3 were achieved by using both our research and the existing results.

TABLE 14

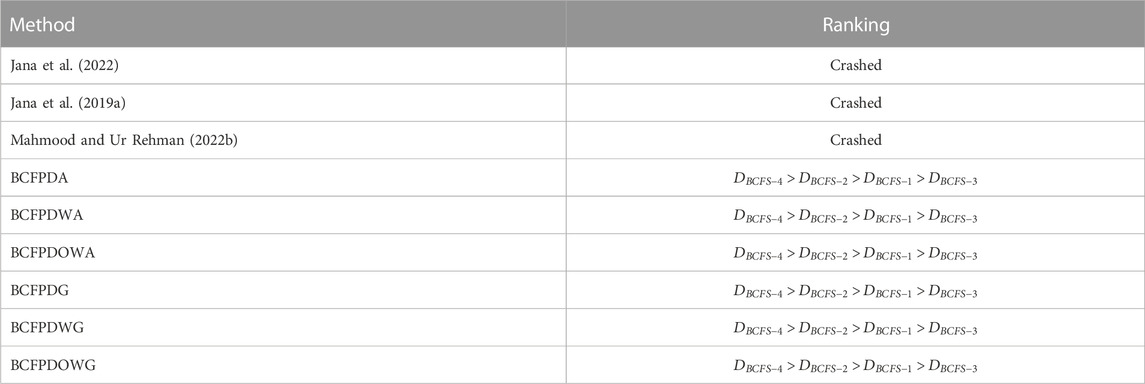
TABLE 14. Ranking order relies on the score values achieved in Table 13.

The works initiated by Jana et al. (2022), Jana et al. (2019a), and Mahmood and Ur Rehman. (2022a) crashed while handling the information from Table 1 as we can see in Table 13 and Table 14. The reason for the crash of Jana et al. (2022) is not being able to account for the negative aspects and the second dimension, i.e., unreal parts as Jana et al. (2022) initiated power Dombi AOs for Pythagorean FS. Furthermore, the reason for the crash of Jana et al. (2019a) is not able to account for the second dimension, i.e., unreal parts, and it is not able to determine ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$, where $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ signifies the support for $D_{BCFS-\mathrm{J}}$ and $D_{BCFS-l}$ as in Jana et al. (2019a) who initiated DAOs for BFS. The DAOs developed by Mahmood and Ur Rehman. (2022b) are in the setting of BCFS and can handle the BCFNs, but these operators do not have the ability to determine ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$, where $\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$ signifies the support for $D_{BCFS-\mathrm{J}}$ and $D_{BCFS-l}$. Thus, the work described by Mahmood and Ur Rehman. (2022a) crashes when one has to find ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right)$. On the contrary, our research can handle negative aspects and unreal parts and can determine ${\rm T}\left(D_{BCFS-\mathrm{J}}\right)={\displaystyle \sum }_{\begin{array}{c}l=1\\ l\ne \mathrm{J}\end{array}}^n\mathit{Sup}\left(D_{BCFS-\mathrm{J}},D_{BCFS-l}\right).$ If we take $\frac{\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}{{\displaystyle \sum }_{\mathrm{J}=1}^n\left(1+{\rm T}\left(D_{BCFS-\mathrm{J}}\right)\right)}={\wp }_{\mathcal{w}-\mathrm{J}}$, then the initiated PDAOs are transformed into DAOs for BCFS. Furthermore, our work modifies FS, BFS, and CFS; we can also easily reduce the proposed operators and the MADM method to FS, BFS, and CFS.

From this discussion, it is clear that for getting fair and better results by solving complicated and awkward data in the setting of BCFS, the invented operators and the method are the best and only tools. None of the existing operators can handle such information. Moreover, the existing parameter $\alpha$ makes them more flexible than existing operators. Various researchers such as Jana et al. (2022), Jana et al. (2019a), and Jiang et al. (2018) in the literature introduced the power Dombi operators but they could not solve the data in the setting of BCFS.

6 Conclusion

This article contains the combination of the three most significant notions which are Dombi t-norm and t-conorm, PA operator, and BCF set. As is well known, BCF is a good model for the management of MADM problems involving ambiguous and uncertain information. Therefore, this article contains power Dombi AOs, i.e., BCFPDA, BCFPDWA, BCFPDOWA, BCFPDG, BCFPDWG, and BCFPDOWG operators in the environment of BCFS. In addition, this paper contains a discussion of climate change and its influence on the environment. Regardless of whether climate change may likewise have natural causes, it is generally related to human movement and ozone-depleting substances. Weather conditions and patterns are changing as a result of climate change. Due to several variables, the climate is changing quickly. It goes without saying that the temperature of the entire planet is rising. We need to take drastic steps to stop climate change since it is affecting the resources and life on our planet. If effective tactics are used to tackle climate change, we can stop it. Here are some strategies for reducing climate challenges: 1) Establish laws and agreements about climate change, 2) spread knowledge about climate change, 3) hold climate change capacity-building initiatives, 4) put clean energy initiatives into action, 5) outlaw tree-cutting and deforestation, 6) steer clear of using chemical fertilizers 7), preserve flora and fauna, 8) increase the number of trees in the neighborhood and nearby places, 9) lower your energy use, 10) keep areas spotless, 11) minimize the wastage of natural resources such as water, 12) purchase appliances and goods that are energy-efficient, and 13) be mindful of the environment and safeguard its resources. To determine the best solution to reducing the effect of climate change on the environment, this study contains a MADM approach in the setting of BCFS using the investigated operators. In addition, we conducted a numerical example on the prioritization of solutions to reduce the influence of climate change on the environment and obtain the best solution which is $D_{BCFS-4}$. Finally, the article contains the superiority and advantages of this study by comparing our study with other investigations. We conclude that in our study, the interpretive power of Dombi AOs and MADM in the setting of BCFS is superior to the existing results and more generalized than certain existing results that can be treated as special cases of BCFS.

In the future, we wish to continue this research in other realms such as health effects of climate change (Costello et al., 2009), complex fuzzy semi-groups (Rehman et al., 2023), complex fuzzy sub-groups (Yang et al., 2022), complex bipolar intuitionistic FS (Jan et al., 2022a), complex bipolar picture FS (Jan et al., 2022b), complex hesitant FS (Mahmood et al., 2021b), and complex T-spherical FS (Zedam et al., 2022).

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The research of Santos-García was funded by the project ProCode-UCM (PID 2019-108528RB-C22) from the Spanish Ministerio de Ciencia e Innovación.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdullah, S., Aslam, M., and Ullah, K. (2014). Bipolar fuzzy soft sets and its applications in decision making problem. J. Intelligent Fuzzy Syst. 27 (2), 729–742. doi:10.3233/ifs-131031

CrossRef Full Text | Google Scholar

Abughazalah, N., Muhiuddin, G., Elnair, M. E., and Mahboob, A. (2022). Bipolar fuzzy set theory applied to the certain ideals in BCI-algebras. Symmetry 14 (4), 815. doi:10.3390/sym14040815

CrossRef Full Text | Google Scholar

Adlassnig, K. P. (1986). Fuzzy set theory in medical diagnosis. IEEE Trans. Syst. Man, Cybern. 16 (2), 260–265. doi:10.1109/tsmc.1986.4308946

CrossRef Full Text | Google Scholar

Akram, M., and Arshad, M. (2020). Bipolar fuzzy TOPSIS and bipolar fuzzy ELECTRE-I methods to diagnosis. Comput. Appl. Math. 39 (1), 7–21. doi:10.1007/s40314-019-0980-8

CrossRef Full Text | Google Scholar

Akram, M. (2011). Bipolar fuzzy graphs. Inf. Sci. 181 (24), 5548–5564. doi:10.1016/j.ins.2011.07.037

CrossRef Full Text | Google Scholar

Alcantud, J. C. R., Santos-García, G., and Akram, M. (2022). OWA aggregation operators and multi-agent decisions with N-soft sets. Expert Syst. Appl. 203, 117430. doi:10.1016/j.eswa.2022.117430

CrossRef Full Text | Google Scholar

Alghamdi, M. A., Alshehri, N. O., and Akram, M. (2018). Multi-criteria decision-making methods in bipolar fuzzy environment. Int. J. Fuzzy Syst. 20 (6), 2057–2064. doi:10.1007/s40815-018-0499-y

CrossRef Full Text | Google Scholar

Alsolame, B., and Alshehri, N. O. (2020). Extension of VIKOR method for MCDM under bipolar fuzzy set. Int. J. Analysis Appl. 18 (6), 989–997. doi:10.28924/2291-8639

CrossRef Full Text | Google Scholar

Barnes, C. S., Alexis, N. E., Bernstein, J. A., Cohn, J. R., Demain, J. G., Horner, E., et al. (2013). Climate change and our environment: The effect on respiratory and allergic disease. J. Allergy Clin. Immunol. Pract. 1 (2), 137–141. doi:10.1016/j.jaip.2012.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Bi, L., Dai, S., and Hu, B. (2018). Complex fuzzy geometric aggregation operators. Symmetry 10 (7), 251. doi:10.3390/sym10070251

CrossRef Full Text | Google Scholar

Bi, L., Dai, S., Hu, B., and Li, S. (2019). Complex fuzzy arithmetic aggregation operators. J. Intelligent Fuzzy Syst. 36 (3), 2765–2771. doi:10.3233/jifs-18568

CrossRef Full Text | Google Scholar

Carlton, S. J., and Jacobson, S. K. (2013). Climate change and coastal environmental risk perceptions in Florida. J. Environ. Manag. 130, 32–39. doi:10.1016/j.jenvman.2013.08.038

CrossRef Full Text | Google Scholar

Chevallier, P., Pouyaud, B., Suarez, W., and Condom, T. (2011). Climate change threats to environment in the tropical andes: Glaciers and water resources. Reg. Environ. Change 11 (1), 179–187. doi:10.1007/s10113-010-0177-6

CrossRef Full Text | Google Scholar

Chung, E. S., and Kim, Y. (2014). Development of fuzzy multi-criteria approach to prioritize locations of treated wastewater use considering climate change scenarios. J. Environ. Manag. 146, 505–516. doi:10.1016/j.jenvman.2014.08.013

CrossRef Full Text | Google Scholar

Costello, A., Abbas, M., Allen, A., Ball, S., Bell, S., Bellamy, R., et al. (2009). Managing the health effects of climate change: Lancet and university college london institute for global health commission. lancet 373 (9676), 1693–1733. doi:10.1016/s0140-6736(09)60935-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahlmann, F., Branicki, L., and Brammer, S. (2019). Managing carbon aspirations: The influence of corporate climate change targets on environmental performance. J. Bus. ethics 158 (1), 1–24. doi:10.1007/s10551-017-3731-z

CrossRef Full Text | Google Scholar

Deveci, M., Pamucar, D., Gokasar, I., Isik, M., and Coffman, D. M. (2022). Fuzzy Einstein WASPAS approach for the economic and societal dynamics of the climate change mitigation strategies in urban mobility planning. Struct. Change Econ. Dyn. 61, 1–17. doi:10.1016/j.strueco.2022.01.009

CrossRef Full Text | Google Scholar

Dombi, J. (1982). A general class of fuzzy operators, the DeMorgan class of fuzzy operators and fuzziness measures induced by fuzzy operators. Fuzzy Sets Syst. 8 (2), 149–163. doi:10.1016/0165-0114(82)90005-7

CrossRef Full Text | Google Scholar

Dong, T., Yin, S., and Zhang, N. (2023). New energy-driven construction industry: Digital green innovation investment project selection of photovoltaic building materials enterprises using an integrated fuzzy decision approach. Systems 11 (1), 11. doi:10.3390/systems11010011

CrossRef Full Text | Google Scholar

Dudziak, U., and Pe, B. (2010). Equivalent bipolar fuzzy relations. Fuzzy Sets Syst. 161 (2), 234–253. doi:10.1016/j.fss.2009.06.016

CrossRef Full Text | Google Scholar

Durkalec, A., Furgal, C., Skinner, M. W., and Sheldon, T. (2015). Climate change influences on environment as a determinant of Indigenous health: Relationships to place, sea ice, and health in an Inuit community. Soc. Sci. Med. 136, 17–26. doi:10.1016/j.socscimed.2015.04.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Escoriza, D., and Hernandez, A. (2021). Buffered microclimate determines the presence of Salamandra corsica. J. For. Res. 32 (3), 1089–1093. doi:10.1007/s11676-020-01142-6

CrossRef Full Text | Google Scholar

Falloon, P., Challinor, A., Dessai, S., Hoang, L., Johnson, J., and Koehler, A. K. (2014). Ensembles and uncertainty in climate change impacts. Front. Environ. Sci. 2, 33. doi:10.3389/fenvs.2014.00033

CrossRef Full Text | Google Scholar

Hu, B., Bi, L., and Dai, S. (2019). Complex fuzzy power aggregation operators. Math. Problems Eng. 2019, 1–7. Article ID 9064385. doi:10.1155/2019/9064385

CrossRef Full Text | Google Scholar

Im, U., Geels, C., Hanninen, R., Kukkonen, J., Rao, S., Ruuhela, R., et al. (2022). Reviewing the links and feedbacks between climate change and air pollution in Europe. Front. Environ. Sci. 10, 954045. doi:10.3389/fenvs.2022.954045

CrossRef Full Text | Google Scholar

Jan, N., Maqsood, R., Nasir, A., Alhilal, M. S., Alabrah, A., and Al-Aidroos, N. (2022). A new approach to model machine learning by using complex bipolar intuitionistic fuzzy information. J. Funct. Spaces 2022, 1–17. doi:10.1155/2022/3147321

CrossRef Full Text | Google Scholar

Jan, N., Akram, B., Nasir, A., Alhilal, M. S., Alabrah, A., and Al-Aidroos, N. (2022). An innovative approach to investigate the effects of artificial intelligence based on complex bipolar picture fuzzy information. Sci. Program. 2022, 1460544. doi:10.1155/2022/1460544

CrossRef Full Text | Google Scholar

Jana, C., and Pal, M. (2021). Multi-criteria decision making process based on some single-valued neutrosophic Dombi power aggregation operators. Soft Comput. 25 (7), 5055–5072. doi:10.1007/s00500-020-05509-z

CrossRef Full Text | Google Scholar

Jana, C., Pal, M., and Wang, J. Q. (2019). Bipolar fuzzy Dombi aggregation operators and its application in multiple-attribute decision-making process. J. Ambient Intell. Humaniz. Comput. 10 (9), 3533–3549. doi:10.1007/s12652-018-1076-9

CrossRef Full Text | Google Scholar

Jana, C., Senapati, T., Pal, M., and Yager, R. R. (2019). Picture fuzzy Dombi aggregation operators: Application to MADM process. Appl. Soft Comput. 74, 99–109. doi:10.1016/j.asoc.2018.10.021

CrossRef Full Text | Google Scholar

Jana, C., Garg, H., and Pal, M. (2022). Multi-attribute decision making for power Dombi operators under Pythagorean fuzzy information with MABAC method. J. Ambient Intell. Humaniz. Comput., 1–18. doi:10.1007/s12652-022-04348-0

CrossRef Full Text | Google Scholar

Javadinejad, S., Dara, R., and Jafary, F. (2021). Analysis and prioritization the effective factors on increasing farmers resilience under climate change and drought. Agric. Res. 10 (3), 497–513. doi:10.1007/s40003-020-00516-w

CrossRef Full Text | Google Scholar

Jiang, W., Wei, B., Liu, X., Li, X., and Zheng, H. (2018). Intuitionistic fuzzy power aggregation operator based on entropy and its application in decision making. Int. J. Intelligent Syst. 33 (1), 49–67. doi:10.1002/int.21939

CrossRef Full Text | Google Scholar

Khan, A. A., Ashraf, S., Abdullah, S., Qiyas, M., Luo, J., and Khan, S. U. (2019). Pythagorean fuzzy Dombi aggregation operators and their application in decision support system. Symmetry 11 (3), 383. doi:10.3390/sym11030383

CrossRef Full Text | Google Scholar

Khan, M., Zeeshan, M., Song, S. Z., and Iqbal, S. (2021). Types of complex fuzzy relations with applications in future commission market. J. Math. 2021, 1–14. Article ID 6685977. doi:10.1155/2021/6685977

CrossRef Full Text | Google Scholar

Khurshid, N., Fiaz, A., Khurshid, J., and Ali, K. (2022). Impact of climate change shocks on economic growth: A new insight from non-linear analysis. Front. Environ. Sci. 10, 128. doi:10.3389/fenvs.2022.1039128

CrossRef Full Text | Google Scholar

Kolk, A., and Pinkse, J. (2004). Market strategies for climate change. Eur. Manag. J. 22 (3), 304–314. doi:10.1016/j.emj.2004.04.011

CrossRef Full Text | Google Scholar

Lee, J. G., and Hur, K. (2019). Bipolar fuzzy relations. Mathematics 7 (11), 1044. doi:10.3390/math7111044

CrossRef Full Text | Google Scholar

Lin, S. S., Shen, S. L., Zhou, A., and Xu, Y. S. (2021). Risk assessment and management of excavation system based on fuzzy set theory and machine learning methods. Automation Constr. 122, 103490. doi:10.1016/j.autcon.2020.103490

CrossRef Full Text | Google Scholar

Liu, P., Akram, M., and Bashir, A. (2021). Extensions of power aggregation operators for decision making based on complex picture fuzzy knowledge. J. Intelligent Fuzzy Syst. 40 (1), 1107–1128. doi:10.3233/jifs-201385

CrossRef Full Text | Google Scholar

Lo Piccolo, E., and Landi, M. (2021). Red-leafed species for urban “greening” in the age of global climate change. J. For. Res. 32 (1), 151–159. doi:10.1007/s11676-020-01154-2

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Ahmmad, J., and Santos-García, G. (2021). Bipolar complex fuzzy Hamacher aggregation operators and their applications in multi-attribute decision making. Mathematics 10 (1), 23. doi:10.3390/math10010023

CrossRef Full Text | Google Scholar

Mahmood, T., Ur Rehman, U., Ali, Z., and Mahmood, T. (2021). Hybrid vector similarity measures based on complex hesitant fuzzy sets and their applications to pattern recognition and medical diagnosis. J. Intelligent Fuzzy Syst. 40 (1), 625–646. doi:10.3233/jifs-200418

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Ali, Z., Aslam, M., and Chinram, R. (2022). Identification and classification of aggregation operators using bipolar complex fuzzy settings and their application in decision support systems. Mathematics 10 (10), 1726. doi:10.3390/math10101726

CrossRef Full Text | Google Scholar

Mahmood, T., ur Rehman, U., Ali, Z., and Aslam, M. (2022). Bonferroni mean operators based on bipolar complex fuzzy setting and their applications in multi-attribute decision making. AIMS Math. 7 (9), 17166–17197. doi:10.3934/math.2022945

CrossRef Full Text | Google Scholar

Mahmood, T., Rehman, U. U., Jaleel, A., Ahmmad, J., and Chinram, R. (2022). Bipolar complex fuzzy soft sets and their applications in decision-making. Mathematics 10 (7), 1048. doi:10.3390/math10071048

CrossRef Full Text | Google Scholar

Mahmood, T., and Ur Rehman, U. (2022a). A novel approach towards bipolar complex fuzzy sets and their applications in generalized similarity measures. Int. J. Intelligent Syst. 37 (1), 535–567. doi:10.1002/int.22639

CrossRef Full Text | Google Scholar

Mahmood, T., and Ur Rehman., U. (2022b). A method to multi-attribute decision making technique based on Dombi aggregation operators under bipolar complex fuzzy information. Comput. Appl. Math. 41 (1), 47–23. doi:10.1007/s40314-021-01735-9

CrossRef Full Text | Google Scholar

Maiers, J., and Sherif, Y. S. (1985). Applications of fuzzy set theory. IEEE Trans. Syst. Man, Cybern. 15 (1), 175–189. doi:10.1109/tsmc.1985.6313408

CrossRef Full Text | Google Scholar

Ramot, D., Milo, R., Friedman, M., and Kandel, A. (2002). Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 10 (2), 171–186. doi:10.1109/91.995119

CrossRef Full Text | Google Scholar

Rasheed, M. S. (2019). Investigation of solar cell factors using fuzzy set technique. Insight-Electronic 1 (1). doi:10.18282/ie.v1.i1.229

CrossRef Full Text | Google Scholar

Rashmanlou, H., Samanta, S., Pal, M., and Borzooei, R. A. (2016). Product of bipolar fuzzy graphs and their degree. Int. J. General Syst. 45 (1), 1–14. doi:10.1080/03081079.2015.1072521

CrossRef Full Text | Google Scholar

Rehman, U. U., Mahmood, T., Albaity, M., Hayat, K., and Ali, Z. (2022). Identification and prioritization of DevOps success factors using bipolar complex fuzzy setting with Frank aggregation operators and analytical hierarchy process. IEEE Access 10, 74702–74721. doi:10.1109/access.2022.3190611

CrossRef Full Text | Google Scholar

Rehman, U. U., Mahmood, T., and Naeem, M. (2023). Bipolar complex fuzzy semigroups. AIMS Math. 8 (2), 3997–4021. doi:10.3934/math.2023200

CrossRef Full Text | Google Scholar

Riaz, M., Pamucar, D., Habib, A., and Jamil, N. (2022). Innovative bipolar fuzzy sine trigonometric aggregation operators and SIR method for medical tourism supply chain. Math. Problems Eng. 2022, 1–17. doi:10.1155/2022/4182740

CrossRef Full Text | Google Scholar

Samanta, S., and Pal, M. (2012). Bipolar fuzzy hypergraphs. Int. J. Fuzzy Log. Syst. 2 (1), 17–28. doi:10.5121/ijfls.2012.2103

CrossRef Full Text | Google Scholar

Seikh, M. R., and Mandal, U. (2021). Intuitionistic fuzzy Dombi aggregation operators and their application to multiple attribute decision-making. Granul. Comput. 6 (3), 473–488. doi:10.1007/s41066-019-00209-y

CrossRef Full Text | Google Scholar

Senapati, T. (2015). Bipolar fuzzy structure of BG-subalgebras. J. Fuzzy Math. 23 (1), 209–220.

Google Scholar

Senent-Aparicio, J., Pérez-Sánchez, J., Carrillo-García, J., and Soto, J. (2017). Using SWAT and Fuzzy TOPSIS to assess the impact of climate change in the headwaters of the Segura River Basin (SE Spain). Water 9 (2), 149. doi:10.3390/w9020149

CrossRef Full Text | Google Scholar

Short, F. T., and Neckles, H. A. (1999). The effects of global climate change on seagrasses. Aquat. Bot. 63 (3-4), 169–196. doi:10.1016/s0304-3770(98)00117-x

CrossRef Full Text | Google Scholar

Singh, P. K., and Kumar, C. A. (2014). Bipolar fuzzy graph representation of concept lattice. Inf. Sci. 288, 437–448. doi:10.1016/j.ins.2014.07.038

CrossRef Full Text | Google Scholar

Stanujkic, D., Karabasevic, D., Zavadskas, E. K., Smarandache, F., and Brauers, W. K. (2019). A bipolar fuzzy extension of the MULTIMOORA method. Informatica 30 (1), 135–152. doi:10.15388/informatica.2018.201

CrossRef Full Text | Google Scholar

Tamir, D. E., Jin, L., and Kandel, A. (2011). A new interpretation of complex membership grade. Int. J. Intelligent Syst. 26 (4), 285–312. doi:10.1002/int.20454

CrossRef Full Text | Google Scholar

Ur Rehman., U., and Mahmood, T. (2022). The generalized dice similarity measures for bipolar complex fuzzy set and its applications to pattern recognition and medical diagnosis. Comput. Appl. Math. 41 (6), 265–330. doi:10.1007/s40314-022-01948-6

CrossRef Full Text | Google Scholar

Wei, G., Alsaadi, F. E., Hayat, T., and Alsaedi, A. (2018). Bipolar fuzzy Hamacher aggregation operators in multiple attribute decision making. Int. J. Fuzzy Syst. 20 (1), 1–12. doi:10.1007/s40815-017-0338-6

CrossRef Full Text | Google Scholar

Wei, G., and Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. Int. J. Intelligent Syst. 33 (1), 169–186. doi:10.1002/int.21946

CrossRef Full Text | Google Scholar

Yager, R. R. (2001). The power average operator. IEEE Trans. Syst. Man, Cybernetics-Part A Syst. Humans 31 (6), 724–731. doi:10.1109/3468.983429

CrossRef Full Text | Google Scholar

Yang, X., Mahmood, T., and ur Rehman, U. (2022). Bipolar complex fuzzy subgroups. Mathematics 10 (16), 2882. doi:10.3390/math10162882

CrossRef Full Text | Google Scholar

Yang, X. P. (2020). Resolution of bipolar fuzzy relation equations with max-Łukasiewicz composition. Fuzzy Sets Syst. 397, 41–60. doi:10.1016/j.fss.2019.08.005

CrossRef Full Text | Google Scholar

Yiarayong, P. (2021). A new approach of bipolar valued fuzzy set theory applied on semigroups. Int. J. Intelligent Syst. 36 (8), 4415–4438. doi:10.1002/int.22465

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8 (3), 338–353. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

Zamani, R., Ali, A. M. A., and Roozbahani, A. (2020). Evaluation of adaptation scenarios for climate change impacts on agricultural water allocation using fuzzy MCDM methods. Water Resour. Manag. 34 (3), 1093–1110. doi:10.1007/s11269-020-02486-8

CrossRef Full Text | Google Scholar

Zedam, L., Pehlivan, N. Y., Ali, Z., and Mahmood, T. (2022). Novel hamacher aggregation operators based on complex T-spherical fuzzy numbers for cleaner production evaluation in gold mines. Int. J. Fuzzy Syst. 24 (5), 2333–2353. doi:10.1007/s40815-022-01262-7

CrossRef Full Text | Google Scholar

Zhang, G., Dillon, T. S., Cai, K., Ma, J., and Lu, J. (2010). “Delta-equalities of complex fuzzy relations,” in Proceeding of the 2010 24th IEEE International Conference on Advanced Information Networking and Applications, Perth, WA, Australia, April 2010 (IEEE), 1218–1224.

CrossRef Full Text | Google Scholar

Zhang, W. R. (1994). “Bipolar fuzzy sets and relations: A computational framework for cognitive modeling and multiagent decision analysis,” in NAFIPS/IFIS/NASA'94. Proceedings of the First International Joint Conference of The North American Fuzzy Information Processing Society Biannual Conference. The Industrial Fuzzy Control and Intellige, San Antonio, TX, USA, December 1994 (IEEE), 305–309.

Google Scholar

Zhu, J. M., Chen, Y., and Zhang, S. (2020). Analysis of the impact of climate change on national vulnerability based on fuzzy comprehensive evaluation. Discrete Dyn. Nat. Soc. 2020, 1–10. doi:10.1155/2020/3527540

CrossRef Full Text | Google Scholar