
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci., 04 January 2023
Sec. Environmental Informatics and Remote Sensing
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.996483
This article is part of the Research TopicDigital Resource Vitalization and Urban Intelligent ComputingView all 6 articles
Optimizing the scheduling algorithm is a key problem to improving the service efficiency of urban heterogeneous computing platforms. In this paper, we propose a novel list-based scheduling algorithm called Modified Predict Earliest Finish Time (MPEFT) for heterogeneous computing systems with the aim to minimize the total execution time. The algorithm consists of two stages: task prioritization and processor selection. In the task prioritization phase, the priority of tasks is calculated by time cost of all paths from a task to the exit task. Compared with the prior works, more accurate task priorities are obtained by considering not only the critical path but also the non-critical ones. In the processor selection phase, the processor is allocated for a task according to whether the computing resources are sufficient to its successive tasks. The experiments on randomly generated workflows and the workflows from practical applications show that the MPEFT outperforms other existing list scheduling algorithms.
In recent years, with the acceleration of smart city construction, the smart city’s computing environment has become more mature, and various urban digital services have emerged quietly. At the same time, the maturity of artificial intelligence algorithms also provides a powerful tool for data analysis. The rapid development of big data, cloud computing and artificial intelligence has promoted the development of smart cities. However, this explosive growth of smart city services presents a higher requirement for the load capacity and performance of urban computing centers. In addition to expanding computing resources, how to improve the efficiency and performance of task scheduling is also a matter of concern (Duan et al., 2020; Li, 2020).
Complex computing in smart cities often consists of multiple tasks. There may be dependencies between these tasks, and data transmission is usually required. These tasks with dependencies form a workflow, a directed acyclic graph (DAG) in which nodes represent the tasks and edges denotes the dependencies. Computing resources are often composed of machines with a certain degree of heterogeneity, e.g., CPUs and GPUs. An example workflow of resources vitalization for urban epidemic analysis and prediction is shown in Figure 1. It contains nine tasks for studying the epidemic situation from different perspectives. The ultimate objective task relies on three modeling sub-tasks, each of which is performed based on five basic services varying from partitioning the maps to assessing the track of infectors. For different types of tasks, specific computation resources are preferred, e.g., high-performance units such as GPUs and FPGAs are more suitable for the modeling and prediction tasks. Scheduling such workflows onto a heterogeneous computing platform so that their total execution time is minimum, is crucial for the efficiency and efficacy of the smart city management (Zheng et al., 2021).
The procedure can be formalized as a celebrated static scheduling problem, in which all information about the tasks and computation resources are known in advance, and its goal is to minimize the total execution time, i.e., the makespan. Due to its key importance in heterogeneous computing systems, the task scheduling problem has been widely studied and many heuristic algorithms were proposed in the literatures. The heuristic algorithms are mainly divided into three groups: list-based scheduling (Topcuoglu et al., 2002; Arabnejad and Barbosa, 2013; Djigal et al., 2019; Madhura et al., 2021),clustering-based scheduling (Wang and Sinnen, 2018), and duplication-based scheduling (Sulaiman et al., 2021). List-based scheduling algorithms have the advantages of low complexity and high efficiency and are widely studied and applied in many scenarios. The list-based scheduling algorithm completes the scheduling through two stages: calculating task priority and assigning processors in sequence Topcuoglu et al. (2002). The existing list-based scheduling algorithms determine the priority of tasks through the critical path, the longest path in the workflow from a task to the last task in DAG Zhou et al. (2017). However, this ignores the impact of other non-critical paths in the DAG, making tasks on other non-critical paths be inappropriately scheduled. For example, in Figure 1, the task Patient Trajectory Data Mining and the task Medical Big Data Analysis may have the same critical path, but the former should have a higher priority because there are more tasks to be calculated on the path from him to the exit task.
In this paper, we propose a new list-based scheduling algorithm, dubbed Modified Predict Earliest Finish Time (MPEFT), for scheduling workflows to fully heterogeneous computing resources with an aim to minimize the makespan. Compared with the existing list scheduling algorithms (Topcuoglu et al., 2002; Arabnejad and Barbosa, 2013; Djigal et al., 2019, 2020; Madhura et al., 2021) that mainly depend on the critical path, the MPEFT adopts more appropriate features to schedule the tasks. The novelty of the MPEFT is the calculation of task priority and the evaluation of critical paths. MPEFT treats critical paths and non-critical paths equally when calculating task priority, and determines priority based on task overhead on all paths. When allocating computing resources for tasks, MPEFT measures the impact of critical paths on the makespan and adjusts the allocation strategy. The impact of critical paths is evaluated by computing the proportion of their time cost in the whole execution cost.
Extensive experiments show that the performance of MPEFT is significantly better than other popular list-based scheduling algorithms in most scenarios.
The scheduling problem studied in this paper is to assign tasks in a workflow onto computing resources. The DAG structure and computation cost matrix in Figure 2 illustrate the details of the example in Figure 1. There are ten tasks and three heterogeneous processors. The tasks will be scheduled onto three processors, such that the runtime of the whole workflow, i.e., the makespan, is minimum.
The computing resource in this paper is the processor set, which we denote by P = {p1, … , pm}. A processor can execute any task, though the number of its executing tasks at any time can be only one. A workflow contains multiple tasks with some dependencies between them.
A workflow can be represented by a directed graph G = (V, E), where V = {t1, … , tn} represents the set of tasks contained in the workflow and E represents the set of dependencies between tasks. Each edge ei,j in E indicates a dependency between a tuple (ti, tj) of tasks, which means that the execution of the task tj depends on the output or the end state of the task ti. For each edge ei,j, the task tj cannot start execution unless the task ti has been performed. We call the task ti the immediate predecessor of the task tj, and the task tj the immediate successor of the task ti. The edge ei,j also has a specific weight ci,j, indicating the communication time that it takes to transfer the result data from the task ti to the task tj. The ci,j are usually defined as:
where
In this paper, we denote the computation cost of all tasks on different processors by the matrix w, in which w (ti, pj) is the processing time of the task ti on the processor pj. Due to the heterogeneity, a task may cost unequal computation times on different processors. For example, in Figure 2, the task t1 takes 14, 16, and nine time units to be executed on p1, p2, and p3, respectively. In addition, we denote by w*(ti) the minimum computation cost of the task ti over all processors. For example, w*(ti) in Figure 2 is 9. To explain the algorithm formally, we first introduce some standard notations.
This paper focuses on the static single-objective workflow scheduling problem with DAG properties under heterogeneous computing resource platforms. The common objective of the problem is the makespan of the workflow. Theoretically, this problem is NP-complete and has not any polynomial algorithm unless NP = ¶(Houssein et al., 2021). Thus, most of the existing methods are heuristic and high-efficient.
We can further classify the heuristic algorithms into the cluster-based (Boeres et al., 2004), the replication-based (Sulaiman et al., 2021) and the list-based (Topcuoglu et al., 2002; Arabnejad and Barbosa, 2013; Madhura et al., 2021; NoorianTalouki et al., 2022), among which the list-based scheduling algorithms have been widely studied due to their lower complexity and higher performance. This kind of algorithm generally consists of two phases: the task priority sorting and the processor selection. At the task prioritizing phase, the scheduling algorithm calculates a priority value for each task and obtains a list based on the priority. It usually takes into account several characteristics of the workflow, such as the execution time of tasks on different processors, dependencies between the tasks, and communication costs, to compute the task priority. At the processor selection phase, the scheduling algorithm progressively selects the most suitable processor for each task by the natural order of the task list. In many algorithms, the two phases are often tangled, i.e., the processor selection would depend on the priority of tasks.
We briefly review some list-based algorithms in Table 2. The critical path plays a certainly important role in the existing list-based algorithms Topcuoglu et al. (2002); Arabnejad and Barbosa (2013); Zhou et al. (2017); Djigal et al. (2019). Many metrics, e.g., ranku in HEFT, rankd in CPOP, and the OCT in PEFT, are calculated along some critical path in the workflow. However, we argue that the impact of the critical path on the final makespan might be overestimated in these algorithms, when there are some other paths that have a similar length as the critical one, i.e., such paths are also vital to the scheduling plan. Especially when the computation resources are limited, exaggerating the effect of the critical path on the final makespan would let the algorithm pay more attention to the critical tasks and the critical processors, whereas overlooking the substantial cost of the non-critical tasks.
For instance, in Example 2, some paths from the task t1 through its different successors have similar length. Nevertheless, when allocating the processors for t1, only the critical path, the path via t2, is considered, which will mislead the algorithm to selecting the processor p2 for t1, since its successive critical task t2 has the minimum runtime on p2. A better scheduling for the task t1 is however p3, as t1 has the minimum EFT on p3, and the other non-critical but also important tasks can benefit from the fast computation of t1. Please refer to Sec 4.4 for more discussions.
Some researches on the scheduling problem utilize more sophisticated meta-heuristic algorithms to iteratively optimize the scheduling solution (Li et al., 2021b; Wang and Zuo, 2021). Though these algorithms might obtain better performance than the heuristic ones, they usually suffer from poor efficiency, as the optimization procedure could be very lengthy. To accelerate the convergence of the optimal solution, many meta-heuristic algorithms often take the optimal solution from some heuristic algorithm as a good initialization (Wu et al., 2019; Pham and Fahringer, 2020; Li et al., 2021a). The proposed MPEFT could also serve as an initializer plugged into these meta-heuristic algorithms. Very Recently, the (deep) reinforcement learning is brought in for the scheduling problem (Tong et al., 2020b,a; Tuli et al., 2021). These approaches aim to learn a heuristic scheduling strategy instead of devising it by hand. The learning procedure involves in a large amount of evaluation and update of the current strategy, and thus are inevitably hindered by the same efficient problem as the meta-heuristic methods.
We briefly summarize some work related to task scheduling, as shown in Table 2. Methods based on list scheduling have been extensively studied. And some researchers try to use meta-heuristic methods and reinforcement learning methods to solve scheduling problems in more complex scenarios, at the cost of higher complexity. For example, in addition to the number of tasks, the complexity of SDHN Li et al. (2021a) based on genetic algorithms also needs to consider a large number of populations n and iterations τ.
Motivated by the deficiency of existing approaches analyzed in the section above, we propose a novel list-based scheduling algorithm, dubbed the Modified Predict Earliest Finish Time (MPEFT) algorithm, for heterogeneous computing systems. Before introducing the MPEFT algorithm, we define some attributes OffspringSet and DCT used for determining the task priorities, and for selecting processors for tasks.
In MPEFT, we use the summed DCT overall offspring to prioritize the tasks:
Contrary to the task ranks used in the prior works that only deal with the critical path, rankAP computes the optimal cost over all paths (AP) from a task to the exit task. More specifically, the rank rankAP (ti) contains the computation and communication cost of all subsequent tasks starting from the task ti to the exit task. The rankAP could provide a more accurate priority of tasks since it takes into account the cost of non-critical tasks, which could also contribute a lot to the value of makespan. The intuition is that in the case where the number of successors of a task is larger than the number of processors, and every successor consumes considerable runtime, the successive tasks cannot be fully paralleled onto the processors and the earlier execution of the preceded task could speed up the whole workflow. Even though sometimes the computation resources are adequate, the processors would not be always available during the running of the workflow, and thus the scheduling performance might still benefit from the proposed rankAP.
Input: A workflow G = (V, E) and the computation cost matrix w
Output: rankAP of all tasks
1: Compute the DCT for each task in G by (6)
2: rankAP ←{}; OffspringSet ←{} ⊳ Initialize as empty dictionaries
3: Get the entry task tentry from G
4: CalcuRankForTask (tentry) ⊳ Recursively compute rankAP
5: return rankAP
6:
7: function CalcuRankForTask (ti)
8: if task ti is exit task then
9: OffspringSet (ti) ←∅
10: else
11: for tj ∈ succ (ti) do
12: if OffspringSet (tj) = ∅ then
13: CalcuRankForTask (tj)
14: end if
15:
16: end for
17: end if
18:
19: end function
The processor selection strategy of MPEFT is built on that of PEFT. During this phase, the Optimistic Cost Table (OCT) (8) is first calculated. It is defined recursively and only the entry task needs to be considered. For the exit task, the OCT (texit, pk) = 0 for all processors pk ∈ P.
where
The assignment of tasks is determined by the Modified Earliest Start Time (MEFT):
where k (ti, pk) is a rational weight controlling the impact of the critical path on the processor selection. Every k (ti, pk) is computed by
Note that CPS(ti, pk) ∈ succ (ti), and thus the weight k (ti, pk) ≤ 1. In other words, the MEFT only diminishes the impact of the critical path, and will degenerate to PEFT if the cost of the critical path dominates the whole time of a task and its offspring. When the number of processors is one larger than the successors of a task, the successors can be paralleled onto multiple processors, and thus MEFT also adopts the original PEFT.
Recall that rankAP corresponds to the total time over all paths from a task to the exit task. The k (ti, pk) evaluates the impact of the critical path by calculating the proportion of the critical path in the total cost over all paths. The smaller fraction of time the critical path occupies, the lower impact it will have.
Compared with the existing scheduling algorithms, MEFT based allocation strategy selects the processor to optimize the cost of the critical path, only when the critical path is vitally important to the final makespan. If there are several comparably costly paths from a task to the exit task, different selections of the processor might not change the whole time of the offspring tasks too much. Subsequently, when selecting the processor, the assignment of a task should pay more attention to the total time of its ahead tasks, i.e., the EFT of the task. For instance, in Figure 2, assigning the task t2 to the processor p3 that has the smallest EFT will produce a better scheduling plan.
The pseudocode of the MPEFT algorithm is shown in Algorithm 2. MPEFT will first calculate the OCT, CPS and rankAP values of all tasks, and then create a ready list with a single entry task. The rankAP value is processed in the order as described in Algorithm 1. Line four will take out the task with the highest rankAP value in the current ready list for processor allocating. Lines 5–12 will select the appropriate processor for the task. The line six calculates the EFT, and lines 7–10 calculate k, the importance of the critical successor of the current task. Line 12 calculates MEFT for the processor selection. Line 15 will put the new ready tasks into the ready-list. Repeat the procedure until all tasks have been executed, and the scheduling plan and the overall computation cost are obtained.
Input: A workflow G = (V, E) and the computation cost matrix w
Output: A scheduling plan with its makespan
1: Compute rankAP and OCT CPS table for all tasks
2: Create Empty ready list L and put entry task as initial task
3: while L is NOT Empty do
4: ti ← the task with highest rankap from L
5: for pj ∈ P do
6: Compute EFT (ti, pj) value using insertion-based scheduling policy
7: if |succ (ti)| < |P| + 1 then
8: k ← 1
9: else
10: Compute k by (11)
11: end if
12: MEFT (ti, pj) = EFT (ti, pj) + OCT (ti, pj) × k
13: end for
14: Assign task ti to the processor pj that minimize MEFT of task ti
15: Update L
16: end while
We analyze the workflow scheduling example shown in Example 2 as a case study. In task prioritizing phase, the rankAP for each task by Eq. 7 is shown in Table 3. The task priority list is (t1, t4, t2, t3, t5, t6, t9, t7, t8, t10).
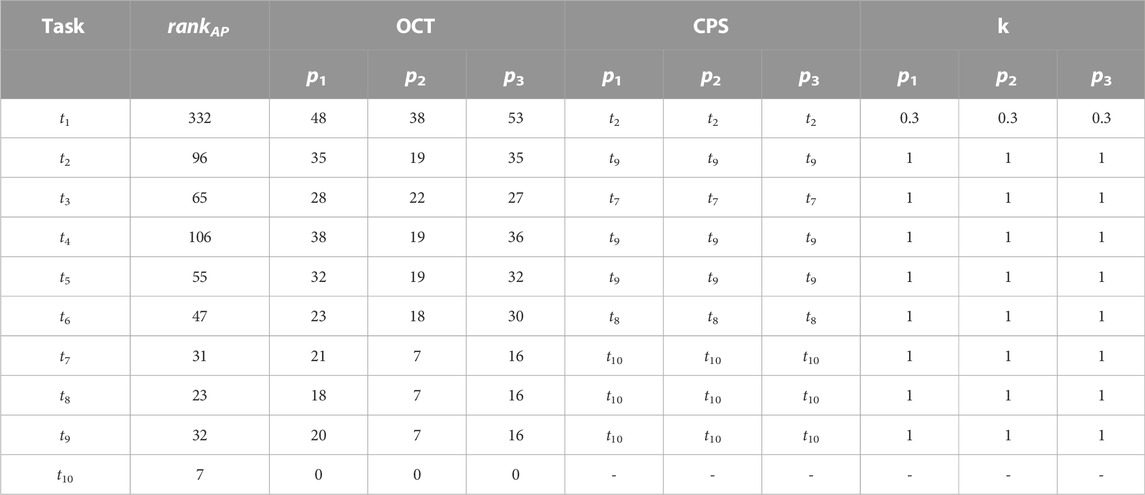
TABLE 3. Produced by Processor Selection Phase on the sample DAG in Figure 2
Table 3 also shows the calculation results of OCT, CPS and k respectively. The value of k of the task t1 is .3. It indicates that the number of direct successor tasks of t1 is more than the number of current processors, and its critical path occupies only 30% of the total time cost. When selecting a processor for task t1, the impact of the critical path is determined according to its CPS and k.
Table 4 shows the scheduling results of each round in MPEFT. The comparison of the scheduling scheme of MPEFT with other list-based scheduling algorithms is shown in Figure 3. The MPEFT algorithm schedules the task t1 to the processor p3, while other algorithms except HEFT consider the processor p2 to be a better choice for t1. However, these algorithms focusing on optimizing task scheduling on the longest path starting from t1 to the exit task would not guarantee global optimization. This is because the assignment of t1 on p2 will cause a delay of t1 compared to p3, and its non-critical successor tasks are also affected by the delay of task t1, which leads to an increased maskpan. In the MPEFT algorithm, the influence of the critical successor of t1 is evaluated by the controlling weight k. The value .3 of k decreases the impact of the critical-path-based metric OCT on the processor selection, which in turn argues the importance of the value of EFT. It makes the algorithm select p3 with the minimum EFT for t1, ensuring the earliest finish of t1 as well as all its successors. Though the critical path from t1 might take a longer time to complete, the total time cost of the workflow, the makespan, in MPEFT is smaller than the prior algorithms.
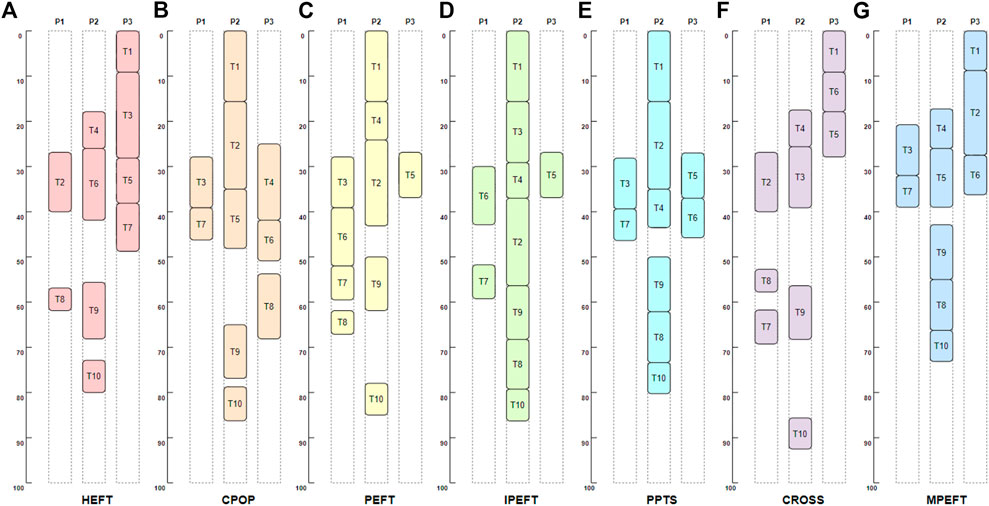
FIGURE 3. Schedules of the sample DAG in Figure 2 with (A) HEFT (makespan = 80), (B) CPOP(makespan = 86), (C) PEFT (makespan = 85), (D) IPEFT (makespan = 95), (E) PPTS (makespan = 80), (F) CROSS(makespan = 93) and (G) MPEFT (makespan = 73).
In this paper, we compare our MPEFT with other list-based scheduling algorithms using the metrics the Scheduling Length Ratio (SLR), the Number of Occurrences of Better Quality of Solutions (NOBQS), makespan standard deviation and running time of the algorithms. Since DAGs may have very different topologies, the SLR is often used to represent the scheduling efficiency of the algorithm, which is defined as follows:
where CP is the critical path from the entry to exit task.
The NOBQS shows the comparison results of the scheduling schemes of different algorithms on all DAG graphs in the form of a table, including better, worse and the same. This paper will compare the MPEFT algorithm with several baselines, including HEFT (Topcuoglu et al., 2002), CPOP (Topcuoglu et al., 2002), PEFT (Arabnejad and Barbosa, 2013), IPEFT (Zhou et al., 2017), PPTS (Djigal et al., 2019) and CROSS (Madhura et al., 2021).
Makespan standard deviation describes the robustness of the algorithms. The makespan standard deviation σmakespan is defined as 13. The smaller the makespan standard deviation, the stronger the robustness of the algorithm.
All experiments were performed on a computer with a 40-core Intel(R) Xeon(R) Gold 5218R 2.10 GHz processor and 32 GB of RAM. We use a simulator, which is realized by Python, to conduct the comparative experiments. The code of the proposed MPEFT is released on the Website https://github.com/MengQiaolan/DAG_Scheduling.
To comprehensively evaluate the effectiveness of the algorithm on different graphs, we use a random graph generator to obtain graphs with different topologies. The random graph generator generates multiple DAG graphs with the given input parameters (frs69wq, 2012). Related parameters are described as follows:
n: the number of computation nodes in the DAG (i.e., tasks in workflow).
fat: the width of the DAG, the maximum number of tasks that can be executed concurrently. A small value will lead to a thin DAG (e.g., chain) with a low task parallelism, while a large value induces a fat DAG (e.g., fork-join) with a high degree of parallelism.
density: determines the number of dependencies between tasks of two consecutive DAG levels.
regular: the regularity of the distribution of tasks between the different levels of the DAG.
jump: the maximum number of levels spanned by inter-task communications. This allows to generate DAGs with execution paths of different lengths.
Regarding the computation cost and data transfer cost, we specify them by setting the following parameters:
communication-to-computation ratio (ccr): the ratio of the sum of edge weights to the sum of the task computation cost in a DAG.
heterogeneity: the heterogeneity factor for processor speeds. A high heterogeneity value indicates higher heterogeneity and different computation costs among processors. A low value indicates that the computation costs on processors for a given task are almost equal.
The average computation cost of a task ti in a given graph
In this experiment, we use the parameter in Table 5 to generate workflow scheduling scenarios randomly. These parameters generate a total of 38,880 different parameter combinations, and for each parameter combination, 10 DAG graphs are randomly generated, so this part has a capacity of 388,800 DAGs for experiments.
Figure 4 shows the average SLR of all algorithms for different DAG sizes. The CROSS algorithm performed worst because of its downward priority calculation method. The CPOP algorithm performed badly because it pays too much attention to the critical path. It may work well in extreme cases where most tasks of workflow are on the critical path. There is a gap between the performance of HEFT, PEFT, IPEFT, PPTS and MPEFT, when the number of tasks is less than 400. When the number of tasks is greater than 400, the average SLRs of these five algorithms are however not much different. This may be due to their similar task priority calculation methods. The MPEFT algorithm outperforms the other four algorithms in every task number.
Figure 5 shows the influence of ccr, heterogeneity, and the number of processors. When the ccr is low, there is no obvious difference between these algorithms except CPOP. With the increase in ccr, the MPEFT algorithm begins to show better performance, and the gap from the baselines becomes more obvious. This shows that MPEFT is more suitable for scenarios with large data transmission between tasks since MPEFT considers all subsequent data transmission costs of the task in the task prioritization stage.
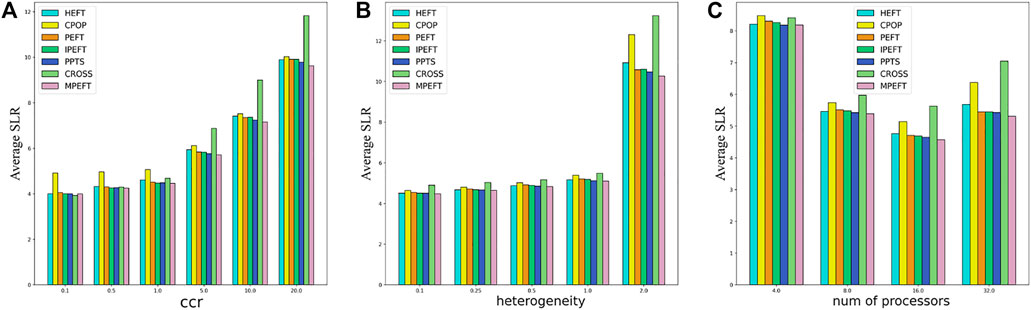
FIGURE 5. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for random DAGs.
In contrast, other algorithms ignore the data transmission costs other than the longest path from the task to the exit task. When the ccr is low, these costs can be ignored, while as the ccr increases, the data transmission requirements between tasks become larger, and the benefits of MPEFT in task sorting will become clear. Similarly, the performance of MPEFT also improves significantly compared with other algorithms under different heterogeneities and numbers of processor conditions.
Figure 6 shows the influence of fat, density, regularity and jump on the algorithm performance. It can be found that the structural parameters of the DAG have no obvious impact on the scheduling performance.
Table 6 shows the NOBQS results. As can be seen, MPEFT performs better than CPOP, HEFT, PEFT, IPEFT, PPTS and CROSS on most DAG graphs. Compared to IPEFT, the best-performing algorithm among other algorithms, MPEFT also performs worse on only 32% of the DAGs.
We evaluate the performance of workflows that appear in some practical applications, including epigenomics, montage, ligo and cybershake. The workflow for these applications is presented in Figure 7, and for the details, please refer to (Djigal et al., 2020). In the experiment, we used epigenomics, montage, ligo and cybershake workflows containing 50, 100, 200 tasks to evaluate the algorithms. And we also evaluated the performance of our algorithm on workflows of Gaussian elimination and molecular dynamics code.
Figure 7A depicts the structure of an epigenomic workflow with 20 tasks. Figure 8A shows the average SLR under different ccr conditions. When ccr <5, the performance of the five algorithms is relatively close, and the MPEFT algorithm performs slightly better. However, when ccr is greater than 5, the MPEFT outperforms other algorithms significantly, especially when ccr is equal to 20. For various heterogeneities, MPEFT also outperforms other algorithms and improves significantly when heterogeneity is 2.0. Finally, MPEFT performs well for different numbers of processors. As shown in Figure 8C, by analyzing the characteristics of the Epigenomic workflow, it can be found that there is no critical path but several paths of the same process. Therefore, the algorithms such as CPOP, HEFT, etc. Tend to perform worse under this workflow since they pay more attention to the critical path. The MPEFT reduces the impact of the critical path on the allocated processor by calculating the k value and achieves better results.
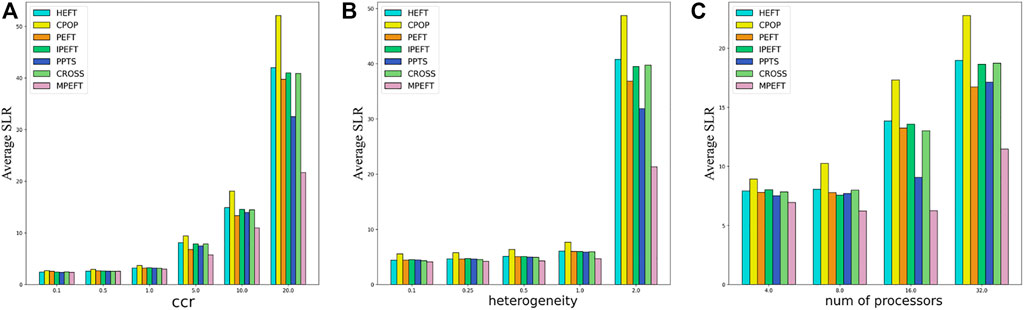
FIGURE 8. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Epigenomic Workflows.
In the simulated scheduling of cybershake workflow, our algorithm outperforms other list scheduling algorithms in most scenarios, as shown in Figure 9. As can be seen from Figure 7B, the workflow has no obvious critical path and the paths are short, so the scheduling performance based on the critical path is not satisfied. Among them, the performance of PPTS is close to that of MPEFT. This is because the PCM of PPTS takes into account the case where the current task and immediate successor tasks are placed on the same processor. In a DAG with a flat structure, PCM can optimize the scheduling strategy. Since there is no obvious critical path, the processor allocation strategy of MPEFT is similar to that of HEFT, that is, the successor tasks are not considered when assigning tasks.
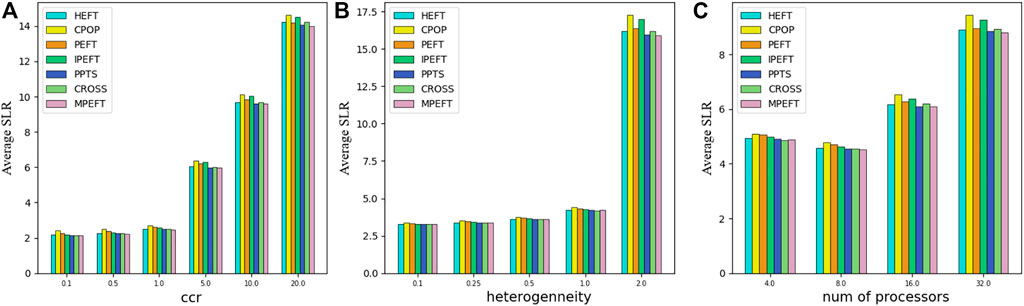
FIGURE 9. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Cybershake Workflows.
In Ligo workflow, MPEFT has better scheduling efficiency, as shown in Figure 10. The structure of Ligo is shown in Figure 7C. When scheduling the task represented by the yellow node in the first row, since there is only one successor node, MPEFT will schedule based on the critical path. When scheduling the task represented by the red node in the third row, since it has many paths to the exit task, MPEFT will schedule it to the node that can complete the task as soon as possible, speeding up the execution of all immediate successor tasks.
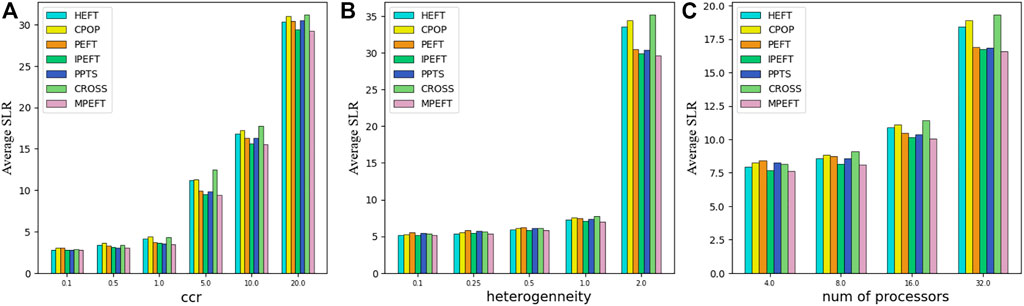
FIGURE 10. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Ligo Workflows.
The Montage Workflow is the worst-performing workflow type for the MPEFT algorithm in our experiments, as shown in Figure 11. On this Workflow, the performance of the five algorithms is very close in general except CPOP and CROSS. Compared with other algorithms, MPEFT only improves by 1%–3% in most scenarios. And MPEFT performs slightly worse than PPTS. Because tasks in the latter part of this kind of workflow are connected one by one, which results in almost no difference in rankAP of predecessors of these tasks. The same is true for other algorithms. Thus all algorithms achieve similar results in the task prioritizing phase.
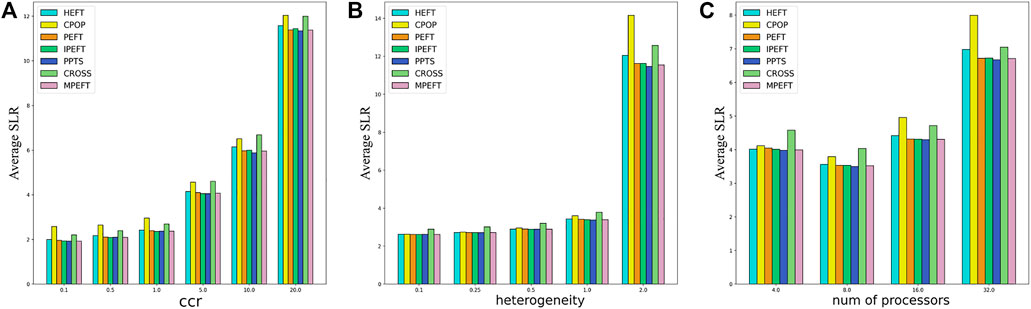
FIGURE 11. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Montage Workflows.
Figure 12A depicts the structure of Molecular Dynamic Code workflow. The experimental results of Molecular Dynamics Code are shown in Figure 13. MPEFT also outperforms the other four algorithms in different parameter environments. As with the previous experimental results, MPEFT performs better and better with increasing ccr. when ccr = .1, MPEFT performs very close to HEFT, PEFT, and IPEFT. But when ccr = 20, the MPEFT performs significantly better than other algorithms. Figure 13B shows that the MPEFT algorithm outperforms most algorithms in different heterogeneity situations. Especially when heterogeneity = 2.0, compared with HEFT, CPOP, PEFT, IPEFT, PPTS and CROSS algorithms, there are 13.1%, 23.6%, 1.9%, 7.0%, 4.8% and 11.8% improvements, respectively. Under the condition of a different number of processors, the performance of the MPEFT algorithm is slightly better than other algorithms. These result shows that MPEFT still performs well even when the workflow structure is chaotic and irregular.

FIGURE 13. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Molecular Dynamics Workflows.
Figure 12B gives the graph of Gaussian Elimination workflow for the special case of m = 4, where m is the dimension of the matrix. On the Gaussian Elimination workflow, our algorithm also does not perform particularly well. As shown in Figure 14, only when the ccr is 10 and 20, the MPEFT algorithm has obvious advantages. Under most other conditions, the MPEFT algorithm only outperforms the CPOP algorithm. By analyzing the structural characteristics of Gaussian Elimination workflow, we believe that this is due to the particularity of the critical path of this type of workflow. In the Gaussian Elimination workflow, its critical path is very clear and important. However, since there are many other paths from the entry task to the exit task, the cost is not much lower than the critical path. The MPEFT algorithm may incorrectly estimate the importance of the critical path due to the influence of other paths.
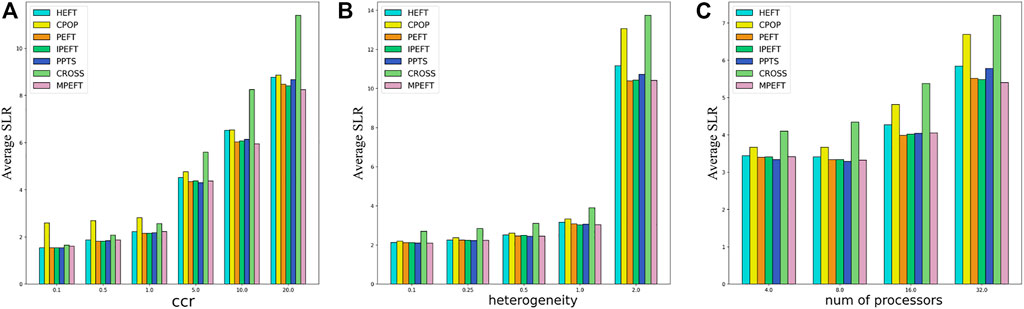
FIGURE 14. Average SLR as function of ccr (A), heterogeneity (B) and number of processors (C) for Gaussian Elimination Workflows.
We carried out experiments on the makespan standard deviation of the algorithms on four scientific workflows under number of tasks, and the results are shown in Table 7. CPOP algorithm has the worst robustness because it relies heavily on critical paths of workflows. HEFT and CROSS did not perform well on montage workflows. The second half of the montage workflow is a single chain structure as shown in Figure 7 (d), that is, the critical path is determined. HEFT and CROSS lack consideration of critical path, resulting in poor performance. PEFT, IPEFT, PPTS and MPEFT have similar makespan standard deviations in most scenarios. And on epigenomics workflows, MPEFT has an obvious advantage when the number of tasks is large.
The average running time of the algorithm for the number of four scientific workflow tasks is shown in Table 8. HEFT, CPOP, and CROSS perform similarly in performance. Because they do not consider different processors when calculating priorities, the performance at this stage is better than other algorithms. The other four algorithms have similar performance because they calculate priority based on the processor.
This paper proposes a new list-based static scheduling algorithm based on a heterogeneous platform, MPEFT. First, MPEFT will sort all tasks in the workflow based on priority, which is determined by the cost of all offspring of the task. Then, MPEFT will allocate the sorted tasks to the corresponding processors in turn based on the number of processors, the number of successors, and the priority of successors. Compared with the current list scheduling algorithm based on the critical path, MPEFT solves the problem that excessive attention to the critical path leads to reduced scheduling efficiency. Experiments on SLR and NOBQS show that MPEFT performs well in terms of makespan compared with other list-based scheduling algorithms. And through makespan standard deviation and running time experiments, MPEFT also has good robustness and operational efficiency.
The current optimization objective of MPEFT is limited to makespan. Our one future research is to expand MPEFT into a multi-objective optimization algorithm, such as optimization for resource utilization.
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
The authors would like to thank the reviewers for their helpful comments.
This work is supported by the National Key R&D Program of China (2021YFB2104800) and the National Science Foundation of China (62177002).
The authors would like to thank the anonymous reviewers for their helpful comments.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Arabnejad, H., and Barbosa, J. G. (2013). List scheduling algorithm for heterogeneous systems by an optimistic cost table. IEEE Trans. Parallel Distributed Syst. 25, 682–694.
Boeres, C., Filho, J. V., and Rebello, V. E. F. (2004). “A cluster-based strategy for scheduling task on heterogeneous processors,” in 16th symposium on computer architecture and high performance computing (IEEE), 214–221.
Chen, H., Zhu, X., Liu, G., and Pedrycz, W. (2018). Uncertainty-aware online scheduling for real-time workflows in cloud service environment. IEEE Trans. Serv. Comput. 14, 1167–1178. doi:10.1109/tsc.2018.2866421
Djigal, H., Feng, J., Lu, J., and Ge, J. (2020). Ippts: An efficient algorithm for scientific workflow scheduling in heterogeneous computing systems. IEEE Trans. Parallel Distributed Syst. 32, 1057–1071. doi:10.1109/tpds.2020.3041829
Djigal, H., Feng, J., and Lu, J. (2019). Task scheduling for heterogeneous computing using a predict cost matrix. In Proceedings of the 48th International Conference on Parallel Processing: Workshops, 1–10.
Duan, Q., Quynh, N. V., Abdullah, H. M., Almalaq, A., Do, T. D., Abdelkader, S. M., et al. (2020). Optimal scheduling and management of a smart city within the safe framework. IEEE Access 8, 161847–161861. doi:10.1109/access.2020.3021196
frs69wq (2012). Daggen: A synthetic task graph generator. Available at: https://github.com/frs69wq/daggen (Accessed December 18, 2022).
Houssein, E. H., Gad, A. G., Wazery, Y. M., and Suganthan, P. N. (2021). Task scheduling in cloud computing based on meta-heuristics: Review, taxonomy, open challenges, and future trends. Swarm Evol. Comput. 62, 100841. doi:10.1016/j.swevo.2021.100841
Hu, B., Cao, Z., and Zhou, M. (2019). Scheduling real-time parallel applications in cloud to minimize energy consumption. IEEE Trans. Cloud Comput. 10, 662–674. doi:10.1109/tcc.2019.2956498
Li, H., Wang, B., Yuan, Y., Zhou, M., Fan, Y., and Xia, Y. (2021a). Scoring and dynamic hierarchy-based nsga-ii for multiobjective workflow scheduling in the cloud. IEEE Trans. Automation Sci. Eng. 19, 982–993. doi:10.1109/tase.2021.3054501
Li, H., Wang, D., Zhou, M., Fan, Y., and Xia, Y. (2021b). Multi-swarm co-evolution based hybrid intelligent optimization for bi-objective multi-workflow scheduling in the cloud. IEEE Trans. Parallel Distributed Syst. 33, 2183–2197. doi:10.1109/tpds.2021.3122428
Li, J. (2020). Resource optimization scheduling and allocation for hierarchical distributed cloud service system in smart city. Future Gener. Comput. Syst. 107, 247–256. doi:10.1016/j.future.2019.12.040
Madhura, R., Elizabeth, B. L., and Uthariaraj, V. R. (2021). An improved list-based task scheduling algorithm for fog computing environment. Computing 103, 1353–1389. doi:10.1007/s00607-021-00935-9
NoorianTalouki, R., Shirvani, M. H., and Motameni, H. (2022). A heuristic-based task scheduling algorithm for scientific workflows in heterogeneous cloud computing platforms. J. King Saud University-Computer Inf. Sci. 34, 4902–4913. doi:10.1016/j.jksuci.2021.05.011
Pham, T.-P., and Fahringer, T. (2020). Evolutionary multi-objective workflow scheduling for volatile resources in the cloud. IEEE Trans. Cloud Comput. 10, 1780–1791. doi:10.1109/tcc.2020.2993250
Sulaiman, M., Halim, Z., Waqas, M., and Aydın, D. (2021). A hybrid list-based task scheduling scheme for heterogeneous computing. J. Supercomput. 77, 10252–10288. doi:10.1007/s11227-021-03685-9
Tong, Z., Chen, H., Deng, X., Li, K., and Li, K. (2020a). A scheduling scheme in the cloud computing environment using deep q-learning. Inf. Sci. 512, 1170–1191. doi:10.1016/j.ins.2019.10.035
Tong, Z., Deng, X., Chen, H., Mei, J., and Liu, H. (2020b). Ql-heft: A novel machine learning scheduling scheme base on cloud computing environment. Neural Comput. Appl. 32, 5553–5570. doi:10.1007/s00521-019-04118-8
Topcuoglu, H., Hariri, S., and Wu, M.-Y. (2002). Performance-effective and low-complexity task scheduling for heterogeneous computing. IEEE Trans. parallel distributed Syst. 13, 260–274. doi:10.1109/71.993206
Tuli, S., Casale, G., and Jennings, N. R. (2021). Mcds: Ai augmented workflow scheduling in mobile edge cloud computing systems. IEEE Trans. Parallel Distributed Syst. 33, 1–2807. doi:10.1109/tpds.2021.3135907
Wang, H., and Sinnen, O. (2018). List-scheduling versus cluster-scheduling. IEEE Trans. Parallel Distributed Syst. 29, 1736–1749. doi:10.1109/tpds.2018.2808959
Wang, Y., and Zuo, X. (2021). An effective cloud workflow scheduling approach combining pso and idle time slot-aware rules. IEEE/CAA J. Automatica Sinica 8, 1079–1094. doi:10.1109/jas.2021.1003982
Wu, Q., Zhou, M., and Wen, J. (2021). Endpoint communication contention-aware cloud workflow scheduling. IEEE Trans. Automation Sci. Eng. 19, 1137–1150. doi:10.1109/tase.2020.3046673
Wu, Q., Zhou, M., Zhu, Q., Xia, Y., and Wen, J. (2019). Moels: Multiobjective evolutionary list scheduling for cloud workflows. IEEE Trans. Automation Sci. Eng. 17, 166–176. doi:10.1109/tase.2019.2918691
Zheng, X., Li, M., and Guo, J. (2021). Task scheduling using edge computing system in smart city. Int. J. Commun. Syst. 34, e4422. doi:10.1002/dac.4422
Keywords: workflow scheduling, DAG scheduling, list-based scheduling, heterogeneous platform, random graphs generator
Citation: Pu J, Meng Q, Chen Y and Sheng H (2023) MPEFT: A novel task scheduling method for workflows. Front. Environ. Sci. 10:996483. doi: 10.3389/fenvs.2022.996483
Received: 17 July 2022; Accepted: 08 December 2022;
Published: 04 January 2023.
Edited by:
Mengchu Zhou, New Jersey Institute of Technology, United StatesReviewed by:
Neeraj Arora, Vardhaman Mahaveer Open University, IndiaCopyright © 2023 Pu, Meng, Chen and Sheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hao Sheng , c2hlbmdoYW9AYnVhYS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.