- 1School of Marine Science and Technology, Tianjin University, Tianjin, China
- 2State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin, China
- 3State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin, China Institute of Water Resources and Hydropower Research, Beijing, China
- 4College of Intelligence and Computing, Tianjin University, Tianjin, China
The velocity field in coastal and oceanic currents is mostly non-uniform, which will result in irregular particle distribution when the fluid is represented by an amount of moving discrete particles as in smoothed particle hydrodynamics (SPH). When the non-uniformity of the flow is big, i.e., with large deformation, the conventional SPH method can hardly solve the associated advection-diffusion process (e.g., substance transport). To accurately simulate the substance transport in flows with large deformation, two types of particle shifting techniques (PSTs) are incorporated into the conventional SPH in this paper. One is based on current particle distance, and the other is based on Fick’s law. In the second type, the repulsive force (RF) term for suppressing the paring instability that occurs in particle shifting technique (PST) is studied and the effect of the kernel function is examined. By introducing a particle disorder measurement, the simulated results of SPH with the two types of PSTs and their modifications are evaluated and the influence of the shifting magnitude is analyzed. The suggestions for how to set reasonable parameters in PSTs are provided by a systematic parametric study. For further illustration, the simulation of the anisotropic diffusion is also examined. To give reliable reference solutions, the high-resolution modified total variation diminishing Lax Friedrichs scheme with Superbee limiter (MTVDLF-Superbee) with fine mesh is also implemented. The validated Lagrangian particle model with optimized PST is applied to a practical application.
1 Introduction
Substances (including sediment, salt and soluble pollutants, etc.) transport in surface and subsurface water is modeled by the advection-diffusion equation, for which various numerical methods have been developed (Finlayson, 1992; Ewing and Wang, 2001; Wang and Hutter, 2001; Alhumaizi, 2004). The difficulties to obtain good solutions for advection-diffusion equation mainly exist in two aspects. One is the treatment of the advection term, especially when the problem is advection dominated, and the other is that there exist steep fronts in the solution. Compared with Eulerian methods, the major advantage of the Lagrangian methods is that the advective term is not involved in the Lagrangian form of the advection-diffusion equation, so that the numerical problems of both spurious oscillations and diffusion error caused by spatial discretization of the advection can be easily eliminated, leading to accurate solutions (Zimmermann et al., 2001; Liu and Liu, 2006; Devkota and Imberger, 2009). Compared with mesh-based Eulerian methods, the smoothed particle hydrodynamics (SPH) is more competitive and attractive due to its good properties of Lagrange and meshfree. It is considered to have the competence to tackle intractable problems in the CFD field, such as big deformation, free-surface and multi-phase flows (Monaghan and Kocharyan, 1995; Kum et al., 2003; Larbe and Price, 2012; Monaghan, 2012; Ye et al., 2019; Gu et al., 2022).
However, SPH has two inherent drawbacks, i.e., boundary deficiency and particle inconsistency, which are still the key issues for research and application in the SPH society (Monaghan, 2000; Kum et al., 2003; Ye et al., 2019; Gu et al., 2022). To solve the governing partial differential equations (PDEs) using SPH, there are two main procedures. One is the kernel approximation in continuous form, and the other is the particle approximation in discretization form. To obtain reasonable solutions, the kernel needs to satisfy some requirements, such as normalization of kernel integration, symmetry of the kernel and anti-symmetry of kernel gradients (Violeau, 2012). These properties can be well preserved in the procedure of particle approximation when the particles maintain regularly spaced, otherwise numerical instability and accuracy degradation cannot be fully avoided. The conventional SPH has second-order accuracy for organized particles, while it cannot even achieve first order as the particles become disorganized (Ye et al., 2019). This is known as particle inconsistency, which mainly results from the discrepancy between kernel approximation and particle approximation when the particles are irregularly spaced.
SPH is applicable in solving the advection-diffusion and heat conduction equations, to which some studies have devoted (Cleary and Monaghan, 1999; Monaghan, 2005; Aristodemo et al., 2010; Bai et al., 2018; Wang et al., 2019). Noticing that both of them have identical form in Lagrangian frame, the discrepancy between them is the zero advection in heat conduction problems, while attention also needs to be paid to particle inconsistency when heat conduction couples with the large deformation flows (Cleary and Monaghan, 1999). Arising from advection, particle disorder affects the simulation of the diffusion process. Chaniotis et al. (2002) approximated the diffusion terms by directly discretizing the second-order derivatives, but this approach is sensitive to particle disorder, then particle remeshing schemes have to be added. Most of the studies (Cleary and Monaghan, 1999; Shao and Lo, 2003; Aristodemo et al., 2010; Ryan et al., 2010; Chang and Chang, 2017; Zheng et al., 2018) adopted a scheme that can be regarded as the hybrid of SPH and difference method. In this scheme, the simulation of diffusion terms merely includes the first-order derivative approximation of SPH. Via this hybrid scheme, Cleary and Monaghan (1999), Aristodemo et al. (2010), Chang and Chang (2017) expressed the diffusion coefficient in a symmetric form to ensure continuity of the flux when the diffusion coefficient is discontinuous and to reduce the influence of particle disorder. Ryan et al. (2010) also used the hybrid scheme to handle the diffusion terms in flows with small deformation, and the focus was on the treatment of the complicated boundary conditions. Recently, Alvarado-Rodríguez et al. (2019) improved the consistency of SPH via setting smoothing length and the number of neighboring particles relevant to the total number of particles, aiming to simulate the anisotropic diffusion with irregular particle distribution. In this paper, the SPH format for diffusion terms differs from the two methods mentioned above. It is a complete SPH form and does not directly approximate the second-order derivatives.
To restore particle consistency, many high-order SPH methods have been proposed, which are known as corrective SPH schemes. To enhance the approximation accuracy, the reproducing kernel particle method (RKPM) modifies the kernel function by a correction function (Liu et al., 1995; Liu and Jun, 1998). The corrective smoothed particle method (CSPM) (Chen et al., 1999; Chen and Beraun, 2000) improves the conventional SPH on the basis of Taylor series expansion, whose discretization form is equivalent to the normalization for the function and its first derivatives. Based on CSPM, the finite particle method (FPM) was put forward by Liu and Liu (2006), which approximates the function and its first derivatives simultaneously and has higher order accuracy than CSPM. The kernel gradient correction (KGC) (Bonet and Lok, 1999; Shao et al., 2012) method corrects the kernel gradient by multiplying the original kernel gradient with an invertible matrix. This method is easy to code on account of retaining the structure of conventional SPH. For the ease of choosing kernel function, the kernel gradient free (KGF) SPH method was proposed (Huang et al., 2015), whose corrective matrix is invertible even if the particles are highly disordered, because the corrective matrix is symmetric. Recently, the decoupled finite particle method (DFPM) (Zhang and Liu, 2018) was developed, in which the corrective matrix is diagonally dominant and it is not necessary to calculate the inverse matrix particle by particle, so it becomes less sensitive to the particle disorder. In fact, the high-order SPH methods mentioned above correct the conventional SPH by some kernel properties which are satisfied only when the particle distribution is regular. On that account, the accuracy of these algorithms will degrade to some extent when particles are disordered.
Apart from the corrective SPH methods, some other ones, namely particle regularization techniques, are also capable of restoring particle consistency. The XSPH scheme (Monaghan, 1988; Shahriari et al., 2013; Ye et al., 2019) uses the adjacent particles to calculate the local velocity, by which the movement of particles tends to mitigate. However, this method may result in non-physical solutions especially when large velocity gradient exists. To improve particle consistency, Monaghan (2000) adopted a repulsive force (RF) term in the equation of motion to avoid the clumping of particles. Similar to RF, Tsuruta et al. (2013) employed a stabilizing force to prevent interparticle penetration. In this work, the same RF term as that of Monaghan (2000) is brought into particle shifting techniques (PST) to redistribute particles. The state of the art PSTs gained much attention in recent years (Nestor et al., 2009; Xu et al., 2009; Lind et al., 2012; Skillen et al., 2013; Antuono et al., 2014; Khorasanizade and Sousa, 2016; Huang et al., 2018). They try to make the particles distribute as uniformly as possible according to certain rules. Xu et al. (2009) brought the PST proposed originally in the finite volume particle method (Nestor et al., 2008; Nestor et al., 2009) into SPH. They applied this technique to simulate incompressible flows by coupling with incompressible SPH (ISPH) method. This PST depends on the calculation of particle distance to decide the shifting of particles. Lind et al. (2012) proposed another type of method on the basis of Fick’s law aiming at the incompressible flows too. Several improvements (Skillen et al., 2013; Khorasanizade and Sousa, 2016; Huang et al., 2018) for Xu et al. (Xu et al., 2009) and Lind et al. (Lind et al., 2012) methods are suggested in succession to stabilize the PSTs. In this paper, we contribute to the parameter optimization and stabilities improvement for the PSTs. The purpose of studying PSTs in this paper is to solve the particle cavity problem which leads to the failure of the simulation of advection-diffusion process.
The rest of the paper is organized as follows. Section 2 presents the governing equation and the SPH-based Lagrangian particle transport model. In Section 3, to deal with substance transport in large deformation flows, several typical PSTs are presented. An evaluation method for the degree of particle disorder is also described. In Section 4, the Lagrangian particle transport model based on SPH combined with PSTs is applied to the isotropic and anisotropic diffusion problems in flows with large deformation, and the results are compared with the exact and reference solutions. The performance of different PSTs and the effect of involved parameters are also evaluated. In Section 5, the SPH method with optimized PST is applied to a case study to show its applicability to practical problems. Section 6 summarizes the concluding remarks.
2 Lagrangian particle transport model
2.1 Governing equations
The governing equation for substance transport adopted in this paper is the two-dimensional (2D) advection-diffusion equation
where
where the diffusion coefficients can be symbolized by a tensor
Note that Eqs 1, 2 are derived for incompressible fluid and hence the divergence of the velocity is zero. The given velocity field in Section 4 is consistent with this assumption. The velocities of the flow field can either be given analytically or numerically calculated by any suitable methods, which are supposed to be known here.
With the definition of the material derivative
on the moving coordinate system
The Lagrangian form of Eq. 2 can be constructed following the same way.
2.2 SPH-based Lagrangian particle model
The SPH method is introduced briefly in this section, the foundation of which is the interpolation theory (Violeau, 2012). The kernel approximation in continuous form and the particle approximation in discretization form are its two main ingredients.
There are three typical approximation forms for second derivatives in SPH. They can be directly approximated via the second derivatives of the kernel (Monaghan, 2005) as
where
To circumvent the weakness of Eq. 5, other forms approximating the second derivatives are developed, among which the hybrid scheme and the approach presented in this work have been widely used. By the hybrid scheme (Cleary and Monaghan, 1999; Monaghan, 2005), the diffusion term can be discretized as
in which only the first derivative of kernel is contained. The formulation (6) can be considered as the hybrid of SPH and finite difference (Cleary and Monaghan, 1999), hence its stability and accuracy is vulnerable to be effected by the finite difference part.
In this paper, another scheme for approximating diffusion terms is applied, in which only first-order derivatives need to be treated (Jeong et al., 2003; Liu et al., 2020). By this scheme, Eq. 1 can be rewritten by the diffusive flux
Again
where
can be used to extend Eq. 8 as
The particle discretization form of Eq. 10 is
Note that Eq. 11 can mitigate the particle inconsistency problem to some degree, although the discretization of Eq. 9 is only true for regularly distributed particles.
Applying Eq. 11 to the first-order derivatives in Eq. 7, the semi-discretization form of the substance transport equation is derived as (Liu et al., 2020)
Note that a similar formulation can be obtained for anisotropic diffusion, which eases the coding of anisotropic diffusion process (Liu et al., 2020). Since the diffusive flux is included, it is also easy to handle Neumann type boundary. The accuracy of Eq. 12 is the same order as that of Eq. 6 when particles are regularly spaced (Fatehi and Manzari, 2011). Together with a time integration algorithm, the above semi-discretization form and the change of the coordinate can be integrated. For simplicity, the first-order one-step Euler method is used here, which gives accurate results if the used time step is sufficiently small.
Equation 12 has been derived in Liu et al. (2020) with more details. In that work, the capability of the Lagrangian particle transport model to handle the grid anisotropic problem, dominated advection, pure advection and discontinuity have been validated in the flows with small deformation. Its accuracy, efficiency and stability were compared with the mesh-based Eulerian method, and the particle cavity problem was also recognized. In this work, the SPH-based model is further applied to substance transport problem in flows with large deformation. Since the model given by Eq. 12 cannot simulate the diffusion process when particles are in cavity state, the PSTs for eliminating particle cavities need to be incorporated, which is presented below.
3 Particle shifting techniques
When the particles become disordered due to non-uniform velocity field, SPH cannot accurately approximate the first- and second-order derivatives (Monaghan, 2000; Xu et al., 2009; Lind et al., 2012), and PSTs are good remedies. PSTs can be categorized into two classes. One is based on the distance between particles (Xu’s approach and its modified ones), and the other is based on the Fick’s law of diffusion (Lind’s approach and its modified ones). The latter ones are more feasible for free surface flow. In this section, the representative PSTs and their modified ones are presented. Moreover, a measurement to evaluate the degree of particle disorder is introduced.
3.1 PST of Xu (Xu et al., 2009)
In Xu’s approach, the particles are shifted in terms of the distance between the center particle and its neighbors (those in the support domain of the kernel). On the basis of Tailor series expansion, the concentration in the new position is interpolated by
where
In Xu’s approach, the regulation directing particle redistribution is given by
where
3.2 Modified Xu’s algorithm
In Xu’s approach,
where
3.3 Lind’s approach
In Lind’s approach, the movement of particles is determined by the gradient of particle concentration. To distinguish the diffusion process of pollutant concentration in Lagrangian Particle Transport Model Section from that of particle number concentration in this section, we use
Colagrossi et al. (2012) showed that
Substituting Eq. 18 into the shifting displacement of particle
The gradient of particle concentration can be discretized by SPH as (Lind et al., 2012)
where
Monaghan (2000) showed that when Eq. 20 is applied, the kernel gradient deviates from its physical meaning and will result in unphysical solution. For instance, the gradient of the cubic spline is zero in the origin, which will impose unphysical influence on the results when particle
where
The parameters
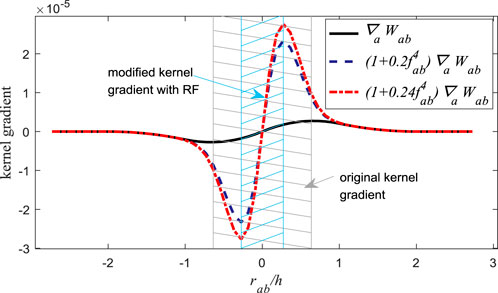
FIGURE 1. Comparison of the original kernel gradient (cubic spline kernel, solid line) with the modified ones by adding RF.
Using the symbol
where
3.4 Modified Lind’s algorithms
Skillen et al. (2013) improved Lind’s approach via the CFL condition for the purpose of bringing in the local velocity which makes a similar sense as
in which
Then the local velocity can be used to control the shifting magnitude. In fact, there should be a dimensionless parameter as
Recently, by using the maximum advection distance to replace one
Note that although these PSTs do not strictly preserve momentum, they are still valuable in solving the particle inconsistency problem because they have good features in convergence, accuracy and stability (Lind et al., 2012).
In Figure 1, the original kernel gradient (derivative with respect to
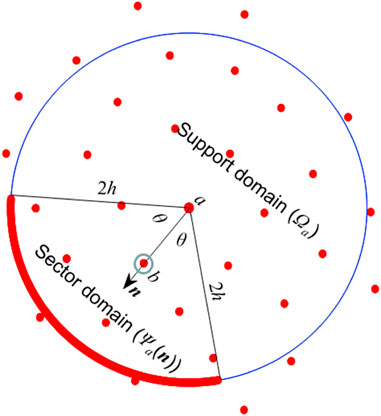
3.5 Particle disorder measurement
For judging the performance of different PSTs and the effect of related parameters, a measurement to evaluate the degree of particle disorder is presented in this section. The algorithm proposed by Antuono et al. (2014) is adopted here to figure out the best choice of parameters in different schemes and to appraise which scheme can lead to the best consequence in the simulation of the advection-diffusion process.
In the evaluation of particle consistency, there are two main steps. The first step is to search the neighbors of particle
In the second step, the sector domain
Accordingly, the maximum value
The function for quantitating particle disorder is given by
Then the effect of particle inconsistency can be evaluated by averaging all of
where
4 Numerical results and discussion
In this section, we aim to confirm the feasibility of SPH coupled with PST in solving the advection-diffusion process when particle cavity problem occurs. An anisotropic rotation flow field with strong deformation (Pudykiewicz and Staniforth, 1984) is used for validation. The pure advection simulation is carried out firstly to illustrate the cavity phenomenon, which still exists even a large number of particles are used. Under this circumstance, the diffusion terms cannot be accurately approximated. For eliminating the cavity problem and regulating the particle distribution, PSTs are added to the Lagrangian particle transport model (Liu et al., 2020) and a series of tests are then conducted. Through the numerical experiments, the efficiency of different PSTs is compared, the factors affecting the stability of PSTs are optimized, and the accuracy is examined by comparing with the reference solution of MTVDLF-Superbee. The performances of PSTs are discussed in detail to guide their possible application to real engineering problems. The anisotropic diffusion simulations are also performed to further state the feasibility of the particle model.
In this test, the flow field is given by the streamline function
Then the velocities in
where
The initial distribution of pollutant is given by the Gaussian as
where
4.1 Advection-diffusion simulation without PSTs
The pure advection case is simulated to verify the existence of cavity problem even a large number of particles are used. First, particles with a uniform spacing of 50 m (4096 particles) are distributed in the domain (see Figure 4A). The time step is 2.5 s and the simulation time is 3400 s, which approximately equals to the time needed for one rotation. As shown in Figure 4B, after one rotation, the particle distribution becomes highly irregular and some cavities appear, which is also shown in (Liu et al., 2020). Note that in the following figures, the color bar means pollutant concentration unless otherwise mentioned.
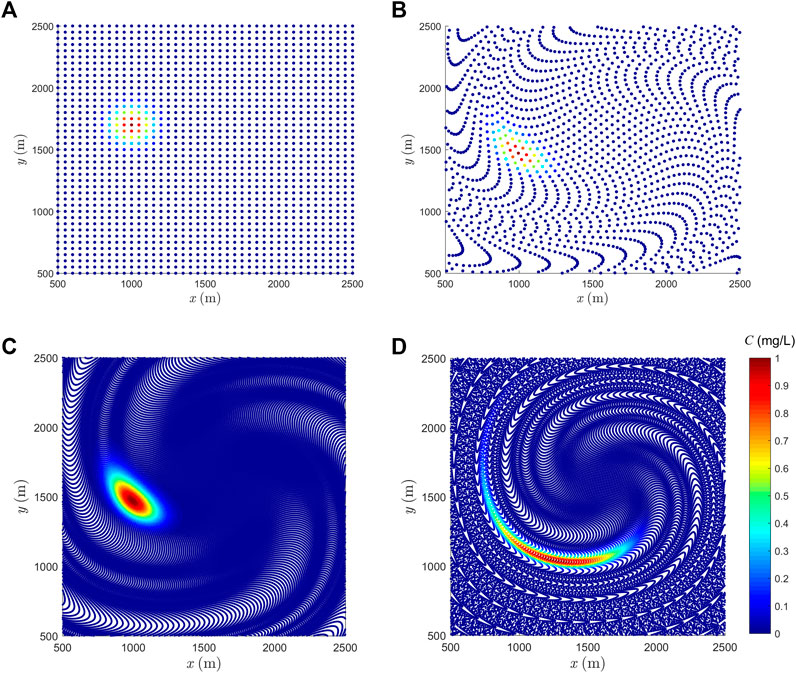
FIGURE 4. Pure advection simulation by SPH: concentration and particle distribution. (A) t = 0 s and 4096 particles, (B) t = 3400 s (roughly one rotation) and 4096 particles, (C) t = 3400 s and 102400 particles and (D) t = 6800 s and 102400 particles.
A uniform spacing of 10 m (102,400 particles) is then applied. The results after one rotation are presented in Figure 4C, where the cavity problem is still evident. After two rotations, the particle cavity phenomenon gets worse (see Figure 4D). They indicate that increasing particle number does not help to remove the cavity problem and higher computational cost will be caused.
For the advection-diffusion process in the given flow field, there is no exact solution available. To provide a good reference solution for comparison and evaluation, MTVDLF-Superbee method is implemented. In this case, the initial concentration distribution is smooth and no steep front forms within the simulation time, for which MTVDLF-Superbee can achieve second-order accuracy (Wang and Hutter, 2001). As the diffusion coefficient is assigned to be 20 m2/s, this is a diffusion dominated case, for which MTVDLF-Superbee gives good reference solutions (Liu et al., 2020). The grid number is 400 by 400 and the time step is 0.005 s. The reference solution after one rotation is shown in Figure 5. On a laptop machine (Core i7-5600U, 2.6 GHz), the CPU time for MTVDLF-Superbee is roughly 6 h.
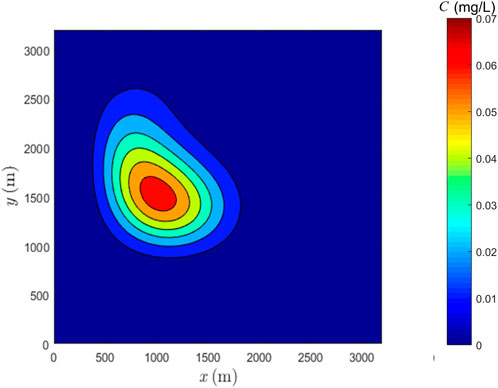
FIGURE 5. Reference solution obtained by MTVDLF-Superbee with grid number 400 by 400 and dt = 0.005 s.
In the SPH-based model, 160 by 160 particles are used to test its performance without PSTs. The smoothing length of
4.2 Advection-diffusion simulation with PSTs
As it is not necessary to arrange a large number of particles in view of applying PSTs, the particle number is set to be 64 by 64 for all the tests in this section. For SPH combined with PSTs, the CPU time is about half an hour. In general, Lind’s PST needs one-third more time than Xu’s PST because it is based on SPH approximations, whereas Xu’s PST is just based on a set of algebraic expressions.
To quantitatively evaluate the SPH results, the L2 norm error is taken here to measure the discrepancy between the solution of SPH with PST and the one of MTVDLF-Superbee with finer grids.
where
Moreover, the irregularity index
4.2.1 Factors affecting the stability of PSTs
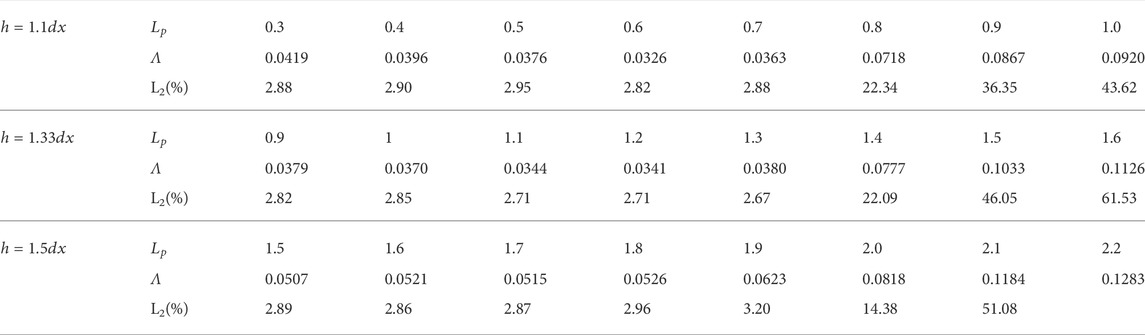
1) Paring instability affected by kernel types in Lind’s PST
In Lind’s PST, the paring instability often occurs. To avoid it, the smoothing length
FIGURE 7. Simulation results for one rotation by Lind’s PST with cubic spline kernel without RF in different smoothing length. (A) h = 1.1dx, (B) h = 1.2dx, (C) h = 1.33dx, (D) h = 1.4dx and (E) h = 1.5dx.
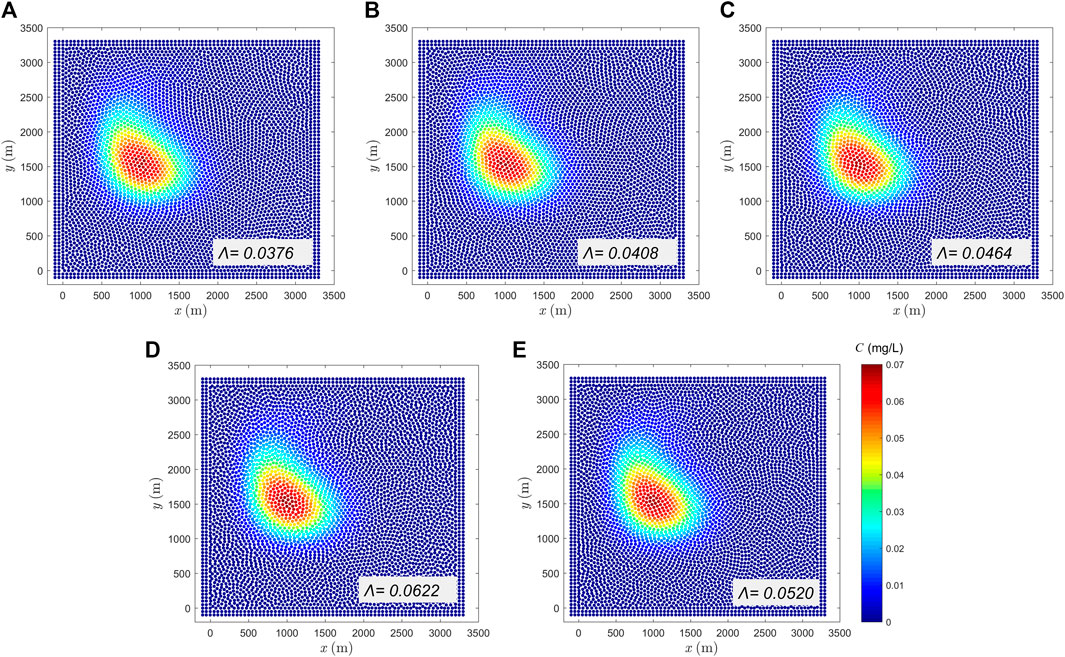
FIGURE 8. Simulation results for one rotation by Lind’s PST with cubic spline kernel with RF in different smoothing length. (A) h = 1.1dx, (B) h = 1.2dx, (C) h = 1.33dx, (D) h = 1.4dx and (E) h = 1.5dx.
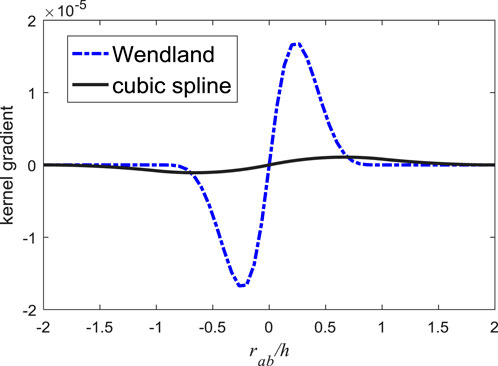
As mentioned in Section 3.4, the misleading portion of the kernel gradient should be narrow to alleviate the paring instability, from which aspect the Wendland type kernel (see Figure 9) is termed to be a better option (Dehnen and Aly, 2012; Alvarado-Rodríguez et al., 2019). Since the paring instability only occurs in PST and the simulation of diffusion is free of it, only the cubic spline kernel is replaced by Wendland. For ease of comparison, the same smoothing length with that in Figure 8E is used. In the solution obtained with the Wendland kernel without RF, paring instability has been completely resolved; see Figure 10. The value of
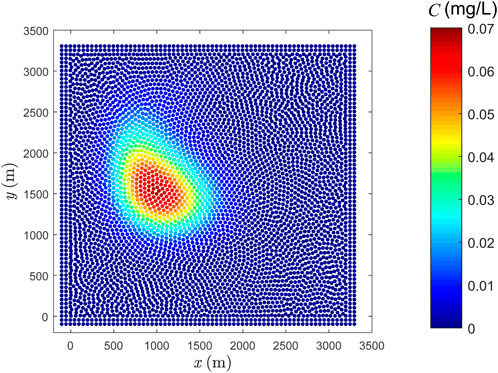
In Figure 11, the contours of simulated result by Lind’s PST with Wendland kernel are compared with the reference solution. For clearness, the concentration profiles along
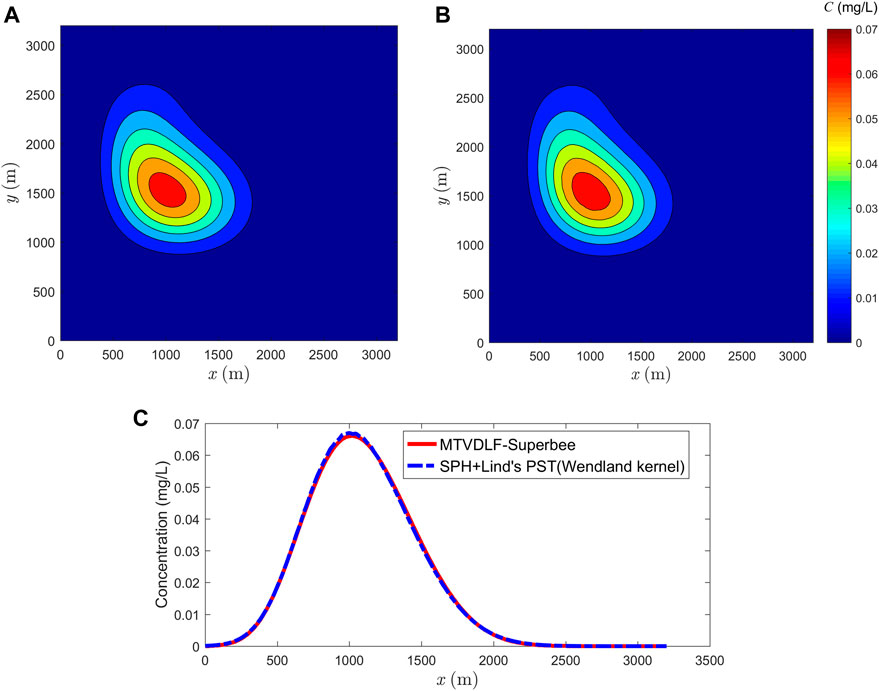
FIGURE 11. Comparison between reference solution and the result obtained by SPH combined with Lind’s PST. (A) Reference solution yielded by MTVDLF-Superbee, (B) solution of particle scheme (Lind’s PST with Wendland kernel) and (C) concentrations along
In summary, when the cubic spline kernel is adopted, paring instability appears, unless small smoothing length is applied or the RF term is added. While when the Wendland kernel is employed, there is no need to add RF to avoid paring instability, even a large smoothing length is used.
2) Parameters controlling the shifting amplitude
In Lind’s approach, the shifting magnitude depends on the value of
To visually show whether the results are stable or not, several simulations with different
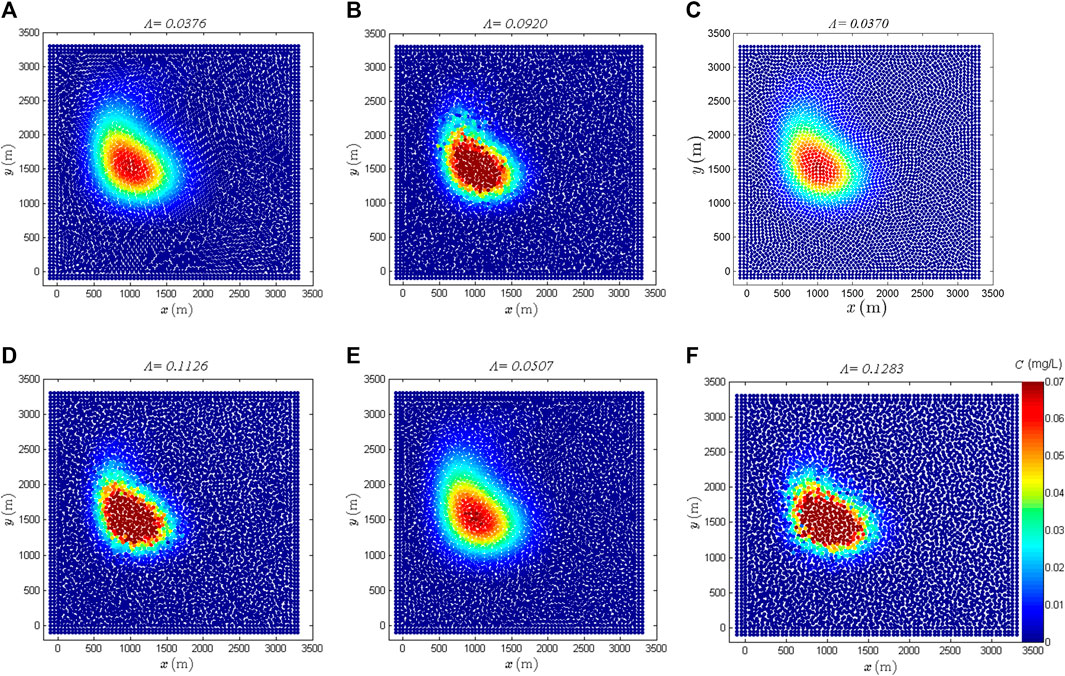
FIGURE 12. Simulation results of SPH combined with Lind’s PST with RF in different smoothing length and different Lp. (A) h = 1.1dx and Lp = 0.5, (B) h = 1.1dx and Lp = 1, (C) h = 1.33dx and Lp = 1, (D) h = 1.33dx and Lp = 1.6, (E) h = 1.5dx and Lp = 1.6 and (F) h = 1.5dx and Lp = 2.2.
In Xu’s approach, the shifting magnitude relies on parameter
The concentration for three typical values of
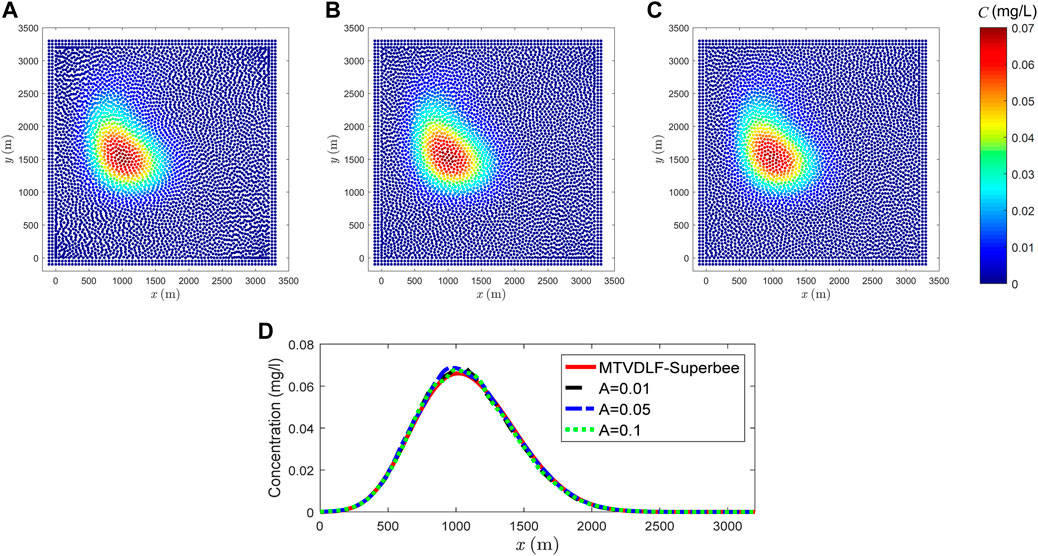
FIGURE 13. Simulation results by Xu’s PST with different A. (A) A = 0.01, (B) A = 0.05, (C) A = 0.1 and (D) concentration profiles along y = 1500 m.
According to the numerical results, it is seen that the solution of Lind’s PST within stable range is more accurate and has more regular particle distribution, while Xu’s PST is more stable. For the key parameter
3) Encoding details for mixed particle position
The test in this section is only for Lind’s PST. In the above simulations, the PST is executed after the advection process, which means that the particle position needs to be updated twice in each time step. For illustration, two symbols are used to distinct the particle positions in the current time step
Note that the PST can be done by solely using
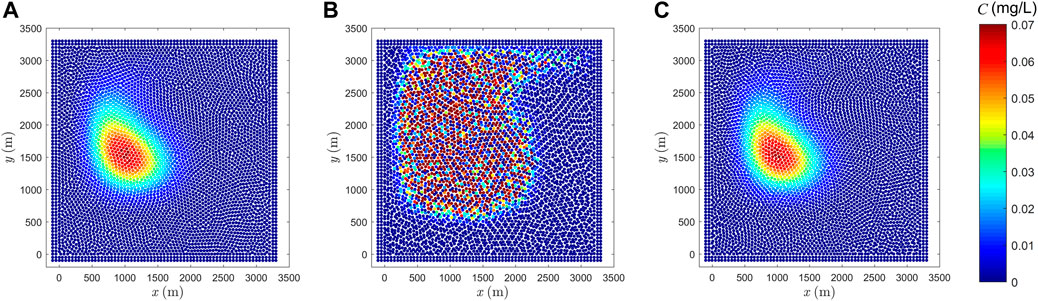
FIGURE 14. Simulation results by SPH with PST using (A) mixed particle position
In terms of the results presented in this section, mixed particle positions after both advection and PST should be used, otherwise the solution will become less stable, if only particle positions after advection are used.
4.2.2 Results of modified PSTs
To better control the shifting distance, the local velocity of particles or the maximum advection distance is introduced in the modified PSTs, which stabilizes the original algorithms and deletes the upper limit for the shifting magnitude. In this section, the results of the modified PSTs presented in Section 3 are compared with those of the original ones. The smoothing length
In the PST of Skillen et al. (2013) (modified Lind), numerical results with three different
4.3 Simulation of anisotropic diffusion
Different from the isotropic diffusion cases studied above, the anisotropic diffusion process brings two mixed derivatives. In this section, the capability of the developed particle scheme to simulate the anisotropic diffusion process with different
4.3.1 Transport in uniform flow
The ability of the SPH-based transport model (Eq. 12) to solve the anisotropic diffusion process is firstly verified by simulating an example with analytical solution.
The initial distribution of the concentration is also the Gaussian type and the exact solution is
where
In this case,
The numerical results of the first group are shown in Figure 15, where the results of both the particle and grid methods agree well with the analytical solution. For more clearness, all of them are compared through the concentration profiles along
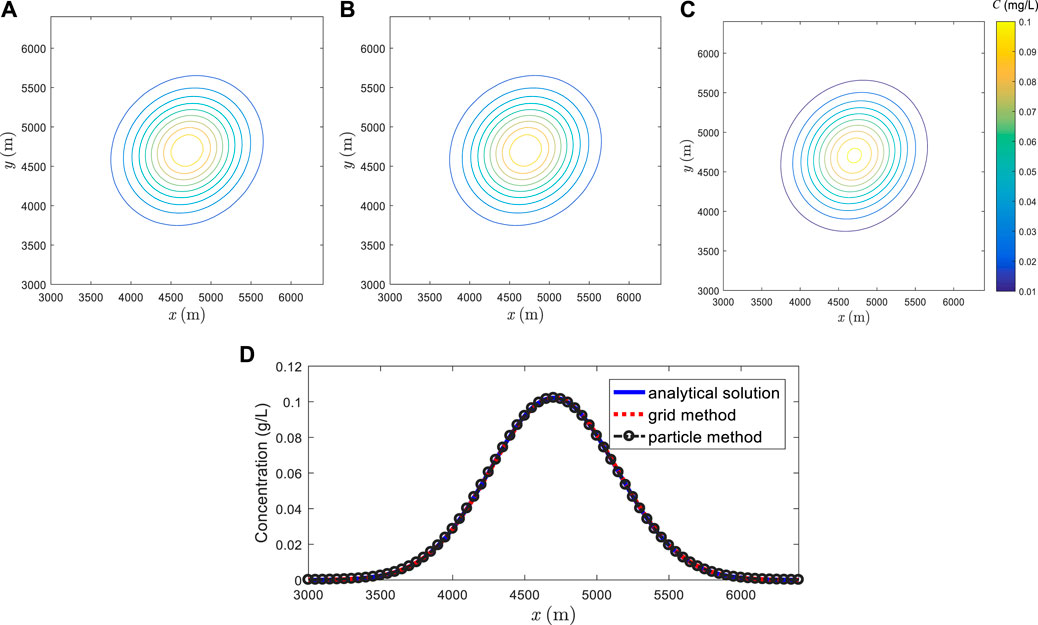
FIGURE 15. Results of the anisotropic diffusion under condition of
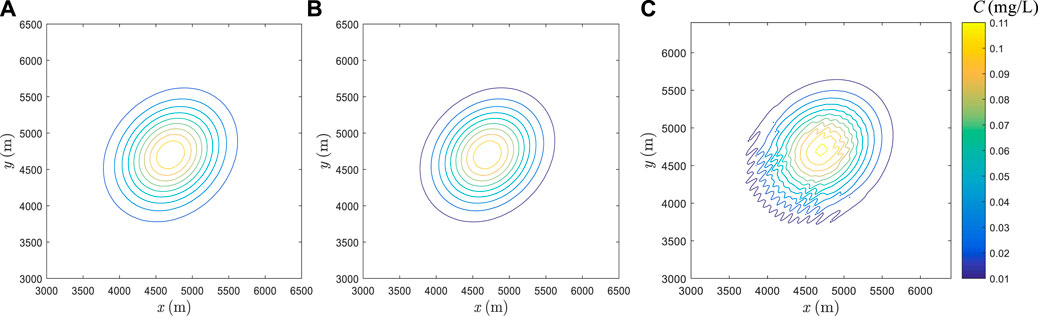
FIGURE 16. Results of the anisotropic diffusion under condition of
4.3.2 Transport in cavity problem
The flow field is still that with large deformation given by Eq. 31 and the initial concentration distribution is identical with that shown in Figure 4A. For the reference solution obtained by the grid method, the parameters are consistent with those used in the isotropic case in Section 4.1. In SPH the particles are 64 by 64 and the time step is 2.5 s. The simulation time is 3400 s. The diffusion coefficients
As shown in Figure 17, although a slight discrepancy still exists, good agreements between particle solution and reference solution are observed. That is, the developed particle model can also give reliable solutions for the anisotropic diffusion in the cavity problem.

FIGURE 17. Simulations of anisotropic diffusion in flow with cavities by (A) grid method and (B) particle method and comparison of concentration profiles along (C)
5 Case study
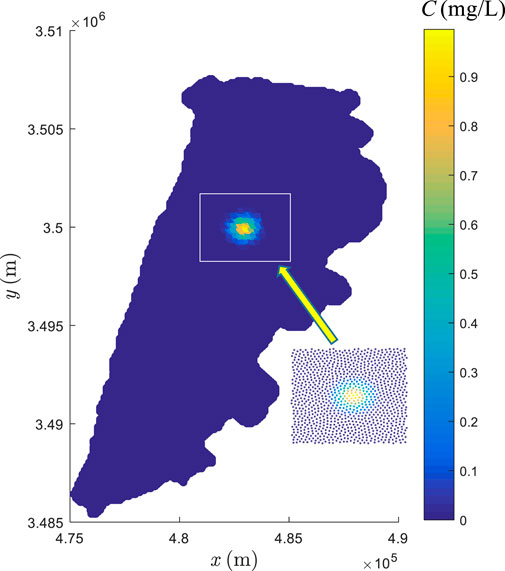
To show the capacity of the developed model for real problems, an engineering case study is presented in this section. The Gehu Lake is an artificial lake located in Jiangsu Province, China, the area of which is about 164 square kilometers. Its geometry is shown in Figure 18. To meet the ecological and landscape needs, the renewal time of the water body has to be determined. As the maximum water depth is only 4 m, the horizontal scale is much larger than the vertical scale. Meanwhile, the calculation of water renewal time involves the convection and diffusion of substances in the water. Therefore, this case study can be simplified into a problem of substance transport in 2D space. With the given shoreline, topography, outlet water level and inlet flow velocity, the flow field is firstly calculated by solving the shallow water equation on triangular meshes (see Figure 18A). As seen from the calculated velocity shown in Figure 18B, the flow is governed by the inlet and the two outlets.
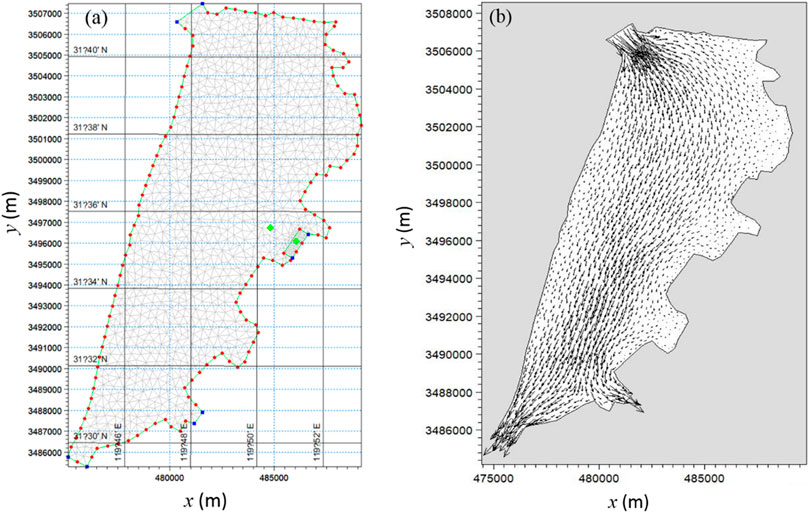
FIGURE 18. The geometry of Gehu Lake discretized with triangular meshes (A) and calculated flow velocity (B).
Different from the idealized case with given analytical velocity field (e.g., Figure 3), the velocity distribution in this real case is known only on the nodes of the triangular meshes (see Figure 18A). To interpolate the velocity of particles moving through the grids, the symmetric smoothed particle hydrodynamics (SSPH) method (Batra and Zhang, 2008) is used, which is third order accurate when up to third-order derivatives are remained in the Taylor’s expansion. Since the computational domain is irregular, the triangular mesh is adopted for initial particle distribution. In this case, as the transportation of pollutants along the central axis of this lake is the main concern, the zero concentration for the dummy particles is applied. For the PST, sufficient dummy particles are needed to prevent fluid particles clustering near the boundary or escaping from the computational domain.
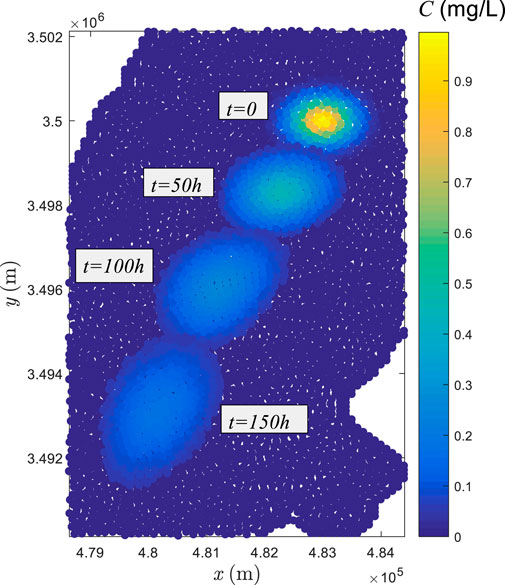
To determine how substances transport in this lake and how long they cross the lake, the Gaussian type pollutant given by Eq. 34 is supposed to be released into the water instantaneously at the upstream (See Figure 19), for which the maximum concentration value is 1 mg/L. Initially 9000 fluid particles are set at the triangular mesh point with a spacing of 100 m. An enlarged view of the area around the pollutants shows that initially the particles are more or less uniformly distributed. The time step can be assigned with a large value, up to 3000 s, which still satisfies the stability condition due to the slow velocity. A constant diffusion coefficient of
6 Conclusion
The SPH method under Lagrangian frame has advantages in solving the advection-diffusion problems. It can well handle the advection-dominated transport problems with discontinuity which are tough for mesh-based Eulerian methods, and has characters of high efficiency and precision (Liu et al., 2020). However, when complicated velocity field is encountered, the particle distribution will become disordered and even forms particle cavities. On this condition, the simulation of the diffusion process easily fails because the insufficient or asymmetry of neighboring particles leads to inaccuracy of kernel approximation. To settle this problem, the particle shifting techniques (PSTs) are introduced to eliminate the particle cavities and make the Lagrangian particle transport model run accurately and smoothly. It can well resolve both the isotropic and anisotropic diffusion process in large deformation flow. Reasonable results are obtained when it is applied in practical flow. The stability, efficiency and accuracy of different PSTs are compared. Lind’s approach gives more regular particle distribution and hence higher accuracy, while Xu’s PST is more stable and its efficiency is higher. When Lind’s approach is adopted, to prevent paring instability, the Wendland kernel is a better choice than the cubic spline, since the RF term is not needed. In addition, to carry out the PST for a given particle, the updated positions of its neighbors after both advection and PST should be applied, otherwise instability might be induced if only the advected positions are used. Comparing with the original PSTs of Xu and Lind, the modified ones do not show noticeable improvements, at least for the cases studied in this work.
The flow field in the present work, either steady in the real case or straightly given by the streamline function, is relatively simple. How the developed scheme performs in the more practical problems, e.g., in the complicated and time-variant ocean flow field (Luo et al., 2021), should be further explored. The involvement of irregular boundaries could be more intractable, which has not been fully discussed in this work. The PST introduced intents to make the particle method available in the transportation simulation of real flows. We will focus on promoting the capability of the proposed numerical model in solving the practical problems in future.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
WL: methodology, investigation, simulation, visualization, validation, analysis, and writing original draft. QH: supervision, conceptualization, methodology, analysis, investigation and writing, review and editing. XL: conceptualization, supervision, review and editing. JL: supervision, review and editing. JD: supervision, review and editing.
Funding
This study was supported by the National Key Research and Development Program of China (No. 2020YFC1807905), National Natural Science Foundation of China (No. 52079090) and Basic Research Program of Qinghai Province (No. 2022-ZJ-704).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alhumaizi, K. (2004). Comparison of finite difference methods for the numerical simulation of reacting flow. Comput. Chem. Eng. 28, 1759–1769. doi:10.1016/j.compchemeng.2004.02.032
Alvarado-Rodríguez, C. E., Sigalotti, L. D. G., and Klapp, J. (2019). Anisotropic dispersion with a consistent smoothed particle hydrodynamics scheme. Adv. Water Resour. 131, 103374. doi:10.1016/j.advwatres.2019.07.004
Antuono, M., Bouscasse, B., Colagrossi, A., and Marrone, S. (2014). A measure of spatial disorder in particle methods. Comput. Phys. Commun. 185, 2609–2621. doi:10.1016/j.cpc.2014.06.008
Aristodemo, F., Federico, I., Veltri, P., and Panizzo, A. (2010). Two-phase SPH modelling of advective diffusion processes. Environ. Fluid Mech. 10, 451–470. doi:10.1007/s10652-010-9166-z
Bai, B., Rao, D. Y., Xu, T., and Chen, P. P. (2018). SPH-FDM boundary for the analysis of thermal process in homogeneous media with a discontinuous interface. Int. J. Heat. Mass Transf. 117, 517–526. doi:10.1016/j.ijheatmasstransfer.2017.10.004
Batra, R. C., and Zhang, G. M. (2008). SSPH basis functions for meshless methods, and comparison of solutions with strong and weak formulations. Comput. Mech. 41, 527–545. doi:10.1007/s00466-007-0209-3
Bonet, J., and Lok, T. S. L. (1999). Variational and momentum preservation aspects of smooth particle hydrodynamic formulations. Comput. Methods Appl. Mech. Eng. 180, 97–115. doi:10.1016/s0045-7825(99)00051-1
Chang, Y. S., and Chang, T. J. (2017). SPH simulations of solute transport in flows with steep velocity and concentration gradients. Water 9, 132. doi:10.3390/w9020132
Chaniotis, A. K., Poulikakos, D., and Koumoutsakos, P. (2002). Remeshed smoothed particle hydrodynamics for the simulation of viscous and heat conducting flows. J. Comput. Phys. 182, 67–90. doi:10.1006/jcph.2002.7152
Chen, J. K., and Beraun, J. E. (2000). A generalized smoothed particle hydrodynamics method for nonlinear dynamic problems. Comput. Methods Appl. Mech. Eng. 190, 225–239. doi:10.1016/s0045-7825(99)00422-3
Chen, J. K., Beraun, J. E., and Carney, T. C. (1999). A corrective smoothed particle method for boundary value problems in heat conduction. Int. J. Numer. Methods Eng. 46, 231–252. doi:10.1002/(sici)1097-0207(19990920)46:2<231::aid-nme672>3.0.co;2-k
Cleary, P. W., and Monaghan, J. J. (1999). Conduction modelling using smoothed particle hydrodynamics. J. Comput. Phys. 148, 227–264. doi:10.1006/jcph.1998.6118
Colagrossi, A., Bouscasse, B., Antuono, M., and Marrone, S. (2012). Particle packing algorithm for SPH schemes. Comput. Phys. Commun. 183, 1641–1653. doi:10.1016/j.cpc.2012.02.032
Dehnen, W., and Aly, H. (2012). Improving convergence in smoothed particle hydrodynamics simulations without pairing instability. Mon. Not. R. Astron. Soc. 425, 1068–1082. doi:10.1111/j.1365-2966.2012.21439.x
Devkota, B. H., and Imberger, J. (2009). Lagrangian modeling of advection-diffusion transport in open channel flow. Water Resour. Res. 45 (12406), 1–14. doi:10.1029/2009wr008364
Ewing, R. E., and Wang, H. (2001). A summary of numerical methods for time-dependent convection-dominated partial differential equations. J. Comput. Appl. Math. 128 (1-2), 423–445. doi:10.1016/S0377-0427(00)00522-7
Fatehi, R., and Manzari, M. T. (2011). Error estimation in smoothed particle hydrodynamics and a new scheme for second derivatives. Comput. Math. Appl. 61, 482–498. doi:10.1016/j.camwa.2010.11.028
Finlayson, B. A. (1992). Numerical methods for problems with moving fronts. Seattle: Ravenna Park Publishing.
Gu, S., Zheng, W., Wu, H., Chen, C., and Shao, S. (2022). DualSPHysics simulations of spillway hydraulics: A comparison between single- and two-phase modelling approaches. J. Hydraulic Res. 60, 835–852. doi:10.1080/00221686.2022.2064343
Huang, C., Lei, J. M., Liu, M. B., and Peng, X. Y. (2015). A kernel gradient free (KGF) SPH method. Int. J. Numer. Meth. Fluids 78, 691–707. doi:10.1002/fld.4037
Huang, C., Zhang, D. H., Shi, Y. X., Si, Y. L., and Huang, B. (2018). Coupled finite particle method with a modified particle shifting technology. Int. J. Numer. Methods Eng. 113, 179–207. doi:10.1002/nme.5608
Jeong, J. H., Jhon, M. S., Halow, J. S., and van Osdol, J. (2003). Smoothed particle hydrodynamics: Applications to heat conduction. Comput. Phys. Commun. 153, 71–84. doi:10.1016/s0010-4655(03)00155-3
Khorasanizade, S., and Sousa, J. M. M. (2016). An innovative open boundary treatment for incompressible SPH. Int. J. Numer. Meth. Fluids 80, 161–180. doi:10.1002/fld.4074
Kum, O., Hoover, W. G., and Hoover, C. G. (2003). Smooth-particle boundary conditions. Phys. Rev. E 68, 017701. doi:10.1103/physreve.68.017701
Larbe, G., and Price, D. J. (2012). Dusty gas with smoothed particle hydrodynamics–II. Implicit time stepping and astrophysical drag regimes. Mon. Not. R. Astron. Soc. 420 (3), 2365–2376. doi:10.1111/j.1365-2966.2011.20201.x
Lind, S. J., Xu, R., Stansby, P. K., and Rogers, B. D. (2012). Incompressible smoothed particle hydrodynamics for free-surface flows: A generalised diffusion-based algorithm for stability and validations for impulsive flows and propagating waves. J. Comput. Phys. 231, 1499–1523. doi:10.1016/j.jcp.2011.10.027
Liu, M. B., and Liu, G. R. (2006). Restoring particle consistency in smoothed particle hydrodynamics. Appl. Numer. Math. 56, 19–36. doi:10.1016/j.apnum.2005.02.012
Liu, W., Hou, Q., Lian, J. J., Zhang, A. M., and Dang, J. W. (2020). Coastal pollutant transport modeling using smoothed particle hydrodynamics with diffusive flux. Adv. Water Resour. 146, 103764. doi:10.1016/j.advwatres.2020.103764
Liu, W. K., and Jun, S. (1998). Multiple-scale reproducing kernel particle methods for large deformation problems. Int. J. Numer. Methods Eng. 41, 1339–1362. doi:10.1002/(sici)1097-0207(19980415)41:7<1339::aid-nme343>3.0.co;2-9
Liu, W. K., Jun, S., and Zhang, Y. (1995). Reproducing kernel particle methods. Int. J. Numer. Meth. Fluids 20, 1081–1106. doi:10.1002/fld.1650200824
Luo, M., Khayyer, A., and Lin, P. (2021). Particle methods in ocean and coastal engineering. Appl. Ocean Res. 114, 102734. doi:10.1016/j.apor.2021.102734
Mlacnik, M. J., and Durlofsky, L. J. (2006). Unstructured grid optimization for improved monotonicity of discrete solutions of elliptic equations with highly anisotropic coefficients. J. Comput. Phys. 216, 337–361. doi:10.1016/j.jcp.2005.12.007
Monaghan, J. J. (1988). An introduction to SPH. Comput. Phys. Commun. 48 (1), 89–96. doi:10.1016/0010-4655(88)90026-4
Monaghan, J. J., and Kocharyan, A. (1995). SPH simulation of multi-phase flow. Comput. Phys. Commun. 87 (1-2), 225–235. doi:10.1016/0010-4655(94)00174-z
Monaghan, J. J. (2005). Smoothed particle hydrodynamics. Rep. Prog. Phys. 68, 1703–1759. doi:10.1088/0034-4885/68/8/r01
Monaghan, J. J. (2012). Smoothed particle hydrodynamics and its diverse applications. Annu. Rev. Fluid Mech. 44, 323–346. doi:10.1146/annurev-fluid-120710-101220
Monaghan, J. J. (2000). SPH without a tensile instability. J. Comput. Phys. 159, 290–311. doi:10.1006/jcph.2000.6439
Nestor, R., Basa, M., Lastiwka, M., and Quinlan, N. (2009). Extension of the finite volume particle method to viscous flow. J. Comput. Phys. 228, 1733–1749. doi:10.1016/j.jcp.2008.11.003
Nestor, R., Basa, M., and Quinlan, N. (2008). Moving boundary problems in the finite volume particle method. in Proceedings of 3rd International SPHERIC Workshop, Lausanne, Switzerland, 4-6 June 2008. 109–114.
Nordbotten, J. M., and Aavatsmark, I. (2005). Monotonicity conditions for control volume methods on uniform parallelogram grids in homogeneous media. Comput. Geosci. 9 (1), 61–72. doi:10.1007/s10596-005-5665-2
Pudykiewicz, J., and Staniforth, A. (1984). Some properties and comparative performance of the semi-Lagrangian method of Robert in the solution of the advection-diffusion equation. Atmosphere-Ocean 22 (3), 283–308. doi:10.1080/07055900.1984.9649200
Ryan, E. M., Tartakovsky, A. M., and Amon, C. (2010). A novel method for modeling Neumann and Robin boundary conditions in smoothed particle hydrodynamics. Comput. Phys. Commun. 181, 2008–2023. doi:10.1016/j.cpc.2010.08.022
Shahriari, S., Hassan, I. G., and Kadem, L. (2013). Modeling unsteady flow characteristics using smoothed particle hydrodynamics. Appl. Math. Model. 37 (3), 1431–1450. doi:10.1016/j.apm.2012.04.017
Shao, J. R., Li, H. Q., Liu, G. R., and Liu, M. B. (2012). An improved SPH method for modeling liquid sloshing dynamics. Comput. Struct. 100-101, 18–26. doi:10.1016/j.compstruc.2012.02.005
Shao, S. D., and Lo, E. Y. M. (2003). Incompressible SPH method for simulating Newtonian and non-Newtonian flows with a free surface. Adv. Water Resour. 26, 787–800. doi:10.1016/s0309-1708(03)00030-7
Skillen, A., Lind, S., Stansby, P. K., and Rogers, B. D. (2013). Incompressible smoothed particle hydrodynamics (SPH) with reduced temporal noise and generalised Fickian smoothing applied to body–water slam and efficient wave–body interaction. Comput. Methods Appl. Mech. Eng. 265, 163–173. doi:10.1016/j.cma.2013.05.017
Tsuruta, N., Khayyer, A., and Gotoh, H. (2013). A short note on dynamic stabilization of moving particle semi-implicit Method. Comput. Fluids 82, 158–164. doi:10.1016/j.compfluid.2013.05.001
Violeau, D. (2012). Fluid mechanics and the SPH method: The theory and applications. Oxford: Oxford University Press.
Wang, J. Q., Hu, W., Zhang, X. B., and Pan, W. X. (2019). Modeling heat transfer subject to inhomogeneous Neumann boundary conditions by smoothed particle hydrodynamics and peridynamics. Int. J. Heat. Mass Transf. 139, 948–962. doi:10.1016/j.ijheatmasstransfer.2019.05.054
Wang, Y. Q., and Hutter, K. (2001). Comparisons of numerical methods with respect to convectively dominated problems. Int. J. Numer. Meth. Fluids 37, 721–745. doi:10.1002/fld.197
Xu, R., Stansby, P., and Laurence, D. (2009). Accuracy and stability in incompressible SPH (ISPH) based on the projection method and a new approach. J. Comput. Phys. 228, 6703–6725. doi:10.1016/j.jcp.2009.05.032
Ye, T., Pan, D. Y., Huang, C., and Liu, M. B. (2019). Smoothed particle hydrodynamics (SPH) for complex fluid flows: Recent developments in methodology and applications. Phys. Fluids 31, 1–41. doi:10.1063/1.5068697
Yuan, G., and Sheng, Z. (2008). Monotone finite volume schemes for diffusion equations on polygonal meshes. J. Comput. Phys. 227, 6288–6312. doi:10.1016/j.jcp.2008.03.007
Zhang, Z. L., and Liu, M. B. (2018). A decoupled finite particle method for modeling incompressible flows with free surfaces. Appl. Math. Model. 60, 606–633. doi:10.1016/j.apm.2018.03.043
Zheng, X., Ma, Q. W., and Shao, S. D. (2018). Study on SPH viscosity term formulations. Appl. Sci. 8, 249. doi:10.3390/app8020249
Keywords: smoothed particle hydrodynamics, anisotropic diffusion, particle shifting technique, particle disorder measurement, MTVDLF-Superbee
Citation: Liu W, Hou Q, Lei X, Lian J and Dang J (2022) SPH modeling of substance transport in flows with large deformation. Front. Environ. Sci. 10:991969. doi: 10.3389/fenvs.2022.991969
Received: 12 July 2022; Accepted: 29 July 2022;
Published: 12 October 2022.
Edited by:
Songdong Shao, Dongguan University of Technology, ChinaReviewed by:
Can Huang, North China University of Technology, ChinaXiaodong Yu, Hohai University, China
Copyright © 2022 Liu, Hou, Lei, Lian and Dang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qingzhi Hou, cWhvdUB0anUuZWR1LmNu
 Wanying Liu
Wanying Liu Qingzhi Hou
Qingzhi Hou Xiaohui Lei3
Xiaohui Lei3 Jianwu Dang
Jianwu Dang