Effects of long-term climate trends on the methane and CO2 exchange processes of Toolik Lake, Alaska

Methane and carbon dioxide effluxes from aquatic systems in the Arctic will affect and likely amplify global change. As permafrost thaws in a warming world, more dissolved organic carbon (DOC) and greenhouse gases are produced and move from soils to surface waters where the DOC can be oxidized to CO₂ and also released to the atmosphere. Our main study objective is to measure the release of carbon to the atmosphere via effluxes of methane (CH₄) and carbon dioxide (CO₂) from Toolik Lake, a deep, dimictic, low-arctic lake in northern Alaska. By combining direct eddy covariance flux measurements with continuous gas pressure measurements in the lake surface waters, we quantified the k₆₀₀ piston velocity that controls gas flux across the air–water interface. Our measured k values for CH₄ and CO₂ were substantially above predictions from several models at low to moderate wind speeds, and only converged on model predictions at the highest wind speeds. We attribute this higher flux at low wind speeds to effects on water-side turbulence resulting from how the surrounding tundra vegetation and topography increase atmospheric turbulence considerably in this lake, above the level observed over large ocean surfaces. We combine this process-level understanding of gas exchange with the trends of a climate-relevant long-term (30 + years) meteorological data set at Toolik Lake to examine short-term variations (2015 ice-free season) and interannual variability (2010–2015 ice-free seasons) of CH₄ and CO₂ fluxes. We argue that the biological processing of DOC substrate that becomes available for decomposition as the tundra soil warms is important for understanding future trends in aquatic gas fluxes, whereas the variability and long-term trends of the physical and meteorological variables primarily affect the timing of when higher or lower than average fluxes are observed. We see no evidence suggesting that a tipping point will be reached soon to change the status of the aquatic system from gas source to sink. We estimate that changes in CH₄ and CO₂ fluxes will be constrained with a range of +30% and −10% of their current values over the next 30 years.

1 Introduction

A vast reservoir of organic matter is preserved in Arctic regions in permafrost, the permanently frozen ground at high latitudes (Schuur et al., 2015). Thawing of permafrost with climate warming exposes organic matter to decomposition, a process which has become a major concern as a positive and undesirable feedback of the Arctic to climate change (Tan and Zhuang, 2015; Elder et al., 2018; Elder et al., 2019; Elder et al., 2020). Greenhouse gases (GHG, here the sum of CO₂ and CH₄) produced by this terrestrial decomposition may be released directly to the atmosphere or they may be transferred by movement of groundwater or soil water into lakes and streams that drain the terrestrial landscape (e.g., Kling et al., 1991; Cole et al., 1994). In addition, newly-thawed dissolved and particulate organic carbon (C) on land can be transferred to surface waters where the C may be oxidized to CO₂ by microbes and sunlight (e.g., Cory et al., 2013; Cory et al., 2014). Open water bodies in the Arctic, which cover up to 48% of the earth surface in some regions of Alaska (Riordan et al., 2006; McGuire et al., 2009) and about 12%–14% of the surface area of the Alaskan North Slope, thus play an important role in greenhouse gas release to the atmosphere (Kling et al., 1991; Kling et al., 1992; McGuire et al., 2009; Cory et al., 2014; Garies and Lesack, 2020).

For over 110 years (see Krogh, 1910) the characteristics and controls of gas exchange across air-water interfaces have been examined, as described in several comprehensive studies and reviews (Brutsaert and Jirka, 1984; Liss and Merlivat, 1986; Jahne and Monahan, 1995; Wanninkhof et al., 2009; Garbe et al., 2014). The fundamental variable controlling gas flux is the gas transfer velocity (piston velocity) typically represented as k in a basic equation of gas flux (F) where F = k(Cw − Co); Cw is the gas concentration beneath the water surface and Co, is the gas concentration at the water surface (modified for solubility or chemical enhancement, e.g., Wanninkhof et al., 2009). Depending on gas solubility and chemical enhancement, the physical-chemical controls on k have been studied from the water-side (less soluble and unreactive gases, e.g., Liss and Slater 1974) or from the air-side (more soluble and reactive gases, e.g., Johnson et al., 2011; Garbe et al., 2014). For gases of intermediate solubility or for processes that extend across the air-water interface (e.g., surface films, Yang et al., 2021, or the effects of wave breaking and bubble clouds, e.g., Deike and Melville, 2018), both air-side and water-side fluid dynamics may be important.

Formulations of k in gas flux models have over time increasingly recognized the role of turbulent kinetic energy (TKE), buoyancy flux (β), and energy dissipation (ε), especially in the hydrodynamic processes of surface waters, and this has improved model fits to empirical data (e.g., MacIntyre et al., 2001; Fredriksson et al., 2016; Esters et al., 2017). However, many studies still find deviations between model predictions and empirically-measured gas transfer velocities (e.g., Zappa et al., 2007; Heikensen et al., 2014), including our results in this paper. These deviations seem especially large at low wind speeds and in lakes (e.g., Read et al., 2012), and in a recent, comprehensive study Klaus and Vachon (2020) showed that existing models that predict k do better than using a mean value of k in only 2%–39% of lakes, and they could not explain what conditions led to the poor predictions of models.

Eugster et al. (2020a) examined the variability in gas fluxes from Toolik Lake, Alaska, using data from 2010–2015 and showed greater interannual than diel variation in CO₂ and CH₄ fluxes. In this paper, we focus on the gas exchange processes between lake surface waters and the near-surface atmosphere measured in detail during the 2015 ice-free season of Toolik Lake. We specifically examine the relationships of environmental conditions and drivers of gas transfer velocities computed with eddy covariance, and suggest that the enhancement of k compared to a range of model predictions, especially at low wind speeds in this small lake (1.5 km² area), are related to the characteristics and dissipation of atmospheric turbulence generated over land as it reaches the lake. We combine the information on environmental controls with a detailed trend analysis of potential driver variables, including rainfall and soil temperature that could influence the amount of C transferred from land to surface waters, that were monitored during the past (up to 33 years) by the Arctic Long-Term Ecological Research project (ARC LTER), also based at Toolik Lake (Hobbie and Kling, 2014). By projecting the past 30+ year trends into the future, and combining this information with the full 2010–2015 flux dataset (see Eugster et al., 2020a), we consider how CO₂ and CH₄ fluxes from deep lakes like Toolik might evolve over the next 30 years, from 2020–2050.

The paper is structured as follows: 1) methods and results of the gas flux measurements, 2) relationships of gas fluxes to environmental variables, 3) controls on gas fluxes, and 4) long-term trends of driver variables and expected trends in gas fluxes.

2 Materials and methods

2.1 Study site

Measurements were made on Toolik Lake (68°37.830′ N, 149°36.366′ W, WGS84 datum) at 719 m asl, and in the Toolik Field Station (TFS) environment. Toolik Lake is a relatively deep glacial lake (maximum depth ≈26 m) located on the tundra north of the Alaskan Brooks Range with a surface area of 1.5 km² (Hobbie and Kling, 2014).

Six ice-free seasons (2010–2015) were covered with eddy covariance flux measurements (Section 2.2), the results of which were presented by Eugster et al. (2020a). In addition, in 2015 an equilibrator system with a dissolved gas extraction unit was used to continuously determine the gas mixing ratios in the Toolik lake surface waters (Section 2.3). And finally, long-term observations were made as a component of the ARC LTER project since the late 1980s. The location of the TFS meteorological station (68°37.698′ N, 149°35.759′ W, 722 m asl) is ∼500 m southeast of the EC flux measurements.

Toolik lake is ice covered during 9–10 months of the year, with CO₂ and CH₄ accumulating under the ice (Kling et al., 1992), an aspect not covered here. Ice on and off dates are typically from mid-June to early July, and ice-on starts in the time period of end of August to late September. Because the Sun does not set at this northern latitude from 23 May to 19 July, there is no dark period of the day and “night” with darkness is not observed before August.

2.2 Eddy covariance flux instrumentation

The instrumentation and methods used in this study were presented in detail in Eugster et al. (2020a). Here we briefly summarize the key aspects of the EC measurements. Flux measurements were made with a three-dimensional ultrasonic anemometer-thermometer (CSAT3, Campbell Scientific, Logan, UT, United States) in combination with a closed-path integrated off-axis cavity output spectrometer (ICOS) for CH₄ (FMA, Los Gatos Research, Inc., San Jose, CA, United States) and a nondispersive infra-red gas analyzer for CO₂ and H₂O (Li-7000, Li-Cor Inc., Lincoln, NE, United States). Instruments were mounted on a floating platform (Supplementary Figure S1A) that was moored at approximately the same location every year ≈400 m from the nearest lake shore. Depth of the lake at this location was ≈12 m. The gap-filling of missing data up to four hours (up to 8 hours for 3-hourly resolved variables) was done by linear interpolation. For longer gaps the following approach was used: 1) the median diel cycle of all available years during the time-of-day of the gap, including a 1-day margin on both sides, was used as a reference; 2) then the beginning of the gap-filling time series was connected to the endpoint of the available data using an offset correction; and 3) finally, the endpoint of the gap was connected to the first valid data point after the gap via linear scaling. In addition, the pyranometer data were offset-corrected to obtain a mean 0 W m⁻² nocturnal flux (this corrects for the offset associated with the instrument temperature of the pyranometer), after which all nocturnal values <0 W m⁻² were set to zero. The main precipitation time series only captured liquid precipitation, hence frozen precipitation in summer (which tends to be a small component) was neglected until a second, heated rain gauge was installed on 19 June 2004. There was very good agreement of the rainfall amounts measured by both gauges [major axis regression slope of 0.0998%, 95% CI 0.995–1.001; Legendre and Legendre (1998)]. Thus, for the analysis here, the gaps in the long-term precipitation time series were filled by inserting the measurements from the newer rain gauge, with no attempt to fill the remaining (mainly winter) gaps. Thus, in the case of precipitation, our analysis is biased towards the warm season with predominantly liquid precipitation. For details on flux calculation, gap-filling of missing data, and the flux footprint of the EC measurements the reader is referred to Eugster et al. (2020a).

2.3 Equilibrator system with dissolved gas extraction unit

During the 2015 ice-free season an equilibrator system with automatic dissolved gas extraction unit was deployed on the EC float (Supplementary Figure S1A). The device used was a modified version of a prototype that Los Gatos Research, Inc., produced for us in 2012–2013, from which the commercial LGR Dissolved Gas Extraction Unit (https://www.lgrinc.com/documents/LGR_Dissolved%20Gas%20Extraction%20System.pdf) evolved. The basic principle (Supplementary Figure S2) is to pull water through a cylindrical Liqui-Cel device containing a gas-permeable membrane separating the water flow from the gas flow. The under-pressure generated by pulling water through the Liqui-Cel device increases the efficiency with which dissolved gases pass the membrane and are incorporated into the air strip-flow section of the device. The strip gas containing the gases extracted from the water are then analyzed by CH₄ and CO₂ analyzers (Supplementary Figures S1,S2), and the equilibrium gas mixing ratio (mol fraction or parts per million by volume) is then calculated using the flow rates of all components of the system, the initial gas mixing ratios in the air strip-flow, and the gas extraction efficiency of the Liqui-Cel membrane.

However, we were unable to achieve the expected accuracy of the equilibration mixing ratios of CO₂ and CH₄ in this configuration because we found no simple way to accurately determine the efficiency of the Liqui-Cel membrane. The reason might have been that Toolik lake has a substantial load of particulate organic matter (POM) in the water (DelSontro, 2011) and the main water filter system was unable to remove 100% of the POM before the water stream entered the Liqui-Cel device. We thus expected that the efficiency of the Liqui-Cel device was a non-trivial function of 1) its age, 2) the elapsed time since replacement of the main water filter, and 3) the POM load in the sample water stream. Thus, we remodeled our prototype to operate in conventional closed-loop equilibration mode (Supplementary Figure S2 for the configuration used in this study).

Equilibrium gas mixing ratios were obtained by scaling the raw mixing ratio measurements obtained from the equilibrator device with the net difference between the gas flow from the Liqui-Cel membrane to the analyzers and the strip gas flow measured with a gas flow meter,

$c_{eq}=\frac{c_{measured}\cdot F_{gas}-F_{stripgas}\cdot c_{ambient}}{F_{gas}-F_{stripgas}}(1)$

with ambient mixing ratio c_ambient of 390 ppmv (parts per million by volume) for CO₂ and 1.85 ppmv for CH₄. The gas flow to the analyzer, Fgas, was ≈5.5·10⁻⁴ m³ s⁻¹ (a 408 cm³ sample cell refreshed every 7.4 s). The strip gas flow Fstripgas was continuously measured by the dissolved gas extraction unit (Supplementary Figures S1B,C). Due to the high variability of the raw mixing ratio measurements, a local polynomial regression smoothing (loess function in R) was applied in the computation of c_measured to obtain the final equilibrium mixing ratio c_eq. Supplementary Figure S3 shows the data used for quality checking this procedure.

2.4 Long-term monitoring and trend analysis

In 1988 long-term meteorological measurements started, and the variables used in this study are shown in Supplementary Table S1. From the available variables, air temperature, barometric pressure, short-wave incoming radiation, lake depth, lake temperature, precipitation, relative humidity (RH), soil temperatures, and wind speed were used for trend analysis. For pre-1996 temperature and RH at 5 m height, we gap-filled from a local station when available, and to correct a degraded RH sensor an offset-correction was applied that sets the moving 7-days maximum to 100% and trims data to 100%. Vapor pressure deficit (VPD) was calculated from the air temperature Ta (in °C), relative humidity RH (in %) and barometric pressure Pa (in hPa) using the procedure by Buck (1981) to yield

$VPD=\left(1-\frac{RH}{100\%}\right)\cdot 6.1121\cdot e^{\frac{17.502\cdot T_a}{T_a}+240.97}\cdot \left(1.0007+3.46\cdot {10}^{-6}\cdot P_a\right)(2)$

Snow depth and wind direction were not included in the trend analysis. Snow depth is only measured since 2014 (Supplementary Table S1) and moreover during the ice-free season an extensive snow cover is missing and thus it is not expected that this variable strongly influences summertime CO₂ and CH₄ fluxes. Wind direction also was excluded from the trend analysis because small trends in wind direction are not expected to influence lake–atmosphere GHG effluxes substantially.

For the trend analyses we used the Theil-Sen median slope estimator (Sen, 1968; Akritas et al., 1995) that takes account for the fact that time-series do not meet the model assumptions of ordinary least-square regression (the x-axis is not a random variable, and values are equally spaced in the time-series and do not follow a random normal distribution). This trend slope estimator was then combined with a quantile regression approach (Easterling, 1969; Lejeune and Sarda, 1988; Patel, 2021); within each year the quantiles of the available measurements are determined for each percentile of the empirical distribution for that year. Then the Theil-Sen median trend slope fit was calculated for each new time-series of the quantiles in each percentile of each year. This approach allows identification of trends that are not uniform across the entire gradient of values observed in a given time-series. To estimate the long-term overall trend of each monitored variable we then used only the percentiles with significant trends to obtain the median change per decade and its 95% confidence interval.

2.5 Statistical analyses

Statistical analyses were carried out with R version 4.1.2 (R Core Team, 2014). To compute the Theil-Sen median trend slope the trend package (Pohlert, 2020) was used, which provides the sens.slope function (Sen, 1968). Significance of the slope was determined using the nonparametric Mann-Kendall test provided by the mk.test function. Major axis (orthogonal) regression was computed using the lmodel2 function of the lmodel2 package (Legendre and Legendre, 1998).

3 Results

Six years of eddy covariance flux measurements of CH₄ and CO₂ during the ice-free season of Toolik lake (Eugster et al., 2020a) allow us to link interannual variability to trend estimates from the long-term ancillary monitoring data to estimate future development of these two most important GHG fluxes (see Section 4.2). The focus here is on the detailed process-level investigations from the 2015 ice-free season during which continuous dissolved gas mixing ratio measurements at fine temporal resolution were carried out, allowing us to assess the gas exchange processes and their short-term responses to variability in atmospheric meteorological and lake water conditions. These measured values allow for increased detail to be extracted from the record instead of using modeled GHG fluxes.

Equilibrium CO₂ mixing ratios of the Toolik lake surface water fluctuated around atmospheric mixing ratios throughout the season (Figure 1A), typically following a 12-h delay behind barometric pressure changes, whereas the water was supersaturated with CH₄ at all times (Figure 1B). The range of equilibrium mixing ratios in the surface waters was much broader than in the atmosphere (Figure 2C), and the distribution of values was close to a normal distribution. In contrast, atmospheric mixing ratios followed a gamma distribution (Figure 2C) with a clear lower daytime boundary around 370 ppmv (Figure 2C), and a long tail towards higher mixing ratios at night. The CO₂ fluxes show a pronounced diel cycle (Figure 2B), but the timing is not synchronous with the diel cycle of the CO₂ mixing ratio (Figure 2A) or the cycle of primary production (driven by light; Miller et al., 1986). Above-average equilibrium CO₂ mixing ratios in the surface waters were observed during the period 0200–1600 h Alaska Daylight Time (AKDT) (Figure 2A), when substantially increased CO₂ fluxes were observed from 0000 to 0600 h AKDT (local midnight is at 0200 h AKDT), thus during the period of lowest net radiation input. Note that the Sun does not set during most of the summer season, and thus “night” does not imply complete darkness at Toolik Lake.

FIGURE 1

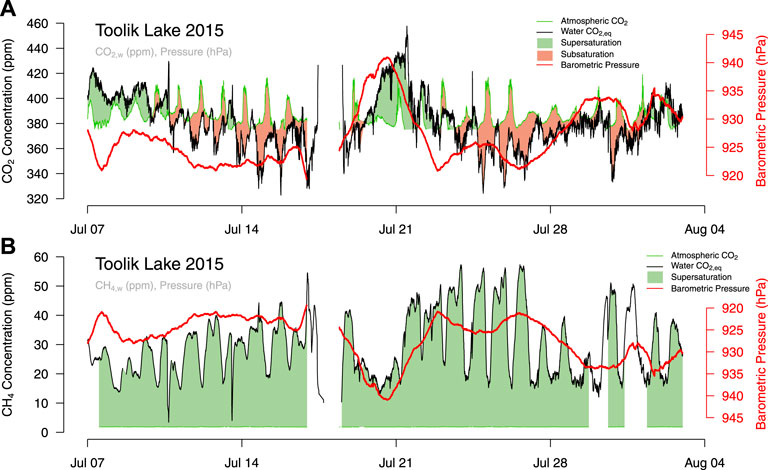
FIGURE 1. Timeseries of (A) CO₂ concentrations and (B) CH₄ concentrations in the atmosphere (green lines) and the surface water (black lines) during the ice-free seasons 2015. Supersaturation of the surface water is shown with a green area between the two concentrations, and subsaturation is shown with a red area. In addition, barometric pressure (bold red lines) are shown; note axes at right, and the inversed barometric pressure axis in (B).

FIGURE 2

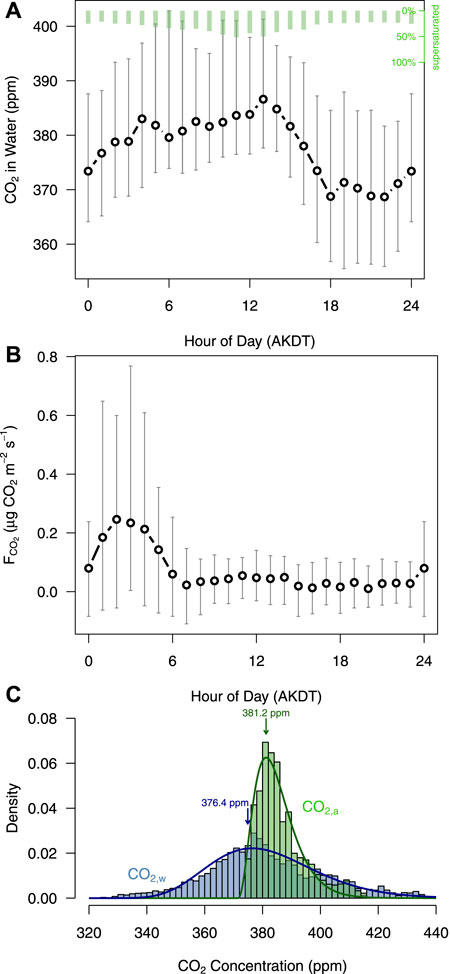
FIGURE 2. Diel cycles of (A) equilibrium surface water CO₂ concentration, (B) CO₂ flux across lake surface interface, and (C) the histograms of surface water (CO_2,w) and atmospheric (CO_2,a) concentrations. Arrows with values show the location of the maximum of the respective distribution. Error bars show the inter-quartal range (inner 50% of hourly data), and circles are hourly medians.

To examine the potential role of CO₂ uptake by photosynthesis, we measured chlorophyll a (an estimate of algal biomass), water column primary production, and concentrations of CO₂ (CO₂ measured with a syringe equilibration method, see Kling et al., 2000) at different depths in Toolik Lake. In 2015 at all depths measured near the surface (0.1, 1, 3 m) the CO₂ concentrations tended to increase as chlorophyll a or primary production increased (Supplementary Figure S4), which is the opposite of what we would expect if CO₂ drawdown from photosynthesis was important in determining surface water gas concentrations. Benthic fluxes of CO₂ or CH₄ were not measured in this study, in part because during the ice-free season this deep lake is stratified (Supplementary Figure S5) and any benthic flux would be essentially trapped in the hypolimnion during our period of measurements.

Dissolved CH₄ in Toolik Lake was supersaturated at all times (Figures 1B, 3C) with 10–58 ppmv higher equilibrium mixing ratios in surface waters than what was observed in the atmosphere. The diel cycle of atmospheric CH₄ mixing ratio (Figure 3A) almost mirrors the diel cycle of CO₂ flux (Figure 2B) with minimum equilibrium CH₄ mixing ratios in the surface waters from 0000 to 0600 h. CH₄ fluxes where slightly higher in the afternoon than in the early morning (Figure 3B).

FIGURE 3

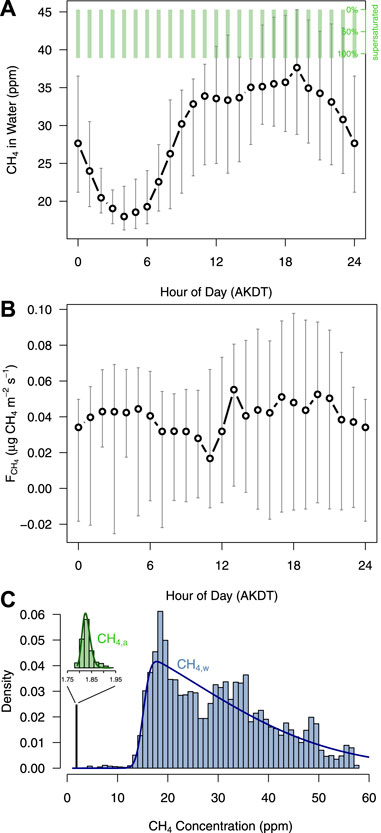
FIGURE 3. Diel cycles of (A) equilibrium surface water CH₄ concentration, (B) CH₄ flux across lake surface interface, and (C) the histograms of surface water (CH_4,w) and atmospheric (CH_4,a) concentrations. The distribution peaks are located at 1.825 and 17.8 ppm for CH_4,a and CH_4,w, respectively. Error bars show the inter-quartal range (inner 50% of hourly data), and circles are hourly medians.

3.1 Principal components of the drivers of CO₂ fluxes

A principal component analysis (PCA) of CO₂ flux measured during 2015 over Toolik Lake combined the potential driving variables at the same temporal resolution as CO₂ fluxes. This analysis includes meteorological variables, eddy flux variables, and temperature and gas mixing ratios in the water, including temperature of the upper mixing layer in the lake (0–4 m depth) and temperature near or below the typical summer thermocline (5 m depth). If arrows are shown perpendicular to each other, the variables are independent (uncorrelated) in the selected PCA axes. Figure 4A shows CO₂ flux as the dominant variable in the second PCA axis. The two first PCA axes in Figure 4A explain a total of 59.5% of the variance in the selected dataset (42.4 % and 17.1%). F_CO2 increases as atmospheric CO₂ density (in mmol m⁻³) increases, but is almost unrelated to CO₂ mixing ratio corrected for variability in density of air, which includes barometric pressure, air temperature, and atmospheric water vapor content. In contrast, the CO₂ mixing ratio gradient across the air-water interface, ΔCO₂ (in ppmv), has a weak, direct negative effect on F_CO2. The sign conventions of F_CO2 and ΔCO₂ are that F_CO2 is positive when gas evades from the water to the atmosphere, and ΔCO₂ is positive when the equilibration mixing ratio of CO₂ in the surface water is higher than the corresponding atmospheric value.

FIGURE 4

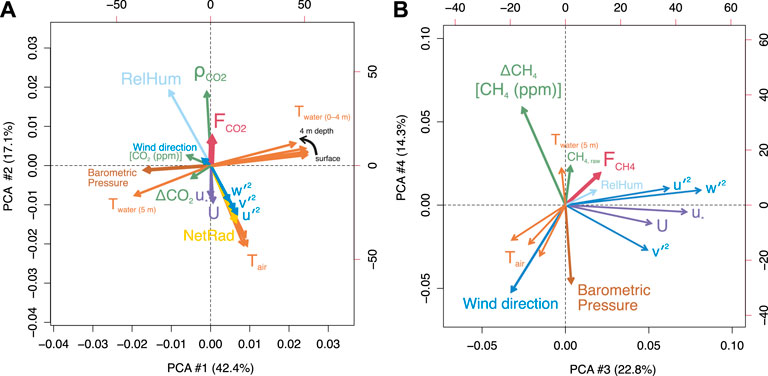
FIGURE 4. Principal component biplots of (A) CO₂ flux and (B) CH₄ flux with the most relevant potential driver variables. The CO₂ flux (F_CO2) already appears prominently in PCA ^#2, thus the first two PCAs are displayed in (A), whereas the CH₄ flux (F_CH4) only appears in PCA ^#3, hence the third and fourth PCAs are shown in (B), and the percentage of explained variance is modified by excluding PCAs #1 and #2 from the total in (B). U is the mean horizontal wind speed, and u_* the friction velocity (downward-directed momentum flux); u′², v′², and w′² are the turbulent variances of horizontal along-wind, across wind, and vertical wind fluctuations, respectively. ρ_CO2 is the CO₂ density in air (mmol m⁻³).

The transfer of CO₂-rich waters from depths lower in the epilimnion or the metalimnion toward the lake surface will enhance flux to the atmosphere. This is seen in Figure 4A as the first temperature below the typical thermocline (water temperature at 5 m depth) correlates positively with ΔCO₂, whereas the epilimnion temperatures down to 4 m depth are negatively correlated with ΔCO₂. There is a slight but important increase in correlation between the epilimnion temperatures and F_CO2 with increasing depth, indicating that temperature effects at the thermocline where CO₂ is typically higher (Supplementary Figure S5) are more important for F_CO2 than is the surface temperature.

Increasing wind speed (U) and turbulence (u_*, u′², v′², w′²) all reduce—not increase—F_CO2, almost in perfect agreement with net radiation, which represents atmospheric stability over the water surface. With increases in net radiation, wind speed and turbulence also increase. Atmospheric stability is negative (z/L < 0 and Ri < 0; e.g., Stull, 1988 and Supplementary Figure S6) most times of the day, except in the afternoon when it is in the near-neutral to slightly unstable range (ca. 1200–2100 h AKDT; data not shown). This indicates the important difference of a lake surface from a terrestrial surface, where over land atmospheric stability is negative when net radiation is high, but positive (stable) at night during times where the lake surface water temperatures are warmer than the terrestrial atmosphere. These conditions where a cooler atmosphere overlies a warmer surface water, leading to convection in the water, lead to the substantial peak in F_CO2 at night between 0000 and 0600 h AKDT (Figure 2B), whereas barometric pressure has no influence on F_CO2. In summary, CO₂ effluxes from Toolik Lake are strongly governed by environmental drivers and thus are a key component in the second PCA axis, indicating a close link between F_CO2 and the observed driver variables.

3.2 Principal components of the drivers of CH₄ fluxes

In contrast to CO₂ efflux from Toolik Lake, the CH₄ fluxes are much less coupled with the same driver variables (Figure 4B) that influence CO₂ evasion (Figure 4A). The first two PC axes (explaining 59.5% of the data subset used in this analysis) do not include F_CH4, thus we only inspect PC axes 3 and 4 which explain 22.8% and 14.3% of the remaining variance, respectively (Figure 4B). For F_CH4 the wind direction has a strong influence with northerly directions (direction towards 360°) reducing F_CH4. This reflects the local daytime foreland–mountain wind system with northwesterly winds (from the coast to the Brooks range) typically prevailing from 0800 to 1400 h AKDT, and south-easterly dominance (winds from the mountains to the foreland of the North Slope) from 1500 to 0600 h AKDT.

However, in contrast to CO₂, equilibrium methane mixing ratios in the water are supersaturated at all times (Figure 3) by a median 27.3 ppmv (95% CI 13.2–51.3 ppmv), and thus both atmospheric CH₄ mixing ratio and the gradient measured acros s the water interface have almost no influence on F_CH4 (the two arrow are almost at a right angle with F_CH4 in Figure 4B, indicating statistical independence). However, not quite as expected, air temperature (represented by three redundant measurements) has a negative effect on F_CH4 with warmer air temperatures reducing CH₄ evasion from the lake. According to Figure 4B warmer air temperatures are associated with lower wind speed and atmospheric turbulence. Also barometric pressure has an influence as high pressure tends to suppress F_CH4. Higher wind speeds and turbulence only have a weak enhancing effect on F_CH4, but it is clearly in contrast to F_CO2 where the same variables seem to reduce F_CO2. Net radiation (and thus atmospheric stability) and water temperatures of the epilimnion were unrelated with F_CH4; only the upper metalimnion temperature (5 m depth) seems to positively influence F_CH4. In the biweekly sampled CH₄ mixing ratio profiles the peak CH₄ mixing ratio is often found at the depth of the thermocline (Supplementary Figure S5), whereas in contrast to the substantial CO₂ storage in the metalimnion there is no such CH₄ storage in deeper waters of Toolik lake.

The diel variation of CH₄ mixing ratio in the water is substantial (Figure 3A), with the lowest median of 18.0 ppmv at 0400 h AKDT and the highest median of 37.6 ppmv at 1900 h AKDT. This range, however, does not translate to a clear diel cycle in F_CH4 (Figure 3B) because the water is strongly supersaturated with CH₄ at all times. Median fluxes during low and high water mixing ratio periods of the day are all on the order of 0.02–0.06 µg CH₄ m⁻² s⁻¹, with no strong pattern in diel variation (Figure 3B).

3.3 Flux–gradient relationships across the lake surface interface

The CO₂ efflux from Toolik Lake is almost insensitive to mean horizontal wind speed (U) (see also Zappa et al., 2007) (Figure 5A; all regression fits to Toolik Lake data are given in Supplementary Table S2). It even appears that the highest observed wind speeds in 2015 actually reduced the CO₂ flux slightly (Figure 5A). If the data are analyzed separately for conditions with subsaturated (Figure 5C) vs. supersaturated (Figure 5D) CO₂ mixing ratios in the lake surface waters, and U is replaced by the friction velocity u_* (representing mechanical turbulence directly driving the gas flux), then CO₂ effluxes are highest under lower turbulence conditions (u_* < 0.2 m s⁻¹) when conditions are subsaturated, and become net neutral at u_* ≥ 0.2 m s⁻¹ (Figure 5C). In contrast, if the surface waters are supersaturated with CO₂, then CO₂ fluxes are similar to the subsaturated condition at low u_*, but become higher and more variable at u_* ≥ 0.2 m s⁻¹ (Figure 5C). This is consistent with surface waters that are supersaturated because increased stirring (via increasing u_*) should more completely outgas the surplus CO₂ in the surface waters.

FIGURE 5

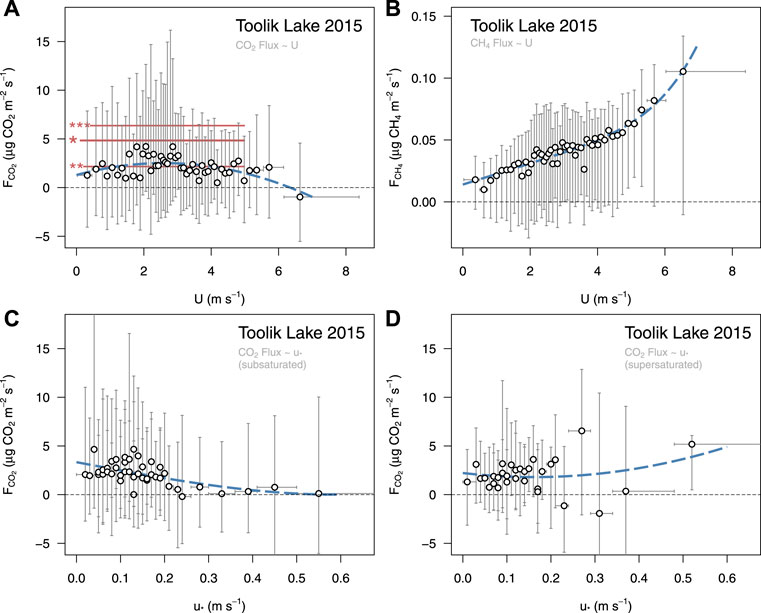
FIGURE 5. CO₂ flux (A) and CH₄ flux (B) at 5-min resolution as a function of mean horizontal wind speed, and CO₂ flux as a function of friction velocity u_* with subsaturated water (C) and supersaturated water (D). The red line with in (A) shows the Eugster et al. (2003) average flux level determined over a few days (*), during stratified conditions (**), and during convective periods (***). Vertical error bars show the inter-quartile range of values (inner 50% of data), whereas the horizontal whiskers show the entire size of the associated bin.

A more direct and clear relationship of CO₂ efflux from Toolik lake was found when the temperature difference between the water surface and the air was used as a reference (Figure 6A). In the range where T_w is colder or less than 5°C warmer than the air, the CO₂ fluxes appear weakly driven by the temperature difference. But at T_w > (T_a + 5°C) an exponential increase of CO₂ efflux with increasing temperature difference was found (Figure 6A).

FIGURE 6

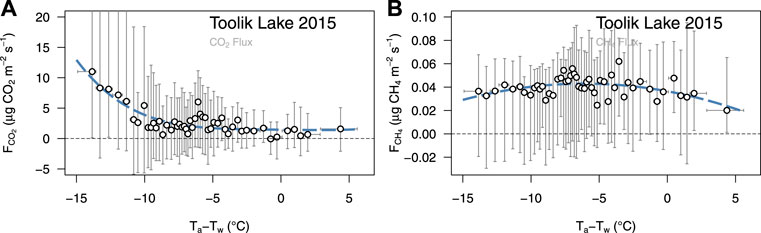
FIGURE 6. Effect of water–air temperature differences on (A) CO₂ fluxes and (B) on CH₄ fluxes at 5-min resolution. Vertical error bars show the inter-quartile range of values (inner 50% of data), whereas the horizontal whiskers show the entire size of the associated bin.

Methane fluxes do not show the same response to the temperature gradient between water and air (Figure 6B). If the water is 5°C colder than the air, the CH₄ effluxes were low and steadily increased to an optimum when the water temperature was around 8°C warmer than the air. If the difference was even larger, then CH₄ efflux decreased slightly (Figure 6B).

In this study we measured both concentrations in water and air, and fluxes of CO₂ and CH₄ fluxes (an advance since the beginning of air–sea exchange measurements, see Wanninkhof et al., 2009). Contrastingly, if only gas gradients are measured across the water–air interface, e.g., by syringe sampling, then the piston velocity normalized to a Schmidt number of 600 (k₆₀₀) must be estimated from horizontal wind speed measurements, although some authors claim that the relation to horizontal wind speed often is weak (Zappa et al., 2007). Most of the models used to predict k₆₀₀ from wind speed at 10 m height (U₁₀) are derived for open ocean environments with a large fetch without obstacles. Over an inland lake with limited surface area such as Toolik, these models of k₆₀₀ inadequately reflect the local conditions. Figure 7 shows that our direct measurements of the k₆₀₀ piston velocity for CO₂ are almost constant, the highest values occur at low U₁₀, and only at U₁₀ > 10 m s⁻¹ do our estimates fall in the range of k₆₀₀ that any model, including the MacIntyre et al. (2010) model that considers the buoyancy flux term, would predict for a stratified lake (Supplementary Table S3). This can be interpreted with the fact that it is actually u_*, not U₁₀, that drives vertical turbulent exchange of gases along the gradient between water surface and atmosphere. If measurements are made over a small lake, then the distance travelled over the lake surface is too short to bring u_* into equilibrium with U₁₀. There is a much higher level of turbulent mixing present in air masses that travelled over rough terrestrial tundra, and thus u_* remains relatively high in comparison to U₁₀.

FIGURE 7

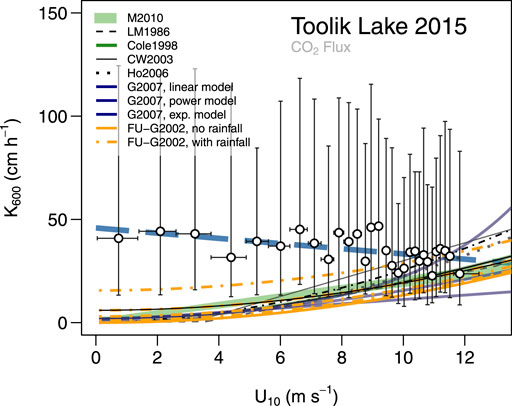
FIGURE 7. Comparison of measured piston velocities normalized to k₆₀₀ for CO₂ flux–gradient relationships at 5-min resolution with a selection of models to estimate the fluxes from simpler water–air gradient measurements. Open circles show the median of each bin, approximated by a dashed blue line. Vertical error bars show the inter-quartile range of values (inner 50% of data), whereas the horizontal whiskers show the entire size of the associated bin. Models used are: M2010: MacIntyre et al. (2010), range given by the buoyancy flux term; LM 1986: Liss and Merlivat (1986); Cole 1998: Cole and Caraco (1998); CW 2004: Crusius and Wanninkhof (2003); Ho 2006: Ho et al. (2006); G2007: Guérin et al. (2007) with three versions (linear, power, and exponential model); and FU-G2002: Frost and Upstill-Goddard (2002), solid line without precipitation, and dashed lines with 0.05, 0.15, and 0.30 mm h⁻¹ rainfall. See Table S3 for K₆₀₀ model equations used. The U₁₀ values derived for the 10-m height from local measurements and then enlarged by Charnock’s relationship that relates true u_∗ to U₁₀ (Figure 10A).

The k₆₀₀ piston velocity for CH₄ differs from that of CO₂ and shows the expected exponential increase with increasing U₁₀ (Figure 8). However, there is a substantially higher turbulent exchange efficiency at low U₁₀ than expected from models, with k₆₀₀ around 14 cm h⁻¹ even at very calm wind conditions (Figure 8). At U₁₀ > 6 m s⁻¹ the k₆₀₀ for CH₄ then merges with the predicted values that most models provide (Figure 8).

FIGURE 8

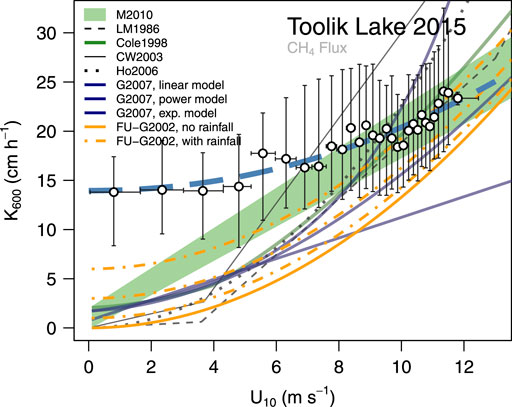
FIGURE 8. Same as Figure 7 but for CH₄ flux–gradient relationships.

The high turbulent exchange efficiency at low wind speeds, and the rather weak dependence of k₆₀₀ on U₁₀ in general, result in an almost constant CO₂ efflux (Figure 9A) and CH₄ efflux (Figure 9B) and mostly independent of the air-water difference in gas mixing ratio.

FIGURE 9

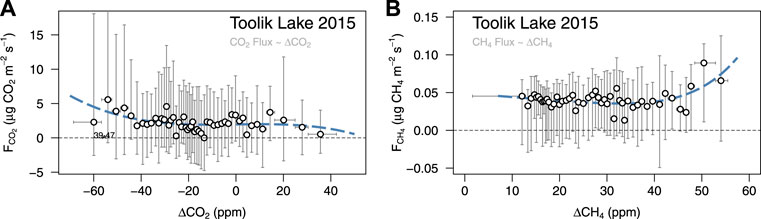
FIGURE 9. Relationships between measurements of the water–air (A) CO₂ gradient (ΔCO₂) and (B) CH₄ gradient (ΔCH₄) and their respective flux across the water interface. Positive Δ values indicate that the mixing ratio in water is above the equilibrium mixing ratio in the air.

Figure 10A clearly shows that the u_*-to-U₁₀ relationship is substantially enhanced over Toolik Lake as compared to what would be expected over the open ocean (red dashed line in Figure 10A). At U₁₀ < 2 m s⁻¹, u_* is rather constant around 0.08 m s⁻¹, which is a factor 2–5× higher than what the Charnok relationship predicts (Figure 10A). Moreover, at low wind speeds the turbulent mixing not only depends on the mean U₁₀ during an average interval, but also on the history of U₁₀ during the previous interval. Over Toolik Lake the threshold of equal antecedent wind speeds is around U₁₀ ≈ 5 m s⁻¹ (Figure 10B); if U₁₀ is below that threshold, it is most likely that U₁₀ was higher with more turbulent mixing during the previous time interval, and if U₁₀ was above that threshold, the U₁₀ in the previous time interval was most likely lower.

FIGURE 10

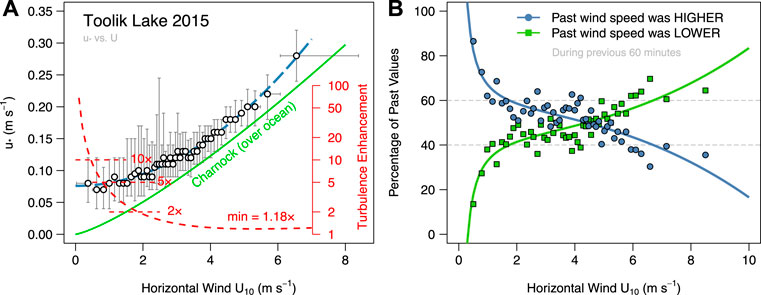
FIGURE 10. Turbulent mixing (A) (expressed by friction velocity u_* as a function of horizontal wind speed) is substantially enhanced over limited-sized Toolik Lake as compared to the widely-used Charnock-relationship over open ocean water surfaces. Moreover, (B) variability of horizontal wind speed over Toolik Lake is high, with past wind speeds (last 60 min) typically having been greater than actual wind speeds <4.4 m s⁻¹. The red dashed line in (A) shows the ratio between measurements (fit to group means) and the expected u_* according to Charnock.

3.4 Long-term trends of driver variables affecting CO₂ and CH₄ fluxes

Long-term trends are available for a few monitoring variables that cover the period from 1988 (or later) to 2020. For CO₂ and CH₄ gas exchange over Toolik Lake we focus on the long-term trends of lake depth (Figure 11A), lake surface water temperature (Figure 11B), horizontal wind speed (Figure 11C), rainfall (Figure 12), air temperature (Figure 13A), relative humidity (Figure 13B), short-wave incoming radiation (Figure 13C), barometric pressure (Figure 13D), and soil temperatures at the surface (in moss at the transition from green active tissue to brown peat) and at the deepest level recorded (1.5 m depth, corresponding to the maximum extension of the thawed active layer in summer) (Figure 14).

FIGURE 11

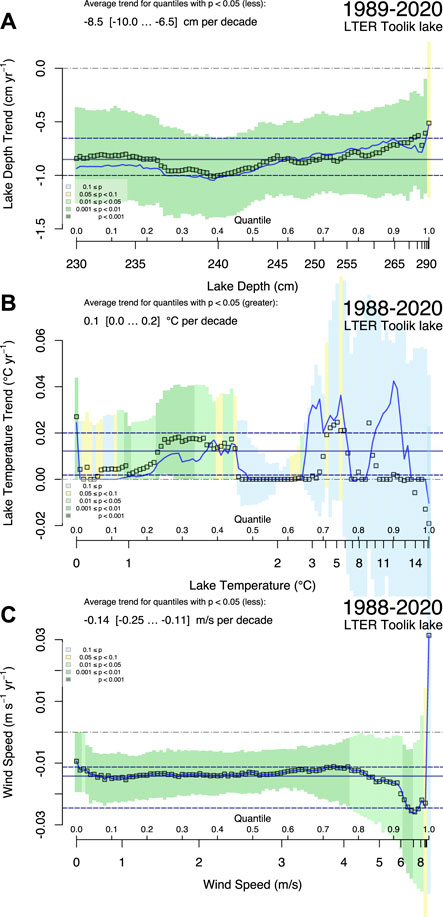
FIGURE 11. Quantile regression trend estimates of (A) lake depth, (B) lake temperature, and (C) horizontal wind speed at 5 m a.g.l. Black squares show the best estimate of the Theil-Sen median trend slope for each percentile of the observed range of quantiles. Color bands show the 95% confidence interval of the slope estimate with color coding from green (significant at p < 0.05 to yellow (marginally significant, p < 0.1) and light blue for insignificant slopes. The analysis was carried out on gap-filled timeseries. For comparison, the best estimates without gap-filling are shown with the solid blue line. A significant downward trend of the lake depth was observed, whereas the warming trend of lake surface waters is only significant at the lower 45% of temperature observations, that is, winter (under ice) temperatures < 1–2°C.

FIGURE12

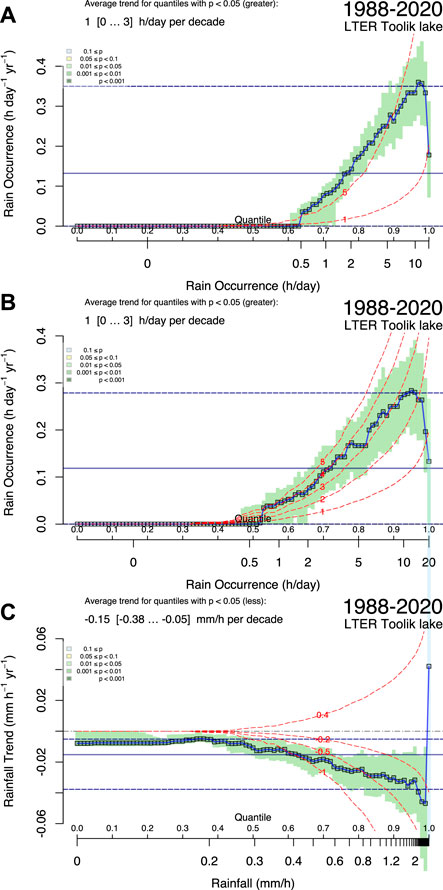
FIGURE12. Quantile regression trend estimates of (A) increasing occurrence of hours with rainfall, (B) as in (A) but restricted to the growing season months May–September, and (C) rainfall amount. Display as in Figure 11, with the addition of red dashed lines indicating equal percentage of change.

FIGURE 13

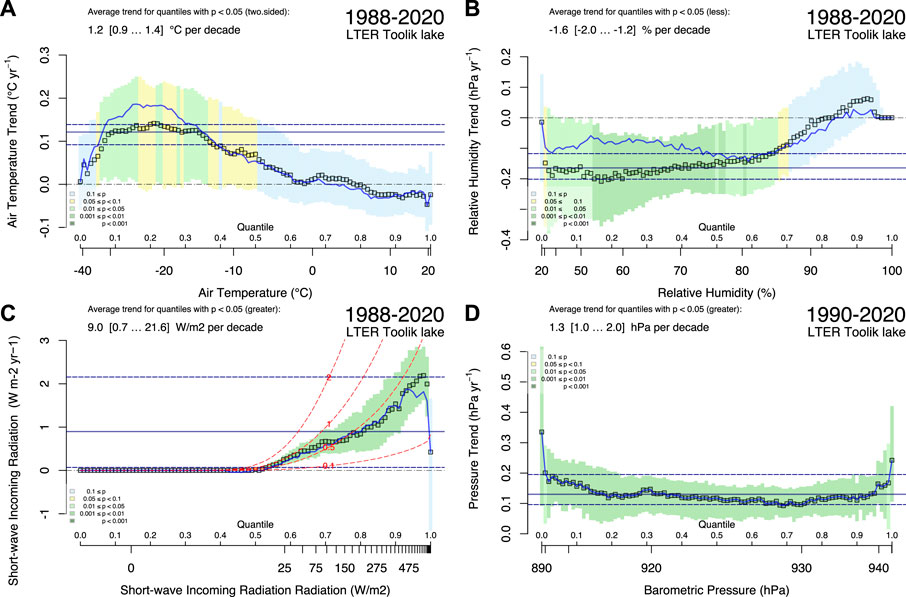
FIGURE 13. Quantile regression trend estimates of (A) air temperatures (two-sided test), (B) decreasing relative humidity at temperatures above freezing, (C) increasing global radiation, and (D) increasing barometric pressure. Display as in Figure 11.

FIGURE 14

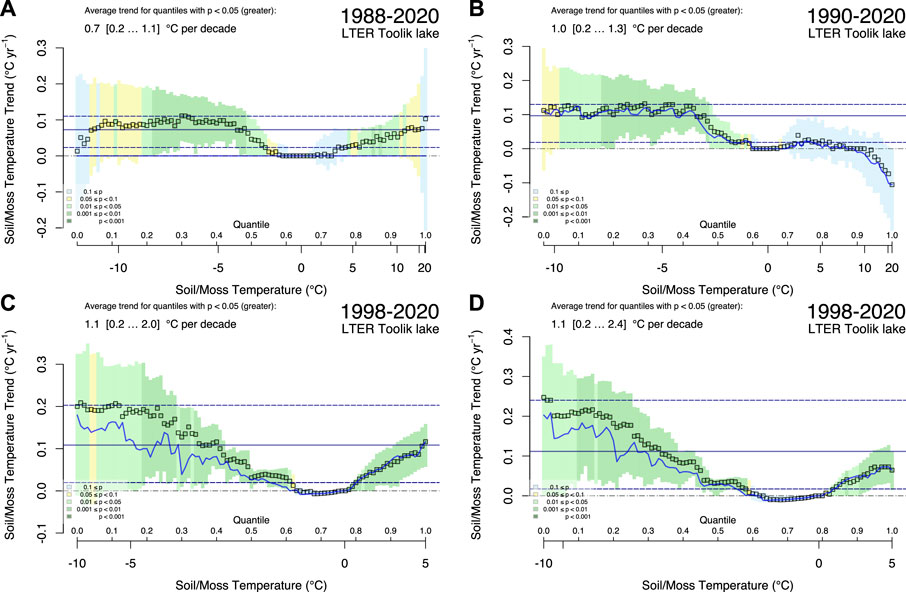
FIGURE 14. Quantile regression trend estimates of (A,B) moss temperatures of two replicates (two-sided test), and (C,D) soil temperatures at 1.5 m depth (typical maximum depth of active layer). Display as in Figure 11.

Because trends tend to be weak or statistically insignificant at annual aggregation of the long-term monitoring variables, all trends were determined via quantile regression that determines the trend slope for each quantile of the full dataset collected in each observation year. In this way, opposing trends at low, intermediate, or high values (quantiles) of the respective monitoring variable can be detected. Depending on the variable and expectation, we either tested the significance of the trend with a one-sided test (for existence of monotonically increasing or decreasing trends), or with a two-sided test to determine if any trend is significantly different from a null trend. Lake depth (Figure 11A) significantly decreased in all quantiles by −8.5 cm per decade, thereby reducing the water pressure on the lake bottom sediments which could increase the flux of gases produced at saturation in the sediments and released as bubbles to the water body (particularly the insoluble CH₄), and potentially thus increase the GHG efflux from organic sediments. However, we have observed very few ebullition events for CH₄ in Toolik Lake, which are the most expected events resulting from changing air pressure (Eugster et al., 2020a).

Lake water temperature did not show any significant trend during the warm season (Figure 11B), only winter conditions with surface water temperatures <2°C show a significant warming trend on the order of 0.1°C per decade (Figure 11B). Wind speed shows a decreasing trend at the lower 50% of the wind speed distribution, whereas wind speeds in the typical gentle breeze range (Beaufort 3, 3.6–5.1 m s⁻¹ according to WMO, Hasse and Isemer, 1986; Arguez and Vose, 2011) remained almost unchanged in the past 33 years. Only the 1% most extreme wind speeds have increased more substantially by 0.3 m s⁻¹ per decade, but this trend is not significant when we test for greater than normal wind speed extremes.

There is a highly significant increasing trend of rainfall events. On a daily basis the number of hours with precipitation has increased since 1988, both at the annual scale (Figure 12A) and during the terrestrial growing season months (May–September, Figure 12B). For days with up to 4 h of precipitation the increase in rainfall hours closely follows the + 5% increase curve during the growing season and follows the + 4% increase in the range of 4–7 h day⁻¹. The trend on days with >7 h of precipitation is less dramatic, although still statistically significantly compared to a null trend. Interestingly, the increasing duration of rain events is associated with significantly decreasing amounts of rainfall (−0.15 mm h⁻¹ per decade; Figure 12C). This combination of prolonged rainfall events with lower precipitation amounts may reduce the risk of terrestrial flushing or erosion due to strong storms, and reduce the terrestrial export of DOC, thus supplying the lake with less carbon to be respired to CO₂ and CH₄.

During the warm season no significant trends in air temperature were found (Figure 13A). Significantly increasing air temperatures only affect winter temperatures < −8°C (Figure 13A), but the trend is rather substantial with a 1.2°C increase per decade.

Trends of relative humidity measured at 5 m a.g.l (above ground level) were separately determined for temperatures above and below freezing (Figure 13B). Above freezing, the high relative humidity (>85%) showed no significant trends. This is in line with the observed rainfall trends with prolonged duration of rainfall events, which tend to dominate conditions with high relative humidity. Although statistically significant, the decreasing trend in relative humidity at humidity values < ∼80% is only a −1.6% reduction per decade, a value that most likely does not strongly affect GHG fluxes from Toolik lake.

Short-wave incoming radiation (Figure 13C) showed a roughly +0.5% increase over 33 years of measurements, which corresponds to a short-wave radiation increase of 9.0 [0.7–21.6] W m⁻² per decade. This decadal trend is 3.3 times the estimate of the human-caused radiative forcing in 2019 as compared to 1750 [2.72 (1.96–3.48) W m⁻²; IPCC AR6 WGI (2021; p.13: A.4.1)], but is in agreement with the global brightening that replaced the trend towards global dimming when the Toolik Lake long-term measurements were initiated in 1988 (Wild, 2005; Wild et al., 2012).

Barometric pressure has significantly increased at all quantiles by an average 1.4 [1.1–2.2] hPa per decade (Figure 13D), against a background range of ∼900–1,000 hPa. Converted to a water column pressure this corresponds to a 1.43 cm increase in water level per decade. This increase in barometric pressure counteracts the effect of the decreasing lake depth trend, but its magnitude is only one sixth of the concurrent decreasing trend in lake depth (Figure 11A).

Soil temperatures from the air-moss interface down to 1.5 m depth show a very consistent warming trend ranging from the lowest values at the soil surface (i.e., in the moss layer) of 0.7–1.0°C per decade (Figures 14A, B) to 1.1°C per decade at 1.5 m depth (Figures 14C, D), which is the transition zone from the maximum extent of the summer active-layer thaw and the permafrost. The warming trend is significant and consistent across all soil depths for temperatures < −1°C and > 1−5°C, but around the freezing point there is no significant trend seen at any depth (Figure 14). This lack of trend at the freezing point is regulated by the physics of the phase transition from solid ice to liquid water; the phase transition remains near 0.0°C irrespective of climate warming trends, but the response is how much heat content is stored in either the deeper permafrost soil or in the seasonally-thawed active layer.

4 Discussion

During the study period, CH₄ was always supersaturated (with respect to the atmosphere) in Toolik Lake surface waters (Figure 3), and there was a consistent flux of CH₄ from the lake to the atmosphere. CO₂ concentrations fluctuated close to atmospheric values, and fluxes to the atmosphere were low but consistently positive (Figure 1). These results are generally consistent with prior results of eddy covariance measurements from Toolik Lake (Eugster et al., 2003; Eugster et al., 2020a). At some times barometric pressure was positively related to dissolved CO₂ and negatively related to dissolved CH₄ in surface waters (Figure 1). Higher atmospheric pressure could increase the partial pressure of CO₂ or CH₄ in the water, but the mixing ratios in water would not change unless the air mass also had a different mixing ratio of these gases. Lower atmospheric pressures may release gases close to saturation in lake sediments, but as mentioned above we found very few if any bubbles in the water column of Toolik Lake (Eugster et al., 2020a).

In the diel cycle CO₂ concentrations were slightly lower during the evening hours, but as with CH₄ there was no obvious relationship between CO₂ concentrations and CO₂ flux to the atmosphere (Figure 2). CO₂ efflux was typically highest at night from 0000 to 0600 h, which has been attributed to greater convective mixing at the lake surface when air temperatures are cooler than lake temperatures (Eugster et al., 2003; Eugster et al., 2020a). Vertical profiles of CO₂ concentrations (Supplementary Figure S5) clearly show increasing concentrations with depth during summer stratification, indicating a near-surface source of CO₂ to be entrained by mixing and support greater flux to the atmosphere. Diel variations in CH₄ mixing ratios were not obviously related to the CH₄ efflux from the lake, which was more or less constant over the day (Figure 3). The difference between higher nighttime fluxes of CO₂ but not CH₄ (Figure 2,3) may be related to the lack of obvious increases in CH₄ concentration with depth (Supplementary Figure S4), and thus the lack of a near-surface supply of CH₄ to the surface during convective mixing at night when air temperatures decrease relative to surface water temperatures.

Natural or deliberate fertilization of lakes can increase algal biomass and rates of algal drawdown of CO₂ during photosynthesis, as demonstrated for a fertilized arctic lake near Toolik (Kling et al., 1992). In that same study results showed no indication of algal drawdown of CO₂ contributing to diel or seasonal variation of dissolved CO₂ concentrations or to atmospheric fluxes in ultra-oligotrophic Toolik Lake. In addition, here we show that the relationships between dissolved CO₂ concentrations and primary production or chlorophyll a in surface waters are positive (Supplementary Figure S4), and thus the opposite of expected if photosynthetic drawdown of CO₂ was important or could affect CO₂ efflux. There is also no clear drawdown of CO₂ concentrations during the middle of the day (1000–1400 h) when photosynthesis would be strongest. Even on short time scales it is unlikely that photosynthetic uptake would substantially influence dissolved CO₂ concentrations and thus gas exchange in this ultra-oligotrophic lake. For example, the highest rates of primary production shown in Supplementary Figure S4 would consume CO₂ at ∼0.2 µmol L⁻¹ hr⁻¹ against a background concentration of ∼20–50 µmol CO₂ L⁻¹ (Supplementary Figure S4). At the same time, there is an input of CO₂ from bacterial respiration in surface waters of at least half the algal uptake rate (Crump et al., 2003). This input of CO₂ is considered a minimum value because it assumes 100% bacterial growth efficiency of respired CO₂ per C incorporated into bacterial cells. If a typical bacterial growth efficiency of 50% was used, then bacterial respiration alone could resupply the maximum photosynthetic uptake of CO₂.

4.1 Gas exchange velocities

Perhaps the most intriguing finding of this study is that measured piston velocities (k) for both CO₂ and CH₄ at wind speeds <10 m s⁻¹ exceed what flux models would predict (Figures 7, 8), and the friction velocities (u_*) at all wind speeds exceed the expected values given the Charnock relationship (Charnock, 1955; Figure 10A). Even updated Charnock relationships (Edson et al., 2013; Jimenez and Dudhia, 2018) that predict increased wind stress at a given U₁₀ still underestimate our measured u_*, especially at lower wind speeds (Figure 10A). Thus the higher friction velocity imparted to the water surface in our study should generate greater TKE in the surface water to enhance gas exchanges (k in Figures 7, 8).

There are several possible explanations for the high gas transfer velocities we measured at medium to low wind speeds (<10 m s⁻¹, Figures 7, 8). First, Munk (1947) proposed that flow over the ocean is laminar up to the Kelvin-Helmholtz instability around 6.5 m s⁻¹ and only becomes turbulent at higher wind speeds (Supplementary Figures S6, S7). Fetch is unlimited over the open ocean, and hence even at low wind speeds an equilibrium can establish between the atmospheric flow and the ocean depending on the previous status of the atmospheric and ocean turbulence (Supplementary Figure S6). Contrastingly, smaller lakes have a limited fetch and are thus more influenced by the surrounding, relatively rough landscape that generates more atmospheric turbulence, and the previous status is always “turbulent” under such conditions (Supplementary Figures S6, S7). There is no wind sheltering at Toolik Lake due to the low canopy structure of the surrounding tundra, but topographical rises of 20 m within 100 m of the shoreline are common and hills can be 30 m above the lake surface within 300 m of the lake shore. This complex terrain, coupled with a lack of wind sheltering to reduce wind speed and turbulence in the air mass reaching the lake (e.g., Markfort et al., 2010), act to generate more TKE in the atmosphere over the lake than is typically generated at the same wind speeds in smooth landscapes or over large lakes or oceans.

Second, the memory effect of turbulent mixing in the atmosphere brings well-mixed conditions from the rough terrestrial surface to the smooth lake water body, but in this small lake even a kilometer of fetch is unlikely sufficient to bring the turbulence state of the near-surface atmosphere into equilibrium with the water surface. However, at the same time the “young” waves generated when the fetch is small are typically shorter and steeper than waves closer to equilibrium with wind speeds in large lakes or oceans, and this steepness can increase the gas exchange (Edson et al., 2013) and increase the form stress on the water surface (Sullivan et al., 2018).

Third, the smaller, shorter waves that develop over shorter-fetch waters for a given wind speed are less likely to break than are larger waves and thus less likely to inject bubbles into the surface water. Bubble-mediated gas exchange is biased toward invasion (Woolf and Thorpe, 1991), and bubbles generated during wave breaking reintroduce atmosphere into the near surface and that reduces gas exchange (e.g., Emerson and Bushinsky, 2016). Note that as wind speed and wave height increase the bubble-mediated gas invasion will also increase, thereby reducing our measured k values compared to model predictions; this behavior is seen in Figures 7, 8.

Fourth, open-water surface roughness tends to increase at shallower depths (e.g., Taylor and Yelland, 2001), which leads to increased surface drag over shallow waters typically unaccounted for in models (Jiménez and Dudhia, 2018). Taken together, these processes tend to increase the measured k values compared to values predicted from models, including those developed for use in lakes and that incorporate buoyancy flux (e.g., MacIntyre et al., 2010). At present, we have no clear means of separating the individual contributions of these potential explanations for the higher than predicted gas exchange velocities we measured.

It is also unclear at present why there is a difference between the flux behavior of CO₂ and CH₄ (e.g., Figures 5–9). Although both of these gases are low enough in solubility to be generally controlled by water-side dynamics (Wanninkhof et al., 2009; Garbe et al., 2014), recent work has highlighted that bubble-dynamics vary between gases (Goddijn-Murphy et al., 2016; Rosentreter et al., 2017), and even gas solubility and transfer is differentially affected in response to films on the water surface (Mesarchaki et al., 2015).

4.2 Summary of environmental drivers of fluxes

A PCA indicated a strong coupling of CO₂ fluxes with environmental variables (meteorological variables, eddy flux variables, and temperature and gas mixing ratios in the water, including temperature of the upper mixing layer in the lake, 0–4 m depth, and temperature near or below the typical summer thermocline at 5 m depth). An increased dissolved CO₂ mixing ratio does not automatically increase the CO₂ efflux from the lake. It seems to represent the important transfer of CO₂-rich waters at the bottom of the epilimnion or in the metalimnion (Supplementary Figure S5) being transferred into the upper epilimnion, thereby increasing CO₂ mixing ratio, but not directly F_CO2 (Figure 4).

The CH₄ fluxes are much less coupled with the same driver variables (Figure 4B) that influence CO₂ evasion (Figure 4A). We only inspected PC axes 3 and 4 where F_CH4 plays a role and which explain 22.8% and 14.3% of the remaining variance (after PC1 and PC2), respectively (Figure 3B). It is probably the constantly high supersaturation of CH₄ (Figure 3A) that leads to a constant CH₄ efflux with a minor diel cycle (Figure 3B), and this makes F_CH4 much less dependent on environmental variables than is F_CO2 (Figure 4A).

4.3 Interannual flux variability

The process-level relationships between GHG mixing ratios in the surface waters and the eddy-covariance flux measurements of CO₂ and CH₄ were only available from summer 2015, but seasonal flux measurements were carried out at Toolik lake during the ice-free seasons 2010–2015. In Eugster et al. (2020a) we provided a detailed comparison of interannual variability of the seasonal fluxes. In summary, the 2012 season provided the highest CO₂ and CH₄ effluxes with 1.3 g CO₂ m⁻² day⁻¹ (30 mmol m⁻² day⁻¹ and 3.2 mg CH₄ m⁻² day⁻¹ (0.20 mmol m⁻² day⁻¹), respectively. During the 2010 season with the lowest CO₂ efflux only 30% of the 2015 efflux was observed, and in the case of CH₄ the following 2011 season had the lowest efflux which was 35% of the 2015 maximum flux. This high interannual variability is not easily explained by the long-term trends of the monitored variables that influence gas exchange across the water surface in the short term and at the process-level. However, given that carbon input (CO₂, CH₄, DOC, and POC) to the lake from streams can be quite variable and can affect microbial processing of DOC to CO₂ or CH₄ (e.g., Kling et al., 2000; Crump et al., 2003, Crump et al., 2007), it is possible that variable inputs of carbon to the lake affect the interannual variability more than meteorological variables that govern gas exchange. Wu et al. (2013) have also reported that diffusive gas fluxes from two lakes were primarily attributable (30%–45%) to inputs and respiration of terrestrial DOC.

A linear, mixed-effect model combining the Eugster et al. (2020a) data with the monitoring variables used in this paper, suggests different processes governing the variability of the CO₂ fluxes (Table 1) versus the CH₄ fluxes (Table 2). The mixed-effect model shows that warm soil temperatures at 10 cm depth increase CO₂ fluxes by 26.5 ± 3.3% (Table 1), but rainfall 12 h ahead reduces CO₂ fluxes substantially by −37.7% ± 15.6%. It is possible that at warm times or in warm years that soil temperatures tend to increase organic matter decomposition in soil and thus increase the transport of CO₂ and CH₄ to the lake, or to increase the production of DOC and POC that feed into Toolik Lake. But rainfall, especially heavier rainfall intensities, are expected to increase effluxes of CO₂ and CH₄ from the lake (Guérin et al., 2007). Stronger winds, and stronger winds in combination with warmer 10-cm soil temperatures, also exert a negative effect on CO₂ fluxes on the order of −10% (Table 1). From other ecosystems it is also known that the near-surface soils are the most important substrate for respiration, in combination with soil temperature but with a dominance of availability of organic matter (e.g., Robinson et al., 2022). In arctic tundra there is substantial organic peat available across the upper soil profile, and thus the importance of the 10-cm conditions (and not the moss or 5 cm temperature) for respiration and decomposition may be most relevant as soils warm and eventually thaw in the Arctic.

TABLE 1

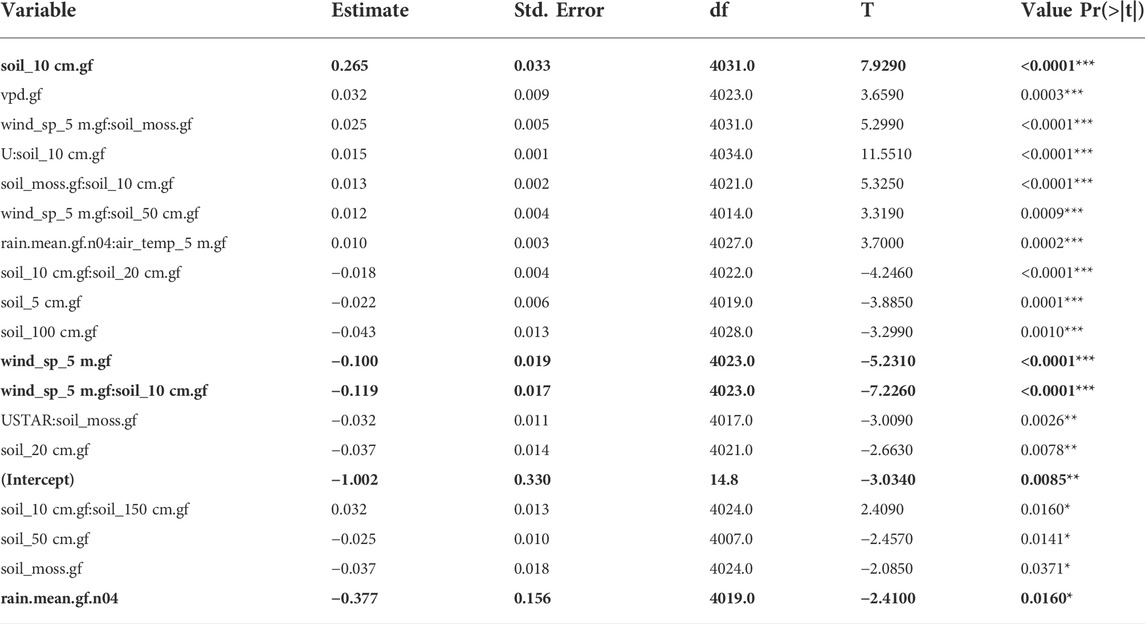
TABLE 1. Linear mixed effect model for CO₂ flux during the Toolik lake ice-free seasons 2010–2015. Predictor variables aggregated to 3-h averages or sums (rainfall) were normalized to look at relative importance (estimate of response slopes). Insignificant effects and those influencing CO₂ flux by less than ± 1% are not included. Effects influencing CO₂ flux by more than ± 10% are shown with bold face font. Stepwise forward selection was used to find the best model. Fixed effects were sorted within each significance level according to their relative importance (Estimate).

TABLE 2

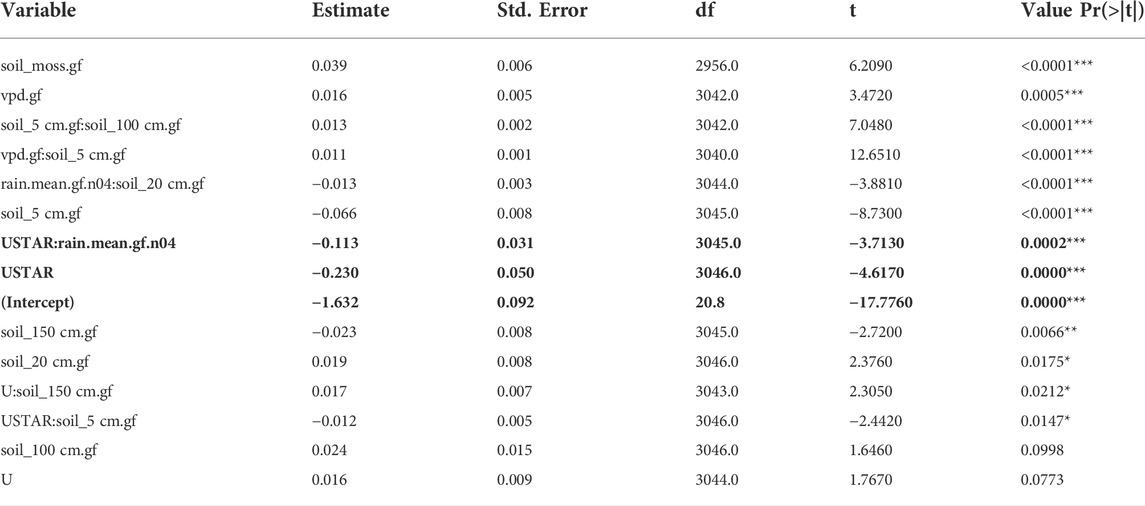
TABLE 2. Linear mixed effect model for CH₄ flux during the Toolik lake ice-free seasons 2010–2015. Predictor variables aggregated to 3-h averages or sums (rainfall) were normalized to look at relative importance (estimate of response slopes). Insignificant effects and those influencing CH₄ flux by less than ± 1% are not included. Effects influencing CH₄ flux by more than ± 10% are shown with bold face font. Stepwise forward selection was used to find the best model. Fixed effects were sorted within each significance level according to their relative importance (Estimate).

The driving forces for CH₄ effluxes include a set of variables that each contribute only a minor percentage to the flux: warmer moss temperatures (i.e., temperature measured at the transition from green living moss matter to brown moss peat), a dry atmosphere (higher vapor pressure deficits, VPD), and warm temperatures in the topsoil (5 cm) in combination with warmer temperatures near the bottom of the active layer (100 cm). A strong negative effect is quite prominent when we observe turbulent mixing above the water surface (u_*) (−23.0 ± 0.5%, Table 2) or high u_* in combination with rainfall intensity 12 h ahead (−11.3% ± 3.1%, Table 2). That the processes affecting CH₄ fluxes differ from those affecting CO₂ is not surprising given the differences in relationships with physical forcing between the two gases (e.g., Figures 4–8). In addition, CH₄ is only produced under anaerobic conditions and will be oxidized to CO₂ when it is exposed to an aerobic environment.

4.4 Expected trends of CO₂ and CH₄ fluxes until 2050

To translate the past and present functional relationships between CO₂ and CH₄ fluxes and their environmental driving forces into the future, we analyze changes in the observed long-term monitoring variables and how they correlate with the GHG fluxes in Toolik Lake. Because the trends of most variables are looking roughly 30 years into the past, our projection is an estimate for conditions 30 years into the future (i.e., a time horizon of 2050). This extrapolation of trends over the last 30 years assumes that, in general, human activities leading to GHG emissions today will continue to increase at the same pace as in the last 30 years (the business as usual or RCP8.5 scenarios). This assumption is made in part because downscaled, regional predictions of future climate for the North Slope of Alaska are unavailable (see Hobbie and Kling, 2014). But projecting the trend observed during the past 30 + years to the next 30 years is not the same as using an IPCC scenario for predictions. Thus, with continued warming the IPCC projections expect that both CO₂ and CH₄ emissions to the atmosphere will increase in the years to come, despite the low confidence (or too little data) in the potential role of Arctic warming (IPCC AR6 WGI, 2021).

In summary, the relevant long-term trends in monitored potential driver variables of CO₂ and CH₄ fluxes are 1) the decreasing trend in lake depth, 2) the increasing trend in barometric pressure, 3) the decreasing trend of the lower 50% of wind speeds, 4) the 4%–5% increase in daily hours with rainfall in combination with the decreasing trend of rainfall intensity (precipitation amount per hour), 5) the increasing global radiation with global brightening since the early 1990s, and 6) the increasing soil temperatures above and below freezing (but not near the freezing point) across the entire 1.5 m depth profile equipped with temperature sensors. Not included in this discussion are 1) photosynthesis, 2) air temperatures that only show significant warming during the winter and thus outside the ice-free period covered with GHG flux measurements in this study, and 3) relative humidity that does not appear to have a strong influence on GHG effluxes from Toolik Lake. Wind direction trends were not included in this analysis (see Eugster et al., 2020a for wind direction analyses).

Starting with substrate availability for CO₂ and CH₄ production in Toolik Lake, the warming trend of the soil and increasing permafrost thaw (Turetsky et al., 2020) is probably an important positive feedback that will increase carbon inputs from land via stream inflow, groundwater, and overland flow to lakes in permafrost terrain (Hobbie and Kling, 2014; Vonk et al., 2015). If part of this increased input of C is in the form of particulate C that settles to the lake bottom, decreasing trends of lake depth might then amplify the outgassing of carbon gases produced from this particulate organic matter (less pressure to keep insoluble gases in the sediments). However, our earlier study (Eugster et al., 2020a) found no relevant role of CO₂ and CH₄ production in the bottom sediments of Toolik Lake, as deduced from the lack of evidence for ebullition. Moreover, the cold hypolimnion temperatures around 5–6°C even in peak summer limit biological activity and thus decomposition of C-rich substrates deposited in the lake bottom sediments. A study by Bayer et al. (2019) suggests that future gas fluxes from permafrost lakes are dependent on carbon inputs from the catchment.

The increasing trend in barometric pressure counteracts the effect of the decreasing trend in lake depth; that is, as the former reduces outgassing of GHGs from the bottom sediments, the latter promotes outgassing when the hydrostatic pressure on GHGs produced in lake sediments decreases. The net result would be toward enhanced outgassing because the magnitude of the barometric pressure trend is only one sixth of the opposing pressure trend exerted by lake depth. Hence we expect that a long-term trend of increasing barometric pressure may influence the short-term timing of GHG efflux from the lake, but the more important lake depth change most likely influences any long-term change in GHG fluxes derived from gases lost from lake bottom sediments.

Because of the weak relationship with CO₂ flux and either U₁₀ or u_*, a reduction of wind speeds below 1 m s⁻¹ or above 5 m s⁻¹ only slightly reduces the average F_CO2 level of 2.5 µg CO₂ m⁻² s⁻¹; at the highest wind speeds there is one data point showing that the CO₂ flux is reduced to near zero (Figure 5A). An assessment of the trend of increasing wind speeds on global ocean gas exchange with the atmosphere (Wanninkhof and Trenanes, 2017) suggested a slight increase in flux to the atmosphere, and more pronounced effects at lower wind speeds. That study did not consider gas fluxes from inland waters, which would generally experience lower wind speeds than do oceans. However, our results indicate that wind speed may be a poor predictor of and underestimate gas effluxes, which could be considered in future predictions of gas fluxes from all surface waters.

The unexpected increasing trend of daily hours with precipitation but decreasing trend in rainfall intensity (mm h⁻¹) indicates that the risk of storm erosion and thus transport of particulate organic matter to the inlet stream and further to Toolik Lake should decrease compared to the past. This could impose an important negative feedback on substrate availability for heterotrophic respiration in Toolik Lake that could even reduce the GHG fluxes from the lake. However, this potential effect must be balanced against the possibility of erosion and carbon inputs to the lake due to thermokarst failures, which are increasing in many arctic areas most likely due to permafrost thaw (Lewkowicz and Way, 2019). In addition, Cherry et al. (2014) predicted a wetter future for the Toolik region, which could increase the amount of DOC exported from land and respired within the lake (Kling et al., 2000, Kling et al., 2014). Finally, rainfall can enhance gas flux when raindrops add mixing energy to the water surface (Ho et al., 2004; Harrison et al., 2010), and longer periods of rainfall, independent of rain intensity, may thus increase gas fluxes. Overall, the effect of changes in precipitation on lake gas fluxes are complex and difficult to predict.

Increasing short-wave incoming radiation of course means more energy available at the Earth’s surface, which reduces atmospheric stability of the near-surface boundary layer and increases turbulent mixing in the atmosphere and thus the transfer of energy to the water surface that affects gas exchange (Erickson, 1993). At the same time, light-energy inputs warm surface waters, and increase buoyancy and water column stability, thus reducing TKE that can drive gas exchange across the lake surface (Imberger, 1985). On land, some of the energy will be used to increase soil heat flux; this is not in the set of long-term monitoring variables, but is key for the heat required to sustain the observed warming trends both below and above freezing in soils as discussed above. At present it is unclear how light energy increases will affect the balance between higher turbulence on land versus lower turbulence in surface waters with respect to controlling gas exchange.

The brightening of the atmosphere (Wild, 2005) reflected by the significantly increasing trend of short-wave incoming radiation has the potential to increase CO₂ fluxes, but most likely has no substantial effect on CH₄ fluxes. In case of the CO₂ fluxes we observed a positive influence of large T_w to T_a differences (Figure 6A), which most likely would be further amplified by increasing radiation inputs. In addition, increased photon flux to surface waters will increase photomineralization of DOC to CO₂ (Cory et al., 2014; Cory and Kling, 2018). Although greater solar radiation has the potential to increase algal photosynthesis, it is unlikely to be important in ultra-oligotrophic arctic lakes (Supplementary Figure S4). However, the warming trend in lake surface temperature (Figure 11B) was not significant at summer temperatures, but a significant warming trend of 0.1°C per decade under the ice cover (water temperature <2°C; Figure 11B) has the potential to increase under-ice microbial respiration, leading to a greater release of GHG accumulating under the ice during winter. However, this warming trend is quite weak and therefore unlikely to strongly impact microbial respiration under ice in the next 30 years.

Given the combined and often complex and counterbalancing effects of changing environmental drivers of gas flux, it is unlikely that Toolik Lake GHG fluxes will reach a tipping point where the system changes state from a source of gas to the atmosphere to a gas sink. The trends in drivers appear to be statistically significant but of low magnitude, most likely modifying present-day CO₂ and CH₄ effluxes in the range of an estimated factor 0.9–1.3. The lower value (0.9) is derived from an average reduction of –0.14 m s⁻¹ in mean wind speed of 3.0 m s⁻¹ per decade (–0.42 m s⁻¹ in 30 years), which translates to almost unchanged F_CO2 and a −10% change in F_CH4 (based on Supplementary Table S2, Figures 5A,5B). The upper estimate (1.3) is derived from changes in the terrestrial environment that may stimulate organic matter respiration and transport to surface waters; for example, moss temperatures (Figure 14A) increasing by 0.7°C per decade (2.1°C in 30 years) above the average temperature of 7.0°C for conditions >0°C. If this temperature increase is linearly related to the inflow of increased CO₂ and CH₄ to the lake as permafrost thaws (and not including DOC transport and subsequent oxidation), we expect a −30% increase in fluxes from the lake.

It is unclear how the identified trends in environmental drivers and the estimated impacts on GHG fluxes apply to other lakes. However, there may be some similarities in response because many of the processes that influence gas fluxes described here (e.g., rainfall and carbon loading, temperature and respiration, photomineralization of DOC) occur in all surface waters. We suggest that lakes deep enough to stratify seasonally may behave similarly to Toolik Lake, while shallower lakes or wetlands may respond differently to environmental change (e.g., greater ebullition than observed in Toolik). In addition, catchment differences in vegetation and surface topography may contribute to highly site-specific responses of lakes to changing environmental conditions.

5 Conclusion

We investigated the flux–gradient relationships between gas mixing ratios of CO₂ and CH₄ measured in lake surface waters during the ice-free season 2015 at Toolik Lake, estimated the relative strength of potential environmental driving forces governing CO₂ and CH₄ effluxes, and then combined this newly gained process-level knowledge with long-term trends of meteorological and soil temperature data to make predictions of how gas fluxes may change in the coming decades. In contrast to expectations, the flux–gradient relationship of CO₂ mixing ratio differences across the air-water interface had an influence on F_CO2 only if the water surface was at least 8–10°C warmer than the air. Otherwise F_CO2 was surprisingly constant over a wide range of horizontal wind speed. F_CH4 showed a typical exponential increase in flux over the full range of observed wind speeds. Overall, the relationship between wind speed and gas exchange coefficients (k) represented by several models compared poorly to our measured values of k for both CO₂ and CH₄. The models substantially under-predict our measured k values for CO₂ and CH₄ at low to medium wind speeds (<8–10 m s⁻¹), above which our k computed from direct measurements converges on the range of values predicted by most models, especially models specific for lakes that include the effects of buoyancy flux. We attribute these higher gas exchange velocities at low wind speeds to the characteristics of the atmospheric turbulence generated on land and carried over water in this tundra lake, and how that affects surface roughness, wave-breaking, and bubble-mediated gas exchange at low wind speeds. Increased turbulence and a higher u_*-to-U₁₀ ratio over smaller lakes as compared to oceans increased both F_CO2 and F_CH4 at low wind speeds well beyond the level expected over the ocean.

Combining the analysis of the effects of environmental drivers on gas flux with the 30 + year long-term trends of driver variables monitored by the LTER program we found both flux-enhancing and flux-reducing effects. The warming trend across the whole 1.5 m soil profile equipped with temperature sensors tends to enhance both CO₂ and CH₄ fluxes, whereas rainfall intensity tends to reduce F_CO2, and also F_CH4 if in combination with low u_*. High u_* alone also reduces F_CH4, whereas in the case of F_CO2 it is rather increased horizontal wind speed than u_* that reduces fluxes.

We argue that the biological processing of carbon-rich substrate that becomes available for decomposition as the tundra soil warms (e.g., Robinson et al., 2022) is key for understanding future trends in GHG fluxes (see also Wu et al., 2013), whereas the variability and long-term trends of the physical and meteorological variables primarily affect the timing when higher or lower than average fluxes are observed. When all aspects are taken into account, we see no strong evidence that a tipping point will be reached to change the status of the system substantially (e.g., source to sink). Instead we suggest that CO₂ and CH₄ fluxes should not increase by more than ∼30% by 2050, and we do not expect them to decrease by more than ∼ –10% within the next 30 years. This range of −10% to +30% characterizes the limitations of the study, including the variance shown for the relationships of environmental variables and gas fluxes. However, we suggest that lakes in the Arctic will remain a clear and strong source of CO₂ and CH₄ fluxes despite their relatively small area in the terrestrial landscape.

Data availability

The long-term meteorological data used in this study can be downloaded from University of Alaska’s Toolik Field Station Environmental Data Center (https://www.uaf.edu/toolik/edc/monitoring/abiotic/met-data-query.php). The CO₂ and CH₄ flux data used in this study are available from: Eugster et al. (2020b). See also Eugster et al. (2020a). Turbulence and flux data from eddy flux platform on Toolik Lake, Alaska 2009–2015 from Environmental Data Initiative, http://dx.doi.org/10.6073/pasta/919cd028d73ef4f8427d951148f974ec. Gap-filling data from: Shaver (2016).

Author contributions

WE and GK designed the study, collected and analyzed data, and prepared the manuscript. JL contributed to data collection and analysis. TD, JL, and GS contributed data. All authors contributed comments on the manuscript.

Acknowledgments

We acknowledge support from the Arctic LTER grants NSF-DEB-1637459, 1026843, 1754835, NSF-PLR 1504006, and supplemental funding from the NSF-NEON and OPP-AON programs. WE acknowledges additional funding received from ETH Zurich scientific equipment grants 0-43350-07 and 0–43683–11. Many thanks also go to numerous technical assistants working at Toolik Lake, and to Toolik Field Station staff members for their support.Dr. Werner Eugster, an esteemed scientist and our colleague and dear friend for decades, passed away in May 2022. We dedicate this paper to Werner—it was his brainchild, and he continued to contribute to it in his last days. Werner was a world leader in the fields of micrometeorology and eddy covariance studies, and a kind and tireless mentor for us and many other scientists. We miss him.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.948529/full#supplementary-material

References

Akritas, M. G., Murphy, S. A., and Lavalley, M. P. (1995). The Theil-Sen estimator with doubly censored data and applications to astronomy. J. Am. Stat. Assoc. 90, 170–177. doi:10.1080/01621459.1995.10476499

CrossRef Full Text | Google Scholar

Arguez, A., and Vose, R. S. (2011). The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Meteorol. Soc. 92, 699–704. doi:10.1175/2010bams2955.1

CrossRef Full Text | Google Scholar

Bayer, T. K., Gustafsson, E., Brakebusch, M., and Beer, C. (2019). Future carbon emission from boreal and permafrost lakes are sensitive to catchment organic carbon loads. J. Geophys. Res. Biogeosci. 124, 1827–1848. doi:10.1029/2018JG004978

CrossRef Full Text | Google Scholar

W. Brutsaert, and G. H. Jirka (Editors) (1984). Gas transfer at water surfaces (Springer Netherlands). doi:10.1007/978-94-017-1660-4

CrossRef Full Text | Google Scholar

Buck, A. L. (1981). New equations for computing vapor pressure and enhancement factor. J. Appl. Meteor. 20, 1527–1532. doi:10.1175/1520-0450(1981)020<1527:nefcvp>2.0.co;2

CrossRef Full Text | Google Scholar

Charnock, H. (1955). Wind stress on a water surface. Q. J. R. Meteorol. Soc. 81, 639–640. doi:10.1002/qj.49708135027

CrossRef Full Text | Google Scholar

Cherry, J. E., Déry, S. J., Cheng, Y., Stieglitz, M., Jacobs, A. S., and Pan, F. (2014). “Climate and hydrometeorology of the Toolik lake region and the kuparuk river basin,” in Alaska’s changing arctic. Editors J. Hobbie, and G. Kling (Oxford University Press). doi:10.1093/acprof:osobl/9780199860401.003.0002

CrossRef Full Text | Google Scholar

Cole, J. J., and Caraco, N. F. (1998). Atmospheric exchange of carbon dioxide in a low-wind oligotrophic lake measured by the addition of SF₆. Limnol. Oceanogr. 43, 647–656. doi:10.4319/lo.1998.43.4.0647

CrossRef Full Text | Google Scholar

Cole, J. J., Caraco, N. F., Kling, G. W., and Kratz, T. K. (1994). Carbon dioxide supersaturation in the surface waters of lakes. Science 265, 1568–1570. doi:10.1126/science.265.5178.1568

PubMed Abstract | CrossRef Full Text | Google Scholar

Cory, R. M., Crump, B. C., Dobkowski, J. A., and Kling, G. W. (2013). Surface exposure to sunlight stimulates CO₂ release from permafrost soil carbon in the Arctic. Proc. Natl. Acad. Sci. U. S. A. 110, 3429–3434. doi:10.1073/pnas.1214104110

PubMed Abstract | CrossRef Full Text | Google Scholar

Cory, R. M., Ward, C. P., Crump, B. C., and Kling, G. W. (2014). Sunlight controls water column processing of carbon in arctic fresh waters. Science 345, 925–928. doi:10.1126/science.1253119

PubMed Abstract | CrossRef Full Text | Google Scholar

Cory, R. M., and Kling, G. W. (2018). Controls on DOM degradation along the aquatic continuum: The influence of interactions between light, chemistry, and biology. Limnol. Oceanogr. Lett. 3 (3), 102–116. doi:10.1002/lol2.10060

CrossRef Full Text | Google Scholar

Crump, B. C., Kling, G. W., Bahr, M., and Hobbie, J. E. (2003). Bacterioplankton community shifts in an arctic lake correlate with seasonal changes in organic matter source. Appl. Environ. Microbiol. 69, 2253–2268. doi:10.1128/aem.69.4.2253-2268.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

Crump, B. C., Adams, H. E., Hobbie, J. E., and Kling, G. W. (2007). Biogeography of bacterioplankton in lakes and streams of an Arctic tundra catchment. Ecology 88, 1365–1378. doi:10.1890/06-0387

PubMed Abstract | CrossRef Full Text | Google Scholar

Crusius, J., and Wanninkhof, R. (2003). Gas transfer velocities measured at low wind speed over a lake. Limnol. Oceanogr. 48, 1010–1017. doi:10.4319/lo.2003.48.3.1010

CrossRef Full Text | Google Scholar

Deike, L., and Melville, W. K. (2018). Gas transfer by breaking waves. Geophys. Res. Lett. 45, 10482–10492. doi:10.1029/2018GL078758

CrossRef Full Text | Google Scholar

DelSontro, T. S. (2011). Quantifying methane emissions from reservoirs: From basin-scale to discrete analyses with a focus on ebullition dynamics. Ph.D. thesis. Switzerland: ETH Zurich, 154pp.

Google Scholar

Easterling, R. G. (1969). Discrimination intervals for percentiles in regression. J. Am. Stat. Assoc. 64, 1031–1041. doi:10.1080/01621459.1969.10501034

CrossRef Full Text | Google Scholar

Edson, J. B., Jampana, V., Weller, R. A., Bigorre, S. P., Plueddemann, A. J., Fairall, C. W., et al. (2013). On the exchange of momentum over the open ocean. J. Phys. Oceanogr. 43, 1589–1610. doi:10.1175/JPO-D-12-0173.1

CrossRef Full Text | Google Scholar

Elder, C. D., Xu, X., Walker, J., Schnell, J. L., Hinkel, K. M., Townsend-Small, A., et al. (2018). Greenhouse gas emissions from diverse Arctic Alaskan lakes are dominated by young carbon. Nat. Clim. Chang. 8, 166–171. doi:10.1038/s41558-017-0066-9

CrossRef Full Text | Google Scholar

Elder, C. D., Schweiger, M., Lam, B., Crook, E. D., Xu, X., Walker, J., et al. (2019). Seasonal sources of whole-lake CH₄ and CO₂ emissions from interior alaskan thermokarst lakes. J. Geophys. Res. Biogeosci. 124, 1209–1229. doi:10.1029/2018jg004735

CrossRef Full Text | Google Scholar

Elder, C. D., Thompson, D. R., Thorpe, A. K., Hanke, P., Anthony, K. M. W., and Miller, C. E. (2020). Airborne mapping reveals emergent power law of arctic methane emissions. Geophys. Res. Lett. 47, e2019GL085707. doi:10.1029/2019gl085707

CrossRef Full Text | Google Scholar

Emerson, S., and Bushinsky, S. (2016). The role of bubbles during air-sea gas exchange. J. Geophys. Res. Oceans 121, 4360–4376. doi:10.1002/2016JC011744

CrossRef Full Text | Google Scholar

Erickson, D. J. (1993). A stability-dependent theory for air-sea gas exchange. J. Geophys. Res. 98, 8471–8488. doi:10.1029/93jc00039

CrossRef Full Text | Google Scholar

Esters, L., Landwehr, S., Sutherland, G., Bell, T. G., Christensen, K. H., Saltzman, E. S., et al. (2017). Parameterizing air-sea gas transfer velocity with dissipation. J. Geophys. Res. Oceans 122, 3041–3056. doi:10.1002/2016JC012088

CrossRef Full Text | Google Scholar

Eugster, W., DelSontro, T., Shaver, G. R., and Kling, G. W. (2020a). Interannual, summer, and diel variability of CH₄ and CO₂ effluxes from Toolik Lake, Alaska, during the ice-free periods 2010–2015. Environ. Sci. Process. Impacts 22, 2181–2198. doi:10.1039/d0em00125b

PubMed Abstract | CrossRef Full Text | Google Scholar

Eugster, W., Kling, G. W., Jonas, T., McFadden, T., Weust, A., MacIntyre, S., et al. (2003). CO₂ exchange between air and water in an arctic Alaskan and mid-latitude Swiss lake: The importance of convective mixing. 108 (D12), 4362. doi:10.1029/2002JD002653

CrossRef Full Text | Google Scholar

Eugster, W., Kling, G., and Laundre, J. (2020b). Turbulence and flux data from eddy flux platform on Toolik Lake, Alaska 2009-2015. ver 1. Environmental data initiative. Available at: https://doi.org/10.6073/pasta/919cd028d73ef4f8427d951148f974ec (Accessed August 19, 2022).

Google Scholar

Fredriksson, S. T., Arneborg, L., Nilsson, H., Zhang, Q., and Handler, R. A. (2016). An evaluation of gas transfer velocity parameterizations during natural convection using DNS. J. Geophys. Res. Oceans 121, 1400–1423. doi:10.1002/2015JC011112

CrossRef Full Text | Google Scholar

Frost, T., and Upstill-Goddard, R. C. (2002). Meteorological controls of gas exchange at a small English lake. Limnol. Oceanogr. 47, 1165–1174. doi:10.4319/lo.2002.47.4.1165

CrossRef Full Text | Google Scholar

Garbe, C. S., Rutgersson, A., Boutin, J., de Leeuw, G., Delille, B., Fairall, C. W., et al. (2014). “Transfer across the air-sea interface,” in Ocean-atmosphere interactions of gases and particles. Editors P. S. Liss, and M. T. Johnson (Springer Earth System Sciences). doi:10.1007/978-3-642-25643-1_2

CrossRef Full Text | Google Scholar

Garies, J. A. L., and Lesack, L. F. W. (2020). Ice-out and freshet fluxes of CO₂ and CH₄ across the air–water interface of the channel network of a great Arctic delta, the Mackenzie. Polar Res. 39, 3528. doi:10.33265/polar.v39.3528

CrossRef Full Text | Google Scholar

Goddijn-Murphy, L., Woolf, D. K., Callaghan, A. H., Nightingale, P. D., and Shutler, J. D. (2016). A reconciliation of empirical and mechanistic models of the air-sea gas transfer velocity. J. Geophys. Res. Oceans 121, 818–835. doi:10.1002/2015JC011096

CrossRef Full Text | Google Scholar

Guérin, F., Abril, G., Serça, D., Delon, C., Richard, S., Delmas, R., et al. (2007) Gas transfer velocities of CO₂ and CH₄ in a tropical reservoir and its river downstream. J. Mar. Syst. 66, 161–172. doi:10.1016/j.jmarsys.2006.03.019

CrossRef Full Text | Google Scholar

Harrison, E. L., Veron, F., Ho, D. T., Reid, M. C., Orton, P., and McGillis, W. R. (2012). Nonlinear interaction between rain- and wind-induced air-water gas exchange. J. Geophys. Res. 117, C03034. doi:10.1029/2011JC007693

CrossRef Full Text | Google Scholar

Hasse, L., and Isemer, H. J. (1986). Annual migration of the North Atlantic zero heat flux line. Naturwissenschaften 73, 550–551. doi:10.1007/bf00368163

CrossRef Full Text | Google Scholar

Heiskanen, J. J., Mammarella, I., Haapanala, S., Pumpanen, J., Vesala, T., MacIntyre, S., et al. (2014). Effects of cooling and internal wave motions on gas transfer coefficients in a boreal lake. Tellus B Chem. Phys. Meteorology 66 (1), 22827. doi:10.3402/tellusb.v66.22827

CrossRef Full Text | Google Scholar

Ho, D., Law, C. S., Smith, M. J., Schlosser, P., Harvey, M., and Hill, P. (2006). Measurements of air–sea gas exchange at high wind speeds in the Southern Ocean: Implications for global parameterizations. Geophys. Res. Lett. 33, L16611. doi:10.1029/2006GL026817

CrossRef Full Text | Google Scholar

Ho, D. T., Zappa, C. J., McGillis, W. R., Bliven, L. F., Ward, B., Dacey, J. W. H., et al. (2004). Influence of rain on air-sea gas exchange: Lessons from a model ocean. J. Geophys. Res. 109, C08S18. doi:10.1029/2003JC001806

CrossRef Full Text | Google Scholar

Hobbie, J. E., and Kling, G. W. (Editors) (2014). Alaska's changing arctic: Ecological consequences for tundra, streams, and lakes (New York, USA: Oxford University Press), 331∼pp.

Google Scholar

Imberger, J. (1985). The diurnal mixed layer1. Limnol. Oceanogr. 30, 737–770. doi:10.4319/lo.1985.30.4.0737

CrossRef Full Text | Google Scholar

IPCC AR6 WGI (2021). Climate change 2021: The physical science basis. Intergovernmental Panel on Climate Change IPCC. Cambridge, United Kingdom: Cambridge University Press, 3949pp. doi:10.1017/9781009157896

CrossRef Full Text | Google Scholar

Jahne, B., and Monahan, E. C. (Editors) (1995). Air-water gas transfer: Selected papers from the third international symposium on air-water gas transfer (Hanau, Germany: Aeon Verlag), 900.

Google Scholar

Jiménez, P. A., and Dudhia, J. (2018). On the need to modify the sea surface roughness formulation over shallow waters. J. Appl. Meteorol. Climatol. 57, 1101–1110. doi:10.1175/JAMC-D-17-0137.1

CrossRef Full Text | Google Scholar

Johnson, M. T., Hughes, C., Bell, T. G., and Liss, P. S. (2011). “A Rumsfeldian analysis of uncertainty in air–sea gas exchange,”. Gas transfer at water surfaces. Editors S. Komori, W. McGillis, and R. Kurose (Kyoto University Press), 464–485.

Google Scholar

Klaus, M., and Vachon, D. (2020). Challenges of predicting gas transfer velocity from wind measurements over global lakes. Aquat. Sci. 82 (53), 53–17. doi:10.1007/s00027-020-00729-9

CrossRef Full Text | Google Scholar

Kling, G. W., Adams, H. E., Bettez, N. D., Bowden, W. B., Crump, B. C., Giblin, A. E., et al. (2014). “Land-water interactions,”. A changing arctic: Ecological consequences for tundra, streams, and lakes. Editors J. E. Hobbie, and G. W. Kling (Oxford University Press), 143–172.

CrossRef Full Text | Google Scholar

Kling, G. W., Kipphut, G. W., and Miller, M. C. (1991). Arctic lakes and streams as gas conduits to the atmosphere: Implications for tundra carbon budgets. Science 251, 298–301. doi:10.1126/science.251.4991.298

PubMed Abstract | CrossRef Full Text | Google Scholar

Kling, G. W., Kipphut, G. W., and Miller, M. C. (1992). The flux of CO₂ and CH₄ from lakes and rivers in arctic Alaska. Hydrobiologia 240, 23–36. doi:10.1007/bf00013449

CrossRef Full Text | Google Scholar

Kling, G. W., Kipphut, G. W., Miller, M. C., and O'Brien, W. J. (2000). Integration of lakes and streams in a landscape perspective: The importance of material processing on spatial patterns and temporal coherence. Freshw. Biol. 43, 477–497. doi:10.1046/j.1365-2427.2000.00515.x

CrossRef Full Text | Google Scholar

Krogh, A. (1910). Some experiments on the invasion of oxygen and carbonic oxide into Water¹. Skand. Arch. Fur Physiol. 23, 224–235. doi:10.1111/j.1748-1716.1910.tb00599.x

CrossRef Full Text | Google Scholar

Legendre, P., and Legendre, L. (1998). Numerical ecology. Amsterdam: Elsevier, 853∼pp.

Google Scholar

Lejeune, M. G., and Sarda, P. (1988). Quantile regression: A nonparametric approach. Comput. Statistics Data Analysis 6, 229–239. doi:10.1016/0167-9473(88)90003-5

CrossRef Full Text | Google Scholar

Lewkowicz, A. G., and Way, R. G. (2019). Extremes of summer climate trigger thousands of thermokarst landslides in a High Arctic environment. Nat. Commun. 10, 1329. doi:10.1038/s41467-019-09314-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Liss, P. S., and Merlivat, L. (1986). “Air–sea gas exchange rates: Introduction and synthesis,” in The role of air–sea exchange in geochemical cycling. Editor P. Buat-Ménard (Dordrecht, Holland: D. Reidel), 113–127.

CrossRef Full Text | Google Scholar

Liss, P., and Slater, P. (1974). Flux of gases across the air-sea interface. Nature 247, 181–184. doi:10.1038/247181a0

CrossRef Full Text | Google Scholar

MacIntyre, S., Eugster, W., and Kling, G. W. (2001). “The critical importance of buoyancy flux for gas flux across the air-water interface,” in Gas transfer at water surfaces. Editors M. A. Donelan, W. M. Drennan, E. S. Saltzman, and R. Wanninkhof (American Geophysical Union).

Google Scholar

MacIntyre, S., Jonsson, A., Jansson, M., Aberg, J., Turney, D. E., and Miller, S. D. (2010). Buoyancy flux, turbulence, and the gas transfer coefficient in a stratified lake. Geophys. Res. Lett. 37, L24604. doi:10.1029/2010GL044164

CrossRef Full Text | Google Scholar

Markfort, C. D., Perez, A. L. S., Thill, J. W., Jaster, D. A., Porté-Agel, G., and Stefan, H. G. (2010). Wind sheltering of a lake by a tree canopy or bluff topography. Water Resour. Res. 46, W03530. doi:10.1029/2009WR007759

CrossRef Full Text | Google Scholar

McGuire, A. D., Anderson, L. G., Christensen, T. R., Dallimore, S., Guo, L., Hayes, D. J., et al. (2009). Sensitivity of the carbon cycle in the Arctic to climate change. Ecol. Monogr. 79, 523–555. doi:10.1890/08-2025.1

CrossRef Full Text | Google Scholar

Mesarchaki, E., Kräuter, C., Krall, K. E., Bopp, M., Helleis, F., Williams, J., et al. (2015). Measuring air–sea gas-exchange velocities in a large-scale annular wind–wave tank. Ocean Sci. 11, 121–138. doi:10.5194/os-11-121-2015

CrossRef Full Text | Google Scholar

Miller, M. C., Spatt, P., Westlake, P., Yeakel, D., and Hater, G. R. (1986). Primary production and its control in Toolik lake, Alaska. Arch. Hydrobiol. Suppl. 74, 97–131.

Google Scholar

Munk, W. H. (1947). A critical wind speed for air–sea boundary processes. J. Mar. Res. 6, 203–218. Available at: https://images.peabody.yale.edu/publications/jmr/jmr06-03-04.pdf.

Google Scholar

Patel, D. (2021). “Quantile regression support vector machine (QRSVM) model for time series data analysis,” in Soft computing and its engineering applications (Springer Singapore). doi:10.1007/978-981-16-0708-0_6

CrossRef Full Text | Google Scholar

Pohlert, T. (2020) trend: Non-Parametric trend tests and change-point detection. R package version 1.1.4.

Google Scholar

R Core Team (2014). R: A language and environment for statistical computing. Vienna, Austria.

Google Scholar

Read, J. S., Hamilton, D. P., Desai, A. R., Rose, K. C., MacIntyre, S., Lenters, J. D., et al. (2012). Lake-size dependency of wind shear and convection as controls on gas exchange. Geophys. Res. Lett. 39, L09405. doi:10.1029/2012gl051886

CrossRef Full Text | Google Scholar

Riordan, B., Verbyla, D., and McGuire, A. D. (2006). Shrinking ponds in subarctic Alaska based on 1950–2002 remotely sensed images. J. Geophys. Res. 111, G04002. doi:10.1029/2005jg000150

CrossRef Full Text | Google Scholar

Robinson, S. I., O’Gorman, E. J., Frey, B., Hagner, M., and Mikola, J. (2022). Soil organic matter, rather than temperature, determines the structure and functioning of subarctic decomposer communities. Glob. Change Biol. 28, 3929–3943. doi:10.1111/gcb.16158

CrossRef Full Text | Google Scholar

Rosentreter, J. A., Maher, D. T., Ho, D. T., Call, M., Barr, J. G., and Eyre, B. D. (2017). Spatial and temporal variability of CO₂ and CH₄ gas transfer velocities and quantification of the CH₄ microbubble flux in mangrove dominated estuaries. Limnol. Oceanogr. 62, 561–578. doi:10.1002/lno.10444

CrossRef Full Text | Google Scholar

Schuur, E. A. G., McGuire, A. D., Schädel, C., Grosse, G., Harden, J. W., Hayes, D. J., et al. (2015). Climate change and the permafrost carbon feedback. Nature 520, 171–179. doi:10.1038/nature14338

PubMed Abstract | CrossRef Full Text | Google Scholar

Sen, P. K. (1968). Estimates of the regression coefficient based on kendall's tau. J. Am. Stat. Assoc. 63, 1379–1389. doi:10.1080/01621459.1968.10480934

CrossRef Full Text | Google Scholar

Shaver, G. (2016). Hourly weather data from the Arctic LTER Moist Acidic Tussock Experimental plots from 1990 to 1999, Toolik Field Station, North Slope, Alaska. ver 5. Environmental data initiative. Available at: https://doi.org/10.6073/pasta/431942c31aad96a5d0314939d68e2421 (Accessed August 19, 2022).

Google Scholar

Stull, R. B. (1988). An introduction to boundary layer meteorology. Dordrecht: Kluwer Academic Publishers, 670.

Sullivan, P., Banner, M. L., Morison, R. P., and Peirson, W. (2018). Turbulent flow over steep steady and unsteady waves under strong wind forcing. J. Phys. Oceanogr. 48, 3–27. doi:10.1175/JPO-D-17-0118.1

CrossRef Full Text | Google Scholar

Tan, Z., and Zhuang, Q. (2015). Arctic lakes are continuous methane sources to the atmosphere under warming conditions. Environ. Res. Lett. 10, 054016. doi:10.1088/1748-9326/10/5/054016

CrossRef Full Text | Google Scholar

Taylor, P. K., and Yelland, M. J. (2001). The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr. 31, 572–590. doi:10.1175/1520-0485(2001)031<0572:tdossr>2.0.co;2

CrossRef Full Text | Google Scholar

Turetsky, M. R., Abbott, B. W., Jones, M. C., Anthony, K. W., Olefeldt, D., Schuur, E. A. G., et al. (2020). Carbon release through abrupt permafrost thaw. Nat. Geosci. 13, 138–143. doi:10.1038/s41561-019-0526-0

CrossRef Full Text | Google Scholar

Vonk, J. E., Tank, S. E., Mann, P. J., Spencer, R. G. M., Treat, C. C., Striegl, R. G., et al. (2015). Biodegradability of dissolved organic carbon in permafrost soils and aquatic systems: A meta-analysis. Biogeosciences 12, 6915–6930. doi:10.5194/bg-12-6915-2015

CrossRef Full Text | Google Scholar

Wanninkhof, R., Asher, W. E., Ho, D. T., Sweeney, C., and McGillis, W. R. (2009). Advances in quantifying air-sea gas exchange and environmental forcing. Ann. Rev. Mar. Sci. 1, 213–244. doi:10.1146/annurev.marine.010908.163742

PubMed Abstract | CrossRef Full Text | Google Scholar

Wanninkhof, R., and Triñanes, J. (2017). The impact of changing wind speeds on gas transfer and its effect on global air‐sea CO₂ fluxes. Glob. Biogeochem. Cycles 31, 961–974. doi:10.1002/2016GB005592

CrossRef Full Text | Google Scholar

Wild, M., Gilgen, H., Roesch, A., Ohmura, A., Long, C. N., Dutton, E. G., et al. (2005). From dimming to brightening: Decadal changes in solar radiation at earth's surface. Science 308, 847–850. doi:10.1126/science.1103215

PubMed Abstract | CrossRef Full Text | Google Scholar

Wild, M., Roesch, A., and Ammann, C. (2012). Global dimming and brightening – evidence and agricultural implications. Cab. Rev. 7, 1–7. doi:10.1079/PAVSNNR20127003

CrossRef Full Text | Google Scholar

Woolf, D., and Thorpe, S. (1991). Bubbles and the air-sea exchange of gases in near-saturation conditions. J. Mar. Res. 49, 435–466. doi:10.1357/002224091784995765

CrossRef Full Text | Google Scholar

Wu, H., Peng, C., Lucotte, M., Soumis, N., Ge´linas, Y., Duchemin, E., et al. (2013). A coupled two-dimensional hydrodynamic and terrestrial input model to simulate CO₂ diffusive emissions from lake systems. Geosci. Model Dev. Discuss. 6, 3509–3556. doi:10.5194/gmdd-6-3509-2013

CrossRef Full Text | Google Scholar

Yang, M., Smyth, T. J., Kitidis, V., Brown, I. J., Wohl, C., Yelland, M. J., et al. (2021). Natural variability in air–sea gas transfer efficiency of CO₂. Sci. Rep. 11, 13584. doi:10.1038/s41598-021-92947-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Zappa, C. J., McGillis, W. R., Raymond, P. A., Edson, J. B., Hintsa, E. J., Zemmelink, H. J., et al. (2007). Environmental turbulent mixing controls on air-water gas exchange in marine and aquatic systems. Geophys. Res. Lett. 34, L10601. doi:10.1029/2006gl028790

CrossRef Full Text | Google Scholar