Impact of a Low-Permeability Layer on the Pumping Efficiency Under Threats of Saltwater Up-Coning

Previous studies on saltwater up-coning are mostly based on the assumption of a homogeneous aquifer and neglect the effect of heterogeneity. A numerical study was carried out to explore the impact of a low-permeability (k) layer on the pumping efficiency under threats of saltwater up-coning. It is found that the presence of the low-k layer could impede up-coning of saltwater, thereby improving significantly pumping efficiency, as expected. For the cases adopted, when the permeability of the 2 m thick low-k layer is three orders of magnitude less than that of the corresponding homogeneous aquifer, the pumping duration (i.e., the time before the salinity of pumped water reaches 2%) can be up to about 10 times longer than that of the homogeneous aquifer case. Additionally, a sound linear relationship could be developed between the normalized pumping duration of the layered case (E) (defined as the difference of the pumping duration between layered and homogeneous cases relative to the pumping duration in the homogeneous case) and the permeability of the homogeneous aquifer relative to that of the low-k layer (β). However, a short low-k layer may lead to the failure of this linear relationship. Moreover, a thicker low-k layer leads to a larger E when all other conditions are unchanged. When varying the location of the low-k layer, the large E occurs for the low-k layer located below and near the well bottom. The results obtained in the current study offer significant implications for preventing saltwater up-coning and improving the pumping efficiency through natural and artificial barriers.

1 Introduction

Coastal aquifers represent a vital component of freshwater resources in many countries worldwide. However, the overexploitation of the coastal aquifer has resulted in seawater intrusion, causing the degradation of groundwater resources and ecological systems (Werner et al., 2013). The existence of fresh groundwater overlaying saltwater in groundwater systems is ubiquitous in most coastal aquifers as well as in many inland aquifers (e.g., Schmorak and Mercado, 1969). The utilization of freshwater resources in those regions is therefore highly constrained by the presence of saltwater up-coning (i.e., the vertical rise of saline water into a production well), which may occur when groundwater is extracted through a partially penetrating well installed in the freshwater zone above a layer of intruded saltwater. It usually takes a long time for the up-coned saltwater to migrate back to the original position prior to pumping, indicating that once a pumping well is abandoned due to salinization, it can be reused for groundwater utilization after a long time (Zhou et al., 2005). Different skimming well options, such as scavenger wells and skimming tube wells, have been introduced to control saltwater up-coning and to enhance the freshwater extraction efficiency (Saeed et al., 2002).

Saltwater up-coning have been receiving attention for several decades, being studied using analytical, numerical, and experimental methods (Werner et al., 2013). These studies revealed that the rate and extent of saltwater up-coning rely on many factors, such as hydraulic properties of the aquifer, pumping rate and duration, initial interface position, density contrast between freshwater and saltwater, and regional flow. Additional factors affecting saltwater up-coning are dispersion and sorption effects, groundwater recharge, and the well and aquifer geometries (e.g., Reilly and Goodman, 1987; Saeed et al., 2002; Hamza, 2006; Werner et al., 2009).

Diersch et al. (1984) were among the first to use numerical models to analyse dispersive processes during saltwater up-coning and found through sensitivity analysis that the salinity at the pumping well is strongly affected by dispersion. Zhou et al. (2005) explored the effect of longitudinal and transversal dispersivities on the pumping duration defined as the time before the salinity of pumped water reaches a specified value. Their numerical simulation results showed that the smaller the dispersivities, the longer the well pumps freshwater. In addition, the effect of the density difference between the freshwater and saltwater on the up-coning process was investigated in their study. The results indicated that the density effect could retard the solute transport toward the pumping well and prolong the pumping duration prior salinization.

Jakovovic et al. (2012) studied the effect of dye tracer (Rhodamine WT) adsorption on saltwater up-coning based on sand-tank experiments and numerical modelling. The results revealed that under low pumping rates, the spatial variability of the velocity is pronounced, increasing from the centre of the plume towards the interface. The dye tracer could be retarded relative to the salt and be preferentially transported along the higher-velocity paths towards the well forming double-peaked up-coning patterns. However, high pumping rates made the adsorption effect insignificant.

Recently, Jakovovic et al. (2016) investigated the problem of saltwater up-coning by analysing the saltwater up-coning zone of influence (SUZI). The SUZI is defined as the region around a pumping well within which significant rise in the saltwater-freshwater interface occurs. They found through both numerical and analytical methods that the SUZI was dependent on the relative magnitudes of pumping, regional flow, distance of the well from the coast, and position of the well above the interface. Moreover, the results of the three-dimensional coastal setting simulations showed an asymmetric shape of the lateral extent of the SUZI, which is largest in the direction parallel to the coast. The occurrence of this phenomenon is attributed to that the ocean and the inland extent of the seawater wedge limit the propagation of the SUZI perpendicular to the coast.

While significant studies have been conducted, there is very limited research investigating the impact of aquifer heterogeneity on the saltwater up-coning processes. Interface up-coning in stratified aquifers has been examined analytically by Dagan and Zeitoun (1998), where the hydraulic conductivity was modelled as a stationary random function of the vertical coordinate. By contrast, a significant number of studies have been carried out to explore the impact of aquifer heterogeneity on seawater intrusion (e.g., Kim et al., 2006; Liu et al., 2014; Strack and Ausk, 2015). Taking an example, Lu et al. (2013) investigated the steady-state mixing zone in stratified coastal aquifers based on laboratory experiments and numerical modelling and observed that a low-permeability (k) layer exerts a high impact on the mixing-zone development. Accordingly, we hypothesize that the presence of a low-k layer would highly affect saltwater up-coning dynamics.

The main aim of this study is to investigate the impact of a low-k layer on saltwater up-coning processes using a variable-density flow and solute transport numerical model, as a first step to analyse the effects of aquifer heterogeneity on the generation and dynamics of saltwater up-coning. The pumping duration, the same definition as in Zhou et al. (2005), will serve as the main indicator for assessing the impact of the low-k layer on the pumping efficiency. The results of layered aquifers and corresponding homogeneous aquifers will be compared to reveal the importance of the low-k layer on controlling groundwater flow and salt transport. More importantly, quantitative relationships between the pumping duration and the k magnitude of the low-k layer are obtained; these provide a simple tool for developing natural and artificial barriers to prevent saltwater up-coning and enhance the pumping efficiency.

2 Methods

2.1 Conceptual Model and Parameter Values

The conceptual model in Zhou et al. (2005), modified from the saltwater up-coning problem presented by Reilly and Goodman (1987) and Voss and Souza (1987), is further modified in our study and is used as a reference case, since the aquifer is homogeneous (Figure 1). An axisymmetric, anisotropic, and confined aquifer is considered; the domain with a radius of 3,000 m and 150 m thickness, initially consists of three zones identified by different concentrations. The upper zone is the freshwater zone (C_f = 0 kg m⁻³) and 98 m thick, while a 50 m thick saltwater zone is located at the bottom of the aquifer with the concentration C_s = 35 kg m⁻³. A 2 m thick mixing zone separates these two zones with a concentration equal to C_s/2. The origin of the coordinate system is located at the bottom left of the model domain. In comparison with the conceptual model used in Zhou et al. (2005), the thickness of the saltwater zone is increased from 20 to 50 m, and the radius of the model is increased from 2000 to 3,000 m. These modifications were necessary to assure that the saltwater zone was deep enough to be able to supply water for length of all simulations. A smaller domain would have caused the concentrations of the water near the bottom boundary to become lower than C_s, this affecting the pumping times.

FIGURE 1

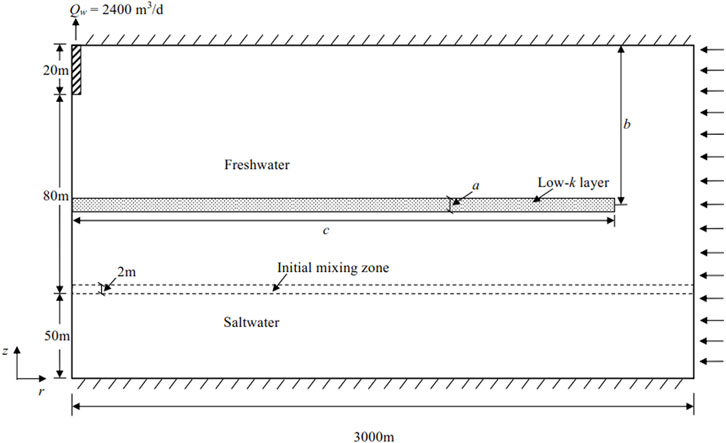
FIGURE 1. Conceptual model of a saltwater up-coning problem (modified from Figure 1 in Zhou et al. (2005).

An extraction well was located at the center of the axisymmetric domain at the top of the freshwater zone with a constant pumping rate Q_w = 2,400 m³ d⁻¹ and a well screen length d_f = 20 m. The initial hydraulic head is set as 10 m above the aquifer top. Recharge of freshwater and saltwater occurred along the external radial boundary with fixed-head and fixed concentration boundary conditions. Note that the fixed concentration is used in our solute boundary condition, while in Zhou et al. (2005), a concentration gradient of zero is prescribed normal to the boundary, and therefore salt can enter from this boundary only through advection. After pumping, saline water beneath the well is gradually drawn upward and the concentration of the extracted water gradually increases. Like in Zhou et al. (2005), it is assumed that, once the concentration of the extracted water reaches 2% of the saltwater concentration (i.e., C_s), the well is shut off.

For the base homogenous case, permeability in the horizontal and vertical directions (k_x and k_z) are $2.56\times {10}^{-11}$ and $1.0\times {10}^{-11}$ m², respectively. A constant value of $1\times {10}^{-3}$ kg m⁻¹ s⁻¹ is used for dynamic viscosity (μ). The porosity (θ) of the aquifer is 0.2. The densities of the freshwater (ρ_w) and saltwater (ρ_s) are 1,000 and 1,025 kg m⁻³, the latter approximately equaling to a common density of seawater. The longitudinal and transversal dispersivities (α_L and α_T) are 1 and 0.5 m, respectively. Molecular diffusion is neglected. The values of the parameters in the homogeneous case, listed in Table 1, are as those assumed for Case A in Zhou et al. (2005).

TABLE 1

TABLE 1. Values of parameters in the homogeneous case.

To study the effect of layered aquifer heterogeneity on saltwater up-coning, a horizontal low-k layer is considered with a thickness of a, distance between the center of the low-k layer and the top of aquifer of b, and extent from the well c. By varying the values of a, b, and c, nine scenarios are designed to test their sensitivity. Three different values of a (2, 4, and 8 m) are selected. For b, five values (6, 20, 32, 46, and 50 m) are chosen; when b = 6 m, the extraction well penetrates the low-k layer. Six values of c (100, 500, 1,000, 1,500, 2000, and 3,000 m) are assumed, where c = 3,000 m means that the low-k layer extended to the entire length of the domain. Moreover, to examine the sensitivity of the k magnitude of the low-k layer, values ranging from one to three orders of magnitude lower than the value in the homogeneous case are adopted. The highest values of k correspond to sands and the lowest values silts (Verruijt, 1970). When varying the value of k, the anisotropic ratio is fixed.

2.2 Numerical Implementation

Numerical simulations are implemented by SEAWAT-2000, a code based on the finite-difference method and developed by USGS for simulating variable-density flow and solute transport in porous media (Langevin et al., 2003). The code SEAWAT-2000 is developed by combining MODFLOW and MT3DMS into a single program that solves the coupled flow and solute transport equations. The governing equations are not shown here for the sake of conciseness and can be found in many references (e.g., Langevin et al., 2003). These three computer programs are originally based on the Cartesian coordinate system. Langevin (2008) showed that axisymmetric flow and transport can be simulated by these programs by adjusting several input parameters to account for the increase in flow area with radial distance from the well. In addition, the logarithmic weighting of interblock transmissivity that is a standard option in MODFLOW can be used for axisymmetric models to represent the linear change in hydraulic conductance within a single finite-difference cell.

For the reference case, the entire domain is discretized into 75 layers and 307 columns, resulting in 23025 cells in total. Each layer is 2 m thick, while the columns are variably spaced with 0.25 m horizontal resolution near the well expanding to 25 m horizontal resolution at the radial boundary. This discretization scheme is similar to that used in Langevin (2008).

2.3 Quantitative Indicators

As mentioned above, the salt concentration distribution (C) and the pumping duration (T) before the salinity of pumped water reaches a specified value (2% in the current study) are taken as quantitative indicators. Here, we define two dimensionless variables based on these two indicators:

$w=\frac{C}{C_s}(1)$

and

$E=\frac{\left(T_L-T_H\right)}{T_H}(2)$

in which T_L and T_H are the pumping durations when the salinity of pumped water reaches 2% in layered and homogeneous cases, respectively. E quantifies the efficiency of well pumping under the threats of saltwater up-coning. In addition, a dimensionless parameter $\beta$ is defined to reflect the relative magnitude of k of the low-k layer to that in the homogenous case:

$\beta =\frac{k_H}{k_L}(3)$

in which k_H and k_L are permeability of the homogenous case and the low-k layer in the horizontal direction, respectively. Since the anisotropy ratio of the aquifer is maintained the same for all cases, the value of β is constant for a given low-k layer regardless of the direction of permeability.

3 Results and Discussion

3.1 Impact on the Flow Field

Figure 2 shows the streamlines developed in the homogeneous aquifer case and layered aquifer case after 1, 2, 5, and 20 years, in which the layered aquifer has the parameters a = 2 m, b = 50 m, c = 3,000 m, and β = 1,000. The streamlines start from the external boundary with the vertical coordinates between 20 and 70 m. The streamlines in both cases change with the time, and the presence of the low-k layer alters significantly their direction. Initially, the streamlines near the external boundary in the homogeneous case are higher than in the layered case (see Figure 2A). With time the relative locations of the streamlines near the external boundary in the two cases are gradually altered (see Figures 2B–D). On the other hand, the presence of the low-k layer cause the streamlines to go up earlier than the counterparts in the homogeneous case. It is interesting that at larger pumping times, the lower streamlines in both cases tend to arrive at the vertical axis with z = 95 m, though this occurs in the homogeneous case earlier.

FIGURE 2

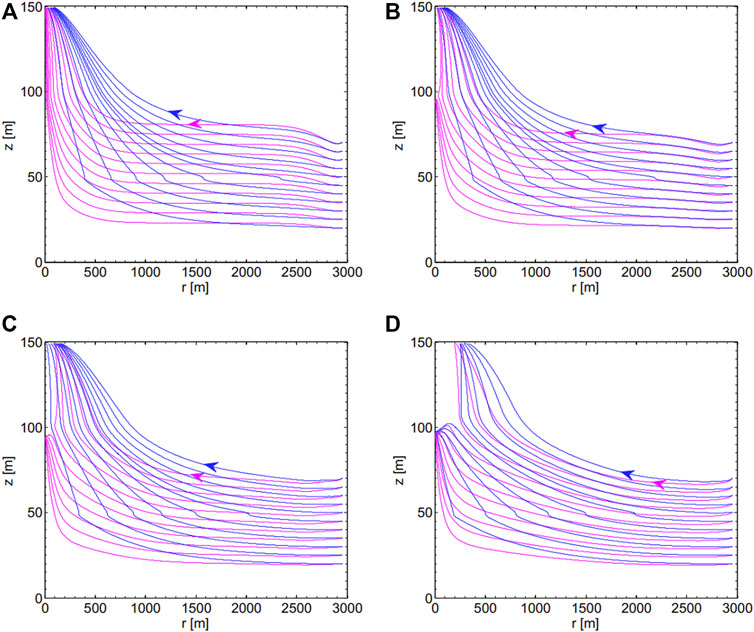
FIGURE 2. Streamlines developed in the homogeneous case (magenta) and the layered case (blue) after (A) 1 year, (B) 2 years, (C) 5 years, and (D) 20 years.

Figure 3 shows the development of the flow regime in the homogeneous aquifer case and layered aquifer case (the same case as in Figure 2). Similar to the findings in Zhou et al. (2005), who used a smaller domain, flow recirculation regimes are developed in both cases at the bottom-left saltwater zone during pumping though they occur at different times. Comparison with additional simulation results (not shown here) shows that the enlarged model domain used here results in the later occurrence of flow recirculation. The flow recirculation beneath the pumping well prevents the high concentration of saltwater in the mixing zone from migrating upward to the well (i.e., up-coning). It is shown that the flow recirculation regime in the homogeneous aquifer case is developed earlier than that in the layered aquifer case. On the other hand, the area of the flow recirculation regime in both cases grows with the time.

FIGURE 3

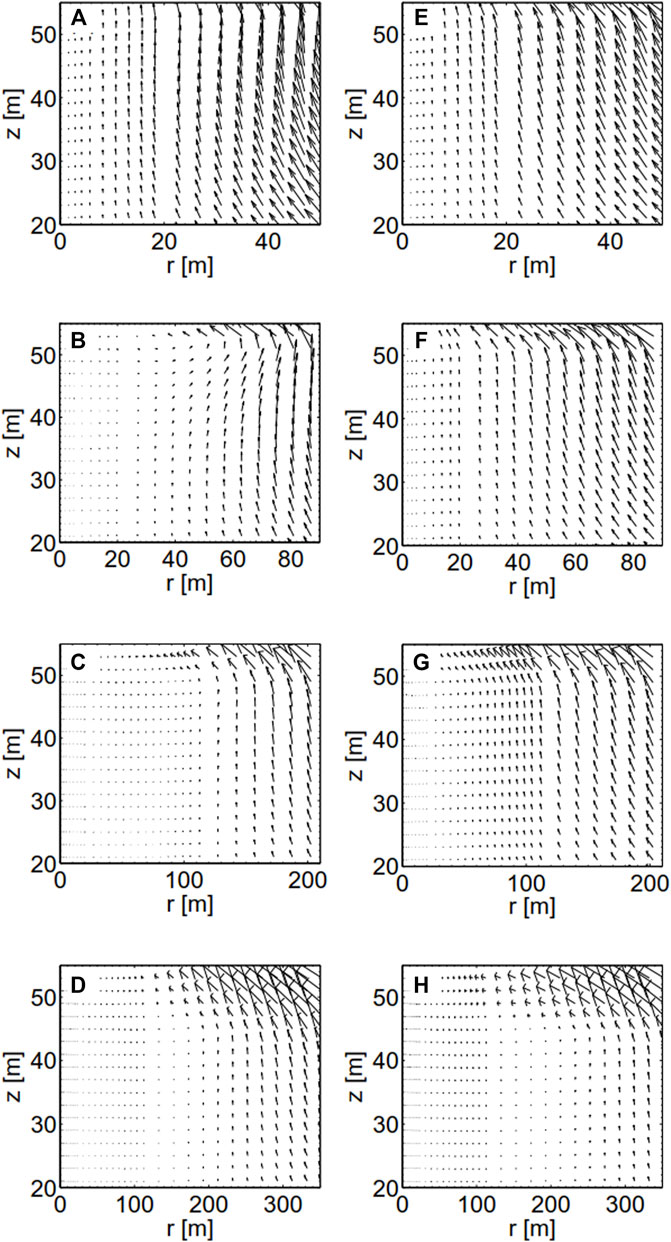
FIGURE 3. The development of the flow regime after 1, 2, 5, and 20 years in the bottom-left saltwater zone in the homogeneous case (A–D) and layered case (E–H).

3.2 Impact on Breakthrough Curves of Pumped Water

Figure 4 shows the breakthrough curves of pumped water for the homogeneous case and layered aquifer case (the same case as in Figure 2). As shown, the rate of saltwater up-coning in the homogenous case is significantly faster than that in the layered case. For the layered aquifer case, during about the first 10 yrs, there is no obvious response of the concentration of pumped water to well pumping, while only about 300 days are found for this phase in the homogeneous aquifer case. The values of T_H = 5.2 yrs and T_L = 47.6 yrs result in a value of E = 8.2 (Eq. (2)). The value of T_H in the current study is smaller than 5.6 yrs in Langevin (2008). With the larger model, saltwater is supplied by the aquifer near the well leading to lower pumping times. With the size of the domain used by Zhou et al. (2005) and Langevin (2008), the saltwater layer at the bottom of the aquifer is not enough to deep and salty water is thus replenished from the external lateral boundary on the right (Figure 1) leading to longer pumping times.

FIGURE 4

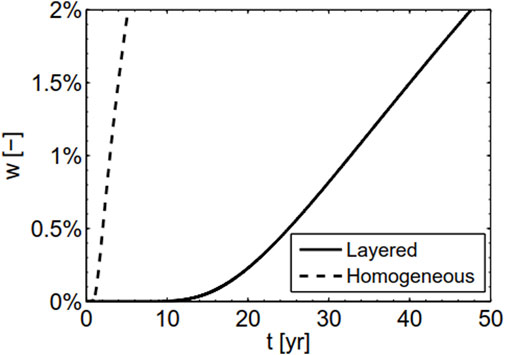
FIGURE 4. The breakthrough curves of pumped water in the homogeneous (dashed line) and layered (solid line) cases. The layered case is the same case as in Figure 2.

3.3 Impact on the Increment of the Total Salt Mass

Figure 5 shows the transient increment of the total salt mass within the model domain for the homogeneous case and layered aquifer case (the same case as in Figure 2). During approximately the initial 6 years, the two curves in the figure are almost overlapping, indicating that the increment of the total salt mass for the two cases are very close, despite of the significant difference of the average salt concentration of pumping water in the two cases (see Figure 4). In other words, the impact of the low-k layer on the increment of the total mass within the model domain during this initial stage is not significant. After that, the curve of the homogeneous aquifer case deviates from that of the layered aquifer case, representing that the increment of the total salt mass in the former case is obviously larger than that in the latter case.

FIGURE 5

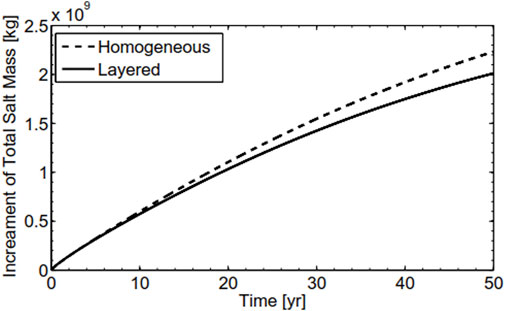
FIGURE 5. The transient increment of the total mass within the model domain for the homogeneous (dashed line) and layered (solid line) cases. The layered case is the same case as in Figure 2.

3.4 Impact on the Salt Concentration Distribution

Figure 6 shows transient salt concentration distributions after 1, 3, 5.2, and 47.6 years of pumping in the homogeneous case and layered aquifer case (the same case as in Figure 2). The salt concentration distributions are characterized by five contour lines of the normalized mass fraction (w = 0.02, 0.2, 0.5, 0.8, and 0.98). One can find from these figures that the concentration contour line w = 0.98 is very close to the concentration contour line w = 0.8 and only slightly lower than its initial position even at large pumping times; this indicates that the thickness of the saltwater layer adopted is sufficient to replenish the up-coned saltwater. This would not occur with the domain used in Zhou et al. (2005) and Langevin (2008) (not shown here).

FIGURE 6

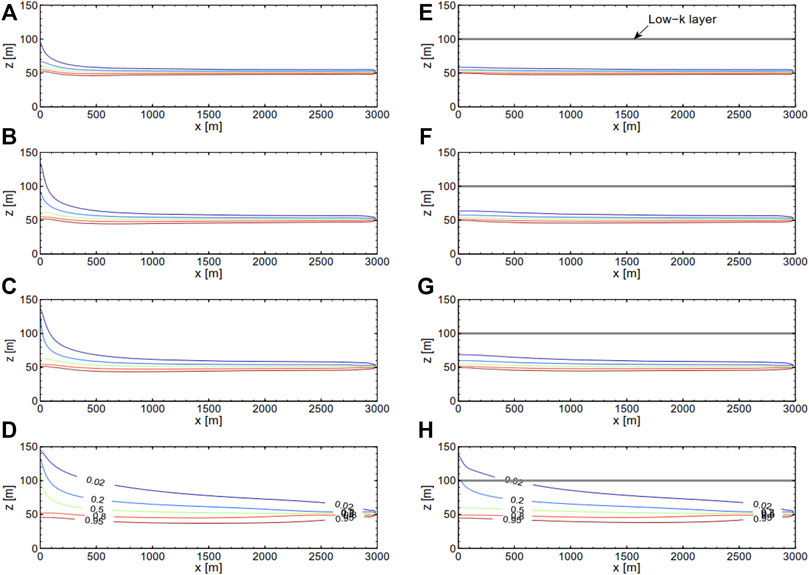
FIGURE 6. Transient salt concentration distributions after 1, 3, 5.2, and 47.6 years of pumping in the homogeneous case (A–D) and layered case (E–H). The layered case is the same case as in Figure 2.

After 1 year of pumping, the salt concentration distribution below the pumping well in the homogeneous case is visibly affected, while negligible effects on the layered aquifer case are found; this shows that the low-k layer exerts a significant impact on preventing saltwater up-coning (Figures 6A,E), as expected. When the well has pumped for 3 years, the mixing zone (defined as the zone between the concentration contour lines of w = 0.02 and 0.98) in the homogeneous case is widened significantly and the concentration contour line of w = 0.02 enters the well (Figure 6B). However, the average concentration of pumped water has not reached the criterion of well shut-off. At the same moment, by contrast, the mixing zone is slightly widened and the salt concentration distribution starts to ascend in the layered aquifer case (Figure 6F).

When the well has pumped for about 5.2 years, in the homogeneous case, the mixing-zone thickness is remained similar and the four concentration contour lines of w = 0.02, 0.5, 0.8, and 0.98 are at similar locations, in comparison to those developed after 3 years of pumping (Figure 6C). However, the concentration contour line of w = 0.2 has been elevated significantly, causing the average concentration of pumped water to reach the well shut-off criterion (i.e., T_H = 5.2 years). At this time, in the layered aquifer case four concentration contour lines are still below the low-k layer, although the thickness of the mixing zone is increased noticeably (Figure 6G). This indicates that the presence of the low-k layer slows dramatically the saltwater up-coning rate, and results in a longer allowable pumping time. The concentration of pumped water in the layered aquifer case reaches the well shut-off criterion when the well has pumped for about T_L = 47.6 years (Figure 6H). If the well shut-off criterion does not apply to the homogeneous aquifer case, the up-coning of saltwater is extensive and the aquifer is highly contaminated by saltwater (Figure 6D). Interestingly, at large pumping times, the highest concentration contour lines (i.e., w = 0.98) could be below the initial condition in both cases, further widening the mixing zone.

3.5 Sensitivity Analysis

3.5.1 Sensitivity to a and β

Figure 7 shows that the sensitivity of E to β for a = 2, 4, and 8 m, with b = 50 m and c = 3,000 m. Sound linear relationships are found for different values of a, with R² all equal to or larger than 0.988. A larger thickness of the low-k layer results in a higher value of E, as expected. In other words, a thicker low-k layer would facilitate preventing saltwater up-coning and increasing the pumping efficiency (i.e., E). When the low-k layer is 8 m thick and its permeability is three orders of magnitude less than that of the homogeneous aquifer, the allowable pumping duration is about 22 times higher than that of the homogeneous aquifer case (i.e., E = 22).

FIGURE 7

FIGURE 7. Sensitivity of E to β for a = 2, 4, and 8 m, with b = 50 m and c = 3000 m.

3.5.2 Sensitivity to b and β

Figure 8 shows the sensitivity of E to β for b = 6, 20, and 50 m, and the sensitivity of E to b when β = 10, 100, 500, and 1,000, in which a = 2 m and c = 3,000 m. Good linear relationships are constructed between E and β for three different values of b (Figure 8A). It is clearly shown that E is not a monotonic function of band the largest E occurs when the low-k layer is below and near the bottom of the well. By contrast, when the low-k layer penetrates the well, E decreases significantly with decreasing b. On the other hand, when b > 30 m, E decreases gradually with increasing b. In particular, when b $\ge$ 100 m (i.e., the low-k layer is located in the initial mixing zone or saltwater zone), the effect of the low-k layer on saltwater up-coning could be neglected.

FIGURE 8

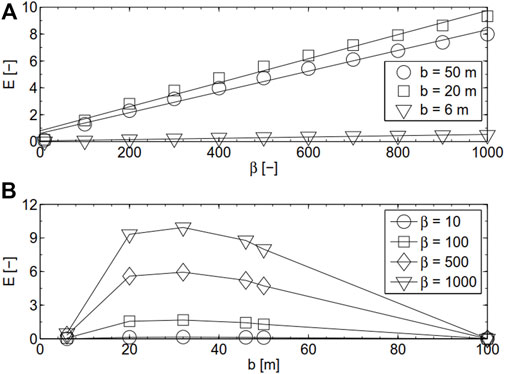
FIGURE 8. (A) Sensitivity of E to β for b = 6, 20, and 50 m, and (B) sensitivity of E to b for β = 10, 100, 500, and 1,000.

3.5.3 Sensitivity to c and β

Figure 9 shows the sensitivity of E to β for c varying between 500 and 3,000 m, with a = 2 m and b = 50 m. When c is equal to or larger than 1,500 m, as shown, the differences of E among different cases are considerably small, i.e., the length effect is negligible. For c = 1,000 m, the length effect is negligible for a large range of β, but remarkable for β larger than 700, resulting in a smaller E and the failure of the linear relationship between E and β. For c = 500 m, the length effect is significant and the impact of β on E is highly weakened.

FIGURE 9

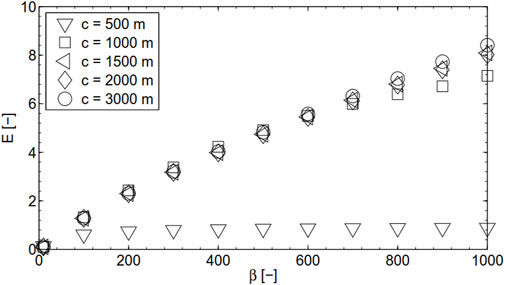
FIGURE 9. Sensitivity of E to β for c varying between 500 and 3,000 m, in which a = 2 m and b = 50 m.

3.5 Implications

To control the saltwater up-coning under pumping wells, skimming wells have been used in practice, as mentioned above. The results obtained in the current study indicate that a geology-based way could be used to improve pumping efficiency. When there is an aquitard in the subsurface, it is suggested that the partially penetrating well does not reach this natural barrier. Otherwise, the efficiency of the well could be significantly lowered. On the other hand, one could develop an artificial barrier below the well bottom to improve pumping efficiency. The technique of developing a plate-shaped stratum capable of offering significant hydraulic resistance is now available (Strack and Ausk, 2016). The obtained linear relationship between β and E together with the understanding of the effects of a, b, and c on E could assist in the design of an artificial barrier.

4 Conclusion

We used a numerical model to explore the impact of a horizontal low-k layer within a homogeneous aquifer on saltwater up-coning. Two main conclusions can be withdrawn as follows:

1) The low-k layer could alter significantly the flow patterns and thus reduce or impede saltwater up-coning. A sound linear relationship can be found between β and E, if the radius of the low-k layer is large enough. A thicker low-k layer leads to a larger E under otherwise the same conditions.

2) The maximum E occurs as the low-k layer is located below and near the well bottom. When the low-k layer penetrates the well, E decreases sharply with decreasing b. When the low-k layer is located below this critical location, by contrast, E decreases relatively gently with increasing b.

Despite that the model is highly simplified and neglects many other factors such as regional flow and unsteady pumping conditions, the results developed could provide significant implications for improving pumping efficiency under the threats of saltwater up-coning through natural and artificial barriers.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

ZW and MT performed the numerical modelling and theortical analysis, and wrote the first draft of the manuscript. ED and CL contributed to conception.

Funding

CL acknowledges the National Key Research and Development Project (2021YFC3200500), National Natural Science Foundation of China (51879088), Fundamental Research Funds for the Central Universities (B200204002), and Natural Science Foundation of Jiangsu Province (BK20190023). Funds received for open access publication fees from Hohai University.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Dagan, G., and Zeitoun, D. G. (1998). Free-surface Flow toward a Well and Interface Upconing in Stratified Aquifers of Random Conductivity. Water Resour. Res. 34 (11), 3191–3196. doi:10.1029/98wr02039

CrossRef Full Text | Google Scholar

Diersch, H.-J., Prochnow, D., and Thiele, M. (1984). Finite-element Analysis of Dispersion-Affected Saltwater Upconing below a Pumping Well. Appl. Math. Model. 8, 305–312. doi:10.1016/0307-904x(84)90143-4

CrossRef Full Text | Google Scholar

Hamza, K. I. (2006). “Numerical Analysis of Saltwater Upconing beneath a Pumping Well,” in The 10th International Water Technology Conference (IWTC-2006), Alexandria, Egypt, March 23–25, 2006. (IWTC10).

Google Scholar

Jakovovic, D., Post, V. E. A., Werner, A. D., Männicke, O., Hutson, J. L., and Simmons, C. T. (2012). Tracer Adsorption in Sand-Tank Experiments of Saltwater Up-Coning. J. Hydrology 414-415, 476–481. doi:10.1016/j.jhydrol.2011.11.024

CrossRef Full Text | Google Scholar

Jakovovic, D., Werner, A. D., De Louw, P. G. B., Post, V. E. A., and Morgan, L. K. (2016). Saltwater Upconing Zone of Influence. Adv. Water Resour. 94, 75–86. doi:10.1016/j.advwatres.2016.05.003

CrossRef Full Text | Google Scholar

Kim, K. Y., Seong, H., Kim, T., Park, K. H., Woo, N. C., Park, Y. S., et al. (2006). Tidal Effects on Variations of Fresh-Saltwater Interface and Groundwater Flow in a Multilayered Coastal Aquifer on a Volcanic Island (Jeju Island, Korea). J. Hydrology 330, 525–542. doi:10.1016/j.jhydrol.2006.04.022

CrossRef Full Text | Google Scholar

Langevin, C. D. (2008). Modeling Axisymmetric Flow and Transport. Groundwater 46 (4), 579–590. doi:10.1111/j.1745-6584.2008.00445.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Langevin, C. D., Shoemaker, W. B., and Guo, W. (2003). MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model--Documentation of the SEAWAT-2000 Version with the Variable-Density Flow Process (VDF) and the Integrated MT3DMS Transport Process (IMT). U.S. Geological Survey Open-File Report 03-426, 43.

CrossRef Full Text | Google Scholar

Liu, Y., Mao, X., Chen, J., and Barry, D. A. (2014). Influence of a Coarse Interlayer on Seawater Intrusion and Contaminant Migration in Coastal Aquifers. Hydrol. Pross. 28, 5162–5175. doi:10.1002/hyp.10002

CrossRef Full Text | Google Scholar

Lu, C., Chen, Y., Zhang, C., and Luo, J. (2013). Steady-state Freshwater-Seawater Mixing Zone in Stratified Coastal Aquifers. J. Hydrology 505, 24–34. doi:10.1016/j.jhydrol.2013.09.017

CrossRef Full Text | Google Scholar

Reilly, T. E., and Goodman, A. S. (1987). Analysis of Saltwater Upconing beneath a Pumping Well. J. Hydrology 89, 169–204. doi:10.1016/0022-1694(87)90179-x

CrossRef Full Text | Google Scholar

Saeed, M. M., Bruen, M., and Asghar, M. N. (2002). A Review of Modelling Approaches to Simulate Saline-Upconing under Skimming Wells. Nord. Hydrol. 33, 165–188. doi:10.2166/nh.2002.0021

CrossRef Full Text | Google Scholar

Schmorak, S., and Mercado, A. (1969). Upconing of Fresh Water - Sea Water Interface below Pumping Wells, Field Study. Water Resour. Res. 5 (6), 1290–1311.

Google Scholar

Strack, O. D. L., and Ausk, B. K. (2015). A Formulation for Vertically Integrated Groundwater Flow in a Stratified Coastal Aquifer. Water Resour. Res. 51, 6756–6775. doi:10.1002/2015wr016887

CrossRef Full Text | Google Scholar

Verruijt, A. (1970). Theory of Groundwater Flow. London: Macmillan.

Google Scholar

Voss, C. I., and Souza, W. R. (1987). Variable Density Flow and Solute Transport Simulation of Regional Aquifers Containing a Narrow Freshwater-Saltwater Transition Zone. Water Resour. Res. 23 (10), 1851–1866. doi:10.1029/wr023i010p01851

CrossRef Full Text | Google Scholar

Werner, A. D., Bakker, M., Post, V. E. A., Vandenbohede, A., Lu, C., Ataie-Ashtiani, B., et al. (2013). Seawater Intrusion Processes, Investigation and Management: Recent Advances and Future Challenges. Adv. Water Resour. 51, 3–26. doi:10.1016/j.advwatres.2012.03.004

CrossRef Full Text | Google Scholar

Werner, A. D., Jakovovic, D., and Simmons, C. T. (2009). Experimental Observations of Saltwater Up-Coning. J. Hydrology 373, 230–241. doi:10.1016/j.jhydrol.2009.05.004

CrossRef Full Text | Google Scholar

Zhou, Q., Bear, J., and Bensabat, J. (2005). Saltwater Upconing and Decay beneath a Well Pumping above an Interface Zone. Transp. Porous Med. 61 (3), 337–363. doi:10.1007/s11242-005-0261-4

CrossRef Full Text | Google Scholar