Time Series Multi-Sensors of Interferometry Synthetic Aperture Radar for Monitoring Ground Deformation

A stack of images is a prerequisite for the multi-temporal interferometric synthetic aperture radar (MT-InSAR) due to the wrapped nature of the interferometric phase. Although the SBAS technique can relieve the requirement of the amount of SAR data, dozens of SAR acquisitions could be regarded as the minimum requirement. However, due to the limitation of the imaging capability of the spaceborne SAR system, the amount of available SAR data acquired from only one SAR sensor is often not enough to satisfy the requirement for phase unwrapping based on the Nyquist sampling assumption. Fortunately, there sometimes may be more than one SAR stack, that is, stacks of SAR data acquired from different SAR systems. In this study, we propose a methodology to detect ground deformation by combining multiple SAR images acquired from different satellite systems for MT-InSAR analysis. First, the low-pass deformation is estimated based on time series SAR acquisitions with low spatial resolution and long wavelengths such as ENVISAT ASAR (ASAR). This information is then incorporated into the processing of time series of SAR acquisitions with high spatial resolution and short wavelength, such as TerraSAR-X (TSX). Specifically, the low-pass deformation will be subtracted from each differential interferogram generated from short-wavelength SAR images, and the rest of the MT-InSAR analysis will be based on the double-differentiation interferograms. Then, the residual deformation will be calculated from these double-differentiation interferograms and together with the low-pass deformation forms the full deformation. As the principal component of deformation has already been subtracted, the phase gradient of those double-differentiated interferograms will be smooth enough to facilitate the phase unwrapping. Between January 2009 and September 2010, 14 ASAR images and 11 TSX images acquired from Tianjin, China are selected as the test data. A root means square error (RMSE) of 9.1 mm/year is achieved from 11 TSX images, while a root means square error of 3.7 mm/year is achieved from 14 ASAR images. However, an RMSE of 1.6 mm/year is achieved when integrating 11 TSX images and 14 ASAR images for MT-InSAR analysis. The experiments show that the proposed method can effectively detect ground deformation.

Introduction

Land subsidence, caused by mining and excessive extraction of groundwater, is a common hazard in contemporary society (Marghany, 2021; Marghany, 2022). Moreover, in coastal areas with low topography, land subsidence can cause more risky damages such as flooding and even inundation (Hu et al., 2009). Measurement of the magnitude of deformation is required to study the land subsidence and control its development.

Differential Synthetic Aperture Radar (DInSAR), a newly emerging space geodetic technique developed in the 1980s (Gabriel et al., 1989; Massonnet et al., 1993), has been proven as a powerful technique for mapping ground deformation caused by earthquake, landslide, and excessive extraction of underground water with high precision and spatial resolution over a large area. Nevertheless, DInSAR may fail due to low correlation caused by spatiotemporal baselines and atmospheric artifacts (Zebker and Villasenor, 1992; Zebker et al., 1997; Bamler and Hartl, 1998; Massonnet and Feigl, 1998; Hanssen et al., 1999; Li et al., 2004), particularly in vegetated areas. Marghany (Marghany, 2013 and Marghany, 2014) have presented two approaches to eliminate the temporal decorrelation to reduce phase unwrapping error.

Fortunately, it was found that some ground targets can maintain the characteristics of stable scattering over long intervals of time (Sousa et al., 2011). With the advantage of these coherent targets, several advanced approaches to multi-temporal InSAR (MT-InSAR) have been presented to overcome the technical limitations of DInSAR since the late 1990s (Ferretti et al., 2000; Ferretti et al., 2001; Berardino et al., 2002; Hooper et al., 2004; Lanari et al., 2004; Wegmüller et al., 2010).

These MT-InSAR approaches differ primarily in the algorithms of coherent target selection and deformation estimation. In some MT-InSAR algorithms, a priori information is required to model the deformation (Hooper et al., 2007). Only this scatterer, whose behavior of deformation is close to the predetermined model, will be identified as a coherent target, also referred to as a permanent scatterer (PS). In contrast, the Stanford Method for PS (StaMPS) algorithm, developed by Hooper et al., uses the spatial correlation of the interferogram phase to identify coherent targets, and it does not require prior knowledge of the variations of deformation in time series (Hooper et al., 2007). Moreover, it is found that the density of coherent targets identified by StaMPS is significantly increased in rural areas with few buildings (Sousa et al., 2011). Therefore, in this study, the StaMPS approach is used while the suburb of Tianjin is chosen as the study area.

The crucial limitation of the MT-InSAR, including the StaMPS, is the wrapped nature of the interferometric phase, which will introduce 2π-ambiguities to the unknown parameters to be estimated. Adding more information, such as an explicit functional model and prior information, to the MT-InSAR is one way to solve this impasse (Heuff and Hanssen, 2020). Dehghani et al. (2013) presented a method that combines DInSAR and Persistent Scatterer InSAR (PSI) to monitor severe ground subsidence. The linear term of subsidence was estimated using DInSAR based on the interferograms with small temporal baselines and then subtracted from all interferograms used for PSI analysis (Dehghani et al., 2013). However, lack of availability of SAR data with high coherent interferograms is mainly the limitation of this method (Sadeghi et al., 2013). In order to overcome this limitation, the periodogram approach is used to estimate the principal component of deformation (Sadeghi et al., 2013). This approach strongly depends on the discretization of the parameter in solution space. However, it is difficult to yield a unique solution as there are alternative solutions based on a different distribution of the unknown parameters (Kampes and Hanssen, 2004). Pawluszek-Filipiak and Borkowski (Pawluszek-Filipiak and Borkowski, 2020) present a method that adopts PSI and DInSAR to estimate the subsidence in the surrounding and central subsidence basins based on the same SAR dataset. Then, the PSI and DInSAR results are merged based on regularized spline functions, yielding the final ground deformation.

The objective of adding more information is to reduce the spatiotemporal variability of the interferometric phase. The interferometric phase will be smooth enough, and the phase gradients are small if the revisit time is short enough. In other words, the deformation can be accurately estimated by MT-InSAR without any additional information if the available SAR images are acquired with high temporal sampling. However, the number of available SAR images is often not enough to satisfy the requirement due to limited capability of the spaceborne sensor to collect SAR acquisitions.

Until now, many spaceborne SAR satellites, such as Envisat, ALOS-1/2, TSX, Tandem-X (TDX), COSMO-SkyMed (CSK), Radarsat-1/2, and Sentinel-1, have been launched, which allows us to observe the Earth with different wavelength, repeat time, spatial resolution, and incidence angle. With the advantage of an increasing number of SAR satellites, there may be more than one SAR stack, for example, several stacks of SAR datasets acquired from several SAR systems covering the same area.

In order to reduce the likelihood of ambiguity errors caused by severe deformation based on finite SAR data, we have developed a new methodology to integrate two different datasets, for example, ASAR with longer and TSX with shorter wavelength, for MT-InSAR analysis. First, the low-pass deformation pattern is estimated based on the time-series ASAR dataset, which represents an initial estimation (that is, the principal component) of the ground deformation. Then, this result will be subtracted from each interferogram generated from the TSX dataset to reduce the phase gradients and meet the Nyquist sampling criterion, and the rest of the MT-InSAR analysis will be based on these double-differentiated TSX interferograms. As the principal component of deformation has already been subtracted, the phase gradient of those double-differentiated TSX interferograms will be smooth enough to better facilitate the phase unwrapping. Therefore, the residual deformation could then be estimated more accurately and reliably from the time-series TSX dataset. As the final step, the residual deformation derived from TSX, together with that from ASAR, forms the full deformation. Through the synergic use of multi-frequency SAR images, the process of deriving ground deformation from time series InSAR analysis can be improved in terms of accuracy and robustness. In addition, the algorithm is capable of extending the applications of achieved SAR data on ground deformation monitoring, especially in the case that considering the historical deformation information. The experiments show that the proposed method can effectively detect the ground deformation with an accuracy of mm/yr by combining multi-sensor SAR data to reduce the phase unwrapping errors.

Methodology

StaMPS was designed by Hooper et al. (Hooper et al., 2007) to overcome the limitation of the absence of man-made buildings on most of the Earth’s surface and prior knowledge of the temporal behavior of the ground deformation, and it has been successfully applied in many cases lacking in anthropogenic features (Costantini et al., 2016; Tiwari et al., 2016; Dwivedi et al., 2017).

The small baseline method implemented in the standard StaMPS software, referred to as StaMPS-SB for simplicity, is used in the following study as there are only a few SAR acquisitions with irregular gaps. StaMPS-SB focuses on these pixels that show a slowly decorrelating filtered phase (SDFP) over a short interval of time to mitigate atmospheric effects and improve the coherence (Hooper, 2008). According to the way that StaMPS-SB selects SDFP pixels, some candidates will be first chosen based on amplitude dispersion with a relatively low threshold. Then, the final SDFP pixels will be selected through an iterative procedure calculating the noise level of each candidate.

As shown in (Hooper et al., 2007), the wrapped interferometric phase, ${\phi }_{x,i}$, of the $x\text{th}$ in the $i\text{th}$ flatted and topographically corrected interferogram can be expressed as the wrapped sum of five terms,

${\phi }_{x,i}=w\left\{{\varphi }_{D,x,i}+{\varphi }_{A,x,i}+{\varphi }_{S,x,i}+{\varphi }_{\theta ,x,i}+{\varphi }_{N,x,i}\right\},(1)$

where ${\varphi }_{D,x,i}$ is the phase contribution due to the movement along the line-of-sight (LoS) direction, ${\varphi }_{A,x,i}$ is the phase caused by changes in atmospheric delay between two SAR acquisitions, ${\varphi }_{S,x,i}$ is the residual phase due to inaccuracies of satellite position, ${\varphi }_{\theta ,x,i}$ is the residual phase due to the look angle error mainly caused by the inaccuracy of DEM such as SRTM-DEM which is usually used to correct the topographic phase, ${\varphi }_{N,x,i}$ is the phase noise term due to variability in scattering, thermal, decorrelation, etc., and $w\{\cdot \}$ is the wrapping operator.

The absolute phase difference between adjacent SDFP pixels may be larger than π due to the spatially uncorrelated component of the signal. Therefore, the spatially uncorrelated portion of ${\varphi }_{\theta ,x,i}$ should be estimated and subtracted from ${\phi }_{x,i}$ before phase unwrapping. The three-dimensional phase unwrapping algorithm adopted by StaMPS-SB contains two steps. First, the differential phase between adjacent pixels is unwrapped in the temporal domain under the Nyquist assumption that the differential phase is less than π. Then, the unwrapped differential phase is used to build a priori probability density functions (PDFs) in each interferogram. Also, these PDFs will be converted into cost functions and fed into the optimization routines of a two-dimensional statistical-cost network-flow algorithm to obtain the final unwrapped results (Hooper, 2010).

After unwrapping, the spatially correlated portion of ${\varphi }_{\theta ,x,i}$ can be estimated using the least squares solution. Then, the atmosphere ${\varphi }_{A,x,i}$ and the orbit errors ${\varphi }_{S,x,i}$ will be estimated by high-pass filtering in the temporal domain followed by low-pass filtering in the spatial domain. Finally, subtracting these nuisance terms leaves the deformation phase ${\varphi }_{D,x,i}$and the spatially uncorrelated errors which can be regarded as random noise.

The phase-unwrapping algorithm adopted by StaMPS-SB is typically based on the Nyquist sampling assumption that the differential phase between adjacent SDFP pixels is less than π. In order to satisfy this condition, the spatially uncorrelated portion of ${\varphi }_{\theta ,x,i}$ should be estimated and subtracted from the original signal before unwrapping. However, the deformation phase ${\varphi }_{D,x,i}$, if too large, can also lead to the differential phase being greater than π, especially when only a few SAR acquisitions are available.

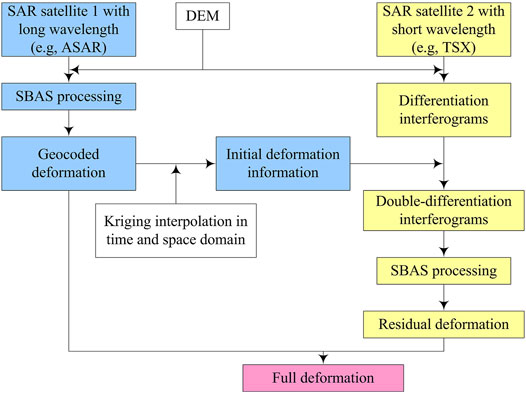
Fortunately, many spaceborne SAR satellites, such as Envisat, ALOS-1/2, TSX, and Sentinel-1., have been launched, which allows us to observe the Earth using multiple SAR sensors with different wavelength, repeat time, spatial resolution, and incidence angle. With the advantage of an increasing number of SAR satellites, there may be more than one SAR stack, for example, several stacks of SAR datasets acquired from different SAR systems covering the same area. In this study, we have developed a new StaMPS-SB procedure to integrate two different SAR datasets, that is, ASAR with longer and TSX with shorter wavelength for MT-InSAR analysis. The flowchart applied in this study is shown in Figure 1.

FIGURE 1

FIGURE 1. Flowchart of the implemented method.

In the proposed method, the deformation ${\varphi }_{D,x,i}$ can be expressed as

${\varphi }_{D,x,i}={\varphi }_{D,x,i}^{lp}+{\varphi }_{D,x,i}^{res},(2)$

where ${\phi }_{D,x,i}^{lp}$ is the low-pass (that is, principal) component deformation and ${\varphi }_{D,x,i}^{res}$ is the residual deformation.

First, ${\varphi }_{D,x,i}^{lp}$ is estimated based on the time-series ASAR dataset, which represents an initial estimation (that is, the principle component) of the ground deformation. Then, this information will be subtracted from each differential interferogram generated from the TSX dataset to fulfill the Nyquist sampling criterion.

It should be noted that the date of ASAR and TSX acquisitions is inconsistent. Also, the location of SDFPs selected from ASAR and TSX is also different from each other. Therefore, the deformation retrieved from ASAR has been first interpolated in time to match the date of TSX data. The quadratic polynomial was used to model the evolution of deformation in time. Then, the time-interpolated deformation was interpolated in the space domain using the Kriging method (Figure 2).

FIGURE 2

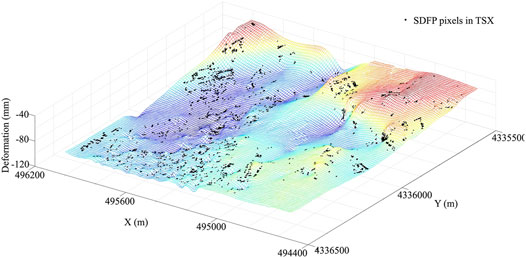
FIGURE 2. Extracting the deformation rate of SDFP pixels in TSX by Kriging interpolation in space. The mesh grid is generated from the deformation rate derived from ASAR images. The black dots denote the SDFP pixels selected from TSX acquisitions.

After interpolation processing in time and space followed by conversion of LoS direction, the low-pass deformation derived from ASAR can be incorporated into the processing of the TSX dataset according to the longitude and latitude of each SDFP. The matching error based on the geographical coordinates is about a few meters, which is acceptable as the deformation is spatially correlated.

Once subtracting the low-pass deformation, further analysis will be based on the double-differentiated TSX interferograms. As the principal component of ground deformation has already been subtracted, the double-differentiated phase will be smooth enough (Figure 3) to facilitate phase unwrapping. Therefore, the residual deformation could then be estimated more accurately and reliably from the time-series TSX dataset using the standard StaMPS-SB procedure. As the final step, the residual deformation derived from TSX, together with that from ASAR, forms the final deformation.

FIGURE 3

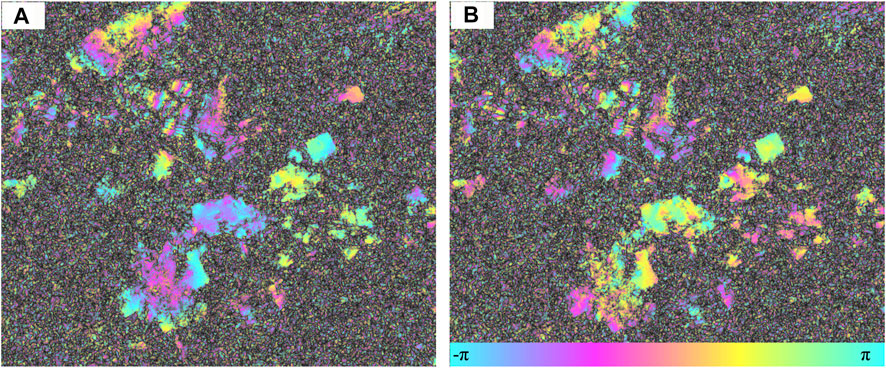
FIGURE 3. TSX interferogram (A) before and (B) after subtracting the initial deformation derived from ASAR acquisitions. The temporal and perpendicular baselines are 429 days and 25 m, respectively.

Study Area and Available Data

The suburb of western Tianjin, shown in Figure 4, is chosen as the study area. Tianjin, one of the four municipalities in China, is located in the North China Plain (Liu et al., 2014). Tianjin lies in a semi-arid and semi-humid climate region and suffers from water shortage as the annual precipitation is less than 500 mm. Due to the shortage of surface water sources and small amount of precipitation, the groundwater has been extracted to meet the agricultural and industrial needs for decades, which leads to severe ground subsidence with maximum cumulative subsidence of 3.22 m in history (Yi et al., 2011). The rates of ground subsidence have visibly increased since the 1950s, reaching 80–100 mm/year from 1967 to 1985 (He et al., 2006a; He et al., 2006b). After the 1980s, some measures, such as injection and restricting exploitation of groundwater, have been taken to reduce the subsidence rate. However, the ground subsidence rate is still very high (approximately 137 mm/year), and the phenomenon of subsidence has even worsened since 2010 (Zhu et al., 2015).

FIGURE 4

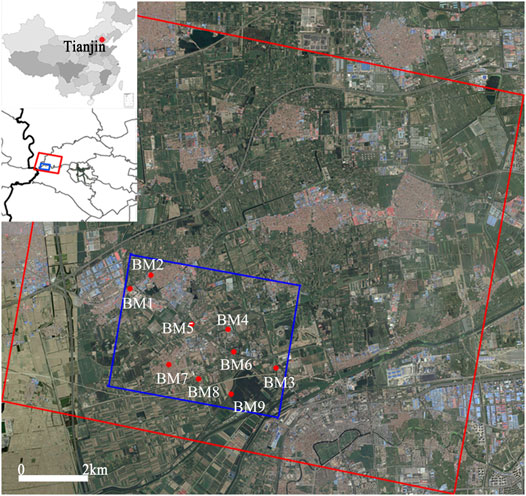
FIGURE 4. Location of the study area. The two insets depict the geographical location of Tianjin in China and the ground coverage of ASAR (red rectangle) and TSX (blue rectangle). The 22 BMs are used to evaluate the results derived from different methods.

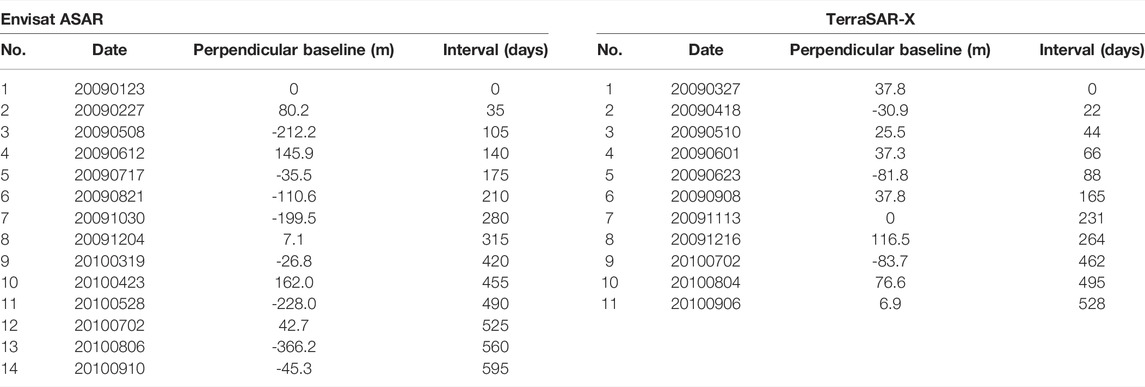
The performance of the presented method will be investigated using ASAR and TSX images with the ground coverage represented by red and blue rectangles, respectively, in Figure 4. The ASAR dataset, which consisted of 14 acquisitions spanning the intervals of time from 23 January 2009 to 10 September 2010 (see Table 1), was acquired in Stripmap mode with an incidence angle of 23° along descending orbit path direction. The ASAR acquisitions have a longer wavelength of about 5.6 cm and a coarser spatial resolution of approximately 5 m in the azimuth direction and 20 m in the ground range direction. The TSX dataset, which consisted of 11 acquisitions spanning the interval time from 27 March 2009 to 6 September 2010 (see Table 1), was acquired in Stripmap mode, with an incidence angle of 41° along descending orbit path direction. The TSX acquisitions have a shorter wavelength of about 3.1 cm and a higher spatial resolution of approximately 3.3 m in the azimuth direction and 2.7 m in the ground range direction.

TABLE 1

TABLE 1. Envisat ASAR and TerraSAR-X dataset.

There are nine leveling bench-marks (BM1-BM9) that are denoted by red dots in Figure 4, located within the study area. The subsidence rate, derived from the leveling data with high-level precision, can be used to evaluate the accuracy of the presented method.

Experimental Results and Discussion

Due to the irregular gaps in SAR acquisitions and serious ground deformation, the StaMPS-SB approach is used in the following experiments. Using the multi-master SBAS approach, only these interferograms with smaller geometric and temporal baselines than the predefined threshold are used for MT-InSAR analysis, which can improve the interferometric coherence by minimizing the decorrelation effects caused by geometric and temporal baselines.

It should be noted that the ground deformation, retrieved from the InSAR technique, is along the LoS direction and composed of the horizontal and uplifted components. However, previous studies (Yi et al., 2011; Zhu et al., 2015) have suggested that the deformation is dominated by vertical components as the ground displacement is mainly caused by over-extraction of groundwater in this study area. Therefore, the ground deformation along the vertical direction is simply obtained by dividing the cosine of the incidence angle.

Results From the Standard StaMPS-SB Approach Based on 11 TSX Acquisitions

In this section, the standard StaMPS-SB approach is used to estimate the ground deformation based on a few SAR acquisitions (i.e., 11 TSX images).

A fully connected network of interferograms is the foundation for MT-InSAR analysis using the StaMPS-SB approach. However, it is difficult to automatically achieve the optimal network due to the irregular intervals of the 11 TSX acquisitions, especially with a wide gap (198 days) between 16 December 2009 and 2 July 2010. Therefore, the interferograms were initially generated with a relatively low threshold, that is, specifying 250 m as the temporal baseline, 90 days as the geometric baselines, and 0.5 as the coherence threshold. Then, on the premise of a connected network, the interferograms with low coherence are manually removed from the network of interferograms. In addition, some interferograms with high coherence were manually generated and appended to the original stacks to increase the temporal sampling. A total of 24 interferograms with high coherence are finally obtained (seen in Figure 5A) and used for MT-InSAR analysis.

FIGURE 5

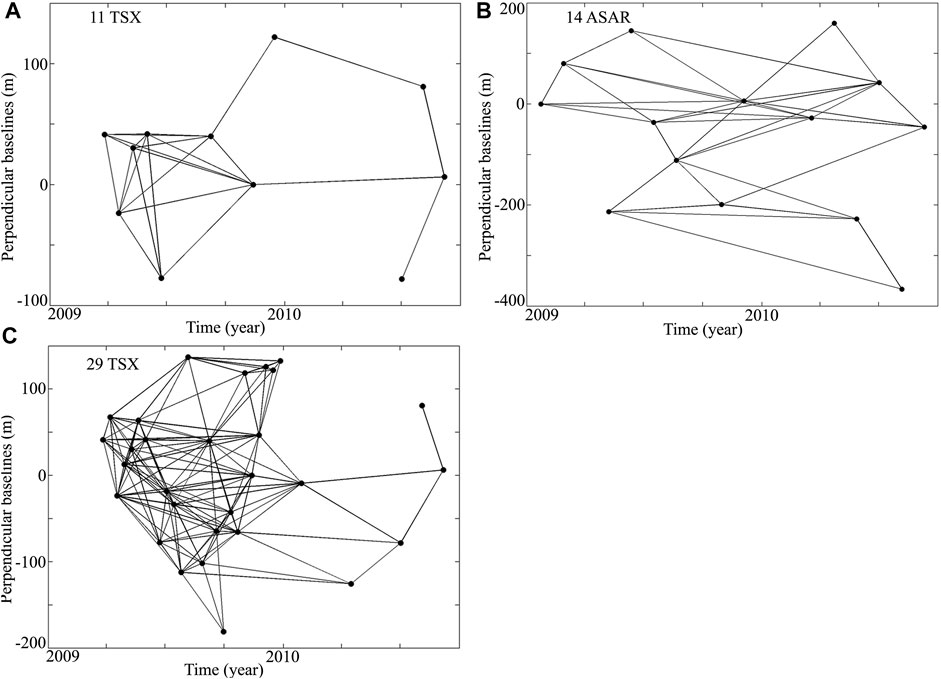
FIGURE 5. Distribution of temporal and perpendicular baselines of interferograms generated from (A) 11 TSX acquisitions, (B) 14 ASAR acquisitions, and (C) 29 TSX acquisitions. The black dots denote the SAR acquisitions; black lines denote the interferograms.

Then, the ground deformation is estimated using the standard StaMPS-SB approach based on the 24 interferograms. Finally, 39892 SDFP pixels have been detected. The mean rate of deformation is converted to the vertical direction and compared with leveling measurements. The result is shown in Figure 6A. The negative rate indicates that the study area suffered ground subsidence during this period. In addition, the spatial pattern of subsidence is almost similar to that detected by Zhu et al. (2015) except for the one in zone Z1. A maximum subsidence rate of 90 mm/year is detected in zone Z1 in this study based on 24 interferograms generated from 11 TSX acquisitions. However, a maximum subsidence rate of 110 mm/year is suggested by Zhu et al. (2015) based on 48 TSX acquisitions.

FIGURE 6

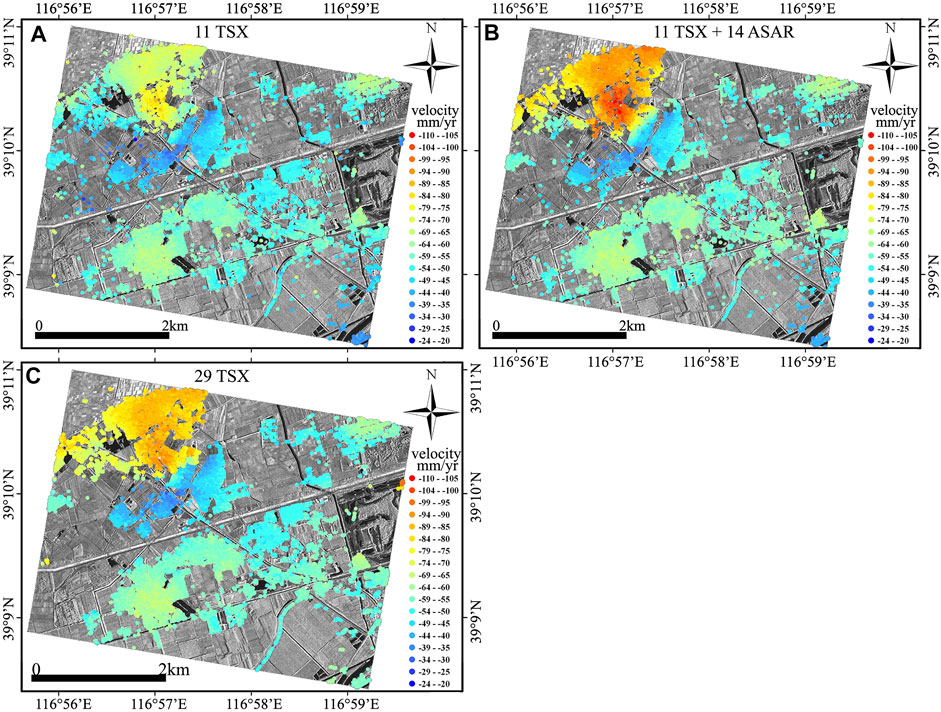
FIGURE 6. Deformation rate derived from (A) 11 TSX acquisitions using the standard StaMPS approach, (B) 11 TSX acquisitions and 14 ASAR acquisitions using the proposed method, and (C) 29 TSX acquisitions using the standard StaMPS approach.

Results From the Proposed Method Based on 11 TSX and 14 ASAR Acquisitions

In this section, the ground deformation is estimated using the proposed method by integrating 11 TSX and 14 ASAR acquisitions.

First, the ground subsidence is estimated using the standard StaMPS-SB approach based on 34 interferograms (as seen in Figure 5B) generated from 14 ASAR acquisitions. Also, the result is evaluated and validated by comparing it with the leveling measurements. The result is shown in Figure 7B. The comparison suggests an RMSE of 3.7 mm/yr and a correlation coefficient of 0.969, which demonstrates that the results derived from the ASAR dataset can be used as prior information. Then, the subsidence is subtracted from each interferogram generated from TSX acquisitions, and the residual deformation is extracted based on these double-differentiated TSX interferograms. Finally, 40147 SDFP pixels have been detected.

FIGURE 7

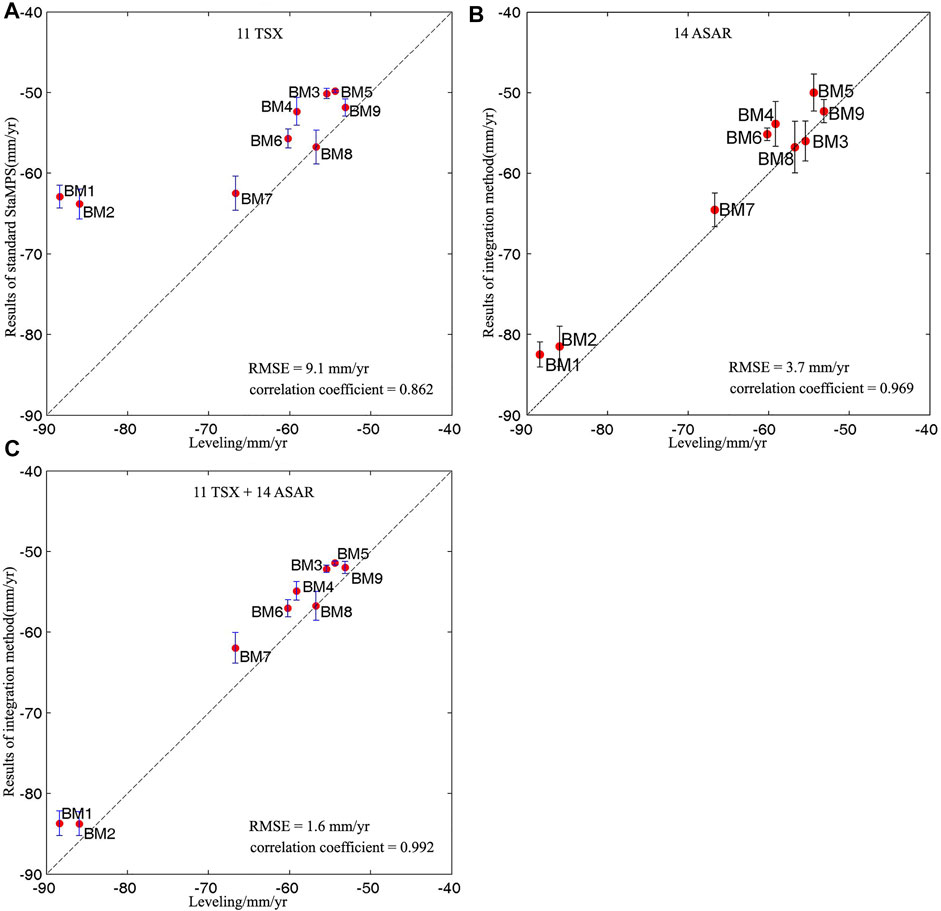
FIGURE 7. Comparison between deformation rates derived from leveling measurement and (A) 11 TSX acquisitions using standard StaMPS-SB, (B) 14 ASAR acquisitions using standard StaMPS-SB and (C) integration of 11 TSX acquisitions and 14 ASAR acquisitions using the proposed method.

Figure 6B depicts the final results derived from the proposed method. As shown in Figure 6, the spatial distribution of the ground subsidence derived from the proposed method agrees with that of 11 TSX images except the one in zone Z1. A subsidence rate of 80–110 mm/yr is detected by the proposed method in zone Z1, and the results agree with those of Zhu et al. (2015) and Luo et al. (2014).

Results From the Standard StaMPS-SB Approach Based on 29 TSX Acquisitions

In order to further evaluate the performance of the presented method, we collect 29 TSX acquisitions used by Zhu et al. (2015). These acquisitions are acquired during the same period as the 11 TSX (i.e., from 27 March 2009 to 6 September 2010). 145 interferograms (as seen in Figure 5C) with a maximum temporal interval of 264 days and geometrical baselines of 117 m are generated based on the 29 acquisitions. Also, the ground subsidence is estimated using the standard StaMPS-SB approach and compared with that from the presented method. The spatial distribution of the subsidence rate is shown in Figure 6C.

Clearly, in Figure 6, the results obtained from the proposed method based on the integration of 11 TSX and 14 ASAR acquisitions (Figure 6B) agree with those of the standard StaMPS-SB approach based on 29 TSX acquisitions (Figure 6C).

Discussion

This section is devoted to analyzing the performance of the proposed method by comparing the results with the leveling measurements.

Comparison Between the Leveling Measurements and the Results From 11 TSX Acquisitions

In order to quantitatively evaluate the performance of the standard StaMPS-SB approach with a few TSX acquisitions, the ground subsidence derived from 11 TSX acquisitions is compared with leveling measurements. Also, the results are shown in Figure 7A. It should be noted that the InSAR-derived subsidence rate is estimated by calculating the mean of the rate of all the SDFP pixels located within a 50 m radius of each leveling bench-marks (BM1–BM9). One standard deviation calculated from these SDFP pixels is also represented by the error bar in Figure 7A.

It can be seen from Figure 7A that the differences between these two distinct measurements are slight (about 5 mm/year) in BM3–BM9, where the rate of ground subsidence is less than 70 mm/year. The slight differences may result from some uncertainties, such as temporal uncertainty due to the different temporal resolution of distinct data, positional uncertainty due to inaccurate coordinate of leveling bench-marks and SDFP pixels, and the uncertainty caused by the conversion of ground subsidence from the LoS direction to the vertical direction.

However, there are significant differences between the two distinct measurements in BM1 (with a difference of 25.5 mm/year) and BM2 (with a difference of 22.1 mm/year), both of which are located in zone Z1. The subsidence is seriously underestimated using the standard StaMPS-SB approach based on the 11 TSX acquisitions. The statistical calculation between the InSAR-derived results and the leveling measurements suggests that the RMSE is up to 9.1 mm/yr, while the correlation coefficient is only 0.862.

Previous studies (Luo et al., 2014; Zhu et al., 2015) show that the ground subsidence is serious in zone Z1, where the maximum rate of subsidence is up to 110 mm/year. In order to detect the serious subsidence, more SAR acquisitions are needed for the standard StaMPS-SB approach to satisfy the assumption that the deformation is strongly correlated in space within a proper distance and can be accurately estimated using the band-pass filtering method. In addition, more SAR acquisitions are also needed to smooth the phase gradient as almost all phase unwrapping methods are based on the assumption that the interferometric phase field varies slowly. However, as only 11 TSX acquisitions are available, the ground subsidence is seriously underestimated using the standard StaMPS-SB approach.

Comparison Between the Leveling Measurements and the Results From 11 TSX and 14 ASAR Acquisitions

For further validation, the subsidence rate obtained from the proposed method is also compared with the leveling measurements, and the linear regression between these two measurements is calculated and shown in Figure 7B. Compared with that of the standard StaMPS-SB, the statistical calculation suggests that the RMSE and maximum difference reduce from 9.1 mm/yr to 1.6 mm/yr and 25.5 mm/yr to 4.7 mm/yr, respectively. Moreover, the correlation coefficient increases from 0.862 to 0.992 at the same time. The comparison demonstrates a significant improvement in the precision of deformation monitoring, which suggests that high-accuracy subsidence can still be achieved from a few TSX images by integrating with ASAR images.

In addition, it can also be seen from Figure 6B that although the accuracy of deformation has been improved, the subsidence rate on all nine benchmarks derived from the proposed method is less than the leveling measurements. These differences may be caused by the error of leveling measurement on BM8 which has been selected as the reference point to calibrate the InSAR results and the inaccurate location of BM8 as well.

In addition, more SDFPs, that is, 40147 SDFPs have been finally detected. According to the method that StaMPS-SB selects SDFP, some candidates will be first selected based on amplitude dispersion. Then, the candidates will be filtered in a small window, such as 50 m × 50 m, to determine the spatially correlated phase. If the difference of deformation between one pixel and others in the small patch is much greater, this pixel, even if it has a very stable phase response in all interferograms, will also be discarded.

Comparison Between the Leveling Measurements and the Results From 29 TSX Acquisitions

The comparison with leveling measurements suggests a correlation coefficient of 0.979 and an RMSE of 3.0 mm/year. Both the statistical analyses demonstrate that the results obtained from 29 TSX images can be used to evaluate the performance of the proposed method.

There are 33087 common SDFP pixels between the ones identified based on 11 TSX acquisitions and those based on 29 TSX acquisitions. Then, we compare the subsidence rate correspondence to these common SDFP pixels. The results are shown in Figure 8A. It can be seen from Figure 8A that there is a significant bias (about 20 mm/yr) between these two measurements. The difference of rate in about 22% of common SDFP pixels is more than 10 mm/yr, which results in a low correlation coefficient of 0.86 and a high RMSE of 7.4 mm/yr. The subsidence derived from 11 TSX acquisitions is underestimated when the deformation velocity reaches over 70 mm/yr in this study. This can be explained by the inference mentioned before, that is, the large deformation cannot be accurately estimated if there are no adequate acquisitions.

FIGURE 8

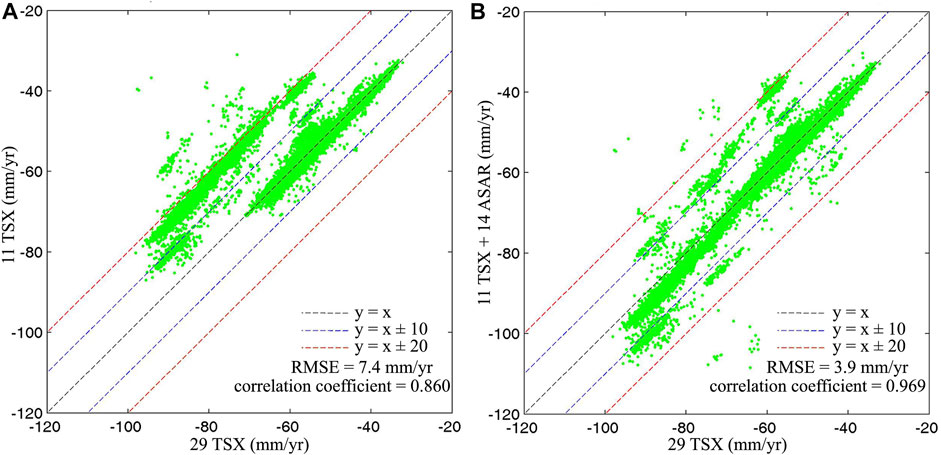
FIGURE 8. Comparison between deformation rates derived from 29 TSX acquisitions and (A) 11 TSX acquisitions using standard StaMPS-SB and (B) integration of 11 TSX acquisitions and 14 ASAR acquisitions using the proposed method.

There are 33306 common SDFP pixels between the ones identified using the proposed method based on the integration of 11 TSX and 14 ASAR acquisitions and those using the standard StaMPS-SB approach based on 29 TSX acquisitions. The subsidence rates in correspondence to these common SDFP pixels are shown in Figure 8B. Compared with the results shown in Figure 8A, the difference between the results derived from the integration of 11 TSX and 14 ASAR acquisitions and that from the 29 TSX acquisitions is significantly reduced. The proportion of the difference with more than 10 mm/yr decreases from 22% to 4.5%. In a few SDFP pixels with a proportion of less than 0.4%, the difference in subsidence rate is more than 20 mm/yr, which may be caused by the errors in initial subsidence information obtained from ASAR data. However, the statistical calculation shows a significant improvement in the correlation coefficient which increases from 0.86 to 0.969, and in the RMSE, which decreases from 7.4 mm/yr to 3.9 mm/yr.

Comparison of Time Series Displacement

Figure 9 shows the evolution of the displacements of SDFPs located within a radius of 50 m of the eight benchmarks. It is difficult to accurately retrieve absolute time-series displacements because only two periods of leveling measurements are available. Therefore, the relative time series displacements at BM1 to BM9 are calculated by reference to these SDFPs near the BM8. It can be seen from Figure 9 that the displacement will be underestimated if only 11 TSX data are available, especially when the actual displacement is relatively large. However, the presented method can effectively detect the time-series displacement by combining multi-sensor SAR data. In addition, the time series displacement derived from the present method is smoother than the other, which is due to the low-pass filtering in the time domain to extract the residual displacement.

FIGURE 9

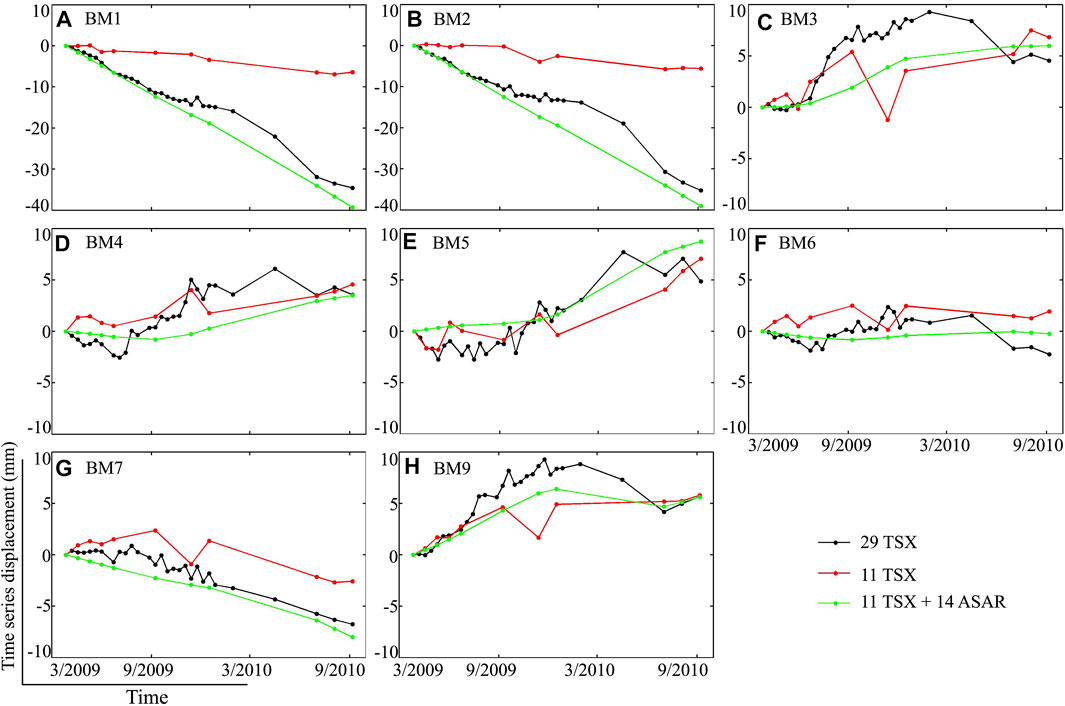
FIGURE 9. Time series of displacement at (A–G) BM1 ∼ BM7 and (H) BM9 derived from three sets of SAR datasets, that is, the 29 TSX acquisitions only, the 11 TSX acquisitions only, and the combination of 11 TSX and 14 ASAR acquisitions. It should be noted that the time series of displacement is relative to BM8.

Overall, the validation of the accuracies using the leveling measurements and the results obtained by different methods with different numbers of SAR acquisitions verify the ability of the proposed method to detect the deformation with high accuracy through a few high spatial resolutions of TSX integrated with the coarser resolution ASAR acquisitions.

Conclusion

In this study, a methodology integrating different SAR acquisitions derived from different SAR satellites with different wavelengths has been presented for MT-InSAR analysis. By integrating multiple SAR sensors, the presented method can overcome the limitation of imaging capability of a single SAR satellite.

We estimate the ground displacement using 11 TSX acquisitions and 14 ASAR acquisitions. In addition, we also estimate the ground displacement by integrating 11 TSX and 14 ASAR acquisitions based on the presented method. Both the InSAR-derived displacements are compared with the leveling data. The statistical calculation shows that the correlation is 0.862, 0.969, and 0.992 and the RMSE is 9.1 mm/yr, 3.7 mm/yr, and 1.6 mm/yr.

In addition, we estimate the ground displacement using 29 TSX acquisitions over the same period and compare the results with that estimated from the integration of 11 TSX and 14 ASAR acquisitions. The correlation coefficient is 0.969 between the two distinct measurements. Furthermore, the RMSE is 3.9 mm/yr, which suggests that the accuracy of the InSAR-derived displacement using the integration of two small SAR datasets coincided with that of one large dataset.

The results from these experiments suggest that the presented method is capable of estimating ground displacement by integrating the datasets from multiple SAR sensors. Still, the presented method can extend the applications of archived SAR data on ground deformation monitoring and will potentially play an important role in the case of insufficient scenes of the image from a single SAR sensor.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

CZ and JZ initiated the study; CZ and SL analyzed the data; CZ provided the software and wrote the manuscript. SL, WW, and LZ provided advice and reviewed the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This research has been supported by the National Natural Science Foundation of China (41901373 and 41877283), the Natural Science Foundation of Hunan Province (grant no. 2019JJ50190), and the Science and Technology Innovation Program of Hunan Province (2021RC4037).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank the StaMPS team for providing the software and the ESA for providing the SAR data. The authors would also like to thank the reviewers for their careful work and insightful suggestions.

References

Bamler, R., and Hartl, P. (1998). Synthetic Aperture Radar Interferometry. Inverse Probl. 14 (4), R1–R54. doi:10.1088/0266-5611/14/4/001

CrossRef Full Text | Google Scholar

Berardino, P., Fornaro, G., Lanari, R., and Sansosti, E. (2002). A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 40 (11), 2375–2383. doi:10.1109/tgrs.2002.803792

CrossRef Full Text | Google Scholar

Costantini, F., Mouratidis, A., Schiavon, G., and Sarti, F. (2016). Advanced InSAR Techniques for Deformation Studies and for Simulating the PS-Assisted Calibration Procedure of Sentinel-1 Data: Case Study from Thessaloniki (Greece), Based on the ENVISAT/ASAR Archive. Int. J. Remote Sens. 37 (4), 729–744. doi:10.1080/01431161.2015.1134846

CrossRef Full Text | Google Scholar

Dehghani, M., Valadan Zoej, M. J., Hooper, A., Hanssen, R. F., Entezam, I., and Saatchi, S. (2013). Hybrid Conventional and Persistent Scatterer SAR Interferometry for Land Subsidence Monitoring in the Tehran Basin, Iran. ISPRS J. Photogramm. Remote Sens. 79 (4), 157–170. doi:10.1016/j.isprsjprs.2013.02.012

CrossRef Full Text | Google Scholar

Dwivedi, R., Narayan, A. B., Tiwari, A., Singh, A. K., and Dikshit, O. (2017). Optimal Estimation of Interferometric Phase for Measuring Surface Deformation. Int. J. Remote Sens. 38 (5-6), 1339–1349. doi:10.1080/01431161.2017.1280627

CrossRef Full Text | Google Scholar

Ferretti, A., Prati, C., and Rocca, F. (2000). Nonlinear Subsidence Rate Estimation Using Permanent Scatterers in Differential SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 38 (5), 2202–2212. doi:10.1109/36.868878

CrossRef Full Text | Google Scholar

Ferretti, A., Prati, C., and Rocca, F. (2001). Permanent Scatterers in SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 39 (1), 8–20. doi:10.1109/36.898661

CrossRef Full Text | Google Scholar

Gabriel, A. K., Goldstein, R. M., and Zebker, H. A. (1989). Mapping Small Elevation Changes over Large Areas: Differential Radar Interferometry. J. Geophys. Res. 94 (B7), 9183–9191. doi:10.1029/jb094ib07p09183

CrossRef Full Text | Google Scholar

Hanssen, R. F., Weckwerth, T. M., Zebker, H. A., and Klees, R. (1999). High-Resolution Water Vapor Mapping from Interferometric Radar Measurements. Science 283 (5406), 1297–1299. doi:10.1126/science.283.5406.1297

PubMed Abstract | CrossRef Full Text | Google Scholar

He, Q. C., Liu, W. B., and Li, Z. M. (2006a). Land Subsidence Survey and Monitoring in the NorthChina Plain. Geol. J. China Univ. 12, 195–209. (In Chinese.). doi:10.3969/j.issn.1006-7493.2006.02.006

CrossRef Full Text | Google Scholar

He, Q. C., Ye, X. B., Li, Z. M., and Liu, W. B. (2006b). The Status and Prevention Strategy of LandSubsidence in China. Geol. J. China Univ. 12, 161–168. (In Chinese.). doi:10.16108/j.issn.1006-7493.2006.02.002

CrossRef Full Text | Google Scholar

Heuff, F. M. G., and Hanssen, R. F. (2020). “InSAR Phase Reduction Using the Remove-Compute-Restore Method,” in IGARSS 2020 - 2020 IEEE International Geoscience and Remote Sensing Symposium, Waikoloa, USA, September 26–October 2, 2020.

CrossRef Full Text | Google Scholar

Hooper, A. (2008). A Multi-Temporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 35 (16), 96–106. doi:10.1029/2008gl034654

CrossRef Full Text | Google Scholar

Hooper, A. (2010). “A Statistical-Cost Approach to Unwrapping the Phase of InSAR Time Series,” in Processing of Fringe 2009 Workshop, Frascati, Italy, November 30–December 4, 2009, 667, 1–5.

Google Scholar

Hooper, A., Segall, P., and Zebker, H. (2007). Persistent Scatterer Interferometric Synthetic Aperture Radar for Crustal Deformation Analysis, with Application to Volcán Alcedo, Galápagos. J. Geophys. Res. Solid Earth 112, B04707. doi:10.1029/2006jb004763

CrossRef Full Text | Google Scholar

Hooper, A., Zebker, H., Segall, O., and Kampes, B. (2004). A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers. Geophys. Res. Lett. 31, 611–615. doi:10.1029/2004gl021737

CrossRef Full Text | Google Scholar

Hu, B., Zhou, J., Wang, J., Chen, Z., Wang, D., and Xu, S. (2009). Risk Assessment of Land Subsidence at Tianjin Coastal Area in China. Environ. Earth Sci. 59 (2), 269–276. doi:10.1007/s12665-009-0024-6

CrossRef Full Text | Google Scholar

Kampes, B. M., and Hanssen, R. F. (2004). Ambiguity Resolution for Permanent Scatterer Interferometry. IEEE Trans. Geosci. Remote Sens. 42 (11), 2446–2453. doi:10.1109/tgrs.2004.835222

CrossRef Full Text | Google Scholar

Lanari, R., Mora, O., Manunta, M., Mallorqui, J. J., Berardino, P., and Sansosti, E. (2004). A Small-Baseline Approach for Investigating Deformations on Full-Resolution Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 42 (7), 1377–1386. doi:10.1109/tgrs.2004.828196

CrossRef Full Text | Google Scholar

Li, Z. W., Ding, X. L., and Liu, G. X. (2004). Modeling Atmospheric Effects on InSAR with Meteorological and Continuous GPS Observations: Algorithms and Some Test Results. J. Atmos. Sol.-Terr. Phys. 66 (11), 907–917. doi:10.1016/j.jastp.2004.02.006

CrossRef Full Text | Google Scholar

Liu, G., Jia, H., Nie, Y., Li, T., Zhang, R., Yu, B., et al. (2014). Detecting Subsidence in Coastal Areas by Ultrashort-Baseline TCPInSAR on the Time Series of High-Resolution TerraSAR-X Images. IEEE Trans. Geosci. Remote Sens. 52 (4), 1911–1923. doi:10.1109/tgrs.2013.2256428

CrossRef Full Text | Google Scholar

Luo, Q., Perissin, D., Lin, H., Zhang, Y., and Wang, W. (2014). Subsidence Monitoring of Tianjin Suburbs by TerraSAR-X Persistent Scatterers Interferometry. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 7 (5), 1642–1650. doi:10.1109/jstars.2013.2271501

CrossRef Full Text | Google Scholar

Marghany, M. (2021). Advanced Algorithms for Mineral and Hydrocarbon Exploration Using Synthetic Aperture Radar. San Diego: Elsevier.

Google Scholar

Marghany, M. (2013). DInSAR Technique for Three-Dimensional Coastal Spit Simulation from Radarsat-1 Fine Mode Data. Acta Geophys. 61 (2), 478–493. doi:10.2478/s11600-012-0061-5

CrossRef Full Text | Google Scholar

Marghany, M. (2014). Hybrid Genetic Algorithm of Interferometric Synthetic Aperture Radar for Three-Dimensional Coastal Deformation. SoMeT 29, 116–131. doi:10.3233/978-1-61499-434-3-116

CrossRef Full Text | Google Scholar

Marghany, M. (2022). Remote Sensing and Image Processing in Mineralogy. Boca Raton, USA: CRC Press.

Google Scholar

Massonnet, D., and Feigl, K. L. (1998). Radar Interferometry and its Application to Changes in the Earth's Surface. Rev. Geophys. 36 (4), 441–500. doi:10.1029/97rg03139

CrossRef Full Text | Google Scholar

Massonnet, D., Rossi, M., Carmona, C., Adragna, F., Peltzer, G., Feigl, K., et al. (1993). The Displacement Field of the Landers Earthquake Mapped by Radar Interferometry. Nature 364 (6433), 138–142. doi:10.1038/364138a0

CrossRef Full Text | Google Scholar

Pawluszek-Filipiak, K., and Borkowski, A. (2020). Monitoring Mining-Induced Subsidence by Integrating Differential Radar Interferometry and Persistent Scatterer Techniques. Eur. J. Remote Sens. 54 (16), 1–13. doi:10.1080/22797254.2020.1759455

CrossRef Full Text | Google Scholar

Sadeghi, Z., Valadan Zoej, M. J., and Dehghani, M. (2013). An Improved Persistent Scatterer Interferometry for Subsidence Monitoring in the Tehran Basin. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 6 (3), 1571–1577. doi:10.1109/jstars.2013.2259221

CrossRef Full Text | Google Scholar

Sousa, J. J., Hooper, A. J., Hanssen, R. F., Bastos, L. C., and Ruiz, A. M. (2011). Persistent Scatterer InSAR: A Comparison of Methodologies Based on a Model of Temporal Deformation vs. Spatial Correlation Selection Criteria. Remote Sens. Environ. 115 (10), 2652–2663. doi:10.1016/j.rse.2011.05.021

CrossRef Full Text | Google Scholar

Tiwari, A., Dwivedi, R., Dikshit, O., and Singh, A. K. (2016). A Study on Measuring Surface Deformation of the L'aquila Region Using the Stamps Technique. Int. J. Remote Sens. 37 (3-4), 819–830. doi:10.1080/01431161.2015.1136449

CrossRef Full Text | Google Scholar

Wegmüller, U., Walter, D., Spreckels, V., and Werner, C. (2010). Nonuniform Ground Motion Monitoring with TerraSAR-X Persistent Scatterer Interferometry. IEEE Trans. Geoscience Remote Sens. 48 (2), 895–904. doi:10.1109/TGRS.2009.2030792

CrossRef Full Text | Google Scholar

Yi, L., Zhang, F., Xu, H., Chen, S. J., Wang, W., and Yu, Q. (2011). Land Subsidence in Tianjin, China. Environ. Earth Sci. 62 (6), 1151–1161. doi:10.1007/s12665-010-0604-5

CrossRef Full Text | Google Scholar

Zebker, H. A., Rosen, P. A., and Hensley, S. (1997). Atmospheric Effects in Interferometric Synthetic Aperture Radar Surface Deformation and Topographic Maps. J. Geophys. Res. 102 (B4), 7547–7563. doi:10.1029/96jb03804

CrossRef Full Text | Google Scholar

Zebker, H. A., and Villasenor, J. (1992). Decorrelation in Interferometric Radar Echoes. IEEE Trans. Geosci. Remote Sens. 30 (5), 950–959. doi:10.1109/36.175330

CrossRef Full Text | Google Scholar

Zhu, C., Zhang, Y., Zhang, J., Zhang, L., Long, S., and Wu, H. (2015). Recent Subsidence in Tianjin, China: Observations from Multi-Looking TerraSAR-X InSAR from 2009 to 2013. Int. J. Remote Sens. 36 (23), 5869–5886. doi:10.1080/01431161.2015.1109729

CrossRef Full Text | Google Scholar