Social cost of carbon: A revisit from a systems analysis perspective

The social cost of carbon (SCC) is estimated by integrated assessment models (IAMs) and is widely used by government agencies to value climate policy impacts. Although there is an ongoing debate about obtained numerical estimates and related uncertainties, little attention has been paid so far to the SCC calculation method itself. This work attempts to fill the gap by providing the theoretical background and economic interpretation of the SCC calculation approach implemented in the DICE (Dynamic Integrated Climate-Economy) IAM. Our analysis indicates that the present calculation method is unable to reflect the linkages between two key IAM components—complex interconnected systems—climate and economy, both influenced by emission abatement policies. Within the modeling framework of DICE, the presently estimated SCC valuates emissions, which are beyond policy control, against consumption of products, which cannot be produced by the economy. This makes the SCC irrelevant for application in climate-economic policies and, therefore, calls for a replacement by a more appropriate indicator. An apparent SCC alternative, which can be considered for policy formulation, is the direct output of the DICE model, the socially optimal marginal abatement cost (SMAC), which corresponds to technological possibilities at the optimal level of carbon emissions abatement. In policymaking, because of the revealed SCC deficiency, great attention needs to be paid to the use of estimates obtained earlier.

1 Introduction

The concept of the social cost of carbon (SCC) appeared in the early publications of Nordhaus (2019) and dates back to the first works on the Dynamic Integrated Climate-Economy (DICE) integrated assessment model (IAM) (DICE, 2022). The SCC gained momentum for policymaking in the 2000s (Pearce, 2003) and since then has been widely used by a large number of organizations, for example, the World Bank (World bank, 2017), US EPA (Technical Support Document, 2010), and UK DEFRA (Pearce, 2003). Although according to more recent publications by Nordhaus (2019) the SCC did not play a decisive role in the evaluation of the US climate-related policies, an earlier publication by Nordhaus (2017) reported “regulations with more than $1 trillion of benefits have been written for the United States that use the SCC in their economic analysis.” The SCC concept is well integrated within the current policy context and, therefore, plays an important role in the assessments of climate-related action. The United States Government Interagency Working Group on the social cost of carbon is using the SCC according to the respective regulation (Technical Support Document, 2010), relying for the purposes of the SCC estimation on the FUND¹ (Anthoff and Tol, 2013; Github, 2022) and PAGE² (Hope, 2008; Github, 2009; Hope, 2013; Frances et al., 2018) models along with the DICE model. There have been other approaches to SCC calculation presented in the literature, for example, those included in Katharine et al. (2018), Rennert et al. (2021), Jin et al. (2020), and Gillingham et al. (2018).

Numerical estimates of the SCC are highly uncertain due to uncertainties in the structure and parameters of respective methods and models, which are employed to assess the SCC. Such parameters include time discounting, climate sensitivity, and—from the structural perspective—the form of representation of the climate system and its parametrization, the form and parametrization of damage functions, and the form and parametrization of welfare function. Various aspects related to uncertainty in SCC estimates in different settings are covered by a large body of the literature, for example, those included in Technical Support Document (2010), Nordhaus (2017), Rennert et al. (2021), Rose et al. (2017), Gillingham et al. (2018), Nordhaus (2014), and Scovronick et al. (2017). Publications hinging on the previously developed methodology call for a modular modeling approach (National Academies of Sciences, Engineering, and Medicine, 2017) and recommend a roadmap for improving numerical SCC estimates embedded in the policy context (Wagner et al., 2021).

Unlike previous publications, in this study, the analysis is focused on the concept of the SCC (as implemented in the DICE model) rather than on numerical values that it can produce. We have selected the DICE model for several reasons: the historical importance of DICE in creating the SCC concept, the prominent use of DICE for SCC estimations in policymaking, DICE’s integrated approach to linking climate with endogenous economic production, and the possibility of drawing implications for other modeling approaches.

There are few definitions of SCC in the literature, for example, “the social cost of carbon refers to the estimate of the monetary value of world-wide damage caused by anthropogenic CO₂ emissions” (Pearce, 2003), “the social cost of carbon is defined as the monetary value of the damage caused by emitting one more ton of carbon at some point of time” (Pearce, 2003), “it is the change in the discounted value of economic welfare from an additional unit of CO₂-equivalent emissions” (Nordhaus, 2019), “it is the change in the discounted value of the utility of consumption per unit of additional emissions, denominated in terms of current consumption” (Nordhaus, 2014), or the “SCC estimates the dollar value of reduced climate change damages associated with a one-metric-ton reduction in carbon dioxide (CO₂) emissions” (Pizer et al., 2014) to name a few. Here, among the definitions, those by Pearce (2003) are more explicit on the intended meaning of the SCC by stating the anthropogenic nature of the emissions (as these are supposed to be subject of climate policies where the SCC is employed), while other formulations are slack on this by not specifying the emissions’ nature.

The DICE model can maximize social utility by finding an optimal level of carbon emissions abatement and—corresponding to that level—socially optimal marginal abatement cost (SMAC)³, which is the direct output of DICE. As opposed to SMAC, the SCC is an additional calculation on top of DICE outputs—it is a ratio between the so-called “marginal” values corresponding to the model’s emissions and consumption equations⁴. As explained by Nordhaus (2014), “the ratio calculates the economic impact of a unit of emissions in terms of t-period consumption as a numéraire”.

A standard DICE 2016 model⁵ run produces different SCC and SMAC values for the tail of the trajectory; see Figure 1A.

The difference between the SCC and SMAC, generally speaking, is not confined to the tail of the optimal trajectory. The same model, therefore, with the exception that per-period industrial emissions are limited to 70% of those optimal in the standard DICE 2016 run, produces visibly different SCC and SMAC outputs also at the head of the optimal trajectory; see Figure 1B. The difference between SCC and SMAC can be positive or negative, as evidenced by these figures. The moment in time when this difference becomes noticeably large can be rather close to the beginning of the modeling time interval, as demonstrated by results obtained from a modified version of the DICE 2016 model where only temperature constraint T < 2.4°C is added and the rest of the model is kept unchanged⁶; see Figure 1C, D.

FIGURE 1

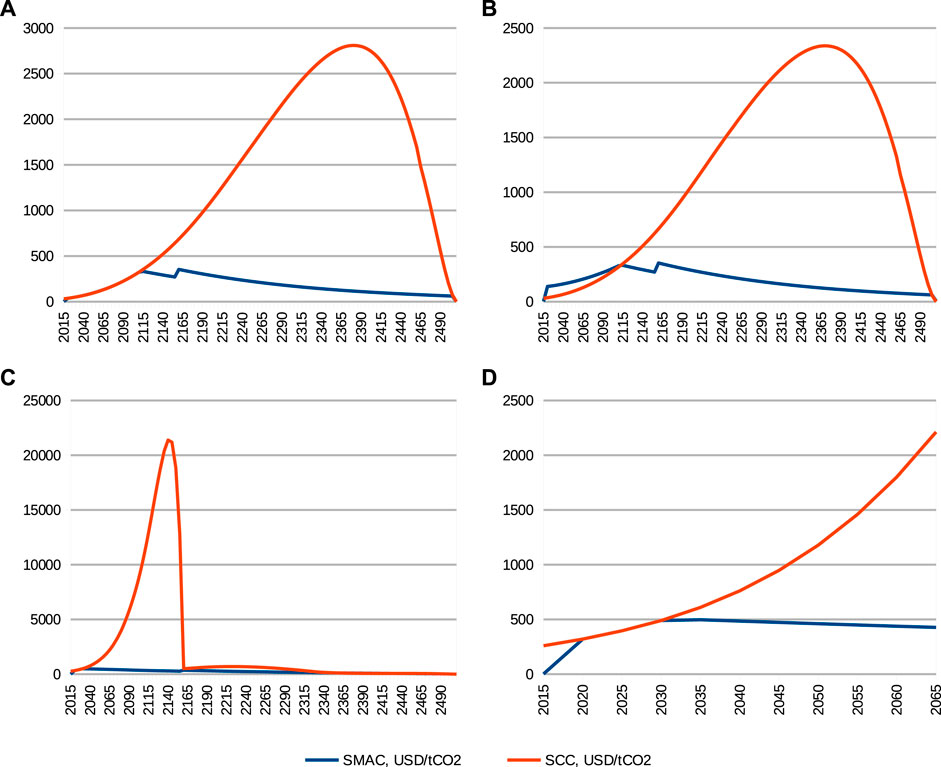
FIGURE 1. Social cost of carbon (SCC) and socially optimal marginal abatement cost of carbon (SMAC) as estimated by (A) the unmodified DICE 2016 model, (B) DICE 2016 model with a 70% cap on industrial emissions (C) DICE 2016 model with added temperature constraint T < 2.4°C, and (D) same as (C) yet zoomed into a shorter 50-year time period 2015–2065.

Although SMAC is the direct result of the DICE’s social welfare optimization, the SCC is a result of an ad hoc calculation, yet both correspond to the same optimal solution of the model. Both SMAC and the SCC are expressed in the same units of US dollars per ton of CO₂ and represent cost of carbon associated, respectively, with abating or emitting one ton of CO₂ at an optimal level of abatement in a particular time period. Intuitively, one may expect that at an optimal level of abatement, these costs will be equal⁷, which is not the case as shown in Figure 1. So the challenging questions for the analysis that follows are 1) why there is a numerical difference between SMAC and the SCC? and 2) what implications does this difference have for policymaking?

Unfortunately, the literature does not say anything clearly on this subject and therefore does not help answering these two questions. For example, the statement that “With an optimized climate policy (abstracting away from complications due to tax or regulatory distortions or inconsistent treatment in different sectors), the SCC will equal the carbon price; this in turn is equal to the marginal cost of emissions reduction” (Nordhaus, 2014) complies with the intuition referred to earlier but contradicts the fact of the difference between SCC and SMAC shown in Figure 1. Additionally, the statement that “the marginal social cost of carbon is the marginal damage caused at the optimal level of abatement” (Pearce, 2003) refers to “damage” and therefore does not inform the relationship between SCC and SMAC. Despite the lack of clarity, policymakers are keen on employing the SCC for various reasons. Therefore, it is of paramount importance to clarify the meaning of the SCC, as manifested by its estimation methodology.

2 Definition and calculation

The SCC in DICE is a combination of two indirect products of the model—two so-called “marginal” values that correspond to two specific model equations and stem from the computational method of finding a solution to the optimization problem. These two marginal values correspond to 1) the emissions equation and 2) the consumption equation in the mathematical formulation of the DICE optimization problem⁸—they are denoted in the DICE GAMS⁹ source code as (a) eeq.m(t) and (b) cc.m(t), where t indicates time period. The equation for the SCC calculation as implemented in DICE is¹⁰

$eeq.m\left(t\right)+x\cdot cc.m\left(t\right)=0,(1)$

where marginal values eeq.m(t) and cc.m(t) are known, and x is the to-be-derived SCC value in the time period t. The value x is calculated from (Eq. 1) after the solution to the DICE optimization problem is found (and hence both eeq.m(t) and cc.m(t) are calculated).

The GAMS documentation¹¹ explains the meaning of such marginal values and the notation used to refer to equations’ marginal values in the GAMS system:

“Marginal values (aka “dual values,” “reduced costs,” “shadow prices,” or “multipliers”) are stored in the “.m” […] equation attribute. The GAMS sign convention is this: the marginal value represents the amount and direction of change in the objective value, given a unit increase in the binding constant ([…] right-hand side [of an equation]).”

So the two marginal values, which are terms in the left-hand side of Eq. 1, have the following meaning: eeq. m(t)—is the increment of the objective value (i.e., the optimal value of DICE’s objective function—social utility) corresponding to one unit (i.e., one ton CO₂) increase in the right-hand side of the emissions equation, and cc. m(t)—is the increment of the objective value corresponding to one unit (i.e. one dollar) increase in the right-hand side of the consumption equation¹²; this one dollar value is scaled to x dollars increase in the right-hand side of the consumption equation, giving x·cc.m(t) increment in the objective value.

In summary, the left-hand side of Eq. 1 represents the total increment of the objective value in a new problem as compared to the original DICE problem. The new optimization problem (further referred to as the “perturbed problem”) differs from the original problem in two equations: (a) the emission equation is perturbed (modified) by adding one ton of CO₂ to its right-hand side, and (b) the consumption equation is perturbed by adding x dollars to its right-hand side¹³.

Since this increment in the objective value of the perturbed problem according to Eq. 1 is equal to zero, there would be no change in the objective value if the original DICE problem would be substituted by the perturbed problem—that is, the objective values in the original and the perturbed problems are equal.

Hence, the SCC equation (Eq. 1) means that the addition of one ton of CO₂ to the right-hand side of the emissions balance equation and simultaneous addition of x dollars to the right-hand side of the consumption equation would lead to a new optimization problem that has the same optimal value of social utility (objective function) as the original problem, that is, one ton of added CO₂ emissions is being compensated by x dollars of added consumption. (*)

This allows one to call x an “exchange rate” between additional emissions and additional consumption that keeps the “status quo” in the sense of keeping utility constant. The “exchange rate” can be seen as a monetary value compensating extra one ton of emissions to keep the societal “status quo,” which justifies the name SCC.

3 Interpretation

Here, we provide the interpretation of the perturbed problem, which is implicitly employed for the SCC calculation through the use of marginal values; it is derived from the original problem by modifying its emissions and consumption equations. We start with a discussion on the meaning of the correction of the emissions equation by one ton of CO₂ in a particular year.

The industry may decide for whatever reason to emit “just a bit” more¹⁴ than planned (whether the plan is optimal or not); however, this would imply that the abated quantity¹⁵ and/or the capital investment¹⁶ (both are the only decision variables in DICE¹⁷) should change so that the total production and associated emissions go up (or just emissions if only the abatement level is reduced). Therefore, in case of changes in human-controlled emissions (in DICE, commonly referred to as industrial emissions), the correction of the emission balance equation is not justified. Such a correction of the equation may be justified if uncontrolled emissions (in DICE, commonly referred to as land emissions) need to be corrected.

According to the meaning of the equation (Eq. 1) highlighted earlier in the text, adding x dollars to the consumption equation would compensate one ton of CO₂ added to the emissions equation¹⁸ so that social utility would be kept constant. This newly added consumption x is not caused by a change in any of the two DICE’s control variables—abatement and savings rate¹⁹—and is, therefore, beyond DICE’s control, that is, out of reach for any climate policy possibly modeled by DICE. Moreover, since, according to DICE’s concept, consumption is entirely based on economic production and regulated by DICE’s decision variables—abatement and savings rate—such consumption added to the consumption equation is not supported by the economy and is, therefore, not justified within the DICE’s IAM concept.

4 Discussion and implications for policy context

The SCC equates additional emissions with additional consumption in a perturbed problem in such a way that the maximum societal utility of this problem remains the same as in the original (unperturbed) problem. This SCC estimate, however, deals with uncontrolled emissions and, therefore, has nothing to do with any deviation of actual emissions under climate policy control from the estimated optimal plan. In DICE’s context, uncontrolled emissions are always more costly than human-made emissions because, while creating economic damage via temperature increase, they are not creating any production, that is, additional consumption possibility. As it regards human-made emissions (i.e. emissions under control in DICE), both over-emitting (e.g., producing more economic output and/or weaker abatement) and under-emitting (e.g., producing less economic output and/or excessive abatement), as compared to the optimal level of emissions, would lead to losses in utility and by that would create net social cost.

The SCC calculation method implicitly relies on the assumed possibility of additional consumption²⁰, which is beyond economic representation in the DICE model. So the SCC is disconnected from the DICE’s economy, and therefore, no economic conclusions whatsoever can be derived from DICE employing such estimated SCC. From this perspective, the SCC, as calculated in (Eq. 1), appears to be an irrelevant concept to justify or enforce, keeping emissions at an optimal level by climate-economic policies in whatever form including the SCC application as a carbon tax.

The SCC only comes in handy if, due to reasons beyond the controls embedded in the model, for example, an unforeseen disaster, the emission equation gets disturbed. In this case, the SCC can only estimate the monetary damage of such a disaster in the sense that if there were an “external” source for increasing consumption by that amount, then that event would not create any impact on the utility. In no case can the SCC provide guidance on how to redistribute consumption and investment after such a disaster; to answer these questions, one has to carry out an optimization of the new (perturbed) problem.

Apparently, the SCC and SMAC have different meanings despite being expressed in the same units. As the DICE model is run and the optimal solution is found, SMAC is the only optimal cost of carbon in the societal context, as reflected by the models’ utility function. This social optimality is unconditional on the SCC value. SMAC “guarantees” the desired optimal abatement level²¹, which is conditional on technological feasibility, as represented in DICE by the marginal cost of abatement specific to a time period and abatement level²².

When there are cases where the numerical value of the SCC in DICE happens to be close to SMAC for a relatively long time of 50–100 years after the beginning of the modeling period (see e.g. Figures 1A), for other highly policy-relevant model setups with a direct temperature constraint, SMAC can be overestimated by the SCC by a factor of four already within 50 years²³ of the beginning of the modeling period (see Figures 1C, D). This overestimation is not conditional on any model parameters’ uncertainty and stems only from the used calculation method. Similarly, SMAC can be also underestimated by the SCC (see Figure 1B).

To better clarify the presented SCC interpretation that refers to a perturbed problem, the “traditional” use of marginal values in economics can be compared to their use for the SCC calculation in DICE. The “traditional” use of marginal values in e.g., the producer’s profit maximization problem constrained by availability of a resource required for production is that it allows us to calculate the marginal price of a resource—the maximum price that the producer would be willing to pay for one additional unit of the resource if it becomes available. This effectively means that the producer is an “open system,” that is, part of a bigger system where more resources can be made accessible, for example, by building additional mines or contracting another supplier [more detailed discussion is presented in Simon and Blume (1994) p. 452]. Similar consideration of an “open system” is conceptually valid also in the climate policy context (Uzawa, 2003) where the world economy is represented by individual countries. When a particular country is considered, it can “borrow” from the rest of the world. Contrary to these examples, there is just one entire world being modeled in DICE, which is the Earth’s “closed system.” This system cannot “borrow” from outside in terms of human-controllable emissions and economic consumption.

The findings obtained from the analysis of the SCC calculation method in the DICE model are relevant beyond the scope of DICE itself. The discovered semantic issue is rooted in the attempt to use the SCC value²⁴ for shaping human-controllable emissions through economic policies. The FUND (Anthoff and Tol, 2013; Github, 2022) and PAGE (Hope, 2008; Github, 2009; Hope, 2013; Frances et al., 2018) IAMs that also estimate the SCC, while being structurally different from DICE²⁵, both use a similar idea of an “emission pulse” that simply increases total emissions by adding to the emission balance equation a pre-defined amount over a certain period of time to generate a new so-called “marginal” model (which is otherwise equal to the original), which then provides a trajectory to derive the SCC value. These newly added emissions are not caused by any change in the abatement and form the basis for SCC estimation. The DICE model vividly demonstrates inconsistencies resulting from the application of such a constructed SCC to estimate the socio-economic value of emissions under a climate policy control.

The presented analysis calls for a clear specification of the meaning of the SCC in applications. Furthermore, regarding DICE, it suggests using the direct model output—socially optimal marginal abatement cost of carbon, SMAC—for the purpose of controlled emissions valuation²⁶. SMAC with its direct meaning shows good potential in replacing the SCC to make climate policy estimates more transparent and, by doing so, could facilitate progress in addressing challenges associated with global climate change.

5 One-sentence summary

The concept of the social cost of carbon (SCC) as manifested through its estimation methodology in DICE and as widely used in policymaking needs to be replaced because it evaluates policy-uncontrolled emissions against the consumption of a product that cannot be produced by the economy, which makes it irrelevant in the climate-economic policy context.

Author contributions

NK has conceptualized the problem; NK and AS have carried out the investigation; MO has contributed to funding acquisition; NK, AS, and MO have discussed the results in the process of investigation; NK has drafted the manuscript; and all co-authors have contributed to writing the manuscript.

Funding

The study was supported by the Austrian Science Fund (FWF): P31796-N29/“Medium Complexity Earth System Risk Management” (ERM) and the European Research Council Synergy Grant number 610028 Imbalance-P: Effects of phosphorus limitations on Life, Earth system, and Society (Seventh Framework Programme of the European Union).

Acknowledgments

The authors acknowledge early discussions around the DICE model with their IIASA colleagues Elena Rovenskaya, Artem Baklanov, Fabian Wagner, Thomas Gasser, and Petr Havlik. These discussions have spurred the interest in a deeper exploration of DICE that ultimately resulted in the presented analysis. The authors are grateful to the former IIASA Deputy Director General for Science Leena Srivastava for her attention and feedback. The authors thank Dr. Linus Mattauch from the University of Oxford for sharing his view on an early draft of this manuscript, Dr. Steven A. Gabriel from the University of Maryland, and Nikita Belyak from the Department of Mathematics and Systems Analysis of Aalto University for their feedback and discussion on the later version of the manuscript. The authors are grateful to their IIASA colleagues Armon Rezai, Michael Kuhn, Stefan Wrzaczek, Michael Freiberger, Jarmo Kikstra, Johannes Bednar, and the participants of the IIASA Economic Forum seminar for useful discussions and feedback. The authors also thank William Nordhaus for making the DICE source code and documentation openly available and the clean and transparent model structure that all made the present research possible. The authors are grateful to two excellent reviewers and the editor for suggestions on this article. The authors acknowledge arXiv for hosting the earlier versions of this manuscript (Khabarov, Smirnov, and Obersteiner).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.923631/full#supplementary-material

Footnotes

¹Climate Framework for Uncertainty, Negotiation, and Distribution (FUND) model.

²Policy Analysis of the Greenhouse Effect (PAGE) model.

³SMAC is the cost of one additional ton CO₂ reduction at the optimal abatement level in a particular year, which is a decision variable denoted in the DICE GAMS source code as MUI(t). SMAC is denoted in the source code as MCABATE(t) “marginal cost of abatement” and additionally as CPRICE(t) “carbon price.” SMAC is calculated as $c_1(t)\cdot {[MIU(t)]}^{c_2}$, where c₁(t) and c₂ are known model parameters.

⁴The compact mathematical formulation of the DICE model is presented in Supplementary Appendix SA: Simplified DICE formulation.

⁵Source: http://www.econ.yale.edu/ ˜ nordhaus/homepage/homepage/DICE2016R-091916ap.gms (accessed on 23 October 2019).

⁶The application of a direct temperature constraint is justified by the property of the damage function, which is unable to capture (or just translate to a monetary value) all potential damage stemming from increased GHG concentrations in the atmosphere. Such a constraint was applied and reported in DICE-2013 (Introduction and User Manual) and later also in DICE-2016 (http://web.archive.org/web/20191205041047/https://data.nber.org/reporter/ 2017number3/nordhaus.html). An alternative constraint---on emissions---would serve the same purpose, however, limiting the temperature only implicitly.

⁷Otherwise, making an assumption that, for example, abatement is more expensive than emitting, that is, SMAC is greater than SCC, the last ton of CO₂ can be saved from abatement, that is, released to the atmosphere, and the resulting cost will become SCC, which is less than the initial SMAC, that is, the new level of abatement would be better, and hence, the initial level is not optimal, which is a contradiction, because the optimal case is being considered. This contradiction makes the initially made assumption (SMAC $>$ SCC) invalid. Similar arguments lead to the conclusion that the case SMAC $<$ SCC is also impossible; hence, SMAC = SCC. Further in the analysis, we do not appeal to this intuition—it only serves the purpose of nurturing reader’s interest.

⁸For details, see Supplementary Appendix SA: Simplified DICE formulation.

⁹https://www.gams.com

¹⁰The equation is adapted for clarity from the DICE source code by removing scaling and regularization factors.

¹¹URL: https://www.gams.com/33/docs/UG_Glossary.html accessed on 2021-10-04.

¹²Both marginal values eeq.m(t) and cc.m(t) computed by a GAMS optimization algorithm (solver) are numerical approximations and, therefore, may have different accuracies depending on a particular DICE formulation and a particular solver employed for optimization.

¹³For a detailed mathematical explanation of the link between the DICE model formulation, considered marginal values, and SCC equation (Eq. 1), please see the appendices—Supplementary Appendix SA: Simplified DICE formulation, Supplementary Appendix SB: DICE and the standard constrained optimization problem, and Supplementary Appendix SC: Interpretation of marginal values in DICE.

¹⁴For the ease of storytelling, we consider adding emissions and refer to the compensating added consumption. A similar consideration of reducing emissions and their compensating adjusted consumption is also valid.

¹⁵The related decision variable is denoted as the emission control rate, MIU(t) in the DICE 2016 GAMS source code.

¹⁶The related decision variable is denoted as the gross savings rate as fraction of the gross world product, S(t) in the DICE 2016 GAMS source code. Savings rate is a direct equivalent of capital investment in DICE as the unconsumed share of the economic product is “saved” by investing on capital.

¹⁷See Supplementary Appendix SA: Simplified DICE formulation.

¹⁸See the paragraph marked with (*) in Section 2.

¹⁹Savings rate is a direct equivalent of capital investment in DICE, as mentioned earlier.

²⁰The respective consumed product was never produced by the economy, which is the only source of product in DICE. (This is in case of a positive consumed quantity. In case of a negative consumed quantity, the respective product was not invested/converted into the capital and was not spent on abatement, so it is completely disconnected from the economy in both cases).

²¹The “guarantee” means here that in case if at the optimum one more ton is being emitted by a part of the industry, and for doing so, SMAC is charged to them by a “policy,” then SMAC would be necessary and sufficient to abate that one ton by whatever part of the industry or “policy” (which is unspecified in, yet consistent with, DICE) and, hence, keep the situation at the optimum.

²²We would like to highlight here the issue of a surplus creation if the SMAC value, being a marginal cost, is applied uniformly by a policy for a non-marginal abated amount. Such an approach would be inconsistent with DICE’s total cost of abatement valuation.

²³The 50-year period is used for SCC estimates by the US EPA (Technical Support Document, 2010).

²⁴This SCC value was obtained via the perturbed problem, that is, it describes human-uncontrollable emissions and consumption of a product, which was never produced by the economy.

²⁵According to the IAM nomenclature suggested by Weyant (2017), FUND and PAGE models are both of the type “benefit–cost” (BC) IAMs, same as DICE, and these three models are the most widely used aggregate BC IAMs.

²⁶While keeping in mind SMAC’s validity for only incremental quantities at the optimal abatement level.

References

Anthoff, D., and Tol, R. S. J. (2013). The uncertainty about the social cost of carbon: A decomposition analysis using FUND. Clim. Change 117, 515–530. doi:10.1007/s10584-013-0706-7

CrossRef Full Text | Google Scholar

DICE (2022). Documentation and source code for the DICE model. Website: online at https://williamnordhaus.com/dicerice-models DICE User’s Manual. Available at: http://www.econ.yale.edu/ñordhaus/homepage/homepage/documents/DICE_Manual_100413r1.pdf.

Google Scholar

Frances, C., Rising, J., Lollo, N., Springer, C., Vasquez, V., Dolginow, A., et al. (2018). Mimi-PAGE, an open-source implementation of the PAGE09 integrated assessment model. Sci. Data 5, 180187. Article number: 180187. doi:10.1038/sdata.2018.187

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillingham, K., Nordhaus, W., Anthoff, D., Blanford, G., Bosetti, V., Christensen, P., et al. (2018). Modeling uncertainty in integrated assessment of climate change: A multimodel comparison. J. Assoc. Environ. Resour. Econ. 54, 791–826. doi:10.1086/698910

CrossRef Full Text | Google Scholar

Github (2022). FUND model source code. Available at: https://github.com/fund-model/MimiFUND.jl.

Google Scholar

Github (2009). PAGE model source code. Available at: https://github.com/anthofflab/MimiPAGE2009.jl.

Google Scholar

Hope, C. (2013). Critical issues for the calculation of the social cost of CO2: Why the estimates from PAGE09 are higher than those from PAGE2002. Clim. Change 117, 531–543. doi:10.1007/s10584-012-0633-z

CrossRef Full Text | Google Scholar

Hope, C. (2008). Discount rates, equity weights and the social cost of carbon. Energy Econ. 30 (3), 1011–1019. ISSN 0140-9883. doi:10.1016/j.eneco.2006.11.006

CrossRef Full Text | Google Scholar

Jin, G., Shi, X., Zhang, L., and Hu, S. (2020). Measuring the SCCs of different Chinese regions under future scenarios. Renew. Sustain. Energy Rev. 130. ISSN 1364-0321. doi:10.1016/j.rser.2020.109949

CrossRef Full Text | Google Scholar

Katharine, R., Drouet, L., Caldeira, K., and Tavoni, M. (2018). Country-level social cost of carbon. Nat. Clim. Chang. 8, 895–10900. doi:10.1038/s41558-018-0282-y

CrossRef Full Text | Google Scholar

Khabarov, N., Smirnov, A., and Obersteiner, M. (2022). Social cost of carbon: What do the numbers really mean? ArXiv. doi:10.48550/arXiv.2001.08935

CrossRef Full Text | Google Scholar

National Academies of Sciences, Engineering, and Medicine (2017). Valuing climate damages: Updating estimation of the social cost of carbon dioxide. Washington, DC: The National Academies Press. . doi:10.17226/24651

CrossRef Full Text | Google Scholar

Nordhaus, W. (2019). Climate change: The ultimate challenge for economics. Am. Econ. Rev. 109 (6), 1991–2014. doi:10.1257/aer.109.6.1991

CrossRef Full Text | Google Scholar

Nordhaus, W. (2014). Estimates of the social cost of carbon: Concepts and results from the DICE-2013R model and alternative approaches. J. Assoc. Environ. Resour. Econ. 1, 273–312. doi:10.1086/676035

CrossRef Full Text | Google Scholar

Nordhaus, W. (2017). Revisiting the social cost of carbon. Proc. Natl. Acad. Sci. U. S. A. 14 (7), 1518–1523. doi:10.1073/pnas.1609244114

PubMed Abstract | CrossRef Full Text | Google Scholar

Pearce, D. (2003). The social cost of carbon and its policy implications. Oxf. Rev. Econ. policy 19 (3), 362–384. Available at: https://academic.oup.com/oxrep/article-abstract/19/3/362/440581. doi:10.1093/oxrep/19.3.362

CrossRef Full Text | Google Scholar

Pizer, W., Adler, M., Aldy, J., Anthoff, D., Cropper, M., Gillingham, K., et al. (2014). Using and improving the social cost of carbon. Science 346 (6214), 1189–1190. doi:10.1126/science.1259774

PubMed Abstract | CrossRef Full Text | Google Scholar

Rennert, K., Brian, C., Prest, W. A. P., Newell, R. G., Anthoff, D., Kingdon, C., et al. (2021). The social cost of carbon: Advances in long-term probabilistic projections of population, GDP, emissions, and discount rates. Resources for the future. URL: Available at: https://www.rff.org/publications/working-papers/the- social-cost-of-carbon-advances-in-long-term- probabilistic-projections-of- population-gdp-emissions-and-discount-rates/.

Google Scholar

Rose, S. K., Diaz, D. B., and Blanford, G. J. (2017). Understanding the social cost of carbon: A model diagnostic and inter-comparison study. Clim. Chang. Econ. (Singap). 08, 1750009. doi:10.1142/S2010007817500099

CrossRef Full Text | Google Scholar

Scovronick, N., Budolfson, M. B., Francis, D., Fleurbaey, M., Siebert, A., Socolow, R. H., et al. (2017). Impact of population growth and population ethics on climate change mitigation policy. Proc. Natl. Acad. Sci. U. S. A. 114 (46), 12338–12343. doi:10.1073/pnas.1618308114

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon, C., and Blume, L. (1994). Mathematics for economists. New York: W. W. Norton & Company.

Google Scholar

Technical Support Document (2010). Social cost of carbon for regulatory impact analysis, under executive order 12866, interagency working Group on social cost of carbon. Washington, DC: United States Government. Available at: https://www.epa.gov/sites/production/files/2016-12/documents/scc_tsd_2010.pdf.

Google Scholar

Uzawa, H. (2003). Economic theory and global warming. Cambridge University Press. 978-0-521-82386-9.

Google Scholar

Wagner, G., Anthoff, D., Cropper, M., Dietz, S., Gillingham, Kenneth T., Groom, B., et al. (2021). Eight priorities for calculating the social cost of carbon. Nature 590, 548–550. doi:10.1038/d41586-021-00441-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Weyant, J. (2017). Some contributions of integrated assessment models of global climate change. Rev. Environ. Econ. Policy 11, 115–137. doi:10.1093/reep/rew018

CrossRef Full Text | Google Scholar

Worldbank (2017). Guidance note on shadow price of carbon in economic analysis. Available at: http://pubdocs.worldbank.org/en/911381516303509498/2017-Shadow-Price-of-Carbon-Guidance-Note-FINAL-CLEARED.pdf.

Google Scholar