
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci. , 28 April 2022
Sec. Environmental Economics and Management
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.893650
This article is part of the Research Topic Export Product Quality, Renewable Energy, and Sustainable Production View all 48 articles
Haze pollution has been a global problem plaguing people for nearly two centuries, especially in developing countries, where haze pollution is getting worse and has become the culprit that restricts global sustainable development. As the largest developing country in the world, China’s regional characteristics of haze pollution are increasingly prominent, and the coverage is expanding, which means that there is a strong spatial interaction of haze pollution. The real world is composed of asymmetric spatial relationships, and asymmetric spatial interactions are more consistent with the reality of haze pollution. To this end, this paper identifies the asymmetric spatial interaction effects of haze pollution by using the time series econometric analysis framework and then constructs asymmetric spatial weights. In this paper, the spatial panel Durbin model and spatial effect decomposition technique are used for the empirical investigation to provide new empirical evidence to reveal the socio-economic influences of haze pollution. The study finds that haze pollution in China has a significant asymmetric spatial interaction and the degree of influence varies among cities. During the sample period, there is a significant inverted U-shaped relationship between economic development and haze pollution. However, the vast majority of cities have not passed the top inflection point of the inverted U-curve and are still in the stage where haze pollution is gradually intensifying with economic growth. High population density, high energy consumption, and unreasonable energy consumption structure aggravate haze pollution, while fixed-asset investment and science and technology expenditure help to reduce haze pollution. However, only the spatial spillover effect of the energy consumption structure is significant. Therefore, the improvement and implementation of more effective socio-economic prevention and control policies in the case of asymmetric interaction is the key to effectively dealing with heavy pollution weather, fighting the defense of the blue sky, and achieving sustainable development.
Haze pollution can seriously threaten the ecological environment, seriously affect the economic quality and the achievement of sustainable development goals, and thus has a strong negative externality. Although the effectiveness of the current haze control in developed countries is relatively significant, and air quality has been improved significantly, the haze still tends to return in many places around the world. In particular, more and more developing countries are also suffering from the haze. From historical experience, severe haze pollution is a natural warning to sloppy growth. Therefore, to improve air quality and achieve sustainable development, haze pollution control is a key part. It is about reducing the haze itself and the fundamental change of economic development and sustainable development (Zhao et al., 2022a). As the world’s largest developing country, it is of great significance to the world to manage the haze pollution, and then to transform the way of economic development and achieve sustainable development.
Although haze pollution is an air pollution phenomenon formed through a series of atmospheric physicochemical processes, no matter how complex the physicochemical process is, socio-economic development essentially causes haze pollution. Therefore, the treatment of haze pollution is a social and economic problem. Currently, China’s haze pollution has shown a large-scale, high-intensity, and persistent trend, which seriously restricts sustainable socio-economic development and threatens the health of the people (Chen et al., 2016; Zhang et al., 2020; Zhou et al., 2021). In particular, fine airborne particles (PM2.5) have become the fourth most lethal factor after diet, hypertension, and smoking (Zhang et al., 2019; Zhao et al., 2022b). More grimly, however, is the fact that due to the increasingly prominent regional spatial characteristics and spatial spillover effect of haze pollution, its prevention and control are becoming more and more difficult. Taking the haze weather that broke out on 20 December 2016, as an example, there were 90 cities with daily average air quality values of severe and above pollution in China, with extensive haze weather in the central-eastern region, and remote sensing data showed that the air pollution covered an area of 1.88 million square kilometers, and its impact reached 17 provinces. Among them, the area of heavy haze pollution accounts for 49% of the total area of haze pollution, more than 920,000 square kilometers. Facing the grim reality of the expanding scope of haze pollution, precise identification of the economic and social influential factors of air pollution can provide a scientific basis for the effective treatment of air pollution.
The real world is composed of asymmetric spatial relationships, and asymmetric spatial interaction effects can better model the reality of haze pollution. It is different from the existing studies based on the assumption of symmetric spatial interaction effects. This paper identifies the spatial asymmetric interaction effects of haze pollution with the help of a time-series econometric analysis framework. It then constructs an asymmetric spatial weight matrix to empirically identify the social and economic influential factors of air pollution with the help of the spatial panel Durbin model. Specifically, this paper collects the official PM2.5 monitoring data in China from 2014 to 2015 published by the Ministry of Ecology and Environment of China and constructs urban PM2.5 day-by-day time series on this basis. Under the framework of time series econometric analysis, three methods such as linear Granger causality test, nonlinear Granger causality test, and variance decomposition is used to identify the asymmetric interaction effects of air pollution in this paper. And then we construct a spatial asymmetric weight matrix of haze pollution based on the above results. This paper uses spatial econometric models to identify the socio-economic influential factors of haze pollution. It is found that there is indeed an obvious asymmetric spatial interaction effect of China’s air pollution. Taking the results of variance decomposition as an example, the impact of haze pollution in Beijing on Tianjin is 0.329%, while the impact of Tianjin on Beijing is 0.553%. During the sample period, the relationship between economic development and haze pollution shows an inverted U-shaped curve, verifying the EKC-Hypothesis. However, most cities fail to pass the inflection point. Under the influence of asymmetric spatial interaction, excessive population density, high energy consumption, and unreasonable energy consumption structure aggravate haze pollution exacerbate the degree of haze pollution, while fixed-asset investment and science and technology expenditure help to reduce haze pollution.
The regional spatial characteristics and spatial effects of haze pollution imply a strong spatial interaction in a certain spatial scale. A large amount of literature uses spatial econometric methods to empirically investigate the influential factors of air pollution (Chen et al., 2019; Lou et al., 2021; Shi and Zhang, 2022), which provides useful references for the formulation of haze pollution control policies. Although spatial measurement provides a feasible tool to explore the influential factors of air pollution based on spatial spillover effects, the hasty setting of spatial weights in existing studies may lead to wrong research results. And thus mislead the tackling policies of haze pollution. When applying the spatial metrology model, the setting of spatial weights is critical and fundamental (Anselin, 2010), and setting spatial weights incorrectly will lead to serious results. In the previous studies, most of the literature has used symmetric spatial weights such as neighborhood weights, geographic distance weights, economic weights, and nested weights (Hao and Liu, 2015; Wang and Fang, 2016; Xie et al., 2016; Du et al., 2018; Kangyin Dong et al., 2019; Zhao et al., 2022c). All these spatial weights are set based on the symmetry assumption of air pollution spatial interaction. However, asymmetric spatial interaction is the most realistic manifestation of haze pollution compared with symmetric spatial interaction. Obviously, ignoring the spatial asymmetric interaction effect of haze pollution may lead to misleading research conclusions. In addition, from the selection of haze pollution data, most of the existing studies have used inter-provincial or urban PM2.5 satellite data published by foreign research institutions. (Lou et al., 2021; Shi and Zhang, 2022). The complex composition and long transmission distance of PM2.5 make the deterioration of haze pollution in one city aggravate the level of air pollution in the surrounding cities or even more distant regions. And this long-distance haze interaction increases with the increase of emissions from pollution sources (Engling and Gelencsér, 2010; Lüthi et al., 2015). Thus, inter-provincial data ignore the spatially non-homogeneous characteristics of haze pollution, while urban monitoring data are more accurate. The monitoring data of PM2.5 have now been published by the Ministry of Ecology and Environment of China, creating conditions for us to use urban data for our study.
The marginal academic contributions of our paper mainly have three points. Firstly, with the help of the time series econometric analysis framework, linear Granger causality test, nonlinear Granger causality test, and variance decomposition technique are applied to identify the asymmetric spatial interaction of air pollution. Secondly, in this paper, the concept of asymmetric spatial interaction of air pollution is proposed, and the asymmetric spatial weights are applied to the study of socio-economic impact factors of haze pollution, which is an extension of spatial measures in the field of haze pollution. Thirdly, by using the spatial panel estimation method, this paper empirically examines the socio-economic influential factors of haze pollution. And further, we analyze the direct effects, indirect effects, and total effects of each influential factor to investigate the influential factors of air pollution more comprehensively.
The air pollution in China has obvious spatial clustering and non-homogeneous characteristics, showing an obvious spatial pattern of “serious in the north and slight in the south, serious in the east and slight in the west.” When studying the socio-economic impact factors of haze pollution, this spatial characteristic should be fully considered, so the spatial measurement method is more applicable. At present, spatial econometric methods have become the mainstream tool to study the economic and social impact factors of air pollution with full consideration of spatial characteristics (Ma et al., 2016; Du et al., 2018). But, the accuracy of spatial econometric regression results critically depends on the setting of spatial weights (Anselin, 2010). Therefore, to accurately reveal the socio-economic impact factors of haze pollution, it is inevitable that the spatial weights must first be accurately constructed. To accurately construct the spatial weights, it is necessary to identify the haze pollution spatial interaction accurately. Existing studies on the socio-economic influential factors of haze pollution make extensive use of spatial measures, but as mentioned before, they all use spatial symmetric weights. In contrast, the real world is composed of asymmetric spatial interaction. Therefore, the continued use of symmetric weights no longer reflects reality, and asymmetric weights are more consistent with the real haze pollution spatial interaction. The use of asymmetric weights is also the trend of spatial measurement and has been used in several research fields (Parent and Lesage, 2008).
According to Zhu et al. (2018), time series econometric techniques provide a feasible research method for identifying the asymmetric interaction effects of haze pollution. Under the time series econometric analysis framework, the asymmetric interaction effects of haze pollution can be identified using at least three tools, which are the traditional linear Granger causality test, nonlinear Granger causality test, and variance decomposition. Therefore, the research framework of asymmetric interaction effects of haze pollution and the construction of spatial weight is shown in Figure 1.
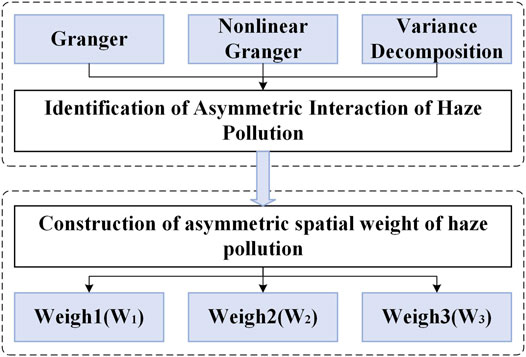
FIGURE 1. Analytical framework for the identification of asymmetric interaction effects and weight construction.
Linear Granger causality test is used to identify asymmetric spatial interaction. The change of haze pollution in a region may affect the change of pollution in other regions. Therefore, this paper identifies the asymmetric interaction effects of haze pollution under the vector autoregressive regression model (VAR) framework. In the VAR framework, the linear Granger causality test approach treats all variables as endogenous and does not require too many a priori constraints on the relationship between variables. It can reveal the asymmetric probability dependence between haze pollution time series and can be used to determine whether there is a lead-lag relationship between two series of haze pollution (Granger, 1969). If the previous information of one time series cannot help to improve the prediction ability of the current value of another time series, the former is said to be not the Granger cause of the latter; otherwise, the former is said to be the Granger cause of the latter. For example, suppose the current or previous information of air pollution in city X helps to improve the predictive ability of future values of haze pollution in city Y. In that case, X is the Granger cause of Y. This paper performs the Granger causality test according to the method proposed by Hsiao (1981). And with the help of the AIC criterion, we select the optimal lag order (Kilian, 2001).
The Nonlinear Granger causality test is used to identify asymmetric spatial interaction. As Granger and Newbold (2014) pointed out, “the real world is full of nonlinear relationships, and nonlinear models can help us simulate the real world more accurately.” For this reason, Diks and Panchenko (2006) proposed a nonlinear Granger causality test based on Hiemstra and Jones (1994). We draw on the idea of Diks and Panchenko (2006) to construct a bivariate VAR model based on a smooth time series. And we filter the linear components among the variables by extracting the VAR residuals and then conduct a nonlinear test on this basis. This paper uses the BDS method (Broock et al., 1996) to identify the air pollution spatial interaction by using the nonlinear Granger causality test under the premise of confirming the existence of a significant nonlinear dynamic trend between the series. In addition, we argue that if the original hypothesis of no nonlinear Granger causality is accepted for all lag orders (1–8), then there must be no asymmetric spatial interaction between haze pollution variables. If the original hypothesis of no nonlinear Granger causality is significantly rejected at all lags, we cannot rule out the existence of asymmetric spatial interaction among the haze pollution variables.
Variance decomposition is used to identify asymmetric spatial interaction. There are still some limitations in the nonlinear Granger causality test. Firstly, the nonlinear Granger causality test only considers the direction of the interaction effect of haze pollution but not the strength of the effect. Secondly, linear Granger and nonlinear Granger are based on a pure information flow perspective, which ignores the characteristics of haze pollution decaying with geographical distance. Whereas the variance decomposition technique, by analyzing the magnitude of the impact of each city’s haze pollution on the degree of another city’s haze pollution, provides relatively important information of all the stochastic perturbation that impacts the variables in the VAR model. Thus, this paper constructs a set of cities that may have asymmetric spatial interaction with each city, based on which VAR modeling is used to reveal the probability dependence and the degree of interaction effects of haze pollution among these cities. However, it is worth noting that the derivation of variance decomposition involves Cholesky decomposition in a certain order of variables, which makes the final analysis depends on the ranking of variables (Campbell, 1991) and cannot take into account the geographical distance factor. Therefore, in this paper, we take the idea of the first law of geography by Tobler (1970) into account. Due to the geographic decay law of the spatial interaction of haze pollution, the intensity of the interaction of haze pollution decreases with the increase of geographic distance. According to the above law, we get the basis for the ranking of variables, i.e., the closer the city is to a city in the Cholesky decomposition process, the more distant the city is, the more distant it is, the more distant it is. This way solves the problem of variable selection and variable ranking of variance decomposition in the VAR model and introduces the law of haze pollution decaying with geographic distance into the variance decomposition.
Anselin and Florax (2012) argued that the better the spatial weight matrix match the spatial structure of data, the better the fit of the model, and the better the explanatory power. In contrast, the existing weights, both symmetric and asymmetric weights, are given a priori and do not change over time, thus neglecting the endogeneity of the weight matrix (Harris et al., 2011; Corrado and Fingleton, 2012). Therefore, to more accurately identify the asymmetric spatial interaction and then construct spatially asymmetric weights that highly match the true spatial structure of real data. This paper identifies the asymmetric spatial interaction of haze pollution in the time series econometric analysis framework and constructs asymmetric spatial weights based on the identification results.
Spatial weight construction based on Granger causality test. In this paper, the spatial weights W1 and W2 are constructed according to the identification results of the linear Granger causality test and the nonlinear Granger causality test respectively, and the matrix elements are shown in Eq. 1.
In Eq. 1, wij is a matrix element, i, j is the sample city (same below).
Spatial weight construction based on variance decomposition. The spatial weights W3 are constructed according to the results of variance decomposition identification, and the matrix elements are shown in Eq. 2.
Where, δij is the contribution of haze pollution derived from variance decomposition, which indicates the degree of influence of city j on the city i. Further, the general form of its weight can be transformed into Eq. 3.
If at
Given that the common theoretical framework for studying environmental pollution impact factors is the STIRPAT model proposed by York et al. (2003). Therefore, we use the STIRPAT model as the basis for selecting impact factors and the model is shown in Eq. 4.
In Eq. 4, i and t denote city and year respectively, Iit represents environmental impact, Pit represents the population, Ait represents wealth, Tit represents technology, εit is the random error term. The STIRPAT is a multivariate nonlinear model, and the linear model is obtained by taking the logarithm of the equation at the same time. The STIRPAT model allows the introduction of other influential factors to analyze. According to the above analysis framework, this paper constructs a spatial econometric analysis model to investigate the social and economic impact factors of haze pollution by combining the spatially non-homogeneous characteristics of haze pollution. According to the existing research, the spatial econometric model should start with the spatial Durbin model. Because we can include the spatial lagged term of the explained variable (WY) and the spatial lagged term of the explanatory variable (WX) into the spatial Durbin model at the same time, which if ignored would result in a loss of consistency in the estimation of the remaining estimates (Elhorst, 2010; Elhorst, 2014). Given this, this paper develops an econometric model as in Eq. 5.
In Eq. 5, t is the year. The explanatory variable Yt is haze pollution, Xt is the relevant influential factor and μt is the random error term. Wij represents the asymmetric spatial weight matrix. ρWYt and βWXt represent the spatial dependence of the explanatory and explanatory variables respectively. ρ is the spatial lag coefficient, which reflects the influence of haze pollution in other cities on the sample city in the current period. β is also the spatial lag coefficient, which represents the influence of other urban impact factors on haze pollution in the sample city in the current period.
Studies have been conducted without spatial correlation tests when adding the spatial lagged terms of explanatory variables (WX) in the construction of spatial Durbin models (Hao and Liu, 2015; Wang and Fang, 2016; Du et al., 2018). Thus, adding all the spatial lagged terms of all explanatory variables to the model can lead to model over-explanation and problems such as multicollinearity. Given this, when adding the WX term in this paper, the Bivariate Moran test (Anselin, 2010) is performed first. Meanwhile, the regression coefficients of the above model cannot directly express the effect of explanatory variables on the explained variable, so further effect decomposition is needed. And we first rewrite the model as in Eq. 6.
The matrix of partial derivatives of E (Yt) (the expected value of Yt) corresponding to the kth explanatory variable in Xt from city one to city n can be written as Eq. 9. These partial derivatives represent the effect of a one-unit change in a particular explanatory variable in one city on the explanatory variables in all other cities, which can be divided into direct effects and indirect effects (Mao et al., 2022). In Eq. 9, IN is the unit matrix,
Explained variables. The explanatory variable is haze pollution (lnpm). PM2.5 is the primary pollutant of haze pollution (Schlesinger, 2007; Zhang et al., 2019) and has the characteristics of complex composition and long transmission distance, which makes the deterioration of air pollution in one city will aggravate the level of air pollution in the surrounding cities. At the same time, the long-distance haze interaction will increase with the increase of pollution source emissions (Engling and Gelencsér, 2010; Lüthi et al., 2015). Thus, PM2.5 is chosen as a proxy variable for air pollution.
Explanatory variables. The explanatory variables in this paper are chosen to expand on the STIRPAT model in the previous paper. Specifically: 1) Population density (lnpopdens). Due to the large differences in population size among cities, it is not accurate enough to directly by using the total population as a proxy variable. Therefore, this paper uses the number of people per square kilometer in each city to measure population density. Generally speaking, the higher the population density of a city, the more active its social and economic activities, the higher energy consumption and pollution emissions, and the greater environmental pressure of the city. 2) Economic development (lnpgdp). Generally speaking, regional GDP per capita can be a good indicator of the city’s economic development (Liu and Pei, 2019). Then we adopt regional GDP per capita as a proxy variable for economic development. Meanwhile, the EKC-Hypothesis suggests that there is an inverted U-shaped curve between economic development and environmental pollution (Grossman and Krueger, 1995). Thus, we also add the square term of GDP per capita into the regression to consider its influence on air pollution. 3) Technological progress (lnrdint and lntechexp). The development of green technology undoubtedly provides important technical support for managing, preventing, and controlling haze pollution (Liu and Pei, 2019). This paper selects R&D intensity and science and technology expenditure as proxy variables for technological progress. Among them, R&D intensity is measured by the proportion of scientific research and technical service personnel to total employees in each city (Fang, 2021). And the expenditure on science and technology is measured by the proportion of the expenditure on science and technology to public finance expenditure in each city. 4) Energy structure (lnenercons and lnenerint) Over the past 30 years, China’s development has been accompanied by high pollution and high energy consumption. There are problems of unreasonable energy consumption structure and high energy intensity in China, which is one of the main causes of haze pollution. Therefore, we choose energy consumption and intensity to measure the energy structure. Among them, energy consumption is measured by the proportion of coal consumption to total energy consumption1 (Shao et al., 2011; Yixuan Dong et al., 2019). Energy intensity is measured by the proportion of comprehensive energy consumption to regional GDP. 5) Investment intensity (lninvestint). Along with the accelerating urbanization process, investment in urban infrastructure construction and real estate development will lead to changes in urban energy structure and dust, which may lead to haze pollution. Therefore, this paper uses the share of total energy consumption in regional GDP to measure. The detailed definitions of all explanatory variables are shown in Table 1.
Currently, real-time urban PM2.5 monitoring data are available from the China General Environmental Monitoring Station2. In addition, other related websites also provide daily data of urban PM2.53. To ensure the accuracy of haze pollution data and to avoid biased research conclusions due to omissions and misplacement in the calculation of daily data from other websites, this paper chooses to calculate daily data for each city directly using hourly data from monitoring stations.
Due to a large amount of these data, it is not easy to meet the needs if the manual collection method is work-intensive and error-prone. In order to obtain data more quickly and accurately, this paper chooses to implement a Web Spider system under the R language platform using tools such as Rvest and Rcurl to capture data from the China General Environmental Monitoring Station pages. Eventually, a PM2.5-based haze pollution database is constructed to create research conditions. The data of other socio-economic influencing factors were obtained from the China Urban Statistical Yearbook and China Energy Statistical Yearbook. Table 2 provides descriptive statistics for all variables.
This paper employs Exploratory Spatial Data Analysis (ESDA) to examine the spatial correlation and spatial clustering characteristics of haze pollution in China.
Global Spatial Autocorrelation is commonly used to analyze the distribution characteristics, which is generally portrayed by Moran’s I (Moran, 1950) and Geary’s C (Geary, 1954). Firstly, the Global Spatial Autocorrelation of urban haze pollution in China is examined using Moran’s I index, and the specific measurement is carried out according to Eq. 10. Where,
Next, Geary’s C index is used to test the Global Spatial Autocorrelation of urban haze pollution in China, measured according to Eq. 11. Unlike Moran’s I index, the value of Geary’s C index greater than one indicates a negative correlation, equal to one indicates no correlation, and less than one indicates a positive correlation.
Using the above method, this paper measures the global Moran’s I and Geary’s C values of PM2.5 in 160 cities. Moran’s I is significantly positive under all three weighting schemes, while Geary’s C is significantly less than one for all of them. This indicates a significant positive spatial correlation characteristic of haze pollution in 160 cities. Therefore, the spatial characteristics of haze pollution should be fully considered; otherwise, it will lead to biased estimation results (Table 3).
The local spatial autocorrelation can be visually portrayed by plotting the Moran scatter plot. As shown in the Moran scatter plot of PM2.5 in 2014 and 2015 (Figure 2), haze pollution has a significant positive spatial correlation and spatial agglomeration effect. That is, for cities with more serious haze pollution, there are usually one or more cities with more serious haze pollution adjacent to them (i.e., high-high positive correlation). Similarly, cities with lighter haze pollution gather together (i.e., low-low positive correlation). In addition, according to the local Moran’s I, about 110 out of 160 cities have positive local Moran’s I for both PM2.5, further indicating the existence of significant spatial clustering characteristics haze pollution.
Bivariate Moran’s I index is used to explore the spatial correlation between the explained variable and explanatory variables, which is used as a basis for adding spatial lagged terms of explanatory variables in the spatial Durbin model as described earlier (Lee, 2001; Anselin, 2010), the index can be expressed as:
In Eq. 12, Zk denotes the normalized Yk values (explanatory variables) and Zl denotes the normalized Xl values (explanatory variables), i.e.,
Before performing the spatial econometric regression, the model is selectively tested by applying the great likelihood estimation and obtaining the likelihood ratio LR. After that, the original hypotheses (H0: β = 0 and H0: β+αρ = 0) are tested by applying the Wald test and LR test. In addition, the spatial Hausman Test is applied to select fixed effects or random effects. In addition, model selection can also be performed based on the great likelihood value of the model, i.e., Likelihood (Lee and Yu, 2010), and the AIC criterion (Akaike, 1974). Table 5 shows the results, and the Wald test and L.R. test for all three weights significantly reject the original hypotheses of (H0: β = 0 and H0: β+αρ = 0), indicating that the SDM model is optimal. In addition, the Hausman test for the SDM model with all three weights is significantly positive, rejecting the random effect. Meanwhile, the Likelihood values of the fixed effects are all greater than the random effects, and the AIC values are all smaller than the random effects, so the fixed effects are more suitable. In summary, this paper selected the SDM model with fixed effects for regression analysis.
This paper conducts regression analyses for the POLS model, the spatial random effects SDM model (SDM-RE), and the spatial fixed effects SDM model (SDM-FE) for PM2.5 under three spatial asymmetric weighting schemes, respectively, and the results are shown in Table 6. Among them, according to the identification results based on the Bivariate Moran test, model (1) and model (2) contain the spatial lagged terms W·lnpopdens, W·lnenercons, W·lninvestint, W·lnenerint, W·lnrdint, and W·lntechexp of the explanatory variables. Model (3) and model (4) contain W·lnpgdp, W·lnpopdens, W·lnenercons and W·lnenerint. Model (5) and model (6) contain W·lnenercons, W·lnenerint, and W·lntechexp. Table 6 shows the regression results. Due to the choice of the fixed-effects SDM model in the above model selection, the regression results of model (3), model (5), and model (7) are used in the analysis below.
According to Table 6, the coefficient of W·lnpm passes the significance test at the 10% significance level among the three spatial weighting schemes, which fully indicates that there are significant spatial clustering characteristics and interaction effects of haze pollution in China at present, that is, the increase of PM2.5 concentration in other cities will further aggravate the degree of haze pollution in this city. Under the effect of asymmetric spatial interaction, haze pollution shows a more significant diffusion effect, and the interaction effect of haze pollution among cities becomes increasingly significant. Therefore, combating haze requires regional joint prevention and control by cities, and the effect of haze prevention and control policies of individual cities or a few cities are becoming less and less obvious. Since haze pollution is essentially a socio-economic problem, identifying the socio-economic influences on haze pollution is essential to improving the current haze pollution prevention and control policies.
Based on the regression results below, we further analyze each factor: 1) Economic development. As shown in columns (3), (5), and (7) of Table 6, the primary terms of economic development are all positive, and the secondary terms are all negative. Except for model (5), which is insignificant, model (3) and model (5) pass the 1% significance level, indicating an inverted U-shaped curve between haze pollution and economic development under the asymmetric interaction. It is consistent with the classical EKC hypothesis that the haze pollution level tends to increase and decrease with increasing levels of economic development. On the surface, the haze pollution level decreases after reaching a peak as the economy continues to develop, so there is no need to prevent and control the increasing haze pollution in economic development. However, it is worth noting that we further calculate the inflection point of the inverted U-shaped curve (in the model (7), for example), which is 150.03 million yuan, and only a few of the 160 sample cities exceeded the inflection point. The cities that exceeded the inflection point in 2014 were Daqing, Dongying, Yangquan, Ordos, and Karamay, and in 2015 were Dongying, Daqing, Yantai, Shenzhen, and Ordos, and about 97% of the cities did not cross the inflection point. Therefore, we cannot expect that haze pollution can be improved just by developing the economy, which requires that we should be aware that the management of haze pollution is a long-term and complex process and focus on continuously improving the prevention and control policies of haze pollution while developing the economy. 2) Population density. Observing the regression results of model (3), model (5), and model (7) in Table 6, it can be found that the regression coefficients of population density show significant positive correlations. It indicates that there is a significant positive correlation between population density and haze pollution. In other words, the higher the population density, the more serious the haze pollution. With the accelerated urbanization process, the population is rapidly concentrated in cities, especially in large and medium-sized cities, and the population density is too large to exceed the carrying capacity of the urban environment. In addition, the increase in fossil energy consumption and traffic congestion caused by the over-concentration of the population are also important reasons for the increase in haze pollution. 3) Technological progress. According to Table 6, R&D intensity has a positive impact on haze pollution under all three spatial weighting schemes, but none of them is significant except for the regression coefficient of the model (7). This paper indicates that the current R&D investment in China is not strong enough, and technological progress does not have a significant positive effect on haze pollution. It also indicates that the directional pair of R&D investment is at odds with improving haze pollution. In addition, in terms of science and technology expenditure, the regression coefficients of models (3), (5), and (7) are significantly negative, indicating that the current government financial investment in science and technology has played a beneficial role in improving haze pollution. Therefore, in the future economic development process, the investment in technology dedicated to improving haze pollution should be strengthened, such as increasing the support for new energy and other green technologies and other measures. 4) Energy consumption. The regression coefficients of models (3), (5), and (7) are all positive, and they pass the 1% significance level except for model (7). This result indicates that the current energy consumption structure of China is not reasonable enough, and the coal-based energy consumption structure aggravates the haze pollution. 5) Energy intensity. From the regression results, it can be seen that the regression coefficients are positive and insignificant except for model (5). This indicates that the energy consumption of China’s 10,000 Yuan GDP is gradually decreasing, but it still aggravates haze pollution. Therefore, it is necessary to strengthen energy conservation and emission reduction and enhance the use of clean energy and new energy to further reduce the energy consumption of 10,000 Yuan GDP. 6) Investment intensity. The regression coefficients of investment intensity in models (3), (5), and (7) are significantly negative, indicating that increasing investment in fixed assets is beneficial to improving haze pollution.
Given that the above regression coefficients can only roughly estimate the effect of each factor on haze pollution and cannot accurately explain its direct and indirect effects on haze pollution, this paper, thus, performs effect decomposition on each explanatory variable, as shown in Table 7. Given that the effect decomposition results under the three weight matrices are in the same direction under the same influencing factor, and the spatial weight W3 can better fit the asymmetric interaction effects of haze pollution, the spatial weight W3 is used as an example for analysis in the later section.
The effect decomposition results in Table 7 show that: 1) The direct effect of population density (lnpopdens) is 0.425, which is significantly positive, showing that the increase of population density will significantly aggravate the haze pollution in the area. The indirect effect is also positive but insignificant, showing that the positive effect of population concentration in the region on haze pollution in other cities is insignificant, leading to a significant positive total effect. This fully indicates that with the current gradual acceleration of urbanization, the over-saturation of the population in megacities and large cities will exacerbate urban haze pollution while also producing spatial spillover effects on other cities. Although the spatial spillover effect is not too obvious at present, with the further increase of urbanization level, the population of big cities will flow to second-tier and even third-tier cities. Suppose the urban population structure is not reasonably adjusted. In that case, it will also aggravate the haze pollution in other areas. 2) The direct effect of science and technology expenditure (lntechexp) is −0.038, which is significantly negative, while the indirect effect and the total effect are simultaneously negative, indicating that an increase in the proportion of science and technology expenditure in the government’s fiscal expenditure helps to improve the haze pollution in the region and beyond. However, the indirect, and total effects are not significant, which may exist because government fiscal expenditure has certain regional characteristics, and it is difficult to impact other regions. 3) The direct effect, indirect effect, and the total effect of R&D intensity (lnrdint) are significantly positive, but the indirect effect is not significant. 4) The direct and indirect effects of energy consumption (lnenercons) are significantly positive, showing that the unreasonable energy consumption structure will not only aggravate the level of haze pollution in this region but also increase the level of haze pollution in other regions. Hence, the total effect is also significantly positive. 5) The direct effect, indirect effect, and total effect of energy intensity (lnenerint) are all positive but insignificant, indicating that the current energy consumption of 10,000 Yuan GDP in China’s cities is not very reasonable, and further energy saving and emission reduction are needed to reduce the energy consumption of 10,000 Yuan GDP. 6) The direct effect of investment intensity (lninvestint) is significantly negative, which indicates that fixed-asset investment helps to reduce haze pollution in this city. However, its indirect effect is not significant, which shows that the current investment structure is not very reasonable and cannot produce spillover effects.
Examining the above factors together, from the direct effects of each influencing factor, investment intensity and science and technology investment are conducive to reducing haze pollution in the region, while high population density, unreasonable energy consumption structure, and deviation in the direction of R&D intensity exacerbate the level of haze pollution in the region. All factors are insignificant except that energy consumption will significantly aggravate the indirect effects of haze pollution in other cities. Through the above analysis, we can clearly understand that there is still disunity in the prevention and control of haze pollution in China, which is the main reason why the implementation effect of joint prevention and control policies in China is far below the expected level.
The regional haze pollution in China has shown an increasingly serious and expanding coverage, while the real world is composed of asymmetric spatial relationships, and asymmetric spatial interaction is more consistent with the reality of haze pollution, which implies that there is a large asymmetric spatial interaction of haze pollution in a large spatial scale. Therefore, this paper identifies the spatial asymmetric interaction effects of haze pollution under the framework of time series econometric analysis and then constructs three asymmetric spatial weight matrices to reveal the socio-economic influences of haze pollution more accurately using a spatial panel Durbin model and combining with effect decomposition techniques. It is found that there is exactly a significant asymmetric spatial interaction of haze pollution in China. Taking the identification of variance decomposition scheme as an example, the influence of Beijing on haze pollution in Tianjin is 0.329%, while the effect of Tianjin on Beijing is 0.553%. At this stage, economic development and haze pollution show an inverted U-shaped curve, consistent with the EKC-Hypothesis. However, it is important to emphasize that most cities have not yet crossed the inflection point and are still at the stage where haze pollution increases with economic growth. Under the asymmetric spatial interaction, high population density, unreasonable energy consumption structure, and high energy consumption of 10,000 Yuan GDP all aggravate haze pollution, while fixed-asset investment and technology expenditure help reduce haze pollution. However, except for the energy consumption structure, the spatial spillover effects of all the above factors are not significant.
The above conclusions provide important policy implications for China to improve and implement more effective socio-economic prevention and control policies and effectively fight the defense of the blue sky. Above all, reconfigure the scope of joint prevention and control. Based on the accurate identification of the spatial asymmetric interaction of haze pollution, the scope of regional joint prevention and control of haze pollution based on the urban perspective are further expanded and redefined, and establish higher-level environmental protection regulatory agencies beyond administrative divisions. The precise definition of the scope of joint prevention and control is the primary link in haze pollution prevention and control. Without proper joint prevention and control of haze pollution, the subsequent treatment will not be smooth. At the same time, environmental incentives should be standardized to avoid the phenomenon of gain without pain. Furthermore, the establishment of long-term governance mechanism construction from the socio-economic factors of influence. Haze pollution is ultimately a socio-economic problem and needs to be solved by socio-economic means. Layout a reasonable population size, prevent excessive concentration of population to large cities, a reasonable layout of the urban population, and to the second and third-tier cities diversion. Continue to promote the transformation and restructuring, especially the continuous adjustment of energy consumption structure, improve energy use efficiency while reducing the percentage of coal in the energy consumption structure. Improve policies to support the development of green industries, expand the improvement of haze reduction technologies, and increase the proportion of public finance expenditures on science and technology. The most important thing is to carry out a region-wide cooperation system. According to the conclusion of the study, the current socio-economic influencing factors of haze pollution only function in the region and do not effectively play its spatial spillover effect. Finally, explore sustainable development models that meet national characteristics and accelerate green and technological cities’ construction. Integrate the concept of sustainable development into the planning and construction of cities, steadily promote circular development and green development, advocate green travel, and accelerate the promotion and policy support of clean energy and new energy vehicles. To achieve the win-win goal of sustainable reduction of haze pollution and transforming the economic development mode to sustainable development, which is the core meaning of the sustainable development concept in dealing with the eternal relationship between environmental protection and economic development. Therefore, haze control is a long-term process, and it is a long way to go.
Publicly available datasets were analyzed in this study. This data can be found here: http://www.cnemc.cn/sssj/ http://www.tianqihoubao.com/.
Conceptualization, Methodology, Writing-original draft WJ; Data collection and sorting, Validation, Writing-review and editing, Funding acquisition YP.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
1In view of the lack of data on total urban energy consumption and coal consumption in China Urban Statistical Yearbook and China Energy Statistical Yearbook, and considering the similarity of energy consumption structure in each province, the data of each province are used to approximate and replace the cities in the province.
Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Trans. Autom. Contr. 19, 716–723. doi:10.1109/TAC.1974.1100705
Anselin, L., and Florax, R. J. G. M. (2012). “New Directions in Spatial Econometrics: Introduction,” in New Directions in Spatial Econometrics (Heidelberg: Springer Science).
Anselin, L. (2010). Thirty Years of Spatial Econometrics. Pap. Reg. Sci. 89, 3–25. doi:10.1111/j.1435-5957.2010.00279.x
Broock, W. A., Scheinkman, J. A., Dechert, W. D., and LeBaron, B. (1996). A Test for Independence Based on the Correlation Dimension. Econ. Rev. 15 (3), 197–235. doi:10.1080/07474939608800353
Campbell, J. Y. (1991). A Variance Decomposition for Stock Returns. Econ. J. 101 (405), 157–179. doi:10.3386/w324610.2307/2233809
Chen, S., Zhang, Y., Zhang, Y., and Liu, Z. (2019). The Relationship between Industrial Restructuring and China's Regional Haze Pollution: A Spatial Spillover Perspective. J. Clean. Prod. 239, 115808. doi:10.1016/j.jclepro.2019.02.078
Chen, X., Zhang, L.-w., Huang, J.-j., Song, F.-j., Zhang, L.-p., Qian, Z.-m., et al. (2016). Long-term Exposure to Urban Air Pollution and Lung Cancer Mortality: A 12-year Cohort Study in Northern China. Sci. Total Environ. 571, 855–861. doi:10.1016/j.scitotenv.2016.07.064
Corrado, L., and Fingleton, B. (2012). Where Is the Economics in Spatial Econometrics?*. J. Reg. Sci. 52 (2), 210–239. doi:10.1111/j.1467-9787.2011.00726.x
Diks, C., and Panchenko, V. (2006). A New Statistic and Practical Guidelines for Nonparametric Granger Causality Testing. J. Econ. Dyn. Control 30 (9), 1647–1669. doi:10.1016/j.jedc.2005.08.008
Dong, K., Hochman, G., Kong, X., Sun, R., and Wang, Z. (2019). Spatial Econometric Analysis of China’s PM10 Pollution and its Influential Factors: Evidence from the Provincial Level. Ecol. Indic. 96, 317–328. doi:10.1016/j.ecolind.2018.09.014
Dong, Y., Shao, S., and Zhang, Y. (2019). Does FDI Have Energy-Saving Spill-Over Effect in China? A Perspective of Energy-Biased Technical Change. J. Clean. Prod. 234, 436–450. doi:10.1016/j.jclepro.2019.06.133
Du, Y., Sun, T., Peng, J., Fang, K., Liu, Y., Yang, Y., et al. (2018). Direct and Spillover Effects of Urbanization on PM2.5 Concentrations in China’s Top Three Urban Agglomerations. J. Clean. Prod. 190, 72–83. doi:10.1016/j.jclepro.2018.03.290
Elhorst, J. P. (2010). Applied Spatial Econometrics: Raising the Bar. Spat. Econ. Anal. 5 (1), 9–28. doi:10.1080/17421770903541772
Elhorst, J. P. (2014). Matlab Software for Spatial Panels. Int. Regional Sci. Rev. 37 (3), 389–405. doi:10.1177/0160017612452429
Engling, G., and Gelencsér, A. (2010). Atmospheric Brown Clouds: From Local Air Pollution to Climate Change. Elements 6 (4), 223–228. doi:10.2113/gselements.6.4.223
Fang, J. (2021). Impacts of High-Speed Rail on Urban Smog Pollution in China: A Spatial Difference-In-Difference Approach. Sci. Total Environ. 777, 146153. doi:10.1016/j.scitotenv.2021.146153
Geary, R. C. (1954). The Contiguity Ratio and Statistical Mapping. Inc. Stat. 5 (3), 115–145. doi:10.2307/2986645
Granger, C. W. J. (1969). Investigating Causal Relations by Econometric Models and Cross-Spectral Methods. Econometrica 37 (3), 424–438. doi:10.2307/1912791
Granger, C. W. J., and Newbold, P. (2014). Forecasting Economic Time Series. Pittsburgh: American Academic Press.
Grossman, G. M., and Krueger, A. B. (1995). Economic Growth and the Environment. Q. J. Econ. 110 (2), 353–377. doi:10.2307/2118443
Hao, Y., and Liu, Y.-M. (2015). The Influential Factors of Urban PM2.5, Concentrations in China: A Spatial Econometric Analysis. J. Clean. Prod. 112 (2), 1443–1453. doi:10.1016/j.jclepro.2015.05.005
Harris, R., Moffat, J., and Kravtsova, V. (2011). In Search of 'W'. Spat. Econ. Anal. 6 (3), 249–270. doi:10.1080/17421772.2011.586721
Hiemstra, C., and Jones, J. D. (1994). Testing for Linear and Nonlinear Granger Causality in the Stock Price-Volume Relation. J. Finance 49 (5), 1639–1664. doi:10.1111/j.1540-6261.1994.tb04776.x
Hsiao, C. (1981). Autoregressive Modelling and Money-Income Causality Detection. J. Monetary Econ. 7 (1), 85–106. doi:10.1016/0304-3932(81)90053-2
Kilian, L. (2001). Impulse Response Analysis in Vector Autoregressions with Unknown Lag Order. J. Forecast. 20 (3), 161–179. doi:10.1002/1099-131X(200104)20:3<161::AID-FOR770>3.0.CO;2-X
Lee, L.-f., and Yu, J. (2010). Some Recent Developments in Spatial Panel Data Models. Regional Sci. Urban Econ. 40 (5), 255–271. doi:10.1016/j.regsciurbeco.2009.09.002
Lee, S.-I. (2001). Developing a Bivariate Spatial Association Measure: An Integration of Pearson’s R, and Moran’s I. J. Geogr. Syst. 3, 369–385. doi:10.1007/s101090100064
Liu, H., and Pei, Y. (2019). Economic Development and China’s Urban Haze Pollution: Based on Spatial Correlation Networks. Chn. J. Urb. Environ.Stud 07 (2), 1950001. doi:10.1142/S2345748119500015
Lou, L., Li, J., and Zhong, S. (2021). Sulfur Dioxide (SO2) Emission Reduction and its Spatial Spillover Effect in High-Tech Industries: Based on Panel Data from 30 Provinces in China. Environ. Sci. Pollut. Res. 28, 31340–31357. doi:10.1007/s11356-021-12755-7
Lüthi, Z. L., Škerlak, B., Kim, S.-W., Lauer, A., Mues, A., Rupakheti, M., et al. (2015). Atmospheric Brown Clouds Reach the Tibetan Plateau by Crossing the Himalayas. Atmos. Chem. Phys. 15 (11), 6007–6021. doi:10.5194/acp-15-6007-2015
Ma, Y.-R., Ji, Q., and Fan, Y. (2016). Spatial Linkage Analysis of the Impact of Regional Economic Activities on PM2.5 Pollution in China. J. Clean. Prod. 139 (15), 1157–1167. doi:10.1016/j.jclepro.2016.08.152
Mao, X., Wang, L., Pan, X., Zhang, M., Wu, X., and Zhang, W. (2022). A Study on the Dynamic Spatial Spillover Effect of Urban Form on PM2.5 Concentration at County Scale in China. Atmos. Res. 269, 106046. doi:10.1016/j.atmosres.2022.106046
Moran, P. A. P. (1950). Notes on Continuous Stochastic Phenomena. Biometrika 37 (1), 17–23. doi:10.2307/2332142
Parent, O., and Lesage, J. P. (2008). Using the Variance Structure of the Conditional Autoregressive Spatial Specification to Model Knowledge Spillovers. J. Appl. Econ. 23 (2), 235–256. doi:10.1002/jae.981
Schlesinger, R. B. (2007). The Health Impact of Common Inorganic Components of Fine Particulate Matter (PM2.5) in Ambient Air: A Critical Review. Inhal. Toxicol. 19 (10), 811–832. doi:10.1080/08958370701402382
Shao, S., Yang, L., Yu, M., and Yu, M. (2011). Estimation, Characteristics, and Determinants of Energy-Related Industrial CO2 Emissions in Shanghai (China), 1994-2009. Energy Policy 39 (10), 6476–6494. doi:10.1016/j.enpol.2011.07.049
Shi, W., and Zhang, L. (2022). Does Technological Innovation Promote Haze Pollution Control? New Evidence Based on Panel Threshold Model and Spatial Econometric Model. Front. Environ. Sci. 9, 800460. doi:10.3389/fenvs.2021.800460
Tobler, W. R. (1970). A Computer Movie Simulating Urban Growth in the Detroit Region. Econ. Geogr. 46 (2), 234–240. doi:10.2307/143141
Wang, Z.-b., and Fang, C.-l. (2016). Spatial-temporal Characteristics and Determinants of PM2.5 in the Bohai Rim Urban Agglomeration. Chemosphere 148, 148–162. doi:10.1016/j.chemosphere.2015.12.118
Xie, R., Fang, J., and Liu, C. (2016). Impact and Spatial Spillover Effect of Transport Infrastructure on Urban Environment. Energy Proc. 104, 227–232. doi:10.1016/j.egypro.2016.12.039
York, R., Rosa, E. A., and Dietz, T. (2003). STIRPAT, IPAT and ImPACT: Analytic Tools for Unpacking the Driving Forces of Environmental Impacts. Ecol. Econ. 46 (3), 351–365. doi:10.1016/S0921-8009(03)00188-5
Zhang, M., Liu, X., Ding, Y., and Wang, W. (2019). How Does Environmental Regulation Affect Haze Pollution Governance? - an Empirical Test Based on Chinese Provincial Panel Data. Sci. Total Environ. 695, 133905. doi:10.1016/j.scitotenv.2019.133905
Zhang, X., Geng, Y., Shao, S., Song, X., Fan, M., Yang, L., et al. (2020). Decoupling PM2.5 Emissions and Economic Growth in China over 1998-2016: A Regional Investment Perspective. Sci. Total Environ. 714, 136841. doi:10.1016/j.scitotenv.2020.136841
Zhao, X., Ma, X., Chen, B., Shang, Y., and Song, M. (2022a). Challenges toward Carbon Neutrality in China: Strategies and Countermeasures. Resour. Conservation Recycl. 176, 105959. doi:10.1016/j.resconrec.2021.105959
Zhao, X., Ma, X., Shang, Y., Yang, Z., and Shahzad, U. (2022b). Green Economic Growth and its Inherent Driving Factors in Chinese Cities: Based on the Metafrontier-Global-SBM Super-efficiency DEA Model. Gondwana Res. 106, 315–328. doi:10.1016/j.gr.2022.01.013
Zhao, X., Mahendru, M., Ma, X., Rao, A., and Shang, Y. (2022c). Impacts of Environmental Regulations on Green Economic Growth in China: New Guidelines Regarding Renewable Energy and Energy Efficiency. Renew. Energy 187, 728–742. doi:10.1016/j.renene.2022.01.076
Zhou, Q., Zhong, S., Shi, T., and Zhang, X. (2021). Environmental Regulation and Haze Pollution: Neighbor-Companion or Neighbor-Beggar? Energy Policy 151, 112183. doi:10.1016/j.enpol.2021.112183
Keywords: asymmetric spatial interaction, socio-economic factors, sustainable development, PM2.5, haze pollution
Citation: Jia W and Pei Y (2022) Study on Socio-Economic Factors of Haze Pollution in the Context of Sustainable Development: Based on Asymmetric Interaction Effects Perspective. Front. Environ. Sci. 10:893650. doi: 10.3389/fenvs.2022.893650
Received: 10 March 2022; Accepted: 21 March 2022;
Published: 28 April 2022.
Edited by:
Lianbiao Cui, Anhui University of Finance and Economics, ChinaReviewed by:
Peixin Li, Shanghai Academy of Social Sciences, ChinaCopyright © 2022 Jia and Pei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yanfeng Pei, cGVpeWFuZmVuZzE5OTMwMUAxNjMuc3VmZS5lZHUuY24=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.