- 1National Oceanography Centre, Southampton, United Kingdom
- 2Freshwater Habitats Trust, Oxford, United Kingdom
- 3Climate Impacts Research Centre, Umeå University, Abisko, Sweden
- 4Department of Ecology and Environmental Science, Umeå University, Abisko, Sweden
Global-scale characterizations of Earth’s lakes and ponds assume their surface areas are power-law distributed across the full size range. However, empirical power-laws only hold across finite ranges of scales. In this paper, we synthesize evidence for upper and lower limits to power-law behavior in lake and pond size-distributions. We find support for the power-law assumption in general. We also find strong evidence for a lower limit to this power-law behavior, although the specific value for this limit is highly variable (0.001–1 km2), corresponding to orders of magnitude differences of the total number of lakes and ponds. The exact mechanisms that break the power-law at this limit are unknown. The power-law extends to the size of Earth’s largest lake. There is inconsistent evidence for an upper limit at regional-scales. Explaining variations in these limits stands to improve the accuracy of global lake characterizations and shed light on the specific mechanism responsible for forming and breaking lake power-law distributions.
1 Introduction
It is often asserted that lake sizes should be power-law distributed Russ (1994); Seekell et al. (2013); Cael et al. (2015); Cael and Seekell (2016); Mandelbrot (1983); Frank (2009). However, empirical power-laws hold across a finite range of scales and frequently exhibit exponential truncation, i.e., a finite system size cutoff. Such limits to power-law behavior are poorly explored for lakes, and estimates of global lake characteristics typically assume power-law behavior across the full size-distribution Downing (2009, 2010); Seekell and Pace (2011); Seekell et al. (2013); Cael and Seekell (2016). This is a critical assumption because ponds and small lakes are omitted from maps Benson and MacKenzie (1995); Seekell (2018). (n.b. throughout this paper we do not distinguish lakes from ponds by a cut-off area; “lake” refers to both lakes and ponds, i.e., stationary water bodies regardless of their surface area, or their residence time, which is uncharacterized for most lakes and ponds. Note we also do not consider depth or volume of lakes and ponds.). The abundance and area of these small lakes is therefore estimated by extrapolating a power-law fit of large, well mapped lakes Meybeck (1995); Birkett and Mason (1995); Ryanzhin (2005); Downing et al. (2006); Downing (2009, 2010); Messsager et al. (2016); Lazzarino et al. (2009); Minns et al. (2008); Chumchal et al. (2016); Seekell (2018); Tamrazyan (1974); Pace and Prairie (2005); Kastowski et al. (2011). This extrapolation will massively overestimate the abundance of lakes, which is important in particular for ecological metrics such as biodiversity and habitat connectivity Hill et al. (2018), if there are limits to power-law behavior not apparent when examining small numbers of large lakes in isolation Seekell and Pace (2011); McDonald et al. (2012); Seekell et al. (2013); Cael and Seekell (2016). These errors are propagated through subsequent analyses. For example, global estimates of photosynthesis in lakes are 45% higher when based on a full power-law distribution compared to a plausible alternate with lower limit to power-law behavior Lewis (2011).
Few studies have actually tested the goodness-of-fit of lake sizes to the power-law distribution Seekell and Pace (2011); Seekell et al. (2013). Such tests often indicate deviation from a power-law, but because these tests are applied across the full size range, it is unresolved if this deviation is due to the complete absence of power-law behavior or because power-law behavior is limited to certain scales Seekell and Pace (2011); Seekell et al. (2013). Lower-limits are likely because the approximate scale-invariance of topography that engenders power-law distributions breaks down at small-scales where there are strong imprints of scale-dependent geological processes Cael and Seekell (2016). Upper-limits to power-law distributions are also possible and have been hypothesized as components of some regional lake-size distributions where large lakes are unable to form within a finite area Hamilton et al. (1992); Cael et al. (2015). Identifying limits to power-law behavior stands to improve the accuracy of global lake characterizations, and also stands to shed light onto the specific mechanisms responsible for shaping lake size-distributions Cael and Seekell (2016).
In this paper, we synthesize the general evidence for a power-law lake size-distribution, as well as evidence for upper and lower limits to power-law behavior. We also contribute new empirical analyses aimed at resolving uncertainties relative to upper and lower limits. We argue that the development of alternate hypotheses for the form of the lake size-distribution and its generating processes, compared through the application of rigorous statistical analyses, is important for the advancement of global limnology.
2 Evidence for the power-law distribution
Empirical power-laws are ubiquitous in scientific reports, but the strength of evidence supporting these power-laws is often weak due lack of statistical support, lack of a generative mechanism, or both Stumpf and Porter (2012). Additionally, few empirical power-laws contribute genuinely new insights Stumpf and Porter (2012). In this context, the power-law distribution of lakes has a moderate level of support.
Widespread acceptance that lake areas may be power-law distributed is credited with precipitating a paradigm shift whereby environmental scientists recognized that there are many more lakes than previously believed, particularly small lakes, and that therefore lakes have a much greater contribution to the global system than previously believed Downing et al. (2006); Downing (2009, 2010, 2014). Historically, lakes were studied individually or as small groups in close proximity. The adoption of a power-law size-distribution is credited with providing a means of generalizing such studies to the global scale, ensuring the relevance of the entire discipline of limnology during a time of immense focus on global change Downing (2009, 2010, 2014). Hence, there is strong evidence that this power-law has led to transformation scientific insights, regardless of the actual level of statistical and mechanistic support. Despite its transformational impact, there is only moderate and incomplete evidence that lakes actually exhibit a power-law distribution. While there is substantial graphical support for a power-law distribution, this is a relatively weak form of evidence Mandelbrot (1963); Perline (2005); Seekell and Pace (2011) (Supplementary Material S1).
In general, the dynamic processes creating power-laws are poorly understood for lakes when compared to other landforms Mandelbrot (1983); Seekell et al. (2013, 2021). One conceptual model used to explain patterns of lake size and abundance is that depressions are randomly located on the landscape, with hypothetical flooding to outlets sills used to identify the location of lakes (e.g., Mandelbrot (1983); Cael et al. (2015); Cael and Seekell (2016); Goodchild (1988); Downing and Duarte (2009); Seekell et al. (2013); Bhang et al. (2019); Mandelbrot (1995)). Connected depressions represent lakes on river networks, with overlapping regions merging to become multi-basin lakes Cael and Seekell (2016); Goodchild (1988); Downing and Duarte (2009). This has been presented as analogous to the processes that give rise to power-laws in percolation theory, in level-set theory for self-similar surfaces, or in the theory of self-organised criticality Goodchild (1988); Seekell et al. (2013); Cael et al. (2015); Cael and Seekell (2016); Mandelbrot (1995); Blaudeck et al. (2006); Bak et al. (1987); Turcotte (1999). There is inconsistent evidence from these models for a generating mechanism. The primary merit of these models is their relative simplicity. Additionally, they typically provide dual criteria for evaluating data, the power-law form and a specific exponent, which is a much stronger test than examining functional form alone Goodchild (1988); Seekell et al. (2013); Cael and Seekell (2016). There have been mixed results when confronting these models with data. In one case, the global lake distribution for lakes ≥ O (1 km2), had the power exponent equal to that expected from percolation theory to four decimal places Messsager et al. (2016), though we note other theories can generate fairly similar exponents. In another case, lakes at the mean landscape elevation had approximately the same exponent as predicted by level set theory based on independent measures of the landscape’s fractal dimension Seekell et al. (2013). However, in other cases, lakes have failed to exhibit power-law behavior or failed to produce the expected power exponent, even under idealized conditions with simulated data Goodchild (1988); Cael and Seekell (2016); Bhang et al. (2019). The reasons for this variable performance have not been studied.
A common feature of these generating models is the assumption of a static, scale-invariant topography, but the actual geologic and hydrological processes responsible for lake formation and disappearance are scale-dependent and evolve over time Cael and Seekell (2016); Englund et al. (2013). The extent to which these simple models capture the collective behavior of these scale-dependent processes is not clear because few studies have sought to directly test theoretical frameworks Mandelbrot (1995); Goodchild (1988); Cael and Seekell (2016); Cael et al. (2015); Seekell et al. (2013). Additionally, it is difficult to discern what theoretical framework might be optimal, both because different frameworks predict similar results, and because the relevant dynamics often occur at temporal scales exceeding observational records Downing (2010).
3 Evidence for a lower limit
By definition, all power-law distributions have a positive lower limit Vidondo et al. (1997); Clauset et al. (2009); Newman (2005). If lakes are power-law distributed across their entire size spectra, this lower limit will be equal to the smallest sized water body that can be perceived by humans to be a lake Vidondo et al. (1997); Downing et al. (2006); Clauset et al. (2009); Newman (2005). Empirical size spectra are typically power-law distributed across part but not the full range of scales Clauset et al. (2009); Newman (2005). In this case there is a lower limit to power-law behavior which is greater than the smallest perceptible lake. This lower limit is visible on rank-size plots as a downward defection from a straight line among small lakes Seekell and Pace (2011); Cael and Seekell (2016); Newman (2005).
It has long been hypothesized that such deviations reflected the omission of small lakes in regional and global lake data sets Benson and MacKenzie (1995); Downing et al. (2006); Muster et al. (2013). While there is no doubt that mapping omission occurs and can contribute to this pattern, it is unlikely to be the primary cause because the defection typically begins with lakes that are much larger than the minimum reliably mapped size (i.e., the deflection is visible for lakes that are reliably mapped) Benson and MacKenzie (1995); Seekell (2018); Seekell and Pace (2011); Cael and Seekell (2016); Muster et al. (2013). For example, in one global study, the deflection began two orders higher than the minimum reliably mapped lake size Cael and Seekell (2016). We examined pond size data from the United Kingdom Centre for Ecology and Hydrology which completed a survey of randomly selected swaths of Britain, measuring all water bodies in those swaths down to 25 m2, totaling just over 1,000 small lakes. This dataset is thus unique in that the sample study design eliminates the possibility of systematic undersampling of smaller lakes. Departure from power-law behavior is clearly visible in these data despite the specific focus on counting very small ponds (Figure 1). Using the maximum likelihood estimation and bootstrap methodology of Clauset et al. Clauset et al. (2009), we estimated that this break point is 800 ± 400m2. The empirical distribution above this break point appears power-law distributed with an exponent τ = 2.04 ± 0.09 highly consistent with the theoretical expectation from percolation theory 187/91 = 2.054 Cael and Seekell (2016), though again we note that other theories can generate similar exponents. Another study specifically focused on very small lakes and ponds (
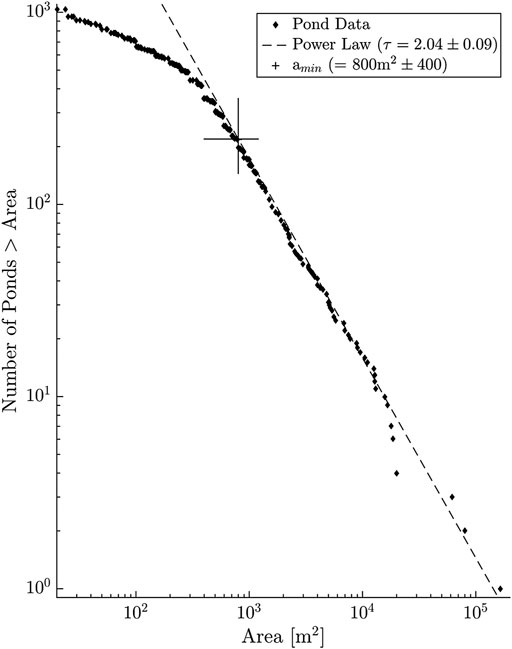
FIGURE 1. Number of ponds greater than a given area versus that area for the CEH dataset, fit by a power law. Diamonds correspond to empirical distribution; dashed line corresponds to a power-law fit with an exponent of 2.04 and a minimum area of 800 m2. Power-law parameters and uncertainties calculated according to Clauset et al. (2009). Note that the slope shown is for the cumulative distribution, which being an integral of the probability distribution has a slope 1 less.
There are several factors that could be responsible for the lower limit to power-law behavior. Earth’s topography is approximately scale-invariant at large scales, but the signature of scale-dependent geological processes can become strong at some smaller scales Dodds and Rothman (2000). This loss of invariance could be reflected in the lake size distribution Cael and Seekell (2016). Another factor could be size-dependent lake formation and destruction processes. For example, a study of lakes in northern Sweden found a power-law lake distribution on young landscapes, but not on older landscapes where small lakes were less abundant than predicted by the power-law distribution, presumably due to the cumulative effects of sedimentation during the longer landscape history Englund et al. (2013). The specific mechanisms that cause deviation from the power-law distribution, including those that cause loss of topography invariance, have not been enumerated but can include by geological processes (e.g., erosion, sedimentation) and human activities (e.g., urbanization, agriculture) that both form and destroy lakes Cael and Seekell (2016); Steele and Heffernan (2014, 2017); Hayes (2016). Quantitative assessments of the lower limit to power-law behavior are rare and current evidence does not allow discrimination among these processes. Visual evidence suggests that lower bounds may vary between 0.001 km2 and 1 km2, depending on the geographic region and scale of the analysis (cf. Downing et al. (2006); Cael and Seekell (2016); Seekell and Pace (2011)). Such a wide uncertainty in the value of the lower cutoff has tremendous implications for the total number of lakes (Supplementary Material S2). The quantification of these patterns, especially relative other landscape characteristics, is the first step to identifying the factors shaping lake size distributions.
4 Evidence for an upper limit
By definition, the upper tails of power-law size-distributions extend infinitely Vidondo et al. (1997); Clauset et al. (2009); Newman (2005). Strictly speaking, this is not possible for empirical power-laws because of Earth’s finite surface area Goodchild (1988); Hamilton et al. (1992); Barton and Pointe (1997). This can create an upper limit for power-law behavior, beyond which large lakes are scarcer than predicted by the power-law. On a rank-size plot, this appears as downward deflection by largest lakes relative to a straight line Hamilton et al. (1992); Cael et al. (2015); Barton and Pointe (1997). Graphical analyses of global-scale lake data by independent research groups using independent data sets have revealed no evidence of such an upper bound impacting the lake size distribution (i.e., the power-law fit is visually good for all large lakes) Meybeck (1995); Barton and Pointe (1997); Downing et al. (2006); Cael and Seekell (2016). However, there is graphical evidence for such boundaries in some smaller scale studies; for example an upper bound was reported for Amazonian floodplain lakes Hamilton et al. (1992). Graphical evaluation of lake size-distributions in the major eco-regions of the United States also suggests deviation from a power-law for large lakes McDonald et al. (2012). However, there is little statistical evidence for an upper limit to power-law behavior at the regional-scale because tests for these patterns are rarely applied. These are a major need because graphical evaluations using rank-size plots can be difficult to interpret and are sometimes misleading Perline (2005); Seekell and Pace (2011). Similar to for lower limits, quantifying the scales of power-law behavior is the first step to shedding light on the factors responsible for upper limits.
A common question related to upper limits is whether the Caspian Sea (374,000 km2) is a lake or a sea. This is relevant to the discussion of upper limits because the Caspian is sometimes excluded from analyses of the global lake size-distribution on the basis that it is an outlier Lehner and Döll (2004); Messsager et al. (2016). Additionally, there is great societal interest in this question. From 1991 to 2018, there was an international dispute relative to the status of the Caspian Sea, which had significant legal consequences for the distribution and extraction of hydrocarbon resources Pietkiewicz (2021); Zimnitskaya and von Geldern (2011). A quick search of many social media networks will reveal substantial and persistent interest in the question from the general public (our favorite is the reviews on Google Maps). In a sense this question relates to whether or not an upper-limit should be imposed on lake size-distributions.
From a limnological perspective, the Caspian Sea is a lake and there is no scientific debate about this status Dumont (1998). We have conducted an empirical analysis to settle the question of whether or not it is an outlier that should be considered differently from other lakes. Specifically, we used the lake size-distribution to develop expectations for the area of Earth’s largest lake by taking many times the largest of N random samples from a power-law distribution with a minimum size of 1 km2 and the same exponent as the lake size distribution, where N is the number of lakes on Earth with areas ≥1 km2. Note that the resulting distribution of maximum values is not itself a power-law. We did this one million times, and compared our simulated estimates with the areas of the Caspian Sea. We found that the Caspian Sea is between the 78th-87th percentile of the distribution depending on the estimates for the relevant parameters (area of Caspian Sea, N, and τ) (Figure 2). In other words, the Caspian Sea is well within the range of sizes expected for Earth’s largest lake, based on the scaling characteristics of its other lakes. Based on this analysis, the Caspian Sea would have to be 4.3x larger to be considered an outlier. For comparison, Earth’s oceans are larger than 99.99% of these simulated largest lake areas. Hence there is a distinct different between lakes and the ocean not seen when comparing lakes to the Caspian Sea. Collectively, these analyses indicate that there is no need to create an artificial upper-limit by excluding the Caspian Sea from lake size analyses.
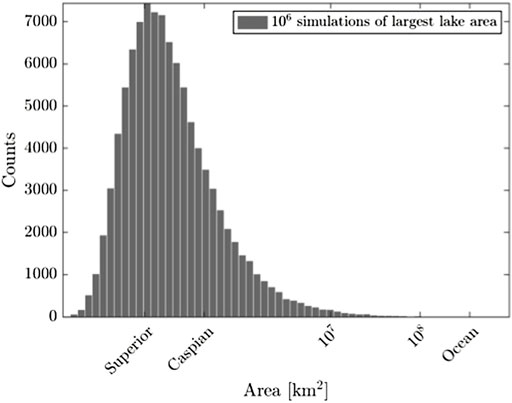
FIGURE 2. Histogram of 1,000,000 simulated values for the area of Earth’s largest lake, based on the total number of Earth’s lakes
5 Discussion
Application of the power-law size-distribution has had a transformational effect on the understanding of Earth’s lakes, but empirical evidence that lakes actually exhibit power-law behavior is still incomplete. Specifically, there has been an over-reliance on rank-size plots that are difficult to interpret when only large lakes are accurately mapped Mandelbrot (1963); Seekell and Pace (2011); Muster et al. (2013). There is a major need for the application of statistical goodness-of-fit tests, such as likelihood calculations and Kolmogorov-Smirnov-like statistics, both to support the general application of the power-law distribution and identify any limits to power-law behavior Clauset et al. (2009); Edwards et al. (2012). These tests have societal relevance because the power-law size distribution is the basis for most estimates of the global contributions of lakes to the carbon cycle, including some of those cited in IPCC reports (e.g., Tranvik et al. (2009); Bastviken et al. (2011)); they also have relevance for ecology, biogeochemistry, and even the study of other planets (Supplementary Material S3). Inclusion of values based on a power law assumption in high profile science-policy interfaces [e.g., Ciais et al. (2013)] engenders a responsibility to ensure accurate characterization, but rigorous evaluations are never completed prior to extrapolation and even cursory evaluations are rare (e.g., Lehner and Döll (2004); Meybeck (1995); Telmer and Costa (2007); Ryaanzhin (2010, 2015); Downing et al. (2006); Chumchal et al. (2016); Raymond et al. (2013); Lazzarino et al. (2009); Minns et al. (2008); Kastowski et al. (2011)). Application of goodness-of-fit tests is a simple and pragmatic way to fulfill this responsibility.
A limitation to the study of lake size-distributions is a lack of plausible alternate hypotheses. Perhaps without exception, every study that has evaluated lakes size distributions has done so based on the premise it should be power-law distributed [e.g., Mandelbrot (1983, 1995); Hamilton et al. (1992); Meybeck (1995); Lehner and Döll (2004); Downing et al. (2006); Messsager et al. (2016); Benson and MacKenzie (1995); Cael et al. (2015); Cael and Seekell (2016); Seekell et al. (2013); Lazzarino et al. (2009); Minns et al. (2008); Chumchal et al. (2016); Kastowski et al. (2011)]. This lack of alternate hypotheses is probably why there has been few substantive changes to the understanding of lake size distributions over the last 50 years Platt (1964). The development of plausible alternate hypotheses and generating mechanisms would promote a thorough understanding of the factors shaping lake size-distributions by forcing the consideration and rejection of alternate patterns and mechanisms, a process needed to engender robust results Chamberlin (1965); Platt (1964).
There is a growing number of regional and global lake databases based on either map compilations or remote sensing (e.g., Lehner and Döll (2004); Messsager et al. (2016); Feng et al. (2019); Verpoorter et al. (2014); Feng et al. (2015); Pekel et al. (2016); Rocher-Ros et al. (2017)). In the future, these data sets may reduce the need to extrapolate small lake abundance from the distribution of large lakes Verpoorter et al. (2014). This is a positive development given the magnitude of potential errors (e.g., a factor of 10, 100, or 1,000 over-/undercounting of total lakes and ponds) that can be caused by these extrapolations Seekell and Pace (2011); Seekell et al. (2013); Verpoorter et al. (2014). These developments do not diminish the need for a thorough characterization of lake size distributions. First and foremost, current global data sets do not have sufficient resolution to accurately resolve small lakes Verpoorter et al. (2014); Feng et al. (2015); Pekel et al. (2016); Downing (2010). There is still a need for improved extrapolation to estimate the abundance of these small systems. Second, improved data sets do not, on their own, resolve the fundamental questions related to the origins of lake size distributions. These new data sets do not supplant the analysis of lake size distributions, but are an important complement to them in advancing the fundamental understanding of lakes at the global scale.
6 Conclusion
Widespread acceptance of a power-law size-distribution for lakes precipitated a paradigm shift from local to global understanding of lakes. Despite this, there is still incomplete evidence for the power-law distribution. In particular, there is evidence for a lower-limit to power-law behavior. The power-law extends to the size of Earth’s largest lake, but exponential truncation may exist regionally. The factors determining the scales exhibiting power-law behavior are poorly studied. Resolving these uncertainties involves the application of rigorous statistics and the development of new alternate hypotheses. Quantifying scales of power-law behavior by identifying these limits is the first step to understanding the ultimate constraints on global-scale patterns of lake properties.
Data availability statement
The data analyzed in this study is subject to the following licenses/restrictions: Requests to access these datasets should be directed to ai5iaWdnc0BmcmVzaHdhdGVyaGFiaXRhdHN0cnVzdC5vcmcudWs=.
Author contributions
BC and DS conceived the study. BC performed analyses. Biggs provided data. BC and DS wrote the paper with input from JB.
Funding
This paper is based on research supported by the Knut and Alice Wallenberg Foundation and Umeå University.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.888735/full#supplementary-material
References
Bak, P., Tang, C., and Wiesenfeld, K. (1987). Self-organized criticality: An explanation of the 1/f noise. Phys. Rev. Lett. 59, 381–384. doi:10.1103/physrevlett.59.381
Barton, C. C., and Pointe, P. R. L. (1997). Fractals in petroleum geology and Earth processes. Berlin, Germany: Springer.
Bastviken, D., Tranvik, L. J., Downing, J. A., Crill, P. M., and Enrich-Prast, A. (2011). Freshwater methane emissions offset the continental carbon sink. Science 331, 50. doi:10.1126/science.1196808
Benson, B. J., and MacKenzie, M. D. (1995). Effects of sensor spatial resolution on landscape structure parameters. Landsc. Ecol. 10, 113–120. doi:10.1007/bf00153828
Bhang, K. J., Schwartz, F. W., Lee, H. W., and Park, S. S. (2019). Scaling effect of lake distribution on power law by coastal area simulation. J. Coast. Res. 91, 301–305. doi:10.2112/si91-061.1
Birkett, C. M., and Mason, I. M. (1995). A new global lakes database for a remote sensing program studying climatically sensitive large lakes. J. Gt. Lakes. Res. 21, 307–318. doi:10.1016/s0380-1330(95)71041-3
Blaudeck, P., Seeger, S., Schulzky, C., Hoffman, K. H., Dutta, T., and Tarafdar, S. (2006). The coastline and lake shores on a fractal island. J. Phys. A Math. Gen. 39, 1609–1618. doi:10.1088/0305-4470/39/7/006
Cael, B. B., Lambert, B., and Bisson, K. (2015). Pond fractals in a tidal flat. Phys. Rev. E 92, 052128. doi:10.1103/physreve.92.052128
Cael, B. B., and Seekell, D. A. (2016). The size-distribution of Earth’s lakes. Sci. Rep. 6, 29633. doi:10.1038/srep29633
Chamberlin, T. C. (1965). The method of multiple working hypotheses. Science 148, 754–759. doi:10.1126/science.148.3671.754
Chumchal, M. M., Drenner, R. W., and Adams, K. J. (2016). Abundance and size distribution of permanent and temporary farm ponds in the southeastern Great Plains. Inland Waters 6, 258–264. doi:10.5268/iw-6.2.954
Ciais, P., Sabine, C., Bala, G., and Peters, W. (2013). Carbon and other biogeochemical cycles. Cambridge: Cambridge University Press, 465–570.
Clauset, A., Shalizi, C. R., and Newman, M. E. J. (2009). Power-law distributions in empirical data. SIAM Rev. Soc. Ind. Appl. Math. 51, 661–703. doi:10.1137/070710111
Dodds, P. S., and Rothman, D. H. (2000). Scaling, universality, and geomorphology. Annu. Rev. Earth Planet. Sci. 28, 571–610. doi:10.1146/annurev.earth.28.1.571
Downing, J. A. (2010). Emerging global role of small lakes and ponds: Little things mean a lot. Limnetica 29, 9–24. doi:10.23818/limn.29.02
Downing, J. A. (2009). Global limnology: Up-scaling aquatic services and processes to planet Earth. SIL Proc. 1922-2010 30, 1149–1166. doi:10.1080/03680770.2009.11923903
Downing, J. A. (2014). Limnology and oceanography: Two estranged twins reuniting by global change. Inland Waters 4, 215–232. doi:10.5268/iw-4.2.753
Downing, J. A., Prairie, Y. T., Cole, J. J., Duarte, C. M., Tranvik, L. J., Striegl, R. G., et al. (2006). The global abundance and size distribution of lakes, ponds, and impoundments. Limnol. Oceanogr. 51, 2388–2397. doi:10.4319/lo.2006.51.5.2388
Dumont, H. J. (1998). The Caspian Lake: History, biota, structure, and function. Limnol. Oceanogr. 43, 44–52. doi:10.4319/lo.1998.43.1.0044
Edwards, A. M., Freeman, M. P., Breed, G. A., and Jonsen, I. D. (2012). Incorrect likelihood methods were used to infer scaling laws of marine predator search behaviour. PLoS One 7, e45174. doi:10.1371/journal.pone.0045174
Englund, G., Eriksson, H., and Nilsson, M. B. (2013). The birth and death of lakes on young landscapes. Geophys. Res. Lett. 40, 1340–1344. doi:10.1002/grl.50281
Feng, M., Sexton, J. O., Channan, S., and Townshend, J. R. (2015). A global, high-resolution (30-m) inland water body dataset for 2000: First results of a topographic-spectral classification algorithm. Int. J. Digit. Earth 9, 113–133. doi:10.1080/17538947.2015.1026420
Feng, S., Liu, S., Huang, Z., Jing, L., Zhao, M., Peng, X., et al. (2019). Inland water bodies in China: Features discovered in the long-term satellite data. Proc. Natl. Acad. Sci. U. S. A. 116, 25491–25496. doi:10.1073/pnas.1910872116
Frank, S. A. (2009). The common patterns of nature. J. Evol. Biol. 22, 1563–1585. doi:10.1111/j.1420-9101.2009.01775.x
Goodchild, M. F. (1988). Lakes on fractal surfaces: A null hypothesis for lake-rich landscapes. Math. Geol. 20, 615–630. doi:10.1007/bf00890580
Håkanson, L. (1994). How many lakes are there in Sweden? Geogr. Ann. Ser. A Phys. Geogr. 76, 203–205. doi:10.2307/521038
Hamilton, S. K., Melack, J. M., Goodchild, M. F., and Lewis, W. M. (1992). Lowland floodplain rivers : Geomorphological perspectives. Chichester, New York: Wiley, 145–163.
Hayes, A. G. (2016). The lakes and seas of titan. Annu. Rev. Earth Planet. Sci. 44, 57–83. doi:10.1146/annurev-earth-060115-012247
Heffernan, J. B., Soranno, P. A., Angilletta, M. J., Buckley, L. B., Gruner, D. S., Keitt, T. H., et al. (2014). Macrosystems ecology: Understanding ecological patterns and processes at continental scales. Front. Ecol. Environ. 12, 5–14. doi:10.1890/130017
Hill, M. J., Hassall, C., Oertli, B., Fahrig, L., Robson, B. J., Biggs, J., et al. (2018). New policy directions for global pond conservation. Conserv. Lett. 11, e12447. doi:10.1111/conl.12447
Kastowski, M., Hinderer, M., and Vecsei, A. (2011). Long-term carbon burial in European lakes: Analysis and estimate. Glob. Biogeochem. Cycles 25, GB3018. doi:10.1029/2010gb003874
Lapierre, J. F., Collins, S. M., Seekell, D. A., Cheruvelil, K. S., Tan, P. N., Skaff, N. K., et al. (2018). Similarity in spatial structure constrains ecosystem relationships: Building a macroscale understanding of lakes. Glob. Ecol. Biogeogr. 27, 1251–1263. doi:10.1111/geb.12781
Lazzarino, J. K., Bachmann, R. W., Hoyer, M. V., and Canfield, D. E. (2009). Carbon dioxide supersaturation in Florida lakes. Hydrobiologia 627, 169–180. doi:10.1007/s10750-009-9723-y
Lehner, B., and Döll, P. (2004). Development and validation of a global database of lakes, reservoirs and wetlands. J. Hydrol. X. 296, 1–22. doi:10.1016/j.jhydrol.2004.03.028
Lewis, W. M. (2011). Global primary production of lakes: 19th baldi memorial lecture. Inland Waters 1, 1–28. doi:10.5268/iw-1.1.384
Mandelbrot, B. B. (1963). New methods in statistical economics. J. Polit. Econ. 71, 421–440. doi:10.1086/258792
McDonald, C. P., Rover, J. A., Stets, E. G., and Striegl, R. G. (2012). The regional abundance and size distribution of lakes and reservoirs in the United States and implications for estimates of global lake extent. Limnol. Oceanogr. 57, 597–606. doi:10.4319/lo.2012.57.2.0597
Messsager, M. L., Lehner, B., Grill, G., Nedeva, I., and Schmitt, O. (2016). Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 7, 13603. doi:10.1038/ncomms13603
Meybeck, M. (1995). Global alteration of riverine geochemistry under human pressure. Berlin: Springer-Verlag, 1–36.
Minns, C. K., Moore, J. E., Shuter, B. J., and Mandrak, N. E. (2008). A preliminary national analysis of some key characteristics of canadian lakes. Can. J. Fish. Aquat. Sci. 65, 1763–1778. doi:10.1139/f08-110
Mosquera, P. V., Hampel, H., Vazquez, R. F., Alonso, M., and Catalan, J. (2017). Abundance and morphometry changes across the high-mountain lake-size gradient in the tropical andes of southern Ecuador. Water Resour. Res. 453, 7269–7280. doi:10.1002/2017wr020902
Muster, S., Heim, B., Abnizova, A., and Boike, J. (2013). Water body distributions across scales: A remote sensing based comparison of three arctic tundra wetlands. Remote Sens. (Basel). 5, 1498–1523. doi:10.3390/rs5041498
Newman, M. (2005). Power laws, pareto distributions and zipf’s law. Contemp. Phys. 46, 323–351. doi:10.1080/00107510500052444
Oertli, B., and Frossard, P. A. (2013). Mares et étangs: Ecologie, conservation, gestion, valorisation. Lausanne, Switzerland: PPUR Presses polytechniques.
Pace, M. L., and Prairie, Y. T. (2005). Respiration in aquatic ecosystems. New York: Oxford University Press, 104–121.
Pekel, J. F., Cottam, A., Gornglick, N., and Belward, A. S. (2016). High-resolution mapping of global surface water and its long-term changes. Nature 540, 418–422. doi:10.1038/nature20584
Perline, R. (2005). Strong, weak and false inverse power laws. Stat. Sci. 20, 68–88. doi:10.1214/088342304000000215
Pietkiewicz, M. (2021). Legal status of caspian sea - problem solved? Mar. Policy 123, 104321. doi:10.1016/j.marpol.2020.104321
Raymond, P., Hartmann, J., Lauerwald, R., Sobek, S., McDonald, C., Hoover, M., et al. (2013). Global carbon dioxide emissions from inland waters. Nature 503, 355–359. doi:10.1038/nature12760
Rocher-Ros, G., Giesler, R., Lundin, E., Salimi, S., Jonsson, A., and Karlsson, J. (2017). Large lakes dominate co2 evasion from lakes in an arctic catchment. Geophys. Res. Lett. 44, 12254–12261.
Ryaanzhin, S. V., Myakisheva, N. V., and Zhumangaliev, Z. M. (2015). Morphometric and hydrochemical characteristics of Kazakhstan lakes. Water Resour. 42, 658–669. doi:10.1134/s0097807815050139
Ryaanzhin, S. V. (2010). Polar lakes of the world: Current data and status of investigation. Water Resour. 37, 427–436.
Ryanzhin, S. V. (2005). New estimates for global surface area and volume or natural world lakes. Dokl. Earth Sci. 401, 253–257.
Seekell, D. A., and Pace, M. L. (2011). Does the pareto distribution adequately describe the size-distribution of lakes? Limnol. Oceanogr. 56, 350–356. doi:10.4319/lo.2011.56.1.0350
Seekell, D. A. (2018). Patterns and variation of littoral habitat size among lakes. Umeå, Sweden: Kungliga Skytteanska Samfundet, 109–119.
Seekell, D., Cael, B., Lindmark, E., and Byström, P. (2021). The fractal scaling relationship for river inlets to lakes. Geophys. Res. Lett. 48, e2021GL093366. doi:10.1029/2021gl093366
Seekell, D., Pace, M. L., Tranvik, L. J., and Verpoorter, C. (2013). A fractal-based approach to lake size-distributions. Geophys. Res. Lett. 40, 517–521. doi:10.1002/grl.50139
Soranno, P. A., Cheruvelil, K. S., Webster, K. E., Bremigan, M. T., Wagner, T., and Stow, C. A. (2010). Using landscape limnology to classify freshwater ecosystems for multi-ecosystem management and conservation. BioScience 60, 440–454. doi:10.1525/bio.2010.60.6.8
Steele, M. K., and Heffernan, J. B. (2017). Land use and topography bend and break fractal rules of water body size-distributions. Limnol. Oceanogr. Lett. 2, 71–80. doi:10.1002/lol2.10038
Steele, M. K., and Heffernan, J. B. (2014). Morphological characteristics of urban water bodies: Mechanisms of change and implications for ecosystem function. Ecol. Appl. 24, 1070–1084. doi:10.1890/13-0983.1
Stumpf, M. P. H., and Porter, M. A. (2012). Critical truths about power laws. Science 335, 665–666. doi:10.1126/science.1216142
Tamrazyan, G. P. (1974). Total lake water resources of the planet. Bull. Geol. Soc. Finl. 46, 23–27. doi:10.17741/bgsf/46.1.004
Telmer, K. H., and Costa, M. P. F. (2007). Sar-based estimates of the size distribution of lakes in Brazil and Canada: A tool for investigating carbon in lakes. Aquat. Conserv. 17, 289–304. doi:10.1002/aqc.854
Tranvik, L. J., Downing, J. A., Cotner, J. B., Loiselle, S. A., Striegl, R. G., Ballatore, T. J., et al. (2009). Lakes and reservoirs as regulators of carbon cycling and climate. Limnol. Oceanogr. 54, 2298–2314. doi:10.4319/lo.2009.54.6_part_2.2298
Turcotte, D. L. (1999). Self-organized criticality. Rep. Prog. Phys. 62, 1377–1429. doi:10.1088/0034-4885/62/10/201
Vadeboncoeur, Y., and Steinman, A. D. (2002). Periphyton function in lake ecosystems. Sci. World J. 2, 1449–1468. doi:10.1100/tsw.2002.294
Verpoorter, C., Kutser, T., Seekell, D. A., and Tranvik, L. J. (2014). A global inventory of lakes based on high-resolution satellite imagery. Geophys. Res. Lett. 41, 6396–6402. doi:10.1002/2014gl060641
Vidondo, B., Prairie, Y. T., Blanco, J. M., and Duarte, C. M. (1997). Some aspects of the analysis of size spectra in aquatic ecology. Limnol. Oceanogr. 42, 184–192. doi:10.4319/lo.1997.42.1.0184
Keywords: limnology, lake size distribution, caspian sea, pond abundance, power law
Citation: Cael BB, Biggs J and Seekell DA (2022) The size-distribution of earth’s lakes and ponds: Limits to power-law behavior. Front. Environ. Sci. 10:888735. doi: 10.3389/fenvs.2022.888735
Received: 03 March 2022; Accepted: 19 July 2022;
Published: 16 August 2022.
Edited by:
Angela Helen Arthington, Griffith University, AustraliaReviewed by:
Markus Aschwanden, Lockheed Martin, United StatesCopyright © 2022 Cael, Biggs and Seekell. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: B. B. Cael, Y2FlbEBub2MuYWMudWs=; D. A. Seekell, ZGF2aWQuc2Vla2VsbEB1bXUuc2U=
 B. B. Cael
B. B. Cael Jeremy Biggs2
Jeremy Biggs2 D. A. Seekell
D. A. Seekell