Trade-Offs in the Water-Energy-Ecosystem Nexus for Cascade Hydropower Systems: A Case Study of the Yalong River, China

The hydropower system’s water-energy-ecosystem nexus (WEEN) has gained particular focus in the last years. The water-use trade-offs between hydropower and ecosystem maintenance are complex and variable for cascade hydropower systems, leading to challenges in water resources management and sustainable development of hydropower. To understand the trade-off in the WEEN of cascade hydropower systems and their changes, a WEEN model using the multi-objective optimization approach is developed in this study, including maximizing cascade power generation, minimizing reservoir water footprint, and minimizing amended annual proportional flow deviation. These optimization objectives characterize the nexus’s water, energy, and ecosystem sectors. And the Pareto non-inferiority solutions are obtained by the third edition of the Non-dominated Sorting Genetic Algorithm. Also, we novelly propose an evaluation index called the Multi-objective Trade-off Index (MTI), a quantitative method with clear physical meaning to explore the trade-offs as revealed between different objectives by the solutions. A case study of the Yalong River, China, has shown that: 1) the larger the incoming water is, the more beneficial to the power generation and ecological benefits of the hydropower system; and 2) the trade-off degrees of the water sector with respect to energy-ecosystem and energy sector with respect to water-ecosystem decreases when the hydrological condition changes from wet to dry, while the degree of ecosystem sector with respect to water-energy increases. In general, the proposed MTI that quantifies trade-offs in the WEEN of cascade hydropower systems is efficient and feasible. Meanwhile, the MTI is also generic and can be applied to other multi-objective optimization problems.

1 Introduction

The water-energy -ecosystem nexus (WEEN) is a focus of much research (Kuriqi et al., 2020; Vinca et al., 2021; Yadav et al., 2021). Hydropower is an important part of WEEN, which is interconnected and interdependent with other sectors of the nexus (Zhang et al., 2018b). Specifically, hydropower plants (HPs) use the kinetic and potential energy of water to generate clean energy (hydropower), and at the same time, reservoirs with regulating capacity provide water for downstream irrigation areas and towns; on the other hand, dams block rivers and affect the survival and reproduction of fish, which may cause enormous adverse impacts on the downstream river ecosystem (Suwal et al., 2020; Kuriqi et al., 2021). This means that there are significant water-use trade-offs between water, energy, and ecosystem sectors for hydropower systems (Zhang et al., 2018b), i.e., the benefit achieved by one objective is often realized at the expense of other objectives (Ma et al., 2020). With rapid population growth, social and economic development, and climate change, coupled with the rapid development of hydropower and the completion of a large number of cascade hydropower systems, the trade-off has become particularly complex and variable. Hence, quantifying the trade-offs in the WEEN for cascade hydropower systems is a challenge and is key to a more comprehensive understanding of hydropower sustainability for decision-makers and stakeholders.

Multi-objective optimization is a crucial tool to identify and analyze the potential trade-offs in the WEEN (Li et al., 2019) and is widely used in hydropower systems(Si et al., 2019; Niu et al., 2021; Wu et al., 2021). For instance, Si et al. (2019) analyzed the trade-off of water-energy-food in the Upper Yellow River Basin through the multi-objective optimization of the cascade reservoirs and determined the benefits of water-energy-food through the operation mode of the Longyangxia Reservoir. However, it is inadequate to obtain the Pareto non-inferiority solutions alone but also needs to explore further the degree of trade-offs as revealed between different objectives by the solutions, which helps decision-makers make more informed operational modes (Unal et al., 2016).

In recent years, various techniques aiming to analyze trade-offs between different objectives in hydropower systems from the perspective of the Pareto non-inferiority solutions have been developed. These methods can be roughly classified into two categories: qualitative and quantitative methods. The qualitative method is usually called pair-wise visualization; that is, the high-dimensional Pareto non-inferiority solution space (Dimension >2) is projected separately in pairs to the two-dimensional plane, which is used to analyze trade-offs between pairs of objectives (Wang et al., 2020; Yu et al., 2021). For instance, Yu et al. (2021) found that there are clear trade-offs between hydropower generation and river ecosystem protection in the Yalong River with the pair-wise visualization method and noted that with the increasing environmental flow requirements, the generation benefits of hydropower systems had decreased significantly. Similarly, Bian et al. (2019) employed the visualization method to reveal the trade-offs between hydropower generation and other objectives in the Yellow River. Their results showed that an increase in the water supply rate would reduce the head of the hydropower plant. However, the disadvantage of the method is evident, as it does not directly show the degree of trade-offs between different objectives.

The quantitative method mainly contains fitting curves and evaluation index methods, which can quantify the degree of trade-offs between different objectives in the multi-objective operation for the cascade HPs and effectively overcome the shortcomings of the qualitative analysis method. The fitted curve method quantifies the trade-offs between objectives by establishing a linear or nonlinear fitting function of the Pareto non-inferiority solutions (Wu et al., 2020). However, this method performs better for two-objective optimization problems; for many-objective optimization problems, the results usually have significant uncertainty, i.e., the Pareto surface produced by each calculation with heuristic algorithms has certain randomness affects the fitted function and thus the analysis of the trade-off.

The evaluation index method measures the trade-off between different objectives by indices extracted from Pareto non-inferiority solutions has the advantages of low complexity, low data requirements, and ease of implementation. Chen et al. (2020) employed the Kendall rank correlation coefficient to evaluate the trade-offs between the water, energy, and ecosystem sectors in the Mekong River Basin. However, the index can only measure the degree of correlation between pairs of objectives. Tang et al. (2019) proposed the Conflict Evaluation Index to quantify trade-offs between objectives in a six-objective reservoir operation problem. Likely, Wu et al. (2021) developed the Multi-objective Correlation Index to quantify the complicated trade-off between hydropower generation, water supply, and ecology of a multi-objective reservoir operation. Unfortunately, the physical meaning of the above assessment indexes is not clear enough to answer similar questions: an increase or decrease of a unit in power generation benefits causes changes in ecological, water supply, and other objective benefits.

The main purposes of this study are: 1) to quantify trade-offs in the water-energy-ecosystem nexus of cascade hydropower systems and their changes under varied hydrological conditions; 2) to propose a new quantitative trade-off analysis method with clear physical meaning from the perspective of the Pareto non-inferiority solutions. For these purposes, we developed a WEEN model using the multi-objective optimization approach, including three objectives: maximizing cascade power generation, minimizing reservoir water footprint, and minimizing amended annual proportional flow deviation of the watershed outlet, and the Pareto non-inferiority solutions are obtained by the third edition of the Non-dominated Sorting Genetic Algorithm. Also, we novelly proposed an evaluation index called Multi-objective Trade-off Index (MTI), a quantitative method with clear physical meaning, to quantify the complex trade-offs of the cascade hydropower system. Yalong River cascade hydropower plants were taken as a case study to verify the effectiveness of the proposed MTI. This study can help managers gain a more comprehensive understanding of the trade-offs between different objectives of hydropower systems and make more appropriate operation decisions.

The rest of this paper is organized as follows. Section 2 provides the details of the case study, including the study area and basic data pertaining thereto. Section 3 provides the details of the trade-off analysis framework and the methods involved. Section 4 shows the results of the multi-objective optimization and trade-off analysis. The impacts of external environmental conditions on trade-offs in the WEEN, the implications of the proposed MTI and its limitations and potential for improvement have been discussed in Section 5. Finally, Section 6 presents the conclusions of this study.

2 Study Area and Basic Data

2.1 Study Area

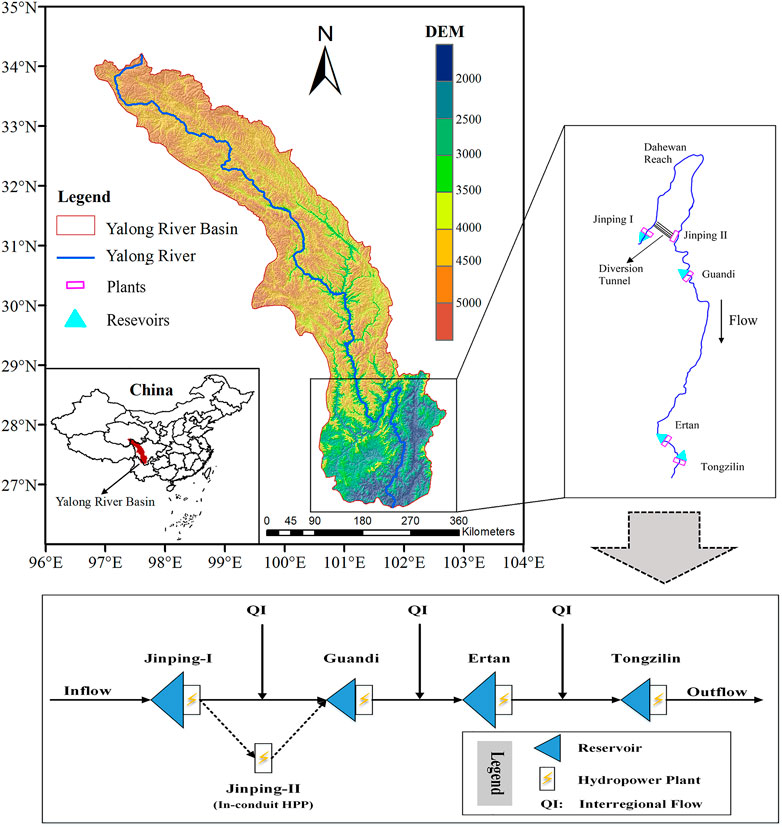
The cascade HPs of the downstream Yalong River (southwest China) were taken as a case study, which is one of the thirteen state hydropower bases in China with an installed capacity of 14.7 GW and an annual power generation of 74.6 TWh (Figure 1). The cascade hydropower system includes five HPs, that is, Jinping-I, Jinping-II, Guandi, Ertan, and Tongzilin, which have different levels of regulation capacity, including annual, seasonal, and daily. Jinping-II is an in-conduit HP and a 119 km dewatered river reach is formed between the water intake and the hydropower plant, which leads to more serious ecological problems. The characteristic parameters of these HPs are shown in Supplementary Table S1. In addition, the primary function of the Yalong River cascade HPs is to power generation, followed by flood control, and maintenance of ecological water in the river, with no water supply for irrigation, residential or industrial use (Yu et al., 2019).

FIGURE 1

FIGURE 1. Study area.

2.2 Basin Data

This study sets the hydrological year and scheduling period of the basin from November to October based on the flood time (June to October) and storage time (the reservoir reaches its normal level at the end of October) of the Yalong River basin. Besides, three typical years, i.e., wet year (2012, p = 10%), normal year (2015, p = 50%), and dry year (2006, p = 90%), are selected for input into the optimization operation model according to the water flow data of the HPs from 1958 to 2018. The inflow to, interregional flow from, and evaporation from the cascade HPs were collected from the China Annual Hydrological Reports, which lists in Supplementary Figure S1 and Supplementary Table S2. Considering the environmental flow requirements in the downstream reach of the river, the HPs need to release a minimum flow as listed in Supplementary Table S2.

3 Methodology

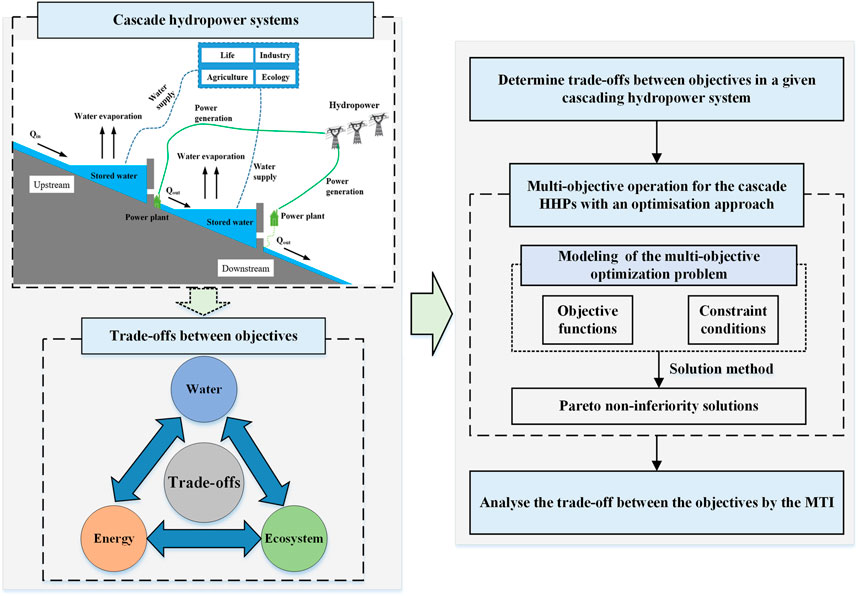
An overview of the methodological framework to quantify the trade-off in the WEEN of cascade hydropower systems is presented in Figure 2. In general, the framework consists of three main steps. The first step is to determine which sectors of the cascade hydropower system (water, energy, food, ecosystem, etc.) have trade-offs with each other. The second step is the multi-objective operation for the cascade hydropower system with an optimization approach, including modeling and solving the multi-objective optimization problem. The third step is to analyze the trade-off between different objectives. Here, we novelly proposed a trade-off analysis index with clear physical meaning based on the concept of change rate, called the MTI.

FIGURE 2

FIGURE 2. The methodological framework of trade-off analysis for cascade hydropower systems.

3.1 Water-Energy-Ecosystem Trade-offs in Cascade Hydropower Systems

Hydropower is considered a non-water user and does not directly consume water resources, but there are two indirect pathways to utilize water resources for a hydropower-reservoir system (Zhang et al., 2018a) (Figure 2). The first pathway is the water evaporated from the open water surface of reservoirs, i.e., the reservoir water footprint (RWF) (Mekonnen and Hoekstra, 2012). As the water level of the reservoir increases, so does the open water surface of the reservoir, and the increased evaporation will match the increased the open water surface. Another pathway is the spatio-temporal occupation of water resources by their storage in the reservoir. An ecological flow (Q_out, Figure 2) must be maintained for the HPs to protect the riverine ecosystem. Through water storage of the reservoir for hydropower production and water supply, this water storage is provided at the cost of a significant reduction in the original Q_out, which inevitably affects the ecosystem downstream (Zhang et al., 2018a). Besides, the biodiversity and ecosystem integrity of the river is the best under natural hydrological conditions (Poff et al., 1997). Human activities have altered the hydrology of rivers, such as those associated with the construction of reservoirs, water intakes, and water diversions. For rivers that have been affected by reservoirs and dams, imitating the natural flow process can reduce its adverse effects on the ecological environment of the river to a certain extent (Shiau and Wu, 2013). The mended annual proportional flow deviation (AAPFD) (Ladson et al., 1999) measures the extent of changes in the hydrological process before and after the reservoir operation, which is one of the effective indicators for quantitatively describing the impact of reservoir operation on river ecosystems. Overall, combining the characteristics and functions of the cascade hydropower system of the Yalong River (i.e., hydropower generation, flood control, and securing ecological flows), the cascade hydropower systems have clear water-use trade-offs between water, energy, and the ecosystem.

3.2 Water-Energy-Ecosystem Nexus Model

Multi-objective optimization can quantify and analyze the potential trade-offs between different objectives, which is an essential tool for the multi-objective operation of cascade hydropower systems. (Zeng et al., 2017). Therefore, we combined the above analysis to develop a multi-objective optimization model for the cascade hydropower system in the Yalong River to reveal the trade-off relationship between its objectives. Specifically, the reservoir water footprint, cascade power generation and AAPFD characterize the water objective, energy objective, and ecosystem objective in the trade-off relationship, respectively. For the flood control of the hydropower system, we achieved this by setting the upper water level during flood season, i.e., the constraint of the model. Thus, the optimization model contains three objectives, i.e., maximizing cascade power generation, minimizing reservoir water footprint, and minimizing amended annual proportional flow deviation of the watershed outlet. The ecological flow and other objectives are considered as constraint conditions. Moreover, the main reservoirs and HPs in the Yalong River were generalized into nodes and the reservoir inflows and outflows were generalized into links to obtain the topological relationship of the study area (Figure 1), which is the physical structure of the WEEN model.

3.2.1 Objective Functions

(1) Energy objective: maximize cascade power generation (CPG)

$\mathbf{Maximize} CPG={\displaystyle \sum }_{i=1}^n{\displaystyle \sum }_{t=1}^T{\eta }_i{H}_{i,t}{Q}_{i,t}^{tur}\mathbf{\Delta }t(1)$

where n represents the number of HPs; T is the number of time periods in the operation period (T = 12); ${\eta }_i$ is comprehensive efficiency coefficient of the ith HP; $H_{i,t}$ denotes the average water head at time t (m); $Q_{i,t}^{tur}$ is the flow through the turbine during power generation (m³/s); $\mathbf{\Delta }t$ is the time step (s).

(2) Water objective: minimize reservoir water footprint of cascade HPs (RWF)

Water footprint analysis can reveal the trade-off between water and energy of hydropower systems (Vaca-Jimenez et al., 2019). Thus, this study employed the RWF to assess water consumption by hydropower for cascade HPs (Mekonnen and Hoekstra, 2012). It should be noted that the evaporation from the original riparian is likely to be negligible for the mountainous rivers because the area of the reservoir is usually much larger than the original river. Also, the main function of the Yalong River cascade HPs is power generation. Thus, the allocation coefficient of the water footprint for functions (e.g., irrigation and water supply) is not considered in this study (Liu et al., 2015).

Thus, the monthly and annual $W{F}_{res}$ (m³) are calculated as follows:

$W{F}_{res,m}\left[t\right]=10\times h_E\left[t\right]\times A\left[t\right](2)$

$W{F}_{res,y}={\displaystyle \sum }_{t=1}^{12}W{F}_{res,m}\left[t\right](3)$

where $W{F}_{res,m}\left[t\right]$ is the RWF on month t (m³/month); factor 10 is applied to convert millimeters into cubic meters per hectare; $h_E\left[t\right]$ is the annual average water evaporation from the open water surface of the reservoir in month t (mm/month); $A\left[t\right]$ is the open water surface area of the reservoir in month t (ha); $W{F}_{res,y}$ represents the annual RWF (m³/year).

The minimizing RWF of cascade HPs is given by:

$\mathbf{Minimize} RWF={\displaystyle \sum }_{i=1}^{n}W{F}_{res,y}^i(4)$

where $W{F}_{res,y}^i$ is the annual RWF in the ith HP (m³).

(3) Ecosystem objective: minimize amended annual proportional flow deviation of the watershed outlet (AAPFD)

Here, we employed the AAPFD (Ladson et al., 1999) as the ecosystem objective, which can measure the extent of changes in the hydrological process before and after the reservoir operation. This indicator characterizes the degree of flow alteration: it is more sensitive when identifying the effect of changes in the runoff on the ecological environment of the river and can better reflect the ecological condition of the river (Ladson et al., 1999). The larger the value of the AAPFD, the greater the change in flow from natural conditions after reservoir operation, and the poorer the ecological condition of the river (Ladson et al., 1999). The specific expression is as follows:

$\mathbf{Minimize} AAPFD={\left[{\displaystyle \sum }_{t=1}^T{\left(\frac{Q_{tzl, t}-Q_{tzl, t}^N}{\overline{Q_{tzl}^N}}\right)}^2\right]}^{0.5}(5)$

where $Q_{tzl, t}$. is the outflow of the Tongzilin HP at time t under joint operation of cascade HPs (m³/s); $Q_{tzl, t}^N$. is the natural flow of the Tongzilin HP at time t (m³/s); $\overline{Q_{tzl}^N}$ the average value of the natural flow through the Tongzilin HP during the operation period (m³/s).

3.2.2 Constraint Conditions

The WEEN model of the Yalong River cascade HPs includes the following constraints:

(1) Water balance constraint

$V_{i,t+1}=V_{i,t}+\left(I_{i,t}-Q_{i,t}\right)\mathbf{\Delta }t-E_{i,t}-L_{i,t}(6)$

where $V_{i,t+1}$ and $V_{i,t}$ are the average storage of reservoir i in the (t + 1)^th and tth periods, respectively (m³); $I_{i,t}$ and $Q_{i,t}$ are the average inflow and outflow of reservoir i at time t (m³/s), respectively; $E_{i,t}$ and $L_{i,t}$ refer to the evaporation and leakage of reservoir i at time t (m³).

(2) Water level constraints

$Z_{i,t}^{lower}\le Z_{i,t}\le Z_{i,t}^{upper}(7)$

where $Z_{i,t}$ denotes the average water level of the reservoir i at time t (m); $Z_{i,t}^{lower}$ and $Z_{i,t}^{upper}$ refer to the lower and upper water levels of reservoir i at time t, respectively (m).

(3) Discharge flow constraints

$Q_{i,t}^{\mathit{min}}\le Q_{i,t}\le Q_{i,t}^{\mathit{max}}(8)$

where $Q_{i,t}^{min}$ and $Q_{i,t}^{max}$ denote the minimum and maximum discharges from reservoir i at time t, respectively (m³/s).

(4) Output constraints

$N_{i,t}^{\mathit{min}}\le N_{i,t}\le N_{i,t}^{\mathit{max}}(9)$

where $N_{i,t}^{min}$ and $N_{i,t}^{max}$ refer to the minimum and the maximum power output of HP i at time t (MW); $N_{i,t}$ refers to power output of HP i at time t (MW).

3.3 Solution Method

The above WEEN model is a nonlinear, multi-objective, and multi-constrained complex optimization problem, and it is generally difficult to obtain the optimal solution mathematically. With modern optimization techniques, intelligent methods have emerged to provide new ways for solving such optimization problems. Multi-objective genetic algorithms are well suited for solving multi-objective optimization problems because of their fast convergence speed, diversity of solution set space, and strong optimization-seeking ability. Thus, we selected the third edition of the non-dominated sorting genetic algorithm, updated by introducing a reference-point-based selection mechanism compared to the second edition of the non-dominated sorting genetic algorithm. This algorithm also inherits most of the functions of the second edition algorithm that have the advantages of rapidity and good convergence (Deb et al., 2002; Jain and Deb, 2014). The algorithm was widely used in solving the multi-objective optimization problems for hydropower systems (Gupta et al., 2020; Zhou et al., 2020; Liu et al., 2021).

Here, we selected three typical years (i.e., wet year, normal year, and dry year) as hydrological conditions, with 1 month as the time step and water level as the decision variable, and used the constraint transformation method to deal with the constraint conditions (more details in Yu et al. (2021)). In addition, the parameters of the third edition of the non-dominated sorting genetic algorithm were set in Supplementary Table S3 and coded in Python.

3.4 The Multi-Objective Trade-off Index

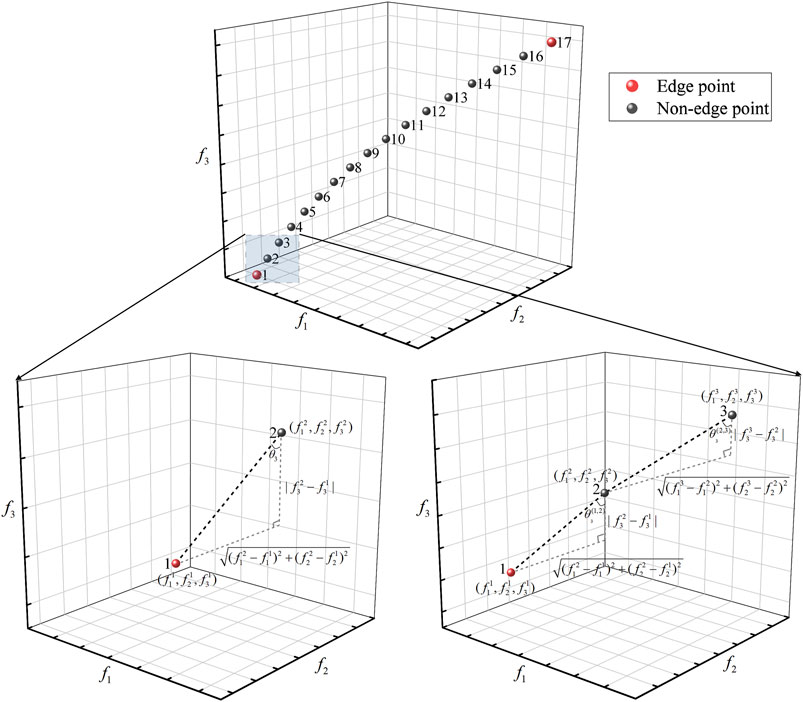
To quantify the water-energy-ecosystem trade-offs of cascade hydropower systems, a trade-off analysis index with clear physical meaning, the MTI, is proposed based on the concept of change rate. In a multi-objective optimization problem, for a specific objective, a 1-unit increase (or decrease) in the value of other objectives requires a ∆-unit decrease (or increase) in the value of that objective to replace it, that is., the concept of the MTI. Based on the feature that each point of the Pareto non-inferiority solution space has different change rates, the specific calculation steps of the MTI for the three-objective optimization problem are as follows.

Step 1 Sorting and numbering of Pareto non-inferiority solutionsThe three-objective optimization problem is solved to obtain a three-dimensional Pareto non-inferiority solution space, each point of which corresponds to a non-inferiority solution. The Pareto non-inferiority solutions are sorted and numbered according to a certain objective value.

Step 2Definition of adjacent pointWhen analyzing the interrelationship of points in the three-dimensional Pareto non-inferiority solution space, it is necessary to define the adjacent points. Adjacent points refer to points that are close to and monotonically related to a given point i. Specifically: Let $f_n$ be the function value of three objectives (n = 1, 2, 3), and points $i^{\text{'}}$ and $i^{\text{'}\text{'}}$ are the points on both sides of point i. When these three points satisfy the closest distance and there exists $f_n^{i^{\text{'}}}>f_n^i>f_n^{i^{\text{'}\text{'}}}$ or $f_n^{i^{\text{'}}}<f_n^i<f_n^{i^{\text{'}\text{'}}}$ (n = 1, 2, 3), then points $i^{\text{'}}$ and $i^{\text{'}\text{'}}$ are adjacent points of point i. In particular, when two adjacent points cannot be found for a given point i, the point nearest to the point i and satisfying $f_n^{i^{\text{'}}}\ne f_n^i$ (n = 1, 2, 3) is taken as the adjacent point. When there are two adjacent points of point i, it is a non-edge point of Pareto non-inferior solution space; when there is only one adjacent point of point i, it is an edge point of Pareto non-inferior solution space.

Step 3Calculation of MTI for single pointFor non-edge points, the MTI of point i is the average of the cotangent of the vector formed by the point and its two adjacent points with each of the objective function axes; for edge points, the MTI of point i is the cotangent of the vector formed by the point and its adjacent point with each of the objective function axes.The non-edge point i:

$k_n^i=\frac{\mathit{cot}{\theta }_n^{\left(i^{\prime },i\right)}+\mathit{cot}{\theta }_n^{\left(i,i^{″}\right)}}{2},n=\mathrm{1,2,3}(10)$

$\mathit{cot}{\theta }_n^{\left(i^{\prime },i\right)}=\frac{|f_n^{i^{\prime }}-f_n^i|}{\sqrt{\left[{{\displaystyle \sum }}_{m=1,m\ne n}^3{\left(f_n^{i^{\prime }}-f_n^i\right)}^2\right]}},n=\mathrm{1,2,3}(11)$

$\mathit{cot}{\theta }_n^{\left(i,i^{″}\right)}=\frac{|f_n^i-f_n^{i^{″}}|}{\sqrt{\left[{{\displaystyle \sum }}_{m=1,m\ne n}^3{\left(f_n^i-f_n^{i^{″}}\right)}^2\right]}},n=\mathrm{1,2,3}(12)$

where $k_n^i$ is the MTI of point i; Points $i^{\prime }$ and $i^{″}$ are the adjacent points of point i; ${\theta }_n^{(i^{\prime },i)}$ and ${\theta }_n^{(i,i^{″})}$ are the angles of the vectors $\underset{\text{Point} i^{\prime } \text{Point} i}{\to }$ and $\underset{\text{Point} i \text{Point} i^{″}}{\to }$ with each objective function axis, respectively; $f_n$ is the function value of the three objectives.The edge point i:

$k_n^i=\mathit{cot}{\theta }_n^{\left(i^{\prime },i\right)}=\frac{|f_n^{i^{\prime }}-f_n^i|}{\sqrt{\left[{{\displaystyle \sum }}_{m=1,m\ne n}^3{\left(f_n^{i^{\prime }}-f_n^i\right)}^2\right]}},n=\mathrm{1,2,3}(13)$

where $k_n^i$ is the MTI of point i; Point $i^{\prime }$ is the adjacent points of point i; ${\theta }_n^{(i^{\prime },i)}$ is the angle of the vector $\underset{\text{Point} i^{\prime } \text{Point} i}{\to }$ with each objective function axis; $f_n$ is the function value of the three objectives.The concept and geometric expression of the MTI are shown in Figure 3.

FIGURE 3

FIGURE 3. Geometric concept of the MTI.

Step 4Calculation of the overall MTIThe overall MTI is used to quantitatively characterize the trade-off degree for the entire Pareto non-inferiority solution space and is calculated as:

$k_n=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{k}_n^i,n=\mathrm{1,2,3}(14)$

where $k_n$ is the overall MTI; N is the total number of Pareto non-inferior solutions.For cascade hydropower systems, the water-energy-ecosystem trade-offs can be expressed by the overall MTI vector $\mathit{k}=(k_1,k_2,k_3)$, and its physical meaning is: 1-unit improvement in RWF and ecological benefits (AAPFD) in the cascade hydropower system, the power generation benefits (CPG) decrease by $k_1$-units; 1-unit improvement in power generation (CPG) and ecological benefits (AAPFD) in the cascade hydropower system, the RWF benefits decrease by $k_2$-units; 1-unit improvement in power generation (CPG) and RWF benefits in the cascade hydropower system, the ecological benefits (AAPFD) decrease by $k_3$-units.

4 Results

4.1 Analysis of Multi-Objective Optimization Results

To better understand the trade-off in the WEEN of cascade hydropower systems, a WEEN model using the multi-objective optimization approach was established in this study. The Pareto non-inferiority solutions (990 solutions) and their two-dimensional plot of the CPG, RWF, and AAPFD for the cascade hydropower system in the Yalong River under three typical years (hydrological conditions) were obtained by using the NSGA-III algorithm, as shown in Figures 4–6.

FIGURE 4

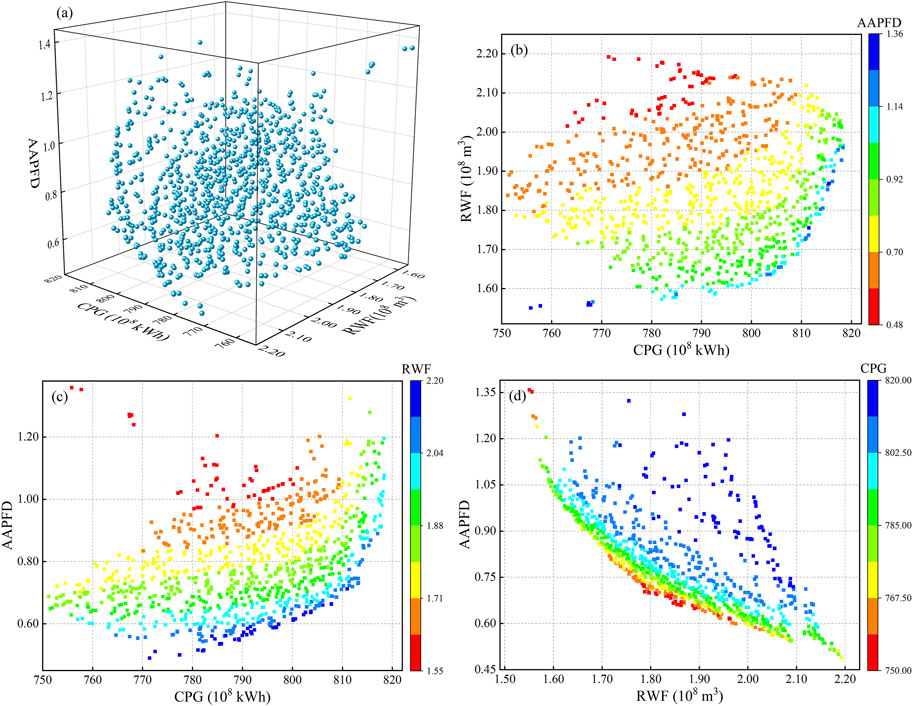
FIGURE 4. The (A) Pareto non-inferiority solutions and their two-dimensional plots for the (B) CPG and RWF, (C) CPG and AAPFD, and (D) RWF and AAPFD under the wetl year.

FIGURE 5

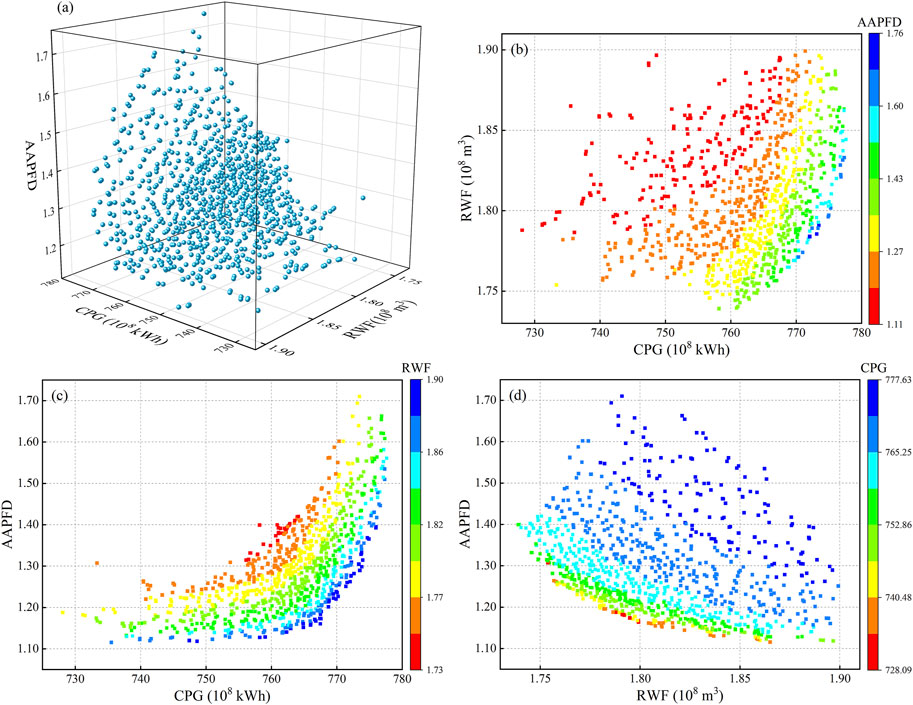
FIGURE 5. The (A) Pareto non-inferiority solutions and their two-dimensional plots for the (B) CPG and RWF, (C) CPG and AAPFD, and (D) RWF and AAPFD under the normal year.

FIGURE 6

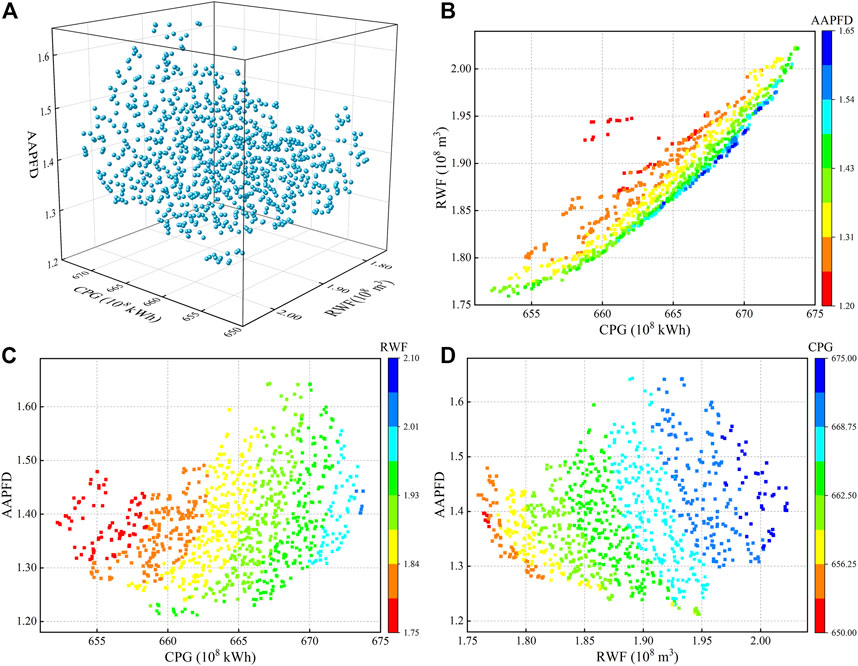
FIGURE 6. The (A) Pareto non-inferiority solutions and their two-dimensional plots for the (B) CPG and RWF, (C) CPG and AAPFD, and (D) RWF and AAPFD under the dry year.

In the wet year, the CPG ranges from 751.23 to 818.40 × 10⁸ kWh with the mean value of 790.84 × 10⁸ kWh, RWF ranges from 1.551 to 2.192 × 108 m³ with the mean value of 1.852 × 108 m³, and AAPFD ranges from 0.490 to 1.359 with the mean value of 0.795 (Figure 4A). In the normal year, the CPG ranges from 728.09 to 777.63 × 10⁸ kWh with the mean value of 762.11 × 10⁸ kWh, RWF ranges from 1.739 to 1.899 × 108 m³ with the mean value of 1.809 × 108 m³, and AAPFD ranges from 1.116 to 1.758 with the mean value of 1.294 (Figure 5A). In the dry year, the CPG ranges from 652.50 to 673.77 × 10⁸ kWh with the mean value of 664.387 × 10⁸ kWh, RWF ranges from 1.759 to 2.023 × 108 m³ with the mean value of 1.881 × 108 m³, and AAPFD ranges from 1.212 to 1.643 with the mean value of 1.384 (Figure 6A). In general, the CPG and AAPFD vary greatly under different hydrological conditions, and both shows: wet year > normal year > dry year, which indicates that the larger the incoming water is, the more beneficial to the power generation and ecological benefits of the cascade hydropower system in the Yalong River. However, hydrological conditions had less influence on the RWF, with the mean value between 1.800 and 1.900 × 108 m³ for the three typical years.

The trade-offs between the three objectives are significant and consistent in the pattern under the three typical years. Figures 4B, 5B, 6B show a significant trade-off relationship between CPG and RWF; that is, with the increase in CPG, the RWF shows an increasing trend. Meanwhile, the higher the power generation, the higher the trade-off degree. This means that more power generation from the cascade hydropower system of the Yalong River comes at the cost of greater water evaporative losses. Figures 4C, 5C, 6C demonstrate a significant trade-off relationship between CPG and AAPFD; with the increase in CPG, the AAPFD shows an increasing trend. Meanwhile, the higher the power generation, the higher the trade-off degree. This means that the cascade hydropower system produces more power generation in the Yalong River at the cost of more drastic changes to the flow and seasonality, which will adversely affect the ecological conditions downstream. Figures 4D, 5D, 6D show a significant trade-off relationship between RWF and AAPFD; that is, with the increase in RWF, the AAPFD shows a decreasing trend. Meanwhile, the larger the RWF, the smaller the trade-off degree. Overall, there is a significant trade-off relationship between the CPG, RWF, and AAPFD, making it is necessary to consider the trade-off between three objectives when decision-makers choose the appropriate mode of operation of cascade HPs.

4.2 Analysis of Trade-offs in the Water-Energy-Ecosystem Nexus

The MTI values of the CPG, RWF, and AAPFD are greatly discrete under the three typical years with large CV (Coefficient of variation) values of significantly >10% (Figure 7; Table 1). The MTI value of the CPG varies from 0.00 to 4,603.40 × 10⁸ kWh with the mean value (±SD) of 22.85 ± 171.22 × 10⁸ kWh, 19.83 ± 113.31 × 10⁸ kWh and 10.09 ± 56.35 × 10⁸ kWh, respectively in the wet, normal, and dry years (Figure 7A; Table 1). The MTI value of the RWF varies from 0.000 to 4.654 × 108 m³ with the mean value (±SD) of 0.571 ± 0.553 × 108 m³, 0.283 ± 0.274 × 108 m³ and 0.197 ± 0.348 × 108 m³, respectively in the wet, normal, and dry year (Figure 7B; Table 1). The MTI value of the AAPFD varies from 0.000 to 54.830 with the mean value (±SD) of 0.544 ± 0.627, 0.919 ± 1.105, and 1.248 ± 2.878, respectively in the wet, normal, and dry years (Figure 7C; Table 1).

FIGURE 7

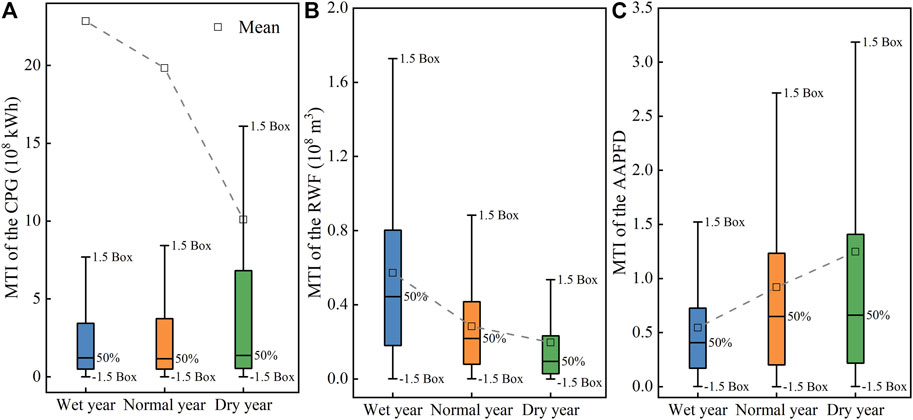
FIGURE 7. Boxplots for the MTI of the (A) cascade power generation (CPG), (B) reservoir water footprint (RWF), and (C) amended annual proportional flow deviation (AAPFD) under the three typical years.

TABLE 1

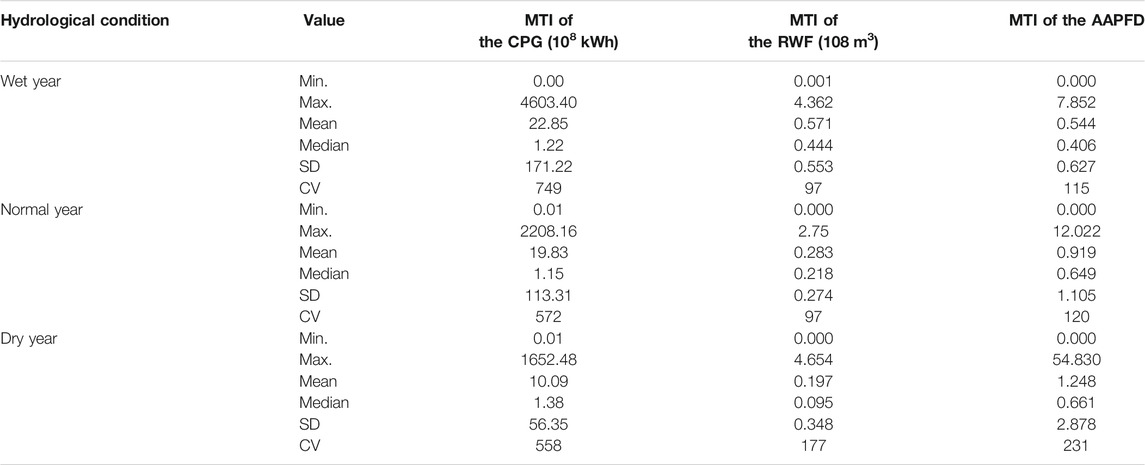
TABLE 1. Statistical results for the MTI of the cascade power generation (CPG), reservoir water footprint (RWF), and amended annual proportional flow deviation of the watershed outlet (AAPFD) under the three typical years. Note: MTI refers to the Multi-objective Trade-off Index. Max and min are the maximum and minimum values, respectively. SD is standard deviation and CV is coefficient of variation (CV = SD/Mean) (%).

For the cascade hydropower system of the Yalong River, the water-energy-ecosystem trade-offs can be expressed by the overall MTI vectors (i.e., mean value of the MTI under the three objectives): $\mathit{ }{\mathit{k}}_{\mathit{w}}=(22.85,0.571,0.544)$, ${\mathit{k}}_{\mathit{n}}=(19.83,0.283,0.919)$ and ${\mathit{k}}_{\mathit{d}}=(10.09,0.197,1.248)$, respectively in the wet, normal, and dry years. The results show that for every 108 m³ of RWF and 1-unit of AAFPD reduction in the cascade hydropower system of Yalong River, the CPG reduction is: wet year > normal year > dry year; for every 10⁸ kWh of CPG increase and 1-unit of AAFPD reduction, the RWF increase is wet year > normal year > dry year; for every 10⁸ kWh of CPG increase and 108 m³ RWF reduction, the AAPFD increases as follows: wet year < normal year < dry year. The trade-off degrees of the water sector with respect to energy-ecosystem and energy sector with respect to water-ecosystem decreases when the hydrological condition changes from wet to dry, while the degree of ecosystem sector with respect to water-energy increases.

5 Discussion

5.1 Implications of the MTI

In this study, a new quantitative trade-off analysis method (i.e., the MTI) from the perspective of the Pareto non-inferiority solutions was proposed, which can quantify the complex trade-offs between different objectives of cascade hydropower systems under changing hydrological conditions. We found that 1 unit improvement in RWF benefits (108 m³) and ecological benefits (AAPFD) in the cascade hydropower system of the Yalong River under a normal year, the power generation benefits (CPG) decrease by 19.83 × 10⁸ kWh. This means that the MTI implies a clear physical meaning, which is a knowledge gap of the previous studies related to the index method (Tang et al., 2020; Wu et al., 2021). It is worth noting that the MTI exhibits some generality and flexibility, which can be applied to other multi-objective optimization problems. Thus, It can guide scholars to quantify the complex trade-offs between different objectives in water resources systems, energy systems, and so on.

Also, we found that the trade-off degrees of the water sector with respect to energy-ecosystem and energy sector with respect to water-ecosystem decreases when the hydrological condition changes from wet to dry in the Yalong River, while the degree of ecosystem sector with respect to water-energy increases. This means that the degree of the water-energy -ecosystem trade-off varies with external environmental conditions, which is consistent with those from previous studies. For example, Wu et al. (2021) noted an increase in the degree of conflict between power generation and water supply or ecological objectives when changing from wet years to dry years in the Jiayan reservoir (China). Yu et al. (2021) showed that the trade-offs between hydropower generation and the assurance rate of power generation vary with riparian ecological conditions in the Yalong River of China. Tang et al. (2019) indicated that the conflict degrees between power generation, reliability, and water shortage become more dramatic with increased water demands in the Nierji Reservoir operation system.

For mountainous rivers like the Yalong River, the CPG is mainly influenced by the operation water level of reservoirs. According to Eq. 2, the water level is also a significant factor in the variation of the RWF. Here, the water level processes of Jinping-I HP (the leading reservoir of the downstream Yalong River with yearly regulation ability) corresponding to all Pareto non-inferior solutions under the three typical years are drawn, including the mean value and interval range (Figure 8). The water level interval is the largest in the wet year, followed by the normal and dry water years. This explains the maximum variation interval of the MTIs of the CPG and RWF under the wet year. During the flood season, the reservoir storage in the dry year is earlier than in the wet and normal years, which dramatically changes the natural runoff. This explains the maximum variation interval of MTIs of AAPFD under the wet year.

FIGURE 8

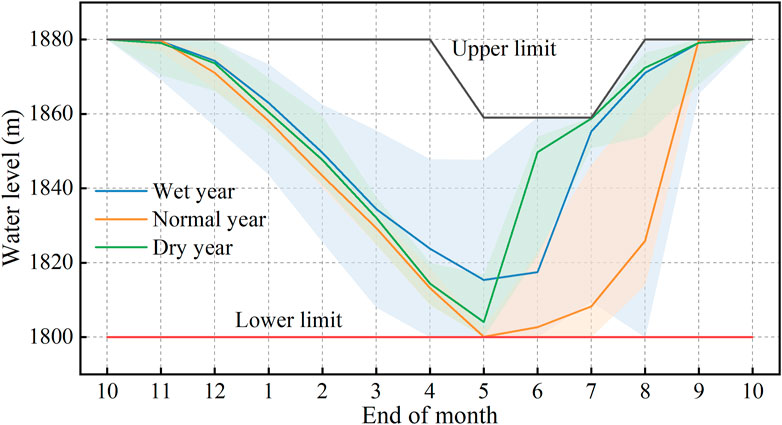
FIGURE 8. The water level of Jinping-Ⅰ HP under the three typical years. Note: The solid line refers to the mean value, and the shading refers to the interval range.

5.2 Limitations and Future Research Directions

This study develops a methodological framework for quantifying the trade-off in the WEEN of cascade hydropower systems, including mainly the WEEN model and the MTI. The WEEN model is based on a multi-objective optimization approach that considers three optimization objectives. However, we use a single indicator to characterize the water, energy and ecosystem sectors of the nexus, which is one of the limitations of this paper. For example, the ecological flow demand of fish in the river is a concern for the ecosystem sector, but it is not considered in this study. From the calculation steps, we can find that MTI only has better performance on 2-objective or 3-objective optimization problems. For the high-dimensional optimization problems (objective number >3), the geometric concept of the MTI becomes blurred, which in turn leads to a lack of clarity in its physical meaning. Therefore, how to extend the application of the MTI to optimization problems with higher dimensional objectives is the future direction to be taken. In the context of global climate change, the intensity and frequency of the interaction between water, energy, and ecosystem sectors of cascade hydropower systems have increased (Zhang X. et al., 2018). Thus, how climate change induces changes in hydropower systems’ water-energy- ecosystem trade-offs is also a topic for future research.

6 Conclusion

To quantify trade-offs in the water-energy-ecosystem nexus (WEEN) of cascade hydropower systems, this study developed a WEEN model using the multi-objective optimization approach and proposed an evaluation index, that is the MTI. A case study of the Yalong River (China) has shown that:

(1) The cascade power generation (CPG) and amended annual proportional flow deviation (AAPFD) vary greatly under different hydrological conditions, and both shows: wet year > normal year > dry year, which indicates that the larger the incoming water is, the more beneficial to the power generation and ecological benefits of the Yalong River cascade HPs. However, hydrological conditions had less influence on the reservoir water footprint (RWF), with the mean value between 1.800 and 1.900 × 108 m³ for the three typical years.

(2) In wet, normal, and dry years, the MTI vectors of CPG, RWF, and AAPFD are ${\mathit{k}}_{\mathit{w}}=(22.85,0.571,0.544)$, ${\mathit{k}}_{\mathit{n}}=(19.83,0.283,0.919)$, and ${\mathit{k}}_{\mathit{d}}=(10.09,0.197,1.248)$, respectively. This means that the trade-off degrees of water with respect to energy-ecosystem and energy with respect to water-ecosystem decreases when the hydrological condition changes from wet to dry, while the degree of the ecosystem with respect to water-energy increases.

The case study results show that the MTI can quantify the complex trade-offs between different objectives under changing hydrological conditions, and the proposed MTI is efficient and feasible. Also, the MTI can be applied to other multi-objective optimization problems. This study can help cascade power plant managers gain a more comprehensive understanding of the trade-offs between different objectives of hydropower systems and make more appropriate operation decisions, which can obtain maximum combined benefits.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This study was supported by the National Key R & D Program of China (Grant No. 2018YFC0407200); the National Natural Science Foundation of China (Grant No. 51709178); a Project funded by China Postdoctoral Science Foundation (Grant No. 2019M661884); the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20200160); and the Special Research Fund of Nanjing Hydraulic Research Institute (Grant No. Y120006).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.857340/full#supplementary-material

References

Bian, J.-q., Dong, Z.-c., Jia, Y.-f., Zhong, D.-y., Dong, Z.-c., Jia, Y.-f., et al. (2019). Research on the Multi-Objective Optimal Operation of cascade Reservoirs in the Upper and Middle Yellow River basin. Water Supply 19 (7), 1918–1928. doi:10.2166/ws.2019.067

CrossRef Full Text | Google Scholar

Chen, X., Zheng, Y., Xu, B., Wang, L., Han, F., and Zhang, C. (2020). Balancing Competing Interests in the Mekong River Basin via the Operation of cascade Hydropower Reservoirs in China: Insights from System Modeling. J. Clean. Prod. 254, 119967. doi:10.1016/j.jclepro.2020.119967

CrossRef Full Text | Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Computat. 6 (2), 182–197. doi:10.1109/4235.996017

CrossRef Full Text | Google Scholar

Gupta, R. S., Hamilton, A. L., Reed, P. M., and Characklis, G. W. (2020). Can Modern Multi-Objective Evolutionary Algorithms Discover High-Dimensional Financial Risk Portfolio Tradeoffs for Snow-Dominated Water-Energy Systems. Adv. Water Resour. 145, 103718. doi:10.1016/j.advwatres.2020.103718

CrossRef Full Text | Google Scholar

Jain, H., and Deb, K. (2014). An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. IEEE Trans. Evol. Computat. 18 (4), 602–622. doi:10.1109/tevc.2013.2281534

CrossRef Full Text | Google Scholar

Kuriqi, A., Pinheiro, A. N., Sordo-Ward, A., Bejarano, M. D., and Garrote, L. (2021). Ecological Impacts of Run -of -river Hydropower Plants ? Current Status and Future Prospects on the Brink of Energy Transition. Renew. Sustain. Energ. Rev. 142, 110833. doi:10.1016/j.rser.2021.110833

CrossRef Full Text | Google Scholar

Kuriqi, A., Pinheiro, A. N., Sordo-Ward, A., and Garrote, L. (2020). Water-energy-ecosystem Nexus: Balancing Competing Interests at a Run-Of-River Hydropower Plant Coupling a Hydrologic-Ecohydraulic Approach. Energ. Convers. Manage. 223, 113267. doi:10.1016/j.enconman.2020.113267

CrossRef Full Text | Google Scholar

Ladson, A. R., White, L. J., Doolan, J. A., Finlayson, B. L., Hart, B. T., Lake, P. S., et al. (1999). Development and Testing of an Index of Stream Condition for Waterway Management in Australia. Freshw. Biol. 41, 453–468. doi:10.1046/j.1365-2427.1999.00442.x

CrossRef Full Text | Google Scholar

Li, M., Fu, Q., Singh, V. P., Liu, D., and Li, T. (2019). Stochastic Multi-Objective Modeling for Optimization of Water-Food-Energy Nexus of Irrigated Agriculture. Adv. Water Resour. 127, 209–224. doi:10.1016/j.advwatres.2019.03.015

CrossRef Full Text | Google Scholar

Liu, C., Zhou, J., Lai, X., and Zhang, T. (2021). Optimization and Mechanism of the Wicket Gate Closing Law for High-Head Pumped Storage Power Stations. Ieee Access 9, 11734–11749. doi:10.1109/access.2021.3049914

CrossRef Full Text | Google Scholar

Liu, J., Zhao, D., Gerbens-Leenes, P. W., and Guan, D. (2015). China's Rising Hydropower Demand Challenges Water Sector. Sci. Rep. 5, 11446. doi:10.1038/srep11446

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, Y., Zhong, P.-a., Xu, B., Bing, J., and Zhang, Y. (2020). Multi-objective and Joint Operation Model for Multistakeholder Cascade Hydropower System. J. Water Resour. Plann. Manage. 146 (11), 1291. doi:10.1061/(asce)wr.1943-5452.0001291

CrossRef Full Text | Google Scholar

Mekonnen, M. M., and Hoekstra, A. Y. (2012). The Blue Water Footprint of Electricity from Hydropower. Hydrol. Earth Syst. Sci. 16 (1), 179–187. doi:10.5194/hess-16-179-2012

CrossRef Full Text | Google Scholar

Niu, W.-j., Feng, Z.-k., Li, Y.-r., and Liu, S. (2021). Cooperation Search Algorithm for Power Generation Production Operation Optimization of Cascade Hydropower Reservoirs. Water Resour. Manage. 35 (8), 2465–2485. doi:10.1007/s11269-021-02842-2

CrossRef Full Text | Google Scholar

Poff, N. L., Allan, J. D., Bain, M. B., Karr, J. R., Prestegaard, K. L., Richter, B. D., et al. (1997). The Natural Flow Regime. Bioscience 47 (11), 769–784. doi:10.2307/1313099

CrossRef Full Text | Google Scholar

Shiau, J.-T., and Wu, F.-C. (2013). Optimizing Environmental Flows for Multiple Reaches Affected by a Multipurpose Reservoir System in Taiwan: Restoring Natural Flow Regimes at Multiple Temporal Scales. Water Resour. Res. 49 (1), 565–584. doi:10.1029/2012wr012638

CrossRef Full Text | Google Scholar

Si, Y., Li, X., Yin, D., Li, T., Cai, X., Wei, J., et al. (2019). Revealing the Water-Energy-Food Nexus in the Upper Yellow River Basin through Multi-Objective Optimization for Reservoir System. Sci. Total Environ. 682, 1–18. doi:10.1016/j.scitotenv.2019.04.427

PubMed Abstract | CrossRef Full Text | Google Scholar

Suwal, N., Huang, X., Kuriqi, A., Chen, Y., Pandey, K. P., and Bhattarai, K. P. (2020). Optimisation of cascade Reservoir Operation Considering Environmental Flows for Different Environmental Management Classes. Renew. Energ. 158, 453–464. doi:10.1016/j.renene.2020.05.161

CrossRef Full Text | Google Scholar

Tang, R., Ding, W., Ye, L., Wang, Y., and Zhou, H. (2019). Tradeoff Analysis Index for Many-Objective Reservoir Optimization. Water Resour. Manage. 33 (13), 4637–4651. doi:10.1007/s11269-019-02363-z

CrossRef Full Text | Google Scholar

Tang, R., Li, K., Ding, W., Wang, Y., Zhou, H., and Fu, G. (2020). Reference Point Based Multi-Objective Optimization of Reservoir Operation: a Comparison of Three Algorithms. Water Resour. Manage. 34 (3), 1005–1020. doi:10.1007/s11269-020-02485-9

CrossRef Full Text | Google Scholar

Unal, M., Warn, G. P., and Simpson, T. W. (2016). Quantifying Tradeoffs to Reduce the Dimensionality of Complex Design Optimization Problems and Expedite Trade Space Exploration. Struct. Multidisc Optim 54 (2), 233–248. doi:10.1007/s00158-015-1389-7

CrossRef Full Text | Google Scholar

Vaca-Jiménez, S., Gerbens-Leenes, P. W., and Nonhebel, S. (2019). Water-electricity Nexus in Ecuador: The Dynamics of the Electricity's Blue Water Footprint. Sci. Total Environ. 696, 133959. doi:10.1016/j.scitotenv.2019.133959

PubMed Abstract | CrossRef Full Text | Google Scholar

Vinca, A., Riahi, K., Rowe, A. M., and Djilali, N. (2021). Climate-Land-Energy-Water Nexus Models across Scales: Progress, Gaps and Best Accessibility Practices. Front. Environ. Sci. 9, 691523. doi:10.3389/fenvs.2021.691523

CrossRef Full Text | Google Scholar

Wang, X., Dong, Z., Ai, X., Dong, X., and Li, Y. (2020). Multi-objective Model and Decision-Making Method for Coordinating the Ecological Benefits of the Three Gorger Reservoir. J. Clean. Prod. 270, 122066. doi:10.1016/j.jclepro.2020.122066

CrossRef Full Text | Google Scholar

Wu, L. Z., Bai, T., and Huang, Q. (2020). Tradeoff Analysis between Economic and Ecological Benefits of the Inter basin Water Transfer Project under Changing Environment and its Operation Rules. J. Clean. Prod. 248, 119294. doi:10.1016/j.jclepro.2019.119294

CrossRef Full Text | Google Scholar

Wu, Z., Mei, Y., Cheng, B., and Hu, T. (2021). Use of a Multi-Objective Correlation Index to Analyze the Power Generation, Water Supply and Ecological Flow Mutual Feedback Relationship of a Reservoir. Water Resour. Manage. 35 (2), 465–480. doi:10.1007/s11269-020-02726-x

CrossRef Full Text | Google Scholar

Yadav, K., Geli, H. M. E., Cibils, A. F., Hayes, M., Fernald, A., Peach, J., et al. (2021). An Integrated Food, Energy, and Water Nexus, Human Well-Being, and Resilience (FEW-WISE) Framework: New Mexico. Front. Environ. Sci. 9, 667018. doi:10.3389/fenvs.2021.667018

CrossRef Full Text | Google Scholar

Yu, L., Jia, B. Y., Wu, S. Q., Wu, X. F., Xu, P., Dai, J. Y., et al. (2019). Cumulative Environmental Effects of Hydropower Stations Based on the Water Footprint Method-Yalong River Basin, China. Sustainability 11 (21), 5958. doi:10.3390/su11215958

CrossRef Full Text | Google Scholar

Yu, L., Wu, X., Wu, S., Jia, B., Han, G., Xu, P., et al. (2021). Multi-objective Optimal Operation of cascade Hydropower Plants Considering Ecological Flow under Different Ecological Conditions. J. Hydrol. 601, 26599. doi:10.1016/j.jhydrol.2021.126599

CrossRef Full Text | Google Scholar

Zeng, X. T., Zhang, S. J., Feng, J., Huang, G. H., Li, Y. P., Zhang, P., et al. (2017). A Multi-Reservoir Based Water-Hydroenergy Management Model for Identifying the Risk Horizon of Regional Resources-Energy Policy under Uncertainties. Energ. Convers. Manage. 143, 66–84. doi:10.1016/j.enconman.2017.02.020

CrossRef Full Text | Google Scholar

Zhang, J., Xu, L., and Cai, Y. (2018a). Water-carbon Nexus of Hydropower: The Case of a Large Hydropower Plant in Tibet, China. Ecol. Indicators 92, 107–112. doi:10.1016/j.ecolind.2017.06.019

CrossRef Full Text | Google Scholar

Zhang, X., Li, H.-Y., Deng, Z. D., Ringler, C., Gao, Y., Hejazi, M. I., et al. (2018b). Impacts of Climate Change, Policy and Water-Energy-Food Nexus on Hydropower Development. Renew. Energ. 116, 827–834. doi:10.1016/j.renene.2017.10.030

CrossRef Full Text | Google Scholar

Zhou, B., Liu, B., Yang, D., Cao, J., and Littler, T. (2020). Multi-objective Optimal Operation of Coastal Hydro-Electrical Energy System with Seawater Reverse Osmosis Desalination Based on Constrained NSGA-III. Energ. Convers. Manage. 207, 112533. doi:10.1016/j.enconman.2020.112533

CrossRef Full Text | Google Scholar

Nomenclature

$h_E\left[t\right]$ annual average water evaporation [mm month⁻¹]

$Q_{tzl}^N$ average value of the natural flow through the Tongzilin hydropower plant during the operation period [m³ s⁻¹]

${\eta }_i$ comprehensive efficiency coefficient [-]

$Q_{i,t}^{tur}$ flow through the turbine [m³ s⁻¹]

$Z_{i,t}^{lower}$ lower water level of reservoir [m]

$Q_{i,t}^{max}$ maximum discharges from reservoir [m³ s⁻¹]

$N_{i,t}^{max}$ maximum power output of hydropower plant [MW]

$Q_{i,t}^{min}$ minimum discharge from reservoir [m³ s⁻¹]

$N_{i,t}^{min}$ minimum power output of hydropower plant [MW]

$Q_{tzl, t}^N$ natural flow of the Tongzilin hydropower plant [m³ s⁻¹]

$A\left[t\right]$ open water surface area of the reservoir [ha]

$Q_{tzl, t}$ outflow of the Tongzilin hydropower plant [m³ s⁻¹]

$N_{i,t}$ power output of hydropower plant [MW]

$E_{i,t}$ reservoir evaporation [m³]

$I_{i,t}$ reservoir inflow [m³ s⁻¹]

$L_{i,t}$ reservoir leakage [m³]

$Q_{i,t}$ reservoir outflow [m³ s⁻¹]

$V_{i,t}$ reservoir storage [m³]

$W{F}_{res,m}\left[t\right]$ reservoir water footprint in a month [m³ month⁻¹]

$W{F}_{res,y}$ reservoir water footprint in a year [m³ year⁻¹]

$H_{i,t}$ reservoir water head [m]

$Z_{i,t}$ reservoir water level [m]

$\mathbf{\Delta }t$ time step [s]

$Z_{i,t}^{upper}$ upper water levels of reservoir [m]

AAPFD amended annual proportional flow deviation [-]

CPG cascade power generation [kWh]

HP hydropower plant

MTI multi-objective trade-off index [-]

n number of hydropower plants

RWF reservoir water footprint [m³]

T number of time periods in the operation period [-]

WEEN water-energy-ecosystem nexus