
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci., 22 March 2022
Sec. Freshwater Science
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.821079
This article is part of the Research TopicRiver and Watershed Restoration, Rehabilitation and Conservation: Challenges, Actions, and PerspectivesView all 6 articles
 Hojat Karami1*
Hojat Karami1* Yashar DadrasAjirlou1
Yashar DadrasAjirlou1 Changhyun Jun2
Changhyun Jun2 Sayed M. Bateni3
Sayed M. Bateni3 Shahab S. Band4*
Shahab S. Band4* Amir Mosavi5,6,7,8
Amir Mosavi5,6,7,8 Massoud Moslehpour9,10
Massoud Moslehpour9,10 Kwok-Wing Chau11
Kwok-Wing Chau11Predicting the amount of sediment in water resource projects is one of the most important measures to be taken, while sediments have an unknown nature in their behavior. In this research, using the data recorded at the Mazrae station between 2002 and 2013, the amount of sediment in the catchment area of Maku Dam has been predicted using different models of intelligent algorithms. Recorded data including river flow (m3/s), sediment concentration (mg/L), and temperature (°C) were considered input data, and sediment load (ton/day) was considered output data. Initially, using the correlation test, the relationship between each input data with output data was considered. The results show high correlation of sediment concentration data and river flow with sediment load and low correlation of temperature data with these data. In order to find the best combination of data for prediction, the combination of single, binary, and triple data was considered in sensitivity analysis. In order to achieve the purpose of this study, first with the classical adaptive neuro-fuzzy inference system (ANFIS), the amount of sediment load was predicted, and then using evolutionary algorithms in ANFIS training, their performance was examined. The intelligent algorithms used in this study were ant colony optimization extended to continuous domain, particle swarm optimization, differential evolution, and genetic algorithm. The results showed that adaptive neuro-fuzzy inference system–ant colony optimization extended to continuous domain, adaptive neuro-fuzzy inference system–particle swarm optimization, adaptive neuro-fuzzy inference system–genetic algorithm, adaptive neuro-fuzzy inference system–differential evolution, and classical ANFIS had the best performance in predicting the amount of sediment load. In the meantime, it was observed that the coefficient of determination, root mean square error, and scatter index in the test mode for the adaptive neuro-fuzzy inference system–ant colony optimization extended to continuous domain algorithm with the best prediction dataset (sediment concentration + river flow) are equal to 0.991, 13.001, and (ton/day), 0.112, and those for the ANFIS with the weakest prediction (temperature + river flow) are equal to 0.490, 107.383 (ton/day), and 0.929, respectively. The present study showed that the use of intelligent algorithms in ANFIS training has been able to improve its performance in predicting the amount of sediment load in the catchment area of Maku Dam.
Understanding the relationships between different components of the river is one of the most important factors in understanding the behavior of these components. Even though many studies have been conducted to understand the behavior of sediment, no reliable relationship has been found to understand the phenomenon of mechanical transfer of sediment and its behavior (Sivakumar and Jayawardena 2002). Studies to estimate the volume of river sediment by scientists are important because they believe that accurate prediction of the amount of river sediment in water resource management projects is considered to be one of its most vital factor (Chang Howard, 2008; Martinez et al., 2009; Omolbani et al., 2010; Omolbani et al., 2012). Predicting the volume of suspended sediment in the river has been described as a very complex process in which many meteorological and hydrological parameters are involved, which emphasizes the complexity of accurately predicting the amount of sediment load (Frings and Kleinhans 2008). Therefore, considering this chaotic nonlinear behavior, the old classical laboratory approaches cannot be used for this purpose (Nourani 2009). However, it has been stated that in order to understand the dependence of the sediment phenomenon on spatial and temporal variables, physical modeling methods can be used (Yaseen et al., 2015), while using intelligent methods can also be helpful in predicting the extent sediment (Kishi 2015).
In the last two decades, many studies and research work have been carried out using artificial intelligence tools to evaluate their efficiency and performance for understanding and modeling hydrological phenomena. One of these efforts was a study to predict river flow with ANFIS (adaptive neuro-fuzzy inference system) and compare it with conventional methods in which ANFIS showed better results than conventional methods for predicting river flow (Nayak et al., 2004). Also, several research studies have been conducted in the field of application of classical intelligent models which were applied to predict water permeability and soil penetration coefficient (Ganjidoost et al., 2015), rainfall-runoff forecast (Tayfur and Singh 2006; Akrami et al., 2014), evaporation and transpiration prediction (Ehteram et al., 2019), canal inlet speed prediction, and spatial distribution of groundwater quality (Khashaei-Siuki and Sarbazi 2013). Predicting the amount of suspended sediment in the river is also one of the fields of interest among scientists to evaluate the performance of intelligent methods, and several studies in this field have been published by them. In order to predict the volume of monthly sediments, ANN (artificial neural network) and ANFIS were used (Firat and Gungor, 2010). Gene programming is also used to study the transport of sediment in the pipes of the municipal sewage system (Ab. Ghani and Azamathulla, 2011) and sediment transport in tropical rivers (Ab. Ghani and Azamathulla, 2012). The ANN (Wang et al., 2009) and intelligent approaches (Chang et al., 2012) are both used for prediction of sediment in tropical rivers. In addition, many researchers have conducted many studies in the field of volume prediction and sediment transport using methods based on artificial intelligence, for example, using ANN to estimate the amount of sediment (Samet et al., 2018). They showed that the ANN can show good result for sediment load. Using some intelligent methods for sediment estimation in Shakkar and Manot watersheds showed good results (Meshram et al., 2020). They noticed that between artificial neural networks, radial basis function (RBF), support vector machine (SVM), and multiple model (MM)-ANNs, The last method showed more successful sediment prediction. Using fuzzy logic theory is another popular method to model sediment transport (Bakhtyar et al., 2008). In some studies, the comparison between intelligent methods such as ANFIS, ANN, and SVM to predict the amount of sediment load was conducted (Batt and Stevens, 2013; Buyukyildiz and Kumcu 2017). In addition, using evolutionary calculations in sediment transport is considered in some cases (Salih et al., 2020). They showed that their mining models performed excellent for the prediction of sediment load. Goyal used the complementary model of wavelet-AI to model sediment transport. However, given the unknown nature of sediments and their behavior in the study areas, researchers are still looking for a more universal method for modeling sediment behavior and predicting its amount in rivers and dam reservoirs (Goyal 2014).
As mentioned above, classical intelligent methods have been shown to be effective in many studies. However, the use of classical intelligent models has drawbacks, such as local search methods, falling into the optimal local trap, time-consuming, and bulky calculations (Peyghami and Khanduzi 2013; Kishi et al., 2018). As mentioned above, ANN and fuzzy neural systems have a good performance in predicting and modeling various hydrological and hydraulic phenomena, but concerning sediment and related issues such as sediment transport and sediment volume in the river, they cannot be expected to perform well because the nature of this phenomenon is extremely complex and chaotic. In the case of rainfall prediction, it is concluded that ANFIS performs better than ANN, where determining the structure of the ANFIS, its fuzzy rules, and how to train the network are the most vital and complex part of this smart model (Akrami et al., 2013). Because classical algorithms use local search methods, they are more likely to fall into the optimal local answers, and the backpropagation method uses time-consuming calculations to train ANFIS which increases the volume and time of calculations (Peyghami and Khanduzi 2013). Therefore, if the number of data is very large and also have a complex nature for forecasting, the forecasting process will be difficult. To solve these problems, evolutionary algorithms have been proposed for use in the training section of the ANFIS.
It has been reported that the use of the DE (differential evolution) algorithm in the ANFIS training section shows good ability to predict sediment transport compared to conventional methods (Ebtehaj and Bonakdari, 2016; Ebtehaj and Bonakdari 2017). In another study, scientists concluded that the use of PSO (particle swarm optimization) and GA (genetic algorithm) for ANFIS training could achieve better results in predicting water quality parameters (Jalalkamali 2015). It has been stated that the combination of the DSOA (direct search optimization algorithm) and FIS (fuzzy inference system) has had a good performance in predicting the runoff of the Taleghan River (Tabari 2016). The fact that the use of evolutionary algorithms has improved the results of traditional intelligent systems in predicting hydrological phenomena is indicated in some studies (Kishi et al., 2017). The amount of sediment transferred in open channels can be estimated by combining the PSO algorithm and ANFIS (Ebtehaj et al., 2019). The basic hypothesis of this research is that the ANFIS has the ability to simulate the amount of sediment in the reservoir of a dam, but the use of evolutionary algorithms can significantly increase the performance of the ANFIS in estimating the amount of sediment and it also assumed that the ANFIS–ACOr (adaptive neuro fuzzy inference system–ant colony optimization extended to continuous domain) algorithm can achieve the best performance among other studied algorithms. To test this hypothesis, the selected data were divided into training and testing, and then by implementing evolutionary algorithms in the training section, the results of each hybrid algorithm were recorded.
Many researchers are focusing on natural phenomena and animal life to introduce more serious and powerful meta-heuristic algorithms in the field of optimization. Between 2006 and 2021, a considerable number of meta heuristic algorithms were introduced (Dragoi and Dafinescu, 2021). Their study reviewed all the meta-heuristic algorithms introduced between 2006 and 2021. They used biological classification of living things in their study and tried to base this classification on simulating the behavior of organisms. They concluded that 61.6% of the algorithms were modeled and developed by vertebrates, while 38.4% of these algorithms were proposed by studying and observing the life of invertebrates. In addition to studying the behavioral mechanisms of these algorithms, they showed that the most widely used mechanism in the development of these algorithms was related to niche classification. They have also prepared a good list of these algorithms in his study, which has provided high usability for researchers in other fields.
In this study, it has been tried to first predict the sediment load in the Maku Dam area using the classic ANFIS on a monthly basis, and then by combining the ACOr, GA, DE, and PSO with the classical ANFIS and using them the training section, its performance was improved and finally the best model was proposed for monthly prediction of the sediment load particles according to statistical evaluation criteria.
The study area in this study belongs to the catchment area of Maku Dam in the geographical range of 38 degrees and 57 s north to 39 degrees and 16 s north and 44 degrees and 06 s east to 44 degrees and 39 s east. This catchment is located in the northwestern region of Iran and has a semi-arid climate. The data used in this study were taken from the farm station archive. Figure 1 shows the geographical area of the farm station with a position of 39 degrees and 10 s north and 44 degrees and 25 s east and an altitude of 1712 m above sea level. The minimum average monthly discharge was recorded in September, which was 1.14 m3/s, and the highest recorded monthly discharge was 10.21 m3/s, recorded in May.
T (temperature) data (C°), Q (river flow) (m3/s), CM (sediment concentration) (mg/L), and SL (sediment load) (ton/day) were the parameters measured at the Mazrae station in which the first three are considered inputs and the last one considered output. The data were recorded monthly between 2002 and 2013. For each type of parameter, 181 numbers are recorded in the station, which is in accordance with what was said, the input data set will be equal to 181 × 3, and the output data set will be equal to 181 × 1. The percentages of data for the training phase and test phase were considered 70 and 30%, respectively. One of the general limitations that can be mentioned is the existence of restrictions on access to data. In this study, the results are based on four types of data. In general, many studies, including the present study, indicate the effectiveness of implementing evolutionary algorithms in the ANFIS, but in order to comprehend to what extent these methods will be able to simulate hydrological phenomena and taking into account which data undoubtedly require much more extensive studies with a much wider data set. Therefore, it is possible that some of the data related to sediment have not been considered. The shortcoming of the data used in this study may also limit the simulation. In short, studies that use broader data and determine the effectiveness of each of them by scientific methods will have a higher scientific rank.
A three-section method has been used to find the average CM. Considering that it is possible to take samples of sediments during floods, a three-section method can be used for this purpose. Only a multi cross-sectional method is effective for sampling and study on first-class stations. However, in some cases, the three-section method can be used in second- and third-degree stations. The sampling steps in this method are as follows: first, a specific section of the river where the flow rate is measured in different parts of that section is selected and then the data were divide it into three parts in a way that the flow rate in all three parts are equal. The concentration of sediment samples is calculated using data collected in the laboratory. The average concentration of each section (CM) is calculated by Eq. 1. The concentration of samples at fixed points (CF) is also calculated in the laboratory. The ratio CM/CF, or in other words K, is also calculated and according to the flow of each section, the graph of changes of K is drawn in terms of Q. Finally, the final value of the CM is calculated using the K graph in terms of Q. It should be noted that the value of K in each section must be calculated for the deepest point of that section. The range of changes K is between 0.4 and 1.6.
where C1, C2, and
ANFIS is one of the neuro-fuzzy models based on artificial intelligence. This system is a tool for estimating continuous-real functions in a specific domain, first introduced by Yang in 1993. The fuzzy part of the ANFIS model establishes a relationship between input and output variables, using membership functions and if–then rules. The parameters of the membership functions are determined using the ANN training algorithm based on the backpropagation error method for the parameters of the input membership functions and the least squares method for the parameters of the output membership functions. The ANFIS model uses the Sugeno system for modeling. For a first-order fuzzy Sugeno model with two inputs (x, y) and one output (f) and two membership functions for each of the inputs, a typical ANFIS model is formed. For such a model, ordinary rules are defined by considering two fuzzy (if–then) rules as follows:
The variables A1, A2, B1, and B2 are membership functions for inputs x and y and p1, q1, r1, p2, q2, and r2 are the parameters of the output function. Therefore, in this case, the formulation in the adaptive neural-fuzzy network follows a forward five-layer neural network arrangement. In the first layer, the input data are linked to each node through the function of it; in other words, the membership function of each node determines the degree of membership of each input data. The second layer does receives the outputs of the first layer and by multiplying them introduces the degree of activity of each fuzzy rule as the output to the next layer. In the third layer, the output of the previous layer gets normalized. The output of the third layer is called normalized firing strengths. In the fourth layer, each node is considered to be corresponding to each output. Finally, each node in the fifth layer calculates the final output as the sum of all inputs (Jang 1993).
In the present study, the ratio of test and training data is 30 and 70%, respectively. The parameters used in the ANFIS for the number of epochs, initial step size, step decrease length, and step increase length are 200, 0.02, 0.8, and 1.2, respectively. It should be noted that hybrid optimization and backpropagation method were used to optimize the effect; the results of hybrid optimization were better than those of the backpropagation method, and the process of continuing the work was carried out with the hybrid optimization method. When using the ANFIS in modeling, it is very important to determine the number of membership functions because membership functions represent the percentage of data belonging to a mathematical set. The number of membership functions is usually determined by clustering. In clustering, data that have closely related properties fall into one category. In the present study, three types of classical ANFIS were used for this purpose: grid partition (GP), subtractive clustering (SC), and fuzzy C-mean clustering (FCM). Considering all inputs together (T + Q + CM) and comparing the performance of the three types of ANFIS (Table 1) according to the statistical criteria of R2 and RMSE, it was concluded that FCM with R2 = 0.8363 and RMSE = 54.4515 (ton/day) in the test section has the best performance in predicting the SL compared to the other two types. Findings of Mirrashid, (2014); Abdulshahed et al., (2015) also confirm that the FCM interface has a better performance than the other two methods.
PSO is a meta-heuristic optimization method that begins by randomly generating a set of particles or solutions in the search space and then searches for the most optimal mode using frequent particle updates (Kennedy and Eberhart, 1995). Inspired by the collective movement of birds, this method is very popular due to its high efficiency in solving complex, costly, and sometimes impossible optimization problems. In this algorithm, the position of each particle represents a point in the answer space of the problem. Each particle has a memory and remembers the best position it reaches in the search space. The motion of each particle can be realized in three directions: 1- continuation of its motion in the same direction as the path it has taken. 2- Moving toward the best position it has taken. 3- Moving toward the best position that the whole group (whole particles) has found. Therefore, changing the position of each particle in the search space will be affected by its own experience and that of other particles. PSO is a reliable algorithm due to its low computational volume, low probability of falling into the local optimal trap, high convergence speed, and easy execution. This algorithm is used for training intelligent models in some studies (Hasanipanah et al., 2016; Kishi et al., 2017).
In a particular problem, each particle in the group can be represented by a velocity vector and a position vector. Changing the position of each particle is possible by changing the previous position structure and velocity. Each particle contains information including the best value (position) ever obtained (personal optimization), the current position (Xi, (t)), and the best response ever given to the whole group has achieved (comprehensive optimization). Each particle uses the current position (Xi, (t)) and the current velocity (Vi, (t)) to change the distance between the current and personal optimal position and the distance between the current position and the all-encompassing optimal position. This gives the best possible answer. Therefore, the new velocity vector (Vi, (t+1)) is computed for the ith particle according to Eq. 2 (Shi and Eberhart 1998):
where r1 and r2 are random vectors between 0 and 1 that are used to maintain the diversity of the group. C1 and C2 are individual and social cognitive parameters, respectively. Selecting the appropriate value for these parameters leads to accelerating the convergence of the algorithm and preventing premature convergence in local optimizations. Larger values are more appropriate for the cognitive parameter C1 than for the social parameter C2, but the condition C1+C2 ≤ 4 must always be met (Goldberg 1989). The parameter
There are several methods for initialization of PSO parameters. Many studies have been carried out in this field (Engelbrecht, 2007; Engelbrecht, 2012; Cazzaniga et al., 2015). One of the limitations of the PSO algorithm is that the choice of initial PSO parameters varies according to the nature of the problem, so one has to do it with trial and error to find the best initial values. However, the choice of initial parameters for the PSO algorithm can itself be a complex optimization problem, especially when different problems with different data are considered, such as premature convergence, inability to solve dynamic optimization problems, and inability to be scaled to accommodate large number of particles (Guo et al., 2020).
In the present study, the maximum value of repetition is 200 because by increasing the number of repetitions, the performance of the algorithm did not differ much while the computation time increased. Particle velocity ranges between −2 and +2 were considered. The number of initial population was 10, the initial inertia weight was equal to 1, individual learning coefficient equal to 1, and social learning coefficient equal to 2.
The GA is a species-based optimization algorithm. This algorithm was first introduced in 1975 by Holland. The GA is one of the most widely used optimization algorithms to solve various problems. Advantages of this algorithm include the ability to search well, be independent of the problem situation, use appropriate complexity in complex problems, and refusal to fall for the optimal local answer (Shihabudeen and Pillai 2018). These traits led to the use of the GA as a good complement to the training of the ANN and ANFIS. In the present study, a GA is used to train the emphysema in order to predict the amount of river sediment. First, the initial population is determined and then the GA obtains the best fitting X with mean and standard deviation. Initially, a set of chromosomes is randomly generated (initial population). The chromosomes that have the most suitable function for sediment prediction are selected. At this point, if the performance of the selected chromosomes is acceptable, the optimization is complete. Otherwise, a new generation is produced, and the previous steps are repeated and the GA produces new chromosomes. This cycle is repeated until the threshold is satisfied. Once the GA is performed, the remaining steps are performed by the ANFIS. The number of iterations of the GA was considered to be 200, and with increasing the number of iterations, no significant change in the performance of the algorithm was observed, while the analysis time increased slightly.
The limitations of the GA include the following: the problem of identifying fitness function, premature convergence occurs, the problem of choosing various parameters such as the size of the population, mutation rate, cross over rate, selection method and its strength, no effective termination point, needs to be coupled with a local search technique, and has trouble finding the exact global optimum (Dahiya and Sangwan, 2018).
The initial population number was considered to be 10, and as the initial population increased, only the computational speed decreased and the performance of the algorithm did not change. The best crossover and mutation values were 0.7 and 0.5, respectively.
The ACO algorithm uses a discrete structure to determine the answer. The concept of discrete structure in ACO is that each of the decision variables in the defined interval is divided into a certain number of states. On the other hand, by discretizing the space of variables, there is a limit to the algorithm, which in turn will reduce the accuracy of the optimization, and by dividing the space between the decision variables, try to increase the accuracy of the answers, the program time is proportional. Will increase with it. In this case, the accuracy may also decrease. In this regard, and to compensate for this problem, the generalization of ACO to continuous space was considered (Socha and Dorigo, 2008).
Sosha and Dorigo proposed in 2008 the use of a Gaussian function to create such a structure. A single-dimensional or single Gaussian function cannot produce a maximum of several points, whereas using a kernel Gaussian function, which is the sum of the weight of several single Gaussian functions, can perform such a task. For example, for the
In order to define this relationship, three parameters
In the ACOr algorithm, an archive is used to store the set of answers. For this purpose, in a system with n decision variables, the number k of a single Gaussian function for each decision variable in the archive is considered. By selecting each of them and generating a new answer, a situation equivalent to a Gaussian kernel function is created for each variable.
In other words, it could be said that the number of answers stored in the archive is equal to
In this regard,
The
To determine
where ξ > 0 is an adjustable parameter and behaves similarly to the pheromone evaporation rate in ACOr. The larger the value of this parameter, the lower the convergence speed of the algorithm. The pheromone evaporation rate in the ACOr algorithm affects long-term memory and causes the worst answers to be forgotten. ξ in ACOr also affects the long-term memory of the algorithm and makes worse answers less likely, thus erasing them.
Now to generate a new answer based on the answer
It is necessary to explain that the lower the amplitude of the bell diagram of the Gaussian function (or in other words, the scatter of all the answers in the archive for the name variable decreases to zero); at that time, any new value generated for the
In addition, by selecting each of the Gaussian functions (for example, for the
Pheromone updating in the ACOr algorithm is carried out by storing the best answers and deleting the weak answers in the answer archive.
The three main limitations of the ACOr algorithm are the stagnation phase, exploration and exploitation rate, and convergence speed of the algorithm (Mulani and Desai, 2018). In this study, the number of iterations of the algorithm was equal to 200, and with more iterations, no improvement was seen in the results. In addition, the initial population of 10 was selected.
Figure 2 shows the steps used for using ACOr to train the ANFIS in order to predict the SL.
In Figure 2, the termination of the algorithm can be carried out in three ways:
1) Lack of progress: That is, all the answers in the archive should be the same so that the new answer produced is not different from the previous answers. Sometimes the algorithm may get stuck in a local optimization, and with the number of consecutive repetitions and the passage of time, it can get out of this state that is based on the type of problem and experience on these algorithms, and their lack of progress can be seen. For this reason, it can be stipulated that if the progress of the algorithm is less than ε with t repetition times, then the algorithm will not be able to progress, and its termination will be announced.
2) Number of repetitions: The stop condition can be performed with a certain number of repetitions. The number of repetitions can be determined experimentally and in the context of the problem.
3) Reaching a certain value: The algorithm can be continued until it converges to a certain value.
The DE strategy is a population-based probabilistic optimization method. This algorithm is similar to the GA in the basic principles of producing the original population and continuing the evolution of future generations and looking at the evaluation function. Only the cut and jump operators in this algorithm are used with a different approach. This algorithm was proposed by Storn and Price (1995). The main difference between this algorithm and other evolutionary algorithms is in choosing the direction and distance of the current population from other members of the population in order to guide the search process in a desirable direction. The general process of this algorithm is as follows: 1) First, the mutation operator is used to generate an optimal vector u(t); the mutation actually occurs from the effect between people in the current population. 2) The main cutting operator, which is discrete, binomial, or exponential, is probabilistically generated to produce a new child using the optimal vector u(t) and a solution x(t) (parent). 3) In the main cutting operation, a child is always produced which almost reduces the volume of calculations, and the orientation of the children is based on the desired vector.
The main problem with DE is that it produces a limited number of different responses in a generation. This constraint prevents the algorithm from finding the right path to reach the global answer. Another disadvantage of this algorithm is that DE is less widespread than other meta-heuristic algorithms. In other words, the degree of convergence of this algorithm may be disturbed, and the global answer may be delayed (Angel et al., 2018). In the present study, for the optimal selection of the number of repetitions, from the number of repetitions of 100 to the number of repetitions of 1,000 numbers were selected, but no change was observed in the limited number of answers. In addition, with the change of the initial population between the numbers 10 and 50, no change in the results was observed.
To evaluate the performance of the designed algorithms to predict the amount SL, three statistical parameters called R2 (coefficient of determination) which normally ranges from 0 to 1; RMSE (root mean square error), which is based on the assumption that data follow normal distribution and also work as a measure of average deviation of model predictions from the actual values in the dataset; and SI (Scatter index), which presents the RMSE difference with respect to mean observations have been used:
In the abovementioned equations,
This section interprets the results obtained from the study of the degree of correlation between input and output data as well as the performance of the simulation of the amount of sediment load by considering the different modes of input data.
The data recorded at the study station include three types of data: T, Q, and CM. Due to the unknown effect of the mentioned parameters in predicting the amount of sediment, this trend was adopted, which was determined by calculating the coefficient of determination by considering the relationship between each of the mentioned parameters and the amount of SL recorded. Figure 3: The calculated R2 for T, Q, and CM data was 0.019, 0.437, and 0.460, respectively, indicating that the CM, Q, and T ranged from highest to lowest correlation. From the results of the regression correlation test, it can be expected that T is the least effective input data in predicting SL, and CM is the most effective input data in predicting SL.
In this section, to understand the impact of each of the input data in predicting the amount of SL, the process was adopted to select data individually or with different combinations as input to algorithms to the most effective data or data combinations on to be determined according to the predicted amount of sediment. For this purpose, the input data in three groups with single nature, binary combination, and separate triple combinations followed the following trend: { T, Q, CM (T + Q) (T + CM) (Q + CM) (T + Q + CM)}.
In this group, the input data are T, Q, and CM, which are used individually in the calculations to determine the effectiveness of each in predicting the amount of sediment. According to the results of calculations, it was observed that the effect of CM, Q, and T was ranked from highest to lowest (Table 2). Taking into account all cases, in general, at this stage, the ANFIS–ACOr hybrid algorithm, considering the input data of CM, recorded the results R2 = 0.708, RMSE = 61.201 (ton/day), and SI = 0.522 in training, and R2 = 0.589, RMSE = 85.655 (ton/day), SI = 0.741 had the best performance, while the classical ANFIS with T as the input had the weakest rate of sediment prediction [R2 = 0.011 and RMSE = 112.668 (ton/day) and SI = 0.961 in training and R2 = 0.0004 and RMSE = 132.587 (ton/day) and SI = 1.147 in the test]. In addition, according to the results, all algorithms emphasized that the T parameter has a very small effect in predicting the amount of sediment. After the ANFIS–ACOr algorithm, the algorithms ANFIS-PSO, ANFIS-GA, and ANFIS-DE were in the next ranks.
Figure 4 confirms the abovementioned results by comparing the observed data and the results of the classical ANFIS algorithm and the ANFIS–ACOr hybrid algorithm. The reason why there is a gap in the last data could be because the input dataset used for this simulation is individual (CM), while as shown in Figures 5, 6 a combined simulation has solved this gap.
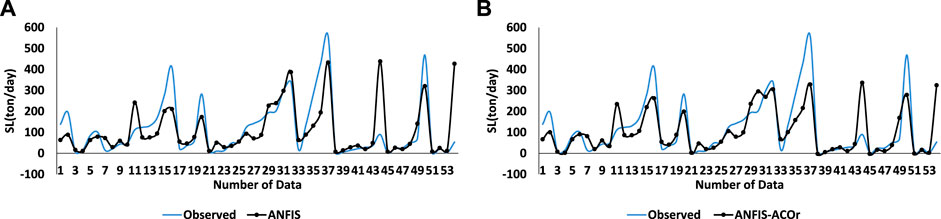
FIGURE 4. Prediction results by ANFIS and ANFIS–ACOr in single input of CM. (A) Comparing the SL observed with the SL predicted in the ANFIS in test mode, (B) Comparing the SL observed with the SL predicted in the ACOr–ANFIS in test mode.
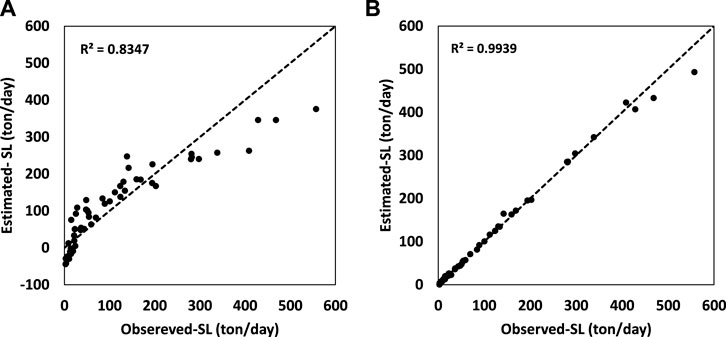
FIGURE 5. Results for ANFIS and ANFIS-ACOr in the combined input of Q+CM, (A) SL predicted by ANFIS in test mode, (B) SL predicted by ANFIS-ACOr in test mode.
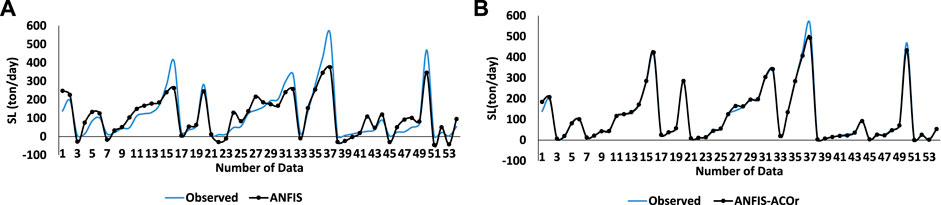
FIGURE 6. Results for ANFIS and ANFIS–ACOr in the input of Q + CM. (A) Comparing the SL observed with the SL predicted in ANFIS in the test mode, (B) Comparing the SL observed with the SL predicted in the ANFIS–ACOr in test mode.
The simulations in the first group showed that the importance of sediment concentration data was much higher than that of river flow and temperature so that the difference between the evaluation criteria in these three inputs is significant. This indicates that the effect of sediment concentration during sampling on sediment load simulation is very high. A noteworthy point in this section is the inability of algorithms to properly predict maximum and minimum points, which is due to the uniqueness of the input data.
The criterion for operation in this section is the binary combination of input data as follows: T + Q, T + CM, Q + CM.
The results of the calculations indicate that the presence of T as part of the input data had a very small positive effect on the performance of the algorithms, while the combination of CM and Q data in all algorithms showed a very good performance. It can be concluded that T can be taken out of its calculations (Table 3). Considering all the cases, in general, in this section, it was observed that the statistical parameters R2, RMSE, and SI in the test mode for the ANFIS–ACOr algorithm with the best prediction (CM + Q) are equal to 0.991, 13.001 (ton/day), and 0.112, respectively, and the ANFIS with the weakest prediction (T + Q) is 0.490, 107.383 (ton/day), and 0.929, respectively. The algorithms ANFIS-PSO and ANFIS-GA were slightly different from each other and ANFIS-DE was in the next ranks. Figure 7 shows the comparison of all five algorithms in Taylor Diagram using standard deviation, Pearson’s correlation, and RMS which supports the calculation above in (Q + CM) the coupled set data.
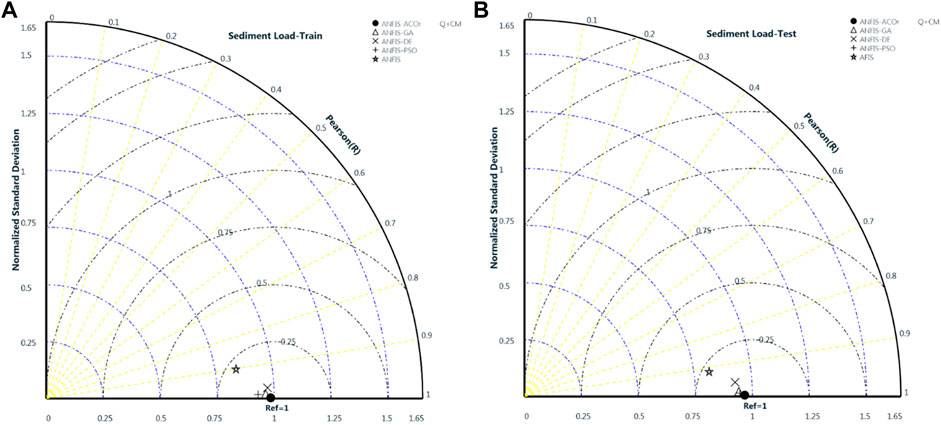
FIGURE 7. Taylor diagram for Comparison between 5 Hybrid Algorithms in Q+CM coupled set data in (A)- Train phase and (B)- Test phase.
Figure 8 and Figure 6 are comparative modes between the performance of the two algorithms ANFIS and ANFIS-ACOr in the
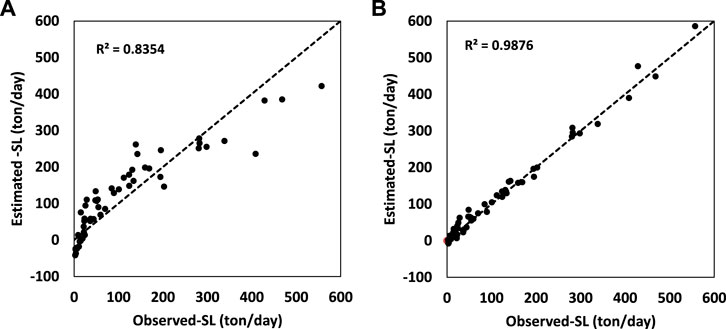
FIGURE 8. Results for ANFIS and ANFIS–ACOr in all inputs. (A) SL predicted by ANFIS in the test mode. (B) SL predicted by ANFIS–ACOr in test mode.
In this case, it is clear that combining data could greatly improve the performance of algorithms. This has significantly increased the poor performance of the algorithms in predicting the maximum and minimum points. In addition, the amount of statistical parameters has been significantly improved. This shows that the hybrid structures used have been able to escape the local optimization with the help of the combination of input data and show significant performance.
Considering all three types of data recorded at the farm station as input data, the results of statistical parameters R2 and RMSE can be seen in Table 4. Algorithm calculations show that the presence of T as part of the input data slightly reduces the performance of the algorithms compared to the CM + Q mode. However, hybrid algorithms still performed satisfactorily compared to the classic ANFIS. ANFIS-PSO, ANFIS-GA, and ANFIS-DE were also in the next ranks of prediction of SL after the ANFIS–ACOr (Table 4). The results of the ANFIS–ACOr hybrid algorithm in the training mode are R2 = 0.989, RMSE = 11.900 (ton/day), and SI = 0.101 and in the test mode are R2 = 0.987, RMSE = 15.507 (ton/day), and SI = 0.134. The ANFIS with the weakest performance was able to record the results of R2 = 0.784, RMSE = 52.992 (ton/day), and SI = 0.452 in the training mode and R2 = 0.835, RMSE = 54.582 (ton/day), and SI = 0.472 in the test mode. The results obtained from this study were in good agreement with the results of other studies (Azad et al., 2017). Their study on predicting water quality parameters concluded that meta-heuristic algorithms could improve the performance of the classical ANFIS. Figure 9 shows the comparison of all five algorithms in Taylor Diagram using standard deviation, Pearson’s correlation, and RMS which supports the calculation above in T + Q + CM set data.
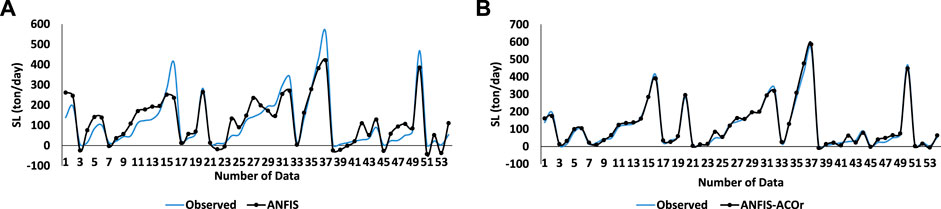
FIGURE 9. Results for ANFIS and ANFIS-ACOr in all inputs. (A) Comparing the SL observed with the SL predicted in ANFIS in the test mode, (B) Comparing the SL observed with the SL predicted in the ANFIS-ACOr in the test mode.
Figure 10 and Figure 5 compare the performance of the two ANFIS algorithms in its classical state and in the optimized state with the ACOr algorithm, in which the input data is T + CM + Q. As can be seen in Figures 7, 9, the results of the ACOr algorithm show the success of this optimization algorithm in improving the performance of the ANFIS. Comparative graphs show that the ANFIS–ACOr has a good ability in predicting the maximum and minimum points (Kishi et al., 2017; Kishi et al., 2017; Yaseen et al., 2017), while the classical ANFIS suffers from this weakness.
The results obtained in this case indicate that the combination of all input data, in fact, could not have a significant impact on the performance of the algorithm. However, by comparing Figures 5, 10 with Figures 6, 8, it can be concluded that the existence of temperature data with a more scattered nature had the opposite function in the training mode. In addition, in the test mode, the predictions for the maximum and minimum points are slightly weaker. This indicates the sensitivity of the hybrid algorithms used for the type of data.
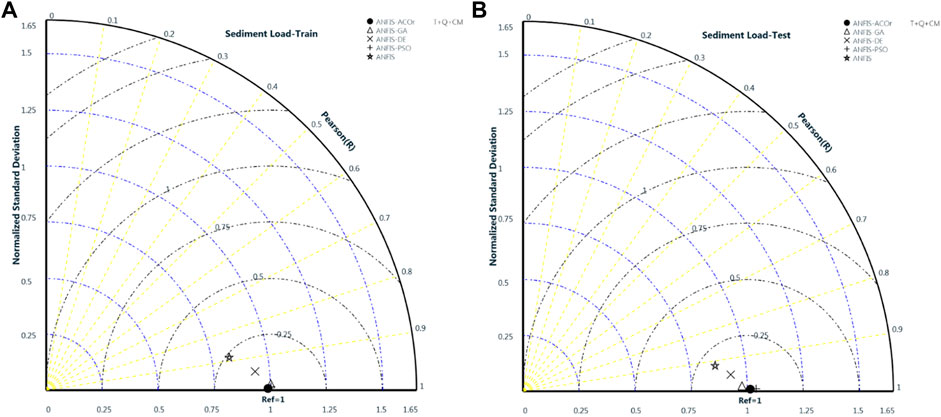
FIGURE 10. Taylor diagram for Comparison between 5 Hybrid Algorithms in T+Q+CM set data in (A)-Train and (B)- Test phase.
In this study, it was hypothesized that hybridization of the ANFIS using four evolutionary algorithms could increase the performance of the ANFIS in predicting the amount of sediment. In addition, in order to be able to understand the impact of each data and their combination, different combinations of data were proposed. Initially, the ANFIS clearly showed that its predictive power was not optimal for sediment load with this data set, so in the first step, the algorithms were evaluated with only one input data set. This method was a determinant of the impact of each data on the scale prediction operation. The results showed that the temperature data (T) in all algorithms led to poor results. After T, the discharge data (Q) showed a significant effect in predicting the amount of sediment. Finally, it was the CM data that showed the highest impact in estimating the amount of sediment. In all the obtained results, the ANFIS–ACOr hybrid algorithm showed the best results, which was in line with the assumption of the research problem. But, the lowest statistical indicators were recorded for the ANFIS algorithm, and the reason for this is that the random selection of data for training and testing tends to overfit the calculations. Comparing the current structure of ANFIS training with the situation in which meta-heuristic algorithms are used, it can be concluded that meta-heuristic algorithms have been able to provide a method that is more independent than the ANFIS and have been able to escape the optimal local trap better than the ANFIS. In other words, it can be said that the overdependence of the ANFIS training process was improved by using these algorithms. The results obtained from the use of meta-heuristic algorithms in ANFIS training showed that all of them have been able to improve its performance, but in the meantime, the ACOr algorithm is better than the others by avoiding falling into the optimal local trap and the problem of over-adaptation. The results of other research studies (Kishi et al., 2018) also confirm this claim. After ACOr, GA, PSO, and DE algorithms were ranked next.
The data were then divided into composite groups consisting of two types of data. In other words, T + Q, T + CM, and Q + CM were the criteria for evaluating the performance of the proposed algorithms. According to the obtained results, it was expected that weaker results would be obtained in the combinations that included T. The results also indicated that the combination of T and Q showed the weakest predictions in this part of the study. This was followed by the combination of T and CM data, which was able to show slightly better predictions, while the best data combination, both in this section and in the whole study, was the combination of Q and CM data, with the lowest error rate. It should be noted that the performance of meta-heuristic algorithms can show a significant effect on the performance of the ANFIS for predicting sediments. In addition, the results of the ANFIS–ACOr algorithm in this section showed the highest correlation and lowest error. Following the effects of the data, the combination of all three data was examined. The noteworthy point in this section was that despite the very good performance of all algorithms in predicting the amount of sediment none of them could show a better performance than the combination of CM + Q data. This result showed that the presence of temperature data can reduce the performance of hybrid algorithms in predicting the amount of sediment in the dam reservoir. In this section, all hybrid algorithms had improved the performance of the ANFIS in predicting the amount of sediment, and among these, the ANFIS–ACOr algorithm had the best performance. According to the results obtained in this section, it was observed that hybrid algorithms when combining data together were still able to show much better performance than a simple ANFIS. This is because the ANFIS performed weaker than the hybrids with the emergence of a parameter that has the least correlation with the observational data, while the algorithms used were able to significantly enhance the ANFIS’s weakness (Azad et al., 2017).
Dam construction studies have very high costs. An important part of dam studies is estimating the amount of sediment in the river. Sedimentation behind dams and studies related to dam construction is one of the most important parts. Laboratory methods undoubtedly require a lot of money to calculate the amount of sediment, but using hybrid algorithms, the amount of sediment in the river can be estimated with a high degree of reliability. Undoubtedly, it is recommended to use laboratory calculations and intelligent algorithms simultaneously in water designs that are of high importance in order to ultimately determine the reliability of these new and low-cost methods. In this study, using recorded information (such as temperature, flow rate, and sediment concentration) upstream of a real dam and using the proposed intelligent method, the amount of sediment is predicted, and it is suggested that this method can be combined with other studies related to sediment estimation.
Figure 11 shows the coherence process of the algorithms used in this study. This figure shows a comparison of the search quality in the answer space. As can be seen, the ANFIS–ACOr algorithm searches the target space better than other algorithms.
In the present study, by performing the coefficient of determination test on the input data of temperature, river flow, and sediment concentration, it was concluded that the sediment concentration data had the highest correlation with the recorded sediment load data, while the temperature had the lowest correlation.
The main purpose of this study was to investigate the performance of meta-heuristic algorithms with classical adaptive neuro-fuzzy inference system. For this purpose, by grouping the input data into single, binary, and ternary groups, the performance of hybrid algorithms and ANFIS was investigated. According to the computations, the best statistical results were recorded when the data were binary (sediment concentration + river flow) in which the ANFIS–ACOr extended to continuous domain algorithm with R2 = 0.991, RMSE = 13.001 (to/day), and SI = 0.112 in the test mode revealed the best performance. In the other two scenarios, also the ANFIS–ACOr extended to continuous domain presented the best prediction which shows it poser for estimating sediment load. Considering the results of the regression test, there was no expectation for the single dataset to provide the best platform for prediction of sediment load; on the other hand, the results showed that for finding the best combination, grouping data were necessary for complete clearance. By considering the outcomes of the dataset in whole (temperature + river flow + sediment concentration), the results were satisfying [R2 = 0.987, RMSE = 15.507 (ton/day), and SI = 0.134]; while it was not the best outcome, it should be mentioned that it needed more time for calculation. Relying on the results obtained from the use of meta-heuristic algorithms in the ANFIS training stage, it can be concluded that these algorithms have a good ability in training and improve the performance of the ANFIS and increase its accuracy in predicting complex hydrological phenomena, such as river sediment prediction. Using the statistical parameters used in the study and comparing the performance of hybrid algorithms in sediment estimation, it was observed that the considered assumption in the problem was proved and in the meantime, the ANFIS–ACOr extended to continuous domain algorithm was able to obtain the best performance among all hybrid algorithms used in this study.
The data analyzed in this study are subject to the following licenses/restrictions: There is no restriction. Requests to access these datasets should be directed to HK, SGthcmFtaUBzZW1uYW4uc2MuaXI=.
Conceptualization: HK, YD, MM, SB, CJ, and SMB. Data curation: HK, YD, SB, CJ, and SMB. Formal analysis: HK, YD, SB, AM, MM, K-WC, CJ, and SMB. Investigation: HK, YD, SB, AM, MM, and K-WC. Methodology: HK, YD, SB, AM, MM, K-WC, CJ, and SMB. Resources: HK, YD and SB. Software: HK and YD. Supervision: HK and SB. Validation: AM, MM, K-WC, CJ, and SMB. Visualization: HK and YD. Writing–original draft: HK and YD. Writing–review and editing: HK, YD, CJ, and SMB.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Ab. Ghani, A., and Azamathulla, H. Md. (2011). Gene-Expression Programming for Sediment Transport in Sewer Pipe Systems. J. Pipeline Syst. Eng. Pract. 2, 102–106. doi:10.1061/(asce)ps.1949-1204.0000076
Ab. Ghani, A., and Azamathulla, H. Md. (2012). Development of GEP-Based Functional Relationship for Sediment Transport in Tropical Rivers. Neural Comput. Appl. 24, 271–276. doi:10.1007/s00521-012-12229
Abdulshahed, A. M., Longstaff, A. P., and Fletcher, S. (2015). The Application of ANFIS Prediction Models for thermal Error Compensation on CNC Machine Tools. Appl. soft Comput. 27, 158–168. doi:10.1016/j.asoc.2014.11.012
Akrami, S. A., El-Shafie, A., and Jaafar, O. (2013). Improving Rainfall Forecasting Efficiency Using Modified Adaptive Neuro-Fuzzy Inference System (MANFIS). Water Resour. Manage. 27 (9), 3507–3523. doi:10.1007/s11269-013-0361-9
Akrami, S. A., Nourani, V., and Hakim, S. J. S. (2014). Development of Nonlinear Model Based on Wavelet-ANFIS for Rainfall Forecasting at Klang Gates Dam. Water Resour. Manage. 28, 2999–3018. doi:10.1007/s11269-014-0651-x
Angel, N., Segura, C., and Cedeño, O. D. (2018). “Explicit Control of Diversity in Differential Evolution,” in IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil (Institute of Electrical and Electronics Engineers). doi:10.1109/CEC.2018.8477682
Azad, A., Karami, H., Farzin, S., Saeedian, A., Kashi, H., and Sayyahi, F. (20172018). Prediction of Water Quality Parameters Using ANFIS Optimized by Intelligence Algorithms (Case Study: Gorganrood River). KSCE J. Civ Eng. 22, 2206–2213. doi:10.1007/s12205-017-1703-6
Bakhtyar, R., Ghaheri, A., Yeganeh-Bakhtiary, A., and Baldock, T. E. (2008). Longshore Sediment Transport Estimation Using a Fuzzy Inference System. Appl. Ocean Res. 30, 273–286. doi:10.1016/j.apor.2008.12.001
Batt, H. A., and Stevens, D. K. (2013). Relevance Vector Machine Models of Suspended Fine Sediment Transport in a Shallow Lake-I: Data Collection. Environ. Eng. Sci. 30 (11), 681–688. doi:10.1089/ees.2012.0487
Buyukyildiz, M., and Kumcu, S. Y. (2017). An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models. Water Resour. Manage. 31, 1343–1359. doi:10.1007/s11269-017-1581-1
Cazzaniga, P., Nobile, M. S., and Besozzi, D. (2015). “The Impact of Particles Initialization in PSO: Parameter Estimation as a Case in point,” in IEEE Conference on Computational Intelligence in Bioinformatics and Computational Biology (CIBCB), Niagara Falls, ON (Institute of Electrical and Electronics Engineers). doi:10.1109/CIBCB.2015.7300288
Chang Howard, H. (2008). River Morphology and River Channel Changes, Trans. Tianjin Univ. 14, 254–262. doi:10.1007/s12209-008-0045-3
Chang, C. K., Azamathulla, H. M., Zakaria, N. A., and Ghani, A. A. (2012). Appraisal of Soft Computing Techniques in Prediction of Total Bed Material Load in Tropical Rivers. J. Earth Syst. Sci. 121 (1), 125–133. doi:10.1007/s12040-012-0138-1
Dahiya, A., and Sangwan, S. (2018). Literature Review on Genetic Algorithm. Int. J. Res. 5 (16), 1142. https://www.researchgate.net/publication/341371936_Literature_Review_on_Genetic_Algorithm.
Dragoi, E. N., and Dafinescu, V. (2021). Review of Metaheuristics Inspired from the Animal Kingdom. Mathematics 9 (18), 2335. doi:10.3390/math9182335
Ebtehaj, I., and Bonakdari, H. (2016). A Comparative Study of Extreme Learning Machines and Support Vector Machines in Prediction of Sediment Transport in Open Channels. Int. J. Eng. 29 (11), 1499–1506.
Ebtehaj, I., and Bonakdari, H. (2017). Design of a Fuzzy Differential Evolution Algorithm to Predict Non-deposition Sediment Transport. Appl. Water Sci. 7, 4287–4299. doi:10.1007/s13201-017-0562-0
Ebtehaj, I., Bonakdari, H., and Es-haghi, M. S. (2019). Design of a Hybrid ANFIS-PSO Model to Estimate Sediment Transport in Open Channels. Iran J. Sci. Technol. Trans. Civ Eng. 43, 851–857. doi:10.1007/s40996-018-0218-9
Ehteram, M., Singh, V. P., Ferdowsi, A., Mousavi, S. F., Farzin, S., Karami, H., et al. (2019). An Improved Model Based on the Support Vector Machine and Cuckoo Algorithm for Simulating Reference Evapotranspiration. PloS one 14 (5), e0217499. doi:10.1371/journal.pone.0217499
Engelbrecht, A. P. (2007). Computational Intelligence: An Introduction. Second Edition. John Wiley & Sons.
Engelbrecht, A. (2012). “Particle Swarm Optimization: Velocity Initialization,” in WCCI 2012 IEEE World Congress on Computational Intelligence, Brisbane, Australia (Institute of Electrical and Electronics Engineers). Available at: https://zenodo.org/record/1266051/files/article.pdf.
Firat, M., and Güngör, M. (2010). Monthly Total Sediment Forecasting Using Adaptive Neuro Fuzzy Inference System. Stoch Environ. Res. Risk Assess. 24, 259–270. doi:10.1007/s00477-009-0315-1
Frings, R. M., and Kleinhans, M. G. (2008). Complex Variations in Sediment Transport at Three Large River Bifurcations during Discharge Waves in the River Rhine. Sedimentology 55, 1145–1171. doi:10.1111/j.1365-3091.2007.00940.x
Ganjidoost, H., Mousavi, S. J., and Soroush, A. (2015). Adaptive Network-Based Fuzzy Inference Systems Coupled with Genetic Algorithms for Predicting Soil Permeability Coefficient. Neural Process. Lett. 44, 53–79. doi:10.1007/s11063-015-9479-5
Goldberg, D. (1989). Genetic Algorithms in Search Optimization and Machine Learning. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc.
Goyal, M. K. (2014). Modeling of Sediment Yield Prediction Using M5 Model Tree Algorithm and Wavelet Regression. Water Resour. Manage. 28, 1991–2003. doi:10.1007/s11269-014-0590-6
Guo, Q., Ba, J., Luo, C., Ba, J., Luo, C., and Xiao, S. (2020). Stability-enhanced Prestack Seismic Inversion Using Hybrid Orthogonal Learning Particle Swarm Optimization. J. Pet. Sci. Eng. 192 (2020), 107313. doi:10.1016/j.petrol.2020.107313
Hasanipanah, M., Noorian-Bidgoli, M., Jahed Armaghani, D., and Khamesi, H. (2016). Feasibility of PSO-ANN Model for Predicting Surface Settlement Caused by Tunneling. Eng. Comput. 32, 705–715. doi:10.1007/s00366-016-0447-0
Jalalkamali, A. (2015). Using of Hybrid Fuzzy Models to Predict Spatiotemporal Groundwater Quality Parameters. Earth Sci. Inform. 8 (4), 885–894. doi:10.1007/s12145-015-0222-6
Jang, J.-S. R. (1993). ANFIS: Adaptive-Network-Based Fuzzy Inference System. IEEE Trans. Syst. Man. Cybern. 23 (3), 665–685. doi:10.1109/21.256541
Kennedy, J., and Eberhart, R. (1995). “Particle Swarm Optimization,” in Proceedings of IEEE International Conference on Neural Networks IV.1000. (Institute of Electrical and Electronics Engineers)
Khashei-Siuki, A., and Sarbazi, M. (2013). Evaluation of ANFIS, ANN, and Geostatistical Models to Spatial Distribution of Groundwater Quality (Case Study: Mashhad plain in Iran). Arab J. Geosci. 8, 903–912. doi:10.1007/s12517-013-1179-8
Kisi, O., Keshavarzi, A., Shiri, J., Zounemat-Kermani, M., and Omran, E.-S. E. (2017). Groundwater Quality Modeling Using Neuro-Particle Swarm Optimization and Neuro-Differential Evolution Techniques. Hydrol. Res. 48 (6), 1508–1519. doi:10.2166/nh.2017.206
Kisi, O., Azad, A., Kashi, H., Saeedian, A., Hashemi, S. A. A., and Ghorbani, S. (2018). Modeling Groundwater Quality Parameters Using Hybrid Neuro-Fuzzy Methods. Water Resour. Manage. 33, 847–861. doi:10.1007/s11269-018-2147-6
Kisi, O. (2015). Streamflow Forecasting and Estimation Using Least Square Support Vector Regression and Adaptive Neuro-Fuzzy Embedded Fuzzy C-Means Clustering. Water Resour. Manage. 29, 5109–5127. doi:10.1007/s11269-015-1107-7
Martinez, J. M., Guyot, J. L., Filizola, N., and Sondag, F. (2009). Increase in Suspended Sediment Discharge of the Amazon River Assessed by Monitoring Network and Satellite Data. Catena 79, 257–264. doi:10.1016/j.catena.2009.05.011
Meshram, S. G., Singh, V. P., Kisi, O., Karimi, V., and Meshram, C. (2020). Application of Artificial Neural Networks, Support Vector Machine and Multiple Model-ANN to Sediment Yield Prediction. Water Resour. Manage. 34, 4561–4575. doi:10.1007/s11269-020-02672-8
Mirrashid, M. (20142014). Earthquake Magnitude Prediction by Adaptive Neuro-Fuzzy Inference System (ANFIS) Based on Fuzzy C-Means Algorithm. Nat. Hazards 74, 1577–1593. doi:10.1007/s11069-014-1264-7
Mulani, M., and Desai, V. L. (2018). Design and Implementation Issues in Ant colony Optimization. Int. J. Appl. Eng. Res. 13 (16), 12877–12882. ISSN 0973-4562 https://www.ripublication.com/ijaer18/ijaerv13n16_69.pdf.
Nayak, P. C., Sudheer, K. P., Rangan, D. M., and Ramasastri, K. S. (2004). A Neuro-Fuzzy Computing Technique for Modeling Hydrological Time Series. J. Hydrol. 291 (1-2), 52–66. doi:10.1016/j.jhydrol.2003.12.010
Nourani, V. (2009). Using Artificial Neural Networks (ANNs) for Sediment Load Forecasting of Talkherood River Mouth. J. Urban Environ. Eng. 3 (1), 1–6. doi:10.4090/juee.2009.v3n1.001006
Omolbani, M. R. P., shui, L. T., and Gehghani, A. A. (2010). Review of Genetic Algorithm Model for Suspended Sediment Estimation. Aust. J. Basic Appl. Sci. 4 (8), 3354–3359. https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.1063.2998&rep=rep1&type=pdf
Omolbani, M. R. P., Lee, T. S., and Amir, A. D. (2012). Comparision of Ant colony Optimization and Genetic Algorithm Models for Identifying the Relation between Flow Discharge and Suspended Sediment Load (Gorgan River - Iran). Sci. Res. Essays 7 (42), 3584–3604. doi:10.5897/SRE11.264
Peyghami, M. R., and Khanduzi, R. (2013). Novel MLP Neural Network with Hybrid Tabu Search Algorithm. Neural Network World 23 (3), 255–270. doi:10.14311/nnw.2013.23.016
Salih, S. Q., Sharafati, A., Khosravi, K., Faris, H., Kisi, O., Tao, H., et al. (2020). River Suspended Sediment Load Prediction Based on River Discharge Information: Application of Newly Developed Data Mining Models. Hydrological Sci. J. 65 (4), 624–637. doi:10.1080/02626667.2019.1703186
Samet, K., Hoseini, K., Karami, H., and Mohammadi, M. (2018). Comparison between Soft Computing Methods for Prediction of Sediment Load in Rivers: Maku Dam Case Study. Iran J. Sci. Technol. Trans. Civ Eng. 43 (3), 93–103. doi:10.1007/s40996-018-0121-4
Shi, Y., and Eberhart, R. C. (1998). “Parameter Selection in Particle Swarm Optimization,” in Evolutionary Programming VII. EP 1998. Editors V. W. Porto, N. Saravanan, D. Waagen, and A. E. Eiben (Berlin, Heidelberg: Springer), 1447, 591–600. Lecture Notes in Computer Science. doi:10.1007/BFb0040810
Shihabudeen, K. V., and Pillai, G. N. (2018). Recent Advances in Neuro-Fuzzy System: A Survey. Knowl.-Based Syst. 152, 136–162. doi:10.1016/j.knosys.2018.04.014
Sivakumar, B., and Jayawardena, A. W. (2002). An Investigation of the Presence of Low-Dimensional Chaotic Behaviour in the Sediment Transport Phenomenon. Hydrological Sci. J. 47 (3), 405–416. doi:10.1080/02626660209492943
Socha, K., and Dorigo, M. (2008). Ant Colony Optimization for Continuous Domains. Eur. J. Oper. Res. 185 (3), 1155–1173. doi:10.1016/j.ejor.2006.06.046
Storn, R., and Price, K. (1995). “Differential Evolution-A Simple and Efficient Adaptive Scheme for Global Optimization over Continuous Spaces,”. Technical Report (International Computer Science Institute), 11.
Mohammad Rezapour Tabari, M. (2016). Prediction of River Runoff Using Fuzzy Theory and Direct Search Optimization Algorithm Coupled Model. Arab J. Sci. Eng. 41 (10), 4039–4051. doi:10.1007/s13369-016-2081-y
Tayfur, G., and Singh, V. P. (2006). ANN and Fuzzy Logic Models for Simulating Event-Based Rainfall-Runoff. J. Hydraul. Eng. 132 (12), 1321–1330. doi:10.1061/(asce)0733-9429(2006)132:12(1321)
Wang, Y. M., Kerh, T., and Traore, S. (2009). Neural Networks Approaches for Modelling River Suspended Sediment Concentration Due to Tropical Storms. Glob. NEST J. 11 (4), 457–466. doi:10.30955/gnj.000628
Yaseen, Z. M., El-shafie, A., Jaafar, O., Afan, H. A., and Sayl, K. N. (2015). Artificial Intelligence Based Models for Stream-Flow Forecasting: 2000-2015. J. Hydrol. 530, 829–844. doi:10.1016/j.jhydrol.2015.10.038
Keywords: sediment load, sediment transport, river flow, machine learning, artificial intelligence, hydrological model, hydrology, big data
Citation: Karami H, DadrasAjirlou Y, Jun C, Bateni SM, Band SS, Mosavi A, Moslehpour M and Chau K-W (2022) A Novel Approach for Estimation of Sediment Load in Dam Reservoir With Hybrid Intelligent Algorithms. Front. Environ. Sci. 10:821079. doi: 10.3389/fenvs.2022.821079
Received: 23 November 2021; Accepted: 11 February 2022;
Published: 22 March 2022.
Edited by:
Arcilan Assireu, Federal University of Itajubá, BrazilReviewed by:
Seyedali Mirjalili, Torrens University Australia, AustraliaCopyright © 2022 Karami, DadrasAjirlou, Jun, Bateni, Band, Mosavi, Moslehpour and Chau. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hojat Karami, SGthcmFtaUBzZW1uYW4uYWMuaXI=; Shahab S. Band, c2hhbXNoaXJiYW5kc0B5dW50ZWNoLmVkdS50dw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.