- 1School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou, China
- 2School of Information and Communication Engineering, Hainan University, Haikou, Hainan, China
- 3School of Electronics and Communication, Guangdong Mechanical & Electronical Polytechnic, Guangzhou, China
Currently, excessive carbon emission is causing visible damage to the ecosystem and will lead to long-term environmental degradation in the future. The manufacturing industry is one of the main contributors to the carbon emission problem. Therefore, the reduction of carbon emissions should be considered at all levels of production activities. In this paper, the carbon emission as a parvenu indicator is considered parallelly with the nobleman indicator, makespan, in the flexible job-shop scheduling problem. Firstly, the carbon emission is modeled based on the energy consumption of machine operation and the coolant treatment during the production process. Then, a deep reinforcement learning-based scheduling model is proposed to handle the carbon emission-aware flexible job-shop scheduling problem. The proposed model treats scheduling as a Markov decision process, where the scheduling agent and the scheduling environment interact repeatedly via states, actions, and rewards. Next, a deep neural network is employed to parameterize the scheduling policy. Then, the proximal policy optimization algorithm is conducted to drive the deep neural network to learn the objective-oriented optimal mapping from the states to the actions. The experimental results verify that the proposed deep reinforcement learning-based scheduling model has prominent optimization and generalization abilities. Moreover, the proposed model presents a nonlinear optimization effect over the weight combinations.
1 Introduction
Production scheduling is a subclass of combinational optimization problems aiming to sequence jobs to machines toward the optimization of one or more scheduling objectives (Fernandes et al., 2022). Production scheduling can be classified into many types according to its inherent properties. For example, the job-shop scheduling problem (JSSP) specifies that one operation can only be processed by one machine (Zhang et al., 2019), while the flexible job-shop scheduling problem (FJSP) allows multiple candidate machines to process an operation (Brucker and Schlie, 1990). The frequently adopted scheduling objectives related to economic benefits include makespan, tardiness, and machine utilization (Allahverdi et al., 2008). In recent years, the steady deterioration of environmental problems (Bhatti et al., 2021; Bhatti et al., 2022a; Bhatti et al., 2022b), such as pollution and climate change, has raised the awareness of environmental protection. Hence, environmental indicators, especially energy consumption and carbon emission, are a growing concern in production scheduling (Gao et al., 2020). Therefore, the FJSP is formulated as a multi-objective optimization problem considering both economic benefit and environmental effect.
The heuristic and meta-heuristic algorithms have been widely applied to achieve multi-objective scheduling. In terms of heuristic algorithms, Zhang et al. (2022) proposed a greedy algorithm and an elite strategy to solve FJSP with the objectives of minimizing both makespan and total energy consumption. Xu et al. (2021) proposed three delayed routing strategies to optimize energy efficiency and mean tardiness in dynamic FJSP. In terms of meta-heuristic algorithms, the multi-objective genetic algorithm (GA) is the most popular scheme due to its excellent global optimization ability and convergence performance (Li and Wang, 2022). Several GA-based algorithms have been proposed to improve search efficiency for minimizing makespan and total energy consumption (Mokhtari and Hasani, 2017; Dai et al., 2019) and to determine machine start/stop time and speed level to save energy (Wu and Sun, 2018). Moreover, none-GA based algorithms including the frog-leaping algorithm (Lei et al., 2017) and the grey wolf algorithm (Luo et al., 2019) are also available for multi-objective scheduling.
However, the above-mentioned scheduling algorithms lack generalization ability (Han and Yang, 2021). To solve an FJSP instance that is different from the solved ones in terms of parameters such as the number of jobs and machines, the existing heuristic algorithms generally require the development of new scheduling rules while the meta-heuristic algorithms require considerable iterative computation time to obtain high-quality scheduling solutions. In contrast, deep reinforcement learning (DRL) based (Arulkumaran et al., 2017) production scheduling can learn and generalize the knowledge from the training samples to new problems. Therefore, the trained DRL models can be applied to different scheduling scenarios to produce satisfactory scheduling solutions in a reasonable computation time. Qu et al. (2016) and van Ekeris et al. (2021) stated that DRL could discover basic heuristic behaviors for production scheduling from scratch, providing a kind of optimization-capable, scalable, and real-time scheduling methods.
Numerous studies have utilized the generalization ability of DRL to solve different-scale production scheduling problems (Ren et al., 2020; Zhang et al., 2020; Monaci et al., 2021; Ni et al., 2021; Park et al., 2021). However, these studies focused on either the single objective JSSP (Han and Yang, 2020; Liu et al., 2020; Zhao et al., 2021; Zeng et al., 2022) or the flow-shop scheduling problem (FSSP) (Pan et al., 2021; Yan et al., 2022). The multi-objective FJSPs have been seldom addressed (Lang et al., 2020; Luo et al., 2021). Furthermore, among the few studies addressing the DRL-based multi-objective FJSP, even fewer studies cared about environmental objectives (Naimi et al., 2021; Du et al., 2022). Therefore, the development of DRL-based methods for solving FJSP is still in the initial stage and not yet systematic (Luo, 2020; Feng et al., 2021; Liu et al., 2022).
In summary, the existing DRL-based methods for FJSP receive less attention compared with those for JSSP. Moreover, most of the studies preferred the optimization of single or multiple economic objectives to the optimization of environmental objectives. Although some studies have attempted to minimize total energy consumption or electricity cost, minimizing carbon emissions has not been yet explicitly considered. Furthermore, a few studies integrated a DRL model with a meta-heuristic algorithm to solve the multi-objective FJSP. However, the DRL model was used as an auxiliary tool to assist the meta-heuristic algorithm to improve search efficiency. To resolve the above-mentioned technical limitation, this paper proposes a DRL-based scheduling method to handle FJSP to minimize both makespan and total carbon emission. The main contributions of this study are listed as follows.
1) The classical FJSP is extended to a carbon emission-aware flexible job-shop scheduling problem (CEA-FJSP), where a carbon emission accounting model is formulated based on the energy consumption of machine operation and coolant treatment during the production process.
2) An intelligent DRL-based scheduling model is developed to directly generate feasible scheduling solutions for CEA-FJSP without extra searching. The solving process is modeled as a Markov decision process (MDP) including generic productive state features, a scheduling rule-based action space, and a composite reward function.
3) The scheduling policy is parameterized by a deep neural network (DNN), that is, optimized by the proximal policy optimization (PPO) algorithm to establish the mapping from the states to the actions.
4) The experimental results on various benchmarks demonstrate that the proposed DRL scheduling model has prominent optimization and generalization abilities. Moreover, the proposed model presents a nonlinear optimization effect over the weight combinations.
The remainder of this paper is organized as follows. The mathematical model of the CEA-FJSP is formulated in Section 2. The DRL scheduling model is described in Section 3. Section 4 presents the experimental results and Section 5 concludes the study.
2 Problem formulation
This section mathematically describes the conditions and constraints of the CEA-FJSP. There are
1) The operations of the same job should be processed following the defined operation precedence.
2) A machine can only process one operation at a time.
3) An operation should be processed without interruption.
4) A machine processes an operation with constant processing power.
5) All machines turn on at the start of the scheduling.
6) The transportation time of jobs and the setup time of machines are negligible.
Based on the above description, a carbon emission accounting model is formulated firstly to identify the main sources and specific computation of carbon emission in CEA-FJSP. Then, the mathematical model of the CEA-FJSP is established. Table 1 lists the notations used in the models.
2.1 Carbon emission accounting model
Carbon emission is produced directly or indirectly by various manufacturing links, such as raw materials consumption, machine operation, transportation, and metal debris treatment (Gutowski et al., 2005). In this paper, the electrical energy consumption of machine operation and the energy consumption of coolant treatment are identified as the main carbon emission sources in CEA-FJSP.
2.1.1 Carbon emission from machine operation
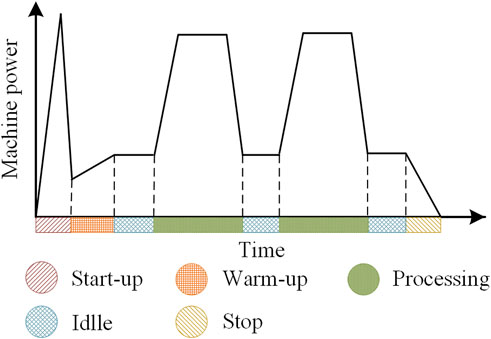
Generally, a machine experiences five working modes in a duty cycle: start-up, warm-up, processing, idle, and stop. Each mode requires a different power level as shown in Figure 1. The modes of start-up, warm-up, and stop appear only once in a duty cycle and the energy consumption in these modes is only related to machine properties rather than scheduling. In contrast, the processing and idle modes tend to alternately appear multiple times. Therefore, only the carbon emission in processing and idle modes are considered in scheduling.
Under processing mode, the carbon emission
where
Under idle mode, the carbon emission
where
2.1.2 Carbon emission from coolant treatment
The coolant is used to reduce the cutting temperature and tool wear and prevent the workpiece from being deformed by heat. The coolant needs to be replaced periodically and the treatment process consumes energy, indirectly producing carbon emissions. To simplify the calculation, it is assumed that the coolant flow rate remains unchanged for the same machine regardless of the processed operations. Hence, the carbon emission of coolant treatment
The total carbon emission
2.2 CEA-FJSP formulation
The CEA-FJSP is a multi-objective optimization problem, considering both economic and environmental benefits. The scheduling objectives are to simultaneously minimize
3 Deep reinforcement learning scheduling modeling
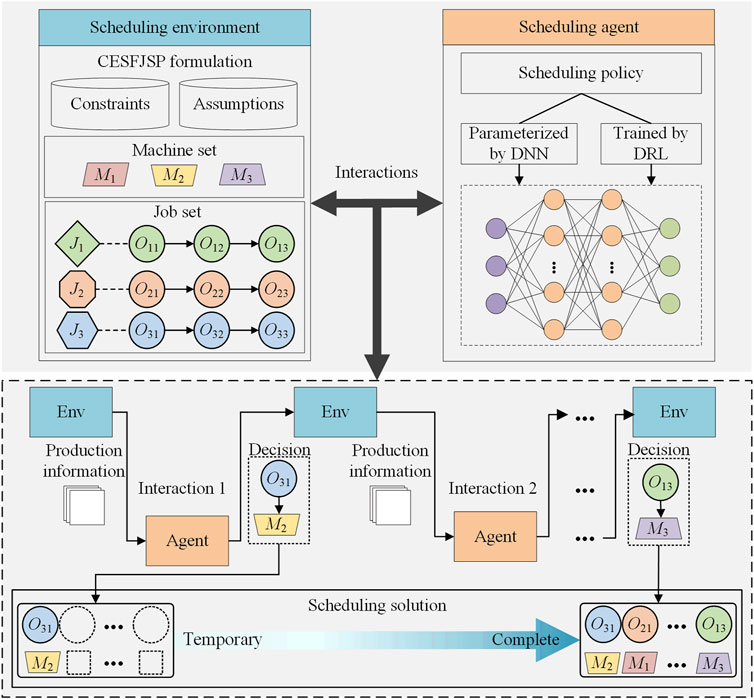
This section proposes a DRL scheduling model for handling CEA-FJSP. Figure 2 shows the framework of the proposed DRL scheduling model. The scheduling environment is an instance of CEA-FJSP initialized with the assumptions and constraints described in Section 2. The scheduling agent embeds a scheduling policy parameterized by a DNN and trained by a DRL algorithm. The agent interacts repeatedly with the environment. In each interaction, the scheduling agent selects an operation and assigns it to a machine, based on the information extracted from the scheduling environment.
The determined operations are queued in a temporary scheduling solution, which is a sequence intuitively describing the precedence of operations. The temporary scheduling solution is turned into a complete and feasible scheduling solution when all operations are determined. Therefore, the scheduling process of a CEA-FJSP instance features an MDP consisting of state, action, and reward. Lastly, the MDP is optimized using a DRL algorithm resulting in a DRL scheduling model.
3.1 Markov decision process formulation
An MDP mainly includes three components: state, action, and reward. A complete decision-making process of MDP is called an episode, consisting of
3.1.1 State representation
The state is the basis of decision making and should provide adequate information about the scheduling environment. The number of scheduled operations of job
A statistic-based representation is adopted to define state features using the dynamic attributes of jobs and machines. Table 2 lists the proposed statistic-based state features. It can be seen from the table that the state is a vector consisting of ten features
3.1.2 Action space
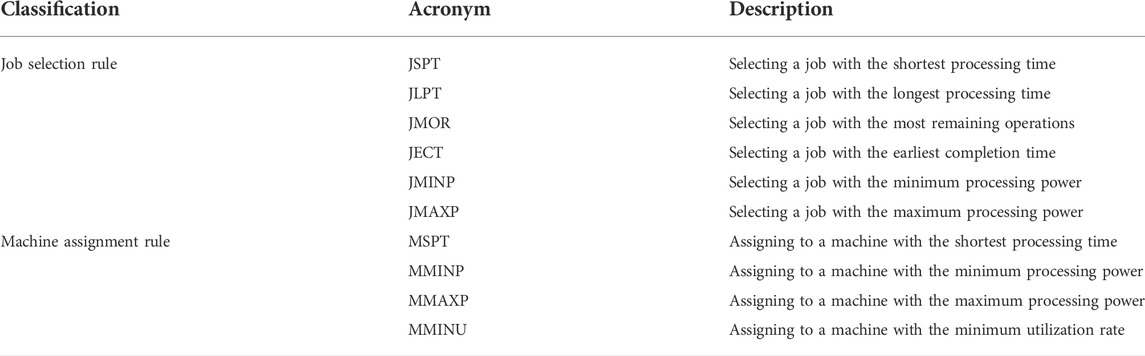
Actions are used to update the scheduling environment, playing a significant role in the quality of scheduling solutions. In the CEA-FJSP, one decision contains two parts: operation selection and machine assignment. Due to the precedence constraint, a job has at most one feasible operation that can be selected at a decision step. Hence, the operation selection can be simplified as the job selection. In this paper, six job selection rules and four machine assignment rules are adopted as shown in Table 3. Nine scheduling rules,
3.1.3 Reward function
As shown in Eq. 7, minimizing
However, the completion time and carbon emission of the scheduled operations can be used as rewards and determined as:
where:
To verify Eq. 13, the cumulative reward is calculated as:
where
Eq. 15 indicates that maximizing the cumulative reward can reach the optimization objectives of minimizing the weighted sum of
3.2 Policy network
The goal of the scheduling policy is to determine the best-matched action for a given state. In this paper, a DNN with parameter
The PPO algorithm is adopted to train the policy network, where the state-value function
3.3 Deep reinforcement learning training process
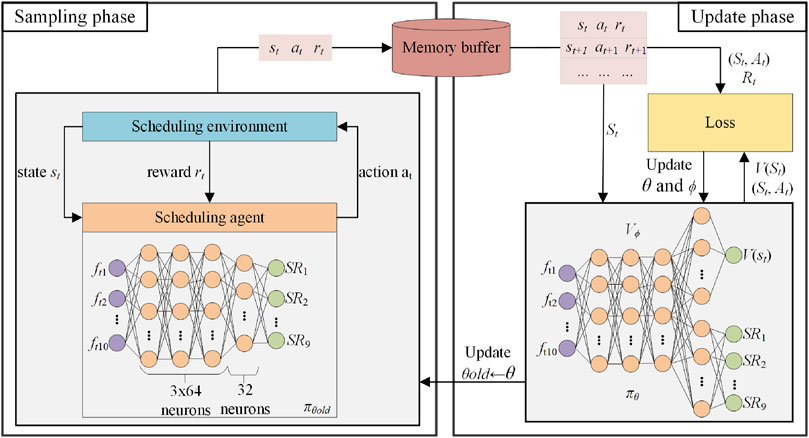
DRL establishes an interaction framework between the agent and the environment using the MDP components: state, action, and reward. The agent learns to optimize its decision-making policy through the interaction, i.e., tunning its policy network
In the sampling phase,
where
The value network is updated through the mean squared error (MSE) loss function:
Due to parameter sharing, the entire network model is trained with the loss function:
where
The pseudo-code of the training process is presented in Algorithm 1. Here, N training instances are initialized at the beginning of a training cycle to prevent the DRL scheduling model from overfitting a specific instance. The data collected from the sampling phase is used to calculate the cumulative gradients to update parameters
Algorithm 1. Training process for CEA-FJSP using PPO
Input: training cycles L; memory buffer M; update epochs K: number of training instances N
Output:
1: Initialize policy network
2: Initialize old policy network
3: for cycle = 1, 2,..., L do
4: Randomly initialize N CEA-FJSP instances
5: for instance = 1, 2,..., N do
6: for step = 1, 2,..., T do
7: Randomly sample action
8: Execute action
9: Receive reward
10: Transfer to the next state
11: Store
12: end for
13: end for
14: for epoch = 1, 2,..., K do
15: Compute
16: Compute
17: Compute
18: Update parameter
19: end for
20:
21: end for
4 Experimental results and discussion
Four numerical experiments were conducted to train the DRL scheduling model, verify the optimization and generalization abilities, and explore the weight effect. The dataset used in the experiments was adapted from the benchmarks in Brandimarte (1993), referred as Brandimarte’s benchmarks hereafter.
4.1 Experimental setting
4.1.1 Dataset adaption
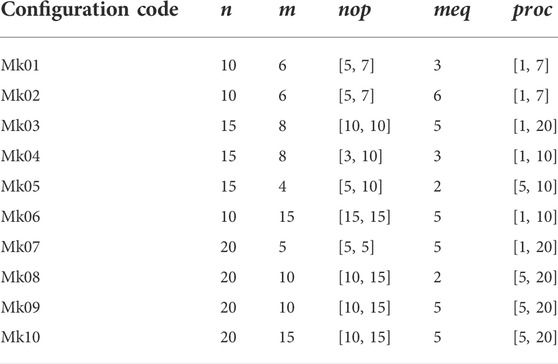
Brandimarte’s benchmarks defined some configurations for FJSP instances, as shown in Table 4. A benchmark is an FJSP instance consisting of
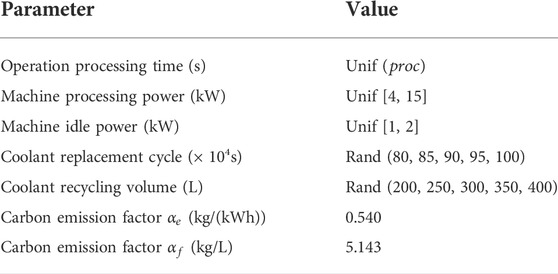
Since the proposed CEA-FJSP considers energy consummation of machine operation and coolant treatment in addition to makespan. Therefore, Brandimarte’s benchmarks are extended by adding seven additional parameters to generate CEA-FJSP scheduling instances. Table 5 lists the added parameters, where Unif denotes uniform distribution of real numbers and Rand denotes random selection. The processing time was measured in seconds instead of the unit time used in the original benchmarks to calculate the specific values of carbon emission. Carbon emission factors were set according to the Hong Kong SME Carbon Audit Toolkit (Liu et al., 2018). The Mki instances of Brandimarte’s benchmarks were changed to MkiEx instances after adding the additional parameters.
4.1.2 Evaluation metrics
Average makespan,
where
4.2 Training dynamics
Five Mk03Ex instances were generated in each training cycle based on the Mk03 configuration in Table 4 with the parameters in Table 5. These instances were used to train the proposed DRL scheduling model to produce the DRL-Mk03Ex scheduling solver. Table 6 lists the values of hyperparameters of Algorithm 1. Both weights
Figure 4A–C show the training histories of the reward,
FIGURE 4. Training histories of (A) the reward, (B) the makespan, and (C) the total carbon emission.
4.3 Optimization ability
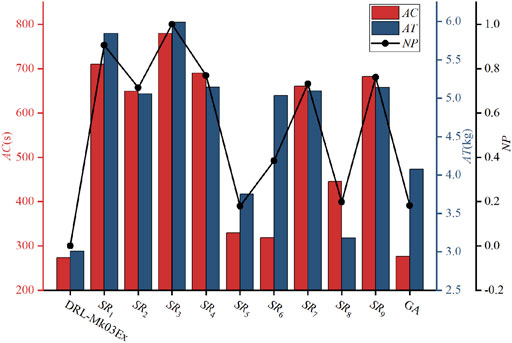
One hundred additional Mk03Ex instances different from those used in the training stage were generated to test the DRL-Mk03Ex against the proposed scheduling rules
Figure 5 shows the performance of DRL-Mk03Ex over the Mk03Ex instances. It can be seen from the figure that DRL-Mk03Ex outperforms all the scheduling rules and GA on the testing instances, i.e., it achieves the lowest average makespan and the lowest average total carbon emission. Although GA and some scheduling rules (
4.4 Generalization ability
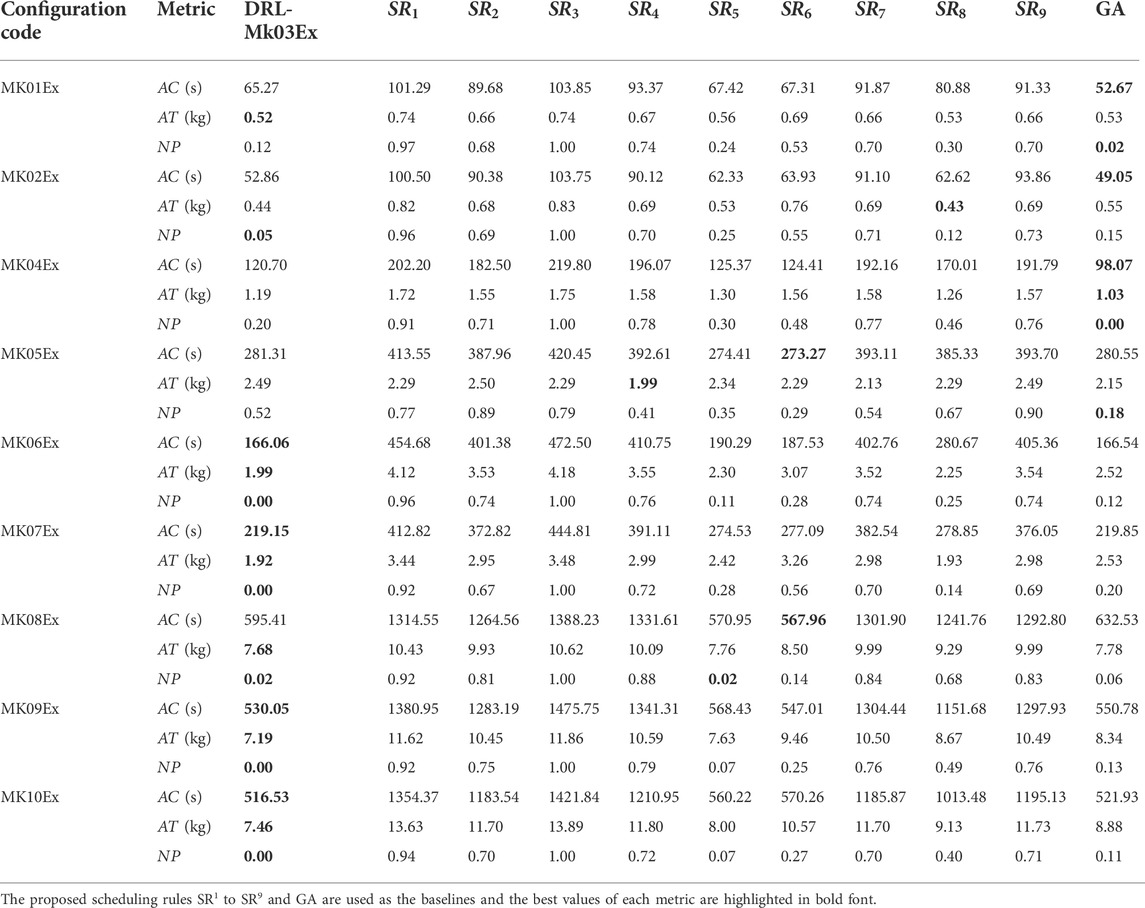
The DRL scheduling solver built on the Mk03Ex instances (DRL-Mk03Ex) was tested on the Mk01Ex, Mk02Ex, and Mk04Ex to Mk10Ex instances. That is, to say, the instances used for testing were different from the ones used for training, and the difference was significant in the sense that the testing and the training instances were sampled from different configurations. To compare the performance, Table 7 shows the average results of three metrics over 100 instances for nine different instance configurations. The proposed scheduling rules
Table 7 shows that DRL-Mk03Ex achieves the best solutions in most instances compared with the scheduling rules and GA. Furthermore, Mk01Ex and Mk02Ex instances have a simpler configuration than the Mk03Ex instances, while Mk04Ex to Mk10Ex instances have a more complex configuration. This means the DRL-Mk03Ex can be bidirectionally generalized. Besides, DRL-Mk03Ex can achieve comparable performance with GA in the simple scheduling instances, while surpassing GA in the complex instances. Moreover, DRL-Mk03Ex is also more robust than the scheduling rules. For example,
4.5 Weight effect
The Mk03Ex instances were used to train the DRL scheduling model under various weight combinations
The results demonstrate the nonlinearity of the DRL scheduling solvers. The
For each weight combination, the three carbon emission components,
5 Conclusion
In this study, a carbon emission-aware flexible job-shop scheduling problem denoted as CEA-FJSP is formulated and a DRL scheduling model is proposed to generate feasible scheduling solutions without extra searching. In the CEA-FJSP, the energy consumption of machine operation and the coolant treatment are identified as two main carbon emission sources. The proposed DRL scheduling model treats the CEA-FJSP as a Markov decision process where the scheduling agent interacts repeatedly with the scheduling environment, i.e., the temporary scheduling solution, to determine an appropriate action for a given state. The interaction is guided by the reward which represents the optimization objectives: minimizing makespan and carbon emission. The experimental results verify that the proposed DRL scheduling model achieves stronger optimization and generalization ability than the scheduling rules and GA, and the DRL scheduling model can be tuned by varying the weight combination. The future work should consider more carbon emission sources, more optimization objectives, and more flexible DRL framework to approach a more practical scheduling solution for the complex production scenarios.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
SW and JL were the principal authors for the text, and responsible for problem formulation, method design, experimental analysis, and manuscript writing. HT contributed to investigation. HT and JW contributed to the visualization together. All authors reviewed the final version of the manuscript and consented to publication.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2020YFB1708500), and the Science and Technology Planning Project of Guangzhou City (Grant No. 202102020882).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor UB declared a shared affiliation with the author HT at the time of review.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Allahverdi, A., Ng, C. T., Cheng, T. E., and Kovalyov, M. Y. (2008). A survey of scheduling problems with setup times or costs. Eur. J. Oper. Res. 187 (3), 985–1032. doi:10.1016/j.ejor.2006.06.060
Arulkumaran, K., Deisenroth, M. P., Brundage, M., and Bharath, A. A. (2017). Deep reinforcement learning: A brief survey. IEEE Signal Process. Mag. 34 (6), 26–38. doi:10.1109/MSP.2017.2743240
Bhatti, U. A., Nizamani, M. M., and Mengxing, H. (2022a). Climate change threatens Pakistan’s snow leopards. Science 377 (6606), 585–586. doi:10.1126/science.add9065
Bhatti, U. A., Yan, Y., Zhou, M., Ali, S., Hussain, A., Qingsong, H., et al. (2021). Time series analysis and forecasting of air pollution particulate matter (PM 2.5): An SARIMA and factor analysis approach. IEEE Access 9, 41019–41031. doi:10.1109/ACCESS.2021.3060744
Bhatti, U. A., Zeeshan, Z., Nizamani, M. M., Bazai, S., Yu, Z., and Yuan, L. (2022b). Assessing the change of ambient air quality patterns in Jiangsu Province of China pre-to post-COVID-19. Chemosphere 288, 132569. doi:10.1016/j.chemosphere.2021.132569
Brandimarte, P. (1993). Routing and scheduling in a flexible job shop by tabu search. Ann. Oper. Res. 41 (3), 157–183. doi:10.1007/BF02023073
Brucker, P., and Schlie, R. (1990). Job-shop scheduling with multi-purpose machines. Computing 45 (4), 369–375. doi:10.1007/BF02238804
Dai, M., Tang, D., Giret, A., and Salido, M. A. (2019). Multi-objective optimization for energy-efficient flexible job-shop scheduling problem with transportation constraints. Robot. Comput. Integr. Manuf. 59, 143–157. doi:10.1016/j.rcim.2019.04.006
Du, Y., Li, J. Q., Chen, X. L., Duan, P. Y., and Pan, Q. K. (2022). Knowledge-based reinforcement learning and estimation of distribution algorithm for flexible job-shop scheduling problem. IEEE Trans. Emerg. Top. Comput. Intell. (Early Access), 1–15. doi:10.1109/TETCI.2022.3145706
Engstrom, L., Ilyas, A., Santurkar, S., Tsipras, D., Janoos, F., Rudolph, L., et al. (2020). Implementation matters in deep policy gradients: A case study on PPO and trpo. arXiv [Preprint]. Available at: https://arxiv.org/abs/2005.12729.
Feng, Y., Zhang, L., Yang, Z., Guo, Y., and Yang, D. (2021). “Flexible job-shop scheduling based on deep reinforcement learning,” in 2021 5th Asian Conference on Artificial Intelligence Technology (ACAIT), Haikou, China, 29-31 October 2021 (IEEE), 660–666. doi:10.1109/ACAIT53529.2021.9731322
Fernandes, J. M., Homayouni, S. M., and Fontes, D. B. (2022). Energy-efficient scheduling in job shop manufacturing systems: A literature review. Sustainability 14 (10), 6264. doi:10.3390/su14106264
Gao, K., Huang, Y., Sadollah, A., and Wang, L. (2020). A review of energy-efficient scheduling in intelligent production systems. Complex Intell. Syst. 6 (2), 237–249. doi:10.1007/s40747-019-00122-6
Gutowski, T., Murphy, C., Allen, D., Bauer, D., Bras, B., Piwonka, T., et al. (2005). Environmentally benign manufacturing: Observations from Japan, europe and the United States. J. Clean. Prod. 13 (1), 1–17. doi:10.1016/j.jclepro.2003.10.004
Han, B. -A., and Yang, J. -J. (2020). Research on adaptive job-shop scheduling problems based on dueling double DQN. IEEE Access 8, 186474–186495. doi:10.1109/ACCESS.2020.3029868
Han, B. A., and Yang, J. J. (2021). A deep reinforcement learning based solution for flexible job-shop scheduling problem. Int. J. Simul. Model. 20 2, 375–386. doi:10.2507/IJSIMM20-2-CO7
Lang, S., Behrendt, F., Lanzerath, N., Reggelin, T., and Müller, M. (2020). “Integration of deep reinforcement learning and discrete-event simulation for real-time scheduling of a flexible job shop production,” in 2020 Winter Simulation Conference (WSC), Orlando, FL, USA, 14-18 December 2020 (IEEE), 3057–3068. doi:10.1109/WSC48552.2020.9383997
Lei, D., Zheng, Y., and Guo, X. (2017). A shuffled frog-leaping algorithm for flexible job-shop scheduling with the consideration of energy consumption. Int. J. Prod. Res. 55 (11), 3126–3140. doi:10.1080/00207543.2016.1262082
Li, M., and Wang, G. G. (2022). A review of green shop scheduling problem. Inf. Sci. (N. Y). 589, 478–496. doi:10.1016/j.ins.2021.12.122
Liu, C. -L., Chang, C. -C., and Tseng, C. -J. (2020). Actor-critic deep reinforcement learning for solving job-shop scheduling problems. IEEE Access 8, 71752–71762. doi:10.1109/ACCESS.2020.2987820
Liu, Q., Tian, Y., Wang, C., Chekem, F. O., and Sutherland, J. W. (2018). Flexible job-shop scheduling for reduced manufacturing carbon footprint. J. Manuf. Sci. Eng. 140 (6), 061006. doi:10.1115/1.4037710
Liu, R., Piplani, R., and Toro, C. (2022). Deep reinforcement learning for dynamic scheduling of a flexible job shop. Int. J. Prod. Res. 60 (13), 4049–4069. doi:10.1080/00207543.2022.2058432
Luo, S. (2020). Dynamic scheduling for flexible job shop with new job insertions by deep reinforcement learning. Appl. Soft Comput. 91, 106208. doi:10.1016/j.asoc.2020.106208
Luo, S., Zhang, L., and Fan, Y. (2021). Dynamic multi-objective scheduling for flexible job shop by deep reinforcement learning. Comput. Ind. Eng. 159, 107489. doi:10.1016/j.cie.2021.107489
Luo, S., Zhang, L., and Fan, Y. (2019). Energy-efficient scheduling for multi-objective flexible job shops with variable processing speeds by grey wolf optimization. J. Clean. Prod. 234, 1365–1384. doi:10.1016/j.jclepro.2019.06.151
Mokhtari, H., and Hasani, A. (2017). An energy-efficient multi-objective optimization for flexible job-shop scheduling problem. Comput. Chem. Eng. 104, 339–352. doi:10.1016/j.compchemeng.2017.05.004
Monaci, M., Agasucci, V., and Grani, G. (2021). An actor-critic algorithm with deep double recurrent agents to solve the job-shop scheduling problem. arXiv [Preprint]. Available at: https://arxiv.org/abs/2110.09076.
Naimi, R., Nouiri, M., and Cardin, O. (2021). A Q-Learning rescheduling approach to the flexible job shop problem combining energy and productivity objectives. Sustainability 13 (23), 13016. doi:10.3390/su132313016
Ni, F., Hao, J., Lu, J., Tong, X., Yuan, M., Duan, J., et al. (2021). “A multi-graph attributed reinforcement learning based optimization algorithm for large-scale hybrid flow shop scheduling problem,” in Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD), Singapore, Aug 14, 2021 - Aug 18, 2021, 3441–3451. doi:10.1109/ICCECE54139.2022.9712705
Pan, Z., Wang, L., Wang, J., and Lu, J. (2021). Deep reinforcement learning based optimization algorithm for permutation flow-shop scheduling. IEEE Trans. Emerg. Top. Comput. Intell. (Early Access), 1–12. doi:10.1109/TETCI.2021.3098354
Park, J., Chun, J., Kim, S. H., Kim, Y., and Park, J. (2021). Learning to schedule job-shop problems: Representation and policy learning using graph neural network and reinforcement learning. Int. J. Prod. Res. 59 (11), 3360–3377. doi:10.1080/00207543.2020.1870013
Qu, S., Wang, J., and Shivani, G. (2016). “Learning adaptive dispatching rules for a manufacturing process system by using reinforcement learning approach,” in 2016 IEEE 21st International Conference on Emerging Technologies and Factory Automation (ETFA), Berlin, Germany, 06-09 September 2016 (IEEE). doi:10.1109/ETFA.2016.7733712
Ren, J. F., Ye, C. M., and Yang, F. (2020). A novel solution to JSPS based on long short-term memory and policy gradient algorithm. Int. J. Simul. Model. 19 (1), 157–168. doi:10.2507/IJSIMM19-1-CO4
van Ekeris, T., Meyes, R., and Meisen, T. (2021). “Discovering heuristics and metaheuristics for job-shop scheduling from scratch via deep reinforcement learning,” in Proceedings of the Conference on Production Systems and Logistics (CPSL), Online, 10-11 August 2021, 709–718. doi:10.15488/11231
Wu, X., and Sun, Y. (2018). A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 172, 3249–3264. doi:10.1016/j.jclepro.2017.10.342
Xu, B., Mei, Y., Wang, Y., Ji, Z., and Zhang, M. (2021). Genetic programming with delayed routing for multiobjective dynamic flexible job-shop scheduling. Evol. Comput. 29 (1), 75–105. doi:10.1162/evco_a_00273
Yan, Q., Wu, W., and Wang, H. (2022). Deep reinforcement learning for distributed flow shop scheduling with flexible maintenance. Machines 10 (3), 210. doi:10.3390/machines10030210
Yin, L., Li, X., Gao, L., Lu, C., and Zhang, Z. (2017). A novel mathematical model and multi-objective method for the low-carbon flexible job shop scheduling problem. Sustain. Comput. Inf. Syst. 13, 15–30. doi:10.1016/j.suscom.2016.11.002
Zeng, Y., Liao, Z., Dai, Y., Wang, R., and Yuan, B. (2022). Hybrid intelligence for dynamic job-shop scheduling with deep reinforcement learning and attention mechanism. arXiv [Preprint]. Available at: https://arxiv.org/abs/2201.00548.
Zhang, C., Song, W., Cao, Z., Zhang, J., Tan, P. S., and Xu, C. (2020). Learning to dispatch for job-shop scheduling via deep reinforcement learning. arXiv [Preprint]. Available at: https://arxiv.org/abs/2010.12367.
Zhang, H., Xu, G., Pan, R., and Ge, H. (2022). A novel heuristic method for the energy-efficient flexible job-shop scheduling problem with sequence-dependent set-up and transportation time. Eng. Optim. 54 (10), 1646–1667. doi:10.1080/0305215X.2021.1949007
Zhang, J., Ding, G., Zou, Y., Qin, S., and Fu, J. (2019). Review of job shop scheduling research and its new perspectives under Industry 4.0. J. Intell. Manuf. 30 (4), 1809–1830. doi:10.1007/s10845-017-1350-2
Keywords: smart manufacturing, production scheduling, deep reinforcement learning, carbon emission, multi-objective optimization
Citation: Wang S, Li J, Tang H and Wang J (2022) CEA-FJSP: Carbon emission-aware flexible job-shop scheduling based on deep reinforcement learning. Front. Environ. Sci. 10:1059451. doi: 10.3389/fenvs.2022.1059451
Received: 01 October 2022; Accepted: 19 October 2022;
Published: 04 November 2022.
Edited by:
Uzair Aslam Bhatti, Hainan University, ChinaReviewed by:
Yongchao Luo, South China University of Technology, ChinaHongyan Shi, Shenzhen University, China
Tao Ku, Shenyang Institute of Automation (SIA) (CAS), China
Copyright © 2022 Wang, Li, Tang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hao Tang, bWVsaW5ldGhAaGFpbmFudS5lZHUuY24=
 Shiyong Wang
Shiyong Wang Jiaxian Li
Jiaxian Li Hao Tang2*
Hao Tang2*