
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci. , 04 January 2023
Sec. Interdisciplinary Climate Studies
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.1045743
This article is part of the Research Topic Building Flood Resilience Under Climate Change View all 6 articles
Episodic inundation from extreme sea-levels (ESLs) will have increasing social and economic impacts in response to relative sea level rise (RSLR). Despite the improved global understanding of ESL frequencies and magnitudes, detailed nationwide inundation maps are unavailable for many countries. This study quantifies New Zealand’s land area exposure to inundation from ESLs and RSLR by: (i) calculating ESL heights for nine annual recurrence intervals (ARI) between 2 and 1,000-years, (ii) converted into space-varying water surface grids, (iii) developing a composite topographical dataset comprised of Airborne Light Detection and Ranging (LIDAR) and bias corrected Shuttle Radar Topography Mission (SRTM), (iv) modifying topographical data to represent mitigation structures, and (v) executing a scalable static model to map land inundation areas for 0.1 m RSLR increments. This modular approach supports continuous integration of new models and data at resolutions appropriate for quantifying inundation hazard and risk trends. In response to 0.1 m–0.4 m RSLR expected in the New Zealand region from 2040 to 2070 under SSP5-8.5 global mean sea level rise scenarios, a rapid cumulative inundation area increase is observed for 10 and 100-year ESL ARIs at national and regional levels. The RSLR time independent maps developed here supports future investigations of ESL inundation hazards and risks for any prescribed RSLR heights or timeframes.
Social and economic impacts from episodic extreme sea-level (ESL) inundation events are expected to increase with rising global sea levels this century. Climate driven global mean level rise (GMSL) could be expose approximately 630 million people to permanent or episodic inundation by 2,100 under high carbon emission scenarios and at least 190 million if emissions are low (Kulp and Strauss 2019). Many exposed people reside in major coastal cities that could sustain expected annual losses of US$52 billion by 2050 and exceed US$1 trillion if no action is taken to mitigate direct infrastructure damages (Hallegatte et al., 2013). These futures faced by coastal populations stress importance for governments at national and local levels to form adaptation policies and strategies that avoid or mitigate socio-economic consequences under changing climate conditions. A first step in this process is to determine what land is exposed to ESL inundation at different spatial and temporal scales.
Nationwide ESL inundation investigations are limited to few countries (Haigh et al., 2014; Sweet and Park 2014; Buchanan et al., 2017; Parotny et al., 2017; Breili et al., 2020; Taherkhani et al., 2020). Several recent large-scale investigations have focused on mapping ESL land inundation across single or multiple countries to demonstrate future changes in response to GMSL (e.g., Vousdoukas et al., 2018a; Bates et al., 2021). Inundation mapping at large-scales have applied either simple ‘static’ or complex ‘dynamic’ approaches (Vousdoukas et al., 2018b). Comparative trade-offs between approaches data inputs, inundation mapping accuracy and computational speed. Static (“bathtub”) approaches are simple and scalable models that often processed in a GIS environment by using logical expressions to identify topographic elevations below a specified water level elevation (Gesch 2018). Static models limit representation of hydrodynamic characteristics causing inundation, including conservation of mass for flows and the effects of land cover roughness and physical structures on lateral flow spreading (Vousdoukas et al., 2016a; Ramirez et al., 2016). Dynamic models numerically simulate inundation from physical processes, but their high computation demand mostly limits applications to inundation mapping to local scales (e.g., Parotny et al., 2018; Breili et al., 2020). Dynamic models for inundation mapping at national levels however, gain computational efficiencies from using lower-resolution topographic data but concede an ability to represent structural controls (e.g., levees) on inundation extents (Vousdoukas et al., 2018b).
Topographic elevation data as digital elevation models (DEMs) are a critical resource for reliable for ESL inundation mapping at any scale (de Moel et al., 2015). Large-scale inundation mapping (e.g., Ward et al., 2015; Kulp and Strauss, 2019) has been supported by consistent spatial resolution and vertical accuracy improvements of satellite DEMs such as Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) and Shuttle Radar Topography Mission (SRTM) (Farr et al., 2007; Abrams et al., 2010). While vegetation and elevated feature removal techniques have improved DEM accuracy (e.g., Yamazaki et al., 2017; Kulp and Strauss 2018), vertical errors in the order of several meters remain with horizontal resolutions at tens of meters (Gesch 2018; Meadows and Wilson, 2021). Horizontal and vertical errors of these magnitudes limit capacity to simulate topographical or structural controls on inundation (Ward et al., 2015), further contributing to the already deep uncertainties when determining the timing and magnitude of future ESL inundation under rising sea levels (Rucket et al., 2019).
Airborne Light Detection and Ranging (LIDAR) is widely recognized as the highest quality topography data for inundation hazard mapping (de Moel et al., 2015). The technique supports digital model development of Earth surface (DSM) features (e.g., vegetation, buildings, roads, mitigation structures) and the ground surface (DEM) (Liu, 2008). Ground surface elevation data can represent vertical errors to centimeter-scale over horizontal resolutions of a few meters. Relatively low errors mean LIDAR DEMs are often used for high-resolution ESL inundation investigations that inform local risk analysis or adaption planning (e.g., Thompson et al., 2019; Habel et al., 2020; Hague et al., 2020; Anderson et al., 2021; Stephens et al., 2021), including trigger determination for future decision points on adaptation actions and pathways (Aerts et al., 2018; Stephens et al., 2018a; Ramm et al., 2018; Shan et al., 2022). LIDAR availability is growing worldwide though data collection and processing is often cost prohibitive and acquired where financially viable for institutions at sub-national scales (Gesch, 2018). Complete or partial LIDAR DEM use in national ESL inundation mapping investigations is currently limited to few countries (e.g., Parotny et al., 2017; Breili et al., 2020), but in combination with satellite DEMs can play a critical role to identify a country’s inundation risk ‘hotspots’, and future timing and magnitude of socio-economic impacts from ESLs and SLR.
This study implements a national land inundation area (IA) assessment from extreme sea-levels (ESLs) and relative sea level rise (RSLR) in New Zealand. The study addresses a significant hazard information gap, producing nationwide inundation maps for 2, 5, 10, 20, 50, 100, 200, 500 and 1,000 annual recurrence interval ESLs for 0.1 m RSLR increments up to 2 m above present-day mean sea levels. We implement a static model approach to map land inundation that 1) balances model complexity and data processing in a GIS environment operating on a personal computer, 2) supports a hybrid national topographical dataset comprising LIDAR and bias corrected SRTM DEMs, with mitigation structure representation 3) supports inundation mapping at different spatial resolutions and 4) that is easily updated with new models or data when available. New Zealand’s ESL inundation exposure is quantified and reported by region, and urban and rural land areas. Finally, we discuss the strengths and limitations of the national inundation mapping approach presented.
Episodic inundation is driven by extreme sea-levels (ESL). ESLs are calculated in this study from linear enumeration of the following components:
where MSL is mean sea level relative to local vertical datum calculated from sea-level gauge records over a recent decade approximately; ST is the storm-tide combination of high tide, meteorological effects (storm-surge) and monthly sea-level anomaly, affected by both seasonal heating and cooling and interannual and inter-decadal climate variability such as the El Niño Southern Oscillation (ENSO) and the 20–30 years Interdecadal Pacific Oscillation (IPO); and WS is the additional wave setup at the shoreline where breaking waves are present. ESLs heights were calculated for locations representing both wave-exposed open coasts and wave-sheltered estuaries, including the transition between high and low energy environments. In this study, ESL heights are estimated for nine ARIs: 2, 5, 10, 20, 50, 100, 200, 500 and 1000-years. ESL heights were calculated at 788 locations spaced at 20 km or less (minimum spacing = 0.35 km) around New Zealand’s mainland coastline. Several detailed regional ESL investigations of ST and WS were used to underpin the development of the national ESL dataset used for this study: Auckland (Auckland Council 2020), Tasman (Stephens et al., 2018b), Bay of Plenty (Stephens 2017; Stephens et al., 2018c), Canterbury (Stephens et al., 2015), Gisborne (Stephens et al., 2014) and Wellington (Stephens et al., 2011).
Inundation mapping requires identification of a “zero-baseline” to define the land-sea boundary to determine land not usually submerged by water. A model of astronomical New Zealand’s tides (Walters et al., 2001) is applied to determine a zero-baseline water level exceeded only by the highest 10% of all high tides (MHWS−10) along the New Zealand coastline relative to a MSL datum of 0 m. MSL offset heights relative to local vertical datum (LVD) available from Bell et al. (2015) were added to MHWS−10, ST and WS height, so that they were relative to LVDs used in the digital elevation model (DEM) (see Section 2.2). Average relative MSL in New Zealand has exhibited an approximately linear rise over the last century of 1.7 ± 0.1 mm yr−1 (Hannah and Bell 2012).
ST estimates were available from Stephens et al. (2020) for 30 locations with sea-level records. Stephens et al. (2020) applied a skew-surge joint-probability method (Batstone et al., 2013) to calculate ST frequency and magnitude distributions for NZ. The authors determine linear relationships between high tide (HT) and ST heights which we applied to calculate ST heights (Table 1) based on mean high-water springs (MHWS) derived from the New Zealand tidal model (Walters et al., 2001). Inside estuaries with no sea-level records, a scaling factor of 1.1 × MHWS height outside the estuary was used, based on observations within the Auckland region of NZ (Auckland Council 2020).
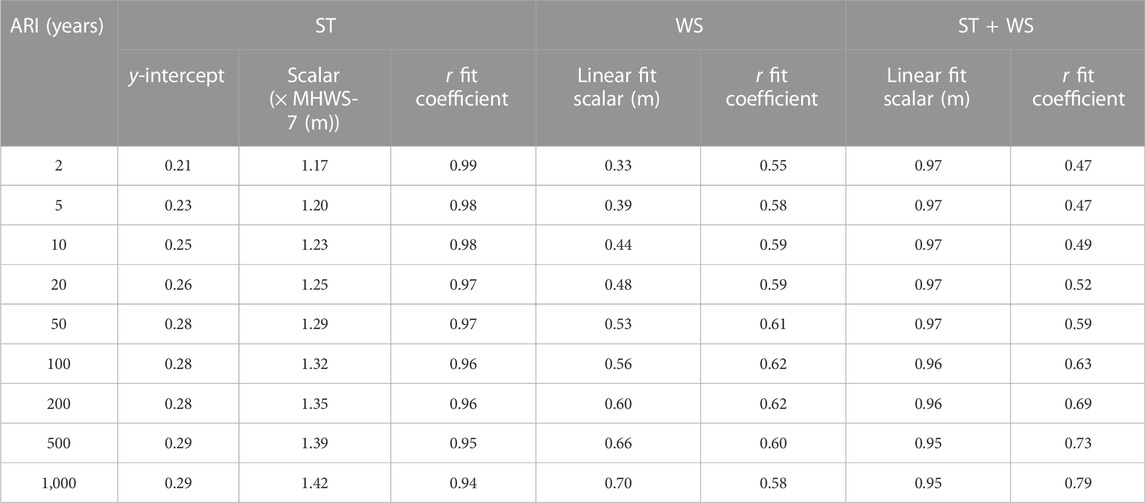
TABLE 1. Linear fit scalars and coefficients used in this study for 1) storm-tide (ST) relationship to MHWS-7, 2) wave-setup (WS) estimation wave model parameters (WS = m × Hs99), and 3) observed and predicted ST + WS heights.
A constant WS height (0.2 m) is applied at ESL locations inside estuaries where regional WS from previous investigations are absent. WS frequency and magnitude are calculated for open coast locations based on local wave climate. Where WS is not available, we reason WS is proportional to wave height around the New Zealand coastline (e.g., Guza and Thornton 1981; King et al., 1990; Hanslow and Nielsen 1993). We then use regional WS and 99th percentile significant wave heights (Hs99) from a 45-year (1957–2002) New Zealand wave hindcast (Godoi et al., 2016) to determine linear relationships (Table 1) between Hs99 and WS for 2–1000-year ARIs (Table 1). These relationships are applied to calculate WS based on Hs99 in regions without a previous WS investigations. Linear r fit coefficients for predicted WS and ST + WS ARIs average 0.59 and 0.57 respectively (Table 1), considerably weaker than predicted ST. The lower WS accuracy is expected as site-specific factors influence across-shore translation of breaking waves into WS along shorelines. Nevertheless, these linear relationships provide a consistent approach to predict ST + WS around New Zealand based on tide, storm-surge and wave energy exposure.
Future SLR rates and timing is uncertain, especially from 2050 onwards (Fox-Kemper et al., 2021). RSLR and its future uncertainty is addressed by evaluating small regular 0.1 m RSLR increments up to 2 m above present-day MSL. Using this approach for inundation mapping creates numerous RSLR scenarios, which are independent of future RSLR projections. This creates flexibility to deal with uncertainty in future RSLR as scenarios can be selected based on the projected RSLR rate and timing. We consider RSLR up to 2 m sufficient representation of projected scenarios and their uncertainties for New Zealand coastlines expected over the next 100-years under various Shared Socioeconomic Pathways (SSPs) (Fox-Kemper et al., 2021).
ESL inundation mapping requires high resolution DEMs (Gesch 2018). LIDAR DEMs represent 71% of New Zealand’s mainland coastlines, with six regions exceeding 90% coverage in 2022 (Figure 1). Regional coverage is variable as LIDAR DEMs are acquired by regional or territorial authorities for coastal and resource management purposes. These organizations have routinely conducted LIDAR surveys since 2003, sampling at point density rates ranging from 1–4 per 1 m2 (urban land) to 1 per 25 m2 (rural land) (Paulik et al., 2020). Higher densities for urban land have higher vertical accuracies ranging between ±0.05 m to ±0.25 m at 1 standard deviation or ±0.07 m to ±0.10 m at the 95% confidence interval. ‘Bare-earth’ DEMs are created for horizontal grids with 1 m representing most urban land. Here, vertical and horizontal LIDAR DEM resolutions were considered sufficient for IA mapping at 0.1 m RSLR increments.
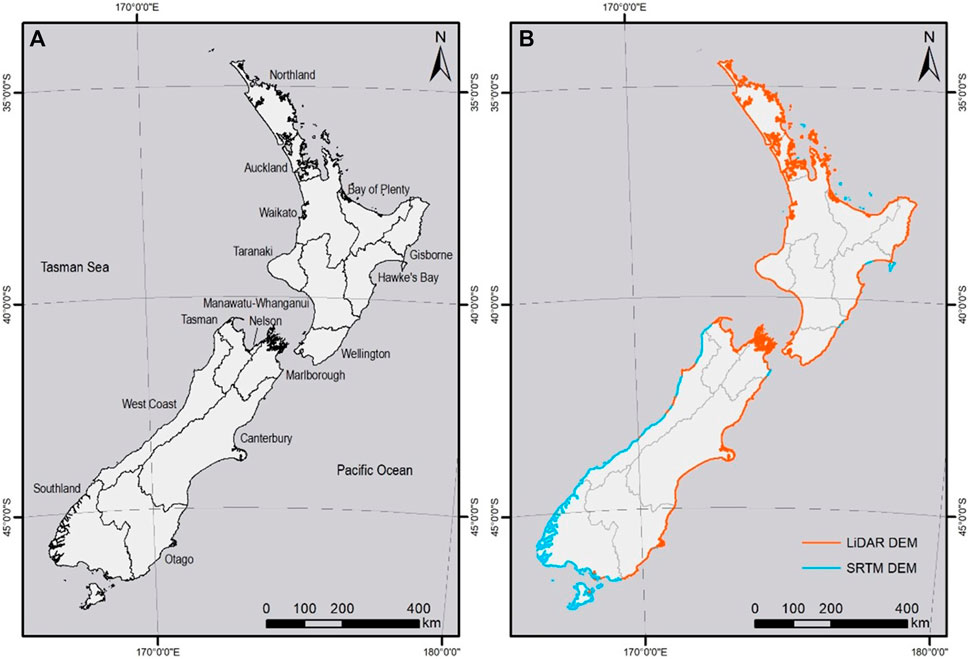
FIGURE 1. (A) New Zealand regional authority boundaries, and (B) coastline coverage represented by LIDAR and SRTM DEMs.
National IA mapping in this study required a composite DEM formed from LIDAR and satellite derived topographic data. Here, we applied a fully convolutional neural network (FCN) model based on Meadows and Wilson (2021) to correct vertical biases in the Shuttle Radar Topography Mission (SRTM) (Farr et al., 2007) for coastal land without LIDAR DEM coverage. Using the SRTM DEM from EarthExplorer (http://earthexplorer.usgs.gov/) at a resolution of 1 arc-second (30 m) (JPL/NASA 2021), the FCN model was trained to correct the DEM over land up to 20 m elevation above MHWS-10. SRTM DEM vertical error reduction for regions with partial LIDAR coverage were evaluated for land overlapping local LIDAR DEMs resampled to 30 m (Supplementary Table ST1).
Topographic elevation data often lacks the resolution to represent mitigation structures acting as barriers to coastal flooding. In large-scale ESL inundation mapping studies, mitigation structures are treated in several ways including parameterization of inundation grids as protected land (Vousdoukas et al., 2016b) and setting uniform levee crest level heights (Scussolini et al., 2016). Here, we adopt the latter approach using the New Zealand Inventory of Stopbanks (NZIS) to represent linear mitigation structures i.e., levees (Crawford-Flett et al., 2021). Structure design levels for ESL protection were absent therefore we implemented 1) a 10 m buffer around polyline features representing the protection structure crest, 2) raster clip of LIDAR and SRTM DEM grid cells within the buffered area polygon, 3) increase grid cell elevation heights up to a minimum 100-year ARI ESL for the corresponding coastline segment, and 4) merge elevation height adjusted grid cells into the original LIDAR and SRTM DEM. This approach assumes land protection up to 100-year ARI ESL heights, consistent with regulatory requirements to manage adverse ESL and RSLR effects over a future 100-year period (Minister of Conservation 2010). We note individual mitigation structure design levels vary, affording land protection less than or exceeding 100-year ARI ESL heights.
ESL inundation is mapped using a static approach as described by Breilh et al. (2013) and Stephens et al. (2021). This has several advantageous for nationwide IA mapping being 1) implementation in a GIS environment using geoprocessing and spatial interpolation functions; 2) low computational demand for operation on a standard personal computer. The static approach was implemented in two phases 1) ESL water surface model and 2), inundation grid development.
ESL heights for coastline segments were converted into space-varying water surface grids prior to inundation mapping. Firstly, ESL height points are converted into polylines with z values forming a connected ESL water surface between points. Polylines were split into 100 m segments, creating 53,000 ESL height points for New Zealand’s mainland coastline. Water surface grids for land above MHWS-10 were produced for ESL heights using a spline interpolation. Several coastal environment areas represented as polygons were created to spatially confine water surfaces which included 1) a WS zone limited to 100 m inland of MHWS-10, and 2) small (e.g., tidal lagoons, tidal river mouth, freshwater river mouths) and large (e.g., shallow drowned valley, deep drowned valley, fjord) estuaries (Hume et al., 2016). This simplified approach limits WS inland influence, assuming land inundation beyond the WS zone and opposite small estuaries is primarily driven by ST.
Water surface grids were applied in a static “bathtub” approach for IA mapping. Horizontal inundation is determined where grid cells at least one of its cardinal neighbors are inundated and hydraulically connected to the coastline (Yunus et al., 2016). Inundation depth above ground can also be computed for DEM grid cells from the difference between ESL water surface height and underlying terrain elevation. Inundation grids for LIDAR DEM coverage were resampled to 2 m in medium to major urban areas, 10 m outside these areas and 30 m for the STRM DEM areas. Variable grid resolution considers the need to represent potential topographical barriers affording land protection from ESL inundation. Finally, IA (km2) is calculated using GIS software for urban [major urban area (pop. ≥100,000); large urban area (pop. 30,000–99,999); medium urban area (pop. 10,000–29,999); small urban area (pop. 1,000–9,999)] and rural [rural settlement (pop. 200–999); rural other] land areas categories (Statistics New Zealand, 2022).
Regional ESL heights for nine ARIs are reported (Section 3.1) at present-day MSL, with corresponding IA in response to RLRS (Section 3.2). We focus on reporting urban and rural IA for 10 and 100-year ARI ESL heights up to 1 m RSLR above present-day MSL. Inundation hazards from 100-year ARI or more frequent ESLs is important for New Zealand as 1) regional and territorial authorities have statutory requirements to investigate and manage hazard effects over a future 100-year timeframe (Minister of Conservation 2010; Lawrence et al., 2018) and (2), 1 m RSLR broadly corresponds to SSP5-8.5 under median (50th percentile) and likely (17th–83rd percentile) projections for New Zealand over this timeframe (Fox-Kemper et al., 2021). Complete national and regional IA information for urban and rural land area categories is provided in Supplementary Tables ST2–ST11.
Since storm surges are relatively small in New Zealand, the spatial pattern of ESL heights is mainly influenced by tidal range and wave exposure (Stephens et al., 2020). New Zealand’s largest 100-year ARI ESL heights are observed along the South Island’s southern (i.e., Southland: mean 4.6 m; SD 1.6 m) and western (i.e., West Coast: mean 3.7 m; SD 1.2 m) coastlines (Figure 2). These regions are exposed to higher wave energy from swells originating in the Southern Ocean (Godoi et al., 2017), leading to relatively higher WS constituents for local ESLs. Similarly, open coastlines in Taranaki (mean 4.3 m; SD 0.8 m) and Northland’s western coast experience relatively higher ESLs due to relative higher WS. On the North Island east coast, ex-tropical cyclone driven ESLs in Bay of Plenty, results in a relatively large increase (mean 0.53 m; SD 0.05) m in regional 100-year ARI ESL heights compared to 10-year ARI ESL heights.
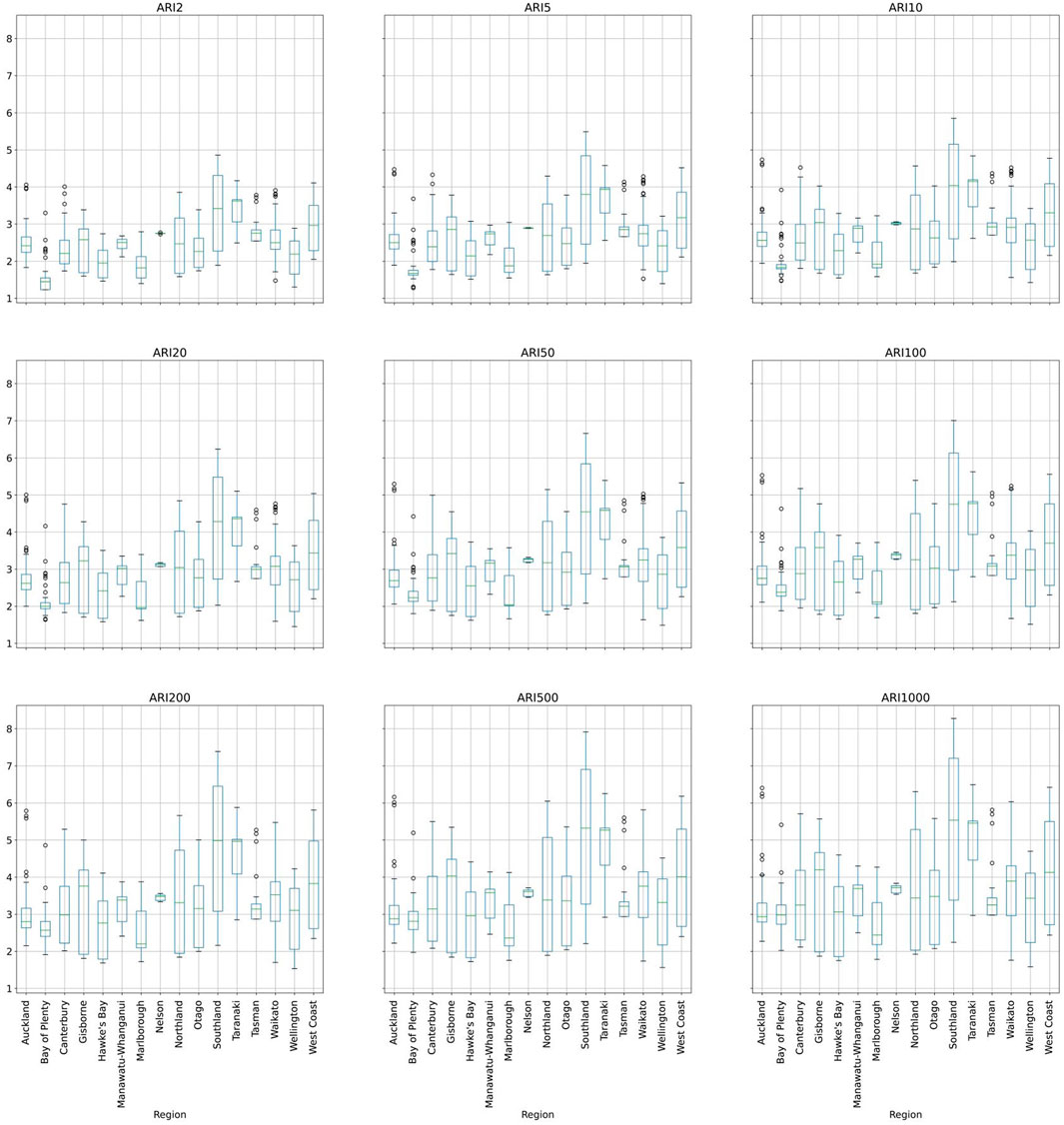
FIGURE 2. Descriptive statistics for 2–1000-year annual recurrence (ARI) ESL heights for New Zealand regions.
Regions with coastlines sheltered from Southern Ocean swells or micro-tidal ranges observe lower ESL heights on average. Wave-sheltering from swells generated from the Southern Ocean or extra-tropical cyclone events reduce ESL heights to <2 m for embayed coastlines along Waikato’s east coast and micro-tidal coastlines in Wellington and Marlborough. Tidal range also plays an important role. For instance, Nelsons sheltered low wave coastline experiences New Zealand’s largest tidal range (∼3.5 m) and sixth largest mean regional 100-year ARI ESL heights (Figure 2). In contrast, Canterbury’s coastline is mostly exposed to a high energy wave environment from the Southern Ocean. The regions small tide range averaging ∼1 m however, means average 100-year ARI ESL heights are considerably lower than equivalent heights for South Island wave sheltered regions such as Nelson and Tasman.
Future ESL land inundation area (IA) in response to RSLR in New Zealand is demonstrated in Figure 3A. IA from 10-year ARI ESLs is approximately 1,593 km2 at present-day MSL, increasing to 1774 km2 for 100-year ARI. A 0.3 m RSLR, projected to occur after 2060 based on median SSP5-8.5 scenarios, respectively increases IA by 713 km2 (31%) and 645 km2 (27%). Cumulative IA trends for ESLs with less than 200-year ARI observe a rapid increase between 0.1 m (200-year ARI ESL) and 0.4 m (2-year ARI ESL) (Figure 3A). IA under 0.3 m RSLR for 5-year to 50-year ARI ESLs is also expected exceed 100-year ARI ESL at present-day MSL. The cumulative IA rate slows thereafter, with a linear IA trend observed in response to RSLR. This trend is similar observed for 500-year and 1000-year ARI ESLs as RSLR exceeds present-day MSL.
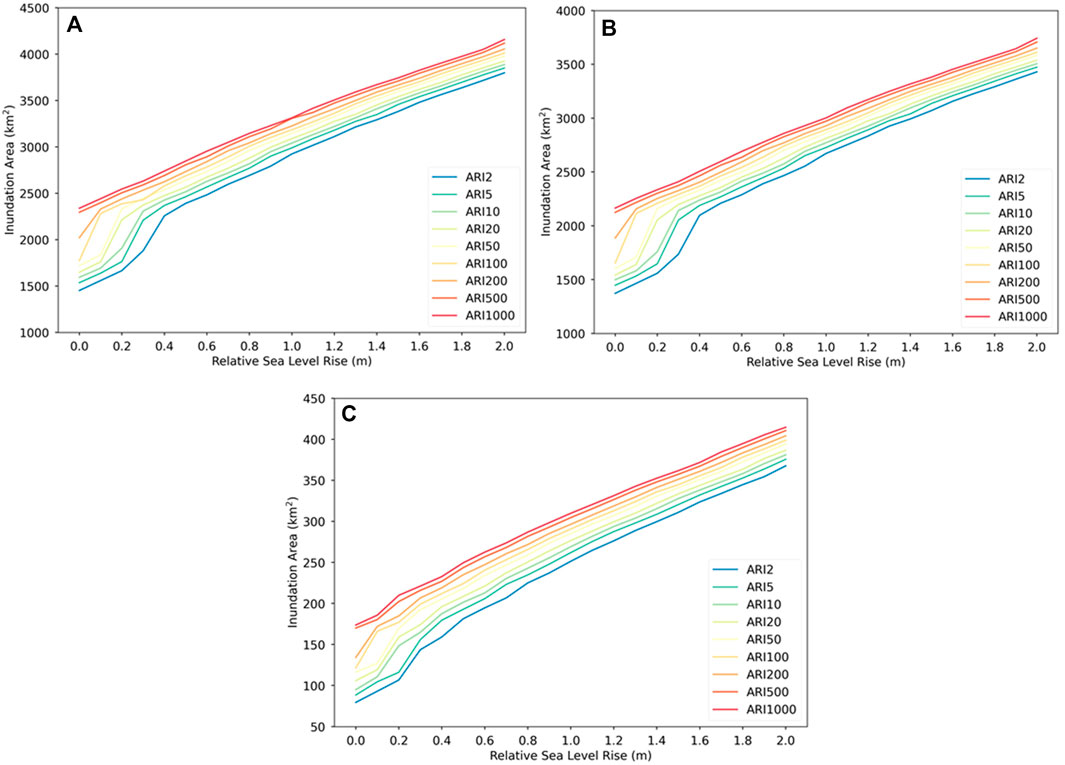
FIGURE 3. Cumulative national ESL inundation area for (A) total, (B) rural, and (C) urban land areas occurring from 2 to 1000-year ARIs and RSLR.
New Zealand’s rural land (Figure 3B) has considerably a larger IA than urban land (Figure 3C). Rural IA exceeds 90% for all ESL and RSLR scenarios. Rural land shows rapid cumulative IA increases between 0.1 m and 0.4 m RSLR for ESLs occurring more frequently than 100-year ARI (Figure 3B). This RSLR range could occur between 2040 and 2070 under likely SSP5-8.5 scenarios for New Zealand. Urban IA exhibits similar a trend though at slightly lower RSLR heights compared to rural IA (Figure 3C). For instance, urban IA for 10-year ARI ESLs shows a linear cumulative IA increase after ∼0.2 m RSLR slightly earlier than rural land at ∼0.3 m RSLR. On urban land this trend could occur after 2050 based on median SSSP5-8.5 scenarios.
Several regions in both North and South islands could experience IA exceeding 100 km2 from both 10-year and 100-year ARI ESLs at present-day MSL (Figures 4A,B). Northland experiences the largest IA in all ESLs and RSLR scenarios. IA estimates should be treated with caution however as despite region-wide LIDAR DEM coverage, limited mitigation structure representation in NZIS could overestimate IA for land protected from ESLs ARIs occurring <100-years. Proportional IA differences from 10-year and 100-year ARI ESLs at present-day MSL varies widely from 4% in Otago and Wellington to 37% in Hawkes Bay. Cumulative 10-year ARI ESL IA in most regions shows a rapid increase in response to 0.1–0.4 m RSLR (Figure 4A). Here, 10-year ARI ESL IA doubles for Waikato, Hawkes Bay and Otago regions becoming comparable with 100-year ARI ESL IA. Comparable regional 10-year and 100-year ESL IAs could signal higher frequency ESLs driving local inundation hazards after RSLR exceeds 0.4 m.
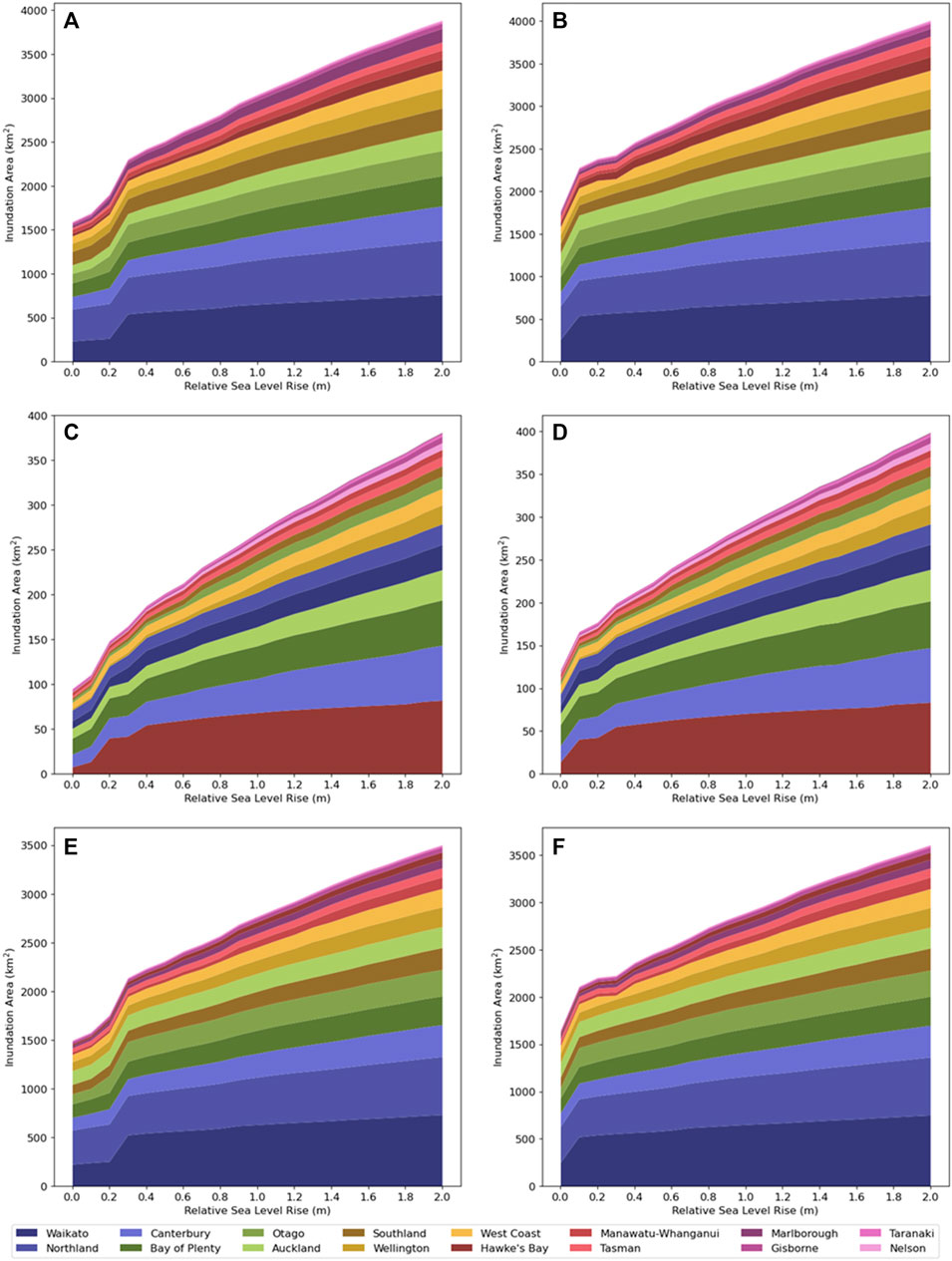
FIGURE 4. Cumulative regional ESL inundation area for total (A) 10-year ARI, (B) 100-year ARI; urban (C) 10-year ARI, (D) 100-year ARI; and rural (E) 10-year ARI, (F) 100-year ARI land areas in response to RSLR.
Urban land IA for 100-year ARI ESL at present-day MSL exceeds 75 km2 for areas with populations >10,000 people (Figures 4C,D). Bay of Plenty and Canterbury urban land IA each exceeds 18 km, half of the national IA (Figures 4A, B). In Hawkes Bay, a 0.3 m RLSR shows considerable IA increase from 11 km2 to 45 km2, a nearly double Bay of Plenty (23 km) and Canterbury (25 km) IAs. In addition, Hawkes Bay’s urban land IA increases from 5 km2 to 35 km2 for 10-year ARI ESL at 0.3 m RLSR, the largest proportional area increase for all regions. Small urban areas with populations <10,000 people are respectively exposed to 35 km2 and 41 km2 IA for 10-year and 100-year ESL ARI at present-day MSL. Several regions, Northland (9 km2), Waikato (7 km2) and West Coast (8 km2) represent half of small urban area IA. In response to 0.3 m RLSR, small urban area IA doubles in Waikato (15 km2) and quadruples in Hawkes Bay from 2 km2 to 9 km2. Regional differences between small urban area IA are small, up to 3.2 km2 for 10-year and 100-year ESL ARIs at 0.3 m RLSR.
Rural land not occupied by settlement (i.e., ‘Other’) has the largest IA for all regions. Northland and Waikato region IA could exceed 250 km2 for 100-year ARI ESLs at present-day MSL, with IA in Waikato doubling with 0.5 m RSLR (Figures 4E,F). Similarly, 100-year ARI ESL IA doubles in Otago and Marlborough with 0.5 m RSLR while several other regions (i.e., Gisborne, Hawkes Bay, Tasman, Canterbury) experience a more than 25% increase. For all regions, a small cumulative rural land IA difference of up to 21 km2 is observed for 10-year and 100-year ARI ESLs at 0.5 m RSLR. Similar IAs could indicate 10-year ARI ESLs in response to 0.5 m RSLR exposes greater rural land areas currently afforded protection to 100-year ARI ESLs.
Corrected STRM DEMs were applied in nine regions (Supplementary Table S1). Compared to LIDAR DEMs, predicted STRM DEM corrections reduced the overall root mean squared error (RMSE) between 46% and 86%. National IA on LIDAR DEMs for 10-year ARI ESLs is 1,423 km2 and 1,584 km2 for 100-year ARI at present-day MSL. Here, STRM DEM representation of national IA 169 km2 (9%) and 189 km2 (10%) respectively with 98% occurring in rural land. Southland (97%) and West Coast (71%) have the largest STRM DEM coverage for regional IAs, with LIDAR DEMs limited to few urban areas. Predicted STRM DEM corrections for these regions reduced RMSE to 1.5 m (46%) and 2.23 m (75%) respectively.
This study applied a practical approach to map New Zealand’s future ESL inundation hazards. ESL inundation maps were produced by: 1) estimating ESL heights for nine ARIs between 2 and 1000-years, 2) converted into space-varying water surface grids, 3) developing a composite topographical dataset comprised of local LIDAR and bias corrected SRTM DEM, 4) modifying topographical data to represent mitigation structures, and 5) executing a scalable static approach to map land inundation area (IA) for 0.1 m RSLR increments up to 2 m above present-day MSL. This modular approach supports continuous integration of new models and data when available at appropriate resolutions to determine future ESL inundation hazard and risk trends.
National ESL inundation mapping here addresses several challenges. We implemented a static model in a GIS environment on a standard personal computer to cost and time-efficiently map IA for nine ESL ARIs and twenty-one RSLR scenarios. Continuous IA mapping along coastlines used 1) spatial interpolated ESL water surfaces within coastline segments at varying horizontal resolutions, and 2) composite LIDAR and STRM DEMs representing several horizontal resolutions to 2 m in major urban areas. ESL inundation scenarios are modelled at time independent 0.1 m RSLR increments. This differs from a common practice of defining future years and or RSLR scenarios (e.g., Heberger et al., 2011; Breili et al., 2020; Amadio et al., 2022). Time independent ESL inundation maps represent GMSL projections over the next century represent shared socioeconomic pathways each with widening sea level height and timing uncertainties. Decision makers are often bound to ESL inundation hazard and risk assessment and reporting for prescribed RSLR heights or timeframes set by statutory and non-statutory instruments (Lawrence et al., 2018). For instance, New Zealand regional and territorial authorities must investigate and implement resource management plans to mitigate ESL inundation hazards and risks within their jurisdictional boundaries over a minimum 100-year period (Minister for Conservation, 2010). Financial institutes manage these risks across spatial scales from individual properties to national portfolios and over short annual timeframes based on mortgage lending or insurance policies e.g., <10-years (Storey et al., 2020). National ESL inundation map coverage representing different ARIs and time independent of projected RSLR then facilities hazard and risk management decision making across different spatial and temporal scales.
There are several important limitations must be noted and improved in future inundation mapping investigations. Dynamic models often determine IA more reliably than static models, particularly on flat terrain where friction effects control on horizontal inundation (e.g., Ramirez et al., 2016; Didier et al., 2018; Kumbier et al., 2019; Stephens et al., 2021). IA overestimation is unquantified though likely, particularly where the static model combined with coarser DEM vertical and horizontal resolutions does not sufficiently represent mitigation structures impeding flood flows (Breilh et al., 2013; Gesch 2018; Paprotny et al., 2018). Incomplete information on mitigation structure geometries and design levels in NZIS (Crawford-Flett et al., 2022), further reduces capacity for the static model to limit inundation over flat terrains where land is protected. This is identified in several large-scale IA investigations (Vousdoukas et al., 2018a; Bates et al., 2021), emphasizing detailed mitigation structure design as a critical input dataset for accurate IA and uncertainty quantification using either static or dynamic model approaches. Despite these limitations, our model approach provides national ESL inundation scenarios that identify hazard exposure across different spatial and temporal scales. This information can be used to signal where dynamic models are required to conduct detailed investigations ESL inundation hazards and risk.
Dynamic inundation approaches based on hydraulic models were not considered here due to their complexity and computational expense. While complex processes driving episodic inundation (e.g., nearshore waves, erosion, wave run-up) are simplified by static-based models (Vousdoukas et al., 2018b), efficient and scalable inundation mapping approaches can outbalance a need for higher resolution maps. Such models hold practical appeal for decision makers with statutory or non-statutory requirements for disclosure of climate hazard and adaptation trends (e.g., United Nations International Strategy for Disaster Reduction, 2015). In this case, static models can suitably inform both national and jurisdictional level ESL inundation hazard exposure and risk ‘hotspot’ identification, monitoring of socio-economic exposure and hazard risk changes in response to land use policy settings or analyse mitigation structure design-level performance requirements for risk avoidance (Mechler et al., 2014; Paprotny and Terefenko 2017). However, users must critically assess inundation map accuracy and limitations to determine appropriateness for statutory hazard and risk management. In the New Zealand context this knowledge requires ongoing research on ESL inundation hazard variability caused by DEM accuracy and resolution, hydrodynamic processes mitigation structure design, static and dynamic model types applied in different coastal settings (Vousdoukas et al., 2018b; Stephens et al., 2021).
The national hazard assessment presented does not aim to quantify socio-economic consequences from ESL inundation hazards. Spatio-temporal hazard maps are critical for determining the future impact magnitude and frequency to social and economic elements (Kappes et al., 2014). ESL inundation hazard scenarios ranging from 2 to 1000-years ARI and 0.1 m RSLR increments up to 2 m above present-day MSL expedites risk quantification (i.e., event loss exceedance and average annualized loss) when combined with information on socio-economic element exposure and vulnerability (Velásquez et al., 2014; Vousdoukas et al., 2018a). Here, New Zealand’s ESL inundation maps enable socio-economic risk quantification of continual population growth and economic development on land with changing inundation hazard exposure under rising sea levels.
We quantified New Zealand’s land area exposure to episodic inundation from ESLs and RSLR. ESL inundation was mapped for nine ARIs between 2 and 1000-years in a GIS environment by: 1) calculating ESL heights at 788 locations, 2) ESL height conversion to space-varying water surface grids, 3) developing a local LIDAR and bias corrected SRTM DEM topographical dataset, 4) modifying topographical data to represent mitigation structures, and 5) executing a scalable static model to map land inundation area (IA) for 0.1 m RSLR increments. This modular approach supports continuous integration of new models and data when available. The time independent ESL inundation maps also represent GMSL projections with widening sea level height and timing uncertainties over the next century. Such information is critical for decision making entities to investigate ESL inundation hazards and risks for any prescribed RSLR heights or timeframes set by statutory and non-statutory instruments.
New Zealand has considerable present and future exposure to ESL inundation. The 10-year and 100-year ARI ESL IA respectively is 1,593 km2 and 1774 km2 at present-day MSL. A 0.3 m RSLR, projected to occur after 2060 based on median SSSP5-8.5 GMSL scenarios, increases these IAs by 713 km2 (31%) and 645 km2 (27%). Rural land represents over 90% of New Zealand’s total IA in all ESL and RSLR scenarios. Bay of Plenty, Hawkes Bay and Canterbury represent over half of New Zealand’s total IA for urban land with populations >10,000 people. Cumulative IA for 10-year and 100-year ARI ESLs at both national and regional levels increases rapidly in response to 0.1–0.4 m RSLR, expected in the New Zealand region between 2040 and 2070 under the SSP5-8.5 GMSL scenario. This short timeframe signals an urgent need to use national ESL inundation maps for hazard and socio-economic risk ‘hotspots’ analyses to identify where to conduct detailed investigations at resolutions suitable for implementing adaptation plans and actions.
The national ESL inundation hazard assessment is not exhaustive with several key limitations. The static model approach creates computational efficiencies but simplifies hydrodynamic processes driving ESL inundation compared to dynamic models. ESL inundation mapping at finer (i.e., 2 m) grid resolutions in medium to major urban areas and modifying topographical data to represent linear mitigation structures exerted physical controls on higher frequency ESLs (2–100-year ARIs). While this approach limited inundation over flat terrains, future model integration of detailed mitigation structure geometry and design level information will be important for continual accurate representations of New Zealand’s increasing ESL inundation hazard and risks over the next 20–50 years.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by RP, AW, SS, RW, and SW. The first draft of the manuscript was written by RP and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
This research was funded by the New Zealand Ministry of Business, Innovation and Employment (MBIE) under a) Deep South Science Challenge (MBIE CONTRACT NUMBER: C01X14121), b) Strategic Science Investment Fund (Project CARH2206—National Institute of Water and Atmospheric Research)” and c) NZ SeaRise Programme (Ministry of Business Innovation and Employment Contract: RTVU1705).
The authors gratefully acknowledge provision of LIDAR (point cloud files or DEMs) from Land Information New Zealand (LINZ), Northland Regional Council, Auckland Council, Waikato Regional Council, Bay of Plenty Regional Council, Gisborne District Council, Hawke’s Bay Regional Council, Taranaki Regional Council, Greater Wellington Regional Council, Environment Canterbury, Christchurch City Council, Otago Regional Council, Dunedin City Council, Nelson City Council, Tasman District Council, Invercargill City Council and West Coast Regional Council.
AW is employed by Aon New Zealand.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.1045743/full#supplementary-material
Abrams, M., Bailey, B., Tsu, H., and Hato, M. (2010). The ASTER global DEM. Photo Eng. Remote Sens. 76, 344–348.
Aerts, J. C., Barnard, P. L., Botzen, W., Grifman, P., Hart, J. F., De Moel, H., et al. (2018). Pathways to resilience: Adapting to sea level rise in los angeles. Ann. N. Y. Acad. Sci. 1427, 1–90. doi:10.1111/nyas.13917
Amadio, M., Essenfelder, A. H., Bagli, S., Marzi, S., Mazzoli, P., Mysiak, J., et al. (2022). Cost–benefit analysis of coastal flood defence measures in the North Adriatic Sea. Nat. Hazards Earth Syst. Sci. 22, 265–286. doi:10.5194/nhess-22-265-2022
Anderson, D. L., Ruggiero, P., Mendez, F. J., Barnard, P. L., Erikson, L. H., O’Neill, A. C., et al. (2021). Projecting climate dependent coastal flood risk with a hybrid statistical dynamical model. Earth's Future 9, e2021EF002285. doi:10.1029/2021EF002285
Auckland Council (2020). “Auckland’s exposure to coastal inundation by storm-tides and waves,”. TR2020/024 (Auckland, New Zealand: Auckland Council), p285.
Bates, P. D., Quinn, N., Sampson, C., Smith, A., Wing, O., Sosa, J., et al. (2021). Combined modeling of US fluvial, pluvial, and coastal flood hazard under current and future climates. Water Resou Res. 57, e2020WR028673. doi:10.1029/2020WR028673
Batstone, C., Lawless, M., Tawn, J., Horsburgh, K., Blackman, D., McMillan, A., et al. (2013). A UK best-practice approach for extreme sea-level analysis along complex topographic coastlines. Ocean. Eng. 71, 28–39. doi:10.1016/j.oceaneng.2013.02.003
Bell, R. G., Paulik, R., and Wadhwa, S. (2015). “National and regional exposure to coastal hazards and sea-level rise. Areal extent,”. Report No: HAM2015-006 (Auckland, New Zealand: NIWA), p134.
Breilh, J. F., Chaumillon, E., Bertin, X., and Gravelle, M. (2013). Assessment of static flood modeling techniques: Application to contrasting marshes flooded during Xynthia (Western France). Nat. Haz Earth Syst. Sci. 13, 1595–1612. doi:10.5194/nhess-13-1595-2013
Breili, K., Simpson, M. J. R., Klokkervold, E., and Roaldsdotter Ravndal, O. (2020). High-accuracy coastal flood mapping for Norway using LIDAR data. Nat. Haz Earth Syst. Sci. 20, 673–694. doi:10.5194/nhess-20-673-2020
Buchanan, M. K., Oppenheimer, M., and Kopp, R. E. (2017). Amplification of flood frequencies with local sea level rise and emerging flood regimes. Env. Res. Lett. 12, 064009. doi:10.1088/1748-9326/aa6cb3
Crawford-Flett, K., Blake, D. M., Pascoal, E., Wilson, M., and Wotherspoon, L. (2022). A standardised inventory for New Zealand's stopbank (levee) network and its application for natural hazard exposure assessments. J. Flood Risk Manag. 15, e12777. doi:10.1111/jfr3.12777
de Moel, H., Jongman, B., Kreibich, H., Merz, B., Penning-Rowsell, E., and Ward, P. J. (2015). Flood risk assessments at different spatial scales. Mitig. Adapt Strateg. Glob. Change 20, 865–890. doi:10.1007/s11027-015-9654-z
Didier, D., Baudry, J., Bernatchez, P., Dumont, D., Sadegh, M., Bismuth, E., et al. (2018). Multihazard simulation for coastal flood mapping: Bathtub versus numerical modelling in an open estuary, Eastern Canada. J. Flood Risk Manag. 12, e12505. doi:10.1111/jfr3.12505
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., et al. (2007). The shuttle radar topography mission. Rev. Geophys 45, RG2004. doi:10.1029/2005rg000183
Fox-Kemper, B., Hewitt, H. T., Xiao, C., et al. (2021). “Ocean, cryosphere and Sea Level change,” in Climate change 2021: The physical science basis. Contribution of working group I to the sixth assessment report of the intergovernmental panel on climate change. Editors P. Zhai, A. Pirani, S. L. Connors, C. Péan, S. Berger, N. Caudet al. (Cambridge, UK: Cambridge University Press).
Gesch, D. B. (2018). Best practices for elevation-based assessments of sea-level rise and coastal flooding exposure. Front. Earth Sci. 6, 230. doi:10.3389/feart.2018.00230
Godoi, V. A., Bryan, K. R., and Gorman, R. M. (2016). Regional influence of climate patterns on the wave climate of the southwestern Pacific: The New Zealand region. J. Geophys Res. Oceans 121, 4056–4076. doi:10.1002/2015JC011572
Godoi, V. A., Bryan, K. R., Stephens, S. A., and Gorman, R. M. (2017). Extreme waves in New Zealand waters. Ocean. Mod. 117, 97–110. doi:10.1016/j.ocemod.2017.08.004
Guza, R. T., and Thornton, E. B. (1981). Wave set-up on a natural beach. J. Geophys Res. Oceans 86, 4133–4137. doi:10.1029/JC086iC05p04133
Habel, S., Fletcher, C. H., Anderson, T. R., and Thompson, P. R. (2020). Sea-level rise induced multi-mechanism flooding and contribution to urban infrastructure failure. Sci. Rep. 3, 3796. doi:10.1038/s41598-020-60762-4
Hague, B. S., McGregor, S., Murphy, B. F., Reef, R., and Jones, D. A. (2020). Sea level rise driving increasingly predictable coastal inundation in Sydney, Australia. Earth's Future 8, e2020EF001607. doi:10.1029/2020EF001607
Haigh, I. D., Wijeratne, E. M. S., McPherson, L. R., Pattiaratchi, C. B., Mason, M. S., Crompton, R. P., et al. (2014). Estimating present day extreme water level exceedance probabilities around the coastline of Australia: Tides, extra-tropical storm surges and mean sea level. Clim. Dyn. 42, 121–138. doi:10.1007/s00382-012-1652-1
Hallegatte, S., Green, C., Nicholls, R., and Corfee-Morlot, J. (2013). Future flood losses in major coastal cities. Nat. Clim. Change 3, 802–806. doi:10.1038/nclimate1979
Hannah, J., and Bell, R. G. (2012). Regional sea level trends in New Zealand. J. Geophys Res. 117, C01004. doi:10.1029/2011JC007591
Hanslow, D. J., and Nielsen, P. (1993). “Wave setup on beaches and in river entrances,” in Proceedings of the 23rd International Conference on Coastal Engineering, Venice, Italy, October 1992. doi:10.1061/9780872629332.018
Heberger, M., Cooley, H., Herrera, P., Gleick, P. H., and Moore, E. (2011). Potential impacts of increased coastal flooding in California due to sea-level rise. Clim. Change 109, 229–249. doi:10.1007/s10584-011-0308-1
Hume, T. M., Gerbeaux, P., Hart, D., Kettles, D., and Neale, D. (2016). A classification of NZ coastal hydrosystems for management purpose. Wellington, New Zealand: Ministry for the Environment, p120.
JPL/NASA (2021). U.S. Releases enhanced shuttle land elevation data. Available online: http://www2.Jpl.Nasa.gov/srtm/.
Kappes, M. S., Keiler, M., von Elverfeldt, K., and Glade, T. (2014). Challenges of analyzing multi-hazard risk: A review. Nat. Hazards 64, 1925–1958. doi:10.1007/s11069-012-0294-2
King, B. A., Blackley, M. W. L., Carr, A. P., and Hardcastle, P. J. (1990). Observations of wave-induced setup on a natural beach. J. Geophys Res. 95, 22289–22297. doi:10.1029/JC095iC12p22289
Kulp, S. A., and Strauss, B. H. (2018). CoastalDEM: A global coastal digital elevation model improved from SRTM using a neural network. Remote Sens. Environ. 206, 231–239. doi:10.1016/j.rse.2017.12.026
Kulp, S. A., and Strauss, B. H. (2019). New elevation data triple estimates of global vulnerability to sea-level rise and coastal flooding. Nat. Commun. 10, 4844. doi:10.1038/s41467-019-12808-z
Kumbier, K., Carvalho, R. C., Vafeidis, A. T., and Woodroffe, C. D. (2019). Comparing static and dynamic flood models in estuarine environments: A case study from south-east Australia. Mar. Freshw. Res. 70, 781. doi:10.1071/MF18239
Lawrence, J., Bell, R. G., Blackett, P., Stephens, S., and Allan, S. (2018). National guidance for adapting to coastal hazards and sea-level rise: Anticipating change, when and how to change pathway. Environ. Sci. Policy 82, 100–107. doi:10.1016/j.envsci.2018.01.012
Liu, X. (2008). Airborne LIDAR for DEM generation: Some critical issues. Prog. Physl Geo Earth Environ. 32, 31–49. doi:10.1177/0309133308089496
Meadows, M., and Wilson, M. A. (2021). A comparison of machine learning approaches to improve free topography data for flood modelling. Remote Sens. 13, 275. doi:10.3390/rs13020275
Mechler, R., Bouwer, L., Linnerooth-Bayer, J., Hochrainer-Stigler, S., Aerts, J. C. J. H., Surminski, S., et al. (2014). Managing unnatural disaster risk from climate extremes. Nat. Clim. Change 4, 235–237. doi:10.1038/nclimate2137
Minister of Conservation (2010). New Zealand coastal policy statement 2010. Wellington, New Zealand: Department of Conservation.
Paprotny, D., Morales-Nápoles, O., Vousdoukas, M. I., Jonkman, S. N., and Nikulin, G. (2018). Accuracy of pan-European coastal flood mapping. J. Flood Risk Manag. 12, e12459. doi:10.1111/jfr3.12459
Paprotny, D., and Terefenko, P. (2017). New estimates of potential impacts of sea level rise and coastal floods in Poland. Nat. Hazards 85, 1249–1277. doi:10.1007/s11069-016-2619-z
Paulik, R., Stephens, S. A., Bell, R. G., Wadhwa, S., and Popovich, B. (2020). National-scale built-environment exposure to 100-year Extreme Sea levels and sea-level rise. Sustainability 12, 1513. doi:10.3390/su12041513
Ramirez, J. A., Lichter, M., Coulthard, T. J., and Skinner, C. (2016). Hyperresolution mapping of regional storm surge and tide flooding: Comparison of static and dynamic models. Nat. Hazards 82, 571–590. doi:10.1007/s11069-016-2198-z
Ramm, T. D., Watson, C. S., and White, C. J. (2018). Strategic adaptation pathway planning to manage sea-level rise and changing coastal flood risk. Environ. Sci. Policy 87, 92–101. doi:10.1016/j.envsci.2018.06.001
Ruckert, K. L., Srikrishnan, V., and Keller, K. (2019). Characterizing the deep uncertainties surrounding coastal flood hazard projections: A case study for norfolk, va. Scien Rep. 9, 11373. doi:10.1038/s41598-019-47587-6
Scussolini, P., Aerts, J. C. J. H., Jongman, B., Bouwer, L. M., Winsemius, H. C., de Moel, H., et al. (2016). Flopros: An evolving global database of flood protection standards. Nat. Haz Earth Syst. Sci. 16, 1049–1061. doi:10.5194/nhess-16-1049-2016
Shan, X., Wang, J., Wen, J., Hu, H., Wang, L., Yin, J., et al. (2022). Using multidisciplinary analysis to develop adaptation options against extreme coastal floods. Int. J. Disaster Risk Sci. 13, 577–591. doi:10.1007/s13753-022-00421-6
Statistics New Zealand (2022). Urban rural 2021 (generalised). Available online: https://datafinder.stats.govt.nz/layer/105158-urban-rural-2021-generalised/(accessed on June 26, 2022).
Stephens, S. A., Allis, M., Gorman, R., Robinson, B., and Goodhue, (2018c). “Storm-tide and wave hazards in the Bay of plenty: Revised and updated september 2018,”. Client Report 2018136HN:125 (Whakatāne, New Zealand: Bay of Plenty Regional Council), p125.
Stephens, S. A., Allis, M., Robinson, B., and Gorman, R. M. (2015). Storm-tides and wave runup in the Canterbury region. NIWA Client Rep. Environ. Canterb., p133.
Stephens, S. A., Bell, R. G., and Haigh, I. D. (2020). Spatial and temporal analysis of extreme storm-tide and skew-surge events around the coastline of New Zealand. Nat. Haz Earth Syst. Sci. 20, 783–796. doi:10.5194/nhess-20-783-2020
Stephens, S. A., Bell, R. G., and Lawrence, J. (2018a). Developing signals to trigger adaptation to sea-level rise. Environ. Res. Lett. 13, 104004. doi:10.1088/1748-9326/aadf96
Stephens, S. A., Gorman, R. M., and Lane, E. (2011). Joint-probability of storm tide and waves on the open coast of Wellington. NIWA Client Rep. HAM, p44.
Stephens, S. A., Paulik, R., Reeve, G., Wadhwa, S., Popovich, B., Shand, T., et al. (2021). Future changes in built environment risk to coastal flooding, permanent inundation and coastal erosion hazards. J. Mar. Scien Eng. 9, 1011. doi:10.3390/jmse9091011
Stephens, S. A., Robinson, B., and Allis, M. (2018b). “Storm-tide and wave hazards in tasman and golden bays,”. NIWA Client Report 20218208HN:61 (Nelson, New Zealand: Tasman District Council and Nelson City Council), p61.
Stephens, S. A., Robinson, B., and Gorman, R. M. (2014). Extreme sea-level elevations from storm-tides and waves along the Gisborne District coastline. NIWA Client Rep. Gisborne Dist. Counc., p106.
Stephens, S. A. (2017). Tauranga harbour Extreme Sea Level analysis. Whakatāne, New Zealand: NIWA Client Report to Bay of Plenty Regional Council, p47.
Storey, B., Owen, S., Noy, I., and Zammit, C. (2020). Insurance retreat: Sea level rise and the withdrawal of residential insurance in aotearoa New Zealand. Wellington, New Zealand: Deep South National Science Challenge, p16.
Sweet, W. V., and Park, J. (2014). From the extreme to the mean: Acceleration and tipping points of coastal inundation from sea-level rise. Earth’s Future 2, 579–600. doi:10.1002/2014EF000272
Taherkhani, M., Vitousek, S., Barnard, P. L., Frazer, N., Anderson, T. R., and Fletcher, C. H. (2020). Sea-level rise exponentially increases coastal flood frequency. Scien Rep. 10, 6466. doi:10.1038/s41598-020-62188-4
Thompson, P. R., Widlansky, M. J., Merrifield, M. A., Becker, J. M., and Marra, J. J. (2019). A statistical model for frequency of coastal flooding in Honolulu, Hawaii, during the 21st century. J. Geophy Res. Oceans 124, 2787–2802. doi:10.1029/2018JC014741
Velásquez, C. A., Cardona, O. D., Mora, M. G., Yamin, L. E., Carreno, M. L., and Barbat, A. H. (2014). Hybrid loss exceedance curve (HLEC) for disaster risk assessment. Nat. Hazards 72, 455–479. doi:10.1007/s11069-013-1017-z
Vousdoukas, M. I., Bouziotas, D., Giardino, A., Bouwer, L. M., Mentaschi, L., Voukouvalas, E., et al. (2018b). Understanding epistemic uncertainty in large-scale coastal flood risk assessment for present and future climates. Nat. Haz Earth Syst. Sci. 16, 2127–2142. doi:10.5194/nhess-18-2127-2018
Vousdoukas, M. I., Mentaschi, L., Voukouvalas, E., Bianchi, A., Dottori, F., and Feyen, L. (2018a). Climatic and socioeconomic controls of future coastal flood risk in Europe. Nat. Clim. Change 8, 776–780. doi:10.1038/s41558-018-0260-4
Vousdoukas, M. I., Voukouvalas, E., Annunziato, A., Giardino, A., and Feyen, L. (2016a). Projections of extreme storm surge levels along Europe. Clim. Dyn. 47, 3171–3190. doi:10.1007/s00382-016-3019-5
Vousdoukas, M. I., Voukouvalas, E., Mentaschi, L., Dottori, F., Giardino, A., Bouziotas, D., et al. (2016b). Developments in large-scale coastal flood hazard mapping. Nat. Haz Earth Syst. Sci. 16, 1841–1853. doi:10.5194/nhess-16-1841-2016
Walters, R. A., Goring, D. G., and Bell, R. G. (2001). Ocean tides around New Zealand. N. Z. J. Mar. Freshw. Res. 35, 567–579. doi:10.1080/00288330.2001.9517023
Ward, P., Jongman, B., Salamon, P., Simpson, A., Bates, P., De Groeve, T., et al. (2015). Usefulness and limitations of global flood risk models. Nat. Clim. Change 5, 712–715. doi:10.1038/nclimate2742
Yamazaki, D., Ikeshima, D., Tawatari, R., Yamaguchi, T., O'Loughlin, F., Neal, J. C., et al. (2017). A high-accuracy map of global terrain elevations. Geophys Res. Lett. 44, 5844–5853. doi:10.1002/2017GL072874
Keywords: extreme sea-levels, sea level rise, coastal flooding, climate change, exposure
Citation: Paulik R, Wild A, Stephens S, Welsh R and Wadhwa S (2023) National assessment of extreme sea-level driven inundation under rising sea levels. Front. Environ. Sci. 10:1045743. doi: 10.3389/fenvs.2022.1045743
Received: 16 September 2022; Accepted: 13 December 2022;
Published: 04 January 2023.
Edited by:
Xiong Zhou, Beijing Normal University, ChinaReviewed by:
Chuanbao Wu, Shandong University of Science and Technology, ChinaCopyright © 2023 Paulik, Wild, Stephens, Welsh and Wadhwa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ryan Paulik, cnlhbi5wYXVsaWtAbml3YS5jby5ueg==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.