- 1Pacific Northwest National Laboratory, Richland, WA, United States
- 2Department of Civil, Environmental and Geodetic Engineering, The Ohio State University, Columbus, OH, United States
- 3Laboratory for Atmospheric Research, Department of Civil and Environmental Engineering, Washington State University, Pullman, WA, United States
Soil respiration in dryland ecosystems is challenging to model due to its complex interactions with environmental drivers. Knowledge-guided deep learning provides a much more effective means of accurately representing these complex interactions than traditional Q10-based models. Mutual information analysis revealed that future soil temperature shares more information with soil respiration than past soil temperature, consistent with their clockwise diel hysteresis. We explicitly encoded diel hysteresis, soil drying, and soil rewetting effects on soil respiration dynamics in a newly designed Long Short Term Memory (LSTM) model. The model takes both past and future environmental drivers as inputs to predict soil respiration. The new LSTM model substantially outperformed three Q10-based models and the Community Land Model when reproducing the observed soil respiration dynamics in a semi-arid ecosystem. The new LSTM model clearly demonstrated its superiority for temporally extrapolating soil respiration dynamics, such that the resulting correlation with observational data is up to 0.7 while the correlations of the Q10-based models and the Community Land Model (CLM) are less than 0.4. Our results underscore the high potential for knowledge-guided deep learning to replace Q10-based soil respiration modules in Earth system models.
1 Introduction
Soil respiration (Rsoil), the emission of carbon dioxide from the soil through belowground autotrophic and heterotrophic respiration, is the second largest source of terrestrial carbon flux in the global carbon budget and plays an important role in regulating climate change (Raich and Potter, 1995; Schlesinger and Andrews, 2000; Bond-Lamberty and Thomson, 2010). Soil temperature (Tsoil) exerts the primary controls on Rsoil in ecosystems not limited by water availability (Lloyd and Taylor, 1994; HoÈgberg et al., 2001; Tang et al., 2005; Sampson et al., 2007; Bond-Lamberty and Thomson, 2010). Rsoil desynchronizes with Tsoil on diurnal cycles, also known as the diel hysteresis (Gaumont-Guay et al., 2006; Riveros-Iregui et al., 2007; Vargas and Allen, 2008; Phillips et al., 2011; Song et al., 2015). In dryland ecosystems, which cover about 41–47% Earth land surface (Lal, 2004; Yao et al., 2020), Rsoil exhibits large interannual variability as the temperature and precipitation regimes shift under the changing climate (Poulter et al., 2014; Ahlström et al., 2015). Soil drying and rewetting cycles reshape the Tsoil dynamics (Wang et al., 2014; Guan et al., 2018; Dusza et al., 2020). Drying soil may reduce Rsoil by limiting root respiration as a result of reduced photosynthesis and high soil temperature (Rustad et al., 2000). However, sporadic rainfall events during a dry period can incur large Rsoil pulses by stimulating the soil microbial activities, a phenomenon known as the Birch effect (Birch, 1958; Jarvis et al., 2007). Such sudden soil rewetting by rainfall may also significantly increase the magnitude of diel hysteresis for both autotrophic and heterotrophic respiration (Song et al., 2015). These complex interactions between Rsoil and its environmental drivers have led to significant uncertainty in predicting Rsoil in dryland ecosystems (Jarvis et al., 2007), consequently for projecting future global carbon budget given the accelerated expansion of drylands (Huang et al., 2016; Yao et al., 2020).
Q10-based methods, which assume an exponential relation between Rsoil and Tsoil (Lloyd and Taylor, 1994; Davidson et al., 2006), are widely adopted to empirically estimate Rsoil in land surface models such as the Community Land Model (CLM) (Lawrence et al., 2019). Q10-based Rsoil modules have evolved over time to account for the dependence of Rsoil on other drivers (e.g., soil wetness and soil organic matter) using either multiplicative coefficients or more complex empirical functions that can be parameterized or calibrated using field observations and lab experiments (Davidson et al., 2006; Phillips et al., 2011; Oikawa et al., 2014; Zhang et al., 2015). Despite the plethora of empirical and semi-empirical models that relate Rsoil to soil temperature and water content, the models fail to capture the pulsed Rsoil spikes in response to sudden soil rewetting during prolonged dry seasons (Lloyd and Taylor, 1994; Jarvis et al., 2007; Wang et al., 2014; Muñoz-Rojas et al., 2016; Yan et al., 2022).
Knowledge-guided deep learning (DL) (Raissi et al., 2017; Shen, 2018; Willard et al., 2020) offers a potential alternative for encoding complex interactions without explicit governing equations into DL models. DL models excel at capturing any nonlinear relationship between inputs and outputs based on observational or simulation data and have been widely applied in earth system studies recently (Shen, 2018; Reichstein et al., 2019). For instance, Long Short-Term Memory (LSTM) model (Hochreiter and Schmidhuber, 1997), a type of recurrent neural network, is well suited to learning long-term dynamic system behaviors, such as sea surface temperature (Zhang et al., 2017), groundwater table depth (Zhang et al., 2018), and watershed surface runoff (Kratzert et al., 2018). Knowledge-guided DL takes one step further by incorporating the domain knowledge of given systems to guide the architectural design of deep neural networks (DNNs) or customize the loss function to impose physical constraints (Jia et al., 2020; Willard et al., 2020). Raissi et al. (2017) proposed physics-informed neural networks to better emulate partial differential equations by constraining the DNNs with the initial and boundary conditions. Sadoughi and Hu (2019) encodes domain knowledge obtained from nonparametric physics-based kernels into a convolutional neural network used for fault diagnosis of rolling element bearings. Despite the rapid development of DL, its applications in modeling Rsoil are few and mostly limited to the usage of artificial neural networks or vanilla machine learning methods (Zhao et al., 2017; Ebrahimi et al., 2019; Lu et al., 2021).
Here, we propose a knowledge-guided DL approach to model the complex interactions between Rsoil and its environmental drivers in dryland ecosystems, which cannot be captured by the traditional Q10-based methods. We apply information theory (Cover and Thomas, 2006) to continuous monitoring data to identify drivers that share significant information with Rsoil. The knowledge gained from the mutual information analysis is used to guide the architectural design of an LSTM model. We hypothesize that the knowledge obtained from the information-theoretic analysis is able to enhance the predictability of the LSTM model, which in turn outperforms the traditional Q10-based modeling. To this end, we compare the DL-based modeling performance in predicting Rsoil with three Q10-based models and CLM simulation. Further, we evaluate both the temporal interpolation and extrapolation capabilities of the DL models in order to assess the applicability of the models in an unseen time period. The new approach reproduces Rsoil dynamics and outperforms the Q10 methods for modeling a semi-arid sagebrush ecosystem in central Washington, United States of America. An automated chamber at this site has continuously monitored soil respiration for a year at a 30-min resolution. An Ameriflux site (US-Hn1) collocated with the soil chamber provides continuous measurements of environmental drivers during the same time window (Missik et al., 2019; Missik et al., 2021). The availability of such comprehensive data facilitates the development of our DNN models.
Below, Section 2 describes the study site, the mathematical framework of mutual information analysis, and the proposed knowledge-guided DL to model Rsoil. In Section 3, we first present the mutual information analysis result which guides the selection of the inputs to the DL models; then, we evaluate the modeling performances of DL-based and CLM/Q10-based Rsoil modeling. Last, Section 4 provides follow-up discussions and draws the conclusion at the end.
2 Methods
2.1 Study site
The studied semi-arid ecosystem is at the AmeriFlux site US-Hn1 in central Washington, USA (Missik et al., 2019) (Figure 1A). The site receives an annual mean precipitation of 170 mm (Duncan et al., 2007), with primary vegetation of shrubs and grasses (Missik et al., 2019). 84% of the soil is composed of loamy sand. The primary source of soil moisture is precipitation with a wilting point around 5%–10% and a field capacity around 10%–20% (O’Geen, 2019). An integrated flux tower system (Missik et al., 2019) has been operated since 2016, which records a variety of environmental fluxes and states at a resolution of 30-min. Continuous observations of Rsoil were collected using an automated chamber system from July 2018 to December 2020 at sub-30-min resolution.
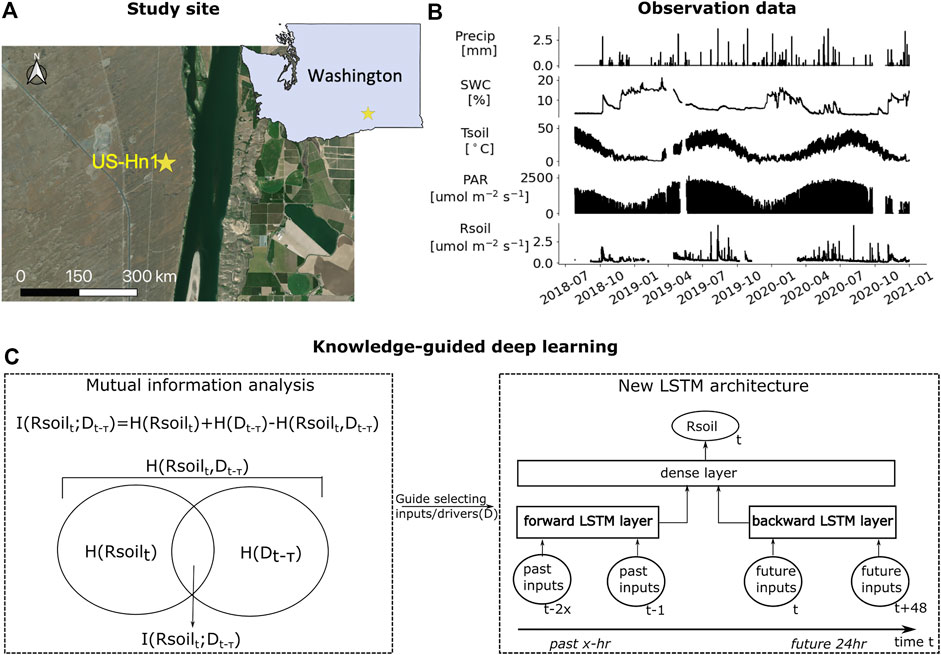
FIGURE 1. Observations of soil respiration (Rsoil) and environmental drivers at the US-Hn1 site. (A) The geographic location of the study site. (B) Time series observations of Rsoil, precipitation (Precip), soil water content at 5 cm depth (SWC), soil temperature at 5 cm depth (Tsoil), and photosynthetic active radiation (PAR) at a temporal resolution of 30-min. (C) The new LSTM architecture whose past and future inputs are informed by mutual information analysis.
In this study, we select precipitation (Precip), photosynthetically active radiation (PAR), Tsoil, and SWC at a depth of 5 cm as the environmental drivers to explore. We aggregated the chamber data to be half-hourly to be consistent with the AmeriFlux data. The remaining analysis and modeling were performed on the time window from July 2018 to December 2020 (Figure 1B).
2.2 Mutual information analysis
To analyze the pairwise dependency between Rsoil and the environmental drivers, we computed mutual information (Cover and Thomas, 2006) between the current state of Rsoil and a lagged state of each driver from the past 24 h to the future 24 h as follows:
Where H is Shannon’s entropy; τ is the time lag, ranging from the prior 24 h to the future 24 h; Rsoilt is Rsoil at time t; Dt−τ is an environmental driver, including Precip, PAR, Tsoil and SWC, at time t − τ; and p is the probability function. The first equation describes that I is the shared uncertainty/entropy between Rsoilt and Dt−τ, which mathematically gives the second equation. We employed the fixed-binning method to estimate a two-dimensional probability space p (r, c) with 50 bins along each dimension (Ruddell and Kumar, 2009). Here, only non-zero Precip is included in the mutual information calculation because the inclusion of data points with zero Precip will significantly dilute the information contained in sporadic rainfall events, which occur rarely compared to data points associated with non-rainy times.
2.3 Knowledge-guided deep learning for soil respiration modeling
The mutual information analysis facilitates the selection of drivers or inputs in DL models by uncovering the lagged dependence between Rsoil and the environmental drivers. To incorporate this dependency into the DL model, we designed a new LSTM architecture that explicitly propagates information about the selected variables forward from their past dynamics and backward from their future dynamics to predict Rsoil. While the past dynamics are mostly causally related with the current state, the future dynamics can be informative when there is a delayed dependency of the inputs. In the example of clockwise Tsoil-Rsoil diel hysteresis, Tsoil lags behind Rsoil due to the delay caused by photosynthesis activities or heat transport across the soil profile; and as a result, the future state of Tsoil probably carries more information of the current state of Rsoil than the current and past Tsoil.
The design of the new LSTM is shown in Figure 1C. The new LSTM uses two LSTM layers to account for both the information transferred from the past input states and the backpropagated information from the future input states. Note that the new LSTM is reduced to an unidirectional LSTM (uniLSTM) in the absence of future inputs. While similar to a bidirectional LSTM (biLSTM) (Graves et al., 2005), the new LSTM is more flexible than a biLSTM for its ability to adopt different numbers of input variables and input temporal lengths for forward and backward LSTM layers.
Here, we vary the past input length from 12 h to 7 days to assess the impact of the temporal length of past dynamics for predicting Rsoil, while a fixed 24 h window is used for the inputs of the future states to maximize the potential impact of diel hysteresis. Further, to study the impact of encoding future dynamics, we also developed the LSTM models that take only past states. Note that the new LSTM is reduced to a uniLSTM model when only past states are taken as inputs. Table 1 lists all cases with different input lengths. For each case, we train both a LSTM model a multilayer perceptron (MLP) model to evaluate which DNN architecture is best suited for predicting Rsoil.
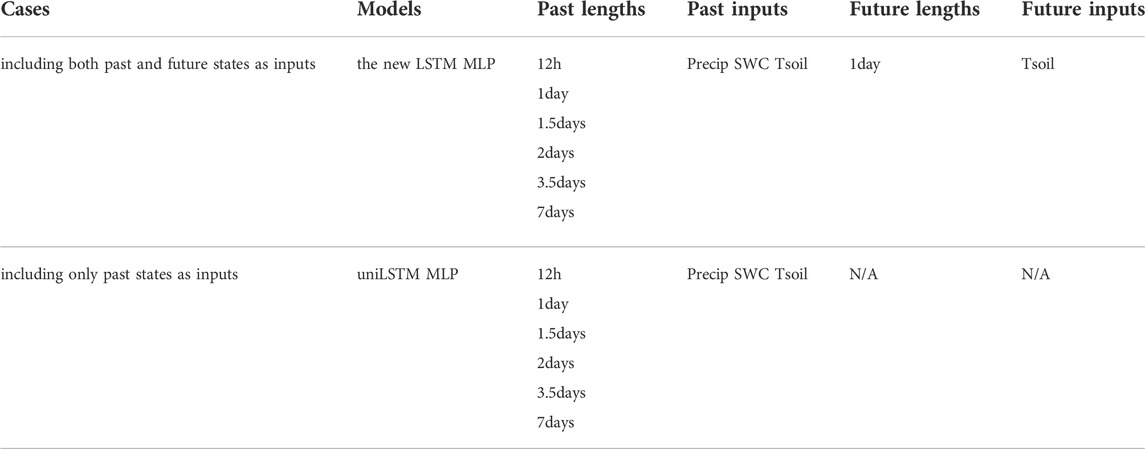
TABLE 1. Cases involving different temporal periods as inputs for estimating Rsoil and Precip/SWC/Tsoil using MLP, uniLSTM, and the new LSTM.
Evaluating the temporal interpolation and extrapolation capabilities of the DL models. We performed two splittings on the observations to prepare two separate sets of training/validation/test data for assessing the interpolation and extrapolation capabilities of the DL models, respectively. The DL models are developed on both interpolation and extrapolation datasets as follows (see the Supplementary Material for the details of model development):
• First, we separated the observations into training, validation, and test data according to either interpolation or extrapolation scenario.
• For each DL model, we then performed the hyperparameter tuning to find the best model architecture (e.g., the number of hidden layers) using the training and validation data.
• Last, we evaluated the performance of the developed DL model with the optimal hyperparameter on the test data.
The interpolation scenario is aimed at assessing the model prediction performance on a dataset sharing the same time window as the training/validation data. We generated the interpolation dataset by randomly splitting the observations into training, validation, and test sets with a proportion of 8:1:1. On the other hand, the extrapolation scenario is used for assessing the model predictability on an untrained or unseen time window (e.g., future time steps). To this end, we selected the time window from 2019-07-01 to 2019-12-31 for testing and randomly split the observations of the remaining time window into training and validation sets with a proportion of 9:1. Supplementary Figure S1 shows the separation of the training, validation, and test data of the two scenarios.
Benchmarks: Q10-based methods and the Community Land Model (CLM). To benchmark the performance of the DL modeling, we developed Rsoil using three Q10-based models and leveraged an existing CLM product calibrated at the same study site (Zhu et al., 2020).
The Q10-based models include the basic Q10 and two SWC-dependent formula, defined as below (Lloyd and Taylor, 1994; Wang et al., 2014):
Where a1, b1, a2, b2, c2, a3, b3, c3, and d3 are model parameters. We estimated the parameters of each model in Eq. 2, based on the training and validation data in the interpolation scenario using the Levenberg-Marquardt least square algorithm (Zobitz et al., 2021; Gelybó et al., 2022). Note that since no hyperparameter tuning is needed for developing these empirical models, both training and validation data is used to estimate the parameters. The calibration leads to a1 = 0.351, b1 = 1.028, a2 = 0.109, b2 = 1.172, c2 = 0.586, a3 = 0.129, b3 = 0.263, c3 = 4.391, and d3 = 0.684. The parameter estimation was performed using a Python package: Scipy version 1.8.
The CLM-based Rsoil simulation is generated from an existing CLM setup at the same study site (Zhu et al., 2020). As a land surface model, the CLM systematically simulates hydrological process, surface energy balance, and biogeochemical process. Rsoil is modeled as a sum of root respiration and heterotrophic respiration parameterized by a variety of dependencies, including Tsoil, SWC, oxygen, etc (Lawrence et al., 2019). To study the local water and carbon budget, this model was calibrated against evapotranspiration and gross primary productivity observations (Zhu et al., 2020) and provides simulation of US-Hn1 in the year 2019. Due to different temporal resolutions of the forcings data, the temporal resolutions of the CLM outputs vary and range from 30 min to 2days (see Supplementary Figure S2 for the time series simulations of the CLM and Q10-based models).
3 Results
In this section, we first present the mutual information analysis results, which guides the design of the new LSTM model. We then present the modeling results. We start by illustrating the deficiencies of CLM and Q10-based modeling in simulating Rsoil, compared with which we show the superiority of the DL models. Particularly, we highlight how the knowledge-guided DL improves predictions of Rsoil. We further evaluate the interpolation and extrapolation capabilities of the DL models and assess the impact of the input time series length on the modeling performance.
3.1 Mutual information analysis and its implications to knowledge-guided DL
The estimated mutual information shown in Figure 2A illustrates that Rsoil shares the most mutual information with SWC and non-zero Precip, followed by Tsoil and PAR, at all lags. We find the dominant role of soil wetness in regulating Rsoil dynamics, indicated by the maximum information provided by SWC and non-zero Precip. Figure 2B shows two diel hysteresis patterns before and after a rainfall event during the summer of 2018. The wetting event significantly increases the diel hysteresis magnitude, consistent with results reported in earlier studies of other dryland ecosystems (Feng et al., 2014; Wang et al., 2014; Song et al., 2015; Guan et al., 2018).
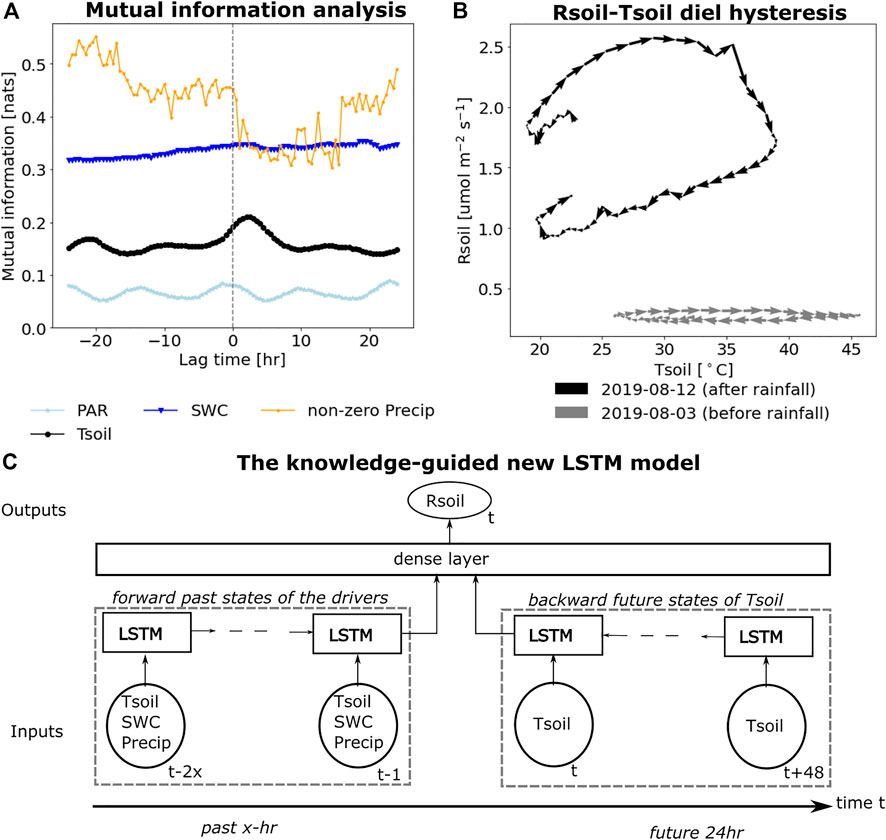
FIGURE 2. Knowledge-guided deep learning (DL) for predicting soil respiration (Rsoil) using mutual information analysis. (A) the quantified mutual information between Rsoil and each of the lagged environmental drivers: non-zero precipitation (Precip), photosynthetic active radiation (PAR), soil temperature (Tsoil), and soil water content (SWC). Positive (negative) time lag represent lagging behind (before) Rsoil. (B) two clockwise diel hysteresis events between Rsoil and Tsoil on two summer days separated by a rainfall event. (C) the new LSTM model for estimating Rsoil that takes past states of Tsoil, SWC, and Precip as well as 24 future hrs of Tsoil as inputs.
The importance of future Tsoil. The computed lagged mutual information suggests that the future states of Tsoil carry more information for the current state of Rsoil than the past states of Tsoil, which peaks at a positive lag of 2 h (the black line in Figure 2A). The importance of future Tsoil is consistent with the clockwise diel hysteresis between Rsoil and Tsoil, shown in the two diel hysteresis examples in Figure 2B.
Implications for the new LSTM. We leveraged the mutual information analysis to explicitly encode diel hysteresis into a DL model for modeling Rsoil. The analysis suggest that: 1) Tsoil, SWC, and Precip can all be significant predictors for Rsoil; and 2) future states of Tsoil provide more useful information for predicting Rsoil than past states. We thus designed the new LSTM model such that the model inputs of the past states include Tsoil, SWC, and Precip dynamics, whereas the inputs of the future states only contain Tsoil (Figure 2C), shown in Table 1.
3.2 CLM and Q10-based modeling
Figure 3 shows the scatter plots of observations versus predictions by the Q10s and CLM. All barely capture the fraction of high Rsoil. The basic Q10, which relates to just Tsoil, has the worst performance with its parameters optimized towards the dominant fraction of Rsoil in the range of 0–0.5 umol m−2s−1 (Figure 3A). Including SWC dependence in a Q10-based model improves model performance, increasing the correlation coefficient between model prediction and observations from nearly 0 to over 0.3. Particularly, representing the dependencies of SWC and Tsoil in a logistic power model best captures the soil respiration dynamics with correlation increasing to almost 0.5, which is consistent with the findings in Wang et al. (2014). Moreover, by using a more complex representation to estimate Rsoil, the CLM simulation demonstrates a modest improvement over the Q10-SWC model. Although both the two SWC-dependent models and CLM can better capture low to medium Rsoil values (Figures 3B,C), they still struggle to capture Rsoil values larger than one umol m−2s−1. Most of these high Rsoil values occur after rainfall events during the prolonged dry summer season.
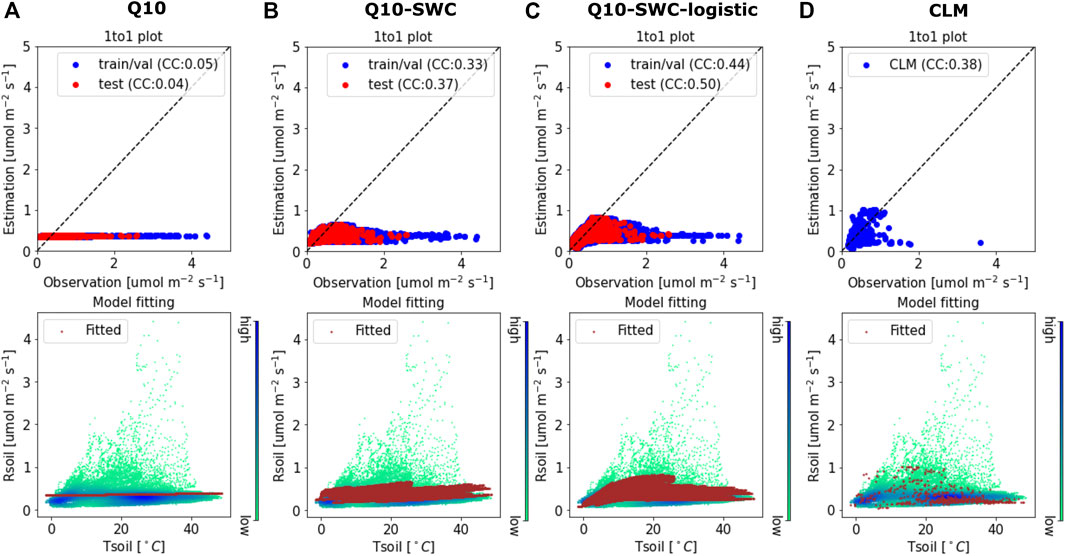
FIGURE 3. The calibrated Q10-based models and CLM simulation. (A) The training and test performances and model fitting of the calibrated Q10 equation:
3.3 Knowledge-guided DL for rsoil modeling
Figure 4 shows the performance of the trained DL models on the test data for both extrapolation and interpolation scenarios listed in Table 1. We assess the prediction performance of each DL model using the following three metrics: mean square error (MSE), Nash–Sutcliffe model efficiency coefficient (NSE), and correlation coefficient (CC). Overall, all the DL models substantially outperform the Q10-based models and the CLM simulation, with CC increasing from less than 0.4 (Figure 3) to approximately 0.6 (extrapolation, Figure 4F) and 1.0 (interpolation, Figure 4C).
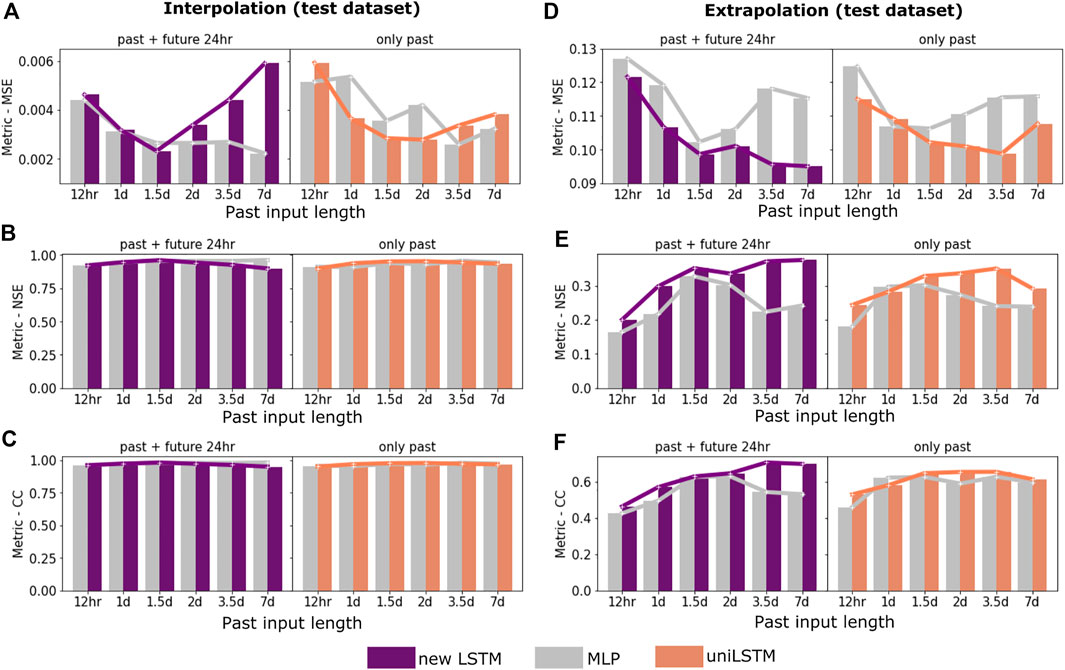
FIGURE 4. Performance of deep learning models for estimating Rsoil. (A-C) model performances on the interpolation scenario test dataset using mean square error (MSE), Nash–Sutcliffe model efficiency coefficient (NSE), and correlation coefficient (CC). (D-F) model performances on the extrapolation scenario test dataset using MSE, NSE, and CC. The selected metric is calculated for all cases with different input temporal ranges in each subplot (see Table 1).
Performance gained by knowledge-guided DL in temporal extrapolation. In general, the knowledge-guided DL models that include future environmental drivers are no worse than or even outperform those that solely rely on past states. When performing interpolation (Figures 4A–C), all DL models show high prediction accuracy (with NSE and CC close to 1). As a result, using future states as inputs slightly improves model performance. The best model type turns out to be the MLP model (grey bars) that takes in both the past and future states. The MLP model shows optimum performance when using as inputs the prior 7 days of states and 24 future hours of Tsoil. For extrapolation scenarios (Figures 4D–F), the newly designed LSTM (purple bars) that includes the future states as inputs shows its superiority over MLP and uniLSTM. The new LSTM increases CC to almost 0.7 when incorporating input data from the prior 7 days, outperforming the other two models whose correlation metrics are only around 0.6. In fact, given a past input length, the new LSTM generally outperforms the corresponding uniLSTM and MLP model with lower MSE and higher NSE/CC values (Figures 4D–F).
Interpolation vs. extrapolation. The DL models generally perform better in temporal interpolation than extrapolation. Figure 5 plots the time series of observed and predicted Rsoil using the best DL models and the corresponding scatter plots on the training, validation, and test datasets. The best interpolation and extrapolation models are the MLP and the new LSTM, respectively. Both models use environmental states of both the past 7 days and one future day as inputs (Figure 4). The models show nearly perfect predictions on the training and validation datasets with NSE and CC close to 1. While the best extrapolation model systematically underestimates Rsoil on the untrained test period (Figure 5B), its correlation metric can still achieve up to around 0.7, greatly outperforming the CLM and Q10-based models whose correlations are no greater than 0.4 (Figure 3).
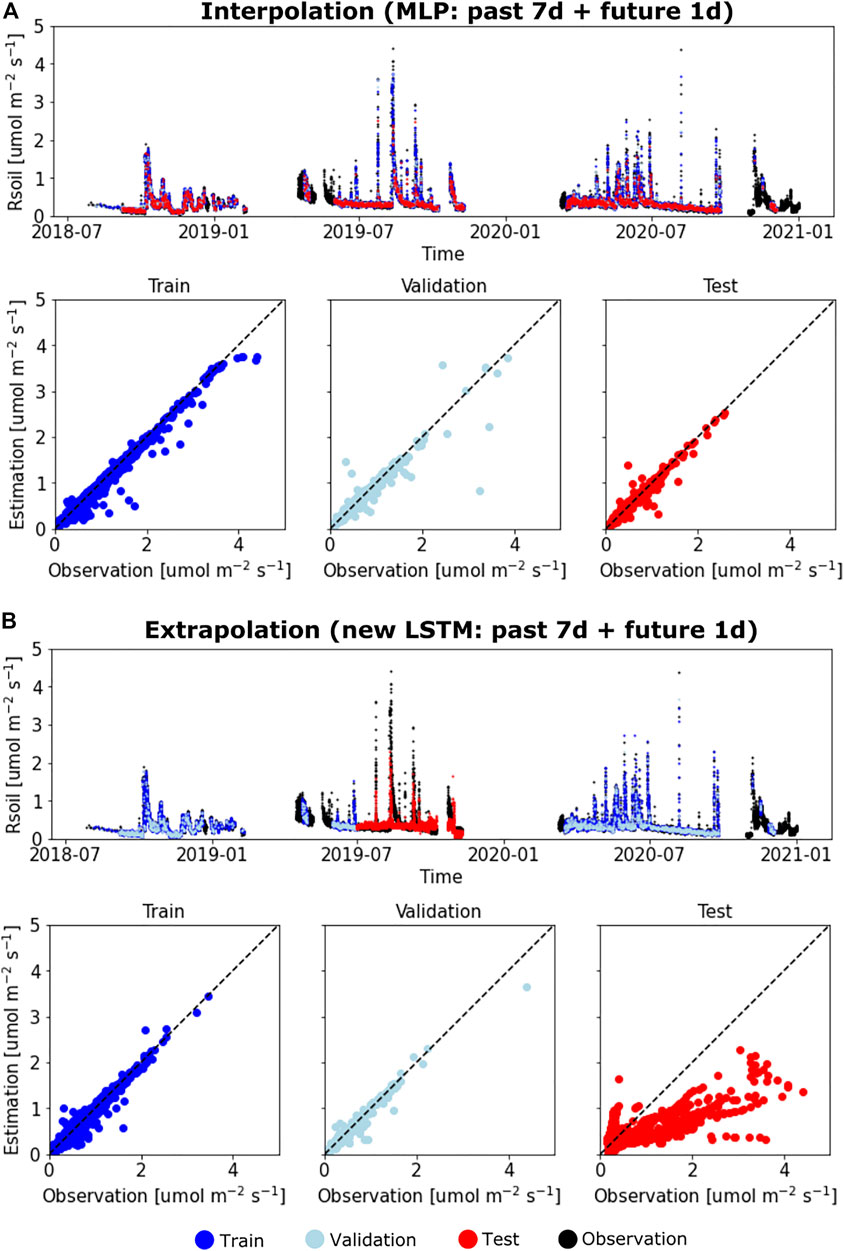
FIGURE 5. Comparison between the best interpolation and extrapolation models. (A) observed and estimated Rsoil for training, validation, and test datasets using the best interpolation model (i.e., MLP that takes the past 7 days of Tsoil/SWC/Precip and 24 future hours of Tsoil as inputs). (B) observed and estimated Rsoil for training, validation, and test datasets using the best extrapolation model (i.e., the new LSTM that takes the past 7 days of Tsoil/SWC/Precip and the future 24 h of Tsoil as inputs).
Furthermore, we find that the performances of the DL models generally increase with the temporal length of the past input, though converging differently between the MLP and LSTM-based models. For the interpolation scenarios, the MLP models achieve better performance on the test dataset than the LSTM-based models when the past input length is longer than 1.5 days (Figures 4A–C). Meanwhile, the LSTM-based models outperform the MLP models in all extrapolation scenarios (Figures 4D–F). Such performance difference between the MLP and LSTM increases with the temporal length of the past states. In fact, the extrapolation predictivity of the new LSTM improves substantially when the past input length increases from 12h (NSE: ∼0.2; CC: ∼0.46) to 7 days (NSE: ∼0.37; CC: ∼0.7).
Modeling the Birch effect. We further zoom into the modeling behaviors after two representative rainfall events with short or long durations (Figures 6A,B), respectively, during the test period of the extrapolation scenarios. The best interpolation DL model (the red line) perfectly reproduces the Rsoil rewetting pulses and the subsequent drying process dynamics. The best extrapolation model (the blue line) captures the Rsoil pulses though mismatches their magnitudes. Yet, neither the Q10-SWC-logistic (the yellow line) nor the CLM (the brown dots) is able to simulate the pulses. It is noted that the fluctuating soil moisture (the cyan line) reflects the diurnal signals as captured by the temperature observations (the green line). Further, while the measured soil moisture does not show abrupt increases due to rainfalls in both events, the developed DL model shows its flexibility to account for the precipitation impact and thus predicts the Rsoil pulses. The unparalleled success of the DL models lies in their ability to encode the dramatic changes in the diel hysteresis patterns during the drying and rewetting cycles by using future Tsoil dynamics as inputs (the right panels in Figure 6). On the other hand, both Q10 and CLM models fail to represent such interactions by exclusively relating Rsoil to the current states of the environmental drivers.
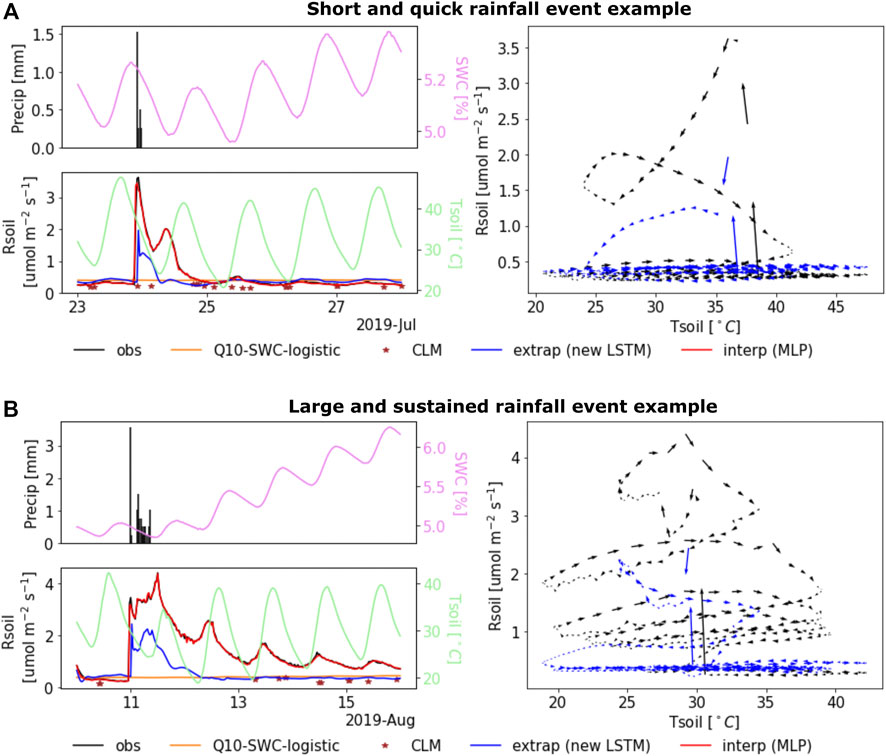
FIGURE 6. The match between modeled and observed Rsoil during and after two rainfall events. (A) Performance of the best interpolation and extrapolation DL models (Figure 5), the Q10-SWC-logistic model, and the CLM simulation for a short and quick rainfall event. (B) Performance of the best interpolation and extrapolation DL models (Figure 5), the Q10-SWC model, and the CLM simulation for a long and sustained rainfall event.
4 Discussions and conclusion
Our study showcases the power of knowledge-guided DL models in emulating complex interactions between dynamic system behaviors and their environmental drivers without knowing the exact functional relations. Due to the clockwise diel hysteresis between Rsoil and Tsoil, including future Tsoil states in DL models led to unprecedented success in predicting Rsoil in a semi-arid ecosystem. The newly configured DL models were able to capture all the large and small Rsoil pulses induced by summer rainfalls. They also captured the dynamics following rainfall events as the soil moisture shifts between wet and dry regimes, overcoming a long-standing challenge of the traditional Q10-based models and other similar empirical representations adopted in process-based models such as the CLM. This data-driven approach can be readily applied to train DL models for other dryland ecosystems with continuous measurements of Rsoil, Tsoil, SWC, and Precip. These results can be ultimately generalized to enable more accurate predictions of Rsoil from monitored or model-projected environmental drivers across global dryland ecosystems.
In addition to showing the importance of the future states, the mutual information-based analysis partially reveals the dominant mechanism that drives the clockwise diel hysteresis at this dryland ecosystem. The least significant role of PAR, revealed by its minimal information shared with Rsoil (Figure 2), may imply that autotrophic respiration contributes little to the total soil respiration due to its sparse vegetation in this ecosystem. Further, contrary to the decoupling between Tsoil and Rsoil, PAR is almost synchronized with the respiration such that the maximum information peaks without lag during a day. This differs from the multiple-hour lead often observed in ecosystems where physiological factors play a more dominant role in controlling Rsoil dynamics (Vargas and Allen, 2008; Kuzyakov and Gavrichkova, 2010). In other words, the diel hysteresis is probably caused by the physical process (i.e., the delay caused by heat transport across the soil profile).
To the best of our knowledge, this is the first implementation of the DL models in estimating soil respiration in a sub-hourly scale. Most existing studies only adopted vanilla machine learning models (e.g., artificial neural networks (Zhao et al., 2017) and random forest (Lu et al., 2021; Yao et al., 2021)) in emulating soil respiration dynamics at coarser temporal scales from daily to annually, which are too coarse to capture the diel hysteresis. Thus, they fail to recognize the importance of future environmental states to the current respiration state in a dryland ecosystem such as this study site. This uniqueness brings the opportunity of explicitly capturing information transferred from both past and future states by using a newly configured LSTM model.
Our proposed DL model shows its superiority in performing temporal extrapolations of Rsoil, which is a common need in Earth system modeling. The modeling performance of the new LSTM model improves with the temporal length of the past input states. Meanwhile, the extrapolation performance of the other models either do not improve over past input length (i.e., MLP) or are consistently inferior to the new LSTM (i.e., uniLSTM). Though slightly worse than MLP for performing interpolation, the new LSTM achieves high accuracy in interpolation (i.e., with both NSE and CC larger than 0.9) and proves to have the best performance in extrapolation. Therefore, the new LSTM can be adopted as the prototyping model in future data-driven modeling development for Rsoil prediction.
One potential future work could be leveraging soil moisture and temperature measurements from multiple layers by including them in the input layers of the LSTM model(s). A straightforward implementation would be directly taking the observations from multiple layers as the inputs of one composite LSTM model. Another alternative is to develop a hybrid modeling framework by coupling the land model (e.g., CLM) with multiple LSTMs, each of which is used to estimate respiration at one soil layer. That is, the DL model serves as the substitute of the corresponding Q10-based module at a given layer for calculating carbon flux. Under such hybrid model, new measurement technology, such as line sensors (Lazik et al., 2019), could provide CO2 concentrations at multiple depths for training, validating, and testing LSTM models.
Although the high Rsoil pulses induced by sporadic sudden rewetting of dry soil are usually short-lived, their accumulation over time and the large coverage of global dryland ecosystems may make them significant global carbon sources. This will only increase with the projected expansion of drylands under the future climate. Therefore, the deficiency in Q10 approaches translates into significant underestimation of soil respiration in dryland ecosystems across the globe by Earth system models like the CLM. Replacing those less accurate dryland soil respiration modules with knowledge-guided DL models will help more accurately model global carbon cycling.
To build a data-driven dryland soil respiration model for Earth system models, future efforts will focus on exploring the transferrability of DL-assisted modeling (Willard et al., 2021) to other locations using community databases of high-resolution Rsoil, such as COSORE (Bond-Lamberty et al., 2020). Such efforts will eventually lead to a generalized global model for dryland Rsoil. The integration of exploratory data analysis and knowledge-guided DL can also be leveraged to model the dynamics of other greenhouse gas fluxes, such as CH4 and N2O, with poorly understood emission mechanisms. Paired with rapid advancements in sensing technologies, knowledge-guided DL can assist Earth scientists in building better and faster Earth system models.
Data availability statement
The data and scripts of this work are available at ESS-DIVE: https://data.ess-dive.lbl.gov/datasets/doi:10.15485/1900529.
Author contributions
PJ and XC designed the research; PJ performed the research; PJ and XC wrote the paper; BV, JM, and ZG collected the data; JM, HL, and ZG helped edit the paper.
Funding
This research was funded by the River Corridor Scientific Focus Area (SFA) project at Pacific Northwest National Laboratory (PNNL), which was supported by the U.S. Department of Energy (DOE), Office of Science (SC) Biological and Environmental Research (BER) program, as part of BER’s Environmental System Science (ESS) program. PNNL is operated for DOE by Battelle Memorial Institute under contract DE-AC05-76RL01830. This paper describes objective technical results and analysis.
Acknowledgments
The authors would like to thank Ben Bond-Lamberty and Vanessa L. Bailey from Pacific Northwest National Laboratory and Rodrigo Vargas from the University of Delaware for their insightful suggestions to improve this work. The authors would also like to acknowledge the assistance of Bowen Zhu from Taiyuan University of Technology in providing the soil respiration simulation of CLM.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2022.1035540/full#supplementary-material
References
Ahlström, A., Raupach, M. R., Schurgers, G., Smith, B., Arneth, A., Jung, M., et al. (2015). The dominant role of semi-arid ecosystems in the trend and variability of the land co2 sink. Science 348, 895–899. doi:10.1126/science.aaa1668
Birch, H. (1958). The effect of soil drying on humus decomposition and nitrogen availability. Plant Soil 10, 9–31. doi:10.1007/bf01343734
Bond-Lamberty, B., Christianson, D. S., Malhotra, A., Pennington, S. C., Sihi, D., AghaKouchak, A., et al. (2020). Cosore: A community database for continuous soil respiration and other soil-atmosphere greenhouse gas flux data. Glob. Chang. Biol. 26, 7268–7283. doi:10.1111/gcb.15353
Bond-Lamberty, B., and Thomson, A. (2010). Temperature-associated increases in the global soil respiration record. Nature 464, 579–582. doi:10.1038/nature08930
Cover, T. M., and Thomas, J. A. (2006). Elements of information theory (wiley series in telecommunications and signal processing). Wiley-Interscience.
Davidson, E. A., Janssens, I. A., and Luo, Y. (2006). On the variability of respiration in terrestrial ecosystems: Moving beyond q10. Glob. Chang. Biol. 12, 154–164. doi:10.1111/j.1365-2486.2005.01065.x
Duncan, J. P., Burk, K. W., Chamness, M. A., Fowler, R. A., Fritz, B. G., Hendrickson, P. L., et al. (2007). Hanford site national environmental policy act (NEPA) characterization. Richland, WA (United States): Tech. rep., Pacific Northwest National Lab.
Dusza, Y., Sanchez-Cañete, E. P., Le Galliard, J.-F., Ferriere, R., Chollet, S., Massol, F., et al. (2020). Biotic soil-plant interaction processes explain most of hysteric soil co 2 efflux response to temperature in cross-factorial mesocosm experiment. Sci. Rep. 10, 905–911. doi:10.1038/s41598-019-55390-6
Ebrahimi, M., Sarikhani, M. R., Safari Sinegani, A. A., Ahmadi, A., and Keesstra, S. (2019). Estimating the soil respiration under different land uses using artificial neural network and linear regression models. CATENA 174, 371–382. doi:10.1016/j.catena.2018.11.035
Feng, W., Zhang, Y., Jia, X., Wu, B., Zha, T., Qin, S., et al. (2014). Impact of environmental factors and biological soil crust types on soil respiration in a desert ecosystem. PLOS ONE 9, 1–10. doi:10.1371/journal.pone.0102954
Gaumont-Guay, D., Black, T. A., Griffis, T. J., Barr, A. G., Jassal, R. S., and Nesic, Z. (2006). Interpreting the dependence of soil respiration on soil temperature and water content in a boreal aspen stand. Agric. For. Meteorology 140, 220–235. The Fluxnet-Canada Research Network: Influence of Climate and Disturbance on Carbon Cycling in Forests and Peatlands. doi:10.1016/j.agrformet.2006.08.003
Gelybó, G., Barcza, Z., Dencső, M., Potyó, I., Kása, I., Horel, A., et al. (2022). Effect of tillage and crop type on soil respiration in a long-term field experiment on chernozem soil under temperate climate. Soil Tillage Res. 216, 105239. doi:10.1016/j.still.2021.105239
Graves, A., Fernández, S., and Schmidhuber, J. (2005). “Bidirectional lstm networks for improved phoneme classification and recognition,” in Artificial neural networks: Formal models and their applications – ICANN 2005. Editors W. Duch, J. Kacprzyk, E. Oja, and S. Zadrożny (Berlin, Heidelberg: Springer Berlin Heidelberg), 799–804.
Guan, C., Li, X., Zhang, P., and Chen, Y. (2018). Diel hysteresis between soil respiration and soil temperature in a biological soil crust covered desert ecosystem. PLOS ONE 13, e0195606–e0195613. doi:10.1371/journal.pone.0195606
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
HoÈgberg, P., Nordgren, A., Buchmann, N., Taylor, A. F., Ekblad, A., HoÈgberg, M. N., et al. (2001). Large-scale forest girdling shows that current photosynthesis drives soil respiration. Nature 411, 789–792. doi:10.1038/35081058
Huang, J., Yu, H., Guan, X., Wang, G., and Guo, R. (2016). Accelerated dryland expansion under climate change. Nat. Clim. Chang. 6, 166–171. doi:10.1038/nclimate2837
Jarvis, P., Rey, A., Petsikos, C., Wingate, L., Rayment, M., Pereira, J., et al. (2007). Drying and wetting of mediterranean soils stimulates decomposition and carbon dioxide emission: The “Birch effect”†. Tree Physiol. 27, 929–940. doi:10.1093/treephys/27.7.929
Jia, X., Willard, J., Karpatne, A., Read, J. S., Zwart, J. A., Steinbach, M., et al. (2020). Physics-guided machine learning for scientific discovery: An application in simulating lake temperature profiles. arXiv preprint arXiv:2001.11086.
Kratzert, F., Klotz, D., Brenner, C., Schulz, K., and Herrnegger, M. (2018). Rainfall–runoff modelling using long short-term memory (lstm) networks. Hydrol. Earth Syst. Sci. 22, 6005–6022. doi:10.5194/hess-22-6005-2018
Kuzyakov, Y., and Gavrichkova, O. (2010). Review: Time lag between photosynthesis and carbon dioxide efflux from soil: A review of mechanisms and controls. Glob. Chang. Biol. 16, 3386–3406. doi:10.1111/j.1365-2486.2010.02179.x
Lal, R. (2004). Carbon sequestration in dryland ecosystems. Environ. Manage. 33, 528–544. doi:10.1007/s00267-003-9110-9
Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., et al. (2019). The community land model version 5: Description of new features, benchmarking, and impact of forcing uncertainty. J. Adv. Model. Earth Syst. 11, 4245–4287. doi:10.1029/2018MS001583
Lazik, D., Vetterlein, D., Salas, S. K., Sood, P., Apelt, B., and Vogel, H.-J. (2019). New sensor technology for field-scale quantification of carbon dioxide in soil. Vadose zone J. 18, 1–14. doi:10.2136/vzj2019.01.0007
Lloyd, J., and Taylor, J. A. (1994). On the temperature dependence of soil respiration. Funct. Ecol. 8, 315–323. doi:10.2307/2389824
Lu, H., Li, S., Ma, M., Bastrikov, V., Chen, X., Ciais, P., et al. (2021). Comparing machine learning-derived global estimates of soil respiration and its components with those from terrestrial ecosystem models. Environ. Res. Lett. 16, 054048. doi:10.1088/1748-9326/abf526
Missik, J. E. C., Liu, H., Gao, Z., Huang, M., Chen, X., Arntzen, E., et al. (2019). Groundwater-river water exchange enhances growing season evapotranspiration and carbon uptake in a semiarid riparian ecosystem. J. Geophys. Res. Biogeosci. 124, 99–114. doi:10.1029/2018JG004666
Missik, J. E. C., Liu, H., Gao, Z., Huang, M., Chen, X., Arntzen, E., et al. (2021). Groundwater regulates interannual variations in evapotranspiration in a riparian semiarid ecosystem. Geophys. Res. Atmos. 126, e2020JD033078. doi:10.1029/2020jd033078
Muñoz-Rojas, M., Lewandrowski, W., Erickson, T. E., Dixon, K. W., and Merritt, D. J. (2016). Soil respiration dynamics in fire affected semi-arid ecosystems: Effects of vegetation type and environmental factors. Sci. Total Environ. 572, 1385–1394. doi:10.1016/j.scitotenv.2016.02.086
Oikawa, P. Y., Grantz, D. A., Chatterjee, A., Eberwein, J. E., Allsman, L. A., and Jenerette, G. D. (2014). Unifying soil respiration pulses, inhibition, and temperature hysteresis through dynamics of labile soil carbon and o2. J. Geophys. Res. Biogeosci. 119, 521–536. doi:10.1002/2013JG002434
Phillips, C. L., Nickerson, N., Risk, D., and Bond, B. J. (2011). Interpreting diel hysteresis between soil respiration and temperature. Glob. Chang. Biol. 17, 515–527. doi:10.1111/j.1365-2486.2010.02250.x
Poulter, B., Frank, D., Ciais, P., Myneni, R. B., Andela, N., Bi, J., et al. (2014). Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 509, 600–603. doi:10.1038/nature13376
Raich, J. W., and Potter, C. S. (1995). Global patterns of carbon dioxide emissions from soils. Glob. Biogeochem. Cycles 9, 23–36. doi:10.1029/94GB02723
Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017). Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv preprint arXiv:1711.10561.
Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., et al. (2019). Deep learning and process understanding for data-driven Earth system science. Nature 566, 195–204. doi:10.1038/s41586-019-0912-1
Riveros-Iregui, D. A., Emanuel, R. E., Muth, D. J., McGlynn, B. L., Epstein, H. E., Welsch, D. L., et al. (2007). Diurnal hysteresis between soil co2 and soil temperature is controlled by soil water content. Geophys. Res. Lett. 34, L17404. doi:10.1029/2007GL030938
Ruddell, B. L., and Kumar, P. (2009). Ecohydrologic process networks: 1. Identification. Water Resour. Res. 45. doi:10.1029/2008WR007279
Rustad, L. E., Huntington, T. G., and Boone, R. D. (2000). Controls on soil respiration: Implications for climate change. Biogeochemistry 48, 1–6. doi:10.1023/a:1006255431298
Sadoughi, M., and Hu, C. (2019). Physics-based convolutional neural network for fault diagnosis of rolling element bearings. IEEE Sens. J. 19, 4181–4192. doi:10.1109/JSEN.2019.2898634
Sampson, D. A., Janssens, I. A., Curiel Yuste, J., and Ceulemans, R. (2007). Basal rates of soil respiration are correlated with photosynthesis in a mixed temperate forest. Glob. Chang. Biol. 13, 2008–2017. doi:10.1111/j.1365-2486.2007.01414.x
Schlesinger, W. H., and Andrews, J. A. (2000). Soil respiration and the global carbon cycle. Biogeochemistry 48, 7–20. doi:10.1023/A:1006247623877
Shen, C. (2018). A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 54, 8558–8593. doi:10.1029/2018WR022643
Song, W., Chen, S., Zhou, Y., Wu, B., Zhu, Y., Lu, Q., et al. (2015). Contrasting diel hysteresis between soil autotrophic and heterotrophic respiration in a desert ecosystem under different rainfall scenarios. Sci. Rep. 5, 1–13. doi:10.1038/srep16779
Tang, J., Baldocchi, D. D., and Xu, L. (2005). Tree photosynthesis modulates soil respiration on a diurnal time scale. Glob. Chang. Biol. 11, 1298–1304. doi:10.1111/j.1365-2486.2005.00978.x
Vargas, R., and Allen, M. F. (2008). Environmental controls and the influence of vegetation type, fine roots and rhizomorphs on diel and seasonal variation in soil respiration. New Phytol. 179, 460–471. doi:10.1111/j.1469-8137.2008.02481.x
Wang, B., Zha, T. S., Jia, X., Wu, B., Zhang, Y. Q., and Qin, S. G. (2014). Soil moisture modifies the response of soil respiration to temperature in a desert shrub ecosystem. Biogeosciences 11, 259–268. doi:10.5194/bg-11-259-2014
Willard, J., Jia, X., Xu, S., Steinbach, M., and Kumar, V. (2020). Integrating physics-based modeling with machine learning: A survey. arXiv preprint arXiv:2003.04919.
Willard, J. D., Read, J. S., Appling, A. P., Oliver, S. K., Jia, X., and Kumar, V. (2021). Predicting water temperature dynamics of unmonitored lakes with meta-transfer learning. Water Resour. Res. 57, e2021WR029579. doi:10.1029/2021WR029579
Yan, J., Feng, Y., Li, J., Li, H., and Ding, G. (2022). Response of soil respiration and q10 to temperature and moisture in naturally regenerated and bare lands based on an 11-year observation period. CATENA 208, 105711. doi:10.1016/j.catena.2021.105711
Yao, J., Liu, H., Huang, J., Gao, Z., Wang, G., Li, D., et al. (2020). Accelerated dryland expansion regulates future variability in dryland gross primary production. Nat. Commun. 11, 1–10. doi:10.1038/s41467-020-15515-2
Yao, Y., Ciais, P., Viovy, N., Li, W., Cresto-Aleina, F., Yang, H., et al. (2021). A data-driven global soil heterotrophic respiration dataset and the drivers of its inter-annual variability. Glob. Biogeochem. Cycles 35, e2020GB006918. doi:10.1029/2020gb006918
Zhang, Q., Katul, G. G., Oren, R., Daly, E., Manzoni, S., and Yang, D. (2015). The hysteresis response of soil co2 concentration and soil respiration to soil temperature. J. Geophys. Res. Biogeosci. 120, 1605–1618. doi:10.1002/2015JG003047
Zhang, Q., Wang, H., Dong, J., Zhong, G., and Sun, X. (2017). Prediction of sea surface temperature using long short-term memory. IEEE Geosci. Remote Sens. Lett. 14, 1745–1749. doi:10.1109/LGRS.2017.2733548
Zhang, J., Zhu, Y., Zhang, X., Ye, M., and Yang, J. (2018). Developing a long short-term memory (lstm) based model for predicting water table depth in agricultural areas. J. Hydrology 561, 918–929. doi:10.1016/j.jhydrol.2018.04.065
Zhao, Z., Peng, C., Yang, Q., Meng, F.-R., Song, X., Chen, S., et al. (2017). Model prediction of biome-specific global soil respiration from 1960 to 2012. Earth's. Future 5, 715–729. doi:10.1002/2016EF000480
Zhu, B., Huang, M., Cheng, Y., Xie, X., Liu, Y., Zhang, X., et al. (2020). Effects of irrigation on water, carbon, and nitrogen budgets in a semiarid watershed in the Pacific northwest: A modeling study. J. Adv. Model. Earth Syst. 12, e2019MS001953. doi:10.1029/2019ms001953
Zobitz, J., Aaltonen, H., Zhou, X., Berninger, F., Pumpanen, J., and Köster, K. (2021). Comparing an exponential respiration model to alternative models for soil respiration components in a canadian wildfire chronosequence (fireresp v1.0). Geosci. Model Dev. 14, 6605–6622. doi:10.5194/gmd-14-6605-2021
Keywords: soil respiration, dryland ecosystem, knowledge-guided deep learning, diel hysteresis, Birch effect
Citation: Jiang P, Chen X, Missik JEC, Gao Z, Liu H and Verbeke BA (2022) Encoding diel hysteresis and the Birch effect in dryland soil respiration models through knowledge-guided deep learning. Front. Environ. Sci. 10:1035540. doi: 10.3389/fenvs.2022.1035540
Received: 05 September 2022; Accepted: 07 November 2022;
Published: 08 December 2022.
Edited by:
Z. Y. Yuan, Chinese Academy of Sciences (CAS), ChinaCopyright © 2022 Jiang, Chen, Missik, Gao, Liu and Verbeke. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peishi Jiang, cGVpc2hpLmppYW5nQHBubmwuZ292
 Peishi Jiang
Peishi Jiang Xingyuan Chen
Xingyuan Chen Justine E. C. Missik2,3
Justine E. C. Missik2,3 Zhongming Gao
Zhongming Gao Heping Liu
Heping Liu