
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Environ. Sci., 11 October 2022
Sec. Environmental Informatics and Remote Sensing
Volume 10 - 2022 | https://doi.org/10.3389/fenvs.2022.1028452
This article is part of the Research TopicAdvances and Applications of Artificial Intelligence and Numerical Simulation in Risk Emergency Management and TreatmentView all 22 articles
Seismic wave travel time is an important seismic attribute information and is widely used in various seismic forward and inversion methods, including seismic migration imaging, seismic tomography, seismic wave forward modeling and other core seismic data processing methods. The accuracy and efficiency of the travel time algorithm are important for the above methods. In the practical application of seismic exploration, it is often carried out under the condition of undulating surface, which has a significant impact on the travel time calculation. Therefore, it is of great significance to study an efficient and high-precision travel time calculation method that can adapt to undulating surface condition. In this paper, Fast iterative method (FIM) is modified to a topography travel time calculation method. The method employs an iterative method to solve the equation of function to obtain seismic wave travel time by maintaining a narrow band called the active list, and the algorithm can update all grid nodes in the active list at a time. We will verify the travel time computing power of the FIM method through several different velocity models.
Seismic exploration has played an important role in the fields of petroleum and mineral resource exploration, geological disaster investigation, hydrological investigation, and engineering quality inspection. Travel time is an important attribute in seismic exploration, and is widely used in data processing technologies such as migration and tomography (Jetschny et al., 2011; Song et al., 2019; Wang et al., 2020; Lu et al., 2022). The travel time calculation method also determines the accuracy and efficiency of the above methods. Since imaging processing often includes models of complex surfaces and strong velocity changes, the ability of travel time calculation methods to adapt to complex models is particularly important (Aki et al., 1977; Hole, 1992; Sun, 2000; Sun, 2004). Therefore, it is of great significance for the theoretical research and practical application of seismic processing methods to study high-efficiency and high-precision seismic wave travel time algorithms that can adapt to complex models (Thurber, 1983; Zelt and Smith, 1992; Eberhart-Phillips and Michael, 1993; Graeber et al., 2002).
Since the finite difference method for travel time calculation was first proposed by Vidale, many scholars have paid enough attention to the method (Vidale, 1988). This method solves the eikonal equation based on the finite difference method, and calculates the travel time of the entire grid area recursively. Van Trier et al. introduced the windward finite difference method to solve the equation of function and then obtained the viscous solution of the equation of function (van Trier and Symes, 1991), which greatly improved the stability of the difference scheme. Based on the Vidale method (Podvin and Lecomte, 1991), Podvin systematically analyzes the different wave propagation forms that may appear at each calculation grid point, and finally determines the wavefront expansion method, which improves the accuracy of the method. Based on the idea of Dijkstra’s algorithm, Qin performs expansion calculation from the actual wave front, and expands the wave front by finding the minimum travel time point, which improves the adaptability of the finite difference method to complex models and the stability of the algorithm (Dijkstra, 1959; Qin et al., 1992). FMM was first proposed by Sethian. This is the most widely used wavefront expansion method (Sethian, 1996; Sethian, 1999). FMM relies on the data structure of the heap to realize the wavefront expansion that meets the narrowband technology, and the algorithm complexity is O(Nlog2N). The performance of the algorithm depends on the size and data structure of the input data. Since the algorithm keeps the data updated by inserting and deleting each element in the heap, the cost of maintaining the heap data structure will be relatively high in the face of large grid computing big. Based on the standard FMM algorithm, Kim proposed a group update method GMM (Group Marching Method) which is based on global boundaries and does not use a sorted data structure. The algorithm complexity is O(N) (Kim and Folie, 2000; Kim, 2001). GMM improves the performance of Computational efficiency. GMM needs to obtain the slowness information of the minimum travel time point in the narrow band to determine the expansion group. If the speed information of the calculation grid point changes greatly, the algorithm may need to perform a large number of iterative calculations, which will reduce the performance of the algorithm. Jeong proposed a new calculation method FIM (Jeong and Whitaker, 2008; Hong and Jeong, 2016), which can effectively solve functional equations on a parallel architecture. FIM manages the active list through an iterative method, and performs grid node insertion and deletion based on convergence metrics. The algorithm does not require active list management. It maintains a special data structure and can update the calculation at multiple points at the same time, thereby effectively improving the calculation efficiency.
The problem of complex undulating surface model is the key problem faced by seismic exploration at present, and the research on forward modeling and imaging method of complex undulating surface is an important geophysical problem. In the study of travel time calculation methods for complex undulating ground, Sun Z et al. studied the calculation of seismic wave travel time under complex surface conditions (Sun et al., 2009), as well as the unequal interval difference method, and compared and analyzed the stepped grid difference method (Sun et al., 2012b), the unequal interval grid finite difference method and the hybrid method. Performance of linear grid interpolation in travel time calculations for complex surface models (Sun et al., 2012a). In the past 50 years, the application scope of geophysical exploration has been expanded rapidly, and the seismic exploration method has been widely used in the monitoring, forecasting and prevention of geological disasters due to its high efficiency and high resolution. Stucchi et al. used seismic survey methods to survey the extension of historical landslides, and the resulting superimposed profiles revealed the deep geometry of the main landslide body and indicated the existence of a potential separation surface at the location of the toe of the landslide (Stucchi and Mazzotti, 2009). Hu G et al. proposed a coal seam seismic exploration technology for predicting coal mine disasters. This method is based on the different propagation velocity of channel waves in the roof and floor of surrounding rock and coal seam, and has dispersion phenomenon, so it can be used to detect geological structures such as voids and faults in coal seams. And achieved good results in practical applications (HU et al., 2013). Maraio et al. used a high-resolution active source seismic exploration method to explore a valley in eastern Italy where a large debris flow occurred, and performed high-precision migration imaging for the measurement results. The processing results reflected the accumulation of sediments behind the debris flow alluvial fan. Characteristics and stratigraphic structure at the top of the bedrock, as well as a quantitative estimate of the total thickness of the valley sediment deposits (Maraio et al., 2018). Feng et al. proposed a modeling method for random noise in seismic exploration in weakly inhomogeneous media, and quantitatively compared the proposed random noise model with the actual random noise. The results show that the proposed noise model is more reliable, The proposed method is successfully applied to construct a complete denoising training set of convolutional neural network to prove the application value of random noise model (Feng et al., 2020). Lei et al. successfully applied the seismic survey method of reflected wave and environmental noise to the survey of urban active faults, and made measurements near actual faults. The research of the combination of the two methods shows that the environmental noise seismic exploration method is feasible for the detection of urban active faults, especially suitable for large-scale regional exploration (Lei et al., 2020). Liu et al. proposed a body wave separation method based on the frequency-domain signal-to-noise ratio, and successfully applied it to the surface wave body wave imaging of passive seismic exploration in actual shallow coverage areas, and the imaging profile was consistent with the active seismic results better (Liu et al., 2021). Fu et al. proposed a seismic prediction and evaluation method for hot dry rock exploration and development, which is based on seismic exploration and combined with other geophysical methods, and can realize nonlinear quantitative prediction and evaluation of hot dry rock reservoirs (Fu et al., 2022). Zhan et al. proposed a 3D structural modeling method for seismic exploration based on knowledge graph, aiming at the problem of image quality degradation in 3D structural modeling in seismic exploration. And under the guidance of the knowledge map, the surface is reconstructed and closed geological bodies are generated. Finally, the effectiveness and feasibility of the method are proved by the field model (Zhan et al., 2022).
In this paper, the FIM algorithm is introduced to solve the seismic wave travel time. Firstly, the basic principle, difference format and algorithm implementation scheme of FIM algorithm are expounded, and then the calculation accuracy and calculation efficiency of FIM algorithm are verified. Finally, the stability of FIM algorithm is verified by different complex models. This method can not only obtain high-precision seismic wave travel time, but also greatly shorten the calculation time, laying a foundation for the accuracy of research results such as tomography and seismic wave inversion.
FIM is a highly efficient numerical algorithm that satisfies the iterative scheme and the narrowband technique, and satisfies the 2D eikonal equations,
Where
FIM uses the time-travel gradient term of the discrete equation of the Godun Windward Differential Formula to obtain the time-traveling time of the seismic waves.
Where the
The main idea of FIM is to selectively solve the equation function equations across all mesh nodes, without the need to maintain a fixed data structure. The wavefront extended narrowband employed by FIM is called the active list, which is used to store the grid node information that is being updated, rather than using a special data structure to track the causal relationship between the grid nodes, FIM keep the relationship loose and update all nodes in the active list at the same time. During each update iteration, all neighboring points of the current calculation point are likely to participate in the update calculation of that point. When the compute node’s solution is up-to-date relative to its proximity (that is, the compute node has converged), the node is removed from the active list and can be reattached to the active list when the value of any windward neighbor node is updated, so FIM is an algorithm that takes a simple data structure and allows each mesh node to be updated multiple times.
Figure 1 shows a 2D schematic of the FIM wavefront expansion. The grid node in the upper left corner is the source point, the black node is the fixed node, that is, the node whose travel time has been calculated, the gray node is the active node, that is, the node that is about to be updated and calculated, the diagonal rectangle containing the active node is the active list, and the black node is the active node. The arrows indicate the forward direction of the narrow band, and the white nodes are the far away points, that is, the nodes that have not yet been calculated when traveling. Figure 1A is the initial stage, the source is initialized, and the initial activity list is constructed; Figure 1B is after the first update step, the wavefront propagates forward, and all neighboring points around the activity list are included for calculation, and the calculation is completed. Nodes of are removed from the active list; Figure 1C is after the second update step, and the wavefront continues to propagate forward until all grid nodes complete the computation. Since grey nodes only depend on their neighbors (black nodes), all grey nodes in the active list can be updated at the same time. If the feature path does not change direction, then all updated gray nodes can be fixed and their white neighbors will form a new narrow band.
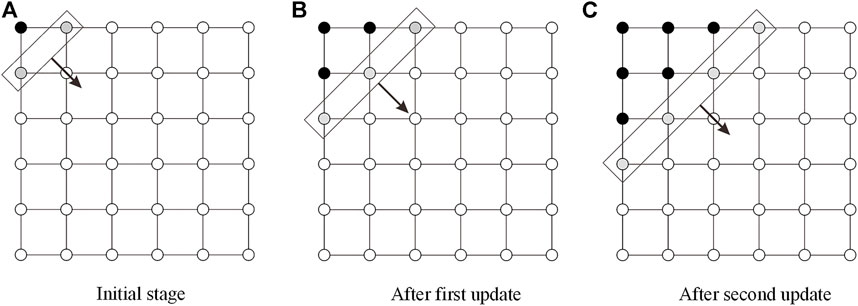
FIGURE 1. Schematic 2D example of FIM wavefront propagation, (A) Initial stage; (B) After first update; (C) After second update.
The implementation scheme of FIM is similar to FMM and is mainly divided into two parts: initialization and active list update:
Initialization process:
Definition: X represents all grid nodes in the calculation area, x represents a grid node in the calculation area, L represents the list of activities, and U(x) represents the timeout value of the calculated point x.
(A1) For all computed grid points, set the time-travel value of the source point to 0, the time-travel value U(x) of the remaining grid nodes to maximum, and the program to set U(x). = 1.0e5;
(A2) Move all adjacent points of the source into L to form an initial list of activities;
Extended update for the list of activities
(B1) For all mesh nodes xi in the active list L, do as follows
1) First, get its time value U(xi), denoted as pi;
2) Use Eq. 1 to get the tick value of xi point, note it as qi, and assign the qi value to U(xi).
(B2) The following judgment is made if pi, qi meets the |pi-qi|<k, then
1) The node information of each neighboring point xj of the compute point xi is judged
2) If xj does not belong to the active list, record the travel time value U (xj) of xj as pj;
3) Use solving Eq. 1 to obtain the travel time value of xj points, denoted as qj;
4) If U (xj)>qj, assign qj to U (xj), otherwise move xj to the active list L;
5) Move the calculation point xi out of the active list.
(B3) Determine whether the active list L is empty, otherwise, return B1 to continue the calculation.
FIM is an iterative calculation method, which means that the nodes are continuously updated until convergence. But for general computational models, most nodes only need one update to converge. When the angle between the direction of the feature path and the direction of advance of the narrowband is less than 45°, an accurate solution at the nodes of the computational mesh can be obtained with only one update. If the angle is greater than 45°, nodes at locations where the eigenpath changes direction will have initial values computed with the wrong upwind neighbors, and they will be replaced in successive iterations as neighbors refine their values renew. So it will continue to update the travel time value of these nodes, instead of removing them from the active list, until the correct result is finally calculated. Unlike FMM, where the wavefront propagates at a point where the wavefront is closed, FIM causes the thicker band to split up where the characteristic path changes direction. Additionally, the wavefront can be moved to a mesh node that has converged and moved back into the active list to update the travel time value when the next mesh node is calculated. In addition, the FIM algorithm is similar to the FMM algorithm in the seismic wave travel time calculation scheme, and the travel time results are obtained by solving the functional equation using the upwind difference scheme, so the results of the FIM algorithm should be similar to the FMM algorithm. The advantage of the FIM algorithm is that it can update the travel time value of all grid nodes in the calculation activity list at the same time. The FMM algorithm can only update the travel time value of one grid node in the narrowband list at a time. Therefore, FIM can obtain close to FMM accuracy on the premise. FIM algorithm program flow chart is shown in Figure 2. Greatly improve computing efficiency. The next section will demonstrate the computational power of the FIM algorithm with numerical examples.
In order to verify the accuracy and efficiency of the algorithm used in this paper, we designed a uniform velocity model with a horizontal width of 4 km, a longitudinal width of 4km, and a seismic wave velocity of 1000 m/s, and placed the epicenter at the center of the model. We use five kinds of distance scattering velocity models between grids and calculate the initial wave travel time of each grid node by FMM, GMM and FIM at the same time, and compare the calculation results with the analytical values. The accuracy index uses the average relative error (L (%)), and the efficiency index uses the calculation time (CPU time consumption(s)), and the results are as shown in Table 1 as shown.
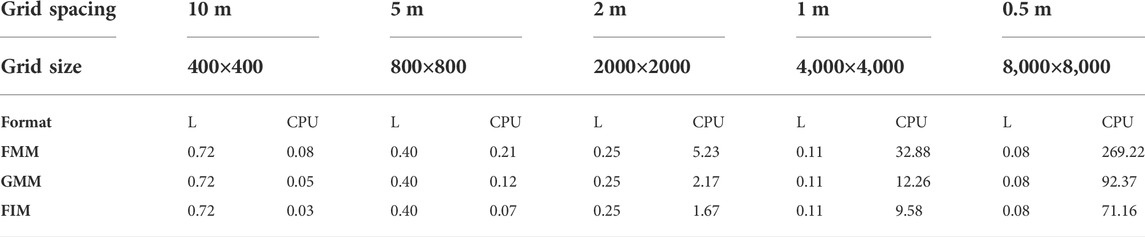
TABLE 1. Analysis of the accuracy and efficiency of the time-travel calculation of the three algorithms.
Table 1 lists the five grid spacings of 0.5m, 1m, 2m, 5m, and 10 m The calculation accuracy and calculation time of the three methods of FMM, GMM and FIM. The law of the change of the average relative error data in the analysis table shows that under different velocity models, the average relative error of the three methods tends to be consistent, and as the grid spacing becomes smaller, the relative error gradually becomes smaller. Overall, all three algorithms have high computational accuracy, and even in the case of a large distance dispersion between meshes of 10 m, the average relative error of all three algorithms is on the order of 0.72%.
The calculation results shown in Figure 3 are calculated on a uniform model with a grid size of 2001×2001, a grid spacing of 2 m×2 m, and a wave speed of 1000 m/s. Since the calculation results of the three methods are similar, only one result graph of each method is shown here. By analyzing the error distribution of these two algorithms, it can be found that the errors of the three algorithms of FMM, GMM, and FIM are concentrated in the diagonal direction, which is due to three The method uses the windward difference scheme to solve the equation function equation to obtain the seismic wave travel time, and only the four neighbors of the calculation point above, down, left and right are included in the calculation when updating the calculation, and the influence of the diagonal neighbors on the overall calculation accuracy is ignored.
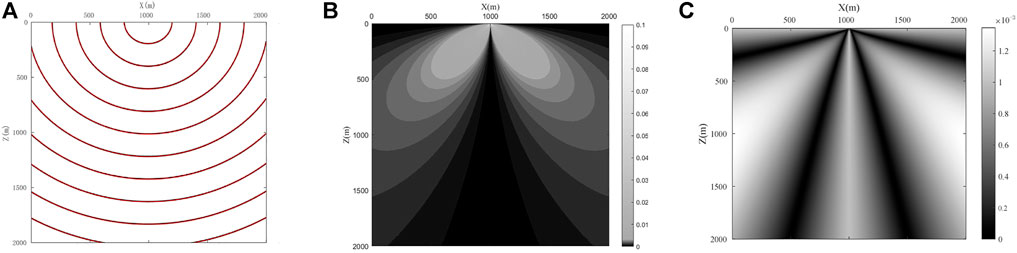
FIGURE 3. Schematic diagram of trial calculation results for homogeneous media, (A) Schematic diagram of FIM travel time contour (calculated value of red line, theoretical value of black line); (B) schematic diagram of relative error of FMM; (C) schematic diagram of absolute error of GMM.
In order to further verify the computing power of the FIM algorithm, we designed three complex models of different degrees and used three methods for trial calculation. Model 1 is a slope velocity model, model 2 is a velocity model with undulating terrain, and model 3 is a high-speed model. The velocity model of the body, the medium velocity distribution range of model 1 and model 2 is 2000 m/s-5000 m/s, the velocity of model 3 is 2000m/s in the low-velocity layer, and the velocity in the high-velocity layer is 5000 m/s. Since the calculation results of the three methods are similar, only the calculation results of one method of each model are shown here. The calculation results are shown in Figure 4. In addition, the calculation efficiency of FIM is about 30% higher than that of GMM, and about 3 times higher than that of FMM algorithm. The calculated results are in good agreement with the above numerical test results.
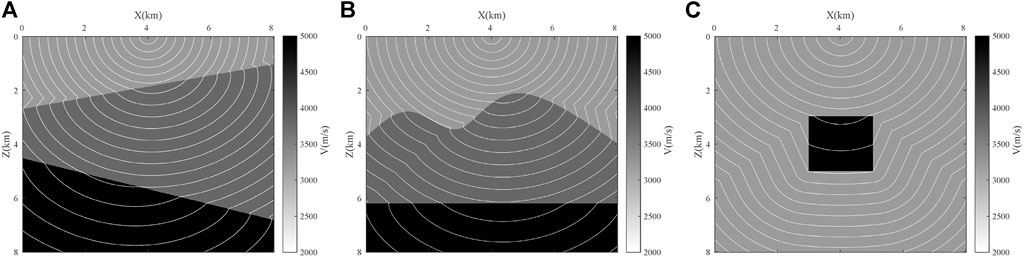
FIGURE 4. Travel time contour maps of the three algorithms, (A) FIM contour; (B) FMM contour; (C) GMM contour.
Table 1 also lists the calculation time of FMM, GMM and FIM under different calculation grids, and the data in the analysis table shows that the calculation efficiency of FIM is the highest, higher than that of GMM algorithm, which is about the same about 4 times the FMM algorithm. Theoretically, FMM and GMM have similar algorithmic structures, both of which are extended in front of the wave through Dijstra algorithm ideas. The biggest difference between the two is narrowband expansion, FMM through the priority queue to achieve the narrowband mesh point removal and insertion operation, the use of heap sorting method for narrowband minimum time point selection, so the FMM time complexity is O(Nlog2N) (N is the total number of calculated grid points). The GMM algorithm performs time-out calculations by traversing the selected group G within a narrow band, so the GMM time complexity is O(N), so GMM The computational efficiency is higher than FMM, but when FIM expands the active list, it incorporates all the neighboring points of the calculation points into the calculation, and updates all the nodes in the active list, so this is also the root cause of the calculation efficiency of the FIM algorithm being higher than the above two algorithms and as the computational model increases, This advantage will be even more pronounced.
The above content mainly focuses on the principle, calculation accuracy and calculation efficiency of the FIM travel time algorithm. The purpose of studying these content is to make the algorithm introduced in this paper suitable for complex surface models. The following will verify the stability and practicability of the FIM algorithm through several complex calculation examples.
Figure 5A is an isochrone diagram of the 4-layer media model, the grid size is 801×801, the grid spacing is 5 m×5 m, and the speed of the three layers from top to bottom is 2000 m/s, 3000 m/s, 4000 m/s, 5000 m/s. Figure 5B shows the Marmousi model, the media velocity distribution range is 2000 m/s-5000 m/s, Figure Figure5C For the Sigsbee model, Figure 5D is the BP model. The above two velocity models are complex models containing high-speed layers, where the low-speed layer speed ranges from 2000 m/s to 3000 m/s and the high-speed layer speed ranges from 6000 m/s to 7,000 m/s. It should be pointed out that in order to make the size of the graphs of the calculation results uniform, we take part of the graphs in the Marmousi model, the Sigsbee model and the BP model. The analysis and calculation results show that the model in Figure 5A is a three-layer homogeneous model, and the contour lines are distributed in each layer of medium when the seismic waves travel, and as the speed of the medium increases, the contour spacing also becomes larger. Figure 5B is a complex surface model with large speed changes, in the face of complex geological structures such as anticline and fault in the model, the time line of seismic waves bends and the distribution gradually becomes sparse, which is due to the rapid propagation speed of seismic waves between high-speed thin layers, so the time contours are more sparse, and the distribution of time lines is denser in areas with smaller speeds. Figures 5C, 4D are time-travel lines of seismic waves containing high-speed bodies, and the time-travel line diagram clearly reflects the propagation law of seismic waves spreading rapidly in the high-speed layer and spreading out slowly in the low-speed layer. Moreover, the time line is still distributed continuously at the boundary between the high-speed layer and the low-speed layer, which shows that the FIM algorithm has good adaptability to the strong speed change model. The comprehensive calculation results show that the distribution of seismic wave time lines conforms to the propagation law of seismic waves in underground media, which further verifies the adaptability of FIM algorithm to complex models.
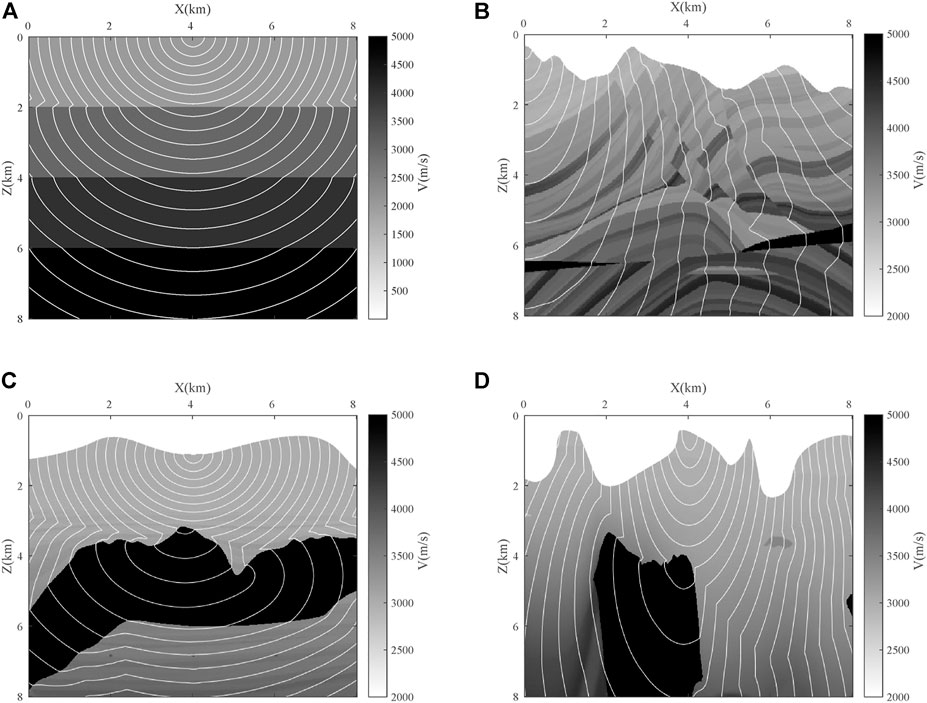
FIGURE 5. Contour maps of different models, (A) 4-layer gradient model, (B) Marmousi (part) model, (C) Sigsbee (part) model,(D) BP (part) model.
In order to efficiently obtain high-quality seismic wave travel time under complex undulating surface conditions, the FIM algorithm in the finite difference algorithm is introduced. The FIM algorithm combines FMM narrowband technology and iterative strategy to update all nodes in the active list at once in the seismic wavefront expansion calculation, and obtain the seismic wavefront time value through multiple iteration calculations. In this paper, the implementation scheme of FIM algorithm to calculate seismic wave travel under undulating surface conditions is given, and the algorithm is compared with FMM algorithm and GMM algorithm. The results show that FIM effectively improves the computational efficiency while maintaining high precision. Finally, through numerical analysis and calculation examples, the FIM algorithm has the following characteristics: 1) The algorithm increases the calculation efficiency by about 4 times compared with the FMM algorithm while taking into account the accuracy of the time-of-action calculation; 2) The algorithm has good stability and adaptability to complex near-surface models and strong velocity change models. The experimental results show that the FIM method can be used as a high-precision and higher-efficiency seismic wave timing calculation method, and has a good application prospect under complex terrain conditions.
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
ML: designed and implemented the algorithm, and initially wrote the manuscript. JiZ: contributed to the data analysis and helped write the manuscript. HS and FG: contributed to model construction. CW: contributed to data calculation. RX and XZ: helped polish the manuscript. All authors have read and agreed to the published version of the manuscript.
This work was supported in part by the pre-research project on Civil Aerospace Technologies No. D020201 funded by China National Space Administration (CNSA), supported in part by the Natural Science Foundation of China under Grant 41,804,100, in part by the China Postdoctoral Science Foundation under Grant 2020T130090 and in part by the China Postdoctoral Science Foundation under Grant 2018M640910.
The authors would thank the National Supercomputer Center in Tianjin for the computer support. The work was carried out at National Supercomputer Center in Tianjin, and this research was supported by Tian He Qingsuo Project special fund project in the field of geoscience.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Aki, K., Christoffersson, A., and Husebye, E. S. (1977). Determination of the three-dimensional seismic structure of the lithosphere. J. Geophys. Res. 82 (2), 277–296. doi:10.1029/JB082i002p00277
Dijkstra, E. W. (1959). A note on two problems in connexion with graphs. Numer. Math. (Heidelb). 1 (1), 269–271. doi:10.1007/bf01386390
Eberhart-Phillips, D., and Michael, A. J. (1993). Three-dimensional velocity structure, seismicity, and fault structure in the Parkfield Region, central California. J. Geophys. Res. 98 (B9), 15737–15758. doi:10.1029/93jb01029
Feng, Q., Li, Y., and Yang, B. (2020). Modeling land seismic exploration random noise in a weakly heterogeneous medium and the application to the training set. IEEE Geosci. Remote Sens. Lett. 17 (4), 701–705. doi:10.1109/lgrs.2019.2926756
Fu, G. Q., Peng, S. P., Wang, R. Z., Zhao, J. T., Yan, F., Xie, J. Y., et al. (2022). Seismic prediction and evaluation techniques for hot dry rock exploration and development. J. Geophys Eng. 19 (4), 694–705. doi:10.1093/jge/gxac042
Graeber, F. M., Houseman, G. A., and Greenhalgh, S. A. (2002). Regional teleseismic tomography of the Western lachlan orogen and the newer volcanic province, southeast Australia. Geophys. J. Int. 149 (2), 249–266. doi:10.1046/j.1365-246X.2002.01598.x
Hole, J. A. (1992). Nonlinear high-resolution three-dimensional seismic travel time tomography. J. Geophys. Res. 97 (B5), 6553–6562. doi:10.1029/92jb00235
Hong, S., and Jeong, W.-K. (2016). A group-ordered fast iterative method for eikonal equations. IEEE Trans. Parallel Distrib. Syst. 28 (2), 1. doi:10.1109/tpds.2016.2567397
Hu, G.-z., Teng, J.-w., Pi, J.-l., and Wang, W. (2013). In-seam seismic exploration techniques——A geophsical method predictting coal-mine disaster. Geophysics 28 (1), 439–451. doi:10.6038/pg20130150
Jeong, W.-K., and Whitaker, R. T. (2008). A fast iterative method for eikonal equations. SIAM J. Sci. Comput. 30 (5), 2512–2534. doi:10.1137/060670298
Jetschny, S., Bohlen, T., and Kurzmann, A. (2011). Seismic prediction of geological structures ahead of the tunnel using tunnel surface waves. Geophys. Prospect. 59 (5), 934–946. doi:10.1111/j.1365-2478.2011.00958.x
Kim, S. (2001). An $\cal O(N)$ level set method for eikonal equations. SIAM J. Sci. Comput. 22 (6), 2178–2193. doi:10.1137/s1064827500367130
Kim, S., and Folie, D. (2000). “The group marching method: An 풪 (N) level set eikonal solver,” in SEG technical program expanded abstracts 2000 (society of exploration geophysicists), Houstone TX USA, 2297–2300. doi:10.1190/1.1815917
Lei, X. Q., Zhang, J., Jin, W. Y., Han, C., and Xu, X. W. (2020). The application of ambient noise and reflection seismic exploration in an urban active fault survey. Interpretation 8 (4), SU1–SU10. doi:10.1190/Int-2020-0085.1
Liu, G. F., Liu, Y., Meng, X. H., Liu, L. B., Su, W. J., Wang, Y. Z., et al. (2021). Surface wave and body wave imaging of passive seismic exploration in shallow coverage area application of Inner Mongolia. Chin. J. Geophysics-Chinese Ed. 64 (3), 937–948. doi:10.6038/cjg2021O0064
Lu, X. L., Hu, X. Q., Xu, Z. Y., Liao, X., Liu, L. H., and Fu, Z. H. (2022). Tunnel concealed karst cave joint detection by tunnel seismic and transient electromagnetic. Lithosphere-Us 2022 (1). 2827582, doi:10.2113/2022/2827582
Maraio, S., Bruno, P. P. G., Picotti, V., Mair, V., and Brardinoni, F. (2018). High-resolution seismic imaging of debris-flow fans, alluvial valley fills and hosting bedrock geometry in Vinschgau/Val Venosta, Eastern Italian Alps. J. Appl. Geophy. 157, 61–72. doi:10.1016/j.jappgeo.2018.07.001
Podvin, P., and Lecomte, I. (1991). Finite difference computation of traveltimes in very contrasted velocity models: A massively parallel approach and its associated tools. Geophys. J. Int. 105 (1), 271–284. doi:10.1111/j.1365-246X.1991.tb03461.x
Qin, F., Luo, Y., Olsen, K. B., Cai, W., and Schuster, G. T. (1992). Finite‐difference solution of the eikonal equation along expanding wavefronts. Geophysics 57 (3), 478–487. doi:10.1190/1.1443263
Sethian, J. A. (1996). A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. U. S. A. 93 (4), 1591–1595. doi:10.1073/pnas.93.4.1591
Sethian, J. A. (1999). Fast marching methods. SIAM Rev. Soc. Ind. Appl. Math. 41 (2), 199–235. doi:10.1137/s0036144598347059
Song, A., Song, B., and Qian, R. Y. (2019). Experiment of 3D seismic reflection technique for forward probing on TBM tunnel face. J. Environ. Eng. Geophys. 24 (4), 609–619. doi:10.2113/Jeeg24.4.609
Stucchi, E., and Mazzotti, A. (2009). 2D seismic exploration of the Ancona landslide (Adriatic Coast, Italy). Geophysics 74 (5), B139–B151. doi:10.1190/1.3157461
Sun, J. (2004). True‐amplitude weight functions in 3D limited‐aperture migration revisited. Geophysics 69 (4), 1025–1036. doi:10.1190/1.1778245
Sun, Z., Sun, J., and Han, F. (2009). Calculation of seismic wave travel time based on linear interpolation and narrowband technique under complex surface conditions. Chin. J. Geophys-Ch 52 (11), 2846–2853. doi:10.3969/j.issn.0001-5733.2009.11.019
Sun, Z., Sun, J., and Han, F. (2012a). Three kinds of seismic wave travel time algorithms for complex terrain and their comparison. Chin. J. Geophys-Ch 55 (2), 560–568. doi:10.6038/j.issn.0001-5733.2012.02.018
Sun, Z., Sun, J., and Han, F. (2012b). Unequal distance upwind difference method for calculating seismic wave travel time under three-dimensional undulating surface conditions. Chin. J. Geophys-Ch 55 (7), 2441–2449. doi:10.6038/j.issn.0001-5733.2012.07.028
Thurber, C. H. (1983). Earthquake locations and three-dimensional crustal structure in the Coyote Lake Area, central California. J. Geophys. Res. 88 (B10), 8226–8236. doi:10.1029/JB088iB10p08226
van Trier, J., and Symes, W. W. (1991). Upwind finite‐difference calculation of traveltimes. Geophysics 56 (6), 812–821. doi:10.1190/1.1443099
Vidale, J. (1988). Finite-difference calculation of travel times. Bull. Seismol. Soc. Am. 78 (6), 2062–2076. doi:10.1785/BSSA0780062062
Wang, J., Liu, J. P., Cheng, F., Yang, H. J., and Huang, Y. F. (2020). Reverse time migration imaging of tunnels via the finite element method using an unstructured mesh. Appl. Geophys. 17 (2), 267–276. doi:10.1007/s11770-020-0814-x
Zelt, C. A., and Smith, R. B. (1992). Seismic traveltime inversion for 2-D crustal velocity structure. Geophys. J. Int. 108 (1), 16–34. doi:10.1111/j.1365-246X.1992.tb00836.x
Keywords: seismic wave travel time calculation, seismic wave numerical simulation, geophysical exploration, fast iterative method (FIM), iterative approach
Citation: Li M, Zhang J, Sun H, Gao F, Wang C, Xu R, Zhao X and Zhou J (2022) Fast iterative method for seismic wave travel time calculation under undulating surface conditions. Front. Environ. Sci. 10:1028452. doi: 10.3389/fenvs.2022.1028452
Received: 26 August 2022; Accepted: 26 September 2022;
Published: 11 October 2022.
Edited by:
Chengyi Pu, Central University of Finance and Economics, ChinaReviewed by:
Chao Li, Chengdu University of Technology, ChinaCopyright © 2022 Li, Zhang, Sun, Gao, Wang, Xu, Zhao and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jian Zhang, emo0NTE3NTU1NjJAZ21haWwuY29t
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.