RSFD: A rough set-based feature discretization method for meteorological data

Meteorological data mining aims to discover hidden patterns in a large number of available meteorological data. As one of the most relevant big data preprocessing technologies, feature discretization can transform continuous features into discrete ones to improve the efficiency of meteorological data mining algorithms. Aiming at the problems of high interaction of multiple attributes, noise interference, and difficulty in obtaining prior knowledge in meteorological data, we propose a rough set-based feature discretization method for meteorological data (RSFD). First, we calculate the information gain of each candidate breakpoint in the meteorological attribute to split the intervals. Then, we use chi-square test to merge these discrete intervals. Finally, we take the variation of indiscernibility relation in rough set as the evaluation criterion for the discretization scheme. We scan each attribute in turn by using the strategy of splitting first and then merging, thus obtaining the optimal discrete feature set. We compare RSFD with the state-of-the-art discretization methods on meteorological data. Experiments show that our method achieves better results in the classification accuracy of meteorological data, and obtains a smaller number of discrete intervals while ensuring data consistency.

1 Introduction

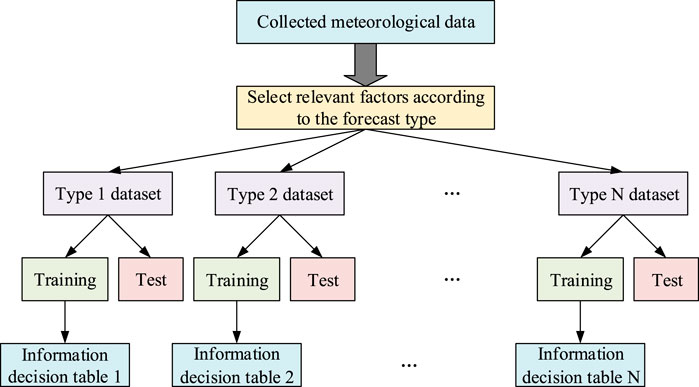
With the continuous improvement of observation and detection technology, the continuous expansion of prediction range, and the continuous improvement of refinement, the meteorological data covers a wider geographical range which has a larger spatial-temporal density, and the more diverse available types and presentation forms (Reichstein et al., 2019; Bhatti et al., 2021a; Bhatti et al., 2022). According to different forecast types, information decision tables of different forecast types in the meteorological dataset can be constructed, as shown in Figure 1. Meteorological data mining aims to find hidden patterns in a large number of available meteorological data from these information decision tables, thus transforming the retrieved information into available meteorological knowledge (Guo, 2016; Aamir et al., 2021; Bhatti et al., 2021b; Hasnain et al., 2021; Galvan et al., 2022). However, the abundant information brings huge space-time overhead and greatly increases the complexity of meteorological data analysis (Xu et al., 2020). Using all collected meteorological information in the process of meteorological big data analysis is easy to lead to information redundancy and weaken the generalization ability of the learning model, thereby significantly reducing the accuracy of meteorological data processing (Zhang and Shi, 2021).

FIGURE 1

FIGURE 1. Information decision tables of different forecast types in meteorological dataset.

Feature discretization is a key technology of intelligent data preprocessing (Chen et al., 2018). It removes redundant information by converting continuous features in meteorological data into discrete ones that are closer to the knowledge layer representation, thus reducing the system overhead and enhancing the robustness of the learning algorithm (Chen et al., 2020; Huang et al., 2020; Chen et al., 2021). In addition, feature discretization can be useful for missing value imputation (Rahman and Islam, 2016). At present, the widely used discretization methods mainly include information entropy-based discretization (de Sá et al., 2016), class-attribute correlation-based discretization (Yan et al., 2014), chi-square-based discretization (Rosati et al., 2015), and rough set-based discretization (Chen and Huang, 2021).

Liu et al. proposed a large-scale data discretization algorithm based on information entropy and inconsistency of meteorological attributes to effectively mine the hidden knowledge in meteorological data (Liu et al., 2017). Moon et al. (2019) devised a selective discretization method that converted a subset of continuous input variables to nominal ones and used principal component analysis to preprocess the meteorological data obtained by the automatic weather station, thus improving the prediction quality of the early warning system (EWS). Kamińska et al. (2020) proposed and tested a multivariate, non-deterministic, and distribution-based discretization algorithm coupled with the well-known rule extraction algorithm APRIORI for modeling of air quality, thus producing more interesting rules with respect to the specific domain-application. Wang et al. discretized the original data by defining a class-attribute contingency coefficient that measures the strength of correlation between variables in Bayesian network, thus mining the correlation between meteorological factors and lightning attributes in the historical data of lightning strikes on transmission lines (Wang et al., 2020).

Although the above feature discretization algorithms have achieved gratifying results in meteorological data mining, they do not take into account the internal stability of discrete intervals and the similarity of adjacent intervals when selecting breakpoints, and cannot ensure that the indiscernibility relationship of information system will not be destroyed. In addition, the prior knowledge of meteorological data in complex environment is usually difficult to obtain, which makes the accuracy of discretization greatly reduced.

To this end, we propose a rough set-based feature discretization method for meteorological data (RSFD). First, we calculate the information gain of each candidate breakpoint in the meteorological attribute to split the intervals. Then, we use chi-square test to merge these discrete intervals. Finally, we take the variation of indiscernibility relation in rough set as the evaluation criterion for the discretization scheme. We scan each attribute in turn by using the strategy of splitting first and then merging, thus obtaining the optimal discrete feature set. We compare RSFD with the state-of-the-art discretization methods on meteorological data. Experiments show that our method achieves better results in the classification accuracy of meteorological data, and obtains a smaller number of discrete intervals while ensuring data consistency.

The remainder of this paper is organized as follows. Section 2 introduces the basic concepts and problem models. Section 3 elaborates the proposed feature discretization method. The experimental results are analyzed and discussed in Section 4. Section 5 summarizes this paper.

2 Problem models

We introduce the definition of feature discretization and the basic flow of meteorological data feature discretization. Then, we describe the rough set model.

2.1 Feature discretization

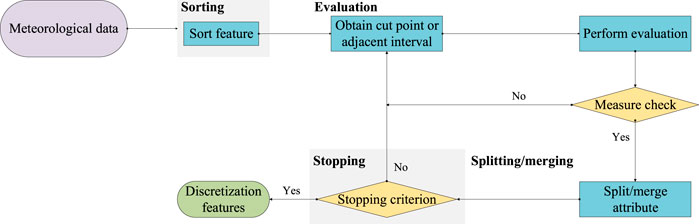
Feature discretization divides continuous attributes into a finite number of sub-intervals, and then associates these sub-intervals with a set of discrete values (Chen et al., 2022a). The basic flow of meteorological data feature discretization is shown in Figure 2. Firstly, the continuous attribute values of meteorological data are sorted and the duplicate values are deleted to obtain a set of candidate breakpoints. Secondly, the breakpoints of continuous attributes are selected from the set of candidate breakpoints, and whether to split the intervals or merge the adjacent sub-intervals is decided according to the judgment criteria of the adopted discretization algorithm. If the termination condition is satisfied, output the meteorological data discretization result, otherwise, continue to select the remaining breakpoints from the set of candidate breakpoints to perform attribute discretization.

FIGURE 2

FIGURE 2. The basic flow of meteorological data feature discretization.

2.2 Rough set

Unlike DS evidence theory and fuzzy set theory, the membership function value of the object in rough set theory depends on the knowledge base, which can be directly obtained from the data without any prior knowledge or additional information about the data (Chen et al., 2022b). Rough set regards the knowledge as the ability to classify the objects on the Universe. An equivalence relation on the Universe represents a knowledge. Two-tuple $K=\left(U,\mathbb{R}\right)$ is a knowledge base, where $U$ is the Universe, and $\mathbb{R}$ is the equivalence relation clusters on $U$. For $x\in U$, $R\in \mathbb{R}$, equivalence class of $x$ under $R$ is: ${\left[x\right]}_R=\left\{y\in U|\left(x,y\right)\in R\right\}$. The quotient set $U/R=\left\{{\left[x\right]}_R|x\in U\right\}$ is called a knowledge. Let $R$ be a binary equivalence relation on $U$, for any $X\subseteq U$, the lower and upper approximations of $X$ with respect to $R$ are:

$R_{-}X=\left\{x\in U|{\left[x\right]}_R\subseteq X\right\},(1)$

$R^{-}X=\left\{x\in U|{\left[x\right]}_R\cap X\ne \varnothing \right\}.(2)$

The rough set-based feature discretization evaluates the discretization results according to the dependence of $X$ to $R$. The dependence of $X$ to $R$ is:

${\gamma }_R\left(X\right)=\frac{\left|R_{-}X\right|}{\left|U\right|},(3)$

where $\left|·\right|$ is the cardinality of the set, $0\le {\gamma }_R\left(X\right)\le 1$. When ${\gamma }_R\left(X\right)\to 1$, the dependence of $X$ to $R$ is high, when ${\gamma }_R\left(X\right)=1$, $X$ is completely dependent on $R$, indicating that the system compatibility is not destroyed.

3 Rough set-based feature discretization

We introduce the process of splitting intervals by information entropy and merging intervals by chi-square test in detail. Then, we explain the discretization scheme evaluation model based on rough set, and point out the defect in the dependence.

3.1 Split intervals by information entropy

We calculate the information gain of each candidate breakpoint in the meteorological attribute to split the intervals. Suppose that the meteorological dataset S contains k categories $\left(C_1,...,C_k\right)$, and $P\left(C_i,S\right)$ represents the occurrence frequency of category $C_i$ in S, then the information entropy of S is defined as:

$Ent\left(S\right)=-{\sum }_{i=1}^{k}P\left(C_i,S\right)\log \left(P\left(C_i,S\right)\right).(4)$

Suppose that S is divided into two subsets $S_1$ and $S_2$ by breakpoint T, then the breakpoint information entropy of S is defined as follows:

$E\left(A,T,S\right)=\frac{\left|S_1\right|}{\left|S\right|}Ent\left(S_1\right)+\frac{\left|S_2\right|}{\left|S\right|}Ent\left(S_2\right).(5)$

where $\left|S\right|$, $\left|S_1\right|$, and $\left|S_2\right|$ are the number of samples contained in S, $\left|S_1\right|$, and $\left|S_2\right|$, respectively, A is the meteorological attribute to be discretized. The breakpoint $T_A$ that minimizes $Ent\left(A,T,S\right)$ is the optimal breakpoint, which is selected to perform binary discretization of A. The information gain of S after discretization is:

$Gains\left(A,T_A,S\right)=Ent\left(S\right)-Ent\left(A,T_A,S\right).(6)$

In addition, the selected breakpoint needs to meet the following conditions:

$Gains\left(A,T_A,S\right)>\frac{{\log }_2\left(N-1\right)}{N}+\frac{\Delta \left(A,T_A,S\right)}{N},(7)$

$\Delta \left(A,T_A,S\right)={\log }_2\left(3^k-2\right)-\left[kEnt\left(S\right)-k_{1}Ent\left(S_1\right)-k_{2}Ent\left(S_2\right)\right],(8)$

where N is the total number of samples in the meteorological dataset, $k_1$ and $k_2$ are the number of categories included in $S_1$ and $S_2$ ($k=k_1+k_2$), respectively.

3.2 Merge intervals by chi-square test

Then, we use chi-square test to merge the discrete intervals generated after the above splitting, as follows:

${\chi }^2={\displaystyle \sum }_{i=1}^2{\displaystyle \sum }_{j=1}^k\frac{{\left(A_{ij}-E_{ij}\right)}^2,}{E_{ij}}(9)$

where ${\chi }^2$ represents the degree of deviation between the observed value and the theoretical value, $A_{ij}$ represents the number of samples belonging to class j in the i-th discrete interval, and $E_{ij}$ represents the expected frequency of class j in the i-th discrete interval. It can be determined by ${\chi }^2$ whether two adjacent discrete intervals should be merged.

3.3 Evaluate intervals by rough set

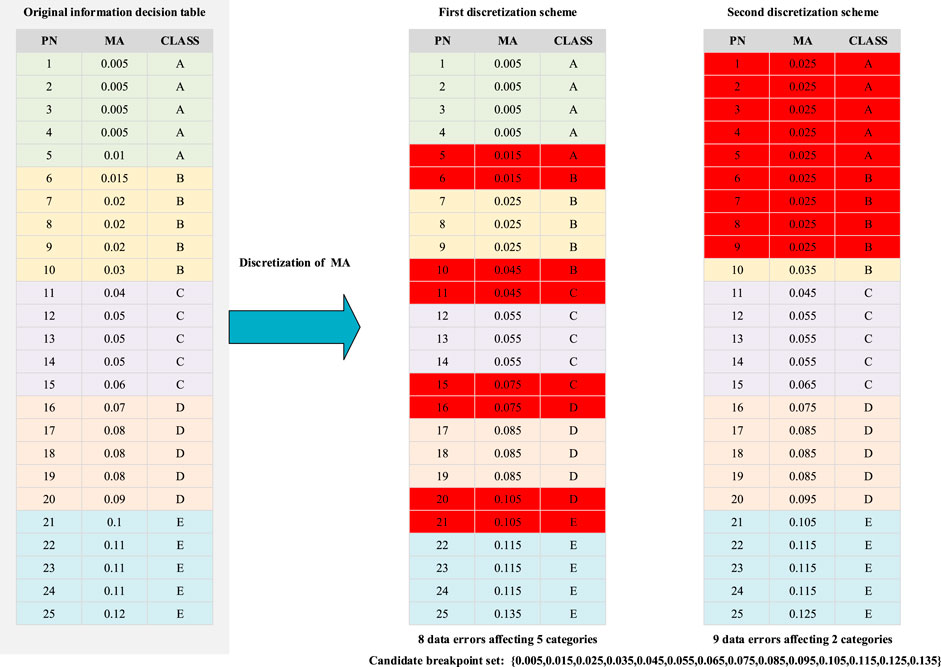
In general, the system compatibility after discretization is measured by the dependence calculated by (3) (Zhang et al., 2008). However, the dependency is only a microscopic reflection of the number of data errors. The indiscernibility relation describes the entire category on a macro level, and its change is directly related to the class-attribute information of meteorological data. As shown in Figure 3, the original information decision table has 25 samples, PN represents the serial number of the sample, MA represents the meteorological attribute, and CLASS is the meteorological category (including five categories of A, B, C, D, and E). Under the first discretization scheme, there are 8 data errors in the information decision table, and the dependence is 0.68. These 8 errors are distributed in five categories. Under the second discretization scheme, there are 9 data errors in the information decision table, and the dependence is 0.64. These 9 errors are only distributed in the two categories of A and B. Although the dependence obtained by the second discretization scheme is less than that obtained by the first discretization scheme, the number of categories correctly identified by the second discretization scheme is more than that correctly identified by the first discretization scheme. Therefore, the dependence cannot directly reflect the accuracy of the discretization result. It is more appropriate to measure the system compatibility through the variation of indiscernibility relation. We use the strategy of splitting first and then merging to scan each meteorological attribute in turn, and then evaluate the discretization scheme by the variation of indiscernibility relation. If the termination conditions are met, RSFD outputs the result; otherwise, it adjusts the thresholds of splitting intervals and merging intervals to rescan all attributes.

FIGURE 3

FIGURE 3. Defect in the dependence.

4 Experiments

We introduce the datasets and the experimental environment configuration. Then, we compare the RSFD with the state-of-the-art discretization methods on meteorological data. Finally, we analyze and discuss the experimental results.

4.1 Datasets and experimental environment

The meteorological data used in the experiment include four main attributes of air pressure, wind direction, wind speed, and temperature. We divide the three meteorological datasets into three rainstorm levels, five rainstorm levels, and seven rainstorm levels, respectively. In the dataset with three rainstorm levels, the number of samples in the training set is 3,000, wherein the number of samples in Level 1 is 1300, the number of samples in Level 2 is 900, and the number of samples in Level 3 is 800. We sort each attribute individually by value and then remove duplicate values in each attribute, totalling 6932 initial breakpoints. In the dataset with five rainstorm levels, the number of samples in the training set is 5000, wherein the number of samples in Level 1 is 1300, the number of samples in Level 2 is 1200, the number of samples in Level 3 is 1000, the number of samples in Level 4 is 800, and the number of samples in Level 5 is 700. We sort each attribute individually by value and then remove duplicate values in each attribute, totalling 10,786 initial breakpoints. In the dataset with seven rainstorm levels, the number of samples in the training set is 7000, wherein the number of samples in Level 1 is 1600, the number of samples in Level 2 is 1300, the number of samples in Level 3 is 1200, the number of samples in Level 4 is 1100, the number of samples in Level 5 is 800, the number of samples in Level 6 is 500, and the number of samples in Level 7 is 500. We sort each attribute individually by value and then remove duplicate values in each attribute, totalling 15,619 initial breakpoints.

To verify the effectiveness of the proposed algorithm, the comparative experiments are carried out under the hardware conditions of Intel Core i5-5200U CPU at 2.20-GHz processor and 12-GB memory. The visualization, programming, simulation, testing, and numerical processing of the experiments are implemented in MATLAB (R2016a version). We select the BP neural networks with three hidden layers as classifiers. Each hidden layer has 20 nodes. The Sigmoid function is selected as the activation function of the hidden layer. The meteorological data used in the experiment contains four main attributes. Correspondingly, we set the number of input nodes of BP neural network to 4. According to the number of rainstorm levels of the three meteorological datasets, we set the number of output nodes of the corresponding BP neural networks to 3, 5, and 7, respectively. The activation function of the output node is the Softmax function.

4.2 Evaluation of discretization scheme

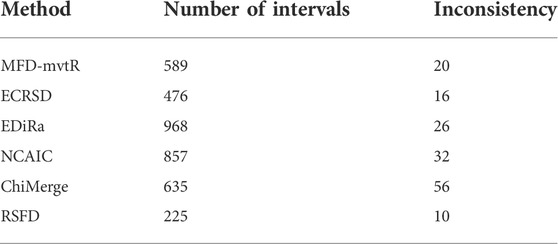
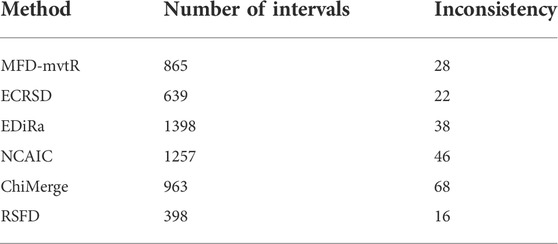
We compare RSFD with MFD-mvtR (Huang et al., 2020), ECRSD (Chen et al., 2021), EDiRa (de Sá et al., 2016), NCAIC (Yan et al., 2014), and ChiMerge (Rosati et al., 2015) in terms of the number of breakpoints and the data inconsistency. The discretization results of all algorithms in the dataset with the three rainstorm levels are shown in Table 1.

TABLE 1

TABLE 1. Discretization results of all algorithms in the dataset with the three rainstorm levels

RSFD obtains the smallest number of breakpoints and the lowest data inconsistency in the dataset with the three rainstorm levels. The number of breakpoints obtained by RSFD is 232 less than that obtained by ECRSD. The data inconsistency obtained by RSFD is 4 lower than that obtained by ECRSD. The discretization results of all algorithms in the dataset with the five rainstorm levels are shown in Table 2.

TABLE 2

TABLE 2. Discretization results of all algorithms in the dataset with the five rainstorm levels.

RSFD obtains the smallest number of breakpoints and the lowest data inconsistency in the dataset with the five rainstorm levels. The number of breakpoints obtained by RSFD is 251 less than that obtained by ECRSD. The data inconsistency obtained by RSFD is 6 lower than that obtained by ECRSD. The discretization results of all algorithms in the dataset with the seven rainstorm levels are shown in Table 3.

TABLE 3

TABLE 3. Discretization results of all algorithms in the dataset with the seven rainstorm levels.

RSFD obtains the smallest number of breakpoints and the lowest data inconsistency in the dataset with the seven rainstorm levels. The number of breakpoints obtained by RSFD is 241 less than that obtained by ECRSD. The data inconsistency obtained by RSFD is 6 lower than that obtained by ECRSD. Then, we train the neural network classifier with the discretization results of all algorithms. The classification results of all algorithms in the dataset with the three rainstorm levels are shown in Table 4.

TABLE 4

TABLE 4. Classification results of all algorithms in the dataset with the three rainstorm levels.

RSFD achieves the highest classification accuracy in the dataset with the three rainstorm levels. The classification accuracy obtained by RSFD is 1.96% and 10.15% higher than that obtained by ECRSD and the original data without discretization, respectively. The classification results of all algorithms in the dataset with the five rainstorm levels are shown in Table 5.

TABLE 5

TABLE 5. Classification results of all algorithms in the dataset with the five rainstorm levels.

RSFD achieves the highest classification accuracy in the dataset with the five rainstorm levels. The classification accuracy obtained by RSFD is 1.21% and 9.13% higher than that obtained by ECRSD and the original data without discretization, respectively. The classification results of all algorithms in the dataset with the seven rainstorm levels are shown in Table 6.

TABLE 6

TABLE 6. Classification results of all algorithms in the dataset with the seven rainstorm levels.

RSFD achieves the highest classification accuracy in the dataset with the seven rainstorm levels. The classification accuracy obtained by RSFD is 2.37% and 9.01% higher than that obtained by ECRSD and the original data without discretization, respectively.

4.3 Discussion

It can be seen that data inconsistency has a great impact on classification accuracy. The smaller the number of data errors, the higher the classification accuracy obtained on the neural network classifier. RSFD scan each attribute in turn by using the strategy of splitting first and then merging, and take the variation of indiscernibility relation in rough set as the evaluation criterion for the discretization scheme, thus obtaining the optimal discrete feature set. EDiRa discretizes only one attribute at a time. Since the correlation between attributes is not considered, the results obtained by EDiRa will destroy the system compatibility to a certain extent. NCAIC uses class-attribute correlation as a criterion for dividing the interval, and considers the upper approximation of each category and the distribution information of the data. However, considering only the upper approximation does not fully characterize the entire equivalence class. The discretization discriminant of NCAIC still has a certain probability to incline to the category with the largest number of samples in the interval, which cannot obtain a satisfactory discretization result. ChiMerge considers the similarity of adjacent intervals, but neglects the internal stability of the intervals. In this way, ChiMerge generates a large number of data errors. On the contrary, MFD-mvtR considers the internal stability of the intervals, but neglects the similarity of adjacent intervals. Although MFD-mvtR can reduce the number of data errors by using the variation of indiscernibility relation as the evaluation criterion for the discretization scheme, it must come at the expense of increasing the number of breakpoints. ECRSD takes into account both the internal stability of the intervals and the similarity of adjacent intervals, thus obtaining a discretization result second only superior to that of RSFD. However, the dependence adopted by ECRSD cannot directly reflect the accuracy of the discretization result. It is more appropriate to measure the system compatibility through the variation of indiscernibility relation. In summary, RSFD has the best performance.

5 Conclusion

Aiming at the problems of high interaction of multiple attributes, noise interference, and difficulty in obtaining prior knowledge in meteorological data, we have proposed a rough set-based feature discretization method for meteorological data (RSFD). Our contributions mainly come from the following aspects: (1) we have calculated the information gain of each candidate breakpoint in the meteorological attribute to split the intervals; (2) we have used chi-square test to merge the discrete intervals generated after the above splitting; (3) we have taken the variation of indiscernibility relation in rough set as the evaluation criterion for the discretization scheme. We have scanned each attribute in turn by using the strategy of splitting first and then merging, thus obtaining the optimal discrete feature set. We have compared RSFD with the state-of-the-art discretization methods on meteorological data. RSFD obtains the smallest number of breakpoints and the lowest data inconsistency. We have trained the neural network classifier with the discretization results of all algorithms. RSFD achieves the highest classification accuracy. However, RSFD is difficult to describe the ambiguity of meteorological data. In future work, we will introduce fuzzy theory to optimize the model, and test RSFD on more meteorological datasets to improve the stability of the algorithm.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LZ and QC contributed equally to method design, experimental analysis, and manuscript writing. MH and QC were responsible for data provision and funding acquisition. All authors reviewed the final version of the manuscript and consented to publication.

Funding

This work was supported in part by the Hainan Provincial Natural Science Foundation of China under Grant 2019CXTD400, in part by the National Key Research and Development Program of China under Grant 2018YFB1404400, and in part by the China Postdoctoral Science Foundation under Grant 2021M701838.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aamir, M., Li, Z., Bazai, S., Wagan, R. A., Bhatti, U. A., Nizamani, M. M., et al. (2021). Spatiotemporal change of air-quality patterns in hubei province—a pre-to post-Covid-19 analysis using path analysis and regression. Atmosphere 12 (10), 1338. doi:10.3390/atmos12101338

CrossRef Full Text | Google Scholar

Bhatti, U. A., Nizamani, M. M., and Huang, M. (2022). Climate change threatens Pakistan’s snow leopards. Science 377 (6606), 585–586. doi:10.1126/science.add9065

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhatti, U. A., Yan, Y., Zhou, M., Ali, S., Hussain, A., Qingsong, H., et al. (2021). ‘Time series analysis and forecasting of air pollution particulate matter (PM_2.5): An SARIMA and factor analysis approach. IEEE Access 9, 41019–41031. doi:10.1109/access.2021.3060744

CrossRef Full Text | Google Scholar

Bhatti, U. A., Yu, Z., Chanussot, J., Zeeshan, Z., Yuan, L., Luo, W., et al. (2021). Local similarity-based spatial–spectral fusion hyperspectral image classification with deep CNN and Gabor filtering. IEEE Trans. Geosci. Remote Sens. 60, 1–15. doi:10.1109/TGRS.2021.3090410

CrossRef Full Text | Google Scholar

Chen, Q., Ding, W., Huang, X., and Wang, H. (2022). Generalized interval type II fuzzy rough model based feature discretization for mixed pixels. IEEE Trans. Fuzzy Syst., 1–15. (Early Access). doi:10.1109/TFUZZ.2022.3190625

CrossRef Full Text | Google Scholar

Chen, Q., and Huang, M. (2021). Rough fuzzy model based feature discretization in intelligent data pre-process. J. Cloud Comp. 10 (1), 5. doi:10.1186/s13677-020-00216-4

CrossRef Full Text | Google Scholar

Chen, Q., Huang, M., and Wang, H. (2021). A feature discretization method for classification of high-resolution remote sensing images in coastal areas. IEEE Trans. Geosci. Remote Sens. 59 (10), 8584–8598. doi:10.1109/tgrs.2020.3016526

CrossRef Full Text | Google Scholar

Chen, Q., Huang, M., Wang, H., and Xu, G. (2022). A feature discretization method based on fuzzy rough sets for high-resolution remote sensing big data under linear spectral model. IEEE Trans. Fuzzy Syst. 30 (5), 1328–1342. doi:10.1109/tfuzz.2021.3058020

CrossRef Full Text | Google Scholar

Chen, Q., Huang, M., Wang, H., Zhang, Y., Feng, W., Wang, X., et al. (2018). “A feature pre-processing framework of remote sensing image for marine targets recognition,” in Proceedings of MTS/IEEE OCEANS Conference, Kobe, Japan, May 28-31, 1–5.

CrossRef Full Text | Google Scholar

Chen, Q., Huang, M., Xu, Q., Wang, H., and Wang, J. (2020). Reinforcement learning-based genetic algo-rithm in optimizing multidimensional data discretization scheme. Math. Probl. Eng. 2020, 1–13. Art. no. 1698323. doi:10.1155/2020/1698323

CrossRef Full Text | Google Scholar

de Sá, C. R., Soares, C., and Knobbe, A. (2016). Entropy-based discretization methods for ranking data. Inf. Sci. (N. Y). 329, 921–936. doi:10.1016/j.ins.2015.04.022

CrossRef Full Text | Google Scholar

Galvan, L. P. C., Bhatti, U. A., Campo, C. C., and Stanojevic, S. (2022). The nexus between CO2 emission, economic growth, trade openness: Evidences from middle-income trap countries. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.938776

CrossRef Full Text | Google Scholar

Guo, X. (2016). “Application of meteorological big data,” in 16th Int. Symp. Comm. Inf. Techn. (ISCIT), Qingdao, China, Sept, 273–279.

CrossRef Full Text | Google Scholar

Hasnain, A., Hashmi, M. Z., Bhatti, U. A., Nadeem, B., Wei, G., Zha, Y., et al. (2021). Assessment of air pollution before, during and after the COVID-19 pandemic lockdown in nanjing, China. Atmosphere 12 (6), 743. doi:10.3390/atmos12060743

CrossRef Full Text | Google Scholar

Huang, M., Chen, Q., and Wang, H. (2020). A multivariable optical remote sensing image feature discreti-zation method applied to marine vessel targets recognition. Multimed. Tools Appl. 79 (7), 4597–4618. doi:10.1007/s11042-019-07920-7

CrossRef Full Text | Google Scholar

Kamińska, J., Lucena-Sánchez, E., Sciavicco, G., and Stan, I. E. (2020). “Rule extraction via dynamic dis-cretization with an application to air quality modelling,” in 4th International Joint Conference Rules and Reasoning (RuleML+RR2020), Oslo, Norway, June 29-Jul 1, 1–16.

Google Scholar

Liu, C., Jin, W., Yu, Y., Qiu, T., Bai, X., and Zou, S. (2017). A discretization algorithm for meteorological data and its parallelization based on Hadoop. J. Phys. Conf. Ser. 910, 012011. doi:10.1088/1742-6596/910/1/012011

CrossRef Full Text | Google Scholar

Moon, S.-H., Kim, Y.-H., Lee, Y. H., and Moon, B.-R. (2019). Application of machine learning to an early warning system for very short-term heavy rainfall. J. Hydrol. X. 568, 1042–1054. doi:10.1016/j.jhydrol.2018.11.060

CrossRef Full Text | Google Scholar

Rahman, Md. G., and Islam, Md. Z. (2016). Discretization of continuous attributes through low frequency numerical values and attribute interdependency. Expert Syst. Appl. 45 (1), 410–423. doi:10.1016/j.eswa.2015.10.005

CrossRef Full Text | Google Scholar

Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N., et al. (2019). Deep learning and process understanding for data-driven Earth system science. Nature 566 (7743), 195–204. doi:10.1038/s41586-019-0912-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Rosati, S., Balestra, G., Giannini, V., Mazzetti, S., Russo, F., and Regge, D. (2015). “Chimerge discretization method: impact on a computer aided diagnosis system for prostate cancer in MRI,” in International Symposium on Medical Measurements and Applications (MeMeA), Turin, Italy, May 6-8, 297–302.

CrossRef Full Text | Google Scholar

Wang, J., Xu, J., Du, Z., Gan, Y., Liu, S., and Hu, J. (2020). “Lightning probability warning of transmission line based on bayesian network,” in 4th Conf. Energ. Intern. Energ. Syst. Integr. (E12), Wuhan, China, Nov, 298–303.

CrossRef Full Text | Google Scholar

Xu, X., Mo, R., Dai, F., Lin, W., Wan, S., and Dou, W. (2020). Dynamic resource provisioning with fault tol-erance for data-intensive meteorological workflows in cloud. IEEE Trans. Ind. Inf. 16 (9), 6172–6181. doi:10.1109/tii.2019.2959258

CrossRef Full Text | Google Scholar

Yan, D., Liu, D., and Sang, Y. (2014). A new approach for discretizing continuous attributes in learning systems. Neurocomputing 133, 507–511. doi:10.1016/j.neucom.2013.12.005

CrossRef Full Text | Google Scholar

Zhang, G., Wu, Z., and Yi, L. (2008). “A remote sensing feature discretization method accommodating uncertainty in classification systems,” in Proceeding 8th International Symposium Spat. Accuracy Assessment. Nat. Res. Environ. Sci., Shanghai, China, Jun, 195–202.

Google Scholar

Zhang, Y., and Shi, Y. (2021). “Application research of unmanned ship route dynamic planning based on meteorological big data,” in Proceeding of 2021 IEEE International Conference Power Electronics Computer Applications (ICPECA), Shenyang, China, Jan 22-24, 1005–1008.

CrossRef Full Text | Google Scholar